energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt
|
|
|
- Noora Hyttinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 14 2 Ensimmäinen pääsääntö 2-1 Lämpömäärä ja työ Termodynaaminen systeemi on jokin maailmankaikkeuden osa, jota rajoittaa todellinen tai kuviteltu rajapinta (engl. boundary). Systeemi voi olla esimerkiksi jokin mekaaninen laite, biologinen organismi tai tietty määrä ainetta. Termofysiikassa on erityisen tärkeää määritellä täsmällisesti, mitä tarkasteltavaan systeemiin kuuluu ja mitä siihen ei kuulu. Esimerkiksi säiliössä olevan kaasun tapauksessa on sovittava, muodostuuko tarkasteltava systeemi vain kaasusta vai kuuluuko siihen myös kaasua ympäröivä säiliö. Jos systeemin ja sen ympäristön välillä on aineen vaihtoa, systeemi on avoin (engl. open). Jos aineen vaihtoa ei ole, systeemi on suljettu (engl. closed). Jos systeemin rajapinnan läpi ei siirry lämpöenergiaa (Q = 0), systeemi on lämpöeristetty (engl. thermally isolated). Rajapinta on tällöin adiabaattinen (engl. adiabatic). Päinvastaisessa tapauksessa, jossa rajapinta johtaa hyvin lämpöä, se on diaterminen (engl. diathermal). Jos systeemin ja sen ympäristön välillä ei ole lainkaan energian vaihtoa (ei lämpöenergian eikä minkään muunkaan energian), systeemi on eristetty (engl. isolated). Tällöin sekä systeemiin siirtynyt lämpömäärä Q että systeemiin tehty työ (merkitään W ) ovat nollia: Q = W = 0. Termodynaaminen prosessi on tapahtumasarja, jossa termodynaamisen systeemin tila muuttuu esimerkiksi kaasun tilavuus muuttuu. Prosessi on erityisen yksinkertainen, jos se on reversiibeli (palautuva, engl. reversible). Tällä tarkoitetaan prosessia, joka voidaan peruuttaa täydellisesti, ts. sekä systeemin että sen ympäristön tilat voidaan palauttaa täsmälleen alkuperäisiksi. Tämä edellyttää, että prosessin suunta voidaan kääntää ilman energiahäviöitä päinvastaiseksi olosuhteiden infinitesimaalisella muutoksella. Esimerkiksi, jos kahden kappaleen lämpötilat poikkeavat hyvin vähän toisistaan, niiden välisen lämpövirran suunta voidaan kääntää päinvastaiseksi lämpötilan vähäisellä muutoksella. Jotta prosessi voisi olla reversiibeli, systeemin täytyy olla koko ajan tasapainotilassa. Tällaista peräkkäisinä tasapainotiloina etenevää prosessia sanotaan kvasistaattiseksi (engl. quasistatic). Koska prosessin suunnan muuttamisen on lisäksi tapahduttava ilman esimerkiksi kitkasta (engl. friction) johtuvia energiahäviöitä (engl. dissipation), siinä ei saa esiintyä hysteresisilmiöitä (joissa systeemin tila riippuu osaksi aikaisemmista olosuhteista). Näitä ehtoja ei mikään todellinen prosessi voi täysin täyttää, joten reversiibeli prosessi on idealisaatio. Todelliset prosessit ovat aina jossakin määrin ei-reversiibelejä eli irreversiibelejä (palautumattomia). Jos todellinen prosessi kuitenkin etenee systeemin relaksaatioaikoihin verrattuna hitaasti ja siinä esiintyy vain vähän kitkaa, sitä voidaan käytännössä pitää reversiibelinä. Tämä on tärkeää, sillä ko. approksimaatio yksinkertaistaa prosessin teoreettista analyysiä ratkaisevasti. Reversiibeliä prosessia voidaan kuvata muutamien tilamuuttujien avulla, esimerkiksi antamalla kaasun paine P sen tilavuuden V yksikäsitteisenä funktiona P = P (V ). Se voidaan
2 esittää myös graafisesti esimerkiksi P V -diagrammina, ts. kaksiulotteisen (P, V )-koordinaatiston käyränä. Lisäksi tilavuuden muutoksen kaasuun tekemä työ voidaan tällöin laskea funktion P (V ) integraalina (kts. yhtälö (2.2)). Jos sen sijaan kaasu ei ole prosessin aikana lähellä tasapainotilaa, sen paine, lämpötila ja tiheys voivat saada eri pisteissä eri arvoja. Tässä tapauksessa prosessia ei voida kuvata yksikäsitteisellä funktiolla P = P (V ) tai sen kuvaajalla (P, V )-koordinaatistossa, eikä tällaista funktiota voida käyttää kaasuun tehdyn työn laskemiseen. Jos taas systeemissä esiintyy kitkaa, se kohdistaa ympäristöönsä paineen P 0, joka ei ole sama kuin kaasun paine P. Tällöinkään systeemiin tehdyn työn laskemiseen ei voida käyttää funktiota P (V ). Suljettuun systeemiin voidaan siirtää energiaa kahdella eri tavalla: tuomalla siihen lämpöä tai tekemällä siihen työtä. Systeemiin tehtyä työtä merkitään symbolilla W. Jos W on negatiivinen, systeemi tekee itse työtä ympäristöönsä. On syytä huomata, että kirjallisuudessa (esim. H. D. Young and R. A. Freedman: University Physics ja F. W. Sears and G. L. Salinger: Thermodynamics, Kinetic Theory, and Statistical Thermodynamics) W määritellään usein vastakkaismerkkisenä. Tällöin W on systeemin tekemä työ. Tätä merkkisopimusta ei käytetä tässä opintojaksossa, vaan systeemin tekemälle työlle käytetään merkintää W (kuten kirjassa F. Mandl: Statistical Physics). Lämpömäärä Q ja työ W spesifioivat eri mekanismeilla systeemiin siirtyneen energian määrän. Kumpikaan ei ole tilamuuttuja. Tämä johtuu siitä, että ei ole olemassa systeemin tilasta riippuvia funktioita (systeemin lämpömäärää ja työtä ), joiden muutoksia Q ja W olisivat. Tästä syystä infinitesimaalista työtä merkitään symbolilla d W (jos käytettäisiin symbolia dw, se voitaisiin virheellisesti tulkita jonkin funktion W differentiaaliksi). Työ ja lämpömäärä ovat eri tavoin siirtyviä energioita: Työ W on energia, joka siirtyy systeemiin makroskooppisesti havaittavien koordinaattien välityksellä. Lämpömäärä Q on energia, joka siirtyy systeemiin lämpötilaeron takia mikroskooppisten (molekyylitason) koordinaattien välityksellä. Tarkastellaan esimerkkinä lämpöeristetyssä sylinterissä olevaa kaasua (kuva 1). Kaasuun voidaan tehdä työtä esimerkiksi puristamalla sitä. Tässä prosessissa makroskooppisena koordinaattina toimii männän paikka x. Puristettaessa kaasu lämpenee, koska 15 Kuva 1.
3 16 Kuva 2. liikkuvaan mäntään törmäävät molekyylit saavat lisää energiaa (kuva 2). Tällä tavoin männän työntämiseen tarvittava energia (työ, jota mitatataan koordinaatilla x) siirtyy systeemiin kaasumolekyylien liike-energiaksi. Vaihtoehtoisesti systeemiin voidaan siirtää energiaa lämmittämällä sitä. Tällöin kaasuun muodostuu lämpötilaeroja, joita voidaan kuvata lämpötilagradienteilla (engl. temperature gradient). Tällaisessa kaasussa tapahtuu energian siirtymistä lämmön johtumisen muodossa, koska lämpimämmästä ja viileämmästä alueesta tulevilla molekyyleillä on erilaiset keskimääräiset liike-energiat. Näin siirtyvää energiaa ei voida mitata millään makroskooppisesti havaittavilla koordinaateilla. Lopputulos on kuitenkin sama kuin kaasua puristettaessa: käytetty energia siirtyy kaasumolekyylien liike-energiaksi. 2-2 Tilavuuden muutoksessa tehty työ Tarkastellaan yleisesti kaasun (tai nesteen) tilavuuden reversiibeliä muutosta. Jos kaasun paine on P, se kohdistaa säiliössä olevaan mäntään voiman F = P A, missä A on männän poikkipinta-ala (kuva 3). Jos männän etäisyys säiliön pohjasta on x (kuten kuvassa 1), säiliön tilavuus on V = Ax. Tällöin infinitesimaalista männän paikan x muutosta dx vastaa infinitesimaalinen säiliön tilavuuden muutos dv = A dx. Kaasua puristettaessa x pienenee, jolloin dx ja dv ovat negatiivisia. Tällöin kaasuun tehdään positiivinen työ d W = F dx = P A dx = P dv. (2.1) Kuva 3.
4 Tämä tulos seuraa suoraan työn määritelmästä: systeemiin tehty työ on mäntään kohdistuvan voiman P A ja männän siirtymän itseisarvon dx tulo (kuva 3). Yhtälö (2.1) pätee myös säiliön tilavuuden kasvaessa: tällöin dx ja dv ovat positiivisia, joten d W on negatiivinen. Näin pitää ollakin, sillä kaasun laajentuessa se tekee itse työtä. Mikroskooppisessa tarkastelussa tilavuuden muutokseen liittyvä työ johtuu siitä, että liikkuvaan mäntään törmäävän molekyylin energia muuttuu: törmäyksessä molekyyli joko saa tai menettää energiaa riippuen siitä, liikkuuko seinämä molekyyliä kohti vai siitä poispäin (kuva 2). Säiliön äärellisessä reversiibelissä tilavuuden muutoksessa alkutilavuudesta lopputilavuuteen V 2 tehty työ, ns. P V -työ, on osuuksien (2.1) summa, ts. integraali 17 V2 W = P (V ) dv. (2.2) Tämän integraalin itseisarvoarvo W on sama kuin P V -tasossa olevien pisteiden P ( ) ja P (V 2 ) välisen käyrän P = P (V ) alla oleva pinta-ala. Jos on suurempi kuin V 2, integraali W on positiivinen. Tämä merkitsee sitä, että systeemiä puristettaessa siihen joudutaan tekemään W :n verran positiivista työtä. Päinvastaisessa tapauksessa integraali on negatiivinen tällöin systeemi tekee laajentuessaan W :n suuruisen positiivisen työn. Kuva 4 esittää kolmen eri prosessin P V -diagrammeja ja systeemin niissä tekemiä töitä (ko. työ on siis W, ei W ). Tarkastellaan esimerkkinä sylinterissä olevan kaasun isotermistä eli vakiolämpötilassa tapahtuvaa puristamista. Tarkasteltavaan systeemiin kuuluu nyt sekä säiliö (sylinteri ja mäntä) että sen sisällä oleva kaasu. Vakiolämpötilan säilyttämiseksi sylinteri on asetettava termiseen kontaktiin lämpötilassa T olevan lämpökylvyn kanssa (kuva 5). Lämpökylpy tai lämpösäiliö (engl. heat bath tai heat reservoir) on systeemi, jonka lämpökapasiteetti on hyvin paljon suurempi kuin tarkasteltavan systeemin (tässä tapauksessa säiliön ja kaasun) lämpökapasiteetti. Tämä merkitsee sitä, että lämpökylvyn lämpötila ei muutu, vaikka se on lämmönvaihdossa tarkasteltavan systeemin kanssa. Kun tarkasteltava systeemi on termisessä tasapainossa lämpökylvyn kanssa, myös sen lämpötila on vakio. Kuva 4.
5 18 Kuva 5. Kvasistaattisessa puristuksessa mäntään kohdistuvaa voimaa lisätään hyvin pienin askelin. Jokaisen lisäyksen jälkeen odotetaan, kunnes systeemi on saavuttanut mekaanisen ja termisen tasapainon. Näin ollen kaasun paine P voidaan kullakin hetkellä laskea tilanyhtälöstä V :n, T :n ja n:n avulla. Jos säiliössä on esimerkiksi ideaalikaasua, paineen lauseke on tilanyhtälön (1.11) mukaan P = nrt/v. Isotermisessä prosessissa kerroin nrt on vakio (kuva 6), joten tällöin reversiibelissä tilavuuden muutoksessa V 2 tehty työ on yhtälön (2.2) mukaan V2 V2 W = P (V ) dv = nrt dv V V = nrt 2 ln V = nrt ln. (2.3) V 2 Jos kaasua puristetaan nopeasti kohdistamalla mäntään ulkopuolelta paine P 0 > P, dv :n suuruisessa tilavuuden muutoksessa tehty työ on d W = P 0 dv > P dv, joten d W > P dv. (2.4) Tämä epäyhtälö pätee myös kaasun tilavuutta nopeasti laajennettaessa. Tällaisen laajenemisen aikana kaasu harvenee männän lähellä ja näin ollen sen mäntään kohdistama paine, P 0, on pienempi kuin paine tasapainotilassa, P. Tästä syystä kaasun tekemä työ d W = P 0 dv on pienempi kuin hitaassa laajentumisessa (huom. dv > 0 ja d W < 0): d W = P 0 dv < P dv, joten d W > P dv. Äärimmäinen esimerkki tämänkaltaisesta Kuva 6.
6 prosessista on kaasun vapaa laajeneminen tyhjiöön. Kun kaasu purkautuu suoraan tyhjiöön vaikuttamatta mäntään, se ei tee lainkaan työtä ( d W = 0), mutta P dv on silti positiivinen, kuten yhtälö (2.4) edellyttää. Tällaiset nopeat prosessit ovat irreversiibelejä. Epäyhtälö (2.4) on voimassa myös kvasistaattiselle prosessille, jos männän ja sylinterin välillä on kitkaa. Tällöin kaasua puristettaessa mäntään on kohdistettava ulkopuolelta paine P 0 = P + f/a, jonka on kitkavoiman f (> 0) voittamiseksi oltava suurempi kuin kaasun paine P (kuva 7). Systeemiin tehty työ on siis d W = P 0 dv = P dv f dv/a > P dv. Vastaavasti kaasun laajentuessa mäntä vaikuttaa systeemin ulkopuolelle paineella P 0 = P f/a, joka on pienempi kuin P. Systeemin tekemä työ on tällöin d W = P 0 dv = P dv f dv/a < P dv. Kuvassa 7 esitetyssä kiertoprosessissa ABCDA mäntään kohdistettu voima tekee (positiivisen) nettotyön, jonka suuruus on kuvion ABCDA pinta-ala. Tämä työ muuttuu kitkan aiheuttamaksi lämpöenergiaksi, ts. lämpötila kohoaa. Jos systeemi on lämpökylvyssä, lämpöenergia siirtyy siihen. Kitka aiheuttaa hysteresisilmiön: systeemin tila (tilavuus V ja paine P ) ei ole ulkoisen paineen P 0 yksikäsitteinen funktio, vaan se riippuu myös P 0 :n aikaisemmista arvoista. Näin ollen prosessi on irreversiibeli: jos ulkoisen paineen P 0 muutos käännetään päinvastaiseksi (kuten esimerkiksi pisteessä B, jossa painetta aletaan pienentää), prosessin suunta ei käänny (siten, että systeemi palaisi alkuperäistä kuvaajaa BA pitkin alkutilaansa A), vaan systeemi alkaa seurata uutta kuvaajaa (BC). Yhteenvetona voidaan todeta, että kun säiliön (esimerkiksi sylinterin ja männän) ja siinä olevan kaasun tai nesteen yhdessä muodostaman systeemin tilavuutta muutetaan dv :n verran, tähän systeemiin tehdään ulkoapäin työ 19 d W P dv, (2.5) missä P on kaasun tai nesteen paine tasapainotilassa. Yhtäsuuruusmerkki on voimassa, jos tilavuuden muutos on reversiibeli, ts. systeemi on mekaanisessa tasapainossa ympäristönsä kanssa (ympäristön paine P 0 on koko ajan sama kuin P ). Suurempi kuin -merkki (>) pätee tilavuuden irreversiibeleille muutoksille. Kuva 7.
7 2-3 Ensimmäinen pääsääntö 20 Makroskooppisen systeemin sisäinen energia E on sen sisäiseen tilaan liittyvää energiaa. Yleensä se liittyy systeemin mikroskooppiseen rakenteeseen, jolloin se muodostuu systeemissä olevien molekyylien satunnaisliikkeen kineettisestä energiasta ja niiden välisten vuorovaikutusten potentiaalienergiasta. Tällöin sitä voidaan sanoa myös termiseksi energiaksi (engl. thermal energy). Sisäinen energia riippuu ainoastaan systeemin tilasta ja on siis tilamuuttuja. Esimerkiksi tasapainotilassa olevan tietyn kaasu- tai nestemäärän (n = vakio) E on muuttujien P, V ja T yksikäsitteinen funktio. Koska mikä tahansa näistä kolmesta muuttujasta voidaan esittää tilanyhtälön avulla kahden muun muuttujan funktiona, kaasun tai nesteen sisäinen energia voidaan esittää muodossa E = E(P, V ) tai E = E(P, T ) tai E = E(V, T ). Yleisesti, jos systeemi on tilassa i, sen sisäinen energia on tämän tilan yksikäsitteinen funktio E(i) E i. Jos systeemin tila muuttuu jossakin prosessissa tilasta 1 tilaksi 2, systeemin sisäinen energia muuttuu alkuarvosta E 1 loppuarvoon E 2. Prosessin aiheuttamaa sisäisen energian muutosta merkitään symbolilla E: E E 2 E 1. (2.6) Jos systeemi ottaa ulkopuolelta vastaan energian U, sen sisäisen energian täytyy kasvaa U:n verran: E = U. Jos näin ei tapahtuisi, energia ei säilyisi. Kuten edellä on todettu, suljettu systeemi voi ottaa ympäristöstään vastaan energiaa kahdella eri tavalla: systeemiin voi siirtyä lämpömäärä Q tai siihen voidaan tehdä työ W. Yleisessä tapauksessa energiaa voi siirtyä molemmilla mekanismeilla. Tällöin systeemin vastaanottama kokonaisenergia on U = Q + W ja näin ollen systeemin sisäisen energian muutos on E = Q + W. (2.7) Tämä on termodynamiikan ensimmäinen pääsääntö suljetuille systeemeille. Se on itse asiassa energian säilymisen laki systeemeille, joihin voi siirtyä energiaa tehdyn työn lisäksi myös näkymättömässä muodossa systeemin mikroskooppisten koordinaattien välityksellä: systeemin sisäisen energian muutos = systeemiin siirtynyt lämpömäärä + siihen tehty työ. Yhtälö (2.7) pätee kaikkien suljettujen systeemien kaikille prosesseille riippumatta siitä, minkälaista työtä (mekaanista, sähköistä,...) niihin tehdään tai siitä, ovatko prosessit reversiibelejä vai irreversiibelejä. Tätä yhtälöä voidaan käyttää myös sisäisen energian E määritelmänä valitsemalla jokin referenssitila j, joka sovitaan E:n nollakohdaksi (ts. sovitaan, että E j = 0). Siirryttäessä tilasta 1 tilaan 2 E ja yhtälön (2.7) mukaan myös summa Q + W ovat yksikäsitteisiä. Sen sijaan Q ja W erikseen riippuvat siitä, miten siirtyminen tapahtuu, ts. millaista tietä prosessi etenee. Tästä seuraa, että lämpömäärä ja työ eivät ole säilyviä suureita. Vain kokonaisenergia säilyy yhtälön (2.7) osoittamalla tavalla. Jos systeemiin tuodaan infinitesimaalinen lämpömäärä d Q ja siihen tehdään infinitesimaalinen työ d W, sen sisäinen energia saa infinitesimaalisen lisäyksen de = d Q + d W. (2.8) Vaikka d Q ja d W eivät ole minkään funktion differentiaaleja, niiden summa de on kuitenkin tilamuuttujan E differentiaali.
8 Jos systeemin tilavuutta muutetaan reversiibelisti dv :n verran, systeemiin tehdään yhtälön (2.1) mukaan työ d W = P dv. Jos systeemiin ei tehdä mitään muuta työtä, ensimmäinen pääsääntö (2.8) saa tässä erikoistapauksessa muodon d Q = de + P dv. (2.9) Jos tilavuuden muutos on irreversiibeli, systeemiin tehty työ noudattaa epäyhtälöä (2.4): d W > P dv. Tällöin ensimmäinen pääsääntö voidaan esittää epäyhtälönä d Q < de + P dv. (2.10) Jos systeemiin tuodaan lämpömäärä d Q pitäen sen tilavuus vakiona (dv = 0), tästä johtuva systeemin sisäisen energian muutos on yhtälön (2.9) mukaan de = d Q. Jos systeemin lämpötila tällöin muuttuu dt :n verran, saadaan systeemin lämpökapasiteetin (1.17) lausekkeeksi ( d ) ( ) ( ) Q de E C V = = =. (2.11) dt V dt V T V Tässä yhtälössä osamäärä (de/dt ) V on tulkittu funktion E(V, T ) (joka on tilamuuttuja) derivaataksi T :n suhteen V :n pysyessä vakiona, siis E(V, T ):n osittaisderivaataksi ( E/ T ) V. (Huomaa, että tällaisen osittaisderivaatan laskemiseksi E on esitettävä nimenomaan riippumattomien muuttujien V ja T funktiona. Muuttuja P voidaan eliminoida tilanyhtälön P = P (V, T ) avulla.) Alaindeksillä V osoitetaan, että kyseessä on systeemin lämpökapasiteetti vakiotilavuudessa. Jos systeemiin tuodaan lämpömäärä d Q pitäen sen paine vakiona (P = vakio), saadaan yhtälöä (2.9) käyttämällä vastaavalla tavalla systeemin lämpökapasiteetiksi vakiopaineessa ( d ) ( ) ( ) ( ) ( ) Q de dv E V C P = = + P = + P. (2.12) dt dt dt T T P P Tässä yhtälössä osamäärät (de/dt ) P ja (dv/dt ) P on voitu tulkita tilamuuttujien E(P, T ) ja V (P, T ) osittaisderivaatoiksi T :n suhteen P :n pysyessä vakiona. (Näiden osittaisderivaattojen laskemiseksi E:n ja V :n riippumattomiksi muuttujiksi on valittava P ja T.) Saatu C P :n lauseke (2.12) ei ole sama kuin C V :n lauseke (2.11). Lämpökapasiteetin arvo riippuu siis siitä, minkälainen prosessi lämmön siirtymiseen liittyy. Koska ideaalikaasussa molekyylien välillä ei ole pitkän kantaman vuorovaikutuksia, kaasun sisäinen energia E ei voi riippua molekyylien välimatkoista. Tästä seuraa, että tietyn kaasumäärän E ei riipu kaasun paineesta eikä tilavuudesta. Näin ollen E riippuu ainoastaan lämpötilasta: E = E(T ). Tämä merkitsee sitä, että tässä erikoistapauksessa osittaisderivaatat ( E/ T ) V ja ( E/ T ) P voidaan korvata kokonaisderivaatalla de/dt : ( E T ) V = ( E T P ) P = de dt. Näin ollen ideaalikaasun lämpökapasiteettien C P ja C V erotukselle saadaan yhtälöitä (2.11) ja (2.12) käyttäen lauseke ( ) V C P C V = P. (2.13) T P Kun vielä käytetään ideaalikaasun tilanyhtälöä V = nrt/p, saadaan tulos ( V/ T ) P = nr/p. Näin ollen ideaalikaasulle on voimassa yksinkertainen yhtälö P P 21 C P C V = nr. (2.14)
9 Jos kaasuun tuodaan vakiopaineessa lämpöenergia d Q, osa siitä kuluu yhtälön (2.9) mukaisesti kaasun laajenemisen vaatimaan työhön (P dv ) ja vain osa kasvattaa kaasun sisäistä energiaa E. Vain tämä jälkimmäinen osa lämmittää kaasua. Tästä syystä kaasun lämpötilan muutos dt on pienempi kuin vastaavassa vakiotilavuudessa tapahtuvassa lämmityksessä. Tämä on fysikaalinen syy siihen, että kaasulla C P on suurempi kuin C V Tilojen väliset tiet Termodynaamisen systeemin siirtyminen alkutilasta 1 lopputilaan 2 tapahtuu tiettyjen välitilojen muodostamaa tietä (engl. path) pitkin. Jos kaikki välitilat ovat hyvin lähellä systeemin tasapainotiloja, tie voidaan esittää P V -tason käyränä P = P (V ). Siitä huolimatta tie ei ole yksikäsitteinen pisteet 1 ja 2 voidaan yhdistää äärettömän monella erilaisella käyrällä. Monissa tapauksissa systeemin jokin ominaisuus pysyy ainakin osassa välitiloista vakiona: Isotermisessä (engl. isothermal) prosessissa systeemin lämpötila T pysyy muuttumattomana. Jos systeemin tilavuus V ei muutu, kyseessä on isokoorinen (engl. isochoric) prosessi. Tällöin tilavuuden muutoksen systeemiin tekemä työ on nolla. Jos systeemiin ei prosessin aikana tehdä mitään muutakaan työtä (esimerkiksi sekoittamalla nestettä siipirattaalla), W = 0. Tässä tapauksessa systeemiin siirtynyt lämpömäärä Q kuluu termodynamiikan ensimmäisen pääsäännön (2.7) mukaan kokonaan systeemin sisäisen energian kasvattamiseen: E = Q. Jos systeemin paine P pysyy vakiona, prosessi on isobaarinen (engl. isobaric). Tällöin tilavuuden muutoksen kaasuun tekemä työ on yhtälön (2.2) mukaan V2 V2 W = P (V ) dv = P dv = P (V 2 ). (2.15) Adiabaattisen prosessin aikana systeemi on lämpöeristetty, joten sen rajapinnan läpi ei kulje lämpövirtaa. Tällöin systeemiin siirtynyt lämpömäärä Q on nolla ja ensimmäisen pääsäännön (2.7) mukaan systeemiin tehty työ W menee kokonaan systeemin sisäisen energian kasvattamiseen: E = W. Jos systeemiä esimerkiksi puristetaan adiabaattisesti, W on positiivinen ja E kasvaa ( E = W > 0). Systeemin sisäisen energian kasvuun liittyy yleensä (mutta ei aina) sen lämpötilan kohoaminen. Monet nopeasti tapahtuvat todelliset prosessit, kuten esimerkiksi polttomoottorin puristustahti, ovat lähes täysin adiabaattisia. Tämä johtuu siitä, että systeemin ja ympäristön välillä ei prosessin lyhyen kestoajan kuluessa ehdi tapahtua merkittävää lämmönvaihtoa. Kuvassa 8 on esitetty suljetussa säiliössä olevan ideaalikaasun isotermisen, isokoorisen, isobaarisen ja adiabaattisen prosessin P V -diagrammit. Näitä prosesseja kuvaavia käyriä sanotaan isotermeiksi (engl. isotherm), isokooreiksi (engl. isochor), isobaareiksi (engl. isobar) ja adiabaateiksi (engl. adiabat). Kuvassa 9 on esitetty kolme erilaista tapaa siirtyä pisteestä 1 (P 1, ) pisteeseen 2 (P 2, V 2 ): Ensin isobaarisesti (so., vakiopaineessa) tilaan 3 (P 1, V 2 ) ja siitä isokoorisesti (so., vakiotilavuudessa) lopputilaan 2 (P 2, V 2 ). Systeemin tässä prosessissa tekemä työ on janan
10 23 Kuva alla olevan suorakulmion pinta-ala P 1 (V 2 ) (kuva 9(b)). (Huomaa, että systeemin tekemälle työlle on kuvissa 9(b), 9(c) ja 9(d) käytetty symbolia W, ei W.) Ensin isokoorisesti tilaan 4 (P 2, ) ja siitä isobaarisesti lopputilaan 2, jolloin systeemin tekemä työ on janan 4 2 alla olevan suorakulmion pinta-ala P 2 (V 2 ) (kuva 9(c)). Kuvan 9(d) mukaisesti suoraan käyrää 1 2 pitkin lopputilaan, jolloin systeemin tekemä työ on tämän käyrän alla olevan kuvion pinta-ala. Kuvista nähdään, että systeemin tekemän työn suuruus on kaikissa kolmessa tapauksessa erilainen. Työ ei siis riipu pelkästään prosessin alku- ja lopputiloista, vaan myös välitiloista, ts. tiestä. Kuva 9.
11 Työ ei yleensä ole nolla edes kiertoprosessissa (engl. cyclic process), jossa systeemi päätyy välitilojen kautta takaisin alkutilaansa. Kun tilasta 1 siirrytään tilaan 2 kuvassa 10 esitettyä käyrää A pitkin, tehdään työ W A = V2 (tie A) P dv. 24 Kiertoprosessissa 1 A 2 B 1 tehty työ on käyrien väliin jäävä pinta-ala ( 0): P dv = W A W B 0. Kvasistaattista kiertoprosessia kuvaa P V -tasossa suljettu käyrä, jonka sisään jäävän alueen pinta-ala on sama kuin prosessin aikana tehdyn työn itseisarvo. Esimerkiksi kuvan 9 kiertoprosessissa systeemi tekee positiivisen nettotyön P 1 (V 2 ) P 2 (V 2 ) = (P 1 P 2 )(V 2 ), joka on prosessia kuvaavan P V -tason suorakulmion pinta-ala. Kiertoprosessin aikana systeemiin tehty kokonaistyö W on positiivinen, jos prosessi etenee sitä kuvaavaa P V -tason suljettua käyrää pitkin vastapäivään, kuten kuvissa 7 ja 10(b). Jos kiertosuunta on myötäpäivään, W on negatiivinen. Myös systeemiin siirtynyt lämpömäärä riippuu prosessin välitiloista. Esimerkkinä voidaan tarkastella yksinkertaista systeemiä, joka muodostuu tietystä määrästä ideaalikaasua. Alkutilassa kaasun lämpötila on 300 K ja sen tilavuus on 2,0 l. Lopputilassa kaasun lämpötila on edelleen 300 K, mutta sen tilavuus on 5,0 l. Kuvassa 11 on esitetty kaksi erilaista tapaa siirtyä alkutilasta lopputilaan: Prosessissa (a) kaasun annetaan laajentua isotermisesti säiliössä, jonka tilavuutta kasvatetaan hitaasti männän avulla. Tällöin kaasu tekee positiivisen työn W, joka voidaan laskea yhtälöllä (2.3). Jotta kaasu ei jäähtyisi, sen menettämä energia on korvattava Kuva 10.
12 25 Kuva 11. siirtämällä siihen ulkopuolelta työtä vastaava lämpömäärä Q = W (ideaalikaasun lämpötila riippuu vain sen sisäisestä energiasta). Prosessissa (b) kaasun annetaan laajentua säiliössä vapaasti tyhjiöön siten, että sen lopputilavuudeksi tulee 5,0 l. Kaasu ei tällöin tee lainkaan työtä, koska se ei ole kosketuksissa minkään liikkuvan seinämän kanssa: W = 0. Tästä syystä kaasu ei menetä laajenemisen aikana sisäistä energiaansa. Näin ollen sen lämpötila ei laske, eikä siihen siirry ulkopuolelta lämpöä: Q = 0. Prosessit (a) ja (b) ovat hyvin erilaisia, vaikka ne johtavat samasta alkutilasta samaan lopputilaan. Prosessia (a) kuvaa P V -tason isotermi P = nrt/v, jonka alla olevan kuvion pinta-ala on sama kuin systeemiin ulkopuolelta siirtynyt lämpömäärä Q tai systeemin tekemä työ W = Q > 0. Sen sijaan prosessi (b) on irreversiibeli, koska se ei etene peräkkäisinä tasapainotiloina. Tästä syystä sitä ei voida lainkaan esittää P V -tason käyrän avulla. Tässä prosessissa sekä systeemiin tehty työ että siihen siirtynyt lämpömäärä ovat nollia. Vaikka systeemiin tehty työ (W ) ja siihen siirtynyt lämpömäärä (Q) riippuvat alku- ja lopputilan välisestä tiestä, niiden summa W + Q on tiestä riippumaton. Tämä summa on termodynamiikan ensimmäisen pääsäännön (2.7) mukaan systeemin sisäisen energian muutos: W + Q = E. Sisäisen energian muutos ei voi riippua tiestä, koska sisäinen energia E on tilamuuttuja systeemin ominaisuus, joka riippuu vain sen tilasta. Kiertoprosessissa systeemi palaa alkutilaansa, joten myös sen sisäinen energia palaa alkuperäiseen arvoonsa: E 1 = E 2. Tästä seuraa, että sisäisen energian muutos E E 2 E 1 on tällaisessa prosessissa nolla: de = 0. (2.16) Tällöin ensimmäisen pääsäännön (2.7) mukaan Q = W. Tämä merkitsee sitä, että kiertoprosessissa systeemin tekemään työhön W kuluva energia on tuotava systeemiin kokonaisuudessaan ulkopuolelta lämpöenergiana. Eristetyn systeemin kaikissa prosesseissa E = 0, mutta tässä tapauksessa sekä W että Q ovat erikseen nollia: W = Q = E = 0.
13 2-5 Ideaalikaasun adiabaattinen tilavuuden muutos 26 Ideaalikaasun reversiibeliä isotermistä tilavuuden muutosta (T = vakio) kuvaava P V -tason käyrä, isotermi, saadaan suoraan kaasun tilanyhtälöstä P = nrt/v. Jos reversiibeli tilavuuden muutos tapahtuu adiabaattisesti (Q = 0), kaasun lämpötilasta tulee tilavuuden funktio: T = T (V ). Esimerkiksi reversiibelissä puristuksessa kaasuun tehdään positiivinen työ W, joka menee kokonaan sen sisäisen energian kasvattamiseen: E = W + Q = W + 0 = W. Tällöin kaasun lämpötila kohoaa. Jos lämpötilan riippuvuus tilavuudesta tunnetaan, adiabaattista prosessia kuvaava P V -tason käyrä voidaan esittää ideaalikaasun tilanyhtälöstä saatavassa muodossa P = nrt (V )/V. Kuinka paljon ideaalikaasun lämpötila muuttuu, jos sen tilavuus muuttuu reversiibelisti ja adiabaattisesti dv :n verran? Tällaisessa prosessissa sen sisäisen energian muutos on ensimmäisen pääsäännön (2.8) ja yhtälön (2.1) mukaan (d Q = 0) de = d Q + d W = d W = P dv. (2.17) Tilavuuden muutoksen jälkeen kaasun lämpötila poikkeaa dt :n verran alkuperäisestä lämpötilasta. Täsmälleen samaan lopputilaan olisi päästy myös toista tietä, muuttamalla kaasun tilavuutta aluksi isotermisesti dv :n verran ja tuomalla siihen sen jälkeen vakiotilavuudessa lämpömäärä d Q = de = P dv. Tällä tavoin päästään oikeaan loppuenergiaan (ja oikeaan loppulämpötilaan), koska ideaalikaasun sisäinen energia riippuu vain lämpötilasta (energia ei siis muutu isotermisen tilavuuden muutoksen aikana). Systeemiin vakiotilavuudessa tuodun lämpömäärän d Q = de = P dv ja sen aiheuttaman lämpötilan muutoksen dt suhde on määrittely-yhtälön (2.11) mukaan systeemin lämpökapasiteetti vakiotilavuudessa C V = ( d Q dt ) V = ( ) de dt V = P ( ) dv dt V. (2.18) Näin ollen ideaalikaasun lämpötilan muutos reversiibelissä ja adiabaattisessa tilavuuden muutoksessa on dt = P dv = nrt dv, (2.19) C V C V V missä on käytetty hyväksi ideaalikaasun tilanyhtälöä P = nrt/v. Yhtälöä (2.14) käyttäen lausekkeessa (2.19) esiintyvä kerroin nr/c V voidaan kirjoittaa muotoon nr C V missä on käytetty lyhennysmerkintää = C P C V C V = γ 1, (2.20) γ C P C V. (2.21) Tämän avulla yhtälö (2.19) voidaan kirjoittaa yksinkertaiseen muotoon dt T + (γ 1)dV V = 0. (2.22) Kun tämä yhtälö integroidaan rajoitetulla lämpötila-alueella, jossa γ voidaan olettaa vakioksi, saadaan lämpötilan ja tilavuuden väliseksi relaatioksi ln T + (γ 1) ln V = ln ( T V γ 1) = vakio, (2.23)
14 josta seuraa tulos 27 T V γ 1 = vakio. (2.24) Jos kaasun lämpötila ja tilavuus ovat alkutilassa (T 1, ) ja lopputilassa (T 2, V 2 ), näiden välillä on yhtälön (2.24) mukaan relaatio T 1 V γ 1 1 = T 2 V γ 1 2. (2.25) Yhtälöstä (2.24) saadaan kaasun paineen ja tilavuuden välinen relaatio eliminoimalla siitä lämpötila ideaalikaasun tilanyhtälöä T = P V/(nR) käyttäen: T V γ 1 = P V nr V γ 1 = P V γ nr Koska n ja R ovat prosessissa vakioita, saadaan yksinkertainen tulos Tämä voidaan esittää muodossa = vakio. (2.26) P V γ = vakio. (2.27) P 1 V γ 1 = P 2V γ 2. (2.28) kun kaasun paine ja tilavuus ovat alkutilassa (P 1, ) ja lopputilassa (P 2, V 2 ). Ideaalikaasun reversiibeliä ja adiabaattista tilavuuden muutosta kuvaava P V -tason käyrä, adiabaatti, on siis yhtälön (2.27) mukaan muotoa P (V ) = vakio V γ. (2.29) Kaasuilla C P on aina suurempi kuin C V, joten γ = C P /C V > 1. Tästä seuraa, että adiabaatti on jyrkemmin muuttuva käyrä kuin isotermi, joka on muotoa Tätä käyttäytymistä havainnollistaa kuva 12. P (V ) = vakio V. (2.30) Kuva 12.
15 Ideaalikaasuun adiabaattisessa ja reversiibelissä tilavuuden muutoksessa tehty työ on yhtälöiden (2.2) ja (2.29) mukaan V2 V2 W = P (V ) dv = vakio ( dv V γ = vakio γ 1 1 V γ ) 1 V γ 1. (2.31) 1 Tässä yhtälössä esiintyvä vakio voidaan yhtälön (2.27) mukaan esittää vaihtoehtoisesti joko muodossa P 1 V γ 1 tai P 2V γ 2, joten työn lausekkeeksi tulee ( ) W = 1 P 2 V γ 2 γ 1 V γ 1 P 1V γ 1 2 V γ 1 = 1 γ 1 (P 2V 2 P 1 ). (2.32) 1 Käyttämällä hyväksi ideaalikaasun tilanyhtälöä (1.11) ja kertoimen γ 1 lauseketta (2.20) saadaan hyvin yksinkertainen lopputulos W = nr γ 1 (T 2 T 1 ) = C V (T 2 T 1 ). (2.33) Kaasuun tehdyn työn lauseke (2.33) olisi voitu kirjoittaa myös suoraan, laskematta integraalia (2.31). Tämä perustuu siihen, että adiabaattisessa prosessissa tehty työ on sama kuin kaasun sisäisen energian muutos: de = d Q + d W = 0 + d W = d W. Toisaalta vakiotilavuudessa tapahtuvassa prosessissa de voidaan esittää lämpökapasiteetin C V määritelmän (2.11) avulla muodossa de = C V dt. (2.34) Lämpötilan äärellisessä muutoksessa T = T 2 T 1 yhtälö (2.34) saa muodon E = C V (T 2 T 1 ), (2.35) jos C V voidaan approksimoida välillä (T 1, T 2 ) vakioksi. Itse asiassa yhtälöt (2.34) ja (2.35) pitävät ideaalikaasun tapauksessa paikkansa kaikissa prosesseissa, myös sellaisissa, joissa tilavuus muuttuu. Tämä johtuu siitä, että ideaalikaasun sisäinen energia riippuu vain sen lämpötilasta: E = E(T ). Tietty T :n muutos aiheuttaa siis aina saman E:n muutoksen (ja päinvastoin) riippumatta siitä, minkälainen prosessi on kyseessä. Jos siis lämpötilan muutos T = T 2 T 1 aiheuttaa vakiotilavuudessa tapahtuvassa prosessissa yhtälön (2.35) mukaisen energian muutoksen E = C V T, sen täytyy aiheuttaa täsmälleen saman energian muutoksen kaikissa muissakin prosesseissa. Näin ollen yhtälön (2.35) täytyy olla voimassa myös ideaalikaasun adiabaattisessa tilavuuden muutoksessa. Koska tällaisessa prosessissa E = W, lauseke (2.33) seuraa suoraan yhtälöstä (2.35). Yhtälön (2.34) mukaan ideaalikaasun sisäisen energian muutos de on kaikissa prosesseissa sama kuin C V dt. Sisäisen energian lauseke E(T ) voidaan tämän avulla ratkaista, jos C V :n riippuvuus lämpötilasta tunnetaan. Jos C V voidaan olettaa vakioksi, E(T ):lle saadaan yksinkertainen lauseke E(T ) = C V T, (2.36) missä integroimisvakio on asetettu nollaksi. Jos C V :lle käytetään yhtälön (2.20) mukaista lauseketta C V = nr/(γ 1), energian lausekkeeksi saadaan E = nrt γ 1 = NkT γ 1, (2.37)
16 missä N on kaasussa olevien molekyylien lukumäärä N = nn A ja k on Boltzmannin vakio k = R/N A. Yhtälön (2.37) mukaan yhden kaasumolekyylin energian keskiarvo on siis ɛ = E N = 29 kt γ 1. (2.38) Esimerkiksi yksiatomisella klassisella ideaalikaasulla γ = 5/3, kuten myöhemmin tullaan osoittamaan. Tässä tapauksessa atomin (liike)energian keskiarvo on siis ɛ = 3 kt. (2.39) 2
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics)
 2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
2 Termodynamiikan ensimmäinen pääsääntö (First Law of Thermodynamics) 1 Tässä luvussa päästää käsittelemään lämmön ja mekaanisen työn välistä suhdetta. 2 Näistä molemmat ovat energiaa eri muodoissa, ja
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
T H V 2. Kuva 1: Stirling kiertoprosessi. Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista (kts. kuva 1):
 1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
1 c 3 p 2 T H d b T L 4 1 a V Kuva 1: Stirling kiertoprosessi. Stirlingin kone Ideaalisen Stirlingin koneen sykli koostuu neljästä osaprosessista kts. kuva 1: 1. Työaineen ideaalikaasu isoterminen puristus
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
Clausiuksen epäyhtälö
 1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
1 Kuva 1: Clausiuksen epäyhtälön johtaminen. Clausiuksen epäyhtälö otesimme Carnot n koneelle, että syklissä lämpötiloissa H ja L vastaanotetuille lämmöille Q H ja Q L pätee Q H H oisin ilmaistuna, Carnot
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 Clausiuksen epäyhtälö
 1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
1 PHYS-C0220 ermodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Clausiuksen epäyhtälö Carnot n koneen syklissä lämpötilassa H ja L vastaanotetuille lämmöille Q H ja Q L pätee oisin ilmaistuna,
IX TOINEN PÄÄSÄÄNTÖ JA ENTROPIA...208
 IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
IX OINEN PÄÄSÄÄNÖ JA ENROPIA...08 9. ermodynaamisen systeemin pyrkimys tasapainoon... 08 9. ermodynamiikan toinen pääsääntö... 0 9.3 Entropia termodynamiikassa... 0 9.3. Entropian määritelmä... 0 9.3.
7 Termodynaamiset potentiaalit
 82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
82 7 ermodynaamiset potentiaalit 7-1 Clausiuksen epäyhtälö Kappaleessa 4 tarkasteltiin Clausiuksen entropiaperiaatetta, joka määrää eristetyssä systeemissä (E, ja N vakioita) tapahtuvien prosessien suunnan.
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 30.10.2017 v. 03 / T. Paloposki Tämän päivän ohjelma: Entropia Termodynamiikan 2. pääsääntö Palautuvat ja palautumattomat prosessit 1 Entropia Otetaan
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
3Työ. 3.1 Yleinen määritelmä
 3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
3Työ Edellisessä luvussa käsittelimme systeemin sisäenergian muutosta termisen energiansiirron myötä, joka tapahtuu spontaanisti kahden eri lämpötilassa olevan kappaleen välillä. Toisena mekanismina systeemin
Ekvipartitioteoreema. Entropia MB-jakaumassa. Entropia tilastollisessa mekaniikassa
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema
 Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
Ekvipartitioteoreema lämpötilan ollessa riittävän korkea, kukin molekyylin liikkeen vapausaste tuo energian ½ kt sekä keskimääräiseen liike-energiaan ja kineettiseen energiaan energian lisäys ja riittävän
VII LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ
 II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
II LÄMPÖOPIN ENSIMMÄINEN PÄÄSÄÄNTÖ 7. Lämpö ja työ... 70 7.2 Kaasun tekemä laajenemistyö... 7 7.3 Laajenemistyön erityistapauksia... 73 7.3. Työ isobaarisessa tilanmuutoksessa... 73 7.3.2 Työ isotermisessä
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
Luku 20. Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde
 Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Luku 20 Kertausta: Termodynamiikan 2. pääsääntö Lämpövoimakoneen hyötysuhde Uutta: Termodynamiikan 2. pääsääntö Jäähdytyskoneen hyötykerroin ja lämpöpumpun lämpökerroin Entropia Tilastollista termodynamiikkaa
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
W el = W = 1 2 kx2 1
 7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
Luento 11: Potentiaalienergia. Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia
 Luento 11: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia 1 / 22 Luennon sisältö Potentiaalienergia Konservatiiviset voimat
Luento 11: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Esimerkkejä ja harjoituksia 1 / 22 Luennon sisältö Potentiaalienergia Konservatiiviset voimat
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
dl = F k dl. dw = F dl = F cos. Kun voima vaikuttaa kaarevalla polulla P 1 P 2, polku voidaan jakaa infinitesimaalisen pieniin siirtymiin dl
 Kun voima vaikuttaa kaarevalla polulla P 2, polku voidaan jakaa infinitesimaalisen pieniin siirtymiin dl Kukin siirtymä dl voidaan approksimoida suoraviivaiseksi, jolloin vastaava työn elementti voidaan
Kun voima vaikuttaa kaarevalla polulla P 2, polku voidaan jakaa infinitesimaalisen pieniin siirtymiin dl Kukin siirtymä dl voidaan approksimoida suoraviivaiseksi, jolloin vastaava työn elementti voidaan
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 4: entropia Pe 3.3.2017 1 Aiheet tänään 1. Klassisen termodynamiikan entropia
Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori!
 6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
6.1 Työ Voima F tekee työtä W vaikuttaessaan kappaleeseen, joka siirtyy paikasta r 1 paikkaan r 2. Työ on skalaarisuure, EI vektori! Siirtymä s = r 2 r 1 Kun voiman kohteena olevaa kappaletta voidaan kuvata
Thermodynamics is Two Laws and a Li2le Calculus
 Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
Thermodynamics is Two Laws and a Li2le Calculus Termodynamiikka on joukko työkaluja, joiden avulla voidaan tarkastella energiaan ja entropiaan lii2yviä ilmiötä kaikissa luonnonilmiöissä ja lai2eissa Voidaan
2. Termodynamiikan perusteet
 Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Statistinen fysiikka, osa A (FYSA241) Tuomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 2. Termodynamiikan perusteet 1 TD ja SM Statistisesta fysiikasta voidaan
Fysiikan maailmankuva 2015 Luento 8. Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa?
 Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
Fysiikan maailmankuva 2015 Luento 8 Aika ja ajan nuoli lisää pohdiskelua Termodynamiikka Miten aika ja termodynamiikka liittyvät toisiinsa? Ajan nuoli Aika on mukana fysiikassa niinkuin jokapäiväisessä
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Luku6 Tilanyhtälö. Ideaalikaasun N V. Yleinen aineen. paine vakio. tilavuus vakio
 Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
Luku6 Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät saadaan leikkaamalla painepinta pv suuntaisilla
PHYS-A0120 Termodynamiikka. Emppu Salonen
 PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
PHYS-A0120 ermodynamiikka Emppu Salonen 1. joulukuuta 2016 ermodynamiikka 1 1 Lämpötila ja lämpö 1.1 ilanyhtälö arkastellaan kolmea yksinkertaista fluidisysteemiä 1, jotka koostuvat kukin vain yhdentyyppisistä
Kemiallinen reaktio
 Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Z 1 = Np i. 2. Sähkömagneettisen kentän värähdysliikkeen energia on samaa muotoa kuin molekyylin värähdysliikkeen energia, p 2
 766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
766328A Termofysiikka Harjoitus no., ratkaisut (syyslukukausi 24). Klassisen ideaalikaasun partitiofunktio on luentojen mukaan Z N! [Z (T, V )] N, (9.) missä yksihiukkaspartitiofunktio Z (T, V ) r e βɛr.
6-1 Hyötysuhde ja tehokerroin
 67 6 Lämpövoimakoneet ja jäähdyttimet 6-1 Hyötysuhde ja tehokerroin Lämpövoimakone (engl. heat engine) on laite, joka muuttaa lämpöenergiaa työksi. Tavallisesti laitteessa tapahtuu kiertoprosessi, jonka
67 6 Lämpövoimakoneet ja jäähdyttimet 6-1 Hyötysuhde ja tehokerroin Lämpövoimakone (engl. heat engine) on laite, joka muuttaa lämpöenergiaa työksi. Tavallisesti laitteessa tapahtuu kiertoprosessi, jonka
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196
 VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
VIII KIERTOPROSESSIT JA TERMODYNAAMISET KONEET 196 8.1 Kiertoprosessin ja termodynaamisen koneen määritelmä... 196 8.2 Termodynaamisten koneiden hyötysuhde... 197 8.2.1 Lämpövoimakone... 197 8.2.2 Lämpöpumpun
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 /
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 7 / 31.10.2016 TERVETULOA! v. 02 / T. Paloposki Tämän päivän ohjelma: Virtaussysteemin energiataseen soveltamisesta Kompressorin energiantarve, tekninen
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 13.11. ja tiistai 14.11. Milloin prosessi on adiabaattinen?
Integroimalla ja käyttämällä lopuksi tilanyhtälöä saadaan T ( ) ( ) H 5,0 10 J + 2,0 10 0,50 1,0 10 0,80 Pa m 70 kj
 S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
S-4.35 Fysiikka (ES) entti 3.8.. ääritä yhden haikaasumoolin (O) (a) sisäenergian, (b) entalian muutos tilanmuutoksessa alkutilasta =, bar, =,8 m3 loutilaan =, bar, =,5 m3. ärähtelyn vaausasteet voidaan
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit
 19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
19.6-7 Harvan kaasun sisäenergia ja lämpökapasiteetit Kokeelliset havainnot ja teoria (mm. luku 18.4) Ainemäärän pysyessä vakiona harvan kaasun sisäenergia riippuu ainoastaan sen lämpötilasta eli U = U(T
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
FY9 Fysiikan kokonaiskuva
 FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
FY9 Sivu 1 FY9 Fysiikan kokonaiskuva 6. tammikuuta 2014 14:34 Kurssin tavoitteet Kerrata lukion fysiikan oppimäärä Yhdistellä kurssien asioita toisiinsa muodostaen kokonaiskuvan Valmistaa ylioppilaskirjoituksiin
y 2 h 2), (a) Näytä, että virtauksessa olevan fluidialkion tilavuus ei muutu.
 Tehtävä 1 Tarkastellaan paineen ajamaa Poisseuille-virtausta kahden yhdensuuntaisen levyn välissä Levyjen välinen etäisyys on 2h Nopeusjakauma raossa on tällöin u(y) = 1 dp ( y 2 h 2), missä y = 0 on raon
Tehtävä 1 Tarkastellaan paineen ajamaa Poisseuille-virtausta kahden yhdensuuntaisen levyn välissä Levyjen välinen etäisyys on 2h Nopeusjakauma raossa on tällöin u(y) = 1 dp ( y 2 h 2), missä y = 0 on raon
Luento 10: Työ, energia ja teho. Johdanto Työ ja kineettinen energia Teho
 Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Luento 10: Työ, energia ja teho Johdanto Työ ja kineettinen energia Teho 1 / 23 Luennon sisältö Johdanto Työ ja kineettinen energia Teho 2 / 23 Johdanto Energia suure, joka voidaan muuttaa muodosta toiseen,
Joukot. Georg Cantor ( )
 Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
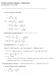 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Vauhti = nopeuden itseisarvo. Nopeuden itseisarvon keskiarvo N:lle hiukkaselle määritellään yhtälöllä
 S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
S-4.35, Fysiikka III (ES) entti 8.3.006. Laske nopeuden itseisarvon keskiarvo v ave ja nopeuden neliöllinen keskiarvo v rms seuraaville 6 molekyylien nopeusjakaumille: a) kaikkien vauhti 0 m/s, b) kolmen
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
Lämpöopin pääsäännöt. 0. pääsääntö. I pääsääntö. II pääsääntö
 Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Lämpöopin pääsäännöt 0. pääsääntö Jos systeemit A ja C sekä B ja C ovat termisessä tasapainossa, niin silloin myös A ja B ovat tasapainossa. Eristetyssä systeemissä eri lämpöiset kappaleet asettuvat lopulta
Käytetään lopuksi ideaalikaasun tilanyhtälöä muutoksille 1-2 ja 3-1. Muutos 1-2 on isokorinen, joten tilanyhtälöstä saadaan ( p2 / p1) = ( T2 / T1)
 LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
LH0- Lämövoimakoneen kiertorosessin vaiheet ovat: a) Isokorinen aineen kasvu arvosta arvoon 2, b) adiabaattinen laajeneminen, jolloin aine laskee takaisin arvoon ja tilavuus kasvaa arvoon 3 ja c) isobaarinen
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
Luento 8 6.3.2015. Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit
 Luento 8 6.3.2015 1 Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) 2 Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Luento 8 6.3.2015 1 Entrooppiset voimat Vapaan energian muunoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) 2 Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
13 KALORIMETRI. 13.1 Johdanto. 13.2 Kalorimetrin lämmönvaihto
 13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 14.11. ja tiistai 15.11. Kurssin aiheet 1. Lämpötila ja lämpö
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 3: Lämpövoimakoneet ja termodynamiikan 2. pääsääntö Maanantai 14.11. ja tiistai 15.11. Kurssin aiheet 1. Lämpötila ja lämpö
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, Luku 7 ENTROPIA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
4. Termodynaamiset potentiaalit
 Statistinen fysiikka, osa A (FYSA241) uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty
Statistinen fysiikka, osa A (FYSA241) uomas Lappi tuomas.v.v.lappi@jyu.fi Huone: FL249. Ei kiinteitä vastaanottoaikoja. kl 2013 4. ermodynaamiset potentiaalit 1 asapainotila Mikrokanoninen ensemble Eristetty
Luento 9: Potentiaalienergia
 Luento 9: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Laskettuja esimerkkejä Luennon sisältö Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta
Luento 9: Potentiaalienergia Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta gradientti Laskettuja esimerkkejä Luennon sisältö Potentiaalienergia Konservatiiviset voimat Voima potentiaalienergiasta
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 5: Termodynaamiset potentiaalit Ke 9.3.2016 1 AIHEET 1. Muut työn laadut sisäenergiassa
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Mikrotila Makrotila Statistinen paino Ω(n) 3 Ω(3) = 4 2 Ω(2) = 6 4 Ω(4) = 1
 76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
76628A Termofysiikka Harjoitus no. 4, ratkaisut (syyslukukausi 204). (a) Systeemi koostuu neljästä identtisestä spin- -hiukkasesta. Merkitään ylöspäin olevien spinien lukumäärää n:llä. Systeemin mahdolliset
Entrooppiset voimat. Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit
 Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
Entrooppiset voimat Entrooppiset voimat Vapaan energian muunnoksen hyötysuhde Kahden tilan systeemit Entrooppiset voimat 3 2 0 0 S k N ln VE S, S f ( N, m) Makroskooppisia voimia, jotka syntyvät pyrkimyksestä
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ
 I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
I PERUSKÄSITTEITÄ JA MÄÄRITELMIÄ 1.1 Tilastollisen fysiikan ja termodynamiikan tutkimuskohde... 2 1.2 Mikroskooppiset ja makroskooppiset teoriat... 3 1.3 Terminen tasapaino ja lämpötila... 5 1.4 Termodynamiikan
Käyttämällä annettua kokoonpuristuvuuden määritelmää V V. = κv P P = P 0 = P. (b) Lämpölaajenemisesta johtuva säiliön tilavuuden muutos on
 766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
