TEKNINEN PIIRUSTUS II
|
|
|
- Anneli Jaana Lattu
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 TEKNINEN PIIRUSTUS II Kevät 2015 PINTAMERKIT TkT Harri Eskelinen 1
2 1 Johdanto 2
3 Pintamerkillä ilmoitettavia vaatimuksia Pintamerkkejä käytetään ilmaistaessa mm. seuraavia pintaa koskevia vaatimuksia: Pinnan karheus Pinnan aaltomaisuus Pinnan kantavuus Suureet ovat pinnan korkeus- tai pituussuuntaisia 3
4 2 Profiilin aritmeettinen keskipoikkeama Ra Ra 1.6 4
5 Perussuureet, joita tarvitaan Ra:n määritelmässä Mittausjakso l i ja mittauspituus l n Mittausjakso l i on mittalaitteen yhdellä mittauskerralla analysoima pituus Mittauspituus l n on tutkittava koneenosan alue / pituus. 5
6 Ra:n matemaattinen määritelmä 6
7 Ra:n ominaisuuksia Yleisimmin käytetty pinnankarheutta kuvaava suure Helppo mitata Ei erota pinnan, ja sen peilikuvan profiileja toisistaan eikä huippuja ja laaksoja toisistaan (itseisarvo) Yksittäiset virheet jäävät helposti osoittamatta (keskiarvo) Lähtökohtana pidetään pinnanprofiilin keskiviivaa, johon nähden poikkeamia ilmoitetaan 7
8 Esimerkiksi alla olevilla pinnoilla on sama Ra 8
9 3 Muita pinnan ominaisuuksia kuvaavia suureita Täydentävät Ra:n antamaa informaatiota (vrt. edellä itseisarvon ja keskiarvon merkitys määritelmässä) Tarvitaan määrittämään joidenkin koneenosien erikoisvaatimuksia (esim. erilaiset tiivistepinnat) Tarvitaan kulumisanalyyseissä (esim. kulumisen syyn ja kulumisnopeuden arviointi) Monet koneenosien mitoitusohjeet perustuvat johonkin muuhun kuin Ra:n käyttöön Kappaleen nk. todellinen pinta koostuu useiden eri virheiden yhteisvaikutuksesta, jolloin tarvitaan korkeus- ja pituussuuntaisia suureita sekä pinnan kantavuusominaisuuksia kuvaavia suureita Suureet voidaan laskea mm. aaltomaisuudelle (esim. Wa) 9
10 Pinnan maksimihuipun korkeus Rp ja minimilaakson syvyys Rv Rp Rv 10
11 Maksimiprofiilin syvyys Rz Rp Rv Rz Rz = Rp + Rv Käytetään monesti Ra:n lisänä rajoittamaan suurimman sallitun yksittäisen virheen suuruutta tiivistepinnoissa Entinen tunnus oli Ry (ei saa sekoittaa myöskään vanhaan Rz:aan, joka oli 5 suurimman ja 5 pienimmän virheen keskiarvo) 11
12 Pinnankarheuden keskihajonta Rq Lasketaan pinnan y(x) virheistä 12
13 Pinnan ominaisuuksia kuvaavia pituussuuntaisia suureita Profiilin epätasaisuuksien keskijako Rsm on profiilin epätasaisuuksien jakojen keskiarvo mittausjaksolla Xs 1 Xs i Xs 2 Xs 3 Xs 4 Xs 5 Xs 6 13
14 Pituussuuntaisia suureita voi hyödyntää esimerkiksi etsittäessä syitä pyörivien koneenosien tai niiden kuormittamien ohjainrakenteiden kulumisvaurioille Monien luisti- ja liukumekanismien toimintaa ja kulumista voi analysoida pituussuuntaisia suureita käyttäen 14
15 Pinnan kantavuusominaisuuksia kuvaavia suureita Profiilin kantopituus p halutulla korkeudella saadaan, kun leikataan pinnan huiput poikki tältä korkeudelta ja lasketaan yhteen jäljelle jääneiden tasattujen huippujen pituudet η n b p i i 1 15
16 Pinnan kanto-osuus t p on kantopituuden ja mittausjakson pituuden suhde halutulla korkeudella t p η l p Yleensä kanto-osuus esitetään prosentteina, suureen lyhenne Rmr Kanto-osuus kuvaa esim. osien todellista kantavaa pinta-alaa sisäänajovaiheen jälkeen tai tietyn kulumisajan jälkeen Jos lasketaan lukuarvo 100%- Rmr, voidaan myös ilmoittaa esimerkiksi jäljellä oleva kulutuspinta 16
17 Profiilin kantokäyrä eli nk. Abbott-käyrä kuvaa kanto-osuuksia (prosentteina ilmaistuna) profiilin eri korkeuksilla esim. ajan funktiona Abbott-käyrää voi käyttää siis joko analysoitaessa todellista kantopinta-alaa tai jäljellä olevaa kulutuspintaa Rmr 17
18 4 Noudatettavat standardit SFS-EN-ISO- ja ISO-standardit antavat yksityiskohtaiset ohjeet pintamerkkien käytöstä sekä määrittelevät yksityiskohtaisesti kaikki standardisoidut pinnan ominaisuuksien ilmoittamiseen käytettävät suureet: SFS-EN-ISO 1302 SFS-EN-ISO 8785 SFS-EN-ISO
19 5 Pintamerkin rakenne ja sisältö a) perusmerkki b) täydennetty pintamerkki, jolla ilmoitetaan että aineen poistoa tarvitaan c) täydennetty pintamerkki, jolla ilmoitetaan, että aineen poistoa ei sallita 19
20 d) Pinnan vaatimus koskee kappaleen kaikkia pintoja 20
21 6 Pinnan ominaisuuksia koskevat täydentävät vaatimukset Erilaiset pinnan ominaisuuksia koskevat vaatimukset on sijoitettavat täydelliseen pintamerkkiin seuraaville paikoille: Paikat a ja b = pinnan ominaisuuksia kuvaavien suureiden lukuarvot allekkain Paikka c = valmistusmenetelmä Paikka d = pintakuvio ja työstönaarmujen suunta Paikka e = työvara (mm) 21
22 7 Pintamerkkien suunta ja sijoittelu Pintamerkki sijoitetaan siten, että se on luettavissa piirustuksesta joko alhaalta tai oikealta 22
23 Pintamerkki sijoitetaan kappaleen ulkopuolelle 1 Osoittamaan muotoviivaan 2 Muotoviivan jatkeelle 3 Viiteviivalle
24 Viiteviivan käyttö projektiosta, joka on edestä 24
25 Viiteviivan hyväksikäyttö, kun tilaa on vähän 25
26 Pintamerkki voidaan sijoittaa myös mittaviivalle 26
27 Pintamerkin sijoittaminen toleranssivaatimusten yhteyteen: 27
28 8 Merkintöjen yksinkertaistaminen Kun useimmilla pinnoilla on sama pinnan ominaisuuksia koskeva vaatimus voidaan yleinen vaatimus esittää esim. otsikkoalueen läheisyydessä (suluissa esitetään poikkeavat vaatimukset) 28
29 Yksinkertaistettua merkintää voidaan käyttää, jos sen merkitys selitettään ko. työkappaleen tai otsikkoalueen läheisyydessä 29
30 Perusmerkkiä ja täydennettyjä perusmerkkejä voidaan käyttää ko. pinnalla, jos merkitys selitetään esim. otsikkoalueen lähellä: 30
31 9 Useampaa valmistusvaihetta koskevien vaatimusten ilmoittaminen Esimerkin työvaiheet: valmistelu pinnoitukselle, pinnoitus ja hionta 31
32 10 Täydellisen pintamerkin sisältö 32
33 Työstönaarmujen suunnan merkitseminen = 33
34 X P 34
35 M C R 35
36 Päästökaista ja mittausjakso väliviivalla erotettuina Mittausjaksojen lkm = suositellaan käytettäväksi oletusarvoja = voidaan jättää pois, jos epäselvyyttä tulkinnasta ei synny 36
37 Määrittelyrajan tulkinta 16%-sääntö Pinta hyväksytään, jos korkeintaan 16% mitatuista suureen arvoista ylittää pintamerkissä annetun rajaarvon Max-sääntö Pinta hyväksytään vain, jos yksikään mitatuista suureen arvoista ei ylitä pintamerkissä annettua rajaarvoa 37
38 11 Lyhyesti mittaustulosten suodatuksesta Tavoitteena on erotella erilaiset pinnanvirheet luotettavasti toisistaan, esimerkiksi pinnan aaltomaisuus ja karheus toisistaan. Käytettävä päästökaista on siksi määritelty standardissa. 38
39 39
40 12 Vanhan ja uuden standardin vertailua Pinnan ominaisuuksia käsittelevien standardien uusitut painokset (monet vahvistettu v ) ovat aiheuttaneet useita merkittäviä muutoksia aikaisempien, 1980-luvulla julkaistujen standardien sisältöön verrattuna. Vanhoja merkintöjä on edelleen käytössä monissa yrityksissä ja tietenkin vanhoissa piirustuksissa Uusi mittaustekniikka muuttaa mittaustulosta siten, että tulos voi pahimmillaan pienetä jopa 37% aikaisempaan mittaustekniikkaan verrattuna, keskimääräiset erot ovat 5-10%. 40
41 Kaksi uutta pintaprofiilia W- (aaltomaisuus) ja P-profiili (rakenne) on määritelty aikaisemman R-profiilin eli karheusprofiilin lisäksi. Kukin kolmesta pintaprofiilista voi nyt olla perustana useille pintasuureille, esim. Ra, Wa ja Pa. Pintasuureiden painoasu on muuttunut. Suureen tunnus kirjoitetaan nyt yhdelle riville, esim. Ra ja Rz. Alaindeksejä, esim. R a ja R z ei enää käytetä. Myös vanha pintamerkin rakenne ja sisältö ovat muuttuneet. Melkein kaikki pinnan ominaisuuksia kuvaavat tunnukset ja olemassa olevien suureiden nimet ovat muuttuneet (SFS-EN-ISO 4287). Aikaisempi pintasuure Rz (profiilinsyvyys, 5 korkeinta huippua ja 5 matalinta laaksoa pinnasta) ei enää ole ISO:n standardisoima. Rz on korvannut aikaisemman tunnuksen Ry (maksimiprofiilinsyvyys). Kolme uutta pintasuureiden ryhmää/ tyyppiä on standardisoitu (standardit SFS-EN-ISO 12085, SFS-EN-ISO ja SFS-EN-ISO , mm. pinnan kantavuutta kuvaavaan käyrään liittyviä suureita). 41
42 13 Pintamerkkien käyttökohteita 42
43 Hammasvaihteen runko 43
44 Laakeripesän kansi 44
45 Säteishuulitiivistimen pesä 45
46 Tiivisteen kohdalla voidaan vaatia Ra:n ylä- ja alaraja, työstönaarmujen suunta ja suurin sallittu yksittäinen virhe Säteishuulitiivistimen kohta akselilla 46
47 Kartiohammaspyörä 47
48 Tekijät, joiden perusteella Ra:n lukuarvo määrätään Koneenosan toiminnalliset vaatimukset Valmistusmenetelmällä saavutettava Ra Ra:n lukuarvon yhteensopivuus toleranssien kanssa Valmistuskustannusten merkitys 48
49 Ra:n ja valmistuskustannusten välinen periaatteellinen yhteys Ra 49
50 Eri valmistusmenetelmillä saavutettava Ra Ra 50
51 14 Kappaleen todellinen pinta Kappaleen todellinen pinta muodostuu useiden eri virheiden yhteisvaikutuksesta Riippuen mm. valmistusmenetelmästä on syntyvän pinnan geometria joko jaksollinen tai jaksoton 51
52 Muotovirhe - suoruus tai tasomaisuus virhe - syynä esim. työkappaleen taipumat tai virhe työstökoneen johteissa 52
53 Luokka 2 - aaltomainen pinnan muoto - syynä esim. työkappaleen epäkeskeinen kiinnitys tai työkalun värähtelyt 53
54 Karheus A - kappaleen pinnassa säännöllisiä uria - syynä esimerkiksi käytetyt lastuamisarvot ja terägeometria (vrt. sorvauksessa nirkon säteen kopioituminen kappaleen pintaan) 54
55 Pinnankarheuden syntyminen sorvauksessa: Nirkon säde kopioituu kappaleen pintaan 55
56 Karheus B - kappaleen pinnassa epäsäännöllisiä uurteita ja painumia - syynä esimerkiksi epäedullinen lastunmuodostus - hiomajäljet tai muun viimeistelymenetelmän jäljet kappaleessa 56
57 Kide- ja hilarakenteen vaikutukset - korroosion vaikutukset - pinnan muutokset kemiallisten vaikutusten takia - kiteytymisen vaikutukset - aineen hilarakenteen vaikutukset 57
58 Todellinen pinta on edellisten virheiden yhdistelmä. Vaadittu tarkkuus esitetään käyttäen: - pintamerkkejä - mittatoleransseja - geometrisia toleransseja - lisämerkintöjä lämpökäsittelyille ja muille pinnan viimeistelymenetelmille 58
59 Ra
60 SILEÄ PINTA EI OLE SAMA ASIA KUIN PAREMPI PINTA Esimerkiksi haluttaessa lisää tartuntapinta-alaa ruiskutettavalle pinnoitteelle tai liima/tiivistemassalle, voi karheampi pinta olla toimivampi. Jos pinnan on tarkoitus olla esim. luistamisen tai liukastumisvaaran välttämiseksi karhea, tai jos karheudella haetaan esim. pitävämpää otetta kappaleesta, ei sileä pinta ole parempi 60
PIKAOPAS PINNANKARHEUDEN MITTAUKSEEN
 PIKAOPAS PINNANKARHEUDEN MITTAUKSEEN Opas laboratorio- ja konepajakäyttöön SUOMIPAINOS Profiilit ja suodattimet (EN ISO 4287 ja EN ISO 16610-21) 01 Varsinainen profiili on profiili, joka syntyy todellisen
PIKAOPAS PINNANKARHEUDEN MITTAUKSEEN Opas laboratorio- ja konepajakäyttöön SUOMIPAINOS Profiilit ja suodattimet (EN ISO 4287 ja EN ISO 16610-21) 01 Varsinainen profiili on profiili, joka syntyy todellisen
Keskeiset aihepiirit
 TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
Standardin ISO 8062 mittatoleranssijärjestelmä
 Valutoleranssilla tarkoitetaan yhteisesti sovittua aluetta, jonka sisälle kappaleiden mittamuutokset mahtuvat. Toleranssit jaotellaan yleensä useaan ryhmään, jossa pienimmissä toleranssiryhmissä hyväksytyt
Valutoleranssilla tarkoitetaan yhteisesti sovittua aluetta, jonka sisälle kappaleiden mittamuutokset mahtuvat. Toleranssit jaotellaan yleensä useaan ryhmään, jossa pienimmissä toleranssiryhmissä hyväksytyt
1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen
 TkT Harri Eskelinen 1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen 2. Standardiosien hyödyntäminen 3. Osien kokoonpanosuunnat ja järjestys 4.
TkT Harri Eskelinen 1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen 2. Standardiosien hyödyntäminen 3. Osien kokoonpanosuunnat ja järjestys 4.
OSA A. MITTATOLERANSSIT
 BK50A0200 TEKNINEN PIIRUSTUS II HARJOITUKSET / KEVÄT 2015/ viikko 11 / TOLERANSSIT Pj/Varapj: Tulosta tehtäväpaperi ja palauta tehtävien ratkaisut luennoitsijalle oman harjoitusajan loppuun mennessä. RYHMÄN
BK50A0200 TEKNINEN PIIRUSTUS II HARJOITUKSET / KEVÄT 2015/ viikko 11 / TOLERANSSIT Pj/Varapj: Tulosta tehtäväpaperi ja palauta tehtävien ratkaisut luennoitsijalle oman harjoitusajan loppuun mennessä. RYHMÄN
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
kartiopinta kartio. kartion pohja, suora ympyräkartio vino pyramidiksi
 5.3 Kartio Kun suora liikkuu avaruudessa niin, että yksi sen piste pysyy paikoillaan ja suoran jokin toinen piste kiertää jossakin tasossa jonkin suljetun käyrän palaten lähtöpaikkaansa, syntyy kaksiosainen
5.3 Kartio Kun suora liikkuu avaruudessa niin, että yksi sen piste pysyy paikoillaan ja suoran jokin toinen piste kiertää jossakin tasossa jonkin suljetun käyrän palaten lähtöpaikkaansa, syntyy kaksiosainen
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Muutoksen arviointi differentiaalin avulla
 Muutoksen arviointi differentiaalin avulla y y = f (x) y = f (x + x) f (x) dy y dy = f (x) x x x x x + x Luento 7 1 of 15 Matematiikan ja tilastotieteen laitos Turun yliopisto Muutoksen arviointi differentiaalin
Muutoksen arviointi differentiaalin avulla y y = f (x) y = f (x + x) f (x) dy y dy = f (x) x x x x x + x Luento 7 1 of 15 Matematiikan ja tilastotieteen laitos Turun yliopisto Muutoksen arviointi differentiaalin
PANK PANK-4122 ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ 1. MENETELMÄN TARKOITUS
 PANK-4122 PANK PÄÄLLYSTEALAN NEUVOTTELUKUNTA ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ Hyväksytty: Korvaa menetelmän: 9.5.2008 26.10.1999 1. MENETELMÄN TARKOITUS 2. MENETELMÄN SOVELTAMISALUE
PANK-4122 PANK PÄÄLLYSTEALAN NEUVOTTELUKUNTA ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ Hyväksytty: Korvaa menetelmän: 9.5.2008 26.10.1999 1. MENETELMÄN TARKOITUS 2. MENETELMÄN SOVELTAMISALUE
ASUINKERROSTALON ÄÄNITEKNISEN LAADUN ARVIOINTI. Mikko Kylliäinen
 ASUINKERROSTALON ÄÄNITEKNISEN LAADUN ARVIOINTI Mikko Kylliäinen Insinööritoimisto Heikki Helimäki Oy Dagmarinkatu 8 B 18, 00100 Helsinki [email protected] 1 JOHDANTO Suomen rakentamismääräyskokoelman
ASUINKERROSTALON ÄÄNITEKNISEN LAADUN ARVIOINTI Mikko Kylliäinen Insinööritoimisto Heikki Helimäki Oy Dagmarinkatu 8 B 18, 00100 Helsinki [email protected] 1 JOHDANTO Suomen rakentamismääräyskokoelman
SUPER TT-, TT- JA HTT -LAATAT
 SUUNNITTELUOHJE SUPER TT-, TT- JA HTT -LAATAT 1 (33) SISÄLLYS 1. YLEISTÄ...2 2. SUUNNITTELU...3 3. VALMISTUS...4 4. KIINNITYSTEN JA RIPUSTUSTEN YLEISOHJE...5 LIITTEET...6 LIITE 1A: SUPERTT-LAATAN POIKKILEIKKAUSMITAT...7
SUUNNITTELUOHJE SUPER TT-, TT- JA HTT -LAATAT 1 (33) SISÄLLYS 1. YLEISTÄ...2 2. SUUNNITTELU...3 3. VALMISTUS...4 4. KIINNITYSTEN JA RIPUSTUSTEN YLEISOHJE...5 LIITTEET...6 LIITE 1A: SUPERTT-LAATAN POIKKILEIKKAUSMITAT...7
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
KISKONHIONNAN TEKNISET TOIMITUSEHDOT
 Kunnossapitoyksikkö/KO 2.11. 2001 1 (11) KISKONHIONNAN TEKNISET TOIMITUSEHDOT Nämä kiskonhionnan tekniset toimitusehdot 1539/731/2001 ovat voimassa Suomen valtion rataverkolla 1.1.2002 lukien. Nämä toimitusehdot
Kunnossapitoyksikkö/KO 2.11. 2001 1 (11) KISKONHIONNAN TEKNISET TOIMITUSEHDOT Nämä kiskonhionnan tekniset toimitusehdot 1539/731/2001 ovat voimassa Suomen valtion rataverkolla 1.1.2002 lukien. Nämä toimitusehdot
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Määrätty integraali. Markus Helén. Mäntän lukio
 Määrätty integraali Markus Helén Pinta-ala Monikulmio on tasokuvio, jota rajoittaa suljettu, itseään leikkaamaton murtoviiva. Monikulmio voidaan aina jakaa kolmioiksi. Alueen pinta-ala on näiden kolmioiden
Määrätty integraali Markus Helén Pinta-ala Monikulmio on tasokuvio, jota rajoittaa suljettu, itseään leikkaamaton murtoviiva. Monikulmio voidaan aina jakaa kolmioiksi. Alueen pinta-ala on näiden kolmioiden
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2014 HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 4.9.04 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 4.9.04 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa
 Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
Virhearviointi. Fysiikassa on tärkeää tietää tulosten tarkkuus.
 Virhearviointi Fysiikassa on tärkeää tietää tulosten tarkkuus. Virhelajit A. Tilastolliset virheet= satunnaisvirheet, joita voi arvioida tilastollisin menetelmin B. Systemaattiset virheet = virheet, joita
Virhearviointi Fysiikassa on tärkeää tietää tulosten tarkkuus. Virhelajit A. Tilastolliset virheet= satunnaisvirheet, joita voi arvioida tilastollisin menetelmin B. Systemaattiset virheet = virheet, joita
Teräsputkipaalujen kalliokärkien suunnittelu, lisäohjeita FEMlaskentaa
 1 (1) Teräsputkipaalujen kalliokärkien suunnittelijoilla Teräsputkipaalujen kalliokärkien suunnittelu, lisäohjeita FEMlaskentaa varten. Teräsputkipaalujen kalliokärkien suunnittelu on tehtävä Liikenneviraston
1 (1) Teräsputkipaalujen kalliokärkien suunnittelijoilla Teräsputkipaalujen kalliokärkien suunnittelu, lisäohjeita FEMlaskentaa varten. Teräsputkipaalujen kalliokärkien suunnittelu on tehtävä Liikenneviraston
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 2.3.2011 T-106.1208 Ohjelmoinnin perusteet Y 2.3.2011 1 / 39 Kertausta: tiedoston avaaminen Kun ohjelma haluaa lukea tai kirjoittaa tekstitiedostoon, on ohjelmalle
Ohjelmoinnin perusteet Y Python T-106.1208 2.3.2011 T-106.1208 Ohjelmoinnin perusteet Y 2.3.2011 1 / 39 Kertausta: tiedoston avaaminen Kun ohjelma haluaa lukea tai kirjoittaa tekstitiedostoon, on ohjelmalle
Pinta-alojen ja tilavuuksien laskeminen 1/6 Sisältö ESITIEDOT: määrätty integraali
 Pinta-alojen ja tilavuuksien laskeminen 1/6 Sisältö ESITIEDOT: Tasoalueen pinta-ala Jos funktio f saa välillä [a, b] vain ei-negatiivisia arvoja, so. f() 0, kun [a, b], voidaan kuvaajan y = f(), -akselin
Pinta-alojen ja tilavuuksien laskeminen 1/6 Sisältö ESITIEDOT: Tasoalueen pinta-ala Jos funktio f saa välillä [a, b] vain ei-negatiivisia arvoja, so. f() 0, kun [a, b], voidaan kuvaajan y = f(), -akselin
1/6 TEKNIIKKA JA LIIKENNE FYSIIKAN LABORATORIO V1.31 9.2011
 1/6 333. SÄDEOPTIIKKA JA FOTOMETRIA A. INSSIN POTTOVÄIN JA TAITTOKYVYN MÄÄRITTÄMINEN 1. Työn tavoite. Teoriaa 3. Työn suoritus Työssä perehdytään valon kulkuun väliaineissa ja niiden rajapinnoissa sädeoptiikan
1/6 333. SÄDEOPTIIKKA JA FOTOMETRIA A. INSSIN POTTOVÄIN JA TAITTOKYVYN MÄÄRITTÄMINEN 1. Työn tavoite. Teoriaa 3. Työn suoritus Työssä perehdytään valon kulkuun väliaineissa ja niiden rajapinnoissa sädeoptiikan
Estemuutokset uusiin sääntöihin
 Estemuutokset uusiin sääntöihin Uusien kansallisten sääntöjen astuessa voimaan tulee voimaan myös tämän liitteen muutokset esteiden osalta. 27.11.2017 Suomen Agilityliitto Yleiset tiedustelut: [email protected]
Estemuutokset uusiin sääntöihin Uusien kansallisten sääntöjen astuessa voimaan tulee voimaan myös tämän liitteen muutokset esteiden osalta. 27.11.2017 Suomen Agilityliitto Yleiset tiedustelut: [email protected]
Kierukkavaihteet GS 50.3 GS 250.3 varustettu jalalla ja vivulla
 Kierukkavaihteet GS 50.3 GS 250.3 varustettu jalalla ja vivulla Käytettäväksi ainoastaan käyttöohjeen yhteydessä! Tämä pikaopas EI korvaa käyttöohjetta! Pikaopas on tarkoitettu ainoastaan henkilöille,
Kierukkavaihteet GS 50.3 GS 250.3 varustettu jalalla ja vivulla Käytettäväksi ainoastaan käyttöohjeen yhteydessä! Tämä pikaopas EI korvaa käyttöohjetta! Pikaopas on tarkoitettu ainoastaan henkilöille,
MS-A0207 Differentiaali- ja integraalilaskenta 2 (CHEM) Luento 2: Usean muuttujan funktiot
 MS-A0207 Differentiaali- ja integraalilaskenta 2 (CHEM) Luento 2: Usean muuttujan funktiot Harri Hakula Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2018 1 Perustuu Antti Rasilan luentomonisteeseen
MS-A0207 Differentiaali- ja integraalilaskenta 2 (CHEM) Luento 2: Usean muuttujan funktiot Harri Hakula Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 2018 1 Perustuu Antti Rasilan luentomonisteeseen
VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN
 Matematiikan kurssikoe, Maa6 Derivaatta RATKAISUT Sievin lukio Torstai 23.9.2017 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN MAOL-taulukkokirja on sallittu. Vaihtoehtoisesti voit käyttää aineistot-osiossa olevaa
Matematiikan kurssikoe, Maa6 Derivaatta RATKAISUT Sievin lukio Torstai 23.9.2017 VASTAA YHTEENSÄ KUUTEEN TEHTÄVÄÄN MAOL-taulukkokirja on sallittu. Vaihtoehtoisesti voit käyttää aineistot-osiossa olevaa
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
ULTRAÄÄNIMUOKAUSLAITTEEN TESTAUS. Mikko Hokkanen Tampereen teknillinen yliopisto
 ULTRAÄÄNIMUOKAUSLAITTEEN TESTAUS Tampereen teknillinen yliopisto Tiivistelmä Tässä tutkimuksessa testattiin nc-ohjatussa sorvissa Elpro Oy:n kehittämää ultraäänimuokkainta erilaisille teräksille ja alumiinille.
ULTRAÄÄNIMUOKAUSLAITTEEN TESTAUS Tampereen teknillinen yliopisto Tiivistelmä Tässä tutkimuksessa testattiin nc-ohjatussa sorvissa Elpro Oy:n kehittämää ultraäänimuokkainta erilaisille teräksille ja alumiinille.
4 LUKUJONOT JA SUMMAT
 Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
Huippu Kertaus Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 0.7.08 4 LUKUJONOT JA SUMMAT ALOITA PERUSTEISTA 45A. Määritetään lukujonon (a n ) kolme ensimmäistä jäsentä ja sadas jäsen a 00 sijoittamalla
PIENOISLINEAARIJOHTEET
 RSR Z ja RSH Z PIENOISLINEAARIJOHTEET MEKAANISET RAKENNEOSAT 2 SKS Mekaniikka Oy Etelä-Suomi Länsi-Suomi Keski-Suomi Tavaraosoite Martinkyläntie 5 Mustionkatu 8 Hämeenkatu 6A Martinkyläntie 5 172 Vantaa
RSR Z ja RSH Z PIENOISLINEAARIJOHTEET MEKAANISET RAKENNEOSAT 2 SKS Mekaniikka Oy Etelä-Suomi Länsi-Suomi Keski-Suomi Tavaraosoite Martinkyläntie 5 Mustionkatu 8 Hämeenkatu 6A Martinkyläntie 5 172 Vantaa
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
Erstantie 2, 15540 Villähde 2 Puh. (03) 872 200, Fax (03) 872 2020 www.anstar.fi [email protected] Käyttöohje
 Erstantie 2, 15540 Villähde 2 Erstantie 2, 15540 Villähde 3 SISÄLLYSLUETTELO Sivu 1 TOIMINTATAPA... 4 2 MATERIAALIT JA RAKENNE... 5 2.1 MATERIAALIT... 5 2.2 RAKENNEMITAT... 5 3 VALMISTUS... 6 3.1 VALMISTUSTAPA...
Erstantie 2, 15540 Villähde 2 Erstantie 2, 15540 Villähde 3 SISÄLLYSLUETTELO Sivu 1 TOIMINTATAPA... 4 2 MATERIAALIT JA RAKENNE... 5 2.1 MATERIAALIT... 5 2.2 RAKENNEMITAT... 5 3 VALMISTUS... 6 3.1 VALMISTUSTAPA...
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Pyramidi 10 Integraalilaskenta harjoituskokeiden ratkaisut sivu 298 Päivitetty
 Pyramidi Integraalilaskenta harjoituskokeiden ratkaisut sivu 98 Päivitetty.5. Pyramidi Harjoituskokeet 6.5.7 Ensimmäinen julkaistu versio..7.7 Korjattu ulkoasua ja painovirheitä..8.7 Täydennetty ratkaisuja
Pyramidi Integraalilaskenta harjoituskokeiden ratkaisut sivu 98 Päivitetty.5. Pyramidi Harjoituskokeet 6.5.7 Ensimmäinen julkaistu versio..7.7 Korjattu ulkoasua ja painovirheitä..8.7 Täydennetty ratkaisuja
Piste ja jana koordinaatistossa
 607 Piste ja jana koordinaatistossa ANALYYTTINEN GEOMETRIA MAA5 Kertausta kurssi Eri asioiden välisten riippuvuuksien havainnollistamiseen kätetään usein koordinaatistoesitstä Pstakselilla riippuvan muuttujan
607 Piste ja jana koordinaatistossa ANALYYTTINEN GEOMETRIA MAA5 Kertausta kurssi Eri asioiden välisten riippuvuuksien havainnollistamiseen kätetään usein koordinaatistoesitstä Pstakselilla riippuvan muuttujan
Yliajokoemenetelmäkuvauksen tarkentava liite
 Versio 1.0 Antopäivä: 3.4.2014 Voimaantulopäivä: 12.5.2014 Voimassa: Toistaiseksi Säädösperusta: Liikenne- ja viestintäministeriön asetus ajoneuvon renkaiden nastoista 408/2003 (viimeisin muutos 466/2009)
Versio 1.0 Antopäivä: 3.4.2014 Voimaantulopäivä: 12.5.2014 Voimassa: Toistaiseksi Säädösperusta: Liikenne- ja viestintäministeriön asetus ajoneuvon renkaiden nastoista 408/2003 (viimeisin muutos 466/2009)
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Vastaus: Määrittelyehto on x 1 ja nollakohta x = 1.
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 4..6 Kokoavia tehtäviä ILMAN TEKNISIÄ APUVÄLINEITÄ. a) Funktion f( ) = määrittelyehto on +, eli. + Ratkaistaan funktion nollakohdat. f(
METROLOGINEN HAKUTEOS
 METROLOGINEN HAKUTEO Muunnostaulukoita, geometrisia toleransseja, kovuusvertailutaulukoita, kolmioiden ratkaisuja, pinnankarheuden mittausta ja materiaalien ominaisuuksia UOMI PAINO isältö 01 Mikä on
METROLOGINEN HAKUTEO Muunnostaulukoita, geometrisia toleransseja, kovuusvertailutaulukoita, kolmioiden ratkaisuja, pinnankarheuden mittausta ja materiaalien ominaisuuksia UOMI PAINO isältö 01 Mikä on
Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE
 Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE Aalto yliopisto LVI-tekniikka 2013 SISÄLLYSLUETTELO TILAVUUSVIRRAN MITTAUS...2 1 HARJOITUSTYÖN TAVOITTEET...2 2 MITTAUSJÄRJESTELY
Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE Aalto yliopisto LVI-tekniikka 2013 SISÄLLYSLUETTELO TILAVUUSVIRRAN MITTAUS...2 1 HARJOITUSTYÖN TAVOITTEET...2 2 MITTAUSJÄRJESTELY
Tasogeometria. Tasogeometrian käsitteitä ja osia. olevia pisteitä. Piste P on suoran ulkopuolella.
 Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
Sisällysluettelo ESIPUHE 1. PAINOKSEEN... 3 ESIPUHE 2. PAINOKSEEN... 3 SISÄLLYSLUETTELO... 4
 Sisällysluettelo ESIPUHE 1. PAINOKSEEN... 3 ESIPUHE 2. PAINOKSEEN... 3 SISÄLLYSLUETTELO... 4 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 6 1.1 KESKEISTEN KÄSITTEIDEN KERTAUSTA... 7 1.2 AIHEESEEN PEREHTYMINEN...
Sisällysluettelo ESIPUHE 1. PAINOKSEEN... 3 ESIPUHE 2. PAINOKSEEN... 3 SISÄLLYSLUETTELO... 4 1. METODOLOGIAN PERUSTEIDEN KERTAUSTA... 6 1.1 KESKEISTEN KÄSITTEIDEN KERTAUSTA... 7 1.2 AIHEESEEN PEREHTYMINEN...
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto)
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 2: Usean muuttujan funktiot Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto)
VeRan laboratoriotietojen siirtoformaatti
 FCG Finnish Consulting Group Oy VERA TOIMINTAOHJEET Rev./pvm 1.03 Hyväksytty 30.4.2010 Sisältö Käyttö Vastuuhenkilö VeRan tiedonsiirtoformaatti Laboratoriot, jotka toimittavat tulokset suoraan VeRaan.
FCG Finnish Consulting Group Oy VERA TOIMINTAOHJEET Rev./pvm 1.03 Hyväksytty 30.4.2010 Sisältö Käyttö Vastuuhenkilö VeRan tiedonsiirtoformaatti Laboratoriot, jotka toimittavat tulokset suoraan VeRaan.
MAA7 7.3 Koe Jussi Tyni Valitse kuusi tehtävää! Tee vastauspaperiin pisteytysruudukko! Kaikkiin tehtäviin välivaiheet näkyviin!
 MAA7 7. Koe Jussi Tyni 1..01 1. Laske raja-arvot: a) 5 x lim x5 x 10 b) x 8x16 lim x x 9 x. a) Määritä erotusosamäärän avulla funktion f (5). b) Onko funktio f x vastauksesi lyhyesti 1 9 x ( ) x f ( x)
MAA7 7. Koe Jussi Tyni 1..01 1. Laske raja-arvot: a) 5 x lim x5 x 10 b) x 8x16 lim x x 9 x. a) Määritä erotusosamäärän avulla funktion f (5). b) Onko funktio f x vastauksesi lyhyesti 1 9 x ( ) x f ( x)
LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TARKISTA TEHTÄVÄT KOKEEN JÄLKEEN JA ANNA PISTEESI RUUTUUN!
 Matematiikan TESTI 4, Maa7 Trigonometriset funktiot ATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TAKISTA TEHTÄVÄT
Matematiikan TESTI 4, Maa7 Trigonometriset funktiot ATKAISUT Sievin lukio II jakso/017 VASTAA JOKAISEEN TEHTÄVÄÄN! MAOL/LIITE/taulukot.com JA LASKIN ON SALLITTU ELLEI TOISIN MAINITTU! TAKISTA TEHTÄVÄT
jakokulmassa x 4 x 8 x 3x
 Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
Laudatur MAA ratkaisut kertausarjoituksiin. Polynomifunktion nollakodat 6 + 7. Suoritetaan jakolasku jakokulmassa 5 4 + + 4 8 6 6 5 4 + 0 + 0 + 0 + 0+ 6 5 ± 5 5 4 ± 4 4 ± 4 4 ± 4 8 8 ± 8 6 6 + ± 6 Vastaus:
l off, mm kuormauksen aikana
 4. Kuormien sijoittaminen vaunuihin 4.1. Vaunuun kuormattujen tavaroiden ja kiinnitysvälineiden yhteenlaskettu paino ei saa ylittää vaunuun merkittyä kantavuutta, ja kun kuorma tukeutuu kahteen vaunuun,
4. Kuormien sijoittaminen vaunuihin 4.1. Vaunuun kuormattujen tavaroiden ja kiinnitysvälineiden yhteenlaskettu paino ei saa ylittää vaunuun merkittyä kantavuutta, ja kun kuorma tukeutuu kahteen vaunuun,
Standardin SFS-EN ISO/IEC 17025:2017 asettamat vaatimukset (mikrobiologisten) menetelmien mittausepävarmuuden arvioinnille ja ilmoittamiselle
 Standardin SFS-EN ISO/IEC 17025:2017 asettamat vaatimukset (mikrobiologisten) menetelmien mittausepävarmuuden arvioinnille ja ilmoittamiselle Annika Wickström, FINAS Esityksen aiheet Mittausepävarmuuden
Standardin SFS-EN ISO/IEC 17025:2017 asettamat vaatimukset (mikrobiologisten) menetelmien mittausepävarmuuden arvioinnille ja ilmoittamiselle Annika Wickström, FINAS Esityksen aiheet Mittausepävarmuuden
Mittaustuloksen esittäminen Virhetarkastelua. Mittalaitetekniikka NYMTES 13 Jussi Hurri syksy 2014
 Mittaustuloksen esittäminen Virhetarkastelua Mittalaitetekniikka NYMTES 13 Jussi Hurri syksy 2014 SI järjestelmä Kansainvälinen mittayksikköjärjestelmä Perussuureet ja perusyksiköt Suure Tunnus Yksikkö
Mittaustuloksen esittäminen Virhetarkastelua Mittalaitetekniikka NYMTES 13 Jussi Hurri syksy 2014 SI järjestelmä Kansainvälinen mittayksikköjärjestelmä Perussuureet ja perusyksiköt Suure Tunnus Yksikkö
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
TRIGONOMETRISTEN FUNKTIOIDEN KUVAAJAT
 3.0.07 0 π TRIGONOMETRISTEN FUNKTIOIDEN KUVAAJAT π = π 3π π = π 5π 6π = 3π 7π TRIGONOMETRISET FUNKTIOT, MAA7 Tarkastellaan aluksi sini-funktiota ja lasketaan sin :n arvoja, kun saa arvoja 0:sta 0π :ään
3.0.07 0 π TRIGONOMETRISTEN FUNKTIOIDEN KUVAAJAT π = π 3π π = π 5π 6π = 3π 7π TRIGONOMETRISET FUNKTIOT, MAA7 Tarkastellaan aluksi sini-funktiota ja lasketaan sin :n arvoja, kun saa arvoja 0:sta 0π :ään
MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET. Jukka-Pekka Rapinoja METSTA
 MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET Jukka-Pekka Rapinoja METSTA Mitä mallipohjainen tuotemäärittely tarkoittaa EN-kielinen termi MBD, Model-based Definition Kaikki tuotetieto on 3D-mallissa
MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET Jukka-Pekka Rapinoja METSTA Mitä mallipohjainen tuotemäärittely tarkoittaa EN-kielinen termi MBD, Model-based Definition Kaikki tuotetieto on 3D-mallissa
Tekstiilien tutkiminen ja testaus
 Tekstiilien tutkiminen ja testaus Yleistä johdatusta tekstiilien tutkimusmenetelmiin elokuu 2006 Riikka Räisänen Helsingin yliopisto Miksi tekstiilejä tutkitaan? Tutkimus (teoreettinen metrologia) Määritykset,
Tekstiilien tutkiminen ja testaus Yleistä johdatusta tekstiilien tutkimusmenetelmiin elokuu 2006 Riikka Räisänen Helsingin yliopisto Miksi tekstiilejä tutkitaan? Tutkimus (teoreettinen metrologia) Määritykset,
LUETTELO ELINKEINOYHTYMÄN JA LIIKKEEN- TAI AMMATINHARJOITTAJAN OMISTAMISTA ARVOPAPEREISTA JA ARVO-OSUUKSISTA (8B)
 LUETTELO ELINKEINOYHTYMÄN JA LIIKKEEN- TAI AMMATINHARJOITTAJAN OMISTAMISTA ARVOPAPEREISTA JA ARVO-OSUUKSISTA (8B) TIETUEKUVAUS 2017 SISÄLTÖ 1 YLEISKUVAUS... 2 2 TIETOVIRRAN ANTAMISTA TARKENTAVAA KUVAUSTA...
LUETTELO ELINKEINOYHTYMÄN JA LIIKKEEN- TAI AMMATINHARJOITTAJAN OMISTAMISTA ARVOPAPEREISTA JA ARVO-OSUUKSISTA (8B) TIETUEKUVAUS 2017 SISÄLTÖ 1 YLEISKUVAUS... 2 2 TIETOVIRRAN ANTAMISTA TARKENTAVAA KUVAUSTA...
4.1 Kaksi pistettä määrää suoran
 4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
4.1 Kaksi pistettä määrää suoran Kerrataan aluksi kurssin MAA1 tietoja. Geometrisesti on selvää, että tason suora on täysin määrätty, kun tunnetaan sen kaksi pistettä. Joskus voi tulla vastaan tilanne,
Kuva 1. Kiillotuksen periaate. 1=alkuperäinen profiili, 2= virtaus, 3=ideaalinen profiili, 4=rekristallisoitunut kohta [Bladergroen 1974]
![Kuva 1. Kiillotuksen periaate. 1=alkuperäinen profiili, 2= virtaus, 3=ideaalinen profiili, 4=rekristallisoitunut kohta [Bladergroen 1974] Kuva 1. Kiillotuksen periaate. 1=alkuperäinen profiili, 2= virtaus, 3=ideaalinen profiili, 4=rekristallisoitunut kohta [Bladergroen 1974]](/thumbs/24/3392447.jpg) Muotin kiillotus Heikki Tikka Tampereen teknillinen yliopisto Periaate Varsin usein kiillotus sekoitetaan hiontaan, jolla pyritään ainetta poistamalla parantamaan työkappaleen mittatarkkuutta ja pinnanlaatua.
Muotin kiillotus Heikki Tikka Tampereen teknillinen yliopisto Periaate Varsin usein kiillotus sekoitetaan hiontaan, jolla pyritään ainetta poistamalla parantamaan työkappaleen mittatarkkuutta ja pinnanlaatua.
( ) B-B 142 `0,3 28-0,2. 36 Ra1.6. 2x45. 1x45. 2x45. Keskiöporaus sallitaan. 0,5x0,5. Ra3.2. Ra1.6. Koneistusnäyttö Aihio: D50x145 S355
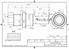 142 `0,3 50 80 M 40 x2 A 20 Ø35 5 n50-0,1 40-0,3 Ø 26-0,05 +0 Ø B + 0,3 55-0 36 Ra1.6 6 2x45 B +0 28-0,2 1x45 0,5x0,5 2x45 b 0,1 A Keskiöporaus sallitaan B-B Ra3.2 Ra1.6 ( ) 3 Designed by Checked by Approved
142 `0,3 50 80 M 40 x2 A 20 Ø35 5 n50-0,1 40-0,3 Ø 26-0,05 +0 Ø B + 0,3 55-0 36 Ra1.6 6 2x45 B +0 28-0,2 1x45 0,5x0,5 2x45 b 0,1 A Keskiöporaus sallitaan B-B Ra3.2 Ra1.6 ( ) 3 Designed by Checked by Approved
Juuri 10 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty
 Juuri 0 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 9..08 Kertaus K. a) Alapaineiden pienin arvo on ja suurin arvo 74, joten vaihteluväli on [, 74]. b) Alapaineiden keskiarvo on 6676870774
Juuri 0 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 9..08 Kertaus K. a) Alapaineiden pienin arvo on ja suurin arvo 74, joten vaihteluväli on [, 74]. b) Alapaineiden keskiarvo on 6676870774
Lisätehtäviä. Rationaalifunktio. x 2. a b ab. 6u x x x. kx x
 MAA6 Lisätehtäviä Laske lisätehtäviä omaan tahtiisi kurssin aikan Palauta laskemasi tehtävät viimeistään kurssikokeeseen. Tehtävät lasketaan ilman laskint Rationaalifunktio Tehtäviä Hyvitys kurssiarvosanassa
MAA6 Lisätehtäviä Laske lisätehtäviä omaan tahtiisi kurssin aikan Palauta laskemasi tehtävät viimeistään kurssikokeeseen. Tehtävät lasketaan ilman laskint Rationaalifunktio Tehtäviä Hyvitys kurssiarvosanassa
y=-3x+2 y=2x-3 y=3x+2 x = = 6
 MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
MAA Koe, Arto Hekkanen ja Jussi Tyni 5.5.015 Loppukoe LASKE ILMAN LASKINTA. 1. Yhdistä kuvaaja ja sen yhtälö a) 3 b) 1 c) 5 d) Suoran yhtälö 1) y=3x ) 3x+y =0 3) x y 3=0 ) y= 3x 3 5) y= 3x 6) 3x y+=0 y=-3x+
SUOMEN RAKENTAMISMÄÄRÄYSKOKOELMA
 SUOMEN RAKENTAMISMÄÄRÄYSKOKOELMA Ilmansuodattimet Tyyppihyväksyntäohjeet 2008 Ympäristöministeriön asetus ilmansuodattimien tyyppihyväksynnästä Annettu Helsingissä 10 päivänä marraskuuta 2008 Ympäristöministeriön
SUOMEN RAKENTAMISMÄÄRÄYSKOKOELMA Ilmansuodattimet Tyyppihyväksyntäohjeet 2008 Ympäristöministeriön asetus ilmansuodattimien tyyppihyväksynnästä Annettu Helsingissä 10 päivänä marraskuuta 2008 Ympäristöministeriön
2. a- ja b-kohdat selviä, kunhan kutakuinkin tarkka, niin a-kohta 1 p b-kohta 1 p
 LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
LYHYT MATEMATIIKKA PRELIMINÄÄRIKOE 2.2.2018 RATKAISUT 1. a) 3,50 b) 56 c) 43300 km d) 15 e) 21.08 f) 23.9. kukin oikea vastaus a-kohdassa pelkkä 3,50 ilman yksikköä kelpuutetaan, samoin c-kohdassa pelkkä
π( f (x)) 2 dx π(x 2 + 1) 2 dx π(x 4 + 2x 2 + 1)dx ) = 1016π 15
 BMA58 Integraalilaskenta ja sovellukset Harjoitus, Kevät 7 Vaikka useissa tehtävissä pyydetään vain lauseketta, ratkaisua tehdessäsi hahmottele aina kuva ja merkitse näkyviin myös lausekkeen osien geometriset
BMA58 Integraalilaskenta ja sovellukset Harjoitus, Kevät 7 Vaikka useissa tehtävissä pyydetään vain lauseketta, ratkaisua tehdessäsi hahmottele aina kuva ja merkitse näkyviin myös lausekkeen osien geometriset
7. Normaalijakauma ja standardipisteet
 33 7. Normaalijakauma ja standardipisteet Aiemmin olemme esittäneet joitakin variaabelin jakaumia histogrammien ja frekvenssipolygonien muodossa. Jos kuvittelemme, että mittaamme varsin tarkasti ja jatkuvaksi
33 7. Normaalijakauma ja standardipisteet Aiemmin olemme esittäneet joitakin variaabelin jakaumia histogrammien ja frekvenssipolygonien muodossa. Jos kuvittelemme, että mittaamme varsin tarkasti ja jatkuvaksi
Ikkunan ja oven tärkeimmät teknilliset ominaisuudet
 Ikkunan ja oven tärkeimmät teknilliset ominaisuudet 12.2.2015 Jorma S. Tiiri Tuotekehityspäällikkö Domus Yhtiöt Oy LOIMAA CE-merkintä Rakennustuoteasetuksen N:o 305/2011 ja tuotestandardin SFS-EN 14351-1
Ikkunan ja oven tärkeimmät teknilliset ominaisuudet 12.2.2015 Jorma S. Tiiri Tuotekehityspäällikkö Domus Yhtiöt Oy LOIMAA CE-merkintä Rakennustuoteasetuksen N:o 305/2011 ja tuotestandardin SFS-EN 14351-1
1 Rationaalifunktio , a) Sijoitetaan nopeus 50 km/h vaihtoaikaa kuvaavan funktion lausekkeeseen.
 Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.06 Rationaalifunktio. a) Sijoitetaan nopeus 50 km/h vaihtoaikaa kuvaavan funktion lausekkeeseen. f (50) 50 8 50 4 8 50 500 400 4 400
Juuri 6 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.7.06 Rationaalifunktio. a) Sijoitetaan nopeus 50 km/h vaihtoaikaa kuvaavan funktion lausekkeeseen. f (50) 50 8 50 4 8 50 500 400 4 400
Ensimmäiseen 2017 vuonna julkaistuun painokseen että 2018 julkaistuun toiseen painokseen tehdyt korjaukset
 Asfalttinormit 2017 korjaukset 1 (9) Ensimmäiseen 2017 vuonna julkaistuun painokseen että 2018 julkaistuun toiseen painokseen tehdyt korjaukset Korjaukset 4.3.2019 Sivu 18 kaavan alapuolella oleva teksti
Asfalttinormit 2017 korjaukset 1 (9) Ensimmäiseen 2017 vuonna julkaistuun painokseen että 2018 julkaistuun toiseen painokseen tehdyt korjaukset Korjaukset 4.3.2019 Sivu 18 kaavan alapuolella oleva teksti
Negatiiviset luvut ja laskutoimitukset
 7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
M 1 ~M 2, jos monikulmioiden vastinkulmat ovat yhtä suuret ja vastinsivujen pituuksien suhteet ovat yhtä suuret eli vastinsivut ovat verrannolliset
 Yhdenmuotoisuus ja mittakaava Tasokuvioiden yhdenmuotoisuus tarkoittaa havainnollisesti sitä, että kuviot ovat samanmuotoiset mutta eivät välttämättä samankokoiset. Kahdella yhdenmuotoisella kuviolla täytyy
Yhdenmuotoisuus ja mittakaava Tasokuvioiden yhdenmuotoisuus tarkoittaa havainnollisesti sitä, että kuviot ovat samanmuotoiset mutta eivät välttämättä samankokoiset. Kahdella yhdenmuotoisella kuviolla täytyy
Asfalttinormit 2017 julkaistiin marraskuussa Ensimmäisen painoksen paperiversio myytiin loppuun ja kesäkuussa 2018 julkaistiin toinen painos
 Asfalttinormit 2017 julkaistiin marraskuussa 2017. Ensimmäisen painoksen paperiversio myytiin loppuun ja kesäkuussa 2018 julkaistiin toinen painos sekä sähköisenä että paperiversiona. Seuraavilla sivuilla
Asfalttinormit 2017 julkaistiin marraskuussa 2017. Ensimmäisen painoksen paperiversio myytiin loppuun ja kesäkuussa 2018 julkaistiin toinen painos sekä sähköisenä että paperiversiona. Seuraavilla sivuilla
Insinöörien kuvakieli. Teknillinen piirustus
 Insinöörien kuvakieli Teknillinen piirustus 1 Tavoite Opiskelija ymmärtää standardin mukaisia koneenpiirustuksia ja osaa tuottaa luonnoksia, työpiirustuksia, kokoonpanokuvia ja osaluetteloita. Hän ymmärtää
Insinöörien kuvakieli Teknillinen piirustus 1 Tavoite Opiskelija ymmärtää standardin mukaisia koneenpiirustuksia ja osaa tuottaa luonnoksia, työpiirustuksia, kokoonpanokuvia ja osaluetteloita. Hän ymmärtää
Lattilämmityksen jakotukki FHF
 Lattilämmityksen jakotukki FHF Käyttö FHF-jakotukkeja käytetään vesikiertoisissa lattialämmityksissä. Rakennusten lattialämmityspiirit kytketään kukin jakotukkeihin, joissa piirien vesimäärät säädetään
Lattilämmityksen jakotukki FHF Käyttö FHF-jakotukkeja käytetään vesikiertoisissa lattialämmityksissä. Rakennusten lattialämmityspiirit kytketään kukin jakotukkeihin, joissa piirien vesimäärät säädetään
Mittaustulosten tilastollinen käsittely
 Mittaustulosten tilastollinen käsittely n kertaa toistetun mittauksen tulos lasketaan aritmeettisena keskiarvona n 1 x = x i n i= 1 Mittaustuloksen hajonnasta aiheutuvaa epävarmuutta kuvaa keskiarvon keskivirhe
Mittaustulosten tilastollinen käsittely n kertaa toistetun mittauksen tulos lasketaan aritmeettisena keskiarvona n 1 x = x i n i= 1 Mittaustuloksen hajonnasta aiheutuvaa epävarmuutta kuvaa keskiarvon keskivirhe
Johanna Tikkanen, TkT, Suomen Betoniyhdistys ry
 Johanna Tikkanen, TkT, Suomen Betoniyhdistys ry Eurooppalainen standardi SFS-EN 206 mahdollistaa vaihtoehtoisen menettelyn käytön jatkuvan tuotannon vaatimustenmukaisuuden osoittamiselle eli niin sanotun
Johanna Tikkanen, TkT, Suomen Betoniyhdistys ry Eurooppalainen standardi SFS-EN 206 mahdollistaa vaihtoehtoisen menettelyn käytön jatkuvan tuotannon vaatimustenmukaisuuden osoittamiselle eli niin sanotun
Differentiaalilaskennan tehtäviä
 Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
MAA4 - HARJOITUKSIA. 1. Esitä lauseke 3 x + 2x 4 ilman itseisarvomerkkejä. 3. Ratkaise yhtälö 2 x 7 3 + 4x = 2 (yksi ratkaisu, eräs neg. kokon.
 MAA4 - HARJOITUKSIA 1. Esitä lauseke 3 + 4 ilman itseisarvomerkkejä.. Ratkaise yhtälö a ) 5 9 = 6 b) 6 9 = 0 c) 7 9 + 6 = 0 3. Ratkaise yhtälö 7 3 + 4 = (yksi ratkaisu, eräs neg. kokon. luku) 4. Ratkaise
MAA4 - HARJOITUKSIA 1. Esitä lauseke 3 + 4 ilman itseisarvomerkkejä.. Ratkaise yhtälö a ) 5 9 = 6 b) 6 9 = 0 c) 7 9 + 6 = 0 3. Ratkaise yhtälö 7 3 + 4 = (yksi ratkaisu, eräs neg. kokon. luku) 4. Ratkaise
Johdantoa. Jokaisen matemaatikon olisi syytä osata edes alkeet jostakin perusohjelmistosta, Java MAPLE. Pascal MathCad
 Johdantoa ALGORITMIT MATEMA- TIIKASSA, MAA Vanhan vitsin mukaan matemaatikko tietää, kuinka matemaattinen ongelma ratkaistaan, mutta ei osaa tehdä niin. Vitsi on ajalta, jolloin käytännön laskut eli ongelman
Johdantoa ALGORITMIT MATEMA- TIIKASSA, MAA Vanhan vitsin mukaan matemaatikko tietää, kuinka matemaattinen ongelma ratkaistaan, mutta ei osaa tehdä niin. Vitsi on ajalta, jolloin käytännön laskut eli ongelman
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 15.2.2010 T-106.1208 Ohjelmoinnin perusteet Y 15.2.2010 1 / 46 Merkkijonot Merkkijonojen avulla ohjelmassa voi esittää tekstitietoa, esim. nimiä, osoitteita ja
Ohjelmoinnin perusteet Y Python T-106.1208 15.2.2010 T-106.1208 Ohjelmoinnin perusteet Y 15.2.2010 1 / 46 Merkkijonot Merkkijonojen avulla ohjelmassa voi esittää tekstitietoa, esim. nimiä, osoitteita ja
f(n) = Ω(g(n)) jos ja vain jos g(n) = O(f(n))
 Määritelmä: on O(g(n)), jos on olemassa vakioarvot n 0 > 0 ja c > 0 siten, että c g(n) kun n > n 0 O eli iso-o tai ordo ilmaisee asymptoottisen ylärajan resurssivaatimusten kasvun suuruusluokalle Samankaltaisia
Määritelmä: on O(g(n)), jos on olemassa vakioarvot n 0 > 0 ja c > 0 siten, että c g(n) kun n > n 0 O eli iso-o tai ordo ilmaisee asymptoottisen ylärajan resurssivaatimusten kasvun suuruusluokalle Samankaltaisia
Derivaatan sovellukset (ääriarvotehtävät ym.)
 Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Derivaatan sovellukset (ääriarvotehtävät ym.) Tehtävät: 1. Tutki derivaatan avulla funktion f kulkua. a) f(x) = x 4x b) f(x) = x + 6x + 11 c) f(x) = x4 4 x3 + 4 d) f(x) = x 3 6x + 1x + 3. Määritä rationaalifunktion
Sinin jatkuvuus. Lemma. Seuraus. Seuraus. Kaikilla x, y R, sin x sin y x y. Sini on jatkuva funktio.
 Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
Sinin jatkuvuus Lemma Kaikilla x, y R, sin x sin y x y. Seuraus Sini on jatkuva funktio. Seuraus Kosini, tangentti ja kotangentti ovat jatkuvia funktioita. Pekka Salmi FUNK 19. syyskuuta 2016 22 / 53 Yhdistetyn
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 6.3.08 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 6.3.08 HYVÄN VASTAUKSEN PIIRTEITÄ Alla oleva vastausten piirteiden, sisältöjen ja pisteitysten luonnehdinta ei sido ylioppilastutkintolautakunnan arvostelua. Lopullisessa
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 1.4.2009 T-106.1208 Ohjelmoinnin perusteet Y 1.4.2009 1 / 56 Tentti Ensimmäinen tenttimahdollisuus on pe 8.5. klo 13:00 17:00 päärakennuksessa. Tämän jälkeen
Ohjelmoinnin perusteet Y Python T-106.1208 1.4.2009 T-106.1208 Ohjelmoinnin perusteet Y 1.4.2009 1 / 56 Tentti Ensimmäinen tenttimahdollisuus on pe 8.5. klo 13:00 17:00 päärakennuksessa. Tämän jälkeen
3.1.2013 LUT CS20A0650 Meluntorjunta [email protected] 1. Tsunamin synty. 3.1.2013 LUT CS20A0650 Meluntorjunta juhani.kuronen@lut.
 Akustiikan perussuureita, desibelit. 3.1.2013 LUT CS20A0650 Meluntorjunta [email protected] 1 Tsunamin synty 3.1.2013 LUT CS20A0650 Meluntorjunta [email protected] 2 1 Tasoaallon synty 3.1.2013
Akustiikan perussuureita, desibelit. 3.1.2013 LUT CS20A0650 Meluntorjunta [email protected] 1 Tsunamin synty 3.1.2013 LUT CS20A0650 Meluntorjunta [email protected] 2 1 Tasoaallon synty 3.1.2013
Uudet tuotteet
 Uudet tuotteet 2017.1 SISÄLTÖ KOVAMETALLIPORAT 4 5 5 Force X Uusi valikoima monipuolisia poria R6011 Kovametalli NC-keskiöporat R7131 Kovametalli porrasporat kierteille SUURTEHO KOVAMETALLIPORAT VAIHDETTAVALLA
Uudet tuotteet 2017.1 SISÄLTÖ KOVAMETALLIPORAT 4 5 5 Force X Uusi valikoima monipuolisia poria R6011 Kovametalli NC-keskiöporat R7131 Kovametalli porrasporat kierteille SUURTEHO KOVAMETALLIPORAT VAIHDETTAVALLA
Avoimet hammashihnat
 Yleistä avoimista haashihnoista Avoimia haashihnoja (metritavarana) löytyy laaja valikoima eri haasjaoilla ja eri materiaaleista valmistettuina. Jokaiseen eri käyttökohteeseen ja olosuhteeseen löytyy sopiva
Yleistä avoimista haashihnoista Avoimia haashihnoja (metritavarana) löytyy laaja valikoima eri haasjaoilla ja eri materiaaleista valmistettuina. Jokaiseen eri käyttökohteeseen ja olosuhteeseen löytyy sopiva
massa vesi sokeri muu aine tuore luumu b 0,73 b 0,08 b = 0,28 a y kuivattu luumu a x 0,28 a y 0,08 = 0,28 0,08 = 3,5
 A1. Tehdään taulukko luumun massoista ja pitoisuuksista ennen ja jälkeen kuivatuksen. Muistetaan, että kuivatuksessa haihtuu vain vettä. Näin ollen sokerin ja muun aineen massa on sama molemmilla riveillä.
A1. Tehdään taulukko luumun massoista ja pitoisuuksista ennen ja jälkeen kuivatuksen. Muistetaan, että kuivatuksessa haihtuu vain vettä. Näin ollen sokerin ja muun aineen massa on sama molemmilla riveillä.
Lataa Hyvää Suomesta -merkki osoitteesta: www.hyvaasuomesta.fi/kuvapankki/hyvää-suomesta-logot
 GRAAFINEN OHJEISTO Hyvää Suomesta -merkin käyttöoikeus on Ruokatieto Yhdistys ry:n jäsenillä sekä niillä MTK:n ja SLC:n jäsenillä, joille Ruokatieto on myöntänyt merkin käyttöoikeuden. Tutustu huolella
GRAAFINEN OHJEISTO Hyvää Suomesta -merkin käyttöoikeus on Ruokatieto Yhdistys ry:n jäsenillä sekä niillä MTK:n ja SLC:n jäsenillä, joille Ruokatieto on myöntänyt merkin käyttöoikeuden. Tutustu huolella
Kojemeteorologia (53695) Laskuharjoitus 1
 Kojemeteorologia (53695) Laskuharjoitus 1 Risto Taipale 20.9.2013 1 Tehtävä 1 Erään lämpömittarin vertailu kalibrointistandardiin antoi keskimääräiseksi eroksi standardista 0,98 C ja eron keskihajonnaksi
Kojemeteorologia (53695) Laskuharjoitus 1 Risto Taipale 20.9.2013 1 Tehtävä 1 Erään lämpömittarin vertailu kalibrointistandardiin antoi keskimääräiseksi eroksi standardista 0,98 C ja eron keskihajonnaksi
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
