MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
|
|
|
- Mikko Ahonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
2 Jaollisuus Luku b on jaollinen luvulla a eli b on a:n monikerta eli a jakaa luvun b jos on olemassa kokonaisluku k siten, että b = ak, eli b az. Tämä merkitään usein a b. Modulofunktio mod Jos n > 0 niin mod (m, n) = j jos 0 j < n ja m = j + kn missä k Z. (mutta mod (m, 0) = m ja mod (m, n) = mod (m, n) jos n < 0). Jos m ja n ovat positiivisia lukuja niin mod (m, n) on jakojäännös joka saadaan kun m jaetaan n:llä mutta jos m < 0 niin tämä jakojäännos ei ole positiivinen. Kongruenssi modulo Luku a on kongruentti luvun b kanssa modulo n jos a b on jaollinen n:llä ja tämä merkitään a n b tai a b (mod n): a n b a b (mod n) n (a b) a = b + kn, k Z mod (a, n) = mod (b, n) G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
3 Z/nZ, kongruenssi- eli jäännösluokat Relaatio n on ekvivalenssirelaatio joukossa Z (x n x, x n y y n x, x n y AND y n z x n z) ja jakaa Z ekvivalenssiluokkiin joita kutsutaan kongruenssi- tai jäännösluokiksi, ja nämä ovat joukot {..., 2n, n, 0, n, 2n...}, {..., 2n + 1, n + 1, 1, n + 1, 2n },..., {..., n 1, 1, n 1, 2n 1,...} joissa kaikki alkiot ovat kongruentteja toistensa kanssa modulo n. Seuraavia merkintöjä käytetään: [k] n def = { m Z : m n k } = { m Z : mod (m, n) = mod (k, n) }, Z/nZ def = { [k] n : k = 0, 1, 2,..., n 1 }, jos n > 0. Huom! Koska mod (m 1, n) = mod (m 2, n) [m 1 ] n = [m 2 ] n niin usein valitaan alkio mod (m, n) edustamaan jäännösluokkaa [m] n niin että voidaan esim. puhua luvuista 0, 1, 2,..., 5 joukon Z/6Z alkioina joukkojen [0] 6, [1] 6,..., [5] 6 sijasta. Joskus kirjoitetaan [k] n :n sijasta k n ja Z/nZ:n sijasta Z n. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
4 Yhteen-, vähennys- ja kertolasku Z/nZ:ssa Voidaan osoittaa, että jos niin a 1 n a 2 ja b 1 n b 2 (a 1 + b 1 ) n (a 2 + b 2 ) (a 1 b 1 ) n (a 2 b 2 ) (a 1 b 1 ) n (a 2 b 2 ) Näin ollen voidaan määritellä laskuoperaatioita joukossa Z/nZ seuraavasti: [a] n + [b] n = [a + b] n, [a] n [b] n = [a b] n, [a] n [b] n = [a b] n, ja kaikki normaalit laskusäännöt (paitsi epäyhtälöihin liittyvät) pätevät edelleen. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
5 Suurin yhteinen tekijä Jos m ja n ovat kokonaislukuja jotka eivät molemmat ole 0 niin niiden suurin yhteinen tekijä on syt (m, n) = max{ d Z : d m ja d n }. (syt=suurin yhteinen tekijä, gcd= greatest common divisor, ja tavallisesti märitellään syt (0, 0) = 0) Jos syt (m, n) = 1 niin luvut m ja n ovat keskenään jaottomia. Huomaa, että määritelmästä seuraa, että syt (m, n) = syt (n, m) = syt ( m, n ). G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
6 Käänteisalkiot Z/nZ:ssa Jos [m] n Z/nZ ja on olemassa jäännösluokka [j] n Z/nZ siten, että [m] n [j] n = [1] n, eli m j n 1 niin sanotaan, että [m] n :llä on käänteisalkio tai että [m] n on kääntyvä Z/nZ:ssa ja käänteisalkio on [j] n = [m] 1 n. Tässä tapauksessa voidaan jakaa [m] n :llä koska se on yhtäpitävää sen kanssa, että kerrotaan [j] n :llä. Koska m j n 1 niin on olemassa kokonaisluku k siten, että m j = 1 + k n. Jos nyt d m ja d n niin pätee d (m j k n) eli d 1 joten d = 1. Näin ollen syt (m, n) = 1. Voidaan osoittaa, että myös käänteinen tulos pätee joten Huom [m] n :llä on käänteisalkio Z/nZ:ssa syt (m, n) = 1. Jos p on alkuluku niin kaikilla Z/pZ:n alkioilla paitsi [0] p :llä on käänteisalkio. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
7 Eukleideen algoritmi ja syt (m, n) Oleta, että m n > 0. Valitse r 0 = m ja r 1 = n. Laske q j ja r j siten, että 0 r j < r j 1 ja kun j 2 ja r j 1 > 0. syt (m, n) = r k 1 jos r k = 0. Miksi Eukleideen algoritmi toimii? r j 2 = q j r j 1 + r j Koska r j 2 = q j r j 1 + r j niin syt (r j 2, r j 1 ) = syt (r j 1, r j ) kun oletetaan, että r j 1 > 0. Koska d 0 kaikilla d niin syt (r k 1, 0) = r k 1 joten syt (m, n) = syt (r 0, r 1 ) =... = syt (r k 1, r k ) = syt (r k 1, 0) = r k 1 jos r k = 0. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
8 Eukleideen algoritmi ja Z/nZ:n käänteisalkiot Jos Eukleideen algoritmissa on valittu r 0 = m, r 1 = n ja sitten laskettu q j ja r j kun j = 2,..., k kaavalla r j 2 = q j r j 1 + r j kunnes r k = 0, jolloin r k 1 = syt (m, n) niin voidaan laskea takaperin lähtien yhtälöstä r k 3 = q k 1 r k 2 + r k 1 joka voidaan kirjoittaa muotoon syt (m, n) = r k 1 = r k 3 q k 1 r k 2 = a j r j + b j r j+1, missä j = k 3. Tähän sijoitetaan r j+1 = r j 1 q j+1 r j yhtälöstä r j 1 = q j+1 r j + r j+1 jolloin nähdään, että syt (m, n) = a j r j + b j r j+1 kaikilla j = k 2, k 1,..., 0, eli lopuksi missä a = a 0 ja b 0. Jos nyt syt (m, n) = 1 niin syt (m, n) = am + bn. [a] n [m] n = [1] n eli [a] n = [m] n 1, [b] m [n] m = [1] m eli [b] m = [n] 1 m. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
9 Eulerin ϕ-funktio ϕ(n) = alkioiden lukumäärä joukossa { m Z : 0 m n 1, syt (m, n) = 1 }, = niiden joukon Z/nZ alkioiden lukumäärä, joilla on käänteisalkio. Huomaa että [0] 1 :llä on käänteisalkio joukossa Z/1Z joten ϕ(1) = 1 mutta [0] n :llä ei tietenkään (?) ole käänteisalkiota joukossa Z/nZ kun n > 1. Matlab/octave:ssä tämän funktion laskemiseksi voidaan käyttää Eulerin lause Jos syt (a, n) = 1 ja n > 1 niin a ϕ(n) n 1 eli mod (a ϕ(n), n) = 1 eli [ a ϕ(n)] n = [1] n. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
10 RSA-algoritmi RSA-algoritmissa käytetään julkista avainta (n, k) viestin saalaamiseen ja yksityistä avainta (n, d) salatun viestin purkamiseen: Salaaminen: Viesti a, joka on luku 0:n ja n 1:n väliltä salataan lähetettäväksi viestiksi b = mod (a k, n). Vastaanotettu viesti b puretaan alkuperäiseksi viestiksi a = mod (b d, n). Menetelmä perustuu siihen, että julkisen avaimen avulla on (pitää olla) ylivoimaisen vaikeata määrittää yksityistä avainta julkisesta avaimesta jolloin kuka tahansa voi lähettää viestin, joka on salattu vastaanottajan julkisella avaimella mutta ainoastaan vastaanottaja, joka tuntee oman yksityisen avaimensa pystyy purkamaan salatun viestin. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
11 Miten RSA-algoritmin avaimet on valittava? Valitaan n = pq missä p ja q ovat kaksi erittäin isoa alkulukua siten, että luvun n jakaminen alkulukutekijöiksi on ylivoimaisen vaikeata (eli esim. myös p q :n on oltava iso ). k on riittävän iso luku siten että syt (k, m) = 1 missä m = (p 1) (q 1) Eukleideen algoritmin avulla voidaan laskea d siten, että [d] m = [k] 1 m ja tähän tarvitaan tieto siitä mitä p ja q ovat. Miksi RSA-algoritmi toimii? Oleta yksinkertaisuuden vuoksi, että syt (a, n) = 1. ϕ(n) = ϕ(p q) = (p 1) (q 1) = m. Eulerin lauseen mukaan [a m ] n = [1] n. Koska [d] m = [k] 1 m niin k d = 1 + r m ja [b d] [ = a k d] = [ a 1+r m] n n n = [a] n [a m ] r n = [a] n [1] r n = [a] n, josta seuraa, että mod (b d, n) = mod (a, n) = a. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
12 RSA-algoritmi ja allekirjoitukset Jos A haluaa lähettää viestin a B:lle ja B haluaa tulla vakuuttuneeksi siitä, että viesti todella on peräisin A:lta niin he voivat toimia seuraavalla tavalla: A laskee tiivisteen eli hajautusarvon h(a) viestistä a. A salaa viestin a B:n julkisella avaimella (n B, k B ) salatuksi viestiksi b = mod (a k B, n B ). A salaa tiivisteen h(a) omalla yksityisella avaimellaan (n A, d A ) allekirjotukseksi s = mod (h(a) d A, n A ). A lähettää b:n ja s:n B:lle. B purkaa b:n yksityisellä avaimellaan (n B, d B ) ja saa tulokseksi a:n. B laskee tiivisteen h(a):n ja purkaa s:n A:n julkisella avaimella (n A, k A ) ja jos tulos on sama kuin h(a) niin hän tulee vakuuttuneeksi siitä, että viesti a todella on peräisin A:lta koska kukaan muu ei pysty salaamaan h(a):ta A:n yksityisellä avaimella (n A, d A ). Koska [k] m = [d] 1 m niin viesti joka on salattu yksityisellä avaimella voidaan purkaa julkisella avaimella. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
13 Väritysongelma Jos meillä on 6 palloa, monellako tavalla voimme värittää 2 niistä mustiksi ja muut valkoisiksi? Jos pallot ovat identtiset on vain yksi tapa, 2 väritetään mustiksi ja 4 valkoisiksi. Jos pallot on numeroitu niin on ( 6 2) = 15 tapaa valita ne, jotka väritetään mustiksi ja loput valkoisiksi. Jos pallot ovat säännöllisen 6-kulmion kulmissa ja tätä 6-kulmiota voi kääntää niin on 3 vaihtoehtoa: Mutta miten ratkaistaan monimutkaisemmat tämäntyyppiset ongelmat? Huomaa, ettei väritystä pidä ymmärtää kirjaimellisesti. Yllä olevat kuvat voivat myös esittää ksyleenin (C 8 H 10 ) isomeerejä missä kaksi vetyatomia on korvattu metyyliryhmillä. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
14 Ryhmät Ryhmä on pari [G, ] missä G on joukko ja on binäärinen operaatio G:ssä eli funktio G G G siten, että Sulkeutuneisuus: a b G jos a ja b G. (Seuraus oletuksesta, että : G G G on funktio.) Assosiatiivisuus: (a b) c = a (b c) jos a, b ja c G. Neutraalialkio: On olemassa alkio e G siten, että e a = a e = a jos a G. Käänteisalkio: Jos a G, niin on olemassa alkio a 1 G (joka osoittautuu yksikäsitteiseksi) siten, että a a 1 = a 1 a = e. Huom! Usein sanotaan G on ryhmä jos on selvää, mikä ryhmäoperaatio on tai jos sillä ei ole merkitystä. Merkinnän a b (tai (a, b)) sijasta kirjoitetaan usein ab, a 0 = e ja a m = a } a {{... a}. Neutraalialkiota merkitään myös 1:llä tai I :llä. m G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
15 Kommutatiiviset eli Abelin ryhmät Jos [G, ] on ryhmä siten, että a b = b a kaikilla a ja b G niin ryhmä on kommutatiivinen eli Abelin ryhmä. Tässä tapauksessa ryhmäoperaatiota merkitään usein +:lla, neutraalikalkiota 0:lla ja a:n käänteisalkiota a:llä. Aliryhmä Jos G (eli [G, ]) on ryhmä niin joukon G ei-tyhjä osajoukko H on G:n aliryhmä jos seuraavat ehdot pätevät ja silloin H (eli [H, H H ]) on myös ryhmä: Jos a ja b H niin a b H. Jos a H niin a 1 H. Jos H on äärellinen joukko niin jälkimmäinen ehto seuraa edellisestä koska a m H kaikilla m 1 ja H < niin on olemassa luvut m > k 1 siten, että a m = a k jolloin a m k = e ja silloin a = e = a 1 H jos m = k + 1 ja a 1 = a m+k 1 H jos m > k + 1. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
16 Homomorfismit ja isomorfismit Oletetaan, että [G 1, 1 ] ja [G 2, 2 ] ovat kaksi ryhmää ja ψ on funktio : G 1 G 2. ψ on homomorfismi jos ψ(a 1 b) = ψ(a) 2 ψ(b) kaikilla a ja b G 1. ψ on isomorfismi jos se on homomorfismi ja bijektio (jolloin myös ψ 1 on homomorfismi). Ryhmät ovat tässä epäolennaisia, oleellista on, että homomorfismi säilyttää struktuurin! Sykliset ryhmät Ryhmä G on syklinen jos on olemassa a G siten, että G = { a j : j Z }. Silloin sanotaan, että G on a:n generoima syklinen ryhmä ja merkitään G = a. Jos G on ryhmä ja a G niin a = { a j : j Z } on a:n generoima G:n syklinen aliryhmä. Koska kaikki sykliset ryhmät, joissa on m alkiota ovat isomorfiset niin tällaista ryhmää merkitään C m :llä. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
17 Sivuluokat Olkoon G ryhmä, H sen aliryhmä ja a G. Joukko ah = { ab : b H } on H:n vasen sivuluokka joka sisältää a:n. Joukko Ha = { ba : b H } on H:n oikea sivuluokka joka sisältää a:n. Sivuluokilla on seuraavia ominaisuuksia (tässä ainoastaan vasemmat sivuluokat): ah = H kaikilla a G. Jos a ja b G niin joko ah = bh tai ah bh =. a G ah = G. Jos a ja b G ja ah = bh niin pätee b 1 a H. G = H { ah : a G } ja näin ollen luku H jakaa luvun G. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
18 Homomorfismit, normaalit aliryhmät ja tekijäryhmät Olkoon G ryhmä. Jos G on ryhmä, jonka neutraalialkio on e ja ψ : G G on homomorfismi niin H = { a G : ψ(a) = e } (ψ:n ydin) on G:n aliryhmä. G:n aliryhmä H on muotoa { a G : ψ(a) = e } jollakin homomorfismilla G G jos ja vain jos ah = Ha kaikilla a G (tai yhtäpitävästi, aba 1 H kaikilla a G ja b H). Tässä tapauksessa sanotaan, että H on G:n normaali aliryhmä. Jos H on G:n normaali aliryhmä niin sivuluokat (vasen sama kuin oikea) muodostavat tekijäryhmän, jota merkitään G/H:lla ja jonka ryhmäoperaatio on (ah)(bh) = (ab)h, neutraalialkio H ja käänteisalkio (ah) 1 = a 1 H. Funktio ψ : G G/H jonka määritelmä on ψ(a) = ah on homomorfismi, jonka ydin on H. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
19 Permutaatiot Joukon A permutaatio on bijektio A A. Kaikki joukon A permutaatiot muodostavat ryhmän kun ryhmäoperaatio on funktioiden yhdistäminen. Koska kaikki m-alkioisten joukkojen kaikkien permutaatioiden muodostamat ryhmät ovat isomorfiset niin tällaista ryhmää merkitään S m :llä. Jokainen ryhmä [G, ] on isomorfinen jonkin joukon permutaatioiden aliryhmän kanssa koska joukoksi voidaan valita G ja isomorfismiksi voidaan valita ψ(a)(b) = a b mutta tästä ei seuraa että aina olisi hyödyllistä käsitellä ryhmää tällaisena permutaatioryhmänä. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
20 Permutaatiot, radat, syklimerkinnät Olkoon A äärellinen ei-tyhjä joukko. Jos α on A:n permutaatio niin α:n radat ovat pienimmät mahdolliset osajoukot A j A, j = 1, 2,... m siten, että A j A k = kun j k, m j=1 A j = A ja α(a j )= { α(a) : a A j } = A j. Sykli on A:n permutaatio α jolle pätee α(x j ) = x j+1, j = 1, 2,..., k 1 ja α(x k ) = x 1 missä x 1, x 2,..., x k A ja α(x) = x kaikilla x A \ {x 1,..., x k }. Syklimerkinnöillä kirjoitetaan α = ( x 1 x 2... x k ). Tällaisen syklin α pituus on k ja sanotaan, että α on k-sykli. Syklin α radat ovat {x 1, x 2,..., x k } ja joukot {x} kaikilla x A \ {x 1,..., x k }. Jos α on permutaatio niin jokaista sen rataa vastaa sykli ja α voidaan esittää näiden syklien tulona (eli yhdistettynä funktiona). Huom! Permutaation α radat ovat ekvivalenssiluokat kun ekvivalenssirelaatioksi määritellään x y kun α j (x) = y jollain j Z. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
21 Parilliset ja parittomat permutaatiot Jokainen sykli, jonka pituus on k 2 voidaan kirjoittaa k 1:n 2-syklin tulona koska ( x1 x 2... x k ) = ( x1 x k ) ( x1 x k 1 )... ( x1 x 3 ) ( x1 x 2 ). Jokainen sykli voidaan kirjoittaa tulona sykleistä joiden pituudet ovat 2 (tai 1). Jos permutaatio α on kirjoitettu sekä r:n että r :n 2-syklin tulona niin ( 1) r = ( 1) r ja permutaation merkki on sign (α) = ( 1) r. Jos α on sykli, jonka pituus on k niin sign (α) = ( 1) k+1. Jos α on n-alkioisen joukon permutaatio ja α:lla on m rataa niin sign (α) = ( 1) n m. Permutaation α on parillinen jos sign (α) = 1 ja muuten pariton. Jos α ja β ovat saman joukon permutaatioita niin sign (αβ) = sign (α)sign (β). G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
22 Ryhmän toiminta Jos G eli [G, ] on ryhmä ja X on joukko niin G:n toiminta joukossa X on homomorfismi G:ltä X :n permutaatioiden ryhmälle. Jos yhdistetty funktio määritellään (normaalilla) tavalla (f g)(x) = f (g(x)) niin saadaan vasen toiminta ja jos määritellään x(f g) = (xf )g niin saadaan oikea toiminta. Sen sijaan että kirjoitettaisiin ψ(a)(x) missä ψ on homomorfismi, a G ja x X kirjoitetaan useimmiten ax ja sanotaan että G toimii joukossa X. Vasemmalle toiminnalle homomorfismiominaisuudeksi tulee (ab)x = a(bx), a, b G, x X. Huom Jos G on ryhmä X :n permutaatioita niin identiteettifunktio on homomorfismi eikä toiminta-käsitettä tarvita. Jos G on ryhmä niin se toimii itsessään esim. siten, että ψ(a)(x) = ax (vasen toiminta), ψ(a)(x) = axa 1 (vasen toiminta), ψ(a)(x) = xa (oikea toiminta) tai ψ(a)(x) = a 1 xa (oikea toiminta). G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
23 Radat ja kiinnittäjäaliryhmät Oletetaan, että ryhmä G toimii joukossa X (vasemmalta). Jos x X niin sen rata G:n toiminnassa on joukko Gx = { ax : a G } X. Jos x X niin sen rata alkion a G toiminnassa on joukko a x = { a j x : j Z } X. ( a on a:n generoima syklinen ryhmä.) Jos x X niin sen kiinnittäjäaliryhmä G:n toiminnassa on joukko G x = { a G : ax = x }, joka on G:n aliryhmä. Jokaisella x X pätee Gx G x = G. Huom! Jos G toimii joukossa X niin voidaan määritellä ekvivalenssirelaatio joukossa X siten, että x y jos ja vain jos x = ay jollakin a G. Radat ovat silloin ekvivalenssiluokat ja usein voi olla hyödyllistä pitää saman ekvivalenssiluokan alkioita samoina. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
24 Sykli-indeksi Joukon X permutaation a tai joukossa X toimivan ryhmän G alkion a sykli-indeksi on monomi ζ a,x (t 1,..., t n ) = t j 1 1 t j tn jn missä j k on k-pituisten ratojen lukumäärä a:n toiminnassa. Joukon X permutaatioryhmän G tai joukossa X toimivan ryhmän G sykli-indeksi on ζ G,X (t 1,..., t n ) = 1 G ζ a,x (t 1,..., t n ). a G G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
25 Ratojen lukumäärä ryhmän toiminnassa (Burnsiden lemma) Oletetaan, että (äärellinen) ryhmä G toimii joukossa X. Jokaiselle a G määritellään kiintopistejoukko X a siten, että X a = { x X : ax = x }. (Tätä joukkoa merkitään joskus myös X a :lla tai F (a):lla.) Silloin ratojen lukumäärä ryhmän G toiminnassa joukossa X on 1 G X a. a G G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
26 Ryhmän toiminta ja väritykset Oletetaan, että ryhmä G toimii joukossa X. Joukon X väritys on funktio ω : X K missä K on joukko värejä. Ryhmä G toimii kaikkien väritysten joukossa K X siten, että (aω)(x) = ω(a 1 x), a G, x X. Tämä on vasen toiminta koska (a(bω))(y) = (bω)(a 1 y) = ω(b 1 a 1 y) = ω((ab) 1 y) = ((ab)ω)(y). Jos Ω K X on X :n väritysten osajoukko niin G toimii joukossa Ω mikäli GΩ = Ω. Ryhmän G toiminta väritysjoukolla Ω määrittelee ekvivalenssirelaation Ω:lla siten, että samaan rataan kuluvat väritykset ovat ekvivalentteja, eli ω η jos ja vain jos ω = aη jollakin a G ja silloin näitä värityksiä pidetään samoina. Näin ollen G:n toiminnan suhteen erilaisten väritysten lukumäärä on sama kuin ratojen lukumäärä, joka on 1 Ω a G missä Ω a = { ω Ω : aω = ω } on niiden väritysten joukko, jotka ovat invariantteja, eli kiintopisteitä, a:n toiminnassa. a G G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
27 Mitkä väritykset ovat invariantteja ryhmäalkion a toiminnassa? Oletetaan, että ryhmä G toimii joukossa X ja että a G ja X :n radat a:n toiminnassa ovat R a,1, R a,2,... R a,ma. Jos ω on X :n väritys (eli funktio: X K missä K on joukko värejä) niin aω = ω jos ja vain jos ω on vakio jokaisella radalla R a,j, j = 1,..., m a. Miksi? Koska aω = ω niin pätee a j ω = ω kaikilla j Z. Jos nyt x ja y kuuluvat samaan rataan a:n toiminnassa niin on olemassa luku j siten, että a j x = y eli a j y = x. Alkion a G toiminnan määritelmän ((aω)(x) = ω(a 1 x)) nojalla ja koska a j ω = ω saamme ω(y) = (a j ω)(y) = ω(a j y) = ω(x). Jos taas ω on vakio jokaisella radalla niin ω(x) = ω(a 1 x) kaikilla x X. Tästä seuraa, että ω(x) = (aω)(x) kaikilla x, eli ω = aω. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
28 Pólyan väritys -lause Oletetaan, että G toimii joukossa X ja että K X on kaikkien X :n väritysten joukko missä värien joukko on K = {v 1, v 2,..., v r }. Silloin monomin v i 1 1 v i v r ir, kerroin polynomissa ζ G,X (v v 1 r, v v 2 r,..., v n v n r ) on niiden X :n väritysten lukumäärä, joissa väriä v j käytetään täsmälleen i j kertaa (eli { x : ω(x) = v j } = i j ) ja jotka eivät ole ekvivalentteja G:n toiminnassa. Jos käytetään r väriä mutta muita rajoituksia ei ole niin ζ G,X (r, r,..., r) on niiden X :n väritysten lukumäärä, jotka eivät ole ekvivalentteja G:n toiminnassa. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
29 Verkot Suunnattu verkko on pari [V, E] missä V on joukko, jonka alkiot ovat verkon solmut ja E on joukon V V osajoukko, jonka alkiot ovat solmujen väliset (suunnatut) kaaret eli linkit. Suuntaamaton verkko (tai vain verkko) on pari [V, E] missä V on joukko, jonka alkiot ovat verkon solmut ja E { {a, b} : a, b V } on verkon solmujen välisten kaarien joukko. Suuntamaton verkko [V, E] on yksinkertainen jos {v, v} = {v} / E kaikilla v V ja suunnatun verkon tapauksessa jos [v, v] / E kaikilla v V. Jos verkon kahden solmun välillä on kaari niin ne ovat toistensa naapureita ja kyseisen kaaren päätesolmut. Useimmiten V :n alkioiden lukumäärä on positiivinen mutta äärellinen. Huom! Näissä verkoissa on siis kahden solmun välillä korkeintaan yksi kaari ja verkko on yksinkertainen jos mikään solmu ei ole oma naapurinsa. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
30 Määritelmiä Verkon [V, E] polku (solmusta v 0 solmuun v n ) on jono [v 0, v 1,..., v n ] missä v j V, j = 0, 1,..., n ja jokaisella j = 1,..., n on olemassa kaari solmujen v j 1 ja v j välillä, (eli {v j 1, v j } E tai [v j 1, v j ] E). Polun [v 0, v 1,..., v n ] pituus on n. Verkon [V, E] sykli on sen polku [v 0, v 1,..., v n ] missä v n = v 0. Polku [v 0, v 1,..., v n ] on yksinkertainen jos v j v k 0 j < k n. Sykli [v 0, v 1,..., v n ] on yksinkertainen jos n 3 ja [v 0, v 1,..., v n 1 ] on yksinkertainen. Verkon [V, E] Eulerin polku (tai sykli) on sen polku (tai sykli) [v 0, v 1,..., v n ], jossa n j=1 {v j 1, v j } = E ja {v j 1, v j } {v k 1, v k } kun 1 j < k n ( n j=1 [v j 1, v j ] = E ja [v j 1, v j ] [v k 1, v k ] kun 1 j < k n) eli se käy läpi verkon kaikki kaaret täsmälleen kerran. Verkon [V, E] Hamiltonin polku (tai sykli) on sen yksinkertainen polku (tai sykli) [v 0, v 1,..., v n ], jossa {v 0,..., v n } = V eli se käy läpi kaikki verkon solmut (syklitapauksessa paitsi v 0 = v n ) täsmälleen kerran. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
31 Määritelmiä, jatk. Verkko on yhtenäinen jos jokaisesta solmusta on polku jokaiseen toiseen solmuun. Verkko on puu jos se on yksinkertainen ja jokaisesta solmusta on täsmälleen yksi yksinkertainen polku jokaiseen toiseen solmuun. Verkko on metsä jos se on yksinkertainen ja jokaisesta solmusta on korkeintaan yksi yksinkertainen polku jokaiseen toiseen solmuun. Verkko [V, E] on kaksijakoinen osilla X ja Y jos V = X Y, X Y = ja E { {x, y} : x X, y Y } (tai E X Y ). Verkon [V, E] pariutus on kaarien osajoukko M E siten, että kahdella eri M:n kaarilla ei ole yhteisiä päätesolmuja, eli jos e 1 = {v 1, v 1 } ja e 2 = {v 2, v 2 } niin e 1 e 2 e 1 = e 2 (jos [v 1, v 1 ] M ja [v 2, v 2 ] M niin {v 1, v 1 } {v 2, v 2 } [v 1, v 1 ] = [v 2, v 2 ]) Yksinkertaisen verkon [V, E] solmujen väritys on funktio ω : V K siten, että ω(v j ) ω(v k ) jos {v j, v k } E ([v j, v k ] E). Verkon kromaattinen luku on pienin solmujen väritykseen tarvittava värien lukumäärä. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
32 Naapurimatriisi Jos [V, E] on verkko, jossa on m solmua V = {v 1,... v m } niin sen naapurimatriisi on m m-matriisi { 1, {v j, v k } E, ( [v j, v k ] E), A(j, k) = 0, {v j, v k } / E, ( [v j, v k ] / E). Jos n 1 niin (A n )(j, k) on n-pituisten polkujen lukumäärä solmusta v j solmuun v k. Huom Jos verkon kaareille annetaan numeroarvoja eli määritellään funktio w : E R, esimerkiksi kuvaamaan solmujen välisiä etäisyyksiä niin kannattaa vaihtaa A:n määritelmäksi A(j, k) = w({v j, v k }) jos {v j, v k } E ja esimerkiksi + muuten. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
33 Isomorfiset verkot Verkot [V, E] ja [V, E ] ovat isomorfiset jos on olemassa bijektio ψ : E E siten, että {ψ(a), ψ(b)} E {a, b} E ( ja suunnatussa tapauksessa [ψ(a), ψ(b)] E [a, b] E) eli naapurit kuvautuvat naapureille. Kaksijakoiset verkot ja pariutukset Olkoon [X Y, E] kaksijakoinen verkko (jonka osat ovat X ja Y ). Silloin on olemassa pariutus M siten, että jokainen x X on jonkin M:n kaaren päätepiste eli M on ns. täydellinen pariutus jos ja vain jos jokaisella A X pätee, että A:n alkioiden lukumäärä A on pienempi tai yhtäsuuri kuin A:n alkioiden naapureiden lukumäärä eli A { y Y : {x, y} E ([x, y] E), x A }. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
34 Ahne väritysalgoritmi Helppo, mutta ei välttämättä optimaalinen tapa solmujen värityksen löytämiseksi on seuraava ahne algoritmi: Aseta solmut johonkin järjestykseen: [v 1, v 2,..., v n ]. Aseta värit johonkin järjestykseen: [c 1, c 2,..., c r ]. Väritä ensimmäinen solmu ensimmäisellä värillä, eli ω(v 1 ) = c 1. Jos solmut v 1,..., v k on väritetty niin väritä solmu v k+1 ensimmäisellä käytettävissä olevalla värillä siten, että ehto ettei naapureita väritetä samalla värillä toteutuu, eli ω(v k+1 ) = c j missä j = min{ i 1 : {v p, v k+1 } E AND p k ω(v p ) c i }. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
35 Minimaalinen virittävä puu, ahne algoritmi I (Prim) Jos [V, E] on yhtenäinen (suuntaamaton) verkko ja jokaiselle kaarelle {v j, v k } on annettu paino w({v j, v k }) (ja w({v j, v k }) = jos {v j, v k } / E) niin minimaalinen virittävä puu on verkko [V, E T ] missä E T E (eli aliverkko) joka on puu ja sellainen, että {v j,v k } E T w({v j, v k }) on mahdollisimman pieni. Minimaalinen virittävä puu voidaan konstruoida esimerkiksi seuraavalla ahneella algoritmilla: Valitse T 1 = [{v 1 }, ] missä v 1 on V :n mielivaltainen alkio. Jos T m = [V m, E m ] on valittu ja V m V niin valitse v j V m ja v k V \ V m siten, että w({v j, v k }) on mahdollisimman pieni jolloin T m+1 = [V m {v k }, E m {{v j, v k }}], eli verkon T m solmuihin lisätään solmu v k ja kaareihin solmujen v j ja v k välinen kaari. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
36 Minimaalinen virittävä puu, ahne algoritmi II (Kruskal) Jos [V, E] on yhtenäinen (suuntaamaton) verkko ja jokaiselle kaarelle {v j, v k } on annettu paino w({v j, v k }) (ja w({v j, v k }) = jos {v j, v k } / E) niin minimaalinen virittävä puu voidaan konstruoida myös seuraavalla ahneella algoritmilla: Valitse E 1 =. Niin kauan kun verkko [V, E m ] ei ole puu niin valitse e E \ E m siten, että w(e) on mahdollisimman pieni ja verkko [V, E m+1 ], missä E m+1 = E m {e}, on metsä. G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
37 Dynaaminen optimointi ja verkot Olkoon [V, E] yksinkertainen ja yhtenäinen (suuntaamaton) verkko jossa jokaiselle kaarelle {v j, v k } on annettu paino w({v j, v k }) 0 (ja w({v j, v k }) = jos {v j, v k } / E). Jos tehtävänä on löytää polku [v 0, v 1,..., v n ] tietystä solmusta v 0 johonkin toiseen solmuun v n siten, että n j=1 w({v j 1, v j }) on mahdollisimman pieni voidaan menetellä seuraavalla tavalla: Määrittele s(v) = min{ k j=1 w({v j 1, v j }) : [v 0, v 1,..., v k ] on polku solmusta v 0 solmuun v k = v}. Huomaa, että funktio s toteuttaa dynaamisen optimoinnin periaatetta: s(v) = min v V (s(v ) + w({v, v}). Määritä optimaliset arvot s(v) seuraavalla tavalla: Valitse V 0 = {v 0 } ja s(v 0 ) = 0. Jos optimaaliset arvot s(v) on määritetty kun v V j niin laske V j :n naapureille testiarvot t(v) = min v V j (s(v ) + w({v, v}), v V \ V j. Valitse V j+1 = V j {v} ja s(v) = t(v) jos v V \ V j ja t(v) = min v V \V j t(v ). G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2. osa huhtikuuta II / 37
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Ryhmät
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Ryhmät
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Permutaatiot
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Permutaatiot
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetyhteenveto, 3. osahuhtikuuta
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetyhteenveto, 3. osahuhtikuuta
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Permutaatiot ja ryhmät Ryhmät
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Permutaatiot ja ryhmät Ryhmät
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 20. lokakuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 20. lokakuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 0. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 0. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Ryhmät Permutaatiot
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Ryhmät Permutaatiot
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä14.
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä14.
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä4. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä4. ym.,
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Permutaatiot
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Permutaatiot
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 204 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 204 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II G. Gripenberg Modulaariaritmetiikka 2 Permutaatiot ja ryhmät Aalto-yliopisto 3. huhtikuuta 204 3 Verkot G. Gripenberg (Aalto-yliopisto)
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa II G. Gripenberg Modulaariaritmetiikka 2 Permutaatiot ja ryhmät Aalto-yliopisto 3. huhtikuuta 204 3 Verkot G. Gripenberg (Aalto-yliopisto)
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos meillä
MS-A0402 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos meillä
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos
MS-A0401 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos
j(j 1) = n(n2 1) 3 + (k + 1)k = (k + 1)(k2 k + 3k) 3 = (k + 1)(k2 + 2k + 1 1)
 MS-A0401 Diskreetin matematiikan perusteet Tentti ja välikokeiden uusinta 10.11.015 Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot! Laskimia tai taulukoita ei saa käyttää tässä kokeessa!
MS-A0401 Diskreetin matematiikan perusteet Tentti ja välikokeiden uusinta 10.11.015 Kirjoita jokaiseen koepaperiin nimesi, opiskelijanumerosi ym. tiedot! Laskimia tai taulukoita ei saa käyttää tässä kokeessa!
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 4: Modulaariaritmetiikka Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Modulaariaritmetiikka Jakoyhtälö Määritelmä 1 Luku
MS-A0402 Diskreetin matematiikan perusteet Osa 4: Modulaariaritmetiikka Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Modulaariaritmetiikka Jakoyhtälö Määritelmä 1 Luku
Esko Turunen MAT Algebra1(s)
 Määritelmä (4.1) Olkoon G ryhmä. Olkoon H G, H. Jos joukko H varustettuna indusoidulla laskutoimituksella on ryhmä, se on ryhmän G aliryhmä. Jos H G on ryhmän G aliryhmä, merkitään usein H G, ja jos H
Määritelmä (4.1) Olkoon G ryhmä. Olkoon H G, H. Jos joukko H varustettuna indusoidulla laskutoimituksella on ryhmä, se on ryhmän G aliryhmä. Jos H G on ryhmän G aliryhmä, merkitään usein H G, ja jos H
Kuvauksista ja relaatioista. Jonna Makkonen Ilari Vallivaara
 Kuvauksista ja relaatioista Jonna Makkonen Ilari Vallivaara 20. lokakuuta 2004 Sisältö 1 Esipuhe 2 2 Kuvauksista 3 3 Relaatioista 8 Lähdeluettelo 12 1 1 Esipuhe Joukot ja relaatiot ovat periaatteessa äärimmäisen
Kuvauksista ja relaatioista Jonna Makkonen Ilari Vallivaara 20. lokakuuta 2004 Sisältö 1 Esipuhe 2 2 Kuvauksista 3 3 Relaatioista 8 Lähdeluettelo 12 1 1 Esipuhe Joukot ja relaatiot ovat periaatteessa äärimmäisen
Lukuteorian kertausta
 Lukuteorian kertausta Jakoalgoritmi Jos a, b Z ja b 0, niin on olemassa sellaiset yksikäsitteiset kokonaisluvut q ja r, että a = qb+r, missä 0 r < b. Esimerkki 1: Jos a = 60 ja b = 11, niin 60 = 5 11 +
Lukuteorian kertausta Jakoalgoritmi Jos a, b Z ja b 0, niin on olemassa sellaiset yksikäsitteiset kokonaisluvut q ja r, että a = qb+r, missä 0 r < b. Esimerkki 1: Jos a = 60 ja b = 11, niin 60 = 5 11 +
Esimerkki A1. Jaetaan ryhmä G = Z 17 H = 4 = {1, 4, 4 2 = 16 = 1, 4 3 = 4 = 13, 4 4 = 16 = 1}.
 Jaetaan ryhmä G = Z 17 n H = 4 sivuluokkiin. Ratkaisu: Koska 17 on alkuluku, #G = 16, alkiona jäännösluokat a, a = 1, 2,..., 16. Määrätään ensin n H alkiot: H = 4 = {1, 4, 4 2 = 16 = 1, 4 3 = 4 = 13, 4
Jaetaan ryhmä G = Z 17 n H = 4 sivuluokkiin. Ratkaisu: Koska 17 on alkuluku, #G = 16, alkiona jäännösluokat a, a = 1, 2,..., 16. Määrätään ensin n H alkiot: H = 4 = {1, 4, 4 2 = 16 = 1, 4 3 = 4 = 13, 4
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013
 Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
a b 1 c b n c n
 Algebra Syksy 2007 Harjoitukset 1. Olkoon a Z. Totea, että aina a 0, 1 a, a a ja a a. 2. Olkoot a, b, c, d Z. Todista implikaatiot: a) a b ja c d ac bd, b) a b ja b c a c. 3. Olkoon a b i kaikilla i =
Algebra Syksy 2007 Harjoitukset 1. Olkoon a Z. Totea, että aina a 0, 1 a, a a ja a a. 2. Olkoot a, b, c, d Z. Todista implikaatiot: a) a b ja c d ac bd, b) a b ja b c a c. 3. Olkoon a b i kaikilla i =
802354A Algebran perusteet Luentorunko Kevät Työryhmä: Markku Niemenmaa, Kari Myllylä, Topi Törmä
 802354A Algebran perusteet Luentorunko Kevät 2017 Työryhmä: Markku Niemenmaa, Kari Myllylä, Topi Törmä Sisältö 1 Lukuteoriaa 3 1.1 Jakoalgoritmi ja alkuluvut.................... 3 1.2 Suurin yhteinen tekijä......................
802354A Algebran perusteet Luentorunko Kevät 2017 Työryhmä: Markku Niemenmaa, Kari Myllylä, Topi Törmä Sisältö 1 Lukuteoriaa 3 1.1 Jakoalgoritmi ja alkuluvut.................... 3 1.2 Suurin yhteinen tekijä......................
Esko Turunen Luku 3. Ryhmät
 3. Ryhmät Monoidia rikkaampi algebrallinen struktuuri on ryhmä: Määritelmä (3.1) Olkoon joukon G laskutoimitus. Joukko G varustettuna tällä laskutoimituksella on ryhmä, jos laskutoimitus on assosiatiivinen,
3. Ryhmät Monoidia rikkaampi algebrallinen struktuuri on ryhmä: Määritelmä (3.1) Olkoon joukon G laskutoimitus. Joukko G varustettuna tällä laskutoimituksella on ryhmä, jos laskutoimitus on assosiatiivinen,
Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen
 Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen anton.mallasto@aalto.fi. 1. 2. Muista. Ryhmän G aliryhmä H on normaali aliryhmä, jos ah = Ha kaikilla a G. Toisin
Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen anton.mallasto@aalto.fi. 1. 2. Muista. Ryhmän G aliryhmä H on normaali aliryhmä, jos ah = Ha kaikilla a G. Toisin
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
R : renkaan R kääntyvien alkioiden joukko; R kertolaskulla varustettuna on
 0. Kertausta ja täydennystä Kurssille Äärelliset kunnat tarvittavat esitiedot löytyvät Algebran kurssista [Alg]. Hyödyksi voivat myös olla (vaikka eivät välttämättömiä) Lukuteorian alkeet [LTA] ja Salakirjoitukset
0. Kertausta ja täydennystä Kurssille Äärelliset kunnat tarvittavat esitiedot löytyvät Algebran kurssista [Alg]. Hyödyksi voivat myös olla (vaikka eivät välttämättömiä) Lukuteorian alkeet [LTA] ja Salakirjoitukset
802354A Lukuteoria ja ryhmät Luentorunko Kevät Työryhmä: Markku Niemenmaa, Kari Myllylä, Juha-Matti Tirilä, Antti Torvikoski, Topi Törmä
 802354A Lukuteoria ja ryhmät Luentorunko Kevät 2014 Työryhmä: Markku Niemenmaa, Kari Myllylä, Juha-Matti Tirilä, Antti Torvikoski, Topi Törmä Sisältö 1 Ekvivalenssirelaatio 3 2 Lukuteoriaa 4 2.1 Lukuteorian
802354A Lukuteoria ja ryhmät Luentorunko Kevät 2014 Työryhmä: Markku Niemenmaa, Kari Myllylä, Juha-Matti Tirilä, Antti Torvikoski, Topi Törmä Sisältö 1 Ekvivalenssirelaatio 3 2 Lukuteoriaa 4 2.1 Lukuteorian
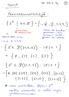 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
802354A Algebran perusteet Luentorunko Kevät Työryhmä: Markku Niemenmaa, Kari Myllylä, Topi Törmä
 802354A Algebran perusteet Luentorunko Kevät 2018 Työryhmä: Markku Niemenmaa, Kari Myllylä, Topi Törmä Sisältö 1 Lukuteoriaa 3 1.1 Jakoalgoritmi ja alkuluvut.................... 3 1.2 Suurin yhteinen tekijä......................
802354A Algebran perusteet Luentorunko Kevät 2018 Työryhmä: Markku Niemenmaa, Kari Myllylä, Topi Törmä Sisältö 1 Lukuteoriaa 3 1.1 Jakoalgoritmi ja alkuluvut.................... 3 1.2 Suurin yhteinen tekijä......................
6. Tekijäryhmät ja aliryhmät
 6. Tekijäryhmät ja aliryhmät Tämän luvun tavoitteena on esitellä konstruktio, jota kutsutaan tekijäryhmän muodostamiseksi. Konstruktiossa lähdetään liikkeelle jostakin isosta ryhmästä, samastetaan alkioita,
6. Tekijäryhmät ja aliryhmät Tämän luvun tavoitteena on esitellä konstruktio, jota kutsutaan tekijäryhmän muodostamiseksi. Konstruktiossa lähdetään liikkeelle jostakin isosta ryhmästä, samastetaan alkioita,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Tekijäryhmiä varten määritellään aluksi sivuluokat ja normaalit aliryhmät.
 3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
HN = {hn h H, n N} on G:n aliryhmä.
 Matematiikan ja tilastotieteen laitos Algebra I Ratkaisuehdoituksia harjoituksiin 8, 23.27.3.2009 5 sivua Rami Luisto 1. Osoita, että kullakin n N + lukujen n 5 ja n viimeiset numerot kymmenkantaisessa
Matematiikan ja tilastotieteen laitos Algebra I Ratkaisuehdoituksia harjoituksiin 8, 23.27.3.2009 5 sivua Rami Luisto 1. Osoita, että kullakin n N + lukujen n 5 ja n viimeiset numerot kymmenkantaisessa
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
{I n } < { I n,i n } < GL n (Q) < GL n (R) < GL n (C) kaikilla n 2 ja
 5. Aliryhmät Luvun 4 esimerkeissä esiintyy usein ryhmä (G, ) ja jokin vakaa osajoukko B G siten, että (B, B ) on ryhmä. Määrittelemme seuraavassa käsitteitä, jotka auttavat tällaisten tilanteiden käsittelyssä.
5. Aliryhmät Luvun 4 esimerkeissä esiintyy usein ryhmä (G, ) ja jokin vakaa osajoukko B G siten, että (B, B ) on ryhmä. Määrittelemme seuraavassa käsitteitä, jotka auttavat tällaisten tilanteiden käsittelyssä.
on Abelin ryhmä kertolaskun suhteen. Tämän joukon alkioiden lukumäärää merkitään
 5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
a ord 13 (a)
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 4, MALLIRATKAISUT Tehtävä 1. Etsi asteet ord p (a) luvuille a 1, 2,..., p 1 kun p = 13 ja kun p = 17. (ii) Mitkä jäännösluokat ovat primitiivisiä juuria (mod
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 4, MALLIRATKAISUT Tehtävä 1. Etsi asteet ord p (a) luvuille a 1, 2,..., p 1 kun p = 13 ja kun p = 17. (ii) Mitkä jäännösluokat ovat primitiivisiä juuria (mod
Fermat n pieni lause. Heikki Pitkänen. Matematiikan kandidaatintutkielma
 Fermat n pieni lause Heikki Pitkänen Matematiikan kandidaatintutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2009 Sisältö Johdanto 3 1. Fermat n pieni lause 3 2. Pseudoalkuluvut
Fermat n pieni lause Heikki Pitkänen Matematiikan kandidaatintutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2009 Sisältö Johdanto 3 1. Fermat n pieni lause 3 2. Pseudoalkuluvut
Transversaalit ja hajoamisaliryhmät
 Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
Eräitä ratkeavuustarkasteluja
 Eräitä ratkeavuustarkasteluja Pro gradu-tutkielma Milla Jantunen 2124227 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2014 Sisältö 1 Ryhmät ja aliryhmät 3 1.1 Ryhmä...............................
Eräitä ratkeavuustarkasteluja Pro gradu-tutkielma Milla Jantunen 2124227 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2014 Sisältö 1 Ryhmät ja aliryhmät 3 1.1 Ryhmä...............................
Kurssikoe on maanantaina 29.6. Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2
 3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 Olen valinnut kunkin luvun teemaksi yhden ryhmän. Ensimmäisen luvun teema on pienin epätriviaali ryhmä, eli ryhmä, jossa on kaksi alkiota. Merkitsen
3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 Olen valinnut kunkin luvun teemaksi yhden ryhmän. Ensimmäisen luvun teema on pienin epätriviaali ryhmä, eli ryhmä, jossa on kaksi alkiota. Merkitsen
Diskreetin matematiikan perusteet Laskuharjoitus 5 / vko 41
 Diskreetin matematiikan perusteet Laskuharjoitus 5 / vko 4 Tuntitehtävät 4-42 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 45-46 loppuviikon harjoituksissa. Kotitehtävät 43-44 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 5 / vko 4 Tuntitehtävät 4-42 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 45-46 loppuviikon harjoituksissa. Kotitehtävät 43-44 tarkastetaan loppuviikon
kaikille a R. 1 (R, +) on kommutatiivinen ryhmä, 2 a(b + c) = ab + ac ja (b + c)a = ba + ca kaikilla a, b, c R, ja
 Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi binääristä assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme muuten samat ominaisuudet kuin kokonaisluvuilta,
Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi binääristä assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme muuten samat ominaisuudet kuin kokonaisluvuilta,
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
pdfmark=/pages, Raw=/Rotate 90 1 LUKUTEORIAA JA MUITA TYÖKALUJA SALAUKSEEN Lukujoukot Sekalaisia merkintöjä...
 pdfmark=/pages, Raw=/Rotate 90 Sisältö 1 LUKUTEORIAA JA MUITA TYÖKALUJA SALAUKSEEN 0-2 2 Merkintöjä 0-3 2.1 Lukujoukot................... 0-3 2.2 Sekalaisia merkintöjä.............. 0-4 2.3 Tärkeitä kaavoja................
pdfmark=/pages, Raw=/Rotate 90 Sisältö 1 LUKUTEORIAA JA MUITA TYÖKALUJA SALAUKSEEN 0-2 2 Merkintöjä 0-3 2.1 Lukujoukot................... 0-3 2.2 Sekalaisia merkintöjä.............. 0-4 2.3 Tärkeitä kaavoja................
MS-A0402 Diskreetin matematiikan perusteet
 MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 6. Alkeislukuteoria 6.1 Jaollisuus Käsitellään kokonaislukujen perusominaisuuksia: erityisesti jaollisuutta Käytettävät lukujoukot: Luonnolliset luvut IN = {0,1,2,3,...
811120P Diskreetit rakenteet 2016-2017 6. Alkeislukuteoria 6.1 Jaollisuus Käsitellään kokonaislukujen perusominaisuuksia: erityisesti jaollisuutta Käytettävät lukujoukot: Luonnolliset luvut IN = {0,1,2,3,...
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa I
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetyhteenveto, 3. osahuhtikuuta
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetyhteenveto, 3. osahuhtikuuta
H = H(12) = {id, (12)},
 7. Normaali aliryhmä ja tekijäryhmä Tarkastelemme luvun aluksi ryhmän ja sen aliryhmien suhdetta. Olkoon G ryhmä ja olkoon H G. Alkiong G vasen sivuluokka (aliryhmän H suhteen) on gh = {gh : h H} ja sen
7. Normaali aliryhmä ja tekijäryhmä Tarkastelemme luvun aluksi ryhmän ja sen aliryhmien suhdetta. Olkoon G ryhmä ja olkoon H G. Alkiong G vasen sivuluokka (aliryhmän H suhteen) on gh = {gh : h H} ja sen
Algebran ja lukuteorian harjoitustehtäviä. 1. Tutki, ovatko seuraavat relaatiot ekvivalenssirelaatioita joukon N kaikkien osajoukkojen
 Algebran ja lukuteorian harjoitustehtäviä Versio 1.0 (27.1.2006) Turun yliopisto Lukuteoria 1. Tutki, ovatko seuraavat relaatiot ekvivalenssirelaatioita joukon N kaikkien osajoukkojen joukolla: a) C D
Algebran ja lukuteorian harjoitustehtäviä Versio 1.0 (27.1.2006) Turun yliopisto Lukuteoria 1. Tutki, ovatko seuraavat relaatiot ekvivalenssirelaatioita joukon N kaikkien osajoukkojen joukolla: a) C D
Algebra I, harjoitus 5,
 Algebra I, harjoitus 5, 7.-8.10.2014. 1. 2 Osoita väitteet oikeiksi tai vääriksi. a) (R, ) on ryhmä, kun asetetaan a b = 2(a + b) aina, kun a, b R. (Tässä + on reaalilukujen tavallinen yhteenlasku.) b)
Algebra I, harjoitus 5, 7.-8.10.2014. 1. 2 Osoita väitteet oikeiksi tai vääriksi. a) (R, ) on ryhmä, kun asetetaan a b = 2(a + b) aina, kun a, b R. (Tässä + on reaalilukujen tavallinen yhteenlasku.) b)
Shorin algoritmin matematiikkaa Edvard Fagerholm
 Edvard Fagerholm 1 Määritelmiä Määritelmä 1 Ryhmä G on syklinen, jos a G s.e. G = a. Määritelmä 2 Olkoon G ryhmä. Tällöin alkion a G kertaluku ord(a) on pienin luku n N \ {0}, jolla a n = 1. Jos lukua
Edvard Fagerholm 1 Määritelmiä Määritelmä 1 Ryhmä G on syklinen, jos a G s.e. G = a. Määritelmä 2 Olkoon G ryhmä. Tällöin alkion a G kertaluku ord(a) on pienin luku n N \ {0}, jolla a n = 1. Jos lukua
MAT Algebra 1(s)
 8. maaliskuuta 2012 Esipuhe Tämä luentokalvot sisältävät kurssin keskeiset asiat. Kalvoja täydennetään luennolla esimerkein ja todistuksin. Materiaali perustuu Jyväskylän, Helsingin ja Turun yliopistojen
8. maaliskuuta 2012 Esipuhe Tämä luentokalvot sisältävät kurssin keskeiset asiat. Kalvoja täydennetään luennolla esimerkein ja todistuksin. Materiaali perustuu Jyväskylän, Helsingin ja Turun yliopistojen
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 6 (8 sivua) OT. 1. a) Määritä seuraavat summat:
 Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 6 (8 sivua) 21.2.-25.2.2011 OT 1. a) Määritä seuraavat summat: [2] 4 + [3] 4, [2] 5 + [3] 5, [2] 6 + [2] 6 + [2] 6, 7 [3]
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 6 (8 sivua) 21.2.-25.2.2011 OT 1. a) Määritä seuraavat summat: [2] 4 + [3] 4, [2] 5 + [3] 5, [2] 6 + [2] 6 + [2] 6, 7 [3]
Tekijäryhmän määrittelemistä varten määritellään aluksi sivuluokat ja normaalit aliryhmät. gh = {gh h H}.
 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
2017 = = = = = = 26 1
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 2, MALLIRATKAISUT Tehtävä 1. Sovella Eukleiden algoritmia ja (i) etsi s.y.t(2017, 753) (ii) etsi kaikki kokonaislukuratkaisut yhtälölle 405x + 141y = 12. Ratkaisu
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 2, MALLIRATKAISUT Tehtävä 1. Sovella Eukleiden algoritmia ja (i) etsi s.y.t(2017, 753) (ii) etsi kaikki kokonaislukuratkaisut yhtälölle 405x + 141y = 12. Ratkaisu
802355A Algebralliset rakenteet Luentorunko Syksy Markku Niemenmaa Kari Myllylä Topi Törmä Marko Leinonen
 802355A Algebralliset rakenteet Luentorunko Syksy 2016 Markku Niemenmaa Kari Myllylä Topi Törmä Marko Leinonen Sisältö 1 Kertausta kurssilta Algebran perusteet 3 2 Renkaat 8 2.1 Renkaiden teoriaa.........................
802355A Algebralliset rakenteet Luentorunko Syksy 2016 Markku Niemenmaa Kari Myllylä Topi Törmä Marko Leinonen Sisältö 1 Kertausta kurssilta Algebran perusteet 3 2 Renkaat 8 2.1 Renkaiden teoriaa.........................
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
1 Lukujen jaollisuudesta
 Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa I
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 30. syyskuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 30.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa I G. Gripenberg Aalto-yliopisto 30. syyskuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 30.
4. Ryhmien sisäinen rakenne
 4. Ryhmien sisäinen rakenne Tässä luvussa tarkastellaan joitakin tapoja päästä käsiksi ryhmien sisäiseen rakenteeseen. Useimmat tuloksista ovat erityisen käyttökelpoisia äärellisten ryhmien tapauksessa.
4. Ryhmien sisäinen rakenne Tässä luvussa tarkastellaan joitakin tapoja päästä käsiksi ryhmien sisäiseen rakenteeseen. Useimmat tuloksista ovat erityisen käyttökelpoisia äärellisten ryhmien tapauksessa.
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi
 7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
7. Olemassaolo ja yksikäsitteisyys Galois n kunta GF(q) = F q, jossa on q alkiota, määriteltiin jäännösluokkarenkaaksi Z p [x]/(m), missä m on polynomirenkaan Z p [x] jaoton polynomi (ks. määritelmä 3.19).
2.1. Tehtävänä on osoittaa induktiolla, että kaikille n N pätee n = 1 n(n + 1). (1)
 Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
(d) 29 4 (mod 7) (e) ( ) 49 (mod 10) (f) (mod 9)
 1. Pätevätkö seuraavat kongruenssiyhtälöt? (a) 40 13 (mod 9) (b) 211 12 (mod 2) (c) 126 46 (mod 3) Ratkaisu. (a) Kyllä, sillä 40 = 4 9+4 ja 13 = 9+4. (b) Ei, sillä 211 on pariton ja 12 parillinen. (c)
1. Pätevätkö seuraavat kongruenssiyhtälöt? (a) 40 13 (mod 9) (b) 211 12 (mod 2) (c) 126 46 (mod 3) Ratkaisu. (a) Kyllä, sillä 40 = 4 9+4 ja 13 = 9+4. (b) Ei, sillä 211 on pariton ja 12 parillinen. (c)
Tekijä Pitkä Matematiikka 11 ratkaisut luku 2
 Tekijä Pitkä matematiikka 11 0..017 170 a) Koska 8 = 4 7, luku 8 on jaollinen luvulla 4. b) Koska 104 = 4 6, luku 104 on jaollinen luvulla 4. c) Koska 4 0 = 80 < 8 ja 4 1 = 84 > 8, luku 8 ei ole jaollinen
Tekijä Pitkä matematiikka 11 0..017 170 a) Koska 8 = 4 7, luku 8 on jaollinen luvulla 4. b) Koska 104 = 4 6, luku 104 on jaollinen luvulla 4. c) Koska 4 0 = 80 < 8 ja 4 1 = 84 > 8, luku 8 ei ole jaollinen
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) OT
 Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) 31.1.-4.2.2011 OT 1. Määritellään kokonaisluvuille laskutoimitus n m = n + m + 5. Osoita, että (Z, ) on ryhmä.
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) 31.1.-4.2.2011 OT 1. Määritellään kokonaisluvuille laskutoimitus n m = n + m + 5. Osoita, että (Z, ) on ryhmä.
Luupit Pro gradu Anni Keränen Matemaattisten tieteiden laitos Oulun yliopisto 2014
 Luupit Pro gradu Anni Keränen Matemaattisten tieteiden laitos Oulun yliopisto 2014 Sisältö Johdanto 2 1 Perusteita 3 1.1 Kuvauksista............................ 3 1.2 Relaatioista............................
Luupit Pro gradu Anni Keränen Matemaattisten tieteiden laitos Oulun yliopisto 2014 Sisältö Johdanto 2 1 Perusteita 3 1.1 Kuvauksista............................ 3 1.2 Relaatioista............................
Salausmenetelmät. Veikko Keränen, Jouko Teeriaho (RAMK, 2006)
 Salausmenetelmät Veikko Keränen, Jouko Teeriaho (RAMK, 2006) LUKUTEORIAA JA ALGORITMEJA 3. Kongruenssit à 3.1 Jakojäännös ja kongruenssi Määritelmä 3.1 Kaksi lukua a ja b ovat keskenään kongruentteja (tai
Salausmenetelmät Veikko Keränen, Jouko Teeriaho (RAMK, 2006) LUKUTEORIAA JA ALGORITMEJA 3. Kongruenssit à 3.1 Jakojäännös ja kongruenssi Määritelmä 3.1 Kaksi lukua a ja b ovat keskenään kongruentteja (tai
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
Diskreetin matematiikan perusteet Esimerkkiratkaisut 3 / vko 10
 Diskreetin matematiikan perusteet Esimerkkiratkaisut / vko 0 Tuntitehtävät - lasketaan alkuviikon harjoituksissa ja tuntitehtävät - loppuviikon harjoituksissa. Kotitehtävät - tarkastetaan loppuviikon harjoituksissa.
Diskreetin matematiikan perusteet Esimerkkiratkaisut / vko 0 Tuntitehtävät - lasketaan alkuviikon harjoituksissa ja tuntitehtävät - loppuviikon harjoituksissa. Kotitehtävät - tarkastetaan loppuviikon harjoituksissa.
MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen
 MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen Tehtävä 1. Onko joukon X potenssijoukon P(X) laskutoimitus distributiivinen laskutoimituksen suhteen? Onko laskutoimitus distributiivinen laskutoimituksen
MAT-41150 Algebra I (s) periodilla IV 2012 Esko Turunen Tehtävä 1. Onko joukon X potenssijoukon P(X) laskutoimitus distributiivinen laskutoimituksen suhteen? Onko laskutoimitus distributiivinen laskutoimituksen
a 2 ba = a a + ( b) a = (a + ( b))a = (a b)a, joten yhtälö pätee mielivaltaiselle renkaalle.
 Harjoitus 10 (7 sivua) Ratkaisuehdotuksia/Martina Aaltonen Tehtävä 1. Mitkä seuraavista yhtälöistä pätevät mielivaltaisen renkaan alkioille a ja b? a) a 2 ba = (a b)a b) (a + b + 1)(a b) = a 2 b 2 + a
Harjoitus 10 (7 sivua) Ratkaisuehdotuksia/Martina Aaltonen Tehtävä 1. Mitkä seuraavista yhtälöistä pätevät mielivaltaisen renkaan alkioille a ja b? a) a 2 ba = (a b)a b) (a + b + 1)(a b) = a 2 b 2 + a
800333A Algebra I Luentorunko Kevät Työryhmä: Markku Niemenmaa, Kari Myllylä, Juha-Matti Tirilä
 800333A Algebra I Luentorunko Kevät 2010 Työryhmä: Markku Niemenmaa, Kari Myllylä, Juha-Matti Tirilä Sisältö 1 Lukuteorian alkeita 3 1.1 Kongruenssiin liittyviä perustuloksia.............. 7 2 Ekvivalenssirelaatio
800333A Algebra I Luentorunko Kevät 2010 Työryhmä: Markku Niemenmaa, Kari Myllylä, Juha-Matti Tirilä Sisältö 1 Lukuteorian alkeita 3 1.1 Kongruenssiin liittyviä perustuloksia.............. 7 2 Ekvivalenssirelaatio
Kokonaislukuoptimointi
 Kokonaislukuoptimointi Algebrallisen geometrian sovelluksia Sisältö Taustaa algebrallisesta geometriasta Gröbnerin kanta Buchbergerin algoritmi Kokonaislukuoptimointi Käypyysongelma Algoritmi ratkaisun
Kokonaislukuoptimointi Algebrallisen geometrian sovelluksia Sisältö Taustaa algebrallisesta geometriasta Gröbnerin kanta Buchbergerin algoritmi Kokonaislukuoptimointi Käypyysongelma Algoritmi ratkaisun
Tekijäryhmät ja homomorsmit
 Tekijäryhmät ja homomorsmit LuK-tutkielma Henna Isokääntä 1953004 henna.isokaanta@gmail.com Matemaattiset tieteet Oulun yliopisto Kevät 2019 Sisältö Johdanto 1 1 Tekijäryhmät 1 2 Homomorsmit 3 Lähdeluettelo
Tekijäryhmät ja homomorsmit LuK-tutkielma Henna Isokääntä 1953004 henna.isokaanta@gmail.com Matemaattiset tieteet Oulun yliopisto Kevät 2019 Sisältö Johdanto 1 1 Tekijäryhmät 1 2 Homomorsmit 3 Lähdeluettelo
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT Tehtävä 1. (i) Olkoot n, d 1 ja d n. Osoita, että (k, n) d jos ja vain jos k ad, missä (a, n/d) 1. (ii) Osoita, että jos (m j, m k ) 1 kun
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT Tehtävä 1. (i) Olkoot n, d 1 ja d n. Osoita, että (k, n) d jos ja vain jos k ad, missä (a, n/d) 1. (ii) Osoita, että jos (m j, m k ) 1 kun
Symmetrisistä ryhmistä symmetriaryhmiin
 Symmetrisistä ryhmistä symmetriaryhmiin 16. marraskuuta 2006 1 Symmetrisistä ryhmistä... Bijektiivistä kuvausta {1,..., n} {1,..., n} kutsutaan n-permutaatioksi. Merkitään n-permutaatioden joukkoa S n.
Symmetrisistä ryhmistä symmetriaryhmiin 16. marraskuuta 2006 1 Symmetrisistä ryhmistä... Bijektiivistä kuvausta {1,..., n} {1,..., n} kutsutaan n-permutaatioksi. Merkitään n-permutaatioden joukkoa S n.
Liite 2. Ryhmien ja kuntien perusteet
 Liite 2. Ryhmien ja kuntien perusteet 1. Ryhmät 1.1 Johdanto Erilaisissa matematiikan probleemoissa törmätään usein muotoa a + x = b tai a x = b oleviin yhtälöihin, joissa tuntematon muuttuja on x. Lukujoukkoja
Liite 2. Ryhmien ja kuntien perusteet 1. Ryhmät 1.1 Johdanto Erilaisissa matematiikan probleemoissa törmätään usein muotoa a + x = b tai a x = b oleviin yhtälöihin, joissa tuntematon muuttuja on x. Lukujoukkoja
(x + I) + (y + I) = (x + y)+i. (x + I)(y + I) =xy + I. kaikille x, y R.
 11. Ideaalit ja tekijärenkaat Rengashomomorfismi φ: R R on erityisesti ryhmähomomorfismi φ: (R, +) (R, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin φ
11. Ideaalit ja tekijärenkaat Rengashomomorfismi φ: R R on erityisesti ryhmähomomorfismi φ: (R, +) (R, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin φ
H = : a, b C M. joten jokainen A H {0} on kääntyvä matriisi. Itse asiassa kaikki nollasta poikkeavat alkiot ovat yksiköitä, koska. a b.
 10. Kunnat ja kokonaisalueet Määritelmä 10.1. Olkoon K rengas, jossa on ainakin kaksi alkiota. Jos kaikki renkaan K nollasta poikkeavat alkiot ovat yksiköitä, niin K on jakorengas. Kommutatiivinen jakorengas
10. Kunnat ja kokonaisalueet Määritelmä 10.1. Olkoon K rengas, jossa on ainakin kaksi alkiota. Jos kaikki renkaan K nollasta poikkeavat alkiot ovat yksiköitä, niin K on jakorengas. Kommutatiivinen jakorengas
ja jäännösluokkien joukkoa
 3. Polynomien jäännösluokkarenkaat Olkoon F kunta, ja olkoon m F[x]. Polynomeille f, g F [x] määritellään kongruenssi(-relaatio) asettamalla g f mod m : m g f g = f + m h jollekin h F [x]. Kongruenssi
3. Polynomien jäännösluokkarenkaat Olkoon F kunta, ja olkoon m F[x]. Polynomeille f, g F [x] määritellään kongruenssi(-relaatio) asettamalla g f mod m : m g f g = f + m h jollekin h F [x]. Kongruenssi
Diofantoksen yhtälön ratkaisut
 Diofantoksen yhtälön ratkaisut Matias Mäkelä Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2017 Sisältö Johdanto 2 1 Suurin yhteinen tekijä 2 2 Eukleideen algoritmi 4 3 Diofantoksen yhtälön
Diofantoksen yhtälön ratkaisut Matias Mäkelä Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2017 Sisältö Johdanto 2 1 Suurin yhteinen tekijä 2 2 Eukleideen algoritmi 4 3 Diofantoksen yhtälön
Algebra I, harjoitus 8,
 Algebra I, harjoitus 8, 4.-5.11.2014. 1. Olkoon G ryhmä ja H sen normaali aliryhmä. Todista, että tällöin G/H on ryhmä, kun määritellään laskutoimitus joukossa G/H asettamalla aina, kun x, y G (lauseen
Algebra I, harjoitus 8, 4.-5.11.2014. 1. Olkoon G ryhmä ja H sen normaali aliryhmä. Todista, että tällöin G/H on ryhmä, kun määritellään laskutoimitus joukossa G/H asettamalla aina, kun x, y G (lauseen
[E : F ]=[E : K][K : F ].
![[E : F ]=[E : K][K : F ]. [E : F ]=[E : K][K : F ].](/thumbs/61/46040569.jpg) ALGEBRA II 35 Lause 4.4 (Astelukulause). Olkoot E/K/Fäärellisiä kuntalaajennuksia. Silloin [E : F ]=[E : K][K : F ]. Todistus. Olkoon {α 1,...,α n } kanta laajennukselle E/K ja {β 1,...,β m } kanta laajennukselle
ALGEBRA II 35 Lause 4.4 (Astelukulause). Olkoot E/K/Fäärellisiä kuntalaajennuksia. Silloin [E : F ]=[E : K][K : F ]. Todistus. Olkoon {α 1,...,α n } kanta laajennukselle E/K ja {β 1,...,β m } kanta laajennukselle
