TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas

Transkriptio

1 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas

2 Keskivirheyksiköllä ilmaistuna voidaan erottaa otantajakaumalta kriittisiä kohtia: Keskimmäinen 95 % otoskeskiarvoista välillä [-1.96,+1.96] Keskimmäinen 99 % otoskeskiarvoista välillä [-2.58,+2.58] Keskimmäinen 99.9 % otoskeskiarvoista välillä [-3.29,+3.29] 99.9 % 99 % 95 % Keskiarvon keskivirhe: s.e.

3 Tutkija B: Kuinka todennäköistä olisi havaita keskiarvo 182 tai sitä suurempi arvo, kun poimitaan satunnaisotos perusjoukosta? Tärkeää: aikaisemman perusteella B ei tiedä voiko otoskeskiarvo olla suurempi vaiko pienempi kuin vertailuarvo 182. Tutkija B on aikaisemmin päättänyt, että jos vertailuarvo 182 on 95 % otantajakauman keskimmäisen keskiarvon joukossa, se ei poikkea tilastollisesti merkitsevästi hänen havaitsemastaan arvosta ts. olisi vielä suhteellisen todennäköistä saada perusjoukosta tällainen keskiarvo Suhteutetaan keskiarvon 182 etäisyys tutkijan B otoksen pohjalta otantajakauman : keskiarvo ja keskivirhe 4.93: z se = ( ) / 4.93 = Koska z se = 2.08 > 1.96, ero on tilastollisesti merkitsevä (ja kysytyn todennäköisyyden tarkka arvo saadaan pinta-ala integraalina p = 0.019) Johtopäätös: B:n otoskeskiarvo on tilastollisesti merkitsevästi matalampi kuin vertailuarvo 182 (p= 0.019). p-arvo on näiden kahden pinta-alan summa

4 ESTIMOINTI Tehdään päätelmiä perusjoukon parametreista (keskiarvo, korrelaatio jne.) Parametrin estimaatti on arvo, jota lasketaan otostiedon perusteella ja edustaa arvioita perusjoukon parametrin arvosta silloin, kun laskentaan liittyvät matemaattiset oletukset ovat voimassa Mitä suurempi otos, sitä tarkemmat estimaatit A. Piste-estimaatit Perusjoukon parametrin arvo vastaa yksi lukuarvo Esim. otoskeskiarvo on perusjoukon keskiarvon pisteestimaatti B. Väliestimaatit Märitetään väli, jolla perusjoukon parametrin arvo sijaitsee valitulla todennäköisyydellä (luottamusväli) Esim. väli, jolla perusjoukon keskiarvo sijaitsee 95 % luottamustasolla

5 KESKIARVON LUOTTAMUSVÄLI Esim. keskiarvon 95 % luottamusväli saadaan määrittämällä väli, jolla 95 % keskimmäisistä otoskeskiarvoista sijaitsee otantajakaumalla Keskivirheyksiköillä ilmaistuna tämä väli sijaitsi ±1.96 keskivirheyksikön etäisyydellä keskiarvosta 95 %

6 ESIMERKKI B:n otoksesta (n = 3) lasketaan Keskiarvo: Keskihajonta: 8.54 Keskivirhe on siis Koska luottamusväli on 1.96 keskivirheyksikön päässä keskiarvon ala- ja yläpuolella, lasketaan Alaraja: = = Yläraja: = = Huom. Tässä laskut on suoritettu tarkoilla arvoilla, jotka on pyöristetty kahden desimaalin tarkkuudelle. Tulkinta: tutkijalla on 95 % luottamus siihen, että perusjoukon keskiarvo sijaitsee välillä[162.11, ]

7 KESKIARVON LUOTTAMUSVÄLI Yleisesti keskiarvon luottamusväli voidaan laskea normaalisti jakautuneelle muuttujalle, kun n> 30 kaavalla: Vakion zarvona käytetään vakiintuneita varmuuden asteita z= 1.96 (95 %) z= 2.58 (99 %) z= 3.29 (99.9 %)

8 Luottamusvälit, joita tutkija A voi laskea kolmen tutkittavan otoksille Otos Otoskeskiarvo Keskivirhe 95% Luottamusväli Otantayksiköt perusjoukossa

9 PITUUSMUUTTUJAN 95% LUOTTAMUSVÄLIT Perusjoukon keskiarvo cm Pituus (cm) Otos (keskiarvon mukaan järjestettynä) 20

10 TULKINTA Lähes kaikki luottamusvälit pitävät sisällään perusjoukon keskiarvon Yksi luottamusväleistä (otos 12, kuvion viimeinen) ei sisällä perusjoukon keskiarvoa Lasketaan: 1/20 = 0.05, eli 5 %, joten 95 % otoskeskiarvon luottamusväleistä sisältää keskiarvon Tulkinta: Tutkija B ei tiedä otostaessaan, minkä erilaisista otoksista hän saa käyttöönsä, joten hän hyväksyy 5 % riskin sille, ettei luottamusväli sisällä perusjoukon keskiarvoa Hänellä on siis 95 % luottamus siihen, että luottamusväli sisältää perusjoukon keskiarvon B:n johtopäätös: 95 % luottamuksella tutkitun muuttujan perusjoukon keskiarvo sisältyy luottamusvälille [162.11, ]

11 VIRHEPÄÄTELMÄN RISKI Luottamustasoon liittyy siis riski virhepäätelmälle 95 % luottamus 5 % riski 99 % luottamus 1 % riski 99.9 % luottamus 0.1 % riski Riskitaso (α) kuvaa todennäköisyyttä tehdä virhepäätelmä väitettäessä, että perusjoukon keskiarvo on luottamusvälin sisällä, vaikka se ei todellisuudessa olekaan Luottamustason valintaan liittyy siis riski tehdä virhepäätelmä Yleisesti tutkimuskäytössä 5 % riskitaso on riittävä Kun määritetään esim. lääkkeiden haittavaikutuksiin liittyviä luottamusvälejä, voidaan käyttää tiukempia riskitasoja

12 KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen empiirisen jakauman esittäminen Frekvenssijakauma Luokittelu Kuviot Tunnusluvut Kaksiulotteisen jakauman esittäminen ja riippuvuus Ristiintaulukko ja kuviot Riippuvuuden tunnusluvut Vähän todennäköisyydestä Otantajakauma Tilastollinen päätöksenteko Estimointi Hypoteesien testaus Perustestejä Keskiarvotestit, varianssianalyysit Riippuvuuden testit

13 TESTAUKSEN TÄRKEIMMÄT VAIHEET Testaushypoteesit: mitä testataan? Nollahypoteesi (ja vastahypoteesi) Riskitaso: millä tasolla tulkitaan p-arvoa? α= 0.05, 0.01 tai Oletukset: sopiiko testi aineistolle? Satunnaisotanta, normaalijakautuneisuus jne. p-arvo: testin tulos nollahypoteesin suhteen Jos p> α, nollahypoteesi jää voimaan Jos p< α, nollahypoteesi hylätään Ennen aineiston tarkastelua Periaatteessa Ennen aineiston tarkastelua Aineiston pohjalta

14 PERUSTESTEJÄ Tarkastellaan eroja Keskiarvotestit Tarkastellaan riippuvuutta Riippuvuustestit Riippumattomat otokset Riippuvat otokset Yhden otoksen t-testi Kahden otoksen t-testi Yksisuuntainen Varianssianalyysi Kahden otoksen t-testi χ 2 -riippumattomuustesti Korrelaatiokertoimen merkitsevyystesti

15 KESKIARVOTESTIT Yhden otoksen keskiarvon testaus Ongelma: Onko perusjoukon keskiarvo sama kuin vertailuarvo? Esim. Poikkeaako jyväskyläläisten miesten kokonaiskolesterolin keskimääräinen arvo merkitsevästi arvosta 5 mmol/l? Hypoteesit: H 0 : µ= µ 0 H 1 : µ µ 0 tai H 1 : µ< µ 0 H 1 : µ> µ 0 Otoksesta laskettu keskiarvo on vertailuarvon suuruinen Keskiarvo poikkeaa vertailuarvosta Keskiarvo on pienempi kuin vertailuarvo Keskiarvo on suurempi kuin vertailuarvo

16 YHDEN OTOKSEN KESKIARVON TESTAUS Oletukset: Muuttuja vähintään välimatka-asteikollinen Otos on riippumaton otos perusjoukosta (ts. se on satunnaisotos) Muuttuja on likimain normaalijakautunut perusjoukossa (vinous, huipukkuus, KS-testi) Riskitaso: Valitaan sopiva α-taso (0.05 / 0.01 / 0.001)

17 YHDEN OTOKSEN KESKIARVON TESTAUS Testisuure: perusjoukon keskihajonta tiedetään tai n> 30 standardoitu normaalijakauma, ks. luentomoniste, liite. yleisemmin keskihajontaa ei tiedetä (lasketaan otoksesta) ja / tai n < 30; käytetään Studentin t-jakaumaa: Otoskeskiarvo ~ t(df) Vertailuarvo Otoskeskihajonta Otoskoko Vapausasteet: lasketaan otoskoon avulla: df= n-1

18 VAPAUSASTEET(DEGREES OF FREEDOM) Useilla otantajakaumilla, jakauman muoto riippuu otoskoosta Esim. pienillä otoksilla (n< 30), kun perusjoukon parametrit ovat tuntemattomia keskiarvoihin liittyvät otantajakaumat noudattavat likimain Studentin t-jakaumaa Jakauman tarkemman muodon eri otoskokojen kohdalla määrittää vapausasteet (vrt. oheinen kuvio t- jakaumasta) Joillain jakaumilla käytettään kahta vapausastetta, esim. varianssianalyysin F-jakaumalle kerrotaan otoskoko (df w ) ja ryhmien lukumäärä (df b )

19 YHDEN OTOKSEN KESKIARVON TESTAUS Johtopäätökset: Jos testisuureeseen liittyvä p-arvo on pienempi kuin riskitaso (p < α), katsotaan testin puoltavan nollahypoteesin hylkäämistä. Tällöin vastahypoteesi selittää tutkittavan ilmiön paremmin ja se astuu voimaan. Jos testisuureeseen liittyvä p-arvo on suurempi kuin riskitaso (p > α), nollahypoteesi saa tukea.

20 YHDEN OTOKSEN KESKIARVON TESTAUS Esimerkki Haluttiin tarkastaa yleisen uimarannan bakteeripitoisuus. Bakteerikanta ei saisi ylittää 200 yksikköä. Otettiin satunnaisista paikoista 10 vesinäytettä, joiden bakteeripitoisuuden keskiarvo oli yksikköä ja keskihajonta Onko uimarannan vesi riittävän puhdasta? Hypoteesit Valitaan yksisuuntainen vastahypoteesi, sillä tämän asian kannalta ei ole merkitystä, jos bakteerikanta on yli 200 yks.: H 0 : µ= 200 H 1 : µ< 200

21 YHDEN OTOKSEN KESKIARVON TESTAUS Oletukset Muuttuja on suhdeasteikollinen Mittauspaikat on valittu satunnaisesti Normaalijakautuneisuus oletetaan voimassa olevaksi (data ei ole saatavilla, joten oletetaan olevan voimassa) Riskitaso Valitaan 0.05, sillä asialla on suhteellisen vakavat seuraukset Testisuure p= df= 10 1 = 9 Johtopäätös Keskiarvo ei ole alle 200, sillä p> 0.05, ja veden bakteeripitoisuutta voidaan siis pitää hälyttävänä.

22 TESTIN JA LUOTTAMUSVÄLIEN ERO Aikaisempien tutkimusten perusteella määritettiin painon keskiarvoksi 75-vuotiaiden jyväskyläläisille miehille 74 kg. Uudesta otoksesta lasketaan painon keskiarvoksi vastaavassa otoksessa 80 kg (keskihajonta 10 kg). Jos n= % luottamusväli keskiarvolle [78.04, 81.96]; 74 ei sijaitse välillä, joten merkitsevä ero suhteessa vertailuarvoon Testi H 0 : µ= 74, p< 0.001: nollahypoteesi hylätään, joten merkitsevä ero suhteessa vertailuarvoon Yleensä käytetään merkitsevyystestiä, jos halutaan tietää eron merkitsevyys; jos taas halutaan tietää minkälaisia eroja olisi mahdollista havaita, lasketaan luottamusväli

23 Kahden riippumattoman otoksen keskiarvojen vertailu Ongelma: Ovatko kahden ryhmän perusjoukkojen keskiarvot yhtä suuret? Esim. Onko jyväskyläläisten miesten keskimääräinen kehon rasvaprosentti yhtä suuri kuin göteborgilaisten miesten? Hypoteesit: H 0 : µ 1 = µ 2 Keskiarvot ovat yhtä suuret (µ 1 -µ 2 = 0) H 1 : µ 1 µ 2 tai H 1 : µ 1 < µ 2 H 1 : µ 1 > µ 2 Keskiarvot eri suuret Ensimmäisen ryhmän keskiarvo on pienempi kuin toisen ryhmän Toisen ryhmän keskiarvo on pienempi kuin ensimmäisen ryhmän

24 Kahden riippumattoman otoksen keskiarvojen vertailu Oletukset: Muuttuja vähintään välimatka-asteikollinen Otos on riippumaton otos perusjoukosta (ts. se on satunnaisotos) ja tarkasteltavat kaksi ryhmää ovat riippumattomia toisistaan Muuttuja on likimain normaalijakautunut kummassakin perusjoukossa (KS-testi) Perusjoukon varianssit ovat yhtä suuret. Jos ovat erisuuret, käytetään erilaista menettelyä kuin tässä esitellään. Riskitaso: Valitaan sopiva α-taso (0.05 / 0.01 / 0.001)

25 Kahden riippumattoman otoksen keskiarvojen vertailu Testisuure: Lasketaan yhteinen varianssiestimaatti s 2 Sitten keskiarvojen erotuksen t-testisuure: ~ t(df) Vapausasteet: lasketaan otoskokojen avulla: df= n 1 + n 2-2

26 Kahden riippumattoman otoksen keskiarvojen vertailu Johtopäätökset: Jos testisuureeseen liittyvä p-arvo on pienempi kuin riskitaso (p< α), nollahypoteesin hylätään ja vastahypoteesi astuu voimaan Jos testisuureeseen liittyvä p-arvo on suurempi kuin riskitaso (p> α), nollahypoteesi saa tukea Esim. jos riskitaso on α= 0.05, hylätään nollahypoteesi, jos p-arvo on tätä pienempi.

27 Kahden riippumattoman otoksen keskiarvojen vertailu Esimerkki Tarkastellaan kehon rasvatonta painoa 75- vuotiailla jyväskyläläisillä ja göteborgilaisilla miehillä. Molemmista perusjoukoista on kerätty satunnaisotos ja havaittiin: Hypoteesit jyväskyläläiset: n 1 = 104, x 1 = (s 1 = 6.35) göteborgilaiset: n 2 = 118, x 2 = (s 2 = 6.43) Valitaan kaksisuuntainen vastahypoteesi, sillä tuloksen suunnasta ei ole tietoa: H 0 : µ 1 = µ 2 H 1 : µ 1 µ 2

28 Kahden riippumattoman otoksen keskiarvojen vertailu Oletukset Muuttuja on suhdeasteikollinen Otokset satunnaisotoksia ja riippumattomia toisistaan Normaalijakautuneisuus: KS-testin perusteella havaitaan: Kolmogorov-Smirnov Paikkakunta Statistic df Sig. NC2618 Kehon 1 Jyväskylä, ,101 rasvaton paino 2 Göteborg, ,200* Varianssit oletetaan yhtä suuriksi (testauksesta myöhemmin) Riskitaso Valitaan 0.05, joka on yleisesti käytetty riskitaso tutkimuksessa.

29 Kahden riippumattoman otoksen keskiarvojen vertailu Testisuure df= = 220 p= Johtopäätös Nollahypoteesi hylätään, koska p< 0.05, ja sanotaan, että kehon rasvattoman painon keskiarvot eroavat toisistaan.

30 Normaalijakautuneisuus ryhmittäin

31 H 0 : Muuttuja on normaalistijakautunut.

32 Esim. suhteellisen tarkka 95 % luottamusväli: ± H 0 : s 12 = s 2 2 H 0 : µ 1 = µ 2 Jyväskyläläisten ja göteborgilaisten miesten ryhmien variansseja voitiin pitää yhtä suurina (p = 0.979). Paikkakuntien välillä rasvaton kehonpaino oli korkeampi göteborgilaisilla miehillä (t= -2.26, df= 220, p= 0.025).

33 RAPORTOINTI Table 1. Means, standard deviations(sd) and group comparisonp-valuesfor 75-year-old menlivingin Jyväskylä and Göteborg in Jyväskylä (n = 103) Göteborg (n = 116) Mean SD Mean SD p-value Lean body mass Glucose Waist girth Diastolic blood pressure

34 NORMAALIJAKAUTUNEISUUS (JÄÄNNÖSTARKASTELU) if (sexcntry=1) z = nc if (sexcntry=3) z = nc Exe.

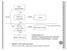
35 Data: järjestysast. Ei Kyllä Jatkuva, normaali Kyllä t-testi Ei Suuria poikkeavia arvoja Ei Mann-Whitney Kyllä Mediaani testi ks. luentomoniste Valintakaavio: Kahden riippumattoman ryhmän jakauman keskikohdan vertailu Jäitkö vielä epävarmaksi: Selvitä antavatko testit samansuuntaisen tuloksen.

36 Kahden riippuvan otoksen keskiarvojen vertailu Ongelma: Ovatko kahden ryhmän perusjoukkojen keskiarvot yhtä suuret, kun ryhmien välillä on riippuvuutta? Esim. Onko jyväskyläläisten miesten keskimääräinen kehon rasvaprosentti yhtä suuri 75 vuotiaana kuin 80 vuotiaana? Hypoteesit: H 0 : µ 1 = µ 2 H 1 : µ 1 µ 2 tai H 1 : µ 1 < µ 2 H 1 : µ 1 > µ 2 pienempi Keskiarvot ovat yhtä suuret Keskiarvot eri suuret Ensimmäisen ryhmän keskiarvo on pienempi kuin toisen ryhmän Toisen ryhmän keskiarvo on kuin ensimmäisen ryhmän

37 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU Riippuvuus Riippuvuutta voi otosten välillä aiheuttaa seuranta-asetelma (alku-vs. seurantamittaukset), kaksosasetelma (kaksosparien vertailu) Esim. seurantatilanteessa voidaan merkitä esim. kehon rasvaprosenttia alkumittauksessa (X) ja seurantamittauksessa (Y) Oletukset: Muuttuja on vähintään välimatka-asteikollinen Havaintoparit riippumaton otos perusjoukosta Vastinparien erotus (d i = x i y i ) on perusjoukossa normaalisti jakautunut (erotusmuuttujaa D voidaan testata esim. KStestillä) Riskitaso: Valitaan sopiva α-taso (0.05 / 0.01 / 0.001)

38 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU Testisuure: Lasketaan erotusten d i keskiarvo ja keskihajonta: Sitten keskiarvojen erotuksen t-testisuure: ~ t(df) Vapausasteet: lasketaan otoskoon avulla: df= n 1

39 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU Johtopäätökset: Jos testisuureeseen liittyvä p-arvo on pienempi kuin riskitaso (p< α), nollahypoteesin hylätään ja vastahypoteesi astuu voimaan Jos testisuureeseen liittyvä p-arvo on suurempi kuin riskitaso (p> α), nollahypoteesi saa tukea

40 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU Esimerkki Lääketehdas on tuottanut kaksi unilääkettä UNI1 ja UNI2. Nyt halutaan tietää kumpi lääke antaa pidemmän unen. Valitaan satunnaisotannallakoehenkilöt, jotka ottavat molempia uni-lääkkeitä ja kertovat unen pituuden. Aineiston perusteella tarkastellaan, onko unilääkkeillä eroa saavutetun nukkumisajan suhteen. Kh UNI1 UNI Yhteensä Keskiarvo

41 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU 8 Unimäärä (tuntia) Keskiarvo

42 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU Hypoteesit Valitaan kaksisuuntainen vastahypoteesi, sillä tuloksen suunnasta ei ole ennakkotietoa: H 0 : µ 1 = µ 2 H 1 : µ 1 µ 2 Oletukset Satunnaisotos ja suhdeasteikollinen muuttuja Erotusten jakauma on normaali KS-testillä Kolmogorov-Smirnov testattuna: Statistic df Sig. Riskitaso D,178 10,200* Valitaan α = 0.05, koska seuraukset eivät ole vakavat.

43 KAHDEN RIIPPUVAN OTOKSEN KESKIARVOJEN VERTAILU Testisuure Kh UNI1 UNI2 d i d i p= Johtopäätös: Nollahypoteesi jää voimaan, sillä p> Yhteensä Keskiarvo

44 H 0 : Muuttuja on normaalistijakautunut.

45 H 0 : ρ= 0 H 0 : µ 1 = µ 2

46 Data: järjestysast. Ei Jatkuva, normaali Ei Symmetrinen Kyllä Kyllä Kyllä Merkkitesti t-testi ks. luentomoniste Wilcoxon Ei Merkkitesti Valintakaavio: Kahden riippuvan ryhmän jakauman keskikohdan vertailu