TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
|
|
|
- Pauliina Lehtonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas
2 JAKAUMAN MUOTO Vinous, skew (g 1, γ 1 ) Kertoo jakauman symmetrisyydestä Vertailuarvona on nolla, joka vastaa symmetristä jakaumaa (mm. normaalijakauma) Vertailuarvona: g 1 < 2, jos jakauman symmetrisyydessä ei ole selkeitä ongelmia Jos g 1 on positiivinen jakauma on vino oikealle (häntä oikealla) Jos g 1 on negatiivinen vinous on vasemmalle (häntä vasemmalla) Merkitsevyystesti: g 1 /[s.e.(g 1 )] < 2, jos vinous ei ole tilastollisesti merkitsevää. Luottamusväli: Jos väli g 1 ± 2 s.e.(g 1 ) sisältää nollan, vinous ei ole tilastollisesti merkitsevää. Esim. miesten pituuden vinous g 1 = ja sen keskivirhe on Ei ylitä vertailuarvoa Ei tilastollisesti merkitsevä, koska merkitsevyystestin arvoksi saadaan / = -1.10; luottamusväli: ± = [-1.748, 0.508] sisältää nollan Jakaumaa voidaan pitää symmetrisenä perusjoukossa
3 JAKAUMAN MUOTO Huipukkuus, kurtosis (g 2, γ 2 ) Kertoo jakauman terävyydestä tai latteudesta symmetrisyydestä (mm. suhteessa normaalijakaumaan) Vertailuarvona on nolla, joka vastaa jakaumaa (mm. normaalijakauma) Vertailuarvona: g 2 < 2, jos jakaumassa ei ole merkittäviä ongelmia huipukkuuden suhteen Positiivinen g 2 tarkoittaa, että jakaumalla on terävä huippu Negatiivinen g 2 tarkoittaa, että jakauma on lattea Merkitsevyystesti ja luottamusväli kuten vinouden tunnusluvulla Esim. miesten pituuden huipukkuusg 2 = 0.41 ja sen keskivirhe on 1.09 Ei ylitä vertailuarvoa Ei tilastollisesti merkitsevä, koska merkitsevyystestin arvoksi saadaan 0.41 / 1.09 = 0.38; luottamusväli: ± = [-1.77, 2.59] sisältää nollan Perusjoukon jakaumaa ei siis pidetä huipukkaana
4 ESIMERKKI Masentuneisuuden oireet Götegorgilaiset 75-vuotiaat Miehet, NORA-tutkimus, /0.217 = > /0.431 = > 2 Positiivinen vinous: Jakauman häntä on oikealla.
5 SUHTEELLINEN OSUUS, PROPORTION Symboli: otoksessa p, perusjoukossa π Havaintoryhmän frekvenssin f osuus koko aineistosta Lasketaan: p = f / n, missä f sisältää sen ryhmän frekvenssin, josta ollaan kiinnostuneita ja n on otoskoko Suhteellinen osuus vaihtelee välillä [0, 1] Prosenttiosuus saadaan kertomalla suhteellinen osuus sadalla: p 100 Mitta-asteikko: vähintään luokitteluasteikko Esim. tutkimukseen osallistui 284, ja heistä 106 oli miehiä. Miesten suhteellinen osuus oli siis p = 106 / 284 = 0.37 (eli 37 %)
6 ESIMERKKEJÄ Havaintoaineistossa oli käytettävissä 690 tutkittavaa ja vastausprosentin kerrottiin olleen n %. Kuinka paljon tutkittavia oli alun perin otostettu? p = f / n = 690 / n n = 690 / = 854 Kuinka moni jätti vastaamatta? = (ts % ei vastannut) = 164 jätti vastaamatta (myös: = 164) Havaintoaineisto koostui n = 50 tutkittavasta. Alkumittauksessa 15 tutkittavalla havaittiin liikuntavaikeuksia. Seurantamittauksessa vaikeuksia oli 12:ta. Mikä oli muutoksen suunta ja suuruus prosenttimuodossa ilmaistuna. 1: p 1 = 15 / 50 = 0.30 (30 %); p 2 = 12 /50 = 0.24 (24 %); eli muutos oli p 2 p 1 = = -6 prosenttiyksikköä, ts. laskua oli 6 prosenttiyksikköä (Huom! Vähennetään aina seurannan prosentit alkumittauksen prosenteista) 2: (p 2 p 1 ) / p 1 = (24 30) / 30 = -6 / 30 = -0.2 (-20 %), eli laskua oli n. 20 prosenttia
7 LAATIKKO-JANA KUVIO (BOX PLOT) Q 3 Md Q 1 - Kuvaa ryhmittäin jatkuvan muuttujan jakauman keskeisiä piirteitä - Laatikko kuvaa kvartiilien rajaamaa aluetta (keskimmäinen 50 % havainnoista), joka jaetaan kahteen osaan mediaanin kohdalta
8 LAATIKKO-JANA KUVIO (BOX PLOT) Q 3 Md Q 1 - Laatikon molemmin puolin erotetaan laskennalliset minimi- ja maksimiarvot (vaakasuorat janat) - Janat ovat 1.5 kertaa (laskennallisen) kvartiilivälin pituuden verran laatikon ylä- ja alapuolella - Laskennallisuuden takia Etäisyys laatikkoon voi olla erilainen laatikon alaja yläpuolella
9 LAATIKKO-JANA KUVIO (BOX PLOT) Q 3 Md Q kertaa kvartiilivälin pituuden etäisyydellä laatikosta: poikkeava havainto (outlier) - yli 3 kertaa kvartiilivälin pituuden etäisyydellä laatikosta: erittäin poikkeava havainto (extreme) *
10 LAATIKKO-JANA KUVIO (BOX PLOT) Q 3 Md Q 1 Kuviosta nähdään mm.: - Miesten jakauman keskikohta on naisia korkeammalla tasolla - Miesten hajonta näyttää olevan hieman suurempaa kuin naisilla - Naisten jakauma on keskittynyttiiviimmin jakauman keskikohtaan - Naisilla osa havainnoista on merkitty poikkeaviksi
11 Kaikki havaitut tapaukset (n = 20) Keskiarvo 171 Keskihajonta 10 Satunnaisesti puuttuvat tapaukset (n = 15) Keskiarvo 171 Keskihajonta 10
12 Kaikki havaitut tapaukset (n = 20) Keskiarvo 171 Keskihajonta 10 Ei-satunnaisesti puuttuvat tapaukset (n = 16) Keskiarvo 175 Keskihajonta 8 Puuttuvat Havaitut
13 Keskiarvo: Keskihajonta: p [318, 418] = 67 % 368 N 50 N p: suhteellinen frekvenssi (tässä yhden keskihajonnan välille keskiarvon ympärillä sijoittuvien osuus ) Data
14 Keskiarvo: Keskihajonta: p [296, 474] = 75 % 385 N 89 N p: suhteellinen frekvenssi (tässä yhden keskihajonnan välille keskiarvon ympärillä sijoittuvien osuus ) Data
15 Keskiarvo: 376 N Keskihajonta: 103 N p [273, 479] = 83 % p: suhteellinen frekvenssi (tässä yhden keskihajonnan välille keskiarvon ympärillä sijoittuvien osuus ) Data
16 ESIMERKKI LONKKAMURTUMAPOTILAIDEN KUNTOUTUS Ote: Salpakoski et al. (2014). Lähde:
17 KUN PITÄÄ TIIVISTÄÄ MUUTTUJAN JAKAUMAN TIETOA Mitta-asteikko Jatkuva Nominaali Ordinaali Raportoi Luokkafrekvenssit Tarkista vinous ja huipukkuus Molemmat < 2 Ainakin toinen > 2 Virhe datassa tms. Muokkaa Selvitä syy Vino/huipukas jakauma, Poikkeava havainto Raportoi Keskiarvo ja -hajonta Raportoi Mediaani ja kvartiilivälin pituus Jos tarkasteltavana on alaryhmiä (miehet / naiset tms.), käy vaiheet läpi kullekin ryhmälle erikseen.
18 KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen empiirisen jakauman esittäminen Frekvenssijakauma Luokittelu Kuviot Tunnusluvut Kaksiulotteisen jakauman esittäminen ja riippuvuus Ristiintaulukko ja kuviot Riippuvuuden tunnusluvut Vähän todennäköisyydestä Otantajakauma Tilastollinen päätöksenteko Estimointi Hypoteesien testaus Perustestejä Keskiarvotestit, varianssianalyysit Riippuvuuden testit
19 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Luokittelu- ja järjestysasteikko: Ristiintaulukko Sukupuoli Mies (1) Nainen (2) Maa Suomi (1) Ruotsi (2) Tanska (3) Yhteensä Arvoparin frekvenssi näkyy taulukon soluista Ehdolliset frekvenssit: kiinnitetään yksi maamuuttujan luokka (esim. Suomi) ja tarkastellaan sukupuolijakaumaa
20 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Sukupuoli Mies (1) Nainen (2) Maa Suomi (1) Ruotsi (2) Tanska (3) Yhteensä Riviprosentit: / 355 = % / 355 = % / 368 = % / 368 = % / 481 = % / 481 = %
21 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Luokitteluasteikko: Ristiintaulukko Sukupuoli Mies (1) Nainen (2) Maa Suomi (1) 119 (34 %) 236 (66 %) 355 (100 %) Ruotsi (2) 159 (43 %) 209 (57 %) 368 (100 %) Tanska (3) 222 (46 %) 259 (54 %) 481 (100 %) Yhteensä Esim. Suomessa otos painottui selkeämmin naisiin (noin kaksi kolmannesta oli naisia)
22 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Sukupuoli Mies (1) Nainen (2) Maa Suomi (1) Ruotsi (2) Tanska (3) Yhteensä Sarakeprosentit: / 500 = % / 500 = % / 500 = % / 704 = % / 704 = % / 704 = %
23 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Sukupuoli Mies (1) Nainen (2) Maa Suomi (1) 119 (24 %) 236 (34 %) 355 Ruotsi (2) 159 (32 %) 209 (30 %) 368 Tanska (3) 222 (44 %) 259 (37 %) 481 Yhteensä 500 (100 %) 704 (100 %) 1204 Esim. pienin osuus miehistä muodostui suomalaisista miehistä, naisista pienin osuus oli ruotsalaisilla
24 RISTIINTAULUKON GRAAFINEN ESITYS Huono: Vaikea erottaa pylväitten keskinäisiä korkeuksia Miehet 100 Naiset 50 0 Suomi Ruotsi Tanska Naiset Miehet
25 RISTIINTAULUKON GRAAFINEN ESITYS Mies Nainen 50 0 Suomi Ruotsi Tanska Maa
26 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Jatkuvat muuttujat: hajontakuvio Koehenkilöiden pituus 75- ja 80-vuotiaana ID Pituus 75 Pituus
27 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Jatkuvat muuttujat: hajontakuvio Koehenkilöiden pituus 75- ja 80-vuotiaana ID Pituus 75 Pituus
28 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Jatkuvat muuttujat: hajontakuvio Koehenkilöiden pituus 75- ja 80-vuotiaana ID Pituus 75 Pituus
29 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Tulkintaa helpottavia kuvaajia Identiteettiviiva
30 KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Tulkintaa helpottavia kuvaajia Identiteettiviiva Regressiosuora
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas f 332 = 3 Kvartiilit(302, 365, 413) Kvartiilit: missä sijaitsee keskimmäinen 50 % aineistosta? Kvartiilit(302, 365, 413) Keskiarvo (362.2) Keskiarvo
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas f 332 = 3 Kvartiilit(302, 365, 413) Kvartiilit: missä sijaitsee keskimmäinen 50 % aineistosta? Kvartiilit(302, 365, 413) Keskiarvo (362.2) Keskiarvo
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas MUITA HAJONNAN TUNNUSLUKUJA Varianssi, variance (s 2, σ 2 ) Keskihajonnan neliö Käyttöä enemmän osana erilaisia menetelmiä (mm. varianssianalyysi),
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas MUITA HAJONNAN TUNNUSLUKUJA Varianssi, variance (s 2, σ 2 ) Keskihajonnan neliö Käyttöä enemmän osana erilaisia menetelmiä (mm. varianssianalyysi),
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Jatkuvat muuttujat: hajontakuvio Koehenkilöiden pituus 75- ja 80-vuotiaana ID Pituus 75 Pituus 80 1 156
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KAKSIULOTTEISEN EMPIIRISEN JAKAUMAN TARKASTELU Jatkuvat muuttujat: hajontakuvio Koehenkilöiden pituus 75- ja 80-vuotiaana ID Pituus 75 Pituus 80 1 156
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas TEOREETTISISTA JAKAUMISTA Usein johtopäätösten teko helpottuu huomattavasti, jos tarkasteltavan muuttujan perusjoukon jakauma noudattaa
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas TEOREETTISISTA JAKAUMISTA Usein johtopäätösten teko helpottuu huomattavasti, jos tarkasteltavan muuttujan perusjoukon jakauma noudattaa
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas Ilman Ruotsia: r = 0.862 N Engl J Med 2012; 367:1562-1564. POIKKEAVAN HAVAINNON VAIKUTUS PAIRWISE VAI LISTWISE? Kun aineistossa on muuttujia, joilla
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas Ilman Ruotsia: r = 0.862 N Engl J Med 2012; 367:1562-1564. POIKKEAVAN HAVAINNON VAIKUTUS PAIRWISE VAI LISTWISE? Kun aineistossa on muuttujia, joilla
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas RIIPPUVUUS ALARYHMISSÄ Riippuvuus saattaa olla erilaista jos samassa aineistossa on esim. tutkittavia molemmista sukupuolista Yhteys saattaa olla erilaista
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas RIIPPUVUUS ALARYHMISSÄ Riippuvuus saattaa olla erilaista jos samassa aineistossa on esim. tutkittavia molemmista sukupuolista Yhteys saattaa olla erilaista
Tilastollisen analyysin perusteet Luento 1: Lokaatio ja hajonta
 Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas AINEISTON TARKASTELU JA MUOKKAUS AINA ennen varsinaista analyysia suoritetaan aineiston tarkastelu ja muokkaus, data-analyysi Tavoitteena:
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas AINEISTON TARKASTELU JA MUOKKAUS AINA ennen varsinaista analyysia suoritetaan aineiston tarkastelu ja muokkaus, data-analyysi Tavoitteena:
Kandidaatintutkielman aineistonhankinta ja analyysi
 Kandidaatintutkielman aineistonhankinta ja analyysi Anna-Kaisa Ylitalo M 315, anna-kaisa.ylitalo@jyu.fi Musiikin, taiteen ja kulttuurin tutkimuksen laitos Jyväskylän yliopisto 2018 2 Havaintomatriisi Havaintomatriisi
Kandidaatintutkielman aineistonhankinta ja analyysi Anna-Kaisa Ylitalo M 315, anna-kaisa.ylitalo@jyu.fi Musiikin, taiteen ja kulttuurin tutkimuksen laitos Jyväskylän yliopisto 2018 2 Havaintomatriisi Havaintomatriisi
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas Keskivirheyksiköllä ilmaistuna voidaan erottaa otantajakaumalta kriittisiä kohtia: Keskimmäinen 95 % otoskeskiarvoista välillä [-1.96,+1.96] Keskimmäinen
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas Keskivirheyksiköllä ilmaistuna voidaan erottaa otantajakaumalta kriittisiä kohtia: Keskimmäinen 95 % otoskeskiarvoista välillä [-1.96,+1.96] Keskimmäinen
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas OTOSTAMISEEN LIITTYVIÄ ONGELMIA Otostamisen ongelmat liittyvä satunnaistamisen epäonnistumiseen Ongelmat otantakehyksen määrittämisessä Väärän otantamenetelmän
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas OTOSTAMISEEN LIITTYVIÄ ONGELMIA Otostamisen ongelmat liittyvä satunnaistamisen epäonnistumiseen Ongelmat otantakehyksen määrittämisessä Väärän otantamenetelmän
HAVAITUT JA ODOTETUT FREKVENSSIT
 HAVAITUT JA ODOTETUT FREKVENSSIT F: E: Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies (1) 59 28 4 91 Nainen (2) 5 14 174 193 Yhteensä 64 42 178 284 Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies
HAVAITUT JA ODOTETUT FREKVENSSIT F: E: Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies (1) 59 28 4 91 Nainen (2) 5 14 174 193 Yhteensä 64 42 178 284 Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas LUENNOT Luento Paikka Vko Päivä Pvm Klo 1 L 304 8 Pe 21.2. 08:15-10:00 2 L 304 9 To 27.2. 12:15-14:00 3 L 304 9 Pe 28.2. 08:15-10:00 4 L 304 10 Ke 5.3.
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas LUENNOT Luento Paikka Vko Päivä Pvm Klo 1 L 304 8 Pe 21.2. 08:15-10:00 2 L 304 9 To 27.2. 12:15-14:00 3 L 304 9 Pe 28.2. 08:15-10:00 4 L 304 10 Ke 5.3.
Til.yks. x y z
 Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas Itse arvioidun terveydentilan ja sukupuolen välinen riippuvuustarkastelu. Jyväskyläläiset 75-vuotiaat miehet ja naiset vuonna 1989.
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas Itse arvioidun terveydentilan ja sukupuolen välinen riippuvuustarkastelu. Jyväskyläläiset 75-vuotiaat miehet ja naiset vuonna 1989.
Tilastollisen analyysin perusteet Luento 1: Lokaatio ja hajonta
 Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Näistä standardoiduista arvoista laskettu keskiarvo on nolla ja varianssi 1, näin on standardoidulle muuttujalle aina.
 [MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, kevät 2019 https://coursepages.uta.fi/mtttp1/kevat-2019/ HARJOITUS 3 Joitain ratkaisuja 1. x =(8+9+6+7+10)/5 = 8, s 2 = ((8 8) 2 + (9 8) 2 +(6 8) 2 + (7 8) 2 ) +
[MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, kevät 2019 https://coursepages.uta.fi/mtttp1/kevat-2019/ HARJOITUS 3 Joitain ratkaisuja 1. x =(8+9+6+7+10)/5 = 8, s 2 = ((8 8) 2 + (9 8) 2 +(6 8) 2 + (7 8) 2 ) +
Näistä standardoiduista arvoista laskettu keskiarvo on nolla ja varianssi 1, näin on standardoidulle muuttujalle aina.
 [MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, Syksy 2017 http://www.uta.fi/sis/mtt/mtttp1/syksy_2017.html HARJOITUS 3 viikko 40 Joitain ratkaisuja 1. Suoritetaan standardointi. Standardoidut arvot ovat z 1 =
[MTTTP1] TILASTOTIETEEN JOHDANTOKURSSI, Syksy 2017 http://www.uta.fi/sis/mtt/mtttp1/syksy_2017.html HARJOITUS 3 viikko 40 Joitain ratkaisuja 1. Suoritetaan standardointi. Standardoidut arvot ovat z 1 =
Mat Tilastollisen analyysin perusteet. Tilastollisten aineistojen kerääminen ja mittaaminen Tilastollisten aineistojen kuvaaminen Väliestimointi
 Mat-2.104 Tilastollisen analyysin perusteet / Ratkaisut Aiheet: Avainsanat: Tilastollisten aineistojen kerääminen ja mittaaminen Tilastollisten aineistojen kuvaaminen Väliestimointi Diskreetit muuttujat,
Mat-2.104 Tilastollisen analyysin perusteet / Ratkaisut Aiheet: Avainsanat: Tilastollisten aineistojen kerääminen ja mittaaminen Tilastollisten aineistojen kuvaaminen Väliestimointi Diskreetit muuttujat,
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KATO (MISSING DATA, ATTRITION) Kun otostetuista havaintoyksiköistä saavutetaan (mitataan) vain osa, tarkoittaa kato sitä osaa tutkittavista tai mittauksista,
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KATO (MISSING DATA, ATTRITION) Kun otostetuista havaintoyksiköistä saavutetaan (mitataan) vain osa, tarkoittaa kato sitä osaa tutkittavista tai mittauksista,
r = 0.221 n = 121 Tilastollista testausta varten määritetään aluksi hypoteesit.
 A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
3. a) Mitkä ovat tilastolliset mitta-asteikot? b) Millä tavalla nominaaliasteikollisen muuttujan jakauman voi esittää?
 Seuraavassa muutamia lisätehtäviä 1. Erään yrityksen satunnaisesti valittujen työntekijöiden poissaolopäivien määrät olivat vuonna 003: 5, 3, 16, 9, 0, 1, 3,, 19, 5, 19, 11,, 0, 4, 6, 1, 15, 4, 0,, 4,
Seuraavassa muutamia lisätehtäviä 1. Erään yrityksen satunnaisesti valittujen työntekijöiden poissaolopäivien määrät olivat vuonna 003: 5, 3, 16, 9, 0, 1, 3,, 19, 5, 19, 11,, 0, 4, 6, 1, 15, 4, 0,, 4,
Til.yks. x y z 1 2 1 20.3 2 2 1 23.5 9 2 1 4.7 10 2 2 6.2 11 2 2 15.6 17 2 2 23.4 18 1 1 12.5 19 1 1 7.8 24 1 1 9.4 25 1 2 28.1 26 1 2-6.2 33 1 2 33.
 Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
Tehtävien ratkaisuja. a) Tilastoyksiköitä ovat työntekijät: Vatanen, Virtanen, Virtanen ja Voutilainen; muuttujina: ikä, asema, palkka, lasten lkm (ja nimikin voidaan tulkita muuttujaksi, jos niin halutaan)
pisteet Frekvenssi frekvenssi Yhteensä
 806118P JOHDATUS TILASTOTIETEESEEN Loppukoe 15.3.2018 (Jari Päkkilä) 1. Kevään -17 Johdaus tilastotieteeseen -kurssin opiskelijoiden harjoitusaktiivisuudesta saatujen pisteiden frekvenssijakauma: Harjoitus-
806118P JOHDATUS TILASTOTIETEESEEN Loppukoe 15.3.2018 (Jari Päkkilä) 1. Kevään -17 Johdaus tilastotieteeseen -kurssin opiskelijoiden harjoitusaktiivisuudesta saatujen pisteiden frekvenssijakauma: Harjoitus-
Esim. Pulssi-muuttujan frekvenssijakauma, aineisto luentomoniste liite 4
 18.9.2018/1 MTTTP1, luento 18.9.2018 KERTAUSTA Esim. Pulssi-muuttujan frekvenssijakauma, aineisto luentomoniste liite 4 pyöristetyt todelliset luokka- frekvenssi luokkarajat luokkarajat keskus 42 52 41,5
18.9.2018/1 MTTTP1, luento 18.9.2018 KERTAUSTA Esim. Pulssi-muuttujan frekvenssijakauma, aineisto luentomoniste liite 4 pyöristetyt todelliset luokka- frekvenssi luokkarajat luokkarajat keskus 42 52 41,5
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen 1 Jakaumaoletuksien testaamiseen soveltuvat testit χ 2 -yhteensopivuustesti yksi otos otoksen
Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen 1 Jakaumaoletuksien testaamiseen soveltuvat testit χ 2 -yhteensopivuustesti yksi otos otoksen
Hannu mies LTK 180 Johanna nainen HuTK 168 Laura nainen LuTK 173 Jere mies NA 173 Riitta nainen LTK 164
 86118P JOHDATUS TILASTOTIETEESEEN Harjoituksen 3 ratkaisut, viikko 5, kevät 19 1. a) Havaintomatriisissa on viisi riviä (eli tilastoyksikköä) ja neljä saraketta (eli muuttujaa). Hannu mies LTK 18 Johanna
86118P JOHDATUS TILASTOTIETEESEEN Harjoituksen 3 ratkaisut, viikko 5, kevät 19 1. a) Havaintomatriisissa on viisi riviä (eli tilastoyksikköä) ja neljä saraketta (eli muuttujaa). Hannu mies LTK 18 Johanna
1.Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet
 VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: 1.Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: 1.Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 11. lokakuuta 2007 Antti Rasila () TodB 11. lokakuuta 2007 1 / 15 1 Johdantoa tilastotieteeseen Peruskäsitteitä Tilastollisen kuvailun ja päättelyn menetelmiä
Sovellettu todennäköisyyslaskenta B Antti Rasila 11. lokakuuta 2007 Antti Rasila () TodB 11. lokakuuta 2007 1 / 15 1 Johdantoa tilastotieteeseen Peruskäsitteitä Tilastollisen kuvailun ja päättelyn menetelmiä
Ennen seuraavia tehtäviä tarkista, että KUNNAT-aineistossasi on 12 muuttujaa ja 416 tilastoyksikköä.
 Tilastollinen tietojenkäsittely / SPSS Harjoitus 3 Tällä harjoituskerralla tarkastellaan harjoituksissa 2 tehtyjä SPSS-havaintoaineistoja KUNNAT, kyselya ja kyselyb. Aineistoihin tutustutaan mm. erilaisten
Tilastollinen tietojenkäsittely / SPSS Harjoitus 3 Tällä harjoituskerralla tarkastellaan harjoituksissa 2 tehtyjä SPSS-havaintoaineistoja KUNNAT, kyselya ja kyselyb. Aineistoihin tutustutaan mm. erilaisten
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-.04 Tilastollisen analyysin perusteet, kevät 007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen Jakaumaoletuksien testaamiseen soveltuvat testit χ -yhteensopivuustesti yksi otos otoksen vertaaminen
Mat-.04 Tilastollisen analyysin perusteet, kevät 007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen Jakaumaoletuksien testaamiseen soveltuvat testit χ -yhteensopivuustesti yksi otos otoksen vertaaminen
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas Marko: Aineisto: Kolme muuttujaa: Tutkimuskysymys: Kaksi ryhmää (koe ja kontrolli), liikuntainterventio Kävelynopeus (metri/sekunti) Polven ojennusvoima
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas Marko: Aineisto: Kolme muuttujaa: Tutkimuskysymys: Kaksi ryhmää (koe ja kontrolli), liikuntainterventio Kävelynopeus (metri/sekunti) Polven ojennusvoima
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas LUENNOT 2017 Luento Paikka Vko Päivä Pvm Klo 1 L 304 3 To 19.1.2016 12:15-14:00 2 MaA 103 3 Pe 20.1.2016 10:15-12:00 3 MaA 103 4 Ke
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas LUENNOT 2017 Luento Paikka Vko Päivä Pvm Klo 1 L 304 3 To 19.1.2016 12:15-14:00 2 MaA 103 3 Pe 20.1.2016 10:15-12:00 3 MaA 103 4 Ke
MTTTA1 Tilastomenetelmien perusteet 5 op Luento , osa 1. 1 Kokonaisuudet johon opintojakso kuuluu
 5.3.2018/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 5.3.2018, osa 1 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2017
5.3.2018/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 5.3.2018, osa 1 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2017
Ennen seuraavia tehtäviä tarkista, että KUNNAT-aineistossasi on 12 muuttujaa ja 416 tilastoyksikköä.
 Tilastollinen tietojenkäsittely / SPSS Harjoitus 3 Tällä harjoituskerralla tarkastellaan harjoituksissa 2 tehtyjä SPSS-havaintoaineistoja KUNNAT, kyselya ja kyselyb. Jos epäilet, että aineistosi eivät
Tilastollinen tietojenkäsittely / SPSS Harjoitus 3 Tällä harjoituskerralla tarkastellaan harjoituksissa 2 tehtyjä SPSS-havaintoaineistoja KUNNAT, kyselya ja kyselyb. Jos epäilet, että aineistosi eivät
5 Lisa materiaali. 5.1 Ristiintaulukointi
 5 Lisa materiaali 5.1 Ristiintaulukointi 270. a) Aineiston koko nähdään frekvenssitaulukon oikeasta alakulmasta: N = 559. Tilastotieteen johdantokurssille osallistui yhteensä 559 opiskelijaa. Huomaa: Opiskelijoiden
5 Lisa materiaali 5.1 Ristiintaulukointi 270. a) Aineiston koko nähdään frekvenssitaulukon oikeasta alakulmasta: N = 559. Tilastotieteen johdantokurssille osallistui yhteensä 559 opiskelijaa. Huomaa: Opiskelijoiden
Tilastotieteen kertaus. Kuusinen/Heliövaara 1
 Tilastotieteen kertaus Kuusinen/Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla reaalimaailman ilmiöistä voidaan tehdä johtopäätöksiä tilanteissa, joissa
Tilastotieteen kertaus Kuusinen/Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla reaalimaailman ilmiöistä voidaan tehdä johtopäätöksiä tilanteissa, joissa
4. Seuraavaan ristiintaulukkoon on kerätty tehtaassa valmistettujen toimivien ja ei-toimivien leikkijunien lukumäärät eri työvuoroissa:
 Lisätehtäviä (siis vanhoja tenttikysymyksiä) 1. Erään yrityksen satunnaisesti valittujen työntekijöiden poissaolopäivien määrät olivat vuonna 003: 5, 3, 16, 9, 0, 1, 3,, 19, 5, 19, 11,, 0, 4, 6, 1, 15,
Lisätehtäviä (siis vanhoja tenttikysymyksiä) 1. Erään yrityksen satunnaisesti valittujen työntekijöiden poissaolopäivien määrät olivat vuonna 003: 5, 3, 16, 9, 0, 1, 3,, 19, 5, 19, 11,, 0, 4, 6, 1, 15,
MTTTA1 Tilastomenetelmien perusteet 5 op Luento Kokonaisuudet johon opintojakso kuuluu
 10.1.2019/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 10.1.2019 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2018 10.1.2019/2
10.1.2019/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 10.1.2019 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2018 10.1.2019/2
Tilastollinen aineisto Luottamusväli
 Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
tilastotieteen kertaus
 tilastotieteen kertaus Keskiviikon 24.1. harjoitukset pidetään poikkeuksellisesti klo 14-16 luokassa Y228. Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla
tilastotieteen kertaus Keskiviikon 24.1. harjoitukset pidetään poikkeuksellisesti klo 14-16 luokassa Y228. Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 18. lokakuuta 2007 Antti Rasila () TodB 18. lokakuuta 2007 1 / 19 1 Tilastollinen aineisto 2 Tilastollinen malli Yksinkertainen satunnaisotos 3 Otostunnusluvut
Sovellettu todennäköisyyslaskenta B Antti Rasila 18. lokakuuta 2007 Antti Rasila () TodB 18. lokakuuta 2007 1 / 19 1 Tilastollinen aineisto 2 Tilastollinen malli Yksinkertainen satunnaisotos 3 Otostunnusluvut
Harjoittele tulkintoja
 Harjoittele tulkintoja Syksy 9: KT (55 op) Kvantitatiivisen aineiston keruu ja analyysi SPSS tulosteiden tulkintaa/til Analyysit perustuvat aineistoon: Haavio-Mannila, Elina & Kontula, Osmo (1993): Suomalainen
Harjoittele tulkintoja Syksy 9: KT (55 op) Kvantitatiivisen aineiston keruu ja analyysi SPSS tulosteiden tulkintaa/til Analyysit perustuvat aineistoon: Haavio-Mannila, Elina & Kontula, Osmo (1993): Suomalainen
Kvantitatiiviset tutkimusmenetelmät maantieteessä
 Kvantitatiiviset tutkimusmenetelmät maantieteessä Harjoitukset: 2 Muuttujan normaaliuden testaaminen, merkitsevyys tasot ja yhden otoksen testit FT Joni Vainikka, Yliopisto-opettaja, GO218, joni.vainikka@oulu.fi
Kvantitatiiviset tutkimusmenetelmät maantieteessä Harjoitukset: 2 Muuttujan normaaliuden testaaminen, merkitsevyys tasot ja yhden otoksen testit FT Joni Vainikka, Yliopisto-opettaja, GO218, joni.vainikka@oulu.fi
Tilastotieteen kertaus. Vilkkumaa / Kuusinen 1
 Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
1. Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet
 VAASAN YLIOPISTO/AVOIN YLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia 1 KURSSIKYSELYAINEISTO: 1. Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
VAASAN YLIOPISTO/AVOIN YLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia 1 KURSSIKYSELYAINEISTO: 1. Työpaikan työntekijöistä laaditussa taulukossa oli mm. seuraavat rivit ja sarakkeet Nimi Ikä v. Asema Palkka
KURSSIKYSELYAINEISTO: HUOM! Aineiston tilastoyksikkömäärä 11 on kovin pieni oikean tilastotieteen tekemiseen, mutta Harjoitteluun se kelpaa kyllä!
 VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: HUOM! Aineiston tilastoyksikkömäärä 11 on kovin pieni oikean tilastotieteen tekemiseen, mutta Harjoitteluun
VAASAN YLIOPISTO/KESÄYLIOPISTO TILASTOTIETEEN PERUSTEET Harjoituksia A KURSSIKYSELYAINEISTO: HUOM! Aineiston tilastoyksikkömäärä 11 on kovin pieni oikean tilastotieteen tekemiseen, mutta Harjoitteluun
... Vinkkejä lopputyön raportin laadintaan. Sisältö 1. Johdanto 2. Analyyseissä käytetyt muuttujat 3. Tulososa 4. Reflektio (korvaa Johtopäätökset)
 LIITE Vinkkejä lopputyön raportin laadintaan Sisältö 1. Johdanto 2. Analyyseissä käytetyt muuttujat 3. Tulososa 4. Reflektio (korvaa Johtopäätökset) 1. Johdanto Kerro johdannossa lukijalle, mitä jatkossa
LIITE Vinkkejä lopputyön raportin laadintaan Sisältö 1. Johdanto 2. Analyyseissä käytetyt muuttujat 3. Tulososa 4. Reflektio (korvaa Johtopäätökset) 1. Johdanto Kerro johdannossa lukijalle, mitä jatkossa
RISKITASO. Riskitaso (α) määrittää virhepäätelmän todennäköisyyden. Käytettyjä riskitasoja:
 RISKITASO Riskitaso (α) määrittää virhepäätelmän todennäköisyyden testattaessa Todennäköisyys, jolla tutkija on valmis hylkäämään nollahypoteesin, vaikka se saattaisikin pitää perusjoukossa paikkansa Käytettyjä
RISKITASO Riskitaso (α) määrittää virhepäätelmän todennäköisyyden testattaessa Todennäköisyys, jolla tutkija on valmis hylkäämään nollahypoteesin, vaikka se saattaisikin pitää perusjoukossa paikkansa Käytettyjä
Pylväsdiagrammi Suomen kunnat lääneittäin vuonna Piirakkadiagrammi Suomen kunnat lääneittäin vuonna 2003 LKM 14.8% 11.2% 19.7% 4.9% 3.6% 45.
 Pylväsdiagrammi Suomen kunnat lääneittäin vuonna Piirakkadiagrammi Suomen kunnat lääneittäin vuonna 8.8% 8.9%.%.% 9.7%.7% Etelä Länsi Itä Oulu Lappi Ahvenanmaa Länsi Etelä Itä Oulu Lappi Ahvenanmaa Läänien
Pylväsdiagrammi Suomen kunnat lääneittäin vuonna Piirakkadiagrammi Suomen kunnat lääneittäin vuonna 8.8% 8.9%.%.% 9.7%.7% Etelä Länsi Itä Oulu Lappi Ahvenanmaa Länsi Etelä Itä Oulu Lappi Ahvenanmaa Läänien
Väliestimointi (jatkoa) Heliövaara 1
 Väliestimointi (jatkoa) Heliövaara 1 Bernoulli-jakauman odotusarvon luottamusväli 1/2 Olkoon havainnot X 1,..., X n yksinkertainen satunnaisotos Bernoulli-jakaumasta parametrilla p. Eli X Bernoulli(p).
Väliestimointi (jatkoa) Heliövaara 1 Bernoulli-jakauman odotusarvon luottamusväli 1/2 Olkoon havainnot X 1,..., X n yksinkertainen satunnaisotos Bernoulli-jakaumasta parametrilla p. Eli X Bernoulli(p).
2. Aineiston kuvailua
 2. Aineiston kuvailua Avaa (File/Open/Data ) aineistoikkunaan tiedosto tilp150.sav. Aineisto on koottu Tilastomenetelmien peruskurssilla olleilta. Tiedot osallistumisesta demoihin, tenttipisteet, tenttien
2. Aineiston kuvailua Avaa (File/Open/Data ) aineistoikkunaan tiedosto tilp150.sav. Aineisto on koottu Tilastomenetelmien peruskurssilla olleilta. Tiedot osallistumisesta demoihin, tenttipisteet, tenttien
Teema 5: Ristiintaulukointi
 Teema 5: Ristiintaulukointi Kahden (tai useamman) muuttujan ristiintaulukointi: aineiston analysoinnin ja tulosten esittämisen perusmenetelmä usein samat tiedot esitetään sekä taulukkona että kuvana mahdollisen
Teema 5: Ristiintaulukointi Kahden (tai useamman) muuttujan ristiintaulukointi: aineiston analysoinnin ja tulosten esittämisen perusmenetelmä usein samat tiedot esitetään sekä taulukkona että kuvana mahdollisen
TUTKIMUSAINEISTON ANALYYSI. LTKY012 Timo Törmäkangas
 TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi Yksiulotteisen
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI. LTKY012 Timo Törmäkangas Gerontologian tutkimuskeskus
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas Gerontologian tutkimuskeskus LUENNOT Luento Paikka Vko Päivä Pvm Klo 1 L 303 3 ke 16.1.2013 10:15-12:00 2 L 303 3 pe 18.1.2013 10:15-12:00
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas Gerontologian tutkimuskeskus LUENNOT Luento Paikka Vko Päivä Pvm Klo 1 L 303 3 ke 16.1.2013 10:15-12:00 2 L 303 3 pe 18.1.2013 10:15-12:00
Matemaatikot ja tilastotieteilijät
 Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Kaavakokoelma, testikaaviot ja jakaumataulukot liitteinä. Ei omia taulukoita! Laskin sallittu.
 Ka6710000 TILASTOLLISEN ANALYYSIN PERUSTEET 2. VÄLIKOE 9.5.2007 / Anssi Tarkiainen Kaavakokoelma, testikaaviot ja jakaumataulukot liitteinä. Ei omia taulukoita! Laskin sallittu. Tehtävä 1. a) Gallupissa
Ka6710000 TILASTOLLISEN ANALYYSIN PERUSTEET 2. VÄLIKOE 9.5.2007 / Anssi Tarkiainen Kaavakokoelma, testikaaviot ja jakaumataulukot liitteinä. Ei omia taulukoita! Laskin sallittu. Tehtävä 1. a) Gallupissa
Luentokalvoja tilastollisesta päättelystä. Kalvot laatinut Aki Taanila Päivitetty 30.11.2012
 Luentokalvoja tilastollisesta päättelystä Kalvot laatinut Aki Taanila Päivitetty 30.11.2012 Otanta Otantamenetelmiä Näyte Tilastollinen päättely Otantavirhe Otanta Tavoitteena edustava otos = perusjoukko
Luentokalvoja tilastollisesta päättelystä Kalvot laatinut Aki Taanila Päivitetty 30.11.2012 Otanta Otantamenetelmiä Näyte Tilastollinen päättely Otantavirhe Otanta Tavoitteena edustava otos = perusjoukko
OHJ-7600 Ihminen ja tekniikka -seminaari, 4 op Käyttäjäkokemuksen kvantitatiivinen analyysi Luento 2
 OHJ-7600 Ihminen ja tekniikka -seminaari, 4 op Käyttäjäkokemuksen kvantitatiivinen analyysi Luento 2 Luento 2 Kuvailevat tilastolliset menetelmät Käytetyimmät tilastolliset menetelmät käyttäjäkokemuksen
OHJ-7600 Ihminen ja tekniikka -seminaari, 4 op Käyttäjäkokemuksen kvantitatiivinen analyysi Luento 2 Luento 2 Kuvailevat tilastolliset menetelmät Käytetyimmät tilastolliset menetelmät käyttäjäkokemuksen
Johdatus tilastotieteeseen Tilastollisten aineistojen kuvaaminen. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteeseen Tilastollisten aineistojen kuvaaminen TKK (c) Ilkka Mellin (2005) 1 Tilastollisten aineistojen kuvaaminen Havaintoarvojen jakauma Tunnusluvut Suhdeasteikollisten muuttujien tunnusluvut
Johdatus tilastotieteeseen Tilastollisten aineistojen kuvaaminen TKK (c) Ilkka Mellin (2005) 1 Tilastollisten aineistojen kuvaaminen Havaintoarvojen jakauma Tunnusluvut Suhdeasteikollisten muuttujien tunnusluvut
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas KURSSIN SISÄLTÖ Johdanto Mittaaminen ja aineiston hankinta Mitta-asteikot Otanta Aineiston esittäminen ja data-analyysi Havaintomatriisi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Kyllä. Kyllä. Jäitkö vielä epävarmaksi: Selvitä antavatko testit samansuuntaisen tuloksen.
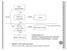 Data: järjestysast. Ei Kyllä Jatkuva, normaali Kyllä t-testi Ei Suuria poikkeavia arvoja Ei Mann-Whitney Kyllä Mediaani testi ks. luentomoniste Valintakaavio: Kahden riippumattoman ryhmän jakauman keskikohdan
Data: järjestysast. Ei Kyllä Jatkuva, normaali Kyllä t-testi Ei Suuria poikkeavia arvoja Ei Mann-Whitney Kyllä Mediaani testi ks. luentomoniste Valintakaavio: Kahden riippumattoman ryhmän jakauman keskikohdan
Leikkijunan kunto toimiva ei-toimiva Työvuoro aamuvuoro päivävuoro iltavuoro
 Lisätehtäviä 1. Erään yrityksen satunnaisesti valittujen työntekijöiden poissaolopäivien määrät olivat vuonna 003: 5, 3, 16, 9, 0, 1, 3,, 19, 5, 19, 11,, 0, 4, 6, 1, 15, 4, 0,, 4, 3, 3, 8, 3, 9, 11, 19,
Lisätehtäviä 1. Erään yrityksen satunnaisesti valittujen työntekijöiden poissaolopäivien määrät olivat vuonna 003: 5, 3, 16, 9, 0, 1, 3,, 19, 5, 19, 11,, 0, 4, 6, 1, 15, 4, 0,, 4, 3, 3, 8, 3, 9, 11, 19,
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Tilastollinen testaus Tilastollinen testaus Tilastollisessa testauksessa tutkitaan tutkimuskohteita koskevien oletusten tai väitteiden paikkansapitävyyttä havaintojen avulla. Testattavat oletukset tai
Tilastollinen testaus Tilastollinen testaus Tilastollisessa testauksessa tutkitaan tutkimuskohteita koskevien oletusten tai väitteiden paikkansapitävyyttä havaintojen avulla. Testattavat oletukset tai
MTTTP1, luento KERTAUSTA JA TÄYDENNYSTÄ. Tunnusluvut. 1) Sijainnin tunnuslukuja. Keskilukuja moodi (Mo) mediaani (Md) keskiarvo, kaava (1)
 20.9.2018/1 MTTTP1, luento 20.9.2018 KERTAUSTA JA TÄYDENNYSTÄ Tunnusluvut 1) Sijainnin tunnuslukuja Keskilukuja moodi (Mo) mediaani (Md) keskiarvo, kaava (1) Muita sijainnin tunnuslukuja ala- ja yläkvartiili,
20.9.2018/1 MTTTP1, luento 20.9.2018 KERTAUSTA JA TÄYDENNYSTÄ Tunnusluvut 1) Sijainnin tunnuslukuja Keskilukuja moodi (Mo) mediaani (Md) keskiarvo, kaava (1) Muita sijainnin tunnuslukuja ala- ja yläkvartiili,
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
1. Normaalisuuden tutkiminen, Bowmanin ja Shentonin testi, Rankit Plot, Wilkin ja Shapiron testi
 Mat-2.2104 Tilastollisen analyysin perusteet / Ratkaisut Aiheet: Avainsanat: Yhteensopivuuden ja homogeenisuden testaaminen Bowmanin ja Shentonin testi, Hypoteesi, 2 -homogeenisuustesti, 2 -yhteensopivuustesti,
Mat-2.2104 Tilastollisen analyysin perusteet / Ratkaisut Aiheet: Avainsanat: Yhteensopivuuden ja homogeenisuden testaaminen Bowmanin ja Shentonin testi, Hypoteesi, 2 -homogeenisuustesti, 2 -yhteensopivuustesti,
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
806109P TILASTOTIETEEN PERUSMENETELMÄT I Hanna Heikkinen Esimerkkejä estimoinnista ja merkitsevyystestauksesta, syksy (1 α) = 99 1 α = 0.
 806109P TILASTOTIETEEN PERUSMENETELMÄT I Hanna Heikkinen Esimerkkejä estimoinnista ja merkitsevyystestauksesta, syksy 2012 1. Olkoon (X 1,X 2,...,X 25 ) satunnaisotos normaalijakaumasta N(µ,3 2 ) eli µ
806109P TILASTOTIETEEN PERUSMENETELMÄT I Hanna Heikkinen Esimerkkejä estimoinnista ja merkitsevyystestauksesta, syksy 2012 1. Olkoon (X 1,X 2,...,X 25 ) satunnaisotos normaalijakaumasta N(µ,3 2 ) eli µ
MTTTP1, luento KERTAUSTA
 26.9.2017/1 MTTTP1, luento 26.9.2017 KERTAUSTA Varianssi, kaava (2) http://www.sis.uta.fi/tilasto/mtttp1/syksy2017/kaavat.pdf n i i n i i x x n x n x x n s 1 2 2 1 2 2 1 1 ) ( 1 1 Mittaa muuttujan arvojen
26.9.2017/1 MTTTP1, luento 26.9.2017 KERTAUSTA Varianssi, kaava (2) http://www.sis.uta.fi/tilasto/mtttp1/syksy2017/kaavat.pdf n i i n i i x x n x n x x n s 1 2 2 1 2 2 1 1 ) ( 1 1 Mittaa muuttujan arvojen
7. laskuharjoituskierros, vko 10, ratkaisut
 7. laskuharjoituskierros, vko 10, ratkaisut D1. a) Oletetaan, että satunnaismuuttujat X ja Y noudattavat kaksiulotteista normaalijakaumaa parametrein E(X) = 0, E(Y ) = 1, Var(X) = 1, Var(Y ) = 4 ja Cov(X,
7. laskuharjoituskierros, vko 10, ratkaisut D1. a) Oletetaan, että satunnaismuuttujat X ja Y noudattavat kaksiulotteista normaalijakaumaa parametrein E(X) = 0, E(Y ) = 1, Var(X) = 1, Var(Y ) = 4 ja Cov(X,
Tilastollisen analyysin perusteet Luento 5: Jakaumaoletuksien. testaaminen
 Tilastollisen analyysin perusteet Luento 5: Sisältö Tilastotieteessä tehdään usein oletuksia havaintojen jakaumasta. Useat tilastolliset menetelmät toimivat tehottomasti tai jopa virheellisesti, jos jakaumaoletukset
Tilastollisen analyysin perusteet Luento 5: Sisältö Tilastotieteessä tehdään usein oletuksia havaintojen jakaumasta. Useat tilastolliset menetelmät toimivat tehottomasti tai jopa virheellisesti, jos jakaumaoletukset
b6) samaan perusjoukkoon kohdistuu samanaikaisesti useampia tutkimuksia.
 806109P TILASTOTIETEEN PERUSMENETELMÄT I 1. välikoe 11.3.2011 (Jari Päkkilä) VALITSE VIIDESTÄ TEHTÄVÄSTÄ NELJÄ JA VASTAA VAIN NIIHIN! 1. Valitse kohdissa A-F oikea (vain yksi) vaihtoehto. Oikeasta vastauksesta
806109P TILASTOTIETEEN PERUSMENETELMÄT I 1. välikoe 11.3.2011 (Jari Päkkilä) VALITSE VIIDESTÄ TEHTÄVÄSTÄ NELJÄ JA VASTAA VAIN NIIHIN! 1. Valitse kohdissa A-F oikea (vain yksi) vaihtoehto. Oikeasta vastauksesta
Tilastollisten aineistojen kuvaaminen
 Ilkka Mellin Tilastolliset menetelmät Osa 1: Johdanto Tilastollisten aineistojen kuvaaminen TKK (c) Ilkka Mellin (2007) 1 Tilastollisten aineistojen kuvaaminen >> Havaintoarvojen jakauma Tunnusluvut Suhdeasteikollisten
Ilkka Mellin Tilastolliset menetelmät Osa 1: Johdanto Tilastollisten aineistojen kuvaaminen TKK (c) Ilkka Mellin (2007) 1 Tilastollisten aineistojen kuvaaminen >> Havaintoarvojen jakauma Tunnusluvut Suhdeasteikollisten
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012. Timo Törmäkangas
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas NORMAALIJAKATUNEISUUDEN TESTAUS H 0 : Muuttuja on perusjoukossa normaalisti jakautunut. H 1 : Muuttuja ei ole perusjoukossa normaalisti
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas NORMAALIJAKATUNEISUUDEN TESTAUS H 0 : Muuttuja on perusjoukossa normaalisti jakautunut. H 1 : Muuttuja ei ole perusjoukossa normaalisti
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
SISÄLTÖ 1 TILASTOJEN KÄYTTÖ...7 MITÄ TILASTOTIEDE ON?
 SISÄLTÖ 1 TILASTOJEN KÄYTTÖ...7 MITÄ TILASTOTIEDE ON?...7 TILASTO...7 TILASTOTIEDE...8 HISTORIAA...9 TILASTOTIETEEN NYKYINEN ASEMA...9 TILASTOLLISTEN MENETELMIEN ROOLIT ERI TYYPPISET AINEISTOT JA ONGELMAT...10
SISÄLTÖ 1 TILASTOJEN KÄYTTÖ...7 MITÄ TILASTOTIEDE ON?...7 TILASTO...7 TILASTOTIEDE...8 HISTORIAA...9 TILASTOTIETEEN NYKYINEN ASEMA...9 TILASTOLLISTEN MENETELMIEN ROOLIT ERI TYYPPISET AINEISTOT JA ONGELMAT...10
Ohjeita kvantitatiiviseen tutkimukseen
 1 Metropolia ammattikorkeakoulu Liiketalouden yksikkö Pertti Vilpas Ohjeita kvantitatiiviseen tutkimukseen Osa 2 KVANTITATIIVISEN TUTKIMUSAINEISTON ANALYYSI Sisältö: 1. Frekvenssi- ja prosenttijakaumat.2
1 Metropolia ammattikorkeakoulu Liiketalouden yksikkö Pertti Vilpas Ohjeita kvantitatiiviseen tutkimukseen Osa 2 KVANTITATIIVISEN TUTKIMUSAINEISTON ANALYYSI Sisältö: 1. Frekvenssi- ja prosenttijakaumat.2
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012
 TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas AINEISTON KERÄÄMINEN Tärkein vaihe tutkimuksen tekemisessä, koska mitatessa tulleita virheitä ei välttämättä voi huomata eikä niitä
TUTKIMUSAINEISTON KVANTITATIIVINEN ANALYYSI LTKY012 Timo Törmäkangas AINEISTON KERÄÄMINEN Tärkein vaihe tutkimuksen tekemisessä, koska mitatessa tulleita virheitä ei välttämättä voi huomata eikä niitä
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Estimointi. Otantajakauma
 Otantajakauma Otantajakauma kuvaa jonkin parametrin arvojen (esim. keskiarvon) jakauman kaikille tietyn kokoisille otoksille. jotka perusjoukosta voidaan muodostaa Histogrammissa otantajakauman parametrin
Otantajakauma Otantajakauma kuvaa jonkin parametrin arvojen (esim. keskiarvon) jakauman kaikille tietyn kokoisille otoksille. jotka perusjoukosta voidaan muodostaa Histogrammissa otantajakauman parametrin
Kynä-paperi -harjoitukset. Taina Lehtinen Taina I Lehtinen Helsingin yliopisto
 Kynä-paperi -harjoitukset Taina Lehtinen 43 Loput ratkaisut harjoitustehtäviin 44 Stressitestin = 40 s = 8 Kalle = 34 pistettä Ville = 5 pistettä Z Kalle 34 8 40 0.75 Z Ville 5 8 40 1.5 Kalle sijoittuu
Kynä-paperi -harjoitukset Taina Lehtinen 43 Loput ratkaisut harjoitustehtäviin 44 Stressitestin = 40 s = 8 Kalle = 34 pistettä Ville = 5 pistettä Z Kalle 34 8 40 0.75 Z Ville 5 8 40 1.5 Kalle sijoittuu
Tilastollinen testaus. Vilkkumaa / Kuusinen 1
 Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
TUTKIMUSOPAS. SPSS-opas
 TUTKIMUSOPAS SPSS-opas Johdanto Tässä oppaassa esitetään SPSS-tilasto-ohjelman alkeita, kuten Excel-tiedoston avaaminen, tunnuslukujen laskeminen ja uusien muuttujien muodostaminen. Lisäksi esitetään esimerkkien
TUTKIMUSOPAS SPSS-opas Johdanto Tässä oppaassa esitetään SPSS-tilasto-ohjelman alkeita, kuten Excel-tiedoston avaaminen, tunnuslukujen laskeminen ja uusien muuttujien muodostaminen. Lisäksi esitetään esimerkkien
Luottamusvälit. Normaalijakauma johnkin kohtaan
 Luottamusvälit Normaalijakauma johnkin kohtaan Perusjoukko ja otanta Jos halutaan tutkia esimerkiksi Suomessa elävien naarashirvien painoa, se voidaan (periaatteessa) tehdä kahdella tavalla: 1. tutkimalla
Luottamusvälit Normaalijakauma johnkin kohtaan Perusjoukko ja otanta Jos halutaan tutkia esimerkiksi Suomessa elävien naarashirvien painoa, se voidaan (periaatteessa) tehdä kahdella tavalla: 1. tutkimalla
Harjoituksessa tarkastellaan miten vapaa-ajan liikunta on yhteydessä..
 Harjoituksessa tarkastellaan miten vapaa-ajan liikunta on yhteydessä.. TEHTÄVÄ 1 Taulukko 1 Kuvailevat tunnusluvut pääkaupunkiseudun terveystutkimuksesta vuonna 2007 (n=941) Keskiarvo (keskihajonta) Ikä
Harjoituksessa tarkastellaan miten vapaa-ajan liikunta on yhteydessä.. TEHTÄVÄ 1 Taulukko 1 Kuvailevat tunnusluvut pääkaupunkiseudun terveystutkimuksesta vuonna 2007 (n=941) Keskiarvo (keskihajonta) Ikä
Estimointi. Luottamusvälin laskeminen keskiarvolle α/2 α/2 0.1
 Estimointi - tehdään päätelmiä perusjoukon ominaisuuksista (keskiarvo, riskisuhde jne.) otoksen perusteella - mitä suurempi otos, sitä tarkemmat estimaatit Otokseen perustuen määritellään otantajakaumalta
Estimointi - tehdään päätelmiä perusjoukon ominaisuuksista (keskiarvo, riskisuhde jne.) otoksen perusteella - mitä suurempi otos, sitä tarkemmat estimaatit Otokseen perustuen määritellään otantajakaumalta
MTTTP1, luento KERTAUSTA
 25.9.2018/1 MTTTP1, luento 25.9.2018 KERTAUSTA Varianssi, kaava (2) http://www.sis.uta.fi/tilasto/mtttp1/syksy2018/kaavat.pdf n i i n i i x x n x n x x n s 1 2 2 1 2 2 1 1 ) ( 1 1 Mittaa muuttujan arvojen
25.9.2018/1 MTTTP1, luento 25.9.2018 KERTAUSTA Varianssi, kaava (2) http://www.sis.uta.fi/tilasto/mtttp1/syksy2018/kaavat.pdf n i i n i i x x n x n x x n s 1 2 2 1 2 2 1 1 ) ( 1 1 Mittaa muuttujan arvojen
MTTTP1, luento KERTAUSTA
 19.3.2019/1 MTTTP1, luento 19.3.2019 KERTAUSTA Varianssi, kaava (2) http://www.sis.uta.fi/tilasto/mtttp1/syksy2018/kaavat.pdf n i i n i i x x n x n x x n s 1 2 2 1 2 2 1 1 ) ( 1 1 Mittaa muuttujan arvojen
19.3.2019/1 MTTTP1, luento 19.3.2019 KERTAUSTA Varianssi, kaava (2) http://www.sis.uta.fi/tilasto/mtttp1/syksy2018/kaavat.pdf n i i n i i x x n x n x x n s 1 2 2 1 2 2 1 1 ) ( 1 1 Mittaa muuttujan arvojen
Kvantitatiiviset menetelmät
 Kvantitatiiviset menetelmät HUOM! Tentti pidetään tiistaina.. klo 6-8 Vuorikadulla V0 ls Muuttujien muunnokset Usein empiirisen analyysin yhteydessä tulee tarve muuttaa aineiston muuttujia Esim. syntymävuoden
Kvantitatiiviset menetelmät HUOM! Tentti pidetään tiistaina.. klo 6-8 Vuorikadulla V0 ls Muuttujien muunnokset Usein empiirisen analyysin yhteydessä tulee tarve muuttaa aineiston muuttujia Esim. syntymävuoden
Ongelma: Poikkeaako perusjoukon suhteellinen osuus vertailuarvosta?
 Yhden otoksen suhteellisen osuuden testaus Ongelma: Poikkeaako perusjoukon suhteellinen osuus vertailuarvosta? Hypoteesit H 0 : p = p 0 H 1 : p p 0 tai H 1 : p > p 0 tai H 1 : p < p 0 Suhteellinen osuus
Yhden otoksen suhteellisen osuuden testaus Ongelma: Poikkeaako perusjoukon suhteellinen osuus vertailuarvosta? Hypoteesit H 0 : p = p 0 H 1 : p p 0 tai H 1 : p > p 0 tai H 1 : p < p 0 Suhteellinen osuus
/1. MTTTP1, luento Normaalijakauma (jatkoa) Olkoon Z ~ N(0, 1). Määritellään z siten, että P(Z > z ) =, graafisesti:
 4.10.2016/1 MTTTP1, luento 4.10.2016 7.4 Normaalijakauma (jatkoa) Olkoon Z ~ N(0, 1). Määritellään z siten, että P(Z > z ) =, graafisesti: Samoin z /2 siten, että P(Z > z /2 ) = /2, graafisesti: 4.10.2016/2
4.10.2016/1 MTTTP1, luento 4.10.2016 7.4 Normaalijakauma (jatkoa) Olkoon Z ~ N(0, 1). Määritellään z siten, että P(Z > z ) =, graafisesti: Samoin z /2 siten, että P(Z > z /2 ) = /2, graafisesti: 4.10.2016/2
Järvi 1 Valkjärvi. Järvi 2 Sysijärvi
 Tilastotiedettä Tilastotieteessä kerätään tietoja yksittäisistä asioista, ominaisuuksista tai tapahtumista. Näin saatua tietoa käsitellään tilastotieteen menetelmin ja saatuja tuloksia voidaan käyttää
Tilastotiedettä Tilastotieteessä kerätään tietoja yksittäisistä asioista, ominaisuuksista tai tapahtumista. Näin saatua tietoa käsitellään tilastotieteen menetelmin ja saatuja tuloksia voidaan käyttää
Monitasomallit koulututkimuksessa
 Metodifestivaali 9.5.009 Monitasomallit koulututkimuksessa Mitä ihmettä? Antero Malin Koulutuksen tutkimuslaitos Jyväskylän yliopisto 009 1 Tilastollisten analyysien lähtökohta: Perusjoukolla on luonnollinen
Metodifestivaali 9.5.009 Monitasomallit koulututkimuksessa Mitä ihmettä? Antero Malin Koulutuksen tutkimuslaitos Jyväskylän yliopisto 009 1 Tilastollisten analyysien lähtökohta: Perusjoukolla on luonnollinen
Ilkka Mellin Tilastolliset menetelmät. Osa 3: Tilastolliset testit. Tilastollinen testaus. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Tilastollinen testaus TKK (c) Ilkka Mellin (2007) 1 Tilastolliset testit >> Tilastollinen testaus Tilastolliset hypoteesit Tilastolliset
Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Tilastollinen testaus TKK (c) Ilkka Mellin (2007) 1 Tilastolliset testit >> Tilastollinen testaus Tilastolliset hypoteesit Tilastolliset
