KOORDINAATTIMITTAUSKONEET JA KONEENOSIEN MITTAAMINEN COORDINATE MEASURING MACHINES AND MEASURING OF MACHINE COMPONENTS
|
|
|
- Helmi Leppänen
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 LAPPEENRANNAN TEKNILLINEN YLIOPISTO Teknillinen tiedekunta Konetekniikan Koulutusohjelma KOORDINAATTIMITTAUSKONEET JA KONEENOSIEN MITTAAMINEN COORDINATE MEASURING MACHINES AND MEASURING OF MACHINE COMPONENTS Lappeenrannassa Ari Pesola
2 SISÄLLYSLUETTELO 1 JOHDANTO KONEENOSIEN MITAT JA TOLERANSSIT Pituustoleranssit Geometriset toleranssit KOORDINAATTIMITTAUSKONEET KOORDINAATTIKONEIDEN MITTAUSPÄÄT Koskettavat anturit Videomittaus Laseranturit MITTAUSOHJELMISTOT KONEISTETUN TUOTTEEN MITTAUKSET Pituusmittojen tarkastus Geometriset toleranssit Koordinaattimittauskoneen käyttö kotelon mittauksissa JOHTOPÄÄTÖKSET YHTEENVETO LÄHTEET 29 LIITEET
3 1 1 JOHDANTO Koneistettujen kappaleiden mittatarkkuus on tänä päivänä yhä isommassa roolissa konepajojen pyrkiessä parantamaan tuotteidensa laatua. Perinteisten käsikäyttöisten mittalaitteiden tarkkuus ei välttämättä aina riitä, tai mittaustulosten saanti vie liian kauan aikaa. Tässä kandidaatintyössä on tutkittu, mitä erilaisia vaihtoehtoja perinteisille käsikäyttöisille mittalaitteille on nykyään olemassa. Työssä on myös mainittu mittaamisen kannalta muutamia seikkoja, joita koneenosien suunnittelussa, mittauslaitteen hankinnassa sekä itse mittaustapahtumassa tulisi ottaa huomioon. Koordinaattimittauskoneet ovat laitteita joiden avulla voidaan mitata vaikeitakin geometrisia muotoja ja tuotteita kuten nokka-akseleita, kampiakseleita, turbiinien siivekkeitä, jne. /1/ Työssä on vertailtu keskenään kosketukseen, lasersäteeseen ja konenäköön perustuvia koordinaattimittauskoneita. Vertailtavien laitteiden valinnassa on otettu huomioon sarjatuotannon tuomat vaatimukset. Toisaalta erittäin tarkat mittauslaitteet asettavat omat vaatimuksensa myös mittausympäristölle mm. siisteyden ja ilmanlaadun suhteen. Tekstissä käsitellään koordinaattimittauskoneita, jotka kykenevät mittaamaan noin 1m 3 tilavuuteen mahtuvia, tasomaisia kappaleita, kuitenkaan menemättä mikroskooppisiin kappaleisiin. Viimeisessä kappaleessa pohditaan erään koneistetun tuotteen mittauksia; tarvitaanko joissain mittauksissa koordinaattimittauslaitetta vai selvitäänkö perinteisillä käsimittauslaitteilla? Tässä työssä tarkastellaan mittauslaitteita vain pituus- ja geometriamittausten kannalta. Pinnanlaadun, kovuuden tms. mittausta ei ole otettu huomioon. Ennen koordinaattimittauskoneita, konepajatekniset mittaukset on suoritettu perinteisillä käsimittavälineillä. Vaikka koordinaattimittauskoneet ovat nopeuttaneet joitain mittauksia sekä tehnyt vaikeimpien geometristen toleranssien mittaamisen ylipäätään mahdolliseksi, eivät ne kuitenkaan koskaan syrjäytä täysin käsimittavälineitä. Varsinkin yksinkertaisissa pituusmittauksissa ja pienissä sarjoissa, käsimittalaitteet ovat nopeampi ja halvempi ratkaisu mittauksen toteuttamiseen.
4 2 Perinteiset käsimittauslaitteet ovat jaoteltu kolmeen eri ryhmään, jotka ovat kiintomitat, osoittavat mittauslaitteet ja muut mittauslaitteet. Kiintomittoihin kuuluvat erilaiset mittapalat, tulkit ja mallit. Konepajoilla on usein käytössä mittapalasarja tai rakotulkki, joiden avulla voidaan tarkistaa esim. raon tai akselin toleranssialue. /2/ Mittapaloja käytetään yleensä muiden mittausvälineiden tarkastuksiin ja asetuksiin /3/. Muut mittauslaitteet tarkoittavat työstökoneiden omia mittasauvoja /2/. Konepajoissa saatetaan joskus käyttää myös luotilankaa tai vesivaakaa mittojen ja kohtisuoruuksien tarkistamiseen /4/. Tyypillisesti tällaisilla perinteisillä mittausvälineillä päästään noin 0,01 0,2 mm tarkkuuteen /5/.
5 3 2 KONEENOSIEN MITAT JA TOLERANSSIT Tuotteet mitoitetaan aina joidenkin toleranssiarvojen väliin. Tällöin pääperiaatteena on luopuminen absoluuttisen mitan käytöstä jolloin se korvataan mitalla, joka saa vaihdella toleranssialueella. Näitä mittamääräyksiä kontrolloidaan mittausvälineillä. /3/ Koska ehdottoman tarkkaa kappaletta on mahdotonta valmistaa, saadaan valmistuksessa toleranssien käytöllä aikaan kustannussäästöjä kuitenkaan tinkimättä tuotteen toimintavarmuudesta. /3, 4/ Konepajateollisuudessa on käytössä periaate, jonka mukaan mittalaitteen mittausepävarmuus saa olla 20 % toleranssialueesta. Tämä periaatteen pohjalta tehdään mittauslaitteen valinta. /3/ 2.1 Pituustoleranssit Pituusmittojen toleransseja varten on olemassa kansainvälinen ISO - toleranssijärjestelmä, jonka käsitteet löytyvät kotimaisesta SFS 2772 standardista. /6/ Järjestelmän avulla voidaan kullekin osalle ilmoittaa perusmitta, rajamitat, eromitat, toleranssiasema ja aste. Perusmitta ilmoittaa osan nimellisen mitan. Rajamitat kertovat ne rajat, joiden väliin osan mitan tulee osua. Eromitoilla ilmoitetaan toleranssirajat perusmitan suhteen. Ne voivat olla joko positiivisia tai negatiivisia. Toleranssiasema ilmoitetaan kirjaimilla ja sen tarkoitus on ilmoittaa toleranssialueen paikka perusmitan suhteen. Akseleille käytetään pieniä kirjaimia ja rei ille isoja kirjaimia. Toleranssiaste kuvaa toleranssin suuruutta. Edellä mainittuja käsitteitä havainnollistaa kuva 1. /4/ Kuva 1. Toleranssien nimikkeitä. /6/
6 4 ISO toleransseissa on perustoleranssiasteet ilmoitettu IT - taulukossa. Taulukossa 1 on osa IT taulukon arvoista. Taulukosta nähdään, että mitä pienempi IT aste on, sitä tarkempi on valmistusvaatimus. Taulukko jatkuu aina 3150 mm perusmittaan ja IT18 asteeseen asti. /7/ Käytännössä siis akseleiden ja reikien kohdalla kirjaimen perässä oleva toleranssiasteen numero kertoo, kuinka paljon mitattu mitta saa poiketa peruseromitasta /8/ Taulukko 1. Osa perustoleranssiasteista IT taulukossa. /14/ Teknisten piirustusten pituusmitat voidaan jaotella kolmeen eri ryhmään. Ryhmät ovat toimintamitat, ei-toimintamitat ja apumitat. Toimintamitat määrittelevät osien muodon ja sijainnin ja nämä mitat vaikuttavat niiden sopivuuteen muiden osien kanssa. Toimintamittaan on yleensä lisätty toleranssi. Ei-toimintamitat vaikuttavat kappaleen ulkonäköön, mutta ei sen toimintaan tai yhteensopivuuteen muiden osien kanssa. Apumitat voidaan yleensä jättää merkitsemättä, koska ne eivät vaikuta kappaleen valmistukseen. Joskus apumitta on kuitenkin tärkeä esim. raaka-aineen tai asennuksen valinnassa. /4/ Ne osat, joita ei ole erikseen piirustuksessa toleroitu, tulee olla valmistettu otsikko-osan yleistoleranssin tarkkuuteen. Ohjeet tähän on ISO 2768 standardissa (taulukko 2). Poikkeuksena ovat apumitat, joihin yleistoleranssi ei vaikuta. /4/ Taulukko 2. ISO 2768-standardin mukaiset toleranssiluokat. /7/
7 5 2.2 Geometriset toleranssit Geometrisilla toleransseilla ilmoitetaan rajat, joiden sisällä muodon ja sijainnin tulee olla. Geometristen toleranssien käyttö on lisääntynyt koordinaattimittauskoneiden myötä. Geometriatoleransseilla voidaan antaa elementille varsinaisesta mittatoleransseista riippumattomia vaatimuksia. Geometriset toleranssit voidaan jakaa muoto- ja sijaintitoleransseihin. /3/ Geometristen toleranssien piirustusmerkinnät ovat kuvassa 2. Muototoleranssit ilmoittavat kuinka paljon elementin muoto saa poiketa sen teoreettisesta muodosta. Tällaisia ovat suoruus, tasomaisuus, ympyrämäisyys, lieriömäisyys sekä tasoviivan ja pinnan muoto. /2/ Sijaintitoleransseilla rajataan kahden tai useamman elementin keskinäistä asentoa toisiinsa. Tällaisia rajoituksia ovat yhdensuuntaisuus, kohtisuoruus, kulma-asento, paikka, samankeskisyys, sama-akselisuus ja symmetria. /2/ Kuva 2. Geometristen toleranssien merkintä. /9/
8 6 Otetaan esimerkiksi auton moottorin sylinterin kansi. Kuvasta 3 voidaan nähdä, kuinka paljon erilaisia geometriatoleransseja auton sylinterin kannesta tulee mitata. Osa pituusmitoista ja toleransseista olisi mahdotonta mitata tehokkaasti perinteisin käsimittauslaittein. Kuva 3. Auton sylinterikannen mittauksessa vaadittavat geometriatoleranssit. Vasemmalla tiivistyspinta (deck face), keskellä venttiilin ohjaimet (valve guide) ja oikealla venttiilitaskut (valve seat). /10/ Geometrisia toleransseja tarkastettaessa on hyvä tarkastaa SFS 4910 standardi. Tässä standardissa annetaan ohjeita, miten eri geometristen toleranssien mittaustapahtuma tulisi suorittaa. /7/ Mittaajan sekä valmistajan kannalta olisi suunnittelijan hyvä suosia säteisheittotoleranssien käyttöä mittauksien helpottamiseksi /8/.
9 7 3 KOORDINAATTIMITTAUSKONEET Ensimmäinen koordinaattimittauskone oli Zeissin tekemä UM 500 vuodelta Se kykeni 0,5 mikrometrin tarkkuuteen ja oli tietokoneohjelmoitu- sekä ohjattu. /5/ Sittemmin markkinoille on tullut niin käsikäyttöisiä halvempia verstasmalleja, kuin auton kokoisten tuotteiden mittaamiseen tarkoitettuja täysin ohjelmoituja portaalimittauslaitteita /12/. Suomessa on tällä hetkellä noin 300 koordinaattimittauskonetta /19/. American machinist lehden mukaan vuonna 2006 huippukonepajoista oli 54,9 %:lla oli käytössään kehittynyt koordinaattimittauslaitetta. /11/ Koordinaattimittauskone koostuu itse mittauskoneesta ja sen referenssikoordinaatistosta, mittausantureista, tietokoneesta, mittausohjelmistosta, työkappaleohjelmasta ja raportoinnista. Koordinaattimittauskone on yleensä sijoitettu erilleen tuotannosta omaan ilmastoituun tilaansa, mutta valmistajat pyrkivät koko ajan kehittämään mittauslaitteita myös huonompiin olosuhteisiin. /12/ Mittauskoneiden toimintatapoja ovat käsikäyttöinen, motorisoitu tai NC - ohjattu. NC - ohjattuja koneita käytetään yleensä sarjatuotannossa. Kone kuljettaa mittauspäätä joka rekisteröi kohteen pinnalta mitattavan pisteen. Mittauspäitä on valtava määrä erilaisiin tarpeisiin. Tietokoneessa olevan mittausohjelmiston ja työkappaleen mittausohjelman avulla saadaan rekisteröidyt mittauspisteet raportoitavaan muotoon. /12/ Mittauspisteiden rekisteröinti perustuu mekaanisen kosketukseen, optiseen kuvaan tai lasermittaukseen. /11/ Viime aikoina mm. saksalainen koordinaattimittauskoneiden valmistaja Werth on kehittänyt myös röntgenkuvaukseen perustuvan mittauslaitteen. Röntgenkuvauslaite muodostaa kappaleesta läpinäkyvän kuvan, josta voidaan tarkistaa esimerkiksi valutuotteiden sisäisiä mittoja. /13/ Mekaanisessa kosketusmittauksessa laite rekisteröi mittaussauvan kosketuksen kappaleen pintaan. Optisissa mittauskoneissa konenäkö tunnistaa kappaleen piirteet. Lasermittauskoneissa koordinaatit saadaan taas mitattua nimensä mukaisesti lasersäteen taittumista. /12/ Koordinaattimittauskoneiden rakennetyyppejä ovat pylväs-, puomi-, portaali- ja siltatyyppiset rungot sekä nivelvartiset rakenteet. Neljä ensimmäistä on esitetty kuvassa 4,
10 8 josta nähdään kuinka kukin runkotyyppi on tarkoitettu hieman erityyppisille ja kokoisille komponenteille. Kuva 4. A) Pylväs- B) puomi- C) portaali- ja D) siltarakenne. /12/ Viimeksi mainittu nivelvartinen rakenne poikkeaa muista siten, että se muistuttaa hieman robotin käsivartta, kun taas muut rakenteet voivat olla huomattavasti kookkaampia. /12/ Kuvassa 5 on Faron valmistama nivelvarsityyppinen mittauslaite. Kuva 5. FaroArm nivelvarsimittauslaite. /14/ Yleisin mittauskone on portaalityyppinen koordinaattimittauskone, joka on varustettu kiinteällä pöydällä ja suoraviivaisilla liikeakseleilla. Koneiden mittausnopeus ja käytettävyys paranee tietotekniikan kehityksen mukana. Rungon ja pöydän materiaaleina käytetään yleensä kiveä, joten kone on kohtalaisen painava. Suomessa olevista koneista suurin osa on tarkoitettu noin koirankopin kokoisten kappaleiden mittaamiseen. Mittauspää
11 9 on yleensä mekaaniseen kosketukseen perustuva, mutta NC-ohjatuissa versioissa voi olla myös kamera- tai lasermittauspää. /12/ Aina mitattaessa erilaisia koneenosia, mittauksiin liittyy mittausepävarmuus. Mittausepävarmuuden suuruus vaikuttaa moneen asiaan ja sen tiedostaminen on sekä valmistajan, että suunnittelijan hyvä tietää. Yleisesti ajatellaan, että mittaustuloksen osuessa toleranssialueelle, tulos on suoraan hyväksyttävissä. Mittaustulosta tarkasteltaessa on kuitenkin huomattava että tuloksen tulee mahtua toleranssialueelle, kun mittauslaitteen virhemarginaali lisätään mittaustulokseen. Mittausepävarmuus siis käytännössä pienentää toleranssialuetta. Mitään valmistusprosessia ei myöskään voida trimmata tarkemmaksi, kuin mitä käytössä olevien mittalaitteiden tarkkuus on. /15/ Koordinaattimittauskoneiden mittausepävarmuutta varten on olemassa omat standardinsa. Valmistajat käyttävät yleisesti standardia ISO 10360, joka antaa ohjeet koskettavan mittauskoneen mittausepävarmuuden selvittämiseksi. Osa valmistajista käyttää taas CMMA, VDI/VDE 2617, ASME B89 tai JIS standardia. Koordinaattimittauskonetta hankkiessa onkin syytä ottaa huomioon, minkä standardin mukaan valmistaja ilmoittaa koneensa mittausepävarmuuden. /1/ Koskettavien koordinaattimittauskoneiden valmistajat ilmoittavat yleensä koneiden suurimman sallitun virheen (eng. Maximum Permissible Error, MPEE) ISO standardin mukaisesti. Se saadaan yhtälöstä = + /1000, (1) jossa A on osa, joka on riippumaton mittauspituudesta. L on mitattu pituus (mm) ja b on mittauspituudesta riippuva osa. Vastaus saadaan mikrometreinä (0,001 mm), josta joissain lähteissä käytetään myös termiä mikroni. Kaavasta nähdään, että mittausvirhe on sitä suurempi, mitä kauempaa koneen referenssipisteestä joudutaan mittaamaan. /12, 16/ Kuten sanottua, toistaiseksi virallisia mittausepävarmuuden määrittäviä standardeja on olemassa vasta koskettavia koordinaattimittauskoneita varten. Laser- tai optista mittalaitetta ostettaessa ollaan mittausepävarmuuden suhteen pitkälti valmistajan
12 10 luotettavuuden armoilla. Valmistajien on täytynyt kehittää omat menetelmänsä mittausepävarmuuden määrittämiseen. Hyvä uutinen on, että edellä mainittuja koneita varten on tulossa ISO-standardiin laajennus ( ), joka todennäköisesti julkaistaan vuoden 2011 ensimmäisellä puoliskolla. /16/ Japanilainen mittauslaitteiden valmistaja Mitutoyo ilmoittaa optisten mittauslaitteensa tarkkuudeen myös MPEE kaavaa käyttäen. Erona on, että mittausepävarmuudet ovat ilmoitettu akselisuunnittain. Esimerkiksi Mitutoyon Ultra Video Check laitteiston mittausepävarmuus ilmoitetaan seuraavasti: E1XY(0,3+L/1000), E1Z(3+2L/1000) ja E2XY(0,5+2L/1000). /26/ Muita käyttötapoja on ilmoittaa virhe 2D tai 3D tasossa /12/.
13 11 4 KOORDINAATTIMITTAUSKONEIDEN MITTAUSPÄÄT Kuten jo aiemmin mainittiin, mittauksen hoitavia mittauspäitä on useita erilaisia. Samassa rungossa voi olla kaksikin eri mittauspäätä. Yleensä toinen niistä on mekaaniseen kosketukseen perustuva. Koordinaattimittauskonetta joissa on enemmän kuin yksi mittauspää, voidaan kutsua monianturimittauskoneeksi. Monianturikoneessa voi olla makasiinissa useita erilaisia mittauspäitä, kuten CCD-kamera tai laseranturi, jotka voivat mitata muita ominaisuuksia kuin dimensioita esim. pinnankarheutta, lämpötilaa, jne. Tässä kappaleessa käsitellään miten eri mittauspäiden ominaisuudet ja käyttö poikkeavat toisistaan. Karkeasti voidaan sanoa, että parhaiten koskettava mittaus soveltuu monen suuntaisille pinnoille, mutta ei nurkkapaikkoihin. Lasermittaus taas sopii parhaiten vaakapinnoille ja videomittaus reunojen tunnistukseen. /12/ 4.1 Koskettavat anturit Koskettavassa käsikäyttöisessä mittauskoneessa puhutaan mittauskärjestä, jonka päässä teräskuula, jota painetaan kappaletta vasten. Kun käyttäjä on valinnut kärjelle sopivan paikan, hän painaa kytkimestä jolloin kone rekisteröi kuulan paikan nivelakselien suhteen. Tällaisessa tapauksessa kuulassa ei ole minkäänlaista anturia. /12/ Mittauspää voi myös reagoida kosketukseen siten, että se aukaisee kytkimen jolloin kone ymmärtää kosketuksen kappaleeseen. Tällöin puhutaan mittausanturista. Anturi voi myös olla täysin aktiivinen, jolloin se mittaa jatkuvasti mittauskärjen paikkaa avaruudessa. /12/ Mittauskärkiä ja antureita on olemassa valtava määrä eri pituuksilla ja mekaanisilla ominaisuuksilla varustettuna. Yksi erittäin tunnettu valmistaja on Renishaw, jonka koskettavia mittauspäitä on saatavissa lähes jokaisen valmistajan laitteeseen. Toinen suosittu valmistaja on Carl Zeiss, joka suosii useammalla erikokoisella anturilla varustettuja mittauspäitä. Kuvassa 6 on Zeissin ja Renishawin mittauspäät. /12/
14 12 Kuva 6. Vasemmalla Renishawn kevyt versio ja oikealla usealla kärjellä varustettu Zeiss:n valmistama mittauspää /12/. Kuvan 6 osakokonaisuuksia kutsutaan siis mittauspäiksi. Zeissin raskas ja iso mittauspää kiinnittyy koneen Z-pinooliin tai luistiin välisovitteilla. Välisovitteen ja mittausanturin väliin tulee adapteri, joka mahdollistaa kärkien vaihdot koneen makasiinista. Renishawin mallissa mittausanturit on kiinnitetty kärkimoduuliin, joka irtoaa mittauskoneesta tai nivelistukasta. Renishawin PH10 on erittäin suosittu kääntyvä nivelistukka, johon voidaan asentaa mekaanisen anturin lisäksi laseranturi. Kuvassa 7 on havainnollistettu tarkemmin mittauspään eri osat. /12/ Kuva 7. Kaksi erilaista mittauspäävaihtoehtoa. Äärimmäisenä vasemmalla Zeissin suosima malli ja siitä oikealle Renishawin nivelistukallisia malleja. /12/ Kuvassa 7 olevien mittauspäiden osat ovat a) mittauskoneen Z-pinooli tai luisti, b) nivelistukka, c) anturi (mittaava, kytkevä), d) välisovite, e) adapteri, f) jatkovarsi, g) mittauskärki tai varsi, h) liitinkappale ja e i) mittauskärkiyhdistelmä. /12/
15 13 Mittausantureita on useita erilaisia riippuen toimintatavasta. Toiset anturit kykenevät mittaamaan vain yhden pisteen kerrallaan, kun taas toisia antureita voidaan kuljettaa pintaa pitkin. Kone painaa mittauskärkeä aina ennalta määrätyllä voimalla kappaletta vasten, jolloin se kykenee erottamaan todellisen kosketuksen ns. ilmapisteistä. Kone osaa myös välttää pahimmat törmäykset, kun kosketusvoima on tiedossa. /12/ Manuaalisesti ohjattavan, koskettavan portaalimallisen koordinaattimittauskoneen voi saada jo alle euron, kun taas NC-ohjatut laitteet maksavat huomattavasti enemmän. Koskettavaan mittaukseen perustuvat laitteet ovat teollisuudessa suosittuja niiden edullisen suorituskyky-hinta suhteensa takia. Niiden tarkkuus ja mittaustulosten luotettavuus on myös parempi mitä esim. lasermittauslaitteilla mitattaessa. Haittapuolena optisiin ja lasereilla toimiviin laitteisiin on korkea operointiaika varsinkin kun kerättävien mittauspisteiden määrä on suuri esim. monimutkaisilla pinnoilla. /12/ Koneenosien geometrisista pinnoista noin 80 % on pyörähdyssymmetrisiä. On siis luontevaa, että ympyrämäisyysmittauksille on omat laitteensa. Ympyränmittauslaitteilla voidaan mitata ympyrämäisyyden lisäksi heittoa, sama-akselisuutta, yhdensuuntaisuutta ja suoruutta. /17/ Karkkilassa toimiva Mansner Oy on investoinut mittaushuoneeseensa noin euron arvoisen ympyrämäisyydenmittauskoneen. Mittauskone skannaa reiän kehää useilta eri tasoilta ja laskee mittaustietojen samankeskisyyttä. Mittauskone pystyy jopa kahden mikronin mittaustarkkuuteen. Kuvassa 8 on kyseinen kone ja oikealla näkyy mittaustulos tietokoneen ruudulla. /18/ Kuva 8. Taylor Hobson Talyrond 385 ympyrämäisyydenmittauskone /18/.
16 Videomittaus Suomen noin 300:sta koordinaattimittauskoneesta noin kolmasosa on videomittauslaitteita. Sen etuna on muun muassa se, ettei kappaletta tarvitse lainkaan koskettaa. Silti videomittauslaitteeseen saattaa olla yhdistettynä myös koskettava mittauskärki. Videomittakonetta ohjaa tietokone ja mittaukset voidaan suorittaa automaattisesti. Mittausohjelmistolla kyetään mittaamaan pituutta, halkaisijaa, kulmaa, suoruutta, yhdensuuntaisuutta sekä ympyrämäisyyttä. /19/ Itse mittaamiseen videomittauslaite käyttää CCD - kameraa, joka saa paikkatietonsa johteisiin asennetuista, tarkoista asteikoista. Kappaleen valaistaan joko objektin läpi tulevalla myötävalolla, objektin ympärillä olevalla rengasvalolla tai alavalolla. /19/ Oikean etäisyyden mittaaminen perustuu kuvan tarkennukseen (fokusointiin). Valaistusta on säädettävä kappaleen mukaan siten, että pinnassa on sekä tummia, että vaaleita kohtia. Tummia ja vaaleita sävyjä tarvitaan erilaisten reunojen ja pintojen muotojen erottamiseen muusta ympäristöstä. Ongelmaksi voi tulla materiaalin pinnoite tai läpinäkyvyys. /12/ Kuvassa 9 on videomittauskoneen laitteisto. Kuva 9. Videomittauskone. /19/ Videomittauslaite on Z-suunnassa erittäin tarkka, kun mitattava pinta on kohtisuorasti kameraa kohti. Videomittauslaitteen ja koskettavan mittauksen ero on, että videomittauskoneella voidaan mitata reunoja mitä koskettavalla mittauksella ei voida tehdä. Koskettavalla mittauksella voidaan taas mitata pystysuoria seinämiä. Siten
17 15 esimerkiksi ympyrän halkaisijan mittauksissa kyseisillä laitteilla saadaan hyvin erilaiset tulokset. Koskettavan mittauksen tulokseen vaikuttaa pinnankarheus ja sen muoto. /12/ Kappaleesta voidaan siis perinteisesti mitata vain kameraan päin oleva pinta. Kappaleen pinnan ja objektin välinen suunta on Z-suunta. Jotta muutkin sivut saadaan kuvattua, on kameraa tai kappaletta käänneltävä, tai käytettävä peilejä joilla saadaan kaikki sivut näkyviin. Tyypillisesti kameran objektissa ei ole liikkuvia linssejä, vaan tarkkuus haetaan liikuttamalla koko objektia Z-suunnassa. Viime aikoina on kuitenkin markkinoille tullut myös muuttuvalla fokusetäisyydellä olevia zoom linssejä ja nivelellisiä kääntyviä kameroita. /12/ Parhaiten videomittauskone soveltuu erityisesti elektroniikan sovelluksiin, mutta sitä käytetään myös mittaamaan ohutseinäisiä muovi- ja metallikappaleita, sekä kappaleita joiden koskettava mittaus on vaikeaa tai mahdotonta. /7/ Myös työstettyjen kappaleiden mittaus onnistuu. Werth on tunnettu koordinaattimittauslaitteiden valmistaja, jonka videomittauskoneilla voi työkappaleen ja objektin väli vaihdella mm välillä. Laitteiston yksi etu on, että syvien reikien mittaus työstetystä kappaleesta voidaan suorittaa luotettavasti ilman pitkiä mekaanisia antureita, jotka voisivat aiheuttaa törmäysvaaran. Laite sopii hyvin yksinkertaisten 2D-muotojen mittauksiin, kuten hammaspyörien mittaamiseen. /20/ Eräs optisen mittaamisen sovellus on lasermittauksestakin tuttu viistokuva- tai kolmiomittaus. Menetelmässä kohde valaistaan valojuovalla. Juovia voi olla yksi tai enemmän ja niiden koko vaihtelee. Juovastolla peitetään kohteen pinta sopivalla tiheydellä. Valojuovia tai kappaletta liikutetaan jolloin samaan aikaan kamera kaappaa kuvia kohteen pinnasta ja näkee valojuovien kulun muutokset kappaleen pinnassa. /12/ Kuvassa 10 on GOM:n valmistama Atos - stereokuvausprojektori kahdella kameralla, joka perustuu tähän menetelmään /11/.
18 16 Kuva 10. GOM:n Atos 3D-stereokuvausprojektori /21/. Viistokuvamittausta voidaan käyttää myös suurille kappaleille. Suomalainen luksuspurjevenevalmistaja Nautor käyttää saksalainen GOM:n valmistamaa stereokuvausprojektoria peräsimien, rungon ja kölien mittaamiseen. Esimerkiksi peräsin voi olla noin 3m pitkä. GOM:n mittaustavassa kappaleen pintaan tai sen ympäristöön kiinnitetään tarralappuja. Lappujen avulla koneen mittausohjelma osaa yhdistää skannatut ruudut. GOM:n Atos-stereokuvausprojektorissa on kaksi kameraa, joiden välinen kulma on tiedossa. Mitattavan kappaleen pinnalle heijastetaan viivoitus, jonka kokoa ja muotoa muutetaan mitattavan kappaleen mukaan. Kohdetta pyöritetään pyörityspöydällä, jotta riittävä määrä kuvia saadaan eri puolilta. Yleensä kohteesta tarvitaan vähintään 5-6 kuvaa, jotta ohjelmisto pystyy luomaan niistä pistepilven. /22/ GOM:n maahantuojan, Cascade Computingin Johan Lundellin mukaan optisen mittaamisen tekniikka on yksinkertaista, mutta sen soveltaminen on vaikeaa. Edellä mainitun järjestelmän käytännön mittausepävarmuus on ±0,005mm ja se täyttää autonvalmistajien käyttämän VDE 2634-standardin vaatimukset. Järjestelmän hinta alkaa n eurosta. Peruspakettiin sisältyy kalibroitu ja toimintavalmis laitteisto, joka sisältää tietokoneen ja tarvittavan mittausohjelmiston. /22/ Samalla laitteistolla voidaan kuvata aina 38mm kokoisista osista jopa 2 m asti /21/.
19 Laseranturit Lasersäteen avulla on mahdollista mitata yhtä pistettä tai pyyhkäistä (scanning) alue pisteestä pisteeseen. Käytettyjä lasermittauksen toimintapoja on kaksi: kolmiomittaus ja fokusoiva laser. Kolmiomittauksessa diodilaser lähettää valoa kohti kappaleen pintaa. Valo heijastuu pinnasta takaisin linssin kautta analogiselle sensorille tai CCD-kennoon, joka muuttaa sen digitaaliseen muotoon. Tästä paikasta mitataan anturin etäisyys kappaleeseen kolmion kulman perusteella. Mittaustarkkuus on hyvä isoilla kulmilla, mutta tällöin mittausalue on pieni. Pienellä kulmalla tarkkuus on huono, mutta mittausalue on suuri. Kuvassa 11 on kolmiomittauslaserin toimintaperiaate. /12/ Kuva 11. Kolmiolaser ja kaavio sen toiminnasta. /12/ Fokusoiva laser toimii kuten CD-soittimen lukupää. Fokusoivassa laseranturissa valon heijastusmatka muutetaan siirtymäksi ns. ±diodille. Valon osumispaikka vaikuttaa ±diodin tuottamaan jännitteeseen ja napaisuuteen. Kohdetta liikutetaan siten että, ±diodin antama jännite on nolla, jolloin valo osuu keskelle diodia ja anturi on sopivalla fokusetäisyydellä. Fokusoivan laserin paras puoli on, että valo kulkee suoraan optista akselia pitkin mitattavaan kappaleeseen ja palaa samaa rataa myös takaisin. Tällöin voidaan mitata luotettavasti lähellä myös olakkeita sekä kapeiden ja syvien reikien pohjia. Kuvassa 12 on esitetty fokusoivan laserin etäisyyden mittauksen periaate. /12/
20 18 Kuva 12. Fokusoivan laserin toimintaperiaate. Differential diode = ±diodi, offset minus/plus = polttopisteen etäisyys optimikohdasta, shutter = varjostin, laser light = laservalo. /12/ Lähtevästä diodilaservalosta peitetään puolet pois (shutter). Loppu säde kulkee kappaleen pinnalle. Kappaleesta heijastuneen säteen poikkeama fokuspisteestä saa aikaan ±diodissa jännite-eron, josta Z-pinooli saa signaalin liikkua ylös tai alas. Fokusetäisyys on oikea, kun valo on jälleen keskellä diodia. Rajoitteena voi olla suuresta suurennoksesta aiheutuva lyhyt fokusetäisyys. Anturi saatetaan joutua asettelemaan hyvin lähelle kappaletta, jolloin törmäysriski on olemassa. /12/. Kolmiomittauksessa yleisimmin käytetty anturi kykenee mittaamaan vain yhtä pistettä kerrallaan. Kun laservalo heijastetaankin pinnalle juovana, käytetään termiä viistokuvamittaus. Kohteen pinnalla olevat epätasaisuudet muuttavat laserjuovan kulkua. Juovan muoto talletetaan yhdellä tai kahdella kameralla. Kahdella kameralla mittaustarkkuus on parempi, koska tietoa tulee kaksi kertaa enemmän. Laserjuovalla mittaavia laitteita kutsutaan myös nauhaskannereiksi. /12/ Laservaloon perustuvat mittauslaitteet ovat suosittuja varsinkin muottien mittaustöissä. Laseranturi voi olla sijoitettu joko perinteiseen koordinaattimittauskoneen runkoon (kuva 4) tai nivelvarsityyppiseen varteen (kuva 5). Faro Technologies on edelläkävijä
21 19 nivelvarsilaitteiden valmistajana. Faron kehittämät kannettavat FaroArm nivelvarsimittauslaitteet voidaan ottaa mukaan ja viedä suoraan paikan päälle, kun kappaletta ei voida esim. kokonsa puolesta tuoda mittaustiloihin. Platinum FaroArm:lla nivelvarsimittauslaitteella päästään 0,005mm tarkkuuteen. /23/ Lasermittauksen uusimpia keksintöjä on patentoitu AFI tekniikka (Accordion Fringe Interferometry), jossa lasersäteen lähteitä on kaksi ja ne heijastavat haitarimaisen kuvion mitattavan kappaleen pintaan (kuva 13). Erittäin tarkka kamera rekisteröi kuvion vaihtelun pinnalla, joka voidaan digitalisoida ja muuttaa mittauspisteiksi. /24/ Kuva 13. Vasemmalla AFI-tekniikan toimintaperiaate ja oikealla kahden laserlähteen muodostama kuvio. /24, 25/ AFI-tekniikan ansiosta mittaustapahtuma ei ole arka ulkoiselle valolle. Se on erittäin tarkka ja projektorissa on hyvä syvyystarkkuus. Myös heijastavien pintojen mittaaminen onnistuu perinteisempää lasermittausta paremmin. /25/
22 20 5 MITTAUSOHJELMISTOT Niin manuaalisiin, kuin NC - ohjattuihinkin koordinaattimittauskoneisiin kuuluu aina tietokone ja mittausohjelma. Mittausohjelmisto käsittelee mitattuja pisteitä; se laskee mittauspään tai kärjen kosketuskohdat tai ohjaa videomittauskoneen CCD - kameran reunatunnistusta. Kosketuspisteistä mittausohjelma laskee mm. geometrioita, uusia elementtejä ja vertailee tuloksia CAD-malliin. Pisteitä voidaan edelleen verrata toleranssivaatimuksiin. Lopuksi ohjelma lähettää kuvat sekä tekstit tiedostona, verkossa tai tulosteena käyttäjälle. Mittausohjelma kannattaa hankkia sertifioituna, jolloin ohjelma on testattu käyttäen pistejoukkoja, jotka haastavat ohjelman haastaviin laskutoimenpiteisiin. /12/ Nykyajan kehittyneet tekoälypohjaiset mittausohjelmistot ja tietojärjestelmät valvovat tulevaisuudessa mittaustapahtumaa. Ne varoittavat huonoista mittauskosketuksista ja mahdollisista vääristä laskelmista mikäli ollaan matemaattisten algoritmien äärialueilla. Tarvittaessa ne saattavat pyytää uuden mittauksen. Käyttäjä voi myös poistaa huonoja mittauspisteitä tai antaa koneen tehdä sen automaattisesti. Käyttäjän on valvottava myös mm. törmäyksien vaikutuksia, mittauspään toimintaa ja sen kalibrointia, kaapeleiden kuntoa, jne. /12/ Ohjelmistot ovat perinteisesti olleet konekohtaisia, mutta esim. ranskalainen Metrologic valmistaa ohjelmistoja useisiin eri koneisiin. Vielä 1990-luvun lopulla ohjelmien käyttö perustui tekstivalikkojen käyttöön, mutta 2000-luvulle tultaessa, mittausohjelmistot ovat tulleet visuaalisimmiksi ja käyttävät enemmän hyödyksi mm. kappaleen CAD mallia. Kuvassa 14 värit indikoivat mitattujen pisteiden eroa CAD mallin pisteisiin. /12/ Kuva 14. Värit paljastavat mitattujen pisteiden heiton CAD mallista. /25/
23 21 6 KONEISTETUN TUOTTEEN MITTAUKSET Yritys tilaa erään tuotteen valmiina alihankkijalta. Asiakas toimittaa tuotteen mukana mittauspöytäkirjat, mutta yritys haluaa selvittää miten he voivat tarpeen vaatiessa myös itse tarkastaa tuotteen mitat. Tuotteen tekniset piirustukset ovat liitteessä III, ja CAD mallin kuvat eri puolilta ovat liitteissä I ja II. Tässä kappaleessa pohditaan miten tuotteen mitat saadaan varmistettua oikeiksi. Koska yrityksellä on ennestään mittaustoimintaa vähän, tarkoituksena on käyttää mahdollisimman paljon perinteisiä käsimittatyökaluja ja kartoittaa, mitkä mittaukset on suoritettava koordinaattimittauskoneella. Piirustuksessa ja kuvissa on valmiin rakenteen toinen puolikas. Valmiissa rakenteessa kaksi tällaista puolikasta on kiinnitettynä vastakkain toisiinsa yhdeksi kokonaisuudeksi. 6.1 Pituusmittojen tarkastus Piirustuksen otsikkoalueella on mainittu niille mitoille standardin 2768-m mukaiset mitat, joita ei ole erikseen toleroitu. Nämä mitat voidaan tarkistaa kappaleen 2.1 taulukosta 1 tai kyseisestä standardista. Tuotteen ulkoiset mitat saadaan helposti tarkistettua esim. viivaimella ja/tai riittävän isolla työntömitalla. Myös tuotteen sisäkehän läpireikien kohdalla olevat suorakulmaiset kolot (6 kpl) voidaan mitata työntömitalla. Tuotteen laakeripesän keskireiän ja sen kahden olakkeen, sekä kaikkien läpireikien halkaisijamitat voidaan tarkastaa tappitulkkien ja litteiden reikätulkkien avulla (kuva 15). Tappitulkit sopivat alle 100mm halkaisijalla olevien reikien mittaamiseen. Tätä isompiin tarvitaan reikätulkki. Yksi mahdollisuus laakeripesän halkaisijatoleranssien mittaamiseen on myös käyttää kolmipistemikrometriä. Kuva 15. a) Vasemmalla litteä (>100mm) ja b) oikealla pyöreä reikätulkki (<100mm). /26/ Tuotteen ulkokehällä olevat 13,5 mm reiät (8 kpl), sekä sisäkehän 9 mm reiät (6 kpl) voidaan tarkastaa sopivan kokoisten tappitulkkien avulla.
24 22 Laakeripesän olakkeissa on säteisvaatimuksena 0,5 mm ja keskimmäisessä maksimissaan 1,5 mm (kuva X). 1,5 mm säteen mittaaminen voidaan tehdä kuvan 16 oikean reunan mukaisella sädetulkilla, mutta sisemmän olakkeen 0,5 mm pyöristyssädettä ei. Markkinoilla olevissa tulkeissa pienin mitattava säde on yleensä 1 mm, kuten kuvan X tulkista voidaan nähdä. Tässä tapauksessa tarvittaisiin tarkkaa koordinaattimittauskonetta. Mikäli laakerin/tiivisteen toiminnan kannalta on mahdollista, olisi olakkeiden koneistuksessa hyvä käyttää tyypillisiä nirkonsäteitä (esim. 0,4 tai 0,8 mm). Kuva 16. a) Vasemmalla laakeripesän pyöristyssäteet, b) oikealla tarkistuksessa käytettävä sädetulkki /27/. 6.2 Geometriset toleranssit Tuotteessa on muutamia erittäin tiukkoja geometrisia toleransseja niin valmistuksen, kuin mittaustenkin kannalta. Otetaan ensimmäisenä käsittelyyn laakeripesän keskiolakkeen lieriömäisyys. ISO 1101 standardia mukaillen, olakkeen pinnan tulee olla kahden samaakselisen lieriöpinnan välissä, joiden väli tässä tapauksessa on 0,0065 mm. Näin pienen arvon mittaaminen heittokellolla, tai millään muulla käsimittavälineellä on käytännössä mahdotonta, koska tarkkuus käsimittavälineillä on yleensä n. 0,01 mm. Tässä kohtaa tarvittaisiin siis koordinaattimittauskonetta. Näin tarkka toleranssivaatimus rajoittaa myös koordinaattimittauskoneen valintaa. Esimerkiksi hyvin tasomaisten ja symmetristen muotojen mittaamisen kykenevä videomittauskone ei kykene lähellekään näin tarkkoja mittauksia. Mittausta varten tarvitaan tarkka ympyrämäisyyden mittauskone tai tavanomainen koskettava koordinaattimittauskone. Tästä on mainittu myös standardissa SFS 4910.
25 23 Yksi mitattava kohde käsimittavälineillä on tuotteen liittymispinnan kohtisuoruustoleranssi suhteessa laakeripesään (kuva 17). Mitattaessa kohtisuoruutta tulee kotelo kiinnittää laakerointikohdasta (elementti A) pyörityselementtiin, esimerkiksi sorviin tai pyörityspöytään, missä ei itsessään ole kohtisuoruusheittoa. Tämä mittaus ei onnistu pelkästään käsimittavälineillä. Koordinaattimittauskoneessa pyörityselementtiä ei tarvita. Kuva 17. Kohtisuoruustoleranssi liittymispinnassa laakeripesän pinnan suhteen. Oikealla mittauksessa tarvittava mittakello. /28/ Mittakello asetetaan tuotteen kehälle nuolen osoittamaan kohtaan jonka jälkeen sitä pyöritetään. Mittakellon pienimmän ja suurimman arvon näyttämä saa olla korkeintaan 0,1 mm. Ohjeet asetteluun löytyvät myös standardista SFS Samaan tapaan tulee mitata myös laakeripesän 100 mm halkaisijalla oleva olake. Kuvan 18 mukaisesti edellä mainitut lieriömäisyys- ja kohtisuoruustoleranssit voidaan muuttaa säteisheiton toleransseiksi. Tällainen muutos voisi selventää mittaustapahtumaa ja helpottaa piirustusten oikein ymmärtämistä. Säteisheitto on merkintänä on selkeämpi ja helpommin ymmärrettävissä kuin lieriömäisyyden toleranssi.
26 24 Kuva 18. Lieriömäisyys- ja kohtisuoruustoleranssin muuttaminen säteisheiton toleransseiksi. /29/ Laakeripesän toleranssimittauksista seuraavana käsitellään olakkeiden sama-akselisuuden mittaus (kuva 19). ISO standardin mukaan toleroitujen pintojen keskiviiva ei saa heittää A-elementin keskiviivasta enempää kuin 0,05 mm. Myös sama-akselisuuden mittaukseen tarvitaan heittokelloa sekä pyörityselementtiä. Tuote tulee tukea laakerointikohdasta pyörityselementtiin. Pyörityselementin ja laakerointikohdan (A-elementin) tulee olla samalla pyörähdysakselilla. Tuotetta pyöritetään ja mitataan toleroitujen pintojen säteisheitot. Säteisheitto ei saa ylittää puolta toleranssiarvosta 0,025 mm. Vaikeudeksi saattaa muodostua mittakellon mahduttaminen varsinkin kapeampaan olakkeen pintaa vasten. Tuotetta pitää myös kääntää työn aikana, joka lisää mittausepävarmuutta. Koordinaattimittauskonetta käyttämällä nämä ongelmat voitaisiin välttää, koska laite kykenee skannaamaan pinnat, eikä kappaletta tarvitse liikutella työvaiheen aikana. Kuva 19. Sama-akselisuuden toleranssit laakeripesässä.
27 25 Tuotteen kahdella kehällä olevien läpireikien paikkatoleranssien mittaaminen ilman koordinaattimittauskonetta aiheuttaa päänvaivaa (kuva 20). Läpireikien keskipisteen paikan heitto tuotteen keskipisteen suhteen ei saa ylittää 0,1 mm. Koska tuotteen keskipistettä on vaikea saada laakeripesän reikien takia selville ja reikien välisen kulman mittaaminenkin käsimittavälineillä on hieman epävarmaa, voisi paikkatoleranssin muuttaa esim. reikien koon toleranssiksi. Tämä sen takia, että todennäköisesti kokoonpannussa rakenteessa laakeripesän ja siitä läpimenevän akselin valmistustarkkuudet määrittävät myös tuotteen puoliskojen asettumisen toisiaan vasten. Koordinaattimittauskoneelle paikkatoleranssi ei aiheuta ongelmia, koska se osaa hakea laskennallisesti kotelon keskipaikan. Kuva 20. Läpireikien paikan toleranssit. Reikiä koon toleranssin suurentamisella myös todennäköisesti nopeutettaisiin valmistusnopeutta ja pienet, 1 2 mm paikan heitot eivät vaikuttaisi kokoonpanon toimintaan, koska läpirei istä tulee pinnapultit/normaalit pultit läpi, jotka pitävät kotelon puolikkaat kiinni toisissaan. 6.3 Koordinaattimittauskoneen käyttö kotelon mittauksissa Kuten jo aiemmin tekstissä on mainittu, koordinaattimittauskoneen käyttö varsinkin geometristen toleranssien mittaamisessa säästäisi aikaa ja etenkin hermoja. Myös mittaustulosten luotettavuus olisi huomattavasti parempi johtuen koneiden tarkkuudesta ja kappaleiden vähäisemmän liikuttelun ansiosta. Isoja sarjoja mitattaessa ajan säästön takia kone olisi varmasti lähes välttämätön. Haittapuolena on laitteiston käytön opettelu mikä voi viedä aikaa. Lisäksi laitteisto vaatii ilmastoidun tilan, jossa lämpötila ja ilmankosteus on oltava standardien vaatimissa rajoissa. Riippuen mittauskoneen koosta, voi myös olla tarpeen tehdä hallin lattiarakenteisiin muutoksia (esim. oma eristetty betonivalupohja). Tämän selvitystyön perusteella kannattaa mittaukset hoitaa koskettavalla anturilla varustetulla koordinaattimittauskoneella. Videomittauskoneiden ongelma on, että ne
28 26 soveltuvat parhaimmillaan reunojen mittaamiseen. Laseranturilla varustetut koneet sopivat taas paremmin esim. valumuottien ynnä muiden ei-lineaaristen kappaleiden mittaamiseen. Yrityksen tapauksessa tuotanto ei oletettavasti ole myöskään niin isoa, että kalliimpia ja nopeampia monianturikoneita olisi tässä vaiheessa syytä edes harkita. Yhtenä vaihtoehtona voisi olla Teräskonttorin jälleenmyymä Mitutoyon CrystaApex koordinaattimittauskone. Kone mittaustarkkuus on noin 1,7µm/metri, joten vaativatkin toleranssivaatimukset saadaan luotettavasti mitattua. Pakettiin sisältyy itse koneen lisäksi vaadittava mittausohjelmisto, joten laite on valmis mittauksiin. Karkea hinta-arvio koneelle on noin /30/ Muita tunnettuja valmistajia ovat mm. Zeiss, Nikon, Leitz, TESA, CEJ ja DEA /12/. Käsimittalaitteet maksavat tietysti murto-osan tästä. Puhutaan sadoista tai korkeintaan tuhansista euroista. Kuitenkin on muistettava että käsimittalaitteet on kalibroitava tasaisin väliajoin, jotka myös lisäävät kustannuksia. Lisäksi mittaustarkkuus ja etenkin mittausten luotettavuus ei vastaa koordinaattimittauskoneella tehtyjä mittauksia.
29 27 7 JOHTOPÄÄTÖKSET Mittauskoneet ovat voimakkaasti kehittyneet niin mittaustarkkuuden kuin tulosten analysoinninkin suhteen. Nykyaikaiset koordinaattimittauskoneet kykenevät jopa muutamien mikrometrien tarkkuuksiin. Tämä tarkkuus on huomattavasti suurempi mitä käsimittavälineillä. Erilaisia mittauskoneita varustettuna eri mittausantureilla ja - päillä on markkinoilla satoja. Konetta valittaessa tulee ottaa huomioon mitattavien tuotteiden koko, muoto, mittausvolyymi, mittausolosuhteet jne. Kokenut mittaaja huomaa virheet, mitä myös koordinaattimittauskoneilla voi tapahtua. Tietotekniikka on koordinaattimittauskoneissa hyvin vahvasti mukana ja mittausohjelmistojen hallitseminen on välttämätöntä koneen käytön kannalta. Suurin osa mittauskoneista vaatii hyvin tasaiset olosuhteet mm. lämpötilan ja ilmankosteuden suhteen, joten näiden olosuhteiden järjestämisestä voi koitua koneen hankkijalle kustannuksia. Kuten luvusta 6 ilmenee, korkea valmistustarkkuus sekä suunnittelijan ratkaisut vaikuttavat huomattavasti mittauksien vaikeustasoon ja siten kustannuksiin. Varsinkin geometristen toleranssien määrällä ja laadulla vaikutettaan pitkälti siihen, tarvitaanko koordinaattimittauskonetta vai ei. Tietysti tarkkoja toleransseja ei voida jo pelkästään koneenosan toiminnan kannalta aina välttää. Kuitenkin toleranssien tarkalla harkinnalla voidaan mittauksia vähintäänkin nopeuttaa varsinkin, kun käytössä on perinteiset käsimittalaitteet. Myös erilaisilla pituuksien mitoitusratkaisuilla voidaan saada aikaan ajan sekä rahan säästöä, kun pituustoleransseista ei tehdä turhan tarkkoja. Mikäli kappaleessa 6 käsitellyn tuotteen kaikki mitat halutaan tarkastaa luotettavasti, on yrityksen hankittava koordinaattimittauskone. Mitat/toleranssit, joihin koordinaattimittauskonetta tarvitaan ovat: laakeripesän keskiolakkeen lieriömäisyystoleranssi, laakeripesän olakkeiden sama-akselisuustoleranssit, kohtisuoruustoleranssit (mikäli sopivaa pyörityselementtiä ei ole saatavilla), läpireikien paikan toleranssi. Toisaalta muutamilla geometristen toleranssien muutoksilla voitaisiin toiminnan kannalta kriittisen laakeripesän mittaaminen tehdä mahdolliseksi myös käsimittavälinein.
30 28 8 YHTEENVETO Koneenosien mittauksia voidaan tehdä perinteisillä käsimittavälineillä tai koordinaattimittauskoneilla. Koordinaattimittauskoneet ovat ohjelmoitavissa samaan tapaan kuin työstökoneet/robotit ja niiden mittaustarkkuus on huomattavasti parempi kuin perinteisten mittalaitteiden. Mitattavat suureet jaotellaan pituusmittoihin ja sen toleransseihin, sekä geometrisiin toleransseihin. Absoluuttisen mittatarkkaa koneenosa on mahdoton valmistaa, joten mitoille annetaan jokin vaihteluväli eli toleranssi. Koneenosien mitoittamisesta sekä toleranssien käytöstä on ohjeet ISO standardeissa. Koordinaattimittauskoneet jaotellaan runkotyyppinsä mukaan pylväs-, puomi-, silta-, portaali- ja nivelvarsirakenteeseen. Kappaleen koko ja muoto päättävät pitkälti minkälaista mittauskoneen runkoa tarvitaan. Mittauskoneen rungossa on mittauspää, jonka mittauskyky perustuu joko mekaaniseen kosketukseen, laservaloon tai optiseen videokuvaukseen. Näistä koskettavat mittauspäät ovat teollisuudessa suosituimpia. Koordinaattimittauskoneessa voi olla myös esim. koskettava- sekä lasermittauspää, jolloin sitä voidaan kutsua monianturikoneeksi. Koordinaattimittauskoneen ohjelmointi ja mittaustulosten tarkastelu vaatii tietokoneen ja mittausohjelmiston. Mittausohjelmiston avulla voidaan mittaustuloksia peilata suoraan 3D malliin, jolloin nähdään suoraan kuinka paljon todelliset mitat poikkeavat halutuista mitoista. Käytännön osuudessa on pohdittu erään yrityksen koordinaattimittauskoneen tarvetta tilaamansa tuotteen mittauksissa. Tuotteen pituusmittojen tarkastuksessa selvitään käsimittalaitteiden avulla. Geometristen toleranssien kohdalla ajaudutaan kuitenkin tilanteeseen, jossa toleranssien mittaaminen käsimittalaitteilla on joko vaikeaa tai mahdotonta. Laitehankinnaksi suositellaan koskettavalla mittausanturilla toimivaa koordinaattimittauskonetta.
31 LÄHTEET 1. Card, G. Selecting Your CMM. Manufacturing Engineering Vol 130. Nro. 6. Lehtiartikkeli. Saatavissa: 2. Andersson, P. Tikka, H. Mittaus- ja laatutekniikat WSOY. Porvoo. 323 s. 3. Ihalainen, E. Konepajan mittaukset. Otakustantamo Espoo. 111s. 4. Keinänen, T., Kärkkäinen, P. Konetekniikan perusteet. WSOYpro Oy. Porvoo. 364 s. 5. Aaltonen, K. Miksi koordinaattimittauskone kannattaa hankkia? AEL-seminaarin luentokalvot Helsinki. 6. Airila, M. Karjalainen, J, A. Mantovaara, U. Nurmi, L. Ranta, A. Verho, A Koneenosien suunnittelu 1 perusteet. Werner Söderström Osakeyhtiö. Porvoo, Helsinki, Juva. 283 s. 7. SFS käsikirja Toleranssit ja pinnankarheus osa 1: ISO toleranssit ja geometriset toleranssit. Suomen standardoimisliitto SFS ry. 1. painos. 12/2008. Helsinki. 8. Eskelinen, H. Tekninen piirustus 2. Luentomateriaali. Lappeenrannan teknillinen yliopisto SFS EN-ISO 1101-standardi. Vahvistettu Metrology for engine components. MAHR GmbH:n tuote-esite. PDF-tiedosto. Päivitetty Viitattu Saatavissa: ileid=10110&contentdataid=35555&save=0
32 11. I Know Where I Am But Where Are You? American Machinist lehden verkkoartikkeli. Julkaistu Viitattu Saatavissa: Tikka, H. Koordinaattimittaus Tampereen Yliopistopaino Oy. Tampere. 473s. 13. Scanning The Horizon. The Machinery. S: August Lehtiartikkeli. 14. Kuva Faron verkkosivuilta. Viitattu Saatavissa: Esala, V-P. Lehto, H. Tikka, H. Konepajatekniset mittaukset ja kalibroinnit. Tekninen tiedotus, 3/2003. Teknologiateollisuus ry. Helsinki. 79 s 16. Morey, B. Accuracy and Uncertainty in Noncontact Metrology. Manufacturing Engineering. Julkaistu 11/2010. S: Lehtiartikkeli. 17. Ympyrämäisyys konepajateollisuudessa. Mittatekniikan keskuksen MIKES:n verkkosivut. Viitattu Saatavissa: Kortelainen, K. Mansner mittaa lisää töitä. Metallitekniikka 11/2009. S: Mittatekniikan keskuksen MIKES:n verkkosivut. Saatavissa: 891%26contentID%3D427, viitattu The Worth Of Werth. The Machinery. S: August Lehtiartikkeli. 21. GOM-yhtiön verkkosivut. Viitattu Saatavissa:
33 22. Tervola, J. Muodot talteen kameralla. Metallitekniikka 8/2008. S: Lehtiartikkeli. 23. Kortelainen, K. Kannettavalla 3d-mittausvarrella 0,005mm tarkkuuteen. Talentumin lehtiarkisto verkossa. Julkaistu Metallitekniikka-lehdessä Viitattu Saatavissa: http//lehtiarkisto.talentum.com/lehtiarkisto/search/show?eid= Dimensional Photonics Internationalin verkkosivut. Viitattu Saatavissa: Bruce, M. Advances in Automotive Metrology. Manufacturing Engineering. September S: Lehtiartikkeli. 26. Kuva Knorring Oy:n verkkosivuilta. Saatavissa: Kuva Teräskonttorin tuotevalikoimasta. Päivitetty Viitattu Saatavissa: e=18327&p=0 28. Kuva Virtasenkauppa.fi sivustolta. Viitattu Saatavissa: SKF laakerikirja Luettelo 4000 Fi. 976 s. 30. Puhelinkeskustelut Teräskonttori Oy:n Harri Salmen kanssa
34 Liite I
35 Liite II
36 Liite III
Keskeiset aihepiirit
 TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
TkT Harri Eskelinen Keskeiset aihepiirit 1 Perusmääritelmät geometrisiä toleransseja varten 2 Toleroitavat ominaisuudet ja niiden määritelmät 3 Teknisiin dokumentteihin tehtävät merkinnät 4 Geometriset
Koneistusyritysten kehittäminen. Mittaustekniikka. Mittaaminen ja mittavälineet. Rahoittajaviranomainen: Satakunnan ELY-keskus
 Koneistusyritysten kehittäminen Mittaustekniikka Mittaaminen ja mittavälineet Rahoittajaviranomainen: Satakunnan ELY-keskus Yleistä Pidä työkalut erillään mittavälineistä Ilmoita rikkoutuneesta mittavälineestä
Koneistusyritysten kehittäminen Mittaustekniikka Mittaaminen ja mittavälineet Rahoittajaviranomainen: Satakunnan ELY-keskus Yleistä Pidä työkalut erillään mittavälineistä Ilmoita rikkoutuneesta mittavälineestä
AKK-MOTORSPORT ry Katsastuksen käsikirja ISKUTILAVUUDEN MITTAAMINEN. 1. Tarkastuksen käyttö
 ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
ISKUTILAVUUDEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet 4. Olosuhteet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin iskutilavuuden mittaaminen ja laskeminen. Kyseinen on mahdollista
OSA A. MITTATOLERANSSIT
 BK50A0200 TEKNINEN PIIRUSTUS II HARJOITUKSET / KEVÄT 2015/ viikko 11 / TOLERANSSIT Pj/Varapj: Tulosta tehtäväpaperi ja palauta tehtävien ratkaisut luennoitsijalle oman harjoitusajan loppuun mennessä. RYHMÄN
BK50A0200 TEKNINEN PIIRUSTUS II HARJOITUKSET / KEVÄT 2015/ viikko 11 / TOLERANSSIT Pj/Varapj: Tulosta tehtäväpaperi ja palauta tehtävien ratkaisut luennoitsijalle oman harjoitusajan loppuun mennessä. RYHMÄN
Säteilijät - aallonpituusnormaalit Stabiloidut laserit rel. 543,5 nm 5 10-10 λ 0
 1/ Säteilijät - aallonpituusnormaalit Stabiloidut laserit 32 nm 1 10-10 λ 0 43, nm 10-10 λ 0 633 nm 1 10-10 λ 0 Pituusmitat Pituuden mittauslaitteet Laser-interferometri 1,0 Peruslaitteisto Kulmapoikkeamien
1/ Säteilijät - aallonpituusnormaalit Stabiloidut laserit 32 nm 1 10-10 λ 0 43, nm 10-10 λ 0 633 nm 1 10-10 λ 0 Pituusmitat Pituuden mittauslaitteet Laser-interferometri 1,0 Peruslaitteisto Kulmapoikkeamien
PROJECT X. 2D tarkastuksen standardi Mittausteknologian edelläkävijä
 PROJECT X 2D tarkastuksen standardi Mittausteknologian edelläkävijä 2-dimensioinen kameramittausjärjestelmä Project X.. 2D mittauksen standardi Project X on erilainen. Siinä on otettu käyttöön aivan uusi,
PROJECT X 2D tarkastuksen standardi Mittausteknologian edelläkävijä 2-dimensioinen kameramittausjärjestelmä Project X.. 2D mittauksen standardi Project X on erilainen. Siinä on otettu käyttöön aivan uusi,
UUDET TUOTTEET Laser Scan -mikrometri, kiinteä USB-näyttö LSM 5200
 UUDET TUOTTEET Laser Scan -mikrometri, kiinteä USB-näyttö LSM 5200 Tarkat tiedot sivulla 336. Sivu 333 335 Sivu 335 336 Anturijärjestelmät Laser Scan -mikrometrit Mittausyksiköt Laser Scan -mikrometrit
UUDET TUOTTEET Laser Scan -mikrometri, kiinteä USB-näyttö LSM 5200 Tarkat tiedot sivulla 336. Sivu 333 335 Sivu 335 336 Anturijärjestelmät Laser Scan -mikrometrit Mittausyksiköt Laser Scan -mikrometrit
AKK-MOTORSPORT ry Katsastuksen käsikirja
 NOKKA-AKSELIEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin nokka-akseli(e)n mittaaminen ja ominaisuuksien laskeminen. Ns. A-(perusympyrä)
NOKKA-AKSELIEN MITTAAMINEN 1. Tarkastuksen käyttö 2. Määritelmät 3. Välineet Kyseisen ohjeen tarkoituksena on ohjeistaa moottorin nokka-akseli(e)n mittaaminen ja ominaisuuksien laskeminen. Ns. A-(perusympyrä)
Tehoa robotiikasta -hanke. 1.1 Koordinaattimittalaitekoulutuksen sisältöjen ja toteutuksen suunnittelu
 Tehoa robotiikasta -hanke 1.1 Koordinaattimittalaitekoulutuksen sisältöjen ja toteutuksen suunnittelu Sisällys MITTAUSTARPEIDEN MÄÄRITTELY... 2 KOORDINAATTIMITTALAITTEEN JA MUIDEN MITTALAITTEIDEN TUOMAT
Tehoa robotiikasta -hanke 1.1 Koordinaattimittalaitekoulutuksen sisältöjen ja toteutuksen suunnittelu Sisällys MITTAUSTARPEIDEN MÄÄRITTELY... 2 KOORDINAATTIMITTALAITTEEN JA MUIDEN MITTALAITTEIDEN TUOMAT
Konepajatekniset mittaukset ja kalibroinnit
 Veli-Pekka Esala - Heikki Lehto - Heikki Tikka Konepajatekniset mittaukset ja kalibroinnit T E K N I N E N T I E D O T U S 3 2 0 0 3 A L K U S A N A T Tarkoitus Tämä tekninen tiedotus on tarkoitettu käytettäväksi
Veli-Pekka Esala - Heikki Lehto - Heikki Tikka Konepajatekniset mittaukset ja kalibroinnit T E K N I N E N T I E D O T U S 3 2 0 0 3 A L K U S A N A T Tarkoitus Tämä tekninen tiedotus on tarkoitettu käytettäväksi
Standardin ISO 8062 mittatoleranssijärjestelmä
 Valutoleranssilla tarkoitetaan yhteisesti sovittua aluetta, jonka sisälle kappaleiden mittamuutokset mahtuvat. Toleranssit jaotellaan yleensä useaan ryhmään, jossa pienimmissä toleranssiryhmissä hyväksytyt
Valutoleranssilla tarkoitetaan yhteisesti sovittua aluetta, jonka sisälle kappaleiden mittamuutokset mahtuvat. Toleranssit jaotellaan yleensä useaan ryhmään, jossa pienimmissä toleranssiryhmissä hyväksytyt
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
3D-kuvauksen tekniikat ja sovelluskohteet. Mikael Hornborg
 3D-kuvauksen tekniikat ja sovelluskohteet Mikael Hornborg Luennon sisältö 1. Optiset koordinaattimittauskoneet 2. 3D skannerit 3. Sovelluskohteet Johdanto Optiset mittaustekniikat perustuvat valoon ja
3D-kuvauksen tekniikat ja sovelluskohteet Mikael Hornborg Luennon sisältö 1. Optiset koordinaattimittauskoneet 2. 3D skannerit 3. Sovelluskohteet Johdanto Optiset mittaustekniikat perustuvat valoon ja
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE
 Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE Aalto yliopisto LVI-tekniikka 2013 SISÄLLYSLUETTELO TILAVUUSVIRRAN MITTAUS...2 1 HARJOITUSTYÖN TAVOITTEET...2 2 MITTAUSJÄRJESTELY
Ene-58.4139 LVI-tekniikan mittaukset ILMAN TILAVUUSVIRRAN MITTAUS TYÖOHJE Aalto yliopisto LVI-tekniikka 2013 SISÄLLYSLUETTELO TILAVUUSVIRRAN MITTAUS...2 1 HARJOITUSTYÖN TAVOITTEET...2 2 MITTAUSJÄRJESTELY
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
2. Määritelmät Puristussuhde: Iskutilavuuden suhde puristustilavuuteen, suhdeluku.
 PALOTILAN JA PURISTUSSUHTEEN MITTAAMINEN 1. Tarkastuksen käyttö Tämän ohjeen tarkoituksena on ohjeistaa moottorin laskennallisen puristustilavuuden ja puristussuhteen laskeminen. Tarkastuksen voi tehdä
PALOTILAN JA PURISTUSSUHTEEN MITTAAMINEN 1. Tarkastuksen käyttö Tämän ohjeen tarkoituksena on ohjeistaa moottorin laskennallisen puristustilavuuden ja puristussuhteen laskeminen. Tarkastuksen voi tehdä
EVTEK/ Antti Piironen & Pekka Valtonen 1/6 TM01S/ Elektroniikan komponentit ja järjestelmät Laboraatiot, Syksy 2003
 EVTEK/ Antti Piironen & Pekka Valtonen 1/6 TM01S/ Elektroniikan komponentit ja järjestelmät Laboraatiot, Syksy 2003 LABORATORIOTÖIDEN OHJEET (Mukaillen työkirjaa "Teknillisten oppilaitosten Elektroniikka";
EVTEK/ Antti Piironen & Pekka Valtonen 1/6 TM01S/ Elektroniikan komponentit ja järjestelmät Laboraatiot, Syksy 2003 LABORATORIOTÖIDEN OHJEET (Mukaillen työkirjaa "Teknillisten oppilaitosten Elektroniikka";
MACHINERY on laadunvarmistaja
 MACHINERY on laadunvarmistaja Mitä tapahtuu huomenna? entä jos omaisuudelle tapahtuu jotain? entä jos kalustolle tapahtuu jotain? entä jos sinulle tapahtuu jotain? MACHINERY ennakoi, ennaltaehkäisee ja
MACHINERY on laadunvarmistaja Mitä tapahtuu huomenna? entä jos omaisuudelle tapahtuu jotain? entä jos kalustolle tapahtuu jotain? entä jos sinulle tapahtuu jotain? MACHINERY ennakoi, ennaltaehkäisee ja
PANK-2206. Menetelmä soveltuu ainoastaan kairasydännäytteille, joiden halkaisija on 32-62 mm.
 PANK-2206 KIVIAINES, PISTEKUORMITUSINDEKSI sivu 1/6 PANK Kiviainekset, lujuus- ja muoto-ominaisuudet PISTEKUORMITUSINDEKSI PANK-2206 PÄÄLLYSTEALAN NEUVOTTELUKUNTA 1. MENETELMÄN TARKOITUS Hyväksytty: Korvaa
PANK-2206 KIVIAINES, PISTEKUORMITUSINDEKSI sivu 1/6 PANK Kiviainekset, lujuus- ja muoto-ominaisuudet PISTEKUORMITUSINDEKSI PANK-2206 PÄÄLLYSTEALAN NEUVOTTELUKUNTA 1. MENETELMÄN TARKOITUS Hyväksytty: Korvaa
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Mittaustekniikka (3 op)
 530143 (3 op) Yleistä Luennoitsija: Ilkka Lassila Ilkka.lassila@helsinki.fi, huone C319 Assistentti: Ville Kananen Ville.kananen@helsinki.fi Luennot: ti 9-10, pe 12-14 sali E207 30.10.-14.12.2006 (21 tuntia)
530143 (3 op) Yleistä Luennoitsija: Ilkka Lassila Ilkka.lassila@helsinki.fi, huone C319 Assistentti: Ville Kananen Ville.kananen@helsinki.fi Luennot: ti 9-10, pe 12-14 sali E207 30.10.-14.12.2006 (21 tuntia)
DIGIBONUSTEHTÄVÄ: MPKJ NCC INDUSTRY OY LOPPURAPORTTI
 DIGIBONUSTEHTÄVÄ: MPKJ NCC INDUSTRY OY LOPPURAPORTTI Tekijä: Marko Olli 16.10.2018 Sisällys 1 Johdanto...3 2 Hankkeen tavoitteet ja vaikuttavuus...3 3 Laitteisto ja mittaustarkkuus...3 4 Pilotointi ja
DIGIBONUSTEHTÄVÄ: MPKJ NCC INDUSTRY OY LOPPURAPORTTI Tekijä: Marko Olli 16.10.2018 Sisällys 1 Johdanto...3 2 Hankkeen tavoitteet ja vaikuttavuus...3 3 Laitteisto ja mittaustarkkuus...3 4 Pilotointi ja
MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET. Jukka-Pekka Rapinoja METSTA
 MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET Jukka-Pekka Rapinoja METSTA Mitä mallipohjainen tuotemäärittely tarkoittaa EN-kielinen termi MBD, Model-based Definition Kaikki tuotetieto on 3D-mallissa
MALLIPOHJAISEN TUOTEMÄÄRITTELYN MAHDOLLISUUDET Jukka-Pekka Rapinoja METSTA Mitä mallipohjainen tuotemäärittely tarkoittaa EN-kielinen termi MBD, Model-based Definition Kaikki tuotetieto on 3D-mallissa
OHUTLEVYTUOTTEIDEN JA TYÖKALUJEN MITTAAMINEN
 OHUTLEVYTUOTTEIDEN JA TYÖKALUJEN MITTAAMINEN Heikki Tikka 2005 TUOTEVAATIMUKSET, MITOITUSTAPA TUOTE TYÖKALUT JA KONEET MITTAUSTAVAT PITUUDEN REALISOINTI c = λ f λ = c / f λ = HeNe Laserin aallonpituus
OHUTLEVYTUOTTEIDEN JA TYÖKALUJEN MITTAAMINEN Heikki Tikka 2005 TUOTEVAATIMUKSET, MITOITUSTAPA TUOTE TYÖKALUT JA KONEET MITTAUSTAVAT PITUUDEN REALISOINTI c = λ f λ = c / f λ = HeNe Laserin aallonpituus
Varausta poistavien lattioiden mittausohje. 1. Tarkoitus. 2. Soveltamisalue. 3. Mittausmenetelmät MITTAUSOHJE 1.6.2001 1 (5)
 1.6.2001 1 (5) Varausta poistavien lattioiden mittausohje 1. Tarkoitus Tämän ohjeen tarkoituksena on yhdenmukaistaa ja selkeyttää varausta poistavien lattioiden mittaamista ja mittaustulosten dokumentointia
1.6.2001 1 (5) Varausta poistavien lattioiden mittausohje 1. Tarkoitus Tämän ohjeen tarkoituksena on yhdenmukaistaa ja selkeyttää varausta poistavien lattioiden mittaamista ja mittaustulosten dokumentointia
DistanceMaster One. Laser 650 nm SPEED SHUTTER
 DistanceMaster One 36 Laser 650 nm SPEED SHUTTER Laser 02 2 x Typ AAA / LR03 1,5V / Alkaline DistanceMaster One x x y = m 2 y z x y x y z = m 3 03 ! Lue käyttöohje kokonaan. Lue myös lisälehti Takuu- ja
DistanceMaster One 36 Laser 650 nm SPEED SHUTTER Laser 02 2 x Typ AAA / LR03 1,5V / Alkaline DistanceMaster One x x y = m 2 y z x y x y z = m 3 03 ! Lue käyttöohje kokonaan. Lue myös lisälehti Takuu- ja
Ratkaisu: Maksimivalovoiman lauseke koostuu heijastimen maksimivalovoimasta ja valonlähteestä suoraan (ilman heijastumista) tulevasta valovoimasta:
 LASKUHARJOITUS 1 VALAISIMIEN OPTIIKKA Tehtävä 1 Pistemäinen valonlähde (Φ = 1000 lm, valokappaleen luminanssi L = 2500 kcd/m 2 ) sijoitetaan 15 cm suuruisen pyörähdysparaboloidin muotoisen peiliheijastimen
LASKUHARJOITUS 1 VALAISIMIEN OPTIIKKA Tehtävä 1 Pistemäinen valonlähde (Φ = 1000 lm, valokappaleen luminanssi L = 2500 kcd/m 2 ) sijoitetaan 15 cm suuruisen pyörähdysparaboloidin muotoisen peiliheijastimen
Kelluvien turvalaitteiden. asennus- ja mittausohje
 Kelluvien turvalaitteiden asennus- ja mittausohje 2009 Versio 0.4 Sivu 1 (9) 14.9.2009 Ohjeen infosivu: Kelluvien turvalaitteiden asennus- ja mittausohje Versio: 0.3 / 28.8.2009 laatinut IK Status: Yleisohje
Kelluvien turvalaitteiden asennus- ja mittausohje 2009 Versio 0.4 Sivu 1 (9) 14.9.2009 Ohjeen infosivu: Kelluvien turvalaitteiden asennus- ja mittausohje Versio: 0.3 / 28.8.2009 laatinut IK Status: Yleisohje
KON C3004 14.10.2015 H03 Ryhmä G Samppa Salmi, 84431S Joel Tolonen, 298618. Koesuunnitelma
 KON C3004 14.10.2015 H03 Ryhmä G Samppa Salmi, 84431S Joel Tolonen, 298618 Koesuunnitelma Sisällysluettelo Sisällysluettelo 1 1 Tutkimusongelma ja tutkimuksen tavoit e 2 2 Tutkimusmenetelmät 3 5 2.1 Käytännön
KON C3004 14.10.2015 H03 Ryhmä G Samppa Salmi, 84431S Joel Tolonen, 298618 Koesuunnitelma Sisällysluettelo Sisällysluettelo 1 1 Tutkimusongelma ja tutkimuksen tavoit e 2 2 Tutkimusmenetelmät 3 5 2.1 Käytännön
2. Sähköisiä perusmittauksia. Yleismittari.
 TURUN AMMATTKORKEAKOULU TYÖOHJE 1 TEKNKKA FYSKAN LABORATORO 2.0 2. Sähköisiä perusmittauksia. Yleismittari. 1. Työn tavoite Tutustutaan tärkeimpään sähköiseen perusmittavälineeseen, yleismittariin, suorittamalla
TURUN AMMATTKORKEAKOULU TYÖOHJE 1 TEKNKKA FYSKAN LABORATORO 2.0 2. Sähköisiä perusmittauksia. Yleismittari. 1. Työn tavoite Tutustutaan tärkeimpään sähköiseen perusmittavälineeseen, yleismittariin, suorittamalla
S-108.3020 Elektroniikan häiriökysymykset. Laboratoriotyö, kevät 2010
 1/7 S-108.3020 Elektroniikan häiriökysymykset Laboratoriotyö, kevät 2010 Häiriöiden kytkeytyminen yhteisen impedanssin kautta lämpötilasäätimessä Viimeksi päivitetty 25.2.2010 / MO 2/7 Johdanto Sähköisiä
1/7 S-108.3020 Elektroniikan häiriökysymykset Laboratoriotyö, kevät 2010 Häiriöiden kytkeytyminen yhteisen impedanssin kautta lämpötilasäätimessä Viimeksi päivitetty 25.2.2010 / MO 2/7 Johdanto Sähköisiä
Suorakulmainen kolmio
 Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Suorakulmainen kolmio 1. Määritä terävä kulma α, β ja γ, kun sinα = 0,5782, cos β = 0,745 ja tanγ = 1,222. π 2. Määritä trigonometristen funktioiden sini, kosini ja tangentti, kun kulma α = ja 3 β = 73,2
Karting tekniikkakoulutus KF 6
 Karting tekniikkakoulutus KF 6 KF6 moottorin luokitus Tarkista aina ensin: Moottorin luokitusnumero esim. 3/KF6/14 Moottorin numero esim. 10022 Onko ko. moottori luokituskuvien mukainen ulkoisesti. 3 KF6
Karting tekniikkakoulutus KF 6 KF6 moottorin luokitus Tarkista aina ensin: Moottorin luokitusnumero esim. 3/KF6/14 Moottorin numero esim. 10022 Onko ko. moottori luokituskuvien mukainen ulkoisesti. 3 KF6
Mittaustulosten tilastollinen käsittely
 Mittaustulosten tilastollinen käsittely n kertaa toistetun mittauksen tulos lasketaan aritmeettisena keskiarvona n 1 x = x i n i= 1 Mittaustuloksen hajonnasta aiheutuvaa epävarmuutta kuvaa keskiarvon keskivirhe
Mittaustulosten tilastollinen käsittely n kertaa toistetun mittauksen tulos lasketaan aritmeettisena keskiarvona n 1 x = x i n i= 1 Mittaustuloksen hajonnasta aiheutuvaa epävarmuutta kuvaa keskiarvon keskivirhe
7.4 PERUSPISTEIDEN SIJAINTI
 67 7.4 PERUSPISTEIDEN SIJAINTI Optisen systeemin peruspisteet saadaan systeemimatriisista. Käytetään seuraavan kuvan merkintöjä: Kuvassa sisäänmenotaso on ensimmäisen linssin ensimmäisessä pinnassa eli
67 7.4 PERUSPISTEIDEN SIJAINTI Optisen systeemin peruspisteet saadaan systeemimatriisista. Käytetään seuraavan kuvan merkintöjä: Kuvassa sisäänmenotaso on ensimmäisen linssin ensimmäisessä pinnassa eli
LaserQC mittauksia laserin nopeudella
 LaserQC mittauksia laserin nopeudella 1/6 prosessi LaserQ mittaustulokset 20 sekunnissa! 2D-aihioiden mittojen manuaalinen tarkastus ja muistiinmerkintä on aikaa vievä prosessi. Lisäksi virheiden mahdollisuus
LaserQC mittauksia laserin nopeudella 1/6 prosessi LaserQ mittaustulokset 20 sekunnissa! 2D-aihioiden mittojen manuaalinen tarkastus ja muistiinmerkintä on aikaa vievä prosessi. Lisäksi virheiden mahdollisuus
Seuraa huolellisesti annettuja ohjeita. Tee taitokset tarkkaan,
 Origami on perinteinen japanilainen paperitaittelumuoto, joka kuuluu olennaisena osana japanilaiseen kulttuuriin. Länsimaissa origami on kuitenkin suhteellisen uusi asia. Se tuli yleiseen tietoisuuteen
Origami on perinteinen japanilainen paperitaittelumuoto, joka kuuluu olennaisena osana japanilaiseen kulttuuriin. Länsimaissa origami on kuitenkin suhteellisen uusi asia. Se tuli yleiseen tietoisuuteen
1 TYÖNTÖMITTA. sisä mittakärjet tuuma-nonio lukitusruuvi. 1.1 Yleistä työntömitasta
 MITTAVAUNU MATERIAALIA 1( 35) 1 TYÖNTÖMITTA 1.1 Yleistä työntömitasta Työntömitta ( tönäri, mauseri ) kuuluu tekniikan alan perustyökaluihin, joten sen oikeaoppinen käyttö on jokaisen ammattilaisen osattava.
MITTAVAUNU MATERIAALIA 1( 35) 1 TYÖNTÖMITTA 1.1 Yleistä työntömitasta Työntömitta ( tönäri, mauseri ) kuuluu tekniikan alan perustyökaluihin, joten sen oikeaoppinen käyttö on jokaisen ammattilaisen osattava.
MITTAUS JA DIGITOINTI. smartscan M I T T A A E T U S I. AICON 3D Systems yritys
 MITTAUS JA DIGITOINTI smartscan M I T T A A E T U S I AICON 3D Systems yritys smartscan Sarja joustavia järjestelmiä suuren tarkkuuden 3D mittaukseen smartscan järjestelmät kaappaavat mittauskohteittesi
MITTAUS JA DIGITOINTI smartscan M I T T A A E T U S I AICON 3D Systems yritys smartscan Sarja joustavia järjestelmiä suuren tarkkuuden 3D mittaukseen smartscan järjestelmät kaappaavat mittauskohteittesi
Laskentaohjelma mittausepävarmuuden
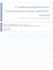 Laskentaohjelma mittausepävarmuuden määrittämiseen Standardin ISO 15530-3 mukainen menetelmä Tekn. Lis. Heikki Lehto, Emeritus-tutkija Toimitustyö ja kuvat: DI Jukka-Pekka Rapinoja METSTA ry 26.10.2018
Laskentaohjelma mittausepävarmuuden määrittämiseen Standardin ISO 15530-3 mukainen menetelmä Tekn. Lis. Heikki Lehto, Emeritus-tutkija Toimitustyö ja kuvat: DI Jukka-Pekka Rapinoja METSTA ry 26.10.2018
Laser FLS 90. Käyttöohje
 Laser FLS 90 fi Käyttöohje L SE R R DI TIO N DO NO T ST R E IN TO BE M L SE R CL S S 2 5 1 2 4 3 3 6 7 B1 B2 1 C1 C2 C3 S1 =S2 = 90 C4 S1 90 S2 D1 D2 D3 D4 D5 D6 E1 S=10m 32 10 E2 C L 1 B E3 L 2 D C L
Laser FLS 90 fi Käyttöohje L SE R R DI TIO N DO NO T ST R E IN TO BE M L SE R CL S S 2 5 1 2 4 3 3 6 7 B1 B2 1 C1 C2 C3 S1 =S2 = 90 C4 S1 90 S2 D1 D2 D3 D4 D5 D6 E1 S=10m 32 10 E2 C L 1 B E3 L 2 D C L
Mittapalat, tulkit ja kulmamitat
 Mittapalat, tulkit ja kulmamitat 66 67 68 69 70 71 72 73 74 Kulmamitat Graniitti mittausalustat Mittausalustat mittakelloille Kulmapalasarjat Alusparallellit Mittapalasarjat työntömittojen tarkastukseen
Mittapalat, tulkit ja kulmamitat 66 67 68 69 70 71 72 73 74 Kulmamitat Graniitti mittausalustat Mittausalustat mittakelloille Kulmapalasarjat Alusparallellit Mittapalasarjat työntömittojen tarkastukseen
FYSP101/K1 KINEMATIIKAN KUVAAJAT
 FYSP101/K1 KINEMATIIKAN KUVAAJAT Työn tavoitteita tutustua kattavasti DataStudio -ohjelmiston käyttöön syventää kinematiikan kuvaajien (paikka, nopeus, kiihtyvyys) hallintaa oppia yhdistämään kinematiikan
FYSP101/K1 KINEMATIIKAN KUVAAJAT Työn tavoitteita tutustua kattavasti DataStudio -ohjelmiston käyttöön syventää kinematiikan kuvaajien (paikka, nopeus, kiihtyvyys) hallintaa oppia yhdistämään kinematiikan
testo 831 Käyttöohje
 testo 831 Käyttöohje FIN 2 1. Yleistä 1. Yleistä Lue käyttöohje huolellisesti läpi ennen laitteen käyttöönottoa. Säilytä käyttöohje myöhempää käyttöä varten. 2. Tuotekuvaus Näyttö Infrapuna- Sensori, Laserosoitin
testo 831 Käyttöohje FIN 2 1. Yleistä 1. Yleistä Lue käyttöohje huolellisesti läpi ennen laitteen käyttöönottoa. Säilytä käyttöohje myöhempää käyttöä varten. 2. Tuotekuvaus Näyttö Infrapuna- Sensori, Laserosoitin
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619
 KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
Mittausjärjestelmän kalibrointi ja mittausepävarmuus
 Mittausjärjestelmän kalibrointi ja mittausepävarmuus Kalibrointi kalibroinnin merkitys kansainvälinen ja kansallinen mittanormaalijärjestelmä kalibroinnin määritelmä mittausjärjestelmän kalibrointivaihtoehdot
Mittausjärjestelmän kalibrointi ja mittausepävarmuus Kalibrointi kalibroinnin merkitys kansainvälinen ja kansallinen mittanormaalijärjestelmä kalibroinnin määritelmä mittausjärjestelmän kalibrointivaihtoehdot
PERUSMITTAUKSIA. 1 Työn tavoitteet
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 PERUSMITTAUKSIA 1 Työn tavoitteet Tässä työssä määrität tutkittavaksesi annetun metallikappaleen tiheyden laskemalla sen suoraan
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 PERUSMITTAUKSIA 1 Työn tavoitteet Tässä työssä määrität tutkittavaksesi annetun metallikappaleen tiheyden laskemalla sen suoraan
Luento 6: 3-D koordinaatit
 Maa-57.300 Fotogrammetrian perusteet Luento-ohjelma 1 2 3 4 5 6 7 8 9 10 11 12 13 Luento 6: 3-D koordinaatit AIHEITA (Alkuperäinen luento: Henrik Haggrén, 16.2.2003, Päivityksiä: Katri Koistinen 5.2.2004
Maa-57.300 Fotogrammetrian perusteet Luento-ohjelma 1 2 3 4 5 6 7 8 9 10 11 12 13 Luento 6: 3-D koordinaatit AIHEITA (Alkuperäinen luento: Henrik Haggrén, 16.2.2003, Päivityksiä: Katri Koistinen 5.2.2004
 MAA4 Abittikokeen vastaukset ja perusteluja 1. Määritä kuvassa olevien suorien s ja t yhtälöt. Suoran s yhtälö on = ja suoran t yhtälö on = + 2. Onko väittämä oikein vai väärin? 2.1 Suorat =5 +2 ja =5
MAA4 Abittikokeen vastaukset ja perusteluja 1. Määritä kuvassa olevien suorien s ja t yhtälöt. Suoran s yhtälö on = ja suoran t yhtälö on = + 2. Onko väittämä oikein vai väärin? 2.1 Suorat =5 +2 ja =5
1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen
 TkT Harri Eskelinen 1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen 2. Standardiosien hyödyntäminen 3. Osien kokoonpanosuunnat ja järjestys 4.
TkT Harri Eskelinen 1. Kokoonpantavan laitteen, sen osakokoonpanojen ja niiden koneenosien toimintaperiaatteiden hyödyntäminen 2. Standardiosien hyödyntäminen 3. Osien kokoonpanosuunnat ja järjestys 4.
geodyna 6800 optima tasapainottamisen uusi standardi
 geodyna 6800 optima tasapainottamisen uusi standardi Täysautomaattinen tasapainotuskone 3 D-laserteknologialla Mikä on GEODYNA 6800 OPTIMA geodyna 6800 optima on täysautomaattinen pyörän tasapainotuskone
geodyna 6800 optima tasapainottamisen uusi standardi Täysautomaattinen tasapainotuskone 3 D-laserteknologialla Mikä on GEODYNA 6800 OPTIMA geodyna 6800 optima on täysautomaattinen pyörän tasapainotuskone
Todellinen 3D-ohjauksensuuntauslaite
 geoliner 680 ja geoliner 780 Huipputarkka Kaikki ajoneuvojen säätöarvot tulevat suoraan autovalmistajilta ja ovat tarkkoja ja luotettavia. Kehittynyt kamerajärjestelmä on erittäin tarkka ja takaa luotettavan
geoliner 680 ja geoliner 780 Huipputarkka Kaikki ajoneuvojen säätöarvot tulevat suoraan autovalmistajilta ja ovat tarkkoja ja luotettavia. Kehittynyt kamerajärjestelmä on erittäin tarkka ja takaa luotettavan
DistanceMaster 80 DE 04 GB 11 NL 18 DK 25 FR 32 ES 39 IT 46 PL 53 FI 60 PT 67 SE 74 NO TR RU UA CZ EE LV LT RO BG GR
 DistanceMaster 80 DE GB NL DK FR ES IT PL PT SE NO TR RU UA CZ EE LV LT RO BG GR 04 11 18 25 32 39 46 53 60 67 74 ! a h i b 2. 4. 6.! 60 Lue lisäohjeet. käyttöohje Noudata kokonaan. annettuja Lue ohjeita.
DistanceMaster 80 DE GB NL DK FR ES IT PL PT SE NO TR RU UA CZ EE LV LT RO BG GR 04 11 18 25 32 39 46 53 60 67 74 ! a h i b 2. 4. 6.! 60 Lue lisäohjeet. käyttöohje Noudata kokonaan. annettuja Lue ohjeita.
Nimi: Muiden ryhmäläisten nimet:
 Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
OHJE 2(5) 25.8.2015 Dnro LIVI/4495/05.00/2015 1 KITKAN MITTAAMISEN MENETELMÄ... 3
 OHJE 2(5) Sisällys 1 KITKAN MITTAAMISEN MENETELMÄ... 3 2 LAATUVAATIMUKSET KITKAMITTAREILLE... 3 2.1 Käyttöturvallisuus... 3 2.2 Kalibroitavuus... 3 2.3 Mittaustarkkuus... 4 2.3.1 Mittarien samankaltaisuuteen
OHJE 2(5) Sisällys 1 KITKAN MITTAAMISEN MENETELMÄ... 3 2 LAATUVAATIMUKSET KITKAMITTAREILLE... 3 2.1 Käyttöturvallisuus... 3 2.2 Kalibroitavuus... 3 2.3 Mittaustarkkuus... 4 2.3.1 Mittarien samankaltaisuuteen
t osatekijät vaikuttavat merkittävästi tuloksen epävarmuuteen Mittaustulosten ilmoittamiseen tulee kiinnittää kriittistä
 Mittausepävarmuuden määrittäminen 1 Mittausepävarmuus on testaustulokseen liittyvä arvio, joka ilmoittaa rajat, joiden välissä on todellinen arvo tietyllä todennäköisyydellä Kokonaisepävarmuusarvioinnissa
Mittausepävarmuuden määrittäminen 1 Mittausepävarmuus on testaustulokseen liittyvä arvio, joka ilmoittaa rajat, joiden välissä on todellinen arvo tietyllä todennäköisyydellä Kokonaisepävarmuusarvioinnissa
Kuva 2. Lankasahauksen periaate.
 Lankasahaus Tampereen teknillinen yliopisto Tuula Höök Lankasahaus perustuu samaan periaatteeseen kuin uppokipinätyöstökin. Kaikissa kipinätyöstömenetelmissä työstötapahtuman peruselementit ovat kipinätyöstöneste,
Lankasahaus Tampereen teknillinen yliopisto Tuula Höök Lankasahaus perustuu samaan periaatteeseen kuin uppokipinätyöstökin. Kaikissa kipinätyöstömenetelmissä työstötapahtuman peruselementit ovat kipinätyöstöneste,
Mittajärjestelmät ja mittasuositukset.
 Mittajärjestelmät ja mittasuositukset. Hannu Hirsi Johdanto: Mittajärjestelmien tarkoitus: Helpottaa eri toimijoiden järjestelmien ja osien yhteensovittamista : suunnittelua, valmistusta, asentamista,
Mittajärjestelmät ja mittasuositukset. Hannu Hirsi Johdanto: Mittajärjestelmien tarkoitus: Helpottaa eri toimijoiden järjestelmien ja osien yhteensovittamista : suunnittelua, valmistusta, asentamista,
Oikeanlaisten virtapihtien valinta Aloita vastaamalla seuraaviin kysymyksiin löytääksesi oikeantyyppiset virtapihdit haluamaasi käyttökohteeseen.
 Oikeanlaisten virtapihtien valinta Aloita vastaamalla seuraaviin kysymyksiin löytääksesi oikeantyyppiset virtapihdit haluamaasi käyttökohteeseen. 1. Tuletko mittaamaan AC tai DC -virtaa? (DC -pihdit luokitellaan
Oikeanlaisten virtapihtien valinta Aloita vastaamalla seuraaviin kysymyksiin löytääksesi oikeantyyppiset virtapihdit haluamaasi käyttökohteeseen. 1. Tuletko mittaamaan AC tai DC -virtaa? (DC -pihdit luokitellaan
Opetusmateriaali. Fermat'n periaatteen esittely
 Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Opetusmateriaali Fermat'n periaatteen esittely Hengenpelastajan tehtävässä kuvataan miten hengenpelastaja yrittää hakea nopeinta reittiä vedessä apua tarvitsevan ihmisen luo - olettaen, että hengenpelastaja
Matterport vai GeoSLAM? Juliane Jokinen ja Sakari Mäenpää
 Matterport vai GeoSLAM? Juliane Jokinen ja Sakari Mäenpää Esittely Tutkimusaineiston laatija DI Aino Keitaanniemi Aino Keitaanniemi työskentelee Aalto yliopiston Rakennetun ympäristön mittauksen ja mallinnuksen
Matterport vai GeoSLAM? Juliane Jokinen ja Sakari Mäenpää Esittely Tutkimusaineiston laatija DI Aino Keitaanniemi Aino Keitaanniemi työskentelee Aalto yliopiston Rakennetun ympäristön mittauksen ja mallinnuksen
33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ
 TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
Kone- ja rakentamistekniikan laboratoriotyöt KON-C3004. Koesuunnitelma: Paineen mittaus venymäliuskojen avulla. Ryhmä C
 Kone- ja rakentamistekniikan laboratoriotyöt KON-C3004 Koesuunnitelma: Paineen mittaus venymäliuskojen avulla Ryhmä C Aleksi Mäki 350637 Simo Simolin 354691 Mikko Puustinen 354442 1. Tutkimusongelma ja
Kone- ja rakentamistekniikan laboratoriotyöt KON-C3004 Koesuunnitelma: Paineen mittaus venymäliuskojen avulla Ryhmä C Aleksi Mäki 350637 Simo Simolin 354691 Mikko Puustinen 354442 1. Tutkimusongelma ja
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
EB-TUTKINTO 2008 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 5. kesäkuuta 2008 (aamupäivä) KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Europpa-koulun antama taulukkovihkonen Funktiolaskin,
Mittausten jäljitettävyysketju
 Mittausten jäljitettävyysketju FINAS-päivä 22.1.2013 Sari Saxholm, MIKES @mikes.fi p. 029 5054 432 Mittatekniikan keskus varmistaa kansainvälisesti hyväksytyt mittayksiköt ja pätevyyden arviointipalvelut
Mittausten jäljitettävyysketju FINAS-päivä 22.1.2013 Sari Saxholm, MIKES @mikes.fi p. 029 5054 432 Mittatekniikan keskus varmistaa kansainvälisesti hyväksytyt mittayksiköt ja pätevyyden arviointipalvelut
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
ZENITHTOO. Nopea, suuren volyymin CNC koordinaattimittauskone Suuren koon CNC mittauskoneet edullisesti
 ZENITHTOO Nopea, suuren volyymin CNC koordinaattimittauskone Suuren koon CNC mittauskoneet edullisesti Nopea, suuren volyymin CNC CMM Zenith too.. seuraavaa sukupolvea Aberlink on kehittänyt mittauskoneitaan
ZENITHTOO Nopea, suuren volyymin CNC koordinaattimittauskone Suuren koon CNC mittauskoneet edullisesti Nopea, suuren volyymin CNC CMM Zenith too.. seuraavaa sukupolvea Aberlink on kehittänyt mittauskoneitaan
www.bosch-professional.fi
 Laadun takeena Bosch! Maailman ensimmäinen lattiapintalaser UUTUUS! Lattiapintalaser GSL 2 Professional Lopultakin voidaan tarkistaa lattioiden, kuten tasoitettujen tai valettujen betonilattioiden, epätasaisuudet
Laadun takeena Bosch! Maailman ensimmäinen lattiapintalaser UUTUUS! Lattiapintalaser GSL 2 Professional Lopultakin voidaan tarkistaa lattioiden, kuten tasoitettujen tai valettujen betonilattioiden, epätasaisuudet
Kuva 104. Kehysten muotoilu. Kuva 105. Kehässä hiekkalistat
 10. Kaavauskehykset Raimo Keskinen, Pekka Niemi Tampereen ammattiopisto Kaavauskehysten päätehtävä on pitää sullottu muotti koossa. Muotin muodostaa useimmiten kaksi päällekkäin olevaa kehystä, joiden
10. Kaavauskehykset Raimo Keskinen, Pekka Niemi Tampereen ammattiopisto Kaavauskehysten päätehtävä on pitää sullottu muotti koossa. Muotin muodostaa useimmiten kaksi päällekkäin olevaa kehystä, joiden
Kombinatorinen optimointi
 Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
DIODIN OMINAISKÄYRÄ TRANSISTORIN OMINAISKÄYRÄSTÖ
 1 IOIN OMINAISKÄYRÄ JA TRANSISTORIN OMINAISKÄYRÄSTÖ MOTIVOINTI Työ opettaa mittaamaan erityyppisten diodien ominaiskäyrät käyttämällä oskilloskooppia XYpiirturina Työssä opetellaan mittaamaan transistorin
1 IOIN OMINAISKÄYRÄ JA TRANSISTORIN OMINAISKÄYRÄSTÖ MOTIVOINTI Työ opettaa mittaamaan erityyppisten diodien ominaiskäyrät käyttämällä oskilloskooppia XYpiirturina Työssä opetellaan mittaamaan transistorin
Laboratorioraportti 3
 KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
7. Resistanssi ja Ohmin laki
 Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Nimi: LK: SÄHKÖ-OPPI Tarmo Partanen Teoria (Muista hyödyntää sanastoa) 1. Millä nimellä kuvataan sähköisen komponentin (laitteen, johtimen) sähkön kulkua vastustavaa ominaisuutta? 2. Miten resistanssi
Kojemeteorologia. Sami Haapanala syksy 2013. Fysiikan laitos, Ilmakehätieteiden osasto
 Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Mittalaitteiden staattiset ominaisuudet Mittalaitteita kuvaavat tunnusluvut voidaan jakaa kahteen luokkaan Staattisiin
Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Mittalaitteiden staattiset ominaisuudet Mittalaitteita kuvaavat tunnusluvut voidaan jakaa kahteen luokkaan Staattisiin
1 Laske ympyrän kehän pituus, kun
 Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
RAKENNUSTEN TIIVIYSMITTAUS MITTALAITTEET
 Rakennusten tiiviysmittaus MITTALAITTTEET 1/6 RAKENNUSTEN TIIVIYSMITTAUS MITTALAITTEET Kuva 1. Retrotec tiiviysmittauslaitteisto. Kuva 2. Minneapolis tiiviysmittauslaitteisto. Kuva 3. Wöhler tiiviysmittauslaitteisto.
Rakennusten tiiviysmittaus MITTALAITTTEET 1/6 RAKENNUSTEN TIIVIYSMITTAUS MITTALAITTEET Kuva 1. Retrotec tiiviysmittauslaitteisto. Kuva 2. Minneapolis tiiviysmittauslaitteisto. Kuva 3. Wöhler tiiviysmittauslaitteisto.
Infrapunalämpömittari CIR350
 Infrapunalämpömittari CIR350 Käyttöopas (ver. 1.2) 5/23/2006 Johdanto Injektor solutionsin CIR350 infrapunalämpömittari tarjoaa sinulle laadukkaan laitteen huokeaan hintaan. Tämän laitteen etuja ovat Optiikka
Infrapunalämpömittari CIR350 Käyttöopas (ver. 1.2) 5/23/2006 Johdanto Injektor solutionsin CIR350 infrapunalämpömittari tarjoaa sinulle laadukkaan laitteen huokeaan hintaan. Tämän laitteen etuja ovat Optiikka
TUTKIMUSRAPORTTI Lintuvaara
 TUTKIMUSRAPORTTI Lintuvaara Helsingin seudun ympäristöpalvelut (HSY) Vesihuolto 16.12.2014 Jukka Sandelin HSY Raportti Opastinsilta 6 A, 00520 Helsinki 1. TAUSTAA Helsingin seudun ympäristöpalvelut / vesihuolto
TUTKIMUSRAPORTTI Lintuvaara Helsingin seudun ympäristöpalvelut (HSY) Vesihuolto 16.12.2014 Jukka Sandelin HSY Raportti Opastinsilta 6 A, 00520 Helsinki 1. TAUSTAA Helsingin seudun ympäristöpalvelut / vesihuolto
Digitaaliset paikoitusmittalaitteet
 Digitaaliset paikoitusmittalaitteet Magnescale Tel: +49 711 5858-777 E-Mail: smse-mp@eu.sony.com www.sonymanufacturing.com Luotettava mittausjärjestelmä korkeampi laatu ja parempi tuottavuus Sonyn magneettiset
Digitaaliset paikoitusmittalaitteet Magnescale Tel: +49 711 5858-777 E-Mail: smse-mp@eu.sony.com www.sonymanufacturing.com Luotettava mittausjärjestelmä korkeampi laatu ja parempi tuottavuus Sonyn magneettiset
Moderni muuntajaomaisuuden kunnonhallinta. Myyntipäällikkö Jouni Pyykkö, Infratek Finland Oy Tuotepäällikkö Juhani Lehto, Vaisala Oyj
 Moderni muuntajaomaisuuden kunnonhallinta Myyntipäällikkö Jouni Pyykkö, Infratek Finland Oy Tuotepäällikkö Juhani Lehto, Vaisala Oyj Kunnonhallinnan strategia Muuntajan kunnossapito ja kunnonhallinta tulee
Moderni muuntajaomaisuuden kunnonhallinta Myyntipäällikkö Jouni Pyykkö, Infratek Finland Oy Tuotepäällikkö Juhani Lehto, Vaisala Oyj Kunnonhallinnan strategia Muuntajan kunnossapito ja kunnonhallinta tulee
FlyMarker PRO merkintälaite. Mark like a Professional
 FlyMarker PRO merkintälaite Mark like a Professional Mark like a Professional FlyMarker PRO Mobile Kannettavan FlyMarker PRO merkintälaitteen avulla suurten, raskaiden ja vaikeasti liikuteltavien kappaleiden
FlyMarker PRO merkintälaite Mark like a Professional Mark like a Professional FlyMarker PRO Mobile Kannettavan FlyMarker PRO merkintälaitteen avulla suurten, raskaiden ja vaikeasti liikuteltavien kappaleiden
PANK PANK-4122 ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ 1. MENETELMÄN TARKOITUS
 PANK-4122 PANK PÄÄLLYSTEALAN NEUVOTTELUKUNTA ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ Hyväksytty: Korvaa menetelmän: 9.5.2008 26.10.1999 1. MENETELMÄN TARKOITUS 2. MENETELMÄN SOVELTAMISALUE
PANK-4122 PANK PÄÄLLYSTEALAN NEUVOTTELUKUNTA ASFALTTIPÄÄLLYSTEEN TYHJÄTILA, PÄÄLLYSTETUTKAMENETELMÄ Hyväksytty: Korvaa menetelmän: 9.5.2008 26.10.1999 1. MENETELMÄN TARKOITUS 2. MENETELMÄN SOVELTAMISALUE
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
Yhtälön oikealla puolella on säteen neliö, joten r. = 5 eli r = ± 5. Koska säde on positiivinen, niin r = 5.
 Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
Tekijä Pitkä matematiikka 5 7..017 31 Kirjoitetaan yhtälö keskipistemuotoon ( x x ) + ( y y ) = r. 0 0 a) ( x 4) + ( y 1) = 49 Yhtälön vasemmalta puolelta nähdään, että x 0 = 4 ja y 0 = 1, joten ympyrän
AXIOMTOO Evoluution kehitysaskel koordinaattimittauskoneissa Introducing the Axiom too range of manual and CNC CMM's
 AXIOMTOO Evoluution kehitysaskel koordinaattimittauskoneissa Introducing the Axiom too range of manual and CNC CMM's - Päivitettävyys koska tahansa manuaalikoneesta CNC-koneeksi - Käyttö tehtaan lattialla
AXIOMTOO Evoluution kehitysaskel koordinaattimittauskoneissa Introducing the Axiom too range of manual and CNC CMM's - Päivitettävyys koska tahansa manuaalikoneesta CNC-koneeksi - Käyttö tehtaan lattialla
Sustainable steel construction seminaari
 Sustainable steel construction seminaari 18.1.2017 Geometrian mittaaminen ja 3D skannaus Timo Kärppä 2017 2 SISÄLTÖ 1. Digitaalisuus mahdollistaa monia asioita 2. Mitä on 3D? 3. 3D skannaus, eri menetelmiä,
Sustainable steel construction seminaari 18.1.2017 Geometrian mittaaminen ja 3D skannaus Timo Kärppä 2017 2 SISÄLTÖ 1. Digitaalisuus mahdollistaa monia asioita 2. Mitä on 3D? 3. 3D skannaus, eri menetelmiä,
S-108-2110 OPTIIKKA 1/10 Laboratoriotyö: Polarisaatio POLARISAATIO. Laboratoriotyö
 S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
S-108-2110 OPTIIKKA 1/10 POLARISAATIO Laboratoriotyö S-108-2110 OPTIIKKA 2/10 SISÄLLYSLUETTELO 1 Polarisaatio...3 2 Työn suoritus...6 2.1 Työvälineet...6 2.2 Mittaukset...6 2.2.1 Malus:in laki...6 2.2.2
15. Sulan metallin lämpötilan mittaus
 15. Sulan metallin lämpötilan mittaus Raimo Keskinen Peka Niemi - Tampereen ammattiopisto Sulan lämpötila joudutan mittaamaan usean otteeseen valmistusprosessin aikana. Sula mitataan uunissa, sekä mm.
15. Sulan metallin lämpötilan mittaus Raimo Keskinen Peka Niemi - Tampereen ammattiopisto Sulan lämpötila joudutan mittaamaan usean otteeseen valmistusprosessin aikana. Sula mitataan uunissa, sekä mm.
TTY Mittausten koekenttä. Käyttö. Sijainti
 TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
TTY Mittausten koekenttä Käyttö Tampereen teknillisen yliopiston mittausten koekenttä sijaitsee Tampereen teknillisen yliopiston välittömässä läheisyydessä. Koekenttä koostuu kuudesta pilaripisteestä (
-Motorracing Electronics. MAP KÄYTTÖOHJE Tuotenumero 1004, 1005 ja MAP Käyttöohje v1.0 11/2011 1/7
 MAP KÄYTTÖOHJE Tuotenumero 1004, 1005 ja 1006 1/7 SISÄLLYSLUETTELO 1. YLEISTÄ... 3 1.1. SPESIFIKAATIO...3 2. ASENNUS... 4 2.1. MEKAANINEN ASENNUS...4 2.2. SÄHKÖINEN ASENNUS...5 3. KÄYTTÖOHJE... 6 3.1.
MAP KÄYTTÖOHJE Tuotenumero 1004, 1005 ja 1006 1/7 SISÄLLYSLUETTELO 1. YLEISTÄ... 3 1.1. SPESIFIKAATIO...3 2. ASENNUS... 4 2.1. MEKAANINEN ASENNUS...4 2.2. SÄHKÖINEN ASENNUS...5 3. KÄYTTÖOHJE... 6 3.1.
Vanhankaupunginkosken ultraäänikuvaukset Simsonar Oy Pertti Paakkolanvaara
 Vanhankaupunginkosken ultraäänikuvaukset 15.7. 14.11.2014 Simsonar Oy Pertti Paakkolanvaara Avaintulokset 2500 2000 Ylös vaellus pituusluokittain: 1500 1000 500 0 35-45 cm 45-60 cm 60-70 cm >70 cm 120
Vanhankaupunginkosken ultraäänikuvaukset 15.7. 14.11.2014 Simsonar Oy Pertti Paakkolanvaara Avaintulokset 2500 2000 Ylös vaellus pituusluokittain: 1500 1000 500 0 35-45 cm 45-60 cm 60-70 cm >70 cm 120
80 AS vesivaakasarja: Mittaustarkkuutta, johon voit luottaa Laadukasta, Saksalaista tekoa
 VUODEN TAKUU* *Lakisääteisten oikeuksien lisäksi, katso yksityiskohdat esitteen takasivulta 80 AS vesivaakasarja: Mittaustarkkuutta, johon voit luottaa Laadukasta, Saksalaista tekoa STABILA 80 AS -sarja:
VUODEN TAKUU* *Lakisääteisten oikeuksien lisäksi, katso yksityiskohdat esitteen takasivulta 80 AS vesivaakasarja: Mittaustarkkuutta, johon voit luottaa Laadukasta, Saksalaista tekoa STABILA 80 AS -sarja:
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
Sääasema Probyte JUNIOR
 Sääasema Probyte JUNIOR JUNIOR sääanturi COM1 12VDC RS-232 signaali PC W9x Excel-tiedosto PROBYTE JUNIOR sääanturin toimintaperiaate Yleistä Probyte SÄÄASEMA JUNIOR1 on sään mittaukseen tarkoitettu ulkoanturi,
Sääasema Probyte JUNIOR JUNIOR sääanturi COM1 12VDC RS-232 signaali PC W9x Excel-tiedosto PROBYTE JUNIOR sääanturin toimintaperiaate Yleistä Probyte SÄÄASEMA JUNIOR1 on sään mittaukseen tarkoitettu ulkoanturi,
dametric AGS-anturi HUOLTOKÄSIKIRJA AGS-XXX Service Manual FI.docx Lokakuu 12, 2010 / BL Sivu 1 (8)
 dametric AGS-anturi AGS-XXX Service Manual FI.docx Lokakuu 12, 2010 / BL Sivu 1 (8) Sisältö 1 Yleistä... 2 2 Anturin asennus ja poisto... 3 3 Kotelon ja putken välinen liitos... 4 4 Kärjen ja kotelon välinen
dametric AGS-anturi AGS-XXX Service Manual FI.docx Lokakuu 12, 2010 / BL Sivu 1 (8) Sisältö 1 Yleistä... 2 2 Anturin asennus ja poisto... 3 3 Kotelon ja putken välinen liitos... 4 4 Kärjen ja kotelon välinen
Yrityksen mittauskyvyn varmistaminen. Heikki Savia Tampereen ammattikorkeakoulu 1
 Yrityksen mittauskyvyn varmistaminen 1 Mittauskyvyn peruselementit Toiminnan rahoitus Oikea mittayksikkö Kunnossa olevat mittavälineet Kelvollinen mittauspaikka Pätevät mittaajat 2 Johdon vastuu Lopulta
Yrityksen mittauskyvyn varmistaminen 1 Mittauskyvyn peruselementit Toiminnan rahoitus Oikea mittayksikkö Kunnossa olevat mittavälineet Kelvollinen mittauspaikka Pätevät mittaajat 2 Johdon vastuu Lopulta
PYP I / TEEMA 4 MITTAUKSET JA MITATTAVUUS
 1 PYP I / TEEMA 4 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen osat Lämpötilan
1 PYP I / TEEMA 4 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen osat Lämpötilan
testo 460 Käyttöohje
 testo 460 Käyttöohje FIN 2 Pikaohje testo 460 Pikaohje testo 460 1 Suojakansi: käyttöasento 2 Sensori 3 Näyttö 4 Toimintonäppäimet 5 Paristokotelo (laitteen takana) Perusasetukset Laite sammutettuna >
testo 460 Käyttöohje FIN 2 Pikaohje testo 460 Pikaohje testo 460 1 Suojakansi: käyttöasento 2 Sensori 3 Näyttö 4 Toimintonäppäimet 5 Paristokotelo (laitteen takana) Perusasetukset Laite sammutettuna >
