Evoluutiopuu. Aluksi. Avainsanat: biomatematiikka, päättely, kombinatoriikka, verkot. Luokkataso: luokka, lukio
|
|
|
- Simo Hänninen
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Evoluutiopuu Avainsanat: biomatematiikka, päättely, kombinatoriikka, verkot Luokkataso: luokka, lukio Välineet: loogiset palat, paperia, kyniä Kuvaus: Tehtävässä tutkitaan bakteerien evoluutiota. Miltä mahtaisi näyttää jonkin bakteerijoukon evoluutiopuu? Entä millainen niiden kantaisä voisi olla? Aluksi Evoluutiopuu (tai fylogeneettinen puu) on jonkin biologisen lajin tai kokonaisuuden syntymistä ja polveutumista kuvaava puumainen kaavio. Tutkijat yrittävät päätellä tutkittavana olevan biologisen kokonaisuuden evoluutiopuun vertailemalla eliöryhmän edustajien muodon ja rakenteen ja/tai perimän eroja ja yhtäläisyyksiä. Ajatellaan esimerkiksi gorillaa, simpanssia ja ihmistä, jotka kaikki kuuluvat isojen ihmisapinoiden heimoon tiettyjen ominaisuuksiensa perusteella. Evoluutiopuun avulla voidaan esittää näiden kolmen lajin keskinäinen lajiutumisjärjestys eli se, onko esimerkiksi näillä lajeilla yksi yhteinen esi-isä, josta lajit ovat polveutuneet likimain yhtä kauan sitten (kuva alla vasemmalla). Evoluutiopuu on aina tutkijoiden valistunut arvaus lajiutumisjärjestyksestä eikä varmaa totuutta asiasta tiedetä. Tästä syystä evoluutiopuuksi on usein monia erilaisia vaihtoehtoja. Kuvissa näkyy kaksi mahdollista evoluutiopuuta. Tutkijat ovat havainneet, että simpanssin ja ihmisen perimä on huomattavan samankaltainen, ja toisaalta erilainen kuin gorillan. Tämä viittaa oikeanpuoleiseen evoluutiopuuhun, eli ihmisellä ja simpanssilla on yhteinen esi-isä, josta lajit ovat polveutuneet ei niin kauan aikaa sitten ja tämä esi-isä on polveutunut samasta esi-isästä kuin gorilla. Sivu 1 / 6
2 Biomatemaatikot tutkivat mm. bakteerien ja virusten evoluutiota ja saavat sitä kautta tärkeää tietoa epidemioiden leviämisestä ja ehkäisemisestä. Viime aikoina uraauurtavaa tutkimusta on tehty mm. sairaalabakteerien tutkimuksen saralla. Tässä tehtävässä tutkitaan bakteerien evoluutiota. Tehtävässä oletetaan, että bakteeri, jota mallintaa looginen pala, leviää ihmisestä toiseen jakautumalla. Jokaisessa jakautumisessa bakteerin perimä muuttuu hieman. Tehtävässä taudinaiheuttajan perimää edustavat loogisten palojen ominaisuudet: 1. muoto 2. koko 3. väri 4. reiällisyys Jokaisessa jakautumisessa täsmälleen yksi näistä ominaisuuksista muuttuu. Esimerkki Kuvassa huipulla oleva ympyrä on alkuperäinen bakteeri, joka alkaa jakautua. Jakautumisessa bakteerin yksi ominaisuus muuttuu: kuvan esittämässä jakautumisessa on muuttunut bakteerin muoto (vasen oksa) ja koko (oikea oksa). Sivu 2 / 6
3 Toteutusehdotus Tehtävä 1 Korvatulehdusbakteereita Kuvassa näet erään tavallisen korvatulehdusta aiheuttavan bakteerin kuvitteellisen evoluutiopuun. Päättele, minkälaisia esi-isiä kuvan bakteereilla saattaa olla! Muista, että jokaisessa bakteerin jakautumisessa täsmälleen yksi seuraavista muuttuu: 1) koko 2) väri 3) muoto tai 4) reiällisyys. kelt. kelt. kelt. kelt. pun. sin. vihr. kelt. Flunssaviruksen evoluutiopuu. Kuinka monta erilaista puuta keksit? Pystytkö päättelemään bakteerien todennäköisimmän kantaisän? Piirrä todennäköisimmät kantaisät alla olevaan laatikkoon. Sivu 3 / 6
4 Tehtävä 2 Pöpöjä päiväkodissa Satu sairastui Streptokokki A:n aiheuttamaan nielutulehdukseen. Vaikka hän ei mennyt enää oireiden ilmaannuttua päiväkotiin, vahinko oli jo tapahtunut, ja pian kaikilla Sadun ryhmän lapsilla oli Streptokokki-tartunta. Kuudelta lapselta otetuista näytteistä löytyivät kuvan bakteerit, jotka kaikki esittävät Streptokokki A:n eri muotoja. Oletetaan, että Satu on alkuperäinen tartunnanlähde, jonka bakteerista kuvan bakteerit ovat muodostuneet jakautumisten kautta. Tilannetta kuvaa oheinen evoluutiopuu. Streptokokki A:n eri muodot. Streptokokki A:n evoluutiopuu. Lisäksi tiedetään, että jos bakteerit ovat hyvin samankaltaisia, eli eroavat vain yhden tai kahden ominaisuuden osalta, niillä on varmasti yhteinen esi-isä joko edellisessä tai sitä edellisessä sukupolvessa. Pystytkö päättelemään, minkälainen Sadun Streptokokki-bakteeri oli? Sivu 4 / 6
5 Vinkkejä ja vastauksia Tehtävä 1 Voidaan aloittaa rakentamalla mikä tahansa ehdot toteuttava puu. Melko pian havaitaan, että puun jokaiseen solmukohtaan, lukuun ottamatta puun latvaa, voidaan sijoittaa muutamia erilaisia paloja (itse asiassa täsmälleen kaksi erilaista). Esimerkiksi puun vasempaan haaraan, toisen jakautumisen kohdalle voi sijoittaa ison keltaisen reiällisen ympyrän tai pienen keltaisen reiällisen neliön. Puun vasen oksa voidaan muodostaa kahdeksalla eri tavalla. Myös puun oikea oksa voidaan muodostaa niin ikään kahdeksalla eri tavalla. Nyt jokainen vasen oksa voidaan yhdistää minkä tahansa oikean oksan kanssa, joten erilaisia puita muodostuu yhteensä 64 kappaletta. Osa puista on kuitenkin mahdottomia sellaiset yhdistelmät eivät ole mahdollisia, joissa vasemman ja oikean oksan ylimmät palat eroavat kolmen tai neljän ominaisuuden osalta. Samoin jos ylimmät palat eroavat vain koon tai vain reiällisyyden osalta, niillä ei voi olla yhteistä esi-isää. Lopulta mahdollisia puita on 20 erilaista. Niistä kuudessa ylimpänä on iso keltainen reiällinen neliö ja kuudessa iso punainen reiätön neliö. Muita paloja esiintyy vähemmän. Bakteerien todennäköisimmät esi-isät ovat siis iso keltainen reiällinen neliö ja kuudessa iso punainen reiätön neliö. Sivu 5 / 6
6 Tehtävä 2 Vasemmalla on kuvattu kaikki mahdolliset puun vasemmat haarat ja oikealla kaikki mahdolliset oikeat haarat. Edellä on kuvattu kaikki mahdolliset puun vasemmat ja oikeat haarat. Nyt haarat täytyy yhdistää! Jokainen mahdollinen vasen haara (11 kpl) on kokeiltava jokaisen mahdollisen oikean haaran kanssa (11 kpl). Vaihtoehtoja on siis 121 kappaletta! Työtä kuitenkin helpottaa havainto, että kaikki yhdistelmät eivät ole mahdollisia. Jotta yhdistelmä on mahdollinen eli on mahdollista, että bakteereilla on yhteinen esi-isä eivät palat saa erota kuin kahden ominaisuuden osalta, tai yhden, jos ominaisuus on väri tai muoto. Koska kaikki vasemman puolen palat ovat pieniä ja reiällisiä ja oikein puolen palat isoja ja reiättömiä, yhteinen esi-isä on mahdollinen ainoastaan, jos jälkeläiset ovat samanvärisiä ja yhdenmuotoisia. Aloitetaan siis karsimalla kaikki mahdottomat tapaukset! Sivu 6 / 6
4. Oheisessa 4x4 ruudukossa jokainen merkki tarkoittaa jotakin lukua. Mikä lukua salmiakki vastaa?
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 30.1.2015 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 30.1.2015 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Kenguru 2019 Ecolier Ratkaisut
 Sivu 0 / 15 3 pistettä TEHTÄVÄ 1 2 3 4 5 6 7 VASTAUS E C A D A A D 4 pistettä TEHTÄVÄ 8 9 10 11 12 13 14 VASTAUS B B C E B A D 5 pistettä TEHTÄVÄ 15 16 17 18 19 20 21 VASTAUS D E B E B E B Kilpailu pidetään
Sivu 0 / 15 3 pistettä TEHTÄVÄ 1 2 3 4 5 6 7 VASTAUS E C A D A A D 4 pistettä TEHTÄVÄ 8 9 10 11 12 13 14 VASTAUS B B C E B A D 5 pistettä TEHTÄVÄ 15 16 17 18 19 20 21 VASTAUS D E B E B E B Kilpailu pidetään
 päättely jatkuva sarja. Päättele miten sarja jatkuu. Jatka sarjaa ainakin kahdella luvulla tai kuviolla. A. 7 8 9 0 0-00 99 98 97 - - - 0 B. 8 0 0 0 9 0 8 00 80 0 0 C. PÄÄT TELY 9 jatkuva sarja. Päättele
päättely jatkuva sarja. Päättele miten sarja jatkuu. Jatka sarjaa ainakin kahdella luvulla tai kuviolla. A. 7 8 9 0 0-00 99 98 97 - - - 0 B. 8 0 0 0 9 0 8 00 80 0 0 C. PÄÄT TELY 9 jatkuva sarja. Päättele
Yhtälönratkaisu oppilaan materiaali
 Yhtälönratkaisu oppilaan materiaali Nimi: Luokka: 1 1. Tosia ja epätosia väitteitä Alkupalat Kirjoita taulukkoon T, jos väite on tosi ja E, jos väite on epätosi. Väite 5 > 3 16 < 8 19 = 26 9 < 28 64 =
Yhtälönratkaisu oppilaan materiaali Nimi: Luokka: 1 1. Tosia ja epätosia väitteitä Alkupalat Kirjoita taulukkoon T, jos väite on tosi ja E, jos väite on epätosi. Väite 5 > 3 16 < 8 19 = 26 9 < 28 64 =
Kenguru 2019 Ecolier 4. ja 5. luokka
 sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
perustelu Noudatetaan sääntöjä. Opetuskortit (tehtävät 16 28), palikoita, supermarketin pohjapiirustus, nuppineuloja, tangram-palat
 Harjoitus 12: INDUKTIIVISEN PÄÄTTELYN KERTAUS Tavoiteltava toiminta: Kognitiivinen taso: Ominaisuuksien ja suhteiden kertaus Toiminnan tavoite ja kuvaus: Oppilaat ratkaisevat paperi- ja palikkatehtäviä
Harjoitus 12: INDUKTIIVISEN PÄÄTTELYN KERTAUS Tavoiteltava toiminta: Kognitiivinen taso: Ominaisuuksien ja suhteiden kertaus Toiminnan tavoite ja kuvaus: Oppilaat ratkaisevat paperi- ja palikkatehtäviä
TEHTÄVÄVINKKEJÄ MATEMATIKKAAN
 Viinikankatu 49a, 33800 TAMPERE Puh (03) 380 5300, Fax (03) 380 5353 E-mail: myynti@tevella.fi, www.tevella.fi TEHTÄVÄVINKKEJÄ MATEMATIKKAAN I LOOGISET PALAT 1) Laita kaikki LOOGISET PALAT eteesi työpöydälle.
Viinikankatu 49a, 33800 TAMPERE Puh (03) 380 5300, Fax (03) 380 5353 E-mail: myynti@tevella.fi, www.tevella.fi TEHTÄVÄVINKKEJÄ MATEMATIKKAAN I LOOGISET PALAT 1) Laita kaikki LOOGISET PALAT eteesi työpöydälle.
INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI TOISELLE LUOKALLE
 INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI TOISELLE LUOKALLE Induktiivisen päättelyn tehtävät Tehtävät 1 5 Suhteet: Vastaavuus eli analogia Mikä kuvio sopii tyhjään ruutuun? 1. VASTAAVUUSTAULUKKO? 2. VASTAAVUUSTAULUKKO?
INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI TOISELLE LUOKALLE Induktiivisen päättelyn tehtävät Tehtävät 1 5 Suhteet: Vastaavuus eli analogia Mikä kuvio sopii tyhjään ruutuun? 1. VASTAAVUUSTAULUKKO? 2. VASTAAVUUSTAULUKKO?
Tehtävä 1 2 3 4 5 6 7 Vastaus
 Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI ESIOPETUKSEEN
 INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI ESIOPETUKSEEN Induktiivisen päättelyn opetuskuvat Tehtävät 1 ja 2 Ryhmän muodostaminen ja ryhmän laajentaminen 1. Jaa palikat kahteen ryhmään. Ryhmän muodostaminen
INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI ESIOPETUKSEEN Induktiivisen päättelyn opetuskuvat Tehtävät 1 ja 2 Ryhmän muodostaminen ja ryhmän laajentaminen 1. Jaa palikat kahteen ryhmään. Ryhmän muodostaminen
Essity Engagement Survey 2018
 Essity Engagement Survey 2018 Tiimiraportin luomisohje EUCUSA Consulting GmbH Mariahilfer Straße 187/39 A-1150 Wien Tel: +43-1-817 40 20-0 Fax: DW 20 FN 174750 k Handelsgericht Wien www.eucusa.com e-mail:
Essity Engagement Survey 2018 Tiimiraportin luomisohje EUCUSA Consulting GmbH Mariahilfer Straße 187/39 A-1150 Wien Tel: +43-1-817 40 20-0 Fax: DW 20 FN 174750 k Handelsgericht Wien www.eucusa.com e-mail:
2.3 Juurien laatu. Juurien ja kertoimien väliset yhtälöt. Jako tekijöihin. b b 4ac = 2
 .3 Juurien laatu. Juurien ja kertoimien väliset yhtälöt. Jako tekijöihin. Toisen asteen yhtälön a + b + c 0 ratkaisukaavassa neliöjuuren alla olevaa lauseketta b b 4ac + a b b 4ac a D b 4 ac sanotaan yhtälön
.3 Juurien laatu. Juurien ja kertoimien väliset yhtälöt. Jako tekijöihin. Toisen asteen yhtälön a + b + c 0 ratkaisukaavassa neliöjuuren alla olevaa lauseketta b b 4ac + a b b 4ac a D b 4 ac sanotaan yhtälön
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, sekä voi olla apua.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
Fibonaccin luvut ja kultainen leikkaus
 Fibonaccin luvut ja kultainen leikkaus Avainsanat: Fibonacci, lukujono, kultainen leikkaus, suhde, yhtälö Luokkataso: 6.-9.-luokka, lukio, yliopisto Välineet: Kynä, paperi (kulmaviivain, sakset) Kuvaus:
Fibonaccin luvut ja kultainen leikkaus Avainsanat: Fibonacci, lukujono, kultainen leikkaus, suhde, yhtälö Luokkataso: 6.-9.-luokka, lukio, yliopisto Välineet: Kynä, paperi (kulmaviivain, sakset) Kuvaus:
Toiminnallinen taso: Luodaan sääntöjä ominaisuuksien perusteella
 Harjoite 10: LUOKITELLAAN KUVIOITA Tavoiteltava toiminta: Materiaalit: Eteneminen: Kognitiivinen taso: P: Aikajärjestys, IR: Suhteet, sarjan järjestäminen Toiminnallinen taso: Luodaan sääntöjä ominaisuuksien
Harjoite 10: LUOKITELLAAN KUVIOITA Tavoiteltava toiminta: Materiaalit: Eteneminen: Kognitiivinen taso: P: Aikajärjestys, IR: Suhteet, sarjan järjestäminen Toiminnallinen taso: Luodaan sääntöjä ominaisuuksien
OMINAISUUS- JA SUHDETEHTÄVIEN KERTAUS. Tavoiteltava toiminta: Kognitiivinen taso: Ominaisuudet ja suhteet -kertaus
 Harjoite 12: Tavoiteltava toiminta: Materiaalit: OMINAISUUS- JA SUHDETEHTÄVIEN KERTAUS Kognitiivinen taso: Ominaisuudet ja suhteet -kertaus Toiminnan tavoite ja kuvaus: Oppilaat ratkaisevat paperi- ja
Harjoite 12: Tavoiteltava toiminta: Materiaalit: OMINAISUUS- JA SUHDETEHTÄVIEN KERTAUS Kognitiivinen taso: Ominaisuudet ja suhteet -kertaus Toiminnan tavoite ja kuvaus: Oppilaat ratkaisevat paperi- ja
INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI ENSIMMÄISELLE LUOKALLE
 INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI ENSIMMÄISELLE LUOKALLE Induktiivisen päättelyn opetuskuvakortit Tehtävät 1 ja 2 Ryhmän muodostaminen ja ryhmän laajentaminen 1. Jaa palikat kahteen ryhmään. Ryhmän
INDUKTIIVISEN PÄÄTTELYN HARJOITUSPAKETTI ENSIMMÄISELLE LUOKALLE Induktiivisen päättelyn opetuskuvakortit Tehtävät 1 ja 2 Ryhmän muodostaminen ja ryhmän laajentaminen 1. Jaa palikat kahteen ryhmään. Ryhmän
4 Matemaattinen induktio
 4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
4 Matemaattinen induktio Joidenkin väitteiden todistamiseksi pitää näyttää, että kaikilla luonnollisilla luvuilla on jokin ominaisuus P. Esimerkkejä tällaisista väitteistä ovat vaikkapa seuraavat: kaikilla
Tekijäryhmiä varten määritellään aluksi sivuluokat ja normaalit aliryhmät.
 3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
Tekijäryhmän määrittelemistä varten määritellään aluksi sivuluokat ja normaalit aliryhmät. gh = {gh h H}.
 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
Mobiilit luontorastit
 Mobiilit luontorastit Kesto: Riippuu reitin pituudesta Kenelle: lukio Missä: ulkona Milloin: kevät ja syksy Tarvikkeet: älypuhelin / tablet -tietokone (muistiinpanovälineet) Eräpassin osio: Luonnossa liikkuminen
Mobiilit luontorastit Kesto: Riippuu reitin pituudesta Kenelle: lukio Missä: ulkona Milloin: kevät ja syksy Tarvikkeet: älypuhelin / tablet -tietokone (muistiinpanovälineet) Eräpassin osio: Luonnossa liikkuminen
Ratkaisu. Tulkitaan de Bruijnin jonon etsimiseksi aakkostossa S := {0, 1} sanapituudelle n = 4. Neljän pituisia sanoja on N = 2 n = 16 kpl.
 iskreetti matematiikka, syksy 00 arjoitus, ratkaisuista. seta 8 nollaa ja 8 ykköstä renkaaksi niin, että jokainen yhdistelmä 0000, 000,..., esiintyy täsmälleen kerran. Vihje: Tulkitse de ruijnin jonon
iskreetti matematiikka, syksy 00 arjoitus, ratkaisuista. seta 8 nollaa ja 8 ykköstä renkaaksi niin, että jokainen yhdistelmä 0000, 000,..., esiintyy täsmälleen kerran. Vihje: Tulkitse de ruijnin jonon
Luonnollisen päättelyn luotettavuus
 Luonnollisen päättelyn luotettavuus Luotettavuuden todistamiseksi määrittelemme täsmällisesti, milloin merkkijono on deduktio. Tässä ei ole sisällytetty päättelysääntöihin iteraatiosääntöä, koska sitä
Luonnollisen päättelyn luotettavuus Luotettavuuden todistamiseksi määrittelemme täsmällisesti, milloin merkkijono on deduktio. Tässä ei ole sisällytetty päättelysääntöihin iteraatiosääntöä, koska sitä
+LISÄTEHTÄVIÄ päättely
 +LISÄTEHTÄVIÄ päättely Ahaa! Aivotreeniä yhdessä on rekisteröity tavaramerkki. Ahaa-materiaalin kopiointi- ja käyttöoikeus vain koulutetuilla ohjaajilla koulutuksenmukaiseen käyttötarkoitukseen. Ahaa!
+LISÄTEHTÄVIÄ päättely Ahaa! Aivotreeniä yhdessä on rekisteröity tavaramerkki. Ahaa-materiaalin kopiointi- ja käyttöoikeus vain koulutetuilla ohjaajilla koulutuksenmukaiseen käyttötarkoitukseen. Ahaa!
MATEMATIIKKA 5 VIIKKOTUNTIA. PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009
 EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
Kenguru 2015 Mini-Ecolier (2. ja 3. luokka) RATKAISUT
 sivu 1 / 10 3 pistettä 1. Kuinka monta pilkkua kuvan leppäkertuilla on yhteensä? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21 Ratkaisu: Pilkkuja on 1 + 1 + 1 + 2 + 2 + 1 + 3 + 2 + 3 + 3 = 19. 2. Miltä kuvan pyöreä
sivu 1 / 10 3 pistettä 1. Kuinka monta pilkkua kuvan leppäkertuilla on yhteensä? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21 Ratkaisu: Pilkkuja on 1 + 1 + 1 + 2 + 2 + 1 + 3 + 2 + 3 + 3 = 19. 2. Miltä kuvan pyöreä
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
 Sivu 0 / 9 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai 5 pistettä.
Sivu 0 / 9 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai 5 pistettä.
Valokuvien matematiikkaa
 Valokuvien matematiikkaa Avainsanat: valokuva, pikseli, päättely Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: Kynä, tehtävämonisteet (liitteenä), mahdollisiin jatkotutkimuksiin tietokone
Valokuvien matematiikkaa Avainsanat: valokuva, pikseli, päättely Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: Kynä, tehtävämonisteet (liitteenä), mahdollisiin jatkotutkimuksiin tietokone
Impedanssitomografia-peli
 Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
Oppitunti 6 - Kynät ja kumit - Osa 1. kynä Tämä on kynä. Kynä on keltainen. pyyhekumi = kumi Tämä on pyyhekumi. Kumi on punainen.
 Oppitunti 6 - Kynät ja kumit - Osa 1 kynä Tämä on kynä. Kynä on keltainen. 1 pyyhekumi = kumi Tämä on pyyhekumi. Kumi on punainen. Kynän päässä on kumi. Kynän päässä on punainen pyyhekumi. Tämän kynän
Oppitunti 6 - Kynät ja kumit - Osa 1 kynä Tämä on kynä. Kynä on keltainen. 1 pyyhekumi = kumi Tämä on pyyhekumi. Kumi on punainen. Kynän päässä on kumi. Kynän päässä on punainen pyyhekumi. Tämän kynän
Avaruuden muoto. Kuvaus: Tehtävässä pohditaan avaruuden muotoa ja pelataan ristinollaa erilaisilla pinnoilla.
 Avaruuden muoto Avainsanat: torus, Kleinin pullo, topologia Luokkataso: 6.-9. luokka, lukio Välineet: kyniä, pelilaudat (liitteenä) Kuvaus: Tehtävässä pohditaan avaruuden muotoa ja pelataan ristinollaa
Avaruuden muoto Avainsanat: torus, Kleinin pullo, topologia Luokkataso: 6.-9. luokka, lukio Välineet: kyniä, pelilaudat (liitteenä) Kuvaus: Tehtävässä pohditaan avaruuden muotoa ja pelataan ristinollaa
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Lineaarinen rakennearvostelu ja rakenneindeksit. Jukka Pösö Faba Jalostus
 Lineaarinen rakennearvostelu ja rakenneindeksit Jukka Pösö Faba Jalostus Lineaarinen rakennearvostelu arvostellaan rakennetta/liikkumista yksityiskohtaisesti esimerkkejä: korkeus jalka-asennot: vuohinen
Lineaarinen rakennearvostelu ja rakenneindeksit Jukka Pösö Faba Jalostus Lineaarinen rakennearvostelu arvostellaan rakennetta/liikkumista yksityiskohtaisesti esimerkkejä: korkeus jalka-asennot: vuohinen
Tasapainotehta via vaakamallin avulla
 Tasapainotehta via vaakamallin avulla Aihepiiri Luokka-aste Kesto Tarvittavat materiaalit / välineet Asiasanat Lausekkeet ja yhtälöt 7.-8. luokka 20 30 minuuttia Piirtoheitin, 2 kalvoa, erimuotoisia paloja
Tasapainotehta via vaakamallin avulla Aihepiiri Luokka-aste Kesto Tarvittavat materiaalit / välineet Asiasanat Lausekkeet ja yhtälöt 7.-8. luokka 20 30 minuuttia Piirtoheitin, 2 kalvoa, erimuotoisia paloja
Toiminnan tavoite ja kuvaus: Oppilaat arvioivat mitä kukin näkee eri tilanteessa. Käytännön toiminnassa: rohkaise jokaista kertomaan tarinaansa
 Harjoite 9: TÄHYSTÄJÄ Tavoiteltava toiminta: Materiaalit: Eteneminen: Kognitiivinen taso: P (spatiaalinen hahmottaminen): IR: suhteet Toiminnan tavoite ja kuvaus: Oppilaat arvioivat mitä kukin näkee eri
Harjoite 9: TÄHYSTÄJÄ Tavoiteltava toiminta: Materiaalit: Eteneminen: Kognitiivinen taso: P (spatiaalinen hahmottaminen): IR: suhteet Toiminnan tavoite ja kuvaus: Oppilaat arvioivat mitä kukin näkee eri
Mobiilit luontorastit
 Mobiilit luontorastit Kesto: Riippuu reitin pituudesta Kenelle: yläkoulu Missä: ulkona Milloin: kevät ja syksy Tarvikkeet: älypuhelin / tablettitietokone (muistiinpanovälineet) Eräpassin osio: Luonnossa
Mobiilit luontorastit Kesto: Riippuu reitin pituudesta Kenelle: yläkoulu Missä: ulkona Milloin: kevät ja syksy Tarvikkeet: älypuhelin / tablettitietokone (muistiinpanovälineet) Eräpassin osio: Luonnossa
5.1 Semanttisten puiden muodostaminen
 Luku 5 SEMNTTISET PUUT 51 Semanttisten puiden muodostaminen Esimerkki 80 Tarkastellaan kysymystä, onko kaava = (( p 0 p 1 ) (p 1 p 2 )) toteutuva Tätä voidaan tutkia päättelemällä semanttisesti seuraavaan
Luku 5 SEMNTTISET PUUT 51 Semanttisten puiden muodostaminen Esimerkki 80 Tarkastellaan kysymystä, onko kaava = (( p 0 p 1 ) (p 1 p 2 )) toteutuva Tätä voidaan tutkia päättelemällä semanttisesti seuraavaan
keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 1 b 3 a 5
 Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
a) Mitkä reaaliluvut x toteuttavat yhtälön x 2 = 7? (1 p.) b) Mitkä reaaliluvut x toteuttavat yhtälön 5 4 x
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 01 Arkkitehtimatematiikan koe, 1..01, Ratkaisut (Sarja A) 1. Anna kohdissa a), b) ja c) vastaukset tarkkoina arvoina. a) Mitkä reaaliluvut x toteuttavat
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 01 Arkkitehtimatematiikan koe, 1..01, Ratkaisut (Sarja A) 1. Anna kohdissa a), b) ja c) vastaukset tarkkoina arvoina. a) Mitkä reaaliluvut x toteuttavat
{ 2v + 2h + m = 8 v + 3h + m = 7,5 2v + 3m = 7, mistä laskemmalla yhtälöt puolittain yhteen saadaan 5v + 5h + 5m = 22,5 v +
 9. 0. ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ö Ø ÙØ 009 È ÖÙ Ö P. Olkoon vadelmien hinta v e, herukoiden h e ja mustikoiden m e rasialta. Oletukset voidaan tällöin kirjoittaa yhtälöryhmäksi v + h + m = 8 v +
9. 0. ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ö Ø ÙØ 009 È ÖÙ Ö P. Olkoon vadelmien hinta v e, herukoiden h e ja mustikoiden m e rasialta. Oletukset voidaan tällöin kirjoittaa yhtälöryhmäksi v + h + m = 8 v +
ARVO - verkkomateriaalien arviointiin
 ARVO - verkkomateriaalien arviointiin Arvioitava kohde: Jenni Rikala: Aloittavan yrityksen suunnittelu, Arvioija: Heli Viinikainen, Arviointipäivämäärä: 12.3.2010 Osa-alue 3/8: Visuaalinen suunnittelu
ARVO - verkkomateriaalien arviointiin Arvioitava kohde: Jenni Rikala: Aloittavan yrityksen suunnittelu, Arvioija: Heli Viinikainen, Arviointipäivämäärä: 12.3.2010 Osa-alue 3/8: Visuaalinen suunnittelu
766320A SOVELTAVA SÄHKÖMAGNETIIKKA, ohjeita tenttiin ja muutamia teoriavinkkejä sekä pari esimerkkilaskua
 7663A OVLTAVA ÄHKÖMAGNTIIKKA, ohjeita tenttiin ja muutamia teoriavinkkejä sekä pari esimerkkilaskua 1. Lue tenttitehtävä huolellisesti. Tehtävä saattaa näyttää tutulta, mutta siinä saatetaan kysyä eri
7663A OVLTAVA ÄHKÖMAGNTIIKKA, ohjeita tenttiin ja muutamia teoriavinkkejä sekä pari esimerkkilaskua 1. Lue tenttitehtävä huolellisesti. Tehtävä saattaa näyttää tutulta, mutta siinä saatetaan kysyä eri
Tehtävä 3: Ongelmanratkaisutehtävä
 Tehtävä 3: Ongelmanratkaisutehtävä Kysymys 3.1 Seuraavat kortit tulee kääntää: ympyrä: tämän kortin selkäpuolen tulee olla punainen sininen: etupuolella ei saa olla ympyrää Seuraavia kortteja ei tarvitse
Tehtävä 3: Ongelmanratkaisutehtävä Kysymys 3.1 Seuraavat kortit tulee kääntää: ympyrä: tämän kortin selkäpuolen tulee olla punainen sininen: etupuolella ei saa olla ympyrää Seuraavia kortteja ei tarvitse
Siltaaminen: Piaget Matematiikka Inductive Reasoning OPS Liikennemerkit, Eläinten luokittelu
 Harjoite 2 Tavoiteltava toiminta: Materiaalit: Eteneminen: TUTUSTUTAAN OMINAISUUS- JA Toiminnan tavoite ja kuvaus: SUHDETEHTÄVIEN TUNNISTAMISEEN Kognitiivinen taso: IR: Toiminnallinen taso: Sosiaalinen
Harjoite 2 Tavoiteltava toiminta: Materiaalit: Eteneminen: TUTUSTUTAAN OMINAISUUS- JA Toiminnan tavoite ja kuvaus: SUHDETEHTÄVIEN TUNNISTAMISEEN Kognitiivinen taso: IR: Toiminnallinen taso: Sosiaalinen
Aasianrunkojäärä. Tilanne Vantaalla 18.11.2015
 Aasianrunkojäärä Tilanne Vantaalla 18.11.2015 Aino-Maija Alanko 18.11.2015 Sisällys Yleistä aasianrunkojäärästä Tilannekatsaus Kivipyykintien esiintymäpaikasta Kartoitukset Jatkotoimenpiteet Aino-Maija
Aasianrunkojäärä Tilanne Vantaalla 18.11.2015 Aino-Maija Alanko 18.11.2015 Sisällys Yleistä aasianrunkojäärästä Tilannekatsaus Kivipyykintien esiintymäpaikasta Kartoitukset Jatkotoimenpiteet Aino-Maija
Kenguru 2019 Cadet (8. ja 9. luokka)
 Sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse vastaus tehtävän numeron alle. Oikeasta vastauksesta saa 3, 4 tai
Sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse vastaus tehtävän numeron alle. Oikeasta vastauksesta saa 3, 4 tai
Tekemistä varhaiskasvatukseen
 Tekemistä varhaiskasvatukseen Ympäristöviikko on vihreitä tekoja ja hauskaa yhdessäoloa! Osallistumalla voit osoittaa ympäristöasioiden tärkeyden ja arvostuksesi luontoa kohtaan. Seuraavilla sivuilla on
Tekemistä varhaiskasvatukseen Ympäristöviikko on vihreitä tekoja ja hauskaa yhdessäoloa! Osallistumalla voit osoittaa ympäristöasioiden tärkeyden ja arvostuksesi luontoa kohtaan. Seuraavilla sivuilla on
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
MATEMATIIKKA JA TAIDE I
 1 MATEMATIIKKA JA TAIDE I Tehtävät sopivat peruskoulun alaluokille. Ne on koostettu Matematiikkalehti Solmun Matematiikkadiplomeista I VI. Sivunumerot viittaavat näiden diplomitehtävien sivuihin. Aihepiirejä:
1 MATEMATIIKKA JA TAIDE I Tehtävät sopivat peruskoulun alaluokille. Ne on koostettu Matematiikkalehti Solmun Matematiikkadiplomeista I VI. Sivunumerot viittaavat näiden diplomitehtävien sivuihin. Aihepiirejä:
Kenguru Écolier (4. ja 5. luokka) sivu 1/5
 Kenguru Écolier (4. ja 5. luokka) sivu 1/5 3 pisteen tehtävät 1. Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2. Aikuisten pääsylippu
Kenguru Écolier (4. ja 5. luokka) sivu 1/5 3 pisteen tehtävät 1. Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2. Aikuisten pääsylippu
FAMILYTREEPAINTER. FamilyTreePainter Käyttöohje
 FAMILYTREEPAINTER FamilyTreePainter Käyttöohje i F A M I L Y T R E E P A I N T E R FamilyTreePainter Käyttöohje Copyright 2006-2013 Timo Vaara Email: timo@vaara.org ii Table of contents 1 YLESIATÄ... 1
FAMILYTREEPAINTER FamilyTreePainter Käyttöohje i F A M I L Y T R E E P A I N T E R FamilyTreePainter Käyttöohje Copyright 2006-2013 Timo Vaara Email: timo@vaara.org ii Table of contents 1 YLESIATÄ... 1
piirrä ohjeen mukaan. Lue ohjeet huolella ja piirrä kuvaan lisää asioita ohjeen mukaisesti.
 kieli piirrä ohjeen mukaan. Lue ohjeet huolella ja piirrä kuvaan lisää asioita ohjeen mukaisesti. Ohjeet: KUVA 1 - Sisällä 1. Piirrä pöydälle kukkaruukku, jossa kasvaa kaksi punaista kukkaa. 2. Kukkaruukun
kieli piirrä ohjeen mukaan. Lue ohjeet huolella ja piirrä kuvaan lisää asioita ohjeen mukaisesti. Ohjeet: KUVA 1 - Sisällä 1. Piirrä pöydälle kukkaruukku, jossa kasvaa kaksi punaista kukkaa. 2. Kukkaruukun
Viivan ulko- vai sisäpuolella?
 Viivan ulko- vai sisäpuolella? Avainsanat: parillisuus, parittomuus, topologia Luokkataso: 1.-2. luokka, 3.-5. luokka Välineet: asfalttiliitua tai narua, puukeppi tai kivi tms. Kuvaus: Tehtävässä tutkitaan
Viivan ulko- vai sisäpuolella? Avainsanat: parillisuus, parittomuus, topologia Luokkataso: 1.-2. luokka, 3.-5. luokka Välineet: asfalttiliitua tai narua, puukeppi tai kivi tms. Kuvaus: Tehtävässä tutkitaan
Puzzle-SM 2000. Loppukilpailu 18.6.2000 Oulu
 Puzzle-SM Loppukilpailu 8.6. Oulu Puzzle Ratkontaaikaa tunti Ratkontaaikaa tunti tsi palat 6 Varjokuva 7 Parinmuodostus 7 Paikallista 7 Metris 7 ominopalapeli Kerrostalot Pisteestä toiseen Heinäsirkka
Puzzle-SM Loppukilpailu 8.6. Oulu Puzzle Ratkontaaikaa tunti Ratkontaaikaa tunti tsi palat 6 Varjokuva 7 Parinmuodostus 7 Paikallista 7 Metris 7 ominopalapeli Kerrostalot Pisteestä toiseen Heinäsirkka
Kaupunkisuunnittelua
 Kaupunkisuunnittelua Avainsanat: geometria, monikulmio, pinta-ala, tasogeometria, diagrammit Luokkataso: 6.-9. luokka, lukio Välineet: kynä, paperi, viivoitin, harppi tai kulmaviivain Kuvaus: Voronoi diagrammien
Kaupunkisuunnittelua Avainsanat: geometria, monikulmio, pinta-ala, tasogeometria, diagrammit Luokkataso: 6.-9. luokka, lukio Välineet: kynä, paperi, viivoitin, harppi tai kulmaviivain Kuvaus: Voronoi diagrammien
Kolikon tie Koululaistehtävät
 Kolikon tie Koululaistehtävät I Tehtävät ennen Heureka-vierailua Rahojen ja Suomen Rahapajan historia 1. Ota selvää missä ja milloin raha otettiin ensimmäisen kerran käyttöön. 2. Minkälaisia ensimmäiset
Kolikon tie Koululaistehtävät I Tehtävät ennen Heureka-vierailua Rahojen ja Suomen Rahapajan historia 1. Ota selvää missä ja milloin raha otettiin ensimmäisen kerran käyttöön. 2. Minkälaisia ensimmäiset
Insinöörimatematiikka A
 Insinöörimatematiikka A Demonstraatio 3, 3.9.04 Tehtävissä 4 tulee käyttää Gentzenin järjestelmää kaavojen johtamiseen. Johda kaava φ (φ ) tyhjästä oletusjoukosta. ) φ ) φ φ 3) φ 4) φ (E ) (E ) (I, ) (I,
Insinöörimatematiikka A Demonstraatio 3, 3.9.04 Tehtävissä 4 tulee käyttää Gentzenin järjestelmää kaavojen johtamiseen. Johda kaava φ (φ ) tyhjästä oletusjoukosta. ) φ ) φ φ 3) φ 4) φ (E ) (E ) (I, ) (I,
STS Uuden Tapahtuma-dokumentin teko
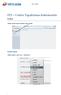 STS Uuden Tapahtuma-dokumentin teko Valitse vasemmasta reunasta kohta Sisällöt. Sisällöt-näkymä Valitse painike Lisää uusi Tapahtuma 1 Valitse kieleksi Suomi Välilehti 1. Perustiedot Musta reunus kieliversioneliön
STS Uuden Tapahtuma-dokumentin teko Valitse vasemmasta reunasta kohta Sisällöt. Sisällöt-näkymä Valitse painike Lisää uusi Tapahtuma 1 Valitse kieleksi Suomi Välilehti 1. Perustiedot Musta reunus kieliversioneliön
Kenguru Écolier (4. ja 5. luokka) ratkaisut sivu 1/5
 Kenguru Écolier (4. ja 5. luokka) ratkaisut sivu 1/5 3 pisteen tehtävät 1) Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2) Aikuisten
Kenguru Écolier (4. ja 5. luokka) ratkaisut sivu 1/5 3 pisteen tehtävät 1) Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2) Aikuisten
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE
 AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Tekstikoe ja Ongelmanratkaisu HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
AMMATTIKORKEAKOULUJEN TEKNIIKAN VALINTAKOE OHJEITA Valintakokeessa on kaksi osaa: TEHTÄVÄOSA: Ongelmanratkaisu VASTAUSOSA: Tekstikoe ja Ongelmanratkaisu HUOMIOI SEURAAVAA: 1. TEHTÄVÄOSAN tehtävään 7 ja
- 4 aloituslaattaa pelaajien väreissä molemmille puolille on kuvattu vesialtaat, joista lähtee eri määrä akvedukteja.
 AQUA ROMANA Vesi oli elintärkeä ja keskeinen edellytys Rooman imperiumin kehitykselle. Vedensaannin turvaamiseksi taitavimmat rakennusmestarit rakensivat valtavan pitkiä akvedukteja, joita pidetään antiikin
AQUA ROMANA Vesi oli elintärkeä ja keskeinen edellytys Rooman imperiumin kehitykselle. Vedensaannin turvaamiseksi taitavimmat rakennusmestarit rakensivat valtavan pitkiä akvedukteja, joita pidetään antiikin
Poistettavien puiden valinta laatuperustein harvennushakkuulla
 Poistettavien puiden valinta laatuperustein harvennushakkuulla Manne Viljamaa TAMK http://puuhuoltooppimispolku.projects.tamk.fi/path.p hp?show=31 1. Harvennushakkuun terminologiasta Käsitteet tuulee olla
Poistettavien puiden valinta laatuperustein harvennushakkuulla Manne Viljamaa TAMK http://puuhuoltooppimispolku.projects.tamk.fi/path.p hp?show=31 1. Harvennushakkuun terminologiasta Käsitteet tuulee olla
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 (opetusmoniste, lauselogiikka )
 T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 opetusmoniste, lauselogiikka 2.1-3.5) 21 24.9.2004 1. Määrittele lauselogiikan konnektiivit a) aina epätoden lauseen ja implikaation
T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 2 opetusmoniste, lauselogiikka 2.1-3.5) 21 24.9.2004 1. Määrittele lauselogiikan konnektiivit a) aina epätoden lauseen ja implikaation
Lukion matematiikkakilpailun alkukilpailun ratkaisut Perussarja P1. Merkitään p:llä paidan ja h:lla housujen hankintahintaa sekä m:llä nä
 11. 10. 007 Lukion matematiikkakilailun alkukilailun ratkaisut Perussarja P1. Merkitään :llä aidan ja h:lla housujen hankintahintaa sekä m:llä näiden yhteistä myyntihintaa. Tiedetään, että m 100% = 0%
11. 10. 007 Lukion matematiikkakilailun alkukilailun ratkaisut Perussarja P1. Merkitään :llä aidan ja h:lla housujen hankintahintaa sekä m:llä näiden yhteistä myyntihintaa. Tiedetään, että m 100% = 0%
Uhanalaisuusarvioinnin keskeiset käsitteet. Annika Uddström, Suomen ympäristökeskus,
 Uhanalaisuusarvioinnin keskeiset käsitteet Annika Uddström, Suomen ympäristökeskus, 2.2.2017 Populaatio ja populaatiokoko (kriteerit A, C ja D) Populaatiolla tarkoitetaan lajin tarkastelualueella elävää
Uhanalaisuusarvioinnin keskeiset käsitteet Annika Uddström, Suomen ympäristökeskus, 2.2.2017 Populaatio ja populaatiokoko (kriteerit A, C ja D) Populaatiolla tarkoitetaan lajin tarkastelualueella elävää
Kenguru 2016 Cadet (8. ja 9. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Tietoturvapolitiikka turvallisuuden perusta
 Tietoturvapolitiikka turvallisuuden perusta TkT Pekka Jäppinen Lappeenrannan Teknillinen yliopisto PROSTEK-yhteistyöfoorumi 18.4.2013 18.4.2013 Pekka Jäppinen Turvallisuus on yhtä vahva kuin sen heikoin
Tietoturvapolitiikka turvallisuuden perusta TkT Pekka Jäppinen Lappeenrannan Teknillinen yliopisto PROSTEK-yhteistyöfoorumi 18.4.2013 18.4.2013 Pekka Jäppinen Turvallisuus on yhtä vahva kuin sen heikoin
Latinalaiset neliöt ja taikaneliöt
 Latinalaiset neliöt ja taikaneliöt LuK-tutkielma Aku-Petteri Niemi Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2018 Sisältö Johdanto 2 1 Latinalaiset neliöt 3 1.1 Latinalainen neliö.........................
Latinalaiset neliöt ja taikaneliöt LuK-tutkielma Aku-Petteri Niemi Matemaattisten tieteiden tutkinto-ohjelma Oulun yliopisto Kevät 2018 Sisältö Johdanto 2 1 Latinalaiset neliöt 3 1.1 Latinalainen neliö.........................
Evoluutio ja luominen. Mian tekemä esitys Jannen esittämänä
 Evoluutio ja luominen Mian tekemä esitys Jannen esittämänä Väite: tiedemiehet ovat todistaneet evoluutioteorian todeksi Evoluutioteorialla tässä tarkoitan teoriaa, jonka mukaan kaikki elollinen on kehittynyt
Evoluutio ja luominen Mian tekemä esitys Jannen esittämänä Väite: tiedemiehet ovat todistaneet evoluutioteorian todeksi Evoluutioteorialla tässä tarkoitan teoriaa, jonka mukaan kaikki elollinen on kehittynyt
Ei välttämättä, se voi olla esimerkiksi Reuleaux n kolmio:
 Inversio-ongelmista Craig, Brown: Inverse problems in astronomy, Adam Hilger 1986. Havaitaan oppositiossa olevaa asteroidia. Pyörimisestä huolimatta sen kirkkaus ei muutu. Projisoitu pinta-ala pysyy ilmeisesti
Inversio-ongelmista Craig, Brown: Inverse problems in astronomy, Adam Hilger 1986. Havaitaan oppositiossa olevaa asteroidia. Pyörimisestä huolimatta sen kirkkaus ei muutu. Projisoitu pinta-ala pysyy ilmeisesti
Nimitys Symboli Merkitys Negaatio ei Konjuktio ja Disjunktio tai Implikaatio jos..., niin... Ekvivalenssi... jos ja vain jos...
 2 Logiikkaa Tässä luvussa tutustutaan joihinkin logiikan käsitteisiin ja merkintöihin. Lisätietoja ja tarkennuksia löytyy esimerkiksi Jouko Väänäsen kirjasta Logiikka I 2.1 Loogiset konnektiivit Väitelauseen
2 Logiikkaa Tässä luvussa tutustutaan joihinkin logiikan käsitteisiin ja merkintöihin. Lisätietoja ja tarkennuksia löytyy esimerkiksi Jouko Väänäsen kirjasta Logiikka I 2.1 Loogiset konnektiivit Väitelauseen
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Varma tapahtuma, Yhdiste, Yhdistetty tapahtuma, Yhteenlaskusääntö
 Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Unioni, Todennäköisyyslaskennan peruskäsitteet Todennäköisyyslaskennan peruslaskusäännöt Alkeistapahtuma, Ehdollinen todennäköisyys,
Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Unioni, Todennäköisyyslaskennan peruskäsitteet Todennäköisyyslaskennan peruslaskusäännöt Alkeistapahtuma, Ehdollinen todennäköisyys,
Tee-se-itse -tekoäly
 Tee-se-itse -tekoäly Avainsanat: koneoppiminen, tekoäly, neuroverkko Luokkataso: 6.-9. luokka, lukio, yliopisto Välineet: kynä, muistilappuja tai kertakäyttömukeja, herneitä tms. pieniä esineitä Kuvaus:
Tee-se-itse -tekoäly Avainsanat: koneoppiminen, tekoäly, neuroverkko Luokkataso: 6.-9. luokka, lukio, yliopisto Välineet: kynä, muistilappuja tai kertakäyttömukeja, herneitä tms. pieniä esineitä Kuvaus:
Liikenneonnettomuuksien määrä eri talvipäivinä
 Liikenneonnettomuuksien määrä eri talvipäivinä Juha Valtonen 7.11.216 1 Liikenneonnettomuuksien määrä eri talvipäivinä Tämä muistio on liite Liikenneturvan lausuntoon ehdotuksesta muuttaa raskaiden ajoneuvojen
Liikenneonnettomuuksien määrä eri talvipäivinä Juha Valtonen 7.11.216 1 Liikenneonnettomuuksien määrä eri talvipäivinä Tämä muistio on liite Liikenneturvan lausuntoon ehdotuksesta muuttaa raskaiden ajoneuvojen
1 Kannat ja kannanvaihto
 1 Kannat ja kannanvaihto 1.1 Koordinaattivektori Oletetaan, että V on K-vektoriavaruus, jolla on kanta S = (v 1, v 2,..., v n ). Avaruuden V vektori v voidaan kirjoittaa kannan vektorien lineaarikombinaationa:
1 Kannat ja kannanvaihto 1.1 Koordinaattivektori Oletetaan, että V on K-vektoriavaruus, jolla on kanta S = (v 1, v 2,..., v n ). Avaruuden V vektori v voidaan kirjoittaa kannan vektorien lineaarikombinaationa:
Paluu paperin taitteluun
 Paluu paperin taitteluun Kotiryhmän nimet: Jakoryhmän nimet: Tehtävä 1 Täydentäkää selitys Väite: Kun paperi taitetaan x kertaa, paperi jakautuu 2 x osaan. Paluu paperin taitteluun Kotiryhmän nimet: Jakoryhmän
Paluu paperin taitteluun Kotiryhmän nimet: Jakoryhmän nimet: Tehtävä 1 Täydentäkää selitys Väite: Kun paperi taitetaan x kertaa, paperi jakautuu 2 x osaan. Paluu paperin taitteluun Kotiryhmän nimet: Jakoryhmän
III Perinnöllisyystieteen perusteita
 Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 15. Populaatiogenetiikka ja evoluutio 1. Avainsanat 2. Evoluutio muuttaa geenipoolia 3. Mihin valinta kohdistuu? 4. Yksilön muuntelua
Perinnöllisyystieteen perusteita III Perinnöllisyystieteen perusteita 15. Populaatiogenetiikka ja evoluutio 1. Avainsanat 2. Evoluutio muuttaa geenipoolia 3. Mihin valinta kohdistuu? 4. Yksilön muuntelua
Diskreetin matematiikan perusteet Laskuharjoitus 3 / vko 10
 Diskreetin matematiikan perusteet Laskuharjoitus 3 / vko 10 Tuntitehtävät 17-18 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 21-22 loppuviikon harjoituksissa. Kotitehtävät 19-20 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 3 / vko 10 Tuntitehtävät 17-18 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 21-22 loppuviikon harjoituksissa. Kotitehtävät 19-20 tarkastetaan loppuviikon
1. Tilastollinen malli??
 1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
Kenguru 2014 Student sivu 1 / 8 (lukion 2. ja 3. vuosi)
 Kenguru 2014 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2014 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko
 DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
Tehtävä 1. Päättele resoluutiolla seuraavista klausuulijoukoista. a. 1 {p 3 } oletus. 4 {p 1, p 2, p 3 } oletus. 5 { p 1 } (1, 2) 7 (4, 6)
 Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
Tehtävä 1 Päättele resoluutiolla seuraavista klausuulijoukoista. a. {{p 0 }, {p 1 }, { p 0, p 2 }, {p 1, p 2, p 3 }, { p 2, p 3 }, {p 3 }}, b. {{ p 0, p 2 }, {p 0, p 1 }, {{ p 1, p 2 }, { p 2 }}, c. {{p
TUULIPUISTON LUONTOSELVITYKSEN TÄYDENNYS SAUVO STENINGEN VARSINAIS-SUOMEN LUONTO- JA YMPÄRISTÖPALVELUT
 TUULIPUISTON LUONTOSELVITYKSEN TÄYDENNYS SAUVO STENINGEN VARSINAIS-SUOMEN LUONTO- JA YMPÄRISTÖPALVELUT 2013 SISÄLLYS 1. Johdanto 2. Uusi rakennuspaikka 3. Rakennuspaikan kuvaus 4. Lepakot 5. Johtopäätökset
TUULIPUISTON LUONTOSELVITYKSEN TÄYDENNYS SAUVO STENINGEN VARSINAIS-SUOMEN LUONTO- JA YMPÄRISTÖPALVELUT 2013 SISÄLLYS 1. Johdanto 2. Uusi rakennuspaikka 3. Rakennuspaikan kuvaus 4. Lepakot 5. Johtopäätökset
Fakta- ja näytenäkökulmat. Pertti Alasuutari Tampereen yliopisto
 Fakta- ja näytenäkökulmat Pertti Alasuutari Tampereen yliopisto Mikä on faktanäkökulma? sosiaalitutkimuksen historia: väestötilastot, kuolleisuus- ja syntyvyystaulut. Myöhemmin kysyttiin ihmisiltä tietoa
Fakta- ja näytenäkökulmat Pertti Alasuutari Tampereen yliopisto Mikä on faktanäkökulma? sosiaalitutkimuksen historia: väestötilastot, kuolleisuus- ja syntyvyystaulut. Myöhemmin kysyttiin ihmisiltä tietoa
Platonin kappaleet. Avainsanat: geometria, matematiikan historia. Luokkataso: 6-9, lukio. Välineet: Polydron-rakennussarja, kynä, paperia.
 Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Värijärjestelmät. Väritulostuksen esittely. Tulostaminen. Värien käyttäminen. Paperinkäsittely. Huolto. Vianmääritys. Ylläpito.
 Tällä tulostimella voidaan tulostaa värillisiä asiakirjoja. Värituloste herättää huomiota, lisää arvostusta ja tulosteen tai tietojen arvoa. käyttö lisää lukijoiden määrää, sillä väritulosteet luetaan
Tällä tulostimella voidaan tulostaa värillisiä asiakirjoja. Värituloste herättää huomiota, lisää arvostusta ja tulosteen tai tietojen arvoa. käyttö lisää lukijoiden määrää, sillä väritulosteet luetaan
BI4 Ihmisen Biologia KAUSTISEN MUSIIKKILUKIO
 BI4 Ihmisen Biologia KAUSTISEN MUSIIKKILUKIO 2016-2017 Tervetuloa BI4-kurssille! Kurssin tavoitteena on, että opiskelija osaa: ihmissolun erilaistumisen pääperiaatteet sekä kudosten ja elinten rakenteet
BI4 Ihmisen Biologia KAUSTISEN MUSIIKKILUKIO 2016-2017 Tervetuloa BI4-kurssille! Kurssin tavoitteena on, että opiskelija osaa: ihmissolun erilaistumisen pääperiaatteet sekä kudosten ja elinten rakenteet
Kiinalaiset kuvakirjaimet ( Kanjit)
 Kiinalaiset kuvakirjaimet ( Kanjit) Japanilaiset omaksuivat kiinalaiset kuvakirjaimet, eli Kanjit, 500-700 luvulla j.kr. mutta tieteiden, taiteiden, ja Buddhismin mukana niitä on omaksuttu lisää mantereelta
Kiinalaiset kuvakirjaimet ( Kanjit) Japanilaiset omaksuivat kiinalaiset kuvakirjaimet, eli Kanjit, 500-700 luvulla j.kr. mutta tieteiden, taiteiden, ja Buddhismin mukana niitä on omaksuttu lisää mantereelta
Kenguru 2015 Benjamin (6. ja 7. luokka)
 sivu 1 / 12 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 12 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi
 Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi LUKUTEORIA JA TODISTAMINEN, MAA11 Esimerkki a) Lauseen Kaikki johtajat ovat miehiä negaatio ei
Lisää kvanttoreista ja päättelyä sekä predikaattilogiikan totuustaulukot 1. Negaation siirto kvanttorin ohi LUKUTEORIA JA TODISTAMINEN, MAA11 Esimerkki a) Lauseen Kaikki johtajat ovat miehiä negaatio ei
Kenguru 2016 Benjamin (6. ja 7. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Lasten ja nuorten maailmankuva Tehtävät
 Lasten ja nuorten maailmankuva Tehtävät TIEDÄ 1. Selitä omin sanoin, mikä on maantieteellinen maailmankuva. 2. Mitä tarkoittaa, että me katsomme maailmaa "kulttuurin värittämien silmälasien läpi"? 3. Miksi
Lasten ja nuorten maailmankuva Tehtävät TIEDÄ 1. Selitä omin sanoin, mikä on maantieteellinen maailmankuva. 2. Mitä tarkoittaa, että me katsomme maailmaa "kulttuurin värittämien silmälasien läpi"? 3. Miksi
Kenguru 2013 Benjamin sivu 1 / 7 (6. ja 7. luokka) yhteistyössä Pakilan ala-asteen kanssa
 Kenguru 2013 Benjamin sivu 1 / 7 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Benjamin sivu 1 / 7 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Matematiikan tukikurssi, kurssikerta 2
 Matematiikan tukikurssi kurssikerta 1 Relaatioista Oletetaan kaksi alkiota a ja b. Näistä kumpikin kuuluu johonkin tiettyyn joukkoon mahdollisesti ne kuuluvat eri joukkoihin; merkitään a A ja b B. Voidaan
Matematiikan tukikurssi kurssikerta 1 Relaatioista Oletetaan kaksi alkiota a ja b. Näistä kumpikin kuuluu johonkin tiettyyn joukkoon mahdollisesti ne kuuluvat eri joukkoihin; merkitään a A ja b B. Voidaan
Vertailukuntien valinta
 Vertailukuntien valinta Vertailukunniksi kannattaa yleensä valita kuntia, jotka mm. ovat suunnilleen samankokoisia kuin oma kunta edustavat suunnilleen samankaltaista rakennetta kuin oma kunta (ikäjakauma,
Vertailukuntien valinta Vertailukunniksi kannattaa yleensä valita kuntia, jotka mm. ovat suunnilleen samankokoisia kuin oma kunta edustavat suunnilleen samankaltaista rakennetta kuin oma kunta (ikäjakauma,
