Matemaattiset apuneuvot II, harjoitus 4
|
|
|
- Jukka-Pekka Aro
- 6 vuotta sitten
- Katselukertoja:
Transkriptio
1 Matemaattiset apuneuvot II, harjoitus 4 K. Tuominen 22. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi assarin nimi. Tehtävät S1 ja S2 ovat ylimääräisiä, ja niistä saa normaalit laskaripisteet, mutta maksimipisteet on mahdollista saada ilmankin. 1. Tarkastellaan vakiokertoimista 1. kertaluvun yhtälöä dx + px = q. dt (a) Ratkaise yhtälöä käyttämällä integroivaa tekijää. (b) Ratkaise yhtälö etsimällä ensin homogeenisen yhtälön ratkaisu x h ja sen jälkeen jokin epähomogeenisen yhtälön yksittäisratkaisu x p. Ratkaisu: (a) Käytetään integroivaa tekijää jolloin yleisen ratkaisun tiedetään olevan I(t) = p(t)dt e = e pdt = e pt x(t)i(t) = I(t)q(t)dt x(t) = q I(t)dt I(t) = q e pt e pt dt ( ) 1 = qe pt p ept + D = q p + qde pt = Ce pt + q p Lopussa otettiin uusi integromisvakio C qd, mikä voidaan tehdä, koska q on vain vakio, eli tulo qd on myös "jokin vakio". (b) Lasketaan ensin homogeenisen ytälön ratkaisu x h
2 matemaattiset apuneuvot ii, harjoitus 4 2 dx dt + px = 0 dx dt = px 1 dx x dt = p dx x = pdt dx x = pdt ln (x) = pt + D x = e pt+d x = e D e pt x = Ce pt Nyt tarvitaan sopiva yrite epähomogeenisen yhtälön yksittäisratkaisuksi. Oikealla puolella yhtälö on nollannen asteen polynomi (eli vakio), siispä yritteeksi riittää x = A. Sijoitetaan yrite. da dx + pa = q pa = q A = q p Saadaan epähomogeenisen yhtälön yleiseksi ratkaisuksi x = x h + x p = Ce pt + q p Siispä saimme molemmilla metodeilla saman vastauksen! 2. Lähetetään valoa vedenpinnan alapuolella suoraan alaspäin. Valon edetessä tapahtuu absorptiota, ja valon intesiteetti pienenee. Intensiteetin pieneneminen syvyydellä h on suoraan verrannollinen intensiteettiin syvyydellä h. Verrannollisuuskerrointa µ kutsutaan lineaariseksi absorptiokertoimeksi. Johda valon intensiteettiä syvyydellä h kuvaava yhtälö ja kirjoita sen yleinen ratkaisu. Veden absorptiokerroin on µ = cm 1. Jos intensiteetti veden pinnassa on I 0, niin millä syvyydellä intensiteetti on puolet alkuperäisestä? Ratkaisu: Koska intensiteetin pieneneminen syvyydellä h on suoraan verrannollinen intensiteettiin ja on annettu lineaarinen absorptiokerroin, saamme yhtälön: di dh = µi Yleinen ratkaisu saadaan, kun muokataan yhtälöä uuteen muotoon ja integroidaan puolittain: di I di I = µdh = µdh ln(i) = µh + C
3 matemaattiset apuneuvot ii, harjoitus 4 I = Ce µh Tiedetään, että veden pinnalla I(h) = I 0 Kun valitaan, että veden pinnalla h = 0, saadaan ratkaistua C: eli C = I 0 ja I(0) = Ce µ0 = I 0 I = I 0 e µh Seuraavaksi selvitetään, millä syvyydellä intensiteetti on puolet alkuperäisestä. I = I 0 2 eli I = I 0 e µh I 0 e µh = I 0 2 e µh = 1 2 µh = ln( 1 2 ) h = ln( 1 2 ) ln( 1 2 = ) µ = 211cm = 21.1m cm 1 Intensiteetti on puolet alkuperäisestä noin 21m syvyydellä vedenpinnasta alaspäin.. Etsi yhtälön ẍ + ẋ 2x = 12e t 6e t yleinen ratkaisu. Ratkaisu: Tehtävä ratkeaa viime viikon tehtävistä tutuksi tullein keinoin. Ratkaisu on homogeenisen yhtälön ratkaisun ja epähomogeenisen yhtälön yksittäisratkaisun summa. Homogeeninen yhtälö on: HY:n karakteristinen yhtälö on: x + x 2x = 0 Joten HY:n ratkaisu on: k 2 + k 2 = 0 k = 1 ± 9 2 k = 1 tai k = 2 x h = C 1 e 2t + C 2 e t Kuten tavallista yksittäisratkaisu selvitetään yritteellä. Hyvä yrite voisi olla x p = Ae t + Be t. Be t on kuitenkin homogeenisen yhtälön ratkaisu, joten yrite on x p = Ae t + Bte t. Sijoitetaan yrite epähomogeeniseen yhtälöön ja ratkaistaan vakiot: x p = Ae t + Bte t x p = Ae t + Bte t + Be t x p = Ae t + Bte t + 2Be t (Ae t + Bte t + 2Be t ) + ( Ae t + Bte t + Be t ) 2(Ae t + Bte t ) = 12e t 6e t Be t 2Ae t = 12e t 6e t A = 6 ja B = 2
4 matemaattiset apuneuvot ii, harjoitus 4 4 Nyt lopullinen vastaus on siis: x = x h + x p = C 1 e 2t + C 2 e t 6e t 2te t 4. Viinilasin värähtelyä voidaan mallintaa yhtälöllä ẍ + λẋ + ω 2 x = 0. Oletetaan, että napautettaessa lasia, se värähtelee taajuudella 660 Hz. (a) Osoita, että 4ω 2 λ 2 = 2640π. (b) Syntynyt ääni vaimenee kuulumattomiin sekunnin kuluessa. Täsmällisemmin sanottuna, kolmen sekunnin kuluessa alkuperäisen värähtelyn amplitudi on vaimentunut tekijällä 1/100. Osoita, että λ = 2 ln(100). Laske λ ja ω kolmen merkitsevän numeron tarkkuudella. Ratkaisu: a) Differentiaaliyhtälön karakteristinen yhtälö on muotoa: Ja sen kompleksiset ratkaisut ovat: γ 2 + λγ + ω 2 γ = λ ± λ 2 4ω 2 2 γ = λ 2 ± i 4ω2 λ 2 2 Jos oletetaan 4ω 2 > λ 2. Yleinen ratkaisu kyseiselle differentiaaliyhtälölle on siis: x(t) = e λt/2 (c 1 cos(at) + c 2 sin(at)) missä ollaan merkitty a = 4ω 2 λ 2 /2. x(t) kuvailee viinilasin värähtelyjä mallissamme. Huomaamme tästä että suure a kuvaa suoraan värähtelyjen kulmataajuutta. Kulmataajuuden ja taajuuden välillä pätee relaatio ν = 2π f (käytämme tässä symbolia ν koska ω on jo käytössä) joten: ν = a = 2π f 4ω 2 λ 2 = 4π f = 4π(660) = 2640π b) Värähtelyjä kuvailevien termien lisäksi löytyy maksimiamplitudia skaalaava termi x(t) n lausekkeessa: x(t) = e λt/2 (c 1 cos(at) + c 2 sin(at)) A(t) = e λt/2 Vakio λ kertoo meille kuinka voimakkaasti viinilasin värähtelyt vaimenevat, koska selvästi kun t saamme x(t) 0. Meille kerrotaan että ajanhetkellä t = maksimiamplitudi on skaalautunut tekijällä 1/100, josta voimme päätellä että: A() = e 2 λ = λ = 2 ln(100).07 Ja a) kohdan kaavasta saadaan lopulta laskettua ω: 4ω 2 (.07) 2 = 2640π
5 matemaattiset apuneuvot ii, harjoitus 4 5 ω 4150 Joka on viinilasin luonnollinen kulmataajuus (ilman vaimennusta vakio λ = 0 ja a = ω). 5. Etsi yleinen ratkaisu yhtälölle d 4 x 16x = 64 sin(2t). dt4 Ratkaisu: Ratkaistaan ensin homogeeninen yhtälö: d 4 x dt 4 16x = 0 Sijoitetaan yhtälöön yrite x(t) = e rt, missä r on vakio: d 4 dt 4 ert 16e rt = 0 r 4 e rt 16e rt = 0 r 4 16 = 0 r 4 = 16 e rt Sitten muistetaan, mitä opittiin kurssin alkupuolella imaginaarilukujen juurista: 2, kun n = 0 ( r = 16e 2πn) 14 = 2e π 2 n 2i, kun n = 1 = 2, kun n = 2 2i, kun n = Homogeenisen yhtälön ratkaisu on siis x h (t) = C 1 e 2t + C 2 e 2t + C e i2t + C 4 e i2t Kurssin alkupuolella esiteltiin myös Eulerin kaava: jonka avulla voimme kirjoittaa: re iφ = cos φ + i sin φ (1) e i2t = cos(2t) + i sin(2t) e i2t = cos( 2t) + i sin( 2t) = cos(2t) i sin(2t) Sijoitetaan nämä homogeenisen yhtälön ratkaisuun ja saamme: x h (t) = C 1 e 2t + C 2 e 2t + C e i2t + C 4 e i2t Tässä tehtävässä epähomogeenitermi on: = C 1 e 2t + C 2 e 2t + C (cos(2t) + i sin(2t)) + C 4 (cos(2t) i sin(2t)) = C 1 e 2t + C 2 e 2t + C cos(2t) + C 4 sin(2t) f (t) = 64 sin(2t) Koska homogeenisen yhtälön ratksisun yksi termi on C 4 sin(2t), muodostetaan yksittäisratkaisun yrite sinin ja kosinin lineaarikombinaationa, ja kerrotaan sitä t:llä. Yritteeksi saadaan: x p (t) = At sin(2t) + Bt cos(2t)
6 matemaattiset apuneuvot ii, harjoitus 4 6 Derivoidaan yritettä ensin neljästi tulon derivoimissääntöä soveltaen: dx p (t) dt = A sin(2t) + 2At cos(2t) + B cos(2t) 2Bt sin(2t) = ( 2Bt + A) sin(2t) + (2At + B) cos(2t) d 2 x p (t) dt 2 = 2B sin(2t) + 2( 2Bt + A) cos(2t) + 2A cos(2t) 2(2At + B) sin(2t) = ( 4At 4B) sin(2t) + ( 4Bt + 4A) cos(2t) d x p (t) dt = 4A sin(2t) + 2( 4At 4B) cos(2t) 4B cos(2t) 2( 4Bt + 4A) sin(2t) = (8Bt 12A) sin(2t) + ( 8At 12B) cos(2t) d 4 x p (t) dt 4 = 8B sin(2t) + 2(8Bt 12A) cos(2t) 8A cos(2t) 2( 8At 12B) sin(2t) = (16At + 2B) sin(2t) + (16Bt 2A) cos(2t) Sijoitetaan yrite yhtälöön: d 4 x p (t) dt 4 + 6x p (t) = 64 sin(2t) (16At + 2B) sin(2t) + (16Bt 2A) cos(2t) + 16(At sin(2t) + Bt cos(2t)) = 64 sin(2t) (2At + 2B) sin(2t) + (2Bt 2A) cos(2t) = 64 sin(2t) (At + B) sin(2t) + (Bt A) cos(2t) = 2 sin(2t) Yltä nähdään, että sinin kertoimien perusteella on oltava A = 0 ja B = 2. Yksittäisratkaisu on siis: x p (t) = 2t cos(2t) Yleinen ratkaisu on nyt: x(t) = x h (t) + x p (t) = C 1 e 2t + C 2 e 2t + C cos(2t) + C 4 sin(2t) + 2t cos(2t) S1. Jatka tehtävän neljä tarkastelua: Lasi kestää deformaation, jonka suuruusluokka on x 1. Lasia kohti suunnataan ääni, jonka taajuus on 660 Hz ja voimakkuus D desibeliä. Tällöin tilannetta kuvaa differentiaaliyhtälö ẍ + λẋ + ω 2 x = 10(D/10) 8 cos(120πt). Mikä äänenvoimakkuuden D tulee olla, jotta lasi särkyy? Ratkaisu: Merkitään yksinkertaisuuden vuoksi F 10(D/10) 8 Differentiaaliyhtälöt, jotka ovat muotoa omaavat yksittäisratkaisun ja ω 0 120π. ẍ + λẋ + ω 2 x = F cos(ω 0 t) x p = C 1 cos(ω 0 t) + C 2 sin(ω 0 t).
7 matemaattiset apuneuvot ii, harjoitus 4 7 Otetaan yksittäisratkaisusta derivaatat: x = C 1 cos(ω 0 t) + C 2 sin(ω 0 t) ẋ = ω 0 C 1 sin(ω 0 t) + ω 0 C 2 cos(ω 0 t) ẍ = ω 2 0 C 1 cos(ω 0 t) ω 2 0 C 2 sin(ω 0 t). Sijoittamalla nämä differentiaaliyhtälöön saadaan muoto: ( ω0 2 C 1 + λω 0 C 2 + ω 2 C 1 ) cos(ω 0 t) + ( ω0 2 C 2 λω 0 C 1 + ω 2 C 2 ) sin(ω 0 t) = F cos(ω 0 t). ] ] [(ω 2 ω0 2)C 1 + λω 0 C 2 cos(ω 0 t) + [(ω 2 ω0 2)C 2 λω 0 C 1 sin(ω 0 t) = F cos(ω 0 t) Vertailemalla kertoimia saadaan muodostettua yhtälöpari, josta voidaan ratkaista C 1 ja C 2 : { (ω 2 ω 2 0 )C 1 + λω 0 C 2 = F (ω 2 ω 2 0 )C 2 λω 0 C 1 = 0 josta saadaan ratkaisuiksi (ω 2 ω0 2 C 1 = )F (ω 2 ω0 2)2 + (ω 0 λ) 2 C 2 = Sijoitetaan nämä takaisin ratkaisun muotoon: x p = ω 0 λf (ω 2 ω 2 0 )2 + (ω 0 λ) 2. (ω 2 ω0 2)F (ω 2 ω0 2)2 + (ω 0 λ) 2 cos(ω ω 0t) + 0 λf (ω 2 ω0 2)2 + (ω 0 λ) 2 sin(ω 0t). Palataan nyt pohtimaan alkuperäistä ongelmaamme. Pystymme tehdä tilanteen pohjalta kaksi yksinkertaistusta, jotka mahdollistavat ongelman ratkaisemisen: 1. Tehtävässä 4 ratkaistiin differentiaaliyhtälön homogeenisen version yleisratkaisu, jossa kaikissa termeissä on tekijä e λt/2. Voidaan hyvin olettaa, että lasin särkyessä aikaa on jo kulunut jonkin verran, jolloin kaikki nämä termit ovat pienentyneet eksponentiaalisesti mitättömiin. 2. Kyseessä on siis lasin särkyminen, jolloin puhutaan resonanssitaajuuksista, eli on ω ω 0. Tarkasteltaessa yksittäisratkaisumme muotoa, huomataan että tällöin termin (ω 2 ω0 2 ) osoittajassa omaava kosinitermi menee nollaksi, ja sinitermi dominoi. Nyt siis jäljelle ratkaisusta jää ainoastaan x = ω 0 λf (ω 2 ω0 2)2 + (ω 0 λ) 2 sin(ω 0t) F ω 0 λ sin(ω 0t). Tiedetään, että lasi kestää deformaation x 1, eli sinitermin kertoimelle tulee päteä F ω 0 λ > 1, eli F > ω 0 λ. Sijoitetaan tähän nyt aiemmin määrittelemämme F sekä ω 0, ja ratkaistaan millä äänenvoimakkuudella lasi hajoaa: F > ω 0 λ 10 (D/10) 8 > 120πλ 10 (D/10) 8 > 960πλ Otetaan molemmilta puolilta lg D 10 8 > lg(960πλ) D > 10 lg(960πλ) Nyt, koska tehtävässä 4 saatiin vaimennuskertoimen arvoksi λ.07, voidaan sanoa lasin hajoavan äänenvoimakkuudella D > 126 db.
8 matemaattiset apuneuvot ii, harjoitus 4 8 S2. Viime viikon (viikko ) S2-tehtävässä osoitettiin, että jos yhtälölle d 2 x dx + p(t) dt2 dt + q(t)x = 0 tunnetaan yksi ratkaisu, u(t), niin toinen ratkaisu voidaan konstruoida määrittelemällä x(t) = u(t)y(t), jolloin y(t) toteuttaa: ẏ = z(t) = Ae p(t)dt u(t) 2. Tarkastellaan yhtälöä ẍ tẋ + x = 0. Yhtälön yksi ratkaisu on u(t) = t. Soveltamalla yllä mainittua tulosta, muodosta toinen ratkaisu x(t). Viimeisen integraalin laskemiseksi, kehitä eksponenttifunktio potentenssisarjaksi ja oleta, että näin saamassasi lausekkeessa voit integroida termi kerrallaan Osoita, että toinen ratkaisu voidaan kirjoittaa muodossa x(t) = A [ 1 + n=1 t 2n 2 n (2n 1)n! ]. Tarkkana p(t):n merkin suhteen! Ratkaisu: Verrataan yhtälöä ẍ tẋ + x = 0 yleiseen muotoon, ja tunnistetaan p(t) = t, q(t) = 1 Tiedetään, että u(t) = t, joten y(t) on ẏ = Ae p(t)dt u(t) 2 ẏ = Ae tdt t 2 ẏ = A t 2 e t2 /2 Käyttämällä Taylorin kehitelmää: y = dy = A t 2 e t2 /2 dt A t 2 e t2 /2 dt Siten e t2 /2 = 1 + (t2 /2) 1! y = y = y = A t 2 e t2 /2 dt + (t2 /2) 2 2! ( A t (t2 /2) 1! ( A t (t2 /2) n n! + (t2 /2) 2 2! + + (t2 /2) n n! 2 1! + t ! + + t2n 2 2 n n! [ 1 y = A + t t 2 + t t 2n 1 ] 2 n (2n 1) n! ) dt ) dt
9 matemaattiset apuneuvot ii, harjoitus 4 9 Nyt muistetaan, että x(t) = u(t)y(t) eli x(t) = t y(t) [ 1 x(t) = t A t t22 t4 x(t) = A [ [ x(t) = A 1 + n=1 + t 2 + t t 2n 1 2 n (2n 1) n! t 2n ] 2 n (2n 1) n! t 2n ] 2 n (2n 1) n! ]
10 matemaattiset apuneuvot ii, harjoitus Consider the following 1st order differential equation with constant coefficients: dx + px = q. dt (a) Solve the equation using integrating factor. (b) Solve the equation by finding first the solution of the homogenoeus equation, x h, and then some particular integral of the inhomogeneous equation, x p. 2. A light beam is travelling downward into the ocean. As it progresses downward, the light is partially absorbed and its intensity decreases. The rate at which the intensity decreases as a function of the depth is proportional to the intensity of that depth. The proportionality constant µ is called the linear absorption coefficient. Write down the equation describing the intensity I as a function of the depth h and derive its general solution. The absorption coefficient of water is µ = cm 1. Determine the depth where the intensity has been reduced to half of its surface intensity I 0.. Find the general solution of the equation ẍ + ẋ 2x = 12e t 6e t. 4. The vibrations of a wine glass can be modelled by the equation ẍ + λẋ + ω 2 x = 0. Suppose that when struck, the glass vibrates at frequency 660 Hz. (a) Show that 4ω 2 λ 2 = 2640π. (b) It takes three seconds for the sound to fade away. This means that after three seconds the amplitude of the vibrations has reduced to 1/100 of its original level. Show, that λ = 2 ln(100). Finally, compute λ and ω to three significant digits. 5. Find the general solution of the equation d4 x 16x = 64 sin(2t). dt 4 S1. Continue the setup of problem 4: The glass can stand deformations of order x 1. A pure tone of frequency 660 Hz is produced at D decibels and directed towards the glass. When this external forcing is taken into account, the situation is described by the differential equation ẍ + λẋ + ω 2 x = 10(D/10) 8 cos(120πt). How loud should the sound be, i.e how large should D be, in order to shatter the glass?
11 matemaattiset apuneuvot ii, harjoitus 4 11 S2. In S2-problem last week (week ) we showed that if one solution,say u(t), to the equation d 2 x dx + p(t) dt2 dt + q(t)x = 0 is known, we can construct another solution by defining x(t) = u(t)y(t), where y(t) is obtained as ẏ = z(t) = Ae p(t)dt u(t) 2. Consider the equation ẍ tẋ + x = 0. One solution is u(t) = t. Construct another solution x(t) by using the formulas above. To carry out the final integral, expand the exponential function as a power series and assume that the resulting expression can be integrated term by term. Hence show that the second solution can be expressed as x(t) = A [ 1 + n=1 ] t 2n 2 n. (2n 1)n! Careful with the sign of p(t)!
Matemaattiset apuneuvot II, harjoitus 3
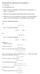 Matemaattiset apuneuvot II, harjoitus 3 K. Tuominen 16. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina 20.11. kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi
Matemaattiset apuneuvot II, harjoitus 3 K. Tuominen 16. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina 20.11. kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi
Esimerkki 1 Ratkaise differentiaaliyhtälö
 Esimerkki 1 Ratkaise differentiaaliyhtälö x 2 y xy =1/x. 1 / K. Tuominen kimmo.i.tuominen@helsinki.fi MApu II 1/20 20 Esimerkki 2 Ratkaise differentiaaliyhtälö x(ln y)y y ln x =0. 2 / K. Tuominen kimmo.i.tuominen@helsinki.fi
Esimerkki 1 Ratkaise differentiaaliyhtälö x 2 y xy =1/x. 1 / K. Tuominen kimmo.i.tuominen@helsinki.fi MApu II 1/20 20 Esimerkki 2 Ratkaise differentiaaliyhtälö x(ln y)y y ln x =0. 2 / K. Tuominen kimmo.i.tuominen@helsinki.fi
2. kl:n DY:t. Lause. Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.
 2. kl:n DY:t Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.) Lause Olkoon f(x 2, x 1, t) funktio, ja oletetaan, että f, f/ x 1 ja f/ x
2. kl:n DY:t Yleisesti yhtälöllä ẍ = f(ẋ, x, t) on (sopivin oletuksin) aina olemassa 1-käs. ratkaisu. (ẋ dx/dt, ẍ d 2 x/dt 2.) Lause Olkoon f(x 2, x 1, t) funktio, ja oletetaan, että f, f/ x 1 ja f/ x
Luento 14: Periodinen liike, osa 2. Vaimennettu värähtely Pakkovärähtely Resonanssi F t F r
 Luento 14: Periodinen liike, osa 2 Vaimennettu värähtely Pakkovärähtely Resonanssi θ F µ F t F r m g 1 / 20 Luennon sisältö Vaimennettu värähtely Pakkovärähtely Resonanssi 2 / 20 Vaimennettu värähtely
Luento 14: Periodinen liike, osa 2 Vaimennettu värähtely Pakkovärähtely Resonanssi θ F µ F t F r m g 1 / 20 Luennon sisältö Vaimennettu värähtely Pakkovärähtely Resonanssi 2 / 20 Vaimennettu värähtely
Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle /
 Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle / 16. 18.5. Lineaariset differentiaaliyhtälöt, homogeeniset differentiaaliyhtälöt Tehtävä 1: a) Määritä differentiaaliyhtälön y 3y = 14e 4x
Differentiaali- ja integraalilaskenta 1 Ratkaisut 6. viikolle / 16. 18.5. Lineaariset differentiaaliyhtälöt, homogeeniset differentiaaliyhtälöt Tehtävä 1: a) Määritä differentiaaliyhtälön y 3y = 14e 4x
y (0) = 0 y h (x) = C 1 e 2x +C 2 e x e10x e 3 e8x dx + e x 1 3 e9x dx = e 2x 1 3 e8x 1 8 = 1 24 e10x 1 27 e10x = e 10x e10x
 BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
Matemaattiset apuneuvot II, harjoitus 2
 Matemaattiset apuneuvot II, harjoitus 2 K. Tuominen 9. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina 13.11. kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi
Matemaattiset apuneuvot II, harjoitus 2 K. Tuominen 9. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina 13.11. kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi
y + 4y = 0 (1) λ = 0
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 6 mallit Kevät 2019 Tehtävä 1. Ratkaise yhtälöt a) y + 4y = x 2, b) y + 4y = 3e x. Ratkaisu: a) Differentiaaliyhtälön yleinen
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 6 mallit Kevät 2019 Tehtävä 1. Ratkaise yhtälöt a) y + 4y = x 2, b) y + 4y = 3e x. Ratkaisu: a) Differentiaaliyhtälön yleinen
Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 MAT-1345 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 9 Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa
1 MAT-1345 LAAJA MATEMATIIKKA 5 Tampereen teknillinen yliopisto Risto Silvennoinen Kevät 9 Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa
4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä
 1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
1 Laaja matematiikka 5 Kevät 010 4. Ensimmäisen ja toisen kertaluvun differentiaaliyhtälöistä Yksi tavallisimmista luonnontieteissä ja tekniikassa esiintyvistä matemaattisista malleista on differentiaaliyhtälö.
MS-A Differentiaali- ja integraalilaskenta 1 (CHEM) Harjoitus 6 loppuviikko
 MS-A0107 - Differentiaali- integraalilaskenta 1 (CHEM) Harjoitus 6 loppuviikko 1 Tehtävä Etsi seuraavien yhtälöiden yleiset ratkaisut: Ratkaisu: a) y y 2y = 4x, b) y + 4y = sin 3x, c) y + 2y + 5y = e x
MS-A0107 - Differentiaali- integraalilaskenta 1 (CHEM) Harjoitus 6 loppuviikko 1 Tehtävä Etsi seuraavien yhtälöiden yleiset ratkaisut: Ratkaisu: a) y y 2y = 4x, b) y + 4y = sin 3x, c) y + 2y + 5y = e x
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt
 MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
MS-C1340 Lineaarialgebra ja differentiaaliyhtälöt Differentiaaliyhtälöt, osa 1 Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 2015 1 / 20 R. Kangaslampi Matriisihajotelmista
lnx x 1 = = lim x = = lim lim 10 = x x0
 BM0A580 - Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 05. (a) (b) ln = sin(t π ) t π t π = = 0 = = cos(t π = ) = 0 t π (c) e [ = ] = = e e 3 = e = 0 = 0 (d) (e) 3 3 + 6 + 8 + 6 5 + 4 4 + 4
BM0A580 - Differentiaalilaskenta ja sovellukset Harjoitus 5, Syksy 05. (a) (b) ln = sin(t π ) t π t π = = 0 = = cos(t π = ) = 0 t π (c) e [ = ] = = e e 3 = e = 0 = 0 (d) (e) 3 3 + 6 + 8 + 6 5 + 4 4 + 4
Matematiikka B3 - Avoin yliopisto
 2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
2. heinäkuuta 2009 Opetusjärjestelyt Luennot 9:15-11:30 Harjoitukset 12:30-15:00 Tentti Lisäharjoitustehtävä Kurssin sisältö (1/2) 1. asteen Differentiaali yhtälöt (1.DY) Separoituva Ratkaisukaava Bernoyulli
4 Korkeamman kertaluvun differentiaaliyhtälöt
 Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Differentiaaliyhtälöt c Pekka Alestalo 2015 Tässä monisteessa käydään läpi tavallisiin differentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Luennolla lasketaan esimerkkitehtäviä
Matemaattinen Analyysi
 Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Vaasan yliopisto, kevät 01 / ORMS1010 Matemaattinen Analyysi. harjoitus, viikko 1 R1 ke 1 16 D11 (..) R to 10 1 D11 (..) 1. Määritä funktion y(x) MacLaurinin sarjan kertoimet, kun y(0) = ja y (x) = (x
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 17. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 17. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
6. Toisen ja korkeamman kertaluvun lineaariset
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 51 6. Toisen ja korkeamman kertaluvun lineaariset differentiaaliyhtälöt Määritelmä 6.1. Olkoon I R avoin väli. Olkoot p i : I R, i = 0, 1, 2,..., n, ja q : I R jatkuvia
Differentiaali- ja integraalilaskenta 1 Ratkaisut 5. viikolle /
 MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
MS-A8 Differentiaali- ja integraalilaskenta, V/7 Differentiaali- ja integraalilaskenta Ratkaisut 5. viikolle / 9..5. Integroimismenetelmät Tehtävä : Laske osittaisintegroinnin avulla a) π x sin(x) dx,
5 Differentiaaliyhtälöryhmät
 5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
5 Differentiaaliyhtälöryhmät 5.1 Taustaa ja teoriaa Differentiaaliyhtälöryhmiä tarvitaan useissa sovelluksissa. Toinen motivaatio yhtälöryhmien käytölle: Korkeamman asteen differentiaaliyhtälöt y (n) =
3 Toisen kertaluvun lineaariset differentiaaliyhtälöt
 3 Toisen kertaluvun lineaariset differentiaaliyhtälöt 3.1 Homogeeniset lineaariset differentiaaliyhtälöt Toisen kertaluvun differentiaaliyhtälö on lineaarinen, jos se voidaan kirjoittaa muotoon Jos r(x)
3 Toisen kertaluvun lineaariset differentiaaliyhtälöt 3.1 Homogeeniset lineaariset differentiaaliyhtälöt Toisen kertaluvun differentiaaliyhtälö on lineaarinen, jos se voidaan kirjoittaa muotoon Jos r(x)
2 dy dx 1. x = y2 e x2 2 1 y 2 dy = e x2 xdx. 2 y 1 1. = ex2 2 +C 2 1. y =
 BM20A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 2, Kevät 207 Päivityksiä: Tehtävän 4b tehtävänanto korjattu ja vastauksia lisätty.. Ratkaise y, kun 2y x = y 2 e x2. Jos y () = 0 niin mikä on ratkaisu
BM20A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 2, Kevät 207 Päivityksiä: Tehtävän 4b tehtävänanto korjattu ja vastauksia lisätty.. Ratkaise y, kun 2y x = y 2 e x2. Jos y () = 0 niin mikä on ratkaisu
Mat Matematiikan peruskurssi K2
 Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
a 1 y 1 (x) + a 2 y 2 (x) = 0 vain jos a 1 = a 2 = 0
 6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
6. Lineaariset toisen kertaluvun yhtälöt Toisen kertaluvun differentiaaliyhtälöt ovat tuntuvasti hankalampia ratkaista kuin ensimmäinen. Käsittelemmekin tässä vain tärkeintä erikoistapausta, toisen kertaluvun
Osa 11. Differen-aaliyhtälöt
 Osa 11. Differen-aaliyhtälöt Differen-aaliyhtälö = yhtälö jossa esiintyy jonkin funk-on derivaa
Osa 11. Differen-aaliyhtälöt Differen-aaliyhtälö = yhtälö jossa esiintyy jonkin funk-on derivaa
Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva).
 6 DIFFERENTIAALIYHTÄLÖISTÄ Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva). Newtonin II:n lain (ma missä Yhtälö dh dt m dh dt F) mukaan mg, on kiihtyvyys ja
6 DIFFERENTIAALIYHTÄLÖISTÄ Esimerkki: Tarkastellaan korkeudella h ht () putoavaa kappaletta, jonka massa on m (ks. kuva). Newtonin II:n lain (ma missä Yhtälö dh dt m dh dt F) mukaan mg, on kiihtyvyys ja
SARJAT JA DIFFERENTIAALIYHTÄLÖT
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 43 0.5 0.4 0.3 0.2 0.1 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.1 0.2 0.3 0.4 0.5 0.1 0.2 0.3 0.4 0.5 0.6 0.7 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 Kuva 12. Esimerkin 4.26(c kuvauksen
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 43 0.5 0.4 0.3 0.2 0.1 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.1 0.2 0.3 0.4 0.5 0.1 0.2 0.3 0.4 0.5 0.6 0.7 1 0.8 0.6 0.4 0.2 0.2 0.4 0.6 0.8 1 Kuva 12. Esimerkin 4.26(c kuvauksen
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Dierentiaaliyhtälöistä Markus Kettunen 4. maaliskuuta 2009 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun yksikäsitteisyydestä.....................
Insinöörimatematiikka D, laskuharjoituksien esimerkkiratkaisut
 Insinöörimatematiikka D, 5.4.06 5. laskuharjoituksien esimerkkiratkaisut. Etsitään homogeenisen vakiokertoimisen lineaarisen differentiaaliyhtälön kaikki ratkaisut (reaalisessa muodossa). y (5) +4y (4)
Insinöörimatematiikka D, 5.4.06 5. laskuharjoituksien esimerkkiratkaisut. Etsitään homogeenisen vakiokertoimisen lineaarisen differentiaaliyhtälön kaikki ratkaisut (reaalisessa muodossa). y (5) +4y (4)
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
10. Toisen kertaluvun lineaariset differentiaaliyhtälöt
 37. Toisen kertaluvun lineaariset differentiaalihtälöt Tarkastelemme muotoa () ( x) + a( x) ( x) + a( x) ( x) = b( x) olevia htälöitä, missä kerroinfunktiot ja oikea puoli ovat välillä I jatkuvia. Edellisen
37. Toisen kertaluvun lineaariset differentiaalihtälöt Tarkastelemme muotoa () ( x) + a( x) ( x) + a( x) ( x) = b( x) olevia htälöitä, missä kerroinfunktiot ja oikea puoli ovat välillä I jatkuvia. Edellisen
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi A. Lepistö alepisto@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2016 M. Hirvensalo V. Junnila A. Lepistö
Luoki?elua: tavallinen vs osi?ais. Osa 11. Differen0aaliyhtälöt. Luoki?elua: kertaluku. Luoki?elua: lineaarisuus 4/13/13
 4/3/3 Osa. Differen0aaliyhtälöt Differen0aaliyhtälö = yhtälö jossa esiintyy jonkin funk0on derivaa?a. Esim: dx = x2 f x + f xy 2 2m d 2 ψ = Eψ dx 2 Luoki?elua: tavallinen vs osi?ais Differen0aaliyhtälöt
4/3/3 Osa. Differen0aaliyhtälöt Differen0aaliyhtälö = yhtälö jossa esiintyy jonkin funk0on derivaa?a. Esim: dx = x2 f x + f xy 2 2m d 2 ψ = Eψ dx 2 Luoki?elua: tavallinen vs osi?ais Differen0aaliyhtälöt
x 4 e 2x dx Γ(r) = x r 1 e x dx (1)
 HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
HY / Matematiikan ja tilastotieteen laitos Todennäköisyyslaskenta IIA, syksy 217 217 Harjoitus 6 Ratkaisuehdotuksia Tehtäväsarja I 1. Laske numeeriset arvot seuraaville integraaleille: x 4 e 2x dx ja 1
3 = Lisäksi z(4, 9) = = 21, joten kysytty lineaarinen approksimaatio on. L(x,y) =
 BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 6, Syksy 2016 1. (a) Olkoon z = z(x,y) = yx 1/2 + y 1/2. Muodosta z:lle lineaarinen approksimaatio L(x,y) siten että approksimaation ja z:n arvot
BM20A5810 Differentiaalilaskenta ja sovellukset Harjoitus 6, Syksy 2016 1. (a) Olkoon z = z(x,y) = yx 1/2 + y 1/2. Muodosta z:lle lineaarinen approksimaatio L(x,y) siten että approksimaation ja z:n arvot
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö
 MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
MS-A010{3,4,5} (ELEC*, ENG*) Differentiaali- ja integraalilaskenta 1 Luento 11: Lineaarinen differentiaaliyhtälö Pekka Alestalo, Jarmo Malinen Aalto-yliopisto, Matematiikan ja systeemianalyysin laitos
2. Viikko. CDH: luvut (s ). Matematiikka on fysiikan kieli ja differentiaaliyhtälöt sen yleisin murre.
 2. Viikko Keskeiset asiat ja tavoitteet: 1. Peruskäsitteet: kertaluku, lineaarisuus, homogeenisuus. 2. Separoituvan diff. yhtälön ratkaisu, 3. Lineaarisen 1. kl yhtälön ratkaisu, CDH: luvut 19.1.-19.4.
2. Viikko Keskeiset asiat ja tavoitteet: 1. Peruskäsitteet: kertaluku, lineaarisuus, homogeenisuus. 2. Separoituvan diff. yhtälön ratkaisu, 3. Lineaarisen 1. kl yhtälön ratkaisu, CDH: luvut 19.1.-19.4.
Insinöörimatematiikka D
 Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Insinöörimatematiikka D M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Matematiikan ja tilastotieteen laitos Turun yliopisto 2015 M. Hirvensalo mikhirve@utu.fi V. Junnila viljun@utu.fi Luentokalvot
Värähdysliikkeet. q + f (q, q, t) = 0. q + f (q, q) = F (t) missä nopeusriippuvuus kuvaa vaimenemista ja F (t) on ulkoinen pakkovoima.
 Torstai 18.9.2014 1/17 Värähdysliikkeet Värähdysliikkeet ovat tyypillisiä fysiikassa: Häiriö oskillaatio Jaksollinen liike oskillaatio Yleisesti värähdysliikettä voidaan kuvata yhtälöllä q + f (q, q, t)
Torstai 18.9.2014 1/17 Värähdysliikkeet Värähdysliikkeet ovat tyypillisiä fysiikassa: Häiriö oskillaatio Jaksollinen liike oskillaatio Yleisesti värähdysliikettä voidaan kuvata yhtälöllä q + f (q, q, t)
Differentiaaliyhtälöt I Ratkaisuehdotuksia, 2. harjoitus, kevät Etsi seuraavien yhtälöiden yleiset ratkaisut (Tässä = d
 Differentiaaliyhtälöt I Ratkaisuehdotuksia,. harjoitus, kevät 016 1. Etsi seuraavien yhtälöiden yleiset ratkaisut (Tässä = d dx ): (a) y + xy = xe x, (b) (1 + x ) y xy = (1 + x ), (c) y sin x y = 1 cos
Differentiaaliyhtälöt I Ratkaisuehdotuksia,. harjoitus, kevät 016 1. Etsi seuraavien yhtälöiden yleiset ratkaisut (Tässä = d dx ): (a) y + xy = xe x, (b) (1 + x ) y xy = (1 + x ), (c) y sin x y = 1 cos
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 7 harjoitus 1 Määritä seuraavien potenssisarjojen suppenemissäteet a) k k x 5)k b) k=1 k x 5)k = k k 1) k ) 1) Suppenemissäteen R käänteisarvo
y = 3x2 y 2 + sin(2x). x = ex y + e y2 y = ex y + 2xye y2
 Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Matematiikan ja tilastotieteen osasto/hy Differentiaaliyhtälöt I Laskuharjoitus 2 mallit Kevät 219 Tehtävä 1. Laske osittaisderivaatat f x = f/x ja f y = f/, kun f = f(x, y) on funktio a) x 2 y 3 + y sin(2x),
Normaaliryhmä. Toisen kertaluvun normaaliryhmä on yleistä muotoa
 Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
Normaaliryhmä Toisen kertaluvun normaaliryhmä on yleistä muotoa x = u(t,x,y), y t I, = v(t,x,y), Funktiot u = u(t,x,y), t I ja v = v(t,x,y), t I ovat tunnettuja Toisen kertaluvun normaaliryhmän ratkaisu
4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt
 4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt 4.1 Homogeeniset lineaariset differentiaaliyhtälöt Homogeeninen yhtälö on muotoa F(x, y,, y (n) ) = 0. (1) Yhtälö on lineaarinen, jos se voidaan
4 Korkeamman kertaluvun lineaariset differentiaaliyhtälöt 4.1 Homogeeniset lineaariset differentiaaliyhtälöt Homogeeninen yhtälö on muotoa F(x, y,, y (n) ) = 0. (1) Yhtälö on lineaarinen, jos se voidaan
Matemaattinen Analyysi
 Vaasan yliopisto, syksy 2016 / ORMS1010 Matemaattinen Analyysi 8. harjoitus, viikko 49 R1 to 12 14 F453 (8.12.) R2 to 14 16 F345 (8.12.) R3 ke 8 10 F345 (7.11.) 1. Määritä funktion f (x) = 1 Taylorin sarja
Vaasan yliopisto, syksy 2016 / ORMS1010 Matemaattinen Analyysi 8. harjoitus, viikko 49 R1 to 12 14 F453 (8.12.) R2 to 14 16 F345 (8.12.) R3 ke 8 10 F345 (7.11.) 1. Määritä funktion f (x) = 1 Taylorin sarja
Dierentiaaliyhtälöistä
 Dierentiaaliyhtälöistä Markus Kettunen 14. helmikuuta 2011 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun olemassaolosta ja yksikäsitteisyydestä...........
Dierentiaaliyhtälöistä Markus Kettunen 14. helmikuuta 2011 1 SISÄLTÖ 1 Sisältö 1 Dierentiaaliyhtälöistä 2 1.1 Johdanto................................. 2 1.2 Ratkaisun olemassaolosta ja yksikäsitteisyydestä...........
Fourier-analyysi, I/19-20, Mallivastaukset, Laskuharjoitus 7
 MS-C14, Fourier-analyysi, I/19- Fourier-analyysi, I/19-, Mallivastaukset, Laskuharjoitus 7 Harjoitustehtävä 7.1. Hetkellä t R olkoon s(t) 1 + cos(4πt) + sin(6πt). Laske tämän 1-periodisen signaalin s Fourier-kertoimet
MS-C14, Fourier-analyysi, I/19- Fourier-analyysi, I/19-, Mallivastaukset, Laskuharjoitus 7 Harjoitustehtävä 7.1. Hetkellä t R olkoon s(t) 1 + cos(4πt) + sin(6πt). Laske tämän 1-periodisen signaalin s Fourier-kertoimet
Epähomogeenisen yhtälön ratkaisu
 Epähomogeenisen yhtälön ratkaisu Lause Olkoot a = a(x), b = b(x) ja f = f(x) jatkuvia funktioita välillä I R ja olkoot y 1 = y 1 (x) ja y 2 = y 2 (x) eräs homogeeniyhtälön y + a(x)y + b(x)y = 0 ratkaisujen
Epähomogeenisen yhtälön ratkaisu Lause Olkoot a = a(x), b = b(x) ja f = f(x) jatkuvia funktioita välillä I R ja olkoot y 1 = y 1 (x) ja y 2 = y 2 (x) eräs homogeeniyhtälön y + a(x)y + b(x)y = 0 ratkaisujen
f (28) L(28) = f (27) + f (27)(28 27) = = (28 27) 2 = 1 2 f (x) = x 2
 BMA581 - Differentiaalilaskenta ja sovellukset Harjoitus 4, Syksy 15 1. (a) Olisiko virhe likimain.5, ja arvio antaa siis liian suuren arvon. (b) Esim (1,1.5) tai (,.5). Funktion toinen derivaatta saa
BMA581 - Differentiaalilaskenta ja sovellukset Harjoitus 4, Syksy 15 1. (a) Olisiko virhe likimain.5, ja arvio antaa siis liian suuren arvon. (b) Esim (1,1.5) tai (,.5). Funktion toinen derivaatta saa
Johdatus diskreettiin matematiikkaan Harjoitus 5, Ratkaise rekursioyhtälö
 Johdatus diskreettiin matematiikkaan Harjoitus 5, 14.10.2015 1. Ratkaise rekursioyhtälö x n+4 2x n+2 + x n 16( 1) n, n N, alkuarvoilla x 1 2, x 2 14, x 3 18 ja x 4 42. Ratkaisu. Vastaavan homogeenisen
Johdatus diskreettiin matematiikkaan Harjoitus 5, 14.10.2015 1. Ratkaise rekursioyhtälö x n+4 2x n+2 + x n 16( 1) n, n N, alkuarvoilla x 1 2, x 2 14, x 3 18 ja x 4 42. Ratkaisu. Vastaavan homogeenisen
Luento 14: Periodinen liike, osa 2
 Luento 14: Periodinen liike, osa 2 Vaimennettu värähtely Pakkovärähtely Resonanssi F ~ µ ~F t F ~ d ~F r m~g Ajankohtaista Poimintoja palautekyselystä Oli mukava luento. Mukavaa että luennoitsija mahdollisti
Luento 14: Periodinen liike, osa 2 Vaimennettu värähtely Pakkovärähtely Resonanssi F ~ µ ~F t F ~ d ~F r m~g Ajankohtaista Poimintoja palautekyselystä Oli mukava luento. Mukavaa että luennoitsija mahdollisti
MS-A0107 Differentiaali- ja integraalilaskenta 1 (CHEM)
 MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
MS-A17 Differentiaali- ja integraalilaskenta 1 CHEM) Laskuharjoitus 4lv, kevät 16 1. Tehtävä: Laske cos x dx a) osittaisintegroinnilla, b) soveltamalla sopivaa trigonometrian kaavaa. Ratkaisu: a) Osittaisintegroinnin
3 TOISEN KERTALUVUN LINEAARISET DY:T
 3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
3 TOISEN KERTALUVUN LINEAARISET DY:T Huomautus epälineaarisista. kertaluvun differentiaaliyhtälöistä Epälineaarisen DY:n ratkaisemiseen ei ole yleismenetelmää. Seuraavat erikoistapaukset voidaan ratkaista
Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 5
 Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 5 1. Kotitehtävä. 2. Lasketaan aluksi korkoa korolle. Jos korkoprosentti on r, ja korko maksetaan n kertaa vuodessa t vuoden ajan, niin kokonaisvuosikorko
Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 5 1. Kotitehtävä. 2. Lasketaan aluksi korkoa korolle. Jos korkoprosentti on r, ja korko maksetaan n kertaa vuodessa t vuoden ajan, niin kokonaisvuosikorko
1 Peruskäsitteet. Dierentiaaliyhtälöt
 Teknillinen korkeakoulu Matematiikka Dierentiaaliyhtälöt Alestalo Tässä monisteessa käydään läpi tavallisiin dierentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Esimerkkejä luennoilla
Teknillinen korkeakoulu Matematiikka Dierentiaaliyhtälöt Alestalo Tässä monisteessa käydään läpi tavallisiin dierentiaaliyhtälöihin liittyviä peruskäsitteitä ja ratkaisuperiaatteita. Esimerkkejä luennoilla
2v 1 = v 2, 2v 1 + 3v 2 = 4v 2.. Vastaavasti ominaisarvoa λ 2 = 4 vastaavat ominaisvektorit toteuttavat. v 2 =
 TKK, Matematiikan laitos Pikkarainen/Tikanmäki Mat-1.1320 Matematiikan peruskurssi K2 Harjoitus 12, A=alku-, L=loppuviikko, T= taulutehtävä, P= palautettava tehtävä, W= verkkotehtävä 21. 25.4.2008, viikko
TKK, Matematiikan laitos Pikkarainen/Tikanmäki Mat-1.1320 Matematiikan peruskurssi K2 Harjoitus 12, A=alku-, L=loppuviikko, T= taulutehtävä, P= palautettava tehtävä, W= verkkotehtävä 21. 25.4.2008, viikko
1 Di erentiaaliyhtälöt
 Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
Taloustieteen mat.menetelmät syksy 2017 materiaali II-5 1 Di erentiaaliyhtälöt 1.1 Skalaariyhtälöt Määritelmä: ensimmäisen kertaluvun di erentiaaliyhtälö on muotoa _y = F (y; t) oleva yhtälö, missä _y
Luento 13: Periodinen liike. Johdanto Harmoninen värähtely Esimerkkejä F t F r
 Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Luento 13: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä θ F t m g F r 1 / 27 Luennon sisältö Johdanto Harmoninen värähtely Esimerkkejä 2 / 27 Johdanto Tarkastellaan jaksollista liikettä (periodic
Harjoitus Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia:
 Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Differentiaaliyhtälöt, Kesä 216 Harjoitus 2 1. Etsi seuraavien autonomisten yhtälöiden kriittiset pisteet ja tutki niiden stabiliteettia: (a) y = (2 y) 3, (b) y = (y 1) 2, (c) y = 2y y 2. 2. Etsi seuraavien
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Kvanttifysiikan perusteet 207 Harjoitus 2: ratkaisut Tehtävä Osoita hyödyntäen Maxwellin yhtälöitä, että tyhjiössä magneettikenttä ja sähkökenttä toteuttavat aaltoyhtälön, missä aallon nopeus on v = c.
Insinöörimatematiikka D, laskuharjoituksien esimerkkiratkaisut
 Insinöörimatematiikka D, 406 6 laskuharjoituksien esimerkkiratkaisut Ratkaistaan differentiaaliyhtälö y = y () Tässä = d dy eli kyseessä on lineaarinen kertaluvun differentiaaliyhtälö: Yhtälön () homogenisoidulle
Insinöörimatematiikka D, 406 6 laskuharjoituksien esimerkkiratkaisut Ratkaistaan differentiaaliyhtälö y = y () Tässä = d dy eli kyseessä on lineaarinen kertaluvun differentiaaliyhtälö: Yhtälön () homogenisoidulle
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi
 Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
Pakotettu vaimennettu harmoninen värähtelijä Resonanssi Tällä luennolla tavoitteena Mikä on pakkovoiman aiheuttama vaikutus vaimennettuun harmoniseen värähtelijään? Mikä on resonanssi? Kertaus: energian
2 1/ /2 ; (a) Todista, että deg P (x)q(x) = deg P (x) + deg Q(x). (b) Osoita, että jos nolla-polynomille pätisi. deg 0(x) Z, Z 10 ; Z 10 [x];
![2 1/ /2 ; (a) Todista, että deg P (x)q(x) = deg P (x) + deg Q(x). (b) Osoita, että jos nolla-polynomille pätisi. deg 0(x) Z, Z 10 ; Z 10 [x]; 2 1/ /2 ; (a) Todista, että deg P (x)q(x) = deg P (x) + deg Q(x). (b) Osoita, että jos nolla-polynomille pätisi. deg 0(x) Z, Z 10 ; Z 10 [x];](/thumbs/97/131422104.jpg) 802656S ALGEBRALLISET LUVUT Harjoituksia 2017 1. Näytä, että (a) (b) (c) (d) (e) 2 1/2, 3 1/2, 2 1/3 ; 2 1/2 + 3 1/2 ; 2 1/3 + 3 1/2 ; e iπ/m, m Z \ {0}; sin(π/m), cos(π/m), tan(π/m), m Z \ {0}; ovat algebrallisia
802656S ALGEBRALLISET LUVUT Harjoituksia 2017 1. Näytä, että (a) (b) (c) (d) (e) 2 1/2, 3 1/2, 2 1/3 ; 2 1/2 + 3 1/2 ; 2 1/3 + 3 1/2 ; e iπ/m, m Z \ {0}; sin(π/m), cos(π/m), tan(π/m), m Z \ {0}; ovat algebrallisia
Matemaattiset apuneuvot II, harjoitus 5
 Matemaattiset apuneuvot II, harjoitus 5 K. Tuominen 29. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina 3.12. kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi
Matemaattiset apuneuvot II, harjoitus 5 K. Tuominen 29. marraskuuta 2017 Palauta ratkaisusi Moodlessa.pdf tiedostona maanantaina 3.12. kello 10:15 mennessä. Merkitse vastauspaperiin laskuharjoitusryhmäsi
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
k = 1,...,r. L(x 1 (t), x
 Mat-2.148 Dynaaminen optimointi Mitri Kitti/Ilkka Leppänen Mallivastaukset, kierros 6 1. Johdetaan välttämättömät ehdot funktionaalin J(y) = t g(y(t), ẏ(t),..., dr y(t), t) dt dt r ekstremaalille, kun
Mat-2.148 Dynaaminen optimointi Mitri Kitti/Ilkka Leppänen Mallivastaukset, kierros 6 1. Johdetaan välttämättömät ehdot funktionaalin J(y) = t g(y(t), ẏ(t),..., dr y(t), t) dt dt r ekstremaalille, kun
H5 Malliratkaisut - Tehtävä 1
 H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa
H5 Malliratkaisut - Tehtävä Eelis Mielonen 30. syyskuuta 07 a) 3a (ax + b)3/ + C b) a cos(ax + b) + C a) Tässä tehtävässä päästään harjoittelemaan lukiosta tuttua integrointimenetelmää. Ensimmäisessä kohdassa
DI matematiikan opettajaksi: Täydennyskurssi, kevät 2010 Luentorunkoa ja harjoituksia viikolle 13: ti klo 13:00-15:30 ja to 1.4.
 DI matematiikan opettajaksi: Täydennyskurssi, kevät Luentorunkoa ja harjoituksia viikolle 3: ti 33 klo 3:-5:3 ja to 4 klo 9:5-: Käydään läpi differentiaaliyhtälöitä Määritelmä Olkoon A R n n (MatLab:ssa
DI matematiikan opettajaksi: Täydennyskurssi, kevät Luentorunkoa ja harjoituksia viikolle 3: ti 33 klo 3:-5:3 ja to 4 klo 9:5-: Käydään läpi differentiaaliyhtälöitä Määritelmä Olkoon A R n n (MatLab:ssa
Ei-inertiaaliset koordinaatistot
 orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
orstai 25.9.2014 1/17 Ei-inertiaaliset koordinaatistot Tarkastellaan seuraavaa koordinaatistomuunnosta: {x} = (x 1, x 2, x 3 ) {y} = (y 1, y 2, y 3 ) joille valitaan kantavektorit: {x} : (î, ĵ, ˆk) {y}
Oletetaan sitten, että γ(i) = η(j). Koska γ ja η ovat Jordan-polku, ne ovat jatkuvia injektiivisiä kuvauksia kompaktilta joukolta, ja määrittävät
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 18 Harjoitus 6 Ratkaisuehdotukset Tehtävä 1. Osoita, että sileille Jordan-poluille on voimassa : I R n ja : J R n (I) = (J) jos ja vain
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi II, syksy 18 Harjoitus 6 Ratkaisuehdotukset Tehtävä 1. Osoita, että sileille Jordan-poluille on voimassa : I R n ja : J R n (I) = (J) jos ja vain
MS-A0104 Differentiaali- ja integraalilaskenta 1 (ELEC2) MS-A0106 Differentiaali- ja integraalilaskenta 1 (ENG2)
 MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
MS-A4 Differentiaali- ja integraalilaskenta (ELEC2) MS-A6 Differentiaali- ja integraalilaskenta (ENG2) Harjoitukset 3L, syksy 27 Tehtävä. a) Määritä luvun π likiarvo käyttämällä Newtonin menetelmää yhtälölle
a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. 8 3 + 4 2 0 = 16 3 = 3 1 3.
 Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
Integraalilaskenta. a) Mikä on integraalifunktio ja miten derivaatta liittyy siihen? Anna esimerkki. b) Mitä määrätty integraali tietyllä välillä x tarkoittaa? Vihje: * Integraali * Määrätyn integraalin
RCL-vihtovirtapiiri: resonanssi
 CL-vihtovirtapiiri: resonanssi Olkoon tarkastelun kohteena tavallinen LC-vaihtovirtapiiri. Piirissä on kolme komponenttia, ohmin vastus, L henryn induktanssi ja C faradin kapasitanssi. Piiriin syötettyyn
CL-vihtovirtapiiri: resonanssi Olkoon tarkastelun kohteena tavallinen LC-vaihtovirtapiiri. Piirissä on kolme komponenttia, ohmin vastus, L henryn induktanssi ja C faradin kapasitanssi. Piiriin syötettyyn
Matemaattinen Analyysi
 Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 8. harjoitus 1. Ratkaise y + y + y = x. Kommentti: Yleinen työlista ratkaistaessa lineaarista, vakiokertoimista toisen kertaluvun differentiaaliyhtälöä
Vaasan yliopisto, 009-010 / ORMS1010 Matemaattinen Analyysi 8. harjoitus 1. Ratkaise y + y + y = x. Kommentti: Yleinen työlista ratkaistaessa lineaarista, vakiokertoimista toisen kertaluvun differentiaaliyhtälöä
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Momenttiemäfunktio ja karakteristinen funktio
 Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
Ilkka Mellin Todennäköisyyslaskenta Osa : Satunnaismuuttujat ja todennäköisyysjakaumat Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (7) 1 Momenttiemäfunktio ja karakteristinen funktio
(a) Järjestellään yhtälöitä siten, että vasemmalle puolelle jää vain y i ja oikealle puolelle muut
 BM0A5830 Differentiaalihtälöiden peruskurssi Harjoitus 7, Kevät 07 Päivitksiä: Tehtävän b tehtävänantoa korjattu, tehtävän 5 vastaus korjattu. b tehtävänantoa sujuvoitettu. Vastauksia lisätt.. Monasti
BM0A5830 Differentiaalihtälöiden peruskurssi Harjoitus 7, Kevät 07 Päivitksiä: Tehtävän b tehtävänantoa korjattu, tehtävän 5 vastaus korjattu. b tehtävänantoa sujuvoitettu. Vastauksia lisätt.. Monasti
Integroimistekniikkaa Integraalifunktio
 . Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
. Integroimistekniikkaa.. Integraalifunktio 388. Vertaa funktioiden ln ja ln, b) arctan ja arctan + k k, c) ln( + 2 ja ln( 2, missä a >, derivaattoja toisiinsa. Tutki funktioiden erotusta muuttujan eri
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Johdatus todennäköisyyslaskentaan Momenttiemäfunktio ja karakteristinen funktio TKK (c) Ilkka Mellin (5) 1 Momenttiemäfunktio ja karakteristinen funktio Momenttiemäfunktio Diskreettien jakaumien momenttiemäfunktioita
Differentiaaliyhtälöt I, kevät 2017 Harjoitus 3
 Differentiaaliyhtälöt I, kevät 07 Harjoitus 3 Heikki Korpela. helmikuuta 07 Tehtävä. Ratkaise alkuarvo-ongelmat a) y + 4y e x = 0, y0) = 4 3 b) Vastaus: xy + y = x 3, y) =.. a) Valitaan integroivaksi tekijäksi
Differentiaaliyhtälöt I, kevät 07 Harjoitus 3 Heikki Korpela. helmikuuta 07 Tehtävä. Ratkaise alkuarvo-ongelmat a) y + 4y e x = 0, y0) = 4 3 b) Vastaus: xy + y = x 3, y) =.. a) Valitaan integroivaksi tekijäksi
Luento 11: Periodinen liike
 Luento 11: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä ~F t m~g ~F r Konseptitesti 1 Tehtävänanto Kuvassa on jouseen kytketyn massan sijainti ajan funktiona. Kuvaile
Luento 11: Periodinen liike Johdanto Harmoninen värähtely Esimerkkejä Laskettuja esimerkkejä ~F t m~g ~F r Konseptitesti 1 Tehtävänanto Kuvassa on jouseen kytketyn massan sijainti ajan funktiona. Kuvaile
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018
 BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
BM20A5840 Usean muuttujan funktiot ja sarjat Harjoitus 7, Kevät 2018 Tehtävä 8 on tällä kertaa pakollinen. Aloittakaapa siitä. 1. Kun tässä tehtävässä sanotaan sopii mahdollisimman hyvin, sillä tarkoitetaan
Numeeriset menetelmät TIEA381. Luento 12. Kirsi Valjus. Jyväskylän yliopisto. Luento 12 () Numeeriset menetelmät / 33
 Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
Numeeriset menetelmät TIEA381 Luento 12 Kirsi Valjus Jyväskylän yliopisto Luento 12 () Numeeriset menetelmät 25.4.2013 1 / 33 Luennon 2 sisältö Tavallisten differentiaaliyhtälöiden numeriikasta Rungen
x (t) = 2t ja y (t) = 3t 2 x (t) + + y (t) Lasketaan pari käyrän arvoa ja hahmotellaan kuvaaja: A 2 A 1
 BM2A582 Integraalilaskenta ja sovellukset Harjoitus 6, Kevät 26 Kaikissa tehtävissä tärkeintä ja riittävää on saada oikea lauseke aikaiseksi. Useissa tehtävissä integraalit eivät tosin ole niin vaikeita
BM2A582 Integraalilaskenta ja sovellukset Harjoitus 6, Kevät 26 Kaikissa tehtävissä tärkeintä ja riittävää on saada oikea lauseke aikaiseksi. Useissa tehtävissä integraalit eivät tosin ole niin vaikeita
Tampere University of Technology
 Tampere University of Technology EDE- Introduction to Finite Element Method. Exercise 3 Autumn 3.. Solve the deflection curve v(x) exactly for the beam shown y,v q v = q z, xxxx x E I z Integroidaan yhtälö
Tampere University of Technology EDE- Introduction to Finite Element Method. Exercise 3 Autumn 3.. Solve the deflection curve v(x) exactly for the beam shown y,v q v = q z, xxxx x E I z Integroidaan yhtälö
Mat Dynaaminen optimointi, mallivastaukset, kierros Johdetaan välttämättömät ehdot funktionaalin. g(y(t), ẏ(t),...
 Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 6 1. Johdetaan välttämättömät ehdot funktionaalin J(y) = g(y(t), ẏ(t),..., dr y(t), t) dt dt r ekstremaalille, kun ja t f ovat kiinteitä ja tiedetään
Mat-2.148 Dynaaminen optimointi, mallivastaukset, kierros 6 1. Johdetaan välttämättömät ehdot funktionaalin J(y) = g(y(t), ẏ(t),..., dr y(t), t) dt dt r ekstremaalille, kun ja t f ovat kiinteitä ja tiedetään
Luento 2: Liikkeen kuvausta
 Luento 2: Liikkeen kuvausta Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Luennon sisältö Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Liikkeen ratkaisu kiihtyvyydestä
Luento 2: Liikkeen kuvausta Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Luennon sisältö Suoraviivainen liike integrointi Kinematiikkaa yhdessä dimensiossa Liikkeen ratkaisu kiihtyvyydestä
Matematiikan tukikurssi
 Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
Matematiikan tukikurssi Kertausluento 2. välikokeeseen Toisessa välikokeessa on syytä osata ainakin seuraavat asiat:. Potenssisarjojen suppenemissäde, suppenemisväli ja suppenemisjoukko. 2. Derivaatan
A B = 100, A = B = 0. D = 1.2. Ce (1.2 D. C (t D) 0, t < 0. t D. )} = Ae πjf D F{Π( t D )} = ADe πjf D sinc(df)
 ELEC-A7 Signaalit ja järjestelmät Syksy 5 Tehtävä 3. a) Suoran tapauksessa ratkaistaan kaksi tuntematonta termiä, A ja B, joten tarvitaan kaksi pistettä, jotka ovat pisteet t = ja t =.. Saadaan yhtälöpari
ELEC-A7 Signaalit ja järjestelmät Syksy 5 Tehtävä 3. a) Suoran tapauksessa ratkaistaan kaksi tuntematonta termiä, A ja B, joten tarvitaan kaksi pistettä, jotka ovat pisteet t = ja t =.. Saadaan yhtälöpari
Kuva 1: Funktion f tasa-arvokäyriä. Ratkaisu. Suurin kasvunopeus on gradientin suuntaan. 6x 0,2
 HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
HY / Matematiikan ja tilastotieteen laitos Vektorianalyysi I, syksy 018 Harjoitus Ratkaisuehdotukset Tehtävä 1. Olkoon f : R R f(x 1, x ) = x 1 + x Olkoon C R. Määritä tasa-arvojoukko Sf(C) = {(x 1, x
. Mitä olisivat y 1 ja y 2, jos tahdottaisiin y 1 (0) = 2 ja y 2 (0) = 0? x (1) = 0,x (2) = 1,x (3) = 0. Ratkaise DY-ryhmä y = Ay.
 BMA583 Differentiaaliyhtälöiden peruskurssi Harjoitus 6, Kevät 7. Oletetaan että saaliskalapopulaation lisääntymisnopeus (ilman kuolemia on suoraan verrannollinen kalapopulaation (merkataan tätä symbolilla
BMA583 Differentiaaliyhtälöiden peruskurssi Harjoitus 6, Kevät 7. Oletetaan että saaliskalapopulaation lisääntymisnopeus (ilman kuolemia on suoraan verrannollinen kalapopulaation (merkataan tätä symbolilla
Insinöörimatematiikka D
 Insinöörimatematiikka D Demonstraatio 7, 6.7... Ratkaise dierentiaalihtälöpari = = Vastaus: DY-pari voidaan esittää muodossa ( = Matriisin ominaisarvot ovat i ja i ja näihin kuuluvat ominaisvektorit (
Insinöörimatematiikka D Demonstraatio 7, 6.7... Ratkaise dierentiaalihtälöpari = = Vastaus: DY-pari voidaan esittää muodossa ( = Matriisin ominaisarvot ovat i ja i ja näihin kuuluvat ominaisvektorit (
Differentiaaliyhtälöt II, kevät 2017 Harjoitus 5
 Differentiaaliyhtälöt II, kevät 27 Harjoitus 5 Heikki Korpela 26. huhtikuuta 27 Tehtävä 2. Määrää seuraavan autonomisen systeemin kriittiset pisteet, ratakäyrät ja luonnostele systeemin aikakehitys: (t)
Differentiaaliyhtälöt II, kevät 27 Harjoitus 5 Heikki Korpela 26. huhtikuuta 27 Tehtävä 2. Määrää seuraavan autonomisen systeemin kriittiset pisteet, ratakäyrät ja luonnostele systeemin aikakehitys: (t)
Muuttujan vaihto. Viikon aiheet. Muuttujan vaihto. Muuttujan vaihto. ) pitää muistaa lausua t:n avulla. Integroimisen työkalut: Kun integraali
 Viikon aiheet Integroimisen työkalut: Rationaalifunktioiden jako osamurtoihin Rekursio integraaleissa CDH: Luku 4, Prujut206: Luvut 4-4.2.5, Prujut2008: s. 89-6 Kun integraali h(x) ei näytä alkeisfunktioiden
Viikon aiheet Integroimisen työkalut: Rationaalifunktioiden jako osamurtoihin Rekursio integraaleissa CDH: Luku 4, Prujut206: Luvut 4-4.2.5, Prujut2008: s. 89-6 Kun integraali h(x) ei näytä alkeisfunktioiden
Kvanttifysiikan perusteet 2017
 Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
Kvanttifysiikan perusteet 7 Harjoitus 3: ratkaisut Tehtävä Tarkastellaan äärettömän syvässä laatikossa (väli [, L) olevaa hiukkasta. Kirjoita energiatiloja E n vastaavat aaltofunktiot muodossa ψ n (x,
Kompleksiluvun logaritmi: Jos nyt z = re iθ = re iθ e in2π, missä n Z, niin saadaan. ja siihen vaikuttava
 Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Kompleksiluvun logaritmi: ln z = w z = e w Jos nyt z = re iθ = re iθ e inπ, missä n Z, niin saadaan w = ln z = ln r + iθ + inπ, n Z Logaritmi on siis äärettömän moniarvoinen funktio. Helposti nähdään että
Useita oskillaattoreita yleinen tarkastelu
 Useita oskillaattoreita yleinen tarkastelu Useita riippumattomia vapausasteita q i, i =,..., n ja potentiaali vastaavasti U(q, q 2,..., q n). Tasapainoasema {q 0, q0 2,..., q0 n} q 0 Käytetään merkintää
Useita oskillaattoreita yleinen tarkastelu Useita riippumattomia vapausasteita q i, i =,..., n ja potentiaali vastaavasti U(q, q 2,..., q n). Tasapainoasema {q 0, q0 2,..., q0 n} q 0 Käytetään merkintää
Vastaus: 10. Kertausharjoituksia. 1. Lukujonot lim = lim n + = = n n. Vastaus: suppenee raja-arvona Vastaus:
 . Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
. Koska F( ) on jokin funktion f ( ) integraalifunktio, niin a+ a f() t dt F( a+ t) F( a) ( a+ ) b( a b) Vastaus: Kertausharjoituksia. Lukujonot 87. + n + lim lim n n n n Vastaus: suppenee raja-arvona
