5 Platonin kappaleet ja niiden symmetriaryhmät
|
|
|
- Heikki Nurmi
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 5 Platonin kappaleet ja niiden symmetriaryhmät Ensimmäisissä luvussa käsittelimme ryhmäteorian peruskonsepteja niin kuin ne on ja 1900-luvuilla määritelty. Nyt palaamme ajassa taaksepäin, ja tutkimme, mitä antiikin kreikkalaiset tiesivät symmetriasta. Pythagoras tunsi kolme säännöllistä kolmiulotteista kappaletta. Kuutio ja tetraedri olivat hyvin tuttuja, ja näiden perusteella hän myöhemmin konstruoi myos dodekaedrin. Platon tai hänen oppilaansa lisäsivät joukkoon oktaedrin ja ikosaedrin, sekä todistivat, että nämä ovat ainoat säännölliset monitahokkaat kolmessa ulottuvuudessa. On tavallaan mielenkiintoista, että Pythagoras ei konstruoinut oktaedria, sillä se on kuitenkin kuution duaalikappale. Määritelmä 5.1. Platonin kappale on säännöllinen monitahokas, jonka tahkot ovat keskenään yhteneviä säännöllisiä monikulmioita, ja jonka jokaisesta kärjestä lähtee yhtä monta särmää. Lause 5.2. Platonin kappaleita on korkeintaan viisi. Todistus. Oletetaan, että säännöllinen monikulmio on n-kulmio, ja jokaisesta kärjestä lähtee k särmää. Todistamme, että mahdollisia pareja (n, k) on korkeintaan viisi. Merkitään säännöllisen n-kulmion sisäkulmaa α:lla, ja tämän komplementtikulmaa β:lla. Tällöin β = 2π n, joten α = π β = π(1 2 n ). Jokaisesta kärjestä lähtee k särmää. Koska nämä särmät eivät kohtaa tasossa, saamme epäyhtälön kα < 2π, josta seuraa kπ(1 2 n ) < 2π k(n 2) < 2n (k 2)(n 2) < 4. Koska monitahokas on kolmiulotteinen, k, n 3. Ainoat kokonaislukuparit (n, k), jotka toteuttavat ylläolevan epäyhtälön ovat (3, 3), (3, 4), (4, 3), (3, 5), (5, 3). Merkitään K monitahokkaan kärkien määrää, S särmien lukumäärää ja T tahkojen lukumäärää. Kokoamme taulukkoon ylläolevat viisi lukuparia, sekä kärkien, särmien ja tahkojen määrä kullekin monitahokkaalle. 29
2 Taulukko 5: Platonin kappaleet nimi K S T n k tetraedri kuutio oktaedri dodekaedri ikosaedri Huomautus 5.3. Platonin kappaleet toteuttavat Eulerin kaavan K S + T = 2. Tämän näkee helpohkosti projisoimalla kunkin kappaleen tasoon planaariverkoksi. Koska Platonin kappaleet elävät kolmiuloitteisessa avaruudessa on niiden symmetriaryhmä äärellinen GL 3 (R):n aliryhmä. Symmetriaryhmä ei myöskään saa muuttaa etäisyyksiä joten ainoastaan alkiot, joiden determinantti on ±1 kelpaavat. Jos rajoitamme etsintämme vain kiertosymmetrioihin, voimme tutkia vain SL 3 (R):n äärellisiä aliryhmiin. Helpoiten hahmotamme nämä ryhmät kuitenkin ryhmän toimintojen ja ratojen avulla kuten alkusanoissa mainittiin. Joten ennen kuin pääsemme käsiksi ryhmiin, tarvitsemme lisää teoriaa. Jotkut teistä varmasti oppivat nämä asiat jo Algebra II:ssa, mutta kertaus ei liene pahitteeksi. Esimerkkinä toiminnasta katsokaamme säännöllisiä monitahokkaita seuraavasta näkökulmasta. Huomaamme yleisesti, että mikä tahansa symmetria, jonka determinantti on 1, on kierto jonkun suoran L ympäri. Jos symmetria on epätriviaali, tämä suora L leikkaa Platonin kappaleen pinnan täsmälleen kahdessa pisteessä P ja Q. Mitä vaihtoehtoja on pisteelle P? Oletetaan että P on jollain tietyllä sivutahkolla. Silloin se voi olla kärjessä, särmällä tai tahkon sisäpinnassa. Jos P on särmällä, mutta ei kärjessä, huomaamme ensin, että kiertosymmetria kiinnittää sekä pisteen P että särmän, jolla P sijaitsee, mutta se vaihtaa särmän päissä olevat kärjet (muussa tapauksessa symmetria ei ole kierto), joten P :n pitää olla särmän keskipisteessä. Samalla tavalla voimme argumentoida, että jos P on tahkon sisäpinnalla, on sen pakko olla tahkon keskipisteessä. Määritelmä 5.4. Olkoon G ryhmä ja Ω joukko. Ryhmä G toimii joukossa Ω, jos on olemassa kuvaus Ω G Ω, jossa (ω, g) ω g joka toteuttaa seuraavat ehdot: (i) ω 1=ω 30
3 (ii) ω (gh) = (ω g) h Tätä kutsutaan vasemmaksi toiminnaksi, koska kohdassa (ii) vasemmanpuoleinen alkio toimii ensin. Oikeanpuoleinen toiminta määritellään vastaavalla tavalla. Lemma 5.5. Toimikoon G joukossa Ω. Tällöin jokainen g G indusoi kuvauksen φ g : Ω Ω, joka määrittää joukon Ω permutaation. Tämän lisäksi, kuvaus α α g φ : G Sym(Ω) g φ g on ryhmähomomorfismi. Tätä kutsutaan myös G:n permutaatioesitykseksi. 1 Todistus. On selvää, että kuvauksen φ g käänteiskuvaus on φ g 1, koska jokaiselle α Ω pätee α(φ g φ g 1) = (α g) g 1 = α g g 1 = α 1=α. Olemme todistaneet, että kuvaus φ g :Ω Ω on bijektio, ja näin ollen se on permutaation määritelmän mukaan Ω:n permutaatio. Ryhmän toiminnan määritelmän kohdasta (i) seuraa, että φ(g 1 g 2 )=φ g1 g 2 = φ g1 φ g2 = φ(g 1 )φ(g 2 ), joten φ : G Sym(Ω) on homomorfismi. Tehtävä Olkoon G ryhmä, G toimii itsessään konjugaation kautta. Tarkemmin, kiinnitetään h G, nyt jokaiselle g G toiminta määritellään g h 1 gh kautta. Osoita, että tämä on toiminta. Onko tämä vasen vai oikea? Jos haluamme määritellä vastakkaistoiminnan, mikä on oikea määritelmä? 1 Permutaatioesitykset ovat tärkeitä esitysteoriassa. Valitettavasti tällä kurssilla meillä ei ole aikaa perehtyä ryhmien esitysteoriaan. Jos joku haluaa, voi tästä aiheesta laatia esseen. 31
4 2. Olkoon GL n (R) kääntyvien n n-matriisien ryhmä. Määrittele GL n (R):lle luonnollinen toiminta avaruudessa R n ja osoita, että tämä on toiminta. Miten toimii ortogonaalisten matriisien ryhmä O n (R) avaruudessa R n. 3. G toimii omissa sivuluokissaan. Tarkemmin, olkoon H G, ja olkoon (G : H) oikeitten sivuluokkien joukko. Määrittelemme toiminnan Osoita, että tämä on toiminta. Hx g = Hxg. 4. Olkoon D 2n diedriryhmä. Osoita, että tämä toimii säännöllisen n- kulmion symmetriaryhmänä. Monet ryhmäteorian lauseet on helppo todistaa toimintojen avulla. Tässä yksi esimerkki klassisesta lauseesta. Lause 5.6 (Cayley). Jokainen äärellinen ryhmä G, jonka kertaluku on pienempi tai yhtäsuuri kuin n, on ryhmän S n aliryhmä. Todistus. Jos k n, on S k S n. Todistukseen riittää, että oletamme G:n kertaluvun olevan tasan n. Nyt meidän täytyy enää osoittaa, että ryhmä, jonka kertaluku on n on symmetrisen ryhmän S n aliryhmä. Voimme määritellä G-toiminnan triviaalin aliryhmän {1} sivuluokissa. Näitä sivuluokkia on luonnollisesti n kappaletta ja ne vastaavat G:n alkioita. Yllä olevan lemman perusteella toiminta määrittelee homomorfismin φ : G S n. Homomorfismin ytimeen kuuluvat sellaiset G:n alkiot, jotka kiinnittävät jokaisen sivuluokan. Näin ollen vain ykkösalkio kuuluu ytimeen ja kuvaus φ on injektio. Tästä seuraa ensimmäisen isomorfialauseen perusteella G = G/{1} = G/Kerφ = Imφ S n. Olkoon H G. Jos G toimii joukossa Ω, myös H määrittää toiminnan joukossa Ω. Tämä aliryhmän toiminta hajottaa joskus Ω:n palasiksi. Kutsumme tätä toimintaa H-toiminnaksi. Määritelmä 5.7. Olkoon G ryhmä, ja toimikoon se joukossa Ω. Olkoon H G. Kun ω Ω, silloin ω:n rata H-toiminnassa on orb H (ω) ={ω g : g H} 32
5 Propositio 5.8. Kun G toimii joukossa Ω ja H G, joukko Ω hajoaa H- ratojen pistevieraaksi unioniksi. Todistus. Tehtävä. Käytiin luennolla läpi. Määritelmä 5.9. Kutsumme ryhmän G toimintaa joukossa Ω transitiiviseksi, jos jokaiselle ω 1,ω 2 Ω, on olemassa g G ja ω 1 g = ω 2. Jos jokaiselle parille pätee sama kuin yllä, kutsumme toimintaa 2- transitiiviseksi, ja edelleen n-transitiiviseksi. Määritelmä Toimikoon ryhmä G joukossa Ω, ja olkoon ω Ω. Alkion ω vakauttaja on joukko G ω = {g G : ω g = ω}. Määritelmä Ryhmän G toimintaa joukossa Ω kutsutaan uskolliseksi, jos ainoa alkio g G, jolle pätee ω g = ω kaikille ω Ω on g =1. Tehtävä Osoita, että G ω on G:n aliryhmä. 2. Olkoon ω = α g, kun G toimii Ω:ssa. Osoita, että G ω ja G α ovat toistensa konjugaatteja. 3. Toimikoon G joukossa Ω = G konjugoimalla. Osoita, että alkion ω vakauttaja on alkion keskittäjä. 4. Osoita, että G:n toiminta oikeissa sivuluokissaan on transitiivinen, ja määrittele sivuluokkien H ja Hg vakauttajat. Määritelmä Toiminnan ydin on G (Ω) = α Ω G α. Tehtävä 31. Osoita, että toiminta on uskollinen, jos toiminnan ydin on triviaali. Yksi hyödyllisimmistä lausesta ryhmäteoriassa on rata-vakauttajalause. Lause Olkoon G äärellinen ryhmä ja Ω äärellinen joukko. Kun G toimii Ω:ssa, jokaiselle α Ω, on voimassa Orb G (α) = G : Stab G (α). Määritellään ensin morfismi kahden toiminnan välillä. 33
6 Määritelmä Kun ryhmä G toimii joukoissa Ω ja kuvaus on G-morfismi, jos ψ :Ω (α Ω g)ψ = αψ g, kaikille α Ω,g G. Kuvausta ψ kutsutaan G-isomorfismiksi, jos se on bijektiivinen. Tämän jälkeen rata-vakauttajalause seuraa seuraavasta lemmasta. Lemma Jos G toimii transitiivisesti Ω:ssa ja ω Ω. Pisteen ω vakauttajaa merkitään G ω. Silloin G:n toiminta Ω:ssa ja G:n toiminta G ω :n sivuluokissa (G : G ω ) ovat isomorfisia. Todistus. Määritellään kuvaus ψ :Ω (G : G ω ) lähettämällä ωx G ω x. Tämä kuvaus on hyvinmääritelty ja injektiivinen, sillä ωx 1 = ωx 2 ωx 1 x 1 2 = ω x 1 x 1 2 G ω G ω x 1 = G ω x 2. Kuvaus on myös selvästi surjektiivinen. Lopuksi tarkistetaan, että se on G- morfismi: ((ωx) g)ψ =(ω xg)ψ = G ω xg =(G ω x)g =(ωx)ψ g kaikille pisteille ωx Ω. Todistetaan nyt rata-vakauttajalause. Todistus. Olkoon α Ω, ja toimikoon G joukossa Orb G (α). Tämä toiminta on luonnollisesti transitiivinen, sillä mikä tahansa radan alkio αg 1 voidaan kuvata mihin tahansa toiseen saman radan alkioon αg 2 :n käyttämällä alkiota g1 1 g 2. Nyt edellisen lemman perusteella G:n toiminnat radalla Orb G (α) ja G α :n sivuluokissa ovat isomorfiset, joten näiden kahden joukon välillä on bijektiivinen kuvaus. Tästä seuraa Orb(α) = [G : G α ]. Yksi sovellutus rata-vakauttajalauseelle on Cauchyn lause. Tämä voidaan nähdä eräänlaisena Lagrangen lauseen käänteistuloksena. Lause 5.16 (Cauchyn lause). Jakakoon p ryhmän kertaluvun G. Tällöin G sisältää alkion, jonka kertaluku on p. 34
7 Todistus. Määritellään Ω= {(x 1,..., x p ):x i G ja x 1 x 2... x p =1}. Olkoon H = σ = C p, missä σ toimii Ω:ssa σ :(x 1,..., x p ) (x 2,..., x p,x 1 ). Rata-vakauttajalause sanoo, että H-radan mahtavuus jakaa H:n kertaluvun. Niinpä saamme, että H-radan mahtavuus on joko 1 tai p. Lisäksi Ω = G p 1, koska voimme valita ensimmäiset p 1 alkiota vapaasti. Nyt p jakaa G :n, jakaa p myös Ω :n. Siispä Ω on H-ratojen pistevieras unioni, ja kukin radoista on joko kokoa p tai 1. Huomaa, että (1, 1,..., 1) muodostaa oman ratansa, joten ainakin yksi rata on mahtavuutta yksi. Olkoon kokoa yksi olevien ratojen määrä a ja kokoa p olevien ratojen lukumäärä b. Silloin Ω = a 1+b p. Koska p jakaa Ω :n, jakaa p myös a:n. Niinpä on olemassa ainakin p rataa, joiden koko on 1. Jotta α:n rata olisi kokoa 1, täytyy olla niin, että x 1 = x 2 = = x p 1. Mutta x 1 x 2 x p =1, joten x p 1 =1ja olemme löytäneet alkion, jonka kertaluku on p. Määritelmä Ryhmän G keskus on joukko {g G : gh = hg h G}. Tästä huomaamme heti, että ykkösalkio kuuluu ryhmän keskukseen. Toisinaan ryhmän keskus on kuitenkin ykkösalkiota suurempi. Tehtävä 32. (i) Osoita, että keskus on normaali aliryhmä. (ii) Imitoimalla ylläolevaa todistusta, osoita, että p-ryhmän keskus on epätriviaali (suurempi kuin ykkösalkio). Tässä tarvittava toiminta on konjugaatiotoiminta. Rata-vakauttajalauseen avulla pystymme nyt tutkimaan Platonin kappaleiden symmetriaryhmiä tarkemmin. 5.1 Ryhmä S 4 Tutkimme ryhmää S 4. Tämä on neljän alkion joukon permutaatioryhmä. Neljä alkiota voidaan permutoida yhteensä 4! = 24 eri tavalla. Niinpä joukossa S 4 on yhteensä 24 alkiota. Symmetriselle ryhmälle on olemassa erityinen tapa merkitä alkioita, eli syklinotaatio, jossa alkiot esitetään erillisten syklien tulona. Esimerkki Permutaatiot ( ) ( , voidaan syklinotaatiossa kirjoittaa muotoon (13)(24) ja (134). 35 )
8 Kutsumme sykliä, jonka pituus on kaksi, transpositioksi. Voimme hajottaa jokaisen n:n pituisen syklin aina transpositioiden (ei välttämättä erillisten) tuloksi. Jos transpositiohajotelmassa on parillinen määrä termejä, kutsumme permutaatiota parilliseksi, muussa tapauksessa parittomaksi. Molemmat ylläolevat permutaatiot ovat parillisia, sillä (134) = (13)(34). Määritelmä Symmetrisen ryhmän alkion syklityyppi määräytyy sen alkiovieraan syklihajotelman perusteella. Syklityyppi listaa yksinkertaisesti eripituisten syklien määrät. Esimerkki Alkion (14) syklityyppi on 2, kun taas alkion (125)(346)(78)(9) syklityyppi on 3 2, 2, 1, huomaa, että =9. Monesti ykkössyklejä ei kirjoiteta ollenkaan. Lause Kaksi symmetrisen ryhmän S n alkiota ovat toistensa konjugaatteja, jos ja vain jos niillä on sama syklityyppi. Todistus. Olkoon (a 1... a m ) m-sykli ja ρ S n, silloin ρ 1 (a 1... a m )ρ = (a 1 ρ... a m ρ) (vakuutu tästä esimerkkien avulla). Olkoon nyt τ = τ 1 τ 2... τ r syklihajotelma. Silloin ρ 1 τρ = ρ 1 τ 1... τ r ρ = ρ 1 τ 1 ρρ 1 τ 2 ρ... ρ 1 τ r ρ, missä jokainen ρ 1 τ i ρ on sykli, jonka pituus on sama kuin τ i :n pituus. Niinpä ρ 1 τρ 1 :lla ja τ:lla on sama syklityyppi. Jos taas τ:lla ja σ:lla on sama syklityyppi, meidän täytyy konstruoida ρ, joka konjugoi nämä alkiot keskenään. Kirjoitetaan τ ja σ sellaiseen järjestykseen, että samanpituiset syklit ovat samassa järjestyksessä. σ =(a 1... a m )(a m+1... a r )(a r+1... )() τ =(b 1... b m )(b m+1... b r )(b r+1... )() Nyt luomme alkion ρ kuvaamaan a i b i mukaan lukien ykkössyklit. Tällainen ρ permutoi {1,..., n} ja on siis ryhmän S n alkio, kuten vaadittua. Tehtävä 33. Osoita, että ryhmän S n parilliset permutaatiot muodostavat normaalin aliryhmän A n, jota kutsutaan alternoivaksi ryhmäksi. 2 Osoita, että tasan puolet S n :n alkioista on parillisia, ja päättele, että A n :n indeksi on kaksi. Huomautus Syklityyppi ei määritä konjugaatiota alternoivassa ryhmässä. Joskus S n :n konjugaatioluokat, voivat hajota, kun konjugoimme niitä ryhmässä A n. 2 Minun mielestäni parempi termi olisi kutsua sitä vuorottelevaksi ryhmäksi. Tai vuorotteluryhmäksi. 36
9 Tehtävä 34. Etsi alkion (123) konjugaatit ryhmässä A 4. Kokoamme taulukkoon S 4 :n alkiot konjugaatioluokkien mukaan Taulukko 6: Ryhmän S 4 alkiot Konjugaatioluokka edustaja 1 (12) (12)(34) (123) (1234) alkion kertaluku konjugaattien määrä keskittäjän koko Koska syklityyppi määrittää konjugaatioluokan, on luonnollista, että normaalit aliryhmät ovat konjugaatioluokkien yhdisteitä. S 4 :ssä on kaksi normaalia aliryhmää. V 4 on konjuvaatioluokkien 1 ja 3 yhdiste ja alternoiva ryhmä A 4 on konjugaatioluokkien 1,3 ja 4 yhdiste. Kokoamme myös ryhmän A 4 vastaavat tiedot taulukkoon. Taulukko 7: Ryhmän A 4 alkiot Konjugaatioluokka 1 2 3a 3b edustaja 1 (12)(34) (123) (134) alkion kertaluku konjugaattien määrä keskittäjän koko Platonin kappaleiden symmetriaryhmät Lause Kuution kiertosymmetriaryhmä on S 4. Todistus. Etsimme siis ryhmää G = {g SO(3) : g :Ω Ω}, missä Ω= {(a, b, c) :a, b, c {1, 1}}. Jaamme todistuksen kolmeen eri osaan. 37
10 1. Aloitamme tarkastelemalla symmetriaryhmän kokoa. Koska symmetriaryhmä toimii transitiivisesti kuution kärjissä, ja jokaisen kärjen vakauttaa kolme alkiota, saamme rata-vakauttajalauseen perusteella ryhmän kooksi 24. Kärjen vakauttavat täsmälleen ne kierrot, joitten symmetria-akseli menee kärjen läpi, ja diagonaalisesti toiseen kärkeen. Tämän akselin ympäri voimme kiertää kuutiota joko 2π/3 tai 4π/3:n verran säilyttäen kuution symmetrian. 2. Toiseksi todistamme, että on olemassa homomorfismi φ : G S 4. Merkitään S:llä kuution päädiagonaalien joukkoa S := {(AA ), (BB ), (CC ), (DD )}. Mikä tahansa kuution symmetriaryhmään kuuluva g G permutoi näitä neljää diagonaalia. Joten G indusoi toiminnan joukossa S joka tuottaa homomorfismin φ : G S 4. Ensimmäisen isomorfialauseen perusteella Imφ = G/Kerφ. 3. Viimeksi todistamme, että Kerφ =1, sillä silloin homomorfismi on injektio, ja koska G = S 4, tästä seuraa, että se on isomorfismi. Olkoon g Kerφ. Tämä tarkoittaa sitä, että g toimii triviaalisti joukossa S, esimerkiksi se kuvaa {A, A } {A, A }. Oletamme, että g 1ja menettämättä mitään, voimme tarkemmin olettaa, että g kuvaa A:n A :ksi. Nyt tarkastelemme B:tä. B on kärki, joka on yhden särmän päässä A:sta, joten g:n pitää kuvata B johonkin sellaiseen kärkeen, joka yhdistyy särmällä A :n. Muistamme, että g : {B, B } {B, B }, joten g kuvaa B:n B :ksi. Samalla tavalla g kuvaa C:n C :ksi ja D:n D :ksi. Nyt muistamme, että g SO(3), jonka alkioita voidaan ajatella myös 3 3-matriiseina. Sellainen 1-dimensioinen R 3 :n aliavaruus, joka sisältää pisteet A ja A on jonkun g:n ominaisvektorin virittämä. Lisäksi tämän ominaisvektorin ominaisarvo on 1. Sama on totta tietysti B, B, C, C ja D, D :lle. Kaikenkaikkiaan siis g:llä on kolme lineaarisesti riippumatonta ominaisvektoria, joiden kaikkien ominaisarvo on 1. Tämä tarkoittaa sitä, että g:n determinantti on 1, mikä on tietysti ristiriita, sillä SO(3):n alkioiden determinanttien pitää olla 1. Kuvaus on siis injektio, kuten haluttua. Korollaari Oktaedrin kiertosymmetriaryhmä on S 4. 38
11 Todistus seuraa siitä, että oktaedri on kuution duaalikappale. Eli voimme käyttää ylläolevaa todistusta suoraan, mutta nyt tarkastelemme kunkin sivutahkon vakauttajaa, kun symmetria-akseli menee sivutahkokolmion keskipisteen lävitse. Lause Tetraedrin kiertosymmetriaryhmä on A 4. Todistus. Tetraedrillä on neljä kärkeä, ja tetraedrin symmetriaryhmän tulee toimia transitiivisesta näissä kärjissä. Kunkin kärjen vakauttaja on kierto, jonka akseli menee yhdestä kärjestä vastakkaisen sivutahkon keskelle. Tähän ryhmään kuuluu kolme alkiota, joten rata-vakauttajalauseen nojalla ryhmän koko on 12. Tämä on ryhmän A 4 koko. Nyt tehtäväksi jää todistaa, että tetraedrin symmetriaryhmä on isomorfinen ryhmän A 4 kanssa. Ryhmän A 5 rakenteen selvitämme seuraavassa luvussa tarkemmin. Tässä vain toteamme seuraavat lauseet. Lause Dodekaedrin kiertosymmetriaryhmä on A 5. Korollaari Ikosaedrin kiertosymmetriaryhmä on A 5. Todistus. Lasketaan symmetriaryhmän koko rata-vakauttajalauseen perusteella. Dodekaedrissä on 12 tahkoa ja kunkin tahkon vakauttaja on viitossykli, jonka akseli menee tahkon viisikulmion kärjen läpi. Näin ollen symmetriaryhmän koko on 5 12 = 60. Palaamme nyt toimintojen teoreettisempaan puoleen, jotta voimme esittää mainion ja hyödyllisen lauseen, jota myös ei-burnsiden lauseeksi kutsutaan. Lauseen nimi kaivannee hieman selittämistä. Noin 1960-luvulta lähtien monet matemaatikot ovat kutsuneet lausetta Burnsiden lauseeksi, ja se kyllä esiintyy William Burnsiden ryhmäteorian opuksessa vuodelta 1897, joten Burnside kyllä tunsi lauseen, kuten myös muut hänen aikalaisensa. Lause itse on vanhempi ja esiintyy ainakin Cauchyn paperissa 1845 ja nykymuodossa Frobeniuksen paperissa 1887 (luultavasti karakteeriateorian yhteydessä). Tavallaan on reilua kutsua lausetta ei-burnsiden lauseeksi, sillä lähes kaikki muut tuon ajan ryhmäteorian lauseista olivat Burnsiden käsialaa. Määritelmä Ryhmä G toimii joukossa Ω. Alkion g kiinnittämien alkioitten joukko on χ(g) ={ω Ω: ω g = ω}. 3 3 Merkitsemme tätä joukkoa kreikkalaisella kirjaimella χ, koska tällä joukolla on yhteys karakteeriteoriaan, josta ehkä jollain myöhemmällä kurssilla. 39
12 Huomautus Tämä ei ole sama joukko kuin alkion vakauttaja Stab G (ω) =G ω = {g G : ω g = ω}. Erityisesti, χ(g) on Ω:n osajoukko, eikä G:n aliryhmä. Lause 5.30 (ei-burnsiden lause). Toimikoon G joukossa Ω. Silloin G:n ratojen lukumäärä Ω:ssa on 1 χ(g). G g G Todistus. Olkoon S järjestettyjen parien joukko {(ω, g) :g G, ω Ω,ω g = ω}. Lasketaan joukon S mahtavuus kahdella eri tavalla. Ensiksi lasketaan tämä G:n alkioiden mukaan. Näin saamme täsmälleen g G χ(g). Lasketaan joukko nyt Ω:n alkioiden mukaan. Ω hajoaa G-radoiksi Ω 1, Ω 2,...Ω k. Voimme edelleen laskea jokaisen Ω i alkiot erikseen. Olkoon ω Ω i, jotta pari (ω, g) S vaaditaan, että ω g = ω, toisin sanoen sopivien alkioiden g lukumäärä on täsmälleen Stab G (ω). Ratavakauttajalauseen perusteella G = Ω i Stab G (ω). Tästä seuraa S = G ratojen luku. 5.3 Platonin kappaleiden väritysongelmat Ei-Burnsiden lause on hyödyllinen erilaisissa kombinatorisissa laskutehtävissä. Esimerkiksi, voimme kysyä, kuinka monta erilaista tapaa on värittää tetraedri kolmella eri värillä. Määrittelemme kaksi tetraedrin väritystä samaksi, jos on olemassa kiertosymmetria, jonka avulla väritykset näyttävät samalta. Koska värejä on kolme, vaikkapa sininen, valkoinen ja punainen, voidaan jokainen tahko värittää 3 tavalla ja koska tahkoja on neljä, on värityksiä yhteensä 3 4 = 81. Nyt tutkimme, mitkä väritykset näistä ovat samoja, eli näyttävät samalta kiertosymmetrian suhteen. Olkoon Ω näiden 81 eri tavalla väritetyn tetraedrin joukko, jonka alkiot ovat siis T 1,T 2,..., T 81. G on tetraedrin kiertosymmetrioiden ryhmä, joka on siis A 4. G toimii Ω:ssa luonnollisella tavalla, eli kuvaa jokaisen T 1,..., T 81 joksikin toiseksi tetraedriksi T 1,..., T 81. Kaksi tetraedria S ja T ovat värityksen suhteen sama tetraedri, jos on olemassa g G, joka S g = T. Tästä seuraa, että tetraedrin väritykset voidaan laskea laskemalla kuinka monta G-rataa on joukossa Ω. Nimittäin jokaiseen rataan on kerätty täsmälleen sellaiset tetraedrit, jotka ovat väritykseltään samat. Voimme käyttää ratojen lukumäärän laskemiseen ei-burnsiden lausetta. Jotta voimme soveltaa sitä, on tarkasteltava kunkin G:n alkion kiinnittämää joukkoa. 40
13 1. Ykkösalkio kiinnittää kaiken, eli χ(1) = Kolmossyklin θ akseli on tetraedrin yksi kärki ja siitä suora vastakkaisen tahkon keskipisteeseen. θ kiinnittää värityksen, jos sivutahkot ovat kaikki samanvärisiä. Tällaisia värityksiä on yhteensä 9, koska on kolme väriä, joilla voimme värittää sivutahkot samanvärisiksi. Pohja voi olla tämän lisäksi minkä värinen tahansa. 3. Alkio φ, jonka kertaluku on kaksi, toimii kuten (12)(34) tahkojen suhteen. Joten, jos halutaan sen kiinnittävän värityksen, vaadimme, että tahkot 1 ja 2 ovat samaa väriä, kuten myös tahkot 3 ja 4. Erilaisia värityksiä saamme jälleen 9. Ryhmässä A 4 on yhteensä kahdeksan kolmossykliä, ja kaikille näille χ(θ) = 9. Kertalukua kaksi olevia alkioita on yhteensä kolme, ja kaikille näille χ(φ) = 9. Nyt ei-burnsiden lause sanoo, että värityksiä on 1 A 4 χ(g) = 1 ( ) = g A 4 Tehtävä 35. sinisellä? 1. Kuinka monta eri tapaa on värittää kuutio keltaisella ja 2. Kuinka monta eri tapaa on luoda helminauha, jonka pituus on 14 helmeä, käyttämällä hopeisia, kultaisia sekä norsunluisia helmiä? 3. Osoita, että on 9099 tapaa värittää dodekaedri kolmella värillä. 41
6 A 5, alternoiva ryhmä ja muita yksinkertaisia ryhmiä
 6 A 5, alternoiva ryhmä ja muita yksinkertaisia ryhmiä Tutustukaamme ensin ryhmään S 5. Jos käytämme syklinotaatiota, toteamme, että se sisältää syklejä, jotka ovat muotoa (12), (123), (1234), (12345),
6 A 5, alternoiva ryhmä ja muita yksinkertaisia ryhmiä Tutustukaamme ensin ryhmään S 5. Jos käytämme syklinotaatiota, toteamme, että se sisältää syklejä, jotka ovat muotoa (12), (123), (1234), (12345),
Esko Turunen MAT Algebra1(s)
 Määritelmä (4.1) Olkoon G ryhmä. Olkoon H G, H. Jos joukko H varustettuna indusoidulla laskutoimituksella on ryhmä, se on ryhmän G aliryhmä. Jos H G on ryhmän G aliryhmä, merkitään usein H G, ja jos H
Määritelmä (4.1) Olkoon G ryhmä. Olkoon H G, H. Jos joukko H varustettuna indusoidulla laskutoimituksella on ryhmä, se on ryhmän G aliryhmä. Jos H G on ryhmän G aliryhmä, merkitään usein H G, ja jos H
3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2
 3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 Olen valinnut kunkin luvun teemaksi yhden ryhmän. Ensimmäisen luvun teema on pienin epätriviaali ryhmä, eli ryhmä, jossa on kaksi alkiota. Merkitsen
3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 Olen valinnut kunkin luvun teemaksi yhden ryhmän. Ensimmäisen luvun teema on pienin epätriviaali ryhmä, eli ryhmä, jossa on kaksi alkiota. Merkitsen
Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen
 Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen anton.mallasto@aalto.fi. 1. 2. Muista. Ryhmän G aliryhmä H on normaali aliryhmä, jos ah = Ha kaikilla a G. Toisin
Mikäli huomaat virheen tai on kysyttävää liittyen malleihin, lähetä viesti osoitteeseen anton.mallasto@aalto.fi. 1. 2. Muista. Ryhmän G aliryhmä H on normaali aliryhmä, jos ah = Ha kaikilla a G. Toisin
Ryhmäteoriaa. 2. Ryhmän toiminta
 Ryhmäteoriaa 2. Ryhmän toiminta Permutaatiot kuvaavat jonkin perusjoukon alkioita toisikseen. Eräät permutaatiot jättävät joitain alkioita paikalleen, toiset liikuttavat kaikkia joukon alkioita. Kaikki
Ryhmäteoriaa 2. Ryhmän toiminta Permutaatiot kuvaavat jonkin perusjoukon alkioita toisikseen. Eräät permutaatiot jättävät joitain alkioita paikalleen, toiset liikuttavat kaikkia joukon alkioita. Kaikki
Symmetrisistä ryhmistä symmetriaryhmiin
 Symmetrisistä ryhmistä symmetriaryhmiin 16. marraskuuta 2006 1 Symmetrisistä ryhmistä... Bijektiivistä kuvausta {1,..., n} {1,..., n} kutsutaan n-permutaatioksi. Merkitään n-permutaatioden joukkoa S n.
Symmetrisistä ryhmistä symmetriaryhmiin 16. marraskuuta 2006 1 Symmetrisistä ryhmistä... Bijektiivistä kuvausta {1,..., n} {1,..., n} kutsutaan n-permutaatioksi. Merkitään n-permutaatioden joukkoa S n.
Algebra I, harjoitus 8,
 Algebra I, harjoitus 8, 4.-5.11.2014. 1. Olkoon G ryhmä ja H sen normaali aliryhmä. Todista, että tällöin G/H on ryhmä, kun määritellään laskutoimitus joukossa G/H asettamalla aina, kun x, y G (lauseen
Algebra I, harjoitus 8, 4.-5.11.2014. 1. Olkoon G ryhmä ja H sen normaali aliryhmä. Todista, että tällöin G/H on ryhmä, kun määritellään laskutoimitus joukossa G/H asettamalla aina, kun x, y G (lauseen
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos meillä
MS-A0402 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos meillä
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos
MS-A0401 Diskreetin matematiikan perusteet Osa 5: Ryhmät ja permutaatiot Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Ryhmät ja permutaatiot Väritysongelma Jos
Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua)
 Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua) 10.12.2012 Tehtävä 1. Osoita, että tuloryhmän R np R sp indeksi Rubikin paikkaryhmässä R p on täsmälleen kaksi. (Tarkkaan
Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua) 10.12.2012 Tehtävä 1. Osoita, että tuloryhmän R np R sp indeksi Rubikin paikkaryhmässä R p on täsmälleen kaksi. (Tarkkaan
Tekijäryhmiä varten määritellään aluksi sivuluokat ja normaalit aliryhmät.
 3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
4. Ryhmien sisäinen rakenne
 4. Ryhmien sisäinen rakenne Tässä luvussa tarkastellaan joitakin tapoja päästä käsiksi ryhmien sisäiseen rakenteeseen. Useimmat tuloksista ovat erityisen käyttökelpoisia äärellisten ryhmien tapauksessa.
4. Ryhmien sisäinen rakenne Tässä luvussa tarkastellaan joitakin tapoja päästä käsiksi ryhmien sisäiseen rakenteeseen. Useimmat tuloksista ovat erityisen käyttökelpoisia äärellisten ryhmien tapauksessa.
H = H(12) = {id, (12)},
 7. Normaali aliryhmä ja tekijäryhmä Tarkastelemme luvun aluksi ryhmän ja sen aliryhmien suhdetta. Olkoon G ryhmä ja olkoon H G. Alkiong G vasen sivuluokka (aliryhmän H suhteen) on gh = {gh : h H} ja sen
7. Normaali aliryhmä ja tekijäryhmä Tarkastelemme luvun aluksi ryhmän ja sen aliryhmien suhdetta. Olkoon G ryhmä ja olkoon H G. Alkiong G vasen sivuluokka (aliryhmän H suhteen) on gh = {gh : h H} ja sen
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013
 Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
Dihedraalinen ryhmä Pro gradu Elisa Sonntag Matemaattisten tieteiden laitos Oulun yliopisto 2013 Sisältö Johdanto 2 1 Ryhmä 3 2 Symmetrinen ryhmä 6 3 Symmetriaryhmä 10 4 Dihedraalinen ryhmä 19 Lähdeluettelo
σ = σ = ( ).
 APPROBATUR 3 (MATP170) Harjoitus 6, Ratkaisut 1. Kirjoita permutaatio perinteisessä kaksirivisessä esitysmuodossa. σ = ( 1 3 6 2 )( 4 5 6 1 )( 2 3 4 5 ) Ratkaisu. Katsotaan alkioden 1, 2, 3, 4, 5, 6 kuvautuminen
APPROBATUR 3 (MATP170) Harjoitus 6, Ratkaisut 1. Kirjoita permutaatio perinteisessä kaksirivisessä esitysmuodossa. σ = ( 1 3 6 2 )( 4 5 6 1 )( 2 3 4 5 ) Ratkaisu. Katsotaan alkioden 1, 2, 3, 4, 5, 6 kuvautuminen
Ryhmäteoria. Pirita Paajanen 26. marraskuuta 2008
 Ryhmäteoria Pirita Paajanen pirita.paajanen@helsinki.fi 26. marraskuuta 2008 Sisältö 1 Merkinnät 3 2 Alkusanat 4 3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 6 3.1 Peruskäsitteet...........................
Ryhmäteoria Pirita Paajanen pirita.paajanen@helsinki.fi 26. marraskuuta 2008 Sisältö 1 Merkinnät 3 2 Alkusanat 4 3 Ryhmäteorian peruskäsitteet ja pienet ryhmät, C 2 6 3.1 Peruskäsitteet...........................
Tekijäryhmän määrittelemistä varten määritellään aluksi sivuluokat ja normaalit aliryhmät. gh = {gh h H}.
 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa suuriin, helpommin käsiteltäviin osiin. Tämän jälkeen voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin
π πρ = ρ, π πρ 3 = ρ 3, πρ 2 πρ = ρ 3 πρ 2 πρ 3 = ρ.
 Rhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 4, ratkaisuehdotus (5 sivua) 26.11.2012 Tehtävä 1. Etsi neliön smmetriarhmän D 8 kaikki alirhmät. Mitkä niistä ovat normaaleja? Ratkaisu. Rhmää D 8
Rhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 4, ratkaisuehdotus (5 sivua) 26.11.2012 Tehtävä 1. Etsi neliön smmetriarhmän D 8 kaikki alirhmät. Mitkä niistä ovat normaaleja? Ratkaisu. Rhmää D 8
1. Tarkastellaan esimerkissä 4.9 esiintynyttä neliön symmetriaryhmää
 Ryhmäteoreettinen näkökulma Rubikin kuutioon Matematiikan ja tilastotieteen laitos Syksy 2010 Harjoitus 2 Ratkaisuehdotus 1. Tarkastellaan esimerkissä 4.9 esiintynyttä neliön symmetriaryhmää D 8 = { id,
Ryhmäteoreettinen näkökulma Rubikin kuutioon Matematiikan ja tilastotieteen laitos Syksy 2010 Harjoitus 2 Ratkaisuehdotus 1. Tarkastellaan esimerkissä 4.9 esiintynyttä neliön symmetriaryhmää D 8 = { id,
HN = {hn h H, n N} on G:n aliryhmä.
 Matematiikan ja tilastotieteen laitos Algebra I Ratkaisuehdoituksia harjoituksiin 8, 23.27.3.2009 5 sivua Rami Luisto 1. Osoita, että kullakin n N + lukujen n 5 ja n viimeiset numerot kymmenkantaisessa
Matematiikan ja tilastotieteen laitos Algebra I Ratkaisuehdoituksia harjoituksiin 8, 23.27.3.2009 5 sivua Rami Luisto 1. Osoita, että kullakin n N + lukujen n 5 ja n viimeiset numerot kymmenkantaisessa
Diskreetin matematiikan perusteet Laskuharjoitus 5 / vko 41
 Diskreetin matematiikan perusteet Laskuharjoitus 5 / vko 4 Tuntitehtävät 4-42 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 45-46 loppuviikon harjoituksissa. Kotitehtävät 43-44 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 5 / vko 4 Tuntitehtävät 4-42 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 45-46 loppuviikon harjoituksissa. Kotitehtävät 43-44 tarkastetaan loppuviikon
5. Ryhmän kompositiotekijät
 5. Ryhmän kompositiotekijät Jos ryhmästä löydetään normaali aliryhmä, sen suhteen voidaan muodostaa tekijäryhmä, jolla saattaa olla yksinkertaisempi rakenne kuin alkuperäisellä ryhmällä. Ryhmä voidaan
5. Ryhmän kompositiotekijät Jos ryhmästä löydetään normaali aliryhmä, sen suhteen voidaan muodostaa tekijäryhmä, jolla saattaa olla yksinkertaisempi rakenne kuin alkuperäisellä ryhmällä. Ryhmä voidaan
Algebra 1, harjoitus 9, h = xkx 1 xhx 1. a) Käytetään molemmissa tapauksissa isomorfialausetta. Tarkastellaan kuvauksia
 Algebra 1, harjoitus 9, 11.-12.11.2014. 1. Olkoon G ryhmä ja H G normaali aliryhmä. Tiedetään, että tällöin xhx 1 H kaikilla x G. Osoita, että itse asiassa xhx 1 = H kaikilla x G. Ratkaisu: Yritetään osoittaa,
Algebra 1, harjoitus 9, 11.-12.11.2014. 1. Olkoon G ryhmä ja H G normaali aliryhmä. Tiedetään, että tällöin xhx 1 H kaikilla x G. Osoita, että itse asiassa xhx 1 = H kaikilla x G. Ratkaisu: Yritetään osoittaa,
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko
 DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
Laitos/Institution Department Matematiikan ja tilastotieteen laitos. Aika/Datum Month and year Huhtikuu 2014
 Tiedekunta/Osasto Fakultet/Sektion Faculty Matemaattis-luonnontieteellinen tiedekunta Laitos/Institution Department Matematiikan ja tilastotieteen laitos Tekijä/Författare Author Anna-Mari Pulkkinen Työn
Tiedekunta/Osasto Fakultet/Sektion Faculty Matemaattis-luonnontieteellinen tiedekunta Laitos/Institution Department Matematiikan ja tilastotieteen laitos Tekijä/Författare Author Anna-Mari Pulkkinen Työn
15. Laajennosten väliset homomorfismit
 15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit niin sanotut automorfismit auttavat vastaavasti
15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit niin sanotut automorfismit auttavat vastaavasti
Esko Turunen Luku 3. Ryhmät
 3. Ryhmät Monoidia rikkaampi algebrallinen struktuuri on ryhmä: Määritelmä (3.1) Olkoon joukon G laskutoimitus. Joukko G varustettuna tällä laskutoimituksella on ryhmä, jos laskutoimitus on assosiatiivinen,
3. Ryhmät Monoidia rikkaampi algebrallinen struktuuri on ryhmä: Määritelmä (3.1) Olkoon joukon G laskutoimitus. Joukko G varustettuna tällä laskutoimituksella on ryhmä, jos laskutoimitus on assosiatiivinen,
Ideaalit ja tekijärenkaat Ryhmähomomorfismin φ : G G ydin on ryhmän G normaali aliryhmä. Esko Turunen Luku 7. Ideaalit ja tekijärenkaat
 Ideaalit ja tekijärenkaat Ryhmähomomorfismin φ : G G ydin on ryhmän G normaali aliryhmä. Ideaalit ja tekijärenkaat Ryhmähomomorfismin φ : G G ydin on ryhmän G normaali aliryhmä. Rengashomomorfismi ψ :
Ideaalit ja tekijärenkaat Ryhmähomomorfismin φ : G G ydin on ryhmän G normaali aliryhmä. Ideaalit ja tekijärenkaat Ryhmähomomorfismin φ : G G ydin on ryhmän G normaali aliryhmä. Rengashomomorfismi ψ :
Algebra I, Harjoitus 6, , Ratkaisut
 Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut (MV 6 sivua 1. Olkoot M ja M multiplikatiivisia monoideja. Kuvaus f : M M on monoidihomomorfismi jos 1 f(ab = f(af(b
Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut Algebra I Harjoitus 6 9. 13.3.2009 Ratkaisut (MV 6 sivua 1. Olkoot M ja M multiplikatiivisia monoideja. Kuvaus f : M M on monoidihomomorfismi jos 1 f(ab = f(af(b
x gxg 1 Esimerkin 3-sykli saatiin siis konjugoimalla siirretyksi toimimaan lukujen 1, 2 ja 3 sijasta luvuilla 5, 8 ja 6.
 4 Konjugointi 4.1 Konjugoinnin määritelmä Usein ryhmän alkiot kuvaavat operaatioita jossain joukossa. Permutaatiot ovat tästä hyvä esimerkki. Tällaisessa tapauksessa voidaan konjugoinnilla siirtää jossain
4 Konjugointi 4.1 Konjugoinnin määritelmä Usein ryhmän alkiot kuvaavat operaatioita jossain joukossa. Permutaatiot ovat tästä hyvä esimerkki. Tällaisessa tapauksessa voidaan konjugoinnilla siirtää jossain
4 Konjugointi. 4.1 Konjugoinnin määritelmä
 4 Konjugointi 4.1 Konjugoinnin määritelmä Usein ryhmän alkiot kuvaavat operaatioita jossain joukossa. Ryhmäteoriassa tätä kutsutaan ryhmän toiminnaksi. Permutaatiot ovat hyvä esimerkki ryhmän toiminnasta.
4 Konjugointi 4.1 Konjugoinnin määritelmä Usein ryhmän alkiot kuvaavat operaatioita jossain joukossa. Ryhmäteoriassa tätä kutsutaan ryhmän toiminnaksi. Permutaatiot ovat hyvä esimerkki ryhmän toiminnasta.
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
{I n } < { I n,i n } < GL n (Q) < GL n (R) < GL n (C) kaikilla n 2 ja
 5. Aliryhmät Luvun 4 esimerkeissä esiintyy usein ryhmä (G, ) ja jokin vakaa osajoukko B G siten, että (B, B ) on ryhmä. Määrittelemme seuraavassa käsitteitä, jotka auttavat tällaisten tilanteiden käsittelyssä.
5. Aliryhmät Luvun 4 esimerkeissä esiintyy usein ryhmä (G, ) ja jokin vakaa osajoukko B G siten, että (B, B ) on ryhmä. Määrittelemme seuraavassa käsitteitä, jotka auttavat tällaisten tilanteiden käsittelyssä.
Ryhmäteoria. Jyrki Lahtonen. Turun yliopisto, helmikuu 2019 keskeneräinen versio
 Ryhmäteoria Jyrki Lahtonen Turun yliopisto, helmikuu 2019 keskeneräinen versio Sisältö 1 Ryhmäteorian peruskäsitteitä 3 1.1 Ryhmä, aliryhmä, homomorfismi.................................. 3 1.2 Generointi,
Ryhmäteoria Jyrki Lahtonen Turun yliopisto, helmikuu 2019 keskeneräinen versio Sisältö 1 Ryhmäteorian peruskäsitteitä 3 1.1 Ryhmä, aliryhmä, homomorfismi.................................. 3 1.2 Generointi,
[E : F ]=[E : K][K : F ].
![[E : F ]=[E : K][K : F ]. [E : F ]=[E : K][K : F ].](/thumbs/61/46040569.jpg) ALGEBRA II 35 Lause 4.4 (Astelukulause). Olkoot E/K/Fäärellisiä kuntalaajennuksia. Silloin [E : F ]=[E : K][K : F ]. Todistus. Olkoon {α 1,...,α n } kanta laajennukselle E/K ja {β 1,...,β m } kanta laajennukselle
ALGEBRA II 35 Lause 4.4 (Astelukulause). Olkoot E/K/Fäärellisiä kuntalaajennuksia. Silloin [E : F ]=[E : K][K : F ]. Todistus. Olkoon {α 1,...,α n } kanta laajennukselle E/K ja {β 1,...,β m } kanta laajennukselle
Jarkko Peltomäki. Aliryhmän sentralisaattori ja normalisaattori
 Jarkko Peltomäki Aliryhmän sentralisaattori ja normalisaattori Matematiikan aine Turun yliopisto Syyskuu 2009 Sisältö 1 Johdanto 2 2 Määritelmiä ja perusominaisuuksia 3 2.1 Aliryhmän sentralisaattori ja
Jarkko Peltomäki Aliryhmän sentralisaattori ja normalisaattori Matematiikan aine Turun yliopisto Syyskuu 2009 Sisältö 1 Johdanto 2 2 Määritelmiä ja perusominaisuuksia 3 2.1 Aliryhmän sentralisaattori ja
Platonin kappaleet. Avainsanat: geometria, matematiikan historia. Luokkataso: 6-9, lukio. Välineet: Polydron-rakennussarja, kynä, paperia.
 Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Alternoivien ryhmien ominaisuuksista
 Alternoivien ryhmien ominaisuuksista Pro gradu -tutkielma Anssi Aska 2257068 Matemaattisten tieteiden laitos Oulun yliopisto 2017 Sisältö 1 Johdanto 2 2 Peruskäsitteitä 3 2.1 Ryhmä ja aliryhmä........................
Alternoivien ryhmien ominaisuuksista Pro gradu -tutkielma Anssi Aska 2257068 Matemaattisten tieteiden laitos Oulun yliopisto 2017 Sisältö 1 Johdanto 2 2 Peruskäsitteitä 3 2.1 Ryhmä ja aliryhmä........................
ja siten kyseisen symmetriaryhmä on toinen dihedraaliryhmä (D 2 )
 APPROBATUR (MATP170) Harjoitus 7, Ratkaisut 1. Kuvaa kirjaimen H smmetriarhmä permutaatioiden avulla ja tee saadulle rhmälle kertotaulu. (Nimeä tätä varten kirjaimesta smmetrian mielessä tärkeitä kohtia
APPROBATUR (MATP170) Harjoitus 7, Ratkaisut 1. Kuvaa kirjaimen H smmetriarhmä permutaatioiden avulla ja tee saadulle rhmälle kertotaulu. (Nimeä tätä varten kirjaimesta smmetrian mielessä tärkeitä kohtia
on Abelin ryhmä kertolaskun suhteen. Tämän joukon alkioiden lukumäärää merkitään
 5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
Johdatus diskreettiin matematiikkaan Harjoitus 2, Osoita että A on hyvin määritelty. Tee tämä osoittamalla
 Johdatus diskreettiin matematiikkaan Harjoitus 2, 23.9.2015 1. Osoita että A on hyvin määritelty. Tee tämä osoittamalla a) että ei ole olemassa surjektiota f : {1,, n} {1,, m}, kun n < m. b) että a) kohdasta
Johdatus diskreettiin matematiikkaan Harjoitus 2, 23.9.2015 1. Osoita että A on hyvin määritelty. Tee tämä osoittamalla a) että ei ole olemassa surjektiota f : {1,, n} {1,, m}, kun n < m. b) että a) kohdasta
Äärellisesti generoitujen Abelin ryhmien peruslause
 Tero Harju (2008/2010) Äärellisesti generoitujen Abelin ryhmien peruslause Merkintä X on joukon koko ( eli #X). Vapaat Abelin ryhmät Tässä kappaleessa käytetään Abelin ryhmille additiivista merkintää.
Tero Harju (2008/2010) Äärellisesti generoitujen Abelin ryhmien peruslause Merkintä X on joukon koko ( eli #X). Vapaat Abelin ryhmät Tässä kappaleessa käytetään Abelin ryhmille additiivista merkintää.
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kuvauksista ja relaatioista. Jonna Makkonen Ilari Vallivaara
 Kuvauksista ja relaatioista Jonna Makkonen Ilari Vallivaara 20. lokakuuta 2004 Sisältö 1 Esipuhe 2 2 Kuvauksista 3 3 Relaatioista 8 Lähdeluettelo 12 1 1 Esipuhe Joukot ja relaatiot ovat periaatteessa äärimmäisen
Kuvauksista ja relaatioista Jonna Makkonen Ilari Vallivaara 20. lokakuuta 2004 Sisältö 1 Esipuhe 2 2 Kuvauksista 3 3 Relaatioista 8 Lähdeluettelo 12 1 1 Esipuhe Joukot ja relaatiot ovat periaatteessa äärimmäisen
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
ei ole muita välikuntia.
 ALGEBRA II 41 Lause 4.15. F q m on polynomin x qm x hajoamiskunta kunnan F q suhteen. Todistus. Olkoon α kunnan F q m primitiivialkio. Nyt F qm =< α > muodostuu täsmälleen polynomin x qm 1 1nollakohdistajatäten
ALGEBRA II 41 Lause 4.15. F q m on polynomin x qm x hajoamiskunta kunnan F q suhteen. Todistus. Olkoon α kunnan F q m primitiivialkio. Nyt F qm =< α > muodostuu täsmälleen polynomin x qm 1 1nollakohdistajatäten
Eräitä ratkeavuustarkasteluja
 Eräitä ratkeavuustarkasteluja Pro gradu-tutkielma Milla Jantunen 2124227 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2014 Sisältö 1 Ryhmät ja aliryhmät 3 1.1 Ryhmä...............................
Eräitä ratkeavuustarkasteluja Pro gradu-tutkielma Milla Jantunen 2124227 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2014 Sisältö 1 Ryhmät ja aliryhmät 3 1.1 Ryhmä...............................
Ratkeavista ryhmistä: teoriaa ja esimerkkejä
 Ratkeavista ryhmistä: teoriaa ja esimerkkejä Pro Gradu-tutkielma Lauri Kangas 2192712 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2015 Sisältö 1 Perusteita 3 1.1 Ryhmät ja aliryhmät.......................
Ratkeavista ryhmistä: teoriaa ja esimerkkejä Pro Gradu-tutkielma Lauri Kangas 2192712 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2015 Sisältö 1 Perusteita 3 1.1 Ryhmät ja aliryhmät.......................
MS-A0003/A0005 Matriisilaskenta Malliratkaisut 5 / vko 48
 MS-A3/A5 Matriisilaskenta Malliratkaisut 5 / vko 48 Tehtävä (L): a) Onko 4 3 sitä vastaava ominaisarvo? b) Onko λ = 3 matriisin matriisin 2 2 3 2 3 7 9 4 5 2 4 4 ominaisvektori? Jos on, mikä on ominaisarvo?
MS-A3/A5 Matriisilaskenta Malliratkaisut 5 / vko 48 Tehtävä (L): a) Onko 4 3 sitä vastaava ominaisarvo? b) Onko λ = 3 matriisin matriisin 2 2 3 2 3 7 9 4 5 2 4 4 ominaisvektori? Jos on, mikä on ominaisarvo?
Tarkastellaan aluksi permutaatioryhmiin liittyvää esimerkkiä.
 5 Tuloryhmät Jotkin ryhmät voidaan jakaa toisistaan riippumattomiin osiin niin, että jokainen ryhmän alkio saadaan tulona eri osista valituista alkioista. Tällöin ryhmää voidaan käsitellä osiensa tulona
5 Tuloryhmät Jotkin ryhmät voidaan jakaa toisistaan riippumattomiin osiin niin, että jokainen ryhmän alkio saadaan tulona eri osista valituista alkioista. Tällöin ryhmää voidaan käsitellä osiensa tulona
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }?
 Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus
2 Permutaatioryhmät. 2.1 Permutaation olemus. 2.2 Permutaatioilla laskeminen
 2 Permutaatioryhmät Rubikin kuution siirrot ovat tietynlaisia permutaatioita Permutaatiot muodostavat ryhmiä, ja tällä tavoin ryhmäteorian työkaluja päästään käyttämään kuutio-ongelman selvittämiseen Tässä
2 Permutaatioryhmät Rubikin kuution siirrot ovat tietynlaisia permutaatioita Permutaatiot muodostavat ryhmiä, ja tällä tavoin ryhmäteorian työkaluja päästään käyttämään kuutio-ongelman selvittämiseen Tässä
g : R R, g(a) = g i a i. Alkio g(a) R on polynomin arvo pisteessä a. Jos g(a) = 0, niin a on polynomin g(x) nollakohta.
 ALGEBRA II 27 on homomorfismi. Ensinnäkin G(a + b) a + b G(a)+G(b) (f), G(ab) ab G(a)G(b) G(a) G(b) (f), ja koska kongruenssien vasempien ja oikeiden puolten asteet ovat pienempiä kuin f:n aste, niin homomorfiaehdot
ALGEBRA II 27 on homomorfismi. Ensinnäkin G(a + b) a + b G(a)+G(b) (f), G(ab) ab G(a)G(b) G(a) G(b) (f), ja koska kongruenssien vasempien ja oikeiden puolten asteet ovat pienempiä kuin f:n aste, niin homomorfiaehdot
Johdatus matematiikkaan
 Johdatus matematiikkaan Luento 7 Mikko Salo 11.9.2017 Sisältö 1. Funktioista 2. Joukkojen mahtavuus Funktioista Lukiomatematiikassa on käsitelty reaalimuuttujan funktioita (polynomi / trigonometriset /
Johdatus matematiikkaan Luento 7 Mikko Salo 11.9.2017 Sisältö 1. Funktioista 2. Joukkojen mahtavuus Funktioista Lukiomatematiikassa on käsitelty reaalimuuttujan funktioita (polynomi / trigonometriset /
2 Permutaatioryhmät. 2.1 Permutaation olemus
 2 Permutaatioryhmät Rubikin kuution siirrot ovat tietynlaisia permutaatioita Permutaatiot muodostavat ryhmiä, ja tällä tavoin ryhmäteorian työkaluja päästään käyttämään kuutioongelman selvittämisessä Tässä
2 Permutaatioryhmät Rubikin kuution siirrot ovat tietynlaisia permutaatioita Permutaatiot muodostavat ryhmiä, ja tällä tavoin ryhmäteorian työkaluja päästään käyttämään kuutioongelman selvittämisessä Tässä
Permutaatioryhmien radoista. Tero Suokas
 Permutaatioryhmien radoista Tero Suokas Pro Gradu -tutkielma Matemaattisten tieteiden laitos Oulun yliopisto 2015 Sisältö 1 Johdanto 2 2 Määritelmiä 3 2.1 Ryhmistä............................. 3 2.2 Homomorsmeista........................
Permutaatioryhmien radoista Tero Suokas Pro Gradu -tutkielma Matemaattisten tieteiden laitos Oulun yliopisto 2015 Sisältö 1 Johdanto 2 2 Määritelmiä 3 2.1 Ryhmistä............................. 3 2.2 Homomorsmeista........................
Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa.
 Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa. Vastaus 2. Vertaillaan
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa. Vastaus 2. Vertaillaan
ÄÄRELLISTEN RYHMIEN VAIHDANNAISUUSVERKOT MIIKKA SILFVERBERG
 ÄÄRELLISTEN RYHMIEN VAIHDANNAISUUSVERKOT MIIKKA SILFVERBERG PRO GRADU HELSINGIN YLIOPISTON MATEMATIIKAN LAITOS TOUKOKUU 2008 SISÄLTÖ 1. Merkinnöistä ja määritelmistä 2 2. Johdanto 3 3. Ryhmäteoriaa 5 3.1.
ÄÄRELLISTEN RYHMIEN VAIHDANNAISUUSVERKOT MIIKKA SILFVERBERG PRO GRADU HELSINGIN YLIOPISTON MATEMATIIKAN LAITOS TOUKOKUU 2008 SISÄLTÖ 1. Merkinnöistä ja määritelmistä 2 2. Johdanto 3 3. Ryhmäteoriaa 5 3.1.
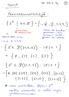 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
1 Lineaariavaruus eli Vektoriavaruus
 1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
1 Lineaariavaruus eli Vektoriavaruus 1.1 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä V epätyhjä joukko. Oletetaan, että joukossa V on määritelty laskutoimitus
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Ryhmät Permutaatiot
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto. huhtikuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot Ryhmät Permutaatiot
4 Abelin ryhmät. 4.1 Suorat tulot ja summat
 4 Abelin ryhmät Ensimmäisellä ryhmäteorian kurssilla käytiin läpi lähinnä syklisiä ryhmiä. Tällä kurssilla keskitymme epäkommutatiivisiin esimerkkeihin. On kuitenkin niin, että äärellisesti viritettyjen
4 Abelin ryhmät Ensimmäisellä ryhmäteorian kurssilla käytiin läpi lähinnä syklisiä ryhmiä. Tällä kurssilla keskitymme epäkommutatiivisiin esimerkkeihin. On kuitenkin niin, että äärellisesti viritettyjen
Lisää ryhmästä A 5 1 / 28. Lisää ryhmästä
 14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 1 / 28 14A.1 14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 Tehtävä: Määrää ryhmän karakteritaulu,
14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 1 / 28 14A.1 14A.1 14A.2 14A.3 14A.4 14A.5 14A.6 14A.7 14A.8 14A.9 14A.10 14A.11 14A.12 14A.13 Tehtävä: Määrää ryhmän karakteritaulu,
a b 1 c b n c n
 Algebra Syksy 2007 Harjoitukset 1. Olkoon a Z. Totea, että aina a 0, 1 a, a a ja a a. 2. Olkoot a, b, c, d Z. Todista implikaatiot: a) a b ja c d ac bd, b) a b ja b c a c. 3. Olkoon a b i kaikilla i =
Algebra Syksy 2007 Harjoitukset 1. Olkoon a Z. Totea, että aina a 0, 1 a, a a ja a a. 2. Olkoot a, b, c, d Z. Todista implikaatiot: a) a b ja c d ac bd, b) a b ja b c a c. 3. Olkoon a b i kaikilla i =
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Kanta ja dimensio 1 / 23
 1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
1 / 23 Kuten ollaan huomattu, saman aliavaruuden voi virittää eri määrä vektoreita. Seuraavaksi määritellään mahdollisimman pieni vektorijoukko, joka virittää aliavaruuden. Jokainen aliavaruuden alkio
6. Tekijäryhmät ja aliryhmät
 6. Tekijäryhmät ja aliryhmät Tämän luvun tavoitteena on esitellä konstruktio, jota kutsutaan tekijäryhmän muodostamiseksi. Konstruktiossa lähdetään liikkeelle jostakin isosta ryhmästä, samastetaan alkioita,
6. Tekijäryhmät ja aliryhmät Tämän luvun tavoitteena on esitellä konstruktio, jota kutsutaan tekijäryhmän muodostamiseksi. Konstruktiossa lähdetään liikkeelle jostakin isosta ryhmästä, samastetaan alkioita,
802320A LINEAARIALGEBRA OSA I
 802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
Approbatur 3, demo 5, ratkaisut
 Approbatur 3, demo 5, ratkaisut 51 Tehtävänä on luetella kaikki joukon S 4 alkiot eli neljän alkion permutaatiot Tämä tarkoittaa kaikkia eri tapoja kuvata joukko {1, 2, 3, 4} bijektiivisesti itselleen
Approbatur 3, demo 5, ratkaisut 51 Tehtävänä on luetella kaikki joukon S 4 alkiot eli neljän alkion permutaatiot Tämä tarkoittaa kaikkia eri tapoja kuvata joukko {1, 2, 3, 4} bijektiivisesti itselleen
15. Laajennosten väliset homomorfismit
 15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit eli niin sanotut automorfismit auttavat vastaavasti
15. Laajennosten väliset homomorfismit Rakenteiden väliset homomorfismit auttavat selvittämään rakenteiden suhteita toisiinsa. Rakenteen sisäiset isomorfismit eli niin sanotut automorfismit auttavat vastaavasti
Permutaatioista alternoivaan ryhmään
 Permutaatioista alternoivaan ryhmään Pro Gradu-tutkielma Sini-Susanna Fetula Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2014 Sisältö 1 Johdanto 2 2 Esitietoja 3 3 Permutaatioista. 6 3.1 Symmetrinen
Permutaatioista alternoivaan ryhmään Pro Gradu-tutkielma Sini-Susanna Fetula Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2014 Sisältö 1 Johdanto 2 2 Esitietoja 3 3 Permutaatioista. 6 3.1 Symmetrinen
Injektio. Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim.
 Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, 2.
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Ryhmät
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Ryhmät
6.4 Ryhmät, joiden kertaluku on pienempi kuin 60
 Lause 6.24 (Liebeck, O Brien, Shalev, Tiep, 2008). Jokaisen epäkommutatiivisen äärellisen yksinkertaisen ryhmän jokainen alkio on vaihdannaistaja. Yksinkertaisten äärellisten ryhmien luokittelu (Classification
Lause 6.24 (Liebeck, O Brien, Shalev, Tiep, 2008). Jokaisen epäkommutatiivisen äärellisen yksinkertaisen ryhmän jokainen alkio on vaihdannaistaja. Yksinkertaisten äärellisten ryhmien luokittelu (Classification
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 2 ratkaisut Tehtävä 1 Olkoon X = {a, b, c} kolmen alkion joukko. a) Mikä on joukon X eri laskutoimitusten lukumäärä? b) Kuinka moni näistä laskutoimituksista on
Äärellisten mallien teoria Harjoituksen 2 ratkaisut Tehtävä 1 Olkoon X = {a, b, c} kolmen alkion joukko. a) Mikä on joukon X eri laskutoimitusten lukumäärä? b) Kuinka moni näistä laskutoimituksista on
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Permutaatiot
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 1 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi 2 Ryhmät ja permutaatiot Permutaatiot
Sylowin lauseet äärellisten ryhmien teoriassa
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Aleksi Heiskanen Sylowin lauseet äärellisten ryhmien teoriassa Luonnontieteiden tiedekunta Matematiikka Marraskuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Aleksi Heiskanen Sylowin lauseet äärellisten ryhmien teoriassa Luonnontieteiden tiedekunta Matematiikka Marraskuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Lineaarialgebra ja differentiaaliyhtälöt Laskuharjoitus 1 / vko 44
 Lineaarialgebra ja differentiaaliyhtälöt Laskuharjoitus 1 / vko 44 Tehtävät 1-3 lasketaan alkuviikon harjoituksissa, verkkotehtävien dl on lauantaina aamuyöllä. Tehtävät 4 ja 5 lasketaan loppuviikon harjoituksissa.
Lineaarialgebra ja differentiaaliyhtälöt Laskuharjoitus 1 / vko 44 Tehtävät 1-3 lasketaan alkuviikon harjoituksissa, verkkotehtävien dl on lauantaina aamuyöllä. Tehtävät 4 ja 5 lasketaan loppuviikon harjoituksissa.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
(xa) = (x) (a) = (x)0 = 0
 11. Ideaalit ja tekijärenkaat Rengashomomorfismi : R! R 0 on erityisesti ryhmähomomorfismi :(R, +)! (R 0, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin
11. Ideaalit ja tekijärenkaat Rengashomomorfismi : R! R 0 on erityisesti ryhmähomomorfismi :(R, +)! (R 0, +) additiivisten ryhmien välillä. Rengashomomorfismin ydin määritellään tämän ryhmähomomorfismin
MS-A0402 Diskreetin matematiikan perusteet
 MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
MS-A040 Diskreetin matematiikan perusteet Osa : Relaatiot ja funktiot Riikka Kangaslampi 017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Relaatiot Relaatio Määritelmä 1 Relaatio joukosta A
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä14.
MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Esimerkkejä14.
4. Ryhmien sisäinen rakenne
 3.5. Sisäiset symmetriat. Kuution väritysesimerkissä 3.14 tarkasteltiin yksittäisten alkioiden sijaan niiden konjugaattiluokkia ja todettiin, että konjugaattiluokkia vastaavat luonnollisella tavalla erityyppiset
3.5. Sisäiset symmetriat. Kuution väritysesimerkissä 3.14 tarkasteltiin yksittäisten alkioiden sijaan niiden konjugaattiluokkia ja todettiin, että konjugaattiluokkia vastaavat luonnollisella tavalla erityyppiset
jonka laskutoimitus on matriisien kertolasku. Vastaavasti saadaan K-kertoiminen erityinen lineaarinen ryhmä
 4. Ryhmät Tässä luvussa tarkastelemme laskutoimituksella varustettuja joukkoja, joiden laskutoimitukselta oletamme muutamia yksinkertaisia ominaisuuksia: Määritelmä 4.1. Laskutoimituksella varustettu joukko
4. Ryhmät Tässä luvussa tarkastelemme laskutoimituksella varustettuja joukkoja, joiden laskutoimitukselta oletamme muutamia yksinkertaisia ominaisuuksia: Määritelmä 4.1. Laskutoimituksella varustettu joukko
14. Juurikunnat Määritelmä ja olemassaolo.
 14. Juurikunnat Mielivaltaisella polynomilla ei välttämättä ole juuria tarkasteltavassa kunnassa. Tässä luvussa tutkitaan sellaisia algebrallisia laajennoksia, jotka saadaan lisäämällä polynomeille juuria.
14. Juurikunnat Mielivaltaisella polynomilla ei välttämättä ole juuria tarkasteltavassa kunnassa. Tässä luvussa tutkitaan sellaisia algebrallisia laajennoksia, jotka saadaan lisäämällä polynomeille juuria.
1 Kertaus. Lineaarinen optimointitehtävä on muotoa:
 1 Kertaus Lineaarinen optimointitehtävä on muotoa: min c 1 x 1 + c 2 x 2 + + c n x n kun a 11 x 1 + a 12 x 2 + + a 1n x n b 1 a 21 x 1 + a 22 x 2 + + a 2n x n b 2 (11) a m1 x 1 + a m2 x 2 + + a mn x n
1 Kertaus Lineaarinen optimointitehtävä on muotoa: min c 1 x 1 + c 2 x 2 + + c n x n kun a 11 x 1 + a 12 x 2 + + a 1n x n b 1 a 21 x 1 + a 22 x 2 + + a 2n x n b 2 (11) a m1 x 1 + a m2 x 2 + + a mn x n
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto
 Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, osa II G. Gripenberg Aalto-yliopisto 14. lokakuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet Yhteenveto, 14.
kaikille a R. 1 (R, +) on kommutatiivinen ryhmä, 2 a(b + c) = ab + ac ja (b + c)a = ba + ca kaikilla a, b, c R, ja
 Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi binääristä assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme muuten samat ominaisuudet kuin kokonaisluvuilta,
Renkaat Tarkastelemme seuraavaksi rakenteita, joissa on määritelty kaksi binääristä assosiatiivista laskutoimitusta, joista toinen on kommutatiivinen. Vaadimme muuten samat ominaisuudet kuin kokonaisluvuilta,
Transversaalit ja hajoamisaliryhmät
 Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
Transversaalit ja hajoamisaliryhmät Graduseminaariesitelmä Miikka Rytty Matemaattisten tieteiden laitos Oulun yliopisto 2006 Motivointi Esimerkki 1 (Ryhmäteorian kurssin harjoitustehtävä). Jos G on ryhmä,
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 20. lokakuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 20. lokakuuta 2016 G. Gripenberg (Aalto-yliopisto) MS-A0401 Diskreetin matematiikan perusteet
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet
MS-A0402 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 2. huhtikuuta 2015 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteet
MS-A0401 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II
 MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MS-A040 Diskreetin matematiikan perusteet Yhteenveto ja esimerkkejä ym., osa II G. Gripenberg Aalto-yliopisto 4. lokakuuta 0 Modulaariaritmetiikka Eukleideen algoritmi RSA-algoritmi Ryhmät ja permutaatiot
MAT Algebra 1(s)
 8. maaliskuuta 2012 Esipuhe Tämä luentokalvot sisältävät kurssin keskeiset asiat. Kalvoja täydennetään luennolla esimerkein ja todistuksin. Materiaali perustuu Jyväskylän, Helsingin ja Turun yliopistojen
8. maaliskuuta 2012 Esipuhe Tämä luentokalvot sisältävät kurssin keskeiset asiat. Kalvoja täydennetään luennolla esimerkein ja todistuksin. Materiaali perustuu Jyväskylän, Helsingin ja Turun yliopistojen
