Johdatus graafiteoriaan
|
|
|
- Eija Hovinen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta
2 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
3 4.1 Eulerin graafi Eulerin graafien tarkastelun alkuna ja itse asiassa koko graafiteorian alkuna oli ns. Königsbergin siltaongelma (ks. esimerkki 4.2): onko mahdollista lähteä jostakin paikasta ja palata takaisin lähtöpaikkaan niin, että on kulkenut jokaisen sillan kautta täsmälleen kerran. Euler julkaisi tämän ongelman ratkaisun vuonna
4 4.1 Eulerin graafi Eulerin graafien tarkastelun alkuna ja itse asiassa koko graafiteorian alkuna oli ns. Königsbergin siltaongelma (ks. esimerkki 4.2): onko mahdollista lähteä jostakin paikasta ja palata takaisin lähtöpaikkaan niin, että on kulkenut jokaisen sillan kautta täsmälleen kerran. Euler julkaisi tämän ongelman ratkaisun vuonna Määritelmä 4.1 Graafin polku (piiri) on Eulerin polku (piiri), jos se sisältää graafin jokaisen särmän täsmälleen kerran. Yhtenäinen epätriviaali graafi on Eulerin graafi, jos siinä on Eulerin piiri. 167
5 168 Esimerkki 4.1 Kuvan 4.1 graafissa on esimerkiksi Eulerin piiri p: v 5, v 6, v 1, v 5, v 2, v 1, v 4, v 3, v 2, v 4, v 5. G: v 6 v 1 v 5 v 2 v 4 v 3 p: v v 1 3 v v 2 v v 3 Kuva 4.1. Graafissa G on Eulerin piiri p.
6 168 Esimerkki 4.1 Kuvan 4.1 graafissa on esimerkiksi Eulerin piiri p: v 5, v 6, v 1, v 5, v 2, v 1, v 4, v 3, v 2, v 4, v 5. G: v 6 v 1 v 5 v 2 v 4 v 3 p: v v 1 3 v v 2 v v 3 Kuva 4.1. Graafissa G on Eulerin piiri p. Eulerin polku tai piiri on aina yksinkertainen, koska siinä ei ole samaa särmää kahdesti.
7 Lause 4.1 Olkoon G jokin yhtenäinen epätriviaali graafi. Tällöin seuraavat väitteet ovat yhtäpitäviä. 1. Graafi G on Eulerin graafi. 169
8 Lause 4.1 Olkoon G jokin yhtenäinen epätriviaali graafi. Tällöin seuraavat väitteet ovat yhtäpitäviä. 1. Graafi G on Eulerin graafi. 2. Graafin G jokaisen solmun aste on parillinen. 169
9 Lause 4.1 Olkoon G jokin yhtenäinen epätriviaali graafi. Tällöin seuraavat väitteet ovat yhtäpitäviä. 1. Graafi G on Eulerin graafi. 2. Graafin G jokaisen solmun aste on parillinen. 3. Graafi G on joidenkin särmiltään erillisten silmukoiden yhdiste. 169
10 Esimerkki 4.2 (Königsbergin sillat) Königsbergin kaupunki Preussissa (nyk. Kaliningrad Venäjällä) on jakaantunut neljään osaan. Königsbergissä oli 1700-luvulla seitsemän siltaa. Kaupunkilaiset yrittivät löytää sunnuntaikävelyllä kotiovelta kotiovelle vievän reitin, joka kulkee jokaisen sillan ylitse täsmälleen kerran. Euler osoitti, että se on mahdotonta muodostamalla Königsbergin siltoja vastaavan graafin, jossa yhtenäiset maa-alueet ovat solmuja ja sillat särmiä. Tämä graafi ei ole Eulerin graafi. G: v 2 v 1 v 3 Kuva 4.2. Königsbergin sillat ja siltoja vastaava multigraafi G. v 4 170
11 Seuraava lause seuraa suoraan lauseesta 4.1. Lause 4.2 Jokainen Eulerin graafin solmu kuuluu johonkin silmukkaan. 171
12 Seuraava lause seuraa suoraan lauseesta 4.1. Lause 4.2 Jokainen Eulerin graafin solmu kuuluu johonkin silmukkaan. Seuraavaksi tarkastelemme, kuinka monella kynänvedolla graafi voidaan piirtää, jos sen paritonasteisten solmujen lukumäärä tiedetään. Lause 4.3 Olkoon G = (V, E) yhtenäinen graafi, jossa on 2k (k 1) paritonasteista solmua. Tällöin E voidaan jakaa epätyhjiin erillisiin osajoukkoihin E 1, E 2,..., E k siten, että jokainen joukoista E 1, E 2,..., E k muodostaa graafin G yksinkertaisen polun. 171
13 Esimerkki 4.3 Kuvan 4.3 graafissa G on neljä paritonasteista solmua. Näin ollen graafin särmäjoukko voidaan jakaa kahteen epätyhjään joukkoon, joista kumpikin muodostaa graafin G yksinkertaisen polun (esimerkiksi polut p 1 ja p 2 ). Kuvan 4.3 solmut w 1 ja w 2 ovat lauseen 4.3 todistuksessa käytettäviä solmuja. G: u 1 u 2 u 1 u 2 u 1 u 2 w 1 w 2 v 1 v 2 v 1 v 2 v 1 v 2 polku p 1 polku p 2 Kuva 4.3. Graafi G ja kaksi sen yksinkertaista polkua. 172
14 Lauseen 4.3 osajoukkoihin jako ei kuitenkaan ole välttämättä yksikäsitteinen. 173
15 Lauseen 4.3 osajoukkoihin jako ei kuitenkaan ole välttämättä yksikäsitteinen. Lause 4.4 Yhtenäisessä graafissa G on Eulerin polku, muttei Eulerin piiriä täsmälleen silloin, kun täsmälleen kahden graafin G solmun aste on pariton. G: v 2 v 1 v 3 v 5 v 4 Kuva 4.4. Graafi G, jossa on Eulerin polku muttei Eulerin piiriä. 173
16 4.2 Hamiltonin graafi Hamiltonin graafi on saanut nimensä irlantilaisen matemaatikon William Rowan Hamiltonin 1857 esittelemästä tehtävästä. Tehtävänä oli kiertää dodekaedrin kärjet särmiä pitkin niin, että käydään jokaisessa kärjessä vain kerran. Tämä tehtävä antoi nimen kaikille sellaisille graafeille, joista löytyy suora polku tai silmukka, jossa on kaikki graafin solmut. Kuva 4.5. Dodekaedri piirrettynä tasoon. 174
17 Määritelmä 4.2 Graafin polku (piiri, silmukka) on Hamiltonin polku (piiri, silmukka), jos se sisältää graafin jokaisen solmun täsmälleen kerran. Graafi on Hamiltonin graafi, jos siinä on Hamiltonin piiri. G: v 2 p: v v 1 v 3 v 1 v v 5 v 4 v 5 v 5 4 Kuva 4.6. Graafissa G on Hamiltonin piiri p. 175
18 Vähintään kolmisolmuisessa graafissa Hamiltonin piiri on aina myös Hamiltonin silmukka. Ei ole tiedossa yksinkertaista välttämätöntä ja riittävää ehtoa sille, että graafi olisi Hamiltonin graafi. Sen sijaan tunnetaan kylläkin useita välttämättömiä ja useita riittäviä ehtoja. Välttämättömiä ehtoja ovat mm. seuraavat. Vähintään kolmisolmuisessa Hamiltonin graafissa ei ole loppusolmuja eikä irrotussolmuja ja kaksijakoisen Hamiltonin graafin kummassakin solmujoukossa on yhtä monta solmua. 176
19 Vähintään kolmisolmuisessa graafissa Hamiltonin piiri on aina myös Hamiltonin silmukka. Ei ole tiedossa yksinkertaista välttämätöntä ja riittävää ehtoa sille, että graafi olisi Hamiltonin graafi. Sen sijaan tunnetaan kylläkin useita välttämättömiä ja useita riittäviä ehtoja. Välttämättömiä ehtoja ovat mm. seuraavat. Vähintään kolmisolmuisessa Hamiltonin graafissa ei ole loppusolmuja eikä irrotussolmuja ja kaksijakoisen Hamiltonin graafin kummassakin solmujoukossa on yhtä monta solmua. Seuraavaksi esitetään muutama riittävä ehto Hamiltonin graafille. 176
20 Lause 4.5 Olkoon G yksinkertainen n-solmuinen graafi, jonka solmut on järjestetty niin, että deg(v 1 ) deg(v 2 ) deg(v n ). Jos tällöin (1) deg(v n k ) n k aina, kun deg(v k ) k < n/2, niin G on Hamiltonin graafi. 177
21 Lause 4.6 Olkoon G = (V, E) yksinkertainen n-solmuinen (n 3) graafi, jonka solmut on järjestetty niin, että deg(v 1 ) deg(v 2 ) deg(v n ). Tällöin G on Hamiltonin graafi, jos jokin seuraavista ehdoista on voimassa. 1. δ(g) n/2. 178
22 Lause 4.6 Olkoon G = (V, E) yksinkertainen n-solmuinen (n 3) graafi, jonka solmut on järjestetty niin, että deg(v 1 ) deg(v 2 ) deg(v n ). Tällöin G on Hamiltonin graafi, jos jokin seuraavista ehdoista on voimassa. 1. δ(g) n/2. 2. deg(u) + deg(v) n aina, kun u, v V ja {u, v} / E. 178
23 Lause 4.6 Olkoon G = (V, E) yksinkertainen n-solmuinen (n 3) graafi, jonka solmut on järjestetty niin, että deg(v 1 ) deg(v 2 ) deg(v n ). Tällöin G on Hamiltonin graafi, jos jokin seuraavista ehdoista on voimassa. 1. δ(g) n/2. 2. deg(u) + deg(v) n aina, kun u, v V ja {u, v} / E. 3. deg(v k ) > k aina, kun 1 k < n/2. 178
24 Lause 4.6 Olkoon G = (V, E) yksinkertainen n-solmuinen (n 3) graafi, jonka solmut on järjestetty niin, että deg(v 1 ) deg(v 2 ) deg(v n ). Tällöin G on Hamiltonin graafi, jos jokin seuraavista ehdoista on voimassa. 1. δ(g) n/2. 2. deg(u) + deg(v) n aina, kun u, v V ja {u, v} / E. 3. deg(v k ) > k aina, kun 1 k < n/2. 4. deg(v j ) + deg(v k ) n aina, kun j < k, deg(v j ) j ja deg(v k ) k
25 4.3 Tasograafi Graafeja piirrettäessä tavoitteena on tietenkin esityksen selkeys. Yksi selkeyttä haittaava piirre on, että särmät leikkaavat toisiaan. Näin ollen graafin esittämisen kannalta on eduksi, jos graafi voidaan piirtää niin, että mitkään graafin särmät eivät leikkaa toisiaan. 179
26 4.3 Tasograafi Graafeja piirrettäessä tavoitteena on tietenkin esityksen selkeys. Yksi selkeyttä haittaava piirre on, että särmät leikkaavat toisiaan. Näin ollen graafin esittämisen kannalta on eduksi, jos graafi voidaan piirtää niin, että mitkään graafin särmät eivät leikkaa toisiaan. Määritelmä 4.3 Tasograafi on graafi, joka voidaan piirtää tasoon niin, että mitkään graafin särmät eivät leikkaa toisiaan. Esitystä, jossa tasograafi piirretään niin, että särmät eivät leikkaa, sanotaan graafin tasoesitykseksi. G: P 1 : P 2 : Kuva 4.7. Graafi G ja graafin G tasoesitykset P 1 ja P
27 Lause 4.7 Jokaisella yksinkertaisella tasograafilla on tasoesitys, jossa kaikki särmät voidaan piirtää suorina viivoina. 180
28 180 Lause 4.7 Jokaisella yksinkertaisella tasograafilla on tasoesitys, jossa kaikki särmät voidaan piirtää suorina viivoina. Määritelmä 4.4 Tasograafin tasoesitys jakaa tason alueisiin. Aluetta reunustavien särmien lukumäärä on alueen aste (deg( )) (sillat lasketaan mukaan kahteen kertaan). G: Kuva 4.8. Graafi G ja graafin G alueiden asteet.
29 181 Tasograafin alueista yksi on ääretön, muut äärellisiä. Stereograafisen projektion avulla voidaan osoittaa, että graafi on esitettävissä tasossa täsmälleen silloin, kun se on esitettävissä pallon pinnalla. Pallon pinnalla kaikki alueet ovat äärellisiä. Koska projektiossa napa voidaan valita vapaasti, tasograafi voidaan aina esittää tasossa siten, että mikä tahansa etukäteen valittu alue on ääretön. f 3 v 1 v 2 f 1 f 2 v 3 v 4 v 3 v 2 f 1 v 1 f 2 f 3 v 4 v 1 f f 3 1 v 4 f v 2 2 v 3 Kuva 4.9. Graafin kolme eri tasoesitystä. Kussakin esityksessä eri alue on ääretön.
30 Määritelmä 4.5 Tasograafin äärellisiä alueita reunustavia silmukoita sanotaan graafin silmiksi. 182
31 182 Määritelmä 4.5 Tasograafin äärellisiä alueita reunustavia silmukoita sanotaan graafin silmiksi. Lause 4.8 (Eulerin kaava) Jos yhtenäisessä tasograafissa on n solmua, m särmää ja r aluetta, niin n m + r = 2.
32 182 Määritelmä 4.5 Tasograafin äärellisiä alueita reunustavia silmukoita sanotaan graafin silmiksi. Lause 4.8 (Eulerin kaava) Jos yhtenäisessä tasograafissa on n solmua, m särmää ja r aluetta, niin n m + r = 2. Eulerin kaavan avulla voidaan joissakin tapauksissa todistaa ylärajoja tasograafin särmien lukumäärälle, kun solmujen lukumäärä tiedetään. Näitä tuloksia voidaan käyttää esimerkiksi sen osoittamiseen, että jokin tietty graafi ei ole tasograafi.
33 Lause 4.9 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää, niin m 3n
34 183 Lause 4.9 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää, niin m 3n 6. Lause 4.10 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää ja graafissa ei ole kolmen särmän pituisia silmukoita, niin m 2n 4.
35 183 Lause 4.9 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää, niin m 3n 6. Lause 4.10 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää ja graafissa ei ole kolmen särmän pituisia silmukoita, niin m 2n 4. Lause 4.11 Graafit K 5 ja K 3,3 eivät ole tasograafeja.
36 183 Lause 4.9 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää, niin m 3n 6. Lause 4.10 Jos yhtenäisessä yksinkertaisessa tasograafissa on n solmua (n 3) ja m särmää ja graafissa ei ole kolmen särmän pituisia silmukoita, niin m 2n 4. Lause 4.11 Graafit K 5 ja K 3,3 eivät ole tasograafeja. Useat graafit, jotka eivät ole tasograafeja, voidaan piirtää toruksen ( donitsi ) pinnalle. Tällaisia graafeja ovat esimerkiksi K 5 ja K 3,3.
37 Lause 4.12 Yksinkertaisessa tasograafissa on ainakin yksi solmu, jonka aste on korkeintaan
38 Lause 4.12 Yksinkertaisessa tasograafissa on ainakin yksi solmu, jonka aste on korkeintaan 5. Lauseen 4.12 perusteella täydellinen graafi K n ei ole tasograafi, kun n 6, täydellinen kaksijakoinen graafi K m,n ei ole tasograafi, kun m, n
39 Lause 4.12 Yksinkertaisessa tasograafissa on ainakin yksi solmu, jonka aste on korkeintaan 5. Lauseen 4.12 perusteella täydellinen graafi K n ei ole tasograafi, kun n 6, täydellinen kaksijakoinen graafi K m,n ei ole tasograafi, kun m, n 6. Lause 4.13 Graafi on tasograafi täsmälleen silloin, kun sillä ei ole aligraafia, joka olisi kutistettavissa graafiksi K 5 tai K 3,3. 184
40 Lause 4.12 Yksinkertaisessa tasograafissa on ainakin yksi solmu, jonka aste on korkeintaan 5. Lauseen 4.12 perusteella täydellinen graafi K n ei ole tasograafi, kun n 6, täydellinen kaksijakoinen graafi K m,n ei ole tasograafi, kun m, n 6. Lause 4.13 Graafi on tasograafi täsmälleen silloin, kun sillä ei ole aligraafia, joka olisi kutistettavissa graafiksi K 5 tai K 3,3. Esimerkki 4.4 Lauseen 4.13 perusteella kaikki täydellisen graafin K 5 aidot aligraafit ovat tasograafeja. 184
41 185 Esimerkki 4.5 Kuvan 4.10 Petersenin graafi ei ole tasograafi, sillä kutistamalla särmät e 1, e 2, e 3, e 4 ja e 5 saadaan K 5. v 1 e 1 v 6 v 5 v 10 v 7 e 2 e 5 v 2 v 4 v 9 e 3 e 4 v 8 v 3 Kuva Petersenin graafi.
42 Määritelmä 4.6 Jos graafin jonkin solmun asteluku on 2, solmuun tulevien särmien sanotaan olevan sarjassa. Olkoot e 1 = {u, v} ja e 2 = {v, w} sarjassa. Tällöin solmun v poistoa ja särmien e 1 ja e 2 korvaamista yhdellä särmällä {u, w} sanotaan sarjan lyhentämiseksi. Jos taas särmään {u, w} lisätään uusi solmu v, jolloin särmä {u, w} korvataan särmillä {u, v} ja {v, w}, puhutaan sarjan pidentämisestä. 186
43 186 Määritelmä 4.6 Jos graafin jonkin solmun asteluku on 2, solmuun tulevien särmien sanotaan olevan sarjassa. Olkoot e 1 = {u, v} ja e 2 = {v, w} sarjassa. Tällöin solmun v poistoa ja särmien e 1 ja e 2 korvaamista yhdellä särmällä {u, w} sanotaan sarjan lyhentämiseksi. Jos taas särmään {u, w} lisätään uusi solmu v, jolloin särmä {u, w} korvataan särmillä {u, v} ja {v, w}, puhutaan sarjan pidentämisestä. Määritelmä 4.7 Kaksi graafia ovat homeomorfisia, jos ne ovat isomorfisia tai ne voidaan tehdä isomorfisiksi peräkkäisillä sarjan lyhentämisillä ja pidentämisillä.
44 Esimerkki 4.6 Kuvan 4.11 graafit G ja H ovat homeomorfiset, sillä lyhentämällä graafista H pois ensin v 5 ja sitten v 1, v 2 ja v 3 saadaan graafi, joka on isomorfinen graafin G kanssa. G: a b c H: v 1 v 2 v 7 d e v 9 v 6 v 5 v 4 v 3 v 8 Kuva Homeomorfiset graafit G ja H. 187
45 Lause 4.14 (Kuratowskin lause) Graafi on tasograafi täsmälleen silloin, kun sillä ei ole aligraafia, joka olisi homeomorfinen graafin K 5 tai K 3,3 kanssa. 188
46 4.4 Graafin värittäminen Graafin väritysongelmaan törmätään useissa eri yhteyksissä. Ehkä klassisin väritysongelma on kartan eri alueiden (esimerkiksi valtioiden) värittäminen eri väreillä niin, että vierekkäiset alueet ovat aina eri väriset. 189
47 4.4 Graafin värittäminen Graafin väritysongelmaan törmätään useissa eri yhteyksissä. Ehkä klassisin väritysongelma on kartan eri alueiden (esimerkiksi valtioiden) värittäminen eri väreillä niin, että vierekkäiset alueet ovat aina eri väriset. Määritelmä 4.8 Graafin värittämisellä tarkoitetaan värien liittämistä graafin solmuihin niin, että vierussolmut ovat aina eriväriset (solmua ei tällöin pidetä itsensä vierussolmuna). 189
48 4.4 Graafin värittäminen Graafin väritysongelmaan törmätään useissa eri yhteyksissä. Ehkä klassisin väritysongelma on kartan eri alueiden (esimerkiksi valtioiden) värittäminen eri väreillä niin, että vierekkäiset alueet ovat aina eri väriset. Määritelmä 4.8 Graafin värittämisellä tarkoitetaan värien liittämistä graafin solmuihin niin, että vierussolmut ovat aina eriväriset (solmua ei tällöin pidetä itsensä vierussolmuna). Määritelmä 4.9 Graafin G väriluku χ(g) on pienin määrä värejä, joka tarvitaan graafin värittämiseen. 189
49 Esimerkki 4.7 Kuvan 4.12 graafien väriluvut ovat χ(g 1 ) = 3, χ(g 2 ) = 2 ja χ(g 3 ) = 4. G 1 : G 2 : G 3 : Kuva Graafit G 1, G 2 ja G
50 Esimerkki 4.8 Graafin värittämistä voidaan käyttää esimerkiksi tenttipäivien valitsemiseen niin, että kukaan ei joudu kahteen tenttiin samana päivänä. Olkoot kurssit graafin solmuja ja tulkitaan särmien tarkoittavan, että kursseilla on yhteisiä opiskelijoita. Koska kuvan 4.13 graafin väriluku on kolme, tiedämme, että kolme tenttipäivää riittää siihen, että kukaan ei joudu kahteen tenttiin samana päivänä. Algebra (punainen) Graafiteoria (keltainen) Analyysi II (punainen) Ohjelmoinnin tekniikka (sininen) Lineaarialgebra I (keltainen) Kuva Joitakin kursseja yhdistävä graafi. 191
51 Lause 4.15 Jos G on yksinkertainen graafi, niin χ(g) (G)
52 Lause 4.15 Jos G on yksinkertainen graafi, niin χ(g) (G) + 1. Esimerkki 4.9 Täydellisen graafin K n värittämiseen tarvitaan (K n ) + 1 = n väriä, sillä kukin solmu on jokaisen muun solmun vierussolmu. 192
53 Lause 4.15 Jos G on yksinkertainen graafi, niin χ(g) (G) + 1. Esimerkki 4.9 Täydellisen graafin K n värittämiseen tarvitaan (K n ) + 1 = n väriä, sillä kukin solmu on jokaisen muun solmun vierussolmu. Esimerkki 4.10 Parittomanpituisen silmukan C 2k+1 (k + ) värittämiseen tarvitaan (C 2n+1 ) + 1 = 3 väriä. Sen sijaan parillisenpituisen silmukan C 2k värittämiseen riittää kaksi väriä. 192
54 Lause 4.16 Olkoon G yhtenäinen yksinkertainen graafi. Jos G ei ole parittoman pituinen silmukka tai täydellinen graafi, niin χ(g) (G). 193
55 Lause 4.16 Olkoon G yhtenäinen yksinkertainen graafi. Jos G ei ole parittoman pituinen silmukka tai täydellinen graafi, niin χ(g) (G). Lause 4.17 (Nelivärilause) Kunkin tasograafin väriluku on korkeintaan neljä. 193
56 Lause 4.16 Olkoon G yhtenäinen yksinkertainen graafi. Jos G ei ole parittoman pituinen silmukka tai täydellinen graafi, niin χ(g) (G). Lause 4.17 (Nelivärilause) Kunkin tasograafin väriluku on korkeintaan neljä. Muiden kuin tasograafien väriluvulle ei ole ylärajaa. Esimerkiksi täydellisen graafin K n väriluku on sama kuin graafin K n solmujen lukumäärä n. 193
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Graafiteoria matematiikkaako?
 Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
0 v i v j / E, M ij = 1 v i v j E.
 Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Kysymys: Voidaanko graafi piirtää tasoon niin, että sen viivat eivät risteä muualla kuin pisteiden kohdalla?
 7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
b) Olkoon G vähintään kaksi solmua sisältävä puu. Sallitaan verkon G olevan
 Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 8 : 1. Tehtävä 8 : 2
 Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
Tehtävä 8 : 1 Merkitään kirjaimella G tarkasteltavaa Petersenin verkkoa. Olkoon A joukon V(G) niiden solmujen joukko, joita vastaavat solmut sijaitsevat tehtäväpaperin kuvassa ulkokehällä. Joukon A jokaisella
GRAAFITEORIAA. Pertti Koivisto Riitta Niemistö
 GRAAFITEORIAA Pertti Koivisto Riitta Niemistö Esipuhe Tämän monisteen tarkoituksena on tutustuttaa lukija graafiteorian peruskäsitteisiin ja -tuloksiin. Vaikka algoritminen graafiteoria on tietokoneiden
GRAAFITEORIAA Pertti Koivisto Riitta Niemistö Esipuhe Tämän monisteen tarkoituksena on tutustuttaa lukija graafiteorian peruskäsitteisiin ja -tuloksiin. Vaikka algoritminen graafiteoria on tietokoneiden
Pertti Koivisto ja Riitta Niemistö. Graafiteoriaa
 Pertti Koivisto ja Riitta Niemistö Graafiteoriaa TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMPERE 2018 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMMIKUU
Pertti Koivisto ja Riitta Niemistö Graafiteoriaa TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMPERE 2018 TAMPEREEN YLIOPISTO INFORMAATIOTIETEIDEN YKSIKÖN RAPORTTEJA 60/2018 TAMMIKUU
Kuva Suomen päätieverkko 1 Moottoritiet on merkitty karttaan vihreällä, muut valtatiet punaisella ja kantatiet keltaisella värillä.
 POHDIN projekti TIEVERKKO Tieverkon etäisyyksien minimointi ja esimerkiksi maakaapeleiden kokonaismäärän minimointi sekä ylipäätään äärellisen pistejoukon yhdistäminen reitityksillä toisiinsa niin, että
POHDIN projekti TIEVERKKO Tieverkon etäisyyksien minimointi ja esimerkiksi maakaapeleiden kokonaismäärän minimointi sekä ylipäätään äärellisen pistejoukon yhdistäminen reitityksillä toisiinsa niin, että
Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005
 Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Diskreetit rakenteet
 Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Tehtävä 10 : 1. Tehtävä 10 : 2
 Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
Tehtävä 0 : Kuvassa Etelä-Amerikan valtioita vastaavat solmut on sijoitettu toisiinsa nähden niiden pääkaupunkien keskinäistä sijaintia vastaavalla tavalla. Kuvioon on joukon {0,, 2, 3 alkioilla merkitty
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko
 DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
DMP / Kevät 2016 / Mallit Harjoitus 6 / viikko 13 / alkuviikko Alkuviikon tuntitehtävä 1: Montako kahdeksaan yhtäsuureen sektoriin leikattua pitsaa voidaan tehdä kolmesta täytteestä siten, että kukin sektori
7.4. Eulerin graafit 1 / 22
 7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
8.5. Järjestyssuhteet 1 / 19
 8.5. Järjestyssuhteet 1 / 19 Määritelmä Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä).
8.5. Järjestyssuhteet 1 / 19 Määritelmä Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä).
= 5! 2 2!3! = = 10. Edelleen tästä joukosta voidaan valita kolme särmää yhteensä = 10! 3 3!7! = = 120
 Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
Tehtävä 1 : 1 Merkitään jatkossa kirjaimella H kaikkien solmujoukon V sellaisten verkkojen kokoelmaa, joissa on tasan kolme särmää. a) Jokainen verkko G H toteuttaa väitteen E(G) [V]. Toisaalta jokainen
6.4. Järjestyssuhteet
 6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
6.4. Järjestyssuhteet Joukon suhteilla voidaan kuvata myös alkioiden järjestystä tietyn ominaisuuden suhteen. Järjestys on myös kaksipaikkainen suhde (ja on monia erilaisia järjestyksiä). Suhde R joukossa
keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 1 b 3 a 5
 Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus verkkoteoriaan 4. luento
 Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
Näin ollen saadaan tulos rad(g) diam(g). Toisaalta huomataan, että verkon G kaikilla solmuilla x ja y pätee kolmioepäyhtälön nojalla havainto
 Tehtävä 3 : 1 Olkoon G mielivaltainen epätyhjä verkko. Erityisesti siltä ei vaadita äärellisyyttä. Polut ovat verkon G koosta riippumatta määritelmän mukaan aina äärellisiä, joten kahden solmun välisen
Tehtävä 3 : 1 Olkoon G mielivaltainen epätyhjä verkko. Erityisesti siltä ei vaadita äärellisyyttä. Polut ovat verkon G koosta riippumatta määritelmän mukaan aina äärellisiä, joten kahden solmun välisen
Tehtävä 4 : 2. b a+1 (mod 3)
 Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Tehtävä 4 : 1 Olkoon G sellainen verkko, jonka solmujoukkona on {1,..., 9} ja jonka särmät määräytyvät oheisen kuvan mukaisesti. Merkitään lisäksi kirjaimella A verkon G kaikkien automorfismien joukkoa,
Liite: Verkot. TKK (c) Ilkka Mellin (2004) 1
 Liite: Verkot TKK (c) Ilkka Mellin (2004) 1 : Mitä opimme? Verkkoteoria on hyödyllinen sovelletun matematiikan osa-alue, jolla on sovelluksia esimerkiksi logiikassa, operaatiotutkimuksessa, peli-ja päätösteoriassa
Liite: Verkot TKK (c) Ilkka Mellin (2004) 1 : Mitä opimme? Verkkoteoria on hyödyllinen sovelletun matematiikan osa-alue, jolla on sovelluksia esimerkiksi logiikassa, operaatiotutkimuksessa, peli-ja päätösteoriassa
Näytetään nyt relaatioon liittyvien ekvivalenssiluokkien olevan verkon G lohkojen särmäjoukkoja. Olkoon siis f verkon G jokin särmä.
 Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Tehtävä 6 : 1 Oletetaan ensin joukon X olevan sisältymisen suhteen minimaalinen solmut a ja b toisistaan erotteleva joukon V(G)\{a, b} osajoukko. Olkoon x joukon X alkio. Oletuksen nojalla joukko X\{x}
Olkoon seuraavaksi G 2 sellainen tasan n solmua sisältävä suunnattu verkko,
 Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen
 V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
Eulerin verkkojen karakterisointi
 Eulerin verkkojen karakterisointi Pro Gradu -tutkielma Jenni Heikkilä 373175 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 018 Sisältö Johdanto 1 Verkkojen peruskäsitteet 3 1.1 Verkon määrittely.........................
Eulerin verkkojen karakterisointi Pro Gradu -tutkielma Jenni Heikkilä 373175 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 018 Sisältö Johdanto 1 Verkkojen peruskäsitteet 3 1.1 Verkon määrittely.........................
Tehtävä 5 : 1. Tehtävä 5 : 2
 Tehtävä 5 : 1 Merkitään kirjaimella H kuvan punaisten solmujen virittämää verkon G yhtenäistä aliverkkoa, jossa on yhteensä kolme särmää. Aliverkosta H voidaan kahdella tavalla valita kahden solmun joukko
Tehtävä 5 : 1 Merkitään kirjaimella H kuvan punaisten solmujen virittämää verkon G yhtenäistä aliverkkoa, jossa on yhteensä kolme särmää. Aliverkosta H voidaan kahdella tavalla valita kahden solmun joukko
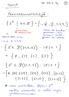 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Johdatus matematiikkaan
 Johdatus matematiikkaan Luento 7 Mikko Salo 11.9.2017 Sisältö 1. Funktioista 2. Joukkojen mahtavuus Funktioista Lukiomatematiikassa on käsitelty reaalimuuttujan funktioita (polynomi / trigonometriset /
Johdatus matematiikkaan Luento 7 Mikko Salo 11.9.2017 Sisältö 1. Funktioista 2. Joukkojen mahtavuus Funktioista Lukiomatematiikassa on käsitelty reaalimuuttujan funktioita (polynomi / trigonometriset /
Ratkaisu: (b) A = x 0 (R(x 0 ) x 1 ( Q(x 1 ) (S(x 0, x 1 ) S(x 1, x 1 )))).
 HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 3 Ratkaisuehdotukset 1. Palataan Partakylään. Olkoon P partatietokanta ja M tästä saatu malli kuten Harjoitusten 1
HY / Matematiikan ja tilastotieteen laitos Johdatus logiikkaan I, syksy 2018 Harjoitus 3 Ratkaisuehdotukset 1. Palataan Partakylään. Olkoon P partatietokanta ja M tästä saatu malli kuten Harjoitusten 1
Kurssikoe on maanantaina 29.6. Muista ilmoittautua kokeeseen viimeistään 10 päivää ennen koetta! Ilmoittautumisohjeet löytyvät kurssin kotisivuilla.
 HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
HY / Avoin ylioisto Johdatus yliopistomatematiikkaan, kesä 201 Harjoitus 7 Ratkaisut palautettava viimeistään perjantaina 26.6.201 klo 16.00. Huom! Luennot ovat salissa CK112 maanantaista 1.6. lähtien.
Berge-perfektit graafit ja Shannonin kapasiteetti
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Joel Syvänen Berge-perfektit graafit ja Shannonin kapasiteetti Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Joel Syvänen Berge-perfektit graafit ja Shannonin kapasiteetti Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
Automaatit. Muodolliset kielet
 Automaatit Automaatit ovat teoreettisia koneita, jotka käsittelevät muodollisia sanoja. Automaatti lukee muodollisen sanan kirjain kerrallaan, vasemmalta oikealle, ja joko hyväksyy tai hylkää sanan. Täten
Automaatit Automaatit ovat teoreettisia koneita, jotka käsittelevät muodollisia sanoja. Automaatti lukee muodollisen sanan kirjain kerrallaan, vasemmalta oikealle, ja joko hyväksyy tai hylkää sanan. Täten
Verkkojen värittäminen
 Verkkojen värittäminen Pro gradu -tutkielma Tiina Aaltonen 165231 Itä-Suomen yliopisto Fysiikan ja matematiikan laitos 10. tammikuuta 2012 Sisältö 1 Johdanto 1 2 Verkkojen peruskäsitteitä 4 2.1 Solmu,
Verkkojen värittäminen Pro gradu -tutkielma Tiina Aaltonen 165231 Itä-Suomen yliopisto Fysiikan ja matematiikan laitos 10. tammikuuta 2012 Sisältö 1 Johdanto 1 2 Verkkojen peruskäsitteitä 4 2.1 Solmu,
Rakenteellinen tasapaino ja transitiivisyys
 1 Hypermedian jatko-opintoseminaari 2008-2009 Rakenteellinen tasapaino ja transitiivisyys 20.2.2009 Seppo Pohjolainen 2 Rakenteellinen tasapaino Käsitteitä: Arvotettu graafi (signed graph) (+ tai - ) Suuntaamaton
1 Hypermedian jatko-opintoseminaari 2008-2009 Rakenteellinen tasapaino ja transitiivisyys 20.2.2009 Seppo Pohjolainen 2 Rakenteellinen tasapaino Käsitteitä: Arvotettu graafi (signed graph) (+ tai - ) Suuntaamaton
Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua)
 Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua) 10.12.2012 Tehtävä 1. Osoita, että tuloryhmän R np R sp indeksi Rubikin paikkaryhmässä R p on täsmälleen kaksi. (Tarkkaan
Ryhmäteoreettinen näkökulma Rubikin kuutioon Harjoitus 6, ratkaisuehdotus (5 sivua) 10.12.2012 Tehtävä 1. Osoita, että tuloryhmän R np R sp indeksi Rubikin paikkaryhmässä R p on täsmälleen kaksi. (Tarkkaan
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Puiden karakterisointi
 Puiden karakterisointi LuK-tutkielma Airta Ella 2502661 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2018 Sisältö Johdanto 2 1 Johdatus verkkoteoriaan 3 1.1 Verkko käsitteenä.........................
Puiden karakterisointi LuK-tutkielma Airta Ella 2502661 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2018 Sisältö Johdanto 2 1 Johdatus verkkoteoriaan 3 1.1 Verkko käsitteenä.........................
Tasograafit ja väritykset
 Solmu /06 Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta
Solmu /06 Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT
 JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT Tehtävä 1. (i) Olkoot n, d 1 ja d n. Osoita, että (k, n) d jos ja vain jos k ad, missä (a, n/d) 1. (ii) Osoita, että jos (m j, m k ) 1 kun
JOHDATUS LUKUTEORIAAN (syksy 2017) HARJOITUS 3, MALLIRATKAISUT Tehtävä 1. (i) Olkoot n, d 1 ja d n. Osoita, että (k, n) d jos ja vain jos k ad, missä (a, n/d) 1. (ii) Osoita, että jos (m j, m k ) 1 kun
Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukko oppi aksiomaattisesti.
 Joukon määritelmä Joukko on alkioidensa kokoelma. Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukko oppi aksiomaattisesti. Näin ei tässä
Joukon määritelmä Joukko on alkioidensa kokoelma. Valitsemalla sopivat alkiot joudutaan tämän määritelmän kanssa vaikeuksiin, jotka voidaan välttää rakentamalla joukko oppi aksiomaattisesti. Näin ei tässä
Algoritmit 1. Luento 1 Ti Timo Männikkö
 Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa.
 Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa. Vastaus 2. Vertaillaan
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus 1. Lasketaan joukkojen alkiot, ja todetaan, että niitä on 3 molemmissa. Vastaus 2. Vertaillaan
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }?
 Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus
Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Miten perustella, että joukossa A = {a, b, c} on yhtä monta alkiota kuin joukossa B = {d, e, f }? Vastaus
VERKKOTEORIAN ALKEITA. Martti E. Pesonen 28.2.2013
 VERKKOTEORIAN ALKEITA Martti E. Pesonen 28.2.2013 1 Sisältö 1 VERKOISTA 1 1.1 Mitä matemaattiset verkot ovat?................ 1 1.1.1 Verkkoteorian synty.................... 1 1.2 Suuntaamaton verkko.......................
VERKKOTEORIAN ALKEITA Martti E. Pesonen 28.2.2013 1 Sisältö 1 VERKOISTA 1 1.1 Mitä matemaattiset verkot ovat?................ 1 1.1.1 Verkkoteorian synty.................... 1 1.2 Suuntaamaton verkko.......................
Graphs in Social Network Analysis And Modeling. Graafit sosiaalisten verkostojen mallintamisessa
 Hypermedian jatko-opintoseminaari 2008 2009 1 Graphs in Social Network Analysis And Modeling Graafit sosiaalisten verkostojen mallintamisessa 28.11.2008 Thumas Miilumäki thumas.miilumaki@tut.fi Sisältö
Hypermedian jatko-opintoseminaari 2008 2009 1 Graphs in Social Network Analysis And Modeling Graafit sosiaalisten verkostojen mallintamisessa 28.11.2008 Thumas Miilumäki thumas.miilumaki@tut.fi Sisältö
 0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
Shorin algoritmin matematiikkaa Edvard Fagerholm
 Edvard Fagerholm 1 Määritelmiä Määritelmä 1 Ryhmä G on syklinen, jos a G s.e. G = a. Määritelmä 2 Olkoon G ryhmä. Tällöin alkion a G kertaluku ord(a) on pienin luku n N \ {0}, jolla a n = 1. Jos lukua
Edvard Fagerholm 1 Määritelmiä Määritelmä 1 Ryhmä G on syklinen, jos a G s.e. G = a. Määritelmä 2 Olkoon G ryhmä. Tällöin alkion a G kertaluku ord(a) on pienin luku n N \ {0}, jolla a n = 1. Jos lukua
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus
 Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Lineaarikombinaatio, lineaarinen riippuvuus/riippumattomuus 1 / 51 Lineaarikombinaatio Johdattelua seuraavaan asiaan (ei tarkkoja määritelmiä): Millaisen kuvan muodostaa joukko {λv λ R, v R 3 }? Millaisen
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) OT
 Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) 31.1.-4.2.2011 OT 1. Määritellään kokonaisluvuille laskutoimitus n m = n + m + 5. Osoita, että (Z, ) on ryhmä.
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 3 (9 sivua) 31.1.-4.2.2011 OT 1. Määritellään kokonaisluvuille laskutoimitus n m = n + m + 5. Osoita, että (Z, ) on ryhmä.
Kenguru 2013 Student sivu 1 / 7 (lukion 2. ja 3. vuosi)
 Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Tasograafit ja väritykset
 Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-Yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta kärkiä; sekä
Tasograafit ja väritykset Esa V. Vesalainen Matematiikan ja systeemianalyysin laitos, Aalto-Yliopisto Graafi on matemaattinen olio, joka koostuu kahdesta eri asiasta: ) äärellisestä joukosta kärkiä; sekä
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 3.5 Reedin-Mullerin koodit Olkoon tässä kappaleessa F = F2 = Z2 ja n = 2 m. Määritellään avaruuteen F n kertolasku koordinaateittain:
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos 3.5 Reedin-Mullerin koodit Olkoon tässä kappaleessa F = F2 = Z2 ja n = 2 m. Määritellään avaruuteen F n kertolasku koordinaateittain:
Tekijäryhmiä varten määritellään aluksi sivuluokat ja normaalit aliryhmät.
 3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
3 Tekijäryhmät Tekijäryhmän käsitteen avulla voidaan monimutkainen ryhmä jakaa osiin. Ideana on, että voidaan erikseen tarkastella, miten laskutoimitus vaikuttaa näihin osiin kokonaisuuksina, ja jättää
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Jenna Laine. Ramseyn teoria
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jenna Laine Ramseyn teoria Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta LAINE, JENNA: Ramseyn teoria Pro
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Jenna Laine Ramseyn teoria Luonnontieteiden tiedekunta Matematiikka Toukokuu 2017 Tampereen yliopisto Luonnontieteiden tiedekunta LAINE, JENNA: Ramseyn teoria Pro
PARITUS KAKSIJAKOISESSA
 PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
Äärellisten mallien teoria
 Äärellisten mallien teoria Harjoituksen 5 ratkaisut (Hannu Niemistö) Tehtävä 1 OlkootGjaG neljän solmun verkkoja Määritä, milloing = 2 G eli verkot ovat osittaisesti isomorfisia kahden muuttujan suhteen
Äärellisten mallien teoria Harjoituksen 5 ratkaisut (Hannu Niemistö) Tehtävä 1 OlkootGjaG neljän solmun verkkoja Määritä, milloing = 2 G eli verkot ovat osittaisesti isomorfisia kahden muuttujan suhteen
Pisteet ja viivat. Multigraafi
 Pisteet ja viivat Josuv on viiva, niin pisteetujav ovat viivanuv päätepisteet (endpoints) ja u jav ovat vierekkäisiä eli vieruspisteitä (neighbours, adjacent points). Piste on irtopiste (isolated point)
Pisteet ja viivat Josuv on viiva, niin pisteetujav ovat viivanuv päätepisteet (endpoints) ja u jav ovat vierekkäisiä eli vieruspisteitä (neighbours, adjacent points). Piste on irtopiste (isolated point)
2.1. Tehtävänä on osoittaa induktiolla, että kaikille n N pätee n = 1 n(n + 1). (1)
 Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
Approbatur 3, demo, ratkaisut Sovitaan, että 0 ei ole luonnollinen luku. Tällöin oletusta n 0 ei tarvitse toistaa alla olevissa ratkaisuissa. Se, pidetäänkö nollaa luonnollisena lukuna vai ei, vaihtelee
Tietojenkäsittelytieteen ja tilastotieteen matematiikkaa 1/137
 Tietojenkäsittelytieteen ja tilastotieteen matematiikkaa 1/137 Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi...
Tietojenkäsittelytieteen ja tilastotieteen matematiikkaa 1/137 Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi...
Hamiltonin sykleistä graateoriassa
 Hamiltonin sykleistä graateoriassa Pro gradu -tutkielma Ohto Nordberg 1335868 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2013 Sisältö Johdanto 2 1 Historiaa 3 1.1 Euler................................
Hamiltonin sykleistä graateoriassa Pro gradu -tutkielma Ohto Nordberg 1335868 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2013 Sisältö Johdanto 2 1 Historiaa 3 1.1 Euler................................
on Abelin ryhmä kertolaskun suhteen. Tämän joukon alkioiden lukumäärää merkitään
 5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
5. Primitiivinen alkio 5.1. Täydennystä lukuteoriaan. Olkoon n Z, n 2. Palautettakoon mieleen, että kokonaislukujen jäännösluokkarenkaan kääntyvien alkioiden muodostama osajoukko Z n := {x Z n x on kääntyvä}
Johdatus graafiteoriaan
 Johdatus graafitoriaan Syksy 2017 Lauri Hlla Tamprn yliopisto Luonnontitidn tidkunta 2 Luku 1 Pruskäsittitä 1.1 Määritlmiä 1.2 Esimrkkjä 1.3 Trminologiaa 1.4 Joitakin rikoisia yksinkrtaisia graafja 1.5
Johdatus graafitoriaan Syksy 2017 Lauri Hlla Tamprn yliopisto Luonnontitidn tidkunta 2 Luku 1 Pruskäsittitä 1.1 Määritlmiä 1.2 Esimrkkjä 1.3 Trminologiaa 1.4 Joitakin rikoisia yksinkrtaisia graafja 1.5
MS-A0003/A0005 Matriisilaskenta Malliratkaisut 5 / vko 48
 MS-A3/A5 Matriisilaskenta Malliratkaisut 5 / vko 48 Tehtävä (L): a) Onko 4 3 sitä vastaava ominaisarvo? b) Onko λ = 3 matriisin matriisin 2 2 3 2 3 7 9 4 5 2 4 4 ominaisvektori? Jos on, mikä on ominaisarvo?
MS-A3/A5 Matriisilaskenta Malliratkaisut 5 / vko 48 Tehtävä (L): a) Onko 4 3 sitä vastaava ominaisarvo? b) Onko λ = 3 matriisin matriisin 2 2 3 2 3 7 9 4 5 2 4 4 ominaisvektori? Jos on, mikä on ominaisarvo?
33. pohjoismainen matematiikkakilpailu 2019 Ratkaisut
 33. pohjoismainen matematiikkakilpailu 2019 Ratkaisut 1. Kutsutaan (eri) positiivisten kokonaislukujen joukkoa merkitykselliseksi, jos sen jokaisen äärellisen epätyhjän osajoukon aritmeettinen ja geometrinen
33. pohjoismainen matematiikkakilpailu 2019 Ratkaisut 1. Kutsutaan (eri) positiivisten kokonaislukujen joukkoa merkitykselliseksi, jos sen jokaisen äärellisen epätyhjän osajoukon aritmeettinen ja geometrinen
Approbatur 3, demo 1, ratkaisut A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat.
 Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Liittomatriisi. Liittomatriisi. Määritelmä 16 Olkoon A 2 M(n, n). Matriisin A liittomatriisi on cof A 2 M(n, n), missä. 1) i+j det A ij.
 Liittomatriisi Määritelmä 16 Olkoon A 2 M(n, n). Matriisin A liittomatriisi on cof A 2 M(n, n), missä (cof A) ij =( 1) i+j det A ij kaikilla i, j = 1,...,n. Huomautus 8 Olkoon A 2 M(n, n). Tällöin kaikilla
Liittomatriisi Määritelmä 16 Olkoon A 2 M(n, n). Matriisin A liittomatriisi on cof A 2 M(n, n), missä (cof A) ij =( 1) i+j det A ij kaikilla i, j = 1,...,n. Huomautus 8 Olkoon A 2 M(n, n). Tällöin kaikilla
TIETOTEKNIIKAN MATEMATIIKKA
 TIETOTEKNIIKAN MATEMATIIKKA Harjoitus 4 syksy 2016 Ratkaisut 1. Mitä ehtoja joukkojen M ja N tulee täyttää (kussakin kohdassa erikseen), jotta seuraavat väittämät olisivat tosia a) M = b) N \ M = c) M
TIETOTEKNIIKAN MATEMATIIKKA Harjoitus 4 syksy 2016 Ratkaisut 1. Mitä ehtoja joukkojen M ja N tulee täyttää (kussakin kohdassa erikseen), jotta seuraavat väittämät olisivat tosia a) M = b) N \ M = c) M
Koodausteoria, Kesä 2014
 Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos Koodausteoria 10 op Kontaktiopetusta 50 h, 26.5. - 26.6. ma 10-14, ti 10-13, to 10-13 Aloitusviikolla poikkeuksellisesti ke 10-13 torstain
Koodausteoria, Kesä 2014 Topi Törmä Matemaattisten tieteiden laitos Koodausteoria 10 op Kontaktiopetusta 50 h, 26.5. - 26.6. ma 10-14, ti 10-13, to 10-13 Aloitusviikolla poikkeuksellisesti ke 10-13 torstain
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 10.4.18 Netspace Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon duaali, verkon upottaminen, verkon genus, verkon komplementti,
Johdatus verkkoteoriaan luento 10.4.18 Netspace Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon duaali, verkon upottaminen, verkon genus, verkon komplementti,
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto
 Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
Matematiikan ja tilastotieteen laitos Algebra I - Kesä 2009 Ratkaisuehdoituksia harjoituksiin 8 -Tehtävät 3-6 4 sivua Heikki Koivupalo ja Rami Luisto 3. Oletetaan, että kunnan K karakteristika on 3. Tutki,
GRAAFITEORIA. Keijo Ruohonen
 GRAAFITEORIA Keijo Ruohonen 2013 Sisältö 1 I MÄÄRITELMIÄ JA PERUSTULOKSIA 1 1.1 Määritelmiä 5 1.2 Kulku. Reitti. Polku. Piiri. Yhtenäisyys. Komponentti 10 1.3 Graafien operaatioita 14 1.4 Irrotus 17 1.5
GRAAFITEORIA Keijo Ruohonen 2013 Sisältö 1 I MÄÄRITELMIÄ JA PERUSTULOKSIA 1 1.1 Määritelmiä 5 1.2 Kulku. Reitti. Polku. Piiri. Yhtenäisyys. Komponentti 10 1.3 Graafien operaatioita 14 1.4 Irrotus 17 1.5
TAMPEREEN YLIOPISTO Pro gradu -tutkielma. Matti Koskinen. Ostomakhion, Antiikin vatsavaivoista nykypäivän ongelmanratkontaan
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Matti Koskinen Ostomakhion, Antiikin vatsavaivoista nykypäivän ongelmanratkontaan Informaatiotieteiden yksikkö Matematiikka Kesäkuu 2014 Tampereen yliopisto Informaatiotieteiden
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Matti Koskinen Ostomakhion, Antiikin vatsavaivoista nykypäivän ongelmanratkontaan Informaatiotieteiden yksikkö Matematiikka Kesäkuu 2014 Tampereen yliopisto Informaatiotieteiden
Todistus (2.2) Todistus (2.2) jatkoa. (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio.
 Todistus (2.2) (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio. Selvästi bittijono f sisältää ainakin yhden1:sen. Voidaan olettaa, että f 1
Todistus (2.2) (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio. Selvästi bittijono f sisältää ainakin yhden1:sen. Voidaan olettaa, että f 1
Diskreetin matematiikan perusteet Esimerkkiratkaisut 3 / vko 10
 Diskreetin matematiikan perusteet Esimerkkiratkaisut / vko 0 Tuntitehtävät - lasketaan alkuviikon harjoituksissa ja tuntitehtävät - loppuviikon harjoituksissa. Kotitehtävät - tarkastetaan loppuviikon harjoituksissa.
Diskreetin matematiikan perusteet Esimerkkiratkaisut / vko 0 Tuntitehtävät - lasketaan alkuviikon harjoituksissa ja tuntitehtävät - loppuviikon harjoituksissa. Kotitehtävät - tarkastetaan loppuviikon harjoituksissa.
802320A LINEAARIALGEBRA OSA I
 802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
802320A LINEAARIALGEBRA OSA I Tapani Matala-aho MATEMATIIKKA/LUTK/OULUN YLIOPISTO SYKSY 2016 LINEAARIALGEBRA 1 / 72 Määritelmä ja esimerkkejä Olkoon K kunta, jonka nolla-alkio on 0 ja ykkösalkio on 1 sekä
Harmoniset funktiot graafeilla
 Harmoniset funktiot graafeilla Henri Raudaskoski Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2017 Tiivistelmä: Henri Raudaskoski, Harmoniset funktiot graafeilla
Harmoniset funktiot graafeilla Henri Raudaskoski Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kevät 2017 Tiivistelmä: Henri Raudaskoski, Harmoniset funktiot graafeilla
Algoritmit 1. Luento 8 Ke Timo Männikkö
 Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Luku 5. Löwenheimin ja Skolemin lause. kompaktisuuslause. Tässä luvussa tutustumme tärkeimpiin täydellisyyslauseen (ja sen todistuksen) seurauksiin.
 Luku 5 Löwenheimin ja Skolemin lause, kompaktisuuslause Tässä luvussa tutustumme tärkeimpiin täydellisyyslauseen (ja sen todistuksen) seurauksiin. Löwenheimin ja Skolemin lause Sanomme, että kaavajoukko
Luku 5 Löwenheimin ja Skolemin lause, kompaktisuuslause Tässä luvussa tutustumme tärkeimpiin täydellisyyslauseen (ja sen todistuksen) seurauksiin. Löwenheimin ja Skolemin lause Sanomme, että kaavajoukko
Helsingin seitsemäsluokkalaisten matematiikkakilpailu 7.2.2013 Ratkaisuita
 Helsingin seitsemäsluokkalaisten matematiikkakilpailu..013 Ratkaisuita 1. Eräs kirjakauppa myy pokkareita yhdeksällä eurolla kappale, ja siellä on meneillään mainoskampanja, jossa seitsemän sellaista ostettuaan
Helsingin seitsemäsluokkalaisten matematiikkakilpailu..013 Ratkaisuita 1. Eräs kirjakauppa myy pokkareita yhdeksällä eurolla kappale, ja siellä on meneillään mainoskampanja, jossa seitsemän sellaista ostettuaan
Todistusmenetelmiä Miksi pitää todistaa?
 Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
Todistusmenetelmiä Miksi pitää todistaa? LUKUTEORIA JA TO- DISTAMINEN, MAA11 Todistus on looginen päättelyketju, jossa oletuksista, määritelmistä, aksioomeista sekä aiemmin todistetuista tuloksista lähtien
14. Juurikunnat Määritelmä ja olemassaolo.
 14. Juurikunnat Mielivaltaisella polynomilla ei välttämättä ole juuria tarkasteltavassa kunnassa. Tässä luvussa tutkitaan sellaisia algebrallisia laajennoksia, jotka saadaan lisäämällä polynomeille juuria.
14. Juurikunnat Mielivaltaisella polynomilla ei välttämättä ole juuria tarkasteltavassa kunnassa. Tässä luvussa tutkitaan sellaisia algebrallisia laajennoksia, jotka saadaan lisäämällä polynomeille juuria.
rm + sn = d. Siispä Proposition 9.5(4) nojalla e d.
 9. Renkaat Z ja Z/qZ Tarkastelemme tässä luvussa jaollisuutta kokonaislukujen renkaassa Z ja todistamme tuloksia, joita käytetään jäännösluokkarenkaan Z/qZ ominaisuuksien tarkastelussa. Jos a, b, c Z ovat
9. Renkaat Z ja Z/qZ Tarkastelemme tässä luvussa jaollisuutta kokonaislukujen renkaassa Z ja todistamme tuloksia, joita käytetään jäännösluokkarenkaan Z/qZ ominaisuuksien tarkastelussa. Jos a, b, c Z ovat
Tehtäväsarja I Tehtävät 1-5 perustuvat monisteen kappaleisiin ja tehtävä 6 kappaleeseen 2.8.
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 8 Harjoitus Ratkaisuehdotuksia Tehtäväsarja I Tehtävät -5 perustuvat monisteen kappaleisiin..7 ja tehtävä 6 kappaleeseen.8..
Johdatus matematiikkaan - tarinaosasto Tero Kilpeläinen
 Tero Kilpeläinen Syksy 2011 Mitä todistettavaa? Seuraavassa esimerkkejä lauseista, joiden todistukset eivät ole ilmeisiä. Aritmetiikan peruslause Jokainen luonnollinen luku voidaan esittää yksikäsitteisellä
Tero Kilpeläinen Syksy 2011 Mitä todistettavaa? Seuraavassa esimerkkejä lauseista, joiden todistukset eivät ole ilmeisiä. Aritmetiikan peruslause Jokainen luonnollinen luku voidaan esittää yksikäsitteisellä
b) Määritä myös seuraavat joukot ja anna kussakin tapauksessa lyhyt sanallinen perustelu.
 Johdatus yliopistomatematiikkaan Helsingin yliopisto, matematiikan ja tilastotieteen laitos Kurssikoe 23.10.2017 Ohjeita: Vastaa kaikkiin tehtäviin. Ratkaisut voi kirjoittaa samalle konseptiarkille, jos
Johdatus yliopistomatematiikkaan Helsingin yliopisto, matematiikan ja tilastotieteen laitos Kurssikoe 23.10.2017 Ohjeita: Vastaa kaikkiin tehtäviin. Ratkaisut voi kirjoittaa samalle konseptiarkille, jos
