Polypropeenin fysikaalisten ominaisuuksien muutokset ekstruusioprosessissa
|
|
|
- Päivi Pesonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Polypropeenin fysikaalisten ominaisuuksien muutokset ekstruusioprosessissa Ossi Parvela Pro Gradu -tutkielma Jyväskylän yliopisto Fysiikan laitos / Paccor Finland 21. toukokuuta 2013 Ohjaajat: Markku Kataja, Heikki Rantanen
2 Tiivistelmä Tässä työssä on tutkittu isotaktisesta polypropeenilevystä lämpömuovaamalla valmistettujen kansien kieroutumista sekä mekaanisten ominaisuuksien muutoksia. Syitä kansien kieroutumiseen on etsitty tutkimalla isotaktisen polypropeenin moolimassajakauman sekä kiteisyysasteen muutoksia eri levynvalmistusprosessin parametreilla. Lisäksi on tutkittu lisäaineiden sekä uudelleenrouhitun raaka-aineen vaikutuksia levyn moolimassajakaumaan. Moolimassajakaumat mittaamiseen käytettiin geelipermeaatiokromatografiaa (GPC) ja kiteisyysasteet mitattiin differentiaalisella pyyhkäisykalorimetrilla (DSC). Prosessiparametreilla ei ollut vaikutusta kansien mekaanisiin ominaisuuksiin, mutta kansien kieroutuminen väheni huomattavasti tietyillä keskitelan lämpötilan arvoilla. i
3 Esipuhe Tämän tutkimuksen lähtökohtana oli laadulliset ongelmat työnantajani Paccor Finlandin valmistamissa muovikansissa. Esitin työnantajalleni ehdotuksen, jossa laatuongelmia lähdettäisiin selvittämään aivan tuotantoprosessin alkuvaiheista - toisin kuin tähän asti oltiin tehty. Tutkimuksen valmisteluissa kului kohtuullisesti aikaa, sillä aluksi lähdin selvittämään, mitkä ominaisuudet muovilevyssä ovat merkittäviä lopputuotteen laadun kannalta. Tämän jälkeen tuli selvittää, miten ja missä kyseisiä ominaisuuksia voidaan luotettavasti mitata sekä miten levynajoprosessin parametreilla pystyisi vaikuttamaan muovilevyn ominaisuuksiin. Lopuksi tarvitsi vielä suunnitella ja suorittaa levykoeajot, joita kertyi yhteensä 17 kappaletta. Tutkimus eteni hyvää vauhtia aina työnantajalle tehtyyn loppuraporttiin asti, mutta itse tutkielman kirjoitusosuus hidastui huomattavasti perheenlisäyksen johdosta. Työn ja lapsiperheen arjen keskellä tutkielmaan käytettävä aika tuntui olevan kortilla. Haluan kiittää kollegoitani saamastani tuesta, sekä erityisesti Hannu Ahosta tutkimuksen koeajovaiheen avustamisesta. Lisäksi haluan kiittää Heikki Rantasta työn tarkastamisesta sekä professori Markku Katajaa avustamisesta sekä työn tarkastamisesta. Tärkeimpänä haluan kuitenkin kiittää avovaimoani Kirsikkaa, joka lapsiperheen kiireiden keskellä mahdollisti tutkielman kirjoittamisen loppuun. Ossi Parvela ossi.t.parvela@jyu.fi Jyväskylässä ii
4 Sisältö Esipuhe ii 1 Johdanto 1 2 Polypropeenin tärkeimmät fysikaaliset ominaisuudet ekstruusiossa Polypropeeni Moolimassajakauma Isotaktinen polypropeeni Kiteytyminen ja polymorfismi Kiteisyysaste Mittausmenetelmät Moolimassajakauma Kiteisyysaste Tehokompensoidun DSC:n toimintaperiaate Sulamisentalpian määrittäminen DSC-käyrästä Maksimikiteisyyden määritys Levykokeet tuotantoprosessissa Levykoneen toimintaperiaate Testilevyjen valmistus puhtaista raaka-aineista Prosessin ajoparametrien muutokset Keskitelan lämpötilan muutos Massan lämpötilan muutos Kokeet syvävetokoneella Tulokset Eri raaka-aineseosten moolimassajakaumia iii
5 5.1.1 Homopolymeeri HB300TF Kopolymeerin vaihdon vaikutukset Rouheen ja lisäaineiden vaikutus levyn moolimassajakaumaan Keskitelan lämpötilan vaikutus levyn kiteisyysasteeseen Massan lämpötilan vaikutus levyn moolimassajakaumaan Levynajoprosessin parametrien vaikutus lopputuotteeseen Johtopäätökset 34 iv
6 1 Johdanto Paccor Finland valmistaa muovista kertakäyttöisiä elintarvikepakkauksia, muovirasioita sekä -kansia. Tuotantoprosessi koostuu kahdesta erillisestä osasta. Ensimmäisessä osassa raaka-aineet sekoitetaan ja sulatetaan ekstruusiolla, jonka jälkeen muovi ajetaan levyksi. Toisessa osassa levy lämmitetään lähelle sulamispistettä ja lämpömuovataan lopputuotteeksi. Pääraaka-aine tuotteiden valmistuksessa on polypropeeni (PP), jonka fysikaaliset ominaisuudet vaikuttavat suurilta osin lopputuotteen ominaisuuksiin. Muita muovilevyn valmistuksessa käytettäviä aineita ovat väriaineet ja levyn staattista sähköisyyttä vähentävä antistaattiaine, joiden osuudet yhteensä muovilevyn massaan suhteutettuna ovat tyypillisesti noin viiden prosentin luokkaa. Tuotannossa käytettävien yksittäisten raaka-aineiden ominaisuudet ovat hyvin tiedossa, mutta niiden yhteisvaikutuksesta muun muassa ekstruusioprosessissa ei löydy aiempia tutkimuksia. Raaka-aineiden valmistajien antamat tiedot tuotteiden ominaisuuksista ovat lähes poikkeuksetta mitattu standardiolosuhteissa, jotka eroavat tuotannon prosessiolosuhteista. Lisäksi raaka-aineiden ominaisuudet hyvin todennäköisesti muuttuvat ekstruusioprosessin aikana, mikä hankaloittaa lopputuotteen ominaisuuksien ja siten myös laadun hallintaa. Tällä hetkellä suurimmat ongelmat tuotannossa liittyvät polypropeenista valmistettuihin rasioiden kansiin. Ensimmäinen ongelma on kansien kieroutuminen muotoiluvaiheessa. Kyseinen ilmiö aiheuttaa ongelmia niin tuotannossa kuin asiakkaallakin. Tuotannossa kierot kannet aiheuttavat häiriöitä painokoneen syöttölaitteessa ja asiakkaalla kannen asettamisessa täytetyn muovirasian päälle. Toinen ongelma liittyy kansien helmojen vahvuuden vaihteluun, joka myös aiheuttaa ongelmia painokoneen syöttölaitteessa. Näihin ongelmiin on yritetty löytää ratkaisua etsimällä oikeita prosessiparametreja lämpömuovaukseen, mutta lämpömuovauksella ei tunnu juurikaan olevan vaikutusta kansien kieroutumiseen eikä helmojen vahvuuteenkaan ole pystytty vaikuttamaan riittävästi. Tästä syystä päätettiin lähteä etsimään ratkaisua näihin ongelmiin tuotantoprosessin alkupäästä eli ekstruusioprosessista. Polypropeenista valmistetussa levyssä on kaksi ominaisuutta, jotka pääosin vaikuttavat lämpömuovauksella valmistettavien kansien ominaisuuksiin. Levyn moolimassajakauma sekä kiteisyysaste määrittävät pitkälti valmiin kannen mekaaniset ominaisuudet sekä vaikuttavat osittain kannen materiaalijakaumaan [1] [2]. Lisäksi levyn kiteiden sekä molekyyliketjujen mahdollinen orientoituminen saattaa vaikuttaa kansien mekaanisiin ominaisuuksiin sekä materiaalijakaumaan [3]. Kiteiden ja molekyyliketjujen orientoitumista ei kuitenkaan voitu resurssien puitteissa tässä tutkimuksessa mitata. 1
7 2 Polypropeenin tärkeimmät fysikaaliset ominaisuudet ekstruusiossa Tämän luvun tarkoituksena on pohjustaa tutkimuksessa esiintyvien ilmiöiden teoreettista taustaa ja antaa tarvittavat lähtötiedot tutkimuksessa esitettyjen tulosten ymmärtämiseksi. Lisäksi luvussa perehdytään tarkemmin polypropeenin rakenteeseen sekä kiteytymiseen tuotannossa tapahtuvien prosessien ymmärtämiseksi. 2.1 Polypropeeni Polypropeenilla tarkoitetaan propeenista (CH 3 ) polymerisoimalla valmistettua polymeeriketjua. Polypropeenin kemiallinen kaava on [CH 2 CH(CH 3 )] n, joka on esitetty havainnollisemmin kuvassa 1. Kemiallinen kaava ilmaisee atomitasolla pienimmän mahdollisen rakennuspalikan, jota monistamalla n kertaa saadaan esitettyä aineen täydellinen rakennekaava. Polymeerien tapauksessa yksittäistä rakennuspalikkaa kutsutaan monomeeriksi. Polypropeenin tapauksessa n voi olla esimerkiksi Kuva 1: Polypropeeni [CH 2 CH(CH 3 )] n Polypropeenin runko muodostuu yksinkertaisilla sidoksilla toisissaan kiinni olevista hiiliatomeista (C). Runkoon on lisäksi kiinnittynyt metyyliryhmiä (CH 3 ) sekä vetyatomeita (H). Metyyliryhmien sijoittuminen toisiinsa nähden hiilirungossa määrittelee pitkälti polypropeenin ominaisuudet. Metyyliryhmä on kiinnittynyt joka toiseen hiilirungon atomiin ja ne voivat järjestäytyä kolmella eri tavalla, jotka on esitettynä kuvassa 2. Isotaktisessa polypropeenissa (ipp) kaikki metyyliryhmät sijaitsevat samalla puolella hiilirunkoa. Polypropeenin isotaktisuudella on suuri vaikutus polypropeenin kykyyn kiteytyä ja tästä syystä valtaosa teollisuudessa käytetystä polypropeenista on nimenomaan isotaktista. Syndiotaktisessa polypropeenissa (spp) metyyliryhmät ovat jakautuneet tasaisesti molemmin puolin hiilirunkoa. Säännöllisen rakenteensa vuoksi se myös kiteytyy hyvin, mutta se ei ole yhtä jäykkää kuin isotaktinen polypropeeni [4, Vol 7, sivu 76]. Isotaktisen polypropeenin esteettinen ongelma on sen sameus, kun taas syndiotaktinen polypropeeni on huomattavasti isotaktista polypropeenia kirkkaampaa. 2
8 Kuva 2: Polypropeenin taktisuus Kolmas polypropeenin esiintymismuoto on ataktinen (app), jossa metyyliryhmät ovat sijoittuneet satunnaisesti hiilirungossa. Ataktisen polypropeenin kiteytyminen on kuitenkin heikkoa ja kiinteässä muodossa se on käytännössä täysin amorfista. Tästä syystä sen valmistaminen kaupalliseen käyttöön on marginaalista. Polypropeenia, joka koostuu ainoastaan kuvassa 1 esitetystä monomeerista [CH 2 CH(CH 3 )], kutsutaan homopolymeeriseksi polypropeeniksi. Polypropeenin fysikaalisiin ja kemiallisiin ominaisuuksiin voidaan vaikuttaa lisäämällä siihen muita monomeereja. Tätä kutsutaan kopolymeroinniksi ja sen avulla muodostettua polypropeenia kopolymeeriseksi polypropeeniksi. Yleisin teollisuudessa polypropeenin yhteydessä kopolymeerina käytetty monomeeri on eteeni C 2 H Moolimassajakauma Valmistettaessa polypropeenia Ziegler-Nattan menetelmällä saadaan aikaiseksi polypropeeniketjuja, joilla on tietty pituusjakauma [5]. Pituusjakauman sijasta yleisemmin käytetään termiä molekyylimassajakauma tai moolimassajakauma. Moolimassa ilmaisee, kuinka monta grammaa painaa yksi mooli ainetta. Mooli tarkoittaa molekyylien, tai molekyyliketjujen, lukumäärää kerrottuna Avogadron luvulla 3
9 6, Näin ollen esimerkiksi yhdessä moolissa polypropeenia on 6, polypropeeniketjua. Aineen keskimääräinen moolimassa M d voidaan laskea kaavalla M d = i N im i i N, (1) i missä i on juokseva numero, joka käy läpi kaikki eripituiset molekyyliketjut. Indeksiä i vastaavan molekyyliketjun moolimassa on M i ja niitä on N i kappaletta. Keskimääräinen moolimassa ei kuitenkaan ole kovin yleisesti käytetty luku polymeerien yhteydessä. Tämä johtuu siitä, että leveän moolimassajakaumat omaavilla polymeereilla pitkät molekyyliketjut antavat keskiarvoon enemmän kontribuutiota kuin pienet molekyyliketjut. Näin ollen näytteestä satunnaisesti poimitun molekyyliketjun moolimassa ei todennäköisesti ole lähellä näytteen keskimääräistä moolimassaa. Keskimääräisen moolimassan sijasta käytetäänkin massapainotettua moolimassaa M w, joka saadaan kaavalla [6, s. 7] M w = i N im 2 i i N im i. (2) Teollisten polymeerien, kuten polyproeenin, moolimassajakauma on logaritmisella asteikolla usein muodoltaan normaalijakauman kaltainen. Tällöin jakauman leveyttä kuvaavat keskihajonta σ sekä varianssi σ 2, joka määritellään yleisesti muuttujalle M σ 2 = M 2 M 2, (3) missä hakaset merkitsevät keskiarvoa. Polymeereille varianssi voidaan määritellä keskimääräisen moolimassajakauman M d avulla kaavaa 1 käyttäen seuraavasti σ 2 i = N im 2 i i N M 2 d. (4) i Kertomalla ja jakamalla ensimmäinen termi sopivasti lausekkeella i N im i saadaan varianssin kaava muotoon σ 2 i = N im 2 i i N im i i N i i N M 2 d. (5) im i Yhtälöiden 1 ja 2 avulla lauseke saadaan sievennettyä muotoon σ 2 = M w M d M 2 d = M 2 d 4 ) 1 M d. (6) ( Mw
10 Täten keskihajonta σ voidaan kirjoittaa muodossa σ = M d Mw M d 1. (7) Jakauman leveyttä kuvaa keskihajonnan lisäksi variaatiokerroin CV, joka on dimensioton suure. Se määritellään keskihajonnan ja keskiarvon suhteena seuraavasti: CV = σ M d = Mw M d 1. (8) Yhtälöstä 8 huomataan, että variaatiokertoimen suuruuteen vaikuttaa ainoastaan termi M w /M d. Tätä termiä kutsutaan polydispersiteetiksi PI ja se siis määritellään PI = M w M d. (9) Polydispersiteettiä voidaan siis käyttää jakauman leveyden kuvaamiseen yhtälön 8 perusteella. Variaatiokertoimen lausekkeen perusteella polydispersiteetin täytyy olla suurempi tai yhtäsuuri kuin yksi. Tämä tarkoittaa, että massapainotetun moolimassan M w täytyy olla suurempi tai yhtäsuuri kuin keskimääräisen moolimassan M d. Tämä pätee kuitenkin kaikille polydisperseille polymeereille [7, s. 22]. Yhtäsuuruus pätee ainoastaan monodisperseille polymeereille, kuten esimerkiksi proteiineille. 2.3 Isotaktinen polypropeeni Kiteytyminen ja polymorfismi Kiteytynyttä polypropeenia esiintyy sekä isotaktisessa, että syndiotaktisessa muodossa. Tässä tutkimuksessa keskitytään kuitenkin ainoastaan isotaktisen polypropeenin kiteytymiseen, sillä Paccor Finland käyttää tuotannossaan vain isotaktista polypropeenia. Isotaktisella polypropeenilla, kuten monilla muillakin kiteytyvillä polymeereillä, esiintyy polymorfismia. Polymorfismi tarkoittaa sitä, että aineella voi olla useita toisistaan eroavia kiderakenteita. Isotaktisella polypropeenilla niitä on neljä: α, β, γ, sekä smektinen kiderakenne. Tarkastelu rajoitetaan kuitenkin ainoastaan α-kiderakenteeseen sekä sen muodostumiseen. Isotaktisen polypropeenin kiteytymisen teoria lähtee liikkeelle ipp-ketjun muodosta, joka on kierteelle kääntynyt spriraali. Yhteen kierrokseen pituusakselin ympäri tarvitaan kolme propeenimolekyyliä [8]. Lisäksi ipp on raseeminen polymeeri, joka tarkoittaa, että ipp-ketjuja esiintyy yhtä paljon sekä vasen- (L) että oikeankätisenä (R). Molemmat ipp-ketjut on esitetty havainnollisemmin kuvassa 3, josta nähdään, 5
11 että vasen- ja oikeankätiset ketjut ovat keskenään peilisymmetrisiä, jolloin vasenkätisestä ketjusta saadaan aikaan oikeankätinen ketju peilaamalla se pituusakselinsa suhteen. Lisäksi ipp-ketjulla on vielä kaksi mahdollista konfiguraatiota, jotka saadaan kääntämällä ketjua 180 pituusakselin normaalin ympäri [9]. Näistä konfiguraatioista käytetään usein nimitystä ylös (u) ja alas (d). Näin ollen ipp-ketjulla on yhteensä neljä erilaista molekyylikonfiguraatiota: L u, L d, R u sekä R d. Kiderakenteita tarkasteltaessa voidaan kuitenkin selkeyden vuoksi jättää u- ja d-konfiguraatiot huomioimatta. Kuva 3: Isotaktisen polypropeenin mahdolliset molekyylikonfiguraatiot [10] Isotaktisen polypropeenin kiteytyessä kiderakenne määräytyy ipp-ketjujen kätisyyden perusteella [11]. α-kiteisen polypropeenin (αipp) kiderakenne muodostuu vuorottelevista L- ja R-ketjutasoista [8]. Kiderakenne ilmenee havainnollisemmin kuvasta 4, jossa α-kiderakenne on kuvattuna ba*-tasossa. L- ja R-ketjutasot ovat suuntautuneet a*-akselin suuntaisesti ja tasot vuorottelevat b-akselin suuntaisesti. Molekyyliketjut ovat kuvattu niin sanotusti ylhäältä päin, toisin sanoen ipp-ketjujen 6
12 pituusakselin normaali on ba*-tason suuntainen. αipp:n kiderakenne voidaan esittää muodossa...rl < > RL < > RL < > RL..., missä symboli < > tarkoittaa, että molekyylitasot ovat sijoittuneet lomittain [11]. Lisäksi on mahdollista, että kiteeseen muodostuu peräkkäin kaksi samankätistä ketjutasoa. Tällöin kiteen kasvusuunta kääntyy joko noin 80 tai noin 100, minkä seurauksena kiderakenne haaroittuu. Haaroittumista voidaan kuvata symbolilla #, jolloin haaroittunut kiderakenne voidaan kirjoittaa muodossa...rl < > RL < > RL > # < LR < > LR < > LR... Kuva 4: α-kiteisen polypropeenin kiderakenne ba*-tasossa [8] Kiderakenteen haaroittuminen αipp:n kiteytymisprosessissa on suhteellisen yleistä ja täten αipp:n kiderakenne on usein oksamainen [11, Fig. 3]. αipp:n kiteytyessä ensisijainen kiderakenne on juuri oksamainen [12]. Oksamaista kiderakennetta ympäröivä alue jää olosuhteista riippuen joko amorfiseksi tai kiteytyy osittain myöhemmin. Kiderakenteen oksat muodostuvat polypropeeniketjujen laskostuessa haitarimaiseksi kiderakenteeksi eli lamelleiksi. Tällöin oksan kasvusuunta on kiderakenteen kasvun suuntainen. Kiderakenteista alkaa usein kasvamaan pallomaisia rakenteita, niin sanottuja sferuliitteja. Sferuliitit koostuvat haaroittuneista kiteistä siten, että kiderakenteen kasvusuunta on sferuliittien säteen suuntainen. Sferuliittien rakenne on esitettynä havainnollisemmin kuvassa 5. Sferuliitit tarvitsevat syntyäkseen kasvualustan, jonka ympärille sferuliitti alkaa muodostua. Kasvualustana voi toimia joko kiteytyvän materiaalin seassa olevat epäpuhtaudet tai sopiva kiderakenne. Sopiva kiderakenne muodostuu, kun lamelli alkaa kasvaan kahteen suuntaan, jonka jälkeen se alkaa haaroittua ja laajeta [4, s ]. 7
13 Kuva 5: Sferuliitin periaatteellinen rakennekuva [13] Sferuliittien säde on hyvin riippuvainen sferuliittien määrästä tutkittavassa aineessa. Sferuliitin kasvu pysähtyy toisen sferuliitin kohtaamiseen, joten sferuliittien määrällinen kasvu pienentää sferuliittien keskimääräistä sädettä. Sferuliittien määrän lisäämiseen voidaan vaikuttaa lisäämällä tarkasteltavaan aineeseen tarkoituksellisesti epäpuhtauksia. Näitä epäpuhtauksia kutsutaan nukleointiaineiksi ja niitä lisätään raaka-aineeseen sen valmistusvaiheessa. Polypropeenin kestävyys laskee huomattavasti sferuliittien keskimääräisen säteen funktiona. Lisäksi nukleoidulla polypropeenilla on huomattavasti suurempi venymäkestävyys [14, s. 84]. Näin ollen sferuliittien koko on hyvä pitää mahdollisimman pienenä, mikäli tuotteella halutaan olevan hyvät mekaaniset ominaisuudet. Tämä tarkoittaa siis sitä, että mekaanisten ominaisuuksien parantamiseksi polypropeeni on syytä nukleoida Kiteisyysaste Polymeerien kiteisyysaste voidaan määritellä usealla eri tavalla mittausmenetelmästä riippuen [15]. Yleisimmät menetelmät kiteisyysasteen mittaukseen ovat laajakulmainen röntgensironta (WAXS), differentiaalinen pyyhkäisykalorimetri (DSC) sekä tiheyksien mittaamiseen perustuva menetelmä. Kaikilla näillä menetelmillä pyritään 8
14 selvittämään kiteytyneiden polymeerien osuutta mitattavassa näytteessä. Kiteisyysasteen määrittäminen röntgensironnalla perustuu röntgendiffraktioon, jossa röntgensäteet siroavat näytteestä Braggin lain mukaan tietyissä kulmissa, jotka ovat riippuvaisia näytteen rakenteesta. Menetelmällä pystytään kiteisyysasteen lisäksi määrittämään näytteestä muun muassa kiderakenteiden tyyppi ja niiden koko. Tiheysmittausmenetelmä perustuu käytännössä näytteen tiheyden määrittämiseen. Kun näytteen tiheys on saatu selville, voidaan näytteen kiteisyysaste laskea sillä edellytyksellä, että tiedetään täysin kiteisen näytteen sekä täysin amorfisen näytteen tiheydet. Menetelmän hyvä puoli on se, ettei kiteisyysasteen määrittämiseen tarvita kallista laitteistoa. Toisaalta menetelmä vaatii, että täysin kiteisen ja täysin amorfisen näytteen tiheydet ovat tiedossa. Yleisin ja suoraviivaisin menetelmä polymeerin kiteisyysasteen määrittämiseen on DSC, jota on myös käytetty tässä tutkimuksessa. DSC:n toimintaperiaate on kuvattu tarkemmin kappaleessa Tämän menetelmän vahvuus on sen suoraviivaisuus ja nopeus, minkä vuoksi DSC on yleisesti käytössä kiteisyysasteiden mittauksessa. Toisin kuin röntgensironnalla, DSC:llä ei saada tietoa näytteen kiderakenteesta tai kiteiden koosta. Lisäksi absoluuttisen kiteisyysasteen määrittämiseen tarvitaan täysin kiteytyneen näytteen sulamisentalpian arvo, joka täytyy etsiä kirjallisuudesta. Näitä kirjallisuusarvoja löytyy kuitenkin vain yleisimmille yksikomponenttisille polymeereille, kuten puhtaalle polypropeenille. Täten absoluuttisen kiteisyysasteen määrittäminen tässäkin työssä tutkittaville monimutkaisille polymeeriseoksille on mahdotonta. Absoluuttisen kiteisyysasteen sijaan voidaan kuitenkin mitata näytteen suhteellinen kiteisyysaste, joka määritellään X c = H s H ref, (10) missä H s on mitatun näytteen sulamisentapia ja H ref on referenssinä pidettävän sulamisentalpian arvo. Referenssiarvo ei siis tässä tapauksessa tarkoita täysin kiteisen näytteen sulamisentalpian arvoa, vaan kokeellisesti mahdollisimman hyvin kiteytetyn näytteen sulamisentalpian arvoa. Yhtälö 10 kuvaa siis sitä, miten hyvin näyte on kiteytynyt suhteessa siihen, kuinka hyvin se voisi kiteytyä. 9
15 3 Mittausmenetelmät 3.1 Moolimassajakauma Polymeerien moolimassajakaumia on mahdollista mitata käyttäen kokoekskluusiokromatografiaa (SEC). Menetelmä perustuu laitteen kykyyn erotella liuotetun näytteen molekyylit niiden koon perusteella. Laitteessa käytetään putkimaisia kolonneja, jotka sisältävät kiinteässä faasissa olevaa huokoista ainetta, jonka läpi liuotettu näyte ajetaan. Kuvassa 6 on esitetty periaatekuva molekyylien separoitumisesta kolonnin sisällä. Pienet molekyylit ajautuvat suuria molekyylejä herkemmin huokosiin, jolloin niiden kulku hidastuu. Täten suuret molekyylit kulkeutuvat nopeimmin kolonnin läpi ja pienimmät molekyylit tulevat kolonnista ulos viimeisenä. Vastaava analogia pätee myös polymeereille, jolloin moolimassaltaan suurimmat polymeerit kulkeutuvat kolonnin läpi nopeimmin. [16, s. 4-5] Kuva 6: Periaatekuva näytteen molekyylien kulkeutumisesta kolonnin läpi Polymeerien moolimassajakaumien mittaamiseen käytetään yleisimmin geelipermeaatiokromatografiaa (GPC), jossa laitteen kolonneissa on käytetty geeliä. Geelin sisältämät mikrohuokoset hidastavat pienempien molekyylien liikettä, jolloin saadaan aikaan haluttu molekyylien separoituminen kolonnin sisällä. Laajan moolimassajakauman omaavilla polymeereillä, kuten polypropeenilla, molekyylien separointiin joudutaan käyttämään useita eri kolonneja. Jokaisessa kolonnissa on erikokoiset huokoset ja jokainen kolonni pystyy separoimaan molekyylit tietyltä moolimassaväliltä. Käyttämällä useita eri kolonneja sarjaan kytkettynä saadaan täten separoinnissa katettua hyvin laaja moolimassaskaala. Tehtaalla kokeissa valmistettujen näytteiden moolimassajakaumat piti alunperin mitata Jyväskylän yliopiston kemian laitoksella. Tähän tarkoitukseen kemian laitoksella on käytössään kokoekskluusiokromatografi. Mittauksia ei kuitenkaan pystytty suorittamaan, sillä polypropeeninäytteet eivät liuenneet huoneenlämmössä mihinkään käytössä olleeseen liuottimeen. Lopulta selvisi, että käyttämämme polypropeenin saa liukenemaan liuottamalla sitä muutaman tunnin ajan triklrooribentseenissä 10
16 (TCB), jonka lämpötila on 140 C. Tähän tarkoitukseen soveltuva laitteisto löytyy Aalto-yliopiston polymeeriteknologian osastolta. Mittauksia ei ollut mahdollista suorittaa itse, joten näytteet lähetettiin postissa polymeeriteknologian osastolle mitattaviksi. Mittaukset suoritti polymeeriteknologian tutkimusryhmään kuuluva henkilö, joka lähetti mittalaitteen antamat mittaustulokset sähköpostilla. Mittaustuloksista löytyy taulukoituna jokaista mittalaitteen erittelemää logaritmista moolimassan arvoa vastaava molekyylien suhteellinen esiintymismäärä. Asettamalla kuvaajaan logaritminen moolimassa vaaka-akselille ja molekyylien suhteellinen esiintymismäärä pystyakselille saadaan aikaiseksi moolimassajakauma. Käytännössä mittaustapahtuma on hyvin yksinkertainen. Ensiksi näyte liuotetaan laitteessa käytettävään ajoliuokseen, tässä tapauksessa TCB:iin. Tämän jälkeen näytteestä suodatetaan pois mahdolliset nukleointiaineet, jolloin jäljelle jää ainoastaan polypropeeniketjut. Sitten näyte asetetaan mittalaitteeseen, joka ajaa näytteen kolonnisarjan läpi 3.2 Kiteisyysaste Tehokompensoidun DSC:n toimintaperiaate Kiteisyysasteen mittaamiseen käytettiin Jyväskylän Yliopiston kemian laitoksen tehokomensoitua Perkin Elmer Pyris Diamond DSC -laitteistoa. Laitteisto koostuu kahdesta toisistaan sekä ympäristöstä lämpöeristetystä uunista, jäähdytys- ja lämmitysjärjestelmästä sekä tietokoneesta. Koko laitteisto tietokonetta lukuunottamatta on rakennettu yhtenäiseksi yksiköksi, joka on esitetty kuvassa 7. Koko yksikkö on hyvin suojattu ja eristetty, joten käyttäjä näkee laitteistosta ainoastaan uunit, joihin mitattava näyte sekä referenssi asetetaan. Uunit sijaitsevat laitteen kannen alla (kuva 8). Kuvassa 9 on esitetty uunien periaatekuva. Uuneihin asetetaan suljetut alumiiniset astiat, joista toisessa on mitattava näyte (S) ja toisessa on referenssi (R). Uuneissa on myös lämpömittari (2) sekä lämmitysvastus (1). Uunien lämmitys tapahtuu siis sähkövastuksen avulla jopa 500 C/min. Uunien jäähdytyksen hoitaa erillinen jäähdytysjärjestelmä, joka jäähdyttää uunien ympärillä olevaa jäähdytysblokkia. Jyväskylän Yliopiston kemian laitoksella jäähdytykseen käytetään nestemäistä typpeä, jonka avulla näytettä pystytään jäähdyttämään nopeimmillaan 200 C/min. Mitattava näyte preparoidaan leikkaamalla siitä ensin alumiiniastiaan sopiva pala siten, että näytteen kontaktipinta alumiiniastian kanssa on mahdollisimman suuri. Näytepala ei kuitenkaan saa olla kosketuksissa astian reunoihin, jotta reunat eivät 11
17 Kuva 7: Jyväskylän Yliopiston kemian laitoksen Perkin Elmer Pyris Diamond DSC -laitteisto Kuva 8: DSC-näytteiden mittauspaikat 12
18 vahingossakaan jää kannattelemaan näytettä. Tällöin on mahdollista, että astian pohjan ja näytteen väliin jää rako, jolloin mittaustuloksista tulee virheelliset. Oikeaoppinen preparointi on esitetty kuvassa 10. Tämän jälkeen astian päälle asetetaan alumiinikansi ja näyteastia puristetaan kiinni siihen tarkoitetulla puristimella. Puristin leikkaa lisäksi näyteastiasta ylimääräisen reunan pois. Mittauksen alussa molempia näyteastioita kuumennetaan yhtä suurella teholla. Mittausohjelmasta valitaan ennen mittauksia nopeus, jolla näytettä halutaan kuumentaa ja laitteen säätöjärjestelmä säätää lämmitystehoa sen mukaisesti. Standardinopeutena useimmissa mittauksissa käytetään arvoa 10 C/min. Laitteisto mittaa kuumennuksen aikana jatkuvasti sekä näytteen että referenssin lämpötilaa. Mikäli näytteen ja referenssin lämpötilat alkavat jossain kohti erota toisistaan, esimerkiksi näytteen sulamisen tai kiteytymisen vuoksi, säädin alkaa kuroa lämpötilaeroa umpeen lisäämällä näytteen lämmitysvastukseen kompensaatiotehon P. Kompensaatiotehon suuruutta säätelee P-säädin, jolloin tehon suuruus on lineaarisesti verrannollinen näytteen ja referenssin lämpötilaeroon T seuraavasti: [17, s. 19] P = k 1 T, (11) missä k 1 on P-säätimen lämpötilasta riippumaton sisäinen korjauskerroin. Lämpötilaerosta T voidaan määrittää myös näytteen ja ympäristön välillä siirtyvä lämpövuo Φ m : Φ m = k 2 T, (12) missä k 2 on mittauslaitteiston kalibroinnin kautta määritettävä vakio. Kalibrointi tehdään aina ennen mittausten aloittamista. Siinä suoritetaan testimittaus standardinäytteellä, jonka lämpövuo lämpötilan funktiona tunnetaan. Mittauksen aikana ohjelma piirtää kuvaajaa, jossa on esitettynä lämpövuo Φ m lämpötilan T funktiona. Mittauksessa tapahtuvat näytteen olomuodon muutokset, kuten sulaminen ja kiteytyminen, ilmenevät poikkeamina (Φ m, T)-käyrällä Sulamisentalpian määrittäminen DSC-käyrästä Aineen sulamisentalpia on voimakkaasti kytköksissä sen lämpökapasiteettiin C. Määritettäessä sulamisentalpiaa DSC-laitteistolla mittaukset suoritetaan vakiopaineessa, joten sulamisentalpian laskemisessa voidaan käyttää vakiopaineista lämpökapasiteettia C p. Mikäli aineen lämpökapasiteetti lämpötilan funktiona tunnetaan, voidaan entalpian muutos H s lämpötilojen T 0 ja T 1 välillä laskea kaavalla [17, s. 121] 13
19 Kuva 9: Tehokompensoidun DSC:n uunien periaatekuva [17, s. 18] Kuva 10: Mitattavan näytteen valmistus 14
20 T1 H s = C p (T )dt. (13) T 0 DSC-laitteet eivät kuitenkaan pysty suoraan mittaamaan näytteen lämpökapasiteettia lämpötilan funktiona. Sen sijaan se pystyy määrittämään näytteen ja ympäristön välisen lämpövuon Φ m lämpötilan funktiona edellisessä kappaleessa mainitulla tavalla. Vakiopaineessa lämpökapasiteetti voidaan esittää muodossa [18, s. 179] C p = 1 ( ) H, (14) m s T p missä m s on mitattavan näytteen massa ja H/ T on differentiaalinen entalpian muutos näytteen kokiessa differentiaalisen lämpötilanmuutoksen T. Yhtälö 14 voidaan muuttaa ajasta riippuvaiseksi ottamalla osittaisdifferentiaali ajan suhteen ( t) sekä entalpian muutoksesta että lämpötilan muutoksesta. Yhtälö 14 saadaan täten muotoon C p = 1 ( ) H/ t. (15) m s T/ t p Yhtälössä 15 esiintyvä termi H/ t on suoraan määritelmän mukaan lämpövuo Φ m lämpötilassa T. Termi T/ t on puolestaan lämpötilan muutosnopeus, jota merkitään usein symbolilla β. Mittauksissa lämpötilan muutosnopeus on ennalta määrätty vakio, joka ei siis riipu ajasta tai lämpötilasta. Täten lämpökapasitetti C p saadaan lopulta muotoon C p = 1 βm s Φ m (T ). (16) Sijoittamalla yhtälö 16 yhtälöön 13 saadaan entalpian muutoksen laskemiseksi lopullinen lauseke H s = 1 T1 Φ m (T )dt. (17) βm s T 0 Mittauksissa käytetty DSC-laitteisto Perkin Elmer Pyris Diamond osaa määrittää kiteisyysasteen määrityksessä tarvittavan sulamisentalpian H s mittaamastaan (Φ m, T)-käyrästä. Laitteen käyttäjän tarvitsee vain normittaa lämpövuon vakiotaso siten, että lämpövuo näytteen ja ympäristön välillä on vakio niiltä osin, kun olomuodonmuutoksia ei tapahdu. Todellisuudessa näytteen ja ympäristön välinen lämpövuo kasvaa näytteen ja ympäristön lämpötilaeron välillä lineaarisesti, mikä nähdään hyvin esimerkiksi kuvasta
21 Kuvan 11 käyrät käännetään siis siten, että käyrien lineaariset osat ovat vaakasuorassa. Mittausohjelmassa on tätä varten automaattinen toiminto, joka normittaa mitatun käyrän vaakasuoraan. Normittamista varten käyttäjän tarvitsee piirtää ohjelmaan mitatun käyrän lineaarista osaa mukaileva viiva, jonka suhteen ohjelma suorittaa normituksen. Lisäksi ohjelma tarvitsee entalpian muutoksen laskemiseen integraalin alku- ja loppulämpötilat. Nämä lämpötilat valitaan silmämääräisesti normitetulta tasolta olomuodonmuutoksen molemmin puolin Maksimikiteisyyden määritys Tässä tutkimuksessa ei ollut tarpeen määrittää näytteistä absoluuttisia kiteisyysasteita, sillä absoluuttisilla arvoilla ei ole tutkimuksen kannalta merkitystä. Sen sijaan keskityttiin määrittämään näytteistä suhteelliset kiteisyysasteet, joiden kautta saadaan selville kiteisyysasteen muutokset tuotantoprosessissa. Polypropeeninäytteiden suhteellisen kiteisyysasteen määritystä varten täytyy keinotekoisesti valmistaa täysin kiteytynyt näyte, jotta saadaan tarvittava sulamisentalpian referenssiarvo kiteisyysasteen laskemiseen yhtälön 10 mukaisesti. Täysin kiteinen näyte valmistetaan kokeellisesti kuumentamalla se ensin huoneenlämpötilasta (25 C) sulamispisteen yläpuolelle, jonka jälkeen se jäähdytetään hyvin hitaasti takaisin huoneenlämpötilaan. Tällöin näytteellä on tarpeeksi aikaa kiteytyä lähelle teoreettista maksimikiteisyyttä. Maksimikiteisyyden määrittämisessä jäähdytysnopeudeksi valittiin 0,5 C/min. Tämä oli käytännössä pienin nopeus, jolla maksimikiteisyyden määritys voitiin tehdä varatun laiteajan puitteissa. Jäähdytysaika on kuitenkin riittävän pitkä käytännön maksimikiteisyyttä määritettäessä, sillä ekstruusioprosessissa jäähdytysajat ovat huomattavasti lyhyempiä. Tässä tapauksessa jäähdytysnopeudella 0,5 C/min näyte jäähtyy sata astetta 200 minuutissa, kun taas ekstruusioprosessissa vastaava jäähtyminen sulamispisteestä 168 C lämpötilaan 68 C kestää joitain sekunteja. Kuvassa 11 on esitettynä maksimikiteisyyden mittaamisen periaatekuvaaja DSC:llä mitattuna. Kuvaajan data on otettu suoraan varsinaisesta mittauksesta. Satunnainen näyte ensin kuumennetaan sulamispisteen yläpuolelle (sininen käyrä) nopeudella 10 C/min. Tämän jälkeen näyte kiteytetään jäähdyttämällä se hyvin hitaasti takaisin huoneenlämpöön (punainen käyrä) nopeudella 0,5 C/min. Lopuksi näyte sulatetaan uudelleen (vihreä käyrä) nopeudella 10 C/min. Viimeisestä sulatuksesta saadaan siis laskettua täysin kiteisen näytteen sulamisentalpia. 16
22 Lämpövuo [mw] Maksimikiteisyyden määritys DSC:llä Näytteen sulatus 2. Hidas jäähdytys 3. Maksimikiteyden mittaus Lämpötila [ C] Kuva 11: Polypropeenin maksimikiteisyyden mittaaminen DSC:llä 17
23 4 Levykokeet tuotantoprosessissa Tutkimuksia varten tuotannossa suoritetaan kokeita, joissa valmistetaan polypropeenilevyä tietyistä raaka-aineista sekä prosessiparametreja muuttaen. Raaka-aineiden erojen tutkimiseen valmistetaan levynäytteitä, joissa on käytetty ainoastaan yhtä raaka-ainetta. Käytetyt raaka-aineet on lueteltu taulukossa 1. Lisäksi valmistetaan tuotantokäyttöön tarkoitettua levyä muuttaen levyn ominaisuuksien kannalta tärkeimpiä prosessiparametreja. Taulukko 1: Tuotannossa suoritettavat kokeet suoritusjärjestyksessä Numero Koe 1 Raaka-aine homopolymeeri HB300TF 2 Raaka-aine kopolymeeri BC240TF 3 Raaka-aine kopolymeeri BC918TF 4 Raaka-aineseos HB300TF 70% / BC918TF 30% 5 Raaka-aine 100% rouhe 6 Telan lämpötilan vaikutus 7 Massan lämpötilan vaikutus 4.1 Levykoneen toimintaperiaate Muovilevyn valmistaminen ekstruusiolla voidaan karkeasti jakaa kolmeen pääkohtaan. Ensin muoviraaka-aine sulatetaan, jonka jälkeen varmistetaan sulan muovimassan tasainen virtaus. Lopuksi sula massa jäähdytetään hallitusti takaisin kiinteäksi muovilevyksi. Lisäksi kaikki kolme osaprosessia täytyy olla synkronoituja keskenään, jotta muovilevyn laatu pysyisi mahdollisimman stabiilina koko valmistusprosessin ajan. Yksinkertaisen levykoneen periaatekuva on esitetty kuvassa 12. Raaka-aine syötetään levykoneeseen suppilon muotoisesta syöttösäiliöstä (1). Raaka-aineet toimitetaan granulaattien muodossa, eli ne ovat koostumukseltaan pieniä muovirakeita. Lisäksi joukkoon sekoitetaan usein muovirouhetta, jota saadaan murskaamalla valmistusprosesissa yli jäänyttä muovilevyä pieneksi silpuksi. Erillinen raakaainejärjestelmä valmistaa ja annostelee käytettäviä raaka-aineita oikeassa suhteessa määrätyn reseptin mukaisesti levykoneen syöttösäiliöön. Säiliön alaosa on avoin, jolloin raaka-aine pääsee putoamaan vapaasti ruuviin (2). Ruuvin tarkoituksena on sulattaa raaka-aine ulkoisen lämmityksen sekä kitkasta aiheutuvan lämmön avulla. Ruuvin toiminta jakautuu kahteen eri osaan. Ruuvissa 18
24 on tihenevä kierre noin ensimmäiset kaksi kolmasosaa ruuvin pituudesta. Tällä osalla tapahtuu raaka-aineen sulatus sekä tiivistys. Ruuvin viimeisessä kolmanneksessa on tasainen kierre, joka syöttää sulaa raaka-ainetta edelleen polymeeripumpulle (3). Polymeeripumppu koostuu kahdesta virtaussuuntaa vastaan pyörivästä rattaasta, joiden tarkoituksena on nostaa sulan massan paine riittävän suureksi sekä syöttää massaa eteenpäin suuttimelle (4). Polymeeripumpun pyörimisnopeudella säädetään suuttimesta ulos tulevan massan määrää. Pumpun pyörimisnopeus määritetään käsin ja ohjausjärjestelmä säätää ruuvin pyörimisnopeutta pitääkseen massan paineen vakiona. Suuttimen jälkeen sula massa kulkee telastolle, jossa massa ajetaan levyksi ja jäähdytetään. Massa tulee ulos suuttimesta ilmaharjan (5) ja keskitelan (6) välistä. Ilmaharja puhaltaa levyn kiinni keskitelaan, josta levy jatkaa matkaansa alatelan ja jäähdytystelan välistä kelaajalle. Levy jäähtyy sulamispisteen alapuolelle hyvin nopeasti ilmaharjan jälkeen, sillä levy on vain 0,45 mm paksua. Nopean jäähtymisen vuoksi levyn kiteytymisen kannalta kriittisin kohta on kontakti keskitelan kanssa. Kiteytyminen on huomattavasti nopeampaa levyn ollessa lähellä sulamispistettä kuin huoneenlämpötilassa. Keskitelan lämpötilaa nostamalla voidaan pidentää levyn kiteytymisaikaa ja täten nostaa levyn kiteisyysastetta. Kuva 12: Levykoneen yksinkertaistettu periaatekuva. 1. Syöttösäiliö 2. Ruuvi 3. Polymeeripumppu 4. Suutin 5. Ilmaharja 6. Keskitela 4.2 Testilevyjen valmistus puhtaista raaka-aineista Käytännön syistä ensimmäiseksi suoritetaan ne kokeet, joissa levyä valmistetaan vain laboratoriomittauksiin tarvittava määrä. Nämä kokeet pyritään suorittamaan siten, ettei levykone pääse sammumaan raaka-aineiden vaihdon välissä. Tässä kohtaa on oltava raaka-aineiden annostelun suhteen tarkkana, ettei raaka-aine pääse loppumaan vaihdon yhteydessä. Levykoneen säiliöön ei kuitenkaan voi laittaa uutta 19
25 raaka-ainetta liian aikaisin, jottei uusi raaka-aine sekoitu vanhan kanssa. Mikäli levykone pääsee sammumaan, ei uudelleenkäynnistyksen jälkeen välttämättä saavuteta täysin samoja ajoparametreja varsinkaan levyn paksuusprofiilin suhteen. Ennen varsinaisia kokeita levykoneen suutin puhdistettiin noin 10 senttimetrin syvyiseltä matkalta käyttäen apuna rakotulkkia. Tämä on rutiinitoimenpide, joka tehdään jokaisen käynnistyksen yhteydessä. Sillä varmistetaan, ettei suuttimessa ole sulan muovimassan virtausta estäviä epäpuhtauksia. Lisäksi vaihdoimme levykoneen sihdin, jottei sulan muovimassan paine ennen massapumppua pääse nousemaan liian korkeaksi kokeiden aikana. Liian korkea massan paine pysäyttää levykoneen, mitä pyrimme kaikin keinoin välttämään. Levykoneen käynnistyksen ja puhdistustoimenpiteiden jälkeen levyn poikkisuuntainen paksuusprofiili säädettiin kohdalleen. Levyn paksuusprofiilin säätö tapahtuu suuttimen huulen yläpuolella sijaitsevista säätömuttereista. Kiristämällä tai löysäämällä säätömutteria huulen rako muuttuu vastaavassa kohdassa. Näin saadaan vaikutettua muovimassan virtauksen määrään kyseisessä kohdassa, mikä on vastaavassa kohdassa suoraan verrannollinen ulos tulevan levyn paksuuteen. Levyn säädössä käytettiin koeajoissa ensin käytettävää raaka-ainetta, joka on homopolymeerinen polypropeeni HB300TF. Kun levyn paksuus oltiin saatu paksuusmittaria ja mikrometriä apuna käyttäen toleranssiin, otettiin levystä ensimmäinen näytepala. Näytteenoton aikana vaihdettiin vaa alle resepti, jolla imettiin siilosta levykoneen säiliöön seuraavassa kokeessa käytettävä raaka-aine BC240TF. Sitten odotettiin, kunnes raaka-aine oli kokonaan vaihtunut, minkä jälkeen todettiin prosessin pysyneen stabiilina raaka-aineen vaihdon jälkeen. Näytteenoton yhteydessä alettiin valmistella seuraavaa koeajoa. Seuraavaa raaka-aine, kopolymeerinen polypropeeni BC918TF, jouduttiin siilon sijasta imemään pahvisesta kontista. Tämä järjestely vaati raaka-aineen imuputken vaihdon siilon kyljestä konttiin. Kun imuputki oli otettu irti siilosta, imettiin putki kokonaan tyhjäksi vanhasta raaka-aineesta ja kaikki vaakajärjestelmässä oleva BC240 laskettiin levykoneen säiliöön. Vasta tämän jälkeen siirrettiin imuputki ottamaan uutta raaka-ainetta kontista. Tällä järjestelyllä pyrittiin jälleen minimoimaan raaka-aineiden sekoittumista keskenään. Näytteenoton jälkeen vaihdettiin seuraavaa koeajoa varten vaa alle uusi resepti, joka sisältää 70% HB300TF:ää ja 30% BC918:aa. Jälleen odotettiin, että raaka-aineet ovat täysin vaihtuneet, minkä jälkeen otettiin levystä näytepala. Lopuksi vaihdoimme vielä vaa alle reseptin, joka sisälsi 100% siilossa olevaa rouhetta. Näytteenoton jälkeen aloimme valmistella seuraavaa koeajoa. 20
26 4.3 Prosessin ajoparametrien muutokset Keskitelan lämpötilan muutos Tämä koe suoritettiin heti edellisen kokeen perään levykonetta sammuttamatta. Levyä valmistettiin tuotannossa käytettävän MKMC409-kansilevyn reseptiä käyttäen kopolymeerin BC240TF sijasta kopolymeeriä BC918. Tässä kokeessa levyä valmistettiin noin 200 kg kutakin koetta kohden, sillä valmistettua levyä käytetään myöhemmin kokeissa syvävetokoneella. Keskitelan lämpötilaa voidaan muuttaa suoraan telaston ohjaustaulusta. Koeajot suoritettiin siten, että haluttu keskitelan lämpötila syötettiin ohjaustauluun ja odotettiin, kunnes keskitela oli saavuttanut pyydetyn lämpötilan. Tämän jälkeen merkittiin rullan kylkeen tussilla merkki, josta lähtien keskitelan lämpötila oli pyydetyssä arvossa. Kun levyä oli valmistettu tarpeeksi, vaihdettiin levy kelautumaan uudelle rullapohjalle ja muutettiin keskitelan lämpötila ohjaustaulusta seuraavaan arvoon. Kokeessa käytetyt lämpötilojen arvot löytyvät taulukosta 2. Alatelan lämpötila pyrittiin pitämään tuotantoajossa käytössä olleessa lämpötilassa 30 C, mutta tämä toteutui vain alhaisimmalla keskitelan lämpötilalla 40 C, joka on myös tuotantoajossa käytössä oleva lämpötila. Jostain syystä alatelan lämpötila nousi 5 C, kun keskitelan lämpötila nostettiin arvosta 40 C arvoon 50 C ja pysyi stabiilina lämpötilassa 35 C tämän jälkeen. Taulukko 2: Kokeessa käytetyt keskitelan lämpötilan arvot Ajo Lämpötila [ C] Keskitelan lämpötilaa oli alunperin tarkoitus nostaa jopa 90 C:een, mutta keskitelan lämpötila ei noussut korkeammaksi kuin 67 C. Lopuksi ajettiin vielä kaksi koeajoa lämpötilojen 40 C ja 67 C välistä, jotta saatiin tarpeeksi mittapisteitä tulosten analysointia varten. Lisäksi havaittiin, että levy pyrkii käyristymään keskitelan lämpötilan ollessa 45 C tai vähemmän. Lämpötilasta 50 C ylöspäin levy alkoi suoristumaan ja korkeimmissa 21
27 lämpötiloissa levy oli jo täysin suoraa Massan lämpötilan muutos Kun keskitelan lämpötilan muutoksia koskevat kokeet saatiin valmiiksi, asetettiin keski- ja alatelan lämpötilat alkuperäisiin arvoihinsa. Keskitelan lämpötila oli alussa 40 C ja alatelan lämpötila 30 C. Tämän jälkeen aloitettiin viimeinen koe levykoneella, jossa muutetaan massan lämpötilaa. Massan lämpötilaan pystyy vaikuttamaan ekstruusioruuvin lämpöelementeillä, mutta lämpöelementtien vaikutus ei kuitenkaan ole kovin suuri, sillä massan kuumeneminen ja sulaminen aiheutuu pääasiassa massan ja ekstruusiokanavan seinämän välisestä kitkasta. Lämpöelementtien avulla massan lämpötilaa saatiin nostettua noin 20 C alimmasta mahdollisesta lämpötilasta, jolla kelvollista levyä pystytään valmistamaan. Koerullat valmistettiin käytännössä vastaavasti kuten edellisessä kokeessa, jossa muutettiin keskitelan lämpötilaa. Ensiksi haimme massan lämpötilalle käytännön alarajan, jolla hyväksyttävää levyä pystyttiin vielä ajamaan. Alaraja tulee vastaan siinä kohdassa, kun levyyn alkaa ilmestyä pieniä paakkuja, jotka vaikuttaisivat olevan sulamattomia granulaatteja. Kun koerulla saatiin valmistettua lämpötilan alarajalla, alettiin massan lämpötilaa vähitellen nostamaan. Taulukossa 3 on listattuna käytetyt massan lämpötilan arvot huulta lähinnä olevasta anturista luettuna. Kokeen aikana havaittiin, että massapumpun paine vaihtelee sitä enemmän, mitä alempi massan lämpötila oli. Massapumpun paineohjauksen automatiikka on säädetty ohjearvoon 45 bar ja alhaisimmalla massan lämpötilalla massapumpun paine vaihteli välillä 40 bar - 51 bar. Korkeimmassa lämpötilassa pumpun paine vaihteli ainoastaan välillä 44 bar - 46 bar. Paine vaihtelee korkeammissa lämpötiloissa vähemmän, sillä massa on juoksevampaa. Levyn laadussa ei kuitenkaan huomattu silminnähtävää eroa eri massan lämpötilan arvoilla. Taulukko 3: Kokeessa käytetyt massan lämpötilan arvot Ajo Lämpötila [ C]
28 4.4 Kokeet syvävetokoneella Levykoneella tehtyjen kokeiden jälkeen tutkittiin keskitelan lämpötilan sekä massan lämpötilan vaikutusta lopputuotteeseen muotoilemalla valmistetuista levyistä kansia. Tällä kokeella haluttiin selvittää massan ja keskitelan lämpötilan vaikutusta kannen kieroutumiseen. Kannen kierouden määrittämiseen ei ole käytettävissä minkäänlaista mittalaitetta, vaan kierous määritetään silmämääräisesti asettamalla kansi suoran metallilevyn päälle. Lisäksi kansista tarkistettiin helmojen levinneisyys silmämääräisesti sekä helmojen vahvuus käsin kokeilemalla. Syvävetokoneen toimintaperiaate on periaatetasolla hyvin yksinkertainen. Levykoneella ajettu levy lämmitetään, jonka jälkeen se johdetaan muottiin, jossa kansien muotoilu tapahtuu. Tässä tutkimuksessa käytetyssä muotissa on kymmenen pesää (1-10), joten vetokoneelta valmistuu 10 kantta kerralla. Kannet muotoillaan ensin mekaanisesti venyttämällä, jonka jälkeen muotoilu viimeistellään paineilmalla. Kansien muotoilussa vetokoneella kaikki vetokoneen parametrit pidettiin vakioina koko koeajon ajan, mikä oli välttämätöntä tulosten tulkitsemisen kannalta. Tässä tutkimuksessa haluttiin selvittää ainoastaan levykoneen parametrien vaikutusta kansien muotoiluun, joten vetokoneen parametrien muuttaminen samanaikaisesti tekisi tulosten tulkitsemisesta mahdotonta. Levyrullia syötettiin yksi kerrallaan vetokoneeseen, jonka jälkeen kansia muotoiltiin tarvittava määrä näytteiden saamiseksi. Tämän jälkeen vetokoneeseen vaihdettiin uusi rulla ja muotoiltiin kannet. Tätä toistettiin, kunnes kaikki rullat oli ajettu. Kansien kieroutta ei mitattu välittömästi muotoilun jälkeen, vaan kansien päätettiin antaa jäähtyä hieman ennen kierouden mittaamista. Mittaamisajankohdaksi valittiin se hetki, jolloin kannet menevät vetokoneelta painoon. Tällöin jäähtymisaika on noin kahdeksan minuuttia. 23
29 5 Tulokset 5.1 Eri raaka-aineseosten moolimassajakaumia Tutkimuksen yhtenä tarkoituksena oli tarkastella raaka-aineiden käyttäytymistä ekstruusiossa sekä lisäaineiden vaikutusta levyn ominaisuuksiin. Tarkastelun kohteena olivat homopolymeeri HB300TF sekä kopolymeerityypit BC240TF ja BC918. Lisäksi haluttiin mielenkiinnosta tutkia yhden raaka-aineen laatuvaihtelua valmistuserien välillä. Raaka-aineiden rakennemuutoksia ekstruusiossa pystytään tutkimaan mittaamalla kyseisen raaka-aineen moolimassajakauma ennen ja jälkeen ekstruusioprosessin. Prosessin sisäisiä muutoksia ei tässä tapauksessa pystytä selvittämään, mutta se ei ole myöskään tarpeellista. Raaka-aineet kokevat prosessin sisällä paljon mekaanista rasitusta ja altistuvat korkealle lämpötilalle. Näiden yhteisvaikutuksesta raaka-aine sulaa ruuvikanavassa ja raaka-aineen ominaisuudet muuttuvat. Alla on taulukoituna raaka-ainetutkimuksia varten mitattujen moolimassajakaumien tunnusluvut, eli massapainotettu keskimääräinen moolimassa M w sekä polydispersiteetti PI. Näytteiden, joissa lukee levy, moolimassajakaumat ovat mitattu ekstruusioprosessilla valmistetuista levyistä. Tarkempi analyysi tuloksista on esitetty seuraavissa kappaleissa. Taulukko 4: Näytteistä mitattujen moolimassajakaumien tunnusluvut: massapainoitettu keskimääräinen moolimassa (M w ) sekä polydispersiteetti (PI) Näyte M w [g/mol] PI Normaali resepti, levy ,7 HB300 granulaatti, erä ,0 HB300 granulaatti, erä ,2 HB300 levy, erä ,0 HB300/BC918, levy ,3 100% rouhe, levy ,6 BC918, granulaatti ,1 BC918, levy ,3 BC240, granulaatti ,2 BC240, levy ,2 24
30 dw t /d(log M w ) Homopolymeeri HB300TF HB300TF:n moolimassajakaumat granulaateista sekä levystä ovat esitettynä kuvassa 13. Kuvaajasta nähdään, että levyksi ajettaessa HB300TF:n jakauma siirtyy hieman vasemmalle. Tämä tarkoittaa, että molekyyliketjut katkeilevat prosessissa. Lisäksi jakauma kapenee hieman, mikä nähdään myös taulukosta 4. Kuvasta 13 nähdään myös, että jakauma kapenee nimenomaan pitkien molekyyliketjujen päästä, kun taas lyhyt pää näyttää kuvaajassa yhtenevältä. Moolimassajakauma, HB300TF 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0, ,5 4 4,5 5 5,5 6 6,5 7 Log M W Granulaatti Levy Kuva 13: Homopolymeerin HB300TF moolimassajakaumat granulaatista sekä valmiista levystä mitattuna Lisäksi vertailtiin HB300TF:n moolimassajakaumia kahden eri tuote-erän välillä ja tulokset on esitetty kuvassa 14. Kuvaajasta nähdään, että kahden peräkkäisen valmistuserän moolimassajakaumien välillä on eroa. Erä on selvästi leveämpi kuin erä , mikä näkyy myös taulukon 4 polydispersiteeteissä. Moolimassajakaumat ovat mitattu prosessoimattomista raaka-aineista, eli tulokset antavat viitteitä raaka-ainevalmistajan valmistusprosessin laatuvaihteluista Kopolymeerin vaihdon vaikutukset Tehtaalla tuotannossa siirryttiin käyttämään uudenlaista kopolymeeria ja tämän tutkimuksen yhteydessä haluttiin selvittää uuden ja vanhan kopolymeerityypin ero- 25
31 dw t /d(log M w ) Moolimassajakauma HB300TF, kaksi eri tuote-erää 0,8 0,7 0,6 0,5 0,4 0,3 0, , ,5 4 4,5 5 5,5 6 6,5 7 Log M W Kuva 14: Homopolymeerin HB300TF moolimassajakaumat granulaateista mitattuna kahdesta eri tuote-erästä ja niin raaka-ainetasolla kuin ekstruusioprosessissakin. Kopolymeerityypin vaihdolla haluttiin parantaa eräiden kirkkaiden tuotteiden, rasioiden ja kansien, läpinäkyvyyttä. Käytettäessä vanhaa kopolymeeriä BC240TF tuotteiden valon läpäisevyys oli melko huono ja tuotteet näyttivät sameilta verrattuna eri raaka-aineista valmistettuihin kirkkaisiin tuotteisiin. Kuvassa 15 on esitettynä kopolymeerigranulaattien moolimassajakaumat. Kuvasta nähdään, että uuden kopolymeerin, BC918, moolimassajakauma eroaa vanhan kopolymeerin jakaumasta selvästi. BC918:n jakaumassa näkyy enemmän lyhyitä molekyyliketjuja, kun taas pitkiä molekyyliketjuja näyttäisi olevan suunnilleen yhtä paljon. Näin ollen BC918:n jakauma on leveämpi, joka näkyy myös taulukon 4 polydispersiteeteistä. Levyksi ajetuista kopolymeerinäytteistä ei kuitenkaan löydetty samanlaista eroa kuin granulaattien tapauksessa. Kuvan 16 perusteella moolimassajakaumat ovat lähes identtiset. Tästä voidaan päätellä, että molemmat kopolymeerit kiteytyvät prosessissa samalla tavalla. Moolimassajakaumien erot tasoittuvat polypropeenin kiteytyessä, sillä liuotettaessa polypropeeninäytteet moolimassamittauksia varten polypropeenin kiderakenteet hajoavat, eikä jäljelle jäänyt moolimassajakauma vastaa kiteytymättömän polypropeenin moolimassajakaumaa. Polypropeenin kiderakenteilla 26
32 dw t /d(log M w ) ei ole muistia, joten kiteen muodostaneet polypropeeniketjut eivät pysy samanmittaisina kiderakenteen hajotessa. 0,8 0,7 0,6 Copolymeerien moolimassajakaumat 0,5 0,4 0,3 0,2 BC918 BC240TF 0, ,5 4 4,5 5 5,5 6 6,5 7 Log M W Kuva 15: Kopolymeerigranulaattien moolimassajakaumat Rouheen ja lisäaineiden vaikutus levyn moolimassajakaumaan Lisäaineettoman levyn, normaalilla reseptillä valmistetun levyn sekä pelkästä rouheesta valmistetun levyn moolimassat on esitettynä taulukossa 5. Vertailussa huomataan, että lisäaineettoman levyn keskimääräinen moolimassa sekä polydispersiteetti ovat suuremmat kuin muissa levyissä. Lisäksi kuvasta 17 nähdään, että lisäaineettoman levyn moolimassajakauma on hieman leveämpi pitkien molekyyliketjujen päästä. Tämä tukee taulukon 5 tuloksia. Tässä tutkimuksessa normaalilla reseptillä valmistettuun levyyn ei oltu lisätty rouhetta, jolloin ainoat erot lisäaineettomaan levyyn ovat valkoinen väri sekä antistaattiaine. Valkoisen värin määrä oli 6% ja antistaattiaineen määrä oli 1,5% käytetyistä raaka-aineista. Taulukosta 5 huomataan, että lisäaineet pienentävät keskimääräistä moolimassaa sekä polydispersiteettiä. Ero on yllättävän suuri ottaen huomioon, että lisäaineiden määrä levyssä on suhteellisen vähäinen. Lisäksi valkoisesta värin massasta huomattavan suuri osa on kantoaineena toimivaa polypropeenia. Moolimassajakaumaan vaikuttaa välillisesti myös se, että levyn valkoisen värin muodostavat titaanidioksidipartikkelit (TiO 2 ) toimivat nukleointiaineina polypropeenin 27
Kiteisyys ja amorfisuus CHEM-C2400 Materiaalit sidoksesta rakenteeseen
 Kiteisyys ja amorfisuus CHEM-C2400 Materiaalit sidoksesta rakenteeseen Pirjo Pietikäinen Crystalline Solids and Amorphous Solids https://www.youtube.com/watch?v=4nzv0zvdm5c 1 Johdanto Silloittumattoman
Kiteisyys ja amorfisuus CHEM-C2400 Materiaalit sidoksesta rakenteeseen Pirjo Pietikäinen Crystalline Solids and Amorphous Solids https://www.youtube.com/watch?v=4nzv0zvdm5c 1 Johdanto Silloittumattoman
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
13 KALORIMETRI. 13.1 Johdanto. 13.2 Kalorimetrin lämmönvaihto
 13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
13 KALORIMETRI 13.1 Johdanto Kalorimetri on ympäristöstään mahdollisimman täydellisesti lämpöeristetty astia. Lämpöeristyksestä huolimatta kalorimetrin ja ympäristön välinen lämpötilaero aiheuttaa lämmönvaihtoa
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä
 Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
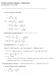 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
Koesuunnitelma. Tuntemattoman kappaleen materiaalin määritys. Kon c3004 Kone ja rakennustekniikan laboratoriotyöt. Janne Mattila.
 Kon c3004 Kone ja rakennustekniikan laboratoriotyöt Koesuunnitelma Tuntemattoman kappaleen materiaalin määritys Janne Mattila Teemu Koitto Lari Pelanne Sisällysluettelo 1. Tutkimusongelma ja tutkimuksen
Kon c3004 Kone ja rakennustekniikan laboratoriotyöt Koesuunnitelma Tuntemattoman kappaleen materiaalin määritys Janne Mattila Teemu Koitto Lari Pelanne Sisällysluettelo 1. Tutkimusongelma ja tutkimuksen
Talon valmistumisvuosi 1999 Asuinpinta-ala 441m2. Asuntoja 6
 Lattialämmitetyn rivitalon perusparannus 2015 Talon valmistumisvuosi 1999 Asuinpinta-ala 441m2. Asuntoja 6 Maakaasukattila Lattialämmitys. Putkipituus tuntematon. Ilmanvaihto koneellinen. Ei lämmön talteenottoa.
Lattialämmitetyn rivitalon perusparannus 2015 Talon valmistumisvuosi 1999 Asuinpinta-ala 441m2. Asuntoja 6 Maakaasukattila Lattialämmitys. Putkipituus tuntematon. Ilmanvaihto koneellinen. Ei lämmön talteenottoa.
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Aineopintojen laboratoriotyöt 1. Veden ominaislämpökapasiteetti
 Aineopintojen laboratoriotyöt 1 Veden ominaislämpökapasiteetti Aki Kutvonen Op.nmr 013185860 assistentti: Marko Peura työ tehty 19.9.008 palautettu 6.10.008 Sisällysluettelo Tiivistelmä...3 Johdanto...3
Aineopintojen laboratoriotyöt 1 Veden ominaislämpökapasiteetti Aki Kutvonen Op.nmr 013185860 assistentti: Marko Peura työ tehty 19.9.008 palautettu 6.10.008 Sisällysluettelo Tiivistelmä...3 Johdanto...3
Kojemeteorologia. Sami Haapanala syksy 2013. Fysiikan laitos, Ilmakehätieteiden osasto
 Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Mittalaitteiden staattiset ominaisuudet Mittalaitteita kuvaavat tunnusluvut voidaan jakaa kahteen luokkaan Staattisiin
Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Mittalaitteiden staattiset ominaisuudet Mittalaitteita kuvaavat tunnusluvut voidaan jakaa kahteen luokkaan Staattisiin
Perusopintojen Laboratoriotöiden Työselostus 1
 Perusopintojen Laboratoriotöiden Työselostus 1 Kalle Hyvönen Työ tehty 1. joulukuuta 008, Palautettu 30. tammikuuta 009 1 Assistentti: Mika Torkkeli Tiivistelmä Laboratoriossa tehdyssä ensimmäisessä kokeessa
Perusopintojen Laboratoriotöiden Työselostus 1 Kalle Hyvönen Työ tehty 1. joulukuuta 008, Palautettu 30. tammikuuta 009 1 Assistentti: Mika Torkkeli Tiivistelmä Laboratoriossa tehdyssä ensimmäisessä kokeessa
Ohjeita fysiikan ylioppilaskirjoituksiin
 Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Ohjeita fysiikan ylioppilaskirjoituksiin Kari Eloranta 2016 Jyväskylän Lyseon lukio 11. tammikuuta 2016 Kokeen rakenne Fysiikan kokeessa on 13 tehtävää, joista vastataan kahdeksaan. Tehtävät 12 ja 13 ovat
Kuva 1. Virtauksen nopeus muuttuu poikkileikkauksen muuttuessa
 8. NESTEEN VIRTAUS 8.1 Bernoullin laki Tässä laboratoriotyössä tutkitaan nesteen virtausta ja virtauksiin liittyviä energiahäviöitä. Yleisessä tapauksessa nesteiden virtauksen käsittely on matemaattisesti
8. NESTEEN VIRTAUS 8.1 Bernoullin laki Tässä laboratoriotyössä tutkitaan nesteen virtausta ja virtauksiin liittyviä energiahäviöitä. Yleisessä tapauksessa nesteiden virtauksen käsittely on matemaattisesti
Alkuaineita luokitellaan atomimassojen perusteella
 IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Kertaus. Integraalifunktio ja integrointi. 2( x 1) 1 2x. 3( x 1) 1 (3x 1) KERTAUSTEHTÄVIÄ. K1. a)
 Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
Juuri 9 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 5.5.6 Kertaus Integraalifunktio ja integrointi KERTAUSTEHTÄVIÄ K. a) ( )d C C b) c) d e e C cosd cosd sin C K. Funktiot F ja F ovat saman
FYSA220/1 (FYS222/1) HALLIN ILMIÖ
 FYSA220/1 (FYS222/1) HALLIN ILMIÖ Työssä perehdytään johteissa ja tässä tapauksessa erityisesti puolijohteissa esiintyvään Hallin ilmiöön, sekä määritetään sitä karakterisoivat Hallin vakio, varaustiheys
FYSA220/1 (FYS222/1) HALLIN ILMIÖ Työssä perehdytään johteissa ja tässä tapauksessa erityisesti puolijohteissa esiintyvään Hallin ilmiöön, sekä määritetään sitä karakterisoivat Hallin vakio, varaustiheys
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619
 KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
KÄYTTÖOHJE LÄMPÖTILA-ANEMOMETRI DT-619 2007 S&A MATINTUPA 1. ILMAVIRTAUKSEN MITTAUS Suora, 1:n pisteen mittaus a) Kytke mittalaitteeseen virta. b) Paina UNITS - näppäintä ja valitse haluttu mittayksikkö
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
Kojemeteorologia (53695) Laskuharjoitus 1
 Kojemeteorologia (53695) Laskuharjoitus 1 Risto Taipale 20.9.2013 1 Tehtävä 1 Erään lämpömittarin vertailu kalibrointistandardiin antoi keskimääräiseksi eroksi standardista 0,98 C ja eron keskihajonnaksi
Kojemeteorologia (53695) Laskuharjoitus 1 Risto Taipale 20.9.2013 1 Tehtävä 1 Erään lämpömittarin vertailu kalibrointistandardiin antoi keskimääräiseksi eroksi standardista 0,98 C ja eron keskihajonnaksi
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
DirAir Oy:n tuloilmaikkunaventtiilien mittaukset 30.11.2012
 Tampereen teknillinen yliopisto Teknisen suunnittelun laitos Pentti Saarenrinne Tilaaja: DirAir Oy Kuoppakatu 4 1171 Riihimäki Mittausraportti: DirAir Oy:n tuloilmaikkunaventtiilien mittaukset 3.11.212
Tampereen teknillinen yliopisto Teknisen suunnittelun laitos Pentti Saarenrinne Tilaaja: DirAir Oy Kuoppakatu 4 1171 Riihimäki Mittausraportti: DirAir Oy:n tuloilmaikkunaventtiilien mittaukset 3.11.212
Pinnoitteen vaikutus jäähdytystehoon
 Pinnoitteen vaikutus jäähdytystehoon Jesse Viitanen Esko Lätti 11I100A 16.4.2013 2 SISÄLLYS 1TEHTÄVÄN MÄÄRITTELY... 3 2TEORIA... 3 2.1Jäähdytysteho... 3 2.2Pinnoite... 4 2.3Jäähdytin... 5 3MITTAUSMENETELMÄT...
Pinnoitteen vaikutus jäähdytystehoon Jesse Viitanen Esko Lätti 11I100A 16.4.2013 2 SISÄLLYS 1TEHTÄVÄN MÄÄRITTELY... 3 2TEORIA... 3 2.1Jäähdytysteho... 3 2.2Pinnoite... 4 2.3Jäähdytin... 5 3MITTAUSMENETELMÄT...
(b) Tunnista a-kohdassa saadusta riippuvuudesta virtausmekaniikassa yleisesti käytössä olevat dimensiottomat parametrit.
 Tehtävä 1 Oletetaan, että ruiskutussuuttimen nestepisaroiden halkaisija d riippuu suuttimen halkaisijasta D, suihkun nopeudesta V sekä nesteen tiheydestä ρ, viskositeetista µ ja pintajännityksestä σ. (a)
Tehtävä 1 Oletetaan, että ruiskutussuuttimen nestepisaroiden halkaisija d riippuu suuttimen halkaisijasta D, suihkun nopeudesta V sekä nesteen tiheydestä ρ, viskositeetista µ ja pintajännityksestä σ. (a)
Mikrokalorimetri - uusi materiaalien palamisominaisuuksien tutkimuslaite hankittu VTT:lle
 Mikrokalorimetri - uusi materiaalien palamisominaisuuksien tutkimuslaite hankittu VTT:lle Johan Mangs & Anna Matala VTT Palotutkimuksen päivät 27.-28.8.2013 2 Mikrokalorimetri (Micro-scale Combustion Calorimeter
Mikrokalorimetri - uusi materiaalien palamisominaisuuksien tutkimuslaite hankittu VTT:lle Johan Mangs & Anna Matala VTT Palotutkimuksen päivät 27.-28.8.2013 2 Mikrokalorimetri (Micro-scale Combustion Calorimeter
Otoskoko 107 kpl. a) 27 b) 2654
 1. Tietyllä koneella valmistettavien tiivisterenkaiden halkaisijan keskihajonnan tiedetään olevan 0.04 tuumaa. Kyseisellä koneella valmistettujen 100 renkaan halkaisijoiden keskiarvo oli 0.60 tuumaa. Määrää
1. Tietyllä koneella valmistettavien tiivisterenkaiden halkaisijan keskihajonnan tiedetään olevan 0.04 tuumaa. Kyseisellä koneella valmistettujen 100 renkaan halkaisijoiden keskiarvo oli 0.60 tuumaa. Määrää
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
ASPIRIININ MÄÄRÄN MITTAUS VALOKUVAAMALLA
 ASPIRIININ MÄÄRÄN MITTAUS VALOKUVAAMALLA Jaakko Lohenoja 2009 Johdanto Asetyylisalisyylihapon määrä voidaan mitata spektrofotometrisesti hydrolysoimalla asetyylisalisyylihappo salisyylihapoksi ja muodostamalla
ASPIRIININ MÄÄRÄN MITTAUS VALOKUVAAMALLA Jaakko Lohenoja 2009 Johdanto Asetyylisalisyylihapon määrä voidaan mitata spektrofotometrisesti hydrolysoimalla asetyylisalisyylihappo salisyylihapoksi ja muodostamalla
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ HYVÄN VASTAUKSEN PIIRTEITÄ
 MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2019 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
MATEMATIIKAN KOE, LYHYT OPPIMÄÄRÄ 24.9.2019 HYVÄN VASTAUKSEN PIIRTEITÄ Alustavat hyvän vastauksen piirteet on suuntaa-antava kuvaus kokeen tehtäviin odotetuista vastauksista ja tarkoitettu ensisijaisesti
luku 1.notebook Luku 1 Mooli, ainemäärä ja konsentraatio
 Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
Luku 1 Mooli, ainemäärä ja konsentraatio 1 Kemian kvantitatiivisuus = määrällinen t ieto Kemian kaavat ja reaktioyhtälöt sisältävät tietoa aineiden rakenteesta ja aineiden määristä esim. 2 H 2 + O 2 2
4757 4h. MAGNEETTIKENTÄT
 TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
TURUN AMMATTIKORKEAKOULU TYÖOHJE 1/7 FYSIIKAN LABORATORIO V 1.6 5.014 4757 4h. MAGNEETTIKENTÄT TYÖN TAVOITE Työssä tutkitaan vitajohtimen aiheuttamaa magneettikentää. VIRTAJOHTIMEN SYNNYTTÄMÄ MAGNEETTIKENTTÄ
l 1 2l + 1, c) 100 l=0 AB 3AC ja AB AC sekä vektoreiden AB ja
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
1/6 TEKNIIKKA JA LIIKENNE FYSIIKAN LABORATORIO V1.31 9.2011
 1/6 333. SÄDEOPTIIKKA JA FOTOMETRIA A. INSSIN POTTOVÄIN JA TAITTOKYVYN MÄÄRITTÄMINEN 1. Työn tavoite. Teoriaa 3. Työn suoritus Työssä perehdytään valon kulkuun väliaineissa ja niiden rajapinnoissa sädeoptiikan
1/6 333. SÄDEOPTIIKKA JA FOTOMETRIA A. INSSIN POTTOVÄIN JA TAITTOKYVYN MÄÄRITTÄMINEN 1. Työn tavoite. Teoriaa 3. Työn suoritus Työssä perehdytään valon kulkuun väliaineissa ja niiden rajapinnoissa sädeoptiikan
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Mitä on huomioitava kaasupäästöjen virtausmittauksissa
 Mitä on huomioitava kaasupäästöjen virtausmittauksissa Luotettavuutta päästökauppaan liittyviin mittauksiin 21.8.2006 Paula Juuti 2 Kaupattavien päästöjen määrittäminen Toistaiseksi CO2-päästömäärät perustuvat
Mitä on huomioitava kaasupäästöjen virtausmittauksissa Luotettavuutta päästökauppaan liittyviin mittauksiin 21.8.2006 Paula Juuti 2 Kaupattavien päästöjen määrittäminen Toistaiseksi CO2-päästömäärät perustuvat
Differentiaalilaskennan tehtäviä
 Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Luvun 12 laskuesimerkit
 Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Matematiikan tukikurssi, kurssikerta 3
 Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Matematiikan tukikurssi, kurssikerta 3 1 Epäyhtälöitä Aivan aluksi lienee syytä esittää luvun itseisarvon määritelmä: { x kun x 0 x = x kun x < 0 Siispä esimerkiksi 10 = 10 ja 10 = 10. Seuraavaksi listaus
Termiikin ennustaminen radioluotauksista. Heikki Pohjola ja Kristian Roine
 Termiikin ennustaminen radioluotauksista Heikki Pohjola ja Kristian Roine Maanpintahavainnot havaintokojusta: lämpötila, kostea lämpötila (kosteus), vrk minimi ja maksimi. Lisäksi tuulen nopeus ja suunta,
Termiikin ennustaminen radioluotauksista Heikki Pohjola ja Kristian Roine Maanpintahavainnot havaintokojusta: lämpötila, kostea lämpötila (kosteus), vrk minimi ja maksimi. Lisäksi tuulen nopeus ja suunta,
Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty c) sin 50 = sin ( ) = sin 130 = 0,77
 Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty.5.07 Kertaus K. a) sin 0 = 0,77 b) cos ( 0 ) = cos 0 = 0,6 c) sin 50 = sin (80 50 ) = sin 0 = 0,77 d) tan 0 = tan (0 80 ) = tan 0 =,9 e)
Juuri 7 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty.5.07 Kertaus K. a) sin 0 = 0,77 b) cos ( 0 ) = cos 0 = 0,6 c) sin 50 = sin (80 50 ) = sin 0 = 0,77 d) tan 0 = tan (0 80 ) = tan 0 =,9 e)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
PANK-2206. Menetelmä soveltuu ainoastaan kairasydännäytteille, joiden halkaisija on 32-62 mm.
 PANK-2206 KIVIAINES, PISTEKUORMITUSINDEKSI sivu 1/6 PANK Kiviainekset, lujuus- ja muoto-ominaisuudet PISTEKUORMITUSINDEKSI PANK-2206 PÄÄLLYSTEALAN NEUVOTTELUKUNTA 1. MENETELMÄN TARKOITUS Hyväksytty: Korvaa
PANK-2206 KIVIAINES, PISTEKUORMITUSINDEKSI sivu 1/6 PANK Kiviainekset, lujuus- ja muoto-ominaisuudet PISTEKUORMITUSINDEKSI PANK-2206 PÄÄLLYSTEALAN NEUVOTTELUKUNTA 1. MENETELMÄN TARKOITUS Hyväksytty: Korvaa
H 2 O. Kuva 1. Kalorimetri. missä on kalorimetriin tuotu lämpömäärä. Lämpökapasiteetti taas määräytyy yhtälöstä
 KALORIMETRI 1 TEORIAA Kalorimetri on laite, jolla voidaan mitata lämpömääriä. Mittaus voidaan suorittaa tarkastelemalla lämpömuutoksia, faasimuutoksia, kemiallisia reaktioita jne. Kun mittaus perustuu
KALORIMETRI 1 TEORIAA Kalorimetri on laite, jolla voidaan mitata lämpömääriä. Mittaus voidaan suorittaa tarkastelemalla lämpömuutoksia, faasimuutoksia, kemiallisia reaktioita jne. Kun mittaus perustuu
PERUSMITTAUKSIA. 1 Työn tavoitteet
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 PERUSMITTAUKSIA 1 Työn tavoitteet Tässä työssä määrität tutkittavaksesi annetun metallikappaleen tiheyden laskemalla sen suoraan
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 PERUSMITTAUKSIA 1 Työn tavoitteet Tässä työssä määrität tutkittavaksesi annetun metallikappaleen tiheyden laskemalla sen suoraan
Hienokiteinen ja pehmeä hunaja
 1 Hienokiteinen ja pehmeä hunaja Hunajan kiteytyminen Hunaja on kemiallisesti ajateltuna sokerien ylikylläinen vesiliuos Hunajassa olevaan veteen on liuennut enemmän sokeria kuin siihen mahtuu. Ylimääräinen
1 Hienokiteinen ja pehmeä hunaja Hunajan kiteytyminen Hunaja on kemiallisesti ajateltuna sokerien ylikylläinen vesiliuos Hunajassa olevaan veteen on liuennut enemmän sokeria kuin siihen mahtuu. Ylimääräinen
Fysiikan laboratoriotyöt 3 Sähkömotorinen voima
 Fysiikan laboratoriotyöt 3 Sähkömotorinen voima Työn suorittaja: Antti Pekkala (1988723) Mittaukset suoritettu 8.10.2014 Selostus palautettu 16.10.2014 Valvonut assistentti Martti Kiviharju 1 Annettu tehtävä
Fysiikan laboratoriotyöt 3 Sähkömotorinen voima Työn suorittaja: Antti Pekkala (1988723) Mittaukset suoritettu 8.10.2014 Selostus palautettu 16.10.2014 Valvonut assistentti Martti Kiviharju 1 Annettu tehtävä
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
RAPORTTI ISOVERIN ERISTEIDEN RADIOTAAJUISTEN SIGNAALIEN VAIMENNUKSISTA
 RAPORTTI ISOVERIN ERISTEIDEN RADIOTAAJUISTEN SIGNAALIEN VAIMENNUKSISTA Tämä on mittaus mittauksista, joilla selvitettiin kolmen erilaisen eristemateriaalin aiheuttamia vaimennuksia matkapuhelinverkon taajuusalueilla.
RAPORTTI ISOVERIN ERISTEIDEN RADIOTAAJUISTEN SIGNAALIEN VAIMENNUKSISTA Tämä on mittaus mittauksista, joilla selvitettiin kolmen erilaisen eristemateriaalin aiheuttamia vaimennuksia matkapuhelinverkon taajuusalueilla.
Differentiaali- ja integraalilaskenta
 Differentiaali- ja integraalilaskenta Opiskelijan nimi: DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona
Differentiaali- ja integraalilaskenta Opiskelijan nimi: DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona
SwemaAir 5 Käyttöohje
 SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
SwemaAir 5 Käyttöohje 1. Esittely SwemaAir 5 on kuumalanka-anemometri lämpötilan, ilmanvirtauksen sekä -nopeuden mittaukseen. Lämpötila voidaan esittää joko C, tai F, ilmannopeus m/s tai fpm ja ilman virtaus
Kahden laboratorion mittaustulosten vertailu
 TUTKIMUSSELOSTUS NRO RTE9 (8) LIITE Kahden laboratorion mittaustulosten vertailu Sisältö Sisältö... Johdanto... Tulokset.... Lämpökynttilät..... Tuote A..... Tuote B..... Päätelmiä.... Ulkotulet.... Hautalyhdyt,
TUTKIMUSSELOSTUS NRO RTE9 (8) LIITE Kahden laboratorion mittaustulosten vertailu Sisältö Sisältö... Johdanto... Tulokset.... Lämpökynttilät..... Tuote A..... Tuote B..... Päätelmiä.... Ulkotulet.... Hautalyhdyt,
29. Annossekoittimet. 29.1 Kollerisekoitin. Raimo Keskinen Pekka Niemi - Tampereen ammattiopisto
 29. Annossekoittimet Raimo Keskinen Pekka Niemi - Tampereen ammattiopisto 29.1 Kollerisekoitin Kollerisekoitin kuuluu annossekoittimiin. Se on valimosekoittimista vanhin; sen toimintaperiaate on tunnettu
29. Annossekoittimet Raimo Keskinen Pekka Niemi - Tampereen ammattiopisto 29.1 Kollerisekoitin Kollerisekoitin kuuluu annossekoittimiin. Se on valimosekoittimista vanhin; sen toimintaperiaate on tunnettu
Via Circonvallazione, 10 13018 Valduggia (VC), Italia Puh: +39 0163 47891 Faksi: +39 0163 47895 www.vironline.com. Kuva 9525.
 Valvoindustria Ing. Rizzio S.p.A. www.vironline.com 9520-sarja DZR messinkinen ON/OFF -linjasäätöventtiili Kuvaus Sinkkikadon kestävästä messingistä valmistettu ON/OFF säätöön soveltuva linjasäätöventtiili
Valvoindustria Ing. Rizzio S.p.A. www.vironline.com 9520-sarja DZR messinkinen ON/OFF -linjasäätöventtiili Kuvaus Sinkkikadon kestävästä messingistä valmistettu ON/OFF säätöön soveltuva linjasäätöventtiili
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Fysikaaliset ja mekaaniset menetelmät kiinteille biopolttoaineille
 Fysikaaliset ja mekaaniset menetelmät kiinteille biopolttoaineille Hans Hartmann Technology and Support Centre of Renewable Raw Materials TFZ Straubing, Saksa Markku Herranen ENAS Oy & Eija Alakangas,
Fysikaaliset ja mekaaniset menetelmät kiinteille biopolttoaineille Hans Hartmann Technology and Support Centre of Renewable Raw Materials TFZ Straubing, Saksa Markku Herranen ENAS Oy & Eija Alakangas,
Liike ja voima. Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä
 Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
Liike ja voima Kappaleiden välisiä vuorovaikutuksia ja niistä aiheutuvia liikeilmiöitä Tasainen liike Nopeus on fysiikan suure, joka kuvaa kuinka pitkän matkan kappale kulkee tietyssä ajassa. Nopeus voidaan
5$32577, 1 (8) Kokeen aikana vaihteisto sijaitsi tasalämpöisessä hallissa.
 5$32577, 1 (8) 5967(&12/2*
5$32577, 1 (8) 5967(&12/2*
Esimerkki - Näkymätön kuu
 Inversio-ongelmat Inversio = käänteinen, päinvastainen Inversio-ongelmilla tarkoitetaan (suoran) ongelman ratkaisua takaperin. Arkipäiväisiä inversio-ongelmia ovat mm. lääketieteellinen röntgentomografia
Inversio-ongelmat Inversio = käänteinen, päinvastainen Inversio-ongelmilla tarkoitetaan (suoran) ongelman ratkaisua takaperin. Arkipäiväisiä inversio-ongelmia ovat mm. lääketieteellinen röntgentomografia
DEE Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen 2 ratkaisuiksi
 DEE-4000 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen ratkaisuiksi Yleistä asiaa lämmönjohtumisen yleiseen osittaisdifferentiaaliyhtälöön liittyen Lämmönjohtumisen yleinen osittaisdifferentiaaliyhtälön
DEE-4000 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen ratkaisuiksi Yleistä asiaa lämmönjohtumisen yleiseen osittaisdifferentiaaliyhtälöön liittyen Lämmönjohtumisen yleinen osittaisdifferentiaaliyhtälön
Experiment Finnish (Finland) Hyppivät helmet - Faasimuutosten ja epätasapainotilojen mekaaninen malli (10 pistettä)
 Q2-1 Hyppivät helmet - Faasimuutosten ja epätasapainotilojen mekaaninen malli (10 pistettä) Lue yleisohjeet erillisestä kuoresta ennen tämän tehtävän aloittamista. Johdanto Faasimuutokset ovat tuttuja
Q2-1 Hyppivät helmet - Faasimuutosten ja epätasapainotilojen mekaaninen malli (10 pistettä) Lue yleisohjeet erillisestä kuoresta ennen tämän tehtävän aloittamista. Johdanto Faasimuutokset ovat tuttuja
KE4, KPL. 3 muistiinpanot. Keuruun yläkoulu, Joonas Soininen
 KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
KE4, KPL. 3 muistiinpanot Keuruun yläkoulu, Joonas Soininen KPL 3: Ainemäärä 1. Pohtikaa, miksi ruokaohjeissa esim. kananmunien ja sipulien määrät on ilmoitettu kappalemäärinä, mutta makaronit on ilmoitettu
Sideaineen talteenoton, haihdutuksen ja tunkeuma-arvon tutkiminen vanhasta päällysteestä. SFS-EN 12697-3
 Sideaineen talteenoton, haihdutuksen ja tunkeuma-arvon tutkiminen vanhasta päällysteestä. SFS-EN 12697-3 1 Johdanto Tutkimus käsittelee testausmenetelmästandardin SFS-EN 12697-3 Bitumin talteenotto, haihdutusmenetelmää.
Sideaineen talteenoton, haihdutuksen ja tunkeuma-arvon tutkiminen vanhasta päällysteestä. SFS-EN 12697-3 1 Johdanto Tutkimus käsittelee testausmenetelmästandardin SFS-EN 12697-3 Bitumin talteenotto, haihdutusmenetelmää.
JÄTEHUOLLON ERIKOISTYÖ
 Jari-Jussi Syrjä 1200715 JÄTEHUOLLON ERIKOISTYÖ Typpioksiduulin mittaus GASMET-monikaasuanalysaattorilla Tekniikka ja Liikenne 2013 1. Johdanto Erikoistyön tavoitteena selvittää Vaasan ammattikorkeakoulun
Jari-Jussi Syrjä 1200715 JÄTEHUOLLON ERIKOISTYÖ Typpioksiduulin mittaus GASMET-monikaasuanalysaattorilla Tekniikka ja Liikenne 2013 1. Johdanto Erikoistyön tavoitteena selvittää Vaasan ammattikorkeakoulun
Nimi: Muiden ryhmäläisten nimet:
 Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
WALTERSCHEID-NIVELAKSELI
 VA K OLA Postios. Helsinki Rukkila Puhelin Helsinki 43 48 1 2 Rautatieas. Pitäjänmäki VALTION MAATALOUSKONEIDEN TUTKIMUSLAITOS 1960 Koetusselostus 344 WALTERSCHEID-NIVELAKSELI Koetuttaja: nuko Oy, Helsinki.
VA K OLA Postios. Helsinki Rukkila Puhelin Helsinki 43 48 1 2 Rautatieas. Pitäjänmäki VALTION MAATALOUSKONEIDEN TUTKIMUSLAITOS 1960 Koetusselostus 344 WALTERSCHEID-NIVELAKSELI Koetuttaja: nuko Oy, Helsinki.
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Virhearviointi. Fysiikassa on tärkeää tietää tulosten tarkkuus.
 Virhearviointi Fysiikassa on tärkeää tietää tulosten tarkkuus. Virhelajit A. Tilastolliset virheet= satunnaisvirheet, joita voi arvioida tilastollisin menetelmin B. Systemaattiset virheet = virheet, joita
Virhearviointi Fysiikassa on tärkeää tietää tulosten tarkkuus. Virhelajit A. Tilastolliset virheet= satunnaisvirheet, joita voi arvioida tilastollisin menetelmin B. Systemaattiset virheet = virheet, joita
Eksimeerin muodostuminen
 Fysikaalisen kemian Syventävät-laboratoriotyöt Eksimeerin muodostuminen 02-2010 Työn suoritus Valmista pyreenistä C 16 H 10 (molekyylimassa M = 202,25 g/mol) 1*10-2 M liuos metyylisykloheksaaniin.
Fysikaalisen kemian Syventävät-laboratoriotyöt Eksimeerin muodostuminen 02-2010 Työn suoritus Valmista pyreenistä C 16 H 10 (molekyylimassa M = 202,25 g/mol) 1*10-2 M liuos metyylisykloheksaaniin.
TEHTÄVIEN RATKAISUT. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 712 p m 105 kg
 TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
TEHTÄVIEN RATKAISUT 15-1. a) Hyökkääjän liikemäärä on p = mv = 89 kg 8,0 m/s = 71 kgm/s. b) 105-kiloisella puolustajalla on yhtä suuri liikemäärä, jos nopeus on kgm 71 p v = = s 6,8 m/s. m 105 kg 15-.
LIIAN TAIPUISA MUOVI TAUSTAA
 LIIAN TAIPUISA MUOVI Muoviteollisuuden laboratoriossa on huomattu, että tuotannosta tullut muovi on liian taipuisaa. Tämän vuoksi laadunvalvontalaboratorio tutkii IR:n avulla eteenin pitoisuuden muovissa.
LIIAN TAIPUISA MUOVI Muoviteollisuuden laboratoriossa on huomattu, että tuotannosta tullut muovi on liian taipuisaa. Tämän vuoksi laadunvalvontalaboratorio tutkii IR:n avulla eteenin pitoisuuden muovissa.
Kertaus. x x x. K1. a) b) x 5 x 6 = x 5 6 = x 1 = 1 x, x 0. K2. a) a a a a, a > 0
 Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
Juuri 8 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty 8.9.07 Kertaus K. a) 6 4 64 0, 0 0 0 0 b) 5 6 = 5 6 = =, 0 c) d) K. a) b) c) d) 4 4 4 7 4 ( ) 7 7 7 7 87 56 7 7 7 6 6 a a a, a > 0 6 6 a
1.1 Tyhjiön permittiivisyyden mittaaminen tasokondensaattorilla
 PERMITTIIVISYYS Johdanto Tarkastellaan tasokondensaattoria, joka koostuu kahdesta yhdensuuntaisesta metallilevystä. Siirretään varausta levystä toiseen, jolloin levyissä on varaukset +Q ja Q ja levyjen
PERMITTIIVISYYS Johdanto Tarkastellaan tasokondensaattoria, joka koostuu kahdesta yhdensuuntaisesta metallilevystä. Siirretään varausta levystä toiseen, jolloin levyissä on varaukset +Q ja Q ja levyjen
Torsioheiluri IIT13S1. Selostuksen laatija: Eerik Kuoppala. Ryhmä B3: Eerik Kuoppala G9024 Petteri Viitanen G8473
 Torsioheiluri IIT3S Selostuksen laatija: Eerik Kuoppala Ryhmä B3: Eerik Kuoppala G904 Petteri Viitanen G8473 Mittauspäivämäärä:..4 Selostuksen jättöpäivä: 4.3.4 Torsioheilurin mitatuilla neljän jakson
Torsioheiluri IIT3S Selostuksen laatija: Eerik Kuoppala Ryhmä B3: Eerik Kuoppala G904 Petteri Viitanen G8473 Mittauspäivämäärä:..4 Selostuksen jättöpäivä: 4.3.4 Torsioheilurin mitatuilla neljän jakson
Sähköstatiikan laskuissa useat kaavat yksinkertaistuvat hieman, jos vakio C kirjoitetaan muotoon
 30 SÄHKÖVAKIO 30 Sähkövakio ja Coulombin laki Coulombin lain mukaan kahden tyhjiössä olevan pistevarauksen q ja q 2 välinen voima F on suoraan verrannollinen varauksiin ja kääntäen verrannollinen varausten
30 SÄHKÖVAKIO 30 Sähkövakio ja Coulombin laki Coulombin lain mukaan kahden tyhjiössä olevan pistevarauksen q ja q 2 välinen voima F on suoraan verrannollinen varauksiin ja kääntäen verrannollinen varausten
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Laboratorioraportti 3
 KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
KON-C3004 Kone-ja rakennustekniikan laboratoriotyöt Laboratorioraportti 3 Laboratorioharjoitus 1B: Ruuvijohde Ryhmä S: Pekka Vartiainen 427971 Jari Villanen 69830F Anssi Petäjä 433978 Mittaustilanne Harjoituksessa
Vedetään kiekkoa erisuuruisilla voimilla! havaitaan kiekon saaman kiihtyvyyden olevan suoraan verrannollinen käytetyn voiman suuruuteen
 4.3 Newtonin II laki Esim. jääkiekko märällä jäällä: pystysuuntaiset voimat kumoavat toisensa: jään kiekkoon kohdistama tukivoima n on yhtäsuuri, mutta vastakkaismerkkinen kuin kiekon paino w: n = w kitka
4.3 Newtonin II laki Esim. jääkiekko märällä jäällä: pystysuuntaiset voimat kumoavat toisensa: jään kiekkoon kohdistama tukivoima n on yhtäsuuri, mutta vastakkaismerkkinen kuin kiekon paino w: n = w kitka
Liian taipuisa muovi
 Muoviteollisuuden laboratoriossa on huomattu, että tuotannosta tullut muovi on liian taipuisaa. Tämän vuoksi laadunvalvontalaboratorio tutkii IR:n avulla eteenin pitoisuuden muovissa. TAUSTAA Polypropeeni
Muoviteollisuuden laboratoriossa on huomattu, että tuotannosta tullut muovi on liian taipuisaa. Tämän vuoksi laadunvalvontalaboratorio tutkii IR:n avulla eteenin pitoisuuden muovissa. TAUSTAA Polypropeeni
Kirjoittaja: tutkija Jyrki Kouki, TTS tutkimus
 TUTKIMUSRAPORTTI 13.03.2009 Mittauksia hormittomalla takalla ( Type: HW Biotakka, tuotekehitysversio) Tilaaja: OY H & C Westerlund AB Kirjoittaja: tutkija Jyrki Kouki, TTS tutkimus 2 SISÄLLYSLUETTELO sivu
TUTKIMUSRAPORTTI 13.03.2009 Mittauksia hormittomalla takalla ( Type: HW Biotakka, tuotekehitysversio) Tilaaja: OY H & C Westerlund AB Kirjoittaja: tutkija Jyrki Kouki, TTS tutkimus 2 SISÄLLYSLUETTELO sivu
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
Aerosolimittauksia ceilometrillä.
 Aerosolimittauksia ceilometrillä. Timo Nousiainen HTB workshop 6.4. 2006. Fysikaalisten tieteiden laitos, ilmakehätieteiden osasto Projektin kuvaus Esitellyt tulokset HY:n, IL:n ja Vaisala Oyj:n yhteisestä,
Aerosolimittauksia ceilometrillä. Timo Nousiainen HTB workshop 6.4. 2006. Fysikaalisten tieteiden laitos, ilmakehätieteiden osasto Projektin kuvaus Esitellyt tulokset HY:n, IL:n ja Vaisala Oyj:n yhteisestä,
Integrointi ja sovellukset
 Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Integrointi ja sovellukset Tehtävät:. Muodosta ja laske yläsumma funktiolle fx) x 5 välillä [, 4], kun väli on jaettu neljään yhtä suureen osaan.. Määritä integraalin x + ) dx likiarvo laskemalla alasumma,
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Lahti Precision Fluidisointijärjestelmä
 Lahti Precision Fluidisointijärjestelmä 100 years of experience Lahti Precision -fluidisointijärjestelmä estää siilojen purkautumishäiriöt Patentoitu fluidisointijärjestelmä jauheiden ja muiden hienojakoisten
Lahti Precision Fluidisointijärjestelmä 100 years of experience Lahti Precision -fluidisointijärjestelmä estää siilojen purkautumishäiriöt Patentoitu fluidisointijärjestelmä jauheiden ja muiden hienojakoisten
Tilastollinen testaus. Vilkkumaa / Kuusinen 1
 Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + 2 ( 1) ( 1) 3 = = 4
 KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
KERTAUS KERTAUSTEHTÄVIÄ K1. P( 1) = 3 ( 1) + ( 1) + 3 ( 1) 3 = 3 + 3 = 4 K. a) x 3x + 7x 5x = 4x + 4x b) 5x 3 (1 x ) = 5x 3 1 + x = 6x 4 c) (x + 3)(x 4) = x 3 4x + 3x 1 = x 3 + 3x 4x 1 Vastaus: a) 4x +
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
9. laskuharjoituskierros, vko 12-13, ratkaisut
 9. laskuharjoituskierros, vko 12-13, ratkaisut D1. Olkoot X i, i = 1, 2,..., n riippumattomia, samaa eksponenttijakaumaa noudattavia satunnaismuuttujia, joiden odotusarvo E(X i = β, toisin sanoen X i :t
9. laskuharjoituskierros, vko 12-13, ratkaisut D1. Olkoot X i, i = 1, 2,..., n riippumattomia, samaa eksponenttijakaumaa noudattavia satunnaismuuttujia, joiden odotusarvo E(X i = β, toisin sanoen X i :t
