Digitaalitekniikan matematiikka Luku 3 Sivu 1 (19) Kytkentäfunktiot ja perusporttipiirit
|
|
|
- Tommi Tikkanen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Digitaalitekniikan matematiikka Luku 3 Sivu (9) &&
2 Digitaalitekniikan matematiikka Luku 3 Sivu 2 (9) Johdanto Tässä luvussa esitetään digitaalilaitteen signaalit ja digitaalipiirien perustyypit esitellään kytkentäfunktiot, joihin koko digitaalitekniikka perustuu käsitellään kytkentäfunktioiden määrittelytavat esitetään totuustaulu, joka on kytkentäfunktion taulukkomuotoinen määrittelytapa määritellään erityiset peruskytkentäfunktiot, joiden avulla kaikki kytkentäfunktiot voidaan esittää esitellään perusporttipiirit J, TI ja EI ja esitetään, miten niillä toteutetaan kytkentäfunktioita esitetään perusporttipiirien sovelluksia esitetään, miten kytkentäfunktio esitetään lausekkeena esitetään, miten lauseke toteutetaan perusporttipiireillä ja miten toteutus kuvataan piirikaaviolla esitellään aikakaavio, jolla kuvataan muuttujien ja funktion arvon muuttumista ajan funktiona
3 Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä joko 0 tai tulosignaalit (input signals) tuovat laitteeseen sen tarvitsemaa tietoa tulosignaalilähteitä ovat esimerkiksi kytkimet, painikkeet, näppäimistöt, hiiri ja erilaiset digitaaliset anturit lähtösignaalit (output signals) antavat laitteesta sen muodostamaa tietoa lähtösignaalien kohteita ovat esimerkiksi lamput, näyttölaitteet, äänilaitteet ja erilaiset digitaaliset toimilaitteet Digitaalilaite ja siihen liittyvät signaalit voidaan kuvata lohkokaaviolla Signaaliviivat Tulosignaalit Lähtösignaalit Esimerkki TS TS2 TS3 Digitaalilaite LS LS2 PL VIL Vilkutin Vilkutin LM Laitteen nimi
4 Digitaalitekniikan matematiikka Luku 3 Sivu 4 (9) Kombinaatiopiirit ja sekvenssipiirit? Kombinaatiopiirin (combinational circuit) lähtösignaalien arvot riippuvat vain tulosignaalien arvoista kyseisellä hetkellä Sama tulosignaaliyhdistelmä aikaansaa aina saman lähtösignaaliyhdistelmän Kombinaatiopiireillä voidaan toteuttaa vain osa digitaalilaitteissa tarvittavista toiminnoista Esimerkki: vipukytkimellä sytytettävä ja sammutettava lamppu Sekvenssipiirin (sequential circuit) lähtösignaalien arvot riippuvat piirin tilasta (state) ja ehkä piirin tulosignaalien arvoista; piiri muistaa tilansa Piirin tila riippuu sen alkutilasta (initial state) ja tulosignaalien aiemmin saamista arvoista Sama tulosignaaliyhdistelmä voi aikaansaada eri tapauksissa eri lähtösignaaliyhdistelmän Sekvenssipiireillä voidaan toteuttaa ne digitaalilaitteiden toiminnot, jotka vaativat muistamista Esimerkki: painonapilla sytytettävä ja sammutettava lamppu
5 Digitaalitekniikan matematiikka Luku 3 Sivu 5 (9) Kytkentämuuttujat ja -funktiot Digitaalilaitteiden toiminta perustuu kytkentäfunktioiden (switching function) eli loogisten funktioiden (logic function) toteuttamiseen Mutkikkaissa digitaalilaitteissa toteutetaan hyvin monta funktiota yhtäaikaa Kytkentäfunktioiden muuttujia (variable) nimitetään kytkentämuuttujiksi, loogisiksi muuttujiksi tai Boolen muuttujiksi Kytkentämuuttujalla on kaksi arvoa tosi (true) eli epätosi (false) eli 0 0 Kytkentäfunktio on yhden tai usean kytkentämuuttujan funktio, jolla niinikään on kaksi arvoa tosi eli epätosi eli 0 0 Käytännön laitteissa kytkentämuuttujia ja -funktioita vastaavat digitaaliset signaalit, joita nimitetään myös loogisiksi signaaleiksi muuttujia vastaavat tulosignaalit funktioita vastaavat lähtösignaalit
6 Digitaalitekniikan matematiikka Luku 3 Sivu 6 (9) Kytkentämuuttujien ja -funktioiden nimet Muuttujien ja funktioiden niminä käytetään usein isoja kirjaimia, B, C ja F, G, H erityisesti teoreettisissa esityksissä joskus käytetään pieniäkin kirjaimia Muuttujat ja funktiot voidaan myös nimetä siten, että nimi eli muistikas (mnemonic) kuvaa kyseistä muuttujaa tai funktiota erityisesti käytännön laitteissa signaaliniminä osana signaalinimeä käytetään usein numeroita esim. nelibittisen binaariluvun bitit B3 B0 signaalin nimi on totta signaalin arvo = UKI 0-5 Esimerkki: lamppua ohjaava kytkin = KYT (kytkin päällä KYT = ) lamppua ohjaava toinen kytkin = KYT2 (kytkin päällä KYT2 = ) näistä muodostettava lampun ohjaussignaali = LMP (lamppu palaa LMP = ) OPEN
7 Digitaalitekniikan matematiikka Luku 3 Sivu 7 (9) Kytkentäfunktion määrittelytavat Sanallinen määrittely Määrittely: Lamppu palaa, kun käyttökelpoinen, kun funktio on yksinkertainen kahdesta kytkimestä jompi kumpi on päällä. esimerkki: Lamppu palaa, kun kahdesta kytkimestä jompi kumpi on päällä. Jos molemmat ovat pois päältä tai molemmat ovat päällä, lamppu ei pala. Jos molemmat ovat pois päältä tai molemmat ovat päällä, lamppu ei pala. Totuustaulu kytkentäfunktion kääntäen yksikäsitteinen taulukkomuotoinen määrittely Perusfunktioiden avulla esitetty lauseke lauseke määrittelee funktion yksikäsitteisesti KYT useat erilaiset lausekkeet voivat määritellä saman funktion digitaalipiireillä toteutetaan lausekkeita 0 0 KYT2 0 0 LMP LMP LMP = KYT KYT KYT2 KYT2 + KYT KYT KYT2 KYT2 LMP LMP = (KYT (KYT + KYT2) KYT2) (KYT (KYT + KYT2) KYT2) 0 0
8 Digitaalitekniikan matematiikka Luku 3 Sivu 8 (9) Totuustaulu Totuustaulussa (truth table) esitetään kaikki muuttujien arvoyhdistelmät ja funktion tai funktioiden vastaavat arvot Eräiden kolmen muuttujan, B ja C funktioiden F ja G totuustaulu:? 2 Muuttujat Kaikki muuttujien arvoyhdistelmät (huomaa järjestys!) B C F G Funktiot Funktioiden saamat arvot Esimerkkifunktion LMP totuustaulu KYT KYT KYT2 KYT2 LMP LMP
9 Digitaalitekniikan matematiikka Luku 3 Sivu 9 (9) Peruskytkentäfunktiot ja perusporttipiirit Kaikki kytkentäfunktiot voidaan esittää kolmen perusfunktion avulla Perusfunktiot ovat J-funktio (ND) J ND TI-funktio (OR) TI OR EI-funktio (NOT) EI Jokainen perusfunktio voidaan toteuttaa sitä vastaavalla perusporttipiirillä (gate) (J, TI, EI) Kytkentäfunktio esitetään lausekkeena (expression), jossa perusfunktioita on sovellettu muuttujiin Kytkentäfunktio voidaan käytännössä toteuttaa lauseketta vastaavana perusporttipiiriyhdistelmänä Usea erilainen lauseke voi esittää samaa funktiota Samaa funktiota esittävistä lausekkeista toiset ovat mutkikkaampia kuin toiset Yksinkertaisin lauseke johtaa yksinkertaisimpaan toteutukseen NOT
10 Digitaalitekniikan matematiikka Luku 3 Sivu 0 (9) J-funktio (ND) J-funktiolla on vähintään kaksi muuttujaa J-funktio saa arvon, kun kaikki sen muuttujat saavat arvon saa arvon 0 aina muulloin J-funktion operaattorin symboli on (piste) Myös muita symboleja on käytössä, mm. &, ja Symboli voidaan jättää pois, ellei ole sekaannuksen vaaraa J-funktiota nimitetään myös muuttujiensa loogiseksi tuloksi (logical product) J-funktio toteutetaan J-portilla Kolmen muuttujan, B, ja C J-funktio F F = B C = B C J ND J-funktion B C totuustaulu B C B C
11 Digitaalitekniikan matematiikka Luku 3 Sivu (9) TI-funktio (OR)? 3 TI-funktiolla on vähintään kaksi muuttujaa TI-funktio saa arvon, kun vähintään yksi sen muuttujista saa arvon saa arvon 0, kun kaikki sen muuttujat saavat arvon 0 TI-funktion operaattorin symboli on + ("plus") Myös muita symboleja on käytössä, mm. #, ja TI-funktiota nimitetään myös muuttujiensa loogiseksi summaksi (logical sum) TI-funktio toteutetaan TI-portilla Kolmen muuttujan, B, ja C TI-funktio F F = + B + C TI TI-funktion +B+C totuustaulu B C OR +B+C +B+C
12 Digitaalitekniikan matematiikka Luku 3 Sivu 2 (9) EI-funktio (NOT)? 4 EI-funktio on yhden muuttujan funktio EI NOT EI-funktio saa arvon, kun sen muuttuja saa arvon 0 saa arvon 0, kun sen muuttuja saa arvon EI-funktion operaattorin symboli on (viiva muuttujan päällä), esim. Myös muita symboleja on käytössä, ainakin!,, -, _, /, ~, ' ja * EI-funktiota nimitetään myös muuttujansa komplementiksi (complement), inversioksi (inversion) ja negaatioksi (negation) EI-funktio toteutetaan EI-piirillä eli invertterillä Muuttujan EI-funktio F EI-funktion totuustaulu 0 0 F =
13 Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Perusporttipiirit Perusfunktio toteutetaan sitä vastaavalla porttipiirillä Haluttu kytkentäfunktio toteutetaan sen lauseketta vastaavalla porttipiiriyhdistelmällä, joka esitetään piirikaaviolla Perusporttipiireille on omat piirrosmerkkinsä (symbol) Kansainvälisen IEC-standardin 6067 mukaiset ja perinteiset amerikkalaiset piirrosmerkit GTE IEC piirrosmerkki Tulosignaalit B J-portti Lähtösignaali TI-portti EI-piiri eli invertteri & B + B B merikkalainen piirrosmerkki Tulot B Lähtö B B + B
14 Digitaalitekniikan matematiikka Luku 3 Sivu 4 (9) J- ja TI-portin sovelluksia Signaalin sallinta ja pakko-ohjaus sallinta/pakko-ohjaus nollaksi esimerkki: energian säästö pakottamalla lamppu pimeäksi VLO SLL & LM J Toiminta SLL SLL LM LM 0 0 VLO VLO Kun SLL = 0, lamppu ei pala. Kun SLL =, lamppu palaa signaalin VLO mukaisesti. sallinta/pakko-ohjaus ykköseksi esimerkki: sireenin koekäyttö SOI PKK SIR TI Toiminta PKK PKK SIR SIR 0 SOI SOI Kun PKK = 0, sireeni soi signaalin SOI mukaisesti. Kun PKK =, sireeni soi koko ajan.
15 Digitaalitekniikan matematiikka Luku 3 Sivu 5 (9) Kytkentäfunktion esitys lausekkeena? 5 Vasemmalla puolella funktion nimi F Funktion nimen perässä voivat olla muuttujien nimet suluissa F(, B, C) Oikealla puolella itse lauseke, jossa on muuttujien nimiä, operaattoreita ja sulkumerkkejä + B C Välissä symboli = F = + B C Funktion arvon laskentajärjestys, ellei sulkumerkeillä toisin osoiteta: ensin yksittäisen muuttujan EI seuraavaksi J sitten TI viimeiseksi usean muuttujan yli ulottuva EI Esimerkkejä: F = + B C G(, B, C) = ( + B) ( + B + C) H = X + Y U + Z(U + V) (W + T) B +B B! B B
16 Digitaalitekniikan matematiikka Luku 3 Sivu 6 (9) Piirikaavio Piirikaavio (circuit diagram, schematic) esittää piirin tai laitteen osat eli komponentit (component) symboleina ja niiden kytkennät signaaliviivoina lla on esitetty kaksi lauseketta ja niitä vastaavan porttipiireillä toteutetun kombinaatiopiirin piirikaavio? 6 Ensimmäinen lauseke F = + B C Toinen lauseke G = ( + B) ( + B + C) B C B C & B C & F G + B + B + C
17 Digitaalitekniikan matematiikka Luku 3 Sivu 7 (9) B C Kytkentäfunktion neljä esitystapaa Rakennekuvaus (structural description) Kuvaa komponentit ja kytkennät Sanallinen F saa saa arvon arvon,, kun kun = tai tai kun kun B = ja ja C = 0, 0, muulloin arvon arvon Piirikaavio & Käyttäytymiskuvauksia (behavioral description) Kuvaavat toiminnan F Lauseke F = + B C Totuustaulu B C F
18 Digitaalitekniikan matematiikka Luku 3 Sivu 8 (9) ikakaavio ikakaavio (timing diagram) on vielä yksi tapa esittää kytkentäfunktio Kuvaa signaalien käyttäytymistä ajan funktioina ika kasvaa vasemmalta oikealle Vastaa täydellisesti piirrettynä totuustaulua Ei välttämättä kuvaa kaikkia eri mahdollisuuksia, vaan vain toiminnan kannalta merkittävät Käytetään simuloitaessa piirin toimintaa tietokoneella ja tutkittaessa sitä logiikka-analysaattorilla Voidaan käyttää myös etenemisviiveiden esittämiseen Esimerkkinä perusporttien ja invertterin aikakaaviot (vastaavat tässä totuustaulua) B B 0 + B Kaaviossa nollaviiveet
19 Digitaalitekniikan matematiikka Luku 3 Sivu 9 (9) Yhteenveto Digitaalilaitteeseen tulee tulee tulo- tulo- ja ja siitä siitä lähtee lähtee lähtösignaaleja Digitaalipiirit ovat ovat joko joko kombinaatiopiirejä tai tai sekvenssipiirejä Kytkentäfunktiot ovat ovat digitaalilaitteiden toteuttamisen perusta perusta Kytkentämuuttujalla ja ja -funktiolla on on joko joko arvo arvo tosi tosi () () tai tai epätosi (0) (0) Muuttujien ja ja funktioiden niminä niminä käytetään joko joko kirjaimia tai tai niiden niiden toimintaa kuvaavia muistikkaita Kytkentäfunktio määritellään sanallisesti, totuustaululla tai tai perusfunktioiden avulla avulla esitetyllä lausekkeella Perusfunktiot ovat ovat J J (ND), (ND), TI TI (OR) (OR) ja ja EI EI (NOT) (NOT) Perusfunktioita vastaavat perusporttipiirit: J-portti, TI-portti ja ja invertteri Perusporttipiirillä voidaan toteuttaa toiminnan sallinta- // pakko-ohjauspiiri Kytkentäfunktio esitetään lausekkeena perusfunktioiden avulla avulla Lausekkeen toteutus perusporttipiireillä esitetään piirikaaviolla Kytkentäfunktion neljä neljä eri eri esitystapaa voidaan johtaa johtaa toisistaan ikakaaviota käytetään piirin piirin toimintaa simuloitaessa ja ja tutkittaessa
Digitaalilaitteen signaalit
 Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä
Digitaalitekniikan matematiikka Luku 3 Sivu 3 (9) Digitaalilaitteen signaalit Digitaalilaitteeseen tai -piiriin tulee ja siitä lähtee digitaalisia signaaleita yksittäisen signaalin arvo on kunakin hetkenä
Digitaalitekniikan matematiikka Harjoitustehtäviä
 arjoitustehtäviä Sivu 6 6.3.2 e arjoitustehtäviä uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä jossa käytävän kummassakin päässä on kytkin ja käytävän keskellä lamppu. amppu
arjoitustehtäviä Sivu 6 6.3.2 e arjoitustehtäviä uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä jossa käytävän kummassakin päässä on kytkin ja käytävän keskellä lamppu. amppu
Digitaalitekniikan matematiikka Luku 6 Sivu 1 (20) Kombinaatiopiirit & & A B A + B
 igitaalitekniikan matematiikka Luku 6 Sivu (20).9.20 e 0 0 0 0 0 + 0 0 0 0 0 0 0 igitaalitekniikan matematiikka Luku 6 Sivu 2 (20).9.20 e Johdanto Tässä luvussa esitellään porttipiirityypit J-EI ja TI-EI
igitaalitekniikan matematiikka Luku 6 Sivu (20).9.20 e 0 0 0 0 0 + 0 0 0 0 0 0 0 igitaalitekniikan matematiikka Luku 6 Sivu 2 (20).9.20 e Johdanto Tässä luvussa esitellään porttipiirityypit J-EI ja TI-EI
Johdatus digitaalitekniikkaan
 Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Johdatus digitaalitekniikkaan Johdanto
Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9. e Johdatus digitaalitekniikkaan Johdanto
Digitaalitekniikan matematiikka Luku 8 Sivu 1 (23) Kombinaatiopiirielimet MUX X/Y 2 EN
 Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe DX G = G EN X/Y Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe Johdanto Tässä luvussa esitetään keskeisiä kombinaatiopiirielimiä ne ovat perusporttipiirejä
Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe DX G = G EN X/Y Digitaalitekniikan matematiikka Luku 8 Sivu ().9. Fe Johdanto Tässä luvussa esitetään keskeisiä kombinaatiopiirielimiä ne ovat perusporttipiirejä
Digitaalitekniikan matematiikka Luku 1 Sivu 1 (19) Johdatus digitaalitekniikkaan
 Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdatus digitaalitekniikkaan Digitaalitekniikan matematiikka Luku Sivu 2 (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdanto
Digitaalitekniikan matematiikka Luku Sivu (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdatus digitaalitekniikkaan Digitaalitekniikan matematiikka Luku Sivu 2 (9) Johdatus digitaalitekniikkaan.9.2 Fe Johdanto
Sekvenssipiirin tilat
 igitaalitekniikka (piirit) Luku Täsmätehtävä Tehtävä Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan seuraavissa sekvenssipiireissä: Painikkeella ohjattava lampun sytytys ja sammutus. Näyttöä ohjaava
igitaalitekniikka (piirit) Luku Täsmätehtävä Tehtävä Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan seuraavissa sekvenssipiireissä: Painikkeella ohjattava lampun sytytys ja sammutus. Näyttöä ohjaava
Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: JA-EI-portti A B. TAI-EI-portti A B = 1
 Digitaalitekniikan matematiikka Luku 6 Sivu () Kombinaatiopiirit.9. Fe J-EI- (NND) ja TI-EI- (NOR) -portit Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: NND? B B & B B = & B + B + B
Digitaalitekniikan matematiikka Luku 6 Sivu () Kombinaatiopiirit.9. Fe J-EI- (NND) ja TI-EI- (NOR) -portit Peruspiirejä yhdistelemällä saadaan seuraavat uudet porttipiirit: NND? B B & B B = & B + B + B
Digitaalitekniikka (piirit) Luku 14 Sivu 1 (16) Sekvenssipiirit. Kombinaatiopiiri. Tilarekisteri
 Digitaalitekniikka (piirit) Luku 4 Sivu (6).8.24 Fe/AKo Tilarekisteri Kombinaatiopiiri Digitaalitekniikka (piirit) Luku 4 Sivu 2 (6).8.24 Fe/AKo Johdanto Tässä luvussa todetaan esimerkin avulla kombinaatiopiirien
Digitaalitekniikka (piirit) Luku 4 Sivu (6).8.24 Fe/AKo Tilarekisteri Kombinaatiopiiri Digitaalitekniikka (piirit) Luku 4 Sivu 2 (6).8.24 Fe/AKo Johdanto Tässä luvussa todetaan esimerkin avulla kombinaatiopiirien
ELEC-C3240 Elektroniikka 2
 ELEC-C324 Elektroniikka 2 Marko Kosunen Marko.kosunen@aalto.fi Digitaalielektroniikka Tilakoneet Materiaali perustuu kurssiins-88. Digitaalitekniikan perusteet, laatinut Antti Ojapelto Luennon oppimistavoite
ELEC-C324 Elektroniikka 2 Marko Kosunen Marko.kosunen@aalto.fi Digitaalielektroniikka Tilakoneet Materiaali perustuu kurssiins-88. Digitaalitekniikan perusteet, laatinut Antti Ojapelto Luennon oppimistavoite
Tervetuloa opiskelemaan DIGITAALI- TEKNIIKKAA!
 igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e Yleistä opintojaksosta Laajuus op = 8 h, kokonaan syyslukukauden
igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e igitaalitekniikan matematiikka Luku Sivu (9) Opintojakson esittely.9. e Yleistä opintojaksosta Laajuus op = 8 h, kokonaan syyslukukauden
ELEC-C3240 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä
 ELE-324 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä Materiaalia otettu myös: https://www.allaboutcircuits.com/textbook/digital/chpt-8/introduction-to-karnaughmapping/
ELE-324 Elektroniikka 2 Digitaalielektroniikka Karnaugh n kartat ja esimerkkejä digitaalipiireistä Materiaalia otettu myös: https://www.allaboutcircuits.com/textbook/digital/chpt-8/introduction-to-karnaughmapping/
Harjoitustehtävien ratkaisut
 Sivu (22) 29.8.2 Fe/Ko Luku Sekvenssipiirit. Tutki luentokalvo- ja opetusmonisteessa esitettyä esimerkkiä synkronisesta sekvenssipiiristä. a) Montako tilaa piirissä on? Koska piirissä on kaksi tilasignaalia,
Sivu (22) 29.8.2 Fe/Ko Luku Sekvenssipiirit. Tutki luentokalvo- ja opetusmonisteessa esitettyä esimerkkiä synkronisesta sekvenssipiiristä. a) Montako tilaa piirissä on? Koska piirissä on kaksi tilasignaalia,
Yhden bitin tiedot. Binaariluvun arvon laskeminen. Koodin bittimäärä ja vaihtoehdot ? 1
 Luku Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Opetuskerta Sivu Luku Opetuskerta Sivu Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista.
Luku Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Digitaalitekniikan matematiikka Täsmätehtävät.9. Fe Opetuskerta Sivu Luku Opetuskerta Sivu Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista.
Yhden bitin tiedot. Digitaalitekniikan matematiikka Luku 1 Täsmätehtävä Tehtävä 1. Luettele esimerkkejä yhden bitin tiedoista.
 Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista. Ovi auki - ovi kiinni Virta kulkee - virta ei kulje Lamppu palaa - lamppu ei pala
Digitaalitekniikan matematiikka Luku Täsmätehtävä Tehtävä Yhden bitin tiedot Luettele esimerkkejä yhden bitin tiedoista. Ovi auki - ovi kiinni Virta kulkee - virta ei kulje Lamppu palaa - lamppu ei pala
Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) Kytkentäalgebra A + 1 = 1 A = A A + B C = (A + B) (A + C) A 0 = 0. Maksimitermi.
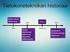 Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) A + 1 = 1 A + B C = (A + B) (A + C) F(A, B, C) = Σ m (2, 3, 5, 7) Maksimitermi A = A m0 A 0 = 0 M7 A + B = A B Minimitermi Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku 4 Sivu 1 (15) A + 1 = 1 A + B C = (A + B) (A + C) F(A, B, C) = Σ m (2, 3, 5, 7) Maksimitermi A = A m0 A 0 = 0 M7 A + B = A B Minimitermi Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku 5 Sivu 1 (22) Lausekkeiden sieventäminen F C F = B + A C. Espresso F = A (A + B) = A A + A B = A B
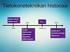 igitaalitekniikan matematiikka Luku 5 Sivu (22).9.2 e = + = ( + ) = + = Espresso igitaalitekniikan matematiikka Luku 5 Sivu 2 (22).9.2 e Johdanto Tässä luvussa esitetään perusteet lausekemuodossa esitettyjen
igitaalitekniikan matematiikka Luku 5 Sivu (22).9.2 e = + = ( + ) = + = Espresso igitaalitekniikan matematiikka Luku 5 Sivu 2 (22).9.2 e Johdanto Tässä luvussa esitetään perusteet lausekemuodossa esitettyjen
Synkronisten sekvenssipiirien suunnittelu
 Digitaalitekniikka (piirit) Luku 6 Sivu (5) Synkronisten sekvenssipiirien suunnittelu.8.24 Fe/AKo Synkronisten sekvenssipiirien suunnittelu Digitaalitekniikka (piirit) Luku 6 Sivu 2 (5) Synkronisten sekvenssipiirien
Digitaalitekniikka (piirit) Luku 6 Sivu (5) Synkronisten sekvenssipiirien suunnittelu.8.24 Fe/AKo Synkronisten sekvenssipiirien suunnittelu Digitaalitekniikka (piirit) Luku 6 Sivu 2 (5) Synkronisten sekvenssipiirien
Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset
 Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset Metropolia/AK. Mealyn koneessa on kolme tulosignaalia, joista yksi vaikuttaa pelkästään lähtösignaaleihin, yksi pelkästään koneen tilaan ja yksi
Digitaalitekniikka (piirit), kertaustehtäviä: Vastaukset Metropolia/AK. Mealyn koneessa on kolme tulosignaalia, joista yksi vaikuttaa pelkästään lähtösignaaleihin, yksi pelkästään koneen tilaan ja yksi
C = P Q S = P Q + P Q = P Q. Laskutoimitukset binaariluvuilla P -- Q = P + (-Q) (-Q) P Q C in. C out
 Digitaalitekniikan matematiikka Luku ivu (2).9.2 Fe C = Aseta Aseta i i = n i > i i i Ei i < i i i Ei i i = Ei i i = i i -- On On On C in > < = CI CO C out -- = + (-) (-) = + = C + Digitaalitekniikan matematiikka
Digitaalitekniikan matematiikka Luku ivu (2).9.2 Fe C = Aseta Aseta i i = n i > i i i Ei i < i i i Ei i i = Ei i i = i i -- On On On C in > < = CI CO C out -- = + (-) (-) = + = C + Digitaalitekniikan matematiikka
Inputs: b; x= b 010. x=0. Elektroniikkajärjestelmät ETT_2068
 Elektroniikkajärjestelmät ETT_2068 tentti 1) Oheisessa sekvenssilogiikassa tiloille on jo annettu bittivaste 000, 001 jne. Tehtävänäsi on nyt konstruoda sekvenssilogiikka vaihe vaiheelta standarditavalla.
Elektroniikkajärjestelmät ETT_2068 tentti 1) Oheisessa sekvenssilogiikassa tiloille on jo annettu bittivaste 000, 001 jne. Tehtävänäsi on nyt konstruoda sekvenssilogiikka vaihe vaiheelta standarditavalla.
13. Loogiset operaatiot 13.1
 13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU
 OPINNÄYTETYÖ - AMMATTIKORKEAKOULUTUTKINTO TEKNIIKAN JA LIIKENTEEN ALA DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU T E K I J Ä : Toni Halonen SAVONIA-AMMATTIKORKEAKOULU OPINNÄYTETYÖ
OPINNÄYTETYÖ - AMMATTIKORKEAKOULUTUTKINTO TEKNIIKAN JA LIIKENTEEN ALA DIGITAALISTEN KOMBINAATIO- PIIRIEN LABORATORIOTÖIDEN SUUNNITTELU T E K I J Ä : Toni Halonen SAVONIA-AMMATTIKORKEAKOULU OPINNÄYTETYÖ
13. Loogiset operaatiot 13.1
 13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
13. Loogiset operaatiot 13.1 Sisällys Loogiset operaatiot AND, OR, XOR ja NOT. Operaatioiden ehdollisuus. Bittioperaatiot. Loogiset operaatiot ohjausrakenteissa. Loogiset operaatiot ja laskentajärjestys.
c) loogiset funktiot tulojen summana B 1 = d) AND- ja EXOR-porteille sopivat yhtälöt
 IGITLITEKNIIKK I 5 Tentti:.. ELEKTRONIIKN LORTORIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) b) minimoituna summien
IGITLITEKNIIKK I 5 Tentti:.. ELEKTRONIIKN LORTORIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) b) minimoituna summien
Digitaalitekniikka (piirit) Luku 15 Sivu 1 (17) Salvat ja kiikut 1D C1 C1 1T 1J C1 1K S R
 igitaalitekniikka (piirit) Luku 5 ivu (7).8.24 Fe/AKo C J C K C T C C J C K igitaalitekniikka (piirit) Luku 5 ivu 2 (7).8.24 Fe/AKo Johdanto Tässä luvussa esitetään salpapiirit, jotka ovat yksinkertaisimpia
igitaalitekniikka (piirit) Luku 5 ivu (7).8.24 Fe/AKo C J C K C T C C J C K igitaalitekniikka (piirit) Luku 5 ivu 2 (7).8.24 Fe/AKo Johdanto Tässä luvussa esitetään salpapiirit, jotka ovat yksinkertaisimpia
Ratkaisu. Ensimmäinen kuten P Q, toinen kuten P Q. Kolmas kuten P (Q R):
 Diskreetti matematiikka, sks 2010 Harjoitus 2, ratkaisuista 1. Seuraavassa on kuvattu kolme virtapiiriä, joissa on paristo, sopiva lamppu L ja katkaisimia P, Q, R, joiden läpi virta kulkee (1) tai ei kulje
Diskreetti matematiikka, sks 2010 Harjoitus 2, ratkaisuista 1. Seuraavassa on kuvattu kolme virtapiiriä, joissa on paristo, sopiva lamppu L ja katkaisimia P, Q, R, joiden läpi virta kulkee (1) tai ei kulje
Käytännön logiikkapiirit ja piirrosmerkit
 Digitaalitekniikan matematiikka Luku 7 Sivu (27) EN 2 EN X/Y X/Y 0 2 3 2 EN X/Y X/Y 0 2 3 Digitaalitekniikan matematiikka Luku 7 Sivu 2 (27) Johdanto Tässä luvussa esitellään käsitteet logiikkaperhe ja
Digitaalitekniikan matematiikka Luku 7 Sivu (27) EN 2 EN X/Y X/Y 0 2 3 2 EN X/Y X/Y 0 2 3 Digitaalitekniikan matematiikka Luku 7 Sivu 2 (27) Johdanto Tässä luvussa esitellään käsitteet logiikkaperhe ja
F = AB AC AB C C Tarkistus:
 Digitaalitekniikka I, tenttitehtäviä ratkaisuineen I 3..995 2. c) esitä seuraava funktio kanonisten summien tulona f(,,) = + Sovelletaan DeMorganin teoreemaa (työläs). Teoriaminimointia ei ole käytetty!
Digitaalitekniikka I, tenttitehtäviä ratkaisuineen I 3..995 2. c) esitä seuraava funktio kanonisten summien tulona f(,,) = + Sovelletaan DeMorganin teoreemaa (työläs). Teoriaminimointia ei ole käytetty!
TIEP114 Tietokoneen rakenne ja arkkitehtuuri, 3 op. FT Ari Viinikainen
 TIEP114 Tietokoneen rakenne ja arkkitehtuuri, 3 op FT Ari Viinikainen Tietokoneen rakenne Keskusyksikkö, CPU Keskusmuisti Aritmeettislooginen yksikkö I/O-laitteet Kontrolliyksikkö Tyypillinen Von Neumann
TIEP114 Tietokoneen rakenne ja arkkitehtuuri, 3 op FT Ari Viinikainen Tietokoneen rakenne Keskusyksikkö, CPU Keskusmuisti Aritmeettislooginen yksikkö I/O-laitteet Kontrolliyksikkö Tyypillinen Von Neumann
Esimerkkitentin ratkaisut ja arvostelu
 Sivu (5) 2.2.2 Fe Seuraavassa on esitetty tenttitehtävien malliratkaisut ja tehtäväkohtainen arvostelu. Osassa tehtävistä on muitakin hyväksyttäviä ratkaisuja kuin malliratkaisu. 2 Tehtävät on esitetty
Sivu (5) 2.2.2 Fe Seuraavassa on esitetty tenttitehtävien malliratkaisut ja tehtäväkohtainen arvostelu. Osassa tehtävistä on muitakin hyväksyttäviä ratkaisuja kuin malliratkaisu. 2 Tehtävät on esitetty
Loogiset konnektiivit
 Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi... jos ja vain jos... Sulkeita ( ) käytetään selkeyden vuoksi
Loogiset konnektiivit Tavallisimmat loogiset konnektiivit ovat negaatio ei konjunktio ja disjunktio tai implikaatio jos..., niin... ekvivalenssi... jos ja vain jos... Sulkeita ( ) käytetään selkeyden vuoksi
ASM-kaavio: reset. b c d e f g. 00 abcdef. naytto1. clk. 01 bc. reset. 10 a2. abdeg. 11 a3. abcdg
 Digitaalitekniikka (piirit) Metropolia / AKo Pikku nnitteluharjoitus: Suunnitellaan sekvenssipiiri, jolla saadaan numerot juoksemaan seitsensegmenttinäytöllä: VHDL-koodin generointi ASM-kaavioista Tässä
Digitaalitekniikka (piirit) Metropolia / AKo Pikku nnitteluharjoitus: Suunnitellaan sekvenssipiiri, jolla saadaan numerot juoksemaan seitsensegmenttinäytöllä: VHDL-koodin generointi ASM-kaavioista Tässä
Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena
 Mikrotietokone Moderni tietokone Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena Sen käyttötarkoitus on yleensä työnteko, kissavideoiden katselu internetistä tai pelien pelaaminen. Tietokoneen
Mikrotietokone Moderni tietokone Ajattelemme tietokonetta yleensä läppärinä tai pöytäkoneena Sen käyttötarkoitus on yleensä työnteko, kissavideoiden katselu internetistä tai pelien pelaaminen. Tietokoneen
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen
 Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2012-2013 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2012-2013 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen
 Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2013-2014 Lasse Lensu 2 Transistori yhdessä
Ongelma(t): Mistä loogisista lausekkeista ja niitä käytännössä toteuttavista loogisista piireistä olisi hyötyä tietojenkäsittelyssä ja tietokoneen rakentamisessa? 2013-2014 Lasse Lensu 2 Transistori yhdessä
Digitaalitekniikan perusteet
 HAMK Riihimäki Versio 1.0 Väinö Suhonen Digitaalitekniikan perusteet Loogiset funktiot ja portit Kombinaatiologiikan elimiä Rekisterilogiikan perusteet Rekisteri- ja sekvenssilogiikan elimiä ena up/ down
HAMK Riihimäki Versio 1.0 Väinö Suhonen Digitaalitekniikan perusteet Loogiset funktiot ja portit Kombinaatiologiikan elimiä Rekisterilogiikan perusteet Rekisteri- ja sekvenssilogiikan elimiä ena up/ down
 LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
LAUSELOGIIKKA (1) Sanalliset ilmaisut ovat usein epätarkkoja. On ilmaisuja, joista voidaan sanoa, että ne ovat tosia tai epätosia, mutta eivät molempia. Ilmaisuja, joihin voidaan liittää totuusarvoja (tosi,
OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012
 OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012 Luento 6: Tiedon esittäminen tietokoneessa, osa 1 Tekijät: Antti Virtanen, Timo Lehtonen, Matti Kujala, Kirsti Ala-Mutka, Petri M. Gerdt et al. Luennon
OHJ-1010 Tietotekniikan perusteet 4 op Syksy 2012 Luento 6: Tiedon esittäminen tietokoneessa, osa 1 Tekijät: Antti Virtanen, Timo Lehtonen, Matti Kujala, Kirsti Ala-Mutka, Petri M. Gerdt et al. Luennon
c) loogiset funktiot tulojen summana B 1 = C 2 C 1 +C 1 C 0 +C 2 C 1 C 0 e) logiikkakaavio
 IGITLITEKNIIKK I 5 Tentti:.. ntti Mäntyniemi ELEKTONIIKN LOTOIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) ykkösten
IGITLITEKNIIKK I 5 Tentti:.. ntti Mäntyniemi ELEKTONIIKN LOTOIO Henkilötunnus - KT Σ. Kaksituloisen multiplekserin toimintaa kuvaa looginen funktio = +. Esitä a) :n toiminta K-kartalla (,5 p) ykkösten
Digitaalitekniikka (piirit) Opetusmoniste
 Sivu (35) 3.2.2 Fe Esko T. Rautanen Digitaalitekniikka (piirit) Sisällysluettelo Sivu Synkroniset sekvenssipiirit 2. Opettavainen tarina 2.2 Digitaalisten piirien ryhmittely 3.3 Synkronisen sekvenssipiirin
Sivu (35) 3.2.2 Fe Esko T. Rautanen Digitaalitekniikka (piirit) Sisällysluettelo Sivu Synkroniset sekvenssipiirit 2. Opettavainen tarina 2.2 Digitaalisten piirien ryhmittely 3.3 Synkronisen sekvenssipiirin
AUTO3030 Digitaalitekniikan jatkokurssi, harjoitus 2, ratkaisuja
 AUTO3030 Digitaalitekniikan jatkokurssi, harjoitus 2, ratkaisuja s2009 1. D-kiikku Toteuta DE2:lla synkroninen laskukone, jossa lasketaan kaksi nelibittistä lukua yhteen. Tulos esitetään ledeillä vasta,
AUTO3030 Digitaalitekniikan jatkokurssi, harjoitus 2, ratkaisuja s2009 1. D-kiikku Toteuta DE2:lla synkroninen laskukone, jossa lasketaan kaksi nelibittistä lukua yhteen. Tulos esitetään ledeillä vasta,
Sekvenssipiirin tilat. Synkroninen sekvenssipiiri ? 1 ? 2
 Luku igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AKo igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AK Opetuskerta Sivu 4 Luku Opetuskerta Sivu Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan
Luku igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AKo igitaalitekniikka (piirit) Täsmätehtävät.8. Fe/AK Opetuskerta Sivu 4 Luku Opetuskerta Sivu Sekvenssipiirin tilat Montako tilaa vähintään tarvitaan
Automaatit. Muodolliset kielet
 Automaatit Automaatit ovat teoreettisia koneita, jotka käsittelevät muodollisia sanoja. Automaatti lukee muodollisen sanan kirjain kerrallaan, vasemmalta oikealle, ja joko hyväksyy tai hylkää sanan. Täten
Automaatit Automaatit ovat teoreettisia koneita, jotka käsittelevät muodollisia sanoja. Automaatti lukee muodollisen sanan kirjain kerrallaan, vasemmalta oikealle, ja joko hyväksyy tai hylkää sanan. Täten
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset
 Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
Kesälukio 2000 PK2 Tauluharjoituksia I Mallivastaukset 2000-08-03T10:30/12:00 Huomaa, että joihinkin kysymyksiin on useampia oikeita vastauksia, joten nämä ovat todellakin vain mallivastaukset. 1 Logiikkaa
LABORAATIOSELOSTUSTEN OHJE H. Honkanen
 LABORAATIOSELOSTUSTEN OHJE H. Honkanen Tämä ohje täydentää ja täsmentää osaltaan selostuskäytäntöä laboraatioiden osalta. Yleinen ohje työselostuksista löytyy intranetista, ohjeen on laatinut Eero Soininen
LABORAATIOSELOSTUSTEN OHJE H. Honkanen Tämä ohje täydentää ja täsmentää osaltaan selostuskäytäntöä laboraatioiden osalta. Yleinen ohje työselostuksista löytyy intranetista, ohjeen on laatinut Eero Soininen
Harjoitustyön 2 aiheiden kuvaukset
 Sivu 1 (5) 1 Raitiovaunun oven avaamis- ja sulkemispiiri Raitiovaunun oven vieressä on matkustajan avauspainike. Kun vaunu on paikallaan, matkustajan avauspainikkeen painaminen antaa signaalin, joka avaa
Sivu 1 (5) 1 Raitiovaunun oven avaamis- ja sulkemispiiri Raitiovaunun oven vieressä on matkustajan avauspainike. Kun vaunu on paikallaan, matkustajan avauspainikkeen painaminen antaa signaalin, joka avaa
BL40A1711 Johdanto digitaalielektroniikkaan: CMOS-tekniikka ja siihen perustuvat logiikkapiiriperheet
 BL40A1711 Johdanto digitaalielektroniikkaan: CMOS-tekniikka ja siihen perustuvat logiikkapiiriperheet Bittioperaatioiden toteuttamisesta Tarvitaan kolmea asiaa: 1. Menetelmät esittää ja siirtää bittejä
BL40A1711 Johdanto digitaalielektroniikkaan: CMOS-tekniikka ja siihen perustuvat logiikkapiiriperheet Bittioperaatioiden toteuttamisesta Tarvitaan kolmea asiaa: 1. Menetelmät esittää ja siirtää bittejä
-Matematiikka on aksiomaattinen järjestelmä. -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi
 -Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
-Matematiikka on aksiomaattinen järjestelmä -uusi tieto voidaan perustella edellisten tietojen avulla, tätä kutsutaan todistamiseksi -mustavalkoinen: asia joko on tai ei (vrt. humanistiset tieteet, ei
1 Logiikkaa. 1.1 Logiikan symbolit
 1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
1 Logiikkaa Tieteessä ja jokapäiväisessä elämässä joudutaan tekemään päätelmiä. Logiikassa tutkimuskohteena on juuri päättelyt. Sen sijaan päätelmien sisältöön ei niinkäään kiinnitetä huomiota. Päätelmät
Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008
 Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008 Kilpailijan nimi: 1) Oheisen kytkennän kokonaisresistanssi on n. 33 Ohm 150 Ohm a) 70 Ohmia b) 100 Ohmia c) 120 Ohmia 120 Ohm 2) Oheisen kytkennän
Taitaja2008, Elektroniikkalajin semifinaali 24.1.2008 Kilpailijan nimi: 1) Oheisen kytkennän kokonaisresistanssi on n. 33 Ohm 150 Ohm a) 70 Ohmia b) 100 Ohmia c) 120 Ohmia 120 Ohm 2) Oheisen kytkennän
BL40A1711 Johdanto digitaaleketroniikkaan: Sekvenssilogiikka, pitopiirit ja kiikut
 BL40A1711 Johdanto digitaaleketroniikkaan: Sekvenssilogiikka, pitopiirit ja kiikut Sekvenssilogiikka Kombinatooristen logiikkapiirien lähtömuuttujien nykyiset tilat y i (n) ovat pelkästään riippuvaisia
BL40A1711 Johdanto digitaaleketroniikkaan: Sekvenssilogiikka, pitopiirit ja kiikut Sekvenssilogiikka Kombinatooristen logiikkapiirien lähtömuuttujien nykyiset tilat y i (n) ovat pelkästään riippuvaisia
Harjoitustehtävien ratkaisuja
 igitaalitekniikan matematiikka arjoitustehtävien ratkaisuja Sivu (22) 6.3.2 e arjoitustehtävien ratkaisuja uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä, jossa käytävän kummassakin
igitaalitekniikan matematiikka arjoitustehtävien ratkaisuja Sivu (22) 6.3.2 e arjoitustehtävien ratkaisuja uku 3 ytkentäfunktiot ja perusporttipiirit 3. äytäväkytkin on järjestelmä, jossa käytävän kummassakin
kwc Nirni: Nimen selvennys : ELEKTRONIIKAN PERUSTEET 1 Tentti La / Matti Ilmonen / Vastaukset kysymyspapereille. 0pisk.
 Tentti La 20.01.2001 / Matti Ilmonen / Vastaukset kysymyspapereille. Nirni: Nimen selvennys : 1 2 3 4 5 z -.. 0pisk.no: ARVOSANA 1. Selvita lyhyesti seuraavat kiitteet ( kohdat a... j ) a) Kokosummain?
Tentti La 20.01.2001 / Matti Ilmonen / Vastaukset kysymyspapereille. Nirni: Nimen selvennys : 1 2 3 4 5 z -.. 0pisk.no: ARVOSANA 1. Selvita lyhyesti seuraavat kiitteet ( kohdat a... j ) a) Kokosummain?
Ohjelmistoradio. Mikä se on:
 1 Mikä se on: SDR = Software Defined Radio radio, jossa ohjelmisto määrittelee toiminnot ja ominaisuudet: otaajuusalue olähetelajit (modulaatio) olähetysteho etuna joustavuus, jota tarvitaan sovelluksissa,
1 Mikä se on: SDR = Software Defined Radio radio, jossa ohjelmisto määrittelee toiminnot ja ominaisuudet: otaajuusalue olähetelajit (modulaatio) olähetysteho etuna joustavuus, jota tarvitaan sovelluksissa,
Digitaalitekniikan matematiikka Luku 10 Sivu 1 (14) Lukujärjestelmämuunnokset. 2 s s
 Digitaalitekniikan matematiikka Luku 10 Sivu 1 (14) k 10 2 10 2 s 10 10 8 10 16 10 2 10 2 s 2 8 8 2 2 16 16 2 Digitaalitekniikan matematiikka Luku 10 Sivu 2 (14) Johdanto Tässä luvussa perustellaan, miksi
Digitaalitekniikan matematiikka Luku 10 Sivu 1 (14) k 10 2 10 2 s 10 10 8 10 16 10 2 10 2 s 2 8 8 2 2 16 16 2 Digitaalitekniikan matematiikka Luku 10 Sivu 2 (14) Johdanto Tässä luvussa perustellaan, miksi
Se mistä tilasta aloitetaan, merkitään tyhjästä tulevalla nuolella. Yllä olevassa esimerkissä aloitustila on A.
 Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
Java-kielen perusteita
 Java-kielen perusteita valintalauseet 1 Johdantoa kontrollirakenteisiin Tähän saakka ohjelmissa on ollut vain peräkkäisyyttä eli lauseet on suoritettu peräkkäin yksi kerrallaan Tarvitsemme myös valintaa
Java-kielen perusteita valintalauseet 1 Johdantoa kontrollirakenteisiin Tähän saakka ohjelmissa on ollut vain peräkkäisyyttä eli lauseet on suoritettu peräkkäin yksi kerrallaan Tarvitsemme myös valintaa
Ehto- ja toistolauseet
 Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
Ehto- ja toistolauseet 1 Ehto- ja toistolauseet Uutena asiana opetellaan ohjelmointilauseet / rakenteet, jotka mahdollistavat: Päätösten tekemisen ohjelman suorituksen aikana (esim. kyllä/ei) Samoja lauseiden
815338A Ohjelmointikielten periaatteet Harjoitus 4 vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 4 vastaukset Harjoituksen aiheena ovat imperatiivisten kielten lauseisiin, lausekkeisiin ja aliohjelmiin liittyvät kysymykset. Tehtävä 1. Mitä
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 4 vastaukset Harjoituksen aiheena ovat imperatiivisten kielten lauseisiin, lausekkeisiin ja aliohjelmiin liittyvät kysymykset. Tehtävä 1. Mitä
1.1 Funktion määritelmä
 1.1 Funktion määritelmä Tämän kappaleen otsikoksi valittu funktio on hyvä esimerkki matemaattisesta käsitteestä, johon usein jopa tietämättämme törmäämme arkielämässä. Tutkiessamme erilaisia Jos joukkojen
1.1 Funktion määritelmä Tämän kappaleen otsikoksi valittu funktio on hyvä esimerkki matemaattisesta käsitteestä, johon usein jopa tietämättämme törmäämme arkielämässä. Tutkiessamme erilaisia Jos joukkojen
Perusteet. Pasi Sarolahti Aalto University School of Electrical Engineering. C-ohjelmointi Kevät Pasi Sarolahti
 C! Perusteet 19.1.2017 Palautteesta (1. kierros toistaiseksi) (Erittäin) helppoa Miksi vain puolet pisteistä? Vaikeinta oli ohjelmointiympäristön asennus ja käyttö Ei selvää että main funktion pitikin
C! Perusteet 19.1.2017 Palautteesta (1. kierros toistaiseksi) (Erittäin) helppoa Miksi vain puolet pisteistä? Vaikeinta oli ohjelmointiympäristön asennus ja käyttö Ei selvää että main funktion pitikin
Elektroniikan laboratorio Lisätehtävät 17.9.2003. Mallivastauksia
 OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät 7.9. Mallivastauksia. Mitkä loogiset operaatiot oheiset kytkennät toteuttavat? Vihje: kytkin johtaa, kun ohjaava signaali =. Käytä
OULUN YLIOPISTO IGITLITEKNIIKK I Elektroniikan laboratorio Lisätehtävät 7.9. Mallivastauksia. Mitkä loogiset operaatiot oheiset kytkennät toteuttavat? Vihje: kytkin johtaa, kun ohjaava signaali =. Käytä
BL40A17x0 Digitaalielektroniikka A/B: Ohjelmoitavat logiikkapiirit
 BL4A17x Digitaalielektroniikka A/B: Ohjelmoitavat logiikkapiirit Ohjelmoitavat logiikkapiirit (PLD, Programmable Logic Device) PLD (Programmable Logic Device) on yleinen nimitys integroidulle piirille,
BL4A17x Digitaalielektroniikka A/B: Ohjelmoitavat logiikkapiirit Ohjelmoitavat logiikkapiirit (PLD, Programmable Logic Device) PLD (Programmable Logic Device) on yleinen nimitys integroidulle piirille,
Approbatur 3, demo 1, ratkaisut A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat.
 Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Luku- ja merkkikoodit. Digitaalitekniikan matematiikka Luku 12 Sivu 1 (15)
 Digitaalitekniikan matematiikka Luku 12 Sivu 1 (15) A = a = i i w i Digitaalitekniikan matematiikka Luku 12 Sivu 2 (15) Johdanto Tässä luvussa esitetään kymmenjärjestelmän lukujen eli BCD-lukujen esitystapoja
Digitaalitekniikan matematiikka Luku 12 Sivu 1 (15) A = a = i i w i Digitaalitekniikan matematiikka Luku 12 Sivu 2 (15) Johdanto Tässä luvussa esitetään kymmenjärjestelmän lukujen eli BCD-lukujen esitystapoja
Sähkötekniikan perusteet
 Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Matematiikan johdantokurssi, syksy 2016 Harjoitus 11, ratkaisuista
 Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Matematiikan johdantokurssi, syksy 06 Harjoitus, ratkaisuista. Valitse seuraaville säännöille mahdollisimman laajat lähtöjoukot ja sopivat maalijoukot niin, että syntyy kahden muuttujan funktiot (ks. monisteen
Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, sekä voi olla apua.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 2 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan erilaisia todistustekniikoita. Luentokalvoista 11, 15-17
Pikapaketti logiikkaan
 Pikapaketti logiikkaan Tämän oppimateriaalin tarkoituksena on tutustua pikaisesti matemaattiseen logiikkaan. Oppimateriaalin asioita tarvitaan projektin tekemisessä. Kiinnostuneet voivat lukea lisää myös
Pikapaketti logiikkaan Tämän oppimateriaalin tarkoituksena on tutustua pikaisesti matemaattiseen logiikkaan. Oppimateriaalin asioita tarvitaan projektin tekemisessä. Kiinnostuneet voivat lukea lisää myös
Negatiiviset luvut ja laskutoimitukset
 7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
Lukujärjestelmät. Digitaalitekniikan matematiikka Luku 9 Sivu 3 (26) Lukujärjestelmät ja lukujen esittäminen Fe
 Digitaalitekniikan matematiikka Luku 9 Sivu 3 (26) Lukujärjestelmät ja lukujen esittäminen.9.2 Fe Lukujärjestelmät Kymmen- eli desimaalijärjestelmä: kantaluku perinteisesti käytetty ja tuttu numerot,,
Digitaalitekniikan matematiikka Luku 9 Sivu 3 (26) Lukujärjestelmät ja lukujen esittäminen.9.2 Fe Lukujärjestelmät Kymmen- eli desimaalijärjestelmä: kantaluku perinteisesti käytetty ja tuttu numerot,,
Perusteet. Pasi Sarolahti Aalto University School of Electrical Engineering. C-ohjelmointi Kevät Pasi Sarolahti
 C! Perusteet 19.1.2017 Palautteesta (1. kierros toistaiseksi) Toistaiseksi helppoa Miksi vain puolet pisteistä? Vaikeinta oli ohjelmointiympäristön asennus ja käyttö Vaikeaa eroavuudet Pythonin ja C:n
C! Perusteet 19.1.2017 Palautteesta (1. kierros toistaiseksi) Toistaiseksi helppoa Miksi vain puolet pisteistä? Vaikeinta oli ohjelmointiympäristön asennus ja käyttö Vaikeaa eroavuudet Pythonin ja C:n
Oppikirjan harjoitustehtävien ratkaisuja
 Sivu (27) 26.2.2 e 7 Muistipiirit 7- Tietokoneen muistin koko on 256 K 6 b. Montako sanaa muistissa on? Mikä on sen sananpituus? Montako muistialkiota muistissa on? Muistissa on 256 kibisanaa eli 262 44
Sivu (27) 26.2.2 e 7 Muistipiirit 7- Tietokoneen muistin koko on 256 K 6 b. Montako sanaa muistissa on? Mikä on sen sananpituus? Montako muistialkiota muistissa on? Muistissa on 256 kibisanaa eli 262 44
PERUSLASKUJA. Kirjoita muuten sama, mutta ota KAKSI välilyöntiä (SEURAA ALUEMERKINTÄÄ) 4:n jälkeen 3/4 +5^2
 PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/4+^2 3 4+ 2 Kirjoita muuten sama, mutta ota KAKSI välilyöntiä (SEURAA ALUEMERKINTÄÄ) 4:n jälkeen 3/4 +^2 3 + 4 2 Kopioi
PERUSLASKUJA Matemaattisten lausekkeiden syöttäminen: Kirjoita ilman välilyöntejä 3/4+^2 3 4+ 2 Kirjoita muuten sama, mutta ota KAKSI välilyöntiä (SEURAA ALUEMERKINTÄÄ) 4:n jälkeen 3/4 +^2 3 + 4 2 Kopioi
Kerta 2. Kerta 2 Kerta 3 Kerta 4 Kerta 5. 1. Toteuta Pythonilla seuraava ohjelma:
 Kerta 2 Kerta 3 Kerta 4 Kerta 5 Kerta 2 1. Toteuta Pythonilla seuraava ohjelma: 2. Tulosta Pythonilla seuraavat luvut allekkain a. 0 10 (eli, näyttää tältä: 0 1 2 3 4 5 6 7 8 9 10 b. 0 100 c. 50 100 3.
Kerta 2 Kerta 3 Kerta 4 Kerta 5 Kerta 2 1. Toteuta Pythonilla seuraava ohjelma: 2. Tulosta Pythonilla seuraavat luvut allekkain a. 0 10 (eli, näyttää tältä: 0 1 2 3 4 5 6 7 8 9 10 b. 0 100 c. 50 100 3.
Python-ohjelmointi Harjoitus 2
 Python-ohjelmointi Harjoitus 2 TAVOITTEET Kerrataan tulostuskomento ja lukumuotoisen muuttujan muuttaminen merkkijonoksi. Opitaan jakojäännös eli modulus, vertailuoperaattorit, ehtorakenne jos, input-komento
Python-ohjelmointi Harjoitus 2 TAVOITTEET Kerrataan tulostuskomento ja lukumuotoisen muuttujan muuttaminen merkkijonoksi. Opitaan jakojäännös eli modulus, vertailuoperaattorit, ehtorakenne jos, input-komento
Digitaalitekniikan matematiikka Sivu 1 (57) Kombinaatiopiirin suunnittelu ja toteutus
 Digitaalitekniikan matematiikka Sivu 1 (57) Kombinaatiopiirin suunnittelu ja toteutus Digitaalitekniikan matematiikka Sivu 2 (57) Harjoitustyön 2 tavoitteet opitaan piirisuunnitteluprosessin vaiheita opitaan
Digitaalitekniikan matematiikka Sivu 1 (57) Kombinaatiopiirin suunnittelu ja toteutus Digitaalitekniikan matematiikka Sivu 2 (57) Harjoitustyön 2 tavoitteet opitaan piirisuunnitteluprosessin vaiheita opitaan
Paavo Räisänen. Ohjelmoijan binaarialgebra ja heksaluvut. www.ohjelmoimaan.net
 Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoimaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
Paavo Räisänen Ohjelmoijan binaarialgebra ja heksaluvut www.ohjelmoimaan.net Tätä opasta saa vapaasti kopioida, tulostaa ja levittää ei kaupallisissa tarkoituksissa. Kuitenkaan omille nettisivuille opasta
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 1: Joukko-oppi ja logiikka Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kiitokset Nämä luentokalvot perustuvat Gustaf
MS-A0402 Diskreetin matematiikan perusteet Osa 1: Joukko-oppi ja logiikka Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kiitokset Nämä luentokalvot perustuvat Gustaf
Ohjelmoitavat logiikkaverkot
 Digitaalitekniikka (piirit) Luku 9 Sivu (3) Ohjelmoitavat logiikkaverkot.8.24 Fe/AKo Ohjelmoitavat logiikkaverkot Ohjelmoitavat logiikkaverkot Programmable logic logic PLD-piirit Programmable logic logic
Digitaalitekniikka (piirit) Luku 9 Sivu (3) Ohjelmoitavat logiikkaverkot.8.24 Fe/AKo Ohjelmoitavat logiikkaverkot Ohjelmoitavat logiikkaverkot Programmable logic logic PLD-piirit Programmable logic logic
Sisällys. 3. Muuttujat ja operaatiot. Muuttujat ja operaatiot. Muuttujat. Operaatiot. Imperatiivinen laskenta. Muuttujat. Esimerkkejä: Operaattorit.
 3. Muuttujat ja operaatiot Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi.. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit. Arvojen
3. Muuttujat ja operaatiot Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi.. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit. Arvojen
LUMECOM. Jyrsinsovellus. 1. Asennusohje 2. Käyttöohje 3. Käyttöönottokortti
 LUMECOM Jyrsinsovellus 1. Asennusohje 2. Käyttöohje 3. Käyttöönottokortti 11.4.2018 Asennusohje - ProJyrsin 1. Avaa Google Play Store tabletiltasi - sovellus ei tue toistaiseksi Apple/IOS käyttöjärjestelmiä
LUMECOM Jyrsinsovellus 1. Asennusohje 2. Käyttöohje 3. Käyttöönottokortti 11.4.2018 Asennusohje - ProJyrsin 1. Avaa Google Play Store tabletiltasi - sovellus ei tue toistaiseksi Apple/IOS käyttöjärjestelmiä
Luento 3: Digitaalilogiikka 29.8.2006. Luento 3. u binary: AND ( ) A B = AB. u unary: NOT ( _ ) A. u precedence: NOT, AND, OR.
 Luento 3 Digital logic Stallings: Appendix B Combinational Circuits Simplification Sequential Circuits Luento 3-1 Luento 3-2 George Boole u ideas 1854 Claude Shannon u apply to circuit design, 1938 u father
Luento 3 Digital logic Stallings: Appendix B Combinational Circuits Simplification Sequential Circuits Luento 3-1 Luento 3-2 George Boole u ideas 1854 Claude Shannon u apply to circuit design, 1938 u father
3. Muuttujat ja operaatiot 3.1
 3. Muuttujat ja operaatiot 3.1 Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi. Operaattorit. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit.
3. Muuttujat ja operaatiot 3.1 Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi. Operaattorit. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit.
Digital logic. Boolean Algebra. Tietokoneen rakenne. Tietokoneen rakenne
 Tietokoneen rakenne Luento 3 Digital logic Stallings: Appendix B Boolean Algebra Combinational Circuits Simplification Sequential Circuits Luento 3-1 Tietokoneen rakenne Boolean Algebra Luento 3-2 Tietokoneen
Tietokoneen rakenne Luento 3 Digital logic Stallings: Appendix B Boolean Algebra Combinational Circuits Simplification Sequential Circuits Luento 3-1 Tietokoneen rakenne Boolean Algebra Luento 3-2 Tietokoneen
Vektoreiden virittämä aliavaruus
 Vektoreiden virittämä aliavaruus Määritelmä Oletetaan, että v 1, v 2,... v k R n. Näiden vektoreiden virittämä aliavaruus span( v 1, v 2,... v k ) tarkoittaa kyseisten vektoreiden kaikkien lineaarikombinaatioiden
Vektoreiden virittämä aliavaruus Määritelmä Oletetaan, että v 1, v 2,... v k R n. Näiden vektoreiden virittämä aliavaruus span( v 1, v 2,... v k ) tarkoittaa kyseisten vektoreiden kaikkien lineaarikombinaatioiden
3. Predikaattilogiikka
 3. Predikaattilogiikka Muuttuja mukana lauseessa. Ei yksikäsitteistä totuusarvoa. Muuttujan kiinnittäminen määrän ilmaisulla voi antaa yksikäsitteisen totuusarvon. Esimerkki. Lauseella x 3 8 = 0 ei ole
3. Predikaattilogiikka Muuttuja mukana lauseessa. Ei yksikäsitteistä totuusarvoa. Muuttujan kiinnittäminen määrän ilmaisulla voi antaa yksikäsitteisen totuusarvon. Esimerkki. Lauseella x 3 8 = 0 ei ole
2_1----~--~r--1.~--~--~--,.~~
 K.Loberg FYSE420 DIGITAL ELECTRONICS 3.06.2011 1. Toteuta alia esitetyn sekvenssin tuottava asynkroninen pun. Anna heditefunktiot, siirtotaulukko ja kokonaistilataulukko ( exitation functions, transition
K.Loberg FYSE420 DIGITAL ELECTRONICS 3.06.2011 1. Toteuta alia esitetyn sekvenssin tuottava asynkroninen pun. Anna heditefunktiot, siirtotaulukko ja kokonaistilataulukko ( exitation functions, transition
Alkuarvot ja tyyppimuunnokset (1/5) Alkuarvot ja tyyppimuunnokset (2/5) Alkuarvot ja tyyppimuunnokset (3/5)
 Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Logiikan kertausta. TIE303 Formaalit menetelmät, kevät Antti-Juhani Kaijanaho. Jyväskylän yliopisto Tietotekniikan laitos.
 TIE303 Formaalit menetelmät, kevät 2005 Logiikan kertausta Antti-Juhani Kaijanaho antkaij@mit.jyu.fi Jyväskylän yliopisto Tietotekniikan laitos TIE303 Formaalit mentetelmät, 2005-01-27 p. 1/17 Luento2Luentomoniste
TIE303 Formaalit menetelmät, kevät 2005 Logiikan kertausta Antti-Juhani Kaijanaho antkaij@mit.jyu.fi Jyväskylän yliopisto Tietotekniikan laitos TIE303 Formaalit mentetelmät, 2005-01-27 p. 1/17 Luento2Luentomoniste
VHDL-kuvauskieli. Digitaalitekniikka (piirit) Luku 17 Sivu 1 (33)
 Digitaalitekniikka (piirit) Luku 7 Sivu (33) Digitaalitekniikka (piirit) Luku 7 Sivu 2 (33) Johdanto Tässä luvussa esitellään laitteiston kuvauskielet ja niistä erityisesti VHDL esitetään VHDL-kuvauskielen
Digitaalitekniikka (piirit) Luku 7 Sivu (33) Digitaalitekniikka (piirit) Luku 7 Sivu 2 (33) Johdanto Tässä luvussa esitellään laitteiston kuvauskielet ja niistä erityisesti VHDL esitetään VHDL-kuvauskielen
15 Opetussuunnitelma OSAAMISEN ARVIOINTI ARVIOINNIN KOHTEET JA AMMATTITAITOVAATIMUKSET OSAAMISEN HANKKIMINEN. osaa: työskentely
 Hyväksymismerkinnät 1 (5) Näytön kuvaus Tutkinnonosan suorittaja osoittaa osaamisensa ammattiosaamisen näytössä tekemällä tutkinnon osan ammattitaitovaatimusten mukaisia työtehtäviä työkohteissa. Työtä
Hyväksymismerkinnät 1 (5) Näytön kuvaus Tutkinnonosan suorittaja osoittaa osaamisensa ammattiosaamisen näytössä tekemällä tutkinnon osan ammattitaitovaatimusten mukaisia työtehtäviä työkohteissa. Työtä
ANSI/IEEE Std
 Digitaalitekniikan matematiikka Luku 9 Sivu 1 (26) Lukujärjestelmät ja lukujen esittäminen ANSI/IEEE Std 754-2008 0 1 0 1 1 0 0 0 B = Σ B i 2 i Digitaalitekniikan matematiikka Luku 9 Sivu 2 (26) Johdanto
Digitaalitekniikan matematiikka Luku 9 Sivu 1 (26) Lukujärjestelmät ja lukujen esittäminen ANSI/IEEE Std 754-2008 0 1 0 1 1 0 0 0 B = Σ B i 2 i Digitaalitekniikan matematiikka Luku 9 Sivu 2 (26) Johdanto
Kappale 20: Kantaluvut
 Kappale 20: Kantaluvut 20 Johdanto: Kantaluvut... 328 Kantalukujen syöttäminen ja muuntaminen... 329 Matemaattiset toiminnot Hex- ja Bin-luvuilla... 330 Bittien vertaileminen ja manipulointi... 331 Huom!
Kappale 20: Kantaluvut 20 Johdanto: Kantaluvut... 328 Kantalukujen syöttäminen ja muuntaminen... 329 Matemaattiset toiminnot Hex- ja Bin-luvuilla... 330 Bittien vertaileminen ja manipulointi... 331 Huom!
Sähkötekniikan perusteet
 Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Sähkötekniikan perusteet 1) Resistanssien rinnankytkentä kuormittaa a) enemmän b) vähemmän c) yhtä paljon sähkölähdettä kuin niiden sarjakytkentä 2) Jännitelähteiden sarjakytkentä a) suurentaa kytkennästä
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8
 Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
1. Tasavirtapiirit ja Kirchhoffin lait
 Kimmo Silvonen, Sähkötekniikka ja elektroniikka, Otatieto 2003. Tasavirtapiirit ja Kirchhoffin lait Sähkötekniikka ja elektroniikka, sivut 5-62. Versio 3..2004. Kurssin Sähkötekniikka laskuharjoitus-,
Kimmo Silvonen, Sähkötekniikka ja elektroniikka, Otatieto 2003. Tasavirtapiirit ja Kirchhoffin lait Sähkötekniikka ja elektroniikka, sivut 5-62. Versio 3..2004. Kurssin Sähkötekniikka laskuharjoitus-,
Säätötekniikan matematiikan verkkokurssi, Matlab tehtäviä ja vastauksia 29.7.2002
 Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
Matlab tehtäviä 1. Muodosta seuraavasta differentiaaliyhtälöstä siirtofuntio. Tämä differentiaaliyhtälö saattaisi kuvata esimerkiksi yksinkertaista vaimennettua jousi-massa systeemiä, johon on liitetty
JOHDATUS ELEKTRONIIKKAAN. Oppitunti 2 Elektroniikan järjestelmät
 JOHDATUS ELEKTRONIIKKAAN Oppitunti 2 Elektroniikan järjestelmät 2 ELEKTRONIIKAN JÄRJESTELMÄT Aktiivisuusranneke Mittaa liikettä Keskustelee käyttäjän kanssa ledeillä ja värinällä Keskustelee radioiden
JOHDATUS ELEKTRONIIKKAAN Oppitunti 2 Elektroniikan järjestelmät 2 ELEKTRONIIKAN JÄRJESTELMÄT Aktiivisuusranneke Mittaa liikettä Keskustelee käyttäjän kanssa ledeillä ja värinällä Keskustelee radioiden
