Tehtävä 1: Massadata (big data) ja sen käytön haasteet
|
|
|
- Merja Hilkka Kinnunen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Tehtävä 1: Massadata (big data) ja sen käytön haasteet Lue ensin seuraava taustamateriaali huolellisesti ja vastaa sen jälkeen siihen liittyviin kysymyksiin. Maailmassa mitataan jatkuvasti monenlaisia asioita, kuten vaikkapa radiosignaalin laatua, ja tästä syntyviä mittausarvoja nimitetään dataksi. Myös sosiaalisen median päivitykset tai kauppaketjujen kassatiedot ovat dataa. Erilaista ja eri lähteistä peräisin olevaa dataa syntyy maailmassa koko ajan enemmän ja sen jakaminen hetkessä ympäri maailmaa on helppoa. Puhutaan massadatasta ( big data ), kun tarkoitetaan niin laajoja ja monimutkaisia datamääriä, että niiden analysointi ja hyödyntäminen on erittäin haastavaa ja vaatii uusien menetelmien kehittämistä. Tästä huolimatta massadatan käytölle on asetettu suuria odotuksia. Ajatellaan, että se tuottaa uusia liiketoimintamahdollisuuksia ja toisaalta antaa mahdollisuuden ratkoa sellaisia ongelmia, joita ennen ei ole pystytty ratkaisemaan. Kun massadataa luonnehditaan, siihen liitetään usein seuraavia sanoja: Volyymi: Dataa syntyy jatkuvasti niin valtavia määriä, että sen käsitteleminen ja tallentaminen on hyvin haastavaa. Se myös saattaa sijaita fyysisesti useassa eri paikassa, mikä edelleen lisää haastetta datan käsittelyyn. Vauhti: Dataa syntyy myös jatkuvasti kiihtyvällä tahdilla. Jo tällä hetkellä on mahdotonta tallettaa kaikkea dataa ja tulevaisuudessa tilanne on aina vain pahempi. Toisaalta kuitenkin olisi tärkeää päästä käsiksi kaikkeen syntyvään dataan, jotta sitä voidaan hyödyntää älykkäästi. Variaatio: Dataa on monen erityyppistä ja erilaisten datalähteiden määrä kasvaa sekin koko ajan. Syntyvän datan standardoiminen käyttämään tiettyjä tallennusmuotoja ei ole toistaiseksi vielä toiminut tyydyttävällä tavalla. Tämä hankaloittaa datan analyysiä ja hyötykäyttöä. Eroja dataan syntyy myös muun muassa erilaisista käytetyistä mittaustavoista, mittayksiköistä, tavoista kirjata numeerisia tietoja ja jopa mittareiden kalibroinnista. Myös kieli- ja kulttuurierot varsinkin tekstimuotoisen datan tallentamisessa voivat aiheuttaa päänvaivaa. Visuaalisen datan eri esitysmuodot voivat nekin aiheuttaa ongelmia, samoin paikkatieto erilaisten koordinaattijärjestelmien takia. Oikeellisuus: Syntyvä data ei välttämättä ole kovin täsmällistä. Se voi myös olla epäselvää tai jopa virheellistä. Joskus datan keruu- ja mittausmenetelmät ovat erilaisia tai niitä ei tunneta, ja siksi eri lähteistä 1
2 tuotetun datan vertailukelpoisuus ei ole itsestään selvää. Pahimmassa tapauksessa esimerkiksi lämpötiladatasta ei tiedetä onko sen mittayksikkö Celsius vai Fahrenheit. Oleellisuus ja arvo: Data on usein reaaliaikaista, jolloin sen hyödyllisyyskin on sidottuna ajanhetkeen. Data ei välttämättä ole kovin kiinnostavaa tai oleellista tietyllä ajanhetkellä tai tietyssä asiayhteydessä, mutta esimerkiksi myöhempänä ajanhetkenä tai toisessa asiayhteydessä sama data saattaa olla hyvin kiinnostavaa ja arvokasta. Toisaalta yhdelle toimijalle tai organisaatiolle data saattaa olla arvotonta, kun taas toiselle se on kullanarvoista. Joskus datan arvo, merkitys, tulee nimenomaan siitä että se tarjoaa tietoa datan muutoksista ajan suhteen. Esimerkkinä tästä on ilmastotutkimukseen liittyvä data, jossa esimerkiksi meren pinnan korkeuden muutokset nimenomaan ajan suhteen ovat olennainen ja kiinnostava tieto. Nämä luonnehdinnat kertovat, että massadata-ilmiössä on kyse muustakin kuin vain valtavan suurista datamääristä. Jotta suuresta määrästä dataa on hyötyä, se pitää jalostaa tiedoksi. Data muuttuu tiedoksi silloin, kun data jäsennetään ja esitetään niin, että sillä on jokin merkitys. Vaikkapa matkapuhelinoperaattorilla voi olla tiedossa kaikkien asiakkaidensa kännyköiden reaaliaikainen sijainti, mutta tämä data muuttuu tiedoksi vasta, kun sitä hyödynnetään sopivasti, esimerkiksi tarjoamalla tietyssä sijainnissa olevien kännyköiden kautta palvelua siten, että kaupungin keskustassa tarjotaan eri palveluja kuin esikaupunkialueella. Vastaavasti sääasemien havaintodatalla ei tee mitään, ennen kuin se on analysoitu sääennusteeksi tai ilmaston muuttumista kuvaavaksi historiatiedoksi. Säähän liittyvän datan määrä kasvaa jatkuvasti ja tänään tietoa voidaan kerätä eri muodossa, eri mittarein ja mittayksiköin kuin vuosia tai vuosikymmeniä sitten. Ilmastodata (lämpötilat, kaasupitoisuudet, meren pinnan korkeudet, jne.), joka ulottuu tästä päivästä taaksepäin aina satojen tuhansien vuosien päähän menneisyyteen, on kerätty eri tekniikoin ja menetelmin, osin laskennallisesti, ja se on erittäin haasteellista analyysin kannalta. Massadatan haasteena esimerkiksi tällaisessa aineistossa on se, miten tuloksista saadaan merkityksellistä ilman että alkuperäistä dataa tulkitaan väärin tai virheellisin oletuksin. Jotta data voi muuttua tiedoksi, tarvitaan paljon erilaisia apuvälineitä: monimutkaisia ohjelmistoja, laskentamalleja ja ratkaisuja, ja niitä tekemään tarvitaan monenlaista eri osaamista: muun muassa ohjelmointitaitoa, tilastojen ymmärtämistä ja liiketoiminnan tajua. Lisäksi itse datasta pitää olla riittävästi tietoa (miten, missä ja kuka mittasi ja millä tekniikoilla). Massadatan käyttöön liittyy usein myös se, että monet toimijat avaavat syntyvän datan avoimesti kenen tahansa käytettäväksi. Esimerkiksi Suomes- 2
3 sa Maanmittauslaitos on avannut keräämänsä karttadatan avoimesti kaikkien saataville, ja tätä dataa hyödyntävät useat yritykset erilaisissa karttapalveluissa. Samoin on avattu Suomen Ilmatieteen laitoksen säätutkien tuottama data, jota hyödynnetään esimerkiksi säätietoja kertovissa sovelluksissa. Esimerkeistä näkyy kuinka uutta liiketoimintaa voi syntyä, kun data on avointa. Tärkeänä osa-alueena massadatan käytössä on luottamus: data ei synny tyhjästä ja väärinkäytönkin vaara on olemassa. Paikkakuntien lämpötilatietoja ei ehkä kovin helposti käytetä väärin, mutta jos kännyköiden sijaintitietoihin kytketään käyttäjän henkilökohtaista tietoa, onkin jo väärinkäytön mahdollisuus suurempi. Toisaalta suurista tietomassoista on kuitenkin mahdollisuus jalostaa hyvinvointia, palveluja ja uutta liiketoimintaa. Sen vuoksi jokaisen yrityksen tai organisaation, joka harkitsee datan avaamista julkiseksi, on tehtävä se harkiten ja etukäteen mietittävä, mitä dataa voidaan julkaista ja millaisilla pelisäännöillä. Kysymykset Vastaa seuraaviin kysymyksiin edellä olevan taustamateriaalin ja yleistietosi perusteella. Kysymyksien yhteenlaskettu maksimipistemäärä on 25 pistettä. Kysymys 1. Kerro konkreettinen esimerkki viidestä eri massadataa luonnehtivasta piirteestä perusteluineen. Valitse esimerkit niin että ne poikkeavat toisistaan, eivätkä ole peräisin taustamateriaalista. Anna siis yhteensä 5 esimerkkiä. Anna 1-2 lausetta perusteluja yhtä esimerkkiä kohden. (maksimipistemäärä 5) Kysymys 2. Viime aikoina on keskusteltu ajoneuvojen reaaliaikaisesta seurannasta autoverotuksen yhteydessä. Jotta ajoneuvon liikkumista voidaan seurata, siihen on käytännössä asennettava GPS-paikannin, joka lähettää jatkuvasti dataa auton sijainnista. Jos oletetaan, että Suomessa otetaan käyttöön tällainen järjestelmä, niin a) mihin muuhun hyödylliseen voitaisiin sillä kerättyä tietoa käyttää, b) mitä eettisiä ongelmia tiedon keräämisessä ja hyödyntämisessä voidaan nähdä, c) mitä teknisiä haasteita järjestelmän luomisessa ja käytössä voidaan kohdata, d) mitä haasteita datan muuttamisessa tiedoksi voidaan tätä järjestelmää käyttäessä kohdata? 3
4 Mainitse kaksi esimerkkiä kustakin kohdasta (a, b, c, d). Perustele. (maksimipistemäärä 8) Kysymys 3. Usein massadataa hyödynnettäessä olemassa olevaa dataa kerätään eri lähteistä analyysiä ja tiedon tuottamista varten. Eri lähteistä kerättävän datan mittaustapa ja tallennusmuoto voi kuitenkin aiheuttaa ongelmia. Esimerkkinä tästä on vaikkapa päivämäärän tallentaminen eri muotoon: amerikkalainen tapa 04/11/2014 ilmaisee vuoden 2014 huhtikuun 11. päivää, kun taas suomalaiselle kyseessä on marraskuun 4. päivä. Anna neljä taustamateriaalista ja toisistaan poikkeavaa esimerkkiä massadatan analyysistä, jossa voi syntyä ongelmia siihen liittyen, että tiedot ovat peräisin eri lähteistä ja datan mittaus-, keräys- ja tallennusmuodot vaihtelevat. Pohdi myös kunkin ongelman kohdalla, miten näitä ongelmia voitaisiin ratkoa. (maksimipistemäärä 12) 4
5 Tehtävä 2: Loppuosataulukko Tutustu tarkoin seuraavaan tekstiin ja vastaa sitä hyväksi käyttäen tehtävän loppuosassa esitettyihin viiteen kysymykseen. Annetun merkkijonon (ns. hahmo) esiintymän haku pidemmästä merkkijonosta (tekstistä) on yksi perustavanlaatuinen tietojenkäsittelytieteen sovellus. Haun voi toteuttaa selaamalla koko tekstin alusta loppuun samalla tutkien, esiintyykö hahmo jossain kohdassa. Tämä lähestymistapa on kuitenkin hidas, jos teksti on hyvin suuri. Hakua voidaan nopeuttaa luomalla tekstistä etukäteen sopiva indeksirakenne, jonka avulla tekstin läpiselaaminen voidaan välttää. Eräs yksinkertainen ja paljon käytetty indeksirakenne on ns. loppuosataulukko. Menetelmää on käytetty yleisesti esimerkiksi laajoihin DNA-aineistoihin, kuten n. 3 miljardia merkkiä käsittävään ihmisen genomiin, kohdistuvien hakujen toteuttamiseen tehokkaasti. Merkkijono koostuu peräkkäisistä merkeistä. Merkkijonoon voidaan viitata merkkijonomuuttujaa käyttäen. Merkkijonon merkkeihin viitataan antamalla merkin indeksi hakasuluissa välittömästi merkkijonomuuttujan perässä. Esimerkiksi x[1] tarkoittaa merkkijonon x ensimmäistä merkkiä. Merkintä x[i..j] tarkoittaa merkkijonon x alimerkkijonoa, joka alkaa indeksistä i ja päättyy indeksiin j. Alimerkkijono, joka jatkuu merkkijonon loppuun asti, on loppuosa. Loppuosan alkukohtaa sanotaan loppuosan indeksiksi. Merkkijonojen x ja y yhteydessä käytämme vertailuoperaattoreita <,, =, ja > kuvaamaan merkkijonojen aakkosjärjestystä. Esimerkiksi merkintä x y tarkoittaa, että x on aakkosjärjestyksessä pienempi tai yhtäsuuri kuin y. Yhtäsuuruus tarkoittaa, että merkkijonot ovat keskenään samanlaiset. Esimerkki 1. Jos merkkijono x on kevät, pätee mm. että: x[1] = k, x[2] = e ja x[4] = ä. x[1..3] = kev, x[3..3] = v ja x[2..5] = evät. Merkkijonon x loppuosat, niiden indeksien eli alkukohtien 1, 2, 3, 4 ja 5 mukaisessa järjestyksessä, ovat x[1..5] = kevät, x[2..5] = evät, x[3..5] = vät, x[4..5] = ät ja x[5..5] = t. Viittaamme tekstiin merkkijonomuuttujalla t ja tekstistä etsittävään hahmoon merkkijonomuuttujalla p. Lisäksi oletamme, että tekstin t pituus on n. Tekstin t loppuosataulukko S on n-alkioinen kokonaislukutaulukko, joka luettelee tekstin loppuosien indeksit loppuosien aakkosjärjestyksen mukaisessa järjestyksessä. Taulukon S indeksin i arvo, josta käytämme merkintää S[i], kertoo, mistä tekstin kohdasta tekstin i:nneksi pienin loppuosa alkaa: S[1] kertoo tekstin aakkosjärjestyksessä pienimmän loppuosan indeksin, S[2] kertoo 1
6 aakkosjärjestyksessä sitä seuraavan loppuosan indeksin, jne. Asian voi ilmaista myös niin, että indekseillä i = 2,..., n pätee ehto t[s[i 1]..n] t[s[i]..n]. Esimerkki 2. Tekstin t = abababba loppuosat ovat abababba, bababba, ababba, babba, abba, bba, ba ja a. Alla on vasemmalla tekstin t loppuosat aakkosjärjestyksessä ja oikealla tekstin t loppuosataulukko S. Huomaa, että loppuosataulukon arvot ovat samat kuin vasemmalla esitetyt loppuosien indeksit. Esimerkiksi arvo S[5] = 7 ilmaisee, että aakkosjärjestyksessä viidenneksi pienin loppuosa alkaa indeksistä 7 eli on t[7..8] = ba. Loppuosa (aakkosjärj.) Loppuosan indeksi Indeksi i S[i] a 8 abababba 1 ababba 3 abba 5 ba 7 bababba 2 babba 4 bba Loppuosien perusominaisuus on, että jos etsitty hahmomerkkijono p esiintyy jossain tekstin kohdassa, esiintyy p samalla tekstin kyseisestä kohdasta alkavan loppuosan alkuosana. Sanomme, että tällöin hahmo p täsmää kyseisen loppuosan kanssa. Hahmo p voidaan etsiä tekstistä etsimällä sellainen loppuosa, jonka kanssa p täsmää. Loppuosataulukon ansiosta tämä onnistuu tehokkaasti käyttäen ns. puolitushakua. Puolitushaku ylläpitää tietoa siitä loppuosataulukon välistä, jonka sisällä voisi senhetkisten tietojen valossa olla hahmon p kanssa täsmäävä loppuosa. Käytämme hakuvälin alkuindeksistä merkintää alku ja loppuindeksistä merkintää loppu. Lisäksi määritämme välin keskimmäisen indeksin keski kaavalla keski = (alku + loppu)/2, jonka arvo pyöristetään lähimpään kokonaislukuun (eli tässä aina ylöspäin), jos summan alku + loppu arvo on pariton. Alkutilanteessa jokainen loppuosa voisi periaatteessa täsmätä eli alku = 1 ja loppu = n. Puolitushaku vertaa hahmoa ja hakuvälin keskimmäistä loppuosaa t[s[keski]..n] keskenään. Jos hahmo täsmää, voidaan haku lopettaa 1. Muuten pätee joko p < t[s[keski]..n] tai p > t[s[keski]..n]. Jos p < t[s[keski]..n] eli hahmo on aakkosjärjestyksessä pienempi kuin indeksin S[keski] omaava loppuosa, ei mikään loppuosataulukon välin keski,..., loppu loppuosa täsmää hahmon kanssa. Tämä on suora seuraus siitä, että loppuosataulukko ilmaisee loppuosat niiden aakkosjärjestyksessä. Tällöin puoli- 1 Tässä tehtävässä keskitytään yhden esiintymän hakuun; hahmo toki voi esiintyä tekstissä monessa eri kohdassa. 2
7 tushaku voi päivittää hakuvälin uudeksi ylärajaksi loppu = keski 1 ja verrata hahmoa seuraavaksi tämän uuden hakuvälin keskimmäiseen loppuosaan. Jos p > t[s[keski]..n], voidaan edellä esitettyyn tapaan todeta, ettei mikään välin alku,..., keski loppuosa voi täsmätä hahmon kanssa. Tällöin hakuvälin alaraja voidaan päivittää asettamalla alku = keski + 1. Jos hakuväli tulee haun aikana tyhjäksi eli ehto alku > loppu astuu voimaan, lopetetaan haku tuloksettomana: teksti ei tässä tapauksessa sisällä yhtään hahmon p esiintymää. Alla on esitetty hahmon p haku tekstistä t loppuosataulukon S avulla vielä hieman täsmällisemmin askeleittain: 1. Aseta hakuvälin alkuindeksi alku = 1 ja loppuindeksi loppu = n. 2. Jos alku > loppu eli hakuväli on tyhjä, lopeta haku: hahmo p ei esiinny tekstissä. 3. Laske alku- ja loppuindeksien puolivälissä oleva indeksi keski: keski = (alku + loppu)/2, pyöristäen arvo tarvittaessa ylöspäin. 4. Vertaile hahmoa p ja hakuvälin keskimmäistä loppuosaa t[s[keski]..n]. Jos p täsmää loppuosan t[s[keski]..n] kanssa, lopeta haku palauttaen tieto, että hahmon p yksi esiintymä löytyi tekstin indeksistä S[keski] alkaen. Jos p ei täsmää loppuosan t[s[keski]..n] kanssa, niin: Jos p < t[s[keski]..n], karsi hakuvälistä indeksit, jotka ovat keski, asettamalla loppu = keski 1 ja jatka hakua palaamalla askeleeseen 2. Jos p > t[s[keski]..n], karsi hakuvälistä indeksit, jotka ovat keski, asettamalla alku = keski + 1 ja jatka hakua palaamalla askeleeseen 2. 3
8 Esimerkki 3. Hahmon p = ababbaba haku tekstistä t = abbaababbababbab. Loppuosa i S[i] aababbababbab 1 4 ab 2 15 ababbab 3 10 ababbababbab 4 5 abbaababbababbab 5 1 abbab 6 12 abbababbab 7 7 b 8 16 baababbababbab 9 3 bab bababbab 11 9 babbab babbababbab 13 6 bbaababbababbab 14 2 bbab bbababbab 16 8 Kysymykset 1. Alkuarvot alku = 1 ja loppu = keski = (1 + 16)/2 = 9, p < t[s[9]..16], loppu = keski 1 = keski = (1 + 8)/2 = 5, p < t[s[5]..16], loppu = keski 1 = keski = (1 + 4)/2 = 3, p > t[s[3]..16], alku = keski + 1 = keski = (4 + 4)/2 = 4, p täsmää loppuosan t[s[4]..16] kanssa ja haku päättyy. Esimerkin puolitushaku joutui tutkimaan 4 tekstinkohtaa. Puolitushaun vahvuus on, että hakuaskeleiden määrä kasvaa varsin hitaasti tekstin koon kasvaessa. Esimerkiksi n. 3 miljardista merkistä koostuvaan ihmisen genomiin kohdistuva puolitushaku joutuu tutkimaan korkeintaan 32 tekstinkohtaa. Kysymys 1. Esitä ne askeleet, jotka puolitushaku tekee etsiessään hahmoa p = babaa esimerkin 3 tekstistä t = abbaababbababbab. Esitä vastauksesi samassa muodossa kuin esimerkissä 3 eli anna kunkin askeleen kohdalla hakuväliä koskevat arvot alku, loppu ja keski. (maksimipistemäärä 3) Kysymys 2. Muodosta merkkijonon t = yhteisvalinta loppuosataulukko. (maksimipistemäärä 4) Kysymys 3. a) Muodosta merkkijonon t = aacatcgatagctagaacat loppuosataulukko. (maksimipistemäärä 4) b) Esitä ne askeleet, jotka puolitushaku tekee etsiessään hahmoa p = cga kohdan a) tekstistä. Esitä vastauksesi samassa muodossa kuin esimerkissä 3 eli anna kunkin askeleen kohdalla hakuväliä koskevat arvot alku, loppu ja keski. (maksimipistemäärä 3) 4
9 Kysymys 4. Muodosta jokin sellainen suomalaisen aakkoston pienistä kirjaimista koostuva merkkijono, jonka loppuosataulukko vastaa alla annettua taulukkoa. Tässä kysymyksessä sallittuun aakkostoon kuuluu siis merkit a, b, c,..., ö. (maksimipistemäärä 4) i S[i] Kysymys 5. Muodosta sellainen pelkästään merkkejä a ja b sisältävä merkkijono, jonka loppuosataulukko vastaa alla annettua taulukkoa. (maksimipistemäärä 7) i S[i]
10 Tehtävä 3: Ongelmanratkaisutehtävä Tässä tehtävässä esitetään kolme toisistaan riippumatonta yleistä ongelmanratkaisukykyä mittaavaa osatehtävää. Kysymys 1. Pöydälle asetetaan neljä pelikorttia. Kaksi näistä korteista on etupuolelta punaisia ja kaksi mustia. Kortit ovat pöydällä selkäpuoli ylöspäin, joten niiden väri ei näy. Valitaan kaksi korttia satunnaisesti, millä todennäköisyydellä ne ovat samaa väriä? (maksimipistemäärä 4) Kysymys 2. (a) Piirrä alla oleva kuvio vastauspaperiin ja sijoita luvut yhdestä kahdeksaan siihen seuraavien ehtojen mukaisesti: kukin luku sijoitetaan omaan ympyräänsä kahta suuruusjärjestyksessä peräkkäistä lukua ei saa sijoittaa siten, että ne sisältävien ympyröiden välillä on viiva Jos esimerkiksi luku 4 sijoitetaan ylimpään ympyrään, silloin lukuja 3 tai 5 ei saa sijoittaa yhteenkään kolmesta sen alla olevasta ympyrästä. (maksimipistemäärä 6) (b) Kaikkiaan on olemassa neljä sellaista lukujen sijoittelua, jotka tuottavat a-kohdan ehtojen mukaisen ratkaisun. Oletetaan, että ratkaistaan a-kohdan tehtävä käymällä läpi kaikki mahdolliset tavat sijoitella luvut kuvioon. Jos yhden sijoittelun kokeiluun menee 10 sekuntia, kauanko tehtävän ratkaisuun pahimmillaan menee? (maksimipistemäärä 4) 1
11 Kysymys 3. Noppapelissä kaksi pelaajaa heittää kukin omaa 6-tahoista noppaansa ja suuremman lukeman saanut voittaa (tasatilanteessa heitetään uudestaan, kunnes peli ratkeaa). Käytettävät nopat ovat kuution muotoisia ja kukin kuudesta tahosta voi tulla heiton päällimmäiseksi yhtä todennäköisesti. Nopat ovat kuitenkin siitä epätavallisia, että niiden tahoihin merkityt arvot on voitu valita mielivaltaisesti lukujoukosta {1, 2, 3, 4, 5, 6}. Sama luku voi siis esiintyä useassa nopan tahossa, ja vastaavasti joitain lukuja voi puuttua kokonaan. (a) Pöydällä on kolme noppaa (A, B ja C), joiden tahoissa on seuraavat lukemat: Noppa A: 2, 2, 2, 5, 5, 5 Noppa B: 3, 3, 3, 3, 3, 6 Noppa C: 1, 1, 1, 4, 4, 4 Pelaaja 1 saa valita ensin pöydältä noppansa, jonka jälkeen pelaaja 2 saa valita omansa jäljelle jääneistä. Perustele, miten pelaajan 1 pitäisi valita, että hänellä olisi aina etu pelissä (toisin sanoen yli 50% voittotodennäköisyys). (maksimipistemäärä 5) (b) Tasoituksen vuoksi pelaaja 2 saa suunnitella uuden 6-tahoisen nopan kysymyksen 3 alussa kuvattujen ehtojen mukaisesti, ja asettaa sen nopan C tilalle. Jälleen, pelaaja 1 valitsee noppansa ensin, sitten pelaaja 2 valitsee jäljelle jääneistä. Suunnittele sellainen noppa C ja pelistrategia pelaajalle 2, joka varmistaa hänelle aina edun pelissä, tai osoita että tämä ei ole mahdollista. (maksimipistemäärä 6) 2
Tehtävä 2: Loppuosataulukko
 Tehtävä 2: Loppuosataulukko Tutustu tarkoin seuraavaan tekstiin ja vastaa sitä hyväksi käyttäen tehtävän loppuosassa esitettyihin viiteen kysymykseen. Annetun merkkijonon (ns. hahmo) esiintymän haku pidemmästä
Tehtävä 2: Loppuosataulukko Tutustu tarkoin seuraavaan tekstiin ja vastaa sitä hyväksi käyttäen tehtävän loppuosassa esitettyihin viiteen kysymykseen. Annetun merkkijonon (ns. hahmo) esiintymän haku pidemmästä
Tehtävä 1: Massadata (big data) ja sen käytön haasteet
 Tehtävä 1: Massadata (big data) ja sen käytön haasteet Lue ensin seuraava taustamateriaali huolellisesti ja vastaa sen jälkeen siihen liittyviin kysymyksiin. Maailmassa mitataan jatkuvasti monenlaisia
Tehtävä 1: Massadata (big data) ja sen käytön haasteet Lue ensin seuraava taustamateriaali huolellisesti ja vastaa sen jälkeen siihen liittyviin kysymyksiin. Maailmassa mitataan jatkuvasti monenlaisia
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Kirjoita ohjelma jossa luetaan kokonaislukuja taulukkoon (saat itse päättää taulun koon, kunhan koko on vähintään 10)
 Tehtävä 40. Kirjoita ohjelma, jossa luetaan 20 lukua, joiden arvot ovat välillä 10 100. Kun taulukko on täytetty, ohjelma tulostaa vain ne taulukon arvot, jotka esiintyvät taulukossa vain kerran. Tehtävä
Tehtävä 40. Kirjoita ohjelma, jossa luetaan 20 lukua, joiden arvot ovat välillä 10 100. Kun taulukko on täytetty, ohjelma tulostaa vain ne taulukon arvot, jotka esiintyvät taulukossa vain kerran. Tehtävä
811312A Tietorakenteet ja algoritmit , Harjoitus 2 ratkaisu
 811312A Tietorakenteet ja algoritmit 2017-2018, Harjoitus 2 ratkaisu Harjoituksen aiheena on algoritmien oikeellisuus. Tehtävä 2.1 Kahvipurkkiongelma. Kahvipurkissa P on valkoisia ja mustia kahvipapuja,
811312A Tietorakenteet ja algoritmit 2017-2018, Harjoitus 2 ratkaisu Harjoituksen aiheena on algoritmien oikeellisuus. Tehtävä 2.1 Kahvipurkkiongelma. Kahvipurkissa P on valkoisia ja mustia kahvipapuja,
Luku 8. Aluekyselyt. 8.1 Summataulukko
 Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Algoritmit 2. Luento 6 To Timo Männikkö
 Algoritmit 2 Luento 6 To 28.3.2019 Timo Männikkö Luento 6 B-puun operaatiot Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2019 Luento 6 To 28.3.2019 2/30 B-puu 40 60 80 130 90 100
Algoritmit 2 Luento 6 To 28.3.2019 Timo Männikkö Luento 6 B-puun operaatiot Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2019 Luento 6 To 28.3.2019 2/30 B-puu 40 60 80 130 90 100
Algoritmit 2. Luento 6 Ke Timo Männikkö
 Algoritmit 2 Luento 6 Ke 29.3.2017 Timo Männikkö Luento 6 B-puun operaatiot B-puun muunnelmia Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2017 Luento 6 Ke 29.3.2017 2/31 B-puu
Algoritmit 2 Luento 6 Ke 29.3.2017 Timo Männikkö Luento 6 B-puun operaatiot B-puun muunnelmia Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2017 Luento 6 Ke 29.3.2017 2/31 B-puu
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 30.4.2019 Timo Männikkö Luento 13 Simuloitu jäähdytys Merkkijonon sovitus Horspoolin algoritmi Ositus ja rekursio Rekursion toteutus Algoritmit 2 Kevät 2019 Luento 13 Ti 30.4.2019
Algoritmit 2 Luento 13 Ti 30.4.2019 Timo Männikkö Luento 13 Simuloitu jäähdytys Merkkijonon sovitus Horspoolin algoritmi Ositus ja rekursio Rekursion toteutus Algoritmit 2 Kevät 2019 Luento 13 Ti 30.4.2019
Todennäköisyyslaskenta I, kesä 2017 Helsingin yliopisto/avoin Yliopisto Harjoitus 1, ratkaisuehdotukset
 Todennäköisyyslaskenta I, kesä 207 Helsingin yliopisto/avoin Yliopisto Harjoitus, ratkaisuehdotukset. Kokeet ja Ω:n hahmottaminen. Mitä tarkoittaa todennäköisyys on? Olkoon satunnaiskokeena yhden nopan
Todennäköisyyslaskenta I, kesä 207 Helsingin yliopisto/avoin Yliopisto Harjoitus, ratkaisuehdotukset. Kokeet ja Ω:n hahmottaminen. Mitä tarkoittaa todennäköisyys on? Olkoon satunnaiskokeena yhden nopan
Syötteen ensimmäisellä rivillä on kokonaisluku n, testien määrä (1 n 10). Tämän jälkeen jokaisella seuraavalla rivillä on kokonaisluku x (0 x 1000).
 A Summat Tehtäväsi on selvittää, monellako tavalla luvun n voi esittää summana a 2 + b 2 + c 2 + d 2. Kaikki luvut ovat ei-negatiivisia kokonaislukuja. Esimerkiksi jos n = 21, yksi tapa muodostaa summa
A Summat Tehtäväsi on selvittää, monellako tavalla luvun n voi esittää summana a 2 + b 2 + c 2 + d 2. Kaikki luvut ovat ei-negatiivisia kokonaislukuja. Esimerkiksi jos n = 21, yksi tapa muodostaa summa
Trafficars - Ruuhkaara
 760104 Trafficars - Ruuhkaara 2 5 pelaajaa Ikäsuositus 5+, 8+ Peliaika 10 15 minuuttia Pelipaketin sisältö 50 autokorttia 12 erikoiskorttia ohjevihko Pelissä: Opitaan liikkumaan lukualueella 0 50. Harjoitellaan
760104 Trafficars - Ruuhkaara 2 5 pelaajaa Ikäsuositus 5+, 8+ Peliaika 10 15 minuuttia Pelipaketin sisältö 50 autokorttia 12 erikoiskorttia ohjevihko Pelissä: Opitaan liikkumaan lukualueella 0 50. Harjoitellaan
 0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
0. 10. 017 a b c d 1. + +. + +. + + 4. + + + 5. + 6. + P1. Lehtipuiden lukumäärä olkoon aluksi n, jolloin havupuiden määrä on 1,4n. Hakkuiden jälkeen lehtipuiden määrä putoaa lukuun n 0,1n = 0,88n ja havupuiden
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6
 Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 11.2.2009 T-106.1208 Ohjelmoinnin perusteet Y 11.2.2009 1 / 33 Kertausta: listat Tyhjä uusi lista luodaan kirjoittamalla esimerkiksi lampotilat = [] (jolloin
Ohjelmoinnin perusteet Y Python T-106.1208 11.2.2009 T-106.1208 Ohjelmoinnin perusteet Y 11.2.2009 1 / 33 Kertausta: listat Tyhjä uusi lista luodaan kirjoittamalla esimerkiksi lampotilat = [] (jolloin
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 10.2.2010 T-106.1208 Ohjelmoinnin perusteet Y 10.2.2010 1 / 43 Kertausta: listat Tyhjä uusi lista luodaan kirjoittamalla esimerkiksi lampotilat = [] (jolloin
Ohjelmoinnin perusteet Y Python T-106.1208 10.2.2010 T-106.1208 Ohjelmoinnin perusteet Y 10.2.2010 1 / 43 Kertausta: listat Tyhjä uusi lista luodaan kirjoittamalla esimerkiksi lampotilat = [] (jolloin
Kenguru 2019 Cadet (8. ja 9. luokka)
 Sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse vastaus tehtävän numeron alle. Oikeasta vastauksesta saa 3, 4 tai
Sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse vastaus tehtävän numeron alle. Oikeasta vastauksesta saa 3, 4 tai
Datatähti 2019 alku. task type time limit memory limit. A Kolikot standard 1.00 s 512 MB. B Leimasin standard 1.00 s 512 MB
 Datatähti 2019 alku task type time limit memory limit A Kolikot standard 1.00 s 512 MB B Leimasin standard 1.00 s 512 MB C Taulukko standard 1.00 s 512 MB D Ruudukko standard 1.00 s 512 MB E Sanalista
Datatähti 2019 alku task type time limit memory limit A Kolikot standard 1.00 s 512 MB B Leimasin standard 1.00 s 512 MB C Taulukko standard 1.00 s 512 MB D Ruudukko standard 1.00 s 512 MB E Sanalista
27. 10. joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja.
 ÄÙ ÓÒÑ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒÔ ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Hiiri juoksee tasaisella
ÄÙ ÓÒÑ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒÔ ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Hiiri juoksee tasaisella
Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 1.2.2013 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 1.2.2013 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
33. pohjoismainen matematiikkakilpailu 2019 Ratkaisut
 33. pohjoismainen matematiikkakilpailu 2019 Ratkaisut 1. Kutsutaan (eri) positiivisten kokonaislukujen joukkoa merkitykselliseksi, jos sen jokaisen äärellisen epätyhjän osajoukon aritmeettinen ja geometrinen
33. pohjoismainen matematiikkakilpailu 2019 Ratkaisut 1. Kutsutaan (eri) positiivisten kokonaislukujen joukkoa merkitykselliseksi, jos sen jokaisen äärellisen epätyhjän osajoukon aritmeettinen ja geometrinen
3. Kirjoita seuraavat joukot luettelemalla niiden alkiot, jos mahdollista. Onko jokin joukoista tyhjä joukko?
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I Seuraavat tehtävät liittyvät luentokalvoihin 1 14. Erityisesti esimerkistä 4 ja esimerkin
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 1 Ratkaisuehdotuksia Tehtäväsarja I Seuraavat tehtävät liittyvät luentokalvoihin 1 14. Erityisesti esimerkistä 4 ja esimerkin
Ongelma(t): Miten merkkijonoja voidaan hakea tehokkaasti? Millaisia hakuongelmia liittyy bioinformatiikkaan?
 Ongelma(t): Miten merkkijonoja voidaan hakea tehokkaasti? Millaisia hakuongelmia liittyy bioinformatiikkaan? 2012-2013 Lasse Lensu 2 Ihmisen, eläinten ja kasvien hyvinvoinnin kannalta nykyaikaiset mittaus-,
Ongelma(t): Miten merkkijonoja voidaan hakea tehokkaasti? Millaisia hakuongelmia liittyy bioinformatiikkaan? 2012-2013 Lasse Lensu 2 Ihmisen, eläinten ja kasvien hyvinvoinnin kannalta nykyaikaiset mittaus-,
1 Lukujen jaollisuudesta
 Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
Matematiikan mestariluokka, syksy 2009 1 1 Lukujen jaollisuudesta Lukujoukoille käytetään seuraavia merkintöjä: N = {1, 2, 3, 4,... } Luonnolliset luvut Z = {..., 2, 1, 0, 1, 2,... } Kokonaisluvut Kun
1 Kannat ja kannanvaihto
 1 Kannat ja kannanvaihto 1.1 Koordinaattivektori Oletetaan, että V on K-vektoriavaruus, jolla on kanta S = (v 1, v 2,..., v n ). Avaruuden V vektori v voidaan kirjoittaa kannan vektorien lineaarikombinaationa:
1 Kannat ja kannanvaihto 1.1 Koordinaattivektori Oletetaan, että V on K-vektoriavaruus, jolla on kanta S = (v 1, v 2,..., v n ). Avaruuden V vektori v voidaan kirjoittaa kannan vektorien lineaarikombinaationa:
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kenguru 2010 Cadet (8. ja 9. luokka) sivu 1 / 5
 Kenguru 2010 Cadet (8. ja 9. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru 2010 Cadet (8. ja 9. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Todennäköisyys (englanniksi probability)
 Todennäköisyys (englanniksi probability) Todennäköisyyslaskenta sai alkunsa 1600-luvulla uhkapeleistä Ranskassa (Pascal, Fermat). Nykyisin todennäköisyyslaskentaa käytetään hyväksi mm. vakuutustoiminnassa,
Todennäköisyys (englanniksi probability) Todennäköisyyslaskenta sai alkunsa 1600-luvulla uhkapeleistä Ranskassa (Pascal, Fermat). Nykyisin todennäköisyyslaskentaa käytetään hyväksi mm. vakuutustoiminnassa,
Pikalajittelu: valitaan ns. pivot-alkio esim. pivot = oikeanpuoleisin
 Pikalajittelu: valitaan ns. pivot-alkio esim. pivot = oikeanpuoleisin jaetaan muut alkiot kahteen ryhmään: L: alkiot, jotka eivät suurempia kuin pivot G : alkiot, jotka suurempia kuin pivot 6 1 4 3 7 2
Pikalajittelu: valitaan ns. pivot-alkio esim. pivot = oikeanpuoleisin jaetaan muut alkiot kahteen ryhmään: L: alkiot, jotka eivät suurempia kuin pivot G : alkiot, jotka suurempia kuin pivot 6 1 4 3 7 2
Tehtävä 2: Säännölliset lausekkeet
 Tehtävä 2: Säännölliset lausekkeet Kun tietokoneohjelmalla luetaan käyttäjän syötettä, olisi syöte aina syytä tarkistaa. Syötteessä voi olla vääriä merkkejä tai merkkejä väärillä paikoilla (syntaktinen
Tehtävä 2: Säännölliset lausekkeet Kun tietokoneohjelmalla luetaan käyttäjän syötettä, olisi syöte aina syytä tarkistaa. Syötteessä voi olla vääriä merkkejä tai merkkejä väärillä paikoilla (syntaktinen
Algoritmit 1. Demot Timo Männikkö
 Algoritmit 1 Demot 1 31.1.-1.2.2018 Timo Männikkö Tehtävä 1 (a) Algoritmi, joka tutkii onko kokonaisluku tasan jaollinen jollain toisella kokonaisluvulla siten, että ei käytetä lainkaan jakolaskuja Jaettava
Algoritmit 1 Demot 1 31.1.-1.2.2018 Timo Männikkö Tehtävä 1 (a) Algoritmi, joka tutkii onko kokonaisluku tasan jaollinen jollain toisella kokonaisluvulla siten, että ei käytetä lainkaan jakolaskuja Jaettava
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
5. Jos x < 1 2,niin x x 1 on aina. , 1] b) pienempi kuin Yhtälön 3 3 x +3 x =4ratkaisujenlukumääräon a) 0 b) 1 c) 2 d) enemmän kuin 2.
![5. Jos x < 1 2,niin x x 1 on aina. , 1] b) pienempi kuin Yhtälön 3 3 x +3 x =4ratkaisujenlukumääräon a) 0 b) 1 c) 2 d) enemmän kuin 2. 5. Jos x < 1 2,niin x x 1 on aina. , 1] b) pienempi kuin Yhtälön 3 3 x +3 x =4ratkaisujenlukumääräon a) 0 b) 1 c) 2 d) enemmän kuin 2.](/thumbs/102/153341150.jpg) 5. Jos x < 1 2,niin x x 1 on aina a) välillä [ 1 2, 1] b) pienempi kuin 1 c) välillä [ 1 2, 3 ] 2 d) ei välttämättä mikään edellisistä. 6. Yhtälön 3 3 x +3 x =4ratkaisujenlukumääräon a) 0 b) 1 c) 2 d)
5. Jos x < 1 2,niin x x 1 on aina a) välillä [ 1 2, 1] b) pienempi kuin 1 c) välillä [ 1 2, 3 ] 2 d) ei välttämättä mikään edellisistä. 6. Yhtälön 3 3 x +3 x =4ratkaisujenlukumääräon a) 0 b) 1 c) 2 d)
Kirjoita oma versio funktioista strcpy ja strcat, jotka saavat parametrinaan kaksi merkkiosoitinta.
 Tehtävä 63. Kirjoita oma versio funktiosta strcmp(),joka saa parametrinaan kaksi merkkiosoitinta. Tee ohjelma, jossa luetaan kaksi merkkijonoa, joita sitten verrataan ko. funktiolla. Tehtävä 64. Kirjoita
Tehtävä 63. Kirjoita oma versio funktiosta strcmp(),joka saa parametrinaan kaksi merkkiosoitinta. Tee ohjelma, jossa luetaan kaksi merkkijonoa, joita sitten verrataan ko. funktiolla. Tehtävä 64. Kirjoita
Injektio. Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim.
 Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
Injektio Funktiota sanotaan injektioksi, mikäli lähtöjoukon eri alkiot kuvautuvat maalijoukon eri alkioille. Esim. Funktio f on siis injektio mikäli ehdosta f (x 1 ) = f (x 2 ) seuraa, että x 1 = x 2.
Kenguru 2019 Student lukio
 sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
Hahmon etsiminen syotteesta (johdatteleva esimerkki)
 Hahmon etsiminen syotteesta (johdatteleva esimerkki) Unix-komennolla grep hahmo [ tiedosto ] voidaan etsia hahmon esiintymia tiedostosta (tai syotevirrasta): $ grep Kisaveikot SM-tulokset.txt $ ps aux
Hahmon etsiminen syotteesta (johdatteleva esimerkki) Unix-komennolla grep hahmo [ tiedosto ] voidaan etsia hahmon esiintymia tiedostosta (tai syotevirrasta): $ grep Kisaveikot SM-tulokset.txt $ ps aux
1. Otetaan perusjoukoksi X := {0, 1, 2, 3, 4, 5, 6, 7}. Piirrä seuraaville kolmelle joukolle Venn-diagrammi ja asettele alkiot siihen.
 Joukko-oppia Matematiikan mestariluokka, syksy 2010 Harjoitus 1, vastaukset 20.2.2010 1. Otetaan perusjoukoksi X := {0, 1, 2, 3, 4, 5, 6, 7}. Piirrä seuraaville kolmelle joukolle Venn-diagrammi asettele
Joukko-oppia Matematiikan mestariluokka, syksy 2010 Harjoitus 1, vastaukset 20.2.2010 1. Otetaan perusjoukoksi X := {0, 1, 2, 3, 4, 5, 6, 7}. Piirrä seuraaville kolmelle joukolle Venn-diagrammi asettele
Tietotekniikan valintakoe
 Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Kohdissa 2 ja 3 jos lukujen valintaan on useita vaihtoehtoja, valitaan sellaiset luvut, jotka ovat mahdollisimman lähellä listan alkua.
 A Lista Aikaraja: 1 s Uolevi sai käsiinsä listan kokonaislukuja. Hän päätti laskea listan luvuista yhden luvun käyttäen seuraavaa algoritmia: 1. Jos listalla on vain yksi luku, pysäytä algoritmi. 2. Jos
A Lista Aikaraja: 1 s Uolevi sai käsiinsä listan kokonaislukuja. Hän päätti laskea listan luvuista yhden luvun käyttäen seuraavaa algoritmia: 1. Jos listalla on vain yksi luku, pysäytä algoritmi. 2. Jos
S: siirtää listan ensimmäisen luvun viimeiseksi V: vaihtaa keskenään listan kaksi ensimmäistä lukua
 A Lista Sinulle on annettu lista, joka sisältää kokonaisluvut 1, 2,, n jossakin järjestyksessä. Tehtäväsi on järjestää luvut pienimmästä suurimpaan käyttäen seuraavia operaatioita: S: siirtää listan ensimmäisen
A Lista Sinulle on annettu lista, joka sisältää kokonaisluvut 1, 2,, n jossakin järjestyksessä. Tehtäväsi on järjestää luvut pienimmästä suurimpaan käyttäen seuraavia operaatioita: S: siirtää listan ensimmäisen
Lineaarialgebra ja matriisilaskenta I, HY Kurssikoe Ratkaisuehdotus. 1. (35 pistettä)
 Lineaarialgebra ja matriisilaskenta I, HY Kurssikoe 26.10.2017 Ratkaisuehdotus 1. (35 pistettä) (a) Seuraavat matriisit on saatu eräistä yhtälöryhmistä alkeisrivitoimituksilla. Kuinka monta ratkaisua yhtälöryhmällä
Lineaarialgebra ja matriisilaskenta I, HY Kurssikoe 26.10.2017 Ratkaisuehdotus 1. (35 pistettä) (a) Seuraavat matriisit on saatu eräistä yhtälöryhmistä alkeisrivitoimituksilla. Kuinka monta ratkaisua yhtälöryhmällä
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8
 Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 1 / vko 8 Tuntitehtävät 1-2 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 5- loppuviikon harjoituksissa. Kotitehtävät 3-4 tarkastetaan loppuviikon
! 7! = N! x 8. x x 4 x + 1 = 6.
 9. 10. 2008 1. Pinnalta punaiseksi maalattu 3 3 3-kuutio jaetaan 27:ksi samankokoiseksi kuutioksi. Mikä osuus 27 pikkukuution kokonaispinta-alasta on punaiseksi maalattu? 2. Positiivisen kokonaisluvun
9. 10. 2008 1. Pinnalta punaiseksi maalattu 3 3 3-kuutio jaetaan 27:ksi samankokoiseksi kuutioksi. Mikä osuus 27 pikkukuution kokonaispinta-alasta on punaiseksi maalattu? 2. Positiivisen kokonaisluvun
Algoritmit 1. Demot Timo Männikkö
 Algoritmit 1 Demot 1 25.-26.1.2017 Timo Männikkö Tehtävä 1 (a) Algoritmi, joka laskee kahden kokonaisluvun välisen jakojäännöksen käyttämättä lainkaan jakolaskuja Jaettava m, jakaja n Vähennetään luku
Algoritmit 1 Demot 1 25.-26.1.2017 Timo Männikkö Tehtävä 1 (a) Algoritmi, joka laskee kahden kokonaisluvun välisen jakojäännöksen käyttämättä lainkaan jakolaskuja Jaettava m, jakaja n Vähennetään luku
Sukelluskeräily. Pelihahmon liikuttaminen. Aarre ja pisteet
 Sukelluskeräily 1 Tässä pelissä keräilet erilaisia aarteita ja väistelet vihollista. Tämän lisäksi pelaajan pitää käydä välillä pinnalla hengittelemässä. Peliin lisätään myös häiriötekijäksi esim. parvi
Sukelluskeräily 1 Tässä pelissä keräilet erilaisia aarteita ja väistelet vihollista. Tämän lisäksi pelaajan pitää käydä välillä pinnalla hengittelemässä. Peliin lisätään myös häiriötekijäksi esim. parvi
11.4. Context-free kielet 1 / 17
 11.4. Context-free kielet 1 / 17 Määritelmä Tyypin 2 kielioppi (lauseyhteysvapaa, context free): jos jokainenp :n sääntö on muotoa A w, missäa V \V T jaw V. Context-free kielet ja kieliopit ovat tärkeitä
11.4. Context-free kielet 1 / 17 Määritelmä Tyypin 2 kielioppi (lauseyhteysvapaa, context free): jos jokainenp :n sääntö on muotoa A w, missäa V \V T jaw V. Context-free kielet ja kieliopit ovat tärkeitä
Algoritmit 2. Luento 9 Ti Timo Männikkö
 Algoritmit 2 Luento 9 Ti 17.4.2018 Timo Männikkö Luento 9 Merkkitiedon tiivistäminen Huffmanin koodi LZW-menetelmä Taulukointi Editointietäisyys Algoritmit 2 Kevät 2018 Luento 9 Ti 17.4.2018 2/29 Merkkitiedon
Algoritmit 2 Luento 9 Ti 17.4.2018 Timo Männikkö Luento 9 Merkkitiedon tiivistäminen Huffmanin koodi LZW-menetelmä Taulukointi Editointietäisyys Algoritmit 2 Kevät 2018 Luento 9 Ti 17.4.2018 2/29 Merkkitiedon
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
1. a) Laske lukujen 1, 1 ja keskiarvo. arvo. b) Laske lausekkeen. c) Laske integraalin ( x xdx ) arvo. MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 13..015 MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 13..015 MATEMATIIKAN MALLIKOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Kenguru 2019 Benjamin 6. ja 7. luokka
 sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai
Algoritmit 2. Luento 12 To Timo Männikkö
 Algoritmit 2 Luento 12 To 3.5.2018 Timo Männikkö Luento 12 Geneettiset algoritmit Simuloitu jäähdytys Merkkijonon sovitus Horspoolin algoritmi Algoritmit 2 Kevät 2018 Luento 12 To 3.5.2018 2/35 Algoritmien
Algoritmit 2 Luento 12 To 3.5.2018 Timo Männikkö Luento 12 Geneettiset algoritmit Simuloitu jäähdytys Merkkijonon sovitus Horspoolin algoritmi Algoritmit 2 Kevät 2018 Luento 12 To 3.5.2018 2/35 Algoritmien
Sekalaiset tehtävät, 11. syyskuuta 2005, sivu 1 / 13. Tehtäviä
 Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Sekalaiset tehtävät, 11. syyskuuta 005, sivu 1 / 13 Tehtäviä Tehtävä 1. Johda toiseen asteen yhtälön ax + bx + c = 0, a 0 ratkaisukaava. Tehtävä. Määrittele joukon A R pienin yläraja sup A ja suurin alaraja
Todennäköisyys. Antoine Gombaud, eli chevalier de Méré?.? Kirjailija ja matemaatikko
 Todennäköisyys TOD.NÄK JA TILASTOT, MAA10 Todennäköisyyslaskennan juuret ovat ~1650-luvun uhkapeleissä. Kreivi de Mérén noppapelit: Jos noppaa heitetään 4 kertaa, niin kannattaako lyödä vetoa sen puolesta,
Todennäköisyys TOD.NÄK JA TILASTOT, MAA10 Todennäköisyyslaskennan juuret ovat ~1650-luvun uhkapeleissä. Kreivi de Mérén noppapelit: Jos noppaa heitetään 4 kertaa, niin kannattaako lyödä vetoa sen puolesta,
c) 22a 21b x + a 2 3a x 1 = a,
 Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. 1. Lukion A ja lukion B oppilasmäärien suhde oli a/b vuoden 2017 lopussa. Vuoden 2017 aikana
Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. 1. Lukion A ja lukion B oppilasmäärien suhde oli a/b vuoden 2017 lopussa. Vuoden 2017 aikana
DIGIBONUSTEHTÄVÄ: MPKJ NCC INDUSTRY OY LOPPURAPORTTI
 DIGIBONUSTEHTÄVÄ: MPKJ NCC INDUSTRY OY LOPPURAPORTTI Tekijä: Marko Olli 16.10.2018 Sisällys 1 Johdanto...3 2 Hankkeen tavoitteet ja vaikuttavuus...3 3 Laitteisto ja mittaustarkkuus...3 4 Pilotointi ja
DIGIBONUSTEHTÄVÄ: MPKJ NCC INDUSTRY OY LOPPURAPORTTI Tekijä: Marko Olli 16.10.2018 Sisällys 1 Johdanto...3 2 Hankkeen tavoitteet ja vaikuttavuus...3 3 Laitteisto ja mittaustarkkuus...3 4 Pilotointi ja
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Kenguru 2013 Student sivu 1 / 7 (lukion 2. ja 3. vuosi)
 Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
8. Kieliopit ja kielet
 8. Kieliopit ja kielet Suomen kielen sanoja voidaan yhdistellä monella eri tavalla. Kielioppi määrää sen, milloin sanojen yhdistely antaa oikein muodostetun lauseen. "Mies räpyttää siipiään" on kieliopillisesti
8. Kieliopit ja kielet Suomen kielen sanoja voidaan yhdistellä monella eri tavalla. Kielioppi määrää sen, milloin sanojen yhdistely antaa oikein muodostetun lauseen. "Mies räpyttää siipiään" on kieliopillisesti
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Kenguru 2012 Student sivu 1 / 8 (lukion 2. ja 3. vuosi)
 Kenguru 2012 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2012 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten. Ratkaisuehdotelma
 Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
Johdatus lukuteoriaan Harjoitus 2 syksy 2008 Eemeli Blåsten Ratkaisuehdotelma Tehtävä 1 1. Etsi lukujen 4655 ja 12075 suurin yhteinen tekijä ja lausu se kyseisten lukujen lineaarikombinaationa ilman laskimen
Algoritmit 1. Luento 7 Ti Timo Männikkö
 Algoritmit 1 Luento 7 Ti 31.1.2017 Timo Männikkö Luento 7 Järjestetty binääripuu Binääripuiden termejä Binääripuiden operaatiot Solmun haku, lisäys, poisto Algoritmit 1 Kevät 2017 Luento 7 Ti 31.1.2017
Algoritmit 1 Luento 7 Ti 31.1.2017 Timo Männikkö Luento 7 Järjestetty binääripuu Binääripuiden termejä Binääripuiden operaatiot Solmun haku, lisäys, poisto Algoritmit 1 Kevät 2017 Luento 7 Ti 31.1.2017
Task list Submit code Submissions Messages Scoreboard View queue Edit contest
 Jäätelö Edit task Translate 1.00 s Uolevi aikoo ostaa kaksi jäätelötötteröä: yhden Maijalle ja yhden itselleen. Tiedossasi on jokaisen myynnissä olevan jäätelötötterön hinta ja paino sekä suurin summa,
Jäätelö Edit task Translate 1.00 s Uolevi aikoo ostaa kaksi jäätelötötteröä: yhden Maijalle ja yhden itselleen. Tiedossasi on jokaisen myynnissä olevan jäätelötötterön hinta ja paino sekä suurin summa,
Tietorakenteet (syksy 2013)
 Tietorakenteet (syksy 2013) Harjoitus 1 (6.9.2013) Huom. Sinun on osallistuttava perjantain laskuharjoitustilaisuuteen ja tehtävä vähintään kaksi tehtävää, jotta voit jatkaa kurssilla. Näiden laskuharjoitusten
Tietorakenteet (syksy 2013) Harjoitus 1 (6.9.2013) Huom. Sinun on osallistuttava perjantain laskuharjoitustilaisuuteen ja tehtävä vähintään kaksi tehtävää, jotta voit jatkaa kurssilla. Näiden laskuharjoitusten
Kenguru 2016 Benjamin (6. ja 7. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
4.1. Olkoon X mielivaltainen positiivinen satunnaismuuttuja, jonka odotusarvo on
 Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Mat-2.090 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Otanta Poisson- Jakaumien tunnusluvut Diskreetit jakaumat Binomijakauma, Diskreetti tasainen jakauma, Geometrinen jakauma, Hypergeometrinen
Algoritmit. Ohjelman tekemisen hahmottamisessa käytetään
 Ohjelmointi Ohjelmoinnissa koneelle annetaan tarkkoja käskyjä siitä, mitä koneen tulisi tehdä. Ohjelmointikieliä on olemassa useita satoja. Ohjelmoinnissa on oleellista asioiden hyvä suunnittelu etukäteen.
Ohjelmointi Ohjelmoinnissa koneelle annetaan tarkkoja käskyjä siitä, mitä koneen tulisi tehdä. Ohjelmointikieliä on olemassa useita satoja. Ohjelmoinnissa on oleellista asioiden hyvä suunnittelu etukäteen.
Negatiiviset luvut ja laskutoimitukset
 7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
7.lk matematiikka Negatiiviset luvut ja laskutoimitukset Hatanpään koulu Syksy 2017 Janne Koponen Negatiiviset luvut ja laskutoimitukset 2 Negatiiviset luvut ja laskutoimitukset Sisällys 1. Negatiiviset
811312A Tietorakenteet ja algoritmit Kertausta kurssin alkuosasta
 811312A Tietorakenteet ja algoritmit 2017-2018 Kertausta kurssin alkuosasta II Perustietorakenteet Pino, jono ja listat tunnettava Osattava soveltaa rakenteita algoritmeissa Osattava päätellä operaatioiden
811312A Tietorakenteet ja algoritmit 2017-2018 Kertausta kurssin alkuosasta II Perustietorakenteet Pino, jono ja listat tunnettava Osattava soveltaa rakenteita algoritmeissa Osattava päätellä operaatioiden
Sukelluskeräily, Pelihahmon liikuttaminen. Tee uusi hahmo: Pelihahmo. Nimeä se. Testaa ikuisesti -silmukassa peräkkäisinä testeinä (jos) onko jokin
 Versio 1.0 1 Sukelluskeräily Tässä pelissä keräilet erilaisia aarteita ja väistelet vihollista. Tämän lisäksi pelaajan pitää käydä välillä pinnalla hengittelemässä. Peliin lisätään myös häiriötekijäksi
Versio 1.0 1 Sukelluskeräily Tässä pelissä keräilet erilaisia aarteita ja väistelet vihollista. Tämän lisäksi pelaajan pitää käydä välillä pinnalla hengittelemässä. Peliin lisätään myös häiriötekijäksi
Joukot. Georg Cantor ( )
 Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Joukot Matematiikassa on pyrkimys määritellä monimutkaiset asiat täsmällisesti yksinkertaisempien asioiden avulla. Tarvitaan jokin lähtökohta, muutama yleisesti hyväksytty ja ymmärretty käsite, joista
Laskennan mallit (syksy 2010) Harjoitus 8, ratkaisuja
 582206 Laskennan mallit (syksy 2010) Harjoitus 8, ratkaisuja 1. Tarkastellaan yhteydetöntä kielioppia S SAB ε A aa a B bb ε Esitä merkkijonolle aa kaksi erilaista jäsennyspuuta ja kummallekin siitä vastaava
582206 Laskennan mallit (syksy 2010) Harjoitus 8, ratkaisuja 1. Tarkastellaan yhteydetöntä kielioppia S SAB ε A aa a B bb ε Esitä merkkijonolle aa kaksi erilaista jäsennyspuuta ja kummallekin siitä vastaava
Sisällys. 3. Muuttujat ja operaatiot. Muuttujat ja operaatiot. Muuttujat. Operaatiot. Imperatiivinen laskenta. Muuttujat. Esimerkkejä: Operaattorit.
 3. Muuttujat ja operaatiot Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi.. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit. Arvojen
3. Muuttujat ja operaatiot Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi.. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit. Arvojen
ja λ 2 = 2x 1r 0 x 2 + 2x 1r 0 x 2
 Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
Johdatus diskreettiin matematiikkaan Harjoitus 4, 7.10.2015 1. Olkoot c 0, c 1 R siten, että polynomilla r 2 c 1 r c 0 on kaksinkertainen juuri. Määritä rekursioyhtälön x n+2 = c 1 x n+1 + c 0 x n, n N,
3. Muuttujat ja operaatiot 3.1
 3. Muuttujat ja operaatiot 3.1 Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi. Operaattorit. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit.
3. Muuttujat ja operaatiot 3.1 Sisällys Imperatiivinen laskenta. Muuttujat. Nimi ja arvo. Muuttujan nimeäminen. Muuttujan tyyppi. Operaattorit. Operandit. Arvon sijoitus muuttujaan. Aritmeettiset operaattorit.
Lauseen erikoistapaus on ollut kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa seuraavassa muodossa:
 Simo K. Kivelä, 13.7.004 Frégier'n lause Toisen asteen käyrillä ellipseillä, paraabeleilla, hyperbeleillä ja niiden erikoistapauksilla on melkoinen määrä yksinkertaisia säännöllisyysominaisuuksia. Eräs
Simo K. Kivelä, 13.7.004 Frégier'n lause Toisen asteen käyrillä ellipseillä, paraabeleilla, hyperbeleillä ja niiden erikoistapauksilla on melkoinen määrä yksinkertaisia säännöllisyysominaisuuksia. Eräs
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 9.2.2011 T-106.1208 Ohjelmoinnin perusteet Y 9.2.2011 1 / 46 Kännykkäpalautetteen antajia kaivataan edelleen! Ilmoittaudu mukaan lähettämällä ilmainen tekstiviesti
Ohjelmoinnin perusteet Y Python T-106.1208 9.2.2011 T-106.1208 Ohjelmoinnin perusteet Y 9.2.2011 1 / 46 Kännykkäpalautetteen antajia kaivataan edelleen! Ilmoittaudu mukaan lähettämällä ilmainen tekstiviesti
a) Sievennä lauseke 1+x , kun x 0jax 1. b) Aseta luvut 2, 5 suuruusjärjestykseen ja perustele vastauksesi. 3 3 ja
 1 YLIOPPILASTUTKINTO- LAUTAKUNTA 1.10.2018 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
1 YLIOPPILASTUTKINTO- LAUTAKUNTA 1.10.2018 MATEMATIIKAN KOE PITKÄ OPPIMÄÄRÄ A-osa Ratkaise kaikki tämän osan tehtävät 1 4. Tehtävät arvostellaan pistein 0 6. Kunkin tehtävän ratkaisu kirjoitetaan tehtävän
Kenguru 2013 Junior sivu 1 / 9 (lukion 1. vuosikurssi)
 Kenguru 2013 Junior sivu 1 / 9 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Junior sivu 1 / 9 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 1 b 3 a 5
 Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
Johdatus diskreettiin matematiikkaan Harjoitus 6, 21.10.2015 1. Ovatko verkot keskenään isomorfiset? (Perustele!) Ratkaisu. Ovat. Tämän näkee indeksoimalla kärjet kuvan osoittamalla tavalla: a 2 b 4 a
5.3 Ensimmäisen asteen polynomifunktio
 Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
1. Jaa blini kolmella suoralla a) neljään, b) viiteen, c) kuuteen ja d) seitsemään osaan. Osien ei tarvitse olla samanlaisia. Piirrä suorat kuviin.
 Peruskoulun matematiikkakilpailu 2015 2016 alkukilpailu 29.10.2015. Ratkaisut 1. Jaa blini kolmella suoralla a) neljään, b) viiteen, c) kuuteen ja d) seitsemään osaan. Osien ei tarvitse olla samanlaisia.
Peruskoulun matematiikkakilpailu 2015 2016 alkukilpailu 29.10.2015. Ratkaisut 1. Jaa blini kolmella suoralla a) neljään, b) viiteen, c) kuuteen ja d) seitsemään osaan. Osien ei tarvitse olla samanlaisia.
OTATKO RISKIN? peli. Heitä noppaa 3 kertaa. Tavoitteena on saada
 OTATKO RISKIN? peli 1. Heitä noppaa 20 kertaa. Tavoitteena on saada vähintään 10 kertaa silmäluku 4, 5 tai 6. Jos onnistut, saat 300 pistettä. Jos et onnistu, menetät 2. Heitä noppaa 10 kertaa. Tavoitteena
OTATKO RISKIN? peli 1. Heitä noppaa 20 kertaa. Tavoitteena on saada vähintään 10 kertaa silmäluku 4, 5 tai 6. Jos onnistut, saat 300 pistettä. Jos et onnistu, menetät 2. Heitä noppaa 10 kertaa. Tavoitteena
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 2014 G. Gripenberg (Aalto-yliopisto) MS-A0402 Diskreetin matematiikan perusteetesimerkkejä,
MS-A0004/MS-A0006 Matriisilaskenta Laskuharjoitus 6 / vko 42
 MS-A0004/MS-A0006 Matriisilaskenta Laskuharjoitus 6 / vko 42 Tehtävät 1-4 lasketaan alkuviikon harjoituksissa ryhmissä, ja ryhmien ratkaisut esitetään harjoitustilaisuudessa (merkitty kirjaimella L = Lasketaan).
MS-A0004/MS-A0006 Matriisilaskenta Laskuharjoitus 6 / vko 42 Tehtävät 1-4 lasketaan alkuviikon harjoituksissa ryhmissä, ja ryhmien ratkaisut esitetään harjoitustilaisuudessa (merkitty kirjaimella L = Lasketaan).
http://www.nelostuote.fi/suomi/rummikubsaan.html
 Sivu 1/5 Pelin sisältö 104 numeroitua laattaa (numeroitu 1-13) 2 laattaa kutakin neljää väriä (musta, oranssi, sininen ja punainen) 2 jokerilaattaa, 4 laattatelinettä, pelisäännöt Pelin tavoite Tavoitteena
Sivu 1/5 Pelin sisältö 104 numeroitua laattaa (numeroitu 1-13) 2 laattaa kutakin neljää väriä (musta, oranssi, sininen ja punainen) 2 jokerilaattaa, 4 laattatelinettä, pelisäännöt Pelin tavoite Tavoitteena
Merkkijono on palindromi, jos se säilyy samana, vaikka sen kääntää väärinpäin.
 A Palindromi Sinulle annetaan merkkijono, ja tehtäväsi on poistaa siitä tarkalleen yksi merkki, minkä jälkeen merkkijonon tulisi olla palindromi. Onko tehtäväsi mahdollinen? Merkkijono on palindromi, jos
A Palindromi Sinulle annetaan merkkijono, ja tehtäväsi on poistaa siitä tarkalleen yksi merkki, minkä jälkeen merkkijonon tulisi olla palindromi. Onko tehtäväsi mahdollinen? Merkkijono on palindromi, jos
Kenguru 2017 Benjamin (6. ja 7. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saat 3, 4 tai 5 pistettä.
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saat 3, 4 tai 5 pistettä.
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä, todistuksia ym., osa I G. Gripenberg Aalto-yliopisto 3. huhtikuuta 014 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteetesimerkkejä,
XXIII Keski-Suomen lukiolaisten matematiikkakilpailu 23.1.2014, tehtävien ratkaisut
 XXIII Keski-Suomen lukiolaisten matematiikkakilpailu 23.1.2014, tehtävien ratkaisut 1. Avaruusalus sijaitsee tason origossa (0, 0) ja liikkuu siitä vakionopeudella johonkin suuntaan, joka ei muutu. Tykki
XXIII Keski-Suomen lukiolaisten matematiikkakilpailu 23.1.2014, tehtävien ratkaisut 1. Avaruusalus sijaitsee tason origossa (0, 0) ja liikkuu siitä vakionopeudella johonkin suuntaan, joka ei muutu. Tykki
Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
 Heli Vaara ja Tiina Komulainen OuLUMA, sivu 1 MERIROSVOJEN AARTEENJAKOPELI Avainsanat: matematiikka, pelit, todennäköisyys Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
Heli Vaara ja Tiina Komulainen OuLUMA, sivu 1 MERIROSVOJEN AARTEENJAKOPELI Avainsanat: matematiikka, pelit, todennäköisyys Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
5.2 Ensimmäisen asteen yhtälö
 5. Ensimmäisen asteen ytälö 5. Ensimmäisen asteen yhtälö Aloitetaan antamalla nimi yhtälön osille. Nyt annettavat nimet eivät riipu yhtälön tyypistä tai asteesta. Tarkastellaan seuraavaa yhtälöä. Emme
5. Ensimmäisen asteen ytälö 5. Ensimmäisen asteen yhtälö Aloitetaan antamalla nimi yhtälön osille. Nyt annettavat nimet eivät riipu yhtälön tyypistä tai asteesta. Tarkastellaan seuraavaa yhtälöä. Emme
Impedanssitomografia-peli
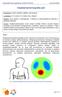 Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja.
 ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ô ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Kauppias on ostanut
ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ô ÖÙ Ö Tehtäviä on kahdella sivulla; kuusi ensimmäistä tehtävää on monivalintatehtäviä, joissa on 0 4 oikeata vastausta. Laskimet eivät ole sallittuja. 1. Kauppias on ostanut
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2018-2019 1. Algoritmeista 1.1 Algoritmin käsite Algoritmi keskeinen laskennassa Määrittelee prosessin, joka suorittaa annetun tehtävän Esimerkiksi Nimien järjestäminen aakkosjärjestykseen
811120P Diskreetit rakenteet 2018-2019 1. Algoritmeista 1.1 Algoritmin käsite Algoritmi keskeinen laskennassa Määrittelee prosessin, joka suorittaa annetun tehtävän Esimerkiksi Nimien järjestäminen aakkosjärjestykseen
{ 2v + 2h + m = 8 v + 3h + m = 7,5 2v + 3m = 7, mistä laskemmalla yhtälöt puolittain yhteen saadaan 5v + 5h + 5m = 22,5 v +
 9. 0. ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ö Ø ÙØ 009 È ÖÙ Ö P. Olkoon vadelmien hinta v e, herukoiden h e ja mustikoiden m e rasialta. Oletukset voidaan tällöin kirjoittaa yhtälöryhmäksi v + h + m = 8 v +
9. 0. ÄÙ ÓÒ Ñ Ø Ñ Ø ÐÔ ÐÙÒ Ð Ù ÐÔ ÐÙÒ Ö Ø ÙØ 009 È ÖÙ Ö P. Olkoon vadelmien hinta v e, herukoiden h e ja mustikoiden m e rasialta. Oletukset voidaan tällöin kirjoittaa yhtälöryhmäksi v + h + m = 8 v +
TEHTÄVIEN RATKAISUT. Luku Kaikki luvut on kokonaislukuja. Luonnollisia lukuja ovat 35, 7 ja 0.
 TEHTÄVIEN RATKAISUT Luku.. Kaikki luvut on kokonaislukuja. Luonnollisia lukuja ovat, 7 ja 0.. a) Luvun vastaluku on, koska + ( ) 0. b) Luvun 7 vastaluku on 7, koska 7 + ( 7) 0. c) Luvun 0 vastaluku on
TEHTÄVIEN RATKAISUT Luku.. Kaikki luvut on kokonaislukuja. Luonnollisia lukuja ovat, 7 ja 0.. a) Luvun vastaluku on, koska + ( ) 0. b) Luvun 7 vastaluku on 7, koska 7 + ( 7) 0. c) Luvun 0 vastaluku on
