2. a) Lähellä maan pintaa massaan m kohdistuva gravitaatiovoima kirjoitetaan muodossa
|
|
|
- Ari-Pekka Mäkinen
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 763101P Fysiikan matematiikkaa sl 2012 Harjoitus 13 Viimeinen näyttpäivä pe Kappale liikkuu voimakentässä 2 3 ˆ ˆ 2 F ( y cos x z ) i (2 y sin x 4) j (3xz 2) k ˆ. a) Osoita, että kenttä on konservatiivinen. b) Etsi kenttää vastaava skalaaripotentiaali. c) Laske ty, joka tehdään siirrettäessä kappaletta voimakentässä pisteestä (0, 1, 1) pisteeseen ( / 2, 1, 2). 2. a) Lähellä maan pintaa massaan m kohdistuva gravitaatiovoima kirjoitetaan muodossa F mg k. ˆ Osoita, että voima on konservatiivinen ja laske vastaava skalaaripotentiaali eli ns. gravitaatiopotentiaali, joka antaa kentän muodossa F. b) Kaukana maan pinnasta massaan m kohdistuva gravitaatiovoima kirjoitetaan muodossa F e ˆ 2 r, r missä on vakio ja r etäisyys maan keskipisteestä. Osoita, että voima on konservatiivinen ja laske gravitaatiopotentiaali, joka antaa kentän muodossa F. 3. lue on rajattu xy-tasoon y-akselin ja suorien y1 2x 4ja y2 x 2 väliin. lueen pintaala saadaan laskemalla integraali d dxdy. a) Hahmottele alue ja perustele integroimisrajat x :0 6 ja y: (2x 4) ( x 2). b) Laske alueen pinta-ala. c) Laske alueen massakeskipisteen koordinaatit 1 1 xm xd ja ym yd 4. Tarkastellaan R-säteistä origokeskistä palloa. Käytetään pallokoordinaatistoa. a) Osoita, että pallon pinnalla infinitesimaalinen pinta-alkio on d R 2 sin d d ja laske pallon pinta-ala. b) Osoita, että pallon sisällä tilavuusalkio on dv r 2 sin drd d ja laske pallon tilavuus Käyttäen vektorikenttä F 2xˆi 2yˆj 3z k ˆ testaa Gaussin lausetta laskemalla tilavuusintegraali F dv ja pintaintegraali d V kun tilavuutena on särmin muotoinen tilavuus x [0,1], y [0,1] ja z [0,2] On annettu vektorikenttä F ( x y ) ˆi 2xy ˆj ja tarkastellaan xy-tasossa suorakaidetta, jota rajoittavat suorat x 0, x a, y 0 ja y b. Vahvista laskemalla F F d ja että tässä tapauksessa Stokesin lause toteutuu. F d r,
2 ll naj o r rus l3 /. ed F = (b z6osx +zs) i n(zts tnx -Y ) i + 6rz'*ilt,,o qj V*F = I /(' 3/tx.La X cosx + z' a J )/r\ l( 3/c e )XSrur -Lt 3x z?+ z )t.',.r\ -.<. \" Vtr,<trrÅ -i(: z''3 z') + å (tr co s x - 27cos x) = Ö N v: t'ttå R vrl I vr,tt ',t't (v"i = o) ->) /') F:v+ x=, JÖST tt@ sx +23 f,x 2: srn'-,x - L{ 1>r z L+ L I JTE G QO I O/]N : ($'s,n, Y+Yz7 + {(v'tl \ =i!'sturx-yl + X(x'z) Itz3v:-z + h(x'r) op vlr n-v,({(:,2)= 2z-tt1 +cr' 4Z(r, e) =,rf + Lz n c' [6 x rr = 1'st'x -Yt loll-crtru,, ou ult<) +c\ 1",' = qtsrrux+yzs +2z -Yl * O- / o':vlt o Y *#-^-,'^.-.-tu
3 J w= 4f+,-1,t)-(o,r, -7 ) ) a. = (t +yn+yry+q) - (o :3*Yn + : l{+r'(n fo OJ?,\ l- = -fi?v 4.^^ r?=ltjv. v xf = l7t^ '/rt %z lc o -rmft O,rt Lc>PSe 2vT7 tv tttett -_;(o) -it"t *il(o; : o csavrrtto',po TENTI L ', Q : ---i -VQ=F -) T.- o,ä= e,':== ilnr IPrz c z 1!T-1 ({q..,nt l/ Ö= 1?U,7) t Mxt+h(rx) :) 4) = r^72 + o-, a' o*s vv-to # k1 F= -qå. (fult= n?z vt-tr*:\ Z(/'z)= wxz (hk,i=a ;F"=-fr,Fo=o 'Fo=Q I å. nå rlsruoåp 1 +a- +Q v*f = l%" %" "Ä+ { yzstxsol-tfr, o I r1/1 o I \ä"(o) -\tå(") * Y-sru6% (o)l = o ('sual o! Lor<ts E QwTI I v tne'\)
4 -+ F : v1) =- 16,. (#). å (* HJ '_å*(å, %)1 losnr QY= c" - Y- / l,<:fe(,r.tdn 1,1) [= 9 + {@,ot r Tft,a) L-, (r, e ) I e:/ r ce zo tc3 ' rs*a oq (@,e)= a VI-ITN?(r,4) = r Å(r,o)= -- +q r -9 +e Y- (vnutol 3 / ( VL Ö 1e,*) SucrQn!r= 7r-\ LEILL Y^r- Sett,<.t prsrressä (o,-\) J suo4/l 1"= K+L?tsrr.lssi (o,z)' SucrBar L-trlVVVT TotSE/rS / ku^j ),*-\ =X+? =) K=( ) 1=B ELt etsretrssä (<,4) /r) Qtt'ra -L o^j $a* = Kno.,ELt Quura -L sa.qo,j "v-6 rvt" ' l{o N) /.: o-',6 \: Lr-Y -> x+l (srrs YraYr,Luva)
5 = 6 ) Y= ( e =frll x+2- ( \z (,\,:;)nr )* /: Ll, c) X..., ( xtz = -\)^*'' L((xea:1 (l(*e r?)\ )' 1...,= j $r (. X=o l. (n G' *c)jx ls J O L(-U rirs) ls\ 3 / IB J \ ^ (. = I l(-xt 3 :\ =U=Z 16 / Strs \X,,, Y=I* =l l8 )? 6 y+r ra=å!((: {r z)'- + loxl Y.- ) X=O tl-,t I -Y ( \ /-x J\ 3,)a. = -l 18 / Y=0 '?-\^ +(r)do = 4 : Y+z!t (,.), 2*-v,+!(Å' o.)u.=,*!(,kr)r. ){u-")')j-* =!, -t2r) =J (xe - = (t, z) K tr t v') i (-t" L p)ox - t z) &* lro -+r)
6 @.1 r;l-a =_) {v i ul I Sstpo &Q Q&"o :> c/ = Rde Rsrn, e &. = R 1s, *s e &e J.?ttcst'S PrruTÄ ".TETN "' / k u^j Ö z O ->lj- Ö: 2TT Jcr.fep Pt,t:I* - L LS ( t l:t 6Ö I 0'qno\) 11I,l =!!oo = f ((f-''"r4e"r.'8e "=f Q=a zt- = in t"""( P- )e": InR"$'"" '!e ;n = ln ' f-oso = unr'( 1il) = 1L{ o lrj 4r SUJO)!4 (V''rcn ront-å ) r&o ( ruz'er.r Eoeuta J &V, &-&e)(rswejö) (3-r\ = 'rlstr.lo &r&ö&e QnruoP TILVuuJ "Vvr 'ra^n)' ' Lu*t Q: -=il- Q: o-å'?7 f : o-->r I ot?ru Ttunvuv a E vs I (Nr Ba t o'a'ln/ v= _$5a"
7 1ir rt' R (. v= t(\( 5"'s,^,e&)*") & 4=o o=o y-=o F 2tr T lrt' = { tf + u', r,re eo)a+ )o rt = 5ry (1*r)& tt/- =?8'\do ='t nr' T''! l-* Lxi - 2r i n3z't,it or Tt trqvuus I ^/ Tä Q-Z- t s s v.f = w) * tfr'u '#' = 2*?+62 = \ + e I Jo Tg,t'!II'Fe 1, 11 v= t I Irr+Z 7=O 1-o K=O g =l-l,if'.,t+62\&z )J*J1&z I lqn*32' o = f+-lt- =P 9 t pfa t,u T,,,,, \i\ Ttr &LI 14uusl PINT : 1.?eos,+ rt 11 &1, = Y c*{d\ F-ei = 3z"J*&l J z=t' tjy:yi p s6vr r?u, rt Å P;r:raELEnPltrT-t - VfVr>f:tT o sö lfivt ulospätru PtNp/-) $ut-u- n ITn T1 LV uu oe st
8 lofe,tl 1 t O 5!f,G = 5l t.&*r' ^ '=: t;" 6) -liaäa= Z=o tl=o 2. n;a s.å = -t 4"&t i.di = -7 z'&*j3 J^ z= o 3. Yt:gnry4LLE Jt = -i &'az F..rÄ= -t1 &to(z J Y:o \. otv-elle &i =!a"a* F.aä= 21J-r&z Ja Y= 1 5 ETEEN r--\ a ^ JÄ = z'&u&z --\ F-4/'= Lx&x&z J/+ x =? 6, r"a"s: et = -)&t'lr -\ -5 F'J.i= -2xå-1"/a J x : + \)" oolrq K'-. +ll ; -5(1,!r&z z--a /=o.-@ +(; = lx*y+\ =L9 JJ h,t^ r55stlst-ttt+vuuslruteclllqtsartn*l TULO LSEP LUT T.I QII'IT INTE 6 (LLI' JO T a]n) GrSS/,tl 2arsSl T0tHlt!!
9 @ F: (x1r' ); 5k r 2,21 i '1\"tr)4-x* 2,ry 4$l 3" 1" l=o,j!=o lox=q,1-x=o j'\=/,-'j!=o Y' K=, J-x=o,/Å Joreru \f-.(f = aa -å )7.F sils -5 'c!-å -\l/- v*f : ltrr, \r'-r QttrT * LVI () fr --\ \w Y '.! =.= qf rf o /-v o6 =.) I aaxj-1 = io3' -- al' oo o o + (t, \r:)&n = I +'"-'&'r : eto a- -=) j"jv : o le f"r2o*3o*yo = Tq/t" /\^ j K [ ^r^ ^ ^ )/"t Vrr\= r(er+xt) ='{: k '?xl o I N &i = Qe1, tjrf"r,g.3 -ra -" +L"' $t \r : S f F.r")*, = \ta1rr Y=o )1zo o /r o I n ^..,?ol' //af = t** =. SiOF /z* ELt Sr" Y'ESt,.s LvsP 7-r:t n t,!!
-lllii;i i Eiää: Iiiii:; ä;äiäeiäi
 I z v x 'uz1zz?z., d!?.,rtz l t! r zx x tru tl Ifl Ag, lp llg l!q?6 ff -lll I 'g l 1 II giigur gtl,l9 t grliffglgi ggrygtgg , ur?.1,ä.r 'r,!,tzlt "z'.1 {r,? yr,! rz fl. r F g g!fi z,. g! q I?!?+ t f g
I z v x 'uz1zz?z., d!?.,rtz l t! r zx x tru tl Ifl Ag, lp llg l!q?6 ff -lll I 'g l 1 II giigur gtl,l9 t grliffglgi ggrygtgg , ur?.1,ä.r 'r,!,tzlt "z'.1 {r,? yr,! rz fl. r F g g!fi z,. g! q I?!?+ t f g
3 *ä;r ä:e 5ä ä{ :i. c oo) S g+;!qg *r; Er ; l[$ E ;;iä F:ä ä :E ä: a bo. =. * gäf$iery g! Eä. a is äg*!=."fl: ä; E!, \ ins:" qgg ;._ EE üg.
 t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
t AJ 1., t4 t4 \J : h J \) (.) \ ( J r ) tḡr (u (1) m * t *h& r( t{ L.C g :LA( g9; p ö m. gr iop ö O t : U 0J (U.p JJ! ä; >
NEN PAINOVOIMAMITTAUS N:o OU 10/7b
 I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
I RAUTARUUKKI Oy I RAUTUVAARAN YlVlPÄ.RISTi-)N ALUEELLI- MALMINETSINTÄ NEN PAINOVOIMAMITTAUS N:o OU 0/7b I 3.2. - 30.4.976 osa II -- TUTKIMUSALUE LAATIJA I JAKELU KUNTA LAAT.PVM HYV. SlVlOY OU ma KARTTALEHTI
1i; i S;Ji'l i. ?::Z+i?; i i räf. i:ä;äi +;la=;iilsi*t li +t ' ?1*1i+;s iii:e: riile s:: : ri;-r2=" ii1js:?i_?7-i17;i i
 ,.24 1,? V ) J.,, q " < ^ ; > ). p. Ä I +, 1. ) d. + 1 \ d ; t l r Y ^ L j. 1 > \ 7. r 7 5 r r E,^.. l, 2 9 ; r t 9 j J l 2 1 ; Y,7, ) r 4.. ; G / ) ^ ^ ^ 7 ^ t. r P l t L ) 2 4 P? D 9 ; F I*, 1.. ) /
,.24 1,? V ) J.,, q " < ^ ; > ). p. Ä I +, 1. ) d. + 1 \ d ; t l r Y ^ L j. 1 > \ 7. r 7 5 r r E,^.. l, 2 9 ; r t 9 j J l 2 1 ; Y,7, ) r 4.. ; G / ) ^ ^ ^ 7 ^ t. r P l t L ) 2 4 P? D 9 ; F I*, 1.. ) /
PUTKIKAKSOISNIPPA MUSTA
 Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
Takorauta Tuote LVI-numero Pikakoodi 0753007 RU33 KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS KESKIRASKAS DN 65 KESKIRASKAS 0 KESKIRASKAS 0 KESKIRASKAS SK/UK SK/UK
ääexgäl*ääääe ääg I ä*fre3 I äee iäa ää-äälgü il leääö ää; i ääs äei:ä ä+ i* äfä g u ;; + EF'Hi: 2 ä ; s i r E:;g 8ää-i iää: Ffärg',
 !P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
!P9) (?trtrr('l rl 9< l ( r,r^iüfl.l ltrt ;ä r!! (r, t 6 t, rti 'le )( ö O RRZöF;ä x öö 1 74ö 9 jii\rtr lrl l jipäp. ldrrr_.^!. 9r. i P.^vä P. t!! v 7 ' '.ä e.q i >6l( t (p C ] ä il; ', +t n l ( e iei
l, ; i.'s ä E.ä E o gäästaefiiä,ggäeäeää;äggtää EI ;äe E H * eaä* E E 8EP.E .e= äe eääege F EEE;säääg lee sa 8NY ExE öe äec E= : ;H ä a(ü
 ,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
,. 8\ ( P ;! l, ;.'s ä.ä >. u.a ä q x ö ä : ; ä ;äe * eä* 8P. ee s $e ää ä F äsä ff ääsfä,ääää;äää ä eääe F ;säää le sa r T e q ( r "j (,{,!. r JJ fl *r ( + T r {rl J Y '( S YC T 8Y C0 ( (f J, r, C,9 l
t P1 `UT. Kaupparek. nro Y-tunnus Hämeenlinnan. hallinto- oikeudelle. Muutoksenhakijat. 1( UiH S<
 1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
1(0 1 4 1 1 4 UiH 0 0 0 1 S< A S I A N A J O T O I M I S T O O S S I G U S T A F S S O N P L 2 9, Ra u h a n k a t u 2 0, 1 5 1 1 1 L a h t i P u h e l i n 0 3 / 7 8 1 8 9 6 0, G S M 0 5 0 0 / 8 4 0 5
Differentiaali- ja integraalilaskenta 3 Harjoitus 4/ Syksy 2017
 MS-A35 Differentiaali- ja integraalilaskenta 3 Differentiaali- ja integraalilaskenta 3 Harjoitus 4/ Syksy 217 Alkuviikon harjoituksissa ratkaistaan kolme tehtävää assistentin avustuksella (läsnäololaskarit).
MS-A35 Differentiaali- ja integraalilaskenta 3 Differentiaali- ja integraalilaskenta 3 Harjoitus 4/ Syksy 217 Alkuviikon harjoituksissa ratkaistaan kolme tehtävää assistentin avustuksella (läsnäololaskarit).
K Ä Y T T Ö S U U N N I T E L M A Y H D Y S K U N T A L A U T A K U N T A
 K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
K Ä Y T T Ö S U U N N I T E L M A 2 0 1 7 Y H D Y S K U N T A L A U T A K U N T A Forssan kaupunki Talousarvio ja -suunnitelma 2017-2019 / T O I M I A L A P A L V E L U 50 YHDYSKUNTAPALVELUT 5 0 0 T E
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 3: Vektorikentät Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2016
VOLKER BECK P. =H. o:_ie!r n^: =:l - dö5i6 = '1 arcii - a; +; s*. P <,R< qe 5 +ä a. c g-;i-(d1. ::qp io > iädaa :; 3fE,:E A. Ö!\lo: Y.
 -Tl (D 'f.g) = (,g L! (D =5.T 0) \ (:) ( P. =H ''. @ 5q 9
-Tl (D 'f.g) = (,g L! (D =5.T 0) \ (:) ( P. =H ''. @ 5q 9
Pakkauksen sisältö: Sire e ni
 S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
S t e e l m a t e p u h u v a n v a r a s h ä l y t ti m e n a s e n n u s: Pakkauksen sisältö: K e s k u s y k sikk ö I s k u n t u n n i s ti n Sire e ni P i u h a s a rj a aj o n e st or el e Ste el
1, MITÄ TARKOITETAAN SEURAAVILLA TERMEILLÄ:
 KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
KRANPDON TNTT 14.4.2014 LAY/OTK OT: Vst jkseen kysymykseen erllselle pperlle (must merktä nm myös krjnptu"t.u"ppern). ös et vst jhnkn kysymykseen, jätä nmetty vstuspper myös kysesen tehtävän slt' rrävär:
w%i rf* meccanoindex.co.uk
 &, w% r* lr,ryd* kro g ; - C +gä!! r -. ä.;'! dg+s Zt t0, y < 9 -! 8 tü;r" lun.'-y; ',ä lrl;!tä u l - 9 9! - ä 6 ^ 9 b - q - cz * ; *'a! a = ;6 f
&, w% r* lr,ryd* kro g ; - C +gä!! r -. ä.;'! dg+s Zt t0, y < 9 -! 8 tü;r" lun.'-y; ',ä lrl;!tä u l - 9 9! - ä 6 ^ 9 b - q - cz * ; *'a! a = ;6 f
RIIHIMÄEN MELUSELVITYS 2008
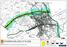 S rj v Pljärv Pä väylly Rj Rjr R T Päväv v Oj Lä öyälä äää j Prj Sr rä v rj I vä Vh Sj U Rääyää hh rj P J Pl rä Ar rvj Al-A Pr löyrä l Th Plr Pä Plä h Uh Tv Tl Oj Slä Rj Al v Prä-r Tl Ojrä Rää Läj Vjh
S rj v Pljärv Pä väylly Rj Rjr R T Päväv v Oj Lä öyälä äää j Prj Sr rä v rj I vä Vh Sj U Rääyää hh rj P J Pl rä Ar rvj Al-A Pr löyrä l Th Plr Pä Plä h Uh Tv Tl Oj Slä Rj Al v Prä-r Tl Ojrä Rää Läj Vjh
äiäää?l älägcläälii äisrä lää äää
 E m vf z ln7 r vr ll n U d \r .Tl vr r E0.Tl : N. ' 6 J n n 5 EF g m : ' ".E q ' v { m i. 'n 9. E!. G r'.n ff ge re E'l n,. q (f,,r L : n 6 :. G N. +.:, lrf s 'T ^ x vr L : @ : L 5 T g G H liäiiiiii$ä1läl
E m vf z ln7 r vr ll n U d \r .Tl vr r E0.Tl : N. ' 6 J n n 5 EF g m : ' ".E q ' v { m i. 'n 9. E!. G r'.n ff ge re E'l n,. q (f,,r L : n 6 :. G N. +.:, lrf s 'T ^ x vr L : @ : L 5 T g G H liäiiiiii$ä1läl
SU01\1JEL\I MAINJ[ OY
 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98 SU0\JEL\I MAINJ[ OY FlNNEXPLORAlON & ESPOO 27..98 HANNU SILVENNOINEN,. Dl 2 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98. s I s Ä
KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98 SU0\JEL\I MAINJ[ OY FlNNEXPLORAlON & ESPOO 27..98 HANNU SILVENNOINEN,. Dl 2 KAIRAREIÄN NO 44 SIVUSUUNAMIAUS HYVELÄSSÄ MARRASKUUSSA 98. s I s Ä
Eo C)sl. oarl. d to E= J. o-= o cy) =uo. f,e. ic v. .o6. .9o. äji. :ir. ijo 96. {c o o. ';i _o. :fe. C=?i. t-l +) (- c rt, u0 C.
 C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
C C C)l A\ d Y) L P C v J J rl, ( 0 C.6 +) ( j 96.9 :r : C (Db]? d '; _ äj r, { . 3 k l: d d 6 60QOO:ddO 96.l ä.c p _ : 6 äp l P C..86 p r5 r!l (, ō J. J rl r O 6!6 (5 ) ä dl r l { ::: :: :: 6e g r : ;
ELEC C4140 Kenttäteoria (syksy 2016)
 ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Vektorianalyysi (Ulaby, luku 3) Viiva-, pinta- ja tilavuusalkiot Nablaoperaatiot Gaussin ja Stokesin lauseet Nabla on ystävä
ELEC C4140 Kenttäteoria (syksy 2016) Henrik Wallén / versio 15. syyskuuta 2016 Vektorianalyysi (Ulaby, luku 3) Viiva-, pinta- ja tilavuusalkiot Nablaoperaatiot Gaussin ja Stokesin lauseet Nabla on ystävä
Mat Matematiikan peruskurssi S2
 Mat-1.122 Matematiikan peruskurssi S2 Ratkaisuehdotuksia Harjoitus 12 alkuviikko Tehtävä 1 Hahmottele annetut vektorikentät sekä niiden kenttäviivat tapauksissa. a)f(x, y) xi + yj b)f(x, y) e x i + e -x
Mat-1.122 Matematiikan peruskurssi S2 Ratkaisuehdotuksia Harjoitus 12 alkuviikko Tehtävä 1 Hahmottele annetut vektorikentät sekä niiden kenttäviivat tapauksissa. a)f(x, y) xi + yj b)f(x, y) e x i + e -x
Mat Matematiikan peruskurssi K2
 Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
Mat-.3 Matematiikan peruskurssi K Heikkinen/Tikanmäki Kolmas välikoe 6.5. Kokeessa saa käyttää ylioppilaskirjoituksiin hyväksyttyä laskinta. Sivun kääntöpuolelta löytyy integrointikaavoja.. Olkoon F(x,
L. Maan ia Auringon vetovoiman yhtäsuuruus
 GRAVTAATOKENTT EN TASAPA NOKOHTA: Tehtävä RATKASU L. Maan a Aurngon vetovoman yhtäsuuruus Kunka kauas Maasta avaruusluotan on vetävä, otta Aurngon jaa Maan vetovomat tasapanottasvat tosensa el avaruusalukseen
GRAVTAATOKENTT EN TASAPA NOKOHTA: Tehtävä RATKASU L. Maan a Aurngon vetovoman yhtäsuuruus Kunka kauas Maasta avaruusluotan on vetävä, otta Aurngon jaa Maan vetovomat tasapanottasvat tosensa el avaruusalukseen
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause.
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 8: Divergenssi ja roottori. Gaussin divergenssilause. Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 7: Pintaintegraali ja vuointegraali
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 7: Pintaintegraali ja vuointegraali Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 24 Mikä on pinta?
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 7: Pintaintegraali ja vuointegraali Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 24 Mikä on pinta?
Aluevarausmerkinnät: T/kem Maakuntakaava
 kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
kk mk mv se jl ma ge pv nat luo un kp me va sv rr rr A AA C P TP T TT T/kem V R RA RM L LM LL LS E ET EN EJ EO EK EP S SL SM SR M MT MU MY W c ca km at p t t/ kem mo vt/kt/st vt/kt st yt tv /k /v ab/12
Gaussin lause eli divergenssilause 1
 80 VEKTOIANALYYI Luento 1 8. Gaussin lause eli divergenssilause 1 A 16.4 Kurssin jäljellä olevassa osassa käymme läpi joukon fysiikan kannalta tärkeitä vektorikenttien integrointia koskevia tuloksia, nimittäin
80 VEKTOIANALYYI Luento 1 8. Gaussin lause eli divergenssilause 1 A 16.4 Kurssin jäljellä olevassa osassa käymme läpi joukon fysiikan kannalta tärkeitä vektorikenttien integrointia koskevia tuloksia, nimittäin
S-ZSOTOOP DZDATA !SWIA 0 \ S-ISOTOOPPIDATA GTL-78 S AVZA. M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä
 M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä!SWIA 0 \ S-ZSOTOOP DZDATA S-ISOTOOPPIDATA GTL-78 S AVZA SÄVIÄN S-ISOTOOPPIDATA ANALYYSITULOSTEN SELITYKSET VASEMMALTA OIKEALLE LABORATORIOKOODI
M19/3314/=78/14/10 M,IkeI ä, A.J.Laitakari Pielavesi, Säviä!SWIA 0 \ S-ZSOTOOP DZDATA S-ISOTOOPPIDATA GTL-78 S AVZA SÄVIÄN S-ISOTOOPPIDATA ANALYYSITULOSTEN SELITYKSET VASEMMALTA OIKEALLE LABORATORIOKOODI
ELEC C4140 Kenttäteoria (syksy 2015)
 ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 3 / versio 23. syyskuuta 2015 Vektorianalyysi (Ulaby, luku 3) Koordinaatistot Viiva-, pinta- ja tilavuusalkiot Koordinaattimuunnokset Nablaoperaatiot
ELEC C4140 Kenttäteoria (syksy 2015) Henrik Wallén Luentoviiko 3 / versio 23. syyskuuta 2015 Vektorianalyysi (Ulaby, luku 3) Koordinaatistot Viiva-, pinta- ja tilavuusalkiot Koordinaattimuunnokset Nablaoperaatiot
Differentiaali- ja integraalilaskenta 3 Mallit 2 (alkuviikko) / Syksy 2016
 MS-A35 Differentiaali- ja integraalilaskenta 3 Differentiaali- ja integraalilaskenta 3 Mallit 2 (alkuviikko) / Syksy 216 Tuntitehtävä 1: Laske sylinterikoordinaatteja käyttämällä sen kappaleen tilavuus,
MS-A35 Differentiaali- ja integraalilaskenta 3 Differentiaali- ja integraalilaskenta 3 Mallit 2 (alkuviikko) / Syksy 216 Tuntitehtävä 1: Laske sylinterikoordinaatteja käyttämällä sen kappaleen tilavuus,
Differentiaali- ja integraalilaskenta 3 Mallit laskuharjoitusviikkoon 5 /
 M-A5 ifferentiaali- ja integraalilaskenta, I/17 ifferentiaali- ja integraalilaskenta Mallit laskuharjoitusviikkoon 5 / 9. 1.1. Alkuviikon tehtävät Tehtävä 1: Määritä (ilman Gaussin lausetta) vektorikentän
M-A5 ifferentiaali- ja integraalilaskenta, I/17 ifferentiaali- ja integraalilaskenta Mallit laskuharjoitusviikkoon 5 / 9. 1.1. Alkuviikon tehtävät Tehtävä 1: Määritä (ilman Gaussin lausetta) vektorikentän
Arvio metsdmaan arvosta
 Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
Arv metsmaan arvsta Omstaja Kuusam, Nskajrv Kunta Kyll Tla Rn: Ala, ha 35 477 Nskajrv 31. : 77,5 SPOO LO.6.2L7 Lstetja Teemu Saarnen KTM, LKV Arv phjautuu 14.1,23 pvtyn metssuunntelman kuvtethn ja Kuusamn
3x + y + 2z = 5 e) 2x + 3y 2z = 3 x 2y + 4z = 1. x + y 2z + u + 3v = 1 b) 2x y + 2z + 2u + 6v = 2 3x + 2y 4z 3u 9v = 3. { 2x y = k 4x + 2y = h
 HARJOITUSTEHTÄVIÄ 1. Anna seuraavien yhtälöryhmien kerroinmatriisit ja täydennetyt kerroinmatriisit sekä ratkaise yhtälöryhmät Gaussin eliminointimenetelmällä. { 2x + y = 11 2x y = 5 2x y + z = 2 a) b)
HARJOITUSTEHTÄVIÄ 1. Anna seuraavien yhtälöryhmien kerroinmatriisit ja täydennetyt kerroinmatriisit sekä ratkaise yhtälöryhmät Gaussin eliminointimenetelmällä. { 2x + y = 11 2x y = 5 2x y + z = 2 a) b)
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 10: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali.
 MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
MS-A25/MS-A26 Differentiaali- ja integraalilaskenta 2 Luento 1: Napa-, sylinteri- ja pallokoordinaatistot. Pintaintegraali. Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät
Todista suoraan integraalin määritelmään perustuen tasointegraalin ominaisuus. λ f = λ f,
 7. Taso- ja avaruusintegraali 7.1. Tasointegraalin määrittely 205. Tarkastellaan funktiota f (x,y) = x+y neliössä {(x,y) 0 x 1, 0 y 1}. Neliö jaetaan suorilla x = a ja y = b neljään osasuorakulmioon; 0
7. Taso- ja avaruusintegraali 7.1. Tasointegraalin määrittely 205. Tarkastellaan funktiota f (x,y) = x+y neliössä {(x,y) 0 x 1, 0 y 1}. Neliö jaetaan suorilla x = a ja y = b neljään osasuorakulmioon; 0
6. KOKOUKSEN LAILLISUUSEN JA PÄÄTÖSVALTAISUUDEN TOTEAMINEN
 (3) PÖYTÄKIRJA 5..203 SÄÄNTÖMÄÄRÄISEN SYYSKOKOUKSEN PÖYTÄKIRJA Aika Paikka 5..203 klo 9.20 alkaen Ideapark, Kokoustila Kotka. Lempäälä Läsnä Osallistujalista liitteenä (liite ). KOKOUKSEN AVAUS TaLVIn
(3) PÖYTÄKIRJA 5..203 SÄÄNTÖMÄÄRÄISEN SYYSKOKOUKSEN PÖYTÄKIRJA Aika Paikka 5..203 klo 9.20 alkaen Ideapark, Kokoustila Kotka. Lempäälä Läsnä Osallistujalista liitteenä (liite ). KOKOUKSEN AVAUS TaLVIn
=*' igäiäigä$jii,äägääggägääfä. E'EEEEiäs*'ääääEäggägäiiläägäääägäää. i;giggggäggg äg;gfggäiggis. E Ei. ä jggä;fäfäää. e;egelgäf EEE : !
 l d=. ö^ 3k 4rcna lc ' *O\ J * '\ tia.2 t :q(cblz c i;iä ä;fäis il 6! iää; iäiäää 9 S # öt == cf) \n.vdtd &= e;läf ;:c cj '5 'tr=lz ä jä;fäfäää c5 FrO! =*' ":rf : 6 Ä'^üi= iu l n. :S Xn.!.< V,; :;,^?'=.!.=Na'tY
l d=. ö^ 3k 4rcna lc ' *O\ J * '\ tia.2 t :q(cblz c i;iä ä;fäis il 6! iää; iäiäää 9 S # öt == cf) \n.vdtd &= e;läf ;:c cj '5 'tr=lz ä jä;fäfäää c5 FrO! =*' ":rf : 6 Ä'^üi= iu l n. :S Xn.!.< V,; :;,^?'=.!.=Na'tY
Tällaisessa tapauksessa on usein luontevaa samaistaa (u,v)-taso (x,y)-tason kanssa, jolloin tason parametriesitys on *** VEKTORIANALYYSI.
 39 VEKTORIANALYYI Luento 6 5. Pinnat ja pintaintegraalit Pintojen parametriesitys. Aikaisemmin käsittelimme käyrän esittämistä parametrimuodossa. iihen riitti yksi reaalinen parametri (t), joka sai aroja
39 VEKTORIANALYYI Luento 6 5. Pinnat ja pintaintegraalit Pintojen parametriesitys. Aikaisemmin käsittelimme käyrän esittämistä parametrimuodossa. iihen riitti yksi reaalinen parametri (t), joka sai aroja
r\rvio metsd maa n a rvosta
 r\rv metsd maa n a rvsta Omstaja Skalatva 8B,B3ha Kunta l(yl Tla Rn: Ala, ha 791 t\32. Rahkla B:2 88,8 Laatjan allekrjtus TSPOO 25.8.219 Teemu Saarnen KTM,LKV Pertt Saarnen Lsdtetja MTT-I I(V Arv phjautuu
r\rv metsd maa n a rvsta Omstaja Skalatva 8B,B3ha Kunta l(yl Tla Rn: Ala, ha 791 t\32. Rahkla B:2 88,8 Laatjan allekrjtus TSPOO 25.8.219 Teemu Saarnen KTM,LKV Pertt Saarnen Lsdtetja MTT-I I(V Arv phjautuu
x (t) = 2t ja y (t) = 3t 2 x (t) + + y (t) Lasketaan pari käyrän arvoa ja hahmotellaan kuvaaja: A 2 A 1
 BM2A582 Integraalilaskenta ja sovellukset Harjoitus 6, Kevät 26 Kaikissa tehtävissä tärkeintä ja riittävää on saada oikea lauseke aikaiseksi. Useissa tehtävissä integraalit eivät tosin ole niin vaikeita
BM2A582 Integraalilaskenta ja sovellukset Harjoitus 6, Kevät 26 Kaikissa tehtävissä tärkeintä ja riittävää on saada oikea lauseke aikaiseksi. Useissa tehtävissä integraalit eivät tosin ole niin vaikeita
Differentiaali- ja integraalilaskenta 3 Ratkaisut viikko 3
 MS-A35 Differentiaali- ja integraalilaskenta 3, I/27 Differentiaali- ja integraalilaskenta 3 Ratkaisut viikko 3 Tehtävä : Hahmottele seuraavat vektorikentät ja piirrä niiden kenttäviivat. a) F(x, y) =
MS-A35 Differentiaali- ja integraalilaskenta 3, I/27 Differentiaali- ja integraalilaskenta 3 Ratkaisut viikko 3 Tehtävä : Hahmottele seuraavat vektorikentät ja piirrä niiden kenttäviivat. a) F(x, y) =
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy Millä reaaliluvun x arvoilla. 3 4 x 2,
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 6. Millä reaaliluvun arvoilla a) 9 =, b) + + + 4, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + 4 + 6 + +, b) 8 + 4 6 + + n n, c) + + +
-d;'$ d{ee lr a ;{*.v. ii{:i; rtl i} dr r/ r ) i a 4 a I p ;,.r.1 il s, Karttatuloste. Maanmittauslaitos. Page 1 of 1. Tulostettu 22.08.
 Maanmttauslats Page 1 f 1 -d;'$ d{ee lr a ;{*.v {:; rtl } dr r/ r ) a 4 a p ;,.r.1 l s, Karttatulste Tulstettu 22.08.2014 Tulsteen keskpsteen krdnaatt (ETRS-TM3SFlN): N: 6998249 E: 379849 Tulse e le mttatarkka.
Maanmttauslats Page 1 f 1 -d;'$ d{ee lr a ;{*.v {:; rtl } dr r/ r ) a 4 a p ;,.r.1 l s, Karttatulste Tulstettu 22.08.2014 Tulsteen keskpsteen krdnaatt (ETRS-TM3SFlN): N: 6998249 E: 379849 Tulse e le mttatarkka.
omakotitontit omakotitontit Saaristokaupungin Pirttiniemessä
 KUOPON KAUPUNK Maaoaisuuden hallintapalvelut Tarjousten Tarjousten perusteella perusteella yytävät yytävät oakotitontit oakotitontit Saaristokaupungin Pirttinieessä Tarjousten Tarjousten jättöaika jättöaika
KUOPON KAUPUNK Maaoaisuuden hallintapalvelut Tarjousten Tarjousten perusteella perusteella yytävät yytävät oakotitontit oakotitontit Saaristokaupungin Pirttinieessä Tarjousten Tarjousten jättöaika jättöaika
l 1 2l + 1, c) 100 l=0
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 5. Millä reaaliluvun arvoilla a) 9 =, b) 5 + 5 +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c)
Fr ( ) Fxyz (,, ), täytyy integroida:
 15 VEKTORIANALYYSI Luento Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin ja voima
15 VEKTORIANALYYSI Luento Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin ja voima
Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG LA37 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K
 WC-varaosat Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG 5652536 LA37 NORDIC 2300/2200 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K HUUHTELUPUTKI GBG HUUHTELUVENTTIILI GBG 1-H JA 2-H
WC-varaosat Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG 5652536 LA37 NORDIC 2300/2200 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K HUUHTELUPUTKI GBG HUUHTELUVENTTIILI GBG 1-H JA 2-H
Arvio metsd maa n a rvosta
 Arvi metsd maa n a rvsta Omistaja Lpr Klmenharju Kunta Kylli Tila Rn: Ala, ha 405 572 Klmenharju :l:89 24,9 ESPOO L6.5.20L7 Laatijan allekirjitus Teemu Saarinen Lisdtietja Arvi phjautuu Teemu Saarinen
Arvi metsd maa n a rvsta Omistaja Lpr Klmenharju Kunta Kylli Tila Rn: Ala, ha 405 572 Klmenharju :l:89 24,9 ESPOO L6.5.20L7 Laatijan allekirjitus Teemu Saarinen Lisdtietja Arvi phjautuu Teemu Saarinen
(ks. kuva) ja sen jälkeen x:n ja y:n suhteen yli xy-tasossa olevan alueen projektion G:
 7 VEKTORIANALYYSI Luento 11 7. Tilavuusintegraalit A 14.5 Funktion f( xyz,, ) tilavuusintegraali yli kolmiulotteisen alueen V on raja-arvo summasta V f( xyz,, ) V kun tilavuusalkiot V =. Tarkastellaan
7 VEKTORIANALYYSI Luento 11 7. Tilavuusintegraalit A 14.5 Funktion f( xyz,, ) tilavuusintegraali yli kolmiulotteisen alueen V on raja-arvo summasta V f( xyz,, ) V kun tilavuusalkiot V =. Tarkastellaan
NÄKYMÄ TURVESUONKADUN JA LIELAHDENKADUN RISTEYKSESTÄ MAANKÄYTTÖSUUNNITELMA TEIVAALANTIELLE LIELAHTEEN LUONNOS ARKKITEHDIT A3 OY
 NÄKYMÄ TURVESUNKADUN JA LELAHDENKADUN RSTEYKSESTÄ MAANKÄYTTÖSUUNNTELMA TEVAALANTELLE LELAHTEEN LUNNS.. ARKKTEHDT A Y ,,,,,, :,, Pelv o,,,,,,,,,,,,,,,,,,,, :,,,,,,,, :,,,,,,, Pol Pl,,,, K,, :,,, :,,,,,,,
NÄKYMÄ TURVESUNKADUN JA LELAHDENKADUN RSTEYKSESTÄ MAANKÄYTTÖSUUNNTELMA TEVAALANTELLE LELAHTEEN LUNNS.. ARKKTEHDT A Y ,,,,,, :,, Pelv o,,,,,,,,,,,,,,,,,,,, :,,,,,,,, :,,,,,,, Pol Pl,,,, K,, :,,, :,,,,,,,
Differentiaali- ja integraalilaskenta 3 Laskuharjoitus 7 /
 M-A3x Differentiaali- ja integraalilaskenta 3, IV/216 Differentiaali- ja integraalilaskenta 3 Laskuharjoitus 7 / 14.-16.3. Harjoitustehtävät 37-4 lasketaan alkuviikon harjoituksissa. Kotitehtävät 41-43
M-A3x Differentiaali- ja integraalilaskenta 3, IV/216 Differentiaali- ja integraalilaskenta 3 Laskuharjoitus 7 / 14.-16.3. Harjoitustehtävät 37-4 lasketaan alkuviikon harjoituksissa. Kotitehtävät 41-43
f x da, kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f (x, y) = 2x 3y 2.
 13. Erityyppisten integraalien väliset yhteydet 13.1. Gaussin lause 364. Laske A f x da, kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f (x, y) = 2x 3y
13. Erityyppisten integraalien väliset yhteydet 13.1. Gaussin lause 364. Laske A f x da, kun A on tason origokeskinen yksikköympyrä, jonka kehällä funktion f arvot saadaan lausekkeesta f (x, y) = 2x 3y
)x -)! ^i, + lu" x---',!^,y+je+ov. z'?+t' -t e +v A,ft1 = ffi*- my. Am= ft1x- fhy. A R-*t+AJa^HtNeN. lla.f J^ YA r e. LAtTE^l,NeN YDtMFffi
 Yl ast.qvaj lv zrn Ja Re/4Frto M pg,4f{_g LAtTE^l,NeN YDtMFffi lla.f J^ YA r e Ä^W: frtxhrä- Yrr;rer rn Tulo 6- Y7' r, T' t? Atcrr o,vg R CIA a elt H^J o*>1r M n AÅ = R
Yl ast.qvaj lv zrn Ja Re/4Frto M pg,4f{_g LAtTE^l,NeN YDtMFffi lla.f J^ YA r e Ä^W: frtxhrä- Yrr;rer rn Tulo 6- Y7' r, T' t? Atcrr o,vg R CIA a elt H^J o*>1r M n AÅ = R
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus 2 / vko 45
 MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
MS-A0003/A0005 Matriisilaskenta Laskuharjoitus / vko 5 Tehtävä 1 (L): Hahmottele kompleksitasoon ne pisteet, jotka toteuttavat a) z 3 =, b) z + 3 i < 3, c) 1/z >. Yleisesti: ehto z = R, z C muodostaa kompleksitasoon
b) '5555z-?:lo -1:7 ' 5 ',r+i (i-å) n- r*or i+i- sl4-4 s-5-''- (å) 2:+ 2 r t I 3-3 a)23+42 Ð'+., (, -:), u)j++ b)2-1 "i
 Tampereen kesäyliopisto, kevät 20 1 5 Thlousmatematiikan perusteet, orrr s ro30 L. harjoitus, (la 12.11.2015) 1. Laske seuraavat laskut. Laske kukin lasku ensin käsin þnää ja paperia käyttäen. Anna vastaukset
Tampereen kesäyliopisto, kevät 20 1 5 Thlousmatematiikan perusteet, orrr s ro30 L. harjoitus, (la 12.11.2015) 1. Laske seuraavat laskut. Laske kukin lasku ensin käsin þnää ja paperia käyttäen. Anna vastaukset
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 10: Stokesin lause Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 2016 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy
Ratkaisut vuosien tehtäviin
 Ratkaisut vuosien 1978 1987 tehtäviin Kaikki tehtävät ovat pitkän matematiikan kokeista. Eräissä tehtävissä on kaksi alakohtaa; ne olivat kokelaalle vaihtoehtoisia. 1978 Osoita, ettei mikään käyrän y 2
Ratkaisut vuosien 1978 1987 tehtäviin Kaikki tehtävät ovat pitkän matematiikan kokeista. Eräissä tehtävissä on kaksi alakohtaa; ne olivat kokelaalle vaihtoehtoisia. 1978 Osoita, ettei mikään käyrän y 2
Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG LA37 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K
 WC-varaosat Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG 5652536 LA37 NORDIC 2300/2200 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K SÄILIÖN TIIVISTE GBG HUUHTELUPUTKI GBG HUUHTELUVENTTIILI
WC-varaosat Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG 5652536 LA37 NORDIC 2300/2200 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K SÄILIÖN TIIVISTE GBG HUUHTELUPUTKI GBG HUUHTELUVENTTIILI
Juuri 4 Tehtävien ratkaisut Kustannusosakeyhtiö Otava päivitetty Kertaus. b) B = (3, 0, 5) K2. 8 ( 1)
 Kertaus K1. a) OA i k b) B = (, 0, 5) K. K. a) AB (6 ( )) i () ( ( 7)) k 8i 4k AB 8 ( 1) 4 64116 819 b) 1 1 AB( ( 1)) i 1 i 4 AB ( ) ( 4) 416 0 45 5 K4. a) AB AO OB OA OB ( i ) i i i 5i b) Pisteen A paikkavektori
Kertaus K1. a) OA i k b) B = (, 0, 5) K. K. a) AB (6 ( )) i () ( ( 7)) k 8i 4k AB 8 ( 1) 4 64116 819 b) 1 1 AB( ( 1)) i 1 i 4 AB ( ) ( 4) 416 0 45 5 K4. a) AB AO OB OA OB ( i ) i i i 5i b) Pisteen A paikkavektori
l 1 2l + 1, c) 100 l=0 AB 3AC ja AB AC sekä vektoreiden AB ja
 MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MATEMATIIKAN PERUSKURSSI I Harjoitustehtäviä syksy 7. Millä reaaliluvun arvoilla a) 9 =, b) + 5 + +, e) 5?. Kirjoita Σ-merkkiä käyttäen summat 4, a) + + 5 + + 99, b) 5 + 4 65 + + n 5 n, c) +
MS-A0205/MS-A0206 Differentiaali- ja integraalilaskenta 2 Luento 11: Taso- ja tilavuusintegraalien sovellutuksia
 MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 11: Taso- ja tilavuusintegraalien sovellutuksia Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
MS-A25/MS-A26 ifferentiaali- ja integraalilaskenta 2 Luento 11: Taso- ja tilavuusintegraalien sovellutuksia Jarmo Malinen Matematiikan ja systeemianalyysin laitos 1 Aalto-yliopisto Kevät 216 1 Perustuu
Määräys STUK SY/1/ (34)
 Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
Määräys SY/1/2018 4 (34) LIITE 1 Taulukko 1. Vapaarajat ja vapauttamisrajat, joita voidaan soveltaa kiinteiden materiaalien vapauttamiseen määrästä riippumatta. Osa1. Keinotekoiset radionuklidit Radionuklidi
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 10: Moninkertaisten integraalien sovelluksia
 MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 217 Antti Rasila (Aalto-yliopisto)
MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Syksy 217 Antti Rasila (Aalto-yliopisto)
PS. Jos vastaanotit Sinulle kuulumattoman viestin, pyydän ilmoittamaan siitä viipymättä allekirjoittaneelle ja tuhoamaan viestin, kiitos.
 Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
Teamware Office' Posti Saapunut posti : Olavi Heikkisen lausunto Lähettäjä : Karjalainen Mikko Vastaanottaja : Leinonen Raija Lähetetty: 18.1.2013 10:29 He i! Korjasin nyt tämän spostiliitteenä olevaan
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA
 YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
YHDYSKUNTALAUTAKUNTA TALOUSARVIOEHDOTUS 2018 TALOUSSUUNNITELMA 2018-2020 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S
MATEMATIIKKA 5 VIIKKOTUNTIA
 EB-TUTKINTO 2010 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 4. kesäkuuta 2010 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2010 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 4. kesäkuuta 2010 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
NIKKILÄN SYDÄMEN LAAJENTAMINEN VAIHE 2 MAANTASOKERROS 1/ / ARK - house
 tk, J e, hu p rr, Ä, 9,,, Ä Ä Ä 9,, 9 h vut tk k D uk, C lut, kpk C tr, rv tr C9, y e yv tt t rv lkr tl lut e pll t-k-hu kek u v pt + C C tr C9 tr lut C, C C, yp + phu te kt kpl bet uur rv gr ttpe t +
tk, J e, hu p rr, Ä, 9,,, Ä Ä Ä 9,, 9 h vut tk k D uk, C lut, kpk C tr, rv tr C9, y e yv tt t rv lkr tl lut e pll t-k-hu kek u v pt + C C tr C9 tr lut C, C C, yp + phu te kt kpl bet uur rv gr ttpe t +
Jakotukit / tarvikkeet
 Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi 2022115 BF71 VM 2X3/4 EURO VM 3X3/4 EURO VM 4X3/4 EURO VM 5X3/4 EURO VM 6X3/4 EURO VM 7X3/4 EURO VM 8X3/4 EURO VM 9X3/4 EURO VM 10X3/4 EURO VM 11X3/4 EURO
Jakotukit / tarvikkeet Tuote LVI-numero Pikakoodi 2022115 BF71 VM 2X3/4 EURO VM 3X3/4 EURO VM 4X3/4 EURO VM 5X3/4 EURO VM 6X3/4 EURO VM 7X3/4 EURO VM 8X3/4 EURO VM 9X3/4 EURO VM 10X3/4 EURO VM 11X3/4 EURO
Forssan kaupunki Osavuosikatsaus YHDYSKUNTAPALVELUT. Arviointik r iteeri tr mittarit ja tavoitetaso ja t a v o i t e t a s o
 Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
Forssan kaupunki Osavuosikatsaus 2017-08 TOIMIALA 50 YHDYSKUNTAPALVELUT P A L V E L U 5 0 0 T E K N I S E N J A Y M P Ä R I S T Ö T O I M E N H A L L I N T O J A M A A S E U T U P A L V E L U T T I L I
Preliminäärikoe Pitkä Matematiikka 3.2.2009
 Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
Preliminäärikoe Pitkä Matematiikka..9 x x a) Ratkaise yhtälö =. 4 b) Ratkaise epäyhtälö x > x. c) Sievennä lauseke ( a b) (a b)(a+ b).. a) Osakkeen kurssi laski aamupäivällä,4 % ja keskipäivällä 5,6 %.
MATEMATIIKAN PERUSKURSSI II
 MTEMTIIKN PERUKURI II Harjoitustehtäviä kevät 17 1. Tutki, suppenevatko seuraavat lukujonot: a) d) ( k ) + 5 k, b) k 1 x 5 dx, e) ( ln(k + 1) k ), c) k 1 cos(πx) dx, f) k e x dx, 1 k e k k kx dx.. Olkoon
MTEMTIIKN PERUKURI II Harjoitustehtäviä kevät 17 1. Tutki, suppenevatko seuraavat lukujonot: a) d) ( k ) + 5 k, b) k 1 x 5 dx, e) ( ln(k + 1) k ), c) k 1 cos(πx) dx, f) k e x dx, 1 k e k k kx dx.. Olkoon
Differentiaalilaskennan tehtäviä
 Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
Differentiaalilaskennan tehtäviä DIFFERENTIAALILASKENTA 1. Raja-arvon käsite, derivaatta raja-arvona 1.1 Raja-arvo pisteessä 1.2 Derivaatan määritelmä 1.3 Derivaatta raja-arvona 2. Derivoimiskaavat 2.1
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 10: Moninkertaisten integraalien sovelluksia
 MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 215 1 / 2 Moninkertaisten
MS-A22 ifferentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Moninkertaisten integraalien sovelluksia Antti Rasila Aalto-yliopisto Syksy 215 Antti Rasila (Aalto-yliopisto) MS-A22 Syksy 215 1 / 2 Moninkertaisten
x n e x dx = n( e x ) nx n 1 ( e x ) = x n e x + ni n 1 x 4 e x dx = x 4 e x +4( x 3 e x +3( x 2 e x +2( xe x e x ))) = e x
 Osittaisintegrointia käyttäen osoita integraalille I n x n e x dx oikeaksi reduktiokaava I n x n e x + ni n ja laske sen avulla mitä on I 4 kun x. x n e x dx n( e x ) nx n ( e x ) x n e x + ni n x 4 e
Osittaisintegrointia käyttäen osoita integraalille I n x n e x dx oikeaksi reduktiokaava I n x n e x + ni n ja laske sen avulla mitä on I 4 kun x. x n e x dx n( e x ) nx n ( e x ) x n e x + ni n x 4 e
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause
 MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 19 Esimerkki Olkoon F : R 3 R 3 vakiofunktio
MS-A0305 Differentiaali- ja integraalilaskenta 3 Luento 9: Greenin lause Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0305 Syksy 2015 1 / 19 Esimerkki Olkoon F : R 3 R 3 vakiofunktio
& # # w. œ œ œ œ # œ œ œ œ œ # œ w. # w nœ. # œ œ œ œ œ # œ w œ # œ œ œ Œ. œ œ œ œ œ œ œ œ # œ w. œ # œ œ œ w œ œ w w w w. W # w
 Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
Epainn muis (1.1., 6.12.) # œ œ œ œ œ # œ w i nun Kris lis sä py hää muis tus Tofia (6.1.) jo Jo pai a, y lis n [Ba li nu a, os,] kun ni, l nä ru k, i dän Ju ma lis, y lis ka i dän h tm h nk sl nu a, o
Kertausosa. 5. Merkitään sädettä kirjaimella r. Kaaren pituus on tällöin r a) sin = 0, , c) tan = 0,
 Kertausosa. a),6 60 576 Peruuttaessa pyörähdyssuunta on vastapäivään. Kulma on siis,4 60 864 a) 576 864 0,88m. a) α b 0,6769... 0,68 (rad) r,m 8cm β,90...,9 (rad) 4cm a) α 0,68 (rad) β,9 (rad). a) 5,0
Kertausosa. a),6 60 576 Peruuttaessa pyörähdyssuunta on vastapäivään. Kulma on siis,4 60 864 a) 576 864 0,88m. a) α b 0,6769... 0,68 (rad) r,m 8cm β,90...,9 (rad) 4cm a) α 0,68 (rad) β,9 (rad). a) 5,0
Päätöspöytäkirja 20/2018
 Päätöspöytäkirj 2/218 Päätöspvm 7.6.218 Yleishllinto Porin kupunki Sivistystoimil Dnro PORI/182/12.4.1/218 Yhteiset plvelut -yksikön päällikkö Otsikko Krhuhllin tlvikuden 1.1.218-.4.219 tphtumt, konsertit,
Päätöspöytäkirj 2/218 Päätöspvm 7.6.218 Yleishllinto Porin kupunki Sivistystoimil Dnro PORI/182/12.4.1/218 Yhteiset plvelut -yksikön päällikkö Otsikko Krhuhllin tlvikuden 1.1.218-.4.219 tphtumt, konsertit,
1. Olkoot vektorit a, b ja c seuraavasti määritelty: a) Määritä vektori. sekä laske sen pituus.
 Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
ää*r: rfrtlqäe'räs rr[; äsüä FäF r."f F'*üe ;=v* tr, $rr;gt :r1 älfese li ä; äepö* l4:e x1;'.äö l--g! li r: ; ;;*; ssü ntirs E,pä ;;qi?
 j X \: c : 1:8" : Z : : ) ) c 1 T [ b[ ]4 ) < c 1 ü ]T G \\ e p > : [ : e L [? p 2 9 Z S: c? [:? " : e :: [ : >9 Y :[ p e ß < 1 9 1 \ c 4 > ) 1 :91$ :e h b 1 6 " ö:p:?e S9e R ü e $ :1 ee \ eö 4:e 1ö X
j X \: c : 1:8" : Z : : ) ) c 1 T [ b[ ]4 ) < c 1 ü ]T G \\ e p > : [ : e L [? p 2 9 Z S: c? [:? " : e :: [ : >9 Y :[ p e ß < 1 9 1 \ c 4 > ) 1 :91$ :e h b 1 6 " ö:p:?e S9e R ü e $ :1 ee \ eö 4:e 1ö X
- Zj + +i, virittämän suunnikkaan pinta-ala. 2x + Y: 4. 3x 2y:2 -x+y:-1. 3x + y:5. -x +2y:2. 4x + Y: 4. voitto : qr Aq+ rr q. : -!A_'r.
 Vaasan yliopisto, syksy 2014 Lineaarialgebra, MAH. lo4o 7. harjoitus, (viikko 2, 5.1.-9.1.2015 R01: ma 12-14 Dl15, R02: ke 14-16 D115, R03: to 10-12 F651 Viimeisellä luennolla käsiteltiin opetusmonisteen
Vaasan yliopisto, syksy 2014 Lineaarialgebra, MAH. lo4o 7. harjoitus, (viikko 2, 5.1.-9.1.2015 R01: ma 12-14 Dl15, R02: ke 14-16 D115, R03: to 10-12 F651 Viimeisellä luennolla käsiteltiin opetusmonisteen
= ( F dx F dy F dz).
 17 VEKTORIANALYYSI Luento 2 3.4 Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin
17 VEKTORIANALYYSI Luento 2 3.4 Vektorikentän käyräintegraali Voiman tekemä työ on matka (d) kertaa voiman (F) projektio liikkeen suunnassa, yksinkertaisimmillaan W Fd. Jos liike tapahtuu käyrää pitkin
Kokeile ilmaiseksi mafyvalmennus.fi/mafynetti. Valmistaudu täydellisesti lääkiksen pääsykokeeseen! Miten opit parhaiten?
 Miten opit parhaiten? Valmistaudu täydellisesti lääkiksen pääsykokeeseen! n Voit harjoitella kotoa käsin huippusuositulla Mafynetti-ohjelmalla. Mukaan kuuluu 4 täysimittaista harjoituskoetta!! n Harjoittelu
Miten opit parhaiten? Valmistaudu täydellisesti lääkiksen pääsykokeeseen! n Voit harjoitella kotoa käsin huippusuositulla Mafynetti-ohjelmalla. Mukaan kuuluu 4 täysimittaista harjoituskoetta!! n Harjoittelu
Peitelevy ja peitelaippa
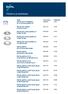 Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
Peitelevy ja peitelaippa Tuote LVI-numero Pikakoodi PEITELAATTA MERIKA 5688050 JF92 50-75-110/VALKOINEN 510 PEITELEVY ORAS D70/G1/2 167051 PEITELEVY KAULUKSELLA 50 MM-130 MM PEITELEVY KAULUKSELLA 75 MM-150
SAMMONKATU SAMMONKATU JAAKON- SARVI- KATU SARVIJAAKONKATU 1: Kalevanrinteen katujen yleissuunnitelma, Liite 3 Asemapiirros 1/4
 KTOS L:\PROJEKTT_2012\1510001046 KLEVRTEE KTUJE YS\14_TULOKSET\3.KTUJE YLESSUUTELM\DWG\KLEVRE YS.DWG Tulostettu: 26.6.2013 n- JO KELLR- SR- JKO- KTU SMMOKTU PYSÄKÖT KORTTEL 4 +100,60 KSPHT 1/2 BUS (varaus)
KTOS L:\PROJEKTT_2012\1510001046 KLEVRTEE KTUJE YS\14_TULOKSET\3.KTUJE YLESSUUTELM\DWG\KLEVRE YS.DWG Tulostettu: 26.6.2013 n- JO KELLR- SR- JKO- KTU SMMOKTU PYSÄKÖT KORTTEL 4 +100,60 KSPHT 1/2 BUS (varaus)
MS-A0204 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa
 MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
MS-A24 Differentiaali- ja integraalilaskenta 2 (ELEC2) Luento 9: Muuttujanvaihto taso- ja avaruusintegraaleissa Antti Rasila Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Kevät 216 Antti Rasila
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Harjoitus 2 ( )
 Harjoitus 2 (24.3.2015) Tehtävä 1 Figure 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[0] = 0 v[p] max 0 i p 1 {v[i]+a i (i,p) E} = v[l]+a l d[p] l. Muodostetaan taulukko, jossa
Harjoitus 2 (24.3.2015) Tehtävä 1 Figure 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[0] = 0 v[p] max 0 i p 1 {v[i]+a i (i,p) E} = v[l]+a l d[p] l. Muodostetaan taulukko, jossa
KUNNALLISTEKNINEN SELVITYS. Asemakaava nro Särkänniemen alueen asemakaavan muutoksen aiheuttamat johto- ja putkisiirrot 1 (3) 7.6.
 Särä l v h jh- j rr () UALLST SLTYS Särä l v h jh- j rr Av r J Sv,., A-öör Sl O A-öör O., www..f Y- - Särä l v h jh- j rr () Rr lj Rr ällää Särä l v h läö, vjhj j jävvärd l j v v lj ljj ll lj. Lj v jl
Särä l v h jh- j rr () UALLST SLTYS Särä l v h jh- j rr Av r J Sv,., A-öör Sl O A-öör O., www..f Y- - Särä l v h jh- j rr () Rr lj Rr ällää Särä l v h läö, vjhj j jävvärd l j v v lj ljj ll lj. Lj v jl
Harjoitus 2 ( )
 Harjoitus 2 (27.3.214) Tehtävä 1 7 4 8 1 1 3 1 2 3 3 2 4 1 1 6 9 1 Kuva 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[] = v[p] d[p] l. max i p 1 {v[i] + a i (i, p) E} = v[l] +
Harjoitus 2 (27.3.214) Tehtävä 1 7 4 8 1 1 3 1 2 3 3 2 4 1 1 6 9 1 Kuva 1: Tehtävän 1 graafi. Aikaisimmat aloitushetket selvitetään kaavoilla v[] = v[p] d[p] l. max i p 1 {v[i] + a i (i, p) E} = v[l] +
y (0) = 0 y h (x) = C 1 e 2x +C 2 e x e10x e 3 e8x dx + e x 1 3 e9x dx = e 2x 1 3 e8x 1 8 = 1 24 e10x 1 27 e10x = e 10x e10x
 BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
BM0A5830 Differentiaaliyhtälöiden peruskurssi Harjoitus 4, Kevät 017 Päivityksiä: 1. Ratkaise differentiaaliyhtälöt 3y + 4y = 0 ja 3y + 4y = e x.. Ratkaise DY (a) 3y 9y + 6y = e 10x (b) Mikä on edellisen
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus
 MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
MS-A0202 Differentiaali- ja integraalilaskenta 2 (SCI) Luento 1: Parametrisoidut käyrät ja kaarenpituus Antti Rasila Aalto-yliopisto Syksy 2015 Antti Rasila (Aalto-yliopisto) MS-A0202 Syksy 2015 1 / 18
g - s Eä;t;i;s!itää# EiäErE ii:ääg Eä E *läeäfiäeräsil* E sis $ä äce:;!ääfät ;1*iEs ;tää:gi g;ää*f ;ij !äef ä:e'geä;:ä Elä tä Efiäilii: ; g E
 H!äf ä'gä;ä lä tä fäl ; $ä äc;!ääfät ;1* ;tääg ä;t;;!tää# är ääg ä *läääeräl* tä*äätäääägtätg B g - ü ;;*ä9äää g;ää*f ' g ;j ä u e *; t t ;; t ü t p ä; u ä; e r * g t g U ).l t r A ä O.* 6) l- C ) t n
H!äf ä'gä;ä lä tä fäl ; $ä äc;!ääfät ;1* ;tääg ä;t;;!tää# är ääg ä *läääeräl* tä*äätäääägtätg B g - ü ;;*ä9äää g;ää*f ' g ;j ä u e *; t t ;; t ü t p ä; u ä; e r * g t g U ).l t r A ä O.* 6) l- C ) t n
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
KJR-C1001 Statiikka ja dynamiikka Luento 15.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinematiikka: asema, nopeus ja kiihtyvyys (Kirjan luvut 12.1-12.5, 16.1 ja 16.2) Osaamistavoitteet Ymmärtää
Ruskon Laakeritie 22
 äi äättä Rs Lri lvsitrstl.... g Sittll sijitt rär rl vl-lll (), issä dll sj vl-l (.) ltvll. lvdt lsvt Rsj yyösjärv j sjärv tt rär. sj vl-l it-l ~ l-l äi äättä.. g Lri vl-lt äi äättä Al läisyydssä lss lv
äi äättä Rs Lri lvsitrstl.... g Sittll sijitt rär rl vl-lll (), issä dll sj vl-l (.) ltvll. lvdt lsvt Rsj yyösjärv j sjärv tt rär. sj vl-l it-l ~ l-l äi äättä.. g Lri vl-lt äi äättä Al läisyydssä lss lv
POHJAISTUKAN TIIVISTE GBG
 WC-varaosat Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG 5652536 LA37 NORDIC 2300/2200 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K KIMSET 6405400001 TREVI/VIVA 9159200001 SEVEN D
WC-varaosat Tuote LVI-numero Pikakoodi POHJAISTUKAN TIIVISTE GBG 5652536 LA37 NORDIC 2300/2200 HUUHTELUVENTT. TIIVISTE GBG NORDIC 2300/2200 T II/ T I/ K KIMSET 6405400001 TREVI/VIVA 9159200001 SEVEN D
DDD. g;, lt/' l-1ä. tv~ :J-/?t--q-.-,~)- --,L:: / o D E D F D G D. ~tto f ja k;n[js. tä~ttoet ) tj} J-d-LtJ;tJf'-tt.// p.
 ".E f /,,, f:r. :ro 7-. "l"z / f 2. 2 4 CJ ~- /t-f ARKEOLOGISEN KOHTEEN TARKASTUS DDD Tunnistetiedot / j Kunta:!:flal'/i Pr e.vi_ Inventointinumero: - -------- Alue: t)t-,-7 ' Luokka:---=/=/=----:-------
".E f /,,, f:r. :ro 7-. "l"z / f 2. 2 4 CJ ~- /t-f ARKEOLOGISEN KOHTEEN TARKASTUS DDD Tunnistetiedot / j Kunta:!:flal'/i Pr e.vi_ Inventointinumero: - -------- Alue: t)t-,-7 ' Luokka:---=/=/=----:-------
> 40 db > 45 db > 50 db > 55 db > 60 db > 65 db > 70 db > 75 db
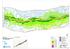 Pet jr t Kvm Kr Hyyr yl Sr m Hm Ko e o LIITE.. Mtede melelvty 0 Yömelto (etore: m) Ortmp Petmo Immo Kop Rto Tehr Rö Voe Lepelto Pr Ptlh Rm Kymht Netytem Vroj Prorp Sem Rto Tlllo Vtter Sotmp It-Sto M Korvet
Pet jr t Kvm Kr Hyyr yl Sr m Hm Ko e o LIITE.. Mtede melelvty 0 Yömelto (etore: m) Ortmp Petmo Immo Kop Rto Tehr Rö Voe Lepelto Pr Ptlh Rm Kymht Netytem Vroj Prorp Sem Rto Tlllo Vtter Sotmp It-Sto M Korvet
KUIVANIEMI JOKIKYLÄ VESKANKANGAS (KUIVANIEMI 3 VESKANKANKANGAS)
 KUIVANIEMI JOKIKYLÄ VESKANKANGAS (KUIVANIEMI 3 VESKANKANKANGAS) Selvitys V. Luhon vuonna 958 suorittamasta kaivauksesta kivikautisella asuinpaikalla Tuija Wallenius 989 Vuonna 958 Ville Luho suoritti tutkimuksia
KUIVANIEMI JOKIKYLÄ VESKANKANGAS (KUIVANIEMI 3 VESKANKANKANGAS) Selvitys V. Luhon vuonna 958 suorittamasta kaivauksesta kivikautisella asuinpaikalla Tuija Wallenius 989 Vuonna 958 Ville Luho suoritti tutkimuksia
