Suora fotonituotto suurienergiaisissa ydintörmäyksissä sähkömagneettisen ja vahvan vuorovaikutuksen

Transkriptio

1 Suora fotonituotto suurienergiaisissa ydintörmäyksissä sähkömagneettisen ja vahvan vuorovaikutuksen kertaluvussa Ç «Ñ «Ë µ Tatu Mustonen Pro Gradu Ohjaaja Prof. Kari J. Eskola Jyväskylän yliopisto Fysiikan laitos Kevät 203

2

3 Sisältö Kiitokset 5 2 Tiivistelmä 6 3 Johdanto 7 4 Vaikutusala 8 5 Suoran fotonituoton mekanismit raskasionitörmäyksissä 0 5. Kinematiikkaa Suoran fotonituoton vaikutusalat 4 6. Fragmentaatiofotonien vaikutusala Nopeiden fotonien vaikutusalat Partonijakaumat 9 7. Protonin partonijakaumat Protonia raskaampien ytimien partonijakaumat Fotonien fragmentaatiofunktiot 22 9 Määritettäviä suureita 25 0 Numeeriset menetelmät Ohjelmallinen toteutus Numeerinen integrointimenetelmä Tulokset 28. Suoran fotonituoton tuloksia LHC-kiihdyttimelle Vaikutusalojen suhteita Ê ½ ¾ Suoria fotoneja prosessista È È Johtopäätökset ja yhteenveto 52 3 Liitteet Laskusääntöjä Spin ½ -hiukkasille tarvittavia laskusääntöjä ¾ 3.3 Sähkömagneettisen ja vahvan vuorovaikutuksen Feynmanin säännöt Esimerkki 2 2-prosessin vaikutusalalaskusta Gaussin integrointimenetelmä käytännössä Ohjelman tärkeimmät moduulit

4

5 Kiitokset Haluan kiittää työn aiheesta ja ohjaamisesta professori Kari J. Eskolaa, sekä perhettä, ystäviä ja tuttavia kaikesta mahdollisesta tuesta, jota olen opiskeluissani saanut. 5

6 2 Tiivistelmä Tämä fysiikan Pro Gradu -tutkielma käsittelee suoraa fotonituottoa suurienergiaisissa ydintörmäyksissä sähkömagneettisen ja vahvan vuorovaikutuksen kertaluvussa Ç «Ñ «Ë µ. Kyseisessä kertaluvussa suora fotonituotto jakaantuu kahteen nopeaan prosessiin ja kahdeksaan fragmentaatioprosessiin. Tässä työssä lasketaan näiden suoran fotonituoton prosessien teoreettiset vaikutusalat ja verrataan näiden ennusteita viimeisimpiin LHC-kiihdyttimeltä mitattuihin suoran fotonituoton tuloksiin. Osoittautuu, että teoreettiset vaikutusalat vastaavat todella hyvin mittaustuloksia. Teoreettisia ja mitattuja vaikutusaloja verrataan toisiinsa laskemalla näiden suhdetta kuvaavat K-tekijät virherajoineen, joiden perusteella nähdään, että fragmentaatio-osuuden vaikutus suoraan fotonituottoon on merkittävä. Lisäksi tutkitaan protoni protoni-sironnan kautta syntyvien suorien fotonien vaikutusalojen suhteita raskasionitörmäyksien vaikutusaloihin sironnoista Ô È, È È, Ù ja Ù Ù. Työssä on käytetty ydinmodifikaatiofunktioita EPS09[2], EKS98[3] ja EPS08[4]. Näiden lisäksi lasketaan K-tekijät eri ydinmodifikaatioilla sironnalle È È käyttämällä CMSkollaboraation mittausdataa [29]. Tulokset osoittavat, että ydinmodifikaatioilla on tärkeä vaikutus laskettaessa teoreettista suoran fotonituoton vaikutusalaa suurienergiaisille raskasionitörmäyksille. 6

7 3 Johdanto Hiukkasfysiikan Standardimallin teoriaan kuuluu kaksi erillistä osaa, nämä ovat sähköheikko yhtenäisteoria ja kvanttiväridynamiikka eli QCD. Sähköheikko yhtenäisteoria puolestaan jakautuu kahdeksi osaksi, joita ovat heikkoja vuorovaikutuksia kuvaava teoria sekä sähkömagneettisia ilmiöitä kuvaava teoria kvanttisähködynamiikka, QED 2. Hiukkasfysiikan Standardimalli on äärimmäisen vahva ja tarkasti luontoa kuvaileva teoriakokonaisuus, fysiikan vuorovaikutuksista ainoastaan gravitaatioilmiöt eivät sisälly Standardimalliin. Standardimalli on ehkäpä ihmiskunnan tarkimmin testattu teoriakokonaisuus. Myös tässä Pro Gradu -tutkielmassa tutkitaan sähkömagneettisen ja vahvan vuorovaikutuksen teorioiden ennusteita sekä verrataan näitä tuloksia viimeisimpiin hiukkaskiihdytinkokeiden tuloksiin. Tutkimuskohteena on suora fotonituotto suurienergiaisista ydintörmäyksistä. Suoran fotonituoton tutkimuksessa yhdistyvät atomiydinten vahvan vuorovaikutuksen ilmiöt sähkömagneettisen vuorovaikutuksen välittäjähiukkasen, fotonin, syntymiseen. Hiukkaskiihdytinkokeiden suoran fotonituoton mittaukset voivat antaa arvokasta tietoa vahvan vuorovaikutuksen hiukkasten, kvarkkien, antikvarkkien ja näitä toisiinsa sitovien gluonien jakaumista atomiytimissä. Suora fotonituotto voi auttaa myös viimeaikaisissa CERN- LHC 3 :n hiukkaskiihdytinkokeissa havaitun Standardimallin Higgsin hiukkasen [] hajoamismekanismien ymmärtämisessä, koska ATLAS- ja CMS-kollaboraatioiden [2], [3] mittauksissa Higgsin hiukkasen hajoaminen kahdeksi fotoniksi on osoittautunut yhdeksi selkeimmistä hajoamiskanavista. Tämän Pro Gradu -tutkielman tarkoituksena on jatkaa erikoistyössä [4] aloitettu suoran fotonituoton tutkimusta. Suorilla fotoneilla tarkoitetaan fotoneja, jotka muodostuvat vahvan vuorovaikutusten sirontaprosessien kautta, eivätkä esimerkiksi jonkin hiukkasen hajoamistuotteena. Erikoistyössä rajoituttiin tutkimaan suoraa fotonituottoa kahdesta perusprosessista, QCD-Compton-sironta ja kvarkki antikvarkki-parin annihilaatio, ja näistä syntyvän fotonin sirontaa ¼ Æ kulmaan törmääviin ytimiin nähden. Näiden kahden prosessin kautta syntyviä suoria fotoneja kutsutaan nopeiksi fotoneiksi, johtuen englannin kielen termistä prompt photons. Tässä työssä jatketaan näiden nopeiden fotonien analyysiä myös muissa sirontakulmissa, ja lisäksi suorien fotonien analyysiin sisällytetään niin sanotut fragmentaatiofotonit. Fragmentaatiofotonit syntyvät suurienergiaisissa ydintörmäyksissä, kun törmäävien atomiytimien sisältämät kvarkit, antikvarkit ja gluonit, muodostavat sirontaprosessin kautta vahvan vuorovaikutuksen hiukkasen, joka säteilee fotonin. Tässä työssä tullaan näkemään, että fragmentaatiofotonit muodostavat merkittävän osuuden suoran fotonituoton vaikutusalasta. Toisinaan tässä Engl. Quantum chromodynamics = Kvanttiväridynamiikka. 2 Engl. Quantum electrodynamics = Kvanttisähködynamiikka. 3 LHC = Large Hadron Collider. 7

8 työssä viitataan nopeisiin fotoneihin lyhenteellä (LO, lowest order ) ja fragmentaatiofotoneihin lyhenteellä (frag). Suoran fotonituoton ymmärtämiseksi tarvitaan sekä sähkömagneettisen että vahvan vuorovaikutuksen ilmiöitä. Näistä ensimmäinen kuvaa sähkömagneettisen säteilyn, fotonien, ja sähköisesti varattujen spin ½ -hiukkasten, fermionien, välistä ¾ dynamiikkaa. Vähintään yhtä tärkeässä osassa tässä työssä on vahvan vuorovaikutuksen ilmiöt, jotka vaikuttavat kvarkkien ja antikvarkkien, jotka ovat spin ½ ¾ - hiukkasia, ja näitä toisiinsa sitovien gluonien välillä. Vahvaa vuorovaikutusta kuvaavan QCD-teorian perusta on että kvarkit, antikvarkit ja gluonit eivät esiinny luonnossa vapaina itsenäisinä hiukkasina, vaan ne esiintyvät QCD-värineutraaleissa kahden tai kolmen kvarkin tai antikvarkin yhdistelminä. Kvarkki antikvarkki-kombinaation yhdistelmiä kutsutaan mesoneiksi ja kolmen kvarkin yhdistelmiä baryoneiksi. Yhteisesti mesoneita ja baryoneita kutsutaan hadroneiksi. Tunnetuimmat hadronit ovat protoni ja neutroni, joista atomiytimet koostuvat. Protonin perusrakenne muodostuu kahdesta u-kvarkista ja yhdestä d-kvarkista sekä neutronin kahdesta d-kvarkista ja yhdestä u-kvarkista, ja näitä kutsutaan protonin ja neutronin valenssikvarkeiksi. Protonin ja neutronin perusrakenteessa on siis kaksi kvarkkimakua, u- ja d-kvarkit. Vaikka protoni ja neutroni koostuvat perusrakenteeltaan u- ja d-kvarkeista, niin silti nämä hadronit sisältävät myös muut tunnetut kvarkkimaut, joita ovat s-, c-, b- ja t-kvarkit. Nämä niin sanotut merikvarkit saadaan hadroneista esille, kun hadroneita kiihdytetään erittäin lähelle valon nopeutta, jolloin valenssikvarkkeihin kytkeytyneisiin gluoneihin muodostuu kvarkki antikvarkki-silmukoita, joissa merikvarkit voivat esiintyä. Merikvarkkien esiintyvyyteen vaikuttaa merkittävästi energiaskaala, jolla näitä hiukkasia pyritään löytämään, esimerkiksi b- ja t-kvarkkien vaikutus tulee näkyviin vasta, kun näille kvarkeille ominaiset massakynnykset ylittyvät. Nämä skaalat ovat Ñ ¾ Î ja Ñ Ø ½ Î [5]. Kvarkkeja, antikvarkkeja ja gluoneja kutsutaan yhteisnimeltään partoneiksi ja näiden jakaumia atomeissa partonijakaumiksi. Partonijakaumat kuvaavat partonien lukumäärätiheyttä hadronissa energiaskaalan ja liikemääräosuuden funktioina. Partonin liikemääräosuus lasketaan tässä alkuperäisen hadronin liikemäärästä. Eräs tämän työn motiiveista on tutkia, miten ydinpartonijakaumat vaikuttavat suorien fotonien syntymiseen suurienergiaisissa raskasionitörmäyksissä. 4 Vaikutusala Hiukkas- ja ydinfysiikassa hiukkasvuorovaikutusten todennäköisyyttä kuvaa vaikutusala, jota merkitään yleensä kreikkalaisella kirjaimella. Vaikutusalalla tarkoitetaan sirontatapahtumien ½ Ò lukumäärää aikayksikössä yhtä kohtiohiukkasta kohti, jaettuna sisään tulevien ammushiukkasten vuolla. 8

9 Hiukkasten ja vuorovaikutusten kautta syntyy Ò kappletta hiukkasia. Käytännössä vaikutusala riippuu törmäävistä hiukkastyypeistä ja, hiukkasvuorovaikutusten voimakkuudesta sekä hiukkasten ja törmäysenergioista. Vaikutusalan dimensio on sama kuin pinta-alan dimensio. Hiukkasfysiikassa käytetään yleensä yksikköjärjestelmää, jossa luonnonvakiot asetetaan ykkösiksi, ½ Tällöin mitattavien suureiden yksikkö on jokin energian potenssi elektronivoltteina. Vaikutusalan dimensio käytettäessä tätä yksikköjärjestelmää on Î ¾. Törmäysprosessissa ½ Ò kvanttimekaaniset hiukkaset ja törmäävät toisiinsa erittäin suurella energialla, jolla tarkoitetaan, että hiukkaset törmäävät toisiinsa lähes valon nopeudella. Merkitään hiukkasten ja energioita ja liikemääriä 4-liikemäärien avulla Ô p µ ja Ô p µ, missä ja ovat hiukkasten energiat sekä p ja p 3-komponenttiset liikemäärät. Sivulla 59 yhtälössä (32) on määritelty nelivektorien sisätulo, jonka avulla saadaan törmääville hiukkasille ja massan, energian ja liikemäärän relaatiot Ñ ¾ Ô ¾ ¾ p ¾ ja Ñ ¾ Ô ¾ ¾ p ¾. Vastaavasti sirontaprosessissa syntyvien hiukkasten 4-liikemäärät ovat ¼k µ ½ Ò, missä ¼ ja k ovat :nnen hiukkasen energia ja 3-liikemäärä. Differentiaalinen vaikutusala sirontaprosessille ½ Ò [6, s.808] on Å Ò ¾ Ò Å Ò ¾ ¾ ¾ Ú Ú Ò ½ k Ò ¾µ ¾ ¼ ¾µ Æ µ Ô Ô µ () missä Å Ò ¾ on spin- ja väri-keskiarvoistettu sironta-amplitudin neliö, törmäävien hiukkasten ja vuotekijä ja Ò lopputilan hiukkasten faasiavaruuselementti. Sironta-amplitudin Å Ò kirjoittamiseksi matematiikan kielelle tarvitaan kvanttikenttäteorioiden Feynmanin sääntöjä, joita sovelletaan kussakin törmäysprosessissa erikseen. Tässä työssä tutkitaan fotoneja, jotka syntyvät atomiydinten kvarkkien ja gluonien sironnoissa, joten tässä työssä tarvitaan sekä sähkömagneettisen että vahvan vuorovaikutuksen Feynmanin sääntöjä. Nämä löytyvät tämän tutkielman liitteistä sivulta 6 kuvasta 36 sekä sivulta 62 kuvasta 37. Vaikutusalassa () esiintyvässä vuotekijässä ¾ ¾ Ú Ú tekijä Ú Ú edustaa törmäävien hiukkasten ja nopeuksia suhteessa toisiinsa. Vuotekijä voidaan ilmaista vaikutusalalaskujen kannalta käytännöllisemmässä Õ muodossa hiukkasten ja 4-liikemäärien ja massojen avulla, Ô Ô µ ¾ Ñ ¾ Ñ ¾, tämän laskun tarkemmat yksityiskohdat ovat liitteiden sivulla 59 yhtälössä (34). 9 ½

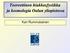
10 Faasiavaruuselementissä Ò esiintyy kunkin lopputilan hiukkasen ½ Ò differentiaalinen liikemääräelementti muodossa, jossa k on hiukkasen 3- k ¾µ ¾ ¼ liikemäärä ja ¼ energia. Elementissä esiintyvä neliulotteinen deltafunktio Æ µ Ô Ô È Ò ½ µ kuvaa energian ja liikemäärän säilymistä sirontaprosessissa, missä siis Ô, Ô ja È Ò ½, ovat kaikkien sirontaprosessissa mukana olevien hiukkasten 4-liikemäärät. 5 Suoran fotonituoton mekanismit raskasionitörmäyksissä Suoran fotonin muodostuminen suurienergiaisesta raskasionitörmäyksestä voi tapahtua kahdella tavalla, joko siten, että fotoni on suoraan osallisena sirontaprosessissa tai siten, että vahvan vuorovaikutuksen sironnassa tuotettu kvarkki tai gluoni säteilee fotonin. Prossessia, jossa fotoni on suoraan osallisena sirontaprosessissa kutsutaan nopeaksi fotoniksi ja jälkimmäisessä tapauksessa syntynyttä fotonia fragmentaatiofotoniksi. Molemmissa tapauksissa suoran fotonituoton sironnat sisältävät sekä vahvan että sähkömagneettisen vuorovaikutuksen ilmiöitä. Suora fotonituotto on teoreettisen tutkimuksen kannalta erinomainen prosessi vahvan vuorovaikutuksen prosessien tutkimiseen, koska prosesseissa syntyvien fotonien fysikaaliset ominaisuudet ovat tarkasti mitattavissa. Tässä työssä sekä nopeat prosessit että fragmentaatioprosessit ovat efektiivisesti verrannollisia vahvan vuorovaikutuksen kytkinvakioon «Ë ¾ Ê µ, jossa ¾ Ê on prosessin vuorovaikutusenergian skaala, ja sähkömagneettisen vuorovaikutuksen voimakkuuteen «Ñ ¾ ½ ½ vuorovaikutusten kertaluvussa Ç «Ñ «Ë µ. Fragmentaation kautta syntyvien fotonien vaikutusalalaskut noudattavat pääpiirteittäin julkaisussa [7] esitettyjä vaikutusalalaskuja, joissa fragmentoituva hiukkanen on hadroni. Häiriöteoreettisesti hiukkasten vuorovaikutusmekanismit voivat sisältää äärettömiä suureita, jotka voidaan sisällyttää QCD:n faktorisaatioteoreeman perusteella partonijakaumien ja fragmentaatiofunktioiden määrittelyihin. QCD:n faktorisaatioteoreeman mukaan suoran fotonituoton vaikutusala fragmentaation kautta on ½ ¾ frag ½ Ü ½ É ¾ µ ¾ Ü ¾ É ¾ µ Ü ½ Ü ¾ É ¾ «Ë ¾ Ê µµ Þ ¾ µ (2) missä atomiytimistä ½ ja ¾ peräisin olevat partonit ja muodostavat partonitason sirontaprosessin kautta hiukkasen, joka säteilee fotonin. Vaikutusalassa (2) esiintyvät funktiot ½ Ü ½ É ¾ µ ja ¾ Ü ¾ É ¾ µ ovat partonien ja ydinpartonijakaumia, joissa Ü ½ ja Ü ¾ ovat partonien ja 4-liikemääräosuudet ydinten ½ ja ¾ 4-liikemääristä ja partonijakaumien energiaskaala on É ¾. Fragmentaatiofunktiossa Þ ¾ µ muuttuja Þ on fotonin ja hiukkasen ener- 0

11 È ½ ½ Ô ½ Ü ½ È ½ Ô ½ Ü ½ É ¾ µ Ë Õ Þ ¾ µ ¾ Ü ¾ É ¾ µ Ë Ô ¾ Ü ¾ È ¾ Ô È ¾ ¾ Kuva : Esimerkki fragmentaatiofotonin synnystä prosessista ½ ¾, jossa atomiytimien ½ ja ¾ sironnan kautta syntyy fotoni ja joukko muita hiukkasia. Kuvassa ytimien ½ ja ¾ 4-liikemäärät ovat È ½ ja È ¾, jolloin näistä ytimistä peräisin olevat partonit ja, 4-liikemääriltään Ô ½ ja Ô ¾, vuorovaikuttavat vahvan vuorovaikutuksen Ë «Ë Ë ¾ µ kautta muodostaen 2 2-sironnan kautta lopputilaan kaksi kvarkkia, 4-liikemäärillä Ô ja Ô, joista toisesta fragmentoituu fotoni. Funktiot ½ Ü ½ É ¾ µ ja ¾ Ü ¾ É ¾ µ ovat alkutilan partonien ja partonijakaumia liikemääräosuuksilla Ü ½ ja Ü ¾ sekä energiaskaalalla É ¾. Fotonin fragmentaatiota kvarkista kuvaa funktio Õ Þ ¾ µ, missä Þ on fotonin energiaosuus kvarkin energiasta, josta fotoni muodostuu, sekä ¾ on fragmentaation energiaskaala. Vahvan vuorovaikutuksen kytkinvakio «Ë ¾ Ê µ on myös riippuvainen vuorovaikutuspisteen kautta kulkevasta energiasta ¾ Ê. gioiden suhde, ja ¾ on fragmentaation energiaskaala. Kuvassa on esimerkki vaikutusalan (2) mukaisesta fragmentaatiofotonin synnystä. Erikoistyössä [4] käsiteltiin kahta nopeaa prosessia, joiden kautta suora fotoni yleisimmin syntyy, nämä prosessit ovat QCD-Compton-sironta ja kvarkki antikvarkki-parin annihilaatio. Näihin prosesseihin viitataan englanninkielisissä artikkeleissa termillä prompt photon, joka tarkoittaa nopeaa fotonia. Nopeiden fotonien vaikutusala QCD:n faktorisaatioteoreeman mukaan on ½ ¾ prompt ½ Ü ½ É ¾ µ ¾ Ü ¾ É ¾ µ Ü ½ Ü ¾ É ¾ «Ë ¾ Ê µµ (3) missä eroaa fragmentaatiofotonien vaikutusalassa (2) esiintyvästä siten, että nopeat fotonit syntyvät suoraan 2 2-sirontaprosesseista eivätkä sironnan jälkeisestä fragmentaatiosta. Kuvassa 2 on nopean fotonituoton periaate QCD-Compton-sironnasta.

12 È ½ ½ Ô ½ Ü ½ È ½ Õ ½ Ü ½ É ¾ µ Õ ¾ Ü ¾ É ¾ µ Ë Ô ¾ Ü ¾ È ¾ Ô È ¾ ¾ Kuva 2: Esimerkkisironta nopean fotonin synnystä QCD-Compton-sironnan kautta. Atomiytimestä ½ peräisin oleva kvarkki vuorovaikuttaa atomiytimestä ¾ peräisin olevan gluonin kanssa, jolloin lopputilaan muodostuu kvarkki ja fotoni. Symbolien selitykset ovat vastaavat kuin kuvassa, mutta lisäksi syntyvän fotonin sähkömagneettista vuorovaikutuspistettä kuvaa Õ, jossa on alkeisvaraus ja Õ kvarkin murtolukuvaraus, sekä Õ fotonin 4-liikemäärä. 5. Kinematiikkaa Tässä työssä nopeiden fotonien tuotto tapahtuu 2 2-sirontojen kautta vuorovaikutuksien kertaluvussa Ç «Ñ «Ë µ, mikä tarkoittaa, että alkutilassa kaksi partonia vuorovaikuttavat keskenään ja lopputilaan syntyy kaksi hiukkasta, joista toinen on fotoni. Alkutilan vuorovaikuttavat partonit ovat peräisin atomiytimistä ½ ja ¾, joilla on 4-liikemäärät È ½ È ¼ ½ P ½µ ja È ¾ È ¼ ¾ P ¾µ. Hiukkaskiihdytinkokeissa atomiytimien kiihdytysenergia esitetään niin sanotun Mandelstamin muuttujan avulla, joka on È ½ È ¾ µ ¾ Ytimien ½ ja ¾ massakeskipistekoordinaatisto määritellään relaatiolla P ½ P ¾ ¼, jonka sijoittamalla muuttujaan ja valitsemalla törmäävien ytimien liikesuunnaksi z-akselin suunta saadaan Ô È ¼ ½ È ¼ ja ¾ Ô Ô È ½ È ¼ P ½ ½µ Ô ¾ ¼ ¼ ¾ Ô µ È ¾ È ¼ P ¾ ¾µ ¾ ¼ ¼ µ (4) ¾ Atomiydinten törmäyksessä ydinten sisältämät kvarkit ja gluonit, jotka siis muodostavat osan ydinten 4-liikemääristä, pääsevät vuorovaikuttamaan keskenään. 2

13 Olkoon ytimestä ½ peräisin olevan partonin 4-liikemäärä Ô ½ ja ytimestä ¾ peräisin olevan Ô ¾. Näiden partonien 4-liikemäärät ovat ytimien ½ ja ¾ (4) avulla ilmaistuna seuraavasti Ô Ô Ô ½ Ü ½ È ½ Ü ½ ¾ ¼ ¼ Ü ½ Ô ¾ Ô µ Ô ¾ Ü ¾ È ¾ Ü ¾ ¾ ¼ ¼ Ü ¾ µ (5) ¾ missä Ü ½ ja Ü ¾ ovat 4-liikemääräosuuksia ydinten ½ ja ¾ 4-liikemääristä, ja Ü ½ Ü ¾ ¾ ¼ ½. Tässä siis oletetaan törmäävien partonien liikkuvan samansuuntaisesti emoytimien kanssa. Tässä työssä käsitellyt partonien sironnat ovat 2 2-sirontoja. Merkitään kyseisessä sirontaprosessissa syntyvien hiukkasten 4-liikemääriä Ô Ô µ Ô Ü Ô Ý Ô Þ µ Ô Ô µ Ô Ü Ô Ý Ô Þ µ (6) missä ja ovat syntyvien hiukkasten energiat sekä Ô Ô Ü Ô Ý Ô Þ µ ja Ô Ô Ü Ô Ý Ô Þ µ 3-liikemäärävektorit. Vaikutusalalaskujen kannalta käytännöllinen kinemaattinen muuttuja on pitkittäissuuntainen rapiditeetti Ý ½ ÔÞ ¾ ÐÒ Ô Þ ØÒ ½ ÔÞ (7) missä on hiukkasen energia ja Ô Þ z-akselin suuntainen liikemääräkomponentti. Määrittelemällä 2 2-törmäyksessä syntyville hiukkasille poikittaisliikemäärävektorit Ô Ì Ô Ü Ô Ý µ ja Ô Ì Ô Ü Ô Ý µ, sekä käyttämällä rapiditeetin määritelmää (7) voidaan 4-liikemäärät (6) kirjoittaa muodossa Ô Ô µ Ô Ì Ó Ý Ô Ì Ô Ì Ò Ý µ Ô Ô µ Ô Ì Ó Ý Ô Ì Ô Ì Ò Ý µ (8) Todellisessa hiukkaskiihdytinkokeessa törmäävillä ytimillä voi olla hieman poikittaisliikemäärää, mutta tässä oletetaan, että alkuperäisillä ytimillä ½ ja ¾ ei ole poikittaisliikemääriä. Tällöin liikemäärän säilymislain perusteella on Ô Ì Ô Ì ¼, josta Ô Ì Ô Ì Ô Ì. Lopputilan hiukkasten 4-liikemäärät (8) poikittaisliikemäärän Ô Ì avulla ovat siten Ô Ô µ Ô Ì Ó Ý Ô Ì Ô Ì Ò Ý µ Ô Ô µ Ô Ì Ó Ý Ô Ì Ô Ì Ò Ý µ (9) Alkutilan partoneiden (5) liikemääräosuudet Ü ½ ja Ü ¾ voidaan ratkaista energian ja liikemäärän säilymislakien avulla rapiditeettien Ý ja Ý suhteen. Energian ja 3

14 liikemäärän säilymislait 4-liikemäärien (5) ja (9) avulla ovat Ô Ü ½ ¾ Ô Ü ½ ¾ Ô Ü ¾ ¾ Ô Ü ¾ ¾ Ô Ì Ó Ý Ô Ì Ó Ý ja Ô Ì Ò Ý Ô Ì Ò Ý (0) Yhtälöistä (0) ylempi kuvaa energian säilymislakia ja alempi liikemäärän säilymistä prosessissa, kun törmäävien partoneiden liikesuunta on z-akselin suuntainen. Yhtälöistä (0) saadaan suoraan liikemääräosuudet Ü ½ ja Ü ¾ ratkaistuksi rapiditeettien Ý ja Ý avulla, eli Ü ½ Ì Ô Ý Ý µ Ü ¾ Ì Ô Ý Ý µ () Määritellään partonien 4-liikemäärien (5) ja (9) avulla partonitason Mandelstamin muuttujat Ô ½ Ô ¾ µ ¾ Ô Ô µ ¾ Ü ½ Ü ¾ Ø Ô ½ Ô µ ¾ Ô ¾ Ô µ ¾ Ü ½ Ô Ì Ô Ý Ù Ô ½ Ô µ ¾ Ô ¾ Ô µ ¾ Ü ¾ Ô Ì Ô Ý (2) joiden liikemääräosuudet Ü ½ ja Ü ¾ ovat yhtälössä (). 6 Suoran fotonituoton vaikutusalat 6. Fragmentaatiofotonien vaikutusala Tässä osassa johdetaan fragmentaation kautta syntyvien fotonien vaikutusalakaavat seuraillen julkaisussa [7] johdettuja yhtälöitä fragmentaation kautta syntyville hadroneille. Vaikutusalakaavan () perusteella partonisironnan Ð vaikutusala massakeskipistekoordinaatistossa on muotoa Ð ½ Šе ¾ Æ µ Ô p p ¾ ½ ¾ ½ Ô ¾ Ô Ô µ ¾ Ð Ø ÙµÆ µ Ô ½ Ô ¾ Ô Ô µ (3) Ø missä Ø Ùµ Šе¾. Vaikutusalan kaavan (3) 3-liikemäärien differentiaalit p Ø ½ ¾ ja p voidaan kirjoittaa poikittaisliikemäärien Ô Ì ja Ô Ì sekä rapiditeettien Ý ja Ý avulla. Esimerkiksi p :lle p p Ü p Ý p Þ ¾ Ô Ì Ý, 4

15 missä poikittaisliikemäärälle p Ü p Ý ¾ Ô Ì ja pitkittäisliikemäärälle p Þ p Þ Ý Ý Ý.Vaikutusalassa (3) esiintyvä Æ µ Ô ½ Ô ¾ Ô Ô µ deltafunktio kuvaa energian ja liikemäärien säilymistä sirontaprosessissa. Deltafunktio voidaan kirjoittaa komponenttimuodossa käyttäen yhtälössä () esiintyviä liikemääräosuuksia Ü ½ ja Ü ¾ sekä poikittaisliikemääriä Ô Ì ja Ô Ì. Deltafunktio tulee muotoon Æ µ Ô ½ Ô ¾ Ô Ô µ ¾ Æ Ü ½ Ô Ì Ô Ý Ý µµæ Ü ¾ Ô Ì Ô Ý Ý µµæ ¾µ Ô Ì Ô Ì µ 4 Sironnan Ð partonit ja katsotaan tulevan atomiytimistä ½ ja ¾, jolloin vaikutusalasta (3) saadaan atomiydintason vaikutusala integroimalla partonien liikemääräosuuksien Ü ½ ja Ü ¾ yli ja summaamalla eri partonimahdollisuudet ÕÕ ½ ¾Ð ¾ ½ ¾Ð Ô ¾ Ì Ô Ì Ý Ý ¾ Ô Ì Ý ¾ Ô Ì Ý ½ ¾ Ô Ì Ü ½ Ü ¾ ½ Ü ½ É ¾ µ ¾ Ü ¾ É ¾ Ð µ ¼ ¾ Ô Ì Ý ¾ Ô Ì Ý ÕÕ Ü ½ ½ Ü ½ É ¾ µü ¾ ¾ Ü ¾ É ¾ µ ½ Ð Ø Ùµ (4) Ø missä deltafunktion yli integroinnit antavat Ü ½ :n ja Ü ¾ :n rapiditeettien ja poikittaisliikemäärän avulla, sekä poikittaisliikemäärän integrointi antaa Ô Ì Ô Ì Ô Ì. Vaikutuslassa (4) esiintyvällä poikittaisliikemäärällä Ô Ì ei ole tarkoin määrättyä referenssisuuntaa atsimuuttikulman suhteen, koska alkutilan törmäävillä partoneilla ja ei katsota olevan poikittaisliikemääriä. Differentiaali ¾ Ô Ì voidaan ilmaista napakoordinaateissa ja keskiarvoistaa atsimuuttikulman suhteen, jolloin ¾ Ô Ì Ô Ì Ô Ì Ô ¾ Ì, ja vaikutusalassa (4) esiintyvästä ½ tekijästä päästään eroon. Käytännössä partonit ja voivat tulla kummasta tahansa ytimestä ½ tai ¾, joten huomioimalla partonien ja mahdolliset alkuperäkombinaatiot vaikutusalasta (4) saadaan ½ ¾Ð Ô ¾ Ì Ý Ý Ü ½ ½ Ð ½ Ü ½ ½ Ü ½ É ¾ µü ¾ ¾ Ü ¾ É ¾ µ Ø Ùµ ½ Æ Ø Ü ½ É ¾ µü ¾ ¾ Ð Ü ¾ É ¾ µ ٠ص (5) Ø missä summauksessa esiintyvät parit Õ Õ ÕÕ Õ Õ ja Õ Õ, sekä kvarkkimaut Õ Ù tai. Vaikutusalassa (5) esiintyvistä partoneista ja Ð jommasta kummasta tai mahdollisesti molemmista halutaan muodostaa kvarkki, antikvarkki tai gluoni, joita 4 Seuraa deltafunktioiden laskusäännöstä Æ µæ µ ¾Æ µæ µ. 5

16 edustaa hiukkanen. Merkitään hiukkasen rapiditeettia Ý, ja huomioimalla jälleen kombinatorisesti, että voi olla kumpi tahansa sironnan tai Ð lopputilan hiukkasista, sekä deltafunktion määritelmästä (33) sivulta 59, saadaan ½ ¾ Ô ¾ Ì Ý Ý Ý Ý Ð Ð ½ ¾Ð ½ Æ Æ Ý Ý µ Æ Ð Æ Ý Ý µ ½ Æ Ð Ô ¾ Ì Ý Ý ½ ½ ½ Æ ½ Æ Ð Ü ½ ½ Ü ½ É ¾ µü ¾ ¾ Ü ¾ É ¾ µ Ü ½ ½ Ü ½ É ¾ µü ¾ ¾ Ü ¾ É ¾ µ Ð Ø ÙµÆ Ð Ù ØµÆ Ð Ø Ø Ð Ù ØµÆ Ð Ø ÙµÆ Ð µ(6) Ø Ø Vaikutusalassa (6) esiintyvän hiukkasen tarkoituksena on säteillä fotoni. Merkitään tämän fragmentaatiofotonin 4-liikemäärää Õ qµ Õ Ì Ó Ý Õ Ì Õ Ì Ò Ý µ missä fotonin energia Õ Ì Ó Ý, rapiditeetti Ý ja poikittaisliikemäärän suuruus Õ Ì Õ Ì. Fragmentoitumisprosessissa vain tietty osa partonin energiasta menee syntyvän fotonin energiaksi, ja tämän kvantifioimiseksi määritellään fotonin energian ja partonin energian välille yhtälö Þ (7) missä Þ ¾ ¼ ½. Sijoittamalla fotonin ja hiukkasen energiat yhtälöön (7) saadaan Õ Ì Ó Ý ÞÔ Ì Ó Ý Þ Fragmentaatioprosessissa fotoni syntyy samansuuntaisesti partonin kanssa, eli 3- liikemäärät q p. Täten fotonin 3-liikemäärävektori voidaan esittää muodossa q p, missä on vakio. Vakio saadaan ratkaistuksi relaatiosta Õ ¾ ¼ ¾ q ¾ Þ ¾ ¾ ¾ p ¾, josta Þ p Þ koska Ô ¾ ¼, eli p. Joten q Õ Ì Õ Ì Ò Ý µ ÞÔ Ì ÞÔ Ì Ò Ý µ Þp, josta seuraa Ý Ý, koska Õ Ì Õ Ì ÞÔ Ì ÞÔ Ì. Vaikutusalan (6) sirontaprosessissa esiintyvän partonin tehtävänä on fragmentatoida fotoni ja luovuttaa tälle osa energiastaan. Fragmentaatiofotonin vai- 6

17 kutusalaksi saadaan ½ ¾ ÕÌ ¾ Ý ½ ¼ ½ Þ ÕÕ Þ ¼ Þ ¾ Þ Þ ¾ ½ Ô ¾ Ì Ý Þ Ý Þ ¾ ¼ Þ Ô ¾ Ì Ý Æ Õ ¾ Ì ÞÔ Ì µ ¾ µæ Ý Ý µ ½ ¾ Ô ¾ Ì Ý Þ ¾ µ Ô ¾ Ì Ý Æ Þ ¾ Õ¾ Ì Þ ¾ Ô¾ Ì µµæ Ý Ý µ ½ ¾ Ô ¾ Ì Ý Þ ¾ µ Ô ¾ Ì ÝÆ Õ¾ Ì Þ ¾ Ô¾ Ì µæ Ý Ý µ ½ ¾ Ô ¾ Ì Ý Þ ¾ µ ½ ¾ Ô ¾ Ì Õ¾ Ì Ð Ü ½ ½ Ü ½ É ¾ µü ¾ ¾ Ü ¾ É ¾ µ Ü ½ ½ Ü ½ É ¾ µü ¾ ¾ Ü ¾ É ¾ µ ½ Þ ¾ Ý Ý Þ ¾ µ ½ ½ Æ ½ Æ Ð Ð Ø Ùµ Þ ¾ Ø µ Р٠ص Ð Þ ¾ Ø µ Р٠ص Þ ¾ Ø µ Ð Ø Ùµ Ð Þ ¾ µ(8) Ø µ Vaikutusalan (8) integrointirajat rapiditeetille Ý saadaan asettamalla liikemääräosuudet Ü ½ Ü ¾ ½, ja ratkaistaan liikemääräosuuksien yhtälöistä () rapiditeetti Ý. Integrointirajat Ý :lle ovat Ô Ô ÐÒ Ý Ý (9) Ô Ì Ý ÐÒ Fragmentaatiomuuttujan Þ integrointirajat saadaan Þ määrittelevän yhtälön (7) avulla. Massakeskipistekoordinaatistossa partonin saavuttama Ô maksimaalinen energia on puolet ytimiä kiihdyttävästä energiasta eli, max, jolloin Þ ¾ min ¾Õ Ô Ì, max Ó Ý. Maksimissaan Þ on silloin, kun partoni luovuttaa kaiken energiansa syntyvälle fotonille, jolloin, ja tulee Þ max ½. Muuttujan Þ integrointirajat ovat siis Ô Ì ¾Õ Ì Ô Ó Ý Þ ½ (20) Vaikutusalassa (8) esiintyy aliprosessien vaikutusaloja muodossa Ð, nämä ovat vahvan vuorovaikutuksen 2 2-sirontoja, joita on vahvan vuorovaikutuksen Ø kertaluvussa Ç «¾ Ë µ yhteensä kahdeksaa eri tyyppiä. Vuorovaikutuksen voimakkuutta kuvaava merkintä Ç «¾ Ë µ tarkoittaa, että vahvan vuorovaikutuksen vuorovaikutuspisteitä on yhteensä kaksi kappaletta. Näiden kahdeksan sirontaprosessin laskemiseen tarvittavat vahvan vuorovaikutuksen Feynmanin säännöt ovat kuvassa 37 sivulla 62. Vahvan vuorovaikutuksen 2 2-sirontoja vahvan kytkinvakion kertaluvussa Ç «¾ Ë µ ovat Õ Õ Õ Õ (Õ Õ ja Õ Õ Õ tai Õ), ÕÕ ÕÕ, Õ Õ Õ Õ, Õ Õ Õ Õ, Õ Õ, 7

18 Vahvan vuorovaikutuksen prosessi Õ Õ Õ Õ (Õ Õ ja Õ Õ Õ tai Õ) ÕÕ ÕÕ ¾ «¾ Ë Ø Ø Ùµ ¾ Ù ¾ Ø ¾ ¾ Ù ¾ Ø ¾ Ø ¾ ¾ ¾ ¾ Ù ¾ ØÙ Õ Õ Õ Õ Õ Õ Õ Õ Ø ¾ Ù ¾ ¾ ؾ Ù ¾ ¾ Ù ¾ ¾Ù¾ ¾ Ø ¾ Ø Õ Õ Ù ¾ µ ½ ØÙ ¾ Õ Õ Ù ¾ µ ½ ØÙ ¾ Õ Õ ¾ Ù ¾ µ ½ Ø ¾ Ù ØÙ Ø ¾ ¾ Ø ¾ Ù ¾ Taulukko : Vahvan vuorovaikutuksen 2 2-sirontojen vaikutusalat Ø-kanavan suhteen vahvan vuorovaikutuksen kertaluvussa Ç «¾ Ë µ, partonitason Mandelstamin muuttujat, Ø ja Ù määriteltiin yhtälöissä (2). Aliprosessien vaikutusalat löytyvät esimerkiksi julkaisusta [8, s. 53]. Õ Õ, Õ Õ ja. Taulukossa on näiden aliprosessien differentiaaliset vaikutusalat Ø-kanavan suhteen. Liitteen sivulta 63 alkaen on esimerkkilaskuna prosessin Õ Õ Õ Õ vaikutusalalasku. Taulukon vaikutusaloissa esiintyvä vahvan vuorovaikutuksen kytkinvakio «Ë ei ole aivan sananmukaisesti vakio, vaan riippuu vuorovaikutuksen energiasta Ê, jota kutsutaan renormalisaatioskaalaksi, ja kvarkkimakujen lukumäärästä. Vahvan vuorovaikutuksen kytkinvakio -silmukkatasolla on, [4, s. 2], «Ë ¾ Ê µ ½¾ ¾Æ µ ÐÒ ¾ Ê ¾ Æ µ (2) missä Æ on kvarkkimakujen lukumäärä, käytännössä 4 tai 5. QCD:n sisäinen skaala Æ on energian skaalaustekijä, jonka numeerinen arvo riippuu käytetystä kvarkkimakujen lukumäärästä, numeerisissa simuloinneissa 4:lle kvarkkimaulle Æ ¼ ¾½ Î ja viidelle Æ ¼ ½ Î, [9]. 8

19 Nopea prosessi ¾ ¾ Õ«Ñ«Ë Ø Ø Ùµ Õ Õ ½ ¾ Ø ¾ Ø Õ Õ Ø ¾ Ù ¾ ØÙ Taulukko 2: Nopeat prosessit suorien fotonien tuottamiseksi kertaluvussa Ç «Ñ «Ë µ. Erikoistyöstä [4] löytyvät näiden prosessien yksityiskohtaiset vaikutusalalaskut. 6.2 Nopeiden fotonien vaikutusalat Erikoistyössä [4] tutkittiin suoraa fotonituottoa nopeiden prosessien kautta, joissa fotoni syntyy suoraan partonisessa primääriverteksissä. Vahvan ja sähkömagneettisen vuorovaikutuksen kertaluvussa Ç «Ñ «Ë µ nopeat prosessit ovat QCD- Compton-sironta ja kvarkki antikvarkkiparin annihilaatio. Näiden prosessien vaikutusalojen yksityiskohtainen johtaminen löytyy erikoistyöstä [4, s. 2 2]. Tässä nopeiden fotoneiden vaikutusala saadaan kaavasta (5) korvaamalla toinen lopputilan partoneista fotonilla. ¾ ½ ¾ Õ ¾ Ì Ý Ý Ü ½ ½ Ü ½ ½ Õ Ü ½ ½ Õ ÕÙ Ü ½ ½ Õ Ü ½ É ¾ µü ¾ ½ Õ Ü ½ É ¾ µü ¾ ¾ Õ Ü ½ É ¾ µü ¾ ¾ Õ Ü ½ É ¾ µ ½ Õ Ü ¾ É ¾ µ ¾ Õ Ü ½ É ¾ µ Ü ¾ ¾ Ü ¾ É ¾ µ Õ Õ Ø Ùµ Ø Ü ¾ É ¾ µ Ø Õ Õ Ü ¾ É ¾ µ ٠ص Ø Ü ¾ É ¾ µ Õ Õ Ø Ùµ Ø Õ Õ Ù Øµ (22) Nopeiden fotonien vaikutusalassa (22) rapiditeetin Ý integrointirajat ovat samat kuin fragmentaatiofotonien tapauksessa, eli Ý :n integrointirajat löytyvät yhtälöstä (9). Vaikutusalan (22) aliprosessien vaikutusalat Ø ovat taulukossa 2. 7 Partonijakaumat Atomiytimet muodostuvat protoneista ja neutroneista, joita sitoo yhteen vahva vuorovaikutus. Protonit ja neutronit puolestaan koostuvat kvarkeista, antikvarkeista ja vahvan vuorovaikutuksen välittäjähiukkasista gluoneista. Kvarkkeja, antikvarkkeja ja gluoneja kutsutaan yhteisnimeltään partoneiksi, joka tulee englannin kielen termistä part-on tarkoittaen osaa. 9

20 7. Protonin partonijakaumat Yleisesti partonin jakaumaa protonissa kuvaa funktio Ô Ü É¾ µ, missä Ü on partonin liikemääräosuus protonin liikemäärästä ja É ¾ on vuorovaikutusenergiaskaala, jolla partoni otetaan protonista ulos. Lähtökohtana protonia raskaampien atomiydinten partonijakaumille on protonin partonijakaumat, koska niiden avulla saadaan myös neutronien partonijakaumat. Protoni ja neutroni kuuluvat ominaisuuksiensa perusteella samaan isospin-duplettiin[0, s. 9], jonka perusteella protonin ja neutronin partonijakaumat ovat samankaltaiset. Käytännössä neutronin partonijakaumat saadaan protonin partonijakaumista isospin-symmetrian nojalla vaihtamalla u- ja d-kvarkkijakaumat keskenään, eli siis u-kvarkille Ù Ô Ü É ¾ µ Ò Ü É ¾ µ ja d-kvarkille Ô Ü É ¾ µ Ù Ò Ü É ¾ µ, missä Ô viittaa protoniin ja Ò neutroniin. Tässä työssä käytetyt protonin partonijakaumat ovat CTEQ-kollaboraation alimman kertaluvun jakaumia CTEQ6L [9]. Kuvassa 3 on numeerisessa simuloinnissa käytetyt CTEQ6L-partonijakaumat kahdella eri energiaskaalalla, É ¾ ½¼ Î ¾ ja É ¾ ½¼¼¼¼ Î ¾. Partonijakaumia ei voida lähtökohtaisesti laskea QCD-teoriasta, vaan ne tarvitsevat parametrisoinnin lähtökohdaksi mittaustuloksia. Tyypillisimmät partonijakaumien mittausprosessit ovat syvä epäelastinen sironta (DIS) ja Drell Yan-prosessi, lyhyt johdattelu näihin prosesseihin löytyy esimerkiksi tutkielmasta [0]. Leptonisessa syvässä epäelastisessa sironnassa protonin rakenne rikotaan törmäyttämällä siihen esimerkiksi elektroni, jolloin sironneen elektronin sirontakulmasta ja energiasta pystytään päättelemään protonin sisäistä rakennetta. Drell Yan-prosessissa puolestaan törmäytetään protoneita, jolloin mahdollisesti syntyy leptoni antileptoni-pareja, joita mittaamalla saadaan myös tietoa protonien rakenteesta. Kun mittauksiin perustuen on sovitettu tietty funktionaalinen muoto partonijakaumille, jollain skaalalla É ¾ ¼, niin sen jälkeen partonijakaumien muutosta energiaskaalan É ¾ suhteen voidaan mallintaa QCD-evoluutioyhtälöiden avulla. Näitä yhtälöitä kutsutaan löytäjiensä mukaisesti DGLAP-yhtälöiksi 5 [], ja ne ovat yleisessä muodossa integro-differentiaaliyhtälöitä, joiden ratkaisemiseen täytyy käyttää numeerisia menetelmiä. Partonijakaumien parametrisoinnissa yleensä käytetty lähtöenergiaskaala on c-kvarkin massakynnys, joka tässä vastaa energiaa É ¾ ¼ ½ ξ. 7.2 Protonia raskaampien ytimien partonijakaumat Protonia raskaampien ytimien partonijakaumat saadaan vapaan protonin partonijakaumista kertomalla protonin partonijakaumaa kullekin ytimelle ominaisella ydinmodifikaatiotekijällä Ê Ü É¾ µ. Ytimen partonijakauma on siis muotoa Ü É ¾ µ Ê Ü É¾ µ Ô Ü É¾ µ (23) 5 DGLAP = Dokshitzer Gribov Lipatov Altarelli Parisi. 20

21 CTEQ6L (LO) partonijakaumat, Q 2 = 0 GeV 2 g/5 uv d v u bar d bar s c CTEQ6L (LO) partonijakaumat, Q 2 = 0000 GeV 2 g/5 uv d v u bar d bar s c x f(x, Q 2 ) x x Kuva 3: Protonin partonijakaumat Ü Ü É ¾ µ, Ù Î Î Ù, jakaumat energiaskaaloilla É ¾ ½¼ Î ¾ ja É ¾ ½¼¼¼¼ Î ¾. Symbolit Ù Î ja Î viittaavat Ù- ja -kvarkkijakaumien valenssikvarkkeihin. Partonijakaumat ovat tässä CTEQ-kollaboraation CTEQ6L -jakaumia [9], versio 6.6 vuodelta

22 missä ydinmodifikaatiofunktio Ê Ü É¾ µ on riippuvainen ytimen massaluvusta, liikemääräosuudesta Ü ja energiaskaalasta É ¾. Tässä työssä käytetyt yhtälön (23) ydinmodifikaatiofunktiot ovat EPS09[2], EKS98[3] ja EPS08[4]. Erityisen mielenkiinnon kohteena ovat EPS09-ydinpartonijakaumat, koska näille jakaumille on saatavissa myös ydinpartonijakaumien parametrisoinnin virherajat. Ydinpartonijakaumat EKS98 ja EPS08 ovat tässä työssä lähinnä verrokkiasemassa. Ydinpartonijakauman (23) avulla kirjoitettuna esimerkiksi u-kvarkin jakauma ytimessä on Ù Ü É ¾ µ Ù Ü µ ɾ µ Ü É¾ µ Ê Ù Ü É¾ µ Ô Ù Ü µ ɾ µ Ê Ü É¾ µ Ô Ü É¾ µ (24) missä ja ovat ytimen massa- ja protoniluvut. Yleisesti ottaen ydinmodifikaatiofunktiot Ê Ü É¾ µ ovat funktionaaliselta muodoltaan varsin monimutkaisia. Esimerkiksi EPS09[2] ydinmodifikaatioiden parametrisoinnissa on käytetty, a priori, 5:tä parametria, jotka sovitetaan mittaustuloksiin ¾ -minimointimenetelmällä. Julkaisussa [2] on tarkat kuvaukset sovituksissa käytetyistä ydinmodifikaatiofunktioista ja näiden parametreista. EPS09- jakaumien 5:lle sovitusparametrille on saatavissa sovitusparametrien virherajat, joiden välissä parametrien arvot voivat vaihdella. Julkaisussa [2, s. 26] suositellaan laskemaan halutun suureen, esimerkiksi vaikutusalan, virheen ylä- ja alarajat erikseen muodossa µ ¾ ½ ½ µ ¾ ½ ½ ÑÜ Ë µ Ë ¼µ Ë µ Ë ¼ µ ¼ ¾ ÑÜ Ë ¼ µ Ë µ Ë ¼µ Ë µ ¼ ¾ missä Ë ¼ edustaa parasta mahdollista sovitusta, ja Ë ½ Ë ½ muiden sovitusparametrien maksimi- ja minimivirheitä. Kuvassa 4 on lyijy-ytimen EPS09- modifikaatiot gluoni-, valenssikvarkki- ja merikvarkkijakaumille yhtälön (25) mukaisine virherajoineen. Kuvan perusteella voi todeta, että erityisesti matalaenergisilla ydinpartonijakaumilla, ja etenkin gluoneilla, on varsin suuret virherajat. 8 Fotonien fragmentaatiofunktiot Fragmentaatiofunktio määritellään dimensiottomaksi funktioksi, joka kuvaa yksittäisen hiukkasen esiintymistodennäköisyysjakaumaa lukumääräjakaumaksi normitettuna hiukkasten törmäysprosessin lopputilassa [5, s. 93]. Fotonin fragmentaatiofunktioiden Þ ¾ µ, Õ, Õ tai, muuttujia ovat Þ, joka kuvaa fragmentoituneen fotonin energian suhdetta emohiukkasen energiaan ja ¾, joka on fragmentaation energiaskaala. 22 (25)

23 .4 EPS09 (LO).4 EPS09 (LO).4 EPS09 (LO) Q 2 = 0 GeV 2 Q 2 = 0 GeV 2 Q 2 = 0 GeV δr Pb g (x,q2 ) R Pb g (x,q2 ) δr Pb v (x,q2 ) R Pb v (x,q2 ) δr Pb s (x,q2 ) R Pb s (x,q2 ).4.2 EPS09 (LO) Q 2 = 0000 GeV EPS09 (LO) Q 2 = 0000 GeV EPS09 (LO) Q 2 = 0000 GeV 2 δr Pb g (x,q2 ) R Pb g (x,q2 ) δr Pb v (x,q2 ) R Pb v (x,q2 ) δr Pb s (x,q2 ) R Pb s (x,q2 ) x x x Kuva 4: Lyijy-ytimen alimman kertaluvun EPS09-ydinpartonimodifikaatiot [2] gluoneille, valenssikvarkeille ja merikvarkeille yhtälön (25) mukaisine virherajoineen energiaskaaloilla É ¾ ½¼ Î ¾ ja É ¾ ½¼¼¼¼ Î ¾. 23

24 Fragmentaatiofunktioiden parametrisointiin tarvitaan myös mittaushavaintoja samaan tapaan kuin partonijakaumissakin. Tyypillinen sirontaprosessi, josta fragmentaatiofotoneita voidaan havainnoida, on annihilaatiosironta. Tässä siis elektroni ja positroni annihiloivat toisensa ja virtuaalisen fotonin tai heikon vuorovaikutuksen ¼ -hiukkasen kautta syntyy fotoni sekä joukko muita hiukkasia. Fragmentaatiofunktioiden arvojen määrittämiseen tarvitaan sekä mittaushavaintoja että häiriöteoreettisesti laskettuja vaikutusaloja. Mittauksissa fragmentaatiofotonin katsotaan syntyvän, kun törmäysprosessissa syntyy hiukkasjetti, jonka keskeltä muodostuu fotoni. Tällöin fotoni ja sen fragmentoinut hiukkanen ovat yhdensuuntaisia. Häiriöteoreettisesti tästä yhdensuuntaisuudesta seuraa, että fragmentaatiofunktiot sisältävät divergenttejä osia, etenkin jos fragmentaatioenergia menee pieneksi. Siksipä fragmentaatioprosesseja täytyy tutkia jostakin energiaskaalasta ¾ ¼ lähtien, jonka tulisi olla niin suuri, että häiriöteorian menetelmiä voidaan käyttää, eli vahvan vuorovaikutuksen kytkinvakiossa (2) «Ë ¾ ¼ µ fragmentaation lähtöenergiaskaala tulee olla ¾ ¼ ¾ Æ. QCD:n faktorisaatioteoreeman mukaan nämä kollineaarisuudesta aiheutuvat divergentit osat voidaan kuitenkin sisällyttää fragmentaatiofunktioiden määrittelyyn. Fotonien fragmentaatiofunktioita osataan jossain määrin laskea puhtaasti häiriöteoreettisin menetelmin. Laskemalla sironnasta Õ Õ syntyvän fotonin vaikutusala QED:n Feynmanin säännöillä, tästä vaikutusalasta voidaan identifioida fragmentaatiofunktiot kertaluvussa Ç «Ñ µ, jotka ovat [6, s. 473] Þ Õ Þ ¾ µ «Ñ ¾ Õ ¾ ½ ½ Þµ¾ ÐÒ ¾ ¾ ¼ µ (26) Þ Þ ¾ µ ¼ Yhtälöissä (26) luonnollisesti Þ ¾ µ ¼, koska kertaluvussa Ç «Ñµ fotoni ei voi fragmentoitua gluonista, vaan tämä tarvitsee pohjalle kvarkki antikvarkkisilmukan, josta fotoni voi muotoutua. Fragmentaatiofunktioiden muotoja voidaan laskea häiriöteoreettisin menetelmin haluttuun vahvan vuorovaikutuksen Ç «Ò Ë µ kertalukuun Ò asti. Fotonien fragmentaatiofunktioiden laskeminen häiriöteoreettisin menetelmin ei suinkaan ole aivan yksinkertaista, ei edes yhtälöiden (26) tapauksessa. Kiinnostunut lukija voi katsoa julkaisusta [7] yhtälöiden (26) ja vahvan vuorovaikutuksen kertaluvun Ç «Ë µ mukaisen kontribuution häiriöteoreettisesti laskettuihin fotonin fragmentaatiofunktioihin käytettäessä divergenttien osien käsittelyyn dimensionaalista regularisaatiota [8]. Kuitenkaan fragmentaatiofunktioiden käyttäytymistä ei voi puhtaasti ymmärtää vain häiriöteoreettisin menetelmin, vaan tarvitaan myös mittaustuloksia. Fragmentaatiofunktioiden energiariippuvuuden hahmottamiseen tarvitaan fragmentaatiofotonien mittauksia jollakin skaalalla ¾ ¼. Yhdistämällä fragmentaatiofotonien mittaushavainnot ja häiriöteorian ennusteet fragmentaatiofunktioiden käyttäytyminen voidaan laskea DGLAP-yhtälöiden [] avulla millä tahansa energiaskaalalla ¾ ¾ ¼. 24

25 Tässä työssä käytetyt fotonin fragmentaatiofunktiot ovat BFG 6 -fragmentaatiofunktioita [9]. BFG-fragmentaatiofunktiot jakaantuvat kahteen osaan, joista toinen on häiriöteoreettisin menetelmin laskettava osa ja toinen, jota ei voida kuvata häiriöteoreettisin menetelmin. Julkaisussa [9] osoittautuukin, että fotonien fragmentaatiofunktioiden ei-häiriöteoreettinen osa on hyvin merkittävä. Tämän ei-häiriöteoreettisen osan kuvaamiseen käytetään VDM-mallia 7 [20], jossa fotonin katsotaan koostuvan kombinaationa ¼, ja mesoneista. Matalilla fragmentaatioenergioilla ¾ ¾ Î ¾ fotonin fragmentaatiofunktioiden määrittämiseen käytetään ensin kvarkkien ja gluonien fragmentoitumista vektorimesoniksi Õ Õ, josta muodostuu edelleen fotoni. BFG-fragmentaatiofunktioiden ei-häiriöteoreettiselle osalle on saatavilla kaksi eri versiota, jotka eroavat toisistaan vain hieman sovitusparametreiltaan. Mallin sovitusparametreihin on käytetty niin ikään ¾ -minimointimenetelmää, jolloin ensimmäiselle sovitukselle ¾ Set I ½ ja toiselle Set ¾ II ½ ¾¾, kuvaus sovitusparametreista löytyy julkaisusta [9, s. 2]. Tämän työn simuloinneissa käytetty ei-häiriöteoreettinen osuus fotonien fragmentaatiofunktioille on Set I. Kuvassa 5 on kuvattu fragmentaatiofotonien simuloinneissa käytetyt fragmentaatiofunktiot kahdella eri fragmentaatioskaalalla. Kuvan 5 fragmentaatioenergiat vastaavat varsin hyvin LHC-hiukkaskiihdyttimeltä mitattuja fotonien energioita. Kuvassa esitettyjen fotonien fragmentaatiofunktioista on kiintoisaa havaita, että fotonien fragmentoituminen kvarkista on huomattavan paljon todennäköisempää kuin gluoneista. Gluonien kontribuutio fotonien fragmentaatiossa näyttäisi olevan maksimissaan 5 % luokkaa kaikista fragmentaatiofotoneista per fragmentoiva partoni. 9 Määritettäviä suureita Tarkoituksena tässä työssä on laskea suoran fotonituoton vaikutusaloja erilaisten ytimien sirontaprosesseista. Noin vuodesta 200 eteenpäin on julkaistu lukuisia ATLAS- ja CMS-kollaboraatioiden suoran fotonituoton mittaustuloksia sironnasta Ô Ô. Näitä mittaustuloksia voidaan verrata tässä työssä laskettuihin teoreettisiin vaikutusaloihin. ATLAS- ja CMS-kollaboraatiot tekevät suorien fotonien mittauksissaan niin sanotun isolaatioleikkauksen fotoneille. Tämä tarkoittaa sitä, että näissä mittauksissa vaaditaan, että fotonin ympärillä olevassa sovitun suuruisessa µ-ympyrässä ei tulisi olla tiettyä määrää suurempaa hadronista poikittaisenergiaa. Tällainen isolaatioleikkaus pienentää fragmentaatiokomponentin osuutta, mutta ei kuitenkaan täysin poista sitä, joten ainoastaan NLO+fragmentaatiofotonilaskun kautta 6 BFG = L. Bourhis M.Fontannaz J. Ph. Guillet. 7 Vector Meson Dominance Model = VDM. 25

26 BFG fragmentaatiofunktiot (Set I), µ 2 F = 0 GeV2 BFG fragmentaatiofunktiot (Set I), µ 2 F = 0000 GeV2 0 g u d s c 0 g u d s c b D γ (z,µ 2 F ) z z Kuva 5: Fotonin Bourhis Fontannaz Guillet -fragmentaatiofunktiot [9] partoneista Ù ja energiaskaaloilla ¾ ½¼ ξ ja ¾ ½¼¼¼¼ ξ. 26

27 on mahdollista suorittaa yksityiskohtaisen tarkka vertailu mittaustuloksiin. Tässä tutkielmassa tarkastellut LO- ja LO+fragmentaatio-tulokset antavat kuitenkin alimman kertaluvun ennustamat ala- ja ylärajat kyseisille isolaatioleikatuille vaikutusaloille, joten tässä tarkastellaan näiden yhteensopivuutta ATLAS- ja CMSkokeiden tuloksiin. 8 Teoreettisen ja mitatun vaikutusalan eroja voidaan tutkia esimerkiksi määrittämällä Ã-kertoimia, jotka kuvaavat teoreettisen ja mitatun vaikutusalan suhdetta. Ã-kertoimen määritys onnistuu esimerkiksi minimoimalla funktiota [7, s. 5] Æ ¾ Ƶ à teoria mittaus ¾ Æ mittaus (27) ½ missä Æ on mittauspisteiden lukumäärä, teoria teoreettinen vaikutusala havainnolle, mittaus mitattu vaikutusala havainnolle ja Æ mittaus on mitatun vaikutusalan mittausvirhe sisältäen sekä statistiset että systemaattiset virheet. ¾ -minimointi on oiva menetelmä laskea numeerisessa parametrisoinnissa tarvittavia kertoimia, jos tunnetaan jonkin fysikaalisen ilmiön mittausdata virherajoineen ja tätä ilmiötä kuvaileva teoreettinen malli. Tässä työssä ¾ -menetelmällä määritetään Ã-kertoimia, joiden selvittäminen onnistuu tässä yhden tuntemattoman parametrin tapauksessa matriisien kertolaskun avulla [2, s ] à ÆÃ Ê Æ ½ ʵ ½ Ê Æ ½ Ý Õ Ê Æ ½ ʵ ½ (28) missä sarakevektori Ê sisältää teoreettisesti lasketun vaikutusalan, matriisi Æ sisältää diagonaalimatriisimuodossa mittausdatan virheen neliön ja sarakevektori Ý mittausdatan. Yksi tämän työn päätavoitteista on tutkia myös protonia raskaampien ytimien vaikutusta suoraan fotonituottoon. Tämä onnistuu esimerkiksi tutkimalla raskaiden ytimien suoran fotonituoton suhdetta protonien kautta tuottettuihin fotoneihin. Eli tutkimalla suhdetta Ê ½ ¾ ¾ ½ ¾ ÕÌ ¾ Ý ½ ¾ ¾ Ô Ô ÕÌ ¾ Ý (29) Toisinaan mittaustulokset ilmoitetaan pseudorapiditeetin avulla rapiditeetin Ý sijaan. Kuitenkin massattomille hiukkasille pseudorapiditeetti ja rapiditeetti ovat samoja Ý ÐÒ ØÒ ¾ missä on sirontakulma törmääviin atomiytimiin nähden. Pseudorapiditeettivälin yli keskiarvoistettu suoran fotonituoton vaikutusala on muotoa [7, s. 5] ÕÌ ¾ ½ ¾ ÕÌ ¾ ½ ÕÌ ¾ Ý (30) 8 Tämä kappale on oleellinen lisähuomautus koskien ATLAS- ja CMS-kokeita, tämä lisäys on tehty professori K. J. Eskolan pyynnöstä. 27

28 0 Numeeriset menetelmät 0. Ohjelmallinen toteutus Käytännössä suoran fotonituoton vaikutusalat (8) ja (22) täytyy laskea tietokoneella numeerisesti. Tätä tarkoitusta varten kirjoitin tietokoneohjelman FORT- RAN90 -ohjelmointikielellä. Ohjelma itsessään on jaettu moduleihin, joiden etuna esimerkiksi FORTRAN77 -kieleen nähden on helppo laajennettavuus ja ohjelman osasten soveltamismahdollisuus myös muihin sirontaprosesseihin. Ohjelman tekemisessä auttoi professori K.J. Eskolan esimerkkiohjelma, josta sain hyviä ideoita ohjelman systematiikkaan. Liitteiden sivulta 67 lähtien on kirjoittamani ohjelman tärkeimmät modulit tiivistetyssä muodossa. Kaikissa simuloinneissa partonijakaumien (23) energiaskaala É Ô Ì, vahvan vuorovaikutuksen (2) renormalisaatioskaala Ê Ô Ì ja fragmentaatiofunktioiden fragmentaatioskaala Õ Ì. Numeerinen integrointimenetelmä Ohjelmassa käytetty numeerinen integrointimenetelmä perustuu gaussin numeeriseen integrointimenetelmään. Integrointimenetelmää käytettäessä hyväksi kompromissiksi laskenta-ajan ja tarkkuuden suhteen osoittautui 6. kertaluvun Gaussin menetelmä, jossa integroinnin osavälit on jaettu vielä 4 osaan. Pystyin vertaamaan tässä laskettuja nopeiden fotonien vaikutusalalaskuja (22) erikoistyössä käytettyyn adaptiivisella integrointimenetelmällä laskettuihin vaikutusaloihin. Erikoistyön adaptiivisessa menetelmässä käytetty laskentatarkkuus oli ½¼, tässä työssä käytetyn moniulotteisen integrointimenetelmän ero adaptiivisella menetelmällä laskettuun vaikutusalaan osoittautui testeissä maksimissaan promillen kymmenesosiksi. Liitteiden sivulta 66 alkaen on Gaussin integroimismenetelmän kuvaus käytännössä. Tulokset Suoran fotonituoton päämekanismit ovat kvarkki antikvarkki-parin annihilaatio ja QCD-Compton-sironta. Fragmentaatiofonien vaikutus suoraan fotonituotoon on joissain tapauksissa lähes samaa luokkaa kuin näiden nopeiden prosessien. Tämä johtuu siitä, että fotonin fragmentaatiofunktioiden energiariippuvuus kompensoi yhden vahvan vuorovaikutuksen kytkinvakion «Ë 2 2-sirontojen vaikutusaloista [5, s. 268]. Tämän kompensaation vaikutus näkyy kuvassa 6, jossa on nopeiden fotonituottoprosessien ja fragmentaation kautta syntyvien suorien fotonien suhteelliset osuudet sironnassa Ô Ô, kun cms-energia Ô ÌÎ, fotonin rapiditeettissa ¼. Fotonin rapiditeetti ¼ vastaa ¼ Æ sirontakulmaa törmääviin protoneihin nähden. Hyvin pienillä fotonin poikittaisliikemääräosuuksilla 28

29 Suhteellinen osuus fotonituoton vaikutusalasta p + p γ + X, s = 7 TeV, η γ =0 LO kertaluvun suorat fotonit LO kertaluvun fragmentaatiofotonit Kuva 6: Alimman kertaluvun nopeiden prosessien ja fragmentaatioprosessien suhteelliset osuudet suoran fotonituoton vaikutusalasta prosessille Ô Ô, kun cms-energia Ô ÌÎ, ja fotonin rapiditeetti ¼. 29

30 LO kertaluvun suorat prosessit LO kertaluvun fragmentaatioprosessit Aliprosessien suhteelliset osuudet vaikutusalasta g q γ q q qbar γ g q i q j q i q j, q i q j ja q i, q j = q tai qbar q q q q q i qbar i q j qbar j, i j q qbar q qbar q qbar g g g g q qbar g q g q g g g g Kuva 7: Vasemmalla ovat QCD-Compton-sironnan ja kvarkki antikvarkkisironnan suhteelliset osuudet nopeiden fotonien vaikutusalasta, ja oikeanpuoleisessa kuvassa on kuvattu fragmentaatioprosessien suhteelliset osuudet fragmentaatiofotonien vaikutusalasta. Suhteelliset osuudet ovat prosessista Ô Ô, kun Ô ÌÎ ja syntyvän fotonin rapiditeetti ¼. suhteessa kiihdytysenergiaan, Õ Ì º ½¼ Î ÌÎ, fragmentaation kautta syntyvä fotoni on jopa nopeita prosesseja todennäköisempi mekanismi suorien fotonien syntymiselle. Mutta myös suuremmilla fotonin poikittaisliikemäärillä fragmentaatiofotonien kontribuutio kokonaisvaikutusalaan on varsin merkittävä, reilusti yli 20 % kautta koko poikittaisliikemääräskaalan. Kuvassa 7 on kahden suoran prosessin ja kahdeksan fragmentaatioprosessin suhteellinen voimakkuus vaikutusalaan fotonin pseudorapiditeetilla ¼. Suorista prosesseista QCD-Compton-sironta on jopa neljä kertaa voimakkaampi kuin kvarkki antikvarkki-parin annihilaatio, tämä vastaa myös erikoistyön havaintoja [4, s. 34]. Erityisen mielenkiintoista on, että fragmentaatioprosesseista dominoivin on sironta Õ Õ, joka on hyvin paljon saman tyyppinen sironta kuin nopeiden prosessin QCD-Compton-sironta. Kuvien 3 ja 5 perusteella voisi olettaa, että todennäköisin fragmentaatioprosessi suoralle fotonituotolle olisi Õ Õ, koska alkutilassa kahden gluonin vaikutus ja lopputilassa kaksi kvarkkia, joista fotonit 30

31 todennäköisimmin fragmentoituvat. Syy, miksi prosessi Õ Õ ei ole todennäköisin fragmentaatiofotonien lähde, johtuu puhtaasti taulukon aliprosessin vaikutusaloista, kirjassa [5, s. 249] on näiden kahdeksan aliprosessin suhteelliset voimakkuudet, kun sirontaa tarkastellaan ¼ Æ sirontakulmassa. Kirjan [5, s. 249] perusteella tässä todennäköisimmäksi havaittu fragmentaatiofotonien aliprosessi Õ Õ on kinemaattisesti noin 40 kertaa voimakkaampi kuin Õ Õ. On todella mielenkiintoista havaita, että puhtaasti aliprosessien vaikutusaloja Ø vertaillen vahvimman ja heikoimman prosessin ero on jopa 200-kertainen.. Suoran fotonituoton tuloksia LHC-kiihdyttimelle Viimeisimmät suoran fotonituoton mittaukset LHC-kiihdyttimeltä löytyvät julkaisuista [22] [25]. Näissä mittauksissa protoneja on kiihdytetty Ô ÌÎ energialla, ja suorien fotonien poikittaisliikemäärät ovat olleet tyypillisesti välillä Î. Protonien suurin mahdollinen kiihdytysenergia LHC-kiihdyttimessä voisi olla jopa Ô ½ ÌÎ, mutta toistaiseksi näin suuria energioita ei ole vielä käytetty. Protonia raskaampien ytimien maksimaalinen kiihdytysenergia LHC-kiihdyttimessä ei ole Ô ÌÎ, vaan ytimien kiihdytysenergia on riippuvainen ytimien massa- ja protoniluvuista. Jos käytetään protonien maksimaalisena kiihdytysenergiana ÌÎ, niin protonia raskaampien ytimien kiihdytysenergia vastaavassa LHC-kiihdyttimen magneettikentässä on [26, s. 7] Ô ÌÎ ½ ¾ ½ ¾ (3) missä ½ ja ¾ ovat törmäävien ytimien massaluvut sekä ½ ja ¾ protoniluvut. Kiihdytysenergiakaavan (3) perusteella Pb Pb-törmäyksien kiihdytysenergia on ¾ ÌÎ ja p Pb-törmäyksien ÌÎ. Suoran fotonituoton mittausdataa protonien törmäyksistä on jo varsin runsaasti lukuisista eri fotonin rapiditeeteista [22] [25]. ATLAS-kollaboraation mittauksissa suoran fotonituoton mittausrapiditeetit ovat välillä 0 2,37 [23], joka vastaa asteina fotonin sirontakulmia välillä ¼ Æ ½¼ Æ ytimien törmäyssuuntaan nähden. CMS-kollaboraation suoran fotonituoton mittausrapiditeetit ovat välillä 0 2,5 [25], joka vastaa sirontakulmia ¼ Æ Æ. Taulukossa 3 on suoran fotonituoton Ã-tekijät kaavan (27) mukaisesti julkaisuissa [22] [25] esitetyille mittaustuloksille. Mittauksissa kukin fotonituoton poikittaisliikemäärän alue on jaettu pienempiin osaväleihin, esimerkiksi ATLASkokeen [22] fotonien poikittaisliikemäärä väli ½ ½¼¼ Î on jaettu osaväleihin ½ ¾¼, ¾¼ ¾, ¾ ¼, ¼, ¼, ¼ ¼, ¼ ¼ ja ¼ ½¼¼ Î, joista jokaisella välillä on mitattu fotonituoton vaikutusalaa. Vaikutusalojen numeerisessa simuloinneissa jokainen osaväli on jaettu vielä 20:een osaan ja teoreettinen vaikutusala 3

32 à Æà Koe Välien lkm Õ Ì Îµ LO LO+frag ATLAS [22] ,00 0,60 ½ ¼ ½½ ½ ¼ ¼ ¼ ATLAS [22] ,60,37 ½ ¼ ½½ ¼ ¼ ¼ ATLAS [22] ,52,8 ½ ¼ ½ ½ ½ ¼ ¼ ATLAS [23] ,00 0,60 ½ ¼ ¼ ½ ¾ ¼ ¼ ATLAS [23] ,60,37 ½ ¼ ¼ ½ ½ ¼ ¼ ATLAS [23] ,52,8 ½ ¼ ½ ½ ¾¾ ¼ ¼ ATLAS [23] ,8 2,37 ½ ¼ ¼ ½ ½¼ ¼ ¼ ATLAS [22], [23] ,00 0,60 ½ ¼ ¼ ½ ¾¾ ¼ ¼ ATLAS [22], [23] ,60,37 ½ ¾ ¼ ¼ ½ ½½ ¼ ¼ ATLAS [22], [23] ,52,8 ½ ¾ ¼ ¼ ½ ¾¼ ¼ ¼ CMS [24] ,00,45 ½ ¼ ¼ ½ ½¼ ¼ ¼ CMS [25] ,00 0,90 ½ ½ ¼ ¼ ½ ½ ¼ ¼ CMS [25] ,90,44 ½ ¼ ¼ ½ ½ ¼ ¼ CMS [25] ,57 2,0 ½ ¼ ¼ ½ ½½ ¼ ¼ CMS [25] ,0 2,50 ½ ¼ ¼ ½ ¼ ¼ ¼ Taulukko 3: Suoran fotonituoton Ã-kertoimet kaavan (27) ¾ -menetelmän avulla laskettuna. Lyhenne (LO) viittaa vaikutusalan (22) nopeisiin prosesseihin sekä (LO+frag) fragmentaatiokontribuution (8) ja nopeiden prosessien (22) yhteisvaikutukseen. ATLAS-kollaboraation mittaukset ovat julkaisuissa [22] ja [23] sekä CMS-kollaboraation [24] ja [25]. Toisessa sarakkeessa on mittausvälien lukumäärä kolmannen sarakkeen poikittaisliikemäärävälillä. Neljännessä mittauksen rapiditeettialue ja viidennessä sekä kuudennessa lasketut Ã-tekijät. Riveillä 8 0 on yhdistetty mittausten [22] ja [23] tulokset yhteensopivilla rapiditeettiväleillä. 32