Rinnakkaistietokannat
|
|
|
- Hannes Hakola
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Rinnakkaistietokannat A. Silberschatz, H. F. Korth & S. Sudarshan: Database System Concepts. Sixth Edition. McGraw-Hill, 2010; sivut , luvun 17 (database-system architectures) kohta 17.3 (parallel systems); sivut , luku 18 (parallel databases); sivut ja , luvun 28 (Oracle) kohdat (partitioning) ja (parallel execution). A. Silberschatz, H. F. Korth & S. Sudarshan: Database System Concepts. Fifth Edition. McGraw-Hill, 2006; sivut , luvun 20 (database-system architectures) kohta 20.3 (parallel systems); sivut , luku 21 (parallel databases); sivut ja , luvun 27 (Oracle) kohdat (partitioning) ja (parallel execution). Rinnakkaisjärjestelmät, s Nopeutuvuus ja mitoittuvuus, s Rinnakkaistietokanta-arkkitehtuurit, s Tiedon osittaminen, s Vinoumien käsittely, s Kyselyiden välinen ja kyselynsisäinen rinnakkaisuus, s Operaationsisäinen rinnakkaisuus, s Rinnakkaisliitos, s Operaatioiden rinnakkaislaskennan kustannus, s Operaatioiden välinen rinnakkaisuus, s Rinnakkaistietokannan kyselynoptimointi, s Rinnakkaisjärjestelmän suunnittelusta, s
2 Rinnakkaisjärjestelmät Rinnakkaisjärjestelmä (parallel system) koostuu joukosta yhdelle maantieteellisesti suppealle tallennusalueelle (konehuoneeseen) sijoitetusta joukosta samanaikaisesti toimivia komponentteja: suorittimia, keskusmuisteja ja levyjä. Komponentit kommunikoivat toistensa kanssa kiinteän ja hyvin nopean yhteenkytkentäverkon (interconnection network) välityksellä. Yleisesti käytettyjä yhteenkytkentäverkkoja ovat väyläverkko (bus network), silmukkaverkko (mesh network) ja hyperkuutio (hypercube network). Rinnakkaistietokantajärjestelmiä (parallel database system) on kehitetty sellaisten tietokantasovellusten tarpeisiin, joissa operoidaan tavattoman suuriin, teratavujen (10 12 tavun) kokoisiin tietokantoihin tai joissa on pystyttävä käsittelemään valtava määrä (tuhansia) transaktioita sekunnissa. Tavanomaiset keskitetyt ja asiakas-palvelinjärjestelmät eivät yleensä ole riittävän tehokkaita sellaisiin sovelluksiin. 170
3 Rinnakkaiskäsittelyssä (parallel processing) useita operaatioita suoritetaan aidosti samanaikaisesti toisin kuin yhden suorittimen tietokoneen osituskäytössä (time sharing). Tietokantaoperaation tai -kyselyn rinnakkaisuuden asteella (degree of parallelism) tarkoitetaan niiden suorittimien lukumäärää, jotka osoitetaan operaation suorittamiseen. Karkearakeinen (coarse-grain) rinnakkaiskone koostuu pienestä määrästä tehokkaita suorittimia. Useimmat tehokäyttöön tarkoitetut koneet tarjoavat jonkinasteista rinnakkaisuutta: kahden tai neljän koneen suorittimet ovat yleisiä. Hienorakeinen (fine-grain) eli massiivisesti rinnakkainen kone käyttää tuhansia pienempiä suorittimia. Useamman sadan suorittimen ja levyn rinnakkaiskoneita on kaupallisesti saatavina. 171
4 Tietokantajärjestelmän suorituskykyä on perinteisesti mitattu suoritusteholla ja vasteajalla. Suoritusteho (throughput) ilmoittaa, kuinka monta tehtävää (transaktiota) järjestelmä pystyy käsittelemään annetun aikavälin kuluessa (esim. sekunnissa). Vasteaika (response time) tarkoittaa sitä aikaa, joka kuluu tehtävän antamisesta sen suorituksen päättymiseen. Järjestelmä, joka käsittelee suuren määrän pieniä transaktioita, voi parantaa suoritustehoaan käsittelemällä useita transaktioita rinnakkaisesti. Järjestelmä, joka käsittelee suuria transaktioita, voi parantaa sekä vasteaikaa että suoritustehoa suorittamalla transaktioiden alitehtäviä rinnakkaisesti. Erityisesti suoritustehon mittaukseen on 1980-luvun alusta lähtien kehitetty erilaisia tietokantakoetinkuormia (database benchmarks). 172
5 Nopeutuvuus ja mitoittuvuus Järjestelmän nopeutuvuus (speedup) tarkoittaa annetun tehtävän käsittelyajan pienentymistä, kun rinnakkaisuutta lisätään. Järjestelmän mitoittuvuus (scaleup) tarkoittaa kykyä käsitellä suurempia (tai enemmän) tehtäviä, kun rinnakkaisuutta lisätään. Tarkastellaan rinnakkaisjärjestelmässä ajettavaa tietokantasovellusta. Lisätään järjestelmän kokoa lisäämällä suorittimien, levyjen ynnä muiden järjestelmäkomponenttien määrää. Tavoitteena on käsitellä tehtävä ajassa, joka on kääntäen verrannollinen suorittimien ja levyjen määrään nähden. Olkoon tehtävän käsittelyaika pienemmällä koneella t S ja suuremmalla koneella t L. Rinnakkaisuudesta johtuvaksi nopeutuvuudeksi määritellään t S /t L. 173
6 Rinnakkaisjärjestelmä on lineaarisesti nopeutuva, jos nopeutuvuus on n, kun suuremman järjestelmän resurssien (keskusyksiköt, levyt ym) määrä on n-kertainen pienempään järjestelmään verrattuna. Jos nopeutuvuus on pienempi kuin n, nopeutuvuuden sanotaan olevan alilineaarinen. Olkoon T tehtävä ja T n sitä n kertaa suurempi tehtävä. Olkoon T :n käsittelyaika pienemmällä koneella t S ja T n :n käsittelyaika n kertaa suuremmalla koneella t n,l. Mitoittuvuudeksi määritellään t S /t n,l. Järjestelmä on lineaarisesti mitoittuva, jos t S = t n,l, ja alilineaarisesti mitoittuva, jos t n,l > t S. 174
7 Tietokantajärjestelmille voidaan määritellä kaksi erilaista mitoittuvuutta siitä riippuen, miten tehtävän koko mitataan. Erämitoittuvuudessa (batch scaleup) tietokannan koko kasvaa ja sen johdosta kasvaa myös yksittäisten tehtävien käsittelyaika. Esimerkkinä transaktio, joka lukee läpi tietokantarelaation, jonka sivujen määrä on suorassa suhteessa tietokannan kokoon. Tietokannan koko on siis tehtävän koon mittari. Transaktiomitoittuvuudessa (transaction scaleup) järjestelmään tulevien transaktioiden määrä aikayksikköä kohti kasvaa ja tietokannan koko kasvaa samassa tahdissa. Transaktiomitoittuvuus on tärkeää transaktionkäsittelyjärjestelmissä, joissa transaktiot ovat pieniä päivityksiä, esim. tilille panoja tai tililtä ottoja, ja transaktioiden määrä aikayksikköä kohti kasvaa sitä mukaa kuin uusia tilejä perustetaan. Tällainen käsittely soveltuu erikoisen hyvin rinnakkaistettavaksi, sillä transaktiot voivat olla suorituksessa samanaikaisesti ja (pitkälti) toisistaan riippumatta, ja kukin transaktio vie suurin piirtein saman ajan, tietokannan koostakin riippumatta. 175
8 Mitoittuvuus on yleensä nopeutuvuutta tärkeämpi tehokkuusmittari rinnakkaisille tietokantajärjestelmille. Tavoitteena on varmistaa, että järjestelmä kykenee toimimaan hyväksyttävällä nopeudella silloinkin, kun tietokannan koko ja transaktioiden määrä lisääntyvät. Olemassa olevan järjestelmän kapasiteetin lisääminen on yritykselle usein helpompaa ja halvempaa kuin keskitetyn järjestelmän korvaaminen kokonaan nopeammalla. Toisaalta on tekijöitä, jotka vähentävät rinnakkaistamisesta saatavia hyötyjä: (1) Uuden prosessin käynnistäminen on kallis operaatio; tuhat rinnakkaista prosessia sisältävän operaation käynnistysaika voi olla suurempi kuin varsinainen käsittelyaika. (2) Rinnakkaiset prosessit eivät suinkaan aina ole toisistaan riippumattomia, vaan käsittelevät yhteisiä resursseja (väylä, levyt, tietoalkioiden lukot), mistä aiheutuu odotuksia. 176
9 (3) Tehtävän jakamisella useampiin rinnakkaisiin osa-askeliin voidaan vähentää keskimääräistä askeleen kokoa, mutta koko tehtävän palveluaika määräytyy hitaimman askeleen mukaan. Tehtävää on usein vaikea jakaa tarkasti samankokoisiin osiin; osien kokojen jakauma voi siis olla vinoutunut (skewed). Jos esimerkiksi 100 yksikön kokoinen tehtävä jaetaan kymmeneen osaan, ja jako on siten vinoutunut, että muutamat osatehtävät ovat pienempiä kuin 10 ja muutamat suurempia kuin 10, joukossa yksi kooltaan 20, niin rinnakkaistamisella saavutettava nopeutuvuus on vain 5 eikä
10 Rinnakkaistietokanta-arkkitehtuurit Rinnakkaiskäsittelyyn kykeneviä tietokonejärjestelmiä on eri tyyppisiä siitä riippuen, mitkä resursseista ovat yhteisiä. Yhteismuistijärjestelmässä (shared-memory system) keskusmuisti on yhteinen kaikkien suorittimien ja levy-yksiköiden kesken muistiväylän tai yhteenkytkentäverkon välityksellä. CPU CPU CPU CPU CPU Muisti Levy Levy Levy 178
11 Yhteismuistijärjestelmän etuna on suorittimien välisen kommunikoinnin tehokkuus: yhteisessä keskusmuistissa olevaan tietoon pääsee mikä tahansa suoritin käsiksi suoraan, eikä mitään ohjelmallista tiedon siirtoa tarvita. Suoritin voi lähettää viestin muille suorittimille kirjoittamalla keskusmuistipaikan, mikä on huomattavasti nopeampaa kuin viestin lähettäminen kommunikointimekanismin välityksellä. Yhteismuistijärjestelmän heikkoutena on, ettei se mitoutu ylitse 64 suorittimen, sillä muistiväylästä tai yhteysverkosta muodostuu pullonkaula (koska se on yhteinen kaikkien suorittimien kesken). Tietyn rajan jälkeen suorittimien lisääminen järjestelmään ei enää lisää tehokkuutta, sillä suorittimet käyttävät enimmän aikaansa odottaen vuoroaan väylälle päästäkseen muistiin. 179
12 Yhteismuistijärjestelmässä on jokaisella suorittimella yleensä suuri välimuisti (cache), jotta yhteiseen muistiin viittaukset vältetään mahdollisimman usein. Välimuistien käyttö yhteismuistijärjestelmässä edellyttää välimuistieheyden (cache coherency) ylläpitoa: Jos jokin suoritin kirjoittaa muistipaikkaan, jonka sisältö on parhaillaan myös toisen suorittimen välimuistissa, myös tämä välimuisti täytyy päivittää tai tieto poistaa sieltä. Välimuistieheyden ylläpitorasite lisääntyy suorittimien määrän kasvaessa. Yhteismuistijärjestelmät eivät tästäkään syystä mitoutu ylitse tietyn rajan; 64 suoritinta on maksimi. 180
13 Yhteislevyjärjestelmässä (shared-disks system, SD system, SD complex) suorittimilla on yksityiset keskusmuistit mutta yhteiset levyt. Kaikki suorittimet voivat lukea ja kirjoittaa kaikkia levyjä yhteenkytkentäverkon välityksellä, mutta suorittimen muistiin pääsee vain kyseinen suoritin yksin. Yhteislevyjärjestelmiä kutsutaan joskus rypäiksi (cluster), esim. Oraclen reaalisovellusryväs (real application cluster). CPU CPU CPU CPU CPU Levy Levy Levy Muisti Muisti Muisti Muisti Muisti 181
14 Muistiväylä ei yhteislevyjärjestelmässä ole pullonkaula. Yhteislevyjärjestelmä on myös vikasietoinen: jos suorittimessa tai muistissa sattuu häiriö, muut suorittimet voivat ottaa sen tehtäviä suorittaakseen. Koska tietokannan levyversio ja lokilevy ovat kaikkien suorittimien saatavilla, yhden suorittimen romahtaessa toinen suoritin voi huolehtia tietokannan elvytyksestä ja uusien transaktioiden vastaanotosta. Ongelmana yhteislevyjärjestelmässä on edelleen mitoittuvuus: yhteys levyjärjestelmään voi muodostua pullonkaulaksi. Yhteismuistijärjestelmään verrattuna yhteislevyjärjestelmä voi mitoittua jonkin verran suurempaan määrään suorittimia, mutta suorittimien välinen kommunikointi on hitaampaa (koska se tapahtuu yhteenkytkentäverkon välityksellä). 182
15 Yhteislevyjärjestelmän kukin suoritin puskuroi yhteisen tietokannan sivuja yksityisessä puskurissaan. Koska sama sivu voi samanaikaisesti olla puskuroituna usean eri suorittimen puskurissa, on huolehdittava puskurieheydestä: Kun tietosivu q on puskuroituna suorittimilla P 1 ja P 2, ja suorittimella P 1 suorituksessa oleva transaktio haluaa lukea tai päivittää puskuroimassaan sivun q kopiossa olevan monikon, pitää taata, että monikko kuuluu tietokannan nykytilaan. Yhteiseen lokiin kirjataan eri suorittimilla suoritettavien transaktioiden tuottamia lokikirjauksia. Eri suorittimilla suoritettavat transaktiot varaavat lukkoja yhteisen tietokannan tietoalkioihin. Näistä aiheutuu kommunikointitarvetta eri suorittimien välillä. Samanaikaisuuden hallinta ja häiriöistä elvytys on monimutkaisempaa kuin keskitetyssä (transaktiopalvelin)järjestelmässä. 183
16 Yksityislevyjärjestelmä (shared-nothing system) eli massiivisesti rinnakkainen järjestelmä (massively-parallel-processing system, MPP system) koostuu itsenäisistä solmuista (node) eli pisteistä (site), joissa kussakin on suoritin, yksityinen keskusmuisti sekä yksi tai useampia yksityisiä levyjä. CPU CPU CPU CPU CPU Muisti Muisti Muisti Muisti Muisti Levy Levy Levy Levy Levy 184
17 Yksityislevyjärjestelmän solmut ovat yhteydessä toisiinsa nopean yhteenkytkentäverkon välityksellä. Solmu toimii järjestelmän palvelimena solmun omistamien tietojen osalta, so. niiden tietojen osalta, joita säilytetään solmun levyillä. Kaiken levyltä haun ja levylle viennin ei nyt tarvitse kulkea yhteisiä linjoja myöten. Ainoastaan kyselyt, joissa viitataan muihin kuin paikallisiin tietoihin, sekä vastaavat tulosrelaatiot täytyy välittää verkon kautta. Yhteenkytkentäverkko suunnitellaan mitoittuvaksi niin, että sen välityskapasiteetti lisääntyy sitä mukaa kuin järjestelmään lisätään uusia solmuja. Yksityislevyjärjestelmä onkin yhteismuisti- ja yhteislevyjärjestelmiä mitoittuvampi ja siihen voidaan liittää suuri määrä solmuja. 185
18 Suorittimien välinen kommunikointi sekä tietojen saanti muulta kuin paikalliselta levyltä ovat yksityislevyjärjestelmässä luonnollisesti hitaampia kuin yhteismuisti- tai yhteislevyjärjestelmässä. Jokainen solmu puskuroi vain omilla levyillään pysyvästi säilytettäviä tietokantasivuja, joten puskurieheyden ylläpito-ongelmaa ei ole. Mikäli jokainen solmu voi itsenäisesti suorittaa transaktioita, on kussakin solmussa oma lokilevy, ja solmussa ylläpidetään transaktioiden hallinnan tarvitsemia keskusmuistirakenteita (lukkotaulu, aktiivisten transaktioiden taulu, päivitettyjen sivujen taulu jne). Solmun lokiin kirjataan paikallisilla levyillä sijaitseviin tietokantasivuihin kohdistuneet päivitykset ja solmun lukkotaulussa säilytetään paikallisilla levyillä sijaitseviin tietoalkioihin varattuja lukkoja. Mikäli transaktio voi operoida useammassa eri solmussa sijaitseviin tietoihin, kysymyksessä on hajautettu transaktio, jonka suoritus joudutaan koordinoimaan (esim. kaksivaiheisella sitoutumiskäytännöllä). Tällaisen yksityislevyjärjestelmän hallinnassa käytetäänkin osin samoja menetelmiä kuin hajautetuissa tietokantajärjestelmissä. 186
19 Hierarkkinen järjestelmä (hierarchical system) yhdistää piirteitä yhteismuisti-, yhteislevy- ja yksityislevyjärjestelmistä. CPU CPU CPU CPU CPU CPU CPU CPU CPU CPU CPU CPU Muisti Muisti Muisti Muisti Levy Levy Levy Levy Levy Levy Levy Levy 187
20 Ylimmällä tasolla hierarkkinen järjestelmä koostuu yhteenkytkentäverkon yhdistämistä solmuista, joilla ei yhteistä muistia eikä levyä. Ylin taso on siis yksityislevyjärjestelmä. Kukin solmu voisi itse asiassa olla yhteismuistia käyttävä pieni joukko suorittimia. Kukin solmu voisi toisaalta olla yhteislevyjärjestelmä, ja kutakin samaa levyjoukkoa käyttävä järjestelmä yhteismuistijärjestelmä. Järjestelmä voidaan siis rakentaa hierarkiaksi, jonka alimmalla tasolla on muutaman suorittimen yhteismuistijärjestelmiä, keskimmäisellä tasolla yhteislevyjärjestelmiä ja ylimmällä tasolla yksityislevyjärjestelmä. 188
21 Tiedon osittaminen Levynkäsittelyn rinnakkaistamisessa (I/O parallelism) tietokantarelaation levyltätuontiaikaa ja levyllevientiaikaa pyritään vähentämään osittamalla (partition) relaatio useammalle levylle. Rinnakkaistietokannoissa yleisimmin käytetty tiedonositusmenetelmä on vaakasuora ositus (horizontal partitioning): Relaatio r ositetaan eli hajautetaan (decluster) n:lle levylle D 0,D 1,...,D n 1 yhtä moneen palaseen (fragment) eli osarelaatioon r 0,r 1,...,r n 1 niin, että (1) palanen r i sijoitetaan levylle D i, i = 0,1,...,n 1, (2) r 0 r 1... r n 1 = r ja (3) palaset ovat erillisiä, so. r i r j = /0, kun i j. Ositukseen on kolme perusmenetelmää: kiertovuoro, hajautus ja osavälit. Kiertovuoroon (round-robin) perustuvassa menettelyssä relaatio r luetaan läpi jossakin järjestyksessä ja r:n i:s monikko sijoitetaan levylle D i mod n. Menettely takaa monikoiden tasaisen jakautumisen levyille, ts. kukin levy saa suurin piirtein saman määrän monikoita. 189
22 Hajautusosituksessa (hash partitioning) jokin relaation r attribuuteista A sovitaan ositusattribuutiksi. Ositusattribuutteja voi olla useampiakin, jolloin ositus perustuu näiden arvokombinaatioon. Määritellään ositusattribuutin A arvojen joukkoon hajautin h, jonka maalijoukko on {0,1,...,n 1}. Relaation r monikko t, jolle h(t[a]) = i, sijoitetaan levylle D i. Osaväliosituksessa (range partitioning) sijoitetaan kullekin levylle relaation r monikot ositusattribuutin A tietyltä arvoväliltä. Ositusattribuutille A valitaan ositusvektori (partitioning vector) [v 0,v 1,...,v n 2 ], jossa v i :t ovat A:n arvojoukkoon kuuluvia arvoja niin että v i < v j aina kun i < j. Relaation r monikko t sijoitetaan (1) levylle D 0, jos t[a] < v 0, (2) levylle D i+1, jos v i t[a] < v i+1, ja (3) levylle D n 1, jos t[a] v n
23 Kun relaatio on ositettu, se voidaan lukea rinnakkaisesti, kukin osa omalta levyltään yhtäaikaa. Vastaavasti relaatiota ositettaessa osat voidaan kirjoittaa levyille samanaikaisesti. Tarkastellaan, miten eri ositusmenetelmät tehostavat erityyppisiä kyselyitä: (1) Koko relaation r tauluselaus (table scan): select from r. (2) Pistekysely (point query), so. relaation r monikon assosiatiivinen haku: select from r where A = a, missä A on (a) ositusattribuutti, (b) muu kuin ositusattribuutti. (3) Osavälikysely (range query), so. relaation r monikoiden haku attribuutin osaväliltä: select from r where A > a 1 and A < a 2, missä A on (a) ositusattribuutti, (b) muu kuin ositusattribuutti. 191
24 Kiertovuoro-ositus sopii ihanteellisesti kyselyihin, joissa selataan koko relaatio läpi eikä järjestyksellä ole väliä. Relaation selausaika on noin (1/n):s osa relaation selausajasta yhden levyn järjestelmässä. Pistekyselyihin ja osavälikyselyihin menettely sopii huonommin, sillä hakuehdon täyttäviä monikoita joudutaan aina hakemaan jokaiselta levyltä. Hajautusositus sopii parhaiten ositusattribuuttiin perustuviin pistekyselyihin: kysely on tarpeen suorittaa vain yhdelle levylle. Koko relaation selaus voidaan toteuttaa kuten kiertovuoro-ositetulle relaatiolle, mutta selaus ei ole yhtä tehokasta, jos eri levyillä on eri määrä relaation monikoita. Hajautusosituksesta ei ole mitään hyötyä pistekyselyissä, jotka perustuvat muihin kuin ositusattribuuttiin, ei liioin osavälikyselyissä. 192
25 Osaväliositus sopii hyvin ositusattribuuttiin perustuville piste- ja osavälikyselyille. Tiedon etsintä voidaan rajoittaa niihin levyihin, joiden osavälit leikkaavat kyselyn osavälejä. Tämä piirre on sekä etu että haitta. Etu on, että pienen (so. vähän monikoita sisältävän) osavälin kysely voidaan laskea lähettämällä se vain yhdelle (tai korkeintaan muutamalle) levylle; muita levyjä voidaan käyttää muiden kyselyiden laskemiseen, mikä lisää suoritustehoa ja ylläpitää hyvää vasteaikaa. Jos taas kyselyn osaväli on suuri, joudutaan hakemaan suuri määrä monikoita yhdeltä tai muutamalta levyltä, mikä voi aiheuttaa pullonkaulan kyseisillä levyillä. 193
26 Vinoumien käsittely Ositettuun tietoon kohdistuvassa kyselynlaskennassa voi esiintyä erilaisia vinoumia (skew). Kun kyselyn laskenta ei ole jakaantunut tasaisesti kaikille levyille, esiintyy suoritusvinouma (execution skew). Kun relaatio ositetaan muulla kuin kiertovuoromenetelmällä, relaation monikoiden jakauma levyille voi olla vino. Tämä voi johtua joko attribuuttiarvovinoumasta tai ositusvinoumasta. Attribuuttiarvovinouma (attribute-value skew) esiintyy, kun relaation ositusattribuutin arvojen jakauma on epätasainen. Hajautusosituksessa ja osaväliosituksessa kaikki tietyllä ositusattribuutin arvolla varustetut monikot joutuvat samalle levylle. Attribuuttiarvovinouma aiheuttaa siis näissä ositusmenetelmissä vinoutta monikoiden jakaumassa levyille. 194
27 Ositusvinoumalla (partition skew) tarkoitetaan osittamisessa esiintymää kuorman epätasapainoa, kun se ei johdu attribuuttiarvovinoumasta. Osaväliositus on altis paitsi attribuuttiarvovinoumalle myös ositusvinoumalle: ositusvektori on saatettu valita alunpitäen huonosti tai välien koot (so. välien sisältämien monikoiden määrät) poikkeavat päivitysten takia suuresti toisistaan. Ositusvinouma on vähemmän todennäköinen hajautusosituksessa, mikäli hajautin on valittu hyvin. 195
28 Vinouma on sitä suurempi ongelma, mitä suurempi on rinnakkaisuuden aste. Olkoon 1000 monikon relaatio r ositettu 10 palaseen. Jos ositus on vinoutunut, joissakin palasissa voi olla vähemmän kuin 100 ja joissakin palasissa enemmän kuin 100 monikkoa. Jos yhdessäkin palasessa on 200 monikkoa, relaation selauksessa rinnakkaistuksella saavutettava nopeutuvuus on vain 5 eikä 10. Oletetaan sitten, että sama relaatio r onkin ositettu 100 palaseen. Silloin yhdessä palasessa on keskimäärin 10 monikkoa. Palasten suuren määrän huomioon ottaen on hyvin mahdollista, että jossain palasessa sattuu olemaan 40 monikkoa tai enemmän. Rinnakkaistuksella saavutettava tauluselauksen nopeutuvuus on silloin vain 25 eikä 100. Nopeutuvuudessa siis menetetään vinouman vuoksi sitä enemmän mitä suurempi on rinnakkaisuuden aste. 196
29 Järjestämällä relaatio voidaan muodostaa tasapainoinen ositusvektori (balanced range-partitioning vector). Olkoon n osituksessa muodostettavien palasten lukumäärä. Relaatio järjestetään ensin ositusattribuutin mukaan. Sitten järjestetty relaatio selataan. Aina kun (1/n):s osa relaatiosta on luettu, seuraavan monikon ositusattribuutin arvo viedään ositusvektoriin. Jos relaatiossa on paha attribuuttiarvovinouma, tuotettu ositus voi yhä olla jonkin verran vino. Pahin haitta on luonnollisesti järjestämisen vaatima ylimääräinen levynkäsittelyaika. 197
30 Ositusvektorin muodostamisesta koituvaa rasitetta voidaan vähentää muodostamalla relaation r kullekin (tärkeälle) attribuutille A sen arvojakaumaa esittävä histogrammi, jota säilytetään tietokannan tietohakemistossa. Relaation r attribuutin A histogrammi on vektori, jonka i:s alkio sisältää ehdon a i t[a] < a i+1 täyttävien r:n monikoiden lukumääräarvion, kun a i on i:nnen osavälin alaraja ja a i+1 on i:nnen osavälin yläraja. Ositusattribuutin histogrammin avulla on suoraviivaista muodostaa ositusvektori, joka on kutakuinkin tasapainoinen. Jos histogrammia ei ole tallennettu, sille voidaan laskea approksimaatio otannalla, poimimalla monikoita satunnaisesti valitusta osasta relaation tietosivuja. 198
31 Toinen menettely erityisesti osaväliosituksen vinouman vaikutusten pienentämiseksi on käyttää virtuaalisuorittimia. Virtuaalisuoritin (virtual processor) on näennäinen (looginen) suoritin, joita voi olla usempia osoitettuna samalle todelliselle (fyysiselle) suorittimelle. Virtuaalisuorittimia voi olla monta kertaa enemmän kuin todellisia suorittimia. Ositus- ja laskentamenetelmät osittavat relaation monikot ja laskennan virtuaalisuorittimille. Virtuaalisuorittimet vuorostaan kuvataan todellisille suorittimille, yleensä käyttäen kiertovuoro-ositusta. Ajatuksena on, että vaikka jollakin osavälillä olisi vinouman takia enemmän monikoita kuin muilla osaväleillä, nämä monikot hajaantuvat useammalle virtuaalisuoritinosavälille. Virtuaalisuorittimien kiertovuoro-ositus hajauttaa ylimääräisen työn useampien todellisten suorittimien kesken, jolloin yksittäisen suorittimen ei tarvitse yksinään kantaa koko taakkaa. 199
32 Kyselyiden välinen ja kyselynsisäinen rinnakkaisuus Kyselyiden välinen rinnakkaisuus (interquery parallelism) tarkoittaa, että eri kyselyitä tai transaktioita suoritetaan samanaikaisesti eri suorittimilla. Transaktionkäsittelyn suoritusteho kasvaa, mutta yksittäisen transaktion vasteaika ei ole sen parempi kuin ajettaessa transaktio yksinään. Kyselyiden välisen rinnakkaisuuden päätarkoituksena onkin mitoittaa transaktionkäsittelyjärjestelmä niin, että se kykenee käsittelemään useampia transaktioita sekunnissa. Kyselyiden välinen rinnakkaisuus on rinnakkaisuuden muodoista se, joka on helpoiten toteutettavissa tietokantajärjestelmässä, erityisesti yhteismuistijärjestelmässä. Yhden suorittimen koneelle suunniteltua tietokantajärjestelmää voidaan käyttää vähäisin muutoksin myös yhteistä keskusmuistia käyttävällä rinnakkaiskoneella, sillä onhan siinä samanaikaisten prosessien hallinta. Transaktiot, jotka osituskäytössä voivat olla samanaikaisesti suorituksessa, voivat yhteismuistijärjestelmässä toimia aidosti rinnakkaisesti. 200
33 Kyselyiden välinen rinnakkaisuus on vaikeampaa toteuttaa yhteislevyjärjestelmässä ja yksityislevyjärjestelmässä. Suorittimien pitää suorittaa eräitä tehtäviä, kuten lukitus ja lokin hallinta, koordinoidusti, mikä edellyttää viestien vaihtoa. Järjestelmän tulee taata, ettei kaksi suoritinta päivitä samaa tietoa toisistaan riippumatta samaan aikaan. Kun suoritin käsittelee yhteisen tietokannan tietoa yksityisessä puskurissaan, järjestelmän täytyy taata puskurieheys, ts. että suorittimella on puskurissaan tietokantasivun tuore versio. Puskurieheyden ylläpitokäytäntö yleensä integroidaan transaktioiden samanaikaisuuden hallintaan. 201
34 Kyselynsisäinen rinnakkaisuus (intraquery parallelism) tarkoittaa, että kyselyn yksittäisiä osatehtäviä suoritetaan samanaikaisesti usealla suorittimella ja levyllä. Tarkoituksena on nopeuttaa pitkäkestoisia kyselyitä. Tarkastellaan esimerkkinä kyselyä, jonka laskenta edellyttää relaation r järjestämistä attribuutin A mukaan. Oletetaan, että r on ositettu usealle levylle attribuutin A osaväleihin perustuen. r voidaan silloin järjestää järjestämällä r:n palaset rinnakkaisesti ja katenoimalla järjestetyt palaset. Kysely voidaan siis rinnakkaistaa rinnakkaistamalla sen yksittäisen operaation laskenta silloin, kun operaatio voidaan jakaa osaoperaatioiksi, joiden tuloksista saadaan helposti koko operaation tulos (operaationsisäinen rinnakkaisuus). Useita operaatioita sisältävä kyselysuunnitelma voidaan rinnakkaistaa laskemalla rinnakkaisesti ne operaatiot, jotka eivät riipu toisistaan (operaatioiden välinen rinnakkaisuus). Toisistaan riippuvat kaksi operaatiota voidaan rinnakkaistaa, kun toisen operaation tuottamaa tulosta voidaan putkittaa toisen operaation kuluttamaksi syötteeksi. 202
35 Seuraavassa tarkastellaan erityyppisten kyselyiden rinnakkaistamista. Kyselyihin ei liity päivityksiä. Algoritmit luonnollisesti riippuvat rinnakkaisjärjestelmän arkkitehtuurista. Algoritmien kuvailussa käytetään kuitenkin yksinomaan yksityislevyjärjestelmää. Ts. kuvataan eksplisiittisesti, milloin tieto pitää siirtää suorittimelta toiselle. Yksityislevyjärjestelmää voidaan simuloida muissa järjestelmissä: tieto voidaan siirtää yhteisen muistin kautta yhteismuistijärjestelmässä ja yhteisten levyjen kautta yhteislevyjärjestelmässä. Yksinkertaisuuden vuoksi oletetaan, että järjestelmässä on n suoritinta, P 0,...,P n 1, ja n levyä, D 0,...,D n 1, missä D i on suorittimeen P i liittyvä levy. Algoritmit ovat helposti yleistettävissä tilanteeseen, jossa suorittimeen liittyy useampia levyjä. 203
36 Operaationsisäinen rinnakkaisuus Operaationsisäinen rinnakkaisuus (intraoperation parallelism) tarkoittaa, että yksittäistä tietokantaoperaatiota (järjestäminen, valinta, projektio, liitos jne) nopeutetaan jakamalla se rinnakkain suoritettaviksi osaoperaatioiksi. Relaation järjestäminen attribuutin A mukaan voidaan rinnakkaistaa seuraavasti. Oletetaan, että relaatio r on ositettu n:ään palaseen r 0,...,r n 1, missä r i on sijoitettu levylle D i. Mikäli ositus perustuu A:n osaväleihin, r voidaan järjestää rinnakkaisesti kuten edellä on todettu. Jos taas ositus on muunlainen, r voidaan ensin osittaa A:n osaväleihin. 204
37 Toinen mahdollisuus on rinnakkainen lomitusjärjestäminen (parallel merge sort): 1. Suoritin P i järjestää oman palasensa r i :n, i = 0,...,n Järjestetyt palaset r 0,...,r n 1 lomitetaan. Lomitusvaihe voidaan rinnakkaistaa seuraavasti: 1. Jaetaan A:n arvojoukko m:ään osaväliin jollakin m n. Ositetaan järjestetty palanen r i attribuutin A osavälien mukaan suorittimille P 0,...,P m 1, jokaisella i = 0,...,m 1. Monikot lähetetään järjestyksessä niin, että kukin suoritin P i saa monikot järjestettynä virtana. 2. Kukin suoritin P i lomittaa saamansa monikkovirrat sitä mukaa kuin niitä saapuu. 3. Suorittimilla P 0,...,P m 1 olevat järjestetyt r:n erät katenoidaan. Suoritusvinouman välttämiseksi pitää askeleessa 1 kunkin suorittimen lähettää monikot seuraavasti: Ensin ensimmäinen erä (esim. sivullinen) osavälin 1 monikoita suorittimelle P 1, sitten ensimmäinen erä osavälin 2 monikoita suorittimelle P 2 jne. Sitten toinen erä osavälin 1 monikoita suorittimelle P 1, sitten toinen erä osavälin 2 monikoita suorittimelle P 2 jne. 205
38 Valinnan σ A=v (r) laskennassa voidaan rajoittua suorittimeen P i, kun r on ositettu attribuutin A mukaan ja arvoa v vastaava r:n palanen on suorittimella P i. Kun relaatio r on ositettu attribuutin A osavälien mukaan, voidaan valinnan σ u A v (r) laskennassa rajoittua niihin suorittimiin, joille sijoitettujen r:n palasten osavälit leikkaavat väliä [u,v]. Muissa tapauksissa valintaoperaatio lasketaan rinnakkaisesti kaikilla niillä suorittimilla, joille r:n palasia on sijoitettu. 206
39 Kaksoiskappaleiden eliminointi relaatiosta r voidaan toteuttaa rinnakkaisjärjestämistä hyväksi käyttäen. Toinen tapa on osittaa r osaväleihin tai hajauttaen ja eliminoida kaksoiskappaleet rinnakkaisesti. Kaksoiskappaleet säilyttävä projektio π X (r) voidaan toteuttaa lukemalla r:n palasia rinnakkaisesti. Jos kaksoiskappaleet pitää eliminoida, menetellään kuten edellä. Ryhmittely- ja koosteoperaatio select X, f (A) from r group by X voidaan laskea osittamalla relaatio r attribuuttijoukon X mukaan osaväleihin (tai hajauttaen) ja laskemalla suorittimella P i sille osoitetut ryhmät. 207
40 Rinnakkaisliitos Relaatioiden r ja s liitoksen laskenta voidaan rinnakkaistaa, kun kysymyksessä on yhtäläisyys- tai luonnollinen liitos. Yhtäläisyysliitoksen r A=B s laskenta ositettuna rinnakkaisliitoksena (partitioned parallel join) tapahtuu seuraavasti: 1. Ositetaan r palasiin r 0,...,r n 1 attribuutin A mukaan hajautusositusta (osaväliositusta) käyttäen, missä r i osoitetaan suorittimelle P i. 2. Ositetaan s palasiin s 0,...,s n 1 attribuutin B mukaan hajautusositusta (osaväliositusta) käyttäen, missä s i osoitetaan suorittimelle P i. Askelissa 1 ja 2 käytetään samaa hajautinta (vast. ositusvektoria). 3. Suoritin P i laskee liitoksen q i = r i A=B s i jollakin tavanomaisella liitosmenetelmällä, i = 0,...,n 1. r 0 s 0 r 1 s 1 r r 2 s 2 r 3 s 3 r 4 s 4 s 4. Lopullinen liitos saadaan yhdisteenä q 0 q n
41 Algoritmi luonnollisesti yksinkertaistuu, jos jompikumpi tai molemmat relaatioista r ja s on jo valmiiksi ositettu liitosattribuutin mukaan. Vinouma on erityinen ongelma osaväliositusta käytettäessä, sillä ositus, joka jakaa relaation r yhtä suuriin palasiin, saattaa jakaa relaation s hyvin vaihtelevankokoisiin palasiin. Ositusvektorin pitää olla sellainen, että palasten r i ja s i monikoiden yhteenlaskettu määrä on kutakuinkin sama kaikilla i = 0, 1,..., n 1. Hajautusositus johtaa yleensä pienempään vinoumaan, paitsi silloin, kun liitosattribuutin jollain arvolla on hyvin monta esiintymää. 209
42 Osittaminen ei sovellu kaikentyyppisiin liitoksiin. Esim. liitoksessa r A<B s on mahdollista, että kaikki r:n monikot liittyvät johonkin s:n monikkoon (tai kääntäen). Ei siis ole mitään helppoa tapaa osittaa r ja s niin, että palasen r i monikot liittyisivät vain palasen s i monikoihin. Tämäntyyppisiä liitoksia r θ s voidaan kuitenkin rinnakkaistaa paloitteluksi ja toisintamiseksi (fragment and replicate) kutsutulla menetelmällä. Tarkastellaan ensin tämän menetelmän erikoistapausta, epäsymmetristä paloittelu- ja toisinnusliitosta (asymmetric fragment-andreplicate join): 1. Ositetaan toinen relaatio, esimerkiksi r, jollakin ositusmenetelmällä, vaikkapa kiertovuoro-osituksella. 2. Toisinnetaan (so. kopioidaan) toinen relaatio, s, kaikille suorittimille. 3. Suoritin P i laskee paikallisesti liitoksen r i θ s jollakin liitosmenetelmällä. r 0 s r 1 s r r 2 s s r 3 s r 4 s 210
43 Yleinen paloittelu- ja toisinnusliitos (fragment-and-replicate join) toimii seuraavasti: 1. Ositetaan r jollakin menetelmällä n:ään palaseen r 0,...,r n Ositetaan s jollakin menetelmällä m:ään palaseen s 0,...,s m 1. Askelissa 1 ja 2 ei tarvitse käyttää samaa ositusmenetelmää eikä n:n tarvitse olla yhtä suuri kuin m. n ja m pitää kuitenkin valita niin, että käytettävissä on vähintään n m suoritinta. 3. Toisinnetaan palanen r i suorittimille P i, j, j = 0,...,m 1, i = 0,...,n Toisinnetaan palanen s j suorittimille P i, j, i = 0,...,n 1, j = 0,...,m Suorittimella P i, j lasketaan liitos r i θ s j jollakin liitosmenetelmällä. r 0 s 0 r 0 s 1 r 0 s 2 r 0 s 3 r 0 s 4 r 1 s 0 r 1 s 1 r 1 s 2 r 1 s 3 r 1 s 4 r 2 s 0 r 2 s 1 r 2 s 2 r 2 s 3 r 2 s 4 r 3 s 0 r 3 s 1 r 3 s 2 r 3 s 3 r 3 s 4 211
44 Tarkastellaan liitoksen r A=B s laskemista tapauksessa, että r on valmiiksi ositettu (jollakin menetelmällä) palasiin r 0,...,r n 1 ja että s on paljon pienempi kuin r. Relaation r ositus ei perustu liitosattribuuttiin B. Oletetaan vielä, että palasen r i tallentavalla suorittimella P i on hakemisto palaseen r i liitosattribuutilla A, i = 0,...,n 1. Lasketaan liitos epäsymmetrisenä paloittelu- ja toisinnusliitoksena, jossa relaatio s toisinnetaan ja r:lle käytetään olemassaolevaa ositusta. Jokainen suoritin P j, jolla on relaation s palanen, toisintaa sen kaikille muille suorittimille. Tämän vaiheen jälkeen kaikilla suorittimilla on toisinnettuna koko relaatio s. Nyt jokainen suoritin P i laskee liitoksen s A=B r i hakemistoliitoksena (indexed nested-loop join). Hakemistoliitokset voidaan laskea limittäin s:n palasten toisintamisen kanssa niin, että vältetään s:n monikoiden viemistä levylle. Liitos ja toisintaminen täytyy tahdistaa niin, että jokaisella suorittimella P i on kylliksi keskusmuistitilaa niiden s:n monikoiden säilyttämiseen, joita ei vielä ole käytetty liitoksen s A=B r i laskennassa. 212
45 Operaatioiden rinnakkaislaskennan kustannus Rinnakkaisuutta saavutetaan osittamalla levynkäsittelyä usealle levylle ja osittamalla keskusmuistikäsittelyä usealle suorittimelle. Jos osittaminen pystytään toteuttamaan aiheuttamatta mitään ylimääräistä rasitetta ja jos työkuorman osituksessa ei esiinny vinoumaa, n:ää suoritinta käyttävä rinnakkaisoperaatio vie vain 1/n-osan siitä ajasta, minkä sama operaatio veisi yhdellä suorittimella. Täytyy kuitenkin ottaa huomioon myös seuraavat lisäkustannukset: (1) Operaation käynnistyskustannus (startup cost), joka koituu operaation käynnistämisestä usealla suorittimella. (2) Vinouma (skew), joka voi esiintyä työkuorman jakelussa prosesssoreille, niin että jotkin suorittimet saavat suuremman työkuorman kuin muut. (3) Kilpailu resursseista (contention for resources), kuten muistista, levystä ja yhteysverkosta, mistä aiheutuu viipeitä. (4) Laskennan lopullisen tuloksen koontikustannus (cost of assembling), mikä sisältää osittaistulosten siirtoja suorittimelta toiselle. 213
46 Rinnakkaisoperaation viemäksi ajaksi voidaan arvioida T part + T asm + max{t 0,T 1,...,T n 1 }, missä T part on relaatioiden ositusaika, T asm on tuloksen koontiaika ja T i on operaation viemä aika suorittimella P i. Mikäli osittamisessa ei esiinny mitään vinoumaa, kukin suoritin saa 1/n-osan monikoiden kokonaismäärästä. Mikäli kilpailua resursseista ei oteta huomioon, kullakin yksittäisellä suorittimella P i suoritettavien operaatioiden kustannukset voidaan arvioida erikseen. Saatu arvio on optimistinen, sillä työkuorman jakaantuminen suorittimille on usein vino. Vaikka yksittäisen kyselyn osittaminen joukoksi rinnakkaisia osatehtäviä pienentää keskimääräisen tehtävän kokoa, kyselyn laskentaajan määrää hitain osatehtävä. Ositettu rinnakkaislaskenta on vain niin nopea kuin hitain yksittäinen laskenta. 214
47 Operaatioiden välinen rinnakkaisuus Operaatioiden välinen rinnakkaisuus (interoperation parallelism) tarkoittaa, että kyselyä nopeutetaan suorittamalla kyselysuunnitelman sisältämiä eri operaatioita rinnakkain. Operaatioiden välistä rinnakkaisuutta on kahta lajia: putkitettua rinnakkaisuutta ja riippumatonta rinnakkaisuutta. Putkitetussa rinnakkaisuudessa (pipelined parallelism) operaatiot o 1 ja o 2 ajetaan rinnakkain eri suorittimilla niin, että o 2 kuluttaa monikoita sitä mukaa kuin o 1 tuottaa niitä. Liitoksen r 1 (AB) r 2 (BC) r 3 (CD) r 4 (DE) laskennassa voidaan hyödyntää putkitettua rinnakkaisuutta käyttämällä liitosten vasemmalle syvää laskentajärjestystä ((r 1 r 2 ) r 3 ) r 4 : (1) s 1 = r 1 r 2 suorittimella P 1, (2) s 2 = s 1 r 3 suorittimella P 2 ja (3) s 3 = s 2 r 4 suorittimella P 3. Rinnakkaisuutta saavutetaan luonnollisesti vain, jos käytetään putkitukseen soveltuvaa liitosmenetelmää. 215
48 Putkitettu rinnakkaisuus on käyttökelpoista pienellä määrällä suorittimia, muttei mitoutu hyvin. Putkiketjut ovat yleensä niin lyhyitä, että rinnakkaisuusaste jää matalaksi. Sellaisia operaatioita (kuten joukkoerotus), jotka voivat tuottaa tulosta vasta kun koko syöte on saatavilla, ei voi putkittaa ollenkaan. Tapauksissa, joissa yhden operaation kustannus on huomattavasti muita korkeampi, putkituksesta saatava nopeutus on marginaalinen. Kun rinnakkaisuusaste on korkea, putkitus on rinnakkaisuuden lähteenä toissijainen tiedon osittamisella saavutettuun rinnakkaisuuteen nähden. Putkituksen tärkein hyöty onkin siinä, että vältytään kirjoittamasta välituloksia levylle. 216
49 Riippumattomassa rinnakkaisuudessa (independent parallelism) kyselyn operaatiot, jotka eivät riipu toisistaan, suoritetaan rinnakkain. Liitoksen r 1 (AB) r 2 (BC) r 3 (CD) r 4 (DE) laskennassa voidaan hyödyntää riippumatonta rinnakkaisuutta käyttämällä liitosten laskentajärjestystä (r 1 r 2 ) (r 3 r 4 ). Tässä liitokset s 1 = r 1 r 2 ja s 2 = r 3 r 4 voidaan laskea toisistaan riippumattomasti rinnakkain eri suorittimilla: lasketaan s 1 suorittimella P 1 ja s 2 suorittimella P 2. Lopullinen liitos s 3 = s 1 s 2 voidaan laskea suorittimella P 3. s 3 :n laskenta voi toimia rinnakkain s 1 :n ja s 2 :n laskennan kanssa, jos käytetään sopivaa liitosalgoritmia, esim. hajautusliitosta. s 3 :n laskennalle P 3 :ssa putkitetaan s 1 :n laskennan tuottamia monikoita P 1 :stä ja s 2 :n laskennan tuottamia monikoita P 2 :sta. P 3 sijoittaa vastaan ottamiaan monikoita liitosattribuutin C mukaan organisoituun hajautusrakenteeseen, jonka perusteella P 3 voi tuottaa lopulliseen liitokseen s 3 tulevia monikoita. Kuten putkitettu rinnakkaisuus, riippumaton rinnakkaisuuskaan ei yleensä tarjoa korkeaa rinnakkaisuuden astetta. 217
50 Rinnakkaistietokannan kyselynoptimointi Kyselynoptimointi rinnakkaisjärjestelmässä on monimutkaisempaa kuin peräkkäisjärjestelmässä (so. yhden suorittimen tietokantajärjestelmässä). Kustannusmallit ovat monimutkaisempia, koska osituskustannukset täytyy ottaa huomioon, samoin kuin vinoumat ja suorittimien kilpailu resursseista. Tärkeimpänä uutena ongelmana on kyselyn rinnakkaistamistavan määrääminen. Oletetaan, että kyselylle on jollain tavalla valittu ekvivalenttien relaatiolausekkeiden joukosta lauseke, jonka mukaan kysely on tarkoitus laskea. Tarkastellaan lauseketta operaatiopuuna. Operaatiopuun laskemiseksi rinnakkaisjärjestelmässä operaatiopuulle on luotava ajoitus (scheduling), so. on tehtävä seuraavat päätökset: (1) Miten kukin operaatio rinnakkaistetaan ja kuinka montaa suoritinta operaation laskentaan käytetään? (2) Mitä operaatioita putkitetaan eri suorittimien välillä, mitkä operaatiot suoritetaan rinnakkaisesti toisistaan riippumattomasti ja mitkä operaatiot suoritetaan peräkkäisesti, yksi toisensa jälkeen? 218
51 Optimointiongelmaan liittyy myös erityyppisten resurssien, kuten suorittimien, levyjen ja muistien, varaaminen kullekin operaatiolle. Saattaa tuntua järkevältä käyttää rinnakkaisuutta hyväksi maksimaalisesti, mutta tietyt operaatiot on syytä toteuttaa peräkkäisesti. Operaatiot, joiden laskentavaatimukset ovat merkittävästi alhaisemmat kuin kommunikoinnista aiheutuva rasite, kannattaa sijoittaa naapuriensa läheisyyteen. Pitkät operaatioputket eivät johda hyvään resurssien käyttöön. Putken viimeinen operaatio saattaa joutua odottamaan pitkään syötettään samalla kun se pitää varattuna kallista resurssia kuten muistia. Rinnakkaisia kyselysuunnitelmia on valittavana paljon suurempi joukko kuin peräkkäisiä kyselysuunnitelmia. Kyselynoptimointi on siis kalliimpaa rinnakkaisjärjestelmässä kuin peräkkäisjärjestelmässä. 219
52 Vaihtoehtoisia kyselysuunnitelmia on syytä karsia heuristisesti. Eräs heuristiikka on rajoittua sellaisiin kyselysuunnitelmiin, joissa jokainen operaatio rinnakkaistetaan kaikille suorittimille ja joissa ei käytetä lainkaan putkitusta. Parhaan kyselysuunnitelman etsiminen on silloin samanlaista kuin peräkkäisjärjestelmässä. Erona on osituksen suorittamistapa sekä käytettävä kustannusarviointikaava. Toinen heuristiikka on valita ensin tehokkain peräkkäinen kyselysuunnitelma ja sitten rinnakkaistaa sen operaatiot. Kyselynoptimointiin vaikuttaa luonnollisesti myös tietojen fyysinen organisointi (hakemistot jne). 220
53 Rinnakkaisjärjestelmän suunnittelusta Suurimittaisia rinnakkaisjärjestelmiä käytetään enimmäkseen suurten tietomäärien tallentamiseen kuten tietovarastointiin (data warehousing) sekä tähän tietoon kohdistuvien, yrityksen päätöksentekoa tukevien kyselyiden (decision-support queries) käsittelyyn. Tietovaraston pääasiallisinta käyttötapaa kutsutaan tosiaikaiseksi tiedonjalostukseksi (online analytic processing, OLAP). Tietovarasto saa tietonsa tavallisista operatiivisista tietokannoista (transaktionkäsittelyjärjestelmistä) ja muista informaatiolähteistä aika ajoin tapahtuvissa latauksissa (loading). Rinnakkaislataus (parallel loading) on keino tehostaa suuren tietomäärän latausta tietovarastoon. 221
54 Kun tietokannan tietomäärä kohoaa teratavuihin, sinänsä yksinkertaiset operaatiot kuten hakemistojen luonti sekä tietokannan kaavion muutokset (esim. attribuutin lisäys relaatioon) voivat viedä hyvin pitkän ajan, useita tunteja tai jopa päiviä. Ei ole suotavaa pitää järjestelmää poissa normaalikäytöstä niin pitkää aikaa. Mainitunlainen tietokannan uudelleenjärjestely (reorganization) pitäisi voida suorittaa tosiaikaisesti (online), normaalin käytön kanssa rinnakkaisesti. Relaation tosiaikaisessa hakemistonluonnissa (online index construction) järjestelmä sallii relaation luku- ja päivitysoperaatioiden suorituksen samanaikaisesti hakemistonluonnin kanssa. Hakemistonluontioperaatio ei siis voi S-lukita koko relaatiota. 222
55 Suuren rinnakkaistietokantajärjestelmän tulee sietää häiriöitä, joita voi sattua joillakin suorittimilla tai levyillä. Kun suorittimia ja levyjä on monta, yhden suorittimen tai levyn toimintahäiriö on merkittävästi todennäköisempi kuin yhden suorittimen ja yhden levyn järjestelmässä. Huonosti suunniteltu rinnakkaisjärjestelmä lopettaa toimintansa yhdenkin komponentin (suorittimen tai levyn) mentyä epäkuntoon. Olettaen, että yksittäisen suorittimen tai levyn häiriön todennäköisyys on pieni, järjestelmän häiriön todennäköisyys kasvaa lineaarisesti järjestelmän suorittimien ja levyjen lukumäärään nähden. Jos yksittäinen suoritin tai levy joutuu epäkuntoon kerran viidessä vuodessa, niin 100 suorittimen järjestelmässä on häiriö joka 18. päivä. 223
56 Suurimittaiset rinnakkaistietokantajärjestelmät on suunniteltu toimimaan, vaikka jokin suoritin tai levy joutuisi epäkuntoon. Kaikki tieto toisinnetaan ainakin kahdelle suorittimelle. Järjestelmä pitää kirjaa epäkuntoon joutuneista suorittimista ja jakelee työkuormaa toimivien suorittimien kesken. Epäkuntoon joutuneessa pisteessä tallennettuun tietoon kohdistuvat kyselyt reititetään automaattisesti sille etävarmistuspisteelle (backup site), jossa tieto on toisinnettuna. Jos romahtaneen suorittimen P kaikki tieto on toisinnettuna ainoastaan suorittimelle P, joutuu P käsittelemään omien kyselyidensä lisäksi myös P:n kyselyt, mikä tekee P :sta pullonkaulan. Yhden suorittimen tallentamat tiedot onkin syytä toisintaa useammalle muulle suorittimelle. 224
Käyttöjärjestelmät: Virtuaalimuisti
 Käyttöjärjestelmät: Virtuaalimuisti Teemu Saarelainen Tietotekniikka teemu.saarelainen@kyamk.fi Lähteet Stallings, W. Operating Systems Haikala, Järvinen, Käyttöjärjestelmät Eri Web-lähteet Muistinhallinta
Käyttöjärjestelmät: Virtuaalimuisti Teemu Saarelainen Tietotekniikka teemu.saarelainen@kyamk.fi Lähteet Stallings, W. Operating Systems Haikala, Järvinen, Käyttöjärjestelmät Eri Web-lähteet Muistinhallinta
Seminaari: Keskusmuistitietokannat. Keskusmuistitietokantojen samanaikaisuuden hallinta Ilkka Pullinen
 Seminaari: Keskusmuistitietokannat Keskusmuistitietokantojen samanaikaisuuden hallinta Ilkka Pullinen Sisältö Johdanto Esiteltävien menetelmien taustoja Hajautetun tietokannan spekuloiva samanaikaisuuden
Seminaari: Keskusmuistitietokannat Keskusmuistitietokantojen samanaikaisuuden hallinta Ilkka Pullinen Sisältö Johdanto Esiteltävien menetelmien taustoja Hajautetun tietokannan spekuloiva samanaikaisuuden
Johdatus diskreettiin matematiikkaan Harjoitus 7, 28.10.2015
 Johdatus diskreettiin matematiikkaan Harjoitus 7, 28.10.2015 1. Onko olemassa yhtenäistä verkkoa, jossa (a) jokaisen kärjen aste on 6, (b) jokaisen kärjen aste on 5, ja paperille piirrettynä sivut eivät
Johdatus diskreettiin matematiikkaan Harjoitus 7, 28.10.2015 1. Onko olemassa yhtenäistä verkkoa, jossa (a) jokaisen kärjen aste on 6, (b) jokaisen kärjen aste on 5, ja paperille piirrettynä sivut eivät
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 8 1 Derivaatta Tarkastellaan funktion f keskimääräistä muutosta tietyllä välillä ( 0, ). Funktio f muuttuu tällä välillä määrän. Kun tämä määrä jaetaan välin pituudella,
Matematiikan tukikurssi Kurssikerta 8 1 Derivaatta Tarkastellaan funktion f keskimääräistä muutosta tietyllä välillä ( 0, ). Funktio f muuttuu tällä välillä määrän. Kun tämä määrä jaetaan välin pituudella,
TILASTOLLINEN LAADUNVALVONTA
 1 Aki Taanila TILASTOLLINEN LAADUNVALVONTA 31.10.2008 2 TILASTOLLINEN LAADUNVALVONTA Tasalaatuisuus on hyvä tavoite, jota ei yleensä voida täydellisesti saavuttaa: asiakaspalvelun laatu vaihtelee, vaikka
1 Aki Taanila TILASTOLLINEN LAADUNVALVONTA 31.10.2008 2 TILASTOLLINEN LAADUNVALVONTA Tasalaatuisuus on hyvä tavoite, jota ei yleensä voida täydellisesti saavuttaa: asiakaspalvelun laatu vaihtelee, vaikka
Lisää segmenttipuusta
 Luku 24 Lisää segmenttipuusta Segmenttipuu on monipuolinen tietorakenne, joka mahdollistaa monenlaisten kyselyiden toteuttamisen tehokkaasti. Tähän mennessä olemme käyttäneet kuitenkin segmenttipuuta melko
Luku 24 Lisää segmenttipuusta Segmenttipuu on monipuolinen tietorakenne, joka mahdollistaa monenlaisten kyselyiden toteuttamisen tehokkaasti. Tähän mennessä olemme käyttäneet kuitenkin segmenttipuuta melko
monissa laskimissa luvun x käänteisluku saadaan näyttöön painamalla x - näppäintä.
 .. Käänteisunktio.. Käänteisunktio Mikäli unktio : A B on bijektio, niin joukkojen A ja B alkioiden välillä vallitsee kääntäen yksikäsitteinen vastaavuus eli A vastaa täsmälleen yksi y B, joten myös se
.. Käänteisunktio.. Käänteisunktio Mikäli unktio : A B on bijektio, niin joukkojen A ja B alkioiden välillä vallitsee kääntäen yksikäsitteinen vastaavuus eli A vastaa täsmälleen yksi y B, joten myös se
D B. Levykön rakenne. pyöriviä levyjä ura. lohko. Hakuvarsi. sektori. luku-/kirjoituspää
 Levyn rakenne Levykössä (disk drive) on useita samankeskisiä levyjä (disk) Levyissä on magneettinen pinta (disk surface) kummallakin puolella levyä Levyllä on osoitettavissa olevia uria (track), muutamasta
Levyn rakenne Levykössä (disk drive) on useita samankeskisiä levyjä (disk) Levyissä on magneettinen pinta (disk surface) kummallakin puolella levyä Levyllä on osoitettavissa olevia uria (track), muutamasta
arvostelija NoSQL-tietokannat Joel Sandborg Helsinki 27.3.2012 HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
 hyväksymispäivä arvosana arvostelija NoSQL-tietokannat Joel Sandborg Helsinki 27.3.2012 HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI
hyväksymispäivä arvosana arvostelija NoSQL-tietokannat Joel Sandborg Helsinki 27.3.2012 HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos HELSINGIN YLIOPISTO HELSINGFORS UNIVERSITET UNIVERSITY OF HELSINKI
Laajan mittakaavan Internet-sovelluksia varten kehitetyt hajautetut tietokannat
 Laajan mittakaavan Internet-sovelluksia varten kehitetyt hajautetut tietokannat Joel Sandborg Helsinki 28.12.2012 Pro gradu -tutkielma HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos HELSINGIN YLIOPISTO
Laajan mittakaavan Internet-sovelluksia varten kehitetyt hajautetut tietokannat Joel Sandborg Helsinki 28.12.2012 Pro gradu -tutkielma HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos HELSINGIN YLIOPISTO
Huomaathan, että ohjeessa olevat näytöistä otetut kuvat voivat poiketa sinun koulutuksesi vastaavien sivujen kuvista.
 OHJE OPISKELIJALLE MOODLEN KÄYTTÖÖN 1/5 2011/2012 MOODLE KOULUTUKSESSA Työterveyslaitoksella käytetään Moodle -verkko-oppimisalustaa. Potilassiirtojen Ergonomia - koulutus on monimuotokoulutusta, johon
OHJE OPISKELIJALLE MOODLEN KÄYTTÖÖN 1/5 2011/2012 MOODLE KOULUTUKSESSA Työterveyslaitoksella käytetään Moodle -verkko-oppimisalustaa. Potilassiirtojen Ergonomia - koulutus on monimuotokoulutusta, johon
Epäyhtälön molemmille puolille voidaan lisätä sama luku: kaikilla reaaliluvuilla a, b ja c on voimassa a < b a + c < b + c ja a b a + c b + c.
 Epäyhtälö Kahden lausekkeen A ja B välisiä järjestysrelaatioita A < B, A B, A > B ja A B nimitetään epäyhtälöiksi. Esimerkiksi 2 < 6, 9 10, 5 > a + + 2 ja ( + 1) 2 2 + 2 ovat epäyhtälöitä. Epäyhtälössä
Epäyhtälö Kahden lausekkeen A ja B välisiä järjestysrelaatioita A < B, A B, A > B ja A B nimitetään epäyhtälöiksi. Esimerkiksi 2 < 6, 9 10, 5 > a + + 2 ja ( + 1) 2 2 + 2 ovat epäyhtälöitä. Epäyhtälössä
Luonnollisten lukujen laskutoimitusten määrittely Peanon aksioomien pohjalta
 Simo K. Kivelä, 15.4.2003 Luonnollisten lukujen laskutoimitusten määrittely Peanon aksioomien pohjalta Aksioomat Luonnolliset luvut voidaan määritellä Peanon aksioomien avulla. Tarkastelun kohteena on
Simo K. Kivelä, 15.4.2003 Luonnollisten lukujen laskutoimitusten määrittely Peanon aksioomien pohjalta Aksioomat Luonnolliset luvut voidaan määritellä Peanon aksioomien avulla. Tarkastelun kohteena on
String-vertailusta ja Scannerin käytöstä (1/2) String-vertailusta ja Scannerin käytöstä (2/2) Luentoesimerkki 4.1
 String-vertailusta ja Scannerin käytöstä (1/2) Vertailuja tehdessä törmätään usein tilanteeseen, jossa merkkijonoa (esimerkiksi merkkijonomuuttujaa) pitää vertailla toiseen merkkijonoon. Tällöin tavanomainen
String-vertailusta ja Scannerin käytöstä (1/2) Vertailuja tehdessä törmätään usein tilanteeseen, jossa merkkijonoa (esimerkiksi merkkijonomuuttujaa) pitää vertailla toiseen merkkijonoon. Tällöin tavanomainen
Tiedon hajauttaminen ja hajautettu kyselynkäsittely
 Tiedon hajauttaminen ja hajautettu kyselynkäsittely M. Kifer, A. Bernstein & P. M. Lewis: Database Systems. An Application-Oriented Approach. Complete Version. Second Edition. Pearson Addison Wesley, 2006;
Tiedon hajauttaminen ja hajautettu kyselynkäsittely M. Kifer, A. Bernstein & P. M. Lewis: Database Systems. An Application-Oriented Approach. Complete Version. Second Edition. Pearson Addison Wesley, 2006;
ESTON LASKENTA VERKOSSA
 J. Virtamo 38.3141 Teleliikenneteoria / Esto verkossa 1 ESTON LASKENTA VERKOSSA Erlangin funktion E(C, a) avulla voidaan laskea esto yhdessä linkissä, jonka kapasiteetti on C (johtoa) ja johon tarjotun
J. Virtamo 38.3141 Teleliikenneteoria / Esto verkossa 1 ESTON LASKENTA VERKOSSA Erlangin funktion E(C, a) avulla voidaan laskea esto yhdessä linkissä, jonka kapasiteetti on C (johtoa) ja johon tarjotun
VÄLIMUISTITIETOISET PUSKURIT. Markus Montonen
 VÄLIMUISTITIETOISET PUSKURIT Markus Montonen Sisällys 1. Johdanto 2. L1-välimuistin puskuroinnin ongelma ja ratkaisuehdotus 3. L1-välimuistin puskurioperaation kokeellinen tutkiminen 4. L2-välimuistin
VÄLIMUISTITIETOISET PUSKURIT Markus Montonen Sisällys 1. Johdanto 2. L1-välimuistin puskuroinnin ongelma ja ratkaisuehdotus 3. L1-välimuistin puskurioperaation kokeellinen tutkiminen 4. L2-välimuistin
Lausuntopyyntö STM 2015
 Lausuntopyyntö STM 2015 1. Vastaajatahon virallinen nimi Nimi - Vaasan sairaanhoitopiirin ky 2. Vastauksen kirjanneen henkilön nimi Nimi - Göran Honga 3. Vastauksen vastuuhenkilön yhteystiedot Nimi Asema
Lausuntopyyntö STM 2015 1. Vastaajatahon virallinen nimi Nimi - Vaasan sairaanhoitopiirin ky 2. Vastauksen kirjanneen henkilön nimi Nimi - Göran Honga 3. Vastauksen vastuuhenkilön yhteystiedot Nimi Asema
Miten korkeakoulujen yhteishaun ja erillishakujen kokonaisuutta tulisi kehittää?
 Miten korkeakoulujen yhteishaun ja erillishakujen kokonaisuutta tulisi kehittää? Nykytilan haasteita, mahdollisen kehittämisen aikataulu ja vaihtoehtoja OKM/KTPO 2.6.2016 Tulevat haut ja kehittämisen aikajanaa
Miten korkeakoulujen yhteishaun ja erillishakujen kokonaisuutta tulisi kehittää? Nykytilan haasteita, mahdollisen kehittämisen aikataulu ja vaihtoehtoja OKM/KTPO 2.6.2016 Tulevat haut ja kehittämisen aikajanaa
Numeeriset menetelmät
 Numeeriset menetelmät Luento 1 Ti 6.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 1 Ti 6.9.2011 p. 1/28 p. 1/28 Numeriikan termejä Simulointi: Reaalimaailman ilmiöiden jäljitteleminen (yleensä)
Numeeriset menetelmät Luento 1 Ti 6.9.2011 Timo Männikkö Numeeriset menetelmät Syksy 2011 Luento 1 Ti 6.9.2011 p. 1/28 p. 1/28 Numeriikan termejä Simulointi: Reaalimaailman ilmiöiden jäljitteleminen (yleensä)
Ratkaisuehdotukset Kesäyliopisto 2014. 1. Kuvassa on esitetty erään ravintolan lounasbuffetin kysyntäfunktio.
 Harjoitukset 2 Taloustieteen perusteet Ratkaisuehdotukset Kesäyliopisto 2014 1. Kuvassa on esitetty erään ravintolan lounasbuffetin kysyntäfunktio. a) Mikä on kysynnän hintajousto 12 :n ja 6 :n välillä?
Harjoitukset 2 Taloustieteen perusteet Ratkaisuehdotukset Kesäyliopisto 2014 1. Kuvassa on esitetty erään ravintolan lounasbuffetin kysyntäfunktio. a) Mikä on kysynnän hintajousto 12 :n ja 6 :n välillä?
Kenguru 2016 Mini-Ecolier (2. ja 3. luokka) Ratkaisut
 sivu 1 / 11 TEHTÄVÄ 1 2 3 4 5 6 VASTAUS E B C D D A TEHTÄVÄ 7 8 9 10 11 12 VASTAUS E C D C E C TEHTÄVÄ 13 14 15 16 17 18 VASTAUS A B E E B A sivu 2 / 11 3 pistettä 1. Anni, Bert, Camilla, David ja Eemeli
sivu 1 / 11 TEHTÄVÄ 1 2 3 4 5 6 VASTAUS E B C D D A TEHTÄVÄ 7 8 9 10 11 12 VASTAUS E C D C E C TEHTÄVÄ 13 14 15 16 17 18 VASTAUS A B E E B A sivu 2 / 11 3 pistettä 1. Anni, Bert, Camilla, David ja Eemeli
SQL-perusteet, SELECT-, INSERT-, CREATE-lauseet
 SQL-perusteet, SELECT-, INSERT-, CREATE-lauseet A271117, Tietokannat Teemu Saarelainen teemu.saarelainen@kyamk.fi Lähteet: Leon Atkinson: core MySQL Ari Hovi: SQL-opas TTY:n tietokantojen perusteet-kurssin
SQL-perusteet, SELECT-, INSERT-, CREATE-lauseet A271117, Tietokannat Teemu Saarelainen teemu.saarelainen@kyamk.fi Lähteet: Leon Atkinson: core MySQL Ari Hovi: SQL-opas TTY:n tietokantojen perusteet-kurssin
5. Luento: Rinnakkaisuus ja reaaliaika. Tommi Mikkonen, tommi.mikkonen@tut.fi
 5. Luento: Rinnakkaisuus ja reaaliaika Tommi Mikkonen, tommi.mikkonen@tut.fi Agenda Perusongelmat Jako prosesseihin Reaaliaika Rinnakkaisuus Rinnakkaisuus tarkoittaa tässä yhteydessä useamman kuin yhden
5. Luento: Rinnakkaisuus ja reaaliaika Tommi Mikkonen, tommi.mikkonen@tut.fi Agenda Perusongelmat Jako prosesseihin Reaaliaika Rinnakkaisuus Rinnakkaisuus tarkoittaa tässä yhteydessä useamman kuin yhden
Helsingin yliopisto/ tktl DO Tietokantojen perusteet, s 2000 Relaatioalgebra 14.9.2000. Harri Laine 1. Relaatioalgebra
 DO NOT PRINT THIS DOCUMENT operaatiot, joilla relaatioista voidaan muodostaa uusia relaatioita joukko opin perusoperaatiot yhdiste, erotus, ristitulo, leikkaus erityisiä relaatioalgebran operaatioita projektio,
DO NOT PRINT THIS DOCUMENT operaatiot, joilla relaatioista voidaan muodostaa uusia relaatioita joukko opin perusoperaatiot yhdiste, erotus, ristitulo, leikkaus erityisiä relaatioalgebran operaatioita projektio,
SKYPE-RYHMÄN LUOMINEN
 SKYPE-RYHMÄN LUOMINEN JA RYHMÄPUHELUN SOITTAMINEN Ryhmän perustaminen on helppoa. Tarvitset internet-yhteyden sekä tietokoneen, jossa on mikrofoni ja webbikamera. Useimmissa kannettavissa tietokoneissa
SKYPE-RYHMÄN LUOMINEN JA RYHMÄPUHELUN SOITTAMINEN Ryhmän perustaminen on helppoa. Tarvitset internet-yhteyden sekä tietokoneen, jossa on mikrofoni ja webbikamera. Useimmissa kannettavissa tietokoneissa
2.2 Täydellinen yhtälö. Ratkaisukaava
 . Täydellinen yhtälö. Ratkaisukaava Tulon nollasäännöstä näkee silloin tällöin omituisia sovellutuksia. Jotkut näet ajattelevat, että on olemassa myöskin tulon -sääntö tai tulon "mikä-tahansa"- sääntö.
. Täydellinen yhtälö. Ratkaisukaava Tulon nollasäännöstä näkee silloin tällöin omituisia sovellutuksia. Jotkut näet ajattelevat, että on olemassa myöskin tulon -sääntö tai tulon "mikä-tahansa"- sääntö.
MAA10 HARJOITUSTEHTÄVIÄ
 MAA0 Määritä se funktion f: f() = + integraalifunktio, jolle F() = Määritä se funktion f : f() = integraalifunktio, jonka kuvaaja sivuaa suoraa y = d Integroi: a) d b) c) d d) Määritä ( + + 8 + a) d 5
MAA0 Määritä se funktion f: f() = + integraalifunktio, jolle F() = Määritä se funktion f : f() = integraalifunktio, jonka kuvaaja sivuaa suoraa y = d Integroi: a) d b) c) d d) Määritä ( + + 8 + a) d 5
Rinnakkaisuuden hyväksikäyttö peleissä. Paula Kemppi
 Rinnakkaisuuden hyväksikäyttö peleissä Paula Kemppi 24.4.2008 Esityksen rakenne Johdantoa Rinnakkaisuus Pelimoottorien rinnakkaisuuden mallit Funktionaalisen rinnakkaisuuden malli Rinnakkaisen tiedon malli
Rinnakkaisuuden hyväksikäyttö peleissä Paula Kemppi 24.4.2008 Esityksen rakenne Johdantoa Rinnakkaisuus Pelimoottorien rinnakkaisuuden mallit Funktionaalisen rinnakkaisuuden malli Rinnakkaisen tiedon malli
Matematiikan tukikurssi 3.4.
 Matematiikan tukikurssi 3.4. Neliömuodot, Hessen matriisi, deiniittisyys, konveksisuus siinä tämän dokumentin aiheet. Neliömuodot ovat unktioita, jotka ovat muotoa T ( x) = x Ax, missä x = (x 1,, x n )
Matematiikan tukikurssi 3.4. Neliömuodot, Hessen matriisi, deiniittisyys, konveksisuus siinä tämän dokumentin aiheet. Neliömuodot ovat unktioita, jotka ovat muotoa T ( x) = x Ax, missä x = (x 1,, x n )
Liitosesimerkki Tietokannan hallinta, kevät 2006, J.Li 1
 Liitosesimerkki 16.02.06 Tietokannan hallinta, kevät 2006, J.Li 1 Esim R1 R2 yhteinen attribuutti C T(R1) = 10,000 riviä T(R2) = 5,000 riviä S(R1) = S(R2) = 1/10 lohkoa Puskuritilaa = 101 lohkoa 16.02.06
Liitosesimerkki 16.02.06 Tietokannan hallinta, kevät 2006, J.Li 1 Esim R1 R2 yhteinen attribuutti C T(R1) = 10,000 riviä T(R2) = 5,000 riviä S(R1) = S(R2) = 1/10 lohkoa Puskuritilaa = 101 lohkoa 16.02.06
Induktio kaavan pituuden suhteen
 Induktio kaavan pituuden suhteen Lauselogiikan objektikieli määritellään kurssilla Logiikka 1B seuraavasti: 1. Lausemuuttujat p 1, p 2, p 3,... ovat kaavoja. 2. Jos A on kaava, niin A on kaava. 3. Jos
Induktio kaavan pituuden suhteen Lauselogiikan objektikieli määritellään kurssilla Logiikka 1B seuraavasti: 1. Lausemuuttujat p 1, p 2, p 3,... ovat kaavoja. 2. Jos A on kaava, niin A on kaava. 3. Jos
Rinnakkaistietokoneet luento S
 Rinnakkaistietokoneet luento 5 521475S Silmukalliset ohjelmat Silmukat joissa ei ole riippuvuussyklejä voidaan vektoroida eli suorittaa silmukan vektorointi Jokainen yksittäinen käsky silmukan rungossa
Rinnakkaistietokoneet luento 5 521475S Silmukalliset ohjelmat Silmukat joissa ei ole riippuvuussyklejä voidaan vektoroida eli suorittaa silmukan vektorointi Jokainen yksittäinen käsky silmukan rungossa
Aluksi. 2.1. Kahden muuttujan lineaarinen epäyhtälö
 Aluksi Matemaattisena käsitteenä lineaarinen optimointi sisältää juuri sen saman asian kuin mikä sen nimestä tulee mieleen. Lineaarisen optimoinnin avulla haetaan ihannearvoa eli optimia, joka on määritelty
Aluksi Matemaattisena käsitteenä lineaarinen optimointi sisältää juuri sen saman asian kuin mikä sen nimestä tulee mieleen. Lineaarisen optimoinnin avulla haetaan ihannearvoa eli optimia, joka on määritelty
Algoritmit ja tietorakenteet Copyright Hannu Laine. 1, kun n= 0. n*(n-1)!, kun n>0;
 1 Rekursio Rekursion periaate ja rekursio määrittelyvälineenä Rekursiota käytetään tietotekniikassa ja matematiikassa erilaisiin tarkoituksiin. Eräänä käyttöalueena on asioiden määrittely. Esimerkkinä
1 Rekursio Rekursion periaate ja rekursio määrittelyvälineenä Rekursiota käytetään tietotekniikassa ja matematiikassa erilaisiin tarkoituksiin. Eräänä käyttöalueena on asioiden määrittely. Esimerkkinä
Diskreetit rakenteet
 Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Väli- ja loppuraportointi
 Väli- ja loppuraportointi Hyvän raportin merkitys hankkeen tulosten kuvaamisessa Sari Ahvenainen ESR-koordinaattori 25.5.2011 Uudenmaan ELY-keskus Väliraportti (1/8) Miksi väliraportti tehdään? - Tarkoituksena
Väli- ja loppuraportointi Hyvän raportin merkitys hankkeen tulosten kuvaamisessa Sari Ahvenainen ESR-koordinaattori 25.5.2011 Uudenmaan ELY-keskus Väliraportti (1/8) Miksi väliraportti tehdään? - Tarkoituksena
Tietokannan hallinta. Kevät 2004 Jan Lindström R&G Chapter 1
 Tietokannan hallinta Kevät 2004 Jan Lindström R&G Chapter 1 Tietokannan hallinta 1. Johdanto (käsitteitä) 2. Tietokannan talletusrakenteet 3. Tietokannan hakemistorakenteet 4. Kyselyiden käsittely ja optimointi
Tietokannan hallinta Kevät 2004 Jan Lindström R&G Chapter 1 Tietokannan hallinta 1. Johdanto (käsitteitä) 2. Tietokannan talletusrakenteet 3. Tietokannan hakemistorakenteet 4. Kyselyiden käsittely ja optimointi
Näkymät ja hakemistot
 Näkymät ja hakemistot A271117, Tietokannat Teemu Saarelainen teemu.saarelainen@kyamk.fi Lähteet: Leon Atkinson: core MySQL Ari Hovi: SQL-opas TTY:n tietokantojen perusteet-kurssin opintomoniste Eri web-lähteet
Näkymät ja hakemistot A271117, Tietokannat Teemu Saarelainen teemu.saarelainen@kyamk.fi Lähteet: Leon Atkinson: core MySQL Ari Hovi: SQL-opas TTY:n tietokantojen perusteet-kurssin opintomoniste Eri web-lähteet
Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on
![Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on Oletetaan, että funktio f on määritelty jollakin välillä ]x 0 δ, x 0 + δ[. Sen derivaatta pisteessä x 0 on](/thumbs/39/20459750.jpg) Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 13 Derivaatan määritelmä Määritelmä
Derivaatta Erilaisia lähestymistapoja: geometrinen (käyrän tangentti sekanttien raja-asentona) fysikaalinen (ajasta riippuvan funktion hetkellinen muutosnopeus) 1 / 13 Derivaatan määritelmä Määritelmä
TKHJ:ssä on yleensä komento create index, jolla taululle voidaan luoda hakemisto
 Indeksin luonti ja hävitys TKHJ:ssä on yleensä komento create index, jolla taululle voidaan luoda hakemisto Komentoa ei ole standardoitu ja niinpä sen muoto vaihtelee järjestelmäkohtaisesti Indeksi voidaan
Indeksin luonti ja hävitys TKHJ:ssä on yleensä komento create index, jolla taululle voidaan luoda hakemisto Komentoa ei ole standardoitu ja niinpä sen muoto vaihtelee järjestelmäkohtaisesti Indeksi voidaan
Dynaamisen järjestelmän siirtofunktio
 Dynaamisen järjestelmän siirtofunktio Nyt päästään soveltamaan matriisilaskentaa ja Laplace muunnosta. Tutkikaamme, miten lineaarista mallia voidaan käsitellä. Kuten edellä on jo nähty säätötekniikassa
Dynaamisen järjestelmän siirtofunktio Nyt päästään soveltamaan matriisilaskentaa ja Laplace muunnosta. Tutkikaamme, miten lineaarista mallia voidaan käsitellä. Kuten edellä on jo nähty säätötekniikassa
3. Muuttujat ja operaatiot 3.1
 3. Muuttujat ja operaatiot 3.1 Sisällys Muuttujat. Nimi ja arvo. Algoritmin tila. Muuttujan nimeäminen. Muuttujan tyyppi. Muuttuja ja tietokone. Operaattorit. Operandit. Arvon sijoitus muuttujaan. Aritmeetiikka.
3. Muuttujat ja operaatiot 3.1 Sisällys Muuttujat. Nimi ja arvo. Algoritmin tila. Muuttujan nimeäminen. Muuttujan tyyppi. Muuttuja ja tietokone. Operaattorit. Operandit. Arvon sijoitus muuttujaan. Aritmeetiikka.
ARVIOINTIPERIAATTEET
 PSYKOLOGIAN YHTEISVALINNAN VALINTAKOE 2012 ARVIOINTIPERIAATTEET Copyright Helsingin yliopisto, käyttäytymistieteiden laitos, Materiaalin luvaton kopiointi kielletty. TEHTÄVÄ 1. (max. 34.5 pistettä) 1 a.i)
PSYKOLOGIAN YHTEISVALINNAN VALINTAKOE 2012 ARVIOINTIPERIAATTEET Copyright Helsingin yliopisto, käyttäytymistieteiden laitos, Materiaalin luvaton kopiointi kielletty. TEHTÄVÄ 1. (max. 34.5 pistettä) 1 a.i)
Sähköpostiohjeet. Tehokas ja huoleton sähköposti
 Sähköpostiohjeet 1 Uuden PST tiedoston luominen sähköposteille... 3 Tärkeää!... 3 Tiedoston luominen... 3 Kansioiden luominen datatiedostoon... 5 Pikatoimintojen luominen... 8 Odottaa vastausta allekirjoitus...
Sähköpostiohjeet 1 Uuden PST tiedoston luominen sähköposteille... 3 Tärkeää!... 3 Tiedoston luominen... 3 Kansioiden luominen datatiedostoon... 5 Pikatoimintojen luominen... 8 Odottaa vastausta allekirjoitus...
HELIA 1 (15) Outi Virkki Tiedonhallinta
 HELIA 1 (15) Luento Suorituskyvyn optimointi... 2 Tiedonhallintajärjestelmän rakenne... 3 Suunnittele... 4 SQL-komentojen viritys... 5 Tekninen ympäristö... 6 Fyysisen tason ratkaisut... 7 Indeksit...
HELIA 1 (15) Luento Suorituskyvyn optimointi... 2 Tiedonhallintajärjestelmän rakenne... 3 Suunnittele... 4 SQL-komentojen viritys... 5 Tekninen ympäristö... 6 Fyysisen tason ratkaisut... 7 Indeksit...
TIES530 TIES530. Moniprosessorijärjestelmät. Moniprosessorijärjestelmät. Miksi moniprosessorijärjestelmä?
 Miksi moniprosessorijärjestelmä? Laskentaa voidaan hajauttaa useammille prosessoreille nopeuden, modulaarisuuden ja luotettavuuden vaatimuksesta tai hajauttaminen voi helpottaa ohjelmointia. Voi olla järkevää
Miksi moniprosessorijärjestelmä? Laskentaa voidaan hajauttaa useammille prosessoreille nopeuden, modulaarisuuden ja luotettavuuden vaatimuksesta tai hajauttaminen voi helpottaa ohjelmointia. Voi olla järkevää
Raportointi hankkeen tulosten kuvaajana ja toteutuksen tukena
 Raportointi hankkeen tulosten kuvaajana ja toteutuksen tukena Tiivistelmät, väli- ja loppuraportit Auli Vuorela ESR-koordinaattori Uudenmaan ELY-keskus 6.5.2013 Raportteja, raportteja, raportteja Loppuraportti
Raportointi hankkeen tulosten kuvaajana ja toteutuksen tukena Tiivistelmät, väli- ja loppuraportit Auli Vuorela ESR-koordinaattori Uudenmaan ELY-keskus 6.5.2013 Raportteja, raportteja, raportteja Loppuraportti
Lausuntopyyntökysely. Ohjeet:
 Lausuntopyyntökysely Ohjeet: Sähköisessä kyselylomakkeessa voi liikkua edestakaisin painamalla Edellinen- tai Seuraava - painikkeita. Kysely on mahdollista lähettää vastaamatta kaikkiin kysymyksiin, mutta
Lausuntopyyntökysely Ohjeet: Sähköisessä kyselylomakkeessa voi liikkua edestakaisin painamalla Edellinen- tai Seuraava - painikkeita. Kysely on mahdollista lähettää vastaamatta kaikkiin kysymyksiin, mutta
Helsingin yliopisto/tktl Kyselykielet, s 2006 Optimointi Harri Laine 1. Kyselyn optimointi. Kyselyn optimointi
 Miksi optimoidaan Relaatiotietokannan kyselyt esitetään käytännössä SQLkielellä. Kieli määrittää halutun tuloksen, ei sitä miten tulos muodostetaan (deklaratiivinen kyselykieli) Tietokannan käsittelyoperaatiot
Miksi optimoidaan Relaatiotietokannan kyselyt esitetään käytännössä SQLkielellä. Kieli määrittää halutun tuloksen, ei sitä miten tulos muodostetaan (deklaratiivinen kyselykieli) Tietokannan käsittelyoperaatiot
Kulttuuripalvelut, toimintamallien vertailu
 Kulttuuripalvelut, toimintamallien vertailu Mitkä asiat on oleellisia? Sitovuus Päätöksenteko Strateginen ohjaus ja toiminnan ohjaus Henkilöstöpolitiikka Asiakasrajapinnat/reagointikyky asiakastarpeisiin
Kulttuuripalvelut, toimintamallien vertailu Mitkä asiat on oleellisia? Sitovuus Päätöksenteko Strateginen ohjaus ja toiminnan ohjaus Henkilöstöpolitiikka Asiakasrajapinnat/reagointikyky asiakastarpeisiin
Luento 6. June 1, 2015. Luento 6
 June 1, 2015 Normaalimuodon pelissä on luontevaa ajatella, että pelaajat tekevät valintansa samanaikaisesti. Ekstensiivisen muodon peleissä pelin jonottaisella rakenteella on keskeinen merkitys. Aluksi
June 1, 2015 Normaalimuodon pelissä on luontevaa ajatella, että pelaajat tekevät valintansa samanaikaisesti. Ekstensiivisen muodon peleissä pelin jonottaisella rakenteella on keskeinen merkitys. Aluksi
SIS. Vinkkejä Ampèren lain käyttöön laskettaessa magneettikenttiä:
 Magneettikentät 2 SISÄLTÖ: Ampèren laki Menetelmän valinta Vektoripotentiaali Ampèren laki Ampèren lain avulla voidaan laskea maneettikenttiä tietyissä symmetrisissä tapauksissa, kuten Gaussin lailla laskettiin
Magneettikentät 2 SISÄLTÖ: Ampèren laki Menetelmän valinta Vektoripotentiaali Ampèren laki Ampèren lain avulla voidaan laskea maneettikenttiä tietyissä symmetrisissä tapauksissa, kuten Gaussin lailla laskettiin
Mielestämme hyvä kannustus ja mukava ilmapiiri on opiskelijalle todella tärkeää.
 Ops-perusteluonnosten palaute Poikkilaakson oppilailta 1 LUKU 2 B Perusopetuksen arvoperusta Suunta on oikea, ja tekstissä kuvataan hyvin sitä, kuinka kaikilla lapsilla kuuluisi olla oikeus opiskella ja
Ops-perusteluonnosten palaute Poikkilaakson oppilailta 1 LUKU 2 B Perusopetuksen arvoperusta Suunta on oikea, ja tekstissä kuvataan hyvin sitä, kuinka kaikilla lapsilla kuuluisi olla oikeus opiskella ja
Helsingin yliopisto/tktl DO Tietokantojen perusteet, s 2000 Johdanto & yleistä Harri Laine 1. Tietokanta. Tiedosto
 Tietokanta Tiedosto Tietokanta (database) jotakin käyttötarkoitusta varten laadittu kokoelma toisiinsa liittyviä säilytettäviä tietoja Ohjelmointikielissä apumuistiin tallennettuja tietoja käsitellään
Tietokanta Tiedosto Tietokanta (database) jotakin käyttötarkoitusta varten laadittu kokoelma toisiinsa liittyviä säilytettäviä tietoja Ohjelmointikielissä apumuistiin tallennettuja tietoja käsitellään
JOENSUUN SEUDUN HANKINTATOIMI KOMISSIOMALLI 28.03.2014
 JOENSUUN SEUDUN HANKINTATOIMI KOMISSIOMALLI 28.03.2014 KOMISSIO Komissio otetaan käyttöön kaikissa kilpailutuksissa, joiden hankintakausi alkaa 1.1.2012 tai sen jälkeen Raha liikkuu Joensuun seudun hankintatoimen
JOENSUUN SEUDUN HANKINTATOIMI KOMISSIOMALLI 28.03.2014 KOMISSIO Komissio otetaan käyttöön kaikissa kilpailutuksissa, joiden hankintakausi alkaa 1.1.2012 tai sen jälkeen Raha liikkuu Joensuun seudun hankintatoimen
Luento 2: Tiedostot ja tiedon varastointi
 HELIA 1 (19) Luento 2: Tiedostot ja tiedon varastointi Muistit... 2 Päämuisti (Primary storage)... 2 Apumuisti (Secondary storage)... 2 Tiedon tallennuksen yksiköitä... 3 Looginen taso... 3 Fyysinen taso...
HELIA 1 (19) Luento 2: Tiedostot ja tiedon varastointi Muistit... 2 Päämuisti (Primary storage)... 2 Apumuisti (Secondary storage)... 2 Tiedon tallennuksen yksiköitä... 3 Looginen taso... 3 Fyysinen taso...
Lue ohjeet huolellisesti ennen laitteen käyttöä.
 1 Väliaikaisen tallennuskansion käyttö Lue ohjeet huolellisesti ennen laitteen käyttöä. Kun skannaat kuvia, dioja, asiakirjoja jne. sekä digitoit LP-levyjä tai C-kasetteja, sinulla on mahdollisuus tallentaa
1 Väliaikaisen tallennuskansion käyttö Lue ohjeet huolellisesti ennen laitteen käyttöä. Kun skannaat kuvia, dioja, asiakirjoja jne. sekä digitoit LP-levyjä tai C-kasetteja, sinulla on mahdollisuus tallentaa
SISÄLLYSLUETTELO. KVALT, 30.11.2015 18:00, Pöytäkirja
 SISÄLLYSLUETTELO KVALT, 30.11.2015 18:00, Pöytäkirja 73 LAUSUNTO ITSEHALLINTOALUEJAON PERUSTEISTA JA SOTE-UUDISTUKSESTA... 1 Pykälän liite: Liite 3: Lopen kunnan lausunto... 2 73, KVALT 30.11.2015 18:00
SISÄLLYSLUETTELO KVALT, 30.11.2015 18:00, Pöytäkirja 73 LAUSUNTO ITSEHALLINTOALUEJAON PERUSTEISTA JA SOTE-UUDISTUKSESTA... 1 Pykälän liite: Liite 3: Lopen kunnan lausunto... 2 73, KVALT 30.11.2015 18:00
Mobiiliturva Palvelun käyttöönotto
 Mobiiliturva Palvelun käyttöönotto Protecting the irreplaceable f-secure.com Sovelluksen lataus Tilattuaan Mobiiliturva palvelun, asiakas saa Android-laitteeseensa latauslinkin*, jota klikkaamalla sovellus
Mobiiliturva Palvelun käyttöönotto Protecting the irreplaceable f-secure.com Sovelluksen lataus Tilattuaan Mobiiliturva palvelun, asiakas saa Android-laitteeseensa latauslinkin*, jota klikkaamalla sovellus
Relaatioalgebra. Kyselyt:
 Relaatioalgebra Relaatiomalliin liittyy malli tietokannan käsittelystä Tietokannasta pitää pystyä hakemaan tietoa ja toisaalta tietokantaa on ylläpidettävä Tietokannan käsittelyn malli relaatioalgebra
Relaatioalgebra Relaatiomalliin liittyy malli tietokannan käsittelystä Tietokannasta pitää pystyä hakemaan tietoa ja toisaalta tietokantaa on ylläpidettävä Tietokannan käsittelyn malli relaatioalgebra
Verkkotehtäviin pohjautuva arviointi matematiikan opetuksessa
 Verkkotehtäviin pohjautuva arviointi matematiikan opetuksessa Linda Blåfield, Helle Majander, Antti Rasila & Pekka Alestalo Aalto-yliopiston teknillinen korkeakoulu Oppimisen arviointi Käytännössä: Tarkastellaan
Verkkotehtäviin pohjautuva arviointi matematiikan opetuksessa Linda Blåfield, Helle Majander, Antti Rasila & Pekka Alestalo Aalto-yliopiston teknillinen korkeakoulu Oppimisen arviointi Käytännössä: Tarkastellaan
Perusopetuksen aamu- ja iltapäivätoiminnan laadun arviointi 2016 Västankvarns skola/ Tukiyhdistys Almus ry.
 Perusopetuksen aamu- ja iltapäivätoiminnan laadun arviointi 06 Västankvarns skola/ toteutti perusopetuksen aamu- ja iltapäivätoiminnan seurantakyselyn lapsille ja huoltajille huhtikuussa 06. Vuoden 06
Perusopetuksen aamu- ja iltapäivätoiminnan laadun arviointi 06 Västankvarns skola/ toteutti perusopetuksen aamu- ja iltapäivätoiminnan seurantakyselyn lapsille ja huoltajille huhtikuussa 06. Vuoden 06
Transaktiot - kertausta
 Hajautettujen järjestelmien perusteet Transaktiot - kertausta Distributed Systems, Concepts and Design, George Coulouris, Jean Dollimore, Tim Kindberg Addison-Wesley 1988,1994. Pearson Education 2001 ISBN:
Hajautettujen järjestelmien perusteet Transaktiot - kertausta Distributed Systems, Concepts and Design, George Coulouris, Jean Dollimore, Tim Kindberg Addison-Wesley 1988,1994. Pearson Education 2001 ISBN:
FROM-lausekkeessa voidaan määritellä useampi kuin yksi taulu, josta tietoja haetaan: Tuloksena on taululistassa lueteltujen taulujen rivien
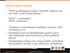 Monen taulun kyselyt FROM-lausekkeessa voidaan määritellä useampi kuin yksi taulu, josta tietoja haetaan: SELECT FROM Tuloksena on taululistassa lueteltujen taulujen rivien karteesinen
Monen taulun kyselyt FROM-lausekkeessa voidaan määritellä useampi kuin yksi taulu, josta tietoja haetaan: SELECT FROM Tuloksena on taululistassa lueteltujen taulujen rivien karteesinen
TK081001 Palvelinympäristö
 TK081001 Palvelinympäristö 5 opintopistettä!! Petri Nuutinen! 8 opintopistettä!! Petri Nuutinen! RAID RAID = Redundant Array of Independent Disks Useasta fyysisestä kiintolevystä muodostetaan yhteinen
TK081001 Palvelinympäristö 5 opintopistettä!! Petri Nuutinen! 8 opintopistettä!! Petri Nuutinen! RAID RAID = Redundant Array of Independent Disks Useasta fyysisestä kiintolevystä muodostetaan yhteinen
Suomen Lions-liitto ry Käyttäjätunnus ja sisäänkirjautuminen MyLCI - Käyttäjäohje Versio 1.2 4.4.2016
 Suomen Lions liitto ry Suomen Lions-liitto ry Käyttäjätunnus ja sisäänkirjautuminen MyLCI - Käyttäjäohje Versio 1.2 4.4.2016 Dokumenttien ja ohjeiden luovutus kolmannelle osapuolelle ilman lupaa, kopioimalla,
Suomen Lions liitto ry Suomen Lions-liitto ry Käyttäjätunnus ja sisäänkirjautuminen MyLCI - Käyttäjäohje Versio 1.2 4.4.2016 Dokumenttien ja ohjeiden luovutus kolmannelle osapuolelle ilman lupaa, kopioimalla,
FYYSINEN SUUNNITTELU
 IIO30120 DATABASE DESIGN / TIETOKANTOJEN SUUNNITTELU JA IIO30220 DATABASE MANAGEMENT / TIETOKANNAN HALLINTA FYYSINEN SUUNNITTELU KIRJAN HOVI, HUOTARI, LAHDENMÄKI: TIETOKANTOJEN SUUNNITTELU & INDEKSOINTI,
IIO30120 DATABASE DESIGN / TIETOKANTOJEN SUUNNITTELU JA IIO30220 DATABASE MANAGEMENT / TIETOKANNAN HALLINTA FYYSINEN SUUNNITTELU KIRJAN HOVI, HUOTARI, LAHDENMÄKI: TIETOKANTOJEN SUUNNITTELU & INDEKSOINTI,
Liitosesimerkki. Esim R1 R2 yhteinen attribuutti C. Vaihtoehdot
 Esim yhteinen attribuutti C Liitosesimerkki T() = 10,000 riviä T() = 5,000 riviä S() = S() = 1/10 lohkoa Puskuritilaa = 101 lohkoa 1 2 Vaihtoehdot Sisäkkäiset silmukat Liitosjärjestys:, Liitosalgoritmit:
Esim yhteinen attribuutti C Liitosesimerkki T() = 10,000 riviä T() = 5,000 riviä S() = S() = 1/10 lohkoa Puskuritilaa = 101 lohkoa 1 2 Vaihtoehdot Sisäkkäiset silmukat Liitosjärjestys:, Liitosalgoritmit:
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
 Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Kyselyt: Lähtökohtana joukko lukuja Laskukaava kertoo miten luvuista lasketaan tulos soveltamalla laskentaoperaatioita
 Relaatioalgebra Relaatiomalliin liittyy malli tietokannan käsittelystä Tietokannasta pitää pystyä hakemaan tietoa ja toisaalta tietokantaa on ylläpidettävä Tietokannan käsittelyn malli relaatioalgebra
Relaatioalgebra Relaatiomalliin liittyy malli tietokannan käsittelystä Tietokannasta pitää pystyä hakemaan tietoa ja toisaalta tietokantaa on ylläpidettävä Tietokannan käsittelyn malli relaatioalgebra
Ohje hakulomakkeen täyttämiseen yliopistohaku.fi -palvelussa
 Hakijan ohje Opetushallitus kevät 2013 Ohje hakulomakkeen täyttämiseen yliopistohaku.fi -palvelussa Tässä ohjeessa on kuvattu miten hakulomake täytetään ja lähetetään yliopistohaku.fi-palvelussa. Näytön
Hakijan ohje Opetushallitus kevät 2013 Ohje hakulomakkeen täyttämiseen yliopistohaku.fi -palvelussa Tässä ohjeessa on kuvattu miten hakulomake täytetään ja lähetetään yliopistohaku.fi-palvelussa. Näytön
Tietokantarakenteet ja -algoritmit 3. harjoitus
 Tietokantarakenteet ja -algoritmit 3. harjoitus Malliratkaisut 1. Analyysivaiheen alussa alustetaan aktiivisten transaktioiden taulu (tyhjä) ja päivitettyjen sivujen taulu (samoin tyhjä) tarkistuspisteestä.
Tietokantarakenteet ja -algoritmit 3. harjoitus Malliratkaisut 1. Analyysivaiheen alussa alustetaan aktiivisten transaktioiden taulu (tyhjä) ja päivitettyjen sivujen taulu (samoin tyhjä) tarkistuspisteestä.
Matkahuolto lisäosa WooCommerce alustalle (c) Webbisivut.org
 Matkahuolto lisäosa WooCommerce alustalle (c) Webbisivut.org Sisällysluettelo Yleistä...3 Asennus... 4 Asetukset... 4 Toimitustavat... 5 Tilauksen käsittely...6 Huomioitavaa... 7 Lähipaketti toimitustapa...
Matkahuolto lisäosa WooCommerce alustalle (c) Webbisivut.org Sisällysluettelo Yleistä...3 Asennus... 4 Asetukset... 4 Toimitustavat... 5 Tilauksen käsittely...6 Huomioitavaa... 7 Lähipaketti toimitustapa...
Terveydenhuollon ATK-päivät
 Terveydenhuollon ATK-päivät Case Medikes Roadmap Järjestelmäasiantuntija Juha Viitala Liikelaitos Medikes Kokonaisarkkitehtuuri Kokonaisarkkitehtuuri on strategisen johtamisen väline, jonka avulla yhtenäistetään
Terveydenhuollon ATK-päivät Case Medikes Roadmap Järjestelmäasiantuntija Juha Viitala Liikelaitos Medikes Kokonaisarkkitehtuuri Kokonaisarkkitehtuuri on strategisen johtamisen väline, jonka avulla yhtenäistetään
ABT 2000kg Haarukkavaunun käyttöohje
 ABT 2000kg Haarukkavaunun käyttöohje HUOM! Käyttäjän tulee lukea käyttöohje ennen käytön aloittamista. 1. YLEISKUVAUS Kapasiteetti Max. haarukoiden korkeus Min. haarukoiden korkeus Haarukoiden pituus Vaunun
ABT 2000kg Haarukkavaunun käyttöohje HUOM! Käyttäjän tulee lukea käyttöohje ennen käytön aloittamista. 1. YLEISKUVAUS Kapasiteetti Max. haarukoiden korkeus Min. haarukoiden korkeus Haarukoiden pituus Vaunun
Luovia ratkaisuja Erasmus-byrokratian kanssa painimiseen KANSAINVÄLISTEN ASIOIDEN KEVÄTPÄIVÄT 10.5.2016, TURKU
 Luovia ratkaisuja Erasmus-byrokratian kanssa painimiseen KANSAINVÄLISTEN ASIOIDEN KEVÄTPÄIVÄT 10.5.2016, TURKU Erasmus+ -ohjelman hallinto Oamkissa - Osin keskitetty, osin hajautettu malli - Kv-palvelut
Luovia ratkaisuja Erasmus-byrokratian kanssa painimiseen KANSAINVÄLISTEN ASIOIDEN KEVÄTPÄIVÄT 10.5.2016, TURKU Erasmus+ -ohjelman hallinto Oamkissa - Osin keskitetty, osin hajautettu malli - Kv-palvelut
Riskienhallinta DTV projektissa. Digi-tv vastaanottimella toteutetut interaktiiviset sovellukset
 Teknillinen korkeakoulu 61 Riskienhallinta DTV projektissa Digi-tv vastaanottimella toteutetut interaktiiviset sovellukset Versio Päiväys Tekijä Kuvaus 1.0 29.10.01 Oskari Pirttikoski Ensimmäinen versio
Teknillinen korkeakoulu 61 Riskienhallinta DTV projektissa Digi-tv vastaanottimella toteutetut interaktiiviset sovellukset Versio Päiväys Tekijä Kuvaus 1.0 29.10.01 Oskari Pirttikoski Ensimmäinen versio
Lausuntopyyntökysely. Ohjeet:
 Lausuntopyyntökysely Ohjeet: Sähköisessä kyselylomakkeessa voi liikkua edestakaisin painamalla Edellinen tai Seuraava painikkeita. Kysely on mahdollista lähettää vastaamatta kaikkiin kysymyksiin, mutta
Lausuntopyyntökysely Ohjeet: Sähköisessä kyselylomakkeessa voi liikkua edestakaisin painamalla Edellinen tai Seuraava painikkeita. Kysely on mahdollista lähettää vastaamatta kaikkiin kysymyksiin, mutta
Relaatioalgebra. Relaatioalgebra. Relaatioalgebra. Relaatioalgebra - erotus (set difference) Kyselyt:
 Relaatiomalliin liittyy malli tietokannan käsittelystä Tietokannasta pitää pystyä hakemaan tietoa ja toisaalta tietokantaa on ylläpidettävä Tietokannan käsittelyn malli relaatioalgebra määrittelee operaatiot,
Relaatiomalliin liittyy malli tietokannan käsittelystä Tietokannasta pitää pystyä hakemaan tietoa ja toisaalta tietokantaa on ylläpidettävä Tietokannan käsittelyn malli relaatioalgebra määrittelee operaatiot,
2.7 Neliöjuuriyhtälö ja -epäyhtälö
 2.7 Neliöjuuriyhtälö ja -epäyhtälö Neliöjuuren määritelmä palautettiin mieleen jo luvun 2.2 alussa. Neliöjuurella on mm. seuraavat ominaisuudet. ab = a b, a 0, b 0 a a b =, a 0, b > 0 b a2 = a a > b, a
2.7 Neliöjuuriyhtälö ja -epäyhtälö Neliöjuuren määritelmä palautettiin mieleen jo luvun 2.2 alussa. Neliöjuurella on mm. seuraavat ominaisuudet. ab = a b, a 0, b 0 a a b =, a 0, b > 0 b a2 = a a > b, a
Algoritmit 2. Luento 8 Ke 13.4.2016. Timo Männikkö
 Algoritmit 2 Luento 8 Ke 13.4.2016 Timo Männikkö Luento 8 Rekursioyhtälöt Master-lause Lähin pistepari Ahne menetelmä Lyhin virittävä puu Kruskalin menetelmä Primin menetelmä Merkkitiedon tiivistäminen
Algoritmit 2 Luento 8 Ke 13.4.2016 Timo Männikkö Luento 8 Rekursioyhtälöt Master-lause Lähin pistepari Ahne menetelmä Lyhin virittävä puu Kruskalin menetelmä Primin menetelmä Merkkitiedon tiivistäminen
LIITTOKOKOUSVAALIT 2016
 1(5) VAALIOHJEET LIITTOHALLITUKSEN JÄSENEHDOKKAIDEN ASETTAMISTA VARTEN 1. Yleistä Liiton sääntöjen 18 :n mukaan liittohallitukseen kuuluvat puheenjohtajan ja varapuheenjohtajan lisäksi 14 varsinaista jäsentä
1(5) VAALIOHJEET LIITTOHALLITUKSEN JÄSENEHDOKKAIDEN ASETTAMISTA VARTEN 1. Yleistä Liiton sääntöjen 18 :n mukaan liittohallitukseen kuuluvat puheenjohtajan ja varapuheenjohtajan lisäksi 14 varsinaista jäsentä
Dynaaminen optimointi
 Dynaaminen optimointi Tapa ratkaista optimointitehtävä Tehtävä ratkaistaan vaiheittain ja vaiheet yhdistetään rekursiivisesti Perustuu optimaalisuusperiaatteeseen: Optimaalisen ratkaisupolun loppuosa on
Dynaaminen optimointi Tapa ratkaista optimointitehtävä Tehtävä ratkaistaan vaiheittain ja vaiheet yhdistetään rekursiivisesti Perustuu optimaalisuusperiaatteeseen: Optimaalisen ratkaisupolun loppuosa on
Relaatiotietokantojen perusteista. Harri Laine Helsingin yliopisto
 Harri Laine Helsingin yliopisto Suosion syy? Yksinkertaisuus vähän käsitteitä helppo hahmottaa Selkeä matemaattinen perusta ei tulkintaongelmia kuten esim. UML:ssä teoria käytäntö kaavio: R(A 1 :D 1, A
Harri Laine Helsingin yliopisto Suosion syy? Yksinkertaisuus vähän käsitteitä helppo hahmottaa Selkeä matemaattinen perusta ei tulkintaongelmia kuten esim. UML:ssä teoria käytäntö kaavio: R(A 1 :D 1, A
Lausuntopyyntö STM 2015
 Lausuntopyyntö STM 2015 1. Vastaajatahon virallinen nimi Nimi - Itä-Savon sairaanhoitopiirin kuntayhtymä 2. Vastauksen kirjanneen henkilön nimi Nimi - Panu Peitsaro 3. Vastauksen vastuuhenkilön yhteystiedot
Lausuntopyyntö STM 2015 1. Vastaajatahon virallinen nimi Nimi - Itä-Savon sairaanhoitopiirin kuntayhtymä 2. Vastauksen kirjanneen henkilön nimi Nimi - Panu Peitsaro 3. Vastauksen vastuuhenkilön yhteystiedot
Sähköstaattisen potentiaalin laskeminen
 Sähköstaattisen potentiaalin laskeminen Potentiaalienegia on tuttu mekaniikan kussilta eikä se ole vieas akielämässäkään. Sen sijaan potentiaalin käsite koetaan usein vaikeaksi. On hyvä muistaa, että staattisissa
Sähköstaattisen potentiaalin laskeminen Potentiaalienegia on tuttu mekaniikan kussilta eikä se ole vieas akielämässäkään. Sen sijaan potentiaalin käsite koetaan usein vaikeaksi. On hyvä muistaa, että staattisissa
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 10 1 Sarjakehitelmiä Palautetaan mieliin, että potenssisarja on sarja joka on muotoa a n (x x 0 ) n = a 0 + a 1 (x x 0 ) + a 2 (x x 0 ) 2 + a 3 (x x 0 ) 3 +. n=0 Kyseinen
Matematiikan tukikurssi Kurssikerta 10 1 Sarjakehitelmiä Palautetaan mieliin, että potenssisarja on sarja joka on muotoa a n (x x 0 ) n = a 0 + a 1 (x x 0 ) + a 2 (x x 0 ) 2 + a 3 (x x 0 ) 3 +. n=0 Kyseinen
1. a) Laadi suoraviivaisesti kyselyä vastaava optimoimaton kyselypuu.
 Helsingin yliopisto, Tietojenkäsittelytieteen laitos Kyselykielet, s 2006, Harjoitus 5 (7.12.2006) Tietokannassa on tietoa tavaroista ja niiden toimittajista: Supplier(sid,sname,city,address,phone,etc);
Helsingin yliopisto, Tietojenkäsittelytieteen laitos Kyselykielet, s 2006, Harjoitus 5 (7.12.2006) Tietokannassa on tietoa tavaroista ja niiden toimittajista: Supplier(sid,sname,city,address,phone,etc);
KUNTIEN ROOLI MUUTOKSESSA Vaikuttamisiltapäivä ja EK-foorumi 3.2.
 Päijät-Hämeen liitto The Regional Council of Päijät-Häme KUNTIEN ROOLI MUUTOKSESSA Vaikuttamisiltapäivä ja EK-foorumi 3.2. @Jari_Parkkonen #PHliitto Lähde: Tilastokeskus Kartta ja analyysi: Timo Aro Lähde:
Päijät-Hämeen liitto The Regional Council of Päijät-Häme KUNTIEN ROOLI MUUTOKSESSA Vaikuttamisiltapäivä ja EK-foorumi 3.2. @Jari_Parkkonen #PHliitto Lähde: Tilastokeskus Kartta ja analyysi: Timo Aro Lähde:
Molemmille yhteistä asiaa tulee kerralla enemmän opeteltavaa on huomattavasti enemmän kuin englannissa
 Molemmille yhteistä alkavat Espoossa 4. luokalta 2 oppituntia viikossa etenemisvauhti on kappaleittain laskettuna hitaampaa kuin englannissa, mutta asiaa tulee kerralla enemmän sanat taipuvat, joten opeteltavaa
Molemmille yhteistä alkavat Espoossa 4. luokalta 2 oppituntia viikossa etenemisvauhti on kappaleittain laskettuna hitaampaa kuin englannissa, mutta asiaa tulee kerralla enemmän sanat taipuvat, joten opeteltavaa
(1) refleksiivinen, (2) symmetrinen ja (3) transitiivinen.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Tietyn ominaisuuden samuus -relaatio on ekvivalenssi; se on (1) refleksiivinen,
Oppimistavoitteet kurssilla Rinnakkaisohjelmointi
 17.5.2006 1/5 Oppimistavoitteet kurssilla Rinnakkaisohjelmointi Rinnakkaisuus ja rinnakkaisuuden soveltaminen tietojenkäsittelyjärjestelmissä Kurssin Tietokoneen toiminta perusteella ymmärtää, miten ohjelman
17.5.2006 1/5 Oppimistavoitteet kurssilla Rinnakkaisohjelmointi Rinnakkaisuus ja rinnakkaisuuden soveltaminen tietojenkäsittelyjärjestelmissä Kurssin Tietokoneen toiminta perusteella ymmärtää, miten ohjelman
HE 226/2008 vp. Esityksessä ehdotetaan muutettavaksi työttömyysturvalakia
 Hallituksen esitys Eduskunnalle laiksi työttömyysturvalain 11 luvun :n muuttamisesta Esityksessä ehdotetaan muutettavaksi työttömyysturvalakia siten, että niitä perusteita, joilla soviteltua työttömyysetuutta
Hallituksen esitys Eduskunnalle laiksi työttömyysturvalain 11 luvun :n muuttamisesta Esityksessä ehdotetaan muutettavaksi työttömyysturvalakia siten, että niitä perusteita, joilla soviteltua työttömyysetuutta
 Sivu 1/5 Mitä CD- tai DVD-muotoa tulisi käyttää? Tässä artikkelissa Tarpeita vastaavan levyn ja muodon valinta Tietoja Live File Systemin ja masteroidun levymuodon eroista Miksi Live File System -muodosta
Sivu 1/5 Mitä CD- tai DVD-muotoa tulisi käyttää? Tässä artikkelissa Tarpeita vastaavan levyn ja muodon valinta Tietoja Live File Systemin ja masteroidun levymuodon eroista Miksi Live File System -muodosta
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus.
 Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden kanssa, joiden lakina on tietyn ominaisuuden samuus. Matematiikassa ja muuallakin joudutaan usein tekemisiin sellaisten relaatioiden
Concurrency - Rinnakkaisuus. Group: 9 Joni Laine Juho Vähätalo
 Concurrency - Rinnakkaisuus Group: 9 Joni Laine Juho Vähätalo Sisällysluettelo 1. Johdanto... 3 2. C++ thread... 4 3. Python multiprocessing... 6 4. Java ExecutorService... 8 5. Yhteenveto... 9 6. Lähteet...
Concurrency - Rinnakkaisuus Group: 9 Joni Laine Juho Vähätalo Sisällysluettelo 1. Johdanto... 3 2. C++ thread... 4 3. Python multiprocessing... 6 4. Java ExecutorService... 8 5. Yhteenveto... 9 6. Lähteet...
Paikallissivuston kumppanin starttipaketti
 Paikallissivuston kumppanin starttipaketti Tervetuloa mukaan paikallissivustolle! Paikallissivusto on osoitteessa www.vantaansanomat.fi Paikallissivustolla on paikallisia uutisia, palveluita, tapahtumatietoja,
Paikallissivuston kumppanin starttipaketti Tervetuloa mukaan paikallissivustolle! Paikallissivusto on osoitteessa www.vantaansanomat.fi Paikallissivustolla on paikallisia uutisia, palveluita, tapahtumatietoja,
Antavatko Kelan standardit mahdollisuuden toteuttaa hyvää kuntoutusta työssä uupuneille ja mielenterveysongelmaisille?
 Antavatko Kelan standardit mahdollisuuden toteuttaa hyvää kuntoutusta työssä uupuneille ja mielenterveysongelmaisille? Sari Kauranen, psykologi Verve Oulu Kokemuksia ja havaintoja kahdesta näkökulmasta
Antavatko Kelan standardit mahdollisuuden toteuttaa hyvää kuntoutusta työssä uupuneille ja mielenterveysongelmaisille? Sari Kauranen, psykologi Verve Oulu Kokemuksia ja havaintoja kahdesta näkökulmasta
Veto-visualisointityökalu
 Ohjelmoinnin suunnittelumallit (design patterns) käyttöliittymissä Vanhin ja keskeisin lähde Gamma E., Helm R., Johnson R., Vlissides J., Design Patterns. Addison-Wesley, USA, 1994. Ajatus ohjelmoinnin
Ohjelmoinnin suunnittelumallit (design patterns) käyttöliittymissä Vanhin ja keskeisin lähde Gamma E., Helm R., Johnson R., Vlissides J., Design Patterns. Addison-Wesley, USA, 1994. Ajatus ohjelmoinnin
