JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 1 Tietojärjestelmätieteen opiskelijavalinta. Väite Oikein Väärin
|
|
|
- Timo Haapasalo
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Vastaa seuraaviin väittämiin oikein tai väärin merkitsemällä rastilla valitsemasi vaihtoehto väittämän perään. Kysymyksiin tulee vastata videoluennon Kyber on kaikkialla sekä kirjallisen aineiston Onko yksilö unohtunut kyberturvallisuudessa? perusteella. Oikeasta vastauksesta saa 1 pisteen ja väärästä vastauksesta menettää 1 pisteen. Tyhjän vastauksen arvo on 0 pistettä. Tehtävän yhteispistemäärä ei voi olla negatiivinen. Väite Oikein Väärin 1. Tietojärjestelmä on ihmisistä, laitteista ja ohjelmistoista koostuva järjestelmä, jonka tarkoituksena on tehostaa ja helpottaa toimintaa tai tehdä jokin toiminta mahdolliseksi. 2. Kyberturvallisuus vaarantaa toteutuessaan kybermaailman ja kriittisen infrastruktuurin oikean ja virheettömän toiminnan. 3. Esineiden internet (engl. Internet of Things, IoT) tarkoittaa niitä palveluita ja järjestelmiä, jotka ovat yhteiskuntamme toiminnalle elintärkeitä. 4. Informaatiovaikuttamiselta suojautuminen perustuu tietoverkkojen ja ohjelmistojen virheettömään toimintaan. 5. Yhteiskunnan verkottuminen vähentää olennaisesti yksilöiden ja organisaatioiden välistä riippuvuutta. 6. Yhteiskunnat ovat monimutkaisia sosiaalisia järjestelmiä, joissa luottamus on tärkeää. Luottamus on muuttanut muotoaan nopeasti viimeisten vuosikymmenten aikana. Nykyisin joudumme luottamaan myös teknisiin järjestelmiin. 7. Häiriötä aiheuttava teknologia on usein helpointa korvata manuaalisen tietojenkäsittelyn avulla. 8. Häiriöiden aiheuttaminen kybertoimintaympäristössä vaatii vain vähäisiä resursseja. 9. Viranomaiset voivat kontrolloida tehokkaasti yhteiskuntaa ennakoimalla kyberuhkia ja niiden vaikutuksia. 10. Edward Snowdenin toimien kaltainen kansalaisaktiivisuus on suositeltavaa, kun se tehdään luottamuksen horjuttamiseksi viranomaistoimintaa kohtaan.
2 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 2 Väite Oikein Väärin 11. Suomella on kyberturvallisuusstrategia, jossa on tarkkaan määritelty yksilöiden ja viranomaisten osallisuus kyberuhkiin varautumisessa, suojautumisessa ja torjunnassa. 12. Suomessa on useita kybertoimintaympäristön muutoksista ja tietoturvaan liittyvistä asioista tiedottavaa viranomaistahoa. 13. Kybermaailman haavoittuvuuksien paljastuminen on heikentänyt sosiaalista pääomaa ja saanut viranomaiset aktiivisesti kehittämään yhteistoimintaa yksilöiden kanssa. 14. Yksilön roolia kyberturvallisuuden toimijana tulisi kehittää tarjoamalla suomalaisille riittävästi tietoa verkottuneen yhteiskunnan uhista. 15. Yksilön roolia kyberturvallisuuden toimijana tulisi kehittää parantamalla yksilöiden mahdollisuuksia varautua kybertoimintaympäristön häiriöihin.
3 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 3 Tehtävä 2. Tehtävän enimmäispistemäärä on 15. Arkemme on viimeisten vuosikymmenten aikana muuttunut nopeasti ja lähes kaikkiin arkemme asioihin liittyy nykyisin kybermaailma. Oikeastaan kukaan ei voi enää jättäytyä kybermaailman ulkopuolelle. Määrittele kybermaailman käsite ja pohdi aineiston perusteella yksilön roolia kybermaailmassa. Esittele mahdollisia kybermaailman häiriöitä ja niiden vaikutuksia yksilön arkeen. Lopuksi argumentoi lyhyesti aineistoa käyttäen, onko yksilö mielestäsi unohtunut kyberturvallisuudessa. Kirjoita sanan mittainen esseevastaus seuraavalle sivulle. Voit tarvittaessa jatkaa sivun kääntöpuolelle, mutta annetun sanamäärän ylittävää osuutta ei arvioida. Laske sanamäärä vastauksesi loppuun. Tehtävään tulee vastata videoluennon Kyber on kaikkialla sekä Aronssonin ja Moilasen artikkelin Onko yksilö unohtunut kyberturvallisuudessa? perusteella. Esitä asia sujuvasti ja selkeästi kokonaisilla virkkeillä. Vastauksesi arvioinnissa kiinnitetään huomiota esseen sisältöön, rakenteeseen ja kieliasuun. Vastaa seuraavalle tyhjälle sivulle.
4 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 4 Vastaus tehtävään 2:
5 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 5 Tehtävä 3. Tehtävän enimmäispistemäärä on 15. Ratkaise kaikki kohdat a), b), c) ja d). Kunkin kohdan pisteytys on kerrottu tehtävän yhteydessä. Kirjoita vastauksesi niille varattuun tilaan. Tehtävän yhteispistemäärä ei voi olla negatiivinen. a) Mikä on alla olevan jonon seuraava luku? 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,? Kirjoita vastauksesi alla olevaan laatikkoon. Oikeasta vastauksesta saa 2 pistettä ja väärästä vastauksesta menettää 1 pisteen. Tyhjän vastauksen arvo on 0 pistettä. b) Ratkaise seuraavat todennäköisyyksiin liittyvät tehtävät. Kirjoita vastauksesi kysymysten alla oleviin laatikoihin. Jokaisesta oikeasta vastauksesta saa 2 pistettä ja väärästä vastauksesta menettää 1 pisteen. Tyhjän vastauksen arvo on 0 pistettä. Kolikkoa on heitetty 10 kertaa ja jokaisella heittokerralla on tullut klaava. Mikä on todennäköisyys sille, että 11. heitto on klaava? Verkkopankki vaatii nelinumeroista tunnuslukua. Jokainen luvun numero voi olla mikä tahansa luku välillä 0-9. Mikä on todennäköisyys sille, että tunnuslukua tietämätön henkilö arvaa luvun oikein yhdellä yrittämällä? Mikä on todennäköisyys sille, että heitettäessä kahta noppaa saadaan pari eli luvut ovat samat molemmissa nopissa (esim. 1 ja 1)?
6 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 6 c) Henkilöllä X on viisi hattua, kolme mustaa ja kaksi valkoista. Henkilö X asettaa hatun opiskelijoiden A, B ja C päähän sattumanvaraisesti. Kukin opiskelija näkee muiden hattujen värit, mutta ei omaansa. Opiskelijat tietävät hattujen lukumäärän ja jakauman. Opiskelijat ilmoittavat järjestyksessä tietävätkö he hattunsa väriä vai eivät. Opiskelija A sanoo: En tiedä hattuni väriä. Opiskelija B sanoo: En tiedä hattuni väriä. Opiskelija C sanoo: Tiedän hattuni värin. Minkä värinen hattu opiskelijalla C on? Kirjoita vastauksesi alla olevaan laatikkoon. Oikeasta vastauksesta saa 2 pistettä ja väärästä vastauksesta menettää 1 pisteen. Tyhjän vastauksen arvo on 0 pistettä. Perustele vastauksesi. Oikeasta vastauksesta saa 2 pistettä. Väärän tai tyhjän vastauksen arvo on 0 pistettä.
7 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 7 d) Jukka, Pekka, Tommi, Ville ja Sami ovat viisi veljestä. Eräänä päivänä yksi veljeksistä rikkoo ikkunan. Veljesten isän kysyessä syyllistä, isä saa seuraavat vastaukset: Jukka: Se oli joko Pekka tai Tommi. Pekka: Se en ollut minä tai Ville. Tommi: Molemmat teistä valehtelevat. Sami: Ei, vain yksi heistä valehtelee. Ville: Ei, Sami, olet väärässä. Perheen äiti näki tapahtuman ja tietää, ketkä pojista valehtelevat. Hän toteaa: Kolme pojistani puhuu totta, mutta kaksi heistä valehtelee. Kuka pojista rikkoi ikkunan? Kirjoita vastauksesi alla olevaan laatikkoon. Oikeasta vastauksesta saa 3 pistettä ja väärästä vastauksesta menettää 2 pistettä. Tyhjän vastauksen arvo on 0 pistettä.
8 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 8 Tehtävä 4. Tehtävän enimmäispistemäärä on 15. Vuokaavioita käytetään kuvaamaan jonkin tietyn prosessin vaiheita. Niillä voidaan kuvata esimerkiksi algoritmien toteutusta tietokoneohjelmia suunniteltaessa. Alla on esitelty joitakin vuokaaviosymboleja ja tavallisia niillä kuvattuja rakenteita. Peräkkäisyys: Toimenpiteet suoritetaan osoitetussa järjestyksessä. Valinta: Seuraava toiminta suoritetaan ehdon totuusarvon perusteella. Toisto: Toimintaa suoritetaan toistuvasti niin kauan kuin ehto on tosi. Esimerkki 1: Alla oleva kaavio kuvaa tietyn matkan soutamista.
9 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 9 a) Keksi jokin esimerkki tapahtumaketjusta, jota seuraava vuokaavio kuvaa. Selitä kaavio kohta kohdalta käyttämällä keksimääsi esimerkkiä, joka ei liity soutamiseen tai auton tankkaamiseen. (6 p.) Vastaus tehtävään 4 a:
10 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 10 b) Auton tankkaus korttimaksulla toimivalla automaatilla on useimmille tuttua. Aluksi asiakas vahvistaa maksun kortilla, jonka jälkeen hän tankkaa autoon haluamansa määrän polttoainetta valitsemastaan tankkauspistoolista. Asiakkaan lopetettua tankkauksen automaatti veloittaa maksuun käytetyltä kortilta oikean summan. Lopuksi asiakkaalla on halutessaan mahdollisuus saada automaatista kuitti ostoksesta. Piirrä seuraavalle sivulle esiteltyjä vuokaaviosymboleja käyttäen kaavio, joka kuvaa tankkausautomaatin toimintaa. Käytä kaaviossa kaikkia ohjeissa mainittuja rakenteita (peräkkäisyys, valinta ja toisto). Kirjoita kaavion viereen tarvittavat selitykset. Kuvauksessa ei tarvitse ottaa huomioon kaikkia mahdollisia poikkeustilanteita. (9 p.) Vastaa seuraavalle tyhjälle sivulle.
11 JYVÄSKYLÄN YLIOPISTO Valintakoe k2017 Sivu 11 Vastaus tehtävään 4 b:
JYVÄSKYLÄN YLIOPISTO Valintakoe k2019 Sivu 1 Tietojärjestelmätieteen opiskelijavalinta. Henkilötunnus:
 JYVÄSKYLÄN YLIOPISTO Valintakoe k2019 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Vastaa seuraaviin väittämiin oikein tai väärin merkitsemällä raksilla valitsemasi vaihtoehto väittämän perään.
JYVÄSKYLÄN YLIOPISTO Valintakoe k2019 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Vastaa seuraaviin väittämiin oikein tai väärin merkitsemällä raksilla valitsemasi vaihtoehto väittämän perään.
JYVÄSKYLÄN YLIOPISTO Valintakoe k2018 Sivu 1 Tietojärjestelmätieteen opiskelijavalinta
 JYVÄSKYLÄN YLIOPISTO Valintakoe k2018 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Vastaa monivalintakysymyksiin erilliselle lomakkeelle (Tenttivastauslomake). Lue huolellisesti erillisen lomakkeen
JYVÄSKYLÄN YLIOPISTO Valintakoe k2018 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Vastaa monivalintakysymyksiin erilliselle lomakkeelle (Tenttivastauslomake). Lue huolellisesti erillisen lomakkeen
JYVÄSKYLÄN YLIOPISTO Valintakoe s2011 Sivu 1 Tietojärjestelmätieteen opiskelijavalinta. Nimi: Henkilötunnus:
 JYVÄSKYLÄN YLIOPISTO Valintakoe s2011 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Esitä lyhyesti äskeisen esityksen keskeinen sisältö. Ilmaise asiasi sujuvasti ja selkeästi, kokonaisilla virkkeillä
JYVÄSKYLÄN YLIOPISTO Valintakoe s2011 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Esitä lyhyesti äskeisen esityksen keskeinen sisältö. Ilmaise asiasi sujuvasti ja selkeästi, kokonaisilla virkkeillä
OTATKO RISKIN? peli. Heitä noppaa 3 kertaa. Tavoitteena on saada
 OTATKO RISKIN? peli 1. Heitä noppaa 20 kertaa. Tavoitteena on saada vähintään 10 kertaa silmäluku 4, 5 tai 6. Jos onnistut, saat 300 pistettä. Jos et onnistu, menetät 2. Heitä noppaa 10 kertaa. Tavoitteena
OTATKO RISKIN? peli 1. Heitä noppaa 20 kertaa. Tavoitteena on saada vähintään 10 kertaa silmäluku 4, 5 tai 6. Jos onnistut, saat 300 pistettä. Jos et onnistu, menetät 2. Heitä noppaa 10 kertaa. Tavoitteena
TIETOPAKETTI EI -KYBERIHMISILLE
 TIETOPAKETTI EI -KYBERIHMISILLE Miksi TIEDOLLA on tässä yhtälössä niin suuri merkitys? Mitä tarkoittaa KYBERTURVALLISUUS? Piileekö KYBERUHKIA kaikkialla? Kaunis KYBERYMPÄRISTÖ? Miten TIETOJÄRJESTELMÄ liittyy
TIETOPAKETTI EI -KYBERIHMISILLE Miksi TIEDOLLA on tässä yhtälössä niin suuri merkitys? Mitä tarkoittaa KYBERTURVALLISUUS? Piileekö KYBERUHKIA kaikkialla? Kaunis KYBERYMPÄRISTÖ? Miten TIETOJÄRJESTELMÄ liittyy
1. Valitse aineiston perusteella oikea vaihtoehto: b) Uudet liiketoimintamallit ovat korvanneet perinteisen musiikkimyynnin vähenemisen.
 JYVÄSKYLÄN YLIOPISTO Valintakoe k2011 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Nimi: Henkilötunnus: Vastaa monivalintakysymyksiin merkitsemällä rastilla valitsemasi vaihtoehto alla olevaan
JYVÄSKYLÄN YLIOPISTO Valintakoe k2011 Sivu 1 Tehtävä 1. Tehtävän enimmäispistemäärä on 15. Nimi: Henkilötunnus: Vastaa monivalintakysymyksiin merkitsemällä rastilla valitsemasi vaihtoehto alla olevaan
Todennäköisyyslaskenta - tehtävät
 Todennäköisyyslaskenta - tehtävät Todennäköisyyslaskentaa käsitellään Pitkän matematiikan kertauskirjan sivuilla 253 276. Klassinen todennäköisyys Kombinatoriikka Binomitodennäköisyys Satunnaismuuttuja,
Todennäköisyyslaskenta - tehtävät Todennäköisyyslaskentaa käsitellään Pitkän matematiikan kertauskirjan sivuilla 253 276. Klassinen todennäköisyys Kombinatoriikka Binomitodennäköisyys Satunnaismuuttuja,
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.2012 klo 10 13 Ratkaisut ja pisteytysohjeet
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.01 klo 10 13 t ja pisteytysohjeet 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 x 3 3 x 1 4, (b)
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.01 klo 10 13 t ja pisteytysohjeet 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 x 3 3 x 1 4, (b)
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe klo 10 13
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.2012 klo 10 13 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 2 x 2 3 2 3 x 1 4, (b) (x + 1)(x 2)
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 11.6.2012 klo 10 13 1. Ratkaise seuraavat yhtälöt ja epäyhtälöt. (a) 3 2 x 2 3 2 3 x 1 4, (b) (x + 1)(x 2)
Kyber uhat. Heikki Silvennoinen, Miktech oy /Safesaimaa 6.9.2013
 Kyber uhat Heikki Silvennoinen, Miktech oy /Safesaimaa 6.9.2013 Taustaa Kyberturvallisuus on kiinteä osa yhteiskunnan kokonaisturvallisuutta Suomi on tietoyhteiskuntana riippuvainen tietoverkkojen ja -järjestelmien
Kyber uhat Heikki Silvennoinen, Miktech oy /Safesaimaa 6.9.2013 Taustaa Kyberturvallisuus on kiinteä osa yhteiskunnan kokonaisturvallisuutta Suomi on tietoyhteiskuntana riippuvainen tietoverkkojen ja -järjestelmien
Approbatur 3, demo 1, ratkaisut A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat.
 Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
Approbatur 3, demo 1, ratkaisut 1.1. A sanoo: Vähintään yksi meistä on retku. Tehtävänä on päätellä, mitä tyyppiä A ja B ovat. Käydään kaikki vaihtoehdot läpi. Jos A on rehti, niin B on retku, koska muuten
KYBERIN TASKUTIETO KESKEISIN KYBERMAAILMASTA JOKAISELLE. Irina Lönnqvist ja Panu Moilanen
 KYBERIN TASKUTIETO KESKEISIN KYBERMAAILMASTA JOKAISELLE Irina Lönnqvist ja Panu Moilanen MIKSI SINÄ TARVITSET TÄMÄN OPPAAN? Kybermaailma saattaa kuulostaa ilmiöltä, josta vain asiantuntijoiden tulee ymmärtää
KYBERIN TASKUTIETO KESKEISIN KYBERMAAILMASTA JOKAISELLE Irina Lönnqvist ja Panu Moilanen MIKSI SINÄ TARVITSET TÄMÄN OPPAAN? Kybermaailma saattaa kuulostaa ilmiöltä, josta vain asiantuntijoiden tulee ymmärtää
Kybersairauden tiedostaminen! Sairaanhoitopiirien kyberseminaari Kari Wirman
 Kybersairauden tiedostaminen! Sairaanhoitopiirien kyberseminaari 19.10.2016 Kari Wirman 19.10.2016 Kari Wirman cybernetics Cybernetics saves the souls, bodies and material possessions from the gravest
Kybersairauden tiedostaminen! Sairaanhoitopiirien kyberseminaari 19.10.2016 Kari Wirman 19.10.2016 Kari Wirman cybernetics Cybernetics saves the souls, bodies and material possessions from the gravest
5/11 6/11 Vaihe 1. 6/10 4/10 6/10 4/10 Vaihe 2. 5/11 6/11 4/11 7/11 6/11 5/11 5/11 6/11 Vaihe 3
 Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Verkot todennäköisyyslaskennassa Satunnaismuuttujat ja todennäköisyysjakaumat Jakaumien tunnusluvut Kertymäfunktio, Momentit, Odotusarvo,
Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Verkot todennäköisyyslaskennassa Satunnaismuuttujat ja todennäköisyysjakaumat Jakaumien tunnusluvut Kertymäfunktio, Momentit, Odotusarvo,
Todennäköisyyslaskenta I, kesä 2017 Helsingin yliopisto/avoin Yliopisto Harjoitus 1, ratkaisuehdotukset
 Todennäköisyyslaskenta I, kesä 207 Helsingin yliopisto/avoin Yliopisto Harjoitus, ratkaisuehdotukset. Kokeet ja Ω:n hahmottaminen. Mitä tarkoittaa todennäköisyys on? Olkoon satunnaiskokeena yhden nopan
Todennäköisyyslaskenta I, kesä 207 Helsingin yliopisto/avoin Yliopisto Harjoitus, ratkaisuehdotukset. Kokeet ja Ω:n hahmottaminen. Mitä tarkoittaa todennäköisyys on? Olkoon satunnaiskokeena yhden nopan
Kenguru 2016 Ecolier (4. ja 5. luokka)
 sivu 1 / 13 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 13 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Espoon kaupunki Pöytäkirja 96. Valtuusto 08.06.2015 Sivu 1 / 1. 96 Valtuustokysymys kyberturvallisuuden järjestämisestä ja uhkiin varautumisesta
 Valtuusto 08.06.2015 Sivu 1 / 1 1909/07.01.00/2015 Kaupunginhallitus 189 25.5.2015 96 Valtuustokysymys kyberturvallisuuden järjestämisestä ja uhkiin varautumisesta Valmistelijat / lisätiedot: Juha Kalander,
Valtuusto 08.06.2015 Sivu 1 / 1 1909/07.01.00/2015 Kaupunginhallitus 189 25.5.2015 96 Valtuustokysymys kyberturvallisuuden järjestämisestä ja uhkiin varautumisesta Valmistelijat / lisätiedot: Juha Kalander,
Tietotekniikan valintakoe
 Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
1. Tässä tehtävässä päätellään kaksilapsisen perheen lapsiin liittyviä todennäköisyyksiä.
 TODENNÄKÖISYYS Aihepiirejä: Yhden ja kahden tapahtuman tuloksien käsittely ja taulukointi, ovikoodit, joukkueen valinta, bussin odotus, pelejä, urheilijoiden testaus kielletyn piristeen käytöstä, linnun
TODENNÄKÖISYYS Aihepiirejä: Yhden ja kahden tapahtuman tuloksien käsittely ja taulukointi, ovikoodit, joukkueen valinta, bussin odotus, pelejä, urheilijoiden testaus kielletyn piristeen käytöstä, linnun
TODENNÄKÖISYYS JA TILASTOT MAA6 KERTAUS
 TODENNÄKÖISYYS JA TILASTOT MAA6 KERTAUS Klassinen todennäköisyys P suotuisten alkeistapausten lkm kaikkien alkeistapausten lkm P( mahdoton tapahtuma ) = 0 P( varma tapahtuma ) = 1 0 P(A) 1 Todennäköisyys
TODENNÄKÖISYYS JA TILASTOT MAA6 KERTAUS Klassinen todennäköisyys P suotuisten alkeistapausten lkm kaikkien alkeistapausten lkm P( mahdoton tapahtuma ) = 0 P( varma tapahtuma ) = 1 0 P(A) 1 Todennäköisyys
Kenguru 2018 Benjamin (6. ja 7. luokka)
 sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saat 3, 4 tai 5 pistettä.
sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saat 3, 4 tai 5 pistettä.
Todennäköisyys (englanniksi probability)
 Todennäköisyys (englanniksi probability) Todennäköisyyslaskenta sai alkunsa 1600-luvulla uhkapeleistä Ranskassa (Pascal, Fermat). Nykyisin todennäköisyyslaskentaa käytetään hyväksi mm. vakuutustoiminnassa,
Todennäköisyys (englanniksi probability) Todennäköisyyslaskenta sai alkunsa 1600-luvulla uhkapeleistä Ranskassa (Pascal, Fermat). Nykyisin todennäköisyyslaskentaa käytetään hyväksi mm. vakuutustoiminnassa,
Valtiovarainministeriön hallinnonalan johdon aamupäivä - puheenvuoroja digitalisaation johtamisesta kyberturvallisuus & riskienhallinta
 Valtiovarainministeriön hallinnonalan johdon aamupäivä - puheenvuoroja digitalisaation johtamisesta kyberturvallisuus & riskienhallinta Kimmo Rousku, VAHTI-pääsihteeri, JulkICT-osasto Esitykseni - viisi
Valtiovarainministeriön hallinnonalan johdon aamupäivä - puheenvuoroja digitalisaation johtamisesta kyberturvallisuus & riskienhallinta Kimmo Rousku, VAHTI-pääsihteeri, JulkICT-osasto Esitykseni - viisi
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6
 Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe klo 10-13
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo -. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x +9, b) log (x) 7, c) x + x 4 =.. Määrää kaikki ne
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo -. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x +9, b) log (x) 7, c) x + x 4 =.. Määrää kaikki ne
Kenguru 2013 Student sivu 1 / 7 (lukion 2. ja 3. vuosi)
 Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2016 Ecolier (4. ja 5. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Vaasan yliopisto (11) Tietotekniikan ja tuotantotalouden kandidaattiohjelma Valintakoe
 Vaasan yliopisto 1.6.2015 1(11) Valintakoe Vastaajan nimi: Tällä hetkellä olen kiinnostunut valitsemaan pääaineeksi Tietotekniikan Tuotantotalouden En tiedä vielä HUOM! Vastauksesi ei ole mitenkään sitova,
Vaasan yliopisto 1.6.2015 1(11) Valintakoe Vastaajan nimi: Tällä hetkellä olen kiinnostunut valitsemaan pääaineeksi Tietotekniikan Tuotantotalouden En tiedä vielä HUOM! Vastauksesi ei ole mitenkään sitova,
Tentti erilaiset kysymystyypit
 Tentti erilaiset kysymystyypit Monivalinta Monivalintatehtävässä opiskelija valitsee vastauksen valmiiden vastausvaihtoehtojen joukosta. Tehtävään voi olla yksi tai useampi oikea vastaus. Varmista, että
Tentti erilaiset kysymystyypit Monivalinta Monivalintatehtävässä opiskelija valitsee vastauksen valmiiden vastausvaihtoehtojen joukosta. Tehtävään voi olla yksi tai useampi oikea vastaus. Varmista, että
Aikamatka digitaaliseen tulevaisuuteen: olemmeko turvassa? Pekka Vepsäläinen, @pveps Jykes & Kyber-INKA, @CyberFinland 18.4.2016
 Aikamatka digitaaliseen tulevaisuuteen: olemmeko turvassa? Pekka Vepsäläinen, @pveps Jykes & Kyber-INKA, @CyberFinland 18.4.2016 Tietojen kalastelua, nettihuijauksia, vai jotain muuta?? Tietojen
Aikamatka digitaaliseen tulevaisuuteen: olemmeko turvassa? Pekka Vepsäläinen, @pveps Jykes & Kyber-INKA, @CyberFinland 18.4.2016 Tietojen kalastelua, nettihuijauksia, vai jotain muuta?? Tietojen
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
MAT-5 Todennäköisyyslaskenta Tentti.. / Kimmo Vattulainen Vastaa jokainen tehtävä eri paperille. Funktiolaskin sallittu.. a) P A). ja P A B).6. Mitä on P A B), kun A ja B ovat riippumattomia b) Satunnaismuuttujan
Tehtävät 1/11. TAMPEREEN YLIOPISTO Informaatiotieteiden tiedekunta Valintakoe Matematiikka ja tilastotiede. Sukunimi (painokirjaimin)
 1/11 Tehtävä 1 2 3 4 5 6 7 8 9 10 Yhteensä Pisteet (tarkastaja merkitsee) Kokeessa on kymmenen tehtävää, joista jokainen on erillisellä paperilla. Jokaisen tehtävän maksimipistemäärä on 6 pistettä. Ratkaise
1/11 Tehtävä 1 2 3 4 5 6 7 8 9 10 Yhteensä Pisteet (tarkastaja merkitsee) Kokeessa on kymmenen tehtävää, joista jokainen on erillisellä paperilla. Jokaisen tehtävän maksimipistemäärä on 6 pistettä. Ratkaise
TIEDOTUSOPIN VALINTAKOE
 TAMPEREEN YLIOPISTO TIEDOTUSOPIN VALINTAKOE 12.6.2006 Tiedotusopin valintakoe koostuu neljästä tehtäväkokonaisuudesta. Valintakokeesta voi saada yhteensä 60 pistettä. Kokeen eri osat tuottavat pisteitä
TAMPEREEN YLIOPISTO TIEDOTUSOPIN VALINTAKOE 12.6.2006 Tiedotusopin valintakoe koostuu neljästä tehtäväkokonaisuudesta. Valintakokeesta voi saada yhteensä 60 pistettä. Kokeen eri osat tuottavat pisteitä
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe 10.6.2013 klo 10-13 Ratkaisut ja pisteytysohjeet
 Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo - Ratkaisut ja pisteytysohjeet. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x+ x +9, b) log (x) 7,
Helsingin, Itä-Suomen, Jyväskylän, Oulun, Tampereen ja Turun yliopisto Matematiikan valintakoe.6. klo - Ratkaisut ja pisteytysohjeet. Ratkaise seuraavat epäyhtälöt ja yhtälö: a) x+ x +9, b) log (x) 7,
2. laskuharjoituskierros, vko 5, ratkaisut
 2. laskuharjoituskierros, vko, ratkaisut Aiheet: Klassinen todennäköisyys, kombinatoriikka, kokonaistodennäköisyys ja Bayesin kaava D1. Eräässä maassa autojen rekisterikilpien tunnukset ovat muotoa XXXXNN,
2. laskuharjoituskierros, vko, ratkaisut Aiheet: Klassinen todennäköisyys, kombinatoriikka, kokonaistodennäköisyys ja Bayesin kaava D1. Eräässä maassa autojen rekisterikilpien tunnukset ovat muotoa XXXXNN,
Kenguru 2015 Benjamin (6. ja 7. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Python-ohjelmointi Harjoitus 5
 Python-ohjelmointi Harjoitus 5 TAVOITTEET Kerrataan silmukkarakenteen käyttäminen. Kerrataan jos-ehtorakenteen käyttäminen. Opitaan if else- ja if elif else-ehtorakenteet. Matematiikan sisällöt Tehtävät
Python-ohjelmointi Harjoitus 5 TAVOITTEET Kerrataan silmukkarakenteen käyttäminen. Kerrataan jos-ehtorakenteen käyttäminen. Opitaan if else- ja if elif else-ehtorakenteet. Matematiikan sisällöt Tehtävät
 päättely jatkuva sarja. Päättele miten sarja jatkuu. Jatka sarjaa ainakin kahdella luvulla tai kuviolla. A. 7 8 9 0 0-00 99 98 97 - - - 0 B. 8 0 0 0 9 0 8 00 80 0 0 C. PÄÄT TELY 9 jatkuva sarja. Päättele
päättely jatkuva sarja. Päättele miten sarja jatkuu. Jatka sarjaa ainakin kahdella luvulla tai kuviolla. A. 7 8 9 0 0-00 99 98 97 - - - 0 B. 8 0 0 0 9 0 8 00 80 0 0 C. PÄÄT TELY 9 jatkuva sarja. Päättele
Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5
 Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Esimerkki 1: auringonkukan kasvun kuvailu
 GeoGebran LASKENTATAULUKKO Esimerkki 1: auringonkukan kasvun kuvailu Auringonkukka (Helianthus annuus) on yksivuotinen kasvi, jonka varren pituus voi aurinkoisina kesinä hyvissä kasvuolosuhteissa Suomessakin
GeoGebran LASKENTATAULUKKO Esimerkki 1: auringonkukan kasvun kuvailu Auringonkukka (Helianthus annuus) on yksivuotinen kasvi, jonka varren pituus voi aurinkoisina kesinä hyvissä kasvuolosuhteissa Suomessakin
Ryhmät. Pauliina Munter/Suvi Junes Tampereen yliopisto/ Tietohallinto 2014
 1 Ryhmät Moodlessa voi jakaa opiskelijoita pienempiin alaryhmiin, joilla toimitaan esim. keskustelualueella tai työskennellään wikissä. Ryhmätoiminto on hyödyllinen, jos kurssilla on paljon osallistujia
1 Ryhmät Moodlessa voi jakaa opiskelijoita pienempiin alaryhmiin, joilla toimitaan esim. keskustelualueella tai työskennellään wikissä. Ryhmätoiminto on hyödyllinen, jos kurssilla on paljon osallistujia
Vaasan yliopisto (10) Tietotekniikka ja tuotantotalous, kauppatieteet Valintakoe
 Vaasan yliopisto 7.6.2013 1(10) Valintakoe Vastaajan nimi: Lue nämä ohjeet ennen kuin aloitat valintakokeen tekemisen! Valintakoe muodostuu kahdesta osiosta: Ensimmäinen osio perustuu valintakoekirjallisuuteen
Vaasan yliopisto 7.6.2013 1(10) Valintakoe Vastaajan nimi: Lue nämä ohjeet ennen kuin aloitat valintakokeen tekemisen! Valintakoe muodostuu kahdesta osiosta: Ensimmäinen osio perustuu valintakoekirjallisuuteen
Vaasan yliopisto (8) Tietotekniikan ja tuotantotalouden kandidaattiohjelma Valintakoe
 Vaasan yliopisto 6.6.2014 1(8) Valintakoe Vastaajan nimi: Lue nämä ohjeet ennen kuin aloitat valintakokeen tekemisen! Valintakokeessa on kolme osiota: Tuotantotalouden osio (tehtävät 1 ja 2, maksimipisteet
Vaasan yliopisto 6.6.2014 1(8) Valintakoe Vastaajan nimi: Lue nämä ohjeet ennen kuin aloitat valintakokeen tekemisen! Valintakokeessa on kolme osiota: Tuotantotalouden osio (tehtävät 1 ja 2, maksimipisteet
Vaasan yliopisto 7.6.2013 1(10) Tietotekniikka ja tuotantotalous, kauppatieteet Valintakoe
 Vaasan yliopisto 7.6.2013 1(10) Valintakoe Vastaajan nimi: Lue nämä ohjeet ennen kuin aloitat valintakokeen tekemisen! Valintakoe muodostuu kahdesta osiosta: Ensimmäinen osio perustuu valintakoekirjallisuuteen
Vaasan yliopisto 7.6.2013 1(10) Valintakoe Vastaajan nimi: Lue nämä ohjeet ennen kuin aloitat valintakokeen tekemisen! Valintakoe muodostuu kahdesta osiosta: Ensimmäinen osio perustuu valintakoekirjallisuuteen
Tietoturvallisuus yhteiskunnan, yritysten ja yksityishenkilöiden kannalta
 Tietoturvallisuus yhteiskunnan, yritysten ja yksityishenkilöiden kannalta Sähköurakoitsijapäivät 21.11.2013 Kari Wirman 7.11.2013 Kari Wirman 21.11.2013 Kari Wirman, ICT-pooli Tieto Tieto on nyky-yhteiskunnan
Tietoturvallisuus yhteiskunnan, yritysten ja yksityishenkilöiden kannalta Sähköurakoitsijapäivät 21.11.2013 Kari Wirman 7.11.2013 Kari Wirman 21.11.2013 Kari Wirman, ICT-pooli Tieto Tieto on nyky-yhteiskunnan
Suomen kyberturvallisuuden nykytila ja tulevaisuus
 Suomen kyberturvallisuuden nykytila ja tulevaisuus 14.3.2018 Jarno Limnéll Professori, kyberturvallisuus, Aalto-yliopisto Dosentti, kyberturvallisuuden johtaminen, Maanpuolustuskorkeakoulu Dosentti, turvallisuus,
Suomen kyberturvallisuuden nykytila ja tulevaisuus 14.3.2018 Jarno Limnéll Professori, kyberturvallisuus, Aalto-yliopisto Dosentti, kyberturvallisuuden johtaminen, Maanpuolustuskorkeakoulu Dosentti, turvallisuus,
ikä (vuosia) on jo muuttanut 7 % 46 % 87 % 96 % 98 % 100 %
 Testaa taitosi 1 1. Noppaa heitetään kahdesti. Merkitse kaikki alkeistapaukset koordinaatistoon. a) Millä todennäköisyydellä ainakin toinen silmäluvuista on 3? b) Mikä on a-kohdan tapahtuman vastatapahtuma?
Testaa taitosi 1 1. Noppaa heitetään kahdesti. Merkitse kaikki alkeistapaukset koordinaatistoon. a) Millä todennäköisyydellä ainakin toinen silmäluvuista on 3? b) Mikä on a-kohdan tapahtuman vastatapahtuma?
Mat Sovellettu todennäköisyyslasku. Aiheet: Todennäköisyyslaskennan peruskäsitteet Todennäköisyyslaskennan peruslaskusäännöt Avainsanat:
 Mat-2.091 Sovellettu todennäköisyyslasku Aiheet: Todennäköisyyslaskennan peruskäsitteet Todennäköisyyslaskennan peruslaskusäännöt Avainsanat: Alkeistapahtuma, Ehdollinen todennäköisyys, Erotustapahtuma,
Mat-2.091 Sovellettu todennäköisyyslasku Aiheet: Todennäköisyyslaskennan peruskäsitteet Todennäköisyyslaskennan peruslaskusäännöt Avainsanat: Alkeistapahtuma, Ehdollinen todennäköisyys, Erotustapahtuma,
Tuen tarpeen tunnistaminen. Lukemisen ja kirjoittamisen ryhmäarviointi. Esitysohjeet opettajalle. toinen luokka syksy
 Tuen tarpeen tunnistaminen Lukemisen ja kirjoittamisen ryhmäarviointi toinen luokka syksy Esitysohjeet opettajalle arvioinnin yleisiä periaatteita Tutustu ennen tehtävien esittämistä ohjeisiin ja materiaaliin
Tuen tarpeen tunnistaminen Lukemisen ja kirjoittamisen ryhmäarviointi toinen luokka syksy Esitysohjeet opettajalle arvioinnin yleisiä periaatteita Tutustu ennen tehtävien esittämistä ohjeisiin ja materiaaliin
A-osio: Ilman laskinta, MAOL:in taulukkokirja saa olla käytössä. Maksimissaan tunti aikaa.
 MAA6 koe 26.9.2016 Jussi Tyni Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A-osio: Ilman laskinta, MAOL:in taulukkokirja
MAA6 koe 26.9.2016 Jussi Tyni Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A-osio: Ilman laskinta, MAOL:in taulukkokirja
Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6
 Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö
Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö
12. Javan toistorakenteet 12.1
 12. Javan toistorakenteet 12.1 Sisällys Yleistä toistorakenteista. Laskurimuuttujat. While-, do-while- ja for-lauseet. Laskuri- ja lippumuuttujat. Tyypillisiä ohjelmointivirheitä. Silmukan rajat asetettu
12. Javan toistorakenteet 12.1 Sisällys Yleistä toistorakenteista. Laskurimuuttujat. While-, do-while- ja for-lauseet. Laskuri- ja lippumuuttujat. Tyypillisiä ohjelmointivirheitä. Silmukan rajat asetettu
(b) Onko hyvä idea laske pinta-alan odotusarvo lähetmällä oletuksesta, että keppi katkeaa katkaisukohdan odotusarvon kohdalla?
 6.10.2006 1. Keppi, jonka pituus on m, taitetaan kahtia täysin satunnaisesti valitusta kohdasta ja muodostetaan kolmio, jonka kateetteina ovat syntyneet palaset. Kolmion pinta-ala on satunnaismuuttuja.
6.10.2006 1. Keppi, jonka pituus on m, taitetaan kahtia täysin satunnaisesti valitusta kohdasta ja muodostetaan kolmio, jonka kateetteina ovat syntyneet palaset. Kolmion pinta-ala on satunnaismuuttuja.
Vaihtoehtoinen tapa määritellä funktioita f : N R on
 Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: 1 (Alkuarvot) Ilmoitetaan funktion arvot
Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: 1 (Alkuarvot) Ilmoitetaan funktion arvot
Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin!
 MAA6 Kurssikoe 1.11.14 Jussi Tyni ja Juha Käkilehto Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A-OSIO: Laske kaikki
MAA6 Kurssikoe 1.11.14 Jussi Tyni ja Juha Käkilehto Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko. Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! A-OSIO: Laske kaikki
Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella:
 8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
8.1 Satunnaismuuttuja Käytetään satunnaismuuttujaa samoin kuin tilastotieteen puolella: Esim. Nopanheitossa (d6) satunnaismuuttuja X kertoo silmäluvun arvon. a) listaa kaikki satunnaismuuttujan arvot b)
Kenguru Benjamin (6. ja 7. luokka) sivu 1 / 5
 Kenguru Benjamin (6. ja 7. luokka) sivu 1 / 5 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö olisi
Kenguru Benjamin (6. ja 7. luokka) sivu 1 / 5 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö olisi
Tentti erilaiset kysymystyypit
 Tentti erilaiset kysymystyypit Kysymystyyppien kanssa kannatta huomioida, että ne ovat yhteydessä tentin asetuksiin ja erityisesti Kysymysten toimintatapa-kohtaan, jossa määritellään arvioidaanko kysymykset
Tentti erilaiset kysymystyypit Kysymystyyppien kanssa kannatta huomioida, että ne ovat yhteydessä tentin asetuksiin ja erityisesti Kysymysten toimintatapa-kohtaan, jossa määritellään arvioidaanko kysymykset
3. laskuharjoituskierros, vko 6, ratkaisut
 Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
Rekursio. Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on
 Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: Rekursio Funktio f : N R määritellään yleensä
Rekursio Funktio f : N R määritellään yleensä antamalla lauseke funktion arvolle f (n). Vaihtoehtoinen tapa määritellä funktioita f : N R on käyttää rekursiota: Rekursio Funktio f : N R määritellään yleensä
Pauliina Munter/Suvi Junes Tietohallinto/Opetusteknologiapalvelut 2015
 Ryhmät Moodlessa voi jakaa opiskelijoita pienempiin alaryhmiin, joilla toimitaan esim. keskustelualueella tai työskennellään wikissä. Ryhmätoiminto on hyödyllinen, jos kurssilla on paljon osallistujia
Ryhmät Moodlessa voi jakaa opiskelijoita pienempiin alaryhmiin, joilla toimitaan esim. keskustelualueella tai työskennellään wikissä. Ryhmätoiminto on hyödyllinen, jos kurssilla on paljon osallistujia
Muistathan, että löytämiäsi aarteita ei saa ottaa mukaan, vaan ne pitää jättää omille paikoilleen muita löytöretkeilijöitä varten.
 TERVETULOA SATUMAISELLE LÖYTÖRETKELLE! Hyvä Löytöretkeilijä, Olet lähdössä seikkailulle Pukstaavin yläkertaan. Voit ratkaista 1 5 rastia joko yksin tai ryhmässä. Tarvittaessa voit pyytää museokaupasta
TERVETULOA SATUMAISELLE LÖYTÖRETKELLE! Hyvä Löytöretkeilijä, Olet lähdössä seikkailulle Pukstaavin yläkertaan. Voit ratkaista 1 5 rastia joko yksin tai ryhmässä. Tarvittaessa voit pyytää museokaupasta
Tietoteoria. Tiedon käsite ja logiikan perusteita. Monday, January 12, 15
 Tietoteoria Tiedon käsite ja logiikan perusteita Tietoteoria etsii vastauksia kysymyksiin Mitä tieto on? Miten tietoa hankitaan? Mitä on totuus? Minkälaiseen tietoon voi luottaa? Mitä voi tietää? Tieto?
Tietoteoria Tiedon käsite ja logiikan perusteita Tietoteoria etsii vastauksia kysymyksiin Mitä tieto on? Miten tietoa hankitaan? Mitä on totuus? Minkälaiseen tietoon voi luottaa? Mitä voi tietää? Tieto?
YHTEISKUNTATIETEIDEN TIEDEKUNTA, LAPIN YLIOPISTO. Tehtävä I (max 15 pistettä) Vastaajan nimi. Hallintotieteen valintakoe
 1 YHTEISKUNTATIETEIDEN TIEDEKUNTA, LAPIN YLIOPISTO Hallintotieteen valintakoe 10.6.2008 Valintakokeessa on tehtävät I, II ja III. Jokaiselle tehtävälle on oma oheismateriaalinsa. Kokeen yhteispistemäärä
1 YHTEISKUNTATIETEIDEN TIEDEKUNTA, LAPIN YLIOPISTO Hallintotieteen valintakoe 10.6.2008 Valintakokeessa on tehtävät I, II ja III. Jokaiselle tehtävälle on oma oheismateriaalinsa. Kokeen yhteispistemäärä
Kenguru Écolier (4. ja 5. luokka) sivu 1/5
 Kenguru Écolier (4. ja 5. luokka) sivu 1/5 3 pisteen tehtävät 1. Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2. Aikuisten pääsylippu
Kenguru Écolier (4. ja 5. luokka) sivu 1/5 3 pisteen tehtävät 1. Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2. Aikuisten pääsylippu
Mihin varautua, kun sairaala varautuu kyberuhkiin? Perttu Halonen Sosiaali- ja terveydenhuollon ATK-päivät,
 Mihin varautua, kun sairaala varautuu kyberuhkiin? Perttu Halonen Sosiaali- ja terveydenhuollon ATK-päivät, 24.5.2017 Sisällys Keskeisimpiä kyberuhkia Liian paljon huomiota kiinnitetään... Liian vähän
Mihin varautua, kun sairaala varautuu kyberuhkiin? Perttu Halonen Sosiaali- ja terveydenhuollon ATK-päivät, 24.5.2017 Sisällys Keskeisimpiä kyberuhkia Liian paljon huomiota kiinnitetään... Liian vähän
Aikamatka digitaaliseen tulevaisuuteen: olemmeko turvassa? Pekka Jykes &
 Aikamatka digitaaliseen tulevaisuuteen: olemmeko turvassa? Pekka Vepsäläinen, @pveps Jykes & Kyber-INKA, @CyberFinland 11.3.2016 on Digitalisaation tukijalka SoTe-sektorillakin Digitalisaatio hyötykäyttöön
Aikamatka digitaaliseen tulevaisuuteen: olemmeko turvassa? Pekka Vepsäläinen, @pveps Jykes & Kyber-INKA, @CyberFinland 11.3.2016 on Digitalisaation tukijalka SoTe-sektorillakin Digitalisaatio hyötykäyttöön
Kenguru 2015 Mini-Ecolier (2. ja 3. luokka) RATKAISUT
 sivu 1 / 10 3 pistettä 1. Kuinka monta pilkkua kuvan leppäkertuilla on yhteensä? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21 Ratkaisu: Pilkkuja on 1 + 1 + 1 + 2 + 2 + 1 + 3 + 2 + 3 + 3 = 19. 2. Miltä kuvan pyöreä
sivu 1 / 10 3 pistettä 1. Kuinka monta pilkkua kuvan leppäkertuilla on yhteensä? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21 Ratkaisu: Pilkkuja on 1 + 1 + 1 + 2 + 2 + 1 + 3 + 2 + 3 + 3 = 19. 2. Miltä kuvan pyöreä
12. Javan toistorakenteet 12.1
 12. Javan toistorakenteet 12.1 Sisällys Yleistä toistorakenteista. Laskurimuuttujat. While-, do-while- ja for-lauseet. Laskuri- ja lippumuuttujat. Tyypillisiä ohjelmointivirheitä. Silmukan rajat asetettu
12. Javan toistorakenteet 12.1 Sisällys Yleistä toistorakenteista. Laskurimuuttujat. While-, do-while- ja for-lauseet. Laskuri- ja lippumuuttujat. Tyypillisiä ohjelmointivirheitä. Silmukan rajat asetettu
Kirjoita jokaiseen erilliseen vastauspaperiin kurssin nimi, tenttipäivä, oma nimesi (selkeästi), opiskelijanumerosi ja nimikirjoituksesi
 Helsingin yliopisto, Tietojenkäsittelytieteen laitos Tietokantojen perusteet, kurssikoe 29.2.2012 (vastauksia) Liitteenä on tiivistelmä SQL-syntaksista Kirjoita jokaiseen erilliseen vastauspaperiin kurssin
Helsingin yliopisto, Tietojenkäsittelytieteen laitos Tietokantojen perusteet, kurssikoe 29.2.2012 (vastauksia) Liitteenä on tiivistelmä SQL-syntaksista Kirjoita jokaiseen erilliseen vastauspaperiin kurssin
ohjekortti #1 Tämä on ehto. Kun se täyttyy pelissä, seuraa tämän siirron sääntöjä.
 ohjekortti #1 tämä on siirron nimi Tämä on ehto. Kun se täyttyy pelissä, seuraa tämän siirron sääntöjä. Tässä on säännöt, joita siirto noudattaa. Säännöt käydään läpi ylhäältä alaspäin Noppien kohdalla
ohjekortti #1 tämä on siirron nimi Tämä on ehto. Kun se täyttyy pelissä, seuraa tämän siirron sääntöjä. Tässä on säännöt, joita siirto noudattaa. Säännöt käydään läpi ylhäältä alaspäin Noppien kohdalla
Yhtälönratkaisu oppilaan materiaali
 Yhtälönratkaisu oppilaan materiaali Nimi: Luokka: 1 1. Tosia ja epätosia väitteitä Alkupalat Kirjoita taulukkoon T, jos väite on tosi ja E, jos väite on epätosi. Väite 5 > 3 16 < 8 19 = 26 9 < 28 64 =
Yhtälönratkaisu oppilaan materiaali Nimi: Luokka: 1 1. Tosia ja epätosia väitteitä Alkupalat Kirjoita taulukkoon T, jos väite on tosi ja E, jos väite on epätosi. Väite 5 > 3 16 < 8 19 = 26 9 < 28 64 =
Kenguru Écolier (4. ja 5. luokka) ratkaisut sivu 1/5
 Kenguru Écolier (4. ja 5. luokka) ratkaisut sivu 1/5 3 pisteen tehtävät 1) Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2) Aikuisten
Kenguru Écolier (4. ja 5. luokka) ratkaisut sivu 1/5 3 pisteen tehtävät 1) Miettisen perhe syö 3 ateriaa päivässä. Kuinka monta ateriaa he syövät viikon aikana? A) 7 B) 18 C) 21 D) 28 E) 37 2) Aikuisten
https://www10.uta.fi/opas/opintojakso.htm?rid=11585&i dx=2&uilang=fi&lang=fi&lvv=2015
 12.1.2016/1 MTTTP5, luento 12.1.2016 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585&i dx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
12.1.2016/1 MTTTP5, luento 12.1.2016 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585&i dx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
Näin käytät GROW-kortteja
 Mikä on GROW? GROW-korttipeli perustuu Graham Alexanderin, Alan Finen ja John Whitmoren kehittämään GROWmalliin, jossa erilaisia pulmatilanteita ja haasteita käsitellään valmentajan kysymysten avulla ratkaisukeskeisesti.
Mikä on GROW? GROW-korttipeli perustuu Graham Alexanderin, Alan Finen ja John Whitmoren kehittämään GROWmalliin, jossa erilaisia pulmatilanteita ja haasteita käsitellään valmentajan kysymysten avulla ratkaisukeskeisesti.
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE Ratkaisut ja arvostelu < X 170
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 4.6.2013 Ratkaisut ja arvostelu 1.1 Satunnaismuuttuja X noudattaa normaalijakaumaa a) b) c) d) N(170, 10 2 ). Tällöin P (165 < X < 175) on likimain
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 4.6.2013 Ratkaisut ja arvostelu 1.1 Satunnaismuuttuja X noudattaa normaalijakaumaa a) b) c) d) N(170, 10 2 ). Tällöin P (165 < X < 175) on likimain
&idx=2&uilang=fi&lang=fi&lvv=2015
 20.10.2015/1 MTTTP5, luento 20.10.2015 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
20.10.2015/1 MTTTP5, luento 20.10.2015 1 Kokonaisuudet, joihin opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=11585 &idx=2&uilang=fi&lang=fi&lvv=2015 2 Osaamistavoitteet Opiskelija osaa
3. Ryhdy kirjoittamaan ja anna kaiken tulla paperille. Vääriä vastauksia ei ole.
 1 Unelma-asiakas Ohjeet tehtävän tekemiseen 1. Ota ja varaa itsellesi omaa aikaa. Mene esimerkiksi kahvilaan yksin istumaan, ota mukaasi nämä tehtävät, muistivihko ja kynä tai kannettava tietokone. Varaa
1 Unelma-asiakas Ohjeet tehtävän tekemiseen 1. Ota ja varaa itsellesi omaa aikaa. Mene esimerkiksi kahvilaan yksin istumaan, ota mukaasi nämä tehtävät, muistivihko ja kynä tai kannettava tietokone. Varaa
CAB Plan. Päivitys 4.5. Asiakas odottaa
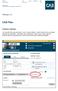 Kent Isacsson 2014-01-20 1 1 of 6 Päivitys 4.5 CAB Plan Asiakas odottaa Jos perustieto ikkunassa laitat rastiin ruutuun asiakas odottaa, muuttuu rekisterinumero punaiseksi työvaiheessa mekaanikko välilehdellä,
Kent Isacsson 2014-01-20 1 1 of 6 Päivitys 4.5 CAB Plan Asiakas odottaa Jos perustieto ikkunassa laitat rastiin ruutuun asiakas odottaa, muuttuu rekisterinumero punaiseksi työvaiheessa mekaanikko välilehdellä,
Kenguru Cadet, ratkaisut (1 / 6) luokka
 Kenguru Cadet, ratkaisut (1 / 6) 3 pisteen tehtävät 1. Mikä luvuista on parillinen? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 Ainoa parillinen on 200 9 = 1800. 2. Kuvan tähti koostuu 12
Kenguru Cadet, ratkaisut (1 / 6) 3 pisteen tehtävät 1. Mikä luvuista on parillinen? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 Ainoa parillinen on 200 9 = 1800. 2. Kuvan tähti koostuu 12
Kenguru 2017 Ecolier (4. ja 5. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai 5 pistettä.
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai 5 pistettä.
(x, y) 2. heiton tulos y
 Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 2, 4, 6, 8, 11 Pistetehtävät: 3, 5, 9, 12 Ylimääräiset tehtävät: 7, 10, 13 Aiheet: Joukko-oppi Todennäköisyys ja sen määritteleminen
Mat-1.2620 Sovellettu todennäköisyyslaskenta B / Tehtävät Demo-tehtävät: 1, 2, 4, 6, 8, 11 Pistetehtävät: 3, 5, 9, 12 Ylimääräiset tehtävät: 7, 10, 13 Aiheet: Joukko-oppi Todennäköisyys ja sen määritteleminen
Kenguru 2017 Ecolier: Ratkaisut (4. ja 5. luokka)
 sivu 1 / 12 Oikeat vastaukset ovat alla. 3 pistettä TEHTÄVÄ 1 2 3 4 5 6 7 VASTAUS C C E B C E A 4 pistettä TEHTÄVÄ 8 9 10 11 12 13 14 VASTAUS D B E A C A C 5 pistettä TEHTÄVÄ 15 16 17 18 19 20 21 VASTAUS
sivu 1 / 12 Oikeat vastaukset ovat alla. 3 pistettä TEHTÄVÄ 1 2 3 4 5 6 7 VASTAUS C C E B C E A 4 pistettä TEHTÄVÄ 8 9 10 11 12 13 14 VASTAUS D B E A C A C 5 pistettä TEHTÄVÄ 15 16 17 18 19 20 21 VASTAUS
Tehtävä 1 2 3 4 5 6 7 Vastaus
 Kenguru Cadet, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Kenguru Cadet, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 1. Algoritmeista 1.1 Algoritmin käsite Algoritmi keskeinen laskennassa Määrittelee prosessin, joka suorittaa annetun tehtävän Esimerkiksi Nimien järjestäminen aakkosjärjestykseen
811120P Diskreetit rakenteet 2016-2017 1. Algoritmeista 1.1 Algoritmin käsite Algoritmi keskeinen laskennassa Määrittelee prosessin, joka suorittaa annetun tehtävän Esimerkiksi Nimien järjestäminen aakkosjärjestykseen
Aaro rakastaa Inkaa tai Ullaa
 VIHJELAPPUSET C.2 I O U I O U A I O B U O O U (U O) (O U) C D I: Aaro rakastaa Inkaa. O: Aaro rakastaa Outia. U: Aaro rakastaa Ullaa. A: I U B: ( I O) U C: ((U O) (O U)) D: O Aaro rakastaa Inkaa tai Ullaa
VIHJELAPPUSET C.2 I O U I O U A I O B U O O U (U O) (O U) C D I: Aaro rakastaa Inkaa. O: Aaro rakastaa Outia. U: Aaro rakastaa Ullaa. A: I U B: ( I O) U C: ((U O) (O U)) D: O Aaro rakastaa Inkaa tai Ullaa
HALLINTOTIETEIDEN KANDIDAATTIOHJELMA (HTK/HTM) Valintakoe Pisteet yhteensä (tarkastaja merkitsee)
 HALLINTOTIETEIDEN KANDIDAATTIOHJELMA (HTK/HTM) Valintakoe 5.6.2017 Pisteet yhteensä (tarkastaja merkitsee) VALINTAKOKEEN PISTEYTYS Valintakokeesta on mahdollisuus saada maksimissaan 60 pistettä. Tehtävät
HALLINTOTIETEIDEN KANDIDAATTIOHJELMA (HTK/HTM) Valintakoe 5.6.2017 Pisteet yhteensä (tarkastaja merkitsee) VALINTAKOKEEN PISTEYTYS Valintakokeesta on mahdollisuus saada maksimissaan 60 pistettä. Tehtävät
Kenguru 2011 Ecolier (4. ja 5. luokka)
 sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
OPPITUNTIMATERIAALIT MEDIAKASVATUS Netiketti Säännöt
 OPPITUNNIN KUVAUS OPPITUNNIN NIMI Sisältö Luokka-aste Suositeltu ohjelmiston kokemustaso Tavoitteet Kesto Tarvikkeet Tehtävän sanastoa Petra s Planet for Schools -ohjelmiston pelisäännöt Käydään läpi netikettiä
OPPITUNNIN KUVAUS OPPITUNNIN NIMI Sisältö Luokka-aste Suositeltu ohjelmiston kokemustaso Tavoitteet Kesto Tarvikkeet Tehtävän sanastoa Petra s Planet for Schools -ohjelmiston pelisäännöt Käydään läpi netikettiä
Kenguru 2014 Ecolier (4. ja 5. luokka)
 sivu 1 / 11 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 11 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Asiakastyytyväisyys Toimiala, yksityisasiakkaat Indeksi 0-100
 EPSI Rating Pankki ja rahoitus 2016 Päivämäärä: 2016-10-03 Lisätietojen saamiseksi, vieraile kotisivuillamme (www.epsi-finland.org) tai ota yhteyttä Tarja Ilvonen, CEO EPSI Rating Suomi Puhelin: +358 50
EPSI Rating Pankki ja rahoitus 2016 Päivämäärä: 2016-10-03 Lisätietojen saamiseksi, vieraile kotisivuillamme (www.epsi-finland.org) tai ota yhteyttä Tarja Ilvonen, CEO EPSI Rating Suomi Puhelin: +358 50
3.5 Todennäköisyyden laskumenetelmiä
 MAB5: Todennäköisyyden lähtökohdat 3.5 Todennäköisyyden laskumenetelmiä Aloitetaan esimerkillä, joka on sitä sarjaa, mihin ei ole mitään muuta yleispätevää ohjetta kuin että on edettävä järjestelmällisesti
MAB5: Todennäköisyyden lähtökohdat 3.5 Todennäköisyyden laskumenetelmiä Aloitetaan esimerkillä, joka on sitä sarjaa, mihin ei ole mitään muuta yleispätevää ohjetta kuin että on edettävä järjestelmällisesti
HALLINTOTIETEIDEN KANDIDAATTIOHJELMA (HTK/HTM) Valintakoe Pisteet yhteensä (tarkastaja merkitsee)
 HALLINTOTIETEIDEN KANDIDAATTIOHJELMA (HTK/HTM) Valintakoe 6.6.2016 Pisteet yhteensä (tarkastaja merkitsee) VALINTAKOKEEN PISTEYTYS Valintakokeesta on mahdollisuus saada maksimissaan 60 pistettä. Tehtävät
HALLINTOTIETEIDEN KANDIDAATTIOHJELMA (HTK/HTM) Valintakoe 6.6.2016 Pisteet yhteensä (tarkastaja merkitsee) VALINTAKOKEEN PISTEYTYS Valintakokeesta on mahdollisuus saada maksimissaan 60 pistettä. Tehtävät
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti
 SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 5.5.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
SGN-1200 Signaalinkäsittelyn menetelmät, Tentti 5.5.2008 Kirjoita nimesi ja opiskelijanumerosi jokaiseen paperiin. Vastauspaperit tullaan irrottamaan toisistaan. Jos tila ei riitä, jatka kääntöpuolelle
Tarkista vielä ennen analysoinnin aloittamista seuraavat seikat:
 Yleistä Tilastoapu on Excelin sisällä toimiva apuohjelma, jonka avulla voit analysoida tilastoaineistoja. Tilastoapu toimii Excelin Windows-versioissa Excel 2007, Excel 2010 ja Excel 2013. Kun avaat Tilastoavun,
Yleistä Tilastoapu on Excelin sisällä toimiva apuohjelma, jonka avulla voit analysoida tilastoaineistoja. Tilastoapu toimii Excelin Windows-versioissa Excel 2007, Excel 2010 ja Excel 2013. Kun avaat Tilastoavun,
KUNTIEN JA HUS:N ASIAKAS- JA POTILASTIETOJÄRJESTELMÄN HANKINTA
 KUNTIEN JA HUS:N ASIAKAS- JA POTILASTIETOJÄRJESTELMÄN HANKINTA Perustelumuistio Liite 4: Toimittajan resurssien ja osaamisen arvioinnin tulokset (vertailuperuste 3.2) 1 Sisällysluettelo 1. Dokumentin tarkoitus
KUNTIEN JA HUS:N ASIAKAS- JA POTILASTIETOJÄRJESTELMÄN HANKINTA Perustelumuistio Liite 4: Toimittajan resurssien ja osaamisen arvioinnin tulokset (vertailuperuste 3.2) 1 Sisällysluettelo 1. Dokumentin tarkoitus
Diskreetin matematiikan perusteet Malliratkaisut 2 / vko 38
 Diskreetin matematiikan perusteet Malliratkaisut 2 / vko 38 Tuntitehtävät 11-12 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 15-16 loppuviikon harjoituksissa. Kotitehtävät 13-14 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Malliratkaisut 2 / vko 38 Tuntitehtävät 11-12 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 15-16 loppuviikon harjoituksissa. Kotitehtävät 13-14 tarkastetaan loppuviikon
Kyberturvallisuuden ja kybersodankäynnin todellisuus
 Kyberturvallisuuden ja kybersodankäynnin todellisuus Jarno Limnéll Professori, kyberturvallisuus, Aalto-yliopisto Kyberturvallisuusjohtaja, Insta Group Oy. Sotatieteiden tohtori, VTM, Kapteeni (evp.) @JarnoLim
Kyberturvallisuuden ja kybersodankäynnin todellisuus Jarno Limnéll Professori, kyberturvallisuus, Aalto-yliopisto Kyberturvallisuusjohtaja, Insta Group Oy. Sotatieteiden tohtori, VTM, Kapteeni (evp.) @JarnoLim
Käyttöopas Mobiilipankkiin ja tunnuslukusovellukseen
 Käyttöopas Mobiilipankkiin ja tunnuslukusovellukseen Käyttöopas tunnuslukusovellukseen sekä mobiilipankkiin Tämä opas on tehty sinulle tueksi Nordean mobiilipalveluiden käytön aloittamiseen Näitä ohjeita
Käyttöopas Mobiilipankkiin ja tunnuslukusovellukseen Käyttöopas tunnuslukusovellukseen sekä mobiilipankkiin Tämä opas on tehty sinulle tueksi Nordean mobiilipalveluiden käytön aloittamiseen Näitä ohjeita
