Kiinalaisen postimiehen ongelma
|
|
|
- Sanna-Kaisa Korpela
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 Aalto-yliopisto Perustieteiden korkeakoulu Teknillisen fysiikan ja matematiikan tutkinto-ohjelma Kiinalaisen postimiehen ongelma Kandidaatintyö Kimmo Kontio Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki oikeudet pidätetään.
2 Aalto-yliopisto, PL 11000, AALTO Tekniikan kandidaatintyön tiivistelmä Tekijä Kimmo Kontio Työn nimi Kiinalaisen postimiehen ongelma Koulutusohjelma Teknillisen fysiikan ja matematiikan koulutusohjelma Pääaine Systeemitieteet Pääaineen koodi F3010 Vastuuopettaja Harri Ehtamo Työn ohjaaja(t) Harri Ehtamo Päivämäärä Sivumäärä Kieli Suomi Tiivistelmä Postinkantajalla on oma alueensa, jolle posti on jaettava. Jotta jokainen asukas saa postinsa, alueen jokainen katu on kuljettava päästä päähän. Kiinalaisen postimiehen ongelma on löytää sellainen reitti, jossa jokainen katu kuljetaan läpi vähintään kerran ja kuljettu kokonaismatka on mahdollisimman pieni. Ongelmalla on monisatavuotinen historia, vaikkakin täsmällinen ongelman määritys ja ratkaisu tapahtui melko tarkalleen viitisenkymmentä vuotta sitten. Ongelman laaja käyttökohteiden kirjo postinkantajan ongelmakentän ulkopuolella, esimerkiksi DNA-ketjun järjestyksen määrittäminen ja matkapuhelimen käyttöliittymän käytettävyyden arviointi, pitää ongelman edelleen aktiivisen tutkimuksen piirissä. Suurin osa ongelman käyttökelpoisista muunnoksista on lisäksi vaikeita ongelmia, joihin alkuperäistä ratkaisua ei voi suoraan käyttää. Kiinalaisen postimiehen ongelma ei ole mikään matematiikan erillinen saareke, vaan sillä on tiivis suhde mm. graafeihin, jotka ovat esiintyneet kumppanina alusta asti. Käytännön laskuesimerkkinä kiinalaisen postimiehen ongelmaa sovelletaan murtomaahiihtoon Yllästunturin alueella. Tarkoituksena on löytää optimaalinen reitti, jossa alueen kaikki ladut hiihdetään läpi kertaalleen kokonaismatka minimoiden. Alueella on reilut 300 km latuja ristiin rastiin muodostaen satakunta risteystä eli hiihdettävää riittää, vaikka kokonaismatkan haluaa pitää mahdollisimman pienenä. Pisimmän yhteen menoon hiihdettävän lenkin lyhentämiseksi tarkastellaan myös muunneltua kiinalaisen postimiehen ongelmaa, joka kuitenkin paljastuu aiempien tutkimusten valossa vaikeaksi ongelmaksi ja varsinainen ratkaisu jää näin ollen tämän työn ulottumattomiin. Avainsanat Kiinalaisen postimiehen ongelma, reititysongelma
3 Sisältö 1 Johdanto 1 2 Termejä Laskennallinen vaativuus Historia 5 4 Algoritmeja Kwanin algoritmi Edmondsin algoritmi Lineaarista ohjelmointia Huomioita Ongelman muunnelmia 14 6 Ongelman sovelluskohteita Konkreettinen ratkaisuesimerkki: hiihtoa Ylläksellä Yhteenveto 21 Viitteet 22 A Ongelman muunnelmia 26
4 1 1 Johdanto Kiinalaisen postimiehen ongelma on optimointitehtävä, jossa haetaan lyhin reitti siten, että reitin jokainen osa tulee kuljettua läpi. Konkreettisesti voidaan ajatella postimiestä, jonka pitää jakaa posti tiettyyn kaupunginosaan. Postimiehen lähtö- ja saapumispaikka on postikonttori ja hänen pitää kulkea kukin kadunpätkä vähintään kerran, jotta kaikki asukkaat saavat postinsa. Lyhin tällainen kierros on vastaus kiinalaisen postimiehen ongelmaan. Kiinalaisen postimiehen ongelma on käyttökelpoinen edellä mainitun suoraviivaisen reititysongelman lisäksi muillakin tieteenalueilla, esimerkiksi biologiassa ja tietotekniikassa. Sovelluskohteiden lukuisan määrän takia - väheksymättä myöskään niiden rahallista merkitystä - ongelman tutkimus on edelleen aktiivista, vaikkakin ongelman perusversioon löytyi hyvä ratkaisu samaisella 1960-luvulla, jolla ongelma varsinaisesti määriteltiin. Tämä työ on yleiskatsaus kiinalaisen postimiehen ongelmaan - uusia tutkimustuloksia ei synny, mutta ymmärrys ongelman luonteesta syvenee. Historiajaksossa aloitetaan 1700-luvulta, pääpaino on kuitenkin 1900-luvun loppupuolen ensimmäisissä ratkaisualgoritmeissa. Käytännön esimerkkinä ongelmaa sovelletaan optimaalisen hiihtolenkin suunnitteluun. Työssä ei rajoituta tiukasti alkuperäisen määrittelyn mukaiseen kiinalaisen postimiehen ongelmaan vaan käsitellään laajemmin siitä johdettuja reititysongelmia ja niiden ratkaisuja. 2 Termejä Tässä luvussa esitellään graateorian termejä. Suomenkieliset termit ovat pääosin Ruohoselta (2013), englannin kieliset termit ovat puolestaan lähteistä Edmonds (1965b), Papadimitriou and Steiglitz (1998) ja Diestel (2010). Graateoriassa eri lähteet eivät ole termien kohdalla täysin yhteneväisiä. Tässä työssä käytetään seuraavia määritelmiä. Graa, solmu, kaari (Graph, vertex, edge) Graa G = (V, E) on joukko solmuja V ja kaaria E. Jokaisen kaaren e kummassakin päässä on solmu v. Solmujen lukumäärä on V ja kaarien lukumäärä on E. Mikäli kaarilla ei ole suuntia, graa on suuntaamaton (undirected ), mikäli kaikilla kaarilla on suunta, graa on suunnattu (directed ).
5 2 Edellisten välimuoto on sekagraa (mixed graph). Graa on painotettu (weighted ), mikäli sen kaarille on annettu painot (esim. pituudet). Solmun v aste (degree) on niiden kaarien määrä, joiden päätesolmu on v - silmukka (loop) eli kaari, jonka alku- ja loppusolmu on sama, lasketaan kahdesti. Solmu on parillinen, mikäli sen aste on parillinen, muutoin se on pariton. Kulku Reitti Polku Kierros Piiri (Walk ) Solmujen ja kaarien yhdistelmä (v 1,e 1,v 2,e 2,...), jossa kaaren e i päätesolmut ovat v i ja v i+1. Lyhin kulku on yksi solmu, jolloin kulun pituus on nolla. Kulku on suljettu, mikäli se päättyy alkusolmuun. (Trail, route) Kulku, jossa graan kukin kaari e i esiintyy vain kerran. (Path) Reitti, jossa graan kukin solmu v i esiintyy vain kerran. Poikkeuksena on suljettu polku, joka päättyy alkusolmuun. (Tour, cycle) Suljettu kulku. (Circuit) Suljettu polku. Yksinkertainen kierros (Simple tour ) Kierros, jossa graan kukin kaari e i esiintyy enintään kerran. Postimiehen kierros (Postman tour ) Kierros, jossa graan kukin kaari e i esiintyy vähintään kerran. Eulerin kierros (Euler tour ) Kierros, jossa graan kukin kaari e i esiintyy täsmälleen kerran. Kiinalaisen postimiehen ongelma (CPP, Chinese Postman Problem ) Optimointiongelma, jossa graa- sta haetaan kokonaismitaltaan lyhin postimiehen kierros. Yksinkertainen graa (Simple graph) Graa, jossa ei ole rinnakkaisia kaaria eikä silmukoita. Rinnakkaisilla kaarilla on samat päätesolmut. Multigraa (Multigraph) Gaa, jossa on silmukoita tai rinnakkaisia kaaria. Yhtenäinen graa (Connected graph) Graa, jonka jokaisesta solmusta on polku kaikkiin muihin solmuihin.
6 3 Vahvasti yhtenäinen graa (Strongly connected graph ). Graa, jonka jokaisesta solmusta on kaarien suuntaa noudattava polku kaikkiin muihin solmuihin. Täydellinen graa (Complete graph) Yksinkertainen graa, jonka jokaisesta solmusta on kaari kaikkiin muihin solmuihin. Eulerin graa (Euler graph) Yhtenäinen graa, jonka kaikki solmut ovat parillisia. Kaksijakoinen graa (Bipartite graph) Graa, jonka solmut V voidaan jakaa kahteen erilliseen joukkoon V 1 ja V 2 siten, että graan jokaisen kaaren toinen päätesolmu kuuluu V 1 :een ja toinen V 2 :een. Aligraa Faktori (Subgraph) Graa G s = (V s,e s ) on graan G = (V,E) aligraa, jos V s V ja E s E. (Factor ) Graan G faktori on G:n aligraa, joka sisältää kaikki graan G solmut. Virittävä aligraa (Spanning subgraph) Sama kuin faktori. Sovitus (Matching) Graan (V, E) kaarien osajoukko M E siten, että M:ään kuuluvilla kaarilla ei ole yhteisiä päätesolmuja. Maksimisovitus (Maximum cardinality matching ) Sovitus, jossa on suurin mahdollinen määrä kaaria. Raskain sovitus (Maximum weighted matching ) Sovitus, jonka kaarien painojen summa on mahdollisimman suuri. Täydellinen sovitus (Perfect matching ) Sovitus, jossa jokainen graan solmu on jonkin sovitukseen kuuluvan kaaren päätesolmu. Kevein täydellinen sovitus (Minimum weighted perfect matching ) Täydellinen sovitus, jonka kaarien painojen summa on mahdollisimman pieni. Metsä (Forest) Piiritön graa.
7 4 Puu (Tree) Yhtenäinen graa, jossa V = E + 1. Vaihtoehtoisesti yhtenäinen metsä. 2.1 Laskennallinen vaativuus Algoritmien laskennallinen vaativuus (vaativuusteoria) arvioi tehtävän ratkaisun vaatimia resursseja (aika, tila) tehtävän kokoon verrattuna (Pohjolainen, 2010; Ruohonen, 2013). O (Big O) O on funktion asymptoottisesta käyttäytymisestä kertova merkintä; f(n) = O(p(n)) tarkoittaa, että on olemassa luku n l N siten, että kun n n l, f(n) Cp(n), C R +. Suurilla n:n arvoilla f(n) käyttäytyy siis korkeintaan kuten vakio p(n). Deterministinen algoritmi Algoritmi, jolla ei ole valinnanmahdollisuuksia etenemisen suhteen. Ei-deterministinen algoritmi Algoritmi, jolla on useita vaihtoehtoja etenemisen suhteen. P N P (Deterministic polynomial time ) Deterministisesti polynomiaikaiset tehtävät ovat polynomiaikaisten algoritmien laskennallinen aikavaativuusluokka. Tehtävä ratkeaa deterministisellä algoritmilla ja ratkaisun vaatima aika f(n) riippuu tehtävän koosta n - graa- en tapauksessa n on esim. solmujen tai kaarien määrä tai niiden yhdistelmä. Tällöin suurilla n:n arvoilla f(n) on kertaluokkaa p(n), missä p(n) on jokin n:n polynomifunktio. (Non-deterministic polynomial time ) Ei-deterministisesti polynomiaikainen tunnistustehtävä ratkeaa ei-deterministisellä algoritmilla ja kuuluu aikavaativuusluokkaan P. Tunnistustehtävässä vastaus annetaan muodossa kyllä tai ei. Esimerkiksi minimointitehtävässä kysytään, onko tehtävän tiettyyn instanssiin löydettävissä pienempää ratkaisua kuin jokin tietty luku k. Mikäli k on käypä ratkaisu ja vastaus on ei, k on myös optimaalinen. N P-täydellinen (N P-complete) N P-täydelliset tehtävät ovat vaikeimpia N P- luokan tehtäviä. Määritelmän mukaan jokainen NP-luokkaan kuuluva tehtävä on redusoitavissa polynomiaikaisesti mihin tahansa N P-täydelliseen tehtävään.
8
9 6 Ongelman ratkaisi sveitsiläinen matemaatikko Leonhard Euler, joka osoitti, ettei haluttua reittiä ole (Euler, 1736). Ja enemmän, Euler ratkaisi ongelman yleisellä tasolla eli millä tahansa siltojen, saarien ja jokihaarojen yhdistelmällä. Tämän dokumentin termein silta on kaari, alue tai saari on solmu ja haluttu reitti on Eulerin reitti. Eulerin reitin olemassaololle Euler esitti seuraavat kolme sääntöä: 1. Jos alueita, joihin johtaa pariton määrä siltoja, on enemmän kuin kaksi, tällaista reittiä ei ole olemassa. 2. Jos kuitenkin täsmälleen kahteen alueeseen johtaa pariton määrä siltoja, reitti on mahdollinen, mikäli se alkaa toisesta näistä alueista. 3. Lopulta, jos ei ole alueita, johon tulee pariton määrä siltoja, reitti on mahdollinen ja se voidaan aloittaa mistä alueesta tahansa. Euler todisti kuitenkin vain ensimmäisen yllä olevista säännöistä (Biggs, 1976) eikä myöskään esittänyt yksityiskohtaisesti, miten Eulerin reitti löydetään, mikäli sellainen on olemassa. Eulerin sääntöjä eli riittäviä ja välttämättömiä ehtoja Eulerin reitin olemassaololle sivusivat myös J. Poinsot 1809 ja J.B. Listing 1847, mutta päästiin 1870-luvulle ennen kuin kaikille säännöille 1-3 esitettiin todistus. Carl Hierholzerin todistus julkaistiin postuumisti 1873 (Hierholzer and Wiener, 1873) - Carl Wiener kirjoitti sen Hierholzerin kanssa käymiensä keskustelujensa pohjalta ilman kirjallisia muistiinpanoja. Todistuksen lisäksi Hierholzer esitti yksityiskohtaisen tavan löytää jokin Eulerin reitti; Hierholzerin algoritmi on vieläpä tehokkaampi kuin myöhempi Fleuryn algoritmi (Wikipedia Eulerian Graph, 2015). Seuraava edistysaskel otettiin suuren harppauksen aikaisessa Kiinassa 1960, jossa Mei-ko Kwan muotoili kysymyksen uudella tavalla (Kwan, 1962, englannin kielinen versio): Kun meillä on yhtenäinen graa, miten saamme piirrettyä jatkuvan graan (kaarien lisäys sallittu) alkaen ja päätyen samaan pisteeseen mahdollisimman pienellä kaarien lisäyksellä. Jatkuvan graan voi mieltää graaksi, jossa voi piirtää jokaisen kaaren mahdollisine toistoineen kynää paperista nostamatta ja päätyä takaisin alkusolmuun - Kwan käytti lähestymistavasta termiä graanen ohjelmointi (graphic programming). Kwan muotoili ongelman optimointiongelmaksi, esitti optimaaliselle ratkai-
10 7 sulle riittävät ja välttämättömät ehdot todistuksineen ja esitti algoritmin tehtävän ratkaisemiseksi. Aikaisemmin oli käsitelty Eulerin reittiä, nyt kyseessä oli kiinalaisen postimiehen kierros (kuva 2). Kuva 2: Kwanin esimerkki ja ratkaisu kiinalaisen postimiehen ongelmaan (Kwan, 1962). Kaarien painot ovat niiden pituudet. Kwanin artikkelin englannin kielinen versio päätyi NBS:n (U.S. National Bureau of Standards, nykyisin NIST) Jack Edmondsin käsiin, joka redusoi ongelman ei-kaksijakoisen graan raskaimpaan sovitukseen ( maximum weighted matching of a non-bipartite graph ) (Edmonds and Johnson, 1973). Suorituksen arvoa nostaa, että juuri Edmonds itse julkaisi ei-kaksijakoisen graan sovitukseen algoritmit ensin graan maksimisovitus (Edmonds, 1965b) ja melkeinpä välittömästi perään graan raskain sovitus (Edmonds, 1965a). Myös ongelman nimi kiinalaisen postimiehen ongelma (CPP) on peräisin Edmondsilta hänen silloisen esimiehensä Alan Goldmanin inspiroimana (Pieterse and Black, 2014). Artikkelissaan 1973 Edmonds esitteli myös kiinalaisen postimiehen ongelman muunnoksia. Alkuperäisessä versiossa ongelmaa kuvaava graa on suuntaamaton; Edmonds otti esille tapaukset, jossa graa on suunnattu, graa on sekagraa, graan joitakin kaaria ei tarvitse kulkea tai että postimiehiä on monta.
11
12
13
14
15
16
17 Huomioita Kiinalaisen postimiehen ongelman ratkaisu ei ole välttämättä yksikäsitteinen - ei kaarien kahdentamisen eikä Eulerin kierrosten kannalta. Kaarien kahdentamisen suhteen tästä ovat esimerkkinä yllä muodostetut Eulerin graat (kuvat 6 ja 9): polut ja ovat yhtä pitkät. Koska jokainen Eulerin kierros on optimaalinen ratkaisu kiinalaisen postimiehen ongelmaan, optimaalisten ratkaisujen lukumäärä on Eulerin kierrosten lukumäärä. Yllä olevassa ratkaisussa (kuva 6) Eulerin kierroksia on 8576 (Wolfram Mathematican funktio FindEulerianCycle). Yleisesti suuntaamattoman graan Eulerin kierrosten laskeminen on vaikea ongelma (Brightwell and Winkler, 2004) ja tässä työssä käytetyssä laskentaympäristössä jo K 7 :n (täydellinen graa, jossa on 7 solmua ja kaari jokaisen solmuparin välillä) Eulerin kierrosten lukumäärän laskenta epäonnistui. Edmondsin (1965b) sovitusalgoritmi kuuluu laskennallisesti luokkaan P ja Edmondsin oma arvio laskennallisesta vaativuudesta oli konservatiivinen O( V 4 ); Kolmogorov (2009) ja Syslo (2006) arvioivat algoritmin kompleksisuuden luokkaa paremmaksi O( E V 2 ). Teoreettisesti nopein algoritmi vuonna 2006 (Syslo et al.) oli Micali-Vaziranin O( E V ), josta todistus (proof of correctness) julkaistiin joitakin vuosia myöhemmin (Vazirani, 2012). 5 Ongelman muunnelmia Liitteessä A on listattu kiinalaisen postimiehen ongelman (CPP) muunnoksia. Joissakin lähteissä C-kirjain tiputetaan pois lyhenteestä, mikäli kaikkia kaaria ei tarvitse kulkea - puhutaan siis postimiehen ongelmasta (PP, Postman Problem). Joissakin lähteissä C jätetään pois pelkästään vain lyhyemmän merkinnän takia. Eri versioissa kiinalaisen postimiehen ongelmaan asetetaan joko lisää rajoituksia tai vaihtoehtoisesti siitä poistetaan rajoituksia. Ehtojen lisäämisestä on esimerkkinä sekalainen kiinalaisen postimiehen ongelma (MCPP), jossa jotkut kaaret ovat yksisuuntaisia - eivät kuitenkaan kaikki, koska tällöin olisi kyseessä suunnattu kiinalaisen postimiehen ongelma (DCPP). Rajoitusten poistosta on esimerkkinä maalaispostimiehen ongelma (RPP), jossa joitakin kaaria ei tarvitse kulkea, mutta niitä pitkin voi kulkea, jos siten kokonaismatkasta saadaan pienempi. Eri vaihtoehtoja voi luonnollisesti yhdistellä, esim. sekalainen maalaispostimiehen ongelma (MRPP), jossa joitakin yksi-
18 15 tai kaksisuuntaisia kaaria ei tarvitse kulkea (Eiselt et al., 1995b). Kiinalaisen postimiehen ongelma (CPP) ja sen suunnattu versio (DCPP) ovat ratkaistavissa polynomiaikaisesti - CPP on redusoitavissa graan sovitustehtävään ja DCPP minimikustannusvirtaustehtävään (minimum cost ow problem). Muut postimiehen ongelman versiot ovat pääsääntöisesti NPvaikeita optimointitehtäviä joitakin yksittäistapauksia lukuun ottamatta. Jälkimmäisestä on esimerkkinä tuulinen kiinalaisen postimiehen ongelma (WCPP), jossa kaarien painot voivat olla erilaiset eri suuntiin kuljettaessa; yleisesti WCPP on N P-vaikea optimointitehtävä, mutta mikäli pohjana oleva graa on Eulerin graa, tehtävälle on olemassa polynomiaikainen ratkaisu (Eiselt et al., 1995a). 6 Ongelman sovelluskohteita Tässä postimiehen ongelmaa käsitellään laajassa merkityksessä reititysongelmana edellisen luvun 5 hengessä eikä rajoituta tiukasti kiinalaisen postimiehen ongelmaan, jossa määritelmän mukaan on kuljettava yhtenäisen suuntaamattoman multigraan kaikki kaaret. Postimiehen ongelmalla on lukuisia käytännön sovelluksia, ongelma on selvästi asetettu, mutta yksinkertaista ja yleispätevää algoritmia ei ole (Kramberger and šerovnik, 2007). Kwanin alkuperäisessä hengessä käyttökohteina ovat kaikki reititysongelmat, joissa on olennaista optimoida kulku pitkin kaarta: postin jakelu, lumen auraus, jätteen keräys, sähkölinjojen tarkastus ja pysäköinnintarkastajien reitin suunnittelu. Postimiehen ongelmaa voidaan soveltaa luovasti myös alkuperäisen käyttötarkoituksensa ulkopuolella. Seuraavaksi joitakin esimerkkejä eri tieteenaloilta yksityiskohtaisemmin käsiteltynä. Leikkuualgoritmeja, joissa yhdestä aihiosta leikataan useita eri kappaleita nostamatta leikkuuterää välillä ylös, voidaan mallintaa maalaispostimiehen ongelmana (Rodrigues and Ferreira, 2012). Elektronisten integroitujen piirien (VLSI) testaukseen, jossa signaalin reitti piirin läpi riippuu syötteestä ja piirin tilasta, voidaan hakea minimimittainen testisuunnitelma, jossa kaikki vaihtoehtoiset reitit käydään läpi, kiinalaisen postimiehen reitillä (Füredi and Kurshan, 2004). Valikkopohjaisten käyttöliittymien (matkapuhelimet, kamerat, pesukoneet ym.) testaus käytettävyyden kannalta on kiinalaisen postimiehen ongelma,
19 16 jonka ratkaisu antaa pienimmän mahdollisen testipolun, jolla kaikki siirtymät tilasta toiseen saadaan testattua. Mallin graassa napin painallus on kaari ja valikon tila on solmu; mikäli napilla ei ole toimintoa kyseisessä tilassa, se on silmukka. Samaan sarjaan kuuluu myös verkkosivustojen linkkien eheyden ja oikeellisuuden analysointi. Kiinalaisen postimiehen reitti ei kerro linkkien laadusta, mutta se antaa lyhimmän tavan testata jokainen linkki. Malligraassa linkki on kaari ja sivu on solmu (Thimbleby, 2003). Bioinformatiikassa käyttökohde on DNA:n rakenneosien (nukleotidien) järjestyksen määrittäminen (DNA fragment assembly ). DNA:ta ei pystytä lukemaan kerralla vaan luku tehdään tietyn pituisissa sekvensseissä. Lukemisen jälkeen oikea DNA-ketju pitäisi koota luetuista sekvensseistä, joiden järjestystä ei tiedetä, joissa on päällekkäisyyksiä ja jotka ovat eri pituisia. Lyhin DNA-ketju, joka sisältää kaikki kerätyt sekvenssit, on osoittautunut kelvolliseksi arvioksi oikealle DNA-ketjulle. Tämä ongelma voidaan muotoilla kiinalaisen postimiehen ongelmana, jossa graana on lukusekvenssien määrämittaisista paloista koottu de Bruijnin graa (Kundeti et al., 2012). Yleispiirteenä voidaan todeta, että kaikki yllä olevat sovellukset ovat mallinnettavissa graafeina, joissa siirtymät ja niiden optimointi ovat oleellisia. 6.1 Konkreettinen ratkaisuesimerkki: hiihtoa Ylläksellä Otetaan konkreettinen esimerkki murtomaahiihdosta Pohjois-Suomessa sijaitsevan Ylläs-tunturin alueelta, jossa on kohtuullisen kattava hiihtolatujen verkosto: yli 300 km yksistään Ylläksen hoitoalueella. Hiihtäjän aikomuksena on sivakoida yhteen menoon kaikki ladut, mutta fyysiset rajansa tuntien hän haluaa minimoida hiihdettävän kokonaismatkan. Alueen laduista on olemassa latukartta (kuva 10), joka voidaan tulkita luontevasti graaksi siten, että solmu on latujen risteys tai päätepiste ja kaari on kahden solmun välinen latuosuus. Kaaren painoksi sopii sen pituus.
20 17 Kuva 10: Ote Ylläksen latukartasta vuodelta 2011 (Ylläksen Rasti ry, 2011). Hiihtäjän ongelma on nyt täsmälleen kiinalaisen postimiehen ongelma, jossa latukarttaa mallintavassa graassa on 98 solmua, 135 kaarta ja kaarien yhteenlaskettu pituus on 299 km (kuva 11). Parittomien solmujen lukumäärä on 74, joten graa ei ole Eulerin graa ja optimaalinen hiihtolenkki on kiinalaisen postimiehen kierros. Huomattakoon, että Kwanin ensimmäinen optimaalisuusehto takaa, että optimiratkaisussa mitään latua ei hiihdetä kahta kertaa enempää. Optimaalisen hiihtolenkin pituudelle saadaan siis triviaalisti alarajaksi kaarien pituuksien summa 299 km ja ylärajaksi sama kahteen kertaan eli 598 km. Sekä kartan muunnos graaksi että kiinalaisen postimiehen ongelman ratkaisu tehtiin Wolfram Mathematicalla, jossa on optimointiin valmis funktio FindPostmanTour. Uudehkolla kannettavalla tietokoneella (ns. ultrabook eikä tehopakkaus) optimointi vei seinäkelloaikaa muutaman millisekunnin eli 1960-luvun termillä voidaan todeta algoritmin olevan hyvä. Lopullinen hiihtomatka venyi latuverkoston 299 kilometristä 355 kilometriin, kahteen kertaan hiihdettävien latujen kokonaispituudeksi tuli siis 56 km 47 pätkässä. Kuvassa (11) ei ole esitetty varsinaisesti postimiehen kierrosta vaan yhteen
21
22 19 (sinisellä) ja kahteen (punaisella) kertaan hiihdettävät ladut siten, että kahteen kertaan hiihdettävien osuuksien yhteenlaskettu pituus on mahdollisimman pieni. Mikäli punaiset kaaret muutetaan kahdeksi rinnakkaiseksi kaareksi (esim. kuva 6), saadaan Eulerin graa, jossa jokainen Eulerin kierros on optimaalinen kiinalaisen postimiehen kierros. Yksittäisiä Eulerin kierroksia voi nyt hakea Hierholzerin algoritmilla (luku 4.1). Ylläksen matkailusivustolla (yllas., 2015) mainitaan Ylläksen hoitoalueen latujen kokonaispituudeksi 330 km, mikä on samaa suuruusluokkaa tässä mallina käytetyn graan kaarien kokonaispituuden 299 km kanssa. Mallissa on poistettu joitakin vähän hoidettuja tai hoitamattomia osuuksia - esim. Pirunkuru ja Aakenuksen laki. Mallin käyttökelpoisuuden kannalta on tietysti olennaista, että 355 km voidaan hiihtää osapuilleen yhteen menoon. Vertailukohta löytyy tarkastelemalla 24 tunnin hiihdon tuloksia: nykyinen naisten ennätys on 344 km (IS, 2015) ja miesten 433 km (ESS, 2010). Koska 24 tunnit hiihdot hiihdetään käytännössä yhteen menoon, 355 km matkana ei tuntuisi ylitsepääsemättömältä. Hiihtäjän huollon järjestäminen vaatinee erityisen huolellisia järjestelyjä: 24 tunnin hiihdot tehdään yleensä tasaisella, lyhyellä (alle 2 km) lenkillä jatkuvasti saatavissa olevan huollon vuoksi. Yllä mainitun miesten ennätyksen hiihtäjä Teemu Virtanen myönsi Etelä- Suomen sanomien haastattelussa kuntonsa olleen hyvä. Passiivisemmalle hiihdon harrastajalle saadaan hiihdettävämpi vaihtoehto, kun kappaleen 5 hengessä malliksi otetaan esimerkiksi MM k-wmcpp:n (Min-Max Windy Mixed k- Chinese Postman Problem). Selkokielellä lyhenne tarkoittaa, että kaikki ladut hiihdetään vähintään kerran (CPP). Tämän voi tehdä kuitenkin k kierroksella (k); kaikkien kierrosten alku ja loppu ovat samassa pisteessä. Kierrosten pituuksien tasoittamiseksi minimoidaan pisimmän lenkin pituus (MM). Jotkin laduista voivat olla yksisuuntaisia (M) latujen turvallisuusohjeen mukaisesti. Kun kaarien painona ei käytetä yksioikoisesti matkaa vaan esim. hiihtämiseen kuluvaa aikaa vakiorasituksella, kaksisuuntaisen kaaren paino voidaan asettaa erilaiseksi eri suuntiin hiihdettäessä (W). Kun k:n arvoa kasvatetaan, intuitiivisesti voi päätellä, että pisimmän lenkin pituus voi pienentyä tiettyyn rajaan asti. Kuvassa (12) on hahmoteltu muutama yksinkertaistettu esimerkkitapaus. Kuvassa 12a maksimikierroksen pituus pienenee k:n arvoon 7 saakka, jolloin lyhin pisimmillään hiihdettävä lenkki on yksi kaaren mitta. Kuvassa 12b arvolla k = 2 saadaan pisin lenkki lyhenemään kahdeksan kaaren mittaiseksi kierrokseksi. Kuvassa 12c pisimmän kierroksen pituus on aina kahdeksan kaarta, mikä on kyettävä hiihtämään kerralla k:n arvosta riippumatta.
23
24 21 7 Yhteenveto Tässä työssä käsiteltiin kiinalaisen postimiehen ongelmaa 1700-luvulta nykypäivään - ajallisesti koko ongelman historia. Periaatetasolla käsiteltiin myös kaksi ensimmäistä ratkaisualgoritmia 1960-luvulta. Kiinalaisen postimiehen ongelma on siitä mielenkiintoinen ongelma, että sille kehitettiin hyvä (polynomiaikainen) ratkaisualgoritmi pian ongelman täsmällisen määrittelyn jälkeen. Tämä ei ole kuitenkaan estänyt algoritmien jatkokehittelyä ja siitä onkin julkaistu useita paranneltuja versioita. Vain alkuperäinen kiinalaisen postimiehen ongelma (mallina suuntaamaton graa- ) ja tämän täysin suunnattu versio ovat ratkaistavissa polynomiaikaisella algoritmilla - muut postimiehen ongelman versiot kuuluvat pääsääntöisesti N P-vaikeisiin ongelmiin, jotka ovat nykyäänkin ratkeamattomia. Jatkotutkimukselle on edelleen tilaus, voidaan parantaa tunnettua hyvää ratkaisua tai keskittyä johonkin ongelman erityisversioon ja lähteä hakemaan ratkaisua vaikeaan ongelmaan. Jälkimmäiseen hyvänä motivaationa on ongelman käyttökelpoisuus moneen alkuperäisen reitinvalintaongelman ulkopuolella olevaan tieteenalaan - yksi työssä käsitelty ongelma oli DNA:n rakenteen määrittäminen. Työn laskennallisessa osassa sovellettiin kiinalaisen postimiehen kierroksen hakua Ylläksen latuverkostoon hiihtäjän näkökulmasta. Laskennassa käytettiin valmista ohjelmistoa ja lopputulos oli positiivinen pettymys - ratkaisu löytyi sekunnin tuhannesosissa tavallisella modernilla kannettavalla tietokoneella. Samassa yhteydessä käsiteltiin monimutkaisemman mallin käyttöä.
25 22 Viitteet Biggs, N., Graph theory Clarendon Press, Oxford [Eng.]. Brightwell, G. R., Winkler, P., Note on counting Eulerian circuits. lanl. arxiv. org.viitattu URL eulerian_circuits.pdf Diestel, R., Graph theory, 4th Edition. No. 173 in Graduate texts in mathematics. Springer, Heidelberg ; New York. Dijkstra, E., A Note on Two Problems in Connexion with Graphs. Numerische Mathematlk 1 (1), URL http: //www-m3.ma.tum.de/foswiki/pub/mn0506/webhome/dijkstra.pdf Edmonds, J., 1965a. Maximum Matching and a Polyhedron with 0,1-Vertices. Journal of Research of the National Bureau of Stantards 69B. URL http: //nvlpubs.nist.gov/nistpubs/jres/69b/jresv69bn1-2p125_a1b.pdf Edmonds, J., 1965b. Paths, trees, and owers. Canadian Journal of mathematics 17 (3), URL http: //cms.math.ca/openaccess/cjm/v17/cjm1965v pdf Edmonds, J., Johnson, E., Matching, Euler tours and the Chinese postman. Mathematical Programming 5 (1), URL Eiselt, H. A., Gendreau, M., Laporte, G., Apr. 1995a. Arc Routing Problems, Part I: The Chinese Postman Problem. Operations Research 43 (2), URL Eiselt, H. A., Gendreau, M., Laporte, G., Jun. 1995b. Arc Routing Problems, Part II: The Rural Postman Problem. Operations Research 43 (3), URL
26 23 ESS, Lahtelainen Teemu Virtanen hiihti vihdoin 24 tunnin maailmanennätyksen. Viitattu URL lahtelainen-teemu-virtanen-hiihti-vihdoin-24-tunnin%e2%80% 93maailmanennatyksen Euler, L., Solutio problematis ad geometriam situs pertinentis. URL Füredi, Z., Kurshan, R., May Minimal length test vectors for multiple-fault detection. Theoretical Computer Science 315 (1), URL Grötschel, M., Yuan, Y.-x., Euler, Mei-Ko Kwan, Königsberg, and a Chinese Postman. Optimization Stories, 43. URL vol-ismp-all.pdf#page=49 Hierholzer, C., Wiener, C., Mar Ueber die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren. Mathematische Annalen 6 (1), URL IS, Iisalmelaishiihtäjä rikkoi 24 tunnin hiihdon maailmanennätyksen. Viitattu URL iisalmelaishiihtaja-rikkoi-24-tunnin-hiihdon%e2%80% 93maailmanennatyksen/ Kolmogorov, V., Blossom V: a new implementation of a minimum cost perfect matching algorithm. Mathematical Programming Computation 1 (1), URL Korte, B. H., Combinatorial optimization: theory and algorithms, 2nd Edition. No. 21 in Algorithms and combinatorics. Springer, Berlin ; New York. Kramberger, T., šerovnik, J., Priority constrained chinese postman problem. Logistics & Sustainable Transport 1 (1). URL
27 24 Kundeti, V., Rajasekaran, S., Dinh, H., An ecient algorithm for Chinese postman walk on bi-directed de Bruijn graphs. Discrete Mathematics, Algorithms and Applications 4 (02), URL http: // Kwan, M.-k., Graphic programming using odd or even points. Chinese Mathematics 1. URL Kwan-Guan-chinese-postman-english.pdf Osterhues, A., Mariak, F., On variants of the k-chinese Postman Problem. Operations Research and Wirtschaftsinformatik, University Dortmund (30). URL publikationen/dispap30.pdf Papadimitriou, C. H., Steiglitz, K., Combinatorial optimization: algorithms and complexity. Dover Publications, Mineola, N.Y. Pieterse, V., Black, P., Chinese postman problem. Viitattu URL Pohjolainen, S. (Ed.), Matemaattinen mallinnus, 1st Edition. WSOYpro Oy. Rodrigues, A. M., Ferreira, J. S., Cutting path as a rural postman problem: solutions by memetic algorithms.viitattu URL Ruohonen, K., Graateoria. Viitattu URL Syslo, M. M., Deo, N., Kowalik, J. S., Dec Discrete Optimization Algorithms: With Pascal Programs. Courier Corporation. Thimbleby, H., The directed chinese postman problem. Software: Practice and Experience 33 (11), URL Vazirani, V. V., A Simplication of the MV Matching Algorithm and its Proof. arxiv preprint arxiv: viitattu URL
28 25 Wikipedia Eulerian Graph, Nov Eulerian path. Page Version ID: Viitattu URL path&oldid= Wolfram reference, The Seven Bridges of Königsberg. Viitattu URL VisualizeEulerianCycles.html yllas., Ladut, reitit ja latukahvilat - Ylläs. Viitattu URL ladut-reitit-ja-latukahvilat.html Ylläksen Rasti ry, Latukartta. Viitattu URL
29 26 A Ongelman muunnelmia Kiinalaisen postimiehen ongelmasta on lukuisia muunnelmia, seuraavassa niistä valikoitu joukko. Eiselt et al. (1995a,b) CPP DCPP MCPP WCPP RPP MRPP SCP HCPP Chinese Postman Problem. Kiinalaisen postimiehen ongelma. Hae kierros graassa G siten, että kaikki kaaret kuljetaan vähintään kerran ja kokonaismatka on pienin mahdollinen. Graa G on yhtenäinen, painotettu, suuntaamaton multigraa. Directed Chinese Postman Problem. Suunnattu kiinalaisen postimiehen ongelma. Kuin CPP, mutta kaikki kaaret ovat suunnattuja. Graan pitää olla vahvasti yhtenäinen. Mixed Chinese Postman Problem. Sekalainen kiinalaisen postimiehen ongelma. Kuin CPP, mutta osa kaarista on suunnattuja. Windy Chinese Postman Problem. Tuulinen kiinalaisen postimiehen ongelma. Kuin CPP, mutta kaarien painot voivat olla erisuuntaisia eri suuntaan kuljettaessa. Rural Postman Problem. Maalaispostimiehen ongelma. Kuin CPP, mutta osaa kaarista ei tarvitse kulkea (voi kyllä, mikäli se pienentää kokonaismatkaa). Mixed Rural Postman Problem. Sekalainen maalaispostimiehen ongelma. Kuin MCPP, mutta osaa kaarista ei tarvitse kulkea (voi kyllä, mikäli se pienentää kokonaismatkaa). Stacker Crane Problem. Hyllynosturiongelma. MRPP, jossa kaikki suunnatut kaaret on kuljettava. Suuntaamattomia kaaria ei tarvitse kulkea kuin tarpeen mukaan. Hierarchical Postman Problem. Hierarkinen postimiehen ongelma. Graan kaaret jaetaan prioriteetin mukaisiin ryhmiin; alemman prioriteetin kaaret palvellaan vasta kun kaikki ylemmän prioriteetin kaaret on palveltu. Kulku pitkin alemman prioriteetin kaarta pitkin on sallittu ennen ylemmän prioriteetin kaaren palvelua.
30 27 Postimiehen tapauksessa palvelu vastaa postin jakoa, kulku ohikävelyä. ARP CARP GRP Arc Routing Problem. Kaarireititysongelma. Yleinen ongelmaluokka, jossa graan kaarien määrätty joukko on kuljettava minimikustannuksin. Capasitated Arc Routing Problem. Kapasitiivinen kaarireititysongelma. Kuin ARP, mutta usealla toimijalla, jolla kullakin on rajoitettu kapasiteetti. General Routing Problem. Yleinen reititysongelma. Yleinen ongelmaluokka, jossa graan kaarien ja solmujen määrätty joukko on kuljettava minimikustannuksin. Osterhues and Mariak (2005) Kaaren painona on sen kulkemiseen tarvittava aika - palveluaika (posti jaetaan) tai läpikulkuaika (postia ei jaeta, puhdas läpikulku). Hiihtäjän tapauksessa matka käy yhtä hyvin. k-cpp k- Chinese Postman Problem. k:n kiinalaisen postimiehen ongelma. Kuin CPP, mutta postimiehiä on k kappaletta. Graan kaikki kaaret on kuljettava. Tehtävässä minimoidaan kaikkien postimiesten käyttämä yhteenlaskettu aika. MM k-cpp Min-Max k-cpp. Min-max k:n kiinalaisen postimiehen ongelma. Kuin k-cpp, mutta nyt minimoidaan pisin postimiehen käyttämä aika. MAD k-cpp Minimum Absolute Deviation k-cpp. k:n kiinalaisen postimiehen ongelma, jossa minimoidaan postimiesten käyttämän ajan yhteenlaskettu poikkeama ohjeellisesta ajasta. MSD k-cpp Minimum Square Deviance k-cpp. k:n kiinalaisen postimiehen ongelma, jossa minimoidaan postimiesten käyttämän ajan yhteenlaskettu neliöllinen poikkeama ohjeellisesta ajasta. MOT k-cpp Minimum Overtime k-cpp. k:n kiinalaisen postimiehen ongelma, jossa minimoidaan postimiesten käyttämän ajan yhteenlaskettu
31 28 ohjeellisen ajan ylitys. Kramberger and šerovnik (2007) GCPP CCPP RPPDC PCCPP Generalized Chinese Postman Problem. Yleistetty kiinalaisen postimiehen ongelma. Kuin CPP, mutta kaaret on jaettu erillisiin joukkoihin. Kustakin kaarijoukosta on kuljettava vähintään yksi kaari siten, että kokonaismatka on pienin mahdollinen. Capacitated Chinese Postman Problem. Kapasitiivinen kiinalaisen postimiehen ongelma. Kuin k-cpp, mutta postimiehillä on rajallinen kapasiteetti (postisäkin koko). Rural Postman Problem with Deadline Classes. Aikarajoitettu maalaispostimiehen ongelma. Kuin RPP, mutta nyt kuljettavat kaaret on jaettu joukkoihin, joilla kullakin on oma määräaikansa, mihin mennessä kaikki sen kaaret on kuljettava. Priority Constrained Chinese Postman Problem. Järjestetty kiinalaisen postimiehen ongelma. Kuin CPP, mutta optimaalisten vastausten joukosta haetaan ratkaisu, joka toteuttaa lisäehdot mahdollisimman hyvin. Lisäehdot ovat tässä järjestetty lista solmuja v 1,v 2,...,v k, joiden kautta halutaan kulkea mahdollisimman aikaisin. Ensin optimaalisten ratkaisujen joukosta valitaan ne, joissa v 1 :ssä vieraillaan mahdollisimman aikaisin, sitten taasen näistä valitaan edelleen ratkaisut, joissa v 2 :n kautta kuljetaan mahdollisimman aikaisin jne.
Kiinalaisen postimiehen ongelma
 Kiinalaisen postimiehen ongelma Kimmo Kontio 1.12.2015 Ohjaaja/Valvoja: Harri Ehtamo [5] Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki oikeudet pidätetään.
Kiinalaisen postimiehen ongelma Kimmo Kontio 1.12.2015 Ohjaaja/Valvoja: Harri Ehtamo [5] Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki oikeudet pidätetään.
0 v i v j / E, M ij = 1 v i v j E.
 Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
Vieruspistematriisi Graafi esitetään tietokoneessa useimmiten matriisin avulla. Graafin G = (V, E), V = {v 1, v 2,..., v n } vieruspistematriisi (adjacency matrix)on n n matriisi M = (M ij ), missä n on
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen
 V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
Joonas Haapala Ohjaaja: DI Heikki Puustinen Valvoja: Prof. Kai Virtanen
 Hävittäjälentokoneen reitin suunnittelussa käytettävän dynaamisen ja monitavoitteisen verkko-optimointitehtävän ratkaiseminen A*-algoritmilla (valmiin työn esittely) Joonas Haapala 8.6.2015 Ohjaaja: DI
Hävittäjälentokoneen reitin suunnittelussa käytettävän dynaamisen ja monitavoitteisen verkko-optimointitehtävän ratkaiseminen A*-algoritmilla (valmiin työn esittely) Joonas Haapala 8.6.2015 Ohjaaja: DI
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 62 Luku 2 Yhtenäisyys 2.1 Polku 2.2 Lyhin painotettu polku 2.3 Yhtenäinen graafi 2.4 Komponentti 2.5 Aste
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 166 Luku 4 Erilaisia graafeja 4.1 Eulerin graafi 4.2 Hamiltonin graafi 4.3 Tasograafi 4.4 Graafin värittäminen
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
A274101 TIETORAKENTEET JA ALGORITMIT VERKOT ELI GRAAFIT Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) HISTORIAA Verkko- eli graafiteorian historia on saanut
Minimilatenssiongelman ratkaisualgoritmeja (valmiin työn esittely)
 Minimilatenssiongelman ratkaisualgoritmeja (valmiin työn esittely) Antti Salmela 03.03.2014 Ohjaaja: Harri Ehtamo Valvoja: Harri Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla.
Minimilatenssiongelman ratkaisualgoritmeja (valmiin työn esittely) Antti Salmela 03.03.2014 Ohjaaja: Harri Ehtamo Valvoja: Harri Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla.
Luku 7. Verkkoalgoritmit. 7.1 Määritelmiä
 Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
PARITUS KAKSIJAKOISESSA
 PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
PARITUS KAKSIJAKOISESSA GRAAFISSA Informaatiotekniikan t iik seminaari i Pekka Rossi 4.3.2008 SISÄLTÖ Johdanto Kaksijakoinen graafi Sovituksen peruskäsitteet Sovitusongelma Lisäyspolku Bipartite matching-algoritmi
Algoritmit 1. Luento 8 Ke Timo Männikkö
 Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005
 Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Königsbergin sillat. Königsberg 1700-luvulla. Leonhard Euler ( )
 Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Königsbergin sillat 1700-luvun Königsbergin (nykyisen Kaliningradin) läpi virtasi joki, jonka ylitti seitsemän siltaa. Sanotaan, että kaupungin asukkaat yrittivät löytää reittiä, joka lähtisi heidän kotoaan,
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
Algoritmit 2. Luento 11 Ti Timo Männikkö
 Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Graafit ja verkot. Joukko solmuja ja joukko järjestämättömiä solmupareja. eli haaroja. Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria
 Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
7.4. Eulerin graafit 1 / 22
 7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
7.4. Eulerin graafit 1 / 22 Viivojen läpikäynti Graafin pisteiden/viivojen läpikäyminen esiintyy usein sovelluksissa: Etsintäalgoritmit, reititykset Läpikäyminen tehdään nopeimmin, kun yhtäkään viivaa/pistettä
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
v 8 v 9 v 5 C v 3 v 4
 Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Algoritmit 1. Luento 13 Ti 23.2.2016. Timo Männikkö
 Algoritmit 1 Luento 13 Ti 23.2.2016 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
Algoritmit 1 Luento 13 Ti 23.2.2016 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
Algoritmit 1. Luento 1 Ti Timo Männikkö
 Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Algoritmi on periaatteellisella tasolla seuraava:
 Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Algoritmit 1. Luento 13 Ma Timo Männikkö
 Algoritmit 1 Luento 13 Ma 26.2.2018 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
Algoritmit 1 Luento 13 Ma 26.2.2018 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä.
 Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkkejä polynomisista ja ei-polynomisista ongelmista
 Esimerkkejä polynomisista ja ei-polynomisista ongelmista Ennen yleisempiä teoriatarkasteluja katsotaan joitain tyypillisiä esimerkkejä ongelmista ja niiden vaativuudesta kaikki nämä ongelmat ratkeavia
Esimerkkejä polynomisista ja ei-polynomisista ongelmista Ennen yleisempiä teoriatarkasteluja katsotaan joitain tyypillisiä esimerkkejä ongelmista ja niiden vaativuudesta kaikki nämä ongelmat ratkeavia
Rekursiolause. Laskennan teorian opintopiiri. Sebastian Björkqvist. 23. helmikuuta Tiivistelmä
 Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Rekursiolause Laskennan teorian opintopiiri Sebastian Björkqvist 23. helmikuuta 2014 Tiivistelmä Työssä käydään läpi itsereplikoituvien ohjelmien toimintaa sekä esitetään ja todistetaan rekursiolause,
Kombinatorinen optimointi
 Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
Johdatus verkkoteoriaan 4. luento
 Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
Johdatus verkkoteoriaan 4. luento 28.11.17 Viikolla 46 läpikäydyt käsitteet Viikolla 47 läpikäydyt käsitteet Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot,
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
Kysymys: Voidaanko graafi piirtää tasoon niin, että sen viivat eivät risteä muualla kuin pisteiden kohdalla?
 7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
7.7. Tasograafit Graafi voidaan piirtää mielivaltaisen monella tavalla. Graafin ominaisuudet voivat näkyä selkeästi jossain piirtämistavoissa, mutta ei toisessa. Eräs tärkeä graafiryhmä, pintagraafit,
Silmukkaoptimoinnista
 sta TIE448 Kääntäjätekniikka, syksy 2009 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. joulukuuta 2009 Sisällys Sisällys Seuraava deadline Vaihe F maanantai 14.12. klo 12 rekisteriallokaatio Arvostelukappale
sta TIE448 Kääntäjätekniikka, syksy 2009 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. joulukuuta 2009 Sisällys Sisällys Seuraava deadline Vaihe F maanantai 14.12. klo 12 rekisteriallokaatio Arvostelukappale
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Algoritmit 1. Luento 9 Ti Timo Männikkö
 Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Graateorian maksimivirtausalgoritmi
 Graateorian maksimivirtausalgoritmi LuK-tutkielma Visa Vallivaara 800283 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 203 Sisältö Johdanto 2 Peruskäsitteitä 3 2 Graateoriaa 6 2. Suunnattu graa.........................
Graateorian maksimivirtausalgoritmi LuK-tutkielma Visa Vallivaara 800283 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 203 Sisältö Johdanto 2 Peruskäsitteitä 3 2 Graateoriaa 6 2. Suunnattu graa.........................
MS-A0402 Diskreetin matematiikan perusteet
 MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
MS-A0402 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks may
811312A Tietorakenteet ja algoritmit 2015-2016. V Verkkojen algoritmeja Osa 2 : Kruskalin ja Dijkstran algoritmit
 811312A Tietorakenteet ja algoritmit 2015-2016 V Verkkojen algoritmeja Osa 2 : Kruskalin ja Dijkstran algoritmit Sisältö 1. Johdanto 2. Leveyshaku 3. Syvyyshaku 4. Kruskalin algoritmi 5. Dijkstran algoritmi
811312A Tietorakenteet ja algoritmit 2015-2016 V Verkkojen algoritmeja Osa 2 : Kruskalin ja Dijkstran algoritmit Sisältö 1. Johdanto 2. Leveyshaku 3. Syvyyshaku 4. Kruskalin algoritmi 5. Dijkstran algoritmi
Optimoinnin sovellukset
 Optimoinnin sovellukset Timo Ranta Tutkijatohtori TTY Porin laitos OPTIMI 4.12.2014 Mitä optimointi on? Parhaan ratkaisun systemaattinen etsintä kaikkien mahdollisten ratkaisujen joukosta Tieteellinen
Optimoinnin sovellukset Timo Ranta Tutkijatohtori TTY Porin laitos OPTIMI 4.12.2014 Mitä optimointi on? Parhaan ratkaisun systemaattinen etsintä kaikkien mahdollisten ratkaisujen joukosta Tieteellinen
Search space traversal using metaheuristics
 Search space traversal using metaheuristics Mika Juuti 11.06.2012 Ohjaaja: Ville Mattila Valvoja: Harri Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki
Search space traversal using metaheuristics Mika Juuti 11.06.2012 Ohjaaja: Ville Mattila Valvoja: Harri Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin kaikki
Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m.
 Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
Hamiltonin sykleistä graateoriassa
 Hamiltonin sykleistä graateoriassa Pro gradu -tutkielma Ohto Nordberg 1335868 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2013 Sisältö Johdanto 2 1 Historiaa 3 1.1 Euler................................
Hamiltonin sykleistä graateoriassa Pro gradu -tutkielma Ohto Nordberg 1335868 Matemaattisten tieteiden laitos Oulun yliopisto Kevät 2013 Sisältö Johdanto 2 1 Historiaa 3 1.1 Euler................................
Malliratkaisut Demot
 Malliratkaisut Demot 4 3.4.017 Tehtävä 1 Tarkastellaan harjoituksen 1 nopeimman reitin ongelmaa ja etsitään sille lyhin virittävä puu käyttämällä kahta eri algoritmia. a) (Primin algoritmi) Lähtemällä
Malliratkaisut Demot 4 3.4.017 Tehtävä 1 Tarkastellaan harjoituksen 1 nopeimman reitin ongelmaa ja etsitään sille lyhin virittävä puu käyttämällä kahta eri algoritmia. a) (Primin algoritmi) Lähtemällä
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
58131 Tietorakenteet (kevät 2009) Harjoitus 11, ratkaisuja (Topi Musto)
 811 Tietorakenteet (kevät 9) Harjoitus 11, ratkaisuja (Topi Musto) 1. Bellmanin-Fordin algoritmin alustusvaiheen jälkeen aloitussolmussa on arvo ja muissa solmuissa on arvo ääretön. Kunkin solmun arvo
811 Tietorakenteet (kevät 9) Harjoitus 11, ratkaisuja (Topi Musto) 1. Bellmanin-Fordin algoritmin alustusvaiheen jälkeen aloitussolmussa on arvo ja muissa solmuissa on arvo ääretön. Kunkin solmun arvo
1 Määrittelyjä ja aputuloksia
 1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
1 Määrittelyjä ja aputuloksia 1.1 Supremum ja infimum Aluksi kerrataan pienimmän ylärajan (supremum) ja suurimman alarajan (infimum) perusominaisuuksia ja esitetään muutamia myöhemmissä todistuksissa tarvittavia
Harjoitus 3 (31.3.2015)
 Harjoitus (..05) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i,j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Harjoitus (..05) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i,j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
14. Luennon sisältö. Kuljetustehtävä. Verkkoteoria ja optimointi. esimerkki. verkkoteorian optimointitehtäviä verkon virittävä puu lyhimmät polut
 JYVÄSKYLÄN YLIOPISTO 14. Luennon sisältö Kuljetustehtävä esimerkki Verkkoteoria ja optimointi verkkoteorian optimointitehtäviä verkon virittävä puu lyhimmät polut kevät 2012 TIEA382 Lineaarinen ja diskreetti
JYVÄSKYLÄN YLIOPISTO 14. Luennon sisältö Kuljetustehtävä esimerkki Verkkoteoria ja optimointi verkkoteorian optimointitehtäviä verkon virittävä puu lyhimmät polut kevät 2012 TIEA382 Lineaarinen ja diskreetti
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Algoritmit 2. Luento 12 Ke Timo Männikkö
 Algoritmit 2 Luento 12 Ke 26.4.2017 Timo Männikkö Luento 12 Rajoitehaku Kauppamatkustajan ongelma Lyhin virittävä puu Paikallinen etsintä Vaihtoalgoritmit Geneettiset algoritmit Simuloitu jäähdytys Algoritmit
Algoritmit 2 Luento 12 Ke 26.4.2017 Timo Männikkö Luento 12 Rajoitehaku Kauppamatkustajan ongelma Lyhin virittävä puu Paikallinen etsintä Vaihtoalgoritmit Geneettiset algoritmit Simuloitu jäähdytys Algoritmit
Algoritmit 1. Luento 14 Ke 25.2.2015. Timo Männikkö
 Algoritmit 1 Luento 14 Ke 25.2.2015 Timo Männikkö Luento 14 Heuristiset menetelmät Heuristiikkoja kapsäkkiongelmalle Kauppamatkustajan ongelma Lähimmän naapurin menetelmä Kertaus ja tenttivinkit Algoritmit
Algoritmit 1 Luento 14 Ke 25.2.2015 Timo Männikkö Luento 14 Heuristiset menetelmät Heuristiikkoja kapsäkkiongelmalle Kauppamatkustajan ongelma Lähimmän naapurin menetelmä Kertaus ja tenttivinkit Algoritmit
Graafin virittävä puu 1 / 20
 Graafin virittävä puu 1 / 20 Graafin virittävä puu PuuT on graafingvirittävä puu (spanning tree), jos se sisältää kaikkig:n pisteet. Virittäviä puita: 2 / 20 Yhdistämisongelma Yhdistämisongelma:(Connector
Graafin virittävä puu 1 / 20 Graafin virittävä puu PuuT on graafingvirittävä puu (spanning tree), jos se sisältää kaikkig:n pisteet. Virittäviä puita: 2 / 20 Yhdistämisongelma Yhdistämisongelma:(Connector
TKT20001 Tietorakenteet ja algoritmit Erilliskoe , malliratkaisut (Jyrki Kivinen)
 TKT0001 Tietorakenteet ja algoritmit Erilliskoe 5.1.01, malliratkaisut (Jyrki Kivinen) 1. [1 pistettä] (a) Esitä algoritmi, joka poistaa kahteen suuntaan linkitetystä järjestämättömästä tunnussolmullisesta
TKT0001 Tietorakenteet ja algoritmit Erilliskoe 5.1.01, malliratkaisut (Jyrki Kivinen) 1. [1 pistettä] (a) Esitä algoritmi, joka poistaa kahteen suuntaan linkitetystä järjestämättömästä tunnussolmullisesta
58131 Tietorakenteet ja algoritmit Uusinta- ja erilliskoe ratkaisuja (Jyrki Kivinen)
 58131 Tietorakenteet ja algoritmit Uusinta- ja erilliskoe 12.9.2018 ratkaisuja (Jyrki Kivinen) 1. [10 pistettä] Iso-O-merkintä. (a) Pitääkö paikkansa, että n 3 + 5 = O(n 3 )? Ratkaisu: Pitää paikkansa.
58131 Tietorakenteet ja algoritmit Uusinta- ja erilliskoe 12.9.2018 ratkaisuja (Jyrki Kivinen) 1. [10 pistettä] Iso-O-merkintä. (a) Pitääkö paikkansa, että n 3 + 5 = O(n 3 )? Ratkaisu: Pitää paikkansa.
Department of Mathematics, Hypermedia Laboratory Tampere University of Technology. Roolit Verkostoissa: HITS. Idea.
 Roolit Tommi Perälä Department of Mathematics, Hypermedia Laboratory Tampere University of Technology 25.3.2011 J. Kleinberg kehitti -algoritmin (Hypertext Induced Topic Search) hakukoneen osaksi. n taustalla
Roolit Tommi Perälä Department of Mathematics, Hypermedia Laboratory Tampere University of Technology 25.3.2011 J. Kleinberg kehitti -algoritmin (Hypertext Induced Topic Search) hakukoneen osaksi. n taustalla
j n j a b a c a d b c c d m j b a c a d a c b d c c j
 TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-38.115 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 12 29.2.2008 D12/1 Tarkastellaan verkkoa, jossa on solmua ja linkkiä.
TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-38.115 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 12 29.2.2008 D12/1 Tarkastellaan verkkoa, jossa on solmua ja linkkiä.
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT GRAAFITEHTÄVIÄ JA -ALGORITMEJA Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) GRAAFIN LÄPIKÄYMINEN Perusta useimmille
A274101 TIETORAKENTEET JA ALGORITMIT GRAAFITEHTÄVIÄ JA -ALGORITMEJA Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) GRAAFIN LÄPIKÄYMINEN Perusta useimmille
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Implementation of Selected Metaheuristics to the Travelling Salesman Problem (valmiin työn esittely)
 Implementation of Selected Metaheuristics to the Travelling Salesman Problem (valmiin työn esittely) Jari Hast xx.12.2013 Ohjaaja: Harri Ehtamo Valvoja: Hari Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston
Implementation of Selected Metaheuristics to the Travelling Salesman Problem (valmiin työn esittely) Jari Hast xx.12.2013 Ohjaaja: Harri Ehtamo Valvoja: Hari Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston
Harjoitus 6 ( )
 Harjoitus 6 (21.4.2015) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s. t. g(x) 0 h(x) = 0 x X olevan optimointitehtävän Lagrangen duaali on missä max θ(u, v) s. t.
Harjoitus 6 (21.4.2015) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s. t. g(x) 0 h(x) = 0 x X olevan optimointitehtävän Lagrangen duaali on missä max θ(u, v) s. t.
Valitaan alkio x 1 A B ja merkitään A 1 = A { x 1 }. Perinnöllisyyden nojalla A 1 I.
 Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
Graafiteoria matematiikkaako?
 Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
Koostanut: Elina Viro, Juho Lauri Opettajalle Graafiteoria matematiikkaako? Kohderyhmä: 7.-9.-luokkalaiset Esitiedot: - Taustalla oleva matematiikka: Graafiteoria, looginen ajattelu Ajankäyttö: Varsinainen
Harjoitus 6 ( )
 Harjoitus 6 (30.4.2014) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s.t. g(x) 0 h(x) = 0 x X (1) olevan optimointitehtävän Lagrangen duaali on max θ(u,v) s.t. u 0,
Harjoitus 6 (30.4.2014) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s.t. g(x) 0 h(x) = 0 x X (1) olevan optimointitehtävän Lagrangen duaali on max θ(u,v) s.t. u 0,
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Algoritmit 2. Luento 14 Ke Timo Männikkö
 Algoritmit 2 Luento 14 Ke 3.5.2017 Timo Männikkö Luento 14 Ositus ja rekursio Rekursion toteutus Kertaus ja tenttivinkit Algoritmit 2 Kevät 2017 Luento 14 Ke 3.5.2017 2/30 Ositus Tehtävän esiintymä ositetaan
Algoritmit 2 Luento 14 Ke 3.5.2017 Timo Männikkö Luento 14 Ositus ja rekursio Rekursion toteutus Kertaus ja tenttivinkit Algoritmit 2 Kevät 2017 Luento 14 Ke 3.5.2017 2/30 Ositus Tehtävän esiintymä ositetaan
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9
 Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Diskreetin matematiikan perusteet Laskuharjoitus 2 / vko 9 Tuntitehtävät 9-10 lasketaan alkuviikon harjoituksissa ja tuntitehtävät 13-14 loppuviikon harjoituksissa. Kotitehtävät 11-12 tarkastetaan loppuviikon
Rakenteellinen tasapaino ja transitiivisyys
 1 Hypermedian jatko-opintoseminaari 2008-2009 Rakenteellinen tasapaino ja transitiivisyys 20.2.2009 Seppo Pohjolainen 2 Rakenteellinen tasapaino Käsitteitä: Arvotettu graafi (signed graph) (+ tai - ) Suuntaamaton
1 Hypermedian jatko-opintoseminaari 2008-2009 Rakenteellinen tasapaino ja transitiivisyys 20.2.2009 Seppo Pohjolainen 2 Rakenteellinen tasapaino Käsitteitä: Arvotettu graafi (signed graph) (+ tai - ) Suuntaamaton
58131 Tietorakenteet ja algoritmit (kevät 2013) Kurssikoe 2, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2013) Kurssikoe 2, 652013, vastauksia 1 [6 pistettä] Vastaa jokaisesta alla olevasta väittämästä onko se tosi vai epätosi ja anna lyhyt perustelu Jokaisesta kohdasta
58131 Tietorakenteet ja algoritmit (kevät 2013) Kurssikoe 2, 652013, vastauksia 1 [6 pistettä] Vastaa jokaisesta alla olevasta väittämästä onko se tosi vai epätosi ja anna lyhyt perustelu Jokaisesta kohdasta
Tarkastelemme ensin konkreettista esimerkkiä ja johdamme sitten yleisen säännön, joilla voidaan tietyissä tapauksissa todeta kielen ei-säännöllisyys.
 Ei-säännöllisiä kieliä [Sipser luku 1.4] Osoitamme, että joitain kieliä ei voi tunnistaa äärellisellä automaatilla. Tulos ei sinänsä ole erityisen yllättävä, koska äärellinen automaatti on äärimmäisen
Ei-säännöllisiä kieliä [Sipser luku 1.4] Osoitamme, että joitain kieliä ei voi tunnistaa äärellisellä automaatilla. Tulos ei sinänsä ole erityisen yllättävä, koska äärellinen automaatti on äärimmäisen
Satunnaisalgoritmit. Topi Paavilainen. Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
 Satunnaisalgoritmit Topi Paavilainen Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 1 Johdanto Satunnaisalgoritmit ovat algoritmeja, joiden
Satunnaisalgoritmit Topi Paavilainen Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 1 Johdanto Satunnaisalgoritmit ovat algoritmeja, joiden
MS-A0401 Diskreetin matematiikan perusteet
 MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
MS-A0401 Diskreetin matematiikan perusteet Osa 6: Verkkoteoria Riikka Kangaslampi Syksy 2017 Matematiikan ja systeemianalyysin laitos Aalto-yliopisto Verkkojen peruskäsitteitä Motivaatiota (...) networks
MS-A0402 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I
 MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
MS-A040 Diskreetin matematiikan perusteet Esimerkkejä ym., osa I G. Gripenberg Aalto-yliopisto. maaliskuuta 05 G. Gripenberg (Aalto-yliopisto) MS-A040 Diskreetin matematiikan perusteet Esimerkkejä. ym.,
Harjoitus 3 (3.4.2014)
 Harjoitus 3 (3..) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i, j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Harjoitus 3 (3..) Tehtävä Olkoon kaaren paino c ij suurin sallittu korkeus tieosuudella (i, j). Etsitään reitti solmusta s solmuun t siten, että reitin suurin sallittu korkeus pienimmillään olisi mahdollisimman
Algoritmit 1. Luento 2 Ke Timo Männikkö
 Algoritmit 1 Luento 2 Ke 11.1.2017 Timo Männikkö Luento 2 Algoritmin esitys Algoritmien analysointi Suoritusaika Asymptoottinen kertaluokka Peruskertaluokkia NP-täydelliset ongelmat Algoritmit 1 Kevät
Algoritmit 1 Luento 2 Ke 11.1.2017 Timo Männikkö Luento 2 Algoritmin esitys Algoritmien analysointi Suoritusaika Asymptoottinen kertaluokka Peruskertaluokkia NP-täydelliset ongelmat Algoritmit 1 Kevät
Diskreetit rakenteet
 Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Oikeasta tosi-epätosi -väittämästä saa pisteen, ja hyvästä perustelusta toisen.
 Tietorakenteet, kevät 2012 Kurssikoe 2, mallivastaukset 2. (a) Järjestämistä ei voi missään tilanteessa suorittaa nopeammin kuin ajassa Θ(n log n), missä n on järjestettävän taulukon pituus. Epätosi: Yleisessä
Tietorakenteet, kevät 2012 Kurssikoe 2, mallivastaukset 2. (a) Järjestämistä ei voi missään tilanteessa suorittaa nopeammin kuin ajassa Θ(n log n), missä n on järjestettävän taulukon pituus. Epätosi: Yleisessä
Kimppu-suodatus-menetelmä
 Kimppu-suodatus-menetelmä 2. toukokuuta 2016 Kimppu-suodatus-menetelmä on kehitetty epäsileiden optimointitehtävien ratkaisemista varten. Menetelmässä approksimoidaan epäsileitä funktioita aligradienttikimpulla.
Kimppu-suodatus-menetelmä 2. toukokuuta 2016 Kimppu-suodatus-menetelmä on kehitetty epäsileiden optimointitehtävien ratkaisemista varten. Menetelmässä approksimoidaan epäsileitä funktioita aligradienttikimpulla.
Eulerin verkkojen karakterisointi
 Eulerin verkkojen karakterisointi Pro Gradu -tutkielma Jenni Heikkilä 373175 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 018 Sisältö Johdanto 1 Verkkojen peruskäsitteet 3 1.1 Verkon määrittely.........................
Eulerin verkkojen karakterisointi Pro Gradu -tutkielma Jenni Heikkilä 373175 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 018 Sisältö Johdanto 1 Verkkojen peruskäsitteet 3 1.1 Verkon määrittely.........................
3. Laskennan vaativuusteoriaa
 3. Laskennan vaativuusteoriaa tähän asti puhuttu siitä, mitä on mahdollista laskea äärellisessä ajassa siirrytään tarkastelemaan laskemista kohtuullisessa ajassa vaihtoehtoisesti voidaan laskenta-ajan
3. Laskennan vaativuusteoriaa tähän asti puhuttu siitä, mitä on mahdollista laskea äärellisessä ajassa siirrytään tarkastelemaan laskemista kohtuullisessa ajassa vaihtoehtoisesti voidaan laskenta-ajan
a b c d
 1. 11. 011!"$#&%(')'+*(#-,.*/103/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + +. 3. 4. 5. 6. + + + + + + + + + + P1. 5 140 8 47 = 5 140 ( 3 ) 47 = 5 140 3 47 = 5 140 141 = (5 ) 140 = 10 140, jossa on
1. 11. 011!"$#&%(')'+*(#-,.*/103/465$*784 /(9:*;9."$ *;5> *@9 a b c d 1. + +. 3. 4. 5. 6. + + + + + + + + + + P1. 5 140 8 47 = 5 140 ( 3 ) 47 = 5 140 3 47 = 5 140 141 = (5 ) 140 = 10 140, jossa on
Osakesalkun optimointi. Anni Halkola Turun yliopisto 2016
 Osakesalkun optimointi Anni Halkola Turun yliopisto 2016 Artikkeli Gleb Beliakov & Adil Bagirov (2006) Non-smooth optimization methods for computation of the Conditional Value-at-risk and portfolio optimization.
Osakesalkun optimointi Anni Halkola Turun yliopisto 2016 Artikkeli Gleb Beliakov & Adil Bagirov (2006) Non-smooth optimization methods for computation of the Conditional Value-at-risk and portfolio optimization.
Lineaaristen monitavoiteoptimointitehtävien
 Lineaaristen monitavoiteoptimointitehtävien ratkaiseminen Jerri Nummenpalo 17.09.2012 Ohjaaja: TkT Juuso Liesiö Valvoja: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla.
Lineaaristen monitavoiteoptimointitehtävien ratkaiseminen Jerri Nummenpalo 17.09.2012 Ohjaaja: TkT Juuso Liesiö Valvoja: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla.
Todistus (2.2) Todistus (2.2) jatkoa. (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio.
 Todistus (2.2) (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio. Selvästi bittijono f sisältää ainakin yhden1:sen. Voidaan olettaa, että f 1
Todistus (2.2) (2.2): Oletetaan, että0 n 1,1 n 1 / P i (F) aina kuni = 1,2,...,n. Olkoonf F painoltaan pienin joukonf alkio. Selvästi bittijono f sisältää ainakin yhden1:sen. Voidaan olettaa, että f 1
13 Lyhimmät painotetut polut
 TIE-20100 Tietorakenteet ja algoritmit 297 13 Lyhimmät painotetut polut BFS löytää lyhimmän polun lähtösolmusta graafin saavutettaviin solmuihin. Se ei kuitenkaan enää suoriudu tehtävästä, jos kaarien
TIE-20100 Tietorakenteet ja algoritmit 297 13 Lyhimmät painotetut polut BFS löytää lyhimmän polun lähtösolmusta graafin saavutettaviin solmuihin. Se ei kuitenkaan enää suoriudu tehtävästä, jos kaarien
Laskennan vaativuus ja NP-täydelliset ongelmat
 Laskennan vaativuus ja NP-täydelliset ongelmat TRAK-vierailuluento 13.4.2010 Petteri Kaski Tietojenkäsittelytieteen laitos Tietojenkäsittelytiede Tietojenkäsittelytiede tutkii 1. mitä tehtäviä voidaan
Laskennan vaativuus ja NP-täydelliset ongelmat TRAK-vierailuluento 13.4.2010 Petteri Kaski Tietojenkäsittelytieteen laitos Tietojenkäsittelytiede Tietojenkäsittelytiede tutkii 1. mitä tehtäviä voidaan
Luku 8. Aluekyselyt. 8.1 Summataulukko
 Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Algoritmit 2. Luento 6 Ke Timo Männikkö
 Algoritmit 2 Luento 6 Ke 29.3.2017 Timo Männikkö Luento 6 B-puun operaatiot B-puun muunnelmia Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2017 Luento 6 Ke 29.3.2017 2/31 B-puu
Algoritmit 2 Luento 6 Ke 29.3.2017 Timo Männikkö Luento 6 B-puun operaatiot B-puun muunnelmia Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2017 Luento 6 Ke 29.3.2017 2/31 B-puu
Kustannustehokkaat riskienhallintatoimenpiteet kuljetusverkostossa (Valmiin työn esittely)
 Kustannustehokkaat riskienhallintatoimenpiteet kuljetusverkostossa (Valmiin työn esittely) Joonas Lanne 23.2.2015 Ohjaaja: Eeva Vilkkumaa Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston
Kustannustehokkaat riskienhallintatoimenpiteet kuljetusverkostossa (Valmiin työn esittely) Joonas Lanne 23.2.2015 Ohjaaja: Eeva Vilkkumaa Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston
Tietotekniikan valintakoe
 Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Jyväskylän yliopisto Tietotekniikan laitos Tietotekniikan valintakoe 2..22 Vastaa kahteen seuraavista kolmesta tehtävästä. Kukin tehtävä arvostellaan kokonaislukuasteikolla - 25. Jos vastaat useampaan
Luento 6: Monitavoiteoptimointi
 Luento 6: Monitavoiteoptimointi Monitavoiteoptimointitehtävässä on useita optimoitavia kohdefunktioita eli ns kriteereitä: f 1,, f m Esimerkiksi opiskelija haluaa oppia mahdollisimman hyvin ja paljon mahdollisimman
Luento 6: Monitavoiteoptimointi Monitavoiteoptimointitehtävässä on useita optimoitavia kohdefunktioita eli ns kriteereitä: f 1,, f m Esimerkiksi opiskelija haluaa oppia mahdollisimman hyvin ja paljon mahdollisimman
= k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko
 238 7.2 Luokka NP Luokka NP on: NP = { NTIME(t) t on polynomi } = k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko P NP Luokan NP ongelmista
238 7.2 Luokka NP Luokka NP on: NP = { NTIME(t) t on polynomi } = k 0 NTIME(n k + k) Siis polynomisessa ajassa epädeterministisellä Turingin koneella tunnistettavien kielten joukko P NP Luokan NP ongelmista
Konsensusongelma hajautetuissa järjestelmissä. Niko Välimäki Hajautetut algoritmit -seminaari
 Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki 30.11.2007 Hajautetut algoritmit -seminaari Konsensusongelma Päätöksen muodostaminen hajautetussa järjestelmässä Prosessien välinen viestintä
Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki 30.11.2007 Hajautetut algoritmit -seminaari Konsensusongelma Päätöksen muodostaminen hajautetussa järjestelmässä Prosessien välinen viestintä
1. Osoita, että joukon X osajoukoille A ja B on voimassa toinen ns. de Morganin laki (A B) = A B.
 HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
HY / Avoin yliopisto Johdatus yliopistomatematiikkaan, kesä 2015 Harjoitus 3 Ratkaisuehdotuksia Tehtäväsarja I Seuraavissa tehtävissä harjoitellaan muun muassa kahden joukon osoittamista samaksi sekä joukon
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle.
 Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
Kombinatoriikka, kesä 2010 Harjoitus 1 Ratkaisuehdotuksia (RT (5 sivua Kaikki kurssin laskuharjoitukset pidetään Exactumin salissa C123. Malliratkaisut tulevat nettiin kurssisivulle. 1. Osoita, että vuoden
NP-täydellisyys. Joonas Järvenpää ja Topi Talvitie. Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos
 NP-täydellisyys Joonas Järvenpää ja Topi Talvitie Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 Sisältö 1 Johdanto 1 2 Ongelman määrittely
NP-täydellisyys Joonas Järvenpää ja Topi Talvitie Laskennan teorian opintopiiri HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Helsinki, 23. helmikuuta 2014 Sisältö 1 Johdanto 1 2 Ongelman määrittely
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Matematiikan tukikurssi Kurssikerta 2 Lisää osamurtoja Tutkitaan jälleen rationaalifunktion P(x)/Q(x) integrointia. Aiemmin käsittelimme tapauksen, jossa nimittäjä voidaan esittää muodossa Q(x) = a(x x
Epädeterministisen Turingin koneen N laskentaa syötteellä x on usein hyödyllistä ajatella laskentapuuna
 Epädeterministisen Turingin koneen N laskentaa syötteellä x on usein hyödyllistä ajatella laskentapuuna. q 0 x solmuina laskennan mahdolliset tilanteet juurena alkutilanne lehtinä tilanteet joista ei siirtymää,
Epädeterministisen Turingin koneen N laskentaa syötteellä x on usein hyödyllistä ajatella laskentapuuna. q 0 x solmuina laskennan mahdolliset tilanteet juurena alkutilanne lehtinä tilanteet joista ei siirtymää,
1 + b t (i, j). Olkoon b t (i, j) todennäköisyys, että B t (i, j) = 1. Siis operaation access(j) odotusarvoinen kustannus ajanhetkellä t olisi.
 Algoritmien DP ja MF vertaileminen tapahtuu suoraviivaisesti kirjoittamalla kummankin leskimääräinen kustannus eksplisiittisesti todennäköisyyksien avulla. Lause T MF ave = 1 + 2 1 i
Algoritmien DP ja MF vertaileminen tapahtuu suoraviivaisesti kirjoittamalla kummankin leskimääräinen kustannus eksplisiittisesti todennäköisyyksien avulla. Lause T MF ave = 1 + 2 1 i
Yleinen paikallinen vakautuva synkronointialgoritmi
 Yleinen paikallinen vakautuva synkronointialgoritmi Panu Luosto 23. marraskuuta 2007 3 4 putki 1 2 α α+1 α+2 α+3 0 K 1 kehä K 2 K 3 K 4 Lähdeartikkeli Boulinier, C., Petit, F. ja Villain, V., When graph
Yleinen paikallinen vakautuva synkronointialgoritmi Panu Luosto 23. marraskuuta 2007 3 4 putki 1 2 α α+1 α+2 α+3 0 K 1 kehä K 2 K 3 K 4 Lähdeartikkeli Boulinier, C., Petit, F. ja Villain, V., When graph
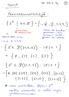 Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
Luento 9: Permutaatiot ja symmetriat 1 MS-A0401 Diskreetin matematiikan perusteet, syksy 2014 Harri Varpanen Aalto-yliopisto Matematiikan ja systeemianalyysin laitos Keskiviikko 8.10.2014 Ryhmän toiminta
