Rationaalinen agentti. Kognitiivinen mallintaminen I. Rationaalinen agentti. Rationaalinen agentti. Kognitiivinen mallintaminen I, kevät /1/08
|
|
|
- Sinikka Seppälä
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Rationaalinen agentti Kognitiivinen mallintaminen I Yksinkertainen refleksiagentti Toiminta perustuu ainoastaan agentin havaintoihin kullakin ajanhetkellä. Luento III Symbolinen mallintaminen Ongelmanratkaisu Produktiosysteemit Rationaalinen agentti Ympäristöä mallintava refleksiagentti agentilla on sisäinen representaatio ympäristön tilasta Rationaalinen agentti Päämärätietoinen agentti (goal-based agent) päämäärä ohjaa agentin käyttäytymistä eri tilanteissa Saara Huhmarniemi 1
2 Rationaalinen agentti Utiliteettiin perustuva agentti jokaiselle agentin tilalle annetaan numeerinen utiliteettiarvo Rationaalinen agentti Oppiminen agentti saa palautteen toiminnastaan Ongelmanratkaisu Rationaalinen agentti Ongelma-avaruus Hakustrategiat ongelma-avaruudessa sokea haku tietoinen haku heuristiikat Ongelmanratkaisu Ongelmanratkaisu yleisesti: miten saavuttaa jokin päämäärä, joka ei ole heti saatavilla? suunnittelu, aikataulutus, vianetsintä, pelit, muut pähkinät kuten ristisanat "Älykäs" toimija ratkaisee ongelmat joko nopeasti tai jonkun "näkemyksen" avulla. Saara Huhmarniemi 2
3 Hyvinmääritellyt ongelmat Hyvinmääritellyt ja tietoon perustuvat ongelmat: Shakki Lähetyssaarnaaja ja ihmissyöjä -ongelma Hanoin torni Aritmetiikan ongelmat Hyvinmääritelty tietoon perustuva ongelma Hyvinmääritelty ongelma: määrittelee yksiselitteisesti ja kokonaan ongelmanratkaisijalle annetun informaation ongelmanratkaisijan vaihtoehdot halutun lopputilan Tietoon perustuva ongelma: ratkaisuun tarvitaan vain rajattu määrä tietoa ratkaisuun ei tarvita ulkopuolista tietoa. Tila-avaruus ja ongelmaavaruus Ongelmat kuvataan tilasiirtyminä ongelmaavaruudessa. Ongelma-avaruuden tila on ote ongelmanratkaisutilanteesta tietyllä ajanhetkellä. kuvaus objekteista ja relaatioista objektien välillä Esimerkiksi shakkipelin alkutila kuvaa nappuloiden värin ja sijainnin laudalla sekä sen että on valkoisen vuoro siirtää. Ongelman tila-avaruus Ongelmanratkaisu on alkutilan muuttaminen halutuksi lopputilaksi käymällä läpi sarja tilasiirtymiä. Usein mahdolliset tilasiirtymät voidaan jakaa luokkiin. sotilaan siirtäminen yhden eteenpäin lähetin siirtäminen diagonaalisesti Siirtymiä kutsutaan seuraajafunktioiksi. Saara Huhmarniemi 3
4 Hyvinmääritelty tietoon perustuva ongelma Täydellisesti määritelty alkutila Seuraajafunktiot Täydellinen määritelmä halutusta lopputilasta tai ne ehdot, jotka halutulla lopputilalla tulee olla. reitti Aradista Bukarestiin reitti Aradista Bukarestiin Alkutila: Arad, Romania Lopputila: Bukarest, Romania Seuraajafunktio: autoilu kaupungista toiseen. Pölynimuriagentti Yksinkertainen refleksiagentti (ympäristöä mallintava agentti) Havainnot: sijainti ja sisältö e.g., [A,Dirty] Toiminnot: Left, Right, Suck, NoOp Saara Huhmarniemi 4
5 Ongelman tila-avaruus Ongelman tila-avaruus muodostuu ongelman tiloista ja siirtymistä jotka muuttavat tilaa. siirtymät esittävät agentin toimintaa tai ympäristön muutosta Tila-avaruus voidaan esittää suunnattuna verkkona tai puuna, jonka solmut vastaavat tiloja ja nuolet siirtymiä tilojen välillä. Ongelma-avaruus Ongelma-avaruus on tila-avaruus laajennettuna alkutilalla ja halutulla lopputilalla. Lopputila annetaan usein ehtoina Onnistunut ongelmanratkaisu on niiden peräkkäisten siirtyminen valitseminen, jotka muuttavat alkutilan halutuksi lopputilaksi. Siirtymille tilasta toiseen voidaan määritellä hinta, jonka avulla ongelmanratkaisua ohjataan. Ongelma-avaruus Ongelma-avaruus Tilat, (alkutila), ehdot lopputilalle, toiminnot (seuraajafunktio), polun hinta? Tila: 0,1 likaisuudelle ja L, R robotin sijainnille (esim. (0,L). Toiminnot: L, R, S Loppuehto: (0,L) & (0,R) Hinta: 1 / toiminto Saara Huhmarniemi 5
6 Etsintä ongelma-avaruudessa Reitti Aradista Bukarestiin Usein ongelma-avaruuden tilassa on useita mahdollisia siirtymiä. Miten löydetään siirtymät, jotka ovat mahdollisia kulloisessakin tilassa? Millä perusteella oikea siirtymä valitaan? Ongelmanratkaisu voidaan nähdä etsintänä (search) ongelma-avaruudessa. Ratkaistakseen ongelman, systeemin on etsittävä oikea polku alkutilasta haluttuun tilaan. Saara Huhmarniemi 6
7 Etsintä ongelma-avaruudessa Hakustrategian arviointi: completeness: does it always find a solution if one exists? time complexity: number of nodes generated space complexity: maximum number of nodes in memory optimality: does it always find a least-cost solution? Time and space complexity are measured in terms of b: maximum branching factor of the search tree d: depth of the least-cost solution m: maximum depth of the state space (may be ) Hakustrategia On olemassa useita algoritmeja lyhimmän polun löytämiseen. Sokeat hakustrategiat (uninformed search, blind search) Tietoinen haku (informed search, heuristic search) Sokeita hakustrategioita syvyyshaku (depth-first) halvin ensin haku (uniform cost) leveyshaku (breadth-first search) rajoitettu syvyyshaku (depth-limited) asteittain syvenevä haku (iterative deepening) kaksisuuntainen haku (bidirectional) leveyshaku leveyshaku puun alkusolmu (juuri) laajennetaan ensin kaikki laajennetut solmut käydään läpi ja laajennetaan ennenkuin edetään syvemmälle puussa. algoritmin suoritus vaatii kaikkien solmujen pitämisen muistissa Saara Huhmarniemi 7
8 Arviointi Löytääkö ratkaisun? Kyllä (jos b on äärellinen) Aika? 1+b+b 2 +b 3 + +b d + b(b d -1) = O(b d+1 ) Tila? O(b d+1 ) (jokainen solmu on muistissa) Optimaalinen? Kyllä (polun hinta=1) Tilankäyttö on ongelma. syvyyshaku laajentaa aina puussa syvimmällä olevan solmun ensin käyttää vain vähän muistia (vain yhden polun kerrallaan syvyyshaku syvyyshaku Saara Huhmarniemi 8
9 Arviointi Löytääkö ratkaisun? Ei, epäonnistuu jos tilaavaruus ei ole äärellinen tai jos polussa on silmukka. Korjataan poissulkemalla toistuvat tilat toimii kun tila-avaruus on äärellinen Aika? O(b m ): paha jos m is on paljon suurempi d (m= maksimisyvyys, d=ratkaisun syvyys) Tila? O(bm), eli lineaarinen tilavaatimus! Optimaalinen? Ei hakustrategioita rajoitettu syvyyshaku asetetaan raja, johon syvyyshaku pysäytetään kullakin polulla ongelma on optimaalisen syvyyden valinta halvin ensin -haku valitaan seuraavaksi laajennettava solmu sen perusteella, mikä on polun "hinta" hinta kasvaa kun polulla edetään, ja jokin toinen polku voi tulla kannattavammaksi asteittain syvenevä haku Asteittain syvenevä haku yhdistää leveys- ja syvyyshaut algoritmi tekee syvyyshakua, mutta etsinnän syvyys on rajoitettu kun koko puu on etsitty rajoitettuun syvyyteen asti, aloitetaan etsintä alusta lisäten etsinnän syvyyttä puu generoidaan uudestaan jokaista syvyyttä varten algoritmi on kuitenkin tehokas Saara Huhmarniemi 9
10 Asteittain syvenevä haku Asteittain syvenevä haku Asteittain syvenevä haku asteittain syvenevä haku Löytääkö ratkaisun? Kyllä Aika? (d+1)b 0 + d b 1 + (d-1)b b d = O(b d ) Tila? O(bd) Optimaalinen? Kyllä. Saara Huhmarniemi 10
11 kaksisuuntainen haku kaksi hakua; toinen eteenpäin alkutilasta ja toinen taaksepäin halutusta lopputilasta haut kohtaavat toisensa lyhimmällä polulla vaatii sen, että mahdolliset lopputilat on eksplisiittisesti listattu siirtyminen ongelma-avaruudessa taaksepäin ei aina ole helppoa Tietoinen haku Tietoisessa haussa käytettävissä on lisätietoa ongelmasta. paras ensin -haku (best first -search) laajennettava solmu valitaan heuristisen funktion avulla. h(n) = halvimman polun arvioitu hinta solmusta n haluttuun lopputilaan. Esimerkkitapauksessa heuristinen funktio h(n) voisi olla esimerkiksi matka linnuntietä kaupungista n Bukarestiin. reitti Aradista Bukarestiin Ahne paras-ensin haku Saara Huhmarniemi 11
12 paras ensin -haku Löytääkö ratkaisun? Ei, voi jäädä silmukkaan, esim. Iasi Neamt Iasi Neamt Aika? O(b m ), mutta parempi heuristiikka parantaa tuloksia dramaattisesti Tila? O(b m ) -- kaikki solmut muistissa Optimaalinen? Ei valittu heuristinen funktio voi yhä antaa huonon alun haulle haku voi eksyä harhapolulle, eikä enää palaa takaisin A*-haku minimoi polun kokonaiskustannuksen: siinä otetaan huomioon g(n) = jo kuljetun polun hinta solmussa n h(n) = arvioitu hinta solmusta n lopputilaan f(n) = arvioitu polun kokonaishinta n:n kautta lopputilaan A*-haku Saara Huhmarniemi 12
13 Etsintä ongelma-avaruudessa Ihmiset eivät yleensä käytä sokeaa hakua vaan käyttävät jotain heuristiikkaa. Esim. Taaksepäinketjutus (backward chaining): edetään lopputilasta kohti alkuehtoja. Välitavoite-analyysi (Means-Ends analysis): valitaan välitavoite johon pyritään lopputilan sijaan. hill-climbing hill-climbing Kukkulalle kapuaminen (hill-climbing): Valitaan aina tila, josta on lyhin matka lopputilaan. Alkutilasta riippuen voidaan juuttua lokaaliin maksimiin hill-climbing ongelmanratkaisija Ongelmanratkaisu voidaan siis nähdä matkana ongelma-avaruudessa seuraavien tilojen löytäminen, evaluointi ja oikean tilan valinta tavoitteiden ja välitavoitteiden asettaminen ja hallinta heuristiikkojen käyttö ongelman representaatio Saara Huhmarniemi 13
14 Produktiosysteemit Tarkastellaan erästä keskeistä kognitiivista mallia: produktiosysteemiä. Produktiosysteemejä on käytetty useissa kognitiivisissa arkkitehtuureissa, kuten ACT (Anderson 1983) ja SOAR (Laird et. al. 1987) Produktiosysteemit Produktiosysteemi on sovelluskohteesta riippumaton päätöksenteon ja järkeilyn malli. Kaksi muistivarastoa työmuisti produktiomuisti Prosessointi tapahtuu kahdessa vaiheessa: Tunnistus, jossa systeemi valitsee säännön. Toiminta, jossa systeemi käyttää sääntöä. Sääntö muuttaa työmuistin sisältöä ja/tai aiheuttaa jonkin ulkoisen toiminnon. Produktiosysteemit Työmuisti on tietokanta, joka on joukko toisistaan riippumattomia propositioita p 1, p 2, p 3,... Produktiosäännöt Sääntömuisti sisältää päättelysääntöjä, jotka ovat muotoa: p 1 " p 2... # act 1 " act 2... esim. shorter(anna, beth) Sääntömuisti sisältää päättelysääntöjä, jotka ovat muotoa: p 1 " p 2...# act 1 " act 2... IF : THEN: shorter(x,y) delete shorter(x,y) add taller(y,x) Saara Huhmarniemi 14
15 Produktiosäännöt Jos työmuistin sisältö on esimerkiksi shorter(anna, beth) voidaan soveltaa produktiosääntöä: IF: THEN: shorter(anna,beth) delete shorter(anna,beth) add taller(beth,anna) Nyt työmuistin uusi sisältö on taller(anna, beth) Produktiosysteemit Mahdollisia toimintoja ovat esimerkiksi elementtien lisääminen ja poistaminen työmuistista. Jokaisella suoritussyklissä systeemi etsii ne säännöt, joiden vasen puoli toteutuu työmuistin sisällön perusteella. (match phase) Tämän jälkeen systeemi päättää, mikä produktioista "laukeaa". (conflict resolution) Jokaisessa syklissä suoritetaan valittujen sääntöjen määrittelemä toiminta. Produktiosysteemit Produktiosysteemiin voidaan lisätä tavoitteita kuvaavia meta-produktioita, jotka ohjaavat ongelmanratkaisua. Konfliktinratkaisussa (conflict resolution) valitaan sopivista produktioista se joka laukeaa. Tähän voidaan käyttää erilaisia strategioita. Produktioille voidaan määritellä esim. että ne laukeavat vain kerran ongelmanratkaisun aikana. Oletetaan seuraava sääntömuisti, jossa kaikki produktiot ovat vain kerran laukeavia: 1. IF: nisäkäs(x) THEN: lisää jalat(x,4) 2. IF: nisäkäs(x) & ihminen(x) THEN: lisää jalat(x,2) 3. IF: jalat(x,2) THEN: lisää seisoo(x) 4. IF: jalat(x) THEN: lisää kävelee(x) 5. IF: kotieläin(x) & ihminen(y) THEN: lisää hoitaa(y,x) Oletetaan työmuisti: { kotieläin(lehmä), ihminen(pekka), nisäkäs(pekka)} Saara Huhmarniemi 15
16 1. syklissä etsitään sopivat säännöt: 1. IF: nisäkäs(x) THEN: lisää jalat(x,4) 2. IF: nisäkäs(x) & ihminen(x) THEN: lisää jalat(x,2), poista nisäkäs(x) 5. IF: kotieläin(x) & ihminen(y) THEN: lisää hoitaa(y,x) Työmuisti: { kotieläin(lehmä), ihminen(pekka), nisäkäs(pekka)} Säännöt 1 ja 2 muodostavat konfliktin, joka ratkaistaan tässä valitsemalla tarkempi sääntö. Suoritettavat toiminnot: lisää jalat(pekka,2), poista nisäkäs(x), lisää hoitaa(pekka, lehmä) Uusi työmuisti: {kotieläin(lehmä), ihminen(pekka), jalat(pekka,2), hoitaa(pekka,lehmä)} Sääntömuisti, josta käytetyt säännöt on poistettu: 1. IF: nisäkäs(x) THEN: lisää jalat(x,4) 3. IF: jalat(x,2) THEN: lisää seisoo(x) 4. IF: seisoo(x) THEN: lisää kävelee(x) 2. syklissä valitaan sääntö 3 jolloin toiminto on: lisää seisoo(pekka) Uusi työmuisti: {kotieläin(lehmä), ihminen(pekka), jalat(pekka,2), hoitaa(pekka,lehmä), seisoo(pekka)} Produktiosysteemin toiminta jatkuu sykleittäin, kunnes sopivia produktioita ei enää löydy tai päästään haluttuun lopputilaan. Oppiminen Systeemi "oppii" muodostamalla päättelyketjuista produktioita. Edellisessä esimerkissä esimerkiksi päättely: IF: nisäkäs(x) & ihminen(x) THEN: jalat(x,2) IF: jalat(x,2) THEN: seisoo(x) IF: seisoo(x) THEN: kävelee(x) voi päättelyketjun suorituksen jälkeen automatisoitua produktioksi: IF: nisäkäs(x) & ihminen(x) THEN: kävelee(x) Saara Huhmarniemi 16
17 Produktiosysteemi Produktiosysteemit Havainnot Tietopohjainen mietintä Refleksit Toiminta Nykyaikaiset modernit produktiosyteemit voivat käsitellä reaaliaikaisesti jopa yli miljoonaa sääntöä. Sääntöjen valinta voidaan toteuttaa rinnakkaisesti, joten se on tehokasta. Sen sijaan sääntöjen sovellus on sarjallista. Produktiosysteemit Mitkä produktiosysteemin ominaisuudet mallintavat ihmisen kognitiota? Psykologinen uskottavuus? Psykologinen uskottavuus? työmuisti, pitkäkestoinen muisti? ajattelu nähdään hahmontunnistuksena Tietty kuvio laukaisee pitkäkestoisesta muistista tietyn toiminnon. Vastaavasti, kun tiettyä vihjettä ei ole läsnä, haluttua ajatusta ei saada mieleen tai toimintoa ei pystytä suorittamaan. modulaarinen Saara Huhmarniemi 17
18 ketjutus ja taaksepäinketjutus Produktiosysteemi on käyttää loogista päättelyä ketjuttamalla (forward chaining): siinä lähdetään atomilauseista soveltaen Modus Ponens -sääntöä ja lisäten faktoja työmuistiin, kunnes kaikki mahdolliset johtopäätökset on tehty. Toinen tapa käyttää loogista päättelyä algoritmissa on taaksepäinketjutus (backward chaining). Tällaiset algoritmit lähtevät lopputilasta taaksepäin, kunnes löytävät faktoja jotka tukevat todistusta. Saara Huhmarniemi 18
Kognitiivinen mallintaminen 1
 Kognitiivinen mallintaminen 1 Uutta infoa: Kurssin kotisivut wikissä: http://wiki.helsinki.fi/display/kognitiotiede/cog241 Suorittaminen tentillä ja laskareilla (ei välikoetta 1. periodissa) Ongelmanratkaisu
Kognitiivinen mallintaminen 1 Uutta infoa: Kurssin kotisivut wikissä: http://wiki.helsinki.fi/display/kognitiotiede/cog241 Suorittaminen tentillä ja laskareilla (ei välikoetta 1. periodissa) Ongelmanratkaisu
Kognitiivinen mallintaminen I
 Kognitiivinen mallintaminen I Symbolinen mallintaminen: 2. luento Ongelmanratkaisu Ongelmanratkaisu Rationaalinen agentti Ongelma-avaruus Hakustrategiat ongelma-avaruudessa sokea haku tietoinen haku heuristiikat
Kognitiivinen mallintaminen I Symbolinen mallintaminen: 2. luento Ongelmanratkaisu Ongelmanratkaisu Rationaalinen agentti Ongelma-avaruus Hakustrategiat ongelma-avaruudessa sokea haku tietoinen haku heuristiikat
Kognitiivinen mallintaminen 1. Kognitiiviset arkkitehtuurit ACT-R
 Kognitiivinen mallintaminen 1 Kognitiiviset arkkitehtuurit ACT-R Kognitiiviset arkkitehtuurit Mielen(tai jonkin älykkään toimijan) mahdollisimman yleisiä piirteitä ja rakenteellista organisaatiota kuvaava
Kognitiivinen mallintaminen 1 Kognitiiviset arkkitehtuurit ACT-R Kognitiiviset arkkitehtuurit Mielen(tai jonkin älykkään toimijan) mahdollisimman yleisiä piirteitä ja rakenteellista organisaatiota kuvaava
Symbolinen mallintaminen: tausta. Kognitiivinen mallintaminen I. Symbolisysteemin hypoteesi. Symbolisysteemin hypoteesi
 Symbolinen mallintaminen: tausta Kognitiivinen mallintaminen I Symbolinen mallintaminen 1 Tausta Symbolisysteemin hypoteesi von Neumannin arkkitehtuuri LOT Esimerkki kognitiivisesta mallista: produktiosysteemit
Symbolinen mallintaminen: tausta Kognitiivinen mallintaminen I Symbolinen mallintaminen 1 Tausta Symbolisysteemin hypoteesi von Neumannin arkkitehtuuri LOT Esimerkki kognitiivisesta mallista: produktiosysteemit
4 Heuristinen haku. Eero Hyvönen Helsingin yliopisto
 4 Heuristinen haku Eero Hyvönen Helsingin yliopisto Strategioita: - Breath-first - Uniform-cost - Depth-first - Depth-limited - Iterative deepening - Bidirectional Tekoäly, Eero Hyvönen, 2004 2 Heuristisen
4 Heuristinen haku Eero Hyvönen Helsingin yliopisto Strategioita: - Breath-first - Uniform-cost - Depth-first - Depth-limited - Iterative deepening - Bidirectional Tekoäly, Eero Hyvönen, 2004 2 Heuristisen
3. Ongelmanratkonta haun avulla. Eero Hyvönen Helsingin yliopisto
 3. Ongelmanratkonta haun avulla Eero Hyvönen Helsingin yliopisto Haku Tavoiteperustaisilla agenteilla Tavoitteen (goal( goal) ) saavuttaminen Ongelman muotoilu (sopivalla yleisyystasolla) Esim. maailma
3. Ongelmanratkonta haun avulla Eero Hyvönen Helsingin yliopisto Haku Tavoiteperustaisilla agenteilla Tavoitteen (goal( goal) ) saavuttaminen Ongelman muotoilu (sopivalla yleisyystasolla) Esim. maailma
1 Ratkaisuja 2. laskuharjoituksiin
 1 1 Ratkaisuja 2. laskuharjoituksiin Tehtävä 1. (a) Yksinkertainen reeksiagentti ei voi toimia rationaalisesti tässä tilanteessa, eli maksimoida suoriutumismittaansa (performance measure). Yksinkertainen
1 1 Ratkaisuja 2. laskuharjoituksiin Tehtävä 1. (a) Yksinkertainen reeksiagentti ei voi toimia rationaalisesti tässä tilanteessa, eli maksimoida suoriutumismittaansa (performance measure). Yksinkertainen
.. X JOHDATUS TEKOÄLYYN TEEMU ROOS
 1 3 1 3 4 3 2 3 4 3 2 3 1 2 3 4 122 31 4 3 1 4 3 1 122 31........ X.... X X 2 3 1 4 1 4 3 2 3 2 4 1 4 JOHDATUS TEKOÄLYYN TEEMU ROOS 2. ETSINTÄ JA PELIT LEVEYSSUUNTAINEN HAKU 1 9 3 2 5 4 6 7 11 16 8 12
1 3 1 3 4 3 2 3 4 3 2 3 1 2 3 4 122 31 4 3 1 4 3 1 122 31........ X.... X X 2 3 1 4 1 4 3 2 3 2 4 1 4 JOHDATUS TEKOÄLYYN TEEMU ROOS 2. ETSINTÄ JA PELIT LEVEYSSUUNTAINEN HAKU 1 9 3 2 5 4 6 7 11 16 8 12
Ongelma 1: Ovatko kaikki tehtävät/ongelmat deterministisiä?
 Ongelma 1: Ovatko kaikki tehtävät/ongelmat deterministisiä? 2012-2013 Lasse Lensu 2 Ongelma 2: Milloin ongelmat muuttuvat oikeasti hankaliksi? 2012-2013 Lasse Lensu 3 Ongelma 3: Miten hankalia ongelmia
Ongelma 1: Ovatko kaikki tehtävät/ongelmat deterministisiä? 2012-2013 Lasse Lensu 2 Ongelma 2: Milloin ongelmat muuttuvat oikeasti hankaliksi? 2012-2013 Lasse Lensu 3 Ongelma 3: Miten hankalia ongelmia
Ongelma 1: Ovatko kaikki tehtävät/ongelmat deterministisiä?
 Ongelma 1: Ovatko kaikki tehtävät/ongelmat deterministisiä? 2013-2014 Lasse Lensu 2 Ongelma 2: Milloin ongelmat muuttuvat oikeasti hankaliksi? 2013-2014 Lasse Lensu 3 Ongelma 3: Miten hankalia ongelmia
Ongelma 1: Ovatko kaikki tehtävät/ongelmat deterministisiä? 2013-2014 Lasse Lensu 2 Ongelma 2: Milloin ongelmat muuttuvat oikeasti hankaliksi? 2013-2014 Lasse Lensu 3 Ongelma 3: Miten hankalia ongelmia
T : Max-flow / min-cut -ongelmat
 T-61.152: -ongelmat 4.3.2008 Sisältö 1 Määritelmät Esimerkki 2 Max-flow Graafin leikkaus Min-cut Max-flow:n ja min-cut:n yhteys 3 Perusajatus Pseudokoodi Tarkastelu 4 T-61.152: -ongelmat Virtausverkko
T-61.152: -ongelmat 4.3.2008 Sisältö 1 Määritelmät Esimerkki 2 Max-flow Graafin leikkaus Min-cut Max-flow:n ja min-cut:n yhteys 3 Perusajatus Pseudokoodi Tarkastelu 4 T-61.152: -ongelmat Virtausverkko
Algoritmit 1. Luento 9 Ti Timo Männikkö
 Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
5. Rajoitelaskenta (Constraint Satisfaction)
 5. Rajoitelaskenta (Constraint Satisfaction) Eero Hyvönen Helsingin yliopisto Solution = An assignment of values for the variables satifying the contraints Some CSPs: optimal solution is the best solution
5. Rajoitelaskenta (Constraint Satisfaction) Eero Hyvönen Helsingin yliopisto Solution = An assignment of values for the variables satifying the contraints Some CSPs: optimal solution is the best solution
811312A Tietorakenteet ja algoritmit Kertausta jälkiosasta
 811312A Tietorakenteet ja algoritmit 2018-2019 Kertausta jälkiosasta V Hashtaulukot ja binääriset etsintäpuut Hashtaulukot Perusajatus tunnettava Tiedettävä mikä on tiivistefunktio Törmäysongelman hallinta:
811312A Tietorakenteet ja algoritmit 2018-2019 Kertausta jälkiosasta V Hashtaulukot ja binääriset etsintäpuut Hashtaulukot Perusajatus tunnettava Tiedettävä mikä on tiivistefunktio Törmäysongelman hallinta:
13 Lyhimmät painotetut polut
 TIE-20100 Tietorakenteet ja algoritmit 297 13 Lyhimmät painotetut polut BFS löytää lyhimmän polun lähtösolmusta graafin saavutettaviin solmuihin. Se ei kuitenkaan enää suoriudu tehtävästä, jos kaarien
TIE-20100 Tietorakenteet ja algoritmit 297 13 Lyhimmät painotetut polut BFS löytää lyhimmän polun lähtösolmusta graafin saavutettaviin solmuihin. Se ei kuitenkaan enää suoriudu tehtävästä, jos kaarien
Algoritmit 2. Luento 11 Ti Timo Männikkö
 Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Algoritmit 2 Luento 11 Ti 24.4.2018 Timo Männikkö Luento 11 Rajoitehaku Kapsäkkiongelma Kauppamatkustajan ongelma Paikallinen etsintä Lyhin virittävä puu Vaihtoalgoritmit Algoritmit 2 Kevät 2018 Luento
Valitaan alkio x 1 A B ja merkitään A 1 = A { x 1 }. Perinnöllisyyden nojalla A 1 I.
 Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
Vaihto-ominaisuudella on seuraava intuition kannalta keskeinen seuraus: Olkoot A I ja B I samankokoisia riippumattomia joukkoja: A = B = m jollain m > 0. Olkoon vielä n = m A B, jolloin A B = B A = n.
A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä.
 Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Kieli merkitys ja logiikka. 2: Helpot ja monimutkaiset. Luento 2. Monimutkaiset ongelmat. Monimutkaiset ongelmat
 Luento 2. Kieli merkitys ja logiikka 2: Helpot ja monimutkaiset Helpot ja monimutkaiset ongelmat Tehtävä: etsi säkillinen rahaa talosta, jossa on monta huonetta. Ratkaisu: täydellinen haku käy huoneet
Luento 2. Kieli merkitys ja logiikka 2: Helpot ja monimutkaiset Helpot ja monimutkaiset ongelmat Tehtävä: etsi säkillinen rahaa talosta, jossa on monta huonetta. Ratkaisu: täydellinen haku käy huoneet
Datatähti 2019 loppu
 Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
Datatähti 2019 loppu task type time limit memory limit A Summa standard 1.00 s 512 MB B Bittijono standard 1.00 s 512 MB C Auringonlasku standard 1.00 s 512 MB D Binääripuu standard 1.00 s 512 MB E Funktio
v 8 v 9 v 5 C v 3 v 4
 Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Verkot Verkko on (äärellinen) matemaattinen malli, joka koostuu pisteistä ja pisteitä toisiinsa yhdistävistä viivoista. Jokainen viiva yhdistää kaksi pistettä, jotka ovat viivan päätepisteitä. Esimerkiksi
Kombinatorinen optimointi
 Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
Kombinatorinen optimointi Sallittujen pisteiden lukumäärä on äärellinen Periaatteessa ratkaisu löydetään käymällä läpi kaikki pisteet Käytännössä lukumäärä on niin suuri, että tämä on mahdotonta Usein
verkkojen G ja H välinen isomorfismi. Nyt kuvaus f on bijektio, joka säilyttää kyseisissä verkoissa esiintyvät särmät, joten pari
 Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
Tehtävä 9 : 1 Merkitään kirjaimella G tehtäväpaperin kuvan vasemmanpuoleista verkkoa sekä kirjaimella H tehtäväpaperin kuvan oikeanpuoleista verkkoa. Kuvan perusteella voidaan havaita, että verkko G on
811312A Tietorakenteet ja algoritmit Kertausta jälkiosasta
 811312A Tietorakenteet ja algoritmit 2016-2017 Kertausta jälkiosasta IV Perustietorakenteet Pino, jono ja listat tunnettava Osattava soveltaa rakenteita algoritmeissa Osattava päätellä operaatioiden aikakompleksisuus
811312A Tietorakenteet ja algoritmit 2016-2017 Kertausta jälkiosasta IV Perustietorakenteet Pino, jono ja listat tunnettava Osattava soveltaa rakenteita algoritmeissa Osattava päätellä operaatioiden aikakompleksisuus
Harjoitus 6 ( )
 Harjoitus 6 (21.4.2015) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s. t. g(x) 0 h(x) = 0 x X olevan optimointitehtävän Lagrangen duaali on missä max θ(u, v) s. t.
Harjoitus 6 (21.4.2015) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s. t. g(x) 0 h(x) = 0 x X olevan optimointitehtävän Lagrangen duaali on missä max θ(u, v) s. t.
Algoritmi on periaatteellisella tasolla seuraava:
 Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
Algoritmi on periaatteellisella tasolla seuraava: Dijkstra(V, E, l, v 0 ): S := { v 0 } D[v 0 ] := 0 for v V S do D[v] := l(v 0, v) end for while S V do valitse v V S jolle D[v] on minimaalinen S := S
JOHDATUS TEKOÄLYYN TEEMU ROOS
 JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 5 OP PERIODI 3: 18.1.2016-6.3.2016 (7 VIIKKOA+KOE) LUENNOT (CK112): MA 14-16, TI 14-16 LASKUHARJOITUKSET: RYHMÄ
JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 5 OP PERIODI 3: 18.1.2016-6.3.2016 (7 VIIKKOA+KOE) LUENNOT (CK112): MA 14-16, TI 14-16 LASKUHARJOITUKSET: RYHMÄ
Algoritmit 1. Luento 8 Ke Timo Männikkö
 Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
Algoritmit 1 Luento 8 Ke 1.2.2017 Timo Männikkö Luento 8 Järjestetty binääripuu Solmujen läpikäynti Binääripuun korkeus Binääripuun tasapainottaminen Graafit ja verkot Verkon lyhimmät polut Fordin ja Fulkersonin
58131 Tietorakenteet (kevät 2009) Harjoitus 11, ratkaisuja (Topi Musto)
 811 Tietorakenteet (kevät 9) Harjoitus 11, ratkaisuja (Topi Musto) 1. Bellmanin-Fordin algoritmin alustusvaiheen jälkeen aloitussolmussa on arvo ja muissa solmuissa on arvo ääretön. Kunkin solmun arvo
811 Tietorakenteet (kevät 9) Harjoitus 11, ratkaisuja (Topi Musto) 1. Bellmanin-Fordin algoritmin alustusvaiheen jälkeen aloitussolmussa on arvo ja muissa solmuissa on arvo ääretön. Kunkin solmun arvo
JOHDATUS TEKOÄLYYN TEEMU ROOS
 JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 4 OP PERIODI 1: 6.9.2012-12.10.2012 (6 VIIKKOA) LUENNOT (B123, LINUS TORVALDS -AUDITORIO): TO 10-12, PE 12-14 LASKUHARJOITUKSET
JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 4 OP PERIODI 1: 6.9.2012-12.10.2012 (6 VIIKKOA) LUENNOT (B123, LINUS TORVALDS -AUDITORIO): TO 10-12, PE 12-14 LASKUHARJOITUKSET
Harjoitus 6 ( )
 Harjoitus 6 (30.4.2014) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s.t. g(x) 0 h(x) = 0 x X (1) olevan optimointitehtävän Lagrangen duaali on max θ(u,v) s.t. u 0,
Harjoitus 6 (30.4.2014) Tehtävä 1 Määritelmän (ks. luentomoniste s. 109) mukaan yleisen, muotoa min f(x) s.t. g(x) 0 h(x) = 0 x X (1) olevan optimointitehtävän Lagrangen duaali on max θ(u,v) s.t. u 0,
JOHDATUS TEKOÄLYYN TEEMU ROOS
 JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 5 OP PERIODI 3: 16.1.2017-3.3.2016 (7 VIIKKOA+KOE) LUENNOT (CK112): MA 14-16, TI 14-16 LASKUHARJOITUKSET: RYHMÄ
JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 5 OP PERIODI 3: 16.1.2017-3.3.2016 (7 VIIKKOA+KOE) LUENNOT (CK112): MA 14-16, TI 14-16 LASKUHARJOITUKSET: RYHMÄ
JOHDATUS TEKOÄLYYN TEEMU ROOS
 JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 5 OP PERIODI 1: 4.9.2014-17.10.2012 (7 VIIKKOA+KOE) LUENNOT (B123, LINUS TORVALDS -AUDITORIO): TO 10-12, PE 12-14
JOHDATUS TEKOÄLYYN TEEMU ROOS KURSSIN PERUSTIEDOT VALINNAINEN AINEOPINTOTASOINEN KURSSI, 5 OP PERIODI 1: 4.9.2014-17.10.2012 (7 VIIKKOA+KOE) LUENNOT (B123, LINUS TORVALDS -AUDITORIO): TO 10-12, PE 12-14
Luku 7. Verkkoalgoritmit. 7.1 Määritelmiä
 Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
811312A Tietorakenteet ja algoritmit V Verkkojen algoritmeja Osa1 : Leveys- ja syvyyshaku
 811312A Tietorakenteet ja algoritmit 2016-2017 V Verkkojen algoritmeja Osa1 : Leveys- ja syvyyshaku Sisältö 1. Johdanto 2. Leveyshaku 3. Syvyyshaku 4. Kruskalin algoritmi 5. Dijkstran algoritmi 811312A
811312A Tietorakenteet ja algoritmit 2016-2017 V Verkkojen algoritmeja Osa1 : Leveys- ja syvyyshaku Sisältö 1. Johdanto 2. Leveyshaku 3. Syvyyshaku 4. Kruskalin algoritmi 5. Dijkstran algoritmi 811312A
Olkoon seuraavaksi G 2 sellainen tasan n solmua sisältävä suunnattu verkko,
 Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
Tehtävä 1 : 1 a) Olkoon G heikosti yhtenäinen suunnattu verkko, jossa on yhteensä n solmua. Määritelmän nojalla verkko G S on yhtenäinen, jolloin verkoksi T voidaan valita jokin verkon G S virittävä alipuu.
811312A Tietorakenteet ja algoritmit 2015-2016. V Verkkojen algoritmeja Osa 2 : Kruskalin ja Dijkstran algoritmit
 811312A Tietorakenteet ja algoritmit 2015-2016 V Verkkojen algoritmeja Osa 2 : Kruskalin ja Dijkstran algoritmit Sisältö 1. Johdanto 2. Leveyshaku 3. Syvyyshaku 4. Kruskalin algoritmi 5. Dijkstran algoritmi
811312A Tietorakenteet ja algoritmit 2015-2016 V Verkkojen algoritmeja Osa 2 : Kruskalin ja Dijkstran algoritmit Sisältö 1. Johdanto 2. Leveyshaku 3. Syvyyshaku 4. Kruskalin algoritmi 5. Dijkstran algoritmi
Malliratkaisut Demot
 Malliratkaisut Demot 6 24.4.2017 Tehtävä 1 Määritelmän (ks. luentomonisteen s. 107) mukaan yleisen muotoa min f(x) s.t. g(x) 0 h(x) = 0 x X (1) olevan optimointitehtävän Lagrangen duaali on min θ(u,v)
Malliratkaisut Demot 6 24.4.2017 Tehtävä 1 Määritelmän (ks. luentomonisteen s. 107) mukaan yleisen muotoa min f(x) s.t. g(x) 0 h(x) = 0 x X (1) olevan optimointitehtävän Lagrangen duaali on min θ(u,v)
Algoritmit 1. Luento 1 Ti Timo Männikkö
 Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Algoritmit 1 Luento 1 Ti 10.1.2017 Timo Männikkö Luento 1 Algoritmi Algoritmin toteutus Ongelman ratkaiseminen Algoritmin tehokkuus Algoritmin suoritusaika Algoritmin analysointi Algoritmit 1 Kevät 2017
Algoritmit 2. Luento 14 Ke Timo Männikkö
 Algoritmit 2 Luento 14 Ke 3.5.2017 Timo Männikkö Luento 14 Ositus ja rekursio Rekursion toteutus Kertaus ja tenttivinkit Algoritmit 2 Kevät 2017 Luento 14 Ke 3.5.2017 2/30 Ositus Tehtävän esiintymä ositetaan
Algoritmit 2 Luento 14 Ke 3.5.2017 Timo Männikkö Luento 14 Ositus ja rekursio Rekursion toteutus Kertaus ja tenttivinkit Algoritmit 2 Kevät 2017 Luento 14 Ke 3.5.2017 2/30 Ositus Tehtävän esiintymä ositetaan
Algoritmit 2. Luento 12 Ke Timo Männikkö
 Algoritmit 2 Luento 12 Ke 26.4.2017 Timo Männikkö Luento 12 Rajoitehaku Kauppamatkustajan ongelma Lyhin virittävä puu Paikallinen etsintä Vaihtoalgoritmit Geneettiset algoritmit Simuloitu jäähdytys Algoritmit
Algoritmit 2 Luento 12 Ke 26.4.2017 Timo Männikkö Luento 12 Rajoitehaku Kauppamatkustajan ongelma Lyhin virittävä puu Paikallinen etsintä Vaihtoalgoritmit Geneettiset algoritmit Simuloitu jäähdytys Algoritmit
Algoritmit 1. Luento 13 Ti 23.2.2016. Timo Männikkö
 Algoritmit 1 Luento 13 Ti 23.2.2016 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
Algoritmit 1 Luento 13 Ti 23.2.2016 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
Algoritmit 2. Luento 4 To Timo Männikkö
 Algoritmit 2 Luento 4 To 21.3.2019 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2019 Luento 4
Algoritmit 2 Luento 4 To 21.3.2019 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2019 Luento 4
Haku osittaisen informaation vallitessa
 136 Haun merkittävä ongelma on mahdollisuus laajentaa uudelleen jo kertaalleen tutkittu tila Näin äärellinen tila-avaruus voi johtaa äärettömään hakupuuhun Ratkeava ongelma voi muuttua käytännössä ratkeamattomaksi
136 Haun merkittävä ongelma on mahdollisuus laajentaa uudelleen jo kertaalleen tutkittu tila Näin äärellinen tila-avaruus voi johtaa äärettömään hakupuuhun Ratkeava ongelma voi muuttua käytännössä ratkeamattomaksi
Tietorakenteet, laskuharjoitus 7, ratkaisuja
 Tietorakenteet, laskuharjoitus, ratkaisuja. Seuraava kuvasarja näyttää B + -puun muutokset lisäysten jälkeen. Avaimet ja 5 mahtuvat lehtisolmuihin, joten niiden lisäys ei muuta puun rakennetta. Avain 9
Tietorakenteet, laskuharjoitus, ratkaisuja. Seuraava kuvasarja näyttää B + -puun muutokset lisäysten jälkeen. Avaimet ja 5 mahtuvat lehtisolmuihin, joten niiden lisäys ei muuta puun rakennetta. Avain 9
Algoritmit 1. Luento 7 Ti Timo Männikkö
 Algoritmit 1 Luento 7 Ti 31.1.2017 Timo Männikkö Luento 7 Järjestetty binääripuu Binääripuiden termejä Binääripuiden operaatiot Solmun haku, lisäys, poisto Algoritmit 1 Kevät 2017 Luento 7 Ti 31.1.2017
Algoritmit 1 Luento 7 Ti 31.1.2017 Timo Männikkö Luento 7 Järjestetty binääripuu Binääripuiden termejä Binääripuiden operaatiot Solmun haku, lisäys, poisto Algoritmit 1 Kevät 2017 Luento 7 Ti 31.1.2017
Ohjelmistotekniikan laitos OHJ-2550 Tekoäly, kevät
 96 Prolog voi päätyä samaan ratkaisuun monen päättelypolun kautta Tällöin sama ratkaisu palautetaan useita kertoja minimum(x,y,x):- X=Y. Molempien sääntöjen kautta löytyyy sama
96 Prolog voi päätyä samaan ratkaisuun monen päättelypolun kautta Tällöin sama ratkaisu palautetaan useita kertoja minimum(x,y,x):- X=Y. Molempien sääntöjen kautta löytyyy sama
AVL-puut. eräs tapa tasapainottaa binäärihakupuu siten, että korkeus on O(log n) kun puussa on n avainta
 AVL-puut eräs tapa tasapainottaa binäärihakupuu siten, että korkeus on O(log n) kun puussa on n avainta pohjana jo esitetyt binäärihakupuiden operaatiot tasapainotus vie pahimmillaan lisäajan lisäys- ja
AVL-puut eräs tapa tasapainottaa binäärihakupuu siten, että korkeus on O(log n) kun puussa on n avainta pohjana jo esitetyt binäärihakupuiden operaatiot tasapainotus vie pahimmillaan lisäajan lisäys- ja
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen
 V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
V. V. Vazirani: Approximation Algorithms, luvut 3-4 Matti Kääriäinen Luento omatoimisen luennan tueksi algoritmiikan tutkimusseminaarissa 23.9.2002. 1 Sisältö Esitellään ongelmat Steiner-puu Kauppamatkustajan
Silmukkaoptimoinnista
 sta TIE448 Kääntäjätekniikka, syksy 2009 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. joulukuuta 2009 Sisällys Sisällys Seuraava deadline Vaihe F maanantai 14.12. klo 12 rekisteriallokaatio Arvostelukappale
sta TIE448 Kääntäjätekniikka, syksy 2009 Antti-Juhani Kaijanaho TIETOTEKNIIKAN LAITOS 8. joulukuuta 2009 Sisällys Sisällys Seuraava deadline Vaihe F maanantai 14.12. klo 12 rekisteriallokaatio Arvostelukappale
Algoritmit 2. Luento 13 Ti Timo Männikkö
 Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
Algoritmit 2 Luento 13 Ti 2.5.2017 Timo Männikkö Luento 13 Merkkijonon sovitus Horspoolin algoritmi Laskennallinen vaativuus Päätösongelmat Epädeterministinen algoritmi Vaativuusluokat NP-täydellisyys
UML -mallinnus TILAKAAVIO
 UML -mallinnus TILAKAAVIO SISÄLLYS 3. Tilakaavio 3.1 Tilakaavion alku- ja lopputilat 3.2 Tilan nimi, muuttujat ja toiminnot 3.3 Tilasiirtymä 3.4 Tilasiirtymän vai tilan toiminnot 3.5 Tilasiirtymän tapahtumat
UML -mallinnus TILAKAAVIO SISÄLLYS 3. Tilakaavio 3.1 Tilakaavion alku- ja lopputilat 3.2 Tilan nimi, muuttujat ja toiminnot 3.3 Tilasiirtymä 3.4 Tilasiirtymän vai tilan toiminnot 3.5 Tilasiirtymän tapahtumat
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
58131 Tietorakenteet ja algoritmit (kevät 2014) Uusinta- ja erilliskoe, 10..2014, vastauksia 1. [9 pistettä] (a) Todistetaan 2n 2 + n + 5 = O(n 2 ): Kun n 1 on 2n 2 + n + 5 2n 2 + n 2 +5n 2 = 8n 2. Eli
Algoritmit 1. Luento 13 Ma Timo Männikkö
 Algoritmit 1 Luento 13 Ma 26.2.2018 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
Algoritmit 1 Luento 13 Ma 26.2.2018 Timo Männikkö Luento 13 Suunnittelumenetelmät Taulukointi Kapsäkkiongelma Ahne menetelmä Verkon lyhimmät polut Dijkstran menetelmä Verkon lyhin virittävä puu Kruskalin
TKT20001 Tietorakenteet ja algoritmit Erilliskoe , malliratkaisut (Jyrki Kivinen)
 TKT0001 Tietorakenteet ja algoritmit Erilliskoe 5.1.01, malliratkaisut (Jyrki Kivinen) 1. [1 pistettä] (a) Esitä algoritmi, joka poistaa kahteen suuntaan linkitetystä järjestämättömästä tunnussolmullisesta
TKT0001 Tietorakenteet ja algoritmit Erilliskoe 5.1.01, malliratkaisut (Jyrki Kivinen) 1. [1 pistettä] (a) Esitä algoritmi, joka poistaa kahteen suuntaan linkitetystä järjestämättömästä tunnussolmullisesta
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT GRAAFITEHTÄVIÄ JA -ALGORITMEJA Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) GRAAFIN LÄPIKÄYMINEN Perusta useimmille
A274101 TIETORAKENTEET JA ALGORITMIT GRAAFITEHTÄVIÄ JA -ALGORITMEJA Lähteet: Timo Harju, Opintomoniste Keijo Ruohonen, Graafiteoria (math.tut.fi/~ruohonen/gt.pdf) GRAAFIN LÄPIKÄYMINEN Perusta useimmille
58131 Tietorakenteet ja algoritmit Uusinta- ja erilliskoe ratkaisuja (Jyrki Kivinen)
 58131 Tietorakenteet ja algoritmit Uusinta- ja erilliskoe 12.9.2018 ratkaisuja (Jyrki Kivinen) 1. [10 pistettä] Iso-O-merkintä. (a) Pitääkö paikkansa, että n 3 + 5 = O(n 3 )? Ratkaisu: Pitää paikkansa.
58131 Tietorakenteet ja algoritmit Uusinta- ja erilliskoe 12.9.2018 ratkaisuja (Jyrki Kivinen) 1. [10 pistettä] Iso-O-merkintä. (a) Pitääkö paikkansa, että n 3 + 5 = O(n 3 )? Ratkaisu: Pitää paikkansa.
Algoritmit 2. Luento 10 To Timo Männikkö
 Algoritmit 2 Luento 10 To 19.4.2018 Timo Männikkö Luento 10 Peruutusmenetelmä Osajoukon summa Verkon 3-väritys Pelipuut Pelipuun läpikäynti Algoritmit 2 Kevät 2018 Luento 10 To 19.4.2018 2/34 Algoritmien
Algoritmit 2 Luento 10 To 19.4.2018 Timo Männikkö Luento 10 Peruutusmenetelmä Osajoukon summa Verkon 3-väritys Pelipuut Pelipuun läpikäynti Algoritmit 2 Kevät 2018 Luento 10 To 19.4.2018 2/34 Algoritmien
T Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet )
 T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet 9.1 9.5) 30.11. 3.12.2004 1. Osoita lauselogiikan avulla oheisten ehtolausekkeiden ekvivalenssi. (a)!(a
T-79.144 Syksy 2004 Logiikka tietotekniikassa: perusteet Laskuharjoitus 12 (opetusmoniste, kappaleet 9.1 9.5) 30.11. 3.12.2004 1. Osoita lauselogiikan avulla oheisten ehtolausekkeiden ekvivalenssi. (a)!(a
Graafit ja verkot. Joukko solmuja ja joukko järjestämättömiä solmupareja. eli haaroja. Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria
 Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Graafit ja verkot Suuntamaton graafi: eli haaroja Joukko solmuja ja joukko järjestämättömiä solmupareja Suunnattu graafi: Joukko solmuja ja joukko järjestettyjä solmupareja eli kaaria Haaran päätesolmut:
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Rekursio Rekursion käyttötapauksia Rekursio määritelmissä Rekursio ongelmanratkaisussa ja ohjelmointitekniikkana Esimerkkejä taulukolla Esimerkkejä linkatulla listalla Hanoin
Tietorakenteet ja algoritmit Rekursio Rekursion käyttötapauksia Rekursio määritelmissä Rekursio ongelmanratkaisussa ja ohjelmointitekniikkana Esimerkkejä taulukolla Esimerkkejä linkatulla listalla Hanoin
Algoritmit 2. Luento 4 Ke Timo Männikkö
 Algoritmit 2 Luento 4 Ke 22.3.2017 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2017 Luento 4
Algoritmit 2 Luento 4 Ke 22.3.2017 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2017 Luento 4
Konsensusongelma hajautetuissa järjestelmissä. Niko Välimäki Hajautetut algoritmit -seminaari
 Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki 30.11.2007 Hajautetut algoritmit -seminaari Konsensusongelma Päätöksen muodostaminen hajautetussa järjestelmässä Prosessien välinen viestintä
Konsensusongelma hajautetuissa järjestelmissä Niko Välimäki 30.11.2007 Hajautetut algoritmit -seminaari Konsensusongelma Päätöksen muodostaminen hajautetussa järjestelmässä Prosessien välinen viestintä
Vasen johto S AB ab ab esittää jäsennyspuun kasvattamista vasemmalta alkaen:
 Vasen johto S AB ab ab esittää jäsennyspuun kasvattamista vasemmalta alkaen: S A S B Samaan jäsennyspuuhun päästään myös johdolla S AB Ab ab: S A S B Yhteen jäsennyspuuhun liittyy aina tasan yksi vasen
Vasen johto S AB ab ab esittää jäsennyspuun kasvattamista vasemmalta alkaen: S A S B Samaan jäsennyspuuhun päästään myös johdolla S AB Ab ab: S A S B Yhteen jäsennyspuuhun liittyy aina tasan yksi vasen
Ohjelmistotekniikan laitos OHJ-2550 Tekoäly, kevät
 128 Näille pätee kolmioepäyhtälö (triangle inequality) muodossa h(n) c([n,a], n') + h(n'), missä n' S(n) (valittu toiminto on a) ja c([n,a], n') on askelkustannus Linnuntie on myös monotoninen heuristiikka
128 Näille pätee kolmioepäyhtälö (triangle inequality) muodossa h(n) c([n,a], n') + h(n'), missä n' S(n) (valittu toiminto on a) ja c([n,a], n') on askelkustannus Linnuntie on myös monotoninen heuristiikka
Kieli merkitys ja logiikka. 4: Luovuus, assosiationismi. Luovuus ja assosiationismi. Kielen luovuus. Descartes ja dualismi
 Luovuus ja assosiationismi Kieli merkitys ja logiikka 4: Luovuus, assosiationismi Käsittelemme ensin assosiationismin kokonaan, sen jälkeen siirrymme kombinatoriseen luovuuteen ja konstituenttimalleihin
Luovuus ja assosiationismi Kieli merkitys ja logiikka 4: Luovuus, assosiationismi Käsittelemme ensin assosiationismin kokonaan, sen jälkeen siirrymme kombinatoriseen luovuuteen ja konstituenttimalleihin
Algoritmit 1. Luento 14 Ke 25.2.2015. Timo Männikkö
 Algoritmit 1 Luento 14 Ke 25.2.2015 Timo Männikkö Luento 14 Heuristiset menetelmät Heuristiikkoja kapsäkkiongelmalle Kauppamatkustajan ongelma Lähimmän naapurin menetelmä Kertaus ja tenttivinkit Algoritmit
Algoritmit 1 Luento 14 Ke 25.2.2015 Timo Männikkö Luento 14 Heuristiset menetelmät Heuristiikkoja kapsäkkiongelmalle Kauppamatkustajan ongelma Lähimmän naapurin menetelmä Kertaus ja tenttivinkit Algoritmit
j n j a b a c a d b c c d m j b a c a d a c b d c c j
 TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-38.115 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 12 29.2.2008 D12/1 Tarkastellaan verkkoa, jossa on solmua ja linkkiä.
TEKNILLINEN KORKEAKOULU Tietoliikenne- ja tietoverkkotekniikan laitos S-38.115 Liikenneteorian perusteet, Kevät 2008 Demonstraatiot Luento 12 29.2.2008 D12/1 Tarkastellaan verkkoa, jossa on solmua ja linkkiä.
Miten käydä läpi puun alkiot (traversal)?
 inääripuut ieman lisää aidon binääripuun ominaisuuksia lehtisolmuja on yksi enemmän kuin sisäsolmuja inääripuut tasolla d on korkeintaan 2 d solmua pätee myös epäaidolle binääripuulle taso 0: 2 0 = 1 solmu
inääripuut ieman lisää aidon binääripuun ominaisuuksia lehtisolmuja on yksi enemmän kuin sisäsolmuja inääripuut tasolla d on korkeintaan 2 d solmua pätee myös epäaidolle binääripuulle taso 0: 2 0 = 1 solmu
58131 Tietorakenteet ja algoritmit (kevät 2013) Kurssikoe 2, , vastauksia
 58131 Tietorakenteet ja algoritmit (kevät 2013) Kurssikoe 2, 652013, vastauksia 1 [6 pistettä] Vastaa jokaisesta alla olevasta väittämästä onko se tosi vai epätosi ja anna lyhyt perustelu Jokaisesta kohdasta
58131 Tietorakenteet ja algoritmit (kevät 2013) Kurssikoe 2, 652013, vastauksia 1 [6 pistettä] Vastaa jokaisesta alla olevasta väittämästä onko se tosi vai epätosi ja anna lyhyt perustelu Jokaisesta kohdasta
Helsingin yliopisto/tktl Kyselykielet, s 2006 Optimointi Harri Laine 1. Kyselyn optimointi. Kyselyn optimointi
 Miksi optimoidaan Relaatiotietokannan kyselyt esitetään käytännössä SQLkielellä. Kieli määrittää halutun tuloksen, ei sitä miten tulos muodostetaan (deklaratiivinen kyselykieli) Tietokannan käsittelyoperaatiot
Miksi optimoidaan Relaatiotietokannan kyselyt esitetään käytännössä SQLkielellä. Kieli määrittää halutun tuloksen, ei sitä miten tulos muodostetaan (deklaratiivinen kyselykieli) Tietokannan käsittelyoperaatiot
Diskreetit rakenteet
 Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
Diskreetit rakenteet 811120P 5 op 7. Oulun yliopisto Tietojenkäsittelytieteiden laitos 2015 / 2016 Periodi 1 Mikä on verkko? verkko (eli graafi) koostuu solmuista ja väleistä, jotka yhdistävät solmuja
815338A Ohjelmointikielten periaatteet
 815338A Ohjelmointikielten periaatteet 2015-2016 VII Logiikkaohjelmointi Sisältö 1. Johdanto 2. Predikaattilogiikan käsitteistöä 3. Prolog 815338A Ohjelmointikielten periaatteet, Logiikkaohjelmointi 2
815338A Ohjelmointikielten periaatteet 2015-2016 VII Logiikkaohjelmointi Sisältö 1. Johdanto 2. Predikaattilogiikan käsitteistöä 3. Prolog 815338A Ohjelmointikielten periaatteet, Logiikkaohjelmointi 2
b) Olkoon G vähintään kaksi solmua sisältävä puu. Sallitaan verkon G olevan
 Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tehtävä 7 : 1 a) Olkoon G jokin epäyhtenäinen verkko. Tällöin väittämä V (G) 2 pätee jo epäyhtenäisyyden nojalla. Jokaisella joukolla X on ehto X 0 voimassa, joten ehdot A < 0 ja F < 0 toteuttavilla joukoilla
Tiedon esittäminen ja päättely. Kognitiivinen mallintaminen I. Merkitys. Merkitys. Kognitiivinen mallintaminen I, kevät /13/07
 Tiedon esittäminen ja päättely Kognitiivinen mallintaminen I Symbolinen mallintaminen 3. luento Tiedon esittäminen ja päättely Merkitys: kompositionaalisuus Malliteoria Loogisen päättelyn malleja Tiedon
Tiedon esittäminen ja päättely Kognitiivinen mallintaminen I Symbolinen mallintaminen 3. luento Tiedon esittäminen ja päättely Merkitys: kompositionaalisuus Malliteoria Loogisen päättelyn malleja Tiedon
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
Joonas Haapala Ohjaaja: DI Heikki Puustinen Valvoja: Prof. Kai Virtanen
 Hävittäjälentokoneen reitin suunnittelussa käytettävän dynaamisen ja monitavoitteisen verkko-optimointitehtävän ratkaiseminen A*-algoritmilla (valmiin työn esittely) Joonas Haapala 8.6.2015 Ohjaaja: DI
Hävittäjälentokoneen reitin suunnittelussa käytettävän dynaamisen ja monitavoitteisen verkko-optimointitehtävän ratkaiseminen A*-algoritmilla (valmiin työn esittely) Joonas Haapala 8.6.2015 Ohjaaja: DI
10. Painotetut graafit
 10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
10. Painotetut graafit Esiintyy monesti sovelluksia, joita on kätevä esittää graafeina. Tällaisia ovat esim. tietoverkko tai maantieverkko. Näihin liittyy erinäisiä tekijöitä. Tietoverkkoja käytettäessä
1. (a) Seuraava algoritmi tutkii, onko jokin luku taulukossa monta kertaa:
 Tietorakenteet, laskuharjoitus 10, ratkaisuja 1. (a) Seuraava algoritmi tutkii, onko jokin luku taulukossa monta kertaa: SamaLuku(T ) 2 for i = 1 to T.length 1 3 if T [i] == T [i + 1] 4 return True 5 return
Tietorakenteet, laskuharjoitus 10, ratkaisuja 1. (a) Seuraava algoritmi tutkii, onko jokin luku taulukossa monta kertaa: SamaLuku(T ) 2 for i = 1 to T.length 1 3 if T [i] == T [i + 1] 4 return True 5 return
isomeerejä yhteensä yhdeksän kappaletta.
 Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävä 2 : 1 Esitetään aluksi eräitä havaintoja. Jokaisella n Z + symbolilla H (n) merkitään kaikkien niiden verkkojen joukkoa, jotka vastaavat jotakin tehtävänannon ehtojen mukaista alkaanin hiiliketjua
Tehtävän V.1 ratkaisuehdotus Tietorakenteet, syksy 2003
 Tehtävän V.1 ratkaisuehdotus Tietorakenteet, syksy 2003 Matti Nykänen 5. joulukuuta 2003 1 Satelliitit Muunnetaan luennoilla luonnosteltua toteutusta seuraavaksi: Korvataan puusolmun p kentät p. key ja
Tehtävän V.1 ratkaisuehdotus Tietorakenteet, syksy 2003 Matti Nykänen 5. joulukuuta 2003 1 Satelliitit Muunnetaan luennoilla luonnosteltua toteutusta seuraavaksi: Korvataan puusolmun p kentät p. key ja
T Syksy 2002 Tietojenkäsittelyteorian perusteet Harjoitus 8 Demonstraatiotehtävien ratkaisut
 T-79.148 Syksy 2002 Tietojenkäsittelyteorian perusteet Harjoitus 8 Demonstraatiotehtävien ratkaisut 4. Tehtävä: Laadi algoritmi, joka testaa onko annetun yhteydettömän kieliopin G = V, Σ, P, S tuottama
T-79.148 Syksy 2002 Tietojenkäsittelyteorian perusteet Harjoitus 8 Demonstraatiotehtävien ratkaisut 4. Tehtävä: Laadi algoritmi, joka testaa onko annetun yhteydettömän kieliopin G = V, Σ, P, S tuottama
Johdatus verkkoteoriaan luento Netspace
 Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Johdatus verkkoteoriaan luento 20.3.18 Netspace Kurssin sijainti muussa suunnitellussa kokonaisuudessa Verkko eli graafi, tasoverkko, solmut, välit, alueet, suunnatut verkot, isomorfiset verkot, verkon
Unify( Tuntee(Jussi, x), Tuntee(y, z) ) { y/jussi, z/x } { y/jussi, x/jussi, z/jussi }
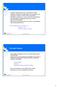 98 Ongelman edellä aiheuttaa saman muuttujanimen käyttö Toisaalta eri lauseiden muuttujanimillä ei ole merkitystä (ennen sidontaa) ja muuttujien nimentä voidaan standardoida Mahdollisia samaistuksia on
98 Ongelman edellä aiheuttaa saman muuttujanimen käyttö Toisaalta eri lauseiden muuttujanimillä ei ole merkitystä (ennen sidontaa) ja muuttujien nimentä voidaan standardoida Mahdollisia samaistuksia on
Johdatus graafiteoriaan
 Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Johdatus graafiteoriaan Syksy 2017 Lauri Hella Tampereen yliopisto Luonnontieteiden tiedekunta 126 Luku 3 Puut 3.1 Puu 3.2 Virittävä puu 3.3 Virittävän puun konstruointi 3.4 Minimaalinen virittävä puu
Pinot, jonot, yleisemmin sekvenssit: kokoelma peräkkäisiä alkioita (lineaarinen järjestys) Yleisempi tilanne: alkioiden hierarkia
 Pinot, jonot, yleisemmin sekvenssit: kokoelma peräkkäisiä alkioita (lineaarinen järjestys) Yleisempi tilanne: alkioiden hierarkia Kukin alkio (viite) talletettuna solmuun (node) vastaa paikan käsitettä
Pinot, jonot, yleisemmin sekvenssit: kokoelma peräkkäisiä alkioita (lineaarinen järjestys) Yleisempi tilanne: alkioiden hierarkia Kukin alkio (viite) talletettuna solmuun (node) vastaa paikan käsitettä
Oikeasta tosi-epätosi -väittämästä saa pisteen, ja hyvästä perustelusta toisen.
 Tietorakenteet, kevät 2012 Kurssikoe 2, mallivastaukset 2. (a) Järjestämistä ei voi missään tilanteessa suorittaa nopeammin kuin ajassa Θ(n log n), missä n on järjestettävän taulukon pituus. Epätosi: Yleisessä
Tietorakenteet, kevät 2012 Kurssikoe 2, mallivastaukset 2. (a) Järjestämistä ei voi missään tilanteessa suorittaa nopeammin kuin ajassa Θ(n log n), missä n on järjestettävän taulukon pituus. Epätosi: Yleisessä
Operatioanalyysi 2011, Harjoitus 3, viikko 39
 Operatioanalyysi 2011, Harjoitus 3, viikko 39 H3t1, Exercise 3.1. H3t2, Exercise 3.2. H3t3, Exercise 3.3. H3t4, Exercise 3.4. H3t5 (Exercise 3.1.) 1 3.1. Find the (a) standard form, (b) slack form of the
Operatioanalyysi 2011, Harjoitus 3, viikko 39 H3t1, Exercise 3.1. H3t2, Exercise 3.2. H3t3, Exercise 3.3. H3t4, Exercise 3.4. H3t5 (Exercise 3.1.) 1 3.1. Find the (a) standard form, (b) slack form of the
Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m.
 Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
Väite: T (n) (a + b)n 2 + a. Induktiotodistus: Tapaus n = 0 selvä; ol. väite pätee kun n < m. Huomaa että funktion x x 2 + (m 1 x) 2 kuvaaja on ylöspäin aukeava paraabeli, joten funktio saavuttaa suurimman
811120P Diskreetit rakenteet
 811120P Diskreetit rakenteet 2016-2017 1. Algoritmeista 1.1 Algoritmin käsite Algoritmi keskeinen laskennassa Määrittelee prosessin, joka suorittaa annetun tehtävän Esimerkiksi Nimien järjestäminen aakkosjärjestykseen
811120P Diskreetit rakenteet 2016-2017 1. Algoritmeista 1.1 Algoritmin käsite Algoritmi keskeinen laskennassa Määrittelee prosessin, joka suorittaa annetun tehtävän Esimerkiksi Nimien järjestäminen aakkosjärjestykseen
Algoritmit 2. Luento 6 Ke Timo Männikkö
 Algoritmit 2 Luento 6 Ke 29.3.2017 Timo Männikkö Luento 6 B-puun operaatiot B-puun muunnelmia Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2017 Luento 6 Ke 29.3.2017 2/31 B-puu
Algoritmit 2 Luento 6 Ke 29.3.2017 Timo Männikkö Luento 6 B-puun operaatiot B-puun muunnelmia Nelipuu Trie-rakenteet Standarditrie Pakattu trie Algoritmit 2 Kevät 2017 Luento 6 Ke 29.3.2017 2/31 B-puu
2. Seuraavassa kuvassa on verkon solmujen topologinen järjestys: x t v q z u s y w r. Kuva 1: Tehtävän 2 solmut järjestettynä topologisesti.
 Tietorakenteet, laskuharjoitus 11, ratkaisuja 1. Leveyssuuntaisen läpikäynnin voi toteuttaa rekursiivisesti käsittelemällä jokaisella rekursiivisella kutsulla kaikki tietyllä tasolla olevat solmut. Rekursiivinen
Tietorakenteet, laskuharjoitus 11, ratkaisuja 1. Leveyssuuntaisen läpikäynnin voi toteuttaa rekursiivisesti käsittelemällä jokaisella rekursiivisella kutsulla kaikki tietyllä tasolla olevat solmut. Rekursiivinen
Algoritmit 2. Luento 7 Ti Timo Männikkö
 Algoritmit 2 Luento 7 Ti 4.4.2017 Timo Männikkö Luento 7 Joukot Joukko-operaatioita Joukkojen esitystapoja Alkiovieraat osajoukot Toteutus puurakenteena Algoritmit 2 Kevät 2017 Luento 7 Ti 4.4.2017 2/26
Algoritmit 2 Luento 7 Ti 4.4.2017 Timo Männikkö Luento 7 Joukot Joukko-operaatioita Joukkojen esitystapoja Alkiovieraat osajoukot Toteutus puurakenteena Algoritmit 2 Kevät 2017 Luento 7 Ti 4.4.2017 2/26
4 INFORMOITU ETSINTÄ AHNE PARAS ENSIN -STRATEGIA
 INFORMOITU ETINTÄ okeilla etsintämenetelmillä ei ole käytössään muuta informaatiota kuin etsintäongelman määrittely. Informoidut etsintämenetelmät (informed search strategies) ovat sellaisia, jotka voivat
INFORMOITU ETINTÄ okeilla etsintämenetelmillä ei ole käytössään muuta informaatiota kuin etsintäongelman määrittely. Informoidut etsintämenetelmät (informed search strategies) ovat sellaisia, jotka voivat
Ratkaisu. Tulkitaan de Bruijnin jonon etsimiseksi aakkostossa S := {0, 1} sanapituudelle n = 4. Neljän pituisia sanoja on N = 2 n = 16 kpl.
 iskreetti matematiikka, syksy 00 arjoitus, ratkaisuista. seta 8 nollaa ja 8 ykköstä renkaaksi niin, että jokainen yhdistelmä 0000, 000,..., esiintyy täsmälleen kerran. Vihje: Tulkitse de ruijnin jonon
iskreetti matematiikka, syksy 00 arjoitus, ratkaisuista. seta 8 nollaa ja 8 ykköstä renkaaksi niin, että jokainen yhdistelmä 0000, 000,..., esiintyy täsmälleen kerran. Vihje: Tulkitse de ruijnin jonon
Graafin 3-värittyvyyden tutkinta T Graafiteoria, projektityö (eksakti algoritmi), kevät 2005
 Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Graafin 3-värittyvyyden tutkinta T-79.165 Graafiteoria, projektityö (eksakti algoritmi), kevät 2005 Mikko Malinen, 36474R 29. maaliskuuta, 2005 Tiivistelmä Artikkelissa käydään läpi teoriaa, jonka avulla
Cog311 Resurssit ja monitehtäväsuoritus
 Cog311 Resurssit ja monitehtäväsuoritus Esko Lehtonen... @helsinki.fi Resursseja? Ihminen havaintokognitiivisena kokonaisuutena voi Keskittyä johonkin kerrallaan Yhteen asiaan keskittyminen sulkee pois
Cog311 Resurssit ja monitehtäväsuoritus Esko Lehtonen... @helsinki.fi Resursseja? Ihminen havaintokognitiivisena kokonaisuutena voi Keskittyä johonkin kerrallaan Yhteen asiaan keskittyminen sulkee pois
Se mistä tilasta aloitetaan, merkitään tyhjästä tulevalla nuolella. Yllä olevassa esimerkissä aloitustila on A.
 Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
Harjoitus 4 (7.4.2014)
 Harjoitus 4 (7.4.2014) Tehtävä 1 Tarkastellaan Harjoituksen 1 nopeimman reitin ongelmaa ja etsitään sille lyhin virittävä puu käyttämällä kahta eri algoritmia. a) (Primin algoritmi) Lähtemällä solmusta
Harjoitus 4 (7.4.2014) Tehtävä 1 Tarkastellaan Harjoituksen 1 nopeimman reitin ongelmaa ja etsitään sille lyhin virittävä puu käyttämällä kahta eri algoritmia. a) (Primin algoritmi) Lähtemällä solmusta
Hakupuut. tässä luvussa tarkastelemme puita tiedon tallennusrakenteina
 Hakupuut tässä luvussa tarkastelemme puita tiedon tallennusrakenteina hakupuun avulla voidaan toteuttaa kaikki joukko-tietotyypin operaatiot (myös succ ja pred) pahimman tapauksen aikavaativuus on tavallisella
Hakupuut tässä luvussa tarkastelemme puita tiedon tallennusrakenteina hakupuun avulla voidaan toteuttaa kaikki joukko-tietotyypin operaatiot (myös succ ja pred) pahimman tapauksen aikavaativuus on tavallisella
