TERÄSRAKENTEISTEN SILTOJEN PARA- METRINEN MALLINNUS
|
|
|
- Jalmari Katajakoski
- 7 vuotta sitten
- Katselukertoja:
Transkriptio
1 TERÄSRAKENTEISTEN SILTOJEN PARA- METRINEN MALLINNUS Mikko Toola Opinnäytetyö Elokuu 2017 Rakennustekniikka Talonrakennustekniikka
2 TIIVISTELMÄ Tampereen ammattikorkeakoulu Rakennustekniikan koulutusohjelma Talonrakennustekniikka TOOLA, MIKKO: Teräsrakenteisten siltojen parametrinen mallinnus Opinnäytetyö 34 sivua, joista liitteitä 0 sivua Elokuu 2017 Opinnäytetyön toimeksiantajana toimi WSP Finland Oy, joka on erikoistunut muun muassa vaativiin siltaprojekteihin Suomessa ja sen ulkopuolella. Työn ohjaajana oli toimeksiantajan siltasuunnittelija, diplomi-insinööri, Olli Perälä. Tavoitteena oli tutkia parametrisen mallintamisen mahdollisuuksia, selvittää siitä aiheutuvia ongelmia ja kehittää visuaalista skriptausta osana mallinnusta. Tässä insinöörityössä toteutettiin Kruunuvuorensillan pylonin teräskotelo ja teräsosien parametrinen malli Tekla Structures -ohjelmaan, mikä on osa Kruunusillat-hanketta. Työ oli käytännönläheinen ja se sisältää tietoa ohjelmista sekä algoritmiavusteisesta mallintamisesta. Työssä esiteltiin myös lyhyesti ja yksinkertaisesti Rhinoceros 3D -ohjelman lisäosa Grasshopper, jolla parametrinen malli toteutettiin. Työtä tehdessä opittiin paljon uutta mallintamisesta ja etenkin Grasshopper -lisäosasta. Grasshopper -lisäosan ja Tekla Structures -ohjelman yhteiskäytöstä selvitettiin paljon huomioitavia asioita. Parametrinen malli toteutettiin onnistuneesti ja todettiin visuaalisen skriptauksen avulla tuotettu malli tarpeelliseksi kyseisessä kohteessa, koska lopullista mitoitusta ei ollut tehty. Siltojen haastavan geometrian ja lähtötietojen muuttumisen vuoksi mallintamista voisi toteuttaa tulevaisuudessa täysin visuaalisella skriptauksella. Asiasanat: algoritmi, algoritmiavusteinen suunnittelu, parametri, parametrinen mallintaminen, Grasshopper
3 ABSTRACT Tampereen ammattikorkeakoulu Tampere University of Applied Sciences Degree Programme in Construction Engineering Building Construction TOOLA, MIKKO: Parametric Modelling of Steel Structure Bridges Bachelor's thesis 34 pages, appendices 0 pages August 2017 The thesis was commissioned by WSP Finland Ltd., which is specialized among other things in demanding bridge projects in Finland and beyond. The work was supervised by Olli Perälä, M.Sc. Bridge Engineer. The objective was to explore the possibilities of parametric modelling, to identify possible problems and to develop visual scripting as part of modelling. In the framework of this thesis a parametric model of Kruunuvuorensilta s pylon steel cage and steel parts was created to Tekla Structures, as part of Kruunusillat project. The thesis was practice-oriented and it includes basic information about programs and algorithm-aided modelling. Rhinoceros 3D program s add-on Grasshopper, used for creating the parametric model, is described briefly and in a simplified way. The thesis offered the opportunity to learn more about modelling and especially about using the Grasshopper plugin. Several issues arose, that are to be considered while using Grasshopper add-on in relation with Tekla Structures program. The parametric model was implemented successfully and the model produced by visual scripting was found necessary for this case, because a final design had not been made. Due to bridges challenging geometry and possible changes of underlying data, the modelling of bridges could be done entirely using visual scripting in the future. Key words: algorithm, algorithm-aided design, parameter, parametric modelling, Grasshopper
4 4 SISÄLLYS 1 JOHDANTO D-mallintaminen Tekla Structures Rhinoceros 3D Grasshopper Grasshopper-Tekla live link Ohjelmien yhteys toisiinsa Algoritminen mallintaminen Algoritmi Parametrinen mallintaminen Algoritmiavusteinen suunnittelu The Morpheus Hotel Yleistä Grasshopperista Matematiikka Grasshopperin apuna Esimerkkitapaus: Kruunuvuorensillan pylonin teräsrakenteiden parametrinen mallinnus Yleistä Kruunuvuorensillasta Lähtötiedot Pylonin teräskotelo Pylonin köysien ankkurointiosat Miksi parametrisoitiin? Esimerkkitapauksen analysointi Visuaaliseen skriptaukseen liittyvät ongelmat Ohjelmien yhteensopivuudesta aiheutuvat ongelmat Sillan geometrian aiheuttamat haasteet Visuaalisen skriptauksen haasteet Grasshopperissa Parametrisen mallintamisen ja visuaalisen skriptauksen hyödyt POHDINTA LÄHTEET... 34
5 5 LYHENTEET JA TERMIT Tekla Rhino Grasshopper Ohjelmakomponentti Tekla komponentti Algoritmi Parametri Visuaalinen skriptaus Lanka Parametrinen malli Input Output Tekla Structures -tietomallinnus ohjelmisto Rhinoceros 3D -mallinnus ohjelmisto Visuaalisen skriptauksen lisäosa Rhinoceros 3D:hen Komponentti, joka suorittaa laskuja Grasshopper -lisäosassa Komponentti, joka mallintaa objekteja Teklaan Grasshopperista Suorittaa tietyn tehtäväsarjan Algoritmissa yksittäinen muuttuja Visuaalisten ohjelmakomponenttien avulla luotu algoritmi Komponenttien yhdistämistä tehtäväsarjaksi Riippuvuussuhteiden rakentamista algoritmia ohjaavien parametrien välille suunnittelumallissa Ohjelmakomponenttiin tai algoritmiin syötettävä data Ohjelmakomponentista saatava data
6 6 1 JOHDANTO Tietomallintaminen on kehittynyt huomattavasti rakentamisessa ja rakennesuunnittelussa 2000-luvun alusta alkaen. Suunnittelu ja mallintaminen tehdään lähes kokonaan tietokoneavusteisesti. Nykyään siltojen suunnittelussa käytetään yhä enemmän tietomalleja suunnittelun apuna. Suurissa siltakohteissa on monen eri alan asiantuntijoita mukana ja suunnittelun eri vaiheissa voidaan tehdä vielä suuria muutoksia, jotka vaikuttavat mallintamiseen. Muutoksiin voidaan varautua tekemällä parametrisia malleja. Tähän tarkoitukseen soveltuu visuaaliseen skriptaukseen perustuva lisäosa Grasshopper. Grasshopper on Rhinoceros 3D -ohjelman lisäosa, jolla voidaan mallintaa Tekla Structures -ohjelmaan objekteja. Lisäosan avulla objekteja on myös mahdollista mallintaa parametrisesti. Muutoksiin pystytään varautumaan etukäteen jo suunnittelun alkuvaiheessa hyödyntämällä parametrista mallinnusta. Tarkoituksena on havainnollistaa Grasshopperin käyttöä, soveltuvuutta ja mahdollisuuksia rakennesuunnittelijan mallintamisen työkaluna. Kokeneiden siltasuunnittelijoiden kanssa käymieni keskustelujen mukaan siltojen mallintamisen kehityksen suunta on yhä enemmän parametrisessa mallinnuksessa ja sillä on potentiaalia jäädä osaksi mallintamista. Opinnäytetyössä tehdään sillan pylonin teräsrakenteiden parametrinen malli ja esitellään algoritmiavusteista mallintamista. Työssä keskitytään mallintamiseen visuaalista skriptausta hyväksi käyttäen Grasshopperin avulla. Työ toteutettiin sekä kirjallisuustutkimuksena, että tapaustutkimuksena. Lopussa selvitetään esimerkkitapauksessa havaittuja ongelmia ja mahdollisia hyötyjä.
7 7 2 3D-mallintaminen 2.1 Tekla Structures Tekla Structures -ohjelmisto on Trimble Solutions Oy:n omistama rakennesuunnitteluohjelmisto, jolla voidaan tehdä tarkkoja, luotettavia ja yksityiskohtaisia tietomalleja. Tarkkoja tietomalleja tarvitaan onnistuneeseen rakentamisen toteutukseen ja ylläpitoon. Tekla Structures toimii kaikkien materiaalien kanssa ja sillä voidaan suunnitella monimutkaisia rakenteita, esimerkiksi geometrialtaan haastavia siltoja. (Trimble Solutions Corporation n.d.) Tekla Structures voidaan yhdistää tärkeimpiin tuotannon- tai resurssisuunnittelujärjestelmiin ja koneiden ohjausjärjestelmiin, joita käyttävät mm. teräsrakenteiden ja raudoitusten valmistajat. Tämä vähentää manuaalisia töitä ja virheitä, sillä tiedot voidaan siirtää automaattisesti Tekla-mallista tuotannon käyttämiin järjestelmiin. (Trimble Solutions Corporation n.d.) Tekla Structures -tietomalli voi parantaa rakennesuunnittelun tietojen laatua ja tarkkuutta. Dokumentointiin ja suunnitteluratkaisuihin jää enemmän aikaan, koska Tekla Structures tuottaa piirustukset ja raportit suoraan mallista. Myös määräluettelot on helppo tuottaa ja vaihtoehtoisten ratkaisujen analysointi on nopeaa. Kun Tekla-malli on kunnossa myös piirustukset pitävät paikkansa. (Trimble Solutions Corporation n.d.) Havainnollistaminen on huomattavasti helpompaa kolmiulotteisena kuin tasopiirustuksena. Siltarakenteissa on valtava määrä raudoitusta, joten kolmiulotteisena tehdyissä rakenteissa on helppo huomata, jos jokin objekti leikkaa toisen objektin kanssa. Tämän ansiosta suunnittelijan virheet saattavat välttyä jo suunnitteluvaiheessa. 2.2 Rhinoceros 3D Rhinoceros 3D, tutummin Rhino, on Robert McNeel & Associatesin kehittämä monipuolinen ja tehokas 3D NURBS -mallinnusohjelma. Sillä voidaan mallintaa tarkasti minkä
8 8 tahansa kappaleen muodon. Rhino soveltuu erinomaisesti käytettäväksi muiden suunnitteluohjelmien kanssa laajan tiedostotuen ansiosta ja sen vahvuus on monipuoliset mallinnusominaisuudet. Ohjelma on helppo oppia, vaikka ei olisikaan aiempaa 3D-mallinnuskokemusta. Rhinoceroksen toimintoja on myös mahdollistaa laajentaa erilaisilla asennettavilla lisäosilla. (Moonsoft 2017.) Tässä opinnäytetyössä ei keskitytä Rhinon käyttöön vaan siihen asennettavaan Grasshopper -lisäosaan, jota ei voida käyttää ilman Rhinocerosta. 2.3 Grasshopper Grasshopper on David Ruttenin luoma algoritmiseen mallintamiseen perustuva ilmainen lisäosa Rhinoceros 3D -ohjelmaan. Poiketen muista skriptaukseen perustuvista ohjelmista, kuten esimerkiksi RhinoScript, perinteistä tekstimuotoista skriptausta ei tarvitse osata Grasshopperissa, sillä se perustuu visuaaliseen skriptaukseen. Ensimmäinen vakaa versio ohjelmasta julkaistiin vuonna (Grasshopper 2017.) Visuaalinen skriptaus ei vaadi aloittelijalta kovin suurta aloituskynnystä. Grasshopperissa luodaan algoritmi visuaalisesti linkittämällä erilaisia ohjelmasta löytyviä komponentteja toisiinsa. Näin ollen tekstimuotoista ohjelmakoodia ei tarvitse kirjoittaa, sillä ohjelmakomponentit sisältävät itsessään kaiken koodin. Ohjelmakomponentteja on monia erilaisia ja jokaisella niistä on tietty toiminto. Komponentteja yhdistelemällä saadaan luotua erilaisia matemaattisia toimintoja ja geometriaa melko yksinkertaisesti. (Tanska & Österlund 2017, 30). Yksinkertaisimmillaan ohjelmakomponentti voi olla esimerkiksi summakomponentti (kuva 1). Komponentti laskee summalaskun, kun sille annetaan ensimmäinen luku ja yhteenlaskettava luku. Lopputuloksena saadaan summa, jonka komponentti laskee itse ilman perinteisesti käsin suoritettavaa skriptausta. KUVA 1. Summakomponentti Grasshopperissa
9 9 2.4 Grasshopper-Tekla live link Grasshopper-Tekla live link mahdollistaa algoritmisen mallintamisen suoraan Grasshopperista reaaliajassa Tekla Structuresiin. Teklaa voidaan ohjata Grasshopperista käsin. Tämä automaattinen linkki ohjelmistojen välille on Trimble Solutions Oy:n kehittämä ja on vielä beta-vaiheessa tätä kirjoittaessa. Linkki julkaistiin vuonna 2016 ja toimiakseen se tarvitsee Rhinon, Grasshopperin ja Tekla Structuresin asennettuna samalle koneelle. (Grasshopper-Tekla Live Link 2017.) KUVA 2. Grasshopper-Tekla live link -lisäosa asennettuna Kun Grasshopper-Tekla live link on asennettu, ilmestyy Grasshopperin komponentteihin Tekla-niminen välilehti (kuva 2). Välilehdeltä löytyvät komponentit ovat kaikki suorassa yhteydessä Tekla Structuresiin ja näillä luodaan haluttuja objekteja Tekla-malliin. Tässä opinnäytetyössä käytetään tätä hyväksi, kun tehdään parametrinen malli esimerkkitapauksessa. 2.5 Ohjelmien yhteys toisiinsa Edellä mainitut ohjelmat ovat kaikki yhteydessä keskenään (kaavio 1). Kun Grasshopperissa tehdään visuaalista skriptausta, tiedot välittyvät Teklaan ja Rhinoon. Teklaan ilmestyy objekti vasta sitten, kun algoritmin loppuun tai tiettyyn osaan on yhdistetty Tekla komponentti Grasshopperissa. Rhinoon päivittyy kaikki Grasshopperin visuaalisella skriptauksella tehdyt vaiheet ja siellä näkyy mm. laskettua geometriaa.
10 10 KAAVIO 1. Ohjelmien yhteys Kuvassa 3 on havainnollistettu, miltä algoritmi näyttää Grasshopperissa, Grasshopperin luomat pisteet Rhinoon sekä näkymä Teklassa, kun Tekla komponentit on mallintanut objektin Teklaan.
11 KUVA 3. Ohjelmistojen näkymät 11
12 12 3 Algoritminen mallintaminen 3.1 Algoritmi Algoritmi tarkoittaa yksinkertaisuudessaan sitä, että suoritetaan tietty komentosarja. Se on sarja, joka kuvaa määriteltyjä tehtäviä, ohjeita ja sääntöjä tietyn päämäärän saavuttamiseksi. Tehtävät määritellään tietyssä järjestyksessä halutun lopputuloksen saamiseksi. Lopputulos on aina sama jokaisen suorituskerran jälkeen, jos algoritmin lähtöarvoja ja komentosarjaa ei muuteta. (Tanska & Österlund 2017, 20.) Algoritmi oli alun alkaen matemaattinen käsite, mutta nykyisin se liittyy yleensä tietokoneiden ohjelmointiin ja tietojenkäsittelyyn. Tietokoneella toteutetut algoritmit ovat huomattavasti nopeampi ja tarkempi toteuttaa kuin manuaalisesti algoritmiin annetut ohjeet. Algoritmi voidaan myös käsittää tosielämässä tietynlaisena tehtäväsarjana. Esimerkiksi tosielämän ruokareseptin ohjeiden noudattaminen on tietynlainen algoritmi. Kun reseptiä noudatetaan, saadaan haluttu lopputulos. Reseptin toimiminen perustuu siihen, että tuodaan oikeat ruoka-aineet, ohjeiden mukaan mitataan oikeat mittasuhteet, valmistetaan tietyssä reseptin määräämässä järjestyksessä ja saadaan haluttu lopputulos. (Tanska & Österlund 2017, 20.) 3.2 Parametrinen mallintaminen Termi parametrinen on peräisin matematiikasta, mutta ei tiedetä tarkalleen milloin suunnittelijat aloittivat sen käytön (Davis 2013). Parametrinen mallinnus tarkoittaa sitä, että asetetaan tiettyjä riippuvuussuhteita, jotka muokkaavat algoritmia tai algoritmin tiettyä osaa halutulla tavalla. Suunnittelija voi parametrista mallinnusta hyväksi käyttäen tehdä parametrisointeja, jossa jo yhden parametrisen arvon muuttaminen muokkaa koko mallin geometriaa tai vain haluttua geometriaa. (Tanska & Österlund 2017, 13.) Parametrisen mallinnuksen avulla voidaan siis esimerkiksi tehdä teräslevyinen laatikko, jossa seinien ja pohjan mitat ovat riippuvuussuhteessa. Kun pohjan leveyttä muutetaan, muuttuu myös seinän sijainti automaattisesti suhteessa pohjan leveyteen. Tässä tapauksessa parametrina on terälevyisen laatikon leveys. Kuvassa 4 on esimerkki parametrisestä mallinnuksesta,
13 jossa pohjan leveys on parametri. Tekla-malli päivittyy automaattisesti, kun arvoa muutetaan Grasshopperin liukusäätimessä eli sliderissa. 13 KUVA 4. Yksinkertainen parametrisoitu Tekla-malli 3.3 Algoritmiavusteinen suunnittelu Algoritmiavusteinen suunnittelu tarkoittaa sitä, että suunnittelija käyttää hyväksi, esimerkiksi mallintamisessa, algoritmeja ja toistuvia sääntöjä rakenteiden luomiseksi. Algoritmiavusteisen suunnittelun avulla voidaan luoda visuaalista skriptausta hyväksi käyttäen algoritmi, jolla luodaan kolmiulotteinen parametrinen malli. Näillä saadaan aikaan haluttu prosessin lopputulos, joka voi olla esimerkiksi teräsrakenteisen sillan pääkannattimet ja poikkipalkit. Suunnittelija määrittelee lähtötiedot, mittaviivat ja geometriat. Algoritmin suunnittelija suunnittelee sääntö ja ohje kerrallaan algoritmin. Grasshopperilla voidaan siis luoda algoritmi visuaalisella skriptauksella, jonka lähtötietoina ovat mittaviivat ja lopputuloksena saadaan Tekla objekteja. Algoritmiavusteinen suunnittelu on arkkitehtien tehokas työväline, koska sillä saadaan tehtyä monia erilaisia vaihtoehtoratkaisuja yhden algoritmin avulla sekä mallinnettua geometrialtaan haastavia kohteita. (Tanska & Österlund 2017, 36.) Algoritmiavusteista
14 14 suunnittelua voi hyödyntää myös rakennesuunnittelijat ja mallintajat, mutta aiheesta on tehty vähän tutkimuksia. Tässä opinnäytetyössä on hyödynnetty algoritmiavusteista suunnittelua osana mallinnusta. 3.4 The Morpheus Hotel The Morpheus Hotel (kuva 5) on Kiinan Macaoon suunniteltu hotelli, joka on suunniteltu algoritmiavusteisesti ja se on parametrisoitu Grasshopperia ja Rhinoa käyttäen. Hotellin julkisivu on geometrialtaan hyvin monimuotoinen ja siinä on käytetty ulkoisena tukirakenteena terästä, joka on verhoiltu alumiinilla. Rakennus on 40-kerroksinen kaksitorninen hotelli, jonka keskellä on kolme vapaamuotoista aukkoa. Rakennuksen arkkitehtuurin suunnitteli Zaha Hadid Architects ja julkisivun tuotannon konsulttina toimi Front Inc. Rakennuksen ennakoidaan valmistuvan vuonna (The Morpheus Hotel: From Design to Production: Live Webinar 2017). KUVA 5. Morpheus -hotelli Kiinassa (Zaha Hadid Architects)
15 15 Ulkoinen tukirakenne on geometrialtaan erittäin haastava, joten mallintamisessa päädyttiin ratkaisuun, jossa tehtiin monta eri mallia rakennuksesta. Rakennuksesta tehtiin 3522 Rhino 3D-mallia, jonka mallintamiseen käytettiin apuna 462:ta erilaista Grasshopper tiedostoa. Yhden tiedoston käyttäminen olisi ollut vaikeaa organisoida, se olisi ollut liian raskas ja sitä olisi voinut käyttää ainoastaan yksi ihminen kerrallaan. Projektissa ulkoista tukirakennetta oli suunnittelemassa neljä ihmistä samanaikaisesti. Ulkoisesta tukirakenteesta laadittiin Grasshopperin avulla automaattisesti konepajapiirustusta ja kokoonpanopiirustusta. Rakennuksen monimuotoisuuden vuoksi, siitä tehtiin FEM-analyysit siirtämällä data automaattisesti Rhinosta ja Grasshopperista laskentaohjelmaan. (The Morpheus Hotel: From Design to Production: Live Webinar 2017). Hotellin suunnittelu on erinomainen näyttö siitä, mitä Grasshopperilla pystytään saamaan aikaan. Arkkitehtien asettamat reunaehdot pystyttiin määrittämään ja parametrisoimaan muuttujat Grasshopperin avulla. Mallintamisen apuna käytettiin Grasshopperin visuaalista skriptausta, mikä säästää aikaa verrattuna perinteiseen koodaamiseen. Projekti antaa mielenkiintoisen lähtökohdan parametrisen suunnittelun maailmaan. 3.5 Yleistä Grasshopperista Tässä kappaleessa esitetään ja käydään läpi Grasshopperin käyttöliittymä ja peruskäsitteet. Kuvassa 6 on esitetty käyttöliittymä mikä aukeaa, kun Rhinon lisäosa Grasshopper avataan, kirjoittamalla Rhinon komentoriviin Grasshopper. Kuvassa 6 alueessa 1 on component menu eli kaikki Grashopperin ohjelmakomponentit, jotka sijaitsevat eri välilehdillä. Tekla live linkin asentamisen jälkeen välilehdeksi ilmestyy myös Tekla-välilehti.
16 16 KUVA 6. Grasshopper käyttöliittymä Alueesta 2 löytyy canvas eli piirtoalue, johon tehdään visuaalinen skriptaus ohjelmakomponenttien avulla. Alueessa 3 on valintapainikkeet, joilla voidaan hallita näkymäasetuksia Rhinon puolella. Kuvassa 7 on esitetty Grasshopperin perusperiaate ja keskeisimmät käsitteet. Tässä lyhyessä algoritmissa on laskettu käyrältä 4000 mm etäisyydellä toisistaan olevien pisteiden koordinaatit. Koodi etenee vasemmalta oikealle, eikä silmukoita (eng. loop) voida tehdä.
17 17 KUVA 7. Grasshopper algoritmi TAULUKKO 1. Kuvan 7 selitykset Nro. Työkalu Selite 1 Data input Lähtötiedot Rhinoon piirretyltä käyrältä 2 Slideri (eng. num slider) Parametri, komponentille välitettävä muuttuja 3 Ohjelmakomponentti Sisältää valmiiksi määriteltyä koodia 4 Komponentin datan sisääntulo, input 5 Komponentin datan ulosmeno, output 6 Lanka (eng. wire) Komponenttien yhdistämistä toisiinsa 7 Paneeli (eng. panel) Voidaan lukea mm. komponenttien outputin sisältämää dataa 3.6 Matematiikka Grasshopperin apuna Grasshopperissa luotu algoritmi käyttää ohjelmakomponentteja, jotka sisältävät itsessään tietyn matemaattisen kaavan. Ohjelmakomponenteilla tehtyyn visuaaliseen skriptaukseen tarvitaan matemaattista ymmärrystä, josta tärkeimmät ovat vektorit, yksikkövektorit ja tason koordinaatiston suunnat avaruudessa, joita voidaan hyödyntää objektien mallintamisessa. Esimerkkitapauksessa luvussa 4 visuaalisessa skriptauksessa käytettiin hyväksi mm. ohjelmakomponenttien outputista saatavia yksikkövektoreita. Yksikkövektoreja kertomalla saatiin mallinnettua objekteista halutun mittaisia ja yksikkövektoreista saatiin myös tärkeitä suuntia, jota käytettiin apuna algoritmia suunniteltaessa. Yksikkövektori on sen vektorin kanssa samansuuntainen ja sen pituus on aina yksi (Kangasaho ym. 2015, 170).
18 18 Kolmiulotteisessa maailmassa taso on äärettömän iso ja sillä on kolme eri akselia, x-, y- ja z-akselit. Grasshopperissa voidaan ohjelmakomponenttien avulla tarkkaan määritellystä tasosta määrittää x-, y- ja z-akselien yksikkövektorit. Tasoja käytettiin esimerkkitapauksessa luvussa 5, sillä siitä saatiin halutut suunnat yksikkövektoreina. Edelleen näitä kertomalla saatiin halutut pituudet. Tasoja käytettiin erittäin paljon myös siksi, että niitä käytettiin viivojen ja tasojen leikkauspisteiden määrittämisessä. Koska tasot ovat äärettömän isoja avaruudessa tarkoittaa se sitä, että kolme erisuuntaista tasoa muodostaa ainoastaan yhden leikkauspisteen, kuvassa 8 vasemmalla. Jos kaksi erisuuntaista tasoa leikkaa toisensa, muodostaa tasojen leikkaus yhden viivan, kuvassa 8 keskellä. Jos viiva ja taso ovat erisuuntaiset, muodostaa niiden leikkaus yhden leikkauspisteen, kuvassa 8 oikealla. KUVA 8. Grasshopper ohjelmakomponentit ja näkymä Rhinossa
19 4 Esimerkkitapaus: Kruunuvuorensillan pylonin teräsrakenteiden parametrinen mallinnus 19 Tässä kappaleessa käydään läpi teräsrakenteisen pylonin parametrinen mallinnus Grasshopperin avulla. Mallinnettuja objekteja ja parametreja havainnollistetaan selventävien kuvien avulla. Mallinnus on rakennussuunnitteluvaiheen alkuvaihetta, sillä lopullista mitoitusta ei ole vielä tässä vaiheessa tehty. Parametrisella mallinnuksella voidaan tehdä vielä muutoksia hyvin pienellä vaivalla malliin. 4.1 Yleistä Kruunuvuorensillasta Kruunuvuorensilta (kuva 9) on osa suurta Kruunusillat-hanketta, joka yhdistää Helsingin kasvavan Laajasalon keskustaan. Laajasalon ja keskustan välille hankkeeseen sisältyy raitiotie sekä kävely- ja pyörätiet. Hankkeen yksi näkyvin osa on Kruunuvuorenrannan ja Korkeasaaren välille rakennettava Kruunuvuorensilta, joka valmistuessaan on Suomen pisin silta. Liittorakenteisen yksipylonisen vinoköysisillan kokonaispituus on noin 1,2 kilometriä, sillan pylonin korkeus on 135 metriä, pisin jänneväli on 260 metriä ja sen suunnittelukäyttöikä on 200 vuotta. Suunnittelukilpailun voitti WSP Finland Oy ja Knight Architects Ltd:n ehdotus Gemma Regalis. Helsingin kaupunginvaltuusto hyväksyi elokuussa 2016 rakentamispäätöksen Kruunusillat-hankkeesta. Rakennustöiden arvioidaan alkavan aikaisintaan vuonna 2019 ja alustava tavoite on, että vuonna 2026 yhteys avataan liikenteelle.
20 20 KUVA 9. Kruunuvuorensilta, katusuunnitelman havainnekuva (WSP Finland Oy) 4.2 Lähtötiedot Koko visuaalisen skriptauksen avulla tehdyn algoritmin lähtötietoina on käytetty ainoastaan yhtä tekstitiedostoa, joka sisältää koordinaattipisteet Kruunuvuorensillan mittalinjasta. Siitä on Grasshopperilla ohjelmakomponenttien avulla skriptattu kaikki muut tarvittavat koordinaattipisteet, viivat ja tasot, joita tarvitaan objektien mallintamiseen. Koko algoritmi lähtee rakentumaan lähtötiedoksi annetusta koordinaattitiedostosta. Tämä mahdollistaa sen, että koko algoritmi muuttuu, jos mittalinjan koordinaatit vaihtuvat projektin edetessä. Lähtötiedot voidaan siis päivittää nopeasti ja se vaikuttaa koko malliin. Visuaalisella skriptauksella on jo mallinnettu sillan teräksiset pääkannattimet ja poikkipalkit. Tämä opinnäytetyö käsittelee ainoastaan sillan pylonin teräskoteloa ja sisälle tulevia ankkurointiosien teräslevyjä. Algoritmi tehtiin Grasshopperilla kahdessa eri tiedostossa. Ensimmäisessä tiedostossa mallinnettiin teräksiset pääkannattimet, poikkipalkit ja köydet. Toisessa tiedostossa mallinnettiin pylonin teräskotelo ja köysien teräksiset ankkurointiosat. Tämä opinnäytetyö käsittelee jälkimmäistä. Jälkimmäisenä mainittuun Grasshopperilla luotuun algoritmiin saatiin lähtötiedot ensimmäisestä tiedostosta. Tietoa vaihdettiin Grasshopper tiedostojen
21 21 välillä siihen asennettavan liitännäisen avulla, joka mahdollistaa ohjelmakomponentin luomisen, jonka avulla voidaan siirtää haluttua dataa. Pylonin teräskotelon ja köysien ankkurointiosien algoritmissa lähtötietoina käytettiin pylonin köysiä, pylonin köysien muodostamaa tasoa, pylonin sijaintia ja tukilinjan T6 yksikkövektoreita (kuva 10). KUVA 10. Data Unpack -komponentin avulla tuodut lähtötiedot Jos ensimmäisenä luotuun toisen suunnittelijan tekemään algoritmiin tehdään muutoksia, ne päivittyvät myös tässä opinnäytetyössä käsiteltävässä algoritmissa, koska ne ovat linkkiketjussa keskenään. Tämä mahdollistaa sen, että esimerkiksi pylonin köysien tulokulmaa pyloniin voidaan muuttaa ensimmäisenä luodussa algoritmissa. Muutokset päivittyvät esimerkkitapauksen algoritmiin siten, että siihen riippuvuussuhteessa olevat teräsosat päivittyvät myös uuden tulokulman mukaan. Tulokulmien muutos päivittää myös Tekla-mallin reaaliaikaisesti. Ennen algoritmin luomista visuaalisella skriptauksella on kannattavaa käyttää hetki aikaa mallintamisen suunnitteluun. Kysymyksiä, joita kannattaa itselleen esittää on listattu seuraavaksi: Mitä lähtötietoja on käytettävissä? Mitä parametreja objekteille tarvitaan? Voiko toisen suunnittelijan tekemästä algoritmista saada tarvittavia tietoja? Miten objektit ovat riippuvuussuhteessa toisiinsa? Mistä objektista visuaalinen skriptaus ja mallintaminen aloitetaan?
22 Pylonin teräskotelo Teräskotelon (kuva 11) mallinnuksessa käytettiin apuna pylonin keskilinjaa. Pylonin keskilinja määriteltiin Grasshopperin avulla, jossa sille annettiin x-, y- ja z-koordinaatit. Teräskotelo on riippuvuussuhteessa pylonin keskilinjan kanssa, joka tarkoittaa sitä, että jos pylonin keskilinjan koordinaatteja muutetaan, muuttuu myös teräskotelon sijainti mallissa. Teräskotelolla on myös toinen riippuvuussuhde, joka liittyy aikaisemmin visuaalisella skriptauksella määritettyyn tukilinjaan. Tukilinjan 6 taso saatiin lähtötiedoista, jonka outputista saadaan teräskotelon sivujen suunnat. Teräskotelo on määritelty kohtisuoraan tukilinjaan nähden. Näin ollen tukilinjan tasosta saatavat yksikkövektorien y- ja x-suunnat ovat tärkeä tieto, sillä siltojen mallintamisessa y-suunta vastaa sillan poikkileikkauksen suuntaa ja x-suunta pituussuunnan tangenttia. KUVA 11. Mallinnettu teräskotelo Seuraavaksi suunniteltiin, mitä parametreja teräskotelolle annetaan. Päädyttiin ratkaisuun, jossa teräskotelo olisi lähes kokonaan muokattavissa parametrisesti. Näin ollen teräskotelon yläpinnan korko, alapinnan korko, kotelon ala- ja yläpinnan pituus sekä leveys ovat muokattavissa reaaliaikaisesti. Teräskotelon sivuille määriteltiin myös parametri-
23 23 sesti ylitulevan levyn pituus. Parametrisoimisessa täytyi myös huomioida levyjen paksuudet siten, että teräslevyt eivät leikkaa toisiaan. Visuaalinen skriptaus suoritettiin yksinkertaisesti pisteitä siirtämällä Grasshopperin avulla. 4.4 Pylonin köysien ankkurointiosat Ankkurointiosien visuaalinen skriptaus ja mallinnus aloitettiin teräksisistä ala- ja päätylevyistä (kuva 12). Teräksiset levyt ovat riippuvuussuhteessa teräskoteloon, joten teräskotelon sijainnin tai koon muuttaminen muuttaa myös levyjen kokoja ja sijaintia mallissa. Ankkurointiköysipareja on 18 molemmin puolin pylonia. Jokainen ankkurointiköysi tulee eri kulmassa teräskoteloon ja näistä on luotu tasot Grasshopperissa. Päätylevyn ehtona on, että se on kohtisuorassa köysiparien muodostamaan tasoon nähden. Alalevy on aina 90 asteen kulmassa päätylevyyn. Visuaalinen skriptaus toteutettiin Grasshopperissa siten, että köysiparien muodostamaa tasoa siirrettiin tietyn etäisyyden päähän alkuperäisestä, jolloin saatiin alalevylle muodostettua taso. Päätylevy toteutettiin niin, että komponenttien avulla luotiin viivoja ja viivojen leikkauspisteitä tasoihin, mistä se mallinnettiin. Pääty- ja alalevy parametrisoitiin niin, että alalevyn pituutta ja etäisyyttä voidaan muuttaa reaaliaikaisesti. Päätylevyn koko muuttuu samalla kun tehdään muutoksia alalevyyn ja se on aina 90 asteen kulmassa siihen nähden. Päätylevyyn parametrisoitiin myös ylituleva pituus alalevystä. KUVA 12. Ala- ja päätylevyn parametrisoinnit
24 24 Seuraavaksi mallinnettiin ankkurointiköysien päihin tulevat teräksiset ankkurointilevyt ja päätyputket (kuva 13). Molemmat ovat riippuvuussuhteessa päätylevyihin ja ankkurointiköysiin. Muutokset edellä mainittuihin objekteihin muuttaa myös ankkurointilevyjen ja päätyputkien sijaintia. Visuaalinen skriptaus toteutettiin pääosin tasoja ja tasojen leikkauksia hyväksi käyttämällä sekä pisteitä liikuttamalla. Ankkurointilevyyn parametrisoitiin leveys, korkeus ja etäisyys päätylevystä. Päätyputkeen parametrisoitiin ainoastaan pituus, sillä putken suunta on sidottu ankkurointiköysiin. KUVA 13. Ankkurointilevyn ja päätyputken parametrisoinnit Viimeisenä mallinnettiin ankkurointilevyn ja päätylevyn väliin tulevat jäykistelevyt (kuva 14). Jäykistelevyjä on neljä kappaletta jokaisessa ankkurointilevyssä ja ne sijaitsevat niiden sivujen puolivälissä. Jäykistelevyt ovat riippuvuussuhteessa päätylevyn ja ankkurointilevyn sijaintiin. Mikäli ankkurointilevyjä tai päätylevyjä siirretään, vaikuttaa se myös jäykistelevyn kokoon. Visuaalinen skriptaus toteutettiin jo aikaisemmin luotujen objektien tasoja ja suuntia apuna käyttäen. Näistä luotiin eri komponenttien avulla uusia pisteitä, josta mallinnettiin levyt. Jäykistelevyyn parametrisoitiin leveys ja pituus viisteeseen. Parametrien muutokset vaikuttavat kaikkiin jäykistelevyihin samanaikaisesti.
25 25 KUVA 14. Jäykistelevyn parametrisoinnit 4.5 Miksi parametrisoitiin? Kruunuvuorensillan pylonin teräskotelon teräsosat ovat geometrialtaan hyvin haastavia ja lähes jokainen osa on eri kulmassa tai asennossa, koska sillan kannen geometria on monimuotoinen ja jokainen köysi on eri kulmassa. Grasshopperilla hyvin luodulla algoritmilla voidaan kuitenkin mallintaa samanaikaisesti monta eri osaa kerralla. Perinteisesti Teklaan mallintamalla olisi jouduttu mallintamaan jokainen osa erikseen. Kuvassa 15 näkyy esimerkkitapauksessa mallinnettu kohde, joka suunniteltiin kokonaan Grasshopperin visuaalisen skriptauksen avulla.
26 26 KUVA 15. Esimerkkitapaus mallinnettu Grasshopperin avulla Kun mallintaminen aloitettiin, projekti oli rakennussuunnitteluvaiheen alkuvaiheessa, jolloin tarkkoja suunnitelmia ei vielä ollut. Näin ollen haluttiin luoda hyvin pitkälle parametrisoitu parametrinen malli. Mallintamista ei tehty vielä täysin loppuun asti, joten detaljitason suunnittelua mm. hitsejä ja lovia ei mallinnettu. Suunnitelmiin tehtävät muutokset ovat helppo ja nopea muuttaa Tekla-mallissa muuttamalla algoritmia tai parametreja Grasshopperissa. Parametrisoinnilla haluttiin myös vertailla erilaisia suunnitteluratkaisuja, koska esimerkiksi köysien tulokulma pyloniin nähden ei ollut tiedossa. Grasshopperilla onnistuttiin luomaan algoritmi, jolla voidaan köysien sijaintia ja kulmia muuttamalla vaikuttaa reaaliaikasesti Tekla-mallin kaikkiin pylonin teräskotelon teräosiin siten, ettei mallintamista tarvitse suorittaa uudestaan.
27 27 5 Esimerkkitapauksen analysointi Tässä kappaleessa analysoidaan ja kerrataan esimerkkitapauksessa havaittuja ongelmia ja saatuja hyötyjä. Ongelmiin pyritään löytämään ratkaisuja ja kerrotaan mitä tulisi tehdä toisin algoritmiavusteisessa suunnittelussa. Osiossa käsitellään mitä hyötyä algoritmiavusteisesta suunnittelusta on siltojen mallintamisessa ja sitä onko se kannattava tapa mallintaa siltoja tulevaisuudessa. 5.1 Visuaaliseen skriptaukseen liittyvät ongelmat Visuaalisessa skriptauksessa algoritmin luettavuus ja selkeys ovat yksi tärkeimmistä asioista, jotta siihen voidaan tehdä muutoksia vielä myöhemmin. Algoritmia on myös vaikea lukea, jos se ei ole selkeä ja toisen tekemää algoritmia voi olla vaikea tulkita. Esimerkkitapauksessa havaittiin ongelma, jossa lähes koko algoritmi jouduttiin tekemään Grasshopperilla uudestaan, koska koodista ei pystynyt lukemaan yksiselitteisesti mitä siinä tapahtuu. Tämän lisäksi algoritmin muutoskyky heikkenee, jos se on vaikeasti ymmärrettävä, eikä muutoksen aiheuttamasta vaikutuksesta ole varmuutta. Ensimmäinen algoritmi oli visuaalisesti sekava ja siinä oli paljon ylimääräisiä komponentteja, joita ei tarvittu mallin luomiseen. Myös komponenttien välisiä lankoja oli liian paljon, jolloin algoritmista tuli vaikeasti hahmotettava. Turhien ohjelmakomponenttien käyttämistä tulisi välttää ja ne pitäisi poistaa algoritmista heti, jos niitä ei tarvita. Selkeyden kannalta myös datavirta on pidettävä vasemmalta oikealle. Jos algoritmin loppuvaiheessa tarvitaan alkuvaiheessa luodun komponentin dataa, tulisi se siirtää data komponentin avulla. Näin saadaan algoritmia luotua selkeämmäksi ja vältytään turhan pitkiltä langoilta. Kuvassa 16 on ylempänä kuvakaappaus ensimmäisenä luodusta epäselkeästä algoritmista ja alempana selkeämpi toinen versio.
28 28 KUVA 16. Epäselkeä ja selkeämpi algoritmi Grasshopperissa Visuaalisessa skriptauksessa havaittiin myös, että algoritmia luodessa voi unohtua missä on tarvittava data, jos skriptauksesta on kulunut aikaa. Mikäli algoritmi on jonkun toisen suunnittelijan luoma niin se aiheuttaa vielä enemmän ongelmia. Visuaalisessa skriptauksessa päädyttiin ratkaisuun, jossa Grasshopperin algoritmiin sijoitettiin havainnollistavaa tekstiä, joten algoritmia on helpompi lukea jälkeenpäin pitkänkin ajan jälkeen. Esimerkkitapauksen yhteydessä huomattiin, että Grasshopper ei tue ns. multi-user tilaa. Se ei myöskään ilmoita Grasshopper-tiedostoa avattaessa, jos se on toisella käyttäjällä auki samanaikaisesti. Tämä aiheuttaa sen, että samassa Grasshopper-tiedostossa on lähes mahdoton työskennellä samanaikaisesti, jos algoritmiin tehdään muutoksia. Kuten esimerkkitapauksessa mainittiin, Grasshopper-tiedostot voidaan yhdistää keskenään siten, että dataa voidaan vaihtaa algoritmien välillä. Kun Grasshopper-tiedostot linkitetään keskenään, täytyy muistaa, että jos muutoksia tehdään, niin kaikki algoritmit täytyy laskea uudestaan ennen kuin ne päivittyvät Tekla-malliin. Tämä aiheutuu siitä, että
29 29 algoritmit ovat riippuvuussuhteissa toisistaan. Esimerkkinä tilanteesta on köysien tulokulmat esimerkkitapauksessa. Jos niitä muutetaan toisen suunnittelijan tekemässä algoritmissa, täytyy myös esimerkkitapauksen algoritmi laskea uudestaan ennen kuin Teklamalli päivittyy täysin uusien geometrioiden mukaan. Mitä enemmän algoritmeja on yhdistelty toisiinsa, sitä suurempi riski on sille, että Tekla-malli ei ole päivittyneenä. 5.2 Ohjelmien yhteensopivuudesta aiheutuvat ongelmat Kuten aiemmin kerrottiin, Grasshopper-Tekla live link -lisäosa on vielä beta-vaiheessa tätä kirjoittaessa eikä se ole täysin vakaa. Lisäosa mahdollistaa linkin Grasshopperista Teklaan ja jos tämä yhteys katoaa, muutokset algoritmiin eivät enään muokkaa Teklamallia. Jotta linkki toimii oikein, ohjelmat täytyy avata tietyssä järjestyksessä. Ensimmäisenä Tekla Structures, sen jälkeen Rhino ja sitten sen lisäosa Grasshopper. Yhteyden katoamisen jälkeen Grasshopperilla luodut objektit tulee poistaa Teklasta ja suorittaa Grasshopperin algoritmi uudelleen, jolloin Tekla-malliin rakentuu algoritmin luomat objektit uudestaan. Tällöin ohjelmien välinen linkki saadaan jälleen toimimaan. Grasshopperilla mallinnetuille objekteille on kannattavaa käyttää samaa phasea, jolloin voidaan helposti poistaa Tekla-mallista ainoastaan Grasshopperilla mallinnetut objektit. Grasshopperilla mallinnettaessa havaittiin myös, että kun visuaalisella skriptauksella tehdään Tekla komponentin avulla objekti Teklaan, ei objekti poistu Teklasta, jos poistaa Grasshopperista Tekla komponentin. Tällöin Tekla-malliin voi jäädä huolimattomasti objektejä, jota ei sinne haluta. Ratkaisu siihen on oikea työjärjestys. Ensin valitaan Grasshopperissa halutut Tekla komponentit aktiiviksiksi, jolloin objektit aktivoituvat automaattisesti myös Teklassa, jos ohjelmien välinen yhteys toimii. Sen jälkeen objektit poistetaan ensin Teklasta ja vasta sen jälkeen Tekla komponentit Grasshopperista. Visuaalisella skriptauksella mallinnettaessa havaittiin myös ongelma, jolloin Tekla-malliin Tekla komponenttien avulla luodut objektit katosivat näkyvistä tai objektin sijoittuivat väärään paikkaan. Tämä johtui siitä, että Teklassa ei ollut käytössä globaalikoordinaatiston työtaso vaan itse määritelty työtaso, joten Grasshopperilla mallinnetut objektit mallintuivat työtason koordinaatiston mukaan. Mallinnettaessa Grasshopperilla objekteja Teklaan on työtason oltava Teklassa origossa.
30 30 Ensimmäisenä luodussa algoritmissa tapahtui ongelma, joka aiheutti tupla geometrian Tekla-malliin eli mallissa oli täsmälleen samankokoisia päällekkäisiä objekteja. Tupla geometriaa on äärimmäisen hankala huomata visuaalisen tarkastuksen yhteydessä ja ongelman aiheuttajaa ei yksiselitteisesti löydetty. Kyseisestä ongelmasta on raportoitu myös Grasshopperin keskustelufoorumilla, mutta kyseessä on todennäköisesti käyttäjän huolimattomuudesta aiheutuva ongelma. Tupla geometrian kanssa tulisi olla tarkkana ja Grasshopperin algoritmia suunniteltaessa tulisi välttää Tekla komponenttien kopioimista. Jos koko algoritmi tai algoritmin osa kopioidaan, jossa sijaitsee Tekla komponentti, Tekla-malliin mallintuu tupla geometria. Tutkimuksessa havaittiin, että algoritmilla mallinnetut objektit ajautuvat Teklassa tehtyjen muutoksien ohi. Esimerkkinä tilanne, jossa halutaan siirtää teräslevyä Teklassa. Tehdään muutos Teklan puolella Grasshopperiin linkitettyyn objektiin. Teräslevy siirtyy Tekla-mallissa, mutta jos algoritmi käynnistetään tai lasketaan uudestaan, objekti siirtyy takaisin algoritmin määrittelemän geometrian mukaan. Mikäli objekteja halutaan siirtää Teklassa perinteisellä tavalla, täytyy algoritmin ja Teklan välinen linkki purkaa, jotta muutokset säilyvät. 5.3 Sillan geometrian aiheuttamat haasteet Kruunuvuorensilta on geometrisesti erittäin haastava mallinnettava kohde (kuva 17). Se on kaareva sekä pysty- että vaakageometrialtaan. Tämä aiheuttaa sen, että esimerkkitapauksessa mallinnettuun teräskoteloon tulevat teräsosat ovat kaikki sijoittuneet eri tavoin toisiinsa nähden, koska kaikki 72 pyloniin tulevaa köyttä ovat eri kulmissa. Grasshopperilla tehdyssä algoritmissa pystyttiin kuitenkin mallintamaan monta eri levyä samanaikaisesti, vaikka ne ovatkin eri kulmissa.
31 31 KUVA 17. Kruunuvuorensillan kannen vaakageometria Kun dataa virtaa ohjelmakomponenttien välillä paljon, voi suunnittelijan olla vaikea lukea sitä. Grasshopperissa listojen käytöllä onnistuttiin kuitenkin muokkaamaan datavirtaa siten, että ne ovat suunnittelijan haluamassa loogisessa järjestyksessä. Yhden langan sisältämä suuri datamäärä on sekä mahdollisuus mallintaa samanaikaisesti, että haaste algoritmin tekemisessä. 5.4 Visuaalisen skriptauksen haasteet Grasshopperissa Visuaalisessa skriptauksessa alkuun pääseminen on huomattavasti helpompaa kuin perinteisesti käsin koodaamalla. Suunnittelijan ei tarvitse laskea itse lähes mitään, sillä Grasshopperin ohjelmakomponentit suorittavat laskutoimitukset. Suunnittelijan haasteena onkin luoda algoritmi ohjelmakomponenteista siten, että loppujen lopuksi päästään haluttuun lopputulokseen eli Tekla objektiin. Aloittelevan käyttäjän voi olla vaikeaa käyttää ja yhdistellä ohjelmakomponentteja, jos ei tiedä mitä tietoa komponentti laskee ja mitä dataa siitä saada ulos.
32 Parametrisen mallintamisen ja visuaalisen skriptauksen hyödyt Kuten aikaisemmin kerrottiin, parametriseen mallintamiseen päädyttiin esimerkkitapauksessa siksi, että teräskotelon teräsosia ei oltu vielä lopullisesti mitoitettu. Mallintamisella pystytään myös vertailemaan erilaisia vaihtoehtoja vielä rakennussuunnitteluvaiheessa tekemättä Tekla-mallia alusta asti uudestaan. Parametrisointi ja Tekla-malli pystyttiin toteuttamaan visuaalisen skriptaukseen tarkoitetulla Grasshopperilla. Parametrisoinnilla ja visuaalisella skriptauksella saadaan paljon hyötyjä, jotka on listattu seuraavaksi: - Tekla-malli on muokattavissa reaaliaikaisesti algoritmin parametrien avulla. - Algoritmiavusteinen suunnittelu mahdollistaa lähtötietojen muuttamisen nopeasti, siten että se vaikuttaa koko sillan geometriaan, esim. tasausviivan muutos. - Joissain tapauksissa visuaalisella skriptauksella tehty mallintaminen voi olla nopeampaa kuin suoraan Teklaan mallintaminen. - Erilaisia suunnitteluratkaisuja voidaan verrata keskenään nopeasti. - Hyvin tehdyllä algoritmilla voidaan mallintaa Teklaan samanaikaisesti keskenään erilaisia objekteja. - Sillan geometria on määritelty Rhinoon Grasshopperin algoritmilla. - Algoritmin avulla mallinnettuja objekteja voidaan siirtää eri Tekla versioiden välillä vaivattomasti. - Geometria voidaan siirtää suoraan laskentaohjelmaan Grasshopperista. - Visuaalisessa skriptauksessa ei tarvitse osata koodata. Visuaalisella skriptauksella voidaan luoda hyvinkin haastavaa geometriaa Grasshopperin monipuolisten ohjelmakomponenttien avulla. Grasshopperin käytöllä vältytään vaikeilta laskuilta ja koordinaattien laskemiselta, koska ohjelmakomponentit sisältävät mitä monimutkaisempia laskukaavoja. Mallintaminen voidaan suorittaa myös ilman objektien parametrisoimista ja käyttää hyväksi mallintamisessa ohjelmakomponentteja geometrian luomisessa.
33 33 6 POHDINTA Suurin haaste Grasshopperista Teklaan mallintamisessa on tiedon rajallinen levinneisyys. Aiheesta on tehty suhteellisen vähän tutkimuksia, aihetta ei opeteta koululaitoksissa ja suoranaisia ohjeita Grasshopperin ja Teklan yhteiskäyttöön ei ole kovinkaan paljon. Ohjelmien välisen yhteyden mahdollistava linkki on ollut käytössä tätä kirjoittaessa vasta vuoden ja käyttäjäpiirit ovat pienet. Aiheesta tulisi tehdä enemmän tutkimuksia, jotta tieto saataisiin liikkumaan rakennesuunnittelijoiden keskuudessa. Näin ollen tutkimustavan valitseminen tapaustutkimukseksi oli erinomainen valinta. Opinnäytetyössä saatiin tehtyä onnistuneesti parametrinen Tekla-malli Grasshopperin algoritmin avulla sillan pylonin teräskotelosta ja sen teräsosista. Ensimmäinen algoritmi saatiin tehtyä onnistuneesti, mutta koodin epäselkeyden vuoksi sitä voidaan pitää epäonnistuneena. Algoritmi tehtiin alusta alkaen uudestaan ja opittujen virheiden myötä se saatiin kohtalaisen selkeäksi. Tekla-malli saatiin parametrisoitua lähes kokonaan ja on vielä helposti muokattavissa jälkikäteen, jos siihen tapahtuu muutoksia. Visuaalisessa skriptauksessa saatiin tärkeitä havaintoja ohjelmien välisestä toimivuudesta ja käytöstä. Grasshopperin ja Teklan yhteiskäytössä on paljon huomioitavia asioita, joista tärkeimmät ovat käyttäjän huolellisuus ohjelmia käyttäessä, algoritmin datavirran hallinta, algoritmin selkeys, yhdistettyjen Grasshopper algoritmien hyvä dokumentointi ja ohjelmien yhteistoiminnan tunteminen. Tärkeimpänä hyötynä saavutetaan Tekla-mallin reaaliaikainen geometrian muokkaus ja lähtötietoihin tuleviin muutoksiin nopea reagointiaika. Tätä insinöörityötä voidaan pitää onnistuneena, sillä esimerkkitapauksen kohde mallinnettiin onnistuneesti ja Grasshopperin käyttöä saatiin edistettyä. Työn tekijä tutustui paljon Grasshopperin käyttöön ja aikaisempaa kokemusta ohjelmasta ei ollut. Tästä saatiin tärkeää tietoa tulevaisuutta ajatellen siirryttäessä parametriseen mallintamiseen. Jatkotutkimuksen aiheena olisi hyvä selvittää mallintamista detaljitasolla Grasshopperilla.
34 34 LÄHTEET Davidson, S Grasshopper www-sivu. Luettu Davis, D A History of Parametric. Luettu Kangasaho, J., Mäkinen, J., Oikkonen, J., Paasonen, J., Salmela, M. & Tahvanainen, J Pitkä matematiikka 14. Kertaus. 2. painos. Helsinki: WSOY Oppimateriaalit Oy. Moonsoft Oy Tuotteet. Robert McNeel & Associates. Luettu Tanska, T. & Österlund, T Algoritmit puurakenteissa. Menetelmät, mahdollisuudet ja tuotanto. 1. painos. Oulun yliopisto, Arkkitehtuurin tiedekunta, DigiWoodLab. The Morpheus Hotel: From Design to Production: Live Webinar Video. Rhino Tutorials. Katsottu Trimble Solutions Corporation Grasshopper-Tekla Live Link. Luettu Trimble Solutions Corporation. Ratkaisut. Rakennesuunnittelijat. Luettu Trimble Solutions Corporation. Tuotteet. Tekla Structures. Luettu
Vektoreita GeoGebrassa.
 Vektoreita GeoGebrassa 1 Miten GeoGebralla piirretään vektoreita? Työvälineet ja syöttökentän komennot Vektoreiden esittäminen GeoGebrassa on luontevaa: vektorien piirtämiseen on kaksi työvälinettä vektoreita
Vektoreita GeoGebrassa 1 Miten GeoGebralla piirretään vektoreita? Työvälineet ja syöttökentän komennot Vektoreiden esittäminen GeoGebrassa on luontevaa: vektorien piirtämiseen on kaksi työvälinettä vektoreita
Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO
 Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Puutekniikan koulutusohjelma Toukokuu 2009 TIIVISTELMÄ OPINNÄYTETYÖSTÄ Yksikkö Aika Ylivieska
Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Puutekniikan koulutusohjelma Toukokuu 2009 TIIVISTELMÄ OPINNÄYTETYÖSTÄ Yksikkö Aika Ylivieska
Julkaisun laji Opinnäytetyö. Sivumäärä 43
 OPINNÄYTETYÖN KUVAILULEHTI Tekijä(t) SUKUNIMI, Etunimi ISOVIITA, Ilari LEHTONEN, Joni PELTOKANGAS, Johanna Työn nimi Julkaisun laji Opinnäytetyö Sivumäärä 43 Luottamuksellisuus ( ) saakka Päivämäärä 12.08.2010
OPINNÄYTETYÖN KUVAILULEHTI Tekijä(t) SUKUNIMI, Etunimi ISOVIITA, Ilari LEHTONEN, Joni PELTOKANGAS, Johanna Työn nimi Julkaisun laji Opinnäytetyö Sivumäärä 43 Luottamuksellisuus ( ) saakka Päivämäärä 12.08.2010
Vektorien pistetulo on aina reaaliluku. Esimerkiksi vektorien v = (3, 2, 0) ja w = (1, 2, 3) pistetulo on
 13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
Built Environment Process Reengineering (PRE)
 RAKENNETTU YMPÄRISTÖ Tarvitaanko tätä palkkia? Built Environment Process Reengineering (PRE) InfraFINBIM PILOTTIPÄIVÄ nro 4, 9.5.2012 Tuotemallinnuksen käyttöönotto Built Environment Process Innovations
RAKENNETTU YMPÄRISTÖ Tarvitaanko tätä palkkia? Built Environment Process Reengineering (PRE) InfraFINBIM PILOTTIPÄIVÄ nro 4, 9.5.2012 Tuotemallinnuksen käyttöönotto Built Environment Process Innovations
S09 04 Kohteiden tunnistaminen 3D datasta
 AS 0.3200 Automaatio ja systeemitekniikan projektityöt S09 04 Kohteiden tunnistaminen 3D datasta Loppuraportti 22.5.2009 Akseli Korhonen 1. Projektin esittely Projektin tavoitteena oli algoritmin kehittäminen
AS 0.3200 Automaatio ja systeemitekniikan projektityöt S09 04 Kohteiden tunnistaminen 3D datasta Loppuraportti 22.5.2009 Akseli Korhonen 1. Projektin esittely Projektin tavoitteena oli algoritmin kehittäminen
AUTOCAD-TULOSTUSOHJE. Tällä ohjeella selitetään Autocadin mittakaavatulostuksen perusasiat (mallin mittayksikkönä millimetrit)
 AUTOCAD-TULOSTUSOHJE Tällä ohjeella selitetään Autocadin mittakaavatulostuksen perusasiat (mallin mittayksikkönä millimetrit) 1. MODEL VS. LAYOUT Autocadista löytyy vasemmasta alakulmasta automaattisesti
AUTOCAD-TULOSTUSOHJE Tällä ohjeella selitetään Autocadin mittakaavatulostuksen perusasiat (mallin mittayksikkönä millimetrit) 1. MODEL VS. LAYOUT Autocadista löytyy vasemmasta alakulmasta automaattisesti
Tekla BIM Awards Suomi ja Baltia 2019 kysymykset
 Yhteystiedot E-mail Etunimi Sukunimi Puhelinnumero Yritys Kilpailuun osallistuvat muut yritykset Projektin tiedot Projektin nimi Valitse sarja - Yleinen sarja - Pienet projektit: Katso tarkempi rajaus
Yhteystiedot E-mail Etunimi Sukunimi Puhelinnumero Yritys Kilpailuun osallistuvat muut yritykset Projektin tiedot Projektin nimi Valitse sarja - Yleinen sarja - Pienet projektit: Katso tarkempi rajaus
Skanska Ruskeasuo Larkas & Laine
 Skanska Ruskeasuo Larkas & Laine Rakennussuunnittelu on muuttunut piirtämisestä rakennusten simuloinniksi. Pelkkä paperikopio ei enää riitä, vaan tilaaja haluaa rakennuksesta usein tietomallin, joka sisältää
Skanska Ruskeasuo Larkas & Laine Rakennussuunnittelu on muuttunut piirtämisestä rakennusten simuloinniksi. Pelkkä paperikopio ei enää riitä, vaan tilaaja haluaa rakennuksesta usein tietomallin, joka sisältää
1. Käytettiinkö projektissa yrityksen omia komponentteja (custom componentit, pluginit, makrot)? a. Kyllä b. Ei Minkä tyyppisiä komponentteja
 1. Yhteystiedot Yritys / Yritykset Tietoja projektin ilmoittajista Kilpailuun osallistuvat yritykset ja niiden tehtävät hankkeessa Ilmoituksen jättäjän yhteystiedot Etunimi Sukunimi Sähköpostiosoite Puhelin
1. Yhteystiedot Yritys / Yritykset Tietoja projektin ilmoittajista Kilpailuun osallistuvat yritykset ja niiden tehtävät hankkeessa Ilmoituksen jättäjän yhteystiedot Etunimi Sukunimi Sähköpostiosoite Puhelin
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla
 Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
AutoCAD blokit. RI Rami Ylä-Pöntinen
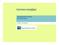 Vakiopaaluperustukset AutoCAD blokit RI Rami Ylä-Pöntinen Dynaaminen blokki = Älykäs blokki Dynaamiset blokit tuovat nopeutta ja tarkkuutta suunnitteluprosessiin Dynaamisia i blokkeja käyttämällä ällä
Vakiopaaluperustukset AutoCAD blokit RI Rami Ylä-Pöntinen Dynaaminen blokki = Älykäs blokki Dynaamiset blokit tuovat nopeutta ja tarkkuutta suunnitteluprosessiin Dynaamisia i blokkeja käyttämällä ällä
GIS-automatisointi ja ohjelmointi/skriptaus. Harri Antikainen
 GIS-automatisointi ja ohjelmointi/skriptaus Harri Antikainen Mistä nyt puhutaan? Automatisointi: Mikä tahansa tapa teettää tietokoneella asioita ilman että käyttäjän tarvitsee tehdä muuta kuin laittaa
GIS-automatisointi ja ohjelmointi/skriptaus Harri Antikainen Mistä nyt puhutaan? Automatisointi: Mikä tahansa tapa teettää tietokoneella asioita ilman että käyttäjän tarvitsee tehdä muuta kuin laittaa
Yleistä vektoreista GeoGebralla
 Vektoreita GeoGebralla Vektoreilla voi laskea joko komentopohjaisesti esim. CAS-ikkunassa tai piirtämällä piirtoikkunassa. Ensimmäisen tavan etuna on, että laskujen tueksi muodostuu kuva. Tästä on varmasti
Vektoreita GeoGebralla Vektoreilla voi laskea joko komentopohjaisesti esim. CAS-ikkunassa tai piirtämällä piirtoikkunassa. Ensimmäisen tavan etuna on, että laskujen tueksi muodostuu kuva. Tästä on varmasti
HB-Harkko-kirjasto asennetaan oletusarvoisesti ArchiCADin kirjastohakemiston alle (C:\Program Files\Graphisoft\ArchiCAD 13\Kirjasto 13).
 HB-HARKKO KÄYTTÖOHJE Lyhyesti Kirjasto sisältää kevytsora- ja eristeharkko-objektin lisäksi laajennuksen, jonka avulla suunnittelija voi tehdä kokonaisen rakennuksen mallin harkoista automaattisesti detaljisuunnittelua
HB-HARKKO KÄYTTÖOHJE Lyhyesti Kirjasto sisältää kevytsora- ja eristeharkko-objektin lisäksi laajennuksen, jonka avulla suunnittelija voi tehdä kokonaisen rakennuksen mallin harkoista automaattisesti detaljisuunnittelua
Oppimateriaali oppilaalle ja opettajalle : GeoGebra oppilaan työkaluna ylioppilaskirjoituksissa 2016 versio 0.8
 Oppimateriaali oppilaalle ja opettajalle : GeoGebra oppilaan työkaluna ylioppilaskirjoituksissa 2016 versio 0.8 Piirtoalue ja algebraikkuna Piirtoalueelle piirretään työvälinepalkista löytyvillä työvälineillä
Oppimateriaali oppilaalle ja opettajalle : GeoGebra oppilaan työkaluna ylioppilaskirjoituksissa 2016 versio 0.8 Piirtoalue ja algebraikkuna Piirtoalueelle piirretään työvälinepalkista löytyvillä työvälineillä
GeoGebra-harjoituksia malu-opettajille
 GeoGebra-harjoituksia malu-opettajille 1. Ohjelman kielen vaihtaminen Mikäli ohjelma ei syystä tai toisesta avaudu toivomallasi kielellä, voit vaihtaa ohjelman käyttöliittymän kielen seuraavasti: 2. Fonttikoon
GeoGebra-harjoituksia malu-opettajille 1. Ohjelman kielen vaihtaminen Mikäli ohjelma ei syystä tai toisesta avaudu toivomallasi kielellä, voit vaihtaa ohjelman käyttöliittymän kielen seuraavasti: 2. Fonttikoon
Pintamallintaminen ja maastomallinnus
 1 / 25 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Pintamallintaminen ja maastomallinnus Muistilista uuden ohjelman opetteluun 2 / 25 1. Aloita käyttöliittymään tutustumisesta: Mitä hiiren näppäintä
1 / 25 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Pintamallintaminen ja maastomallinnus Muistilista uuden ohjelman opetteluun 2 / 25 1. Aloita käyttöliittymään tutustumisesta: Mitä hiiren näppäintä
Matopeli C#:lla. Aram Abdulla Hassan. Ammattiopisto Tavastia. Opinnäytetyö
 Matopeli C#:lla Aram Abdulla Hassan Ammattiopisto Tavastia Opinnäytetyö Syksy 2014 1 Sisällysluettelo 1. Johdanto... 3 2. Projektin aihe: Matopeli C#:lla... 3 3. Projektissa käytetyt menetelmät ja työkalut
Matopeli C#:lla Aram Abdulla Hassan Ammattiopisto Tavastia Opinnäytetyö Syksy 2014 1 Sisällysluettelo 1. Johdanto... 3 2. Projektin aihe: Matopeli C#:lla... 3 3. Projektissa käytetyt menetelmät ja työkalut
TUULIKKI TANSKA ALGORITMIT PUURAKENTAMISESSA
 TUULIKKI TANSKA ALGORITMIT PUURAKENTAMISESSA Tarkoituksena kehittää ja tutkia puurakenteita ja puurakentamista julkisen rakennuksen mittakaavassa käyttäen algoritmisia suunnittelumenetelmiä, sekä tietokoneavusteisia
TUULIKKI TANSKA ALGORITMIT PUURAKENTAMISESSA Tarkoituksena kehittää ja tutkia puurakenteita ja puurakentamista julkisen rakennuksen mittakaavassa käyttäen algoritmisia suunnittelumenetelmiä, sekä tietokoneavusteisia
Loppuraportti. Virtuaali-Frami, CAVE-ohjelmisto. Harri Mähönen projektiassistentti Seinäjoen ammattikorkeakoulu. Versio
 1 Loppuraportti Virtuaali-Frami, CAVE-ohjelmisto Harri Mähönen projektiassistentti Seinäjoen ammattikorkeakoulu Versio 1.0 15.1.2006 2 Sisällys Tiivistelmä... 3 1 Johdanto... 4 1.1 Dokumentin tarkoitus...
1 Loppuraportti Virtuaali-Frami, CAVE-ohjelmisto Harri Mähönen projektiassistentti Seinäjoen ammattikorkeakoulu Versio 1.0 15.1.2006 2 Sisällys Tiivistelmä... 3 1 Johdanto... 4 1.1 Dokumentin tarkoitus...
7 tapaa mallintaa maasto korkeuskäyristä ja metodien yhdistäminen
 1 / 11 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto 7 tapaa mallintaa maasto korkeuskäyristä ja metodien yhdistäminen Kertauslista yleisimmistä komennoista 2 / 11 Kuvan tuominen: PictureFrame Siirtäminen:
1 / 11 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto 7 tapaa mallintaa maasto korkeuskäyristä ja metodien yhdistäminen Kertauslista yleisimmistä komennoista 2 / 11 Kuvan tuominen: PictureFrame Siirtäminen:
Solmu 3/2001 Solmu 3/2001. Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä:
 Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Frégier n lause Simo K. Kivelä Kevään 2001 ylioppilaskirjoitusten pitkän matematiikan kokeessa oli seuraava tehtävä: Suorakulmaisen kolmion kaikki kärjet sijaitsevat paraabelilla y = x 2 ; suoran kulman
Sonera Viestintäpalvelu VIP VIP Laajennettu raportointi Ohje
 Sonera Viestintäpalvelu VIP VIP Laajennettu raportointi Ohje Sisällysluettelo VIP Laajennettu raportointi... 3 Luo raportti Laajennetun raportoinnin työkaluilla... 4 Avaa Laajennettu raportointi... 4 Valitse
Sonera Viestintäpalvelu VIP VIP Laajennettu raportointi Ohje Sisällysluettelo VIP Laajennettu raportointi... 3 Luo raportti Laajennetun raportoinnin työkaluilla... 4 Avaa Laajennettu raportointi... 4 Valitse
Maastotietokannan torrent-jakelun shapefile-tiedostojen purkaminen zip-arkistoista Windows-komentojonoilla
 Maastotietokannan torrent-jakelun shapefile-tiedostojen purkaminen zip-arkistoista Windows-komentojonoilla Viimeksi muokattu 5. toukokuuta 2012 Maastotietokannan torrent-jakeluun sisältyy yli 5000 zip-arkistoa,
Maastotietokannan torrent-jakelun shapefile-tiedostojen purkaminen zip-arkistoista Windows-komentojonoilla Viimeksi muokattu 5. toukokuuta 2012 Maastotietokannan torrent-jakeluun sisältyy yli 5000 zip-arkistoa,
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Perusteet 5, pintamallinnus
 Perusteet 5, pintamallinnus Juho Taipale, Tuula Höök Tampereen teknillinen yliopisto Ota piirustus fin_basic_4.pdf (Sama piirustus kuin harjoituksessa basic_4). Käytä piirustuksessa annettuja mittoja ja
Perusteet 5, pintamallinnus Juho Taipale, Tuula Höök Tampereen teknillinen yliopisto Ota piirustus fin_basic_4.pdf (Sama piirustus kuin harjoituksessa basic_4). Käytä piirustuksessa annettuja mittoja ja
Käyttöohje. Energent MagiCAD plugin
 Käyttöohje Energent MagiCAD plugin Sisältö 1. Yleistä 1 Dokumentin sisältö... 1 Ohjelman asennus... 1 Vaadittavat ohjelmistot... 1 Asennus... 1 Ohjelman käynnistys... 2 2. Toiminnallisuudet 3 Insert Energent
Käyttöohje Energent MagiCAD plugin Sisältö 1. Yleistä 1 Dokumentin sisältö... 1 Ohjelman asennus... 1 Vaadittavat ohjelmistot... 1 Asennus... 1 Ohjelman käynnistys... 2 2. Toiminnallisuudet 3 Insert Energent
Tekijä Pitkä matematiikka
 K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
K1 Tekijä Pitkä matematiikka 5 7..017 a) 1 1 + 1 = 4 + 1 = 3 = 3 4 4 4 4 4 4 b) 1 1 1 = 4 6 3 = 5 = 5 3 4 1 1 1 1 1 K a) Koska 3 = 9 < 10, niin 3 10 < 0. 3 10 = (3 10 ) = 10 3 b) Koska π 3,14, niin π
Condes. Quick Start opas. Suunnistuksen ratamestariohjelmisto. Versio 7. Quick Start - opas Condes 7. olfellows www.olfellows.net 1.
 Condes Suunnistuksen ratamestariohjelmisto Versio 7 Quick Start opas Yhteystiedot: olfellows Jouni Laaksonen Poijukuja 4 21120 RAISIO jouni.laaksonen@olfellows.net www.olfellows.net olfellows www.olfellows.net
Condes Suunnistuksen ratamestariohjelmisto Versio 7 Quick Start opas Yhteystiedot: olfellows Jouni Laaksonen Poijukuja 4 21120 RAISIO jouni.laaksonen@olfellows.net www.olfellows.net olfellows www.olfellows.net
S11-04 Kompaktikamerat stereokamerajärjestelmässä. Projektisuunnitelma
 AS-0.3200 Automaatio- ja systeemitekniikan projektityöt S11-04 Kompaktikamerat stereokamerajärjestelmässä Projektisuunnitelma Ari-Matti Reinsalo Anssi Niemi 28.1.2011 Projektityön tavoite Projektityössä
AS-0.3200 Automaatio- ja systeemitekniikan projektityöt S11-04 Kompaktikamerat stereokamerajärjestelmässä Projektisuunnitelma Ari-Matti Reinsalo Anssi Niemi 28.1.2011 Projektityön tavoite Projektityössä
Työvälineistä komentoihin
 Työvälineistä komentoihin Miten GeoGebralla piirretään funktioita? Kohtasitko ongelmia GeoGebran käytössä? Millaisia? Kohtaisitko tilanteita, joissa jonkin funktion piirtäminen GeoGebralla ei onnistunutkaan?
Työvälineistä komentoihin Miten GeoGebralla piirretään funktioita? Kohtasitko ongelmia GeoGebran käytössä? Millaisia? Kohtaisitko tilanteita, joissa jonkin funktion piirtäminen GeoGebralla ei onnistunutkaan?
AutoCAD-natiiviobjektin toteutus
 AutoCAD-natiiviobjektin toteutus Kontiotuote OY Maailman toiseksi suurin hirsitalotoimittaja Aloittanut toimintansa 70-luvulla Liikevaihto vuonna 2003-37,355 Milj. euroa josta vientiä 7,376 Milj. euroa
AutoCAD-natiiviobjektin toteutus Kontiotuote OY Maailman toiseksi suurin hirsitalotoimittaja Aloittanut toimintansa 70-luvulla Liikevaihto vuonna 2003-37,355 Milj. euroa josta vientiä 7,376 Milj. euroa
A-Tiilikate objektikirjasto
 A-Tiilikate objektikirjasto 15.1.2014 A-Tiilikate-objektikirjasto toimii ArchiCAD 14, 15, 16 ja 17 -versioissa. Kirjaston käyttöön tarvitaan Graphisoftin Tarvikkeet-laajennus. Tarvikkeet-laajennuksen käyttöönotto
A-Tiilikate objektikirjasto 15.1.2014 A-Tiilikate-objektikirjasto toimii ArchiCAD 14, 15, 16 ja 17 -versioissa. Kirjaston käyttöön tarvitaan Graphisoftin Tarvikkeet-laajennus. Tarvikkeet-laajennuksen käyttöönotto
Taso 1/5 Sisältö ESITIEDOT: vektori, koordinaatistot, piste, suora
 Taso 1/5 Sisältö Taso geometrisena peruskäsitteenä Kolmiulotteisen alkeisgeometrian peruskäsitteisiin kuuluu taso pisteen ja suoran lisäksi. Intuitiivisesti sitä voidaan ajatella joka suunnassa äärettömyyteen
Taso 1/5 Sisältö Taso geometrisena peruskäsitteenä Kolmiulotteisen alkeisgeometrian peruskäsitteisiin kuuluu taso pisteen ja suoran lisäksi. Intuitiivisesti sitä voidaan ajatella joka suunnassa äärettömyyteen
Suorat ja tasot, L6. Suuntajana. Suora xy-tasossa. Suora xyzkoordinaatistossa. Taso xyzkoordinaatistossa. Tason koordinaattimuotoinen yhtälö.
 Suorat ja tasot, L6 Suora xyz-koordinaatistossa Taso xyz-koordinaatistossa stä stä 1 Näillä kalvoilla käsittelemme kolmen laisia olioita. Suora xyz-avaruudessa. Taso xyz-avaruudessa. Emme nyt ryhdy pohtimaan,
Suorat ja tasot, L6 Suora xyz-koordinaatistossa Taso xyz-koordinaatistossa stä stä 1 Näillä kalvoilla käsittelemme kolmen laisia olioita. Suora xyz-avaruudessa. Taso xyz-avaruudessa. Emme nyt ryhdy pohtimaan,
KUVANKÄSITTELY THE GIMP FOR WINDOWS OHJELMASSA
 KUVANKÄSITTELY THE GIMP FOR WINDOWS OHJELMASSA Ohjeistuksessa käydään läpi kuvan koon ja kuvan kankaan koon muuntaminen esimerkin avulla. Ohjeistus on laadittu auttamaan kuvien muokkaamista kuvakommunikaatiota
KUVANKÄSITTELY THE GIMP FOR WINDOWS OHJELMASSA Ohjeistuksessa käydään läpi kuvan koon ja kuvan kankaan koon muuntaminen esimerkin avulla. Ohjeistus on laadittu auttamaan kuvien muokkaamista kuvakommunikaatiota
Tekijä Pitkä matematiikka b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta.
 Tekijä Pitkä matematiikka 4 9.1.016 79 a) Kuvasta nähdään, että a = 3i + j. b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta. 5a b = 5(3i + j) ( i 4 j)
Tekijä Pitkä matematiikka 4 9.1.016 79 a) Kuvasta nähdään, että a = 3i + j. b) Kuvasta nähdään, että b = i 4 j. c) Käytetään a- ja b-kohtien tuloksia ja muokataan lauseketta. 5a b = 5(3i + j) ( i 4 j)
Harjoitus Bones ja Skin
 LIITE 3 1(6) Harjoitus Bones ja Skin Harjoituksessa käsiteltävät asiat: Yksinkertaisen jalan luominen sylinteristä Luurangon luominen ja sen tekeminen toimivaksi raajaksi Luurangon yhdistäminen jalka-objektiin
LIITE 3 1(6) Harjoitus Bones ja Skin Harjoituksessa käsiteltävät asiat: Yksinkertaisen jalan luominen sylinteristä Luurangon luominen ja sen tekeminen toimivaksi raajaksi Luurangon yhdistäminen jalka-objektiin
Workflow-esimerkki: Leikkaus
 1 / 18 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Workflow-esimerkki: Leikkaus Workflow-esimerkki: Leikkaus Rhinossa 2 / 18 1. Rhinossa Clipping Planella saa tehtyä leikkaavan tason 2. Section-komennolla
1 / 18 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Workflow-esimerkki: Leikkaus Workflow-esimerkki: Leikkaus Rhinossa 2 / 18 1. Rhinossa Clipping Planella saa tehtyä leikkaavan tason 2. Section-komennolla
Rakennesuunnittelija ja teräsrunkotoimittaja samassa tietomallissa
 JKMM Arkkitehdit Rakennesuunnittelija ja teräsrunkotoimittaja samassa tietomallissa Max Levander, Ramboll Tero Ollikainen, Peikko Group Oy Teräsrakennepäivä 2016, Scandic Park 8.11.2016 RAMBOLL SUOMESSA
JKMM Arkkitehdit Rakennesuunnittelija ja teräsrunkotoimittaja samassa tietomallissa Max Levander, Ramboll Tero Ollikainen, Peikko Group Oy Teräsrakennepäivä 2016, Scandic Park 8.11.2016 RAMBOLL SUOMESSA
Automaattinen regressiotestaus ilman testitapauksia. Pekka Aho, VTT Matias Suarez, F-Secure
 Automaattinen regressiotestaus ilman testitapauksia Pekka Aho, VTT Matias Suarez, F-Secure 2 Mitä on regressiotestaus ja miksi sitä tehdään? Kun ohjelmistoon tehdään muutoksia kehityksen tai ylläpidon
Automaattinen regressiotestaus ilman testitapauksia Pekka Aho, VTT Matias Suarez, F-Secure 2 Mitä on regressiotestaus ja miksi sitä tehdään? Kun ohjelmistoon tehdään muutoksia kehityksen tai ylläpidon
Matterport vai GeoSLAM? Juliane Jokinen ja Sakari Mäenpää
 Matterport vai GeoSLAM? Juliane Jokinen ja Sakari Mäenpää Esittely Tutkimusaineiston laatija DI Aino Keitaanniemi Aino Keitaanniemi työskentelee Aalto yliopiston Rakennetun ympäristön mittauksen ja mallinnuksen
Matterport vai GeoSLAM? Juliane Jokinen ja Sakari Mäenpää Esittely Tutkimusaineiston laatija DI Aino Keitaanniemi Aino Keitaanniemi työskentelee Aalto yliopiston Rakennetun ympäristön mittauksen ja mallinnuksen
MAA5 Vektori, Opintokortti
 MAA5 Vektori, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin täytettynä
MAA5 Vektori, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin täytettynä
Symmetrioiden tutkiminen GeoGebran avulla
 Symmetrioiden tutkiminen GeoGebran avulla Tutustutaan esimerkkien kautta siihen, miten geometrista symmetriaa voidaan tutkia ja havainnollistaa GeoGebran avulla: peilisymmetria: peilaus pisteen ja suoran
Symmetrioiden tutkiminen GeoGebran avulla Tutustutaan esimerkkien kautta siihen, miten geometrista symmetriaa voidaan tutkia ja havainnollistaa GeoGebran avulla: peilisymmetria: peilaus pisteen ja suoran
Pohjan ja leikkauksen tekeminen Casa Parrista
 1 / 12 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto 24.11.2015 Pohjan ja leikkauksen tekeminen Casa Parrista Talon sijoittaminen maastoon 2 / 12 1. File --> import --> valitse maastotiedosto (tai
1 / 12 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto 24.11.2015 Pohjan ja leikkauksen tekeminen Casa Parrista Talon sijoittaminen maastoon 2 / 12 1. File --> import --> valitse maastotiedosto (tai
3D-Win 5.3. Tierakenneohje. 3D-system Oy Kielotie 14 B 01300 VANTAA puh. 09-2532 4411 www.3d-system.fi (10/2008)
 3D-Win 5.3 Tierakenneohje 3D-system Oy Kielotie 14 B 01300 VANTAA puh. 09-2532 4411 www.3d-system.fi (10/2008) Sisällysluettelo: 1 LÄHTÖAINEISTOT... 3 2 TIHENNYS... 3 3 AINEISTOT MITTALAITTEISIIN... 4
3D-Win 5.3 Tierakenneohje 3D-system Oy Kielotie 14 B 01300 VANTAA puh. 09-2532 4411 www.3d-system.fi (10/2008) Sisällysluettelo: 1 LÄHTÖAINEISTOT... 3 2 TIHENNYS... 3 3 AINEISTOT MITTALAITTEISIIN... 4
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
STL:n luonti IronCADillä
 STL:n luonti IronCADillä STL-tiedoston luonti IronCADilla etenee seuraavasti: 1. Avataan haluttu kappale IronCADilla. 2. Kappaletta napsautetaan hiiren oikealla näppäimellä ja valitse pudotusvalikosta
STL:n luonti IronCADillä STL-tiedoston luonti IronCADilla etenee seuraavasti: 1. Avataan haluttu kappale IronCADilla. 2. Kappaletta napsautetaan hiiren oikealla näppäimellä ja valitse pudotusvalikosta
Muodonmuutostila hum 30.8.13
 Muodonmuutostila Tarkastellaan kuvan 1 kappaletta Ω, jonka pisteet siirtvät ulkoisen kuormituksen johdosta siten, että siirtmien tapahduttua ne muodostavat kappaleen Ω'. Esimerkiksi piste A siirt asemaan
Muodonmuutostila Tarkastellaan kuvan 1 kappaletta Ω, jonka pisteet siirtvät ulkoisen kuormituksen johdosta siten, että siirtmien tapahduttua ne muodostavat kappaleen Ω'. Esimerkiksi piste A siirt asemaan
ETAPPI ry JOOMLA 2.5 Mediapaja. Artikkeleiden hallinta ja julkaisu
 ETAPPI ry JOOMLA 2.5 Artikkeleiden hallinta ja julkaisu ETAPPI ry JOOMLA 2.5 Sivu 1(16) Sisällysluettelo 1 Joomla! sivuston sisällöntuotanto... 2 2 Artikkeleiden julkaisu sivustolla... 4 3 Artikkelin julkaisemista
ETAPPI ry JOOMLA 2.5 Artikkeleiden hallinta ja julkaisu ETAPPI ry JOOMLA 2.5 Sivu 1(16) Sisällysluettelo 1 Joomla! sivuston sisällöntuotanto... 2 2 Artikkeleiden julkaisu sivustolla... 4 3 Artikkelin julkaisemista
Tämän lisäksi listataan ranskalaisin viivoin järjestelmän tarjoama toiminnallisuus:
 Dokumentaatio, osa 1 Tehtävämäärittely Kirjoitetaan lyhyt kuvaus toteutettavasta ohjelmasta. Kuvaus tarkentuu myöhemmin, aluksi dokumentoidaan vain ideat, joiden pohjalta työtä lähdetään tekemään. Kuvaus
Dokumentaatio, osa 1 Tehtävämäärittely Kirjoitetaan lyhyt kuvaus toteutettavasta ohjelmasta. Kuvaus tarkentuu myöhemmin, aluksi dokumentoidaan vain ideat, joiden pohjalta työtä lähdetään tekemään. Kuvaus
Ennakkosuunnitelman luonti
 Elokuu 2019 JETI-pikaohje Ennakkosuunnitelman luonti Tämän dokumentin sisällöstä Tämä dokumentti on pikaohje ennakkosuunnitelman laadinnasta ja koskee seuraavia ennakkosuunnitelman luomisen vaiheita: 1.
Elokuu 2019 JETI-pikaohje Ennakkosuunnitelman luonti Tämän dokumentin sisällöstä Tämä dokumentti on pikaohje ennakkosuunnitelman laadinnasta ja koskee seuraavia ennakkosuunnitelman luomisen vaiheita: 1.
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 2017 Insinöörivalinnan matematiikan koe , Ratkaisut (Sarja A)
 Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Diplomi-insinööri- ja arkkitehtikoulutuksen yhteisvalinta 017 Insinöörivalinnan matematiikan koe 30..017, Ratkaisut (Sarja A) 1. a) Lukujen 9, 0, 3 ja x keskiarvo on. Määritä x. (1 p.) b) Mitkä reaaliluvut
Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ (ja MITTAA) a) jana toinen jana, jonka pituus on 3 b) kulma toinen kulma, jonka
Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ (ja MITTAA) a) jana toinen jana, jonka pituus on 3 b) kulma toinen kulma, jonka
Visma Fivaldi -käsikirja Tehtävienhallinta- ohje käyttäjälle
 Visma Fivaldi -käsikirja Tehtävienhallinta- ohje käyttäjälle 2 Sisällys 1 Palvelunhallinta... 3 1.1 Käyttäjäryhmän luominen... 3 2 Tehtävienhallinta- perustiedot... 4 2.1 Yhtiön perustiedot... 4 2.2 Tehtävä-/
Visma Fivaldi -käsikirja Tehtävienhallinta- ohje käyttäjälle 2 Sisällys 1 Palvelunhallinta... 3 1.1 Käyttäjäryhmän luominen... 3 2 Tehtävienhallinta- perustiedot... 4 2.1 Yhtiön perustiedot... 4 2.2 Tehtävä-/
Painevalut 3. Teoriatausta Revolved Pattern. Mallinnuksen vaiheet. CAD työkalut harjoituksessa diecasting_3_1.sldprt
 Painevalut 3 Tuula Höök Tampereen teknillinen yliopisto Hae aloituskappale start_diecasting_3_1.sldprt. Tehtävänäsi on suunnitella kansi alueille, jotka on merkitty kuvaan punaisella, vihreällä ja sinisellä
Painevalut 3 Tuula Höök Tampereen teknillinen yliopisto Hae aloituskappale start_diecasting_3_1.sldprt. Tehtävänäsi on suunnitella kansi alueille, jotka on merkitty kuvaan punaisella, vihreällä ja sinisellä
Johdantoa. Jokaisen matemaatikon olisi syytä osata edes alkeet jostakin perusohjelmistosta, Java MAPLE. Pascal MathCad
 Johdantoa ALGORITMIT MATEMA- TIIKASSA, MAA Vanhan vitsin mukaan matemaatikko tietää, kuinka matemaattinen ongelma ratkaistaan, mutta ei osaa tehdä niin. Vitsi on ajalta, jolloin käytännön laskut eli ongelman
Johdantoa ALGORITMIT MATEMA- TIIKASSA, MAA Vanhan vitsin mukaan matemaatikko tietää, kuinka matemaattinen ongelma ratkaistaan, mutta ei osaa tehdä niin. Vitsi on ajalta, jolloin käytännön laskut eli ongelman
SAMI ERKKILÄ ALGORITMIAVUSTEISEN SUUNNITTELUN HYÖDYNTÄMINEN BETONIELEMENTTIRAKENTEIDEN SUUNNITTELUSSA
 SAMI ERKKILÄ ALGORITMIAVUSTEISEN SUUNNITTELUN HYÖDYNTÄMINEN BETONIELEMENTTIRAKENTEIDEN SUUNNITTELUSSA Diplomityö Tarkastaja: professori Mikko Malaska Tarkastaja ja aihe hyväksytty Talouden ja rakentamisen
SAMI ERKKILÄ ALGORITMIAVUSTEISEN SUUNNITTELUN HYÖDYNTÄMINEN BETONIELEMENTTIRAKENTEIDEN SUUNNITTELUSSA Diplomityö Tarkastaja: professori Mikko Malaska Tarkastaja ja aihe hyväksytty Talouden ja rakentamisen
Ristitulolle saadaan toinen muistisääntö determinantin avulla. Vektoreiden v ja w ristitulo saadaan laskemalla determinantti
 14 Ristitulo Avaruuden R 3 vektoreille voidaan määritellä pistetulon lisäksi niin kutsuttu ristitulo. Pistetulosta poiketen ristitulon tulos ei ole reaaliluku vaan avaruuden R 3 vektori. Ristitulosta on
14 Ristitulo Avaruuden R 3 vektoreille voidaan määritellä pistetulon lisäksi niin kutsuttu ristitulo. Pistetulosta poiketen ristitulon tulos ei ole reaaliluku vaan avaruuden R 3 vektori. Ristitulosta on
Kuva: Ilpo Okkonen
 OodiHOPS OHJAAJAN OHJE 14.2.2017 Kuva: Ilpo Okkonen OodiHOPS Oulun yliopistossa Oulun yliopiston koulutusneuvosto on päättänyt, että OodiHOPS-toiminto otetaan käyttöön vähintään aloittavilla opiskelijoilla
OodiHOPS OHJAAJAN OHJE 14.2.2017 Kuva: Ilpo Okkonen OodiHOPS Oulun yliopistossa Oulun yliopiston koulutusneuvosto on päättänyt, että OodiHOPS-toiminto otetaan käyttöön vähintään aloittavilla opiskelijoilla
Sweco Rakennetekniikka Oy. KORKEAN RAKENTAMISEN HAASTEET, CASE REDI. Copyright Helin & Co / Voima Graphics Arkkitehti Helin & Co
 Sweco Rakennetekniikka Oy. KORKEAN RAKENTAMISEN HAASTEET, CASE REDI Copyright Helin & Co / Voima Graphics Arkkitehti Helin & Co 1 Työmaa 10.8.2016 web-liittymästä Haastavuus näkyy jo tästä 2 Näkymiä Tekla
Sweco Rakennetekniikka Oy. KORKEAN RAKENTAMISEN HAASTEET, CASE REDI Copyright Helin & Co / Voima Graphics Arkkitehti Helin & Co 1 Työmaa 10.8.2016 web-liittymästä Haastavuus näkyy jo tästä 2 Näkymiä Tekla
2020 Fusion. What s New in Version 6? What s New in Version 6? 1 of Fusion
 2020 Fusion What s New in Version 6? What s New in Version 6? 1 of 17 2020 Fusion Uusi 2020 Fusion 6 nopeuttaa ja helpottaa työskentelyäsi: Täysin uudistettu renderöinti Useiden tuotteiden muokkaus samalla
2020 Fusion What s New in Version 6? What s New in Version 6? 1 of 17 2020 Fusion Uusi 2020 Fusion 6 nopeuttaa ja helpottaa työskentelyäsi: Täysin uudistettu renderöinti Useiden tuotteiden muokkaus samalla
Kiinteistö- ja rakennusalan digitalisaatio: BIM & GIS
 Kiinteistö- ja rakennusalan digitalisaatio: BIM & GIS Kiinteistön elinkaari Kiinteistö- ja rakennusalan digitalisaatio. Miten tämän perinteisen alan digitalisaatio käytännössä tapahtuu ja mitä hyötyjä
Kiinteistö- ja rakennusalan digitalisaatio: BIM & GIS Kiinteistön elinkaari Kiinteistö- ja rakennusalan digitalisaatio. Miten tämän perinteisen alan digitalisaatio käytännössä tapahtuu ja mitä hyötyjä
2 Pistejoukko koordinaatistossa
 Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
Pistejoukko koordinaatistossa Ennakkotehtävät 1. a) Esimerkiksi: b) Pisteet sijaitsevat pystysuoralla suoralla, joka leikkaa x-akselin kohdassa x =. c) Yhtälö on x =. d) Sijoitetaan joitain ehdon toteuttavia
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 23.2.2016 Susanna Hurme Tervetuloa kurssille! Mitä on statiikka? Mitä on dynamiikka? Miksi niitä opiskellaan? Päivän aihe: Voiman käsite ja partikkelin tasapaino
KJR-C1001 Statiikka ja dynamiikka Luento 23.2.2016 Susanna Hurme Tervetuloa kurssille! Mitä on statiikka? Mitä on dynamiikka? Miksi niitä opiskellaan? Päivän aihe: Voiman käsite ja partikkelin tasapaino
MAB3 - Harjoitustehtävien ratkaisut:
 MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
MAB - Harjoitustehtävien ratkaisut: Funktio. Piirretään koordinaatistoakselit ja sijoitetaan pisteet:. a) Funktioiden nollakohdat löydetään etsimällä kuvaajien ja - akselin leikkauspisteitä. Funktiolla
www.kotisivukone.fi Pikaopas kotisivujen tekoon
 Kotisivut helposti! www.kotisivukone.fi Pikaopas kotisivujen tekoon Näin Kotisivukone toimii Kun olet kirjautunut sisään kotisivuillesi, tulet helppokäyttöiseen ylläpitotilaan ja voit heti aloittaa kotisivujen
Kotisivut helposti! www.kotisivukone.fi Pikaopas kotisivujen tekoon Näin Kotisivukone toimii Kun olet kirjautunut sisään kotisivuillesi, tulet helppokäyttöiseen ylläpitotilaan ja voit heti aloittaa kotisivujen
2016/06/21 13:27 1/10 Laskentatavat
 2016/06/21 13:27 1/10 Laskentatavat Laskentatavat Yleistä - vaakageometrian suunnittelusta Paalu Ensimmäinen paalu Ensimmäisen paalun tartuntapiste asetetaan automaattisesti 0.0:aan. Tämä voidaan muuttaa
2016/06/21 13:27 1/10 Laskentatavat Laskentatavat Yleistä - vaakageometrian suunnittelusta Paalu Ensimmäinen paalu Ensimmäisen paalun tartuntapiste asetetaan automaattisesti 0.0:aan. Tämä voidaan muuttaa
TIETOMALLINNUS TEKNIIKKALAJIEN KYPSYYSASTEET PUISTOSUUNNITTELU JÄTKÄSAARI, HELSINKI
 TIETOMALLINNUS TEKNIIKKALAJIEN KYPSYYSASTEET PUISTOSUUNNITTELU JÄTKÄSAARI, HELSINKI INFRAMALLINTAMISEN PÄIVÄ 1.2.2017 Veli-Pekka Koskela ESITYKSEN SISÄLTÖ Hanke-esittely Yhteistoiminta puistosuunnitteluhankkeessa
TIETOMALLINNUS TEKNIIKKALAJIEN KYPSYYSASTEET PUISTOSUUNNITTELU JÄTKÄSAARI, HELSINKI INFRAMALLINTAMISEN PÄIVÄ 1.2.2017 Veli-Pekka Koskela ESITYKSEN SISÄLTÖ Hanke-esittely Yhteistoiminta puistosuunnitteluhankkeessa
Ohjelmistojen mallintaminen, mallintaminen ja UML
 582104 Ohjelmistojen mallintaminen, mallintaminen ja UML 1 Mallintaminen ja UML Ohjelmistojen mallintamisesta ja kuvaamisesta Oliomallinnus ja UML Käyttötapauskaaviot Luokkakaaviot Sekvenssikaaviot 2 Yleisesti
582104 Ohjelmistojen mallintaminen, mallintaminen ja UML 1 Mallintaminen ja UML Ohjelmistojen mallintamisesta ja kuvaamisesta Oliomallinnus ja UML Käyttötapauskaaviot Luokkakaaviot Sekvenssikaaviot 2 Yleisesti
KOIRANKOPPI ARK. Tietomalliseloste. Havainnollistuskuva kohteesta. Heidi Sumkin. Mallintaja. Kohde
 Tietomalliseloste Havainnollistuskuva kohteesta KOIRANKOPPI ARK Aloituspvm Mallintaja Kohde Mallinnustarkoitus Käytettävät ohjelmistot, tiedonsiirto Lisätietoja, huomioita yms. 15.5.2009 Nimi Heidi Sumkin
Tietomalliseloste Havainnollistuskuva kohteesta KOIRANKOPPI ARK Aloituspvm Mallintaja Kohde Mallinnustarkoitus Käytettävät ohjelmistot, tiedonsiirto Lisätietoja, huomioita yms. 15.5.2009 Nimi Heidi Sumkin
Ohjelmointi 1. Kumppanit
 Ohjelmointi 1 Kumppanit November 20, 2012 2 Contents 1 Mitä ohjelmointi on 7 2 Ensimmäinen C#-ohjelma 9 2.1 Ohjelman kirjoittaminen......................... 9 A Liite 11 3 4 CONTENTS Esipuhe Esipuhe 5
Ohjelmointi 1 Kumppanit November 20, 2012 2 Contents 1 Mitä ohjelmointi on 7 2 Ensimmäinen C#-ohjelma 9 2.1 Ohjelman kirjoittaminen......................... 9 A Liite 11 3 4 CONTENTS Esipuhe Esipuhe 5
Määrittelydokumentti
 Määrittelydokumentti Aineopintojen harjoitustyö: Tietorakenteet ja algoritmit (alkukesä) Sami Korhonen 014021868 sami.korhonen@helsinki. Tietojenkäsittelytieteen laitos Helsingin yliopisto 23. kesäkuuta
Määrittelydokumentti Aineopintojen harjoitustyö: Tietorakenteet ja algoritmit (alkukesä) Sami Korhonen 014021868 sami.korhonen@helsinki. Tietojenkäsittelytieteen laitos Helsingin yliopisto 23. kesäkuuta
KiMeWebin käyttöohjeet
 KiMeWebin käyttöohjeet 5.3.2017 Miten saan käyttäjätunnuksen? Jos haluat käyttäjätunnuksen (eli oikeuden muokata sivuja) laita viesti webvelho@kime.fi ja kerro viestissä nimi pesti lippukunnassa (esim.
KiMeWebin käyttöohjeet 5.3.2017 Miten saan käyttäjätunnuksen? Jos haluat käyttäjätunnuksen (eli oikeuden muokata sivuja) laita viesti webvelho@kime.fi ja kerro viestissä nimi pesti lippukunnassa (esim.
Ota tämä paperi mukaan, merkkaa siihen omat vastauksesi ja tarkista oikeat vastaukset klo 11:30 jälkeen osoitteesta
 MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
MAA5.2 Loppukoe 26.9.2012 Jussi Tyni Valitse 6 tehtävää Muista merkitä vastauspaperiin oma nimesi ja tee etusivulle pisteytysruudukko Kaikkiin tehtävien ratkaisuihin välivaiheet näkyviin! 1. Olkoon vektorit
OpenOffice.org Impress 3.1.0
 OpenOffice.org Impress 3.1.0 Sisällysluettelo 1 Esityksen luominen...1 2 Dian rakenne...2 3 Dian lisääminen, poistaminen, siirtäminen ja kopioiminen...3 4 Diojen koon muuttaminen...3 5 Pohjatyylisivut...4
OpenOffice.org Impress 3.1.0 Sisällysluettelo 1 Esityksen luominen...1 2 Dian rakenne...2 3 Dian lisääminen, poistaminen, siirtäminen ja kopioiminen...3 4 Diojen koon muuttaminen...3 5 Pohjatyylisivut...4
0, niin vektorit eivät ole kohtisuorassa toisiaan vastaan.
 Tekijä Pitkä matematiikka 4 9.1.016 168 a) Lasketaan vektorien a ja b pistetulo. a b = (3i + 5 j) (7i 3 j) = 3 7 + 5 ( 3) = 1 15 = 6 Koska pistetulo a b 0, niin vektorit eivät ole kohtisuorassa toisiaan
Tekijä Pitkä matematiikka 4 9.1.016 168 a) Lasketaan vektorien a ja b pistetulo. a b = (3i + 5 j) (7i 3 j) = 3 7 + 5 ( 3) = 1 15 = 6 Koska pistetulo a b 0, niin vektorit eivät ole kohtisuorassa toisiaan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9.2.2011
 PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
PRELIMINÄÄRIKOE PITKÄ MATEMATIIKKA 9..0 Kokeessa saa vastata enintään kymmeneen tehtävään.. Sievennä a) 9 x x 6x + 9, b) 5 9 009 a a, c) log 7 + lne 7. Muovailuvahasta tehty säännöllinen tetraedri muovataan
Oppilaan pikaopas. Project 2013 käyttöliittymä ja näkymät
 1 Oppilaan pikaopas Project 2013 käyttöliittymä ja näkymät Kun avaat Project 2013 -ohjelman, näet ensimmäisenä pelkistetyn näkymän. Uusi Project 2013 voi auttaa projektinhallinnassa kuten esim. projektitietojen
1 Oppilaan pikaopas Project 2013 käyttöliittymä ja näkymät Kun avaat Project 2013 -ohjelman, näet ensimmäisenä pelkistetyn näkymän. Uusi Project 2013 voi auttaa projektinhallinnassa kuten esim. projektitietojen
Digitaalisen arkkitehtuurin alkeet
 1 / 18 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Digitaalisen arkkitehtuurin alkeet Miten tehdä mallin loppuosat? 2 / 18 Patch on helppo tehdä sisäosille, mutta alueen rajan ja korkeuskäyrien
1 / 18 Digitaalisen arkkitehtuurin yksikkö Aalto-yliopisto Digitaalisen arkkitehtuurin alkeet Miten tehdä mallin loppuosat? 2 / 18 Patch on helppo tehdä sisäosille, mutta alueen rajan ja korkeuskäyrien
Oppimistavoitematriisi
 Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Arvosanaan 1 2 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä ja yhtälöpareja Osaan muokata
Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Arvosanaan 1 2 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä ja yhtälöpareja Osaan muokata
Oppimistavoitematriisi
 Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Esitiedot Arvosanaan 1 2 riittävät Arvosanaan 3 4 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä
Oppimistavoitematriisi Lineaarialgebra ja matriisilaskenta I Esitiedot Arvosanaan 1 2 riittävät Arvosanaan 3 4 riittävät Arvosanaan 5 riittävät Yhtälöryhmät (YR) Osaan ratkaista ensimmäisen asteen yhtälöitä
Projektinhallintaa paikkatiedon avulla
 Projektinhallintaa paikkatiedon avulla Tampereen Teknillinen Yliopisto / Porin laitos Teemu Kumpumäki teemu.kumpumaki@tut.fi 25.6.2015 1 Paikkatieto ja projektinhallinta Paikkatiedon käyttäminen projektinhallinnassa
Projektinhallintaa paikkatiedon avulla Tampereen Teknillinen Yliopisto / Porin laitos Teemu Kumpumäki teemu.kumpumaki@tut.fi 25.6.2015 1 Paikkatieto ja projektinhallinta Paikkatiedon käyttäminen projektinhallinnassa
3 TOISEN ASTEEN POLYNOMIFUNKTIO
 3 TOISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Kuvasta voidaan arvioida, että frisbeegolfkiekko käy noin 9 metrin korkeudella ja se lentää noin 40 metrin päähän. Vastaus: Frisbeegolfkiekko käy n. 9 m:n
3 TOISEN ASTEEN POLYNOMIFUNKTIO POHDITTAVAA 1. Kuvasta voidaan arvioida, että frisbeegolfkiekko käy noin 9 metrin korkeudella ja se lentää noin 40 metrin päähän. Vastaus: Frisbeegolfkiekko käy n. 9 m:n
PRINCIPLES OF PROGRAMMING LANGUAGES - DEBUGGER
 PRINCIPLES OF PROGRAMMING LANGUAGES - DEBUGGER Group 16 Ville Laatu Henri Myllyoja - i SISÄLLYSLUETTELO 1. DEBUGGERI YLEISESTI... II 1.1 Debuggerin käyttämien... ii 1.2 Debuggerin käynnistäminen... ii
PRINCIPLES OF PROGRAMMING LANGUAGES - DEBUGGER Group 16 Ville Laatu Henri Myllyoja - i SISÄLLYSLUETTELO 1. DEBUGGERI YLEISESTI... II 1.1 Debuggerin käyttämien... ii 1.2 Debuggerin käynnistäminen... ii
GeoGebran 3D paketti
 GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
Pikaohje QPR-käyttöön
 Pikaohje QPR-käyttöön SOTE-arkkitehtuuri 1 11.3.2019 QPR-pikaohje Sisältö Aloittaminen Peruskomennot Elementtien hallinnointi Mallihierarkian rakentaminen Tätä ohjetta täydentää mallinnuskäsikirja, joka
Pikaohje QPR-käyttöön SOTE-arkkitehtuuri 1 11.3.2019 QPR-pikaohje Sisältö Aloittaminen Peruskomennot Elementtien hallinnointi Mallihierarkian rakentaminen Tätä ohjetta täydentää mallinnuskäsikirja, joka
Pistepilvien hyödyntäminen rakennusvalvonnassa
 Pistepilvien hyödyntäminen rakennusvalvonnassa CubiCasa X Oulun Rakennusvalvonta Tiivistettynä: CubiCasan nopeassa kokeilussa kartoitettiin erilaisia rakennusten digitaalisia tallennustapoja, sekä kuinka
Pistepilvien hyödyntäminen rakennusvalvonnassa CubiCasa X Oulun Rakennusvalvonta Tiivistettynä: CubiCasan nopeassa kokeilussa kartoitettiin erilaisia rakennusten digitaalisia tallennustapoja, sekä kuinka
Kerro kuvin 3:n uudet ominaisuudet
 Verkkosivu: www.haltija.fi Puhelin: 09 612 2250 Sähköposti: asiakaspalvelu@haltija.fi Kerro kuvin 3:n uudet ominaisuudet Kerro kuvin 3 on kehitetty uudelleen perusteista lähtien. Kaikki, mikä oli mahdollista
Verkkosivu: www.haltija.fi Puhelin: 09 612 2250 Sähköposti: asiakaspalvelu@haltija.fi Kerro kuvin 3:n uudet ominaisuudet Kerro kuvin 3 on kehitetty uudelleen perusteista lähtien. Kaikki, mikä oli mahdollista
SELVITYS PRO GRADUJEN KÄYTÖSTÄ TAIDEKIRJASTOSSA
 SELVITYS PRO GRADUJEN KÄYTÖSTÄ TAIDEKIRJASTOSSA Tapani Takalo Lapin korkeakoulukirjasto, yliopisto, taide 17.11.2011 1. Johdanto Lapin yliopiston taidekirjastossa on selvitetty taidekirjaston kokoelmiin
SELVITYS PRO GRADUJEN KÄYTÖSTÄ TAIDEKIRJASTOSSA Tapani Takalo Lapin korkeakoulukirjasto, yliopisto, taide 17.11.2011 1. Johdanto Lapin yliopiston taidekirjastossa on selvitetty taidekirjaston kokoelmiin
Tilastolliset ohjelmistot 805340A. Pinja Pikkuhookana
 Tilastolliset ohjelmistot 805340A Pinja Pikkuhookana Sisältö 1 SPSS 1.1 Yleistä 1.2 Aineiston syöttäminen 1.3 Aineistoon tutustuminen 1.4 Kuvien piirtäminen 1.5 Kuvien muokkaaminen 1.6 Aineistojen muokkaaminen
Tilastolliset ohjelmistot 805340A Pinja Pikkuhookana Sisältö 1 SPSS 1.1 Yleistä 1.2 Aineiston syöttäminen 1.3 Aineistoon tutustuminen 1.4 Kuvien piirtäminen 1.5 Kuvien muokkaaminen 1.6 Aineistojen muokkaaminen
1. Olkoot vektorit a, b ja c seuraavasti määritelty: a) Määritä vektori. sekä laske sen pituus.
 Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
Matematiikan kurssikoe, Maa4 Vektorit RATKAISUT Sievin lukio Keskiviikko 12.4.2017 VASTAA YHTEENSÄ VIITEEN TEHTÄVÄÄN! MAOL JA LASKIN/LAS- KINOHJELMAT OVAT SALLITTUJA! 1. Olkoot vektorit a, b ja c seuraavasti
Luento 4. Timo Savola. 21. huhtikuuta 2006
 UNIX-käyttöjärjestelmä Luento 4 Timo Savola 21. huhtikuuta 2006 Osa I Shell Lausekkeet Komentoriville kirjotettu komento on lauseke echo "foo" echo $USER MUUTTUJA=1 ls -l Rivinvaihto
UNIX-käyttöjärjestelmä Luento 4 Timo Savola 21. huhtikuuta 2006 Osa I Shell Lausekkeet Komentoriville kirjotettu komento on lauseke echo "foo" echo $USER MUUTTUJA=1 ls -l Rivinvaihto
Käyttöliittymän muokkaus
 Käyttöliittymän muokkaus Ohjelman pitkän kehityshistorian takia asetukset ovat jakaantuneet useampaan eri kohtaan ohjelmassa. Ohessa yhteenveto nykyisistä asetuksista (versio 6.4.1, 2/2018). Ylä- ja sivupalkkien
Käyttöliittymän muokkaus Ohjelman pitkän kehityshistorian takia asetukset ovat jakaantuneet useampaan eri kohtaan ohjelmassa. Ohessa yhteenveto nykyisistä asetuksista (versio 6.4.1, 2/2018). Ylä- ja sivupalkkien
PÄIVITÄ TIETOSI OPTIMASTA! KOOSTE
 PÄIVITÄ TIETOSI OPTIMASTA! KOOSTE IT-palvelut / Hannele Rajaniemi optima-support@jyu.fi www.jyu.fi/itp/optima-ohjeet 2 Sisältö Mikä on koosteen idea? Miten saan kooste-työkalun käyttööni? Miten luon koosteen?
PÄIVITÄ TIETOSI OPTIMASTA! KOOSTE IT-palvelut / Hannele Rajaniemi optima-support@jyu.fi www.jyu.fi/itp/optima-ohjeet 2 Sisältö Mikä on koosteen idea? Miten saan kooste-työkalun käyttööni? Miten luon koosteen?
ASCII-taidetta. Intro: Python
 Python 1 ASCII-taidetta All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/18cplpy to find out what to do.
Python 1 ASCII-taidetta All Code Clubs must be registered. Registered clubs appear on the map at codeclubworld.org - if your club is not on the map then visit jumpto.cc/18cplpy to find out what to do.
