Antiikin Kreikan kartografit Ilppo Soininvaara
|
|
|
- Kristiina Korpela
- 9 vuotta sitten
- Katselukertoja:
Transkriptio
1 Antiikin Kreikan kartografit Ilppo Soininvaara Antiikin Kreikan historia, ja sen filosofit ovat tunnettuja saavutuksistaan useilla tieteenaloilla. Kreikkalaisten aikaansaannoksista lukiessa ei voi kun hämmästellä, miten pitkälle kreikkalaiset filosofit ja yleisnerot olivat taiteiden lisäksi kehittäneet luonnontieteiden osaamista. Antiikin tieteentekijöillä ei ollut käytössään meidän aikamme välineistöä, mutta he kykenivät puhtaasti loogisella päättelyllä suorituksiin, jotka tuntuvat uskomattomilta. Maantiede oli yksi tärkeistä tieteenaloista antiikin kreikassa, olivathan tuon ajan kreikkalaiset tunnettuja kauppiaita ja matkaajia, jotka perustivat siirtokuntia ympäri Välimerta. Tieto alueista ja kansoista, sekä reiteistä oli elintärkeää kaupanteon kannalta. Me olemme nykyisin tottuneet esittämään kartalla lähes mitä tahansa, mutta varhaisantiikin aikana kartat olivat vielä tuntematon käsite. Kreikkalaiset tukeutuivatkin matkoillaan matkakuvauksiin ja erinäisiin katalogeihin, joissa lueteltiin kaupunkeja, kyliä tai muita maamerkkejä tietyn matkareitin varrelta, ja näiden maamerkkien tai välipisteiden avulla suunnistettiin haluttuun paikkaan. Varsinaisia mittauksia välimatkoista ei tehty, vaan etäisyydet kerrottiin matka-aikoina, jotka luonnollisesti etenkin merialueilla saattoivat olla hyvin epäluotettavia. Antiikin filosofien töihin kuuluu paljon maantieteellisiä kuvauksia; kreikkalaiset olivat kiinnostuneita ympäristöstään, mutta maantieteessä keskityttiin lähinnä asuttujen alueiden ja eri kansojen kuvailuihin. Luonto ei juuri kiinnostanut varhaisia maantieteilijöitä, ellei siitä ollut hyötyä suunnistuksen kannalta, maantieteelliset kuvailut olivat lähinnä ihmismaantiedettä. (Raaflaub et al. 2009) Suurin osa siitä tiedosta, mitä meillä on antiikin kreikkalaisista ja heidän saavutuksistaan, on peräisin aikalaiskirjoituksista ja myöhäisemmistä historiateoksista, jotka ovat käyttäneet vielä lähteinään aikalaisteoksia. Iso osa alkuperäisistä kirjoituksista ja etenkin kartoista ovat hävinneet. Strabo, joka oli itsekin yksi antiikin merkittävimpiä maantieteilijöitä, on muutaman muun ohella yksi tärkeimpiä lähteitä varhaisempien kreikkalaistieteilijöiden saavutuksiin (Perseus Encyclopedia). Vaikka kiitettävän paljon antiikin kirjoituksia on säilynyt, ja näin ollen meillä periaatteessa on saatavillamme hyvin tietoa aiheesta, tulee muistaa lähteiden konteksti. Antiikin kreikkalaisilla oli oma tyylinsä tallentaa tietoja, eikä lähteitä aina voida pitää täysin luotettavina. Uskomukset ja uskonnot linkittyivät empiirisen tiedon kanssa saumattomasti yhteen etenkin varhaisempien tieteilijöiden maailmankuvissa. Samaan aikaan tieteilijä pystyi harrastamaan pitkälle vietyä matematiikkaa vuoren korkeuteen ja kulmiin liittyen, pitämään uskottavana, että vuoren päällä todella asui jumalia tai henkiä (Raaflaub et al. 2009). Samoin antiikin filosofeille on omintakeista samat paheet kuin meille nykyään, he esimerkiksi omivat surutta omien suurmiestensä keksinnöiksi muualta lainattuja asioita, vaikkapa mittaukseen käytetyn gnomon kepin (Daly 1879). Myös muinaiskreikan kieli aiheuttaa päänvaivaa, esimerkiksi Pothecary (1997) on selvittänyt Strabon käyttämän meidän aikanamme - ilmauksen todellista merkitystä; tämä on oiva esimerkki siitä, että emme voi täysin varmasti aina luottaa töihin sellaisenaan. Antiikin lähteissä on myös jonkin verran ristiriitaisuuksia.
2 Antiikin historioitsijat antavat yleensä Anaksimandrokselle kunnian olla ensimmäisen (kreikkalaisen) maailmankartan tekijä (Raaflaub et al. 2009; Daly 1879; Harley & Woodward 1987). Anaksimandros (n eaa.) oli Thaleen, kuuluisan astronomin, oppilas. Tuohon aikaan kartalle ei luonnollisestikaan ollut mitään omaa sanaa kreikan kielessä, ja karttojen yleistyminen käyttöesineiksi oli hidasta. Alkuun kartat olivat lähinnä filosofien välineitä maailman ja sen rakenteen pohdinnassa. Anaksimandroksen kartta (kuva 1), kuten suuri osa hänen muistakaan töistään, ei ole säilynyt, mutta siitä löytyy kirjoitettuja kuvauksia, joiden avulla on luotu rekonstruktioita. Anaksimandroksen maailmankuvan mukaan maa oli sylinterin mallinen (Daly 1879), ja asutun alueen olevan sylinterin päällä. Kartta muistuttaa keskiajan TO-karttaa: maailma on jakautunut kolmeen mantereeseen, joita vesistöt erottavat toisistaan. Maa-alueita ympäröi Oceanus-joki, joka rajasi sylinterin reunoja, ja näin ollen toimi maailman rajana (Daly 1879; Harley & Woodward 1987). Tällainen maailmankuva on ilmeisesti ollut varsin yleinen, mutta ei vailla kritiikkiä. Herodotos kirjoitti pitävänsä ajatuksia maailmaa ympäröivästä, tyhjyyteen rajautuvasta joesta naurettavina, mutta häntä aiemmin maailmankuva on hyvinkin voinut olla kyseisen kaltainen (Raaflaub et al. 2009). Anaksimandroksen kartta oli vielä hyvin alkeellinen ja yksinkertainen, pelkkä havainnollistus maailman mahdollisesta rakenteesta. Se oli kuitenkin alku kartografiselle esittämismuodolle. Hekataios (n eaa.) paranteli Anaksimandroksen karttaa asettamalla karttaan lisää sisältöä, yksityiskohtaisempaa tietoa tunnettujen paikkojen sijainneista. Hekataios oli tunnettu Aasian matkaaja, jonka kaksi matkakertomusta eivät ole säilyneet, mutta jotka ovat olleet aikanaan merkittäviä tiedonlähteitä (Daly 1879; Raaflaub et al. 2009). Hekataioksen myötä voidaan ajatella alkaneen tieteellisemmän otteen (kreikkalaisessa) kartografiassa. Hän yhdisti empiiristä tietoa paikoista karttaan pelkän maailmanpohdinnan sijaan. Kartat yleistyivät hyvin hitaasti filosofien töistä kansan pariin käyttöesineiksi. Vasta 300-luvulla eaa. kartat alkoivat olla arkipäivää, mutta on olemassa varhaisempia tarinoita ja vitsejä karttoja ymmärtämättömistä, oppimattomista, joiden tietämättömyydelle naurettiin. Yksi kenties tunnetuimpia tarinoita varhaisista kartoista, ja niiden käyttämisestä kartanlukutaidottomuutta hyödyntäen on Herodotuksen kertomus Aristagoraasta. Miletoksen johtaja Aristagoras pyrki saamaan Spartan kuninkaan Cleomeneksen mukaansa sotaretkelle Persiaa vastaan, ja toi tämän eteen kartan, johon oli merkitty koko matka Spartasta Persian pääkaupunkiin Susaan saakka. Aristagoraan tarkoituksena ei ollut näyttää Cleomenekselle reittiä perille, vaan nimenomaan huijata tätä matkan pituudesta, sillä Cleomenes ei kyennyt ymmärtämään mittakaavaa. (Raaflaub et al. 2009) Pikkuhiljaa kartat kuitenkin alkoivat tulla tutummiksi ja Harley & Woodward (1987) antavatkin viitteitä kartoista ja pohjapiirroksista, jotka kertovat karttamaisen esitystavan yleistymisestä käytännön elämän asteille, esimerkiksi kaivoksen ja rakennusten pohjapiirroksia 400-luvulta eaa. Kolmannella vuosisadalla eaa. kartografia alkoi kehittyä nopeasti teoriasta käytäntöön. Yksi tärkeimmistä tekijöistä maailmankarttojen kehitykselle olivat
3 matkakertomukset, ja niiden avulla saatu tieto kaukaisista maista. Aleksanteri Suuren sotaretki kauas Intiaan oli hyvin merkittävä tekijä Aasian tuntemuksen kannalta. Aleksanteri määräsi mukaansa suuren joukon tieteilijöitä, joista osan tehtävä oli taltioida kuljetut matkat ja etäisyydet tarkasti, ja näin luotiin ensi kertaa ajan mittapuulla tarkkoja karttoja itäisistä alueista. Toinen merkittävä matkaaja oli Massilialainen Pytheas, joka oli kaupankävijä, ja tutkimusmatkaaja sekä etevä matemaatikko. Pytheas purjehti Atlantilla Britanniaan, Orkneysaarille ja aina pohjoisen jäisille vesille saakka, ja kertoo löytäneensä sieltä tarujen Thulen, kenties Islannin. Aikalaiset ja historioitsijat, kuten Strabo, pitivät Pytheasta huijarina, ainakin koskien pohjoisia alueita. Nykytietämyksen valossa Pytheaan kertomukset kuulostavat uskottavammilta, mutta tuolloin yleinen käsitys oli, että Euroopan keskiosien korkeudella oli jo äärimmäisen kylmää. Matkakertomuksista ja mittauksista oli varmasti apua kartografian kehittymiselle, mutta tuon ajan karttoja ei ole säilynyt, emmekä tiedä niistä juurikaan. Joitakin kirjallisia kuvauksia kartoista on olemassa, mutta ne eivät kerro kaikkea. Oman lisänsä asian tulkintaan tuo esimerkiksi Strabon oma negatiivinen asenne Pytheaan suhteen. (Harley & Woodward 1987) Arvailuja maapallon pyöreydestä esiintyvät jo varhaisissa teoksissa. Historioitsija Diogenes Laertius mainitsee Parmenideen olleen ensimmäinen, joka esitti ajatuksen maapallosta, ja pallo sijaitsi tämän mukaan universumin keskellä. Ilmeisesti Sokrates ( eaa.), jota toisinaan on pidetty yhtenä merkittävimmistä ajattelijoista maapallon todellisen muodon suhteen, on saanut ajatuksen juuri Parmenideeltä (Daly 1879). Toisten arvioiden mukaan ensimmäisenä pallosta olisikin puhunut Archytas Tarentumilainen (Dutka 1993). Aristoteles ( ekr.) oli kuitenkin jo vakuuttunut maan pyöreydestä, ja perusteli asiaa muun muassa maan varjolla auringonpimennyksen aikana. Aristoteleellä oli jopa ehdotuksensa maan ympärysmitaksi, stadionia, joka käyttäen Herodotosta lähteenä stadionin mitaksi, olisi hämmästyttävän lähellä todellista. Aristoteleen jälkeen käsitys pallon muotoisesta maailmasta oli muodostunut yleiseksi oppineiden keskuudessa, joskaan ei kansan parissa. (Dutka 1993; Daly 1879) Yksi merkittävimmistä kreikkalaisista maantieteilijöistä oli Eratosthenes ( eaa.). Eratosthenestä voidaan pitää jopa tieteellisen kartografian isänä, niin merkittävä on hänen asemansa tieteenalan kehitykselle ollut. Eratosthenes oli monitieteilijä useiden kreikkalaisten suurmiesten tapaan, mutta hänen merkittävimmät työnsä liittyivät maapallon tuntemuksen ja maailmankartan kehitykseen (Harley & Woodward 1987). Eratosthenes oli syntyjään kyreneläinen, opiskellut Ateenassa ja toimi lopulta Aleksandrian kirjaston johtajana. Hänen tunnetuin työnsä oli maapallon ympärysmitan laskeminen. Eratostheneksen omia töitä ei ole säilynyt, mutta aikalaiskirjoitukset ovat selostaneet tämän metodeja, joskin hieman kiistanalaisesti. Edes Eratostheneksen käyttämistä mitoista ei ole täyttä yksimielisyyttä. Hän käyttää mittayksikkönä Stadionia, mutta sen sisällöstä on eri käsityksiä, jonka vuoksi hänen työnsä ja tuloksensa herättävät keskustelua yhä edelleen (Brown 1979, Dutka 1993). Eratostheneksen metodi maapallon ympärysmitan laskemiseksi oli yksinkertaisen nerokas. Hän perusti laskelmansa kolmeen alkuhavaintoon tai oletukseen:
4 maahan saapuvat auringonsäteet ovat yhdensuuntaisia, matka kahden mittauspisteen välillä Aleksandriasta Syeneen on 5000 stadionia, mittauspisteet sijaitsevat samalla pituuspiirillä, ja että Syene sijaitsee kääntöpiirillä. Näin ollen Eratosthenes määritti mittauspisteissä auringon gnomon-mittakepille luoman varjojen pituuden avulla mittapisteiden välisen ympyrän sektorin pituuden, ja sen avulla koko maapallon ympäryksen. Hän joutui kuitenkin lisäämään tulokseensa 2000 stadionia, saadakseen 60:lla jaollisen luvun, ja päätyi näin tulokseen Stadionia. (Dutka 1993; Brown 1979; Daly 1879; Harley & Woodward 1987) Mittaus ei ollut lopulta kovin tarkka. Mittapisteiden välimatka ei ollut täsmällinen, pisteet eivät tosiasiassa sijainneetkaan täsmälleen samalla meridiaanilla eikä Syene sijainnut aivan kääntöpiirillä. Näin ollen Eratostheneksen alkuarvot olivat jo pielessä, ja lisäksi gnomon ja varjon pituuden laskeminen olivat ilmeisen epätarkkoja mittauskeinoja. Eratosthenes tuskin myöskään ymmärsi riittävästi valonsäteiden taittumisesta tai muista asiaan liittyvistä fysikaalisista ilmiöistä (Dutka 1993). Suurin kiista koskee kuitenkin Stadionin pituutta, ei ole selvää, kuinka pitkä oli Eratostheneksen käyttämä stadion, sillä mittayksikön pituus on historian saatossa vaihdellut. Jos käytetään hyväksi keskimääräistä käsitystä stadionin pituudesta, on Eratostheneksen stadionia noin kilometriä, mikä on hyvin lähellä totuutta (Dutka 1993; Brown 1979). On kuvaavaa, että Aristoteles päätyi lukemaan stadionia, mikä oli myös hyvin lähellä totuutta, mikäli stadionin mittaa tulkitaan eritavalla. Eratostheneksen mittaustapa ja tulos olivat merkittäviä, mutta Poseidoniuksen hieman myöhemmin määrittelemä arvo, minkä Strabo vielä virheellisesti välitti eteenpäin huomattavasti pienemmäksi vääristyneenä, valikoitui aikanaan oikeana pidetyksi (Brown 1979). Eratostheneksen toinen päätyö oli kolmeosainen Geographica, jossa hän antoi tarkat ohjeet maailmankartan tekemiseen (Harley & Woodward 1987). Eratosthenes oli omaksunut Dicearchuksen ajatuksen jakaa maailma kahtia eteläiseen ja pohjoiseen, sekä itäiseen ja läntiseen osaan. Eratosthenes määritti vertausleveyspiirinsä kulkemaan Gibraltarilta Ateenan kautta Pohjois-Intiaan, sekä keskimeridiaanin kulkemaan Rhodoksen kautta, ja määritti sijainteja näiden suhteen. On kuitenkin sanottu, että etäisyydet, joita Eratosthenes käytti paikkojen sijoittamiseen kartallaan, eivät olleet hänen omiaan, vaan summittaisia lainauksia eri lähteistä. Hän kuitenkin laski tunnetun maailma koon, ja asetti sen pallon pinnalle, ja määritteli asumiskelvollisen vyöhykkeen, joka kiersi maapallon vyönkaltaisesti tiettyjen leveysasteiden välillä, ja piti mahdollisena, että asuttuja saarekkeita tällä vyöhykkeellä on enemmänkin, kuin pelkkä tuolloin tunnettu maailma (Brown 1979; Harley & Woodward 1987). Eratosthenes tavallaan keksi pituus ja leveyspiirit, mutta ei käyttänyt niitä vielä kovin tieteellisesti. Hän määritti pituuspiirejä kulkemaan tunnettujen paikkojen kautta, eikä matemaattisten laskelmien suhteen. Hipparkhos myöhemmin esitti tästä voimakasta kritiikkiä. Eratostheneksen kartta ei ole säilynyt, mutta siitäkin löytyy rekonstruktio (Kuva 2), jota Harley & Woodward kuitenkin varoittavat pitämästä kovin tarkkana kopiona. Vaikka Strabo, ja muut aikalaiset eivät pitäneet Eratostheneksen karttoja tarpeeksi tieteellisinä tai luotettavina, jäi tämä kuitenkin elämään suurena kartografina ja astronomina sekä
5 matemaatikkona, joka oli yksi harvoista, jota Strabo piti kritiikkinsä arvoisena (Brown 1979). Eratosthenestä voidaan pitää ensimmäisenä, joka aloitti projektioiden ja koordinaatistojen kehittämisen (Harley & Woodward 1987), ja joka puhtaan matemaattisesti määritti maapallon kokoluokkaa ja etäisyyksiä matka-aika-arvioiden sijaan (Daly 1879). Eratosthenes myös esitti jo varhain, että purjehtiminen suoraan Gibraltarilta länteen johtaisi matkaajan Intiaan (Brown 1979). Hipparkhos ( eaa.) tunnetaan parhaiten astronomina ja matemaatikkona, trigonometrian isänä. Hän määritteli esimerkiksi Kuun ja Auringon etäisyyksiä maapallosta (Toomer 1974), mutta oli kuitenkin myös merkittävä kartografi, joka kehitti pidemmälle ja tieteellisemmäksi Eratostheneksen pituus- ja leveyspiirejä. Hipparkhos keksi jakaa maapallon 360 asteeseen, navalta navalle kulkeviin pituuspiireihin, ja päiväntasaajan suuntaisiin leveyspiireihin, jotka kulkivat matemaattisessa suhteessa toisiinsa, ja joiden väliin voitiin aina muodostaa uusia, tarkkaan määriteltyjä pituus- tai leveyspiirejä (Daly 1879). Hipparkhosta voidaan pitää ensimmäisenä puhtaan tieteellisenä kartografina. Hän perusti kaikki havaintonsa vain tarkkaan laskettuihin mittauksiin, ja kritisoikin Eratosthenestä paitsi tämän summittaisista pituus- ja leveyspiireistä, niin myös tämän ajatuksista Intian sijainnista. Eratosthenes määritteli Intian liian pohjoiseen, luottaen liiaksi vanhempaan tietämykseen. Hipparkhos oli puolestaan valmis hylkäämään vanhan, varmana pidetyn tiedon, ja luottamaan pelkästään astronomisiin laskuihinsa. Vaikka Hipparkhoksenkaan laskut eivät aina olleet täydellisen oikeassa, olivat ne huomattavasti kehittyneempiä, kuin aiemmin. Paljon kertoo myös Hipparkhoksen kyvyistä, että Strabo, joka on pääasiallinen lähde suurimpaan osaan aiemmista maantieteilijöistä, ei ymmärtänyt Hipparkhoksen töitä, vaan tallensi ne Geographicaansa väärin (Shcheglov 2005). Hipparkhos myös kyseenalaisti vallitsevat käsitykset asumiskelpoisesta maailmasta. Hän väitti, että asuttava maailma jatkuu huomattavan pitkälle tunnetun maailman ulkopuolelle, esimerkiksi etelässä päiväntasaajalle saakka. Joidenkin tutkijoiden mielestä Hipparkhos ei edes aina yrittänyt ratkoa maantieteellisiä ongelmia, vaan keskittyi puhtaasti kritisoimaan edeltäjiään näiden virheistä kehittääkseen parempia metodeja kartan tekoon (Shcheglov 2005). Hipparkhoksen kartta (kuva 3) on jo selkeästi tieteellisemmän oloinen. Hän ei kuitenkaan kyennyt ratkaisemaan maapallon kaarevuuden ongelmaa kaksiulotteisessa kartassaan kovin tehokkaasti, mutta hänen työnsä astronomian ja kartografian saralla olivat huomattavan merkittävässä asemassa tuleville kartografeille, ja näiden töille. Ptolemaios, jota pidetään yhtenä kartografian merkkipaaluna, on selkeästi saanut vaikutteita Hipparkhoksen uraauurtavasta tavasta jakaa maapallo asteisiin, joita käytämme yhä edelleen.
6 LÄHTEET Brown, L. A. (1979, 1. p. 1949). The story of maps. Dover Publications Inc., New York. Daly, C (1879). The Early History of Cartography, or What We Know of Maps and Map- Making before the Time of Mercator, Journal of the American Geographical Society of New York, Vol. 11 (1879), pp Dutka, Jacques (1993). Eratosthenes' measurement of the earth reconsidered. Archive for History of Exact Sciences 20. VIII. 46/1993, sivut Harley, J & Woodward, D (1987). Cartography in prehistoric, ancient, and medieval Europe and the Mediterranean. 622 s. University of Chicago Press. Perseus Encyclopedia < text?doc=perseus%3atext%3a %3aid%3dstrabo&redirect=true> Pothecary, S (1997). The expression "our times" in Strabo's Geography, Classical Philology Vol. 92, No. 3 (Jul., 1997), pp , The University of Chicago Press Raaflaub, K (2009). Geography and ethnography : Perceptions of the world in pre-modern societies, Wiley-Blackwell, Hoboken, NJ, Yhdysvallat Shcheglov, D (2005). Hipparchus on the Latitude of Southern India. Greek, Roman, and Byzantine Studies 45/2005, sivut Toomer, G (1974). Hipparchus on the distances of the sun and moon. Archive for History of Exact Sciences 31. XII. 14/1974, 2, sivut LIITTEET Kuva 1. Rekonstruktio Anaksimandroksen kartasta (
7 Kuva 2. Rekonstruktio Eratostheneen kartasta ( Kuva 3. Kartta vuodelta 100 eaa., mahdollisesti Hipparkhoksen (
Kartografian historiaa ja perusteita. Taru Tiainen
 Kartografian historiaa ja perusteita Taru Tiainen 18.4.2016 Alkutehtävä Piirrä Joensuun kartta Aikaa n. 5 minuuttia Alkutehtävä Mikä vaikuttaa karttasi tekoon? Miksi kartta on näköisensä? Mitä tämän tehtävän
Kartografian historiaa ja perusteita Taru Tiainen 18.4.2016 Alkutehtävä Piirrä Joensuun kartta Aikaa n. 5 minuuttia Alkutehtävä Mikä vaikuttaa karttasi tekoon? Miksi kartta on näköisensä? Mitä tämän tehtävän
PIKAOPAS 1. Kellotaulun kulma säädetään sijainnin leveys- asteen mukaiseksi.
 Käyttöohje PIKAOPAS 1. Kellotaulun kulma säädetään sijainnin leveysasteen mukaiseksi. Kellossa olevat kaupungit auttavat alkuun, tarkempi leveysasteluku löytyy sijaintisi koordinaateista. 2. Kello asetetaan
Käyttöohje PIKAOPAS 1. Kellotaulun kulma säädetään sijainnin leveysasteen mukaiseksi. Kellossa olevat kaupungit auttavat alkuun, tarkempi leveysasteluku löytyy sijaintisi koordinaateista. 2. Kello asetetaan
1) Maan muodon selvittäminen. 2) Leveys- ja pituuspiirit. 3) Mittaaminen
 1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
1) Maan muodon selvittäminen Nykyään on helppo sanoa, että maa on pallon muotoinen olet todennäköisesti itsekin nähnyt kuvia maasta avaruudesta kuvattuna. Mutta onko maapallomme täydellinen pallo? Tutki
Miina ja Ville etiikkaa etsimässä
 Miina ja Ville etiikkaa etsimässä Elämänkatsomustieto Satu Honkala, Antti Tukonen ja Ritva Tuominen Sisällys Opettajalle...4 Oppilaalle...5 Työtavoista...6 Elämänkatsomustieto oppiaineena...6 1. HYVÄ ELÄMÄ...8
Miina ja Ville etiikkaa etsimässä Elämänkatsomustieto Satu Honkala, Antti Tukonen ja Ritva Tuominen Sisällys Opettajalle...4 Oppilaalle...5 Työtavoista...6 Elämänkatsomustieto oppiaineena...6 1. HYVÄ ELÄMÄ...8
Tähtitieteen historiaa, avaruusgeometrian tehtäviä ja muita tehtäviä
 Tähtitieteen historiaa, avaruusgeometrian tehtäviä ja muita tehtäviä A1. Antiikin kreikkalainen monitieteilijä Eratosthenes (276-194) eaa. onnistui ensimmäisenä mittaamaan 240 eaa. maapallon ympärysmitan
Tähtitieteen historiaa, avaruusgeometrian tehtäviä ja muita tehtäviä A1. Antiikin kreikkalainen monitieteilijä Eratosthenes (276-194) eaa. onnistui ensimmäisenä mittaamaan 240 eaa. maapallon ympärysmitan
Vektorien pistetulo on aina reaaliluku. Esimerkiksi vektorien v = (3, 2, 0) ja w = (1, 2, 3) pistetulo on
 13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
13 Pistetulo Avaruuksissa R 2 ja R 3 on totuttu puhumaan vektorien pituuksista ja vektoreiden välisistä kulmista. Kuten tavallista, näiden käsitteiden yleistäminen korkeampiulotteisiin avaruuksiin ei onnistu
Alkukartoitus Opiskeluvalmiudet
 Alkukartoitus Opiskeluvalmiudet Päivämäärä.. Oppilaitos.. Nimi.. Tehtävä 1 Millainen kielenoppija sinä olet? Merkitse rastilla (x) lauseet, jotka kertovat sinun tyylistäsi oppia ja käyttää kieltä. 1. Muistan
Alkukartoitus Opiskeluvalmiudet Päivämäärä.. Oppilaitos.. Nimi.. Tehtävä 1 Millainen kielenoppija sinä olet? Merkitse rastilla (x) lauseet, jotka kertovat sinun tyylistäsi oppia ja käyttää kieltä. 1. Muistan
1) Ymmärrä - ja tule asiantuntijaksi askel askeleelta
 Tarkkailuharjoitus 4..4. Tarkkailu- harjoitus Tarkkailuvihkotekniikka Alla on kuvattu askel askeleelta etenevät ohjeet siitä, kuinka kuluttajien tarpeita voidaan paljastaa. Tämä metodi auttaa sinua tekemään
Tarkkailuharjoitus 4..4. Tarkkailu- harjoitus Tarkkailuvihkotekniikka Alla on kuvattu askel askeleelta etenevät ohjeet siitä, kuinka kuluttajien tarpeita voidaan paljastaa. Tämä metodi auttaa sinua tekemään
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
Yhtälönratkaisusta. Johanna Rämö, Helsingin yliopisto. 22. syyskuuta 2014
 Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Yhtälönratkaisusta Johanna Rämö, Helsingin yliopisto 22. syyskuuta 2014 Yhtälönratkaisu on koulusta tuttua, mutta usein sitä tehdään mekaanisesti sen kummempia ajattelematta. Jotta pystytään ratkaisemaan
Geometrian kertausta. MAB2 Juhani Kaukoranta Raahen lukio
 Geometrian kertausta MAB2 Juhani Kaukoranta Raahen lukio Ristikulmat Ristikulmat ovat yhtä suuret keskenään Vieruskulmien summa 180 Muodostavat yhdessä oikokulman 180-50 =130 50 Samankohtaiset kulmat Kun
Geometrian kertausta MAB2 Juhani Kaukoranta Raahen lukio Ristikulmat Ristikulmat ovat yhtä suuret keskenään Vieruskulmien summa 180 Muodostavat yhdessä oikokulman 180-50 =130 50 Samankohtaiset kulmat Kun
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Selkokartat Pohjoismaat ja Baltia
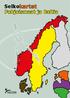 Selkokartat ohjoismaat ja Baltia Selkokartat - ohjoismaat ja Baltia Tekijä:... Tuija iili-jokinen Kuvitus:...Jussi Koskela Asiantuntijakonsultointi:...Ilkka skola Taitto ja kansikuva:...jussi Koskela Kustantaja:...Valteri-koulu
Selkokartat ohjoismaat ja Baltia Selkokartat - ohjoismaat ja Baltia Tekijä:... Tuija iili-jokinen Kuvitus:...Jussi Koskela Asiantuntijakonsultointi:...Ilkka skola Taitto ja kansikuva:...jussi Koskela Kustantaja:...Valteri-koulu
MYYTIT Totta vai tarua?
 MYYTIT Totta vai tarua? MYYTTI ON TARINA Arkikielessä myytti merkitsee usein epätotta, satua, juttua vain. Tämä on myytin todellisen olemuksen sivuuttamista ja vähättelyä! Maailmassa on muitakin totuuksia
MYYTIT Totta vai tarua? MYYTTI ON TARINA Arkikielessä myytti merkitsee usein epätotta, satua, juttua vain. Tämä on myytin todellisen olemuksen sivuuttamista ja vähättelyä! Maailmassa on muitakin totuuksia
Yksilöllisen oppimisen menetelmä. Ville Aitlahti, @matikkamatskut, www.matikkamatskut.com
 Yksilöllisen oppimisen menetelmä Yksilöllisen oppimisen menetelmä Tarve menetelmän takana: http://youtu.be/dep6mcnbh_c Oman oppimisen omistaminen Opettajan tietyt raamit toiminnalle Oman oppimisen omistaminen
Yksilöllisen oppimisen menetelmä Yksilöllisen oppimisen menetelmä Tarve menetelmän takana: http://youtu.be/dep6mcnbh_c Oman oppimisen omistaminen Opettajan tietyt raamit toiminnalle Oman oppimisen omistaminen
OSA 3: GEOMETRIAA. Alkupala. Kokoa neljästä alla olevasta palasesta M kirjain.
 OSA 3: GEOMETRIAA Tekijät: Ari Heimonen, Hellevi Kupila, Katja Leinonen, Tuomo Talala, Hanna Tuhkanen, Pekka Vaaraniemi Alkupala Kokoa neljästä alla olevasta palasesta M kirjain. G. GEOMETRIAA Hannu ja
OSA 3: GEOMETRIAA Tekijät: Ari Heimonen, Hellevi Kupila, Katja Leinonen, Tuomo Talala, Hanna Tuhkanen, Pekka Vaaraniemi Alkupala Kokoa neljästä alla olevasta palasesta M kirjain. G. GEOMETRIAA Hannu ja
Lataa Tieteen lyhyt historia - vai pitkä tie luonnonfilosofian ja empirismin kohtaamiseen - Tuomo Suntola. Lataa
 Lataa Tieteen lyhyt historia - vai pitkä tie luonnonfilosofian ja empirismin kohtaamiseen - Tuomo Suntola Lataa Kirjailija: Tuomo Suntola ISBN: 9789526723686 Sivumäärä: 290 Formaatti: PDF Tiedoston koko:
Lataa Tieteen lyhyt historia - vai pitkä tie luonnonfilosofian ja empirismin kohtaamiseen - Tuomo Suntola Lataa Kirjailija: Tuomo Suntola ISBN: 9789526723686 Sivumäärä: 290 Formaatti: PDF Tiedoston koko:
Sävel Oskar Merikanto Sanat Pekka Ervast
 Sävel Oskar Merikanto Sanat Pekka Ervast KUOLEMAN KUNNIAKSI Pekka Ervast Oskar Merikanto Teoksen taustaa Tukholman kongressi 1913 ja Oskar Merikanto. Kuten lukijamme tietävät, pidetään ensi kesänä Tukholmassa
Sävel Oskar Merikanto Sanat Pekka Ervast KUOLEMAN KUNNIAKSI Pekka Ervast Oskar Merikanto Teoksen taustaa Tukholman kongressi 1913 ja Oskar Merikanto. Kuten lukijamme tietävät, pidetään ensi kesänä Tukholmassa
MATEMAATTIS- LUONNONTIETEELLINEN OSAAMINEN
 MATEMAATTIS- LUONNONTIETEELLINEN OSAAMINEN Matematiikka ja matematiikan soveltaminen, 4 osp Pakollinen tutkinnon osa osaa tehdä peruslaskutoimitukset, toteuttaa mittayksiköiden muunnokset ja soveltaa talousmatematiikkaa
MATEMAATTIS- LUONNONTIETEELLINEN OSAAMINEN Matematiikka ja matematiikan soveltaminen, 4 osp Pakollinen tutkinnon osa osaa tehdä peruslaskutoimitukset, toteuttaa mittayksiköiden muunnokset ja soveltaa talousmatematiikkaa
Tieteellisiä havaintoja kännykällä
 Tieteellisiä havaintoja kännykällä Havainto Arkipäivässäkin voi tehdä tieteellisiä havaintoja erilaisista luonnonilmiöistä. Tieteellisiin havaintoihin kuuluu havainnon dokumentointi ja erilaisten mittausten
Tieteellisiä havaintoja kännykällä Havainto Arkipäivässäkin voi tehdä tieteellisiä havaintoja erilaisista luonnonilmiöistä. Tieteellisiin havaintoihin kuuluu havainnon dokumentointi ja erilaisten mittausten
LIITE 1 VIRHEEN ARVIOINNISTA
 1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
1 Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi miten uudenaikainen tai kallis tahansa ja mittaaja olisi alansa huippututkija Tästä johtuen mittaustuloksista
GeoGebran 3D paketti
 GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
GeoGebran 3D paketti vielä kehittelyvaiheessa joitakin puutteita ja virheitä löytyy! suomennos kesken parhaimmillaan yhdistettynä 3D-lasien kanssa tilattavissa esim. netistä (hinta noin euron/lasit) 3D-version
1 Laske ympyrän kehän pituus, kun
 Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
Ympyrään liittyviä harjoituksia 1 Laske ympyrän kehän pituus, kun a) ympyrän halkaisijan pituus on 17 cm b) ympyrän säteen pituus on 1 33 cm 3 2 Kuinka pitkä on ympyrän säde, jos sen kehä on yhden metrin
Tähtitieteen historiaa
 Tähtitiede Sisältö: Tähtitieteen historia Kokeellisen tiedonhankinnan menetelmät Perusteoriat Alkuräjähdysteoria Gravitaatiolaki Suhteellisuusteoria Alkuaineiden syntymekanismit Tähtitieteen käsitteitä
Tähtitiede Sisältö: Tähtitieteen historia Kokeellisen tiedonhankinnan menetelmät Perusteoriat Alkuräjähdysteoria Gravitaatiolaki Suhteellisuusteoria Alkuaineiden syntymekanismit Tähtitieteen käsitteitä
AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla
 AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla Tähtitieteellinen merenkulkuoppi on oppi, jolla määrätään aluksen sijainti taivaankappaleiden perusteella. Paikanmääritysmenetelmänäon ristisuuntiman
AVOMERINAVIGOINTI eli paikanmääritys taivaankappaleiden avulla Tähtitieteellinen merenkulkuoppi on oppi, jolla määrätään aluksen sijainti taivaankappaleiden perusteella. Paikanmääritysmenetelmänäon ristisuuntiman
Radiotekniikan sovelluksia
 Poutanen: GPS-paikanmääritys sivut 72 90 Kai Hahtokari 11.2.2002 Konventionaalinen inertiaalijärjestelmä (CIS) Järjestelmä, jossa z - akseli osoittaa maapallon impulssimomenttivektorin suuntaan standardiepookkina
Poutanen: GPS-paikanmääritys sivut 72 90 Kai Hahtokari 11.2.2002 Konventionaalinen inertiaalijärjestelmä (CIS) Järjestelmä, jossa z - akseli osoittaa maapallon impulssimomenttivektorin suuntaan standardiepookkina
4. Varastossa on 24, 23, 17 ja 16 kg:n säkkejä. Miten voidaan toimittaa täsmälleen 100 kg:n tilaus avaamatta yhtään säkkiä?
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 3.2.2012 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 3.2.2012 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Matematiikka vuosiluokat 7 9
 Matematiikka vuosiluokat 7 9 Matematiikan opetuksen ydintehtävänä on tarjota oppilaille mahdollisuus hankkia sellaiset matemaattiset taidot, jotka antavat valmiuksia selviytyä jokapäiväisissä toiminnoissa
Matematiikka vuosiluokat 7 9 Matematiikan opetuksen ydintehtävänä on tarjota oppilaille mahdollisuus hankkia sellaiset matemaattiset taidot, jotka antavat valmiuksia selviytyä jokapäiväisissä toiminnoissa
Kieli merkitys ja logiikka. 2: Helpot ja monimutkaiset. Luento 2. Monimutkaiset ongelmat. Monimutkaiset ongelmat
 Luento 2. Kieli merkitys ja logiikka 2: Helpot ja monimutkaiset Helpot ja monimutkaiset ongelmat Tehtävä: etsi säkillinen rahaa talosta, jossa on monta huonetta. Ratkaisu: täydellinen haku käy huoneet
Luento 2. Kieli merkitys ja logiikka 2: Helpot ja monimutkaiset Helpot ja monimutkaiset ongelmat Tehtävä: etsi säkillinen rahaa talosta, jossa on monta huonetta. Ratkaisu: täydellinen haku käy huoneet
Oppilas vahvistaa opittuja taitojaan, kiinnostuu oppimaan uutta ja saa tukea myönteisen minäkuvan kasvuun matematiikan oppijana.
 Tavoitteet S L 3. lk 4. lk 5. lk 6. lk Merkitys, arvot ja asenteet T1 pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta L1, L3, L5
Tavoitteet S L 3. lk 4. lk 5. lk 6. lk Merkitys, arvot ja asenteet T1 pitää yllä oppilaan innostusta ja kiinnostusta matematiikkaa kohtaan sekä tukea myönteistä minäkuvaa ja itseluottamusta L1, L3, L5
Fysiikan historia Luento 2
 Fysiikan historia Luento 2 Ibn al- Haytham (Alhazen), ensimmäinen tiedemies Keskiajan tiede Kiinnostus =iloso=iaa ja luonnontiedettä kohtaan alkoi laantua Rooman vallan kasvaessa Osa vanhasta tiedosta
Fysiikan historia Luento 2 Ibn al- Haytham (Alhazen), ensimmäinen tiedemies Keskiajan tiede Kiinnostus =iloso=iaa ja luonnontiedettä kohtaan alkoi laantua Rooman vallan kasvaessa Osa vanhasta tiedosta
Luento 6: 3-D koordinaatit
 Maa-57.300 Fotogrammetrian perusteet Luento-ohjelma 1 2 3 4 5 6 7 8 9 10 11 12 13 Luento 6: 3-D koordinaatit AIHEITA (Alkuperäinen luento: Henrik Haggrén, 16.2.2003, Päivityksiä: Katri Koistinen 5.2.2004
Maa-57.300 Fotogrammetrian perusteet Luento-ohjelma 1 2 3 4 5 6 7 8 9 10 11 12 13 Luento 6: 3-D koordinaatit AIHEITA (Alkuperäinen luento: Henrik Haggrén, 16.2.2003, Päivityksiä: Katri Koistinen 5.2.2004
9. Vektorit. 9.1 Skalaarit ja vektorit. 9.2 Vektorit tasossa
 9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
9. Vektorit 9.1 Skalaarit ja vektorit Skalaari on koon tai määrän mitta. Tyypillinen esimerkki skalaarista on massa. Lukumäärä on toinen hyvä esimerkki skalaarista. Vektorilla on taas suuruus ja suunta.
TUKIMATERIAALI: Arvosanan kahdeksan alle jäävä osaaminen
 MAANTIETO Maantiedon päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Sisältöalueet Maantieteellinen tieto ja ymmärrys T1 tukea oppilaan jäsentyneen karttakuvan
MAANTIETO Maantiedon päättöarvioinnin kriteerit arvosanalle 8 ja niitä täydentävä tukimateriaali Opetuksen tavoite Sisältöalueet Maantieteellinen tieto ja ymmärrys T1 tukea oppilaan jäsentyneen karttakuvan
Mikä ihmeen Global Mindedness?
 Ulkomaanjakson vaikutukset opiskelijan asenteisiin ja erilaisen kohtaamiseen Global Mindedness kyselyn alustavia tuloksia Irma Garam, CIMO LdV kesäpäivät 4.6.2 Jun- 14 Mikä ihmeen Global Mindedness? Kysely,
Ulkomaanjakson vaikutukset opiskelijan asenteisiin ja erilaisen kohtaamiseen Global Mindedness kyselyn alustavia tuloksia Irma Garam, CIMO LdV kesäpäivät 4.6.2 Jun- 14 Mikä ihmeen Global Mindedness? Kysely,
Pisan 2012 tulokset ja johtopäätökset
 Pisan 2012 tulokset ja johtopäätökset Jouni Välijärvi, professori Koulutuksen tutkimuslaitos Jyväskylän yliopisto PISA ja opettajankoulutuksen kehittäminen-seminaari Tampere 14.3.2014 17.3.2014 PISA 2012
Pisan 2012 tulokset ja johtopäätökset Jouni Välijärvi, professori Koulutuksen tutkimuslaitos Jyväskylän yliopisto PISA ja opettajankoulutuksen kehittäminen-seminaari Tampere 14.3.2014 17.3.2014 PISA 2012
Harjoittelijoiden palaute yliopiston tukemasta harjoittelusta 2012
 Harjoittelijoiden palaute yliopiston tukemasta harjoittelusta 2012 Urapalvelut/ Susan Blomberg Yliopisto tukee opiskelijoidensa työharjoittelua myöntämällä harjoittelutukea tutkintoon sisällytettävään
Harjoittelijoiden palaute yliopiston tukemasta harjoittelusta 2012 Urapalvelut/ Susan Blomberg Yliopisto tukee opiskelijoidensa työharjoittelua myöntämällä harjoittelutukea tutkintoon sisällytettävään
Herra on Paimen. Ps. 100:3 Tietäkää, että Herra on Jumala. Hän on meidät luonut, ja hänen me olemme, hänen kansansa, hänen laitumensa lampaat.
 Herra on Paimen Ps. 100:3 Tietäkää, että Herra on Jumala. Hän on meidät luonut, ja hänen me olemme, hänen kansansa, hänen laitumensa lampaat. Joh. 10:11 Minä olen se hyvä paimen. Joh. 10:11 Minä olen
Herra on Paimen Ps. 100:3 Tietäkää, että Herra on Jumala. Hän on meidät luonut, ja hänen me olemme, hänen kansansa, hänen laitumensa lampaat. Joh. 10:11 Minä olen se hyvä paimen. Joh. 10:11 Minä olen
Vuosilustot ilmastohistorian tulkkina
 Esitelmä Voitto Valio Viinasen Inarin rajahistoria II kirjan julkistamistilaisuudessa Inarin Siidassa 16.12.2006 Vuosilustot ilmastohistorian tulkkina Mauri Timonen Metla, Rovaniemen tutkimusyksikkö Metsäntutkimuslaitos
Esitelmä Voitto Valio Viinasen Inarin rajahistoria II kirjan julkistamistilaisuudessa Inarin Siidassa 16.12.2006 Vuosilustot ilmastohistorian tulkkina Mauri Timonen Metla, Rovaniemen tutkimusyksikkö Metsäntutkimuslaitos
Asiakirjojen vertailu-kurssi
 Asiakirjojen vertailu-kurssi Revussa voi verrata keskenään kahta PDF:ää ja automaattisesti näyttää niiden väliset erot. Piirrosten ja kaaviokuvien vertailu sujuu siten helposti ja nopeasti. Kun haluat
Asiakirjojen vertailu-kurssi Revussa voi verrata keskenään kahta PDF:ää ja automaattisesti näyttää niiden väliset erot. Piirrosten ja kaaviokuvien vertailu sujuu siten helposti ja nopeasti. Kun haluat
Viestintätieteet VIESTINTÄTIETEET , N = 193
 Viestintätieteet 2013-15 VIESTINTÄTIETEET 2013-15, N = 193 Viestintätieteiden opiskelijoilla pitkä matematiikka (27 %) on pienemmällä osuudella kuin lyhyt (40 %) tai ei matematiikkaa (33 %). Reaaliaineista
Viestintätieteet 2013-15 VIESTINTÄTIETEET 2013-15, N = 193 Viestintätieteiden opiskelijoilla pitkä matematiikka (27 %) on pienemmällä osuudella kuin lyhyt (40 %) tai ei matematiikkaa (33 %). Reaaliaineista
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon
 Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Ohje tutkielman tekemiseen
 Sauvon koulukeskus 2011 Ohje tutkielman tekemiseen Aiheen valinta Etsi materiaalia Valitse itseäsi kiinnostava aihe. Sovi opettajan kanssa aiheen rajaus. Pyydä opettajalta tutkielmapassiin merkintä aiheen
Sauvon koulukeskus 2011 Ohje tutkielman tekemiseen Aiheen valinta Etsi materiaalia Valitse itseäsi kiinnostava aihe. Sovi opettajan kanssa aiheen rajaus. Pyydä opettajalta tutkielmapassiin merkintä aiheen
Evoluutiopuu. Aluksi. Avainsanat: biomatematiikka, päättely, kombinatoriikka, verkot. Luokkataso: 6.-9. luokka, lukio
 Evoluutiopuu Avainsanat: biomatematiikka, päättely, kombinatoriikka, verkot Luokkataso: 6.-9. luokka, lukio Välineet: loogiset palat, paperia, kyniä Kuvaus: Tehtävässä tutkitaan bakteerien evoluutiota.
Evoluutiopuu Avainsanat: biomatematiikka, päättely, kombinatoriikka, verkot Luokkataso: 6.-9. luokka, lukio Välineet: loogiset palat, paperia, kyniä Kuvaus: Tehtävässä tutkitaan bakteerien evoluutiota.
Trigonometriset funktiot 1/7 Sisältö ESITIEDOT: reaalifunktiot
 Trigonometriset funktiot 1/7 Sisältö Trigonometriset funktiot suorakulmaisessa kolmiossa a c b Olkoon suorakulmaisen kolmion terävä kulma, a tämän vastainen kateetti, b viereinen kateetti ja c kolmion
Trigonometriset funktiot 1/7 Sisältö Trigonometriset funktiot suorakulmaisessa kolmiossa a c b Olkoon suorakulmaisen kolmion terävä kulma, a tämän vastainen kateetti, b viereinen kateetti ja c kolmion
1.2 Yhtälön avulla ratkaistavat probleemat
 1.2 Yhtälön avulla ratkaistavat probleemat Kun matemaattista probleemaa lähdetään ratkaisemaan yhtälöä hyväksi käyttäen, tilanne on vaikeampi kuin ratkaistaessa yhtälöä mekaanisesti. Nyt on näet itse laadittava
1.2 Yhtälön avulla ratkaistavat probleemat Kun matemaattista probleemaa lähdetään ratkaisemaan yhtälöä hyväksi käyttäen, tilanne on vaikeampi kuin ratkaistaessa yhtälöä mekaanisesti. Nyt on näet itse laadittava
Humanistiset tieteet
 Humanistiset tieteet 2013-15 Kielet kuuluvat humanistisiin tieteisiin, joten aluksi tarkastellaan humanistisia tieteitä yleensä. Kielissä on todistusvalinnan kannalta peräti 17 vaihtoehtoa, joista monet
Humanistiset tieteet 2013-15 Kielet kuuluvat humanistisiin tieteisiin, joten aluksi tarkastellaan humanistisia tieteitä yleensä. Kielissä on todistusvalinnan kannalta peräti 17 vaihtoehtoa, joista monet
10.11.2011. Ja Pohjolan karttakuvan hahmottuminen (n. 1427-1626) Olaus Magnus ja Pohjolan karttakuvan hahmottuminen 1500-luvulla
 Ja Pohjolan karttakuvan hahmottuminen (n. 1427-1626) Olaus Magnus ja Pohjolan karttakuvan hahmottuminen 1500-luvulla 1 Maanmittaus määrittää mittauksin maastokohteiden sijaintia, muotoa ja kokoa (pinta-ala).
Ja Pohjolan karttakuvan hahmottuminen (n. 1427-1626) Olaus Magnus ja Pohjolan karttakuvan hahmottuminen 1500-luvulla 1 Maanmittaus määrittää mittauksin maastokohteiden sijaintia, muotoa ja kokoa (pinta-ala).
Fysikaaliset tieteet, kemia ja matemaattiset tieteet
 Fysikaaliset tieteet, kemia ja matemaattiset tieteet LUONNONTIETEET 2013-15 Tarkastellaan kokonaiskuvan saamiseksi ensin luonnontieteitä kokonaisuutena. Luonnontieteissä pitkän matematiikan paino on suuri
Fysikaaliset tieteet, kemia ja matemaattiset tieteet LUONNONTIETEET 2013-15 Tarkastellaan kokonaiskuvan saamiseksi ensin luonnontieteitä kokonaisuutena. Luonnontieteissä pitkän matematiikan paino on suuri
Kuva Suomen päätieverkko 1 Moottoritiet on merkitty karttaan vihreällä, muut valtatiet punaisella ja kantatiet keltaisella värillä.
 POHDIN projekti TIEVERKKO Tieverkon etäisyyksien minimointi ja esimerkiksi maakaapeleiden kokonaismäärän minimointi sekä ylipäätään äärellisen pistejoukon yhdistäminen reitityksillä toisiinsa niin, että
POHDIN projekti TIEVERKKO Tieverkon etäisyyksien minimointi ja esimerkiksi maakaapeleiden kokonaismäärän minimointi sekä ylipäätään äärellisen pistejoukon yhdistäminen reitityksillä toisiinsa niin, että
SIIVOJA HALLITSEE EKG-REKISTERÖINNIN, VAIKKA SE ON VAIKEAA JOPA KLIINISEN FYSIOLOGIAN ERIKOISHOITAJILLE!
 Hanna-Maarit Riski Yliopettaja Turun ammattikorkeakoulu SIIVOJA HALLITSEE EKG-REKISTERÖINNIN, VAIKKA SE ON VAIKEAA JOPA KLIINISEN FYSIOLOGIAN ERIKOISHOITAJILLE! JOHDANTO Iltasanomissa 17.3.2011 oli artikkeli,
Hanna-Maarit Riski Yliopettaja Turun ammattikorkeakoulu SIIVOJA HALLITSEE EKG-REKISTERÖINNIN, VAIKKA SE ON VAIKEAA JOPA KLIINISEN FYSIOLOGIAN ERIKOISHOITAJILLE! JOHDANTO Iltasanomissa 17.3.2011 oli artikkeli,
Raamatun lainaukset vuoden 1992 raamatunkäännöksestä.
 elämä alkaa tästä 2008 Evangelism Explosion International Kaikki oikeudet pidätetään. Ei saa kopioida missään muodossa ilman kirjallista lupaa. Raamatun lainaukset vuoden 1992 raamatunkäännöksestä. Asteikolla
elämä alkaa tästä 2008 Evangelism Explosion International Kaikki oikeudet pidätetään. Ei saa kopioida missään muodossa ilman kirjallista lupaa. Raamatun lainaukset vuoden 1992 raamatunkäännöksestä. Asteikolla
Eikev 5. Moos 7: 12-11: 25
 1 Eikev 5. Moos 7: 12-11: 25 Hepreankielisessä sanassa eikev on hyvin paljon tarkoitusta. Ensimmäinen tarkoitus on: johdonmukainen, askel askeleelta eteenpäin. Sana eikev tarkoittaa myös kantapäätä. Kaikkivaltias
1 Eikev 5. Moos 7: 12-11: 25 Hepreankielisessä sanassa eikev on hyvin paljon tarkoitusta. Ensimmäinen tarkoitus on: johdonmukainen, askel askeleelta eteenpäin. Sana eikev tarkoittaa myös kantapäätä. Kaikkivaltias
1 Tieteellinen esitystapa, yksiköt ja dimensiot
 1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
1 Tieteellinen esitystapa, yksiköt ja dimensiot 1.1 Tieteellinen esitystapa Maan ja auringon välinen etäisyys on 1 AU. AU on astronomical unit, joka määritelmänsä mukaan on maan ja auringon välinen keskimääräinen
Cantorin joukon suoristuvuus tasossa
 Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
Cantorin joukon suoristuvuus tasossa LuK-tutkielma Miika Savolainen 2380207 Matemaattisten tieteiden laitos Oulun yliopisto Syksy 2016 Sisältö Johdanto 2 1 Cantorin joukon esittely 2 2 Suoristuvuus ja
ELOKUVATYÖKALUN KÄYTTÖ ANIMAATION LEIKKAAMISESSA. Kun aloitetaan uusi projekti, on se ensimmäisenä syytä tallentaa.
 ELOKUVATYÖKALUN KÄYTTÖ ANIMAATION LEIKKAAMISESSA Kun aloitetaan uusi projekti, on se ensimmäisenä syytä tallentaa. Projekti kannattaa tallentaa muutenkin aina sillöin tällöin, jos käy niin ikävästi että
ELOKUVATYÖKALUN KÄYTTÖ ANIMAATION LEIKKAAMISESSA Kun aloitetaan uusi projekti, on se ensimmäisenä syytä tallentaa. Projekti kannattaa tallentaa muutenkin aina sillöin tällöin, jos käy niin ikävästi että
JEESUS RUKOILEE GETSEMANESSA
 Suomen Tunnustuksellinen PYHÄKOULUMATERIAALI 1(5) JEESUS RUKOILEE GETSEMANESSA 1. Kertomuksen taustatietoja a) Missä kertomus tapahtui Getsemane-niminen puutarha, yrttitarha Öljymäellä. b) Ajallinen yhteys
Suomen Tunnustuksellinen PYHÄKOULUMATERIAALI 1(5) JEESUS RUKOILEE GETSEMANESSA 1. Kertomuksen taustatietoja a) Missä kertomus tapahtui Getsemane-niminen puutarha, yrttitarha Öljymäellä. b) Ajallinen yhteys
Työ 5: Putoamiskiihtyvyys
 Työ 5: Putoamiskiihtyvyys Työryhmä: Tehty (pvm): Hyväksytty (pvm): Hyväksyjä: 1. Tavoitteet Työssä määritetään putoamiskiihtyvyys kolmella eri tavalla. Ennakko-oletuksena mietitään, pitäisikö jollain tavoista
Työ 5: Putoamiskiihtyvyys Työryhmä: Tehty (pvm): Hyväksytty (pvm): Hyväksyjä: 1. Tavoitteet Työssä määritetään putoamiskiihtyvyys kolmella eri tavalla. Ennakko-oletuksena mietitään, pitäisikö jollain tavoista
KESKEISET SISÄLLÖT Keskeiset sisällöt voivat vaihdella eri vuositasoilla opetusjärjestelyjen mukaan.
 VUOSILUOKAT 6 9 Vuosiluokkien 6 9 matematiikan opetuksen ydintehtävänä on syventää matemaattisten käsitteiden ymmärtämistä ja tarjota riittävät perusvalmiudet. Perusvalmiuksiin kuuluvat arkipäivän matemaattisten
VUOSILUOKAT 6 9 Vuosiluokkien 6 9 matematiikan opetuksen ydintehtävänä on syventää matemaattisten käsitteiden ymmärtämistä ja tarjota riittävät perusvalmiudet. Perusvalmiuksiin kuuluvat arkipäivän matemaattisten
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö
 3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
3.3 Paraabeli toisen asteen polynomifunktion kuvaajana. Toisen asteen epäyhtälö Yhtälön (tai funktion) y = a + b + c, missä a 0, kuvaaja ei ole suora, mutta ei ole yhtälökään ensimmäistä astetta. Funktioiden
MAA8 Juuri- ja logaritmifunktiot, Opintokortti
 MAA8 Juuri- ja logaritmifunktiot, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin
MAA8 Juuri- ja logaritmifunktiot, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin
33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ
 TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
TYÖOHJE 14.7.2010 JMK, TSU 33 SOLENOIDIN JA TOROIDIN MAGNEETTIKENTTÄ Laitteisto: Kuva 1. Kytkentä solenoidin ja toroidin magneettikenttien mittausta varten. Käytä samaa digitaalista jännitemittaria molempien
Mihin teoreettista filosofiaa tarvitaan?
 Mihin teoreettista filosofiaa tarvitaan? Puhe virtaa virtaavassa maailmassa, puhe virtaa virtaavassa maailmassa ja sinun täytyy itse tietää miltei kaikki. Paavo Haavikko TIETÄMISEN HAASTEET TIETOYHTEISKUNNASSA
Mihin teoreettista filosofiaa tarvitaan? Puhe virtaa virtaavassa maailmassa, puhe virtaa virtaavassa maailmassa ja sinun täytyy itse tietää miltei kaikki. Paavo Haavikko TIETÄMISEN HAASTEET TIETOYHTEISKUNNASSA
Kolminaisuusoppi. Jumala: Isä - Poika - Pyhä Henki
 Kolminaisuusoppi Jumala: Isä - Poika - Pyhä Henki KOLMINAISUUSOPPI - KIRKON TÄRKEIN OPPI Kolminaisuusoppia pidetään yhtenä kristinuskon tärkeimmistä opeista. Se erottaa kirkon uskon muista uskonnoista.
Kolminaisuusoppi Jumala: Isä - Poika - Pyhä Henki KOLMINAISUUSOPPI - KIRKON TÄRKEIN OPPI Kolminaisuusoppia pidetään yhtenä kristinuskon tärkeimmistä opeista. Se erottaa kirkon uskon muista uskonnoista.
2.12.2011. Titta Hänninen
 2.12.2011 Titta Hänninen Kotitehtävätekstit! Palauta viimeistään, viimeistään, viimeistään ensi viikolla (koska meillä on viimeinen tunti)! OHJE JEŠTĔ JEDNOU: 1. Etsi internetistä jokin suomenkielinen
2.12.2011 Titta Hänninen Kotitehtävätekstit! Palauta viimeistään, viimeistään, viimeistään ensi viikolla (koska meillä on viimeinen tunti)! OHJE JEŠTĔ JEDNOU: 1. Etsi internetistä jokin suomenkielinen
Platonin kappaleet. Avainsanat: geometria, matematiikan historia. Luokkataso: 6-9, lukio. Välineet: Polydron-rakennussarja, kynä, paperia.
 Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Kolmannen ja neljännen asteen yhtälöistä
 Solmu /019 7 Kolmannen neljännen asteen yhtälöistä Esa V. Vesalainen Matematik och statistik, Åbo Akademi Tämän pienen artikkelin tarkoituksena on satuilla hieman algebrallisista yhtälöistä. Erityisesti
Solmu /019 7 Kolmannen neljännen asteen yhtälöistä Esa V. Vesalainen Matematik och statistik, Åbo Akademi Tämän pienen artikkelin tarkoituksena on satuilla hieman algebrallisista yhtälöistä. Erityisesti
Lajittelumenetelmät ilmakehän kaukokartoituksen laadun tarkkailussa (valmiin työn esittely)
 Lajittelumenetelmät ilmakehän kaukokartoituksen laadun tarkkailussa (valmiin työn esittely) Viivi Halla-aho 30.9.2013 Ohjaaja: Dos. Johanna Tamminen Valvoja: Prof. Harri Ehtamo Työn saa tallentaa ja julkistaa
Lajittelumenetelmät ilmakehän kaukokartoituksen laadun tarkkailussa (valmiin työn esittely) Viivi Halla-aho 30.9.2013 Ohjaaja: Dos. Johanna Tamminen Valvoja: Prof. Harri Ehtamo Työn saa tallentaa ja julkistaa
Tekijä Pitkä matematiikka Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4).
 Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tekijä Pitkä matematiikka 4 9.12.2016 212 Suoran pisteitä ovat esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4). Vastaus esimerkiksi ( 5, 2), ( 2,1), (1, 0), (4, 1) ja ( 11, 4) 213 Merkitään pistettä
Tuntisuunnitelma Maanjäristykset Kreikassa Työohje
 Tuntisuunnitelma Maanjäristykset Kreikassa Työohje Johdanto: Kreikassa on Euroopan maista eniten maanjäristyksiä ja se on yksi koko maailman seismisesti aktiivisimmista maista. Siksi tietämys maanjäristysten
Tuntisuunnitelma Maanjäristykset Kreikassa Työohje Johdanto: Kreikassa on Euroopan maista eniten maanjäristyksiä ja se on yksi koko maailman seismisesti aktiivisimmista maista. Siksi tietämys maanjäristysten
3 Suorat ja tasot. 3.1 Suora. Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta.
 3 Suorat ja tasot Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta. 3.1 Suora Havaitsimme skalaarikertolaskun tulkinnan yhteydessä, että jos on mikä tahansa nollasta
3 Suorat ja tasot Tässä luvussa käsitellään avaruuksien R 2 ja R 3 suoria ja tasoja vektoreiden näkökulmasta. 3.1 Suora Havaitsimme skalaarikertolaskun tulkinnan yhteydessä, että jos on mikä tahansa nollasta
Lataa Fysiikka - Hannu Karttunen. Lataa
 Lataa Fysiikka - Hannu Karttunen Lataa Kirjailija: Hannu Karttunen ISBN: 9789525329322 Sivumäärä: 133 Formaatti: PDF Tiedoston koko: 39.85 Mb Fysiikka on jaoteltu oppikirjoissa perinteisesti sellaisiin
Lataa Fysiikka - Hannu Karttunen Lataa Kirjailija: Hannu Karttunen ISBN: 9789525329322 Sivumäärä: 133 Formaatti: PDF Tiedoston koko: 39.85 Mb Fysiikka on jaoteltu oppikirjoissa perinteisesti sellaisiin
AURINKO VALON JA VARJON LÄHDE
 AURINKO VALON JA VARJON LÄHDE Tavoite: Tarkkaillaan auringon vaikutusta valon lähteenä ja sen vaihtelua vuorokauden ja vuodenaikojen mukaan. Oppilaat voivat tutustua myös aurinkoenergian käsitteeseen.
AURINKO VALON JA VARJON LÄHDE Tavoite: Tarkkaillaan auringon vaikutusta valon lähteenä ja sen vaihtelua vuorokauden ja vuodenaikojen mukaan. Oppilaat voivat tutustua myös aurinkoenergian käsitteeseen.
Vastaajan nimi. Yhteiskuntatieteiden tiedekunta Hallintotieteiden valintakoe Valintakokeesta saatava yhteispistemäärä max. 40 pist.
 1 Yhteiskuntatieteiden tiedekunta Hallintotieteiden valintakoe 14.6.2005 Valintakokeesta saatava yhteispistemäärä max. 40 pist. TEHTÄVÄ I (max. 15 pistettä) Artikkeli Epäluottamusta luovat tekijät kunnanhallituksen
1 Yhteiskuntatieteiden tiedekunta Hallintotieteiden valintakoe 14.6.2005 Valintakokeesta saatava yhteispistemäärä max. 40 pist. TEHTÄVÄ I (max. 15 pistettä) Artikkeli Epäluottamusta luovat tekijät kunnanhallituksen
Tentti erilaiset kysymystyypit
 Tentti erilaiset kysymystyypit Monivalinta Monivalintatehtävässä opiskelija valitsee vastauksen valmiiden vastausvaihtoehtojen joukosta. Tehtävään voi olla yksi tai useampi oikea vastaus. Varmista, että
Tentti erilaiset kysymystyypit Monivalinta Monivalintatehtävässä opiskelija valitsee vastauksen valmiiden vastausvaihtoehtojen joukosta. Tehtävään voi olla yksi tai useampi oikea vastaus. Varmista, että
ARVI-järjestelmän ohje arvioinnin syöttäjälle 13.4. 2015
 ARVI-järjestelmän ohje arvioinnin syöttäjälle 13.4. 2015 Sisältö ARVI-menettelyn perusteet... 1 Arvioinnin syöttäminen... 2 Arvion lähettäminen TE-toimistoon... 5 Sovelluksen sulkeminen... 6 Virhetilanteiden
ARVI-järjestelmän ohje arvioinnin syöttäjälle 13.4. 2015 Sisältö ARVI-menettelyn perusteet... 1 Arvioinnin syöttäminen... 2 Arvion lähettäminen TE-toimistoon... 5 Sovelluksen sulkeminen... 6 Virhetilanteiden
JEESUS ARMAHTAA AVIONRIKKOJANAISEN
 Suomen Tunnustuksellinen PYHÄKOULUMATERIAALI 1(5) JEESUS ARMAHTAA AVIONRIKKOJANAISEN 1. Kertomuksen taustatietoja a) Kertomuksen tapahtumapaikka - pyhäkössä Suomen Tunnustuksellinen PYHÄKOULUMATERIAALI
Suomen Tunnustuksellinen PYHÄKOULUMATERIAALI 1(5) JEESUS ARMAHTAA AVIONRIKKOJANAISEN 1. Kertomuksen taustatietoja a) Kertomuksen tapahtumapaikka - pyhäkössä Suomen Tunnustuksellinen PYHÄKOULUMATERIAALI
Kristuksen kaksiluonto-oppi
 Kristuksen kaksiluonto-oppi Katolinen kirkko muotoili kolminaisuusopin 300- ja 400-luvuilla ja täydensi sitä Kristuksen kaksiluonto-opilla Khalkedonin kirkolliskokouksessa vuonna 451. Kirkolla on ollut
Kristuksen kaksiluonto-oppi Katolinen kirkko muotoili kolminaisuusopin 300- ja 400-luvuilla ja täydensi sitä Kristuksen kaksiluonto-opilla Khalkedonin kirkolliskokouksessa vuonna 451. Kirkolla on ollut
Löydätkö tien. taivaaseen?
 Löydätkö tien taivaaseen? OLETKO KOSKAAN EKSYNYT? LÄHDITKÖ KULKEMAAN VÄÄRÄÄ TIETÄ? Jos olet väärällä tiellä, et voi löytää perille. Jumala kertoo Raamatussa, miten löydät tien taivaaseen. Jumala on luonut
Löydätkö tien taivaaseen? OLETKO KOSKAAN EKSYNYT? LÄHDITKÖ KULKEMAAN VÄÄRÄÄ TIETÄ? Jos olet väärällä tiellä, et voi löytää perille. Jumala kertoo Raamatussa, miten löydät tien taivaaseen. Jumala on luonut
Osaava henkilöstö kotouttaa kulttuurien välisen osaamisen arviointi. Työpaja 8.5.2014 Hämeenlinna
 Osaava henkilöstö kotouttaa kulttuurien välisen osaamisen arviointi Työpaja 8.5.2014 Hämeenlinna Osaamisen arviointi Osaamisen arvioinnin tavoitteena oli LEVEL5:n avulla tunnistaa osaamisen taso, oppiminen
Osaava henkilöstö kotouttaa kulttuurien välisen osaamisen arviointi Työpaja 8.5.2014 Hämeenlinna Osaamisen arviointi Osaamisen arvioinnin tavoitteena oli LEVEL5:n avulla tunnistaa osaamisen taso, oppiminen
Lukutaitotutkimukset arviointiprosessina. Sari Sulkunen Koulutuksen tutkimuslaitos, JY sari.sulkunen@jyu.fi
 Lukutaitotutkimukset arviointiprosessina Sari Sulkunen Koulutuksen tutkimuslaitos, JY sari.sulkunen@jyu.fi Kansainväliset arviointitutkimukset Arvioinnin kohteena yleensä aina (myös) lukutaito Kansallisista
Lukutaitotutkimukset arviointiprosessina Sari Sulkunen Koulutuksen tutkimuslaitos, JY sari.sulkunen@jyu.fi Kansainväliset arviointitutkimukset Arvioinnin kohteena yleensä aina (myös) lukutaito Kansallisista
MATEMATIIKKA 5 VIIKKOTUNTIA. PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009
 EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
EB-TUTKINTO 2009 MATEMATIIKKA 5 VIIKKOTUNTIA PÄIVÄMÄÄRÄ: 8. kesäkuuta 2009 KOKEEN KESTO: 4 tuntia (240 minuuttia) SALLITUT APUVÄLINEET: Eurooppa-koulun antama taulukkovihkonen Funktiolaskin, joka ei saa
Mercatorin kartta. Antti Rasila Matematiikan laitos, Teknillinen korkeakoulu
 Solmu 1/2007 1 Mercatorin kartta Antti Rasila Matematiikan laitos, Teknillinen korkeakoulu Matematiikasta yleistajuisesti kirjoittamisen tekee usein haasteelliseksi konkreettisten esimerkkien ja sovellusten
Solmu 1/2007 1 Mercatorin kartta Antti Rasila Matematiikan laitos, Teknillinen korkeakoulu Matematiikasta yleistajuisesti kirjoittamisen tekee usein haasteelliseksi konkreettisten esimerkkien ja sovellusten
MAA5 Vektori, Opintokortti
 MAA5 Vektori, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin täytettynä
MAA5 Vektori, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin täytettynä
Tietoteoria. Tiedon käsite ja logiikan perusteita. Monday, January 12, 15
 Tietoteoria Tiedon käsite ja logiikan perusteita Tietoteoria etsii vastauksia kysymyksiin Mitä tieto on? Miten tietoa hankitaan? Mitä on totuus? Minkälaiseen tietoon voi luottaa? Mitä voi tietää? Tieto?
Tietoteoria Tiedon käsite ja logiikan perusteita Tietoteoria etsii vastauksia kysymyksiin Mitä tieto on? Miten tietoa hankitaan? Mitä on totuus? Minkälaiseen tietoon voi luottaa? Mitä voi tietää? Tieto?
Luku 7. Verkkoalgoritmit. 7.1 Määritelmiä
 Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Luku 7 Verkkoalgoritmit Verkot soveltuvat monenlaisten ohjelmointiongelmien mallintamiseen. Tyypillinen esimerkki verkosta on tieverkosto, jonka rakenne muistuttaa luonnostaan verkkoa. Joskus taas verkko
Vetelin kunta Oppimisen seurantalomake 0-2 lk
 Vetelin kunta Oppimisen seurantalomake 0-2 lk Koulu: Oppilas: ÄIDINKIELI Lukeminen 20. Luet kokonaisia kirjoja. 19. Osaat tehdä johtopäätöksiä lukemastasi. 18. Löydät lukemastasi tarvittavia tietoja. 17.
Vetelin kunta Oppimisen seurantalomake 0-2 lk Koulu: Oppilas: ÄIDINKIELI Lukeminen 20. Luet kokonaisia kirjoja. 19. Osaat tehdä johtopäätöksiä lukemastasi. 18. Löydät lukemastasi tarvittavia tietoja. 17.
KURSSIVALINNAT & YLIOPPILASKIRJOITUKSET
 KURSSIVALINNAT & YLIOPPILASKIRJOITUKSET Ohjeita kurssivalintojen tekemiseen ylioppilaskirjoitusten näkökulmasta Tämän koonnin tavoitteena on auttaa Sinua valitsemaan oikeat kurssit oikeaan aikaan suhteessa
KURSSIVALINNAT & YLIOPPILASKIRJOITUKSET Ohjeita kurssivalintojen tekemiseen ylioppilaskirjoitusten näkökulmasta Tämän koonnin tavoitteena on auttaa Sinua valitsemaan oikeat kurssit oikeaan aikaan suhteessa
Nimi: Muiden ryhmäläisten nimet:
 Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
Nimi: Muiden ryhmäläisten nimet: PALKKIANTURI Työssä tutustutaan palkkianturin toimintaan ja havainnollistetaan sen avulla pienten ainepitoisuuksien havainnointia. Työn mittaukset on jaettu kolmeen osaan,
Matematiikan tukikurssi, kurssikerta 1
 Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Matematiikan tukikurssi, kurssikerta 1 1 Joukko-oppia Matematiikassa joukko on mikä tahansa kokoelma objekteja. Esimerkiksi joukkoa A, jonka jäseniä ovat numerot 1, 2 ja 5 merkitään A = {1, 2, 5}. Joukon
Kuuluisat matemaatikot tutuiksi
 Koostanut: Elina Viro Opettajalle Kuuluisat matemaatikot tutuiksi Kohderyhmä: Projekti voidaan toteuttaa 7., 8., 9. luokalla, mutta 9. luokalla taustalla oleva matematiikka on tutuinta. Esitiedot: - Taustalla
Koostanut: Elina Viro Opettajalle Kuuluisat matemaatikot tutuiksi Kohderyhmä: Projekti voidaan toteuttaa 7., 8., 9. luokalla, mutta 9. luokalla taustalla oleva matematiikka on tutuinta. Esitiedot: - Taustalla
KuLTTuuRiERoT asukkaiden Tavoissa
 4 Kulttuurierot asukkaiden tavoissa Moderni tiedonvälitysteknologia on muutamassa vuosikymmenessä kutistanut maapallon meidän omaksi takapihaksemme. Ehkäpä juuri siksi unohdamme nykyään helposti kulttuurien
4 Kulttuurierot asukkaiden tavoissa Moderni tiedonvälitysteknologia on muutamassa vuosikymmenessä kutistanut maapallon meidän omaksi takapihaksemme. Ehkäpä juuri siksi unohdamme nykyään helposti kulttuurien
Talousmatematiikan perusteet ORMS.1030
 kevät 2014 Talousmatematiikan perusteet Matti Laaksonen, (Matemaattiset tieteet / Vaasan yliopisto) Vastaanotto to 11-12 huone D110/Tervahovi Sähköposti: matti.laaksonen@uva.fi Opettajan kotisivu: http://lipas.uwasa.fi/
kevät 2014 Talousmatematiikan perusteet Matti Laaksonen, (Matemaattiset tieteet / Vaasan yliopisto) Vastaanotto to 11-12 huone D110/Tervahovi Sähköposti: matti.laaksonen@uva.fi Opettajan kotisivu: http://lipas.uwasa.fi/
Taulukot. Jukka Harju, Jukka Juslin 2006 1
 Taulukot Jukka Harju, Jukka Juslin 2006 1 Taulukot Taulukot ovat olioita, jotka auttavat organisoimaan suuria määriä tietoa. Käsittelylistalla on: Taulukon tekeminen ja käyttö Rajojen tarkastus ja kapasiteetti
Taulukot Jukka Harju, Jukka Juslin 2006 1 Taulukot Taulukot ovat olioita, jotka auttavat organisoimaan suuria määriä tietoa. Käsittelylistalla on: Taulukon tekeminen ja käyttö Rajojen tarkastus ja kapasiteetti
MAY1 Luvut ja lukujonot, opintokortti
 MAY1 Luvut ja lukujonot, opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin
MAY1 Luvut ja lukujonot, opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää. Opiskelija palauttaa viimeistään kokeeseen o Opintokortin
Nöykkiön koulu Opetussuunnitelma Maantieto. Espoon kaupungin opetussuunnitelmalinjaukset VUOSILUOKAT 7 9. 7.lk
 Nöykkiön koulu Opetussuunnitelma Maantieto 9.10 b Maantieto Oppiaineen opetussuunnitelmaan on merkitty oppiaineen opiskelun yhteydessä toteutuva aihekokonaisuuksien( = AK) käsittely seuraavin lyhentein:
Nöykkiön koulu Opetussuunnitelma Maantieto 9.10 b Maantieto Oppiaineen opetussuunnitelmaan on merkitty oppiaineen opiskelun yhteydessä toteutuva aihekokonaisuuksien( = AK) käsittely seuraavin lyhentein:
 AINEISTOKOKEEN KYSYMYKSET Vastaa aineistokokeen tekstien ja muistiinpanojesi perusteella seuraaviin tehtäviin (1 2). Vastaa täydellisillä suomen kielen virkkeillä. Vastausaikaa on 55 minuuttia (klo 13.55
AINEISTOKOKEEN KYSYMYKSET Vastaa aineistokokeen tekstien ja muistiinpanojesi perusteella seuraaviin tehtäviin (1 2). Vastaa täydellisillä suomen kielen virkkeillä. Vastausaikaa on 55 minuuttia (klo 13.55
KURSSIVALINNAT & YLIOPPILASKIRJOITUKSET
 KURSSIVALINNAT & YLIOPPILASKIRJOITUKSET Ohjeita kurssivalintojen tekemiseen ylioppilaskirjoitusten näkökulmasta Tämän koonnin tavoitteena on auttaa Sinua valitsemaan oikeat kurssit oikeaan aikaan suhteessa
KURSSIVALINNAT & YLIOPPILASKIRJOITUKSET Ohjeita kurssivalintojen tekemiseen ylioppilaskirjoitusten näkökulmasta Tämän koonnin tavoitteena on auttaa Sinua valitsemaan oikeat kurssit oikeaan aikaan suhteessa
MAB2 Geometria, Opintokortti. Nimi:
 MAB2 Geometria, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää Opiskelija palauttaa viimeistään kokeeseen o Opintokortin täytettynä
MAB2 Geometria, Opintokortti Nimi: Minimivaatimukset kurssin suorittamiseksi: Vihkoon on laskettu laadukkaasti vähintään 50 tehtävää Opiskelija palauttaa viimeistään kokeeseen o Opintokortin täytettynä
Suhteellisuusteorian vajavuudesta
 Suhteellisuusteorian vajavuudesta Isa-Av ain Totuuden talosta House of Truth http://www.houseoftruth.education Sisältö 1 Newtonin lait 2 2 Supermassiiviset mustat aukot 2 3 Suhteellisuusteorian perusta
Suhteellisuusteorian vajavuudesta Isa-Av ain Totuuden talosta House of Truth http://www.houseoftruth.education Sisältö 1 Newtonin lait 2 2 Supermassiiviset mustat aukot 2 3 Suhteellisuusteorian perusta
