Luku 3 Puhtaiden aineiden ominaisuudet
|
|
|
- Ida Salo
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 3 Puhtaiden aineiden ominaisuudet Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Tavoitteet Esitetään puhtaan aineen käsite. Tarkastellaan faasi-muutos prosessien fysiikkaa. Esitetään P-v, T-v, ja P-T ominaisuuskaaviot ja P-v-T pinnat puhtaille aineille. Puhtaiden aineiden ominaisuuksien määrittäminen taulukoista ja aineominaisuustiedoista. Kuvataan hypoteettinen aine: ideaali-kaasu ja sen ideaalikaasutilayhtälö. Sovelletaan ideaali-kaasun tilayhtälöä tyypillisten ongelmien ratkaisuun. Esitellään kokoonpuristuvuuskerroin, joka ottaa huomioon reaali-kaasujen poikkeamat ideaali-kaasun käyttäytymisestä. Esitellään joitakin parhaita tilayhtälöitä. 2 1
2 PUHTAAT AINEET Puhdas aine: Aine jolla sama kauttaaltaan koostumus. Ilma on useiden kaasujen seos, mutta sitä käsitellään puhtaana aineena. Typpi ja kaasumainen ilma ovat puhtaita aineita. Nestemäisen ja kaasumaisen veden seos on puhdas aine, mutta nestemäisen ja kaasumaisen ilman seos ei ole. 3 PUHTAAN AINEEN FAASIT Kiinteän aineen molekyylit pitää paikallaan suuret jousimaiset molekyylien väliset voimat Kiinteässä aineessa, molekyylien väliset attraktiiviset ja repulsiiviset voimat pyrkivät pitämään ne vakio etäisyyksillä toisistaan. Atomien järjestys eri faaseissa : (a) molekyylit ovat melko kiinteissä paikoissa kinteässä aineessa, (b) molekyyliryhmät liikkuvat keskenään nestemäisessä aineessa ja (c) kaasufaasissa molekyyllit likkuvat satunnaisesti. 4 2
3 PUHTAIDEN AINEIDEN FAASI-MUUTOS PROSESSIT Kokoon puristettu neste (alijäähtynyt neste): Aine, joka ei ole lähellä höyrystymistä. Kylläinen neste: Neste, joka on lähellä höyrystymistä. 1 atm ja 20 C, vesi esiintyy nestefaasissa (kokoon puristettu neste). 1 atm paineessa ja 100 C, vesi on lähellä höyrystymistä (kylläinen neste). 5 Kylläinen höyry: Höyry, joka on lähellä kondensoitumista. Kylläinen neste höyry seos: Tila, jossa neste ja höyry esiintyvät yhtäaikaa tasapainossa. Tulistettu höyry: Höyry, joka ei ole lauhtumassa (eli, ei kylläinen höyry). Kun lisää lämpöä siiryy, osa kylläisestä nesteestä höyrystyy (kylläinen nestehöyryseos). 1 atm paineessa, lämpötila pysyy vakiona 100 C:ssa kunnes viimeinen pisara nestettä on höyrystynyt (kylläinen höyry). Kun lisää lämpöä siiryy, höyryn lämpötila alkaa nousta (tulistettu höyry). 6 3
4 Koko prosessi tilojen1 ja 5 välillä (kuva) tapahtuu käänteisesti, jos vettä jäähdytetetään, jos paine pysyy vakiona. Vesi palautuu tilaan 1, kulkien täsmälleen samaa polkua ja tällöin vapautuva lämpöenergia vastaa tarkasti lämmitysprosessissa tuotua lämpöenergiaa. Veden vakio paine lämmitysprosessin T-v kaavio 7 Kyllästyslämpötila ja kyllästyspaine Lämpötila, jossa vesi alkaa kiehua, riippuu paineesta, siksi, jos paine on kiinnitetty, on myös kiehumislämpötila kiinnitetty. Vesi kiehuu 100 C 1 atm paineessa. Kyllästyslämpötila T sat : Lämpötila, jossa puhdas aine vaihtaa olomuotoa tietyssä paineessa. Kyllästyspaine P sat : Paine, jossa puhdas aine vaihtaa olomuotoa tietyssä lämpötilassa. Puhtaan aineen nestehöyry kyllästyskäyrä (numeriset arvot ovat veden arvoja). 8 4
5 Latentti lämpö: Olomuodon muutoksessa absorboitunut tai vapautunut lämpöenergia faasimuutos prosessissa. Latentti fuusiolämpö: Sulamisessa absorboitu lämpöenergia. Se on yhtäsuuri kuin jähmettymisessä vapautuva energia. Latentti höyrystymislämpö : Höyrystymisessä absorboitu lämpöenergia, joka on yhtäsuuri kuin lauhtumisessa vapautuva lämpöenergia. Latenttien lämpöjen suuruus riippuu lämpötilasta ja paineesta, jossa faasimuutos tapahtuu. 1 atm paineessa, veden fuusiolämpö on kj/kg ja höyrystymisen latentti lämpö on kj/kg. Ilmakehän paine ja veden kiehumislämpötila laskevat korkeusaseman kasvaessa. 9 T sat ja P sat riippuvuuden joitakin seurausilmiöitä Hedelmien ja vihannesten lämpötilan muuttuminen paineen mukana tyhjöjäähdytykse ssä 25 C:sta 0 C:seen Nestemäisen typen lämpötila ilmakehän olosuhteissa pysyy vakiona -196 C, ja siten säilyttää koekammion lämpötilassa -196 C. Jo 1775, jäätä tehtiin pumppaamalla tyhjö vesisäiliön ilmatilaan. 10 5
6 FAASIMUUTOSPROSESSIEN OMINAISUUSKAAVIOT Ominaisuuksien muuttumista faasimuutosprosesseissa voidaan parhaiten tutkia ominaisuuskaavioiden avulla kuten T-v, P-v, ja P-T kaaviot puhtaille aineille. Puhtaan aineent-v kaavio vakiopaine faasimuutos prosessille eri paineissa (numeroarvot kuuluvat vedelle). 11 Kylläisen nesteen viiva Kylläisen höyryn viiva Kokoonpuristetun nesteen alue tulistetun höyryn alue Kylläisen neste höyry seoksen alua (märkä alue) Ylikriittisissä paineissa (P >P cr ), ei tapahdu erotettavissa olevaa faasimuutos- (kiehumis) prosessia. Puhtaan aineen T-v kaavio. Kriittinen piste: Tilapiste, jossa kylläisen nesteen ja kylläisen höyryn tilat ovat samat. 12 6
7 Puhtaan aineen P-v kaavio. Mäntä-sylinterilaitteen painetta voidaan pienentää poistamalla painoja männän päältä. 13 Otetaan kaavioihin mukaan kiinteäfaasi Vedelle, T tp = 0.01 C P tp = kpa Trippeli-pisteen paineessa ja lämpötilassa aineen kolme olomuotoa ovat tasapainossa. P-v kaavio aineelle, joka supistuu jäätyessään. P-v kaavio aineelle, joka laajenee jäätyessään (kuten vesi). 14 7
8 Sublimatio: Siirrytään kiinteästä faasista suoraan höyry faasiin. Faasi kaavio Alhaisessa paineessa (alle trippeli-pisteen arvon), kiinteät aineet höyrystyvät sulamatta ensin (sublimaatio). P-T kaavio puhtaalle aineelle. 15 P-v-T pinnoilla on paljon informaatiota, mutta termodynaamiset analyysit on helpompi suorittaa kaksi-dimensoisilla kaavioilla, kuten P-v ja T-v kaaviot. P-v-T pinta aineelle, joka supistuu jäätyessään. P-v-T pinta aineelle joka laajenee jäätyessään (kuten vesi). 16 8
9 OMINAISUUSTAULUKOT Useimmille aineille, termodynaamisten ominaisuuksien väliset riippuvuudet ovat liian monimutkaisia lausuttaviksi yksinkertaisista yhtälöistä. Siksi, ominaisuudet annetaan usein taulukoissa. Jotkin termodynaamiset ominaisuudet voidaan mitata helposti, mutta joitakin ei voida ja lasketaan käytäen niiden ja mitattujen suureiden välisiä riippuvuuksia. Näiden mittausten ja laskelmien tulokset esitetään taulukoissa tavanomaiseen tapaan. Entalpia Yhdistetty ominaisuus Yhdistelmää u + Pv käytetään usein kontrollitilavuu ksien analyysissä. Tulolla paine tilavuus on energian yksikkö. 17 Kyllläinen neste ja höyry tilat Taulukko A 4: Kylläisen veden ominaisuudet lämpötilan funktiona. Taulukko A 5: Kylläisen veden ominaisuudet paineen funktiona. Osa taulukosta A 4. Höyrystymisentalpia, h fg (Latent heat of vaporization): Energiamäärä joka tarvitaan höyrystämään yhden massayksikön nestettä tietyssä paineessa tai lämpötilassa. 18 9
10 Esimerkkejä: Veden kylläisen nesteen ja höyryn tilat T-v ja P-v kaavioissa. 19 Kylläinen neste höyry seos Massaosuus (Quality), x : Höyryn massaosus koko seoksen massaan. Massaosuus on välillä : kylläinen neste, 1: kylläinen höyry. Kylläisen nesteen tai höyryn ominaisuudet ovat samat esiintyvätpä ne yksin tai seoksena. Lämpötila ja paine ovat seoksen riippuvia ominaisuksia Neste- ja höyryfaasien suhteellinen osuus kylläisessä seoksessa määritetään suureella (quality) x. Kaksifaasi seos voidaan käsitellä homogeneenisena seoksena
11 y v, u, or h. Massaosuus riippuu pisteen vaakasuorasta etäisyyksitä P-v ja T-v -kaavioissa. Kylläisen nestehöyryseoksen v:n arvo on v f ja v g arvojen välillä tietyllä T:n tai P:n arvolla. 21 Esimerkkejä: Kylläisen nestehöyryseoksen tilat T-v ja P-v kaavioissa
12 Aine esiintyy tulistettuna höyrynä alueella, joka on kylläisen höyryn viivan oikealla puolella ja kriittisen pisteen lämpötilan yläpuolella. Tällä alueella, lämpötila ja paine ovat toisistaan riippumattomia ominaisuuksia. Tulistettu höyry Kylläisen höyryyn verrattuna, tulistettua höyryä luonnehtii Tietyssä P, tulistettu höyry saa korkeampia h arvoja kuin kylläinen höyry Osa taulukosta A Kokoonpuristetun nesteen ominaisuudet riippuvat lämpötilasta paljon voimakkaammin kuin ne riippuvat paineesta. y v, u, or h Tarkempi yhtälö h:lle Kokoonpuristettu neste Kokoonpuristettua nestettä luonnehtii Kokoonpuristettu neste voidaan approksimoida kylläisenä nesteenä tietyssä lämpötilassa. Tietyssä P ja T, puhdas aine esiintyy kokoonpuristettuna nesteenä jos 24 12
13 Referenssitila ja referenssiarvot u, h, ja s arvoja ei voida mitata suoraan siksi ne laskettava mitattavissa olevista suureista käytäen ominaisuuksien välisiä riippuvuksia. Kuitenkin, nämä yhtälöt antavat ominaisuuksien muutokset, ei ominaisuuksien arvoja tietyssä tilassa. Siksi täytyy valita sopivat referenssi tilat ja liittää arvo nolla tietylle ominaisuudelle tai ominaisuuksille tässä tilassa. Veden referenssi tila on 0.01 C ja R-134a:lle on -40 C taulukoissa. Jotkin ominaisuudet voivat saada negatiivisiä arvoja valitun referenssitilan vuoksi. Joissakin tapauksissa eri taulukot antavat ei arvot joillekki n ominaisuksille samassa tilassa käytettyjen eri referenssiarvojen vuoksi. Termodynamiikassa tarkastellaan ominaisuuksien muutoksia ja valitulla referenssi tilalla ei ole merkitystä laskelmissa. 25 IDEAALIKAASUN TILANYHTÄLÖ Tilanyhtälö: Mikä tahansa yhtälö paineen, lämpötilan ja ominaisuustilavuuden välillä. Yksinkertaisin ja parhaiten tunnettu aineen tilanyhtälö kaasufaasissa on ideaali-kaasun tilan yhtälö. Tämä yhtälö antaa kaasun P-v-T käyttäytymisen melko tarkasti tietyllä arvoalueella. Ideaalikaasun tilanyhtälö R: kaasuvakio M: molaarinen massa (kg/kmol) R u : yleinen kaasuvakio Eri aineilla on eri kaasuvakion arvot
14 Massa = Moolimassa Moolien lukumäärä Ideaalikaasun tilanyhtälö kahdelle tilalle tietylle massalle Reaalikaasut Ideaalikaasun yhtälön eri esitysmuodot käyttäytyvät kuten ideaalikaasu alhaisilla tiheyksillä (eli alhaisissa paineissa, korkeissa lämpötiloissa). Ideaali-kaasun tilanyhtälö ei ole käypä reaalikaasuille; joten sitä on käyttettävä harkiten. Aineominaisuudet moolia kohden laskettaessa ilmoitetaan muuttujan yläviivalla 27 Onko vesihöyry ideaalikaasu? Alle10 kpa paineessa, vesihöyry voidaan käsitellä ideaalikaasuna, riippumatta sen lämpötilasta vähäisellä virheellä (pienempi kuin 0.1 %). Korkeammissa paineissa, kuitenkin, ideaalikaasu olettamus johtaa liian suriin virheisiin, erityisesti kriittisen pisteen ja kylläisen höyryn viivan läheisyydessä. Ilmastointisovelluksissa ilman vesihöyry voidaan käsitellä ideaalikaasuna. Miksi? Höyryvoimalaitossovelluksissa, kuitenkin, paineet ovat yleensä hyvin korkeita; siksi, ideaalikaasu yhtälöitä ei pidä käyttää. Prosentuaalinen virhe ([ v table - v ideal /v table ] 100) joka liittyy höyryn ideaalikaasu ja alue, jossa höyry voidaan käsitellä ideaalikaasuna pinemmällä kuin 1 % virheellä
15 KOKOONPURISTUVUUSKERROIN MITTA POIKKEAMISESTA IDEAALIKAASU KÄYTTÄYTYMISESTÄ Kokoonpuristuvuuskerroin Z Kerroin, joka korjaa ideaalikaasun käyttäytymisestä poikkeamisesta tietyssä lämpötilassa. Mitä kauempana Z on yhdestä, sitä enemmän kaasu poikkeaa ideaalikaasusta. Kaasut käyttäytyvät kuten ideaalikaasu alhaisissa tiheyksissä (eli alhaisessa paineessa, korkeissa lämpötiloissa). Kysymys: Milloin on kyse alhaisesta paineesta ja korkeasta lämpötilasta? Vastaus: Kaasun paine tai lämpötila on alhainen verratuna kriittisen tilan arvoihin. Kokoonpurituvuuskerroin saa arvon yksi ideaalikaasulle. Hyvin alhaisissa paineissa kaikki kaasut lähestyvät ideaalikaasun käyttäytymistä (riippumatta lämpötilasta). 29 Redusoitu paine Redusoitu lämpötila Pseudo-redusoitu ominaistilavuus Z voidaan määrittää myös P R ja v R.avulla. Eri kaasujen Z kertoimet. Kaasut poikkevat ideaalikaasun käyttätymisestä eniten kriittisen pisteen läheisyydessä
16 MUUT TILANYHTÄLÖT Useita eri yhtälöitä on ehdotettu aineiden P-v-T käyttätymiselle laajalla alueella ilman rajoituksia. Van der Waals tilan yhtälö Puhtaan aineen kriittisellä isotermillä on käännepiste kriittisessä pisteessä. Tässä mallissa on kaksi tekijää joita ei käsitelty ideaalikaasumallissa: molekyylien välnenvetovoima ja tilavuutta jonka molekyylit täyttävät. van der Waals yhtälön tarkkuus on usein riittämätön. 31 Beattie-Bridgeman tilanyhtälö Benedict-Webb-Rubin tilanyhtälö Vakioiden arvot on annettu taulukossa 3 4 eri aineille Sen on todettu olevan melko tarkka aina tihyksiin 0.8 cr. asti. Vakioiden arvot on annettu taulukossa 3 4. Tämä yhtälö voi käsitellä aineita aina tiheyksiin 2.5 cr. asti. Virial tilanyhtälö Kertoimia a(t), b(t), c(t), jne, jotka ovat ainoastaan lämpötilan funktiota kutsutaan virial kertoimiksi
17 Prosentuaallinen virhe eri tilanyhtälöille typelle (% error = [( v table - v equation )/v table ] 100). Monimutkaiset tilanyhtälöt esittävät kaasujen P-v-T käyttäytymisen tarkemmin kuin laajalla alueella. 33 Yhteenveto Puhtaat aineet Puhtaiden aineiden faasit Puhtaiden aineiden faasimuuos prosessit Kokoonpuristettu neste, kylläinen neste, kylläinen höyry, tulistettu höyry Kyllästyslämpötila ja kyllästyspaine Faasimuutosprosessien ominaisuus kaaviot T-v kaavio, P-v kaavio, P-T kaavio, P-v-T pinta Ominaisuustaulukot Entalpia Kylläinen neste, kylläinen höyry, kylläisen nesteen ja höyryn seokset, tulistettu höyry, kokoonpuristettu neste Referenssi tila ja referenssiarvot Ideaalikaasun tilanyhtälö Onko vesihöyry ideaalikaasu? Kokoonpuristuvuuskerroin Muut tilanyhtälöt 34 17
Luku 13 KAASUSEOKSET
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 4 SULJETTUJEN SYSTEEMIEN ENERGIA- ANALYYSI Copyright The McGraw-Hill Companies, Inc. Permission
Lämpöoppi. Termodynaaminen systeemi. Tilanmuuttujat (suureet) Eristetty systeemi. Suljettu systeemi. Avoin systeemi.
 Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Lämpöoppi Termodynaaminen systeemi Tilanmuuttujat (suureet) Lämpötila T (K) Absoluuttinen asteikko eli Kelvinasteikko! Paine p (Pa, bar) Tilavuus V (l, m 3, ) Ainemäärä n (mol) Eristetty systeemi Ei ole
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 10: Reaalikaasut Pe 1.4.2016 1 AIHEET 1. Malleja, joissa pyritään huomioimaan
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 10: Reaalikaasut Pe 1.4.2016 1 AIHEET 1. Malleja, joissa pyritään huomioimaan
Aineen olomuodot ja olomuodon muutokset
 Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Aineen olomuodot ja olomuodon muutokset Jukka Sorjonen sorjonen.jukka@gmail.com 8. helmikuuta 2017 Jukka Sorjonen (Jyväskylän Normaalikoulu) Aineen olomuodot ja olomuodon muutokset 8. helmikuuta 2017 1
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, Luku 7 ENTROPIA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 7 ENTROPIA Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Teddy 1. välikoe kevät 2008
 Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 1. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
LUKU 16 KEMIALLINEN JA FAASITASAPAINO
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 LUKU 16 KEMIALLINEN JA FAASITASAPAINO Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 LUKU 16 KEMIALLINEN JA FAASITASAPAINO Copyright The McGraw-Hill Companies, Inc. Permission required
Luku 14 KAASU HÖYRY SEOKSET JA ILMASTOINTI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 14 KAASU HÖYRY SEOKSET JA ILMASTOINTI Copyright The McGraw-Hill Companies, Inc. Permission
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 14 KAASU HÖYRY SEOKSET JA ILMASTOINTI Copyright The McGraw-Hill Companies, Inc. Permission
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Ilman suhteellinen kosteus saadaan, kun ilmassa olevan vesihöyryn osapaine jaetaan samaa lämpötilaa vastaavalla kylläisen vesihöyryn paineella:
 ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
ILMANKOSTEUS Ilmankosteus tarkoittaa ilmassa höyrynä olevaa vettä. Veden määrä voidaan ilmoittaa höyryn tiheyden avulla. Veden osatiheys tarkoittaa ilmassa olevan vesihöyryn massaa tilavuusyksikköä kohti.
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus HÖYRYTEKNIIKKA 1. Vettä (0 C) höyrystetään 2 bar paineessa 120 C kylläiseksi höyryksi. Laske
RATKAISUT: 12. Lämpöenergia ja lämpöopin pääsäännöt
 Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
Physica 9 1. painos 1(7) : 12.1 a) Lämpö on siirtyvää energiaa, joka siirtyy kappaleesta (systeemistä) toiseen lämpötilaeron vuoksi. b) Lämpöenergia on kappaleeseen (systeemiin) sitoutunutta energiaa.
L7 Kaasun adsorptio kiinteän aineen pinnalle
 CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle 1
CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle 1
L7 Kaasun adsorptio kiinteän aineen pinnalle
 CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle Oppimistavoitteet
CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle Oppimistavoitteet
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
8 Aineen olomuodot. 8-1 Olomuodon muutokset
 96 8 Aineen olomuodot 8-1 Olomuodon muutokset Vesi voi esiintyä eri lämpötiloissa hyvin erilaisissa tiloissa jäänä, nestemäisenä vetenä ja höyrynä. Tällaisia tiloja sanotaan aineen olomuodoiksi (engl.
96 8 Aineen olomuodot 8-1 Olomuodon muutokset Vesi voi esiintyä eri lämpötiloissa hyvin erilaisissa tiloissa jäänä, nestemäisenä vetenä ja höyrynä. Tällaisia tiloja sanotaan aineen olomuodoiksi (engl.
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Veden ja höyryn termodynaamiset ominaisuudet IAPWS-IF97. Funktiolohkot Siemens PLC
 Veden ja höyryn termodynaamiset ominaisuudet IAPWS-IF97 lohkot Siemens PLC SoftControl Oy 1.0 IAPWS-IF97 FUNKTIOLOHKOT... 3 1.1 Yleistä... 3 1.2 Laskennan tarkkuus... 4 2.0 Vesi... 5 2.1 cplbt Veden ominaislämpökapasiteetti...
Veden ja höyryn termodynaamiset ominaisuudet IAPWS-IF97 lohkot Siemens PLC SoftControl Oy 1.0 IAPWS-IF97 FUNKTIOLOHKOT... 3 1.1 Yleistä... 3 1.2 Laskennan tarkkuus... 4 2.0 Vesi... 5 2.1 cplbt Veden ominaislämpökapasiteetti...
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
Luku 12 THERMODYNAAMISTEN OMINAISUUKSIEN YHTÄLÖT
 hermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 011 Luku 1 HERMODYNAAMISEN OMINAISUUKSIEN YHÄLÖ Copyright he McGraw-Hill Companies, Inc. ermission required
hermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 011 Luku 1 HERMODYNAAMISEN OMINAISUUKSIEN YHÄLÖ Copyright he McGraw-Hill Companies, Inc. ermission required
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 6.11. ja tiistai 7.11. Pohdintaa Mitä tai mikä ominaisuus lämpömittarilla
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2017 Emppu Salonen Lasse Laurson Touko Herranen Toni Mäkelä Luento 11: Faasitransitiot Ke 29.3.2017 1 AIHEET 1. 1. kertaluvun transitioiden (esim.
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2017 Emppu Salonen Lasse Laurson Touko Herranen Toni Mäkelä Luento 11: Faasitransitiot Ke 29.3.2017 1 AIHEET 1. 1. kertaluvun transitioiden (esim.
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Ideaalikaasulaki. Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua
 Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
Ideaalikaasulaki Ideaalikaasulaki on esimerkki tilanyhtälöstä, systeemi on nyt tietty määrä (kuvitteellista) kaasua ja tilanmuuttujat (yhä) paine, tilavuus ja lämpötila Isobaari, kun paine on vakio Kaksi
1. Laske ideaalikaasun tilavuuden lämpötilakerroin (1/V)(dV/dT) p ja isoterminen kokoonpuristuvuus (1/V)(dV/dp) T.
 S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
S-35, Fysiikka III (ES) välikoe Laske ideaalikaasun tilavuuden lämpötilakerroin (/V)(dV/d) p ja isoterminen kokoonpuristuvuus (/V)(dV/dp) ehtävän pisteyttäneen assarin kommentit: Ensimmäisen pisteen sai
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 4.12. ja tiistai 5.12. Metallilangan venytys Metallilankaan tehty työ menee atomien välisten
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 28.9.2015 / T. Paloposki / v. 01 Tämän päivän ohjelma: Tilanyhtälöt (kertaus) Termodynamiikan 1. pääsääntö (energian häviämättömyyden laki)
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 28.9.2015 / T. Paloposki / v. 01 Tämän päivän ohjelma: Tilanyhtälöt (kertaus) Termodynamiikan 1. pääsääntö (energian häviämättömyyden laki)
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Luku 15 KEMIALLISET REAKTIOT
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 15 KEMIALLISET REAKTIOT Copyright The McGraw-Hill Companies, Inc. Permission required for
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 15 KEMIALLISET REAKTIOT Copyright The McGraw-Hill Companies, Inc. Permission required for
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT
 TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
TERMODYNAMIIKAN KURSSIN FYS 2 KURS- SIKOKEEN RATKAISUT (lukuun ottamatta tehtävää 12, johon kukaan ei ollut vastannut) RATKAISU TEHTÄVÄ 1 a) Vesi haihtuu (höyrystyy) ja ottaa näin ollen energiaa ympäristöstä
Termodynamiikka. Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt. ...jotka ovat kaikki abstraktioita
 Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Termodynamiikka Termodynamiikka on outo teoria. Siihen kuuluvat keskeisinä: Systeemit Tilanmuuttujat Tilanyhtälöt...jotka ovat kaikki abstraktioita Miksi kukaan siis haluaisi oppia termodynamiikkaa? Koska
Luento 4. Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit
 Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2. pääsääntö Termodynaamiset potentiaalit Luento 4 Termodynamiikka Termodynaamiset prosessit ja 1. pääsääntö Entropia ja 2.
1. van der Waalsin tilanyhtälö: 2 V m RT. + b2. ja C = b2. Kun T = 273 K niin B = cm 3 /mol ja C = 1200 cm 6 mol 2
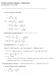 FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
FYSIKAALINEN KEMIA KEMA22) Laskuharjoitus 2, 28..2009. van der Waalsin tilanyhtälö: p = RT V m b a Vm V 2 m pv m = RT V m b = RT = RT a ) V m RT a b/v m V m RT ) [ b/v m ) a V m RT Soveltamalla sarjakehitelmää
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2017 Emppu Salonen Lasse Laurson Toni Mäkelä Touko Herranen Luento 2: kineettistä kaasuteoriaa Pe 24.2.2017 1 Aiheet tänään 1. Maxwellin ja Boltzmannin
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 4: Entropia Maanantai 21.11. ja tiistai 22.11. Ideaalikaasun isoterminen laajeneminen Kaasuun tuodaan määrä Q lämpöä......
HSC-ohje laskuharjoituksen 1 tehtävälle 2
 HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
= 84. Todennäköisin partitio on partitio k = 6,
 S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
S-435, Fysiikka III (ES) entti 43 entti / välikoeuusinta I Välikokeen alue Neljän tunnistettavissa olevan hiukkasen mikrokanonisen joukon mahdolliset energiatasot ovat, ε, ε, 3ε, 4ε,, jotka kaikki ovat
Palautus yhtenä tiedostona PDF-muodossa viimeistään torstaina
 PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
PHYS-A0120 Termodynamiikka, syksy 2018 Kotitentti Vastaa tehtäviin 1/2/3, 4, 5/6, 7/8, 9 (yhteensä viisi vastausta). Tehtävissä 1, 2, 3 ja 9 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla
Ohjeellinen pituus: 2 3 sivua. Vastaa joko tehtävään 2 tai 3
 PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
PHYS-A0120 Termodynamiikka, syksy 2017 Kotitentti Vastaa tehtäviin 1, 2/3, 4/5, 6/7, 8 (yhteensä viisi vastausta). Tehtävissä 1 ja 7 on annettu ohjeellinen pituus, joka viittaa 12 pisteen fontilla sekä
Lämpöopin pääsäännöt
 Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
Lämpöopin pääsäännöt 0. Eristetyssä systeemissä lämpötilaerot tasoittuvat. Systeemin sisäenergia U kasvaa systeemin tuodun lämmön ja systeemiin tehdyn työn W verran: ΔU = + W 2. Eristetyn systeemin entropia
KEMIAN MIKROMAAILMA, KE2 VESI
 VESI KEMIAN MIKROMAAILMA, KE2 Johdantoa: Vesi on elämälle välttämätöntä. Se on hyvä liuotin, energian ja aineiden siirtäjä, lämmönsäätelijä ja se muodostaa vetysidoksia, jotka tekevät siitä poikkeuksellisen
VESI KEMIAN MIKROMAAILMA, KE2 Johdantoa: Vesi on elämälle välttämätöntä. Se on hyvä liuotin, energian ja aineiden siirtäjä, lämmönsäätelijä ja se muodostaa vetysidoksia, jotka tekevät siitä poikkeuksellisen
Spontaanissa prosessissa Energian jakautuminen eri vapausasteiden kesken lisääntyy Energia ja materia tulevat epäjärjestyneemmäksi
 KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
KEMA221 2009 TERMODYNAMIIKAN 2. PÄÄSÄÄNTÖ ATKINS LUKU 3 1 1. TERMODYNAMIIKAN TOINEN PÄÄSÄÄNTÖ Lord Kelvin: Lämpöenergian täydellinen muuttaminen työksi ei ole mahdollista 2. pääsääntö kertoo systeemissä
4 Aineen olomuodot. 4.2 Höyrystyminen POHDI JA ETSI
 4 Aineen olomuodot 4.2 Höyrystyminen POHDI JA ETSI 4-1. a) Vesi asettuu astiassa vaakatasoon Maan vetovoiman ja veden herkkäliikkeisyyden takia. Painovoima tekee työtä, kunnes veden potentiaalienergia
4 Aineen olomuodot 4.2 Höyrystyminen POHDI JA ETSI 4-1. a) Vesi asettuu astiassa vaakatasoon Maan vetovoiman ja veden herkkäliikkeisyyden takia. Painovoima tekee työtä, kunnes veden potentiaalienergia
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä.
 FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
FAASIDIAGRAMMIT Määritelmiä Faasi: Aineen tila, jonka kemiallinen koostumus ja fysikaalinen ominaisuudet ovat homogeeniset koko näytteessä. P = näytteen faasien lukumäärä. Esimerkkejä: (a) suolaliuos (P=1),
FYSA242 Statistinen fysiikka, Harjoitustentti
 FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
FYSA242 Statistinen fysiikka, Harjoitustentti Tehtävä 1 Selitä lyhyesti: a Mikä on Einsteinin ja Debyen kidevärähtelymallien olennainen ero? b Mikä ero vuorovaikutuksessa ympäristön kanssa on kanonisella
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka. Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU
 MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
Tämän päivän ohjelma: ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 9/26/2016
 ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 26.9.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 1 Kotilasku 2 Kotilasku 2 2 Termodynamiikan
ENY-C2001 Termodynamiikka ja lämmönsiirto Luento 3 / 26.9.2016 v. 03 / T. Paloposki Tämän päivän ohjelma: Kommentti kotilaskuun 2 Termodynamiikan 1. pääsääntö 1 Kotilasku 2 Kotilasku 2 2 Termodynamiikan
Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta
 Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 4 Tavoite Oppia tulkitsemaan 2-komponenttisysteemien faasipiirroksia 1 Binääriset
Faasipiirrokset, osa 2 Binääristen piirrosten tulkinta Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 4 Tavoite Oppia tulkitsemaan 2-komponenttisysteemien faasipiirroksia 1 Binääriset
W el = W = 1 2 kx2 1
 7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
7.2 Elastinen potentiaalienergia Paitsi gravitaatioon, myös materiaalien deformaatioon (muodonmuutoksiin) liittyy systeemin rakenneosasten keskinäisiin paikkoihin liittyvää potentiaalienergiaa Elastinen
ln2, missä ν = 1mol. ja lopuksi kaasun saama lämpömäärä I pääsäännön perusteella.
 S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
S-114.42, Fysiikka III (S 2. välikoe 4.11.2002 1. Yksi mooli yksiatomista ideaalikaasua on alussa lämpötilassa 0. Kaasu laajenee tilavuudesta 0 tilavuuteen 2 0 a isotermisesti, b isobaarisesti ja c adiabaattisesti.
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Puhtaat aineet ja seokset
 Puhtaat aineet ja seokset KEMIAA KAIKKIALLA, KE1 Määritelmä: Puhdas aine sisältää vain yhtä alkuainetta tai yhdistettä. Esimerkiksi rautatanko sisältää vain Fe-atomeita ja ruokasuola vain NaCl-ioniyhdistettä
Puhtaat aineet ja seokset KEMIAA KAIKKIALLA, KE1 Määritelmä: Puhdas aine sisältää vain yhtä alkuainetta tai yhdistettä. Esimerkiksi rautatanko sisältää vain Fe-atomeita ja ruokasuola vain NaCl-ioniyhdistettä
η = = = 1, S , Fysiikka III (Sf) 2. välikoe
 S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
S-11445 Fysiikka III (Sf) välikoe 710003 1 Läpövoiakoneen kiertoprosessin vaiheet ovat: a) Isokorinen paineen kasvu arvosta p 1 arvoon p b) adiabaattinen laajeneinen jolloin paine laskee takaisin arvoon
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma
 KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
V T p pv T pv T. V p V p p V p p. V p p V p
 S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
S-45, Fysiikka III (ES välikoe 004, RAKAISU Laske ideaalikaasun tilavuuden lämötilakerroin ( / ( ja isoterminen kokoonuristuvuus ( / ( Ideaalikaasun tilanyhtälö on = ν R Kysytyt suureet ovat: ilavuuden
Dislokaatiot - pikauusinta
 Dislokaatiot - pikauusinta Ilman dislokaatioita Kiteen teoreettinen lujuus ~ E/8 Dislokaatiot mahdollistavat deformaation Kaikkien atomisidosten ei tarvitse murtua kerralla Dislokaatio etenee rakeen läpi
Dislokaatiot - pikauusinta Ilman dislokaatioita Kiteen teoreettinen lujuus ~ E/8 Dislokaatiot mahdollistavat deformaation Kaikkien atomisidosten ei tarvitse murtua kerralla Dislokaatio etenee rakeen läpi
6. Yhteenvetoa kurssista
 Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
Statistinen fysiikka, osa A (FYSA241) Vesa Apaja vesa.apaja@jyu.fi Huone: YN212. Ei kiinteitä vastaanottoaikoja. kl 2016 6. Yhteenvetoa kurssista 1 Keskeisiä käsitteitä I Energia TD1, siirtyminen lämpönä
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 28.11. ja tiistai 29.11. Kotitentti Julkaistaan to 8.12., palautus viim. to 22.12.
KOSTEUS. Visamäentie 35 B 13100 HML
 3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
3 KOSTEUS Tapio Korkeamäki Visamäentie 35 B 13100 HML tapio.korkeamaki@hamk.fi RAKENNUSFYSIIKAN PERUSTEET KOSTEUS LÄMPÖ KOSTEUS Kostea ilma on kahden kaasun seos -kuivan ilman ja vesihöyryn Kuiva ilma
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 8 Vaimennettu värähtely Elävässä elämässä heilureiden ja muiden värähtelijöiden liike sammuu ennemmin tai myöhemmin. Vastusvoimien takia värähtelijän
. Veden entropiamuutos lasketaan isobaariselle prosessille yhtälöstä
 LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
LH- Kilo vettä, jonka lämpötila on 0 0 asetetaan kosketukseen suuren 00 0 asteisen kappaleen kanssa Kun veden lämpötila on noussut 00 0, mitkä ovat veden, kappaleen ja universumin entropian muutokset?
Kryogeniikan termodynamiikkaa DEE Kryogeniikka Risto Mikkonen 1
 DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
DEE-54030 Kryogeniikka Kryogeniikan termodynamiikkaa 4.3.05 DEE-54030 Kryogeniikka Risto Mikkonen Open ystem vs. Closed ystem Open system Melting Closed system Introduced about 900 Cryocooler Boiling Cold
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
FYSA240/3 (FYS242/3) HÖYRYNPAINE JA HÖYRYSTYMISLÄMPÖ
 FYSA240/3 (FYS242/3) HÖYRYNPAINE JA HÖYRYSTYMISLÄMPÖ 1 Johdanto Höyrystyminen Tarkastellaan nesteen ja kaasun, esim. veden ja ilman rajapintaa. Nesteen molekyylit ovat lämpöliikkeessä toistensa vetovoimakentässä.
FYSA240/3 (FYS242/3) HÖYRYNPAINE JA HÖYRYSTYMISLÄMPÖ 1 Johdanto Höyrystyminen Tarkastellaan nesteen ja kaasun, esim. veden ja ilman rajapintaa. Nesteen molekyylit ovat lämpöliikkeessä toistensa vetovoimakentässä.
Peruslaskutehtävät fy2 lämpöoppi kurssille
 Peruslaskutehtävät fy2 lämpöoppi kurssille Muista että kurssissa on paljon käsitteitä ja ilmiöitä, jotka on myös syytä hallita. Selvitä itsellesi kirjaa apuna käyttäen mitä tarkoittavat seuraavat fysiikan
Peruslaskutehtävät fy2 lämpöoppi kurssille Muista että kurssissa on paljon käsitteitä ja ilmiöitä, jotka on myös syytä hallita. Selvitä itsellesi kirjaa apuna käyttäen mitä tarkoittavat seuraavat fysiikan
Lämpöistä oppia Fysiikan ja kemian perusteet ja pedagogiikka
 Lämpöistä oppia Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2012 Alkudemonstraatio Käsi lämpömittarina Laittakaa kolmeen eri altaaseen kylmää, haaleaa ja lämmintä vettä. 1) Pitäkää
Lämpöistä oppia Fysiikan ja kemian perusteet ja pedagogiikka Kari Sormunen Kevät 2012 Alkudemonstraatio Käsi lämpömittarina Laittakaa kolmeen eri altaaseen kylmää, haaleaa ja lämmintä vettä. 1) Pitäkää
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 2: Kaasujen kineettistä teoriaa Pe 26.2.2016 1 AIHEET 1. Maxwellin-Boltzmannin
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 2: Työ ja termodynamiikan 1. pääsääntö Maanantai 7.11. ja tiistai 8.11. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan
1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa?
 Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Kysymys 1. Kumpi painaa enemmän normaalipaineessa: 1m2 80 C ilmaa vai 1m2 0 C ilmaa? 2. EXTRA-PÄHKINÄ (menee yli aiheen): Heität vettä kiukaalle. Miksi vesihöyry nousee voimakkaasti kiukaasta ylöspäin?
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
Luku 5 KONTROLLI- TILAVUUKSIEN MASSA- JA ENERGIA-ANALYYSI
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 5 KONTROLLI- TILAVUUKSIEN MASSA- JA ENERGIA-ANALYYSI Copyright The McGraw-Hill Companies,
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 5 KONTROLLI- TILAVUUKSIEN MASSA- JA ENERGIA-ANALYYSI Copyright The McGraw-Hill Companies,
Kaasu Neste Kiinteä aine Plasma
 Olomuodot Kaasu: atomeilla/molekyyleillä suuri nopeus, vuorovaikuttavat vain törmätessään toisiinsa Neste: atomit/molekyylit/ionit liukuvat toistensa lomitse, mutta pysyvät yhtenä nestetilavuutena (molekyylien
Olomuodot Kaasu: atomeilla/molekyyleillä suuri nopeus, vuorovaikuttavat vain törmätessään toisiinsa Neste: atomit/molekyylit/ionit liukuvat toistensa lomitse, mutta pysyvät yhtenä nestetilavuutena (molekyylien
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut
 Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Ch 19-1&2 Lämpö ja sisäenergia
 Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
Ch 19-1&2 Lämpö ja sisäenergia Esimerkki 19-1 Olet syönyt liikaa täytekakkua ja havaitset, että sen energiasisältö oli 500 kcal. Arvioi kuinka korkealle mäelle sinun pitää pitää kiivetä, jotta kuluttaisit
