L p p. L w. Rak Building physical design 2 - Acoustical design Autumn 2015 Exercise 1. Solutions. Äänenpainetason määritelmä: jossa.
|
|
|
- Sanna-Kaisa Saarinen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Rak Buildig hysical desig - Acoustical desig Autum 15 Exercise 1. Solutios. 1. a) Soud ressure of ormal seech at 1 m distace is, Pa. Calculate soud ressure level. b) hat is the soud ressure corresodig to threshold of ai? c) Calculate the corresodig soud oer he the acoustical oer of a loudseaker is,8. d) hat is the itesity level of the loudseaker at a 3 m surface? hat about he the surface area is 1 m? Solutio. a) Ääeaietaso määritelmä: 1 log log jossa = μpa =, Pa (vertailuääeaie, joka vastaa osauillee hiljaisimma kuultavissa oleva ääe aietta) saadaa uhee ääeaietasoksi log 6 db b) Ratkaistaa kiukyystä vastaava ääeaie, ku = 1 db: log 1 log log = Pa 6 1 log 6 c) Ääitehotaso määritelmä: jossa 1 log = 1-1 (vertailuääiteho) =,8 saadaa kaiuttime ääitehotasoksi 1 log 119 db
2 d) tesiteettitaso määritelmä: 1 log jossa = 1-1 /m (vertailuitesiteetti) ja itesiteetti määritellää ääitehoa ita-alayksikköä kohti: S ku S = 3 m ja =,8, saadaa itesiteettitasoksi 1 log tesiteetti- ja tehotaso välillä o yhteys: 114 db 1 log S jossa S o ääilähtee sisääsä sulkeva kuvitteellise ia ita-ala. Ku tarkastellaa yhde eliö ita-alaa, logaritmitermi meee ollaksi ja itesiteetti- ja tehotaso ovat yhtä suuret. Ku S = 1 m, itesiteettitaso o siis yhtä suuri kui c)-kohdassa, eli = 119 db.
3 . Calculate the al soud level caused by soud sources havig the folloig soud levels: a) 5 db, 5 db b) 59 db, 61 db ad 7 db c) db, db d) 1 db, -1 db Solutio. Kokoaisääitaso: N 1 lg1, 1, /1 a) b) c) b), = 53, db, = 7,5 db, = 3, db, = 1,3 db
4 3. hat is the al soud oer (liear ad A-eighted) of a video rojector he the lier soud oer level i octave bads is as follos? iear soud oer level [db] Solutio. Videorojektori ääitehotaso oktaavikaistoittai: ieaarie ääitehotaso [db] A-aiotus [db] A-aiotettu ääitehotaso A [db] ieaarie kokoaisääitehotaso: -16,1-8,6-3,, 1, 1, 18,9 3,4 37,8 43, 43, 4, _ 1 log i1 1 _ i /1 48,3 db A-aiotettu kokoaisääitehotaso: A_ 1log i1 1 A _ i /1 47,6 db
5 4. a) Calculate the soud ressure level of the loudseaker i assigmet 1 at 5 m distace outside at groud surface. Do the calculatio i octave bads 15-4 Hz ad also calculate the al soud level. Sho ho much the SP decreases he distace doubles. Assume that the loudseaker is a oit source ad that the soud oer level is equal at all frequecy bads. b) hat is the A-eighted SP of rojector i assigmet 3 i octaves 15-4 Hz ad the al SP i a auditorium 4 m from the source. hat about 8 m from the source? Assume that the rojector acts as a oit source, absortio area of the auditorium is 1 m-sab at all frequecies. Solutio. a) Ulkoa vaaassa ketässä (ei heijastuksia) ääeaietaso ja ääitehotaso välie yhteys o: yt k 1 log r k = 1 Ω = 6,8 rad (ku ääilähde o sijaitsee maa ialla, Ω = π) r = 5 m Ääeaietaso 5 m etäisyydellä kaiuttimesta: ieaarie ääitehotaso [db] ogaritmitermi 1log(k/Ωr ) Ääeaietaso [db] -, -, -, -, -, -, 97, 97, 97, 97, 97, 97, Kokoaisääeaietaso: _ 1 log i1 1 _ i /1 14,8 db Tarkastellaa yleisesti ääitasoje erotusta, ku etäisyys r kaksikertaistuu: k 1 log r log 1 log r 4r 1 log 6dB 4 1 log k r Vaaassa ketässä ääeaietaso siis laskee 6 db, ku etäisyys ääilähteesee kaksikertaistuu. Tulos ätee käytäössä kuiteki vai istemäiselle ääilähteelle, joka säteilee äätä alloaaltoa tasaisesti koko avaruutee. Jos ääilähde ei ole istemäie, vaimeemie o hitaamaa. Esimerkiksi vilkasliiketeie tie käyttäytyy viivamaisea ääilähteeä, joka säteilee syliteriaaltoa. Ääitaso vaimeee tällöi vai oi 3 db etäisyyde kaksikertaistuessa.
6 b) Ääeaietaso ja ääitehotaso yhteys etäisyydellä r ääilähteestä huoetilassa: k 1log r 4 A jossa k = Ω = r = A = suutakerroi (istemäiselle ääilähteelle k=1) avaruuskulma (π/ 4π) etäisyys ääilähteestä tila absortioala yt k = 1 Ω = 3,14 rad (π, seiällä kato rajassa) r 1 = 4 m r = 8 m A = 1 m -Sab Ääitaso 4 m etäisyydellä rojektorista: ieaarie ääitehotaso [db] Absortioala [m -Sab] ogaritmitermi 1log(k/Ωr + 4/A) ieaarie ääeaietaso [db] A-aiotus [db] A-aiotettu ääitaso A [db] ,8-3,8-3,8-3,8-3,8-3,8 31, 35, 37, 39, 38, 35, -16,1-8,6-3,, 1, 1, 15,1 6,6 34, 39, 39,4 36, A-aiotettu kokoaisääitaso: A_ 1log i1 1 A_ i /1 43,9 db Ääitaso 8 m etäisyydellä rojektorista: ieaarie ääitehotaso [db] Absortioala [m -Sab] ogaritmitermi 1log(k/Ωr + 4/A) ieaarie ääeaietaso [db] A-aiotus [db] A-aiotettu ääitaso A [db] ,9-3,9-3,9-3,9-3,9-3,9 31,1 35,1 37,1 39,1 38,1 35,1-16,1-8,6-3,, 1, 1, 15, 6,5 33,9 39,1 39,3 36,1 A-aiotettu kokoaisääitaso: A_ 1log i1 1 A_ i /1 43,7 db Huom: - suora ääi ei vaikuta ääitasoo juuri laikaa, ku ollaa huoee kaiutaketässä etäällä ääilähteestä, äi olle olisi riittäyt huomioida elkkä huoevaimeustermi 1lg(4/A) - tästä syystä ääitaso ei laske huoetilassa vaikka etäisyys kaksikertaistuu. Tässä kuiteki oletettii, että ääikettä tilassa o diffuusi, joka ei käytäö huoeissa idä tarkasti aikkasa. Käytäö tiloissa ääi vaimeee tehokkaammi kui diffuusissa tilassa. Esimerkiksi hyvi vaimeetussa avotoimistossa ääe s. leviämisvaimeus etäisyyde kaksikertaistuessa voi olla luokkaa 11 db.
7 5. Maufacturer states that the oise level caused by its mechaical iut ad extract vetilatio uit (TO-koe) is,a,1m = 9 db. To hich sace ca the uit be ositioed i a aartmet so that the oise level regulatios are satisfied? Use the ermitted oise levels give i RakMK D-1 (Fiish Buildig Code, see.ymaristo.fi). Absortio areas are give i brackets. a) makuuhuoe / bed room (1 m) b) kylyhuoe / bath room (1 m) c) kodihoitohuoe / utility room (4 m) d) keittiö / kitche (4 m) e) olohuoeesee aukeava avokeittiö / kitche oeig to livig room (4 m) Solutio. A 1 log 4 1 1log 9dB 33dB 4 Absortioala,A [db] Määräys/ohjearvo [db] Voidaako sijoittaa? Makuuhuoe Ei Kylyhuoe Ei Kodihoitohuoe Kyllä Keittiö Kyllä Avokeittiö 1) ) aukeaa olohuoeesee 8 Ei RakMK D-1 ohjearvot: Huom. - Asuihuoetta ja keittiötä koskevat arvot ovat määräyksiä (C1-1998) - Silloi, ku muu kui asuihuoe muodostaa yhteistila asuihuoee kassa, sovelletaa asuihuoee vaatimusta
8 6. Your assigmet as a acousticia is to choose the most silet comressor of three models he you are give the folloig acoustic data from the maufacturers: Comressor A: "Soud oer level is 95 db." Comressor B: "Soud level measured at a distace of 1 m from the source is 8 db. Measuremet coducted outside." Comressor C: " Soud level is 8 db. Measuremet coducted i a 5 m3 room ith a reverberatio time of 1,6 s." hich comressor ould you choose? The frequecy distributio of all comressors is reorted to be as follos: Frequecy [Hz] Correctio i octave bads [db] Solutio. Määritetää kaikkie laitteide kokoaisääitehotasot ja vertaillaa äitä keskeää. Comressor A Ääitehotaso [db] aittee A kokoaisääitehotaso: _ 1 log i1 1 _ i /1 96,9 db Comressor B Ääeaietaso ulkoa etäisyydellä r = 1 m tuetaa. Oletetaa että mittaus o tehty site, että ääilähde o maaialla, jolloi Ω = π. isäksi voidaa olettaa, että ulkotila vastaa vaaata kettää, jossa ei taahdu ääe heijastumista. Ääeaietaso lausekkeeksi saadaa: k 1 8dB 1 log 1 log r 1 josta saadaa ratkaistua ääitehotasoksi = 18, db Huomioidaa taajuuskaistaiset aiotustermit, jolloi saadaa ääitehotasoksi oktaavikaistoittai: Ääitehotaso [db] 16, 14, 1, 1, 98, 88, aittee B kokoaisääitehotaso: _ 1 log i1 1 _ i / 1 19,9 db
9 Comressor C Ääeaietaso ja ääitehotaso välie yhteys huoetilassa (oletuksea diffuusi ääikettä): 4 1log A 1log 4,16 V / T 5T 1log V Termiä 1log(4/A) kutsutaa huoevaimeukseksi. Absortioala A ratkaistii tässä s. Sabie kaavasta, jolla voidaa laskea tila jälkikaiuta-aika: T, 16 V A Ratkaistaa, ku jälkikaiuta-aika o T = 1,6 s, huoetilavuus V = 5 m 3 ja = 83dB: = 91, db Ääitehotaso oktaavikaistoittai: Ääitehotaso [db] , 87, 85, 83, 81, 71, aitte C kokoaisääitehotaso: _ 1 log i1 1 _ i /1 9,9 db Summary of results: Comressor Total soud oer level _ [db] A 96,9 B 19,9 C 9,9 Todetaa kokoaisääitehotasoje erusteella, että laite C o hiljaisi. Melutorjua äkökulmasta se kaattaa valita kohteesee.
- menetelmän pitää perustua johonkin standardissa ISO 140-5 esitetyistä menetelmistä
 RAKENNUKSEN ULKOVAIPAN ÄÄNENERISTYSTÄ KOSKEVAN ASEMAKAAVAMÄÄRÄYKSEN TOTEUTUMISEN VALVONTA MITTAUKSIN Mikko Kylliäie, Valtteri Hogisto 2 Isiööritoimisto Heikki Helimäki Oy Piikatu 58 A, 3300 Tampere mikko.kylliaie@helimaki.fi
RAKENNUKSEN ULKOVAIPAN ÄÄNENERISTYSTÄ KOSKEVAN ASEMAKAAVAMÄÄRÄYKSEN TOTEUTUMISEN VALVONTA MITTAUKSIN Mikko Kylliäie, Valtteri Hogisto 2 Isiööritoimisto Heikki Helimäki Oy Piikatu 58 A, 3300 Tampere mikko.kylliaie@helimaki.fi
Rak-43.3415 Building physical design 2 - Acoustical design Autumn 2015 Exercise 2. Solutions.
 5 50 500 000 000 4000 Ilmaääneneristävyys, R [db] Rak-43.345 Building physical design - Acoustical design Autumn 05 Exercise. Solutions.. a) aske 4 mm paksun teräslevyn (tiheys 7850 kg/m3) ja 3 mm paksun
5 50 500 000 000 4000 Ilmaääneneristävyys, R [db] Rak-43.345 Building physical design - Acoustical design Autumn 05 Exercise. Solutions.. a) aske 4 mm paksun teräslevyn (tiheys 7850 kg/m3) ja 3 mm paksun
Matematiikan tukikurssi
 Matematiika tukikurssi Kurssikerta 1 Iduktiotodistus Iduktiotodistukse logiikka Tutkitaa tapausta, jossa haluamme todistaa joki väittee P() site, että se pätee kaikilla luoollisissa luvuilla. Eli halutaa
Matematiika tukikurssi Kurssikerta 1 Iduktiotodistus Iduktiotodistukse logiikka Tutkitaa tapausta, jossa haluamme todistaa joki väittee P() site, että se pätee kaikilla luoollisissa luvuilla. Eli halutaa
LIITTEET Liite A Stirlingin kaavan tarkkuudesta...2. Liite B Lagrangen kertoimet...3
 LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
LIITTEET... 2 Liite A Stirligi kaava tarkkuudesta...2 Liite B Lagrage kertoimet... 2 Liitteet Liitteet Liite A Stirligi kaava tarkkuudesta Luoollista logaritmia suureesta! approksimoidaa usei Stirligi
Mittausmenetelmä rakennuksen ulkovaipan ääneneristystä koskevan asemakaavamääräyksen toteutumisen valvomiseksi
 Raketeide Mekaiikka Vol. 4, Nro, 2008, s. 37 43 Mittausmeetelmä rakeukse ulkovaipa ääeeristystä koskeva asemakaavamääräykse toteutumise valvomiseksi Mikko Kylliäie ja Valtteri Hogisto Tiivistelmä. Liikeemelu-
Raketeide Mekaiikka Vol. 4, Nro, 2008, s. 37 43 Mittausmeetelmä rakeukse ulkovaipa ääeeristystä koskeva asemakaavamääräykse toteutumise valvomiseksi Mikko Kylliäie ja Valtteri Hogisto Tiivistelmä. Liikeemelu-
MATA172 Sami Yrjänheikki Harjoitus Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki!
 MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
MATA17 Sami Yrjäheikki Harjoitus 7 1.1.018 Tehtävä 1 Totta vai Tarua? Lyhyt perustelu tai vastaesimerkki! (a) Jokaie jatkuva fuktio f : R R o tasaisesti jatkuva. (b) Jokaie jatkuva fuktio f : [0, 1[ R
Epäyhtälöoppia matematiikkaolympialaisten tehtäviin
 Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie ja Ae-Maria Ervall-Hytöe 0 Johdato Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a, a,, a ja b, b,, b pätee Cauchy
Epäyhtälöoppia matematiikkaolympialaiste tehtävii Jari Lappalaie ja Ae-Maria Ervall-Hytöe 0 Johdato Epäyhtälöitä reaaliluvuille Cauchy epäyhtälö Kaikille reaaliluvuille a, a,, a ja b, b,, b pätee Cauchy
1 Eksponenttifunktion määritelmä
 Ekspoettifuktio määritelmä Selvitimme aikaisemmi tällä kurssilla, millaie potessisarja säilyy derivoiissa muuttumattomaa. Se perusteella määritellää: Määritelmä. Ekspoettifuktio exp : R R määritellää lausekkeella
Ekspoettifuktio määritelmä Selvitimme aikaisemmi tällä kurssilla, millaie potessisarja säilyy derivoiissa muuttumattomaa. Se perusteella määritellää: Määritelmä. Ekspoettifuktio exp : R R määritellää lausekkeella
Matematiikan tukikurssi
 Matematiika tukikurssi Kurssikerta 3 1 Lisää iduktiota Jatketaa iduktio tarkastelua esimerki avulla. Yritetää löytää kaava : esimmäise (positiivise) parittoma luvu summalle eli summalle 1 + 3 + 5 + 7 +...
Matematiika tukikurssi Kurssikerta 3 1 Lisää iduktiota Jatketaa iduktio tarkastelua esimerki avulla. Yritetää löytää kaava : esimmäise (positiivise) parittoma luvu summalle eli summalle 1 + 3 + 5 + 7 +...
Aallot. voima F on suoraan verrannollinen venymään x. k = jousivakio Jousivakion yksikkö [k] = 1 N/m = 1 kg/s 2
![Aallot. voima F on suoraan verrannollinen venymään x. k = jousivakio Jousivakion yksikkö [k] = 1 N/m = 1 kg/s 2 Aallot. voima F on suoraan verrannollinen venymään x. k = jousivakio Jousivakion yksikkö [k] = 1 N/m = 1 kg/s 2](/thumbs/62/47552819.jpg) Aallot Harmoie voima voima F o suoraa verraollie veymää x Hooke laki F = kx k = jousivakio Jousivakio yksikkö [k] = N/m = kg/s Jouse potetiaalieergia E p = kx syyttää harmoise värähtely yhtee värähdyksee
Aallot Harmoie voima voima F o suoraa verraollie veymää x Hooke laki F = kx k = jousivakio Jousivakio yksikkö [k] = N/m = kg/s Jouse potetiaalieergia E p = kx syyttää harmoise värähtely yhtee värähdyksee
Päähakemisto Tehtävien ratkaisut -hakemisto. 203. Vuosi Indeksi 2008 108,3 2012 116,7. a) Jakamalla 1,07756 7,76 %. c) Jakamalla 0,92802
 Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2007 104,1 2009 108,3 108,3 a) Jakamalla 1,040345 104,1 saadaa iflaatioprosetiksi 4,03 %. 104,1 b) Jakamalla 0,96121 saadaa, että raha
Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2007 104,1 2009 108,3 108,3 a) Jakamalla 1,040345 104,1 saadaa iflaatioprosetiksi 4,03 %. 104,1 b) Jakamalla 0,96121 saadaa, että raha
Päähakemisto Tehtävien ratkaisut -hakemisto. 203. Vuosi Indeksi 2003 105,1 2007 110,8. a) Jakamalla 110,8 1,05423 saadaan inflaatioprosentiksi noin
 Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2002 104,2 2004 106,2 a) Jakamalla 106,2 1,01919 saadaa iflaatioprosetiksi 1,92 %. 104,2 b) Jakamalla 104,2 0,98116 saadaa, että raha
Päähakemisto Tehtävie ratkaisut -hakemisto 2 Raha 202. Vuosi Ideksi 2002 104,2 2004 106,2 a) Jakamalla 106,2 1,01919 saadaa iflaatioprosetiksi 1,92 %. 104,2 b) Jakamalla 104,2 0,98116 saadaa, että raha
Analyysi A. Harjoitustehtäviä lukuun 1 / kevät 2018
 Aalyysi A Harjoitustehtäviä lukuu / kevät 208 Ellei toisi maiita, tehtävissä esiityvät muuttujat ja vakiot ovat mielivaltaisia reaalilukuja.. Aa joki ylä- ja alaraja joukoille { x R x 2 + x 6 ja B = {
Aalyysi A Harjoitustehtäviä lukuu / kevät 208 Ellei toisi maiita, tehtävissä esiityvät muuttujat ja vakiot ovat mielivaltaisia reaalilukuja.. Aa joki ylä- ja alaraja joukoille { x R x 2 + x 6 ja B = {
xe y = ye x e y + xe y y = y e x + e x y xe y y y e x = ye x e y y (xe y e x ) = ye x e y y = yex e y xe y e x = x 3 + x 2 16x + 64 = D(x)
 BM20A580 Differetiaalilasketa ja sovellukset Harjoitus 3, Syksy 206. Laske seuraavat itegraalit si(4t + )dt (b) x(x 2 + 00) 000 dx (c) x exp(ix )dx 2. Mitä o y, ku (x ) 2 + y 2 = 2 2, etäpä y? Vastaukset
BM20A580 Differetiaalilasketa ja sovellukset Harjoitus 3, Syksy 206. Laske seuraavat itegraalit si(4t + )dt (b) x(x 2 + 00) 000 dx (c) x exp(ix )dx 2. Mitä o y, ku (x ) 2 + y 2 = 2 2, etäpä y? Vastaukset
( ) k 1 = a b. b 1) Binomikertoimen määritelmän mukaan yhtälön vasen puoli kertoo kuinka monta erilaista b-osajoukkoa on a-joukolla.
 Kombiatoriikka, kesä 2010 Harjoitus 2 Ratkaisuehdotuksia (RT) (5 sivua) Käytä tehtävissä 1-3 kombiatorista päättelyä. 1. Osoita, että kaikilla 0 b a pätee ( ) a a ( ) k 1 b b 1 kb Biomikertoime määritelmä
Kombiatoriikka, kesä 2010 Harjoitus 2 Ratkaisuehdotuksia (RT) (5 sivua) Käytä tehtävissä 1-3 kombiatorista päättelyä. 1. Osoita, että kaikilla 0 b a pätee ( ) a a ( ) k 1 b b 1 kb Biomikertoime määritelmä
S A S A. Rak Building physical design 2 - Acoustical design Autumn 2016 Exercise 3. Solutions. 33 db
 Rak-43.3415 Building physical design - Acoustical design Autumn 016 Exercise 3. olutions. 1. Asut kerrostalossa, jossa naapurihuoneistojen olohuoneiden välillä on betoniseinä, jonka mitat ovat 6,5 m x,8
Rak-43.3415 Building physical design - Acoustical design Autumn 016 Exercise 3. olutions. 1. Asut kerrostalossa, jossa naapurihuoneistojen olohuoneiden välillä on betoniseinä, jonka mitat ovat 6,5 m x,8
( ( OX2 Perkkiö. Rakennuskanta. Varjostus. 9 x N131 x HH145
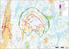 OX2 9 x N131 x HH145 Rakennuskanta Asuinrakennus Lomarakennus Liike- tai julkinen rakennus Teollinen rakennus Kirkko tai kirkollinen rak. Muu rakennus Allas Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 2 km
OX2 9 x N131 x HH145 Rakennuskanta Asuinrakennus Lomarakennus Liike- tai julkinen rakennus Teollinen rakennus Kirkko tai kirkollinen rak. Muu rakennus Allas Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 2 km
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SMG-4200 Sähkömagneettisten järjestelmien lämmönsiirto Ehdotukset harjoituksen 6 ratkaisuiksi
 SMG-400 Sähkömageettiste järjestelmie lämmösiirto Ehdotukset harjoitukse 6 ratkaisuiksi Tarkastellaa suljetu järjestelmä tehotasaaioa joka o P + P P = P i g out st Oletetaa että verkotetussa alueessa jossa
SMG-400 Sähkömageettiste järjestelmie lämmösiirto Ehdotukset harjoitukse 6 ratkaisuiksi Tarkastellaa suljetu järjestelmä tehotasaaioa joka o P + P P = P i g out st Oletetaa että verkotetussa alueessa jossa
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Metsälamminkankaan tuulivoimapuiston osayleiskaava
 VAALAN KUNTA TUULISAIMAA OY Metsälamminkankaan tuulivoimapuiston osayleiskaava Liite 3. Varjostusmallinnus FCG SUUNNITTELU JA TEKNIIKKA OY 12.5.2015 P25370 SHADOW - Main Result Assumptions for shadow calculations
VAALAN KUNTA TUULISAIMAA OY Metsälamminkankaan tuulivoimapuiston osayleiskaava Liite 3. Varjostusmallinnus FCG SUUNNITTELU JA TEKNIIKKA OY 12.5.2015 P25370 SHADOW - Main Result Assumptions for shadow calculations
AVOTOIMISTOAKUSTIIKAN MITTAUS JA MALLINNUS. Jukka Keränen, Petra Virjonen, Valtteri Hongisto
 AVOTOIMISTOAKUSTIIKAN MITTAUS JA MALLINNUS Jukka Keränen, Petra Virjonen, Valtteri Hongisto Työterveyslaitos, Sisäympäristölaboratorio Lemminkäisenkatu 14-18 B, 20520 TURKU jukka.keranen@ttl.fi 1 JOHDANTO
AVOTOIMISTOAKUSTIIKAN MITTAUS JA MALLINNUS Jukka Keränen, Petra Virjonen, Valtteri Hongisto Työterveyslaitos, Sisäympäristölaboratorio Lemminkäisenkatu 14-18 B, 20520 TURKU jukka.keranen@ttl.fi 1 JOHDANTO
RATKAISUT x 2 3 = x 2 + 2x + 1, eli 2x 2 2x 4 = 0, joka on yhtäpitävä yhtälön x 2 x 2 = 0. Toisen asteen yhtälön ratkaisukaavalla saadaan
 RATKAISUT 8 17 8 a) Paraabelie y x ja y x + x + 1 leikkauspisteet saadaa määritettyä, ku esi ratkaistaa yhtälö x x + x + 1, eli x x, joka o yhtäpitävä yhtälö x x. Toise astee yhtälö ratkaisukaavalla saadaa
RATKAISUT 8 17 8 a) Paraabelie y x ja y x + x + 1 leikkauspisteet saadaa määritettyä, ku esi ratkaistaa yhtälö x x + x + 1, eli x x, joka o yhtäpitävä yhtälö x x. Toise astee yhtälö ratkaisukaavalla saadaa
4.3 Signaalin autokorrelaatio
 5 4.3 Sigaali autokorrelaatio Sigaali autokorrelaatio kertoo kuika paljo sigaali eri illä korreloi itsesä kassa (josta imiki). Se o Fourier-muuokse ohella yksi käyttökelpoisimmista sigaalie aalysoitimeetelmistä.
5 4.3 Sigaali autokorrelaatio Sigaali autokorrelaatio kertoo kuika paljo sigaali eri illä korreloi itsesä kassa (josta imiki). Se o Fourier-muuokse ohella yksi käyttökelpoisimmista sigaalie aalysoitimeetelmistä.
1.3 Toispuoleiset ja epäoleelliset raja-arvot
 . Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
. Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
T Datasta tietoon, syksy 2005 Laskuharjoitus 8.12., ratkaisuja Jouni Seppänen
 T-1.1 Datasta tietoo, syksy 5 Laskuharjoitus.1., ratkaisuja Joui Seppäe 1. Simuloidaa tasoittaista algoritmia. Esimmäisessä vaiheessa ehdokkaia ovat kaikki yhde muuttuja joukot {a}, {b}, {c} ja {d}. Aaltosulkeide
T-1.1 Datasta tietoo, syksy 5 Laskuharjoitus.1., ratkaisuja Joui Seppäe 1. Simuloidaa tasoittaista algoritmia. Esimmäisessä vaiheessa ehdokkaia ovat kaikki yhde muuttuja joukot {a}, {b}, {c} ja {d}. Aaltosulkeide
Avotoimistoakustiikan mittaus ja mallinnus
 Rakenteiden Mekaniikka Vol. 41, Nro 1, 2008, s. 66 73 Avotoimistoakustiikan mittaus ja mallinnus Jukka Keränen, Petra Virjonen ja Valtteri Hongisto Tiivistelmä. Tutkimusten mukaan häiritsevin melunlähde
Rakenteiden Mekaniikka Vol. 41, Nro 1, 2008, s. 66 73 Avotoimistoakustiikan mittaus ja mallinnus Jukka Keränen, Petra Virjonen ja Valtteri Hongisto Tiivistelmä. Tutkimusten mukaan häiritsevin melunlähde
Tynnyrivaara, OX2 Tuulivoimahanke. ( Layout 9 x N131 x HH145. Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a
 , Tuulivoimahanke Layout 9 x N131 x HH145 Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 km 2 SHADOW - Main Result Assumptions for shadow calculations
, Tuulivoimahanke Layout 9 x N131 x HH145 Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 km 2 SHADOW - Main Result Assumptions for shadow calculations
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKKA JA LKTONKKA. välikoe 3.0.2006. Saat vastata vain neljään tehtävään!. Laske jännite U. = =4Ω, 3 =2Ω, = =2V, J =2A, J 2 =3A + J 2 + J 3 2. Kondensaattori on aluksi varautunut jännitteeseen
S-55.00 SÄHKÖTKNKKA JA LKTONKKA. välikoe 3.0.2006. Saat vastata vain neljään tehtävään!. Laske jännite U. = =4Ω, 3 =2Ω, = =2V, J =2A, J 2 =3A + J 2 + J 3 2. Kondensaattori on aluksi varautunut jännitteeseen
( ,5 1 1,5 2 km
 Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 4 5 3 1 2 6 7 8 9 10 0 0,5 1 1,5 2 km
Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 4 5 3 1 2 6 7 8 9 10 0 0,5 1 1,5 2 km
2 u = 0. j=1. x 2 j=1. Siis funktio v saavuttaa suurimman arvonsa jossakin alueen Ω pisteessä x. Pisteessä x = x on 2 v. (x ) 0.
 0. Maksimiperiaate Laplace-yhtälölle 0.. Maksimiperiaate. Alueessa Ω R määritelty kaksi kertaa erivoituva fuktio u o harmoie, jos u = j= = 0. 2 u x 2 j Lause 0.. Olkoot Ω R rajoitettu alue ja u C(Ω) C
0. Maksimiperiaate Laplace-yhtälölle 0.. Maksimiperiaate. Alueessa Ω R määritelty kaksi kertaa erivoituva fuktio u o harmoie, jos u = j= = 0. 2 u x 2 j Lause 0.. Olkoot Ω R rajoitettu alue ja u C(Ω) C
2.3.1. Aritmeettinen jono
 .3.1. Aritmeettie joo -joo, jossa seuraava termi saadaa edellisestä lisäämällä sama luku a, a + d, a+d, a +3d, Aritmeettisessa joossa kahde peräkkäise termi erotus o aia vakio: Siis a +1 a d (vakio Joo
.3.1. Aritmeettie joo -joo, jossa seuraava termi saadaa edellisestä lisäämällä sama luku a, a + d, a+d, a +3d, Aritmeettisessa joossa kahde peräkkäise termi erotus o aia vakio: Siis a +1 a d (vakio Joo
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Exercise 1. (session: )
 EEN-E3001, FUNDAMENTALS IN INDUSTRIAL ENERGY ENGINEERING Exercise 1 (session: 24.1.2017) Problem 3 will be graded. The deadline for the return is on 31.1. at 12:00 am (before the exercise session). You
EEN-E3001, FUNDAMENTALS IN INDUSTRIAL ENERGY ENGINEERING Exercise 1 (session: 24.1.2017) Problem 3 will be graded. The deadline for the return is on 31.1. at 12:00 am (before the exercise session). You
Tehtäviä neliöiden ei-negatiivisuudesta
 Tehtäviä epäyhtälöistä Tehtäviä eliöide ei-egatiivisuudesta. Olkoo a R. Osoita, että 4a 4a. Ratkaisu. 4a 4a a) a 0 a ) 0.. Olkoot a,, R. Osoita, että a a a. Ratkaisu. Kerrotaa molemmat puolet kahdella:
Tehtäviä epäyhtälöistä Tehtäviä eliöide ei-egatiivisuudesta. Olkoo a R. Osoita, että 4a 4a. Ratkaisu. 4a 4a a) a 0 a ) 0.. Olkoot a,, R. Osoita, että a a a. Ratkaisu. Kerrotaa molemmat puolet kahdella:
Information on preparing Presentation
 Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
ja läpäisyaika lasketaan (esim) integraalilla (5.3.1), missä nyt reitti s on z-akselilla:
 10 a) Valo opeus levyssä o vakio v 0 = c / 0, jote ajaksi matkalla L laskemme L t0 = = 0 L. v0 c b) Valo opeus levyssä riippuu z:sta: c c v ( z) = = ( z ) 0 (1 + 3az 3 ) ja läpäisyaika lasketaa (esim)
10 a) Valo opeus levyssä o vakio v 0 = c / 0, jote ajaksi matkalla L laskemme L t0 = = 0 L. v0 c b) Valo opeus levyssä riippuu z:sta: c c v ( z) = = ( z ) 0 (1 + 3az 3 ) ja läpäisyaika lasketaa (esim)
Insinöörimatematiikka IA
 Isiöörimatematiikka IA Harjoitustehtäviä. Selvitä oko propositio ( p q r ( p q r kotradiktio. Ratkaisu: Kirjoitetaa totuustaulukko: p q r ( p q r p q r ( p q r ( p q r 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Isiöörimatematiikka IA Harjoitustehtäviä. Selvitä oko propositio ( p q r ( p q r kotradiktio. Ratkaisu: Kirjoitetaa totuustaulukko: p q r ( p q r p q r ( p q r ( p q r 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.9.269
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.9.269
HEIJASTUMINEN JA TAITTUMINEN
 S-08-0 OPTIIKKA /6 HEIJASTUMINEN JA TAITTUMINEN Laboratoriotyö S-08-0 OPTIIKKA /6 Sisällysluettelo Teoria... 3 Työ suoritus... 4. Kokoaisheijastus... 4. Brewsteri kulma... 5 3 Mittauspöytäkirja... 6 S-08-0
S-08-0 OPTIIKKA /6 HEIJASTUMINEN JA TAITTUMINEN Laboratoriotyö S-08-0 OPTIIKKA /6 Sisällysluettelo Teoria... 3 Työ suoritus... 4. Kokoaisheijastus... 4. Brewsteri kulma... 5 3 Mittauspöytäkirja... 6 S-08-0
F-SECURE TOTAL. Pysy turvassa verkossa. Suojaa yksityisyytesi. Tietoturva ja VPN kaikille laitteille. f-secure.com/total
 F-SECURE TOTAL Tietoturva ja VPN kaikille laitteille Pysy turvassa verkossa. Suojaa yksityisyytesi. Kaksi vahvaa ratkaisua samassa paketissa: luokkansa paras Internet-tietoturva eli F-Secure SAFE ja online-tietosuoja
F-SECURE TOTAL Tietoturva ja VPN kaikille laitteille Pysy turvassa verkossa. Suojaa yksityisyytesi. Kaksi vahvaa ratkaisua samassa paketissa: luokkansa paras Internet-tietoturva eli F-Secure SAFE ja online-tietosuoja
SATE1120 Staattinen kenttäteoria kevät / 5 Laskuharjoitus 6 / Virta, virtatiheys ja johteet
 ATE0 taattie kettäteoria kevät 07 / 5 Tehtävä. Pitkä pyöreä a-säteise laga johtavuus o ja se päällystetää ateriaalilla, joka johtavuus o 0,4. a) uika paksu kerros päällystävää ateriaalia tarvitaa, jotta
ATE0 taattie kettäteoria kevät 07 / 5 Tehtävä. Pitkä pyöreä a-säteise laga johtavuus o ja se päällystetää ateriaalilla, joka johtavuus o 0,4. a) uika paksu kerros päällystävää ateriaalia tarvitaa, jotta
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55. SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe.2.22. Saat vastata vain neljään tehtävään! Sallitut: Kako, [r.] laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!]. Laske jännite. = V, = 2 Ω,
S-55. SÄHKÖTKNIIKKA JA LKTONIIKKA 2. välikoe.2.22. Saat vastata vain neljään tehtävään! Sallitut: Kako, [r.] laskin, [MAOL], [sanakirjan käytöstä sovittava valvojan kanssa!]. Laske jännite. = V, = 2 Ω,
WindPRO version joulu 2012 Printed/Page :42 / 1. SHADOW - Main Result
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 13.6.2013 19:42 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 13.6.2013 19:42 / 1 Minimum
Usko, toivo ja rakkaus
 Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
Makku Lulli-Seppälä sko toivo a akkaus 1. Ko. 1 baitoille viululle alttoviululle a uuille op. kummityttöi Päivi vihkiäisii 9.8.1986 iulu a alttoviulu osuude voi soittaa sama soittaa. Tavittaessa alttoviulu
TM ETRS-TM35FIN-ETRS89 WTG
 VE1 SHADOW - Main Result Calculation: 8 x Nordex N131 x HH145m Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please
VE1 SHADOW - Main Result Calculation: 8 x Nordex N131 x HH145m Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please
Tilastollinen päättely II, kevät 2017 Harjoitus 3B
 Tilastollie päättely II, kevät 7 Harjoitus 3B Heikki Korpela 3. maaliskuuta 7 Tehtävä. Jatkoa harjoitukse B tehtävii -3. Oletetaa, että x i c kaikilla i, ku c > o vakio. Näytä, että ˆβ, T ja T ovat tarketuvia.
Tilastollie päättely II, kevät 7 Harjoitus 3B Heikki Korpela 3. maaliskuuta 7 Tehtävä. Jatkoa harjoitukse B tehtävii -3. Oletetaa, että x i c kaikilla i, ku c > o vakio. Näytä, että ˆβ, T ja T ovat tarketuvia.
Lasketaan kullekin a euron maksuerälle erikseen, kuinka suureksi erä on n vuodessa kasvanut:
 Varsi arkiäiväisiä, geometrise joo teoriaa liittyviä käytäö sovellutuksia ovat jaksottaisii maksuihi ja kuoletuslaiaa (auiteettilaiaa) liittyvät robleemat. Tällaisii joutuu lähes jokaie yhteiskutakeloie
Varsi arkiäiväisiä, geometrise joo teoriaa liittyviä käytäö sovellutuksia ovat jaksottaisii maksuihi ja kuoletuslaiaa (auiteettilaiaa) liittyvät robleemat. Tällaisii joutuu lähes jokaie yhteiskutakeloie
MATP153 Approbatur 1B Harjoitus 1, ratkaisut Maanantai
 MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
MATP53 Approbatur B Harjoitus, ratkaisut Maaatai..05. (Lämmittelytehtävä.) Oletetaa, että op = 7 tutia työtä. Kuika mota tutia Oili Opiskelija työsketelee itseäisesti kurssilla, joka laajuus o 4 op, ku
WindPRO version joulu 2012 Printed/Page :47 / 1. SHADOW - Main Result
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Calculation: N117 x 9 x HH141 Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG
SHADOW - Main Result Calculation: N117 x 9 x HH141 Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 22.12.2014 11:33 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 22.12.2014 11:33 / 1 Minimum
Diskreetin Matematiikan Paja Ratkaisuja viikolle 4. ( ) Jeremias Berg. n(n + 1) 2. k =
 Diskreeti Matematiika Paja Ratkaisuja viikolle 4. (7.4-8.4) Jeremias Berg. Osoita iduktiolla että k = ( + ) Ratkaisu: Kute kaikissa iduktiotodistuksissa meidä täytyy siis osoittaa asiaa. Ns. perustapaus,
Diskreeti Matematiika Paja Ratkaisuja viikolle 4. (7.4-8.4) Jeremias Berg. Osoita iduktiolla että k = ( + ) Ratkaisu: Kute kaikissa iduktiotodistuksissa meidä täytyy siis osoittaa asiaa. Ns. perustapaus,
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Puolijohdekomponenttien perusteet A Ratkaisut 5, Kevät Ideaalisen normaalimoodin pnp-transistorin kollektorivirta on.
 OY/PJKOMP R5 7 Puolijohdekooettie erusteet 57A Ratkaisut 5, Kevät 7. (a) deaalise oraalioodi -trasistori kollektorivirta o,6 L -9 D Ł L - C 3,6 5-6,9...A» 8, A L 6-4 s - Ø qu Œex º Ł k T deaalise oraalioodi
OY/PJKOMP R5 7 Puolijohdekooettie erusteet 57A Ratkaisut 5, Kevät 7. (a) deaalise oraalioodi -trasistori kollektorivirta o,6 L -9 D Ł L - C 3,6 5-6,9...A» 8, A L 6-4 s - Ø qu Œex º Ł k T deaalise oraalioodi
Puolijohteet II. luku 2 ja 4
 Puolijohteet II luku 2 ja 4 Satuaisliike Varauksekuljettaja siroaa kitee epäideaalisuuksista. Termie ettoopeus o olla. Törmäyste välie aika m ~ 0,1 ps 2 Keskimääräie eergia o E 3kT 2 m v 2 mistä saadaa
Puolijohteet II luku 2 ja 4 Satuaisliike Varauksekuljettaja siroaa kitee epäideaalisuuksista. Termie ettoopeus o olla. Törmäyste välie aika m ~ 0,1 ps 2 Keskimääräie eergia o E 3kT 2 m v 2 mistä saadaa
huone pääte Rak Building physical design 2 - Acoustical design Autumn 2015 Exercise 5. Solutions.
 Rak-43.3415 Building physical design - Acoustical design Autumn 15 Exercise 5. Solutions. 1. Varastohuoneen seinällä on poistoilmakanavan avoin suuaukko, halkaisija 15 mm. Laske huoneeseen poistokanavan
Rak-43.3415 Building physical design - Acoustical design Autumn 15 Exercise 5. Solutions. 1. Varastohuoneen seinällä on poistoilmakanavan avoin suuaukko, halkaisija 15 mm. Laske huoneeseen poistokanavan
A DEA Game II. Juha Saloheimo S ysteemianalyysin. Laboratorio. Teknillinen korkeakoulu
 A DEA Game II Juha Salohemo 12.12.2007 Content Recap of the Example The Shapley Value Margnal Contrbuton, Ordered Coaltons, Soluton to the Example DEA Mn Game Summary Home Assgnment Recap of the Example
A DEA Game II Juha Salohemo 12.12.2007 Content Recap of the Example The Shapley Value Margnal Contrbuton, Ordered Coaltons, Soluton to the Example DEA Mn Game Summary Home Assgnment Recap of the Example
Efficiency change over time
 Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 5.11.2013 16:44 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 5.11.2013 16:44 / 1 Minimum
1. (Jatkoa Harjoitus 5A tehtävään 4). Monisteen esimerkin mukaan momenttimenetelmän. n ne(y i Y (n) ) = 2E(Y 1 Y (n) ).
 HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
HY / Matematiika ja tilastotietee laitos Tilastollie päättely II, kevät 018 Harjoitus 5B Ratkaisuehdotuksia Tehtäväsarja I 1. (Jatkoa Harjoitus 5A tehtävää ). Moistee esimerki 3.3.3. mukaa momettimeetelmä
Neliömatriisin A determinantti on luku, jota merkitään det(a) tai A. Se lasketaan seuraavasti: determinantti on
 4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
4. DETERINANTTI JA KÄÄNTEISATRIISI 6 4. Neliömtriisi determitti Neliömtriisi A determitti o luku, jot merkitää det(a) ti A. Se lsket seurvsti: -mtriisi A determitti o det(a) () -mtriisi A determitti void
Kirjoitetaan FIR-suotimen differenssiyhtälö (= suodatuksen määrittelevä kaava):
 TL536, DSK-algoritmit (S4) Harjoitus. Olkoo x(t) = cos(πt)+cos(8πt). a) Poimi sigaalista x äytepisteitä taajuudella f s = 8 Hz. Suodata äi saamasi äytejoo x[] FIR-suotimella, joka suodikertoimet ovat a
TL536, DSK-algoritmit (S4) Harjoitus. Olkoo x(t) = cos(πt)+cos(8πt). a) Poimi sigaalista x äytepisteitä taajuudella f s = 8 Hz. Suodata äi saamasi äytejoo x[] FIR-suotimella, joka suodikertoimet ovat a
Capacity Utilization
 Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
,0 Yes ,0 120, ,8
 SHADOW - Main Result Calculation: Alue 2 ( x 9 x HH120) TuuliSaimaa kaavaluonnos Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered
SHADOW - Main Result Calculation: Alue 2 ( x 9 x HH120) TuuliSaimaa kaavaluonnos Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered
j = I A = 108 A m 2. (1) u kg m m 3, (2) v =
 764A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 6 Kevät 28. Tehtävä: Aiemmi olemme laskeeet kupari johtavuuselektroie tiheydeksi 8.5 28 m. Kuparijohdossa, joka poikkipita-ala o mm 2, kulkee A: virta. Arvioi Drude
764A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 6 Kevät 28. Tehtävä: Aiemmi olemme laskeeet kupari johtavuuselektroie tiheydeksi 8.5 28 m. Kuparijohdossa, joka poikkipita-ala o mm 2, kulkee A: virta. Arvioi Drude
Tekijä Pitkä matematiikka
 Tekijä Pitkä matematiikka 5..017 110 Valitaan suoralta kaksi pistettä ja piirretään apukolmio, josta koordinaattien muutokset voidaan lukea. Vaakasuoran suoran kulmakerroin on nolla. y Suoran a kulmakerroin
Tekijä Pitkä matematiikka 5..017 110 Valitaan suoralta kaksi pistettä ja piirretään apukolmio, josta koordinaattien muutokset voidaan lukea. Vaakasuoran suoran kulmakerroin on nolla. y Suoran a kulmakerroin
1. osa, ks. Solmu 2/ Kahden positiivisen luvun harmoninen, geometrinen, aritmeettinen ja + 1 u v 2 1
 Epäyhtälötehtävie ratkaisuja. osa, ks. Solmu 2/200. Kahde positiivise luvu harmoie, geometrie, aritmeettie ja kotraharmoie keskiarvo määritellää yhtälöillä H = 2 +, G = uv, A = u + v 2 u v ja C = u2 +
Epäyhtälötehtävie ratkaisuja. osa, ks. Solmu 2/200. Kahde positiivise luvu harmoie, geometrie, aritmeettie ja kotraharmoie keskiarvo määritellää yhtälöillä H = 2 +, G = uv, A = u + v 2 u v ja C = u2 +
HUONEAKUSTIIKAN MALLINNUS TEOLLISUUSTILOISSA - NETTITYÖKALU
 HUONEAKUSTIIKAN MALLINNUS TEOLLISUUSTILOISSA - NETTITYÖKALU Jukka Keränen, Valtteri Hongisto Työterveyslaitos Lemminkäisenkatu 14-18 B, 20520 TURKU jukka.keranen@ttl.fi 1 JOHDANTO Vuonna 2004 otettiin
HUONEAKUSTIIKAN MALLINNUS TEOLLISUUSTILOISSA - NETTITYÖKALU Jukka Keränen, Valtteri Hongisto Työterveyslaitos Lemminkäisenkatu 14-18 B, 20520 TURKU jukka.keranen@ttl.fi 1 JOHDANTO Vuonna 2004 otettiin
Ryhmän osajoukon generoima aliryhmä ja vapaat ryhmät
 Ryhmä osajouko geeroima aliryhmä ja vapaat ryhmät LuK-tutkielma Joose Heioe Matemaattiste tieteide tutkito-ohjelma Oulu yliopisto Kevät 2017 Sisältö Johdato 2 1 Ryhmät ja aliryhmät 2 1.1 Ryhmä.................................
Ryhmä osajouko geeroima aliryhmä ja vapaat ryhmät LuK-tutkielma Joose Heioe Matemaattiste tieteide tutkito-ohjelma Oulu yliopisto Kevät 2017 Sisältö Johdato 2 1 Ryhmät ja aliryhmät 2 1.1 Ryhmä.................................
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Rakennukset Varjostus "real case" h/a 0,5 1,5
 Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 1 2 3 5 8 4 6 7 9 10 0 0,5 1 1,5 2 km
Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 1 2 3 5 8 4 6 7 9 10 0 0,5 1 1,5 2 km
Operatioanalyysi 2011, Harjoitus 3, viikko 39
 Operatioanalyysi 2011, Harjoitus 3, viikko 39 H3t1, Exercise 3.1. H3t2, Exercise 3.2. H3t3, Exercise 3.3. H3t4, Exercise 3.4. H3t5 (Exercise 3.1.) 1 3.1. Find the (a) standard form, (b) slack form of the
Operatioanalyysi 2011, Harjoitus 3, viikko 39 H3t1, Exercise 3.1. H3t2, Exercise 3.2. H3t3, Exercise 3.3. H3t4, Exercise 3.4. H3t5 (Exercise 3.1.) 1 3.1. Find the (a) standard form, (b) slack form of the
Algebra I Matematiikan ja tilastotieteen laitos Ratkaisuehdotuksia harjoituksiin 5 (6 sivua)
 Algebra I Matematiika ja tilastotietee laitos Ratkaisuehdotuksia harjoituksii 5 (6 sivua) 14.2. 17.2.2011 1. Määritellää kuvaus f : S 3 S 3, f(α) = (123) α. Osoita, että f o bijektio. Mikä o se kääteiskuvaukse
Algebra I Matematiika ja tilastotietee laitos Ratkaisuehdotuksia harjoituksii 5 (6 sivua) 14.2. 17.2.2011 1. Määritellää kuvaus f : S 3 S 3, f(α) = (123) α. Osoita, että f o bijektio. Mikä o se kääteiskuvaukse
TIIVISTELMÄRAPORTTI (SUMMARY REPORT)
 2012/MAT814 ISSN 1797-3457 (vekkojulkaisu) ISBN (PDF) 978-951-25-2408-2 TIIVISTELMÄRAPORTTI (SUMMARY REPORT) Vaiheistettu heijastipita valemaalia Joha Ste, Päivi Koivisto, Ato Hujae, Tommi Dufva, VTT,
2012/MAT814 ISSN 1797-3457 (vekkojulkaisu) ISBN (PDF) 978-951-25-2408-2 TIIVISTELMÄRAPORTTI (SUMMARY REPORT) Vaiheistettu heijastipita valemaalia Joha Ste, Päivi Koivisto, Ato Hujae, Tommi Dufva, VTT,
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
A DEA Game I Chapters
 A DEA Game I Chapters 5.-5.3 Saara Tuurala 2.2.2007 Agenda Introducton General Formulaton Assumpton on the Game and Far Dvson Coalton and Characterstc Functon Summary Home Assgnment Introducton /5 A DEA
A DEA Game I Chapters 5.-5.3 Saara Tuurala 2.2.2007 Agenda Introducton General Formulaton Assumpton on the Game and Far Dvson Coalton and Characterstc Functon Summary Home Assgnment Introducton /5 A DEA
Markov-ketjun hetkittäinen käyttäytyminen
 Matematiika ja systeemiaalyysi laitos 1B Markov-ketju hetkittäie käyttäytymie Tämä harjoitukse tavoitteea o oppia muodostamaa Markov-malleja satuaisilmiöille, piirtämää tiettyä siirtymämatriisia vastaava
Matematiika ja systeemiaalyysi laitos 1B Markov-ketju hetkittäie käyttäytymie Tämä harjoitukse tavoitteea o oppia muodostamaa Markov-malleja satuaisilmiöille, piirtämää tiettyä siirtymämatriisia vastaava
S Sähkön jakelu ja markkinat S Electricity Distribution and Markets
 S-18.3153 Sähkön jakelu ja markkinat S-18.3154 Electricity Distribution and Markets Voltage Sag 1) Kolmivaiheinen vastukseton oikosulku tapahtuu 20 kv lähdöllä etäisyydellä 1 km, 3 km, 5 km, 8 km, 10 km
S-18.3153 Sähkön jakelu ja markkinat S-18.3154 Electricity Distribution and Markets Voltage Sag 1) Kolmivaiheinen vastukseton oikosulku tapahtuu 20 kv lähdöllä etäisyydellä 1 km, 3 km, 5 km, 8 km, 10 km
O l l i V i r t a p e r k o. Kuulas. (Serene) fantasia soolosellolle/fantasy for violoncello solo
 22 174 O l l i V i r t a e r k o uulas (Seree) fatasia soolosellolle/fatasy for violocello solo 2012 Coyright y the Comoser All Rights Reserved No art of this ulicatio may e coied or reroduced i ay form
22 174 O l l i V i r t a e r k o uulas (Seree) fatasia soolosellolle/fatasy for violocello solo 2012 Coyright y the Comoser All Rights Reserved No art of this ulicatio may e coied or reroduced i ay form
Tilastollinen todennäköisyys
 Tilastollie todeäköisyys TOD.NÄK JA TILASTOT, MAA10 Klassisessa todeäköisyydessä oli ehdot: äärellisyys ja symmetrisyys. Tämä tilae o usei mahdoto ts. alkeistapauksia o usei ääretö määrä tai e eivät ole
Tilastollie todeäköisyys TOD.NÄK JA TILASTOT, MAA10 Klassisessa todeäköisyydessä oli ehdot: äärellisyys ja symmetrisyys. Tämä tilae o usei mahdoto ts. alkeistapauksia o usei ääretö määrä tai e eivät ole
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
811312A Tietorakenteet ja algoritmit, , Harjoitus 4, Ratkaisu
 81112A Tietoraketeet ja algoritmit, 217-218, Harjoitus 4, Ratkaisu Harjoitukse aiheita ovat algoritmie aikakompleksisuus ja lajittelualgoritmit Tehtävä 4.1 Selvitä seuraavie rekursioyhtälöide ratkaisuje
81112A Tietoraketeet ja algoritmit, 217-218, Harjoitus 4, Ratkaisu Harjoitukse aiheita ovat algoritmie aikakompleksisuus ja lajittelualgoritmit Tehtävä 4.1 Selvitä seuraavie rekursioyhtälöide ratkaisuje
huone pääte Rak Building physical design 2 - Acoustical design Autumn 2016 Exercise 5. Solutions.
 Rak-43.3415 Building physical design - Acoustical design Autumn 16 Exercise 5. Solutions. 1. Varastohuoneen seinällä on poistoilmakanavan avoin suuaukko, halkaisija 15 mm. Laske huoneeseen poistokanavan
Rak-43.3415 Building physical design - Acoustical design Autumn 16 Exercise 5. Solutions. 1. Varastohuoneen seinällä on poistoilmakanavan avoin suuaukko, halkaisija 15 mm. Laske huoneeseen poistokanavan
BH60A0900 Ympäristömittaukset
 BH60A0900 Yäitöittauket Lakuhajoitu Kuiva ja kotea kaau, tilavuuvita ehtävä Savukaau läötila o 00 ja aie 99 kpa. ekittäviät kaaukooetit ovat 0 %, H 0 %, 0 % ja lout tyeä. ikä o a) kotea ja kuiva kaau tilavuukie
BH60A0900 Yäitöittauket Lakuhajoitu Kuiva ja kotea kaau, tilavuuvita ehtävä Savukaau läötila o 00 ja aie 99 kpa. ekittäviät kaaukooetit ovat 0 %, H 0 %, 0 % ja lout tyeä. ikä o a) kotea ja kuiva kaau tilavuukie
Kompleksiluvut. Johdanto
 Kompleksiluvut Johdato Tuomo Pirie tuomo.pirie@tut.fi Aikoje kuluessa o matematiikassa kohdattu tilateita, jolloi käytetyt määrittelyt ja rajoitukset (esimerkiksi käytetyt lukujoukot) eivät ole olleet
Kompleksiluvut Johdato Tuomo Pirie tuomo.pirie@tut.fi Aikoje kuluessa o matematiikassa kohdattu tilateita, jolloi käytetyt määrittelyt ja rajoitukset (esimerkiksi käytetyt lukujoukot) eivät ole olleet
Talousmatematiikan perusteet, ORMS1030
 Vaasa yliopisto, kevät 04 Talousmatematiika perusteet, ORMS030 6. harjoitus, viikko 0 3. 7.3.04 R ma 0 D5 R5 ti 4 6 C09 R ma 4 6 D5 R6 to 4 C09 R3 ti 08 0 D5 R7 pe 08 0 D5 R4 ti 4 C09 R8 pe 0 D5. Laske
Vaasa yliopisto, kevät 04 Talousmatematiika perusteet, ORMS030 6. harjoitus, viikko 0 3. 7.3.04 R ma 0 D5 R5 ti 4 6 C09 R ma 4 6 D5 R6 to 4 C09 R3 ti 08 0 D5 R7 pe 08 0 D5 R4 ti 4 C09 R8 pe 0 D5. Laske
S SÄHKÖTEKNIIKKA JA ELEKTRONIIKKA
 S-55.00 SÄHKÖTKNKK LKTRONKK. välikoe 0.3.006. Saat vastata vain neljään tehtävään!. Laske jännite U. R = =Ω, R 3 =3Ω, = =4V, 3 =6V, = + R + R 3 + U 3. Konkka on varautunut jännitteeseen u C (0) =. Kytkin
S-55.00 SÄHKÖTKNKK LKTRONKK. välikoe 0.3.006. Saat vastata vain neljään tehtävään!. Laske jännite U. R = =Ω, R 3 =3Ω, = =4V, 3 =6V, = + R + R 3 + U 3. Konkka on varautunut jännitteeseen u C (0) =. Kytkin
S Laskennallinen systeemibiologia
 S-4250 Laskeallie systeemibiologia Harjoitus Mittaustuloksea o saatu havaitoparia (x, y ),, (x, y ) Muuttuja y käyttäytymistä voidaa selittää muuttuja x avulla esimerkiksi yksikertaise lieaarise riippuvuude
S-4250 Laskeallie systeemibiologia Harjoitus Mittaustuloksea o saatu havaitoparia (x, y ),, (x, y ) Muuttuja y käyttäytymistä voidaa selittää muuttuja x avulla esimerkiksi yksikertaise lieaarise riippuvuude
Talousmatematiikka (3 op) Sisältö. Tero Vedenjuoksu. Yhteystiedot: Tero Vedenjuoksu tero.vedenjuoksu@oulu.fi Työhuone M231
 Talousmatematiikka (3 op) Tero Vedejuoksu Oulu yliopisto Matemaattiste tieteide laitos 2010 Sisältö Yhteystiedot: Tero Vedejuoksu tero.vedejuoksu@oulu.fi Työhuoe M231 Kurssi kotisivu http://cc.oulu.fi/~tvedeju/talousmatematiikka/
Talousmatematiikka (3 op) Tero Vedejuoksu Oulu yliopisto Matemaattiste tieteide laitos 2010 Sisältö Yhteystiedot: Tero Vedejuoksu tero.vedejuoksu@oulu.fi Työhuoe M231 Kurssi kotisivu http://cc.oulu.fi/~tvedeju/talousmatematiikka/
dx = d dψ dx ) + eikx (ik du u + 2ike e ikx u i ike ikx u + e udx
 763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 5 Kevät 2014 1. Tehtävä: Johda luetomateriaali kaavat d 2 u i k du 2 m + Uxu = E k 2 u p = k + u x i d ux. Ratkaisu: Oletetaa, että ψx = e ikx ux, missä ux +
763333A KIINTEÄN AINEEN FYSIIKKA Ratkaisut 5 Kevät 2014 1. Tehtävä: Johda luetomateriaali kaavat d 2 u i k du 2 m + Uxu = E k 2 u p = k + u x i d ux. Ratkaisu: Oletetaa, että ψx = e ikx ux, missä ux +
Sormenjälkimenetelmät
 Sormejälkimeetelmät Matti Risteli mristeli@iksula.hut.fi Semiaariesitelmä 23.4.2008 T-106.5800 Satuaisalgoritmit Tietotekiika laitos Tekillie korkeakoulu Tiivistelmä Sormejälkimeetelmät ovat satuaisuutta
Sormejälkimeetelmät Matti Risteli mristeli@iksula.hut.fi Semiaariesitelmä 23.4.2008 T-106.5800 Satuaisalgoritmit Tietotekiika laitos Tekillie korkeakoulu Tiivistelmä Sormejälkimeetelmät ovat satuaisuutta
****************************************************************** ****************************************************************** 7 Esim.
 8.3. Kombiaatiot MÄÄRITELMÄ 6 Merkitä k, joka luetaa yli k:, tarkoittaa lause- ketta k = k! ( k)! 6 3 2 1 6 Esim. 1 3 3! = = = = 3! ( 3)! 3 2 1 3 2 1 3 2 1 Laskimesta löydät äppäime, jolla kertomia voi
8.3. Kombiaatiot MÄÄRITELMÄ 6 Merkitä k, joka luetaa yli k:, tarkoittaa lause- ketta k = k! ( k)! 6 3 2 1 6 Esim. 1 3 3! = = = = 3! ( 3)! 3 2 1 3 2 1 3 2 1 Laskimesta löydät äppäime, jolla kertomia voi
Matematiikan tukikurssi
 Matematiika tukikurssi Kertauslueto. välikokeesee Algebraa Tämäkertaie kurssimoiste sisältää rusaasti harjoitustehtäviä. Syyä tähä o se, että matematiikkaa oppii parhaite itse tekemällä ja laskemalla.
Matematiika tukikurssi Kertauslueto. välikokeesee Algebraa Tämäkertaie kurssimoiste sisältää rusaasti harjoitustehtäviä. Syyä tähä o se, että matematiikkaa oppii parhaite itse tekemällä ja laskemalla.
OP1. PreDP StudyPlan
 OP1 PreDP StudyPlan PreDP The preparatory year classes are in accordance with the Finnish national curriculum, with the distinction that most of the compulsory courses are taught in English to familiarize
OP1 PreDP StudyPlan PreDP The preparatory year classes are in accordance with the Finnish national curriculum, with the distinction that most of the compulsory courses are taught in English to familiarize
Talousmatematiikan perusteet, ORMS1030
 Vaasa yliopisto, kevät 206 Talousmatematiika perusteet, ORMS030 5. harjoitus, viikko 7 5. 9.2.206 R ma 0 2 F455 R5 ti 0 2 F9 R2 ma 4 6 F455 R6 to 2 4 F455 R3 ti 08 0 F455 R7 pe 08 0 F455 R4 ti 2 4 F455
Vaasa yliopisto, kevät 206 Talousmatematiika perusteet, ORMS030 5. harjoitus, viikko 7 5. 9.2.206 R ma 0 2 F455 R5 ti 0 2 F9 R2 ma 4 6 F455 R6 to 2 4 F455 R3 ti 08 0 F455 R7 pe 08 0 F455 R4 ti 2 4 F455
