Time Series Model for Forecasting the Sales of a Functional Dairy Product
|
|
|
- Miina Hakola
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 Aalto University School of Science Degree Programme in Engineering Physics and Mathematics Time Series Model for Forecasting the Sales of a Functional Dairy Product Bachelor s Thesis Anton von Schantz The document can be stored and made available to the public on the open internet pages of Aalto University. All other rights are reserved.
2 Aalto University School of Science ABSTRACT OF Degree Programme in Engineering Physics and Mathematics BACHELOR S THESIS Author: Anton von Schantz Title: Time-series Model for Forecasting the Sales of a Functional Dairy Product Date: November 20, 2013 Number of pages: Professorship: Systems Sciences Code: Mat-2 Supervisor: Professor Ahti Salo Instructor: PhD Antti Vassinen The effect of marketing and advertising functions on the sales of a large Finnish food company s functional dairy product is measured. In order to model the effects of marketing procedures we have to form a picture of the baseline sales levels. For the estimation of the baseline sales levels product sales and marketing expenditure data is used. Marketing data often includes measures on, for example, sales or marketing mix variables at equally spaced intervals over time. Time series models are uniquely suited to capture the time dependencies in these variables. An Seasonal AutoRegressive Integrated Moving Average with external inputs (SARIMAX) model is used to model the baseline sales levels. The model is identified, estimated and validated with the Box-Jenkins procedure. In the resulting model the sales is explained by random shocks in the demand and the price promotion of the product. The aforementioned variables also cause a permanent stochastic trend in the sales. Keywords: SARIMAX, sales, price promotion Language: English i
3 Aalto-yliopisto Perustieteiden korkeakoulu KANDIDAATINTYÖN Teknillisen fysiikan ja matematiikan tutkinto-ohjelma TIIVISTELMÄ Tekijä: Anton von Schantz Työn nimi: Tehojuoman myynnin mallintaminen aikasarjamenetelmällä Päiväys: 20. marraskuuta 2013 Sivumäärä: Professuuri: Systeemitieteet Koodi: Mat-2 Valvoja: Professori Ahti Salo Ohjaaja: KTT Antti Vassinen Työssä tutkittiin suuren suomalaisen elintarvikeyhtiön markkinointi- sekä mainostoimenpiteiden vaikutusta myyntituloihin. Jotta markkinointi- ja mainostoimenpiteiden vaikutusta voidaan mitata, täytyy myynnin perustasosta kuitenkin luoda perusteltu arvio. Myynnin perustason estimoimiseksi käytetään myynti- sekä mainostoimenpidedataa. Markkinointidata sisältää usein muuttujia jotka riippuvat ajasta. Tämän takia käytämme aikasarja-analyysiä näiden muuttujien välisten yhteyksien selvittämiseen. Työssä myynnin perustasoa on mallinnettu SARIMAX mallilla. SARIMAX mallissa myyntituloja selitetään myynnin omalla historialla, satunnaisvaihtelulla sekä ulkoisilla muuttujilla. Tässä tapauksessa markkinointi- ja mainontatoimenpiteet toimivat ulkoisina muuttujina. Mallin tunnistamiseen, estimointiin ja validoimiseen käytetään Box-Jenkins menetelmää. Box-Jenkins menetelmällä saadaan malli, jossa myyntitulot selitetään satunnaisilla shokkeilla sekä tuotteen hintapromootiolla. Edellä mainitut selittäjät aiheuttavat myös pidempiaikaista stokastista trendiä tuotteen myyntiin. Asiasanat: SARIMAX, myyntitulot, hintapromootio Kieli: Englanti ii
4 Table of Contents Abbrevations and Acronyms... iv 1 Introduction Time Series in Marketing ARMA Processes Stationary and Non-stationary Processes Seasonal Processes Methodology Correlation functions The Box-Jenkins procedure Identification Estimation Diagnostic Checks Case study: Functional Dairy Product Description of data Results Identification Estimation Diagnostic Checks Backtesting Discussion References Appendix Summation of the Thesis in Finnish iii
5 Abbrevations and Acronyms uto egressive oving verage uto egressive oving verage uto egressive ntegrated uto egressive ntegrated oving verage oving verage with e ternal variables easonal uto egressive ntegrated oving verage with e ternal variables t discrete time the value of a time series at a discrete time t s seasonal length B backward shift operator defined by and mean level of the process (often normally independently distributed white noise residual with mean 0 and variance (written as ) nonseasonal autoregressive ( ) operator or polynomial of order such that the roots of the characteristic equation lie outside the unit circle for nonseasonal stationarity and the are the nonseasonal parameters nonseasonal differencing operator of order to produce nonseasonal stationarity of the th differences, usually or 2 roots of seasonal operator of order such that the lie outside the unit circle for seasonal stationarity and the are the seasonal parameters stationary series formed by differencing series nonseasonal moving average ( ) operator or polynomial of order such that the roots of that the roots of lie outside the unit circle for invertibility and are the nonseasonal parameters iv
6 seasonal operator of order such that the roots of lie outside the unit circle for invertibility and the are the seasonal parameters The notation is used to represent the seasonal model. v
7 1 Introduction The justification of marketing spending almost always involves estimating the incremental effects of the marketing or advertising procedure under evaluation. In order to model the effects of marketing procedures we have to form a picture of the baseline sales levels. Estimates of baseline sales levels establish a benchmark for evaluating the incremental sales generated by specific marketing activities. This baseline also helps isolate incremental sales from the effects of other influences, such as seasonality or competitive promotions [1]. The aim of this thesis is to model the baseline sales levels of a large Finnish food company s functional dairy product. The product is a dairy product with added health benefits, thus it bought more during influenza seasons. For the estimation of the baseline sales levels product sales and marketing expenditure data is used. By comparing marketing and advertising activities to the difference between actualized and estimated sales one can form versatile models of marketing functions. In order to model the influence of marketing expenditures, we have to build a model of the sales, where marketing activities constitute as a variable. Marketing data often includes measures on, for example, sales or marketing mix variables at equally spaced intervals over time. Time series models are uniquely suited to capture the time dependencies in these variables [2]. The biggest challenges in modeling sales are the changing dynamics between the variables and the problem of endogeneity. Market responsiveness may not be the same over time. Advertising effectiveness might decline over the life cycle of a product, which means that the dynamics between the variables will change over the life cycle of the product as well [3]. With the problem of endogeneity is meant, that the exogenous variables such as price, promotion, advertising, etc., are themselves endogenous. In statistics an exogenous variable affects a model without being affected by it, and whose qualitative characteristics and method of generation are not specified by the model builder [11]. In turn, an endogenous variable is generated within a model and, therefore, a variable whose value is changed by one of the functional relationships in that model [12]. Marketing managers set the marketing-mix variables based on market information which may be in part unobservable to the researcher but which nevertheless affects consumer choice. This would create a situation where the marketing-mix variables could be correlated with the error terms [2]. An extensively used model in marketing science, to describe effects of marketing activities on sales, is a ector uto egressive ( ) model, as it takes in account the dynamic changes of variables. Because of difficulties in getting the package to function in the statistics software R, a easonal uto egressive ntegrated oving verage with e ternal inputs ( ) model is used instead [4, 5]. The theoretical background of the model is explained in Chapter 2 and the Box- Jenkins methodology for fitting a model to a time series is described in Chapter 3. In Chapter 4 the case study for the functional dairy product is presented. First the sales and marketing data are described and after that the Box-Jenkins procedure is applied for the data. The goodness of the model is evaluated with Akaike s Information Criterion (AIC) and backtesting 1
8 experiments. We will arrive with a baseline sales model for the dairy product. Chapter 5 is for discussion and conclusions. 2 Time Series in Marketing The following theoretical background about time series in marketing is following closely the presentation by Horváth et al. [2]. 2.1 ARMA Processes Let be the sales of a product in a period t. A common and fairly simple way to describe fluctuations in sales over time is with a first-order autoregressive process. In this process, it is assumed that sales at t-1,, affect sales at period t where a constant, the error term, a parameter, the starting condition is, and T is the sample length. The model is indicated as, which means autoregressive process of order 1. It is possible that there is a correlation between higher order lags as well. Values of variables occurring prior to the current observation are called lag values [13]. The order of an ( process is the highest lag of that appears in the model. The general -order AR process is where ( ) Here denotes the backshift operator defined by. A first-order moving average process assumes that a random shock at,, affects sales levels at time This model is indicated as. Notice that from here on the error term will be called a random shock. Note also that the past shock does not come from past sales (past values of ) as in the model, but it stems from the random component of. The order of an process is the highest lag of that appears in the model. The general -order process is where ( ) 2 (1) (2) (3) (4)
9 and processes can be combined into a single model to reflect the idea that both past sales and past random shocks affect. For example, the process The orders of a process are the highest lags of and respectively that appear in the model. For example, for an process, and. The general process is If we are interested in estimating the effects of marketing variables such as price, advertising and competitive behavior on sales when the latter variable is also a subject to other complex patterns, we can include these variables in an model, and obtain the following model with e ogenous variables ( (5) (6) (7) 2.2 Stationary and Non-stationary Processes In order to use statistical tests for an model selection, we need to estimate the underlying stochastic process. We can do this by deriving the mean, variance, and co-variance of the sample data. However, these quantities are only meaningful, for obtaining the probability distribution and the statistical tests based on it, if they are independent of time. This is the case if the series is stationary. There are different forms of stationarity. The most commonly considered is covariance stationarity. A series is said to be covariance stationary if the following conditions hold: for all [ ] for all [ ] for all and for all (8) where and are all finite-valued numbers. In practice, we often use the requirement that the roots of what are called the characteristic equations, lie outside the unit circle. For an process this requirement implies that the root is larger than one in absolute value. The characteristic equation is. The root equals, which is greater than one in absolute sense if. The root is called a unit root if. Thus, the process is stationary if and non-stationary (not stationary) if it has a unit root. A time series might exhibit a stochastic trend, which implies that the variation is systematic but hardly predictable. If the time series is not stationary, because it has a stochastic trend, the series can be formulated as a stationary process in differences. The differencing operation removes 3
10 the stochastic trend from the data. It may be necessary to take the differences of the series more than once before it becomes stationary. A model for the differences of is called a (Auto Regressive Integrated Moving Average) model. As an example we consider a model (9) 2.3 Seasonal Processes Many time series in marketing display seasonal patterns caused by managerial decisions, weather conditions, events, holidays, etc. A seasonal model may apply, with orders and respectively for the, and components, denoted by, where is the seasonal lag. To illustrate, suppose there exists a seasonal pattern in monthly data, such that any month s value contains a component that resembles the previous year s value in the same month. Then a purely seasonal model is. (10) In practice, seasonal and non-seasonal processes usually occur together. The examination of and may suggest patterns in these functions at different lags. This general process is indicated as an process In Eq. 11 the seasonal and non-seasonal, and differencing operators are multiplied. In practice, the orders and are small, ranging from 0 to 2 in most cases. (11) 3 Methodology When applying an model it is recommended to use the three stage Box-Jenkins procedure. The description of the procedure in this chapter widely follows [4]. In order to understand the Box- Jenkins procedure the theory behind correlation functions is first described by following closely the representations in [6] and [7]. 4
11 3.1 Correlation functions The cross-correlation between two time series describes the normalized cross-covariance function. Let represent a pair of stochastic processes that are covariance stationary. Then the crosscovariance is given by [ ( )] (12) where and are the means of and respectively. The cross-correlation function is the normalized cross-covariance function (13) where and are the standard deviations of processes and respectively. If, then the cross-correlation function is simply the autocorrelation function [6]. We are often interested in the relationship between two points in time in a time series. One way to measure the linear relationship is with autocorrelation, i.e., to determine the correlation between these two variables. Another way to measure the relationship between variables and is to filter the linear dependency that is caused by the variables between the variables ja, and after that to calculate the correlation between the random variables. This is called partial autocorrelation, autocorrelation of k:th degree is ( ) (14) where is the best linear projection from to, i.e. where is the covariance matrix of the regressors and is the variance between and. With the best linear projection we mean a linear projection, which minimizes the square sum of the errors. An equivalent definition is the solution to the equation system where (15) ( ) and and. This equation system is also called the Yule- Walker equations for an AR(k) process. The last coefficient is the autocorrelation of kth degree. Because we are only interested in this coefficient, the equation system can be solved with regards to, using the Cramer rule. We get 5
12 (16) where corresponds to the matrix, where the kth column has been replaced by. In this context means the determinant. Because this can be applied to different values of k, we can construct a partial autocorrelation function (PACF). From the definition of PACF we can see that there is no difference between the first degree PACF and ACF: 3.2 The Box-Jenkins procedure The first step in the procedure is to identify the form of model that may fit the given data. The second stage is to estimate the model parameters by employing the method of maximum likelihood. The third stage is to employ diagnostic checks to check the model for possible inadequacies Identification The purpose of the identification stage is to transform the data so that it becomes stationary and determine the number of parameters in the model. The first stage is to plot the original time series, it s ACF (autocorrelation function, PACF (partial autocorrelation function) and CCF (cross-correlation function) with external inputs, and check for seasonality, trends either in the mean level or in the variance of the series, long-term cycles and extreme values and outliers. Whether the data is stationary can be checked with the Augmented Dickey-Fuller test. It s a test for a unit root in a time series sample [5]. After the data have been differenced just enough to produce nonseasonal stationarity for a nonseasonal time series and both seasonal and nonseasonal stationarity for seasonal data, then the ACF and PACF of the stationarized series are inspected to determine the number of and parameters required in the model [4]. The lagged effects of the external inputs in the model can be determined from the CCF Estimation The model parameters are estimated with the maximum likelihood method. Given a sample and a parametric distribution, the method estimates the parameters in the distribution so that the sample is most likely to be drawn from the distribution. 6
13 If the distribution of is where is a known distribution function and is an unknown vector, we say that the distribution is parametric and that is the parameter of the distribution. The space is the set of permissible value for. In this setting the method of maximum likelihood is the appropriate technique for estimation and inference on. If the distribution is continuous then the density of can be written as and the joint density of a random sample is ( ) (17) The likelihood of the sample is this joint density evaluated at the observed sample values, viewed as a function of. The log-likelihood function is its natural log (18) If the distribution is discrete, the likelihood and log-likelihood are constructed by setting. The maximum likelihood estimator or MLE is the parameter value which maximizes the likelihood (equivalently, which maximizes the log-likelihood). We can write this as (19) In some simple cases, we can find an explicit expression for as a function of the data, but these cases are rare. More typically, the MLE must be found by numerical methods [8] Diagnostic Checks Diagnostic checks are designed to test model adequacy. We are mainly interested in testing if including parameters improves the fit and also to test if the residual assumptions hold. The residuals should be independent, homoscedastic, and normally distributed. Residual estimates are needed for the tests. The estimates for are automatically calculated at the estimation stage along with the MLE for the parameters. Transforming the data cannot correct dependence of the residuals because the lack of independence indicates the present model is inadequate. Rather, the identification and estimation stages must be repeated in order to determine a suitable model [4]. a. Overfitting Overfitting involves fitting a more elaborate model than the one estimated to see if including one or more parameters greatly improves the fit. Extra parameters should be estimated for the more complex model only where it is feared that the simpler model may require more parameters. A 7
14 common approach to model selection is a selection criterion. One popular choice is the Akaike Information Criterion (AIC). The AIC for a model m is (20) where is the variance estimate for model, and is the number of coefficients in the model. The AIC can be derived as an estimate of the Kullback-Leibler information distance between the true density and the model density. The rule is to select if, else select. Another method of testing model adequacy is by calculating the likelihood ratio. Let denote the maximum likelihood estimator of for the likelihood function., where the likelihood function is treated as a function of the parameters and the are fixed. Similarly, let denote the maximum likelihood estimator of when is true; that is, for the likelihood function. Now, form the ratio (21) This is the ratio of the two likelihood functions and when their parameters have been replaced by their maximum likelihood estimators. Since the maximum likelihood estimators are functions of the random variables the ratio is a function of only and is therefore an observable random variable. The test statistic is (22) The model with more parameters will always fit at least as well (have a greater log-likelihood). Whether it fits significantly better and should thus be preferred is determined by deriving the probability or p-value of the difference D. In many cases, the probability distribution of the test statistic is approximately a chi-square distribution with degrees of freedom equal to df2-df1, if the nested model with fewer parameters is correct. Symbols df1 and df2 represent the number of free parameters of models 1 and 2, the null model and alternate model, respectively [8]. b. Test for whiteness of the residuals. To determine whether the residual are white noise, an appropriate procedure is to examine the residual autocorrelation function. Another way to check for white noise is to perform the Ljung-Box test. To test the hypothesis that the residuals are independent and identically distributed random variables we can use the portmanteau test. We consider the statistic (23) 8
15 If is a finite-variance iid sequence, Q is approximately distributed as the sum of squares of the independent (0,1) random variables,, i.e., as chi-squared with h degrees of freedom. A large value of Q suggests that the sample autocorrelations of the data are too large for the data to be a sample from i.i.d. sequence. We therefore reject the i.i.d. hypothesis at level if, where is the quantile of the chi-squared distribution with h degrees of freedom. The program ITSM conducts a refinement of this test, formulated by Ljung and Box (1978), in which is replaced by (24) whose distribution is better approximated by the chi-squared distribution with h degrees of freedom [8]. c. Homoscedasticity checks of the residuals. The check for homoscedasticity of residuals is done in this thesis, by only observing the residual plot. d. Tests for normality of the residuals. The normality assumption of the residuals is tested to examine the goodness of the fit. The normality assumption is tested by testing for skewness and kurtosis of residuals. Skewness is tested with D Agostino skewness test and kurtosis with Anscomble-Glynn kurtosis test [9]. 4 Case study: Functional Dairy Product 4.1 Description of data In this thesis the baseline sales of a functional dairy product is modeled, with data from weeks 2/ /2011. There was a vast amount of data available of different marketing expenditures, which could be used as external variables in the model, the advertising of the product in different media, the advertising of substitute products and price promotions. But after examination of the correlation matrix between the sales data and the possible external variables the conclusion was that the price promotion was the only variable with a significant correlation. The time series of the product s sales is plotted in Figure 1. The sales are the amount sold to a specific retailer. The sales of the product are measured in kilograms. The data has been partitioned into estimation and forecasting intervals. The 104 first weeks are used to estimate the model, the 16 last weeks are used for backtesting of the model. Unfortunately, the time series is relatively short for determining seasonal patterns. Even though, it would be reasonable to assume that the functional 9
16 dairy product would be bought more during typical influenza seasons. Thus the time series will not be seasonally differentiated in this case study. Figure 1: The sales of the functional dairy product to a retailer during weeks 2/ /2011 measured in kilograms. The products price promotion time series in the retailer chain is plotted in Figure 2. Price promotion is a variable, assuming the value 4 if the prices are at highest and the value 0 if the prices are at lowest. 10
17 Figure 2: The product s price promotions in the retail chain during weeks 2/ / Results Identification First a logarithmic transformation of the data was used to stabilize the variance in the data [10]. The log-transformed sales data is plotted in Figure 3. 11
18 Figure 3: Log-transformed sales of the product in the retailer chain during weeks 2/ /2011 measured in kilograms. Using the ADF-test we can check if the log-transformed sales data is stationary. We use the ADFtest with 4 lags. The p-value of the test statistic is , so we can t reject the null that a unit root exists and the data is non-stationary. We need to remove a stochastic trend of first degree by differencing the data in order to be able to estimate an ARIMAX model. The differenced and logtransformed sales data is plotted in Figure 4. 12
19 Figure 4: Differenced and log-transformed sales of the product in the retailer chain during weeks 2/ /2011 measured in kilograms. Now the time series seems relatively stationary. We use the ADF-test again with 4 lags to check the stationarity assumption. The p-value of the test statistic is 0.01, which means that we can reject the null that there exists a unit root and assume that the data is stationary. From looking at the ACF and PACF functions (Figure 5) for the stationary data, we can identify the model parameters. It s not however that unambiguous to determine the order of and parts. It looks like the PACF function abates exponentially and that the ACF function cuts at the first lag. This indicates, that one should use a model. 13
20 Figure 5: ACF and PACF of the differenced and transformed sales data. The cross-correlation function (CCF) between the transformed sales data and external variables helps us to determine at which lag the external variable affects sales. The CCF can only be counted for wide-sense stationary series, so we need to differentiate the price promotion time series first. From Figure 6 we see that the correlation between sales and price promotion. Price promotion is highest at the zero lag. 14
21 Figure 6: CCF between sales and price promotion data. Estimation The next step is to estimate the model parameters with maximum likelihood method. The time series model was estimated with several parameter combinations because of the ambiguity of the model parameters. The log-likelihood and AIC was calculated for all these models in Table 1. 15
22 Table 1: Model statistics. (p,d,q) Loglikelihood AIC (0,1,1) 73,83-141,65 (1,1,0) 69,35-132,7 (1,1,1) 74,15-140,29 (0,1,2) 74,27-140,55 (2,1,0) 74,7-141,4 (1,1,2) 75,89-141,79 (2,1,1) 74,71-139,42 (2,1,2) 75,91-139,83 (0,1,3) 74,84-139,68 (3,1,0) 74,7-139,41 (1,1,3) 75,91-139,82 (3,1,1) 75,24-138,48 (2,1,3) 75,92-137,83 (3,1,2) 75,88-137,77 (3,1,3) 75,9-135,79 (0,1,4) 75,98-139,96 (1,1,4) 76,03-138,06 (2,1,4) 76,1-136,2 (4,1,4) 78,15-136,3 (4,1,0) 75,52-139,03 (4,1,1) 75,92-137,85 (4,1,2) 75,93-135,86 (4,1,3) 75,93-133,86 (3,1,4) 77,67-137,34 It seems that the has the lowest AIC, so it s considered as the best model. Diagnostic Checks After the most suitable model is chosen, we have to check for model adequacy. The residuals should be white noise. In Figure 7 we see that the residuals have a constant mean, the variance is also relatively constant except for few spikes. 16
23 Figure 7: The residual time series. For the residuals to be white noise, we also need to make sure that they are not autocorrelated. From both the residual ACF (Figure 8) and Ljung-Box test (Figure 9) we see that the residuals aren t autocorrelated. 17
24 Figure 8: Residual ACF. 18
25 Figure 9: The p-values corresponding to the Ljung-Box test statistic plotted against number of lags. If the model fit is good the residuals should be normally distributed. The residual histogram is plotted in Figure 10. The residuals seem to be relatively normally distributed, but we check the normality assumption by performing D Agostino skewness test and Anscomble-Glynn kurtosis test. The p-value of the skewness test is meaning that there doesn t exist skewness in the data. But the kurtosis test p-value is equal to , which means that the kurtosis is not equal to that of a normal distribution. But when the Anscomble-Glynn kurtosis test was performed to other model parameter combinations, they didn t either have the kurtosis of a normal distribution. Thus, the model is not going to be rejected based on this test. 19
26 Figure 10: Residual histogram. The value of the parameter coefficients, standard errors and variance are listed in Table 2. Table 2: Parameter statistics. MA(1) ppvaliokeskotehojuoma coefficient standard error variance
27 Thus, the final model takes the form or (25) The original and fitted time series are plotted in Figure 11 to demonstrate the goodness of the fit. The pseudo- adjusted statistic was also calculated for the goodness of fit [14]. The statistic value is 0.89 which means that the model describes the sales data relatively well. Figure 11: Original (black) and fitted (red) time series. Backtesting After fitting the model to the data, the model was used to predict the sales of the 16 next weeks. The forecast was compared to the actualized sales of the 16 next weeks. The ex-post forecast and 95% confidence intervals are plotted with the actualized sales in Figure 12. It can be noticed that the forecast is quit poor since the actualized sales doesn t even stay inside the 95% confidence intervals. 21
28 Figure 12: Ex-post forecast (red) with 95% confidence intervals (blue) and the actualized sales (black). 22
29 5 Discussion The aim of this thesis was to model the baseline sales of a large Finnish food company s functional dairy product. The baseline sales level was needed for measuring the effect of marketing and advertising functions. Sales data from the manufacturer to a retail chain and marketing and advertising expenditures for end-customers in the retail chain was available for estimation of the model. Because the variables were equally spaced in time, a time series analysis was used to model the baseline sales level. The preferable time series model to model baseline sales would have been a model, as it would have been able to take product life cycle into account. That is, the fact that the effect of advertising on sales changes through product life cycle. But, there were difficulties in getting the package in R statistics software to function. Thus a model was used instead. A model would have been more preferable, because of the seasonal nature of the product, but the time series was too short for seasonal differencing of the model. The Box-Jenkins procedure was used to identify, estimate and validate the model. The best model derived from the Box-Jenkins procedure was. The model is a model, meaning that it is a pure first order Moving Average model that has a first order integrated part. There was no remarkable difference in how well the different models described the data and the model with smallest AIC was chosen. The model described the data relatively well, with a pseudo- adjusted statistic of After finding the best model, the sales for the next 16 weeks were forecasted and compared to the actualized sales. The forecast was pretty poor, since the actualized sales didn t even fit in the 95% confidence interval of the forecast. The difference in the forecasted and actualized sales can however be explained by the marketing and advertising activities that occurred during the forecast interval. During the forecast interval there was an advertising campaign, which could not be explained by our model, since price promotion is the only external variable in the model. The interpretation of the model is that a random shock at time affects the difference in sales between and negatively. This means that the random shock causes a descending stochastic trend in the sales. It can be difficult to state what the random shock represents, but it could be the product life cycle or some competing product that is eating up the market share of this functional dairy product. Obviously, the price promotion of the dairy product affects the difference in sales positively. This means that price promotions create an ascending stochastic trend in the sales. The reason for this could be that customers buy more of the product during price promotion and this simultaneously creates a brand awareness, which makes the customers want to buy of the product in the future, even though the product is then not price promoted. As can be seen from the ex-post forecast the model is not that reliable in forecasting, but can be used to model baseline sales. When there is a noticeable difference in the actualized sales and estimated sales, the effect can be attributed to a marketing or advertising function. However, it 23
30 would be advisable to perform the Box-Jenkins procedure with a longer time series if possible. That way the seasonal effect might also be captured. 6 References [1] Rust, Roland T., Tim Ambler, Gregory S. Carpenter, V. Kumar, and Rajendra K. Srivastava. "Measuring marketing productivity: current knowledge and future directions." Journal of Marketing (2004): [2] Csilla, Horváth, Marcel Kornelis, and Peter SH Leeflang. What marketing scholars should know about time series analysis: time series applications in marketing. No. 02F17. University of Groningen, Research Institute SOM (Systems, Organisations and Management), [3] Pauwels, Koen, Imran Currim, Marnik G. Dekimpe, Dominique M. Hanssens, Natalie Mizik, Eric Ghysels, and Prasad Naik. "Modeling marketing dynamics by time series econometrics." Marketing Letters 15, no. 4 (2004): [4] Hipel, Keith William, Angus Ian McLeod, and William C. Lennox. "Advances in Box-Jenkins modeling: 1. Model construction." Water Resources Research 13, no. 3 (1977): [5] Said, Said E., and David A. Dickey. "Testing for unit roots in autoregressive-moving average models of unknown order." Biometrika 71, no. 3 (1984): [6] (retrieved ) [7] Box, George EP, Gwilym M. Jenkins, and Gregory C. Reinsel. Time series analysis: forecasting and control. 3rd ed. Prentice Hall, Englewood Cliffs, NJ, [8] (retrieved ) [9] Pearson, Egon S. "I. Note on Tests for Normality." Biometrika 22, no. 3-4 (1931): [10] Lütkepohl, Helmut, and Fang Xu. "The role of the log transformation in forecasting economic variables." Empirical Economics 42, no. 3 (2012): [11] (retrieved ) [12] (retrieved ) [13] (retrieved ) [14] Long, J. Scott, and Jeremy Freese. "Regression models for categorical dependent variables using Stata." Stata Press Books (2006). 24
31 7 Appendix 7.1 Summation of the Thesis in Finnish Markkinointitoimenpiteiden perustelu sisältää niiden myynnin lisäämisen arvioimista. Markkinointitoimenpiteiden vaikutuksen arvioimiseksi täytyy ensimmäiseksi muodostaa estimaatti perusmyynnin tasosta, jonka perusteella luodaan vertailuindeksi myynnille. Tämän estimaatin avulla on myös mahdollista eristää muiden myyntiin vaikuttavien seikkojen, kuten kausivaihtelun ja kilpailijoiden hintakampanjoiden vaikutukset [1]. Tämän työn tarkoitus on mallintaa suuren suomalaisen elintarvikeyhtiön tehojuoman perusmyynnin taso. Tuote on maitotuote, johon on lisätty terveysvaikutuksia. Myönteisten terveysvaikutuksien takia tuotetta ostetaan selkeästi enemmän influenssakausina. Perusmyynnin mallintamiseksi käytetään sekä tuotteen myynti- että mainospanosdataa. Mainospanosdata kuvaa paljonko varoja eri markkinointitoimenpiteisiin on käytetty. Varojen käytön tehokkuutta voidaan mallintaa vertailemalla markkinointitoimenpiteitä toteutuneen sekä arvioidun myynnin erotukseen. Markkinointidata sisältää usein aikariippuvaista dataa, jonka takia aikasarjamallit soveltuvat erinomaisesti kuvaamaan datan muuttujien riippuvaisuuksia. Aikasarjamalleissa mallin muuttujat riippuvat ajasta [2]. Kaksi suurinta ongelmaa myynnin mallintamisessa ovat vaihtelevat dynamiikat muuttujien välillä ja endogeenisyyden ongelma. Eli markkinoiden reagointikyky ei välttämättä ole vakio ajan suhteen. Mainonnan vaikutus saattaa hiipua tuotteen elinkaaren ajan, mikä puolestaan johtaa muuttujien välisten dynamiikkojen vaihteluun tuotteen tarkasteluvälillä [3]. Endogeenisyyden ongelmalla tarkoitetaan, että eksogeeniset muuttujat kuten hinta, hintapromootiot ja mainonta ovat tosiasiassa endogeenisiä. Tilastotieteen määritelmien mukaisesti eksogeeninen muuttuja on muuttuja, joka vaikuttaa malliin ilman, että malli vaikuttaa siihen. Eksogeenisen muuttujan kvalitatiiviset ominaisuudet ja tuottamismenetelmät eivät ole mallinrakentajan määrittämiä [11]. Endogeeninen muuttuja on taas tuotettu mallin sisällä ja täten sen arvo vaihtuu mallin funktionaalisten suhteiden kautta [12]. Markkinointijohtajat asettavat markkinointimuuttujien arvot markkinainformaation pohjalta, joka saattaa osittain olla piilevää tutkijalle mutta kuitenkin vaikuttaa asiakkaiden käyttäytymiseen. Tämä luo tilanteen, missä markkinointitoimenpidemuuttujat voivat olla korreloituneita virhetermien kanssa [2]. Markkinointitutkimuksessa yleisesti käytetty malli on vektoriautoregressiomalli ( ), mitä käytetään kuvaamaan markkinointitoimenpiteiden vaikutusta myyntiin. Tässä työssä päädyttiin kuitenkin käyttämään -mallia, koska sen jatkokehitysmahdollisuudet ovat huomattavasti laajemmat [4, 5]. -malli on aikasarjoihin perustuva tilastollinen malli. Kun :ia sovelletaan myynnin perustason mallintamiseen, selitettävänä muuttujana on tuotteen myyntitulot. Myyntituloja 25
32 selitetään myyntitulojen omalla historialla. Lisäksi myynnin satunnaisshokkien historiallista dataa käytetään selittäjänä. Mallissa on myös mahdollista käyttää ulkoisia muuttujia, kuten mainospanosdataa [2]. Selitettävän muuttujan datan on oltava stationaarista, jotta -mallia voidaan käyttää. Stationaarisuus tarkoittaa, että selitettävän muuttujan aikasarjan keskiarvo sekä varianssi ovat aina vakioita. Toisin sanoen aikasarjan tilastolliset ominaisuudet pysyvät vakiona ajan suhteen. Malli ottaa myös huomioon stokastiset trendit myynnissä sekä myynnin kausivaihtelut. Datan stokastinen trendi voidaan ottaa huomioon differentioimalla data, eli laskemalla erotus peräkkäisten aikaaskelien väliltä [2]. -mallin soveltaminen dataan ei kuitenkaan ole täysin triviaalia, vaan se suoritetaan ns. Box-Jenkins menetelmän avulla. Box-Jenkins menetelmä voidaan jakaa kolmeen vaiheeseen; mallin identifiointi, estimointi sekä validointi. Identifioinnin tarkoitus on muokata data stationaariseksi sekä määritellä -mallin parametrien lukumäärä. Datan stationaarisuutta voidaan tutkia ns. täydennetyllä Dickey-Fullerin testillä. Parametrien lukumäärä taas saadaan määriteltyä tutkimalla muuttujien korrelaatiofunktioita. Korrelaatiofunktioista nähdään millä viiveellä muuttujat korreloivat itsensä ja toisten muuttujien kanssa [4]. Kun mallin parametrit on identifioitu, ne estimoidaan suurimman uskottavuuden menetelmällä. Suurimman uskottavuuden menetelmässä käytetään tilastollista otantaa ja arviota siitä, mistä parametrisoidusta jakaumasta kyseinen otanta on otettu. Suurimman uskottavuuden menetelmä estimoi jakaumalle sellaiset parametrit, että otanta on otettu suurimmalla todennäköisyydellä kyseisestä jakaumasta [4]. Mallin validointi koostuu lähinnä residuaalien tutkimisesta. Residuaalien kuuluisi olla riippumattomia, homoskedastisia sekä normaalijakautuneita. Homoskedastisuus tarkoittaa, että residuaalien varianssi ja keskiarvo ovat vakioarvoisia. Lisäksi tarkastellaan parantaako lisäparametrien lisääminen malliin huomattavasti mallin tarkkuutta [4]. Työssä käytettiin -mallia tehojuomatuotteen myynnin perustason mallintamiseen. Myyntitulodatana käytettiin yhtiön myyntituloja jälleenmyyjille. Huomattavaa on, että myyntitulodatana ei siis käytetä määrää, joka loppukäyttäjälle on myyty. Koska tarkastelukohteena on tässä tapauksessa maitotuote, jonka hyllyikä on hyvin lyhyt, voidaan olettaa, että jälleenmyyjät osaavat mitoittaa tilauksensa niin, että se vastaa suhteellisen hyvin loppukäyttäjän kulutusta. Tällöin jälleenmyyjiltä saadut myyntitulot toimivat hyvänä approksimaationa loppukäyttäjiltä saadusta myynnistä. Tuotteen myynnissä esiintyi selkeää kausivaihtelua, mutta sitä ei pystytty mallintamaan datan lyhyen aikajakson takia. Ulkoisiksi muuttujiksi oli mahdollista valita tuotteen mainospanosdata eri medioissa, tuotteen hintatiedot, tuotteen hintapromootiotiedot ja substituuttituotteiden markkinointitoimenpidedata. Korrelaatiomatriisin perusteella kuitenkin huomattiin, että tuotteen hintapromootiodata on yksinään tarpeeksi merkittävä selittämään myyntituloja. Myyntitulodata muutettiin stationaariseksi ja sen korrelaatiofunktiosta pääteltiin, että sopivin -malli olisi sellainen, jossa myyntituloja selitettiin edellisen viikon myyntituloilla, 26
33 satunnaisshokilla ja tuotteen hintapromootiodatalla. Mallin validointivaiheessa todettiin, että tämä oli oikea päättely. Parhaaksi -malliksi saatiin, missä on myyntitulojen erotus ajanhetkillä ja, on myynnin satunnaishokki ajanhetkellä ja on mallin ulkoinen muuttuja, joka tässä tapauksessa on tuotteen hintapromootiodata. Mallin tulkinta on se, että myynnin satunnaisshokki ajanhetkellä vaikuttaa myynnin erotukseen aikavälillä ja negatiivisesti. Tämä tarkoittaa sitä, että satunnaisshokki aiheuttaa laskevan stokastisen trendin myyntituloissa. On vaikea sanoa, mistä satunnaishokki johtuu. Se voi esimerkiksi johtua tuotteen elinkaaresta tai siitä, että kilpaileva tuote syö tuotteen markkinaosuutta. Ilmeisesti hintapromootio vaikuttaa tuotteen myyntiin positiivisesti. Tässä tapauksessa se kuitenkin vaikuttaa myös myynnin erotukseen aikavälillä ja positiivisesti. Tämä tarkoittaa sitä, että hintapromootiot luovat nousevan stokastisen trendin myyntituloihin. Selitys tähän voisi olla, että hintapromootiot saavat asiakkaat ostamaan enemmän tuotetta, joka taas lisää bränditietoisuutta, mikä saa asiakkaat ostamaan lisää tuotetta tulevaisuudessa. 27
Capacity Utilization
 Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Efficiency change over time
 Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
T Statistical Natural Language Processing Answers 6 Collocations Version 1.0
 T-61.5020 Statistical Natural Language Processing Answers 6 Collocations Version 1.0 1. Let s start by calculating the results for pair valkoinen, talo manually: Frequency: Bigrams valkoinen, talo occurred
T-61.5020 Statistical Natural Language Processing Answers 6 Collocations Version 1.0 1. Let s start by calculating the results for pair valkoinen, talo manually: Frequency: Bigrams valkoinen, talo occurred
The CCR Model and Production Correspondence
 The CCR Model and Production Correspondence Tim Schöneberg The 19th of September Agenda Introduction Definitions Production Possiblity Set CCR Model and the Dual Problem Input excesses and output shortfalls
The CCR Model and Production Correspondence Tim Schöneberg The 19th of September Agenda Introduction Definitions Production Possiblity Set CCR Model and the Dual Problem Input excesses and output shortfalls
Gap-filling methods for CH 4 data
 Gap-filling methods for CH 4 data Sigrid Dengel University of Helsinki Outline - Ecosystems known for CH 4 emissions; - Why is gap-filling of CH 4 data not as easy and straight forward as CO 2 ; - Gap-filling
Gap-filling methods for CH 4 data Sigrid Dengel University of Helsinki Outline - Ecosystems known for CH 4 emissions; - Why is gap-filling of CH 4 data not as easy and straight forward as CO 2 ; - Gap-filling
Network to Get Work. Tehtäviä opiskelijoille Assignments for students. www.laurea.fi
 Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward.
 START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
E80. Data Uncertainty, Data Fitting, Error Propagation. Jan. 23, 2014 Jon Roberts. Experimental Engineering
 Lecture 2 Data Uncertainty, Data Fitting, Error Propagation Jan. 23, 2014 Jon Roberts Purpose & Outline Data Uncertainty & Confidence in Measurements Data Fitting - Linear Regression Error Propagation
Lecture 2 Data Uncertainty, Data Fitting, Error Propagation Jan. 23, 2014 Jon Roberts Purpose & Outline Data Uncertainty & Confidence in Measurements Data Fitting - Linear Regression Error Propagation
Valuation of Asian Quanto- Basket Options
 Valuation of Asian Quanto- Basket Options (Final Presentation) 21.11.2011 Thesis Instructor and Supervisor: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta
Valuation of Asian Quanto- Basket Options (Final Presentation) 21.11.2011 Thesis Instructor and Supervisor: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta
The Viking Battle - Part Version: Finnish
 The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
16. Allocation Models
 16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
Other approaches to restrict multipliers
 Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Statistical design. Tuomas Selander
 Statistical design Tuomas Selander 28.8.2014 Introduction Biostatistician Work area KYS-erva KYS, Jyväskylä, Joensuu, Mikkeli, Savonlinna Work tasks Statistical methods, selection and quiding Data analysis
Statistical design Tuomas Selander 28.8.2014 Introduction Biostatistician Work area KYS-erva KYS, Jyväskylä, Joensuu, Mikkeli, Savonlinna Work tasks Statistical methods, selection and quiding Data analysis
19. Statistical Approaches to. Data Variations Tuomas Koivunen S ysteemianalyysin. Laboratorio. Optimointiopin seminaari - Syksy 2007
 19. Statistical Approaches to Data Variations Tuomas Koivunen 24.10.2007 Contents 1. Production Function 2. Stochastic Frontier Regressions 3. Example: Study of Texas Schools 4. Example Continued: Simulation
19. Statistical Approaches to Data Variations Tuomas Koivunen 24.10.2007 Contents 1. Production Function 2. Stochastic Frontier Regressions 3. Example: Study of Texas Schools 4. Example Continued: Simulation
Information on preparing Presentation
 Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
Bounds on non-surjective cellular automata
 Bounds on non-surjective cellular automata Jarkko Kari Pascal Vanier Thomas Zeume University of Turku LIF Marseille Universität Hannover 27 august 2009 J. Kari, P. Vanier, T. Zeume (UTU) Bounds on non-surjective
Bounds on non-surjective cellular automata Jarkko Kari Pascal Vanier Thomas Zeume University of Turku LIF Marseille Universität Hannover 27 august 2009 J. Kari, P. Vanier, T. Zeume (UTU) Bounds on non-surjective
Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition)
 Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen Click here if your download doesn"t start automatically Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen
Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen Click here if your download doesn"t start automatically Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen
Alternative DEA Models
 Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
MUSEOT KULTTUURIPALVELUINA
 Elina Arola MUSEOT KULTTUURIPALVELUINA Tutkimuskohteena Mikkelin museot Opinnäytetyö Kulttuuripalvelujen koulutusohjelma Marraskuu 2005 KUVAILULEHTI Opinnäytetyön päivämäärä 25.11.2005 Tekijä(t) Elina
Elina Arola MUSEOT KULTTUURIPALVELUINA Tutkimuskohteena Mikkelin museot Opinnäytetyö Kulttuuripalvelujen koulutusohjelma Marraskuu 2005 KUVAILULEHTI Opinnäytetyön päivämäärä 25.11.2005 Tekijä(t) Elina
HARJOITUS- PAKETTI A
 Logistiikka A35A00310 Tuotantotalouden perusteet HARJOITUS- PAKETTI A (6 pistettä) TUTA 19 Luento 3.Ennustaminen County General 1 piste The number of heart surgeries performed at County General Hospital
Logistiikka A35A00310 Tuotantotalouden perusteet HARJOITUS- PAKETTI A (6 pistettä) TUTA 19 Luento 3.Ennustaminen County General 1 piste The number of heart surgeries performed at County General Hospital
Kvanttilaskenta - 1. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
LYTH-CONS CONSISTENCY TRANSMITTER
 LYTH-CONS CONSISTENCY TRANSMITTER LYTH-INSTRUMENT OY has generate new consistency transmitter with blade-system to meet high technical requirements in Pulp&Paper industries. Insurmountable advantages are
LYTH-CONS CONSISTENCY TRANSMITTER LYTH-INSTRUMENT OY has generate new consistency transmitter with blade-system to meet high technical requirements in Pulp&Paper industries. Insurmountable advantages are
Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat
 Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat Esityksen sisältö: 1. EU:n energiapolitiikka on se, joka ei toimi 2. Mihin perustuu väite, etteivät
Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat Esityksen sisältö: 1. EU:n energiapolitiikka on se, joka ei toimi 2. Mihin perustuu väite, etteivät
Returns to Scale II. S ysteemianalyysin. Laboratorio. Esitelmä 8 Timo Salminen. Teknillinen korkeakoulu
 Returns to Scale II Contents Most Productive Scale Size Further Considerations Relaxation of the Convexity Condition Useful Reminder Theorem 5.5 A DMU found to be efficient with a CCR model will also be
Returns to Scale II Contents Most Productive Scale Size Further Considerations Relaxation of the Convexity Condition Useful Reminder Theorem 5.5 A DMU found to be efficient with a CCR model will also be
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007
 National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007 Chapter 2.4 Jukka Räisä 1 WATER PIPES PLACEMENT 2.4.1 Regulation Water pipe and its
National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007 Chapter 2.4 Jukka Räisä 1 WATER PIPES PLACEMENT 2.4.1 Regulation Water pipe and its
C++11 seminaari, kevät Johannes Koskinen
 C++11 seminaari, kevät 2012 Johannes Koskinen Sisältö Mikä onkaan ongelma? Standardidraftin luku 29: Atomiset tyypit Muistimalli Rinnakkaisuus On multicore systems, when a thread writes a value to memory,
C++11 seminaari, kevät 2012 Johannes Koskinen Sisältö Mikä onkaan ongelma? Standardidraftin luku 29: Atomiset tyypit Muistimalli Rinnakkaisuus On multicore systems, when a thread writes a value to memory,
Results on the new polydrug use questions in the Finnish TDI data
 Results on the new polydrug use questions in the Finnish TDI data Multi-drug use, polydrug use and problematic polydrug use Martta Forsell, Finnish Focal Point 28/09/2015 Martta Forsell 1 28/09/2015 Esityksen
Results on the new polydrug use questions in the Finnish TDI data Multi-drug use, polydrug use and problematic polydrug use Martta Forsell, Finnish Focal Point 28/09/2015 Martta Forsell 1 28/09/2015 Esityksen
Constructive Alignment in Specialisation Studies in Industrial Pharmacy in Finland
 Constructive Alignment in Specialisation Studies in Industrial Pharmacy in Finland Anne Mari Juppo, Nina Katajavuori University of Helsinki Faculty of Pharmacy 23.7.2012 1 Background Pedagogic research
Constructive Alignment in Specialisation Studies in Industrial Pharmacy in Finland Anne Mari Juppo, Nina Katajavuori University of Helsinki Faculty of Pharmacy 23.7.2012 1 Background Pedagogic research
Land-Use Model for the Helsinki Metropolitan Area
 Land-Use Model for the Helsinki Metropolitan Area Paavo Moilanen Introduction & Background Metropolitan Area Council asked 2005: What is good land use for the transport systems plan? At first a literature
Land-Use Model for the Helsinki Metropolitan Area Paavo Moilanen Introduction & Background Metropolitan Area Council asked 2005: What is good land use for the transport systems plan? At first a literature
MRI-sovellukset. Ryhmän 6 LH:t (8.22 & 9.25)
 MRI-sovellukset Ryhmän 6 LH:t (8.22 & 9.25) Ex. 8.22 Ex. 8.22 a) What kind of image artifact is present in image (b) Answer: The artifact in the image is aliasing artifact (phase aliasing) b) How did Joe
MRI-sovellukset Ryhmän 6 LH:t (8.22 & 9.25) Ex. 8.22 Ex. 8.22 a) What kind of image artifact is present in image (b) Answer: The artifact in the image is aliasing artifact (phase aliasing) b) How did Joe
1. Liikkuvat määreet
 1. Liikkuvat määreet Väitelauseen perussanajärjestys: SPOTPA (subj. + pred. + obj. + tapa + paikka + aika) Suora sanajärjestys = subjekti on ennen predikaattia tekijä tekeminen Alasääntö 1: Liikkuvat määreet
1. Liikkuvat määreet Väitelauseen perussanajärjestys: SPOTPA (subj. + pred. + obj. + tapa + paikka + aika) Suora sanajärjestys = subjekti on ennen predikaattia tekijä tekeminen Alasääntö 1: Liikkuvat määreet
I. Principles of Pointer Year Analysis
 I. Principles of Pointer Year Analysis Fig 1. Maximum (red) and minimum (blue) pointer years. 1 Fig 2. Principle of pointer year calculation. Fig 3. Skeleton plot graph created by Kinsys/Kigraph programme.
I. Principles of Pointer Year Analysis Fig 1. Maximum (red) and minimum (blue) pointer years. 1 Fig 2. Principle of pointer year calculation. Fig 3. Skeleton plot graph created by Kinsys/Kigraph programme.
FinFamily PostgreSQL installation ( ) FinFamily PostgreSQL
 FinFamily PostgreSQL 1 Sisällys / Contents FinFamily PostgreSQL... 1 1. Asenna PostgreSQL tietokanta / Install PostgreSQL database... 3 1.1. PostgreSQL tietokannasta / About the PostgreSQL database...
FinFamily PostgreSQL 1 Sisällys / Contents FinFamily PostgreSQL... 1 1. Asenna PostgreSQL tietokanta / Install PostgreSQL database... 3 1.1. PostgreSQL tietokannasta / About the PostgreSQL database...
7.4 Variability management
 7.4 Variability management time... space software product-line should support variability in space (different products) support variability in time (maintenance, evolution) 1 Product variation Product
7.4 Variability management time... space software product-line should support variability in space (different products) support variability in time (maintenance, evolution) 1 Product variation Product
Characterization of clay using x-ray and neutron scattering at the University of Helsinki and ILL
 Characterization of clay using x-ray and neutron scattering at the University of Helsinki and ILL Ville Liljeström, Micha Matusewicz, Kari Pirkkalainen, Jussi-Petteri Suuronen and Ritva Serimaa 13.3.2012
Characterization of clay using x-ray and neutron scattering at the University of Helsinki and ILL Ville Liljeström, Micha Matusewicz, Kari Pirkkalainen, Jussi-Petteri Suuronen and Ritva Serimaa 13.3.2012
anna minun kertoa let me tell you
 anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto
 Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto If you are searched for a book by Miikka Poikselkä;Harri Holma;Jukka Hongisto Voice over LTE (VoLTE) in pdf form, then you have come
Voice Over LTE (VoLTE) By Miikka Poikselkä;Harri Holma;Jukka Hongisto If you are searched for a book by Miikka Poikselkä;Harri Holma;Jukka Hongisto Voice over LTE (VoLTE) in pdf form, then you have come
Choose Finland-Helsinki Valitse Finland-Helsinki
 Write down the Temporary Application ID. If you do not manage to complete the form you can continue where you stopped with this ID no. Muista Temporary Application ID. Jos et onnistu täyttää lomake loppuun
Write down the Temporary Application ID. If you do not manage to complete the form you can continue where you stopped with this ID no. Muista Temporary Application ID. Jos et onnistu täyttää lomake loppuun
Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO
 Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Puutekniikan koulutusohjelma Toukokuu 2009 TIIVISTELMÄ OPINNÄYTETYÖSTÄ Yksikkö Aika Ylivieska
Jussi Klemola 3D- KEITTIÖSUUNNITTELUOHJELMAN KÄYTTÖÖNOTTO Opinnäytetyö KESKI-POHJANMAAN AMMATTIKORKEAKOULU Puutekniikan koulutusohjelma Toukokuu 2009 TIIVISTELMÄ OPINNÄYTETYÖSTÄ Yksikkö Aika Ylivieska
Salasanan vaihto uuteen / How to change password
 Salasanan vaihto uuteen / How to change password Sisällys Salasanakäytäntö / Password policy... 2 Salasanan vaihto verkkosivulla / Change password on website... 3 Salasanan vaihto matkapuhelimella / Change
Salasanan vaihto uuteen / How to change password Sisällys Salasanakäytäntö / Password policy... 2 Salasanan vaihto verkkosivulla / Change password on website... 3 Salasanan vaihto matkapuhelimella / Change
MEETING PEOPLE COMMUNICATIVE QUESTIONS
 Tiistilän koulu English Grades 7-9 Heikki Raevaara MEETING PEOPLE COMMUNICATIVE QUESTIONS Meeting People Hello! Hi! Good morning! Good afternoon! How do you do? Nice to meet you. / Pleased to meet you.
Tiistilän koulu English Grades 7-9 Heikki Raevaara MEETING PEOPLE COMMUNICATIVE QUESTIONS Meeting People Hello! Hi! Good morning! Good afternoon! How do you do? Nice to meet you. / Pleased to meet you.
812336A C++ -kielen perusteet, 21.8.2010
 812336A C++ -kielen perusteet, 21.8.2010 1. Vastaa lyhyesti seuraaviin kysymyksiin (1p kaikista): a) Mitä tarkoittaa funktion ylikuormittaminen (overloading)? b) Mitä tarkoittaa jäsenfunktion ylimääritys
812336A C++ -kielen perusteet, 21.8.2010 1. Vastaa lyhyesti seuraaviin kysymyksiin (1p kaikista): a) Mitä tarkoittaa funktion ylikuormittaminen (overloading)? b) Mitä tarkoittaa jäsenfunktion ylimääritys
AYYE 9/ HOUSING POLICY
 AYYE 9/12 2.10.2012 HOUSING POLICY Mission for AYY Housing? What do we want to achieve by renting apartments? 1) How many apartments do we need? 2) What kind of apartments do we need? 3) To whom do we
AYYE 9/12 2.10.2012 HOUSING POLICY Mission for AYY Housing? What do we want to achieve by renting apartments? 1) How many apartments do we need? 2) What kind of apartments do we need? 3) To whom do we
FIS IMATRAN KYLPYLÄHIIHDOT Team captains meeting
 FIS IMATRAN KYLPYLÄHIIHDOT 8.-9.12.2018 Team captains meeting 8.12.2018 Agenda 1 Opening of the meeting 2 Presence 3 Organizer s personell 4 Jury 5 Weather forecast 6 Composition of competitors startlists
FIS IMATRAN KYLPYLÄHIIHDOT 8.-9.12.2018 Team captains meeting 8.12.2018 Agenda 1 Opening of the meeting 2 Presence 3 Organizer s personell 4 Jury 5 Weather forecast 6 Composition of competitors startlists
Kvanttilaskenta - 2. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 8, 05 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem The inner product of + and is. Edelleen false, kts. viikon tehtävä 6..
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 8, 05 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem The inner product of + and is. Edelleen false, kts. viikon tehtävä 6..
Miksi Suomi on Suomi (Finnish Edition)
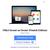 Miksi Suomi on Suomi (Finnish Edition) Tommi Uschanov Click here if your download doesn"t start automatically Miksi Suomi on Suomi (Finnish Edition) Tommi Uschanov Miksi Suomi on Suomi (Finnish Edition)
Miksi Suomi on Suomi (Finnish Edition) Tommi Uschanov Click here if your download doesn"t start automatically Miksi Suomi on Suomi (Finnish Edition) Tommi Uschanov Miksi Suomi on Suomi (Finnish Edition)
BLOCKCHAINS AND ODR: SMART CONTRACTS AS AN ALTERNATIVE TO ENFORCEMENT
 UNCITRAL EMERGENCE CONFERENCE 13.12.2016 Session I: Emerging Legal Issues in the Commercial Exploitation of Deep Seabed, Space and AI BLOCKCHAINS AND ODR: SMART CONTRACTS AS AN ALTERNATIVE TO ENFORCEMENT
UNCITRAL EMERGENCE CONFERENCE 13.12.2016 Session I: Emerging Legal Issues in the Commercial Exploitation of Deep Seabed, Space and AI BLOCKCHAINS AND ODR: SMART CONTRACTS AS AN ALTERNATIVE TO ENFORCEMENT
7. Product-line architectures
 7. Product-line architectures 7.1 Introduction 7.2 Product-line basics 7.3 Layered style for product-lines 7.4 Variability management 7.5 Benefits and problems with product-lines 1 Short history of software
7. Product-line architectures 7.1 Introduction 7.2 Product-line basics 7.3 Layered style for product-lines 7.4 Variability management 7.5 Benefits and problems with product-lines 1 Short history of software
1.3Lohkorakenne muodostetaan käyttämällä a) puolipistettä b) aaltosulkeita c) BEGIN ja END lausekkeita d) sisennystä
 OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
Nuku hyvin, pieni susi -????????????,?????????????????. Kaksikielinen satukirja (suomi - venäjä) (www.childrens-books-bilingual.com) (Finnish Edition)
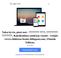 Nuku hyvin, pieni susi -????????????,?????????????????. Kaksikielinen satukirja (suomi - venäjä) (www.childrens-books-bilingual.com) (Finnish Edition) Click here if your download doesn"t start automatically
Nuku hyvin, pieni susi -????????????,?????????????????. Kaksikielinen satukirja (suomi - venäjä) (www.childrens-books-bilingual.com) (Finnish Edition) Click here if your download doesn"t start automatically
EUROOPAN PARLAMENTTI
 EUROOPAN PARLAMENTTI 2004 2009 Kansalaisvapauksien sekä oikeus- ja sisäasioiden valiokunta 2008/0101(CNS) 2.9.2008 TARKISTUKSET 9-12 Mietintöluonnos Luca Romagnoli (PE409.790v01-00) ehdotuksesta neuvoston
EUROOPAN PARLAMENTTI 2004 2009 Kansalaisvapauksien sekä oikeus- ja sisäasioiden valiokunta 2008/0101(CNS) 2.9.2008 TARKISTUKSET 9-12 Mietintöluonnos Luca Romagnoli (PE409.790v01-00) ehdotuksesta neuvoston
RINNAKKAINEN OHJELMOINTI A,
 RINNAKKAINEN OHJELMOINTI 815301A, 18.6.2005 1. Vastaa lyhyesti (2p kustakin): a) Mitkä ovat rinnakkaisen ohjelman oikeellisuuskriteerit? b) Mitä tarkoittaa laiska säikeen luominen? c) Mitä ovat kohtaaminen
RINNAKKAINEN OHJELMOINTI 815301A, 18.6.2005 1. Vastaa lyhyesti (2p kustakin): a) Mitkä ovat rinnakkaisen ohjelman oikeellisuuskriteerit? b) Mitä tarkoittaa laiska säikeen luominen? c) Mitä ovat kohtaaminen
Mat Seminar on Optimization. Data Envelopment Analysis. Economies of Scope S ysteemianalyysin. Laboratorio. Teknillinen korkeakoulu
 Mat-2.4142 Seminar on Optimization Data Envelopment Analysis Economies of Scope 21.11.2007 Economies of Scope Introduced 1982 by Panzar and Willing Support decisions like: Should a firm... Produce a variety
Mat-2.4142 Seminar on Optimization Data Envelopment Analysis Economies of Scope 21.11.2007 Economies of Scope Introduced 1982 by Panzar and Willing Support decisions like: Should a firm... Produce a variety
Huom. tämä kulma on yhtä suuri kuin ohjauskulman muutos. lasketaan ajoneuvon keskipisteen ympyräkaaren jänteen pituus
 AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
TIEKE Verkottaja Service Tools for electronic data interchange utilizers. Heikki Laaksamo
 TIEKE Verkottaja Service Tools for electronic data interchange utilizers Heikki Laaksamo TIEKE Finnish Information Society Development Centre (TIEKE Tietoyhteiskunnan kehittämiskeskus ry) TIEKE is a neutral,
TIEKE Verkottaja Service Tools for electronic data interchange utilizers Heikki Laaksamo TIEKE Finnish Information Society Development Centre (TIEKE Tietoyhteiskunnan kehittämiskeskus ry) TIEKE is a neutral,
Oma sininen meresi (Finnish Edition)
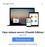 Oma sininen meresi (Finnish Edition) Hannu Pirilä Click here if your download doesn"t start automatically Oma sininen meresi (Finnish Edition) Hannu Pirilä Oma sininen meresi (Finnish Edition) Hannu Pirilä
Oma sininen meresi (Finnish Edition) Hannu Pirilä Click here if your download doesn"t start automatically Oma sininen meresi (Finnish Edition) Hannu Pirilä Oma sininen meresi (Finnish Edition) Hannu Pirilä
Returns to Scale Chapters
 Return to Scale Chapter 5.1-5.4 Saara Tuurala 26.9.2007 Index Introduction Baic Formulation of Retur to Scale Geometric Portrayal in DEA BCC Return to Scale CCR Return to Scale Summary Home Aignment Introduction
Return to Scale Chapter 5.1-5.4 Saara Tuurala 26.9.2007 Index Introduction Baic Formulation of Retur to Scale Geometric Portrayal in DEA BCC Return to Scale CCR Return to Scale Summary Home Aignment Introduction
S Sähkön jakelu ja markkinat S Electricity Distribution and Markets
 S-18.3153 Sähkön jakelu ja markkinat S-18.3154 Electricity Distribution and Markets Voltage Sag 1) Kolmivaiheinen vastukseton oikosulku tapahtuu 20 kv lähdöllä etäisyydellä 1 km, 3 km, 5 km, 8 km, 10 km
S-18.3153 Sähkön jakelu ja markkinat S-18.3154 Electricity Distribution and Markets Voltage Sag 1) Kolmivaiheinen vastukseton oikosulku tapahtuu 20 kv lähdöllä etäisyydellä 1 km, 3 km, 5 km, 8 km, 10 km
Kysymys 5 Compared to the workload, the number of credits awarded was (1 credits equals 27 working hours): (4)
 Tilasto T1106120-s2012palaute Kyselyn T1106120+T1106120-s2012palaute yhteenveto: vastauksia (4) Kysymys 1 Degree programme: (4) TIK: TIK 1 25% ************** INF: INF 0 0% EST: EST 0 0% TLT: TLT 0 0% BIO:
Tilasto T1106120-s2012palaute Kyselyn T1106120+T1106120-s2012palaute yhteenveto: vastauksia (4) Kysymys 1 Degree programme: (4) TIK: TIK 1 25% ************** INF: INF 0 0% EST: EST 0 0% TLT: TLT 0 0% BIO:
SIMULINK S-funktiot. SIMULINK S-funktiot
 S-funktio on ohjelmointikielellä (Matlab, C, Fortran) laadittu oma algoritmi tai dynaamisen järjestelmän kuvaus, jota voidaan käyttää Simulink-malleissa kuin mitä tahansa valmista lohkoa. S-funktion rakenne
S-funktio on ohjelmointikielellä (Matlab, C, Fortran) laadittu oma algoritmi tai dynaamisen järjestelmän kuvaus, jota voidaan käyttää Simulink-malleissa kuin mitä tahansa valmista lohkoa. S-funktion rakenne
Capacity utilization
 Mat-2.4142 Seminar on optimization Capacity utilization 12.12.2007 Contents Summary of chapter 14 Related DEA-solver models Illustrative examples Measure of technical capacity utilization Price-based measure
Mat-2.4142 Seminar on optimization Capacity utilization 12.12.2007 Contents Summary of chapter 14 Related DEA-solver models Illustrative examples Measure of technical capacity utilization Price-based measure
KONEISTUSKOKOONPANON TEKEMINEN NX10-YMPÄRISTÖSSÄ
 KONEISTUSKOKOONPANON TEKEMINEN NX10-YMPÄRISTÖSSÄ https://community.plm.automation.siemens.com/t5/tech-tips- Knowledge-Base-NX/How-to-simulate-any-G-code-file-in-NX- CAM/ta-p/3340 Koneistusympäristön määrittely
KONEISTUSKOKOONPANON TEKEMINEN NX10-YMPÄRISTÖSSÄ https://community.plm.automation.siemens.com/t5/tech-tips- Knowledge-Base-NX/How-to-simulate-any-G-code-file-in-NX- CAM/ta-p/3340 Koneistusympäristön määrittely
Graph. COMPUTE x=rv.normal(0,0.04). COMPUTE y=rv.normal(0,0.04). execute.
 COMPUTE x=rv.ormal(0,0.04). COMPUTE y=rv.ormal(0,0.04). execute. compute hplib_man_r = hplib_man + x. compute arvokons_man_r = arvokons_man + y. GRAPH /SCATTERPLOT(BIVAR)=hplib_man_r WITH arvokons_man_r
COMPUTE x=rv.ormal(0,0.04). COMPUTE y=rv.ormal(0,0.04). execute. compute hplib_man_r = hplib_man + x. compute arvokons_man_r = arvokons_man + y. GRAPH /SCATTERPLOT(BIVAR)=hplib_man_r WITH arvokons_man_r
Alternatives to the DFT
 Alternatives to the DFT Doru Balcan Carnegie Mellon University joint work with Aliaksei Sandryhaila, Jonathan Gross, and Markus Püschel - appeared in IEEE ICASSP 08 - Introduction Discrete time signal
Alternatives to the DFT Doru Balcan Carnegie Mellon University joint work with Aliaksei Sandryhaila, Jonathan Gross, and Markus Püschel - appeared in IEEE ICASSP 08 - Introduction Discrete time signal
LX 70. Ominaisuuksien mittaustulokset 1-kerroksinen 2-kerroksinen. Fyysiset ominaisuudet, nimellisarvot. Kalvon ominaisuudet
 LX 70 % Läpäisy 36 32 % Absorptio 30 40 % Heijastus 34 28 % Läpäisy 72 65 % Heijastus ulkopuoli 9 16 % Heijastus sisäpuoli 9 13 Emissiivisyys.77.77 Auringonsuojakerroin.54.58 Auringonsäteilyn lämmönsiirtokerroin.47.50
LX 70 % Läpäisy 36 32 % Absorptio 30 40 % Heijastus 34 28 % Läpäisy 72 65 % Heijastus ulkopuoli 9 16 % Heijastus sisäpuoli 9 13 Emissiivisyys.77.77 Auringonsuojakerroin.54.58 Auringonsäteilyn lämmönsiirtokerroin.47.50
Toppila/Kivistö 10.01.2013 Vastaa kaikkin neljään tehtävään, jotka kukin arvostellaan asteikolla 0-6 pistettä.
 ..23 Vastaa kaikkin neljään tehtävään, jotka kukin arvostellaan asteikolla -6 pistettä. Tehtävä Ovatko seuraavat väittämät oikein vai väärin? Perustele vastauksesi. (a) Lineaarisen kokonaislukutehtävän
..23 Vastaa kaikkin neljään tehtävään, jotka kukin arvostellaan asteikolla -6 pistettä. Tehtävä Ovatko seuraavat väittämät oikein vai väärin? Perustele vastauksesi. (a) Lineaarisen kokonaislukutehtävän
Lokaali bilineaarinen (lokaali Lee-Carter) kuolevuusmalli
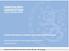 Lokaali bilineaarinen (lokaali Lee-Carter) kuolevuusmalli Aktuaariyhdistyksen kuolevuusseminaari 9.4.2013 Vesa Ronkainen 9.4.2013 Vesa Ronkainen Stochastic modeling of financing longevity risk in pension
Lokaali bilineaarinen (lokaali Lee-Carter) kuolevuusmalli Aktuaariyhdistyksen kuolevuusseminaari 9.4.2013 Vesa Ronkainen 9.4.2013 Vesa Ronkainen Stochastic modeling of financing longevity risk in pension
Integration of Finnish web services in WebLicht Presentation in Freudenstadt 2010-10-16 by Jussi Piitulainen
 Integration of Finnish web services in WebLicht Presentation in Freudenstadt 2010-10-16 by Jussi Piitulainen Who we are FIN-CLARIN University of Helsinki The Language Bank of Finland CSC - The Center for
Integration of Finnish web services in WebLicht Presentation in Freudenstadt 2010-10-16 by Jussi Piitulainen Who we are FIN-CLARIN University of Helsinki The Language Bank of Finland CSC - The Center for
Karkaavatko ylläpitokustannukset miten kustannukset ja tuotot johdetaan hallitusti?
 For professional use only Not for public distribution Karkaavatko ylläpitokustannukset miten kustannukset ja tuotot johdetaan hallitusti? 08.02.2012 Jyrki Merjamaa, Head of Asset Management Aberdeen Asset
For professional use only Not for public distribution Karkaavatko ylläpitokustannukset miten kustannukset ja tuotot johdetaan hallitusti? 08.02.2012 Jyrki Merjamaa, Head of Asset Management Aberdeen Asset
ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin. Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana
 ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana Taustaa KAO mukana FINECVET-hankeessa, jossa pilotoimme ECVETiä
ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana Taustaa KAO mukana FINECVET-hankeessa, jossa pilotoimme ECVETiä
Tutkimusdata ja julkaiseminen Suomen Akatemian ja EU:n H2020 projekteissa
 Tutkimusdata ja julkaiseminen Suomen Akatemian ja EU:n H2020 projekteissa Tutkimusasiamies Kaisa Männikkö Tutkimus- ja innovaatiopalvelut Suomen Akatemian projektit Suomen Akatemia kehottaa avoimeen tieteelliseen
Tutkimusdata ja julkaiseminen Suomen Akatemian ja EU:n H2020 projekteissa Tutkimusasiamies Kaisa Männikkö Tutkimus- ja innovaatiopalvelut Suomen Akatemian projektit Suomen Akatemia kehottaa avoimeen tieteelliseen
Julkaisun laji Opinnäytetyö. Sivumäärä 43
 OPINNÄYTETYÖN KUVAILULEHTI Tekijä(t) SUKUNIMI, Etunimi ISOVIITA, Ilari LEHTONEN, Joni PELTOKANGAS, Johanna Työn nimi Julkaisun laji Opinnäytetyö Sivumäärä 43 Luottamuksellisuus ( ) saakka Päivämäärä 12.08.2010
OPINNÄYTETYÖN KUVAILULEHTI Tekijä(t) SUKUNIMI, Etunimi ISOVIITA, Ilari LEHTONEN, Joni PELTOKANGAS, Johanna Työn nimi Julkaisun laji Opinnäytetyö Sivumäärä 43 Luottamuksellisuus ( ) saakka Päivämäärä 12.08.2010
Miehittämätön meriliikenne
 Rolls-Royce & Unmanned Shipping Ecosystem Miehittämätön meriliikenne Digimurros 2020+ 17.11. 2016 September 2016 2016 Rolls-Royce plc The 2016 information Rolls-Royce in this plc document is the property
Rolls-Royce & Unmanned Shipping Ecosystem Miehittämätön meriliikenne Digimurros 2020+ 17.11. 2016 September 2016 2016 Rolls-Royce plc The 2016 information Rolls-Royce in this plc document is the property
Olet vastuussa osaamisestasi
 Olet vastuussa osaamisestasi Ohjelmistoammattilaisuuden uudet haasteet Timo Vehmaro 02-12-2015 1 Nokia 2015 Mitä osaamista tulevaisuudessa tarvitaan? Vahva perusosaaminen on kaiken perusta Implementaatio
Olet vastuussa osaamisestasi Ohjelmistoammattilaisuuden uudet haasteet Timo Vehmaro 02-12-2015 1 Nokia 2015 Mitä osaamista tulevaisuudessa tarvitaan? Vahva perusosaaminen on kaiken perusta Implementaatio
TAMPEREEN TEKNILLINEN YLIOPISTO Teollisuustalous
 Muista merkita nimesi Ja opiskeliianumerosi iokaiseen paperiin. Myös optiseen lomakkeeseen. Älii irroita papereita nipusta. Kaikki paperit on palautettava. TAMPEREEN 290 10 10 Tuotannonohjauksen tentti
Muista merkita nimesi Ja opiskeliianumerosi iokaiseen paperiin. Myös optiseen lomakkeeseen. Älii irroita papereita nipusta. Kaikki paperit on palautettava. TAMPEREEN 290 10 10 Tuotannonohjauksen tentti
4x4cup Rastikuvien tulkinta
 4x4cup Rastikuvien tulkinta 4x4cup Control point picture guidelines Päivitetty kauden 2010 sääntöihin Updated for 2010 rules Säännöt rastikuvista Kilpailijoiden tulee kiinnittää erityistä huomiota siihen,
4x4cup Rastikuvien tulkinta 4x4cup Control point picture guidelines Päivitetty kauden 2010 sääntöihin Updated for 2010 rules Säännöt rastikuvista Kilpailijoiden tulee kiinnittää erityistä huomiota siihen,
DIGITAL MARKETING LANDSCAPE. Maatalous-metsätieteellinen tiedekunta
 DIGITAL MARKETING LANDSCAPE Mobile marketing, services and games MOBILE TECHNOLOGIES Handset technologies Network technologies Application technologies INTRODUCTION TO MOBILE TECHNOLOGIES COMPANY PERSPECTIVE
DIGITAL MARKETING LANDSCAPE Mobile marketing, services and games MOBILE TECHNOLOGIES Handset technologies Network technologies Application technologies INTRODUCTION TO MOBILE TECHNOLOGIES COMPANY PERSPECTIVE
ELEMET- MOCASTRO. Effect of grain size on A 3 temperatures in C-Mn and low alloyed steels - Gleeble tests and predictions. Period
 1 ELEMET- MOCASTRO Effect of grain size on A 3 temperatures in C-Mn and low alloyed steels - Gleeble tests and predictions Period 20.02-25.05.2012 Diaarinumero Rahoituspäätöksen numero 1114/31/2010 502/10
1 ELEMET- MOCASTRO Effect of grain size on A 3 temperatures in C-Mn and low alloyed steels - Gleeble tests and predictions Period 20.02-25.05.2012 Diaarinumero Rahoituspäätöksen numero 1114/31/2010 502/10
Rekisteröiminen - FAQ
 Rekisteröiminen - FAQ Miten Akun/laturin rekisteröiminen tehdään Akun/laturin rekisteröiminen tapahtuu samalla tavalla kuin nykyinen takuurekisteröityminen koneille. Nykyistä tietokantaa on muokattu niin,
Rekisteröiminen - FAQ Miten Akun/laturin rekisteröiminen tehdään Akun/laturin rekisteröiminen tapahtuu samalla tavalla kuin nykyinen takuurekisteröityminen koneille. Nykyistä tietokantaa on muokattu niin,
KANNATTAVUUDEN ARVIOINTI JA KEHITTÄMINEN ELEMENTTILIIKETOIMINNASSA
 LAPPEENRANNAN TEKNILLINEN YLIOPISTO TEKNISTALOUDELLINEN TIEDEKUNTA Tuotantotalouden koulutusohjelma KANNATTAVUUDEN ARVIOINTI JA KEHITTÄMINEN ELEMENTTILIIKETOIMINNASSA Diplomityöaihe on hyväksytty Tuotantotalouden
LAPPEENRANNAN TEKNILLINEN YLIOPISTO TEKNISTALOUDELLINEN TIEDEKUNTA Tuotantotalouden koulutusohjelma KANNATTAVUUDEN ARVIOINTI JA KEHITTÄMINEN ELEMENTTILIIKETOIMINNASSA Diplomityöaihe on hyväksytty Tuotantotalouden
Jatko-opintovaihtoehdot/ Further studies
 Jatko-opintovaihtoehdot/ Further studies Lukion jälkeen.. Ammatillinen toinen aste 2v. Ammattikorkeakoulut 3,5-4v. Yliopistot 5,5-6 v. Opinnot ulkomailla After Upper Secondary Vocational school, 2 years
Jatko-opintovaihtoehdot/ Further studies Lukion jälkeen.. Ammatillinen toinen aste 2v. Ammattikorkeakoulut 3,5-4v. Yliopistot 5,5-6 v. Opinnot ulkomailla After Upper Secondary Vocational school, 2 years
Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi
 Ideasta projektiksi - kumppanuushankkeen suunnittelun lähtökohdat Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi Erasmus+ -ohjelman hakuneuvonta ammatillisen koulutuksen kumppanuushanketta
Ideasta projektiksi - kumppanuushankkeen suunnittelun lähtökohdat Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi Erasmus+ -ohjelman hakuneuvonta ammatillisen koulutuksen kumppanuushanketta
The role of 3dr sector in rural -community based- tourism - potentials, challenges
 The role of 3dr sector in rural -community based- tourism - potentials, challenges Lappeenranta, 5th September 2014 Contents of the presentation 1. SEPRA what is it and why does it exist? 2. Experiences
The role of 3dr sector in rural -community based- tourism - potentials, challenges Lappeenranta, 5th September 2014 Contents of the presentation 1. SEPRA what is it and why does it exist? 2. Experiences
Categorical Decision Making Units and Comparison of Efficiency between Different Systems
 Categorical Decision Making Units and Comparison of Efficiency between Different Systems Mat-2.4142 Optimointiopin Seminaari Source William W. Cooper, Lawrence M. Seiford, Kaoru Tone: Data Envelopment
Categorical Decision Making Units and Comparison of Efficiency between Different Systems Mat-2.4142 Optimointiopin Seminaari Source William W. Cooper, Lawrence M. Seiford, Kaoru Tone: Data Envelopment
Miten koulut voivat? Peruskoulujen eriytyminen ja tuki Helsingin metropolialueella
 Miten koulut voivat? Peruskoulujen eriytyminen ja tuki Helsingin metropolialueella 26.4.2012 1 "There is often a property bubble around catchment areas. If a school makes a house more saleable or desirable,
Miten koulut voivat? Peruskoulujen eriytyminen ja tuki Helsingin metropolialueella 26.4.2012 1 "There is often a property bubble around catchment areas. If a school makes a house more saleable or desirable,
Tork Paperipyyhe. etu. tuotteen ominaisuudet. kuvaus. Väri: Valkoinen Malli: Vetopyyhe
 etu Monikäyttöpaperi hoitaa useimmat pyyhintätehtävät Sopiva lasipintojen pyyhintään Sopii käsien kuivaamiseen Elintarvikekäyttöön hyväksytty Tork Easy Handling, pakkaus, jota on helppo kantaa mukana,
etu Monikäyttöpaperi hoitaa useimmat pyyhintätehtävät Sopiva lasipintojen pyyhintään Sopii käsien kuivaamiseen Elintarvikekäyttöön hyväksytty Tork Easy Handling, pakkaus, jota on helppo kantaa mukana,
SELL Student Games kansainvälinen opiskelijaurheilutapahtuma
 SELL Student Games kansainvälinen opiskelijaurheilutapahtuma Painonnosto 13.5.2016 (kansallinen, CUP) Below in English Paikka: Nääshalli Näsijärvenkatu 8 33210 Tampere Alustava aikataulu: Punnitus 12:00-13:00
SELL Student Games kansainvälinen opiskelijaurheilutapahtuma Painonnosto 13.5.2016 (kansallinen, CUP) Below in English Paikka: Nääshalli Näsijärvenkatu 8 33210 Tampere Alustava aikataulu: Punnitus 12:00-13:00
MS-A0504 First course in probability and statistics
 MS-A0504 First course in probability and statistics Week 6 Statistical dependence and linear regression Heikki Seppälä Department of mathematics and system analysis School of science Aalto University Spring
MS-A0504 First course in probability and statistics Week 6 Statistical dependence and linear regression Heikki Seppälä Department of mathematics and system analysis School of science Aalto University Spring
3 9-VUOTIAIDEN LASTEN SUORIUTUMINEN BOSTONIN NIMENTÄTESTISTÄ
 Puhe ja kieli, 27:4, 141 147 (2007) 3 9-VUOTIAIDEN LASTEN SUORIUTUMINEN BOSTONIN NIMENTÄTESTISTÄ Soile Loukusa, Oulun yliopisto, suomen kielen, informaatiotutkimuksen ja logopedian laitos & University
Puhe ja kieli, 27:4, 141 147 (2007) 3 9-VUOTIAIDEN LASTEN SUORIUTUMINEN BOSTONIN NIMENTÄTESTISTÄ Soile Loukusa, Oulun yliopisto, suomen kielen, informaatiotutkimuksen ja logopedian laitos & University
Supplementary Table S1. Material list (a) Parameters Sal to Str
 Tooth wear as a means to quantify intra-specific variations in diet and chewing movements - Scientific Reports 2016, 6:3037 Ivan Calandra, Gaëlle Labonne, Ellen Schulz-Kornas, Thomas M. Kaiser & Sophie
Tooth wear as a means to quantify intra-specific variations in diet and chewing movements - Scientific Reports 2016, 6:3037 Ivan Calandra, Gaëlle Labonne, Ellen Schulz-Kornas, Thomas M. Kaiser & Sophie
Infrastruktuurin asemoituminen kansalliseen ja kansainväliseen kenttään Outi Ala-Honkola Tiedeasiantuntija
 Infrastruktuurin asemoituminen kansalliseen ja kansainväliseen kenttään Outi Ala-Honkola Tiedeasiantuntija 1 Asemoitumisen kuvaus Hakemukset parantuneet viime vuodesta, mutta paneeli toivoi edelleen asemoitumisen
Infrastruktuurin asemoituminen kansalliseen ja kansainväliseen kenttään Outi Ala-Honkola Tiedeasiantuntija 1 Asemoitumisen kuvaus Hakemukset parantuneet viime vuodesta, mutta paneeli toivoi edelleen asemoitumisen
Counting quantities 1-3
 Counting quantities 1-3 Lukumäärien 1 3 laskeminen 1. Rastita Tick (X) (X) the kummassa box that has laatikossa more on balls enemmän in it. palloja. X. Rastita Tick (X) (X) the kummassa box that has laatikossa
Counting quantities 1-3 Lukumäärien 1 3 laskeminen 1. Rastita Tick (X) (X) the kummassa box that has laatikossa more on balls enemmän in it. palloja. X. Rastita Tick (X) (X) the kummassa box that has laatikossa
make and make and make ThinkMath 2017
 Adding quantities Lukumäärienup yhdistäminen. Laske yhteensä?. Countkuinka howmonta manypalloja ballson there are altogether. and ja make and make and ja make on and ja make ThinkMath 7 on ja on on Vaihdannaisuus
Adding quantities Lukumäärienup yhdistäminen. Laske yhteensä?. Countkuinka howmonta manypalloja ballson there are altogether. and ja make and make and ja make on and ja make ThinkMath 7 on ja on on Vaihdannaisuus
Operatioanalyysi 2011, Harjoitus 4, viikko 40
 Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
Automaatiojärjestelmän hankinnassa huomioitavat tietoturva-asiat
 Automaatiojärjestelmän hankinnassa huomioitavat tietoturva-asiat Teollisuusautomaation tietoturvaseminaari Purchasing Manager, Hydro Lead Buyer, Industrial Control Systems 1 Agenda / esityksen tavoite
Automaatiojärjestelmän hankinnassa huomioitavat tietoturva-asiat Teollisuusautomaation tietoturvaseminaari Purchasing Manager, Hydro Lead Buyer, Industrial Control Systems 1 Agenda / esityksen tavoite
Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine Centre for Language and Communication Studies
 Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine 4.1.2018 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve
Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine 4.1.2018 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve
Heisingin kaupungin tietokeskus Helsingfors stads faktacentral City of Helsinki Urban Facts 0N THE EFFECTS 0F URBAN NATURAL AMENITIES, ARCHITECTURAL
 Heisingin kaupungin tietokeskus - /igc' ^' 0N THE EFFECTS 0F URBAN NATURAL TIEOUSTELUT FÖRFÄGNINGAR INQUIRIES Henrik Lönnqvist, p. - tel. 09 310 36534 etunimi.sukunimi@hel.fi JULKAISIJA UTGIVARE PUBLISHER
Heisingin kaupungin tietokeskus - /igc' ^' 0N THE EFFECTS 0F URBAN NATURAL TIEOUSTELUT FÖRFÄGNINGAR INQUIRIES Henrik Lönnqvist, p. - tel. 09 310 36534 etunimi.sukunimi@hel.fi JULKAISIJA UTGIVARE PUBLISHER
