SUOMALAISTEN VEDONLYÖJIEN KÄYTTÄYTYMINEN SIJOITTAJIA VAI PELUREITA?
|
|
|
- Olavi Honkanen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 TAMPEREEN YLIOPISTO Taloustieteiden laitos SUOMALAISTEN VEDONLYÖJIEN KÄYTTÄYTYMINEN SIJOITTAJIA VAI PELUREITA? Laskentatoimi Pro gradu -tutkielma Lokakuu 2005 Ohjaaja: Petri Vehmanen Marko Virtanen Mikko Vänni
2 TIIVISTELMÄ Tampereen yliopisto Taloustieteiden laitos; laskentatoimi Tekijät: VIRTANEN, MARKO & VÄNNI, MIKKO Tutkielman nimi: Suomalaisten vedonlyöjien käyttäytyminen sijoittajia vai pelureita Pro gradu -tutkimus: 116 sivua, 17 liitesivua Aika: Lokakuu 2005 Avainsanat: vedonlyönti, markkinoiden tehokkuus, vedonlyöntikäyttäytyminen, suosikki altavastaaja-harha Tutkimuksen tarkoituksena on tutkia suomalaisten Internet-vedonlyöjien käyttäytymistä. Tutkimuksen tavoitteena on tutkia suomalaisten Internet-vedonlyöjien käytössä olevia keinoja ja resursseja, ja selvittää riittävätkö ne kannattavaan vedonlyöntiin. Tutkielman teoriaosuudessa perehdytään vedonlyöntiteoriaan. Tehdään vedonlyöntimarkkinoiden tehokkuutta käsittelevä kirjallisuus katsaus ja verrataan eri vedonlyöntitoimistojen tarjoamia kiinteitä kertoimia sekä toimistojen kohdetarjonnan laajuutta. Lisäksi teoriaosuudessa tehdään arvopaperimarkkinoiden ja vedonlyöntimarkkinoiden yhtäläisyyksiä ja vedonlyöntikäyttäytymistä käsittelevä kirjallisuuskatsaus. Vedonlyöntikäyttäytymistä käsittelevässä luvussa tarkastellaan markkinoilla esiintyviä vedonlyöntiharhoja. Tutkielman empiirisessä osuudessa tutkitaan suomalaisten Internet-vedonlyöjien vedonlyöntikäyttäytymistä. Tutkimuksen kohderyhmän muodostavat vedonlyöntiaiheisen keskustelupalstan, rekisteröityneet käyttäjät. Kyselytutkimus toteutettiin sitä varten avatulla Internet-sivustolla. Kyselytutkimus sisälsi 20 kysymystä, jotka oli ryhmitelty viiteen eri osioon. Ne käsittelivät vastanneiden taustatietoja, vedonlyöntiprosessia, vedonlyöntitoimistoja, kohdevalikoimaa sekä yleistä vedonlyöntikäyttäytymistä. Tutkimuksen aineisto analysoitiin ristiintaulukoimalla kaikki vastaukset keskenään. Tutkimuksen ristiintaulukoinnin tilastollisia riippuvuuksia tutkittiin ²- (khiin neliö) riippumattomuustestin sekä kontingenssikertoimen avulla. Tutkimuksessa selvisi, että Internet-vedonlyöjien asettamat tavoitteet vedonlyöntiin ovat korkeat, jos verrataan heidän käyttämiään keinoja ja resursseja. Suurimmat puutteet olivat havaittavissa vedonlyöjien ajan käytössä sekä riskienhallinnassa. Tutkimuksessa havaittiin, että suomalaisilla Internet-vedonlyöjillä on mielenkiintoa vedonlyöntiin, ja kun jaksetaan pitkäjänteisesti hankkia tarpeeksi hyvä tietämyspohja vedonlyönnistä, myös kannattaviin tuloksiin pääsy on mahdollista. 2
3 1 JOHDANTO Tutkielman tausta Tutkimuksen tarkoitus ja tavoitteet Rajaukset Tutkimuksen rakenne Tutkimusote ja -menetelmä VEDONLYÖNTITEORIA Palautusprosentti Kertoimet ja niiden muodostuminen Kiinteät kertoimet Muuttuvat kertoimet (totalisaattoripeli) Todennäköisyyden määrittäminen Subjektiivinen todennäköisyys Objektiivinen todennäköisyys Odotusarvo Pelikassa ja kirjanpito Hajonnan ja riskin merkitys vedonlyönnissä Vedonlyönnissä käytettäviä kaavoja Kellyn kaava Harvillen kaava Poisson-kaava Arbitraasit Arbitraasin riski Arbitraasin riski Arbitraasin riski Vedonlyöntisanastoa ja tutkimuksessa käytettyjen termien selityksiä Vedonlyöntimuotoja VEDONLYÖNTIMARKKINAT JA NIIDEN TEHOKKUUS Yleinen markkinoiden tehokkuus Vedonlyöntimarkkinoiden tehokkuus Sisäpiiritieto vedonlyöntimarkkinoilla Vedonlyöntitoimistot Toimistojen esittelyä Toimistojen vertailua VEDONLYÖNTI SIJOITUSMUOTONA Erilaiset pelaajaryhmät Vedonlyönti sijoitus vai hyödyke? Yhtäläisyydet osake- ja vedonlyöntimarkkinoiden välillä Rationaalinen pelaaja Pelikassa ja panoksen määritys Pitkäjänteisyys Vedonlyönnin kustannukset Keskustelupalstat ja vihjepalvelut Kerroinvertailut Vedonlyöjän harha Suosikki altavastaaja-harha Poikkeuksia suosikki-altavastaajaharhaan Selityksiä suosikki - altavastaajaharhaan Tunteella pelaamisen harha
4 4.8. Lähtöpaikka harha Kotikenttäetu TUTKIMUSAINEISTON ESITTELY JA TUTKIMUKSEN TOTEUTUS Kyselytutkimuksen kohdejoukko Tutkimuksen vastausmäärät ja toteutus Tutkimuksessa käytetyt tilastolliset riippumattomuusmallit ² riippumattomuustesti (khiin neliö) Kontingenssikerroin TULOKSET Vastanneiden taustatietoja Sukupuoli Ikä Elämäntilanne Vedonlyöntiprosessi Vedonlyöntiaktiivisuus Pelikohteen valinta Panoksen määritys Panoksen koko Kirjanpito Vedonlyöntitoimistot Toimistojen suosio Suosikkitoimisto Lajivalikoima Lajien suosio Päälaji Yleistä vedonlyönnistä Tiedonvaihto Suosikki altavastaaja-harha Tunnesyyt Muu sijoittaminen Arbitraasit Ansiotaso ja tulevaisuuden tavoitteet Vedonlyöjien tulevaisuuden ansaintamahdollisuudet PÄÄTELMÄT LÄHTEET LIITE 1: Tutkimuksessa esitetyt kontingenssikertoimet sekä p-arvot LIITE 2: Kyselylomake
5 1 JOHDANTO 1.1 Tutkielman tausta Urheiluvedonlyönti tarjoaa monelle vedonlyöjälle mahdollisuuden jännittää urheilutapahtuman lopputulosta. Vedonlyöntioppaassaan Vuoksenmaa (1999, 36) toteaa, että suurimmalle osalle pelaajista vedonlyönti on harrastus mutta osa pelaajista suhtautuu urheiluvedonlyöntiin kuin mihin tahansa sijoitustoimintaan. Tarkoituksena sijoitustoiminnassa on maksimoida tuotto sijoitetulle pääomalle. Vedonlyöntiä sijoitustarkoituksessa harjoittavat pelaajat analysoivat markkinoita ja pyrkivät löytämään tuottavia vedonlyöntikohteita, joiden odotusarvo on yli yhden. Vedonlyöntiä koskevat tutkimukset mm. Asch et al. (1984), Hausch & Ziemba (1990), Terrell & Farmer (1996) keskittyvät pääosin vedonlyöntimarkkinoiden tehokkuuden tutkimiseen ja mittaamiseen. Vedonlyöntimarkkinoiden tehokkuutta voidaan tutkia samalla tapaa kuin arvopaperimarkkinoiden tehokkuutta, koska näillä markkinoilla on monia yhtäläisyyksiä (mm. Thaler & Ziemba 1988; Avery & Chevalier 1999; Gabriel & Marsden 1990). Vedonlyöntimarkkinoita on tutkittu vähän verrattuna arvopaperimarkkinoihin ja muihin rahoitusinstrumentteihin. Varsinkin arvopaperimarkkinoiden tehokkuudesta on tehty lukuisia tutkimuksia, mm. Fama (1970), Malkiel (1999). Vedonlyöntimarkkinoita koskevista tutkimuksista suurin osa käsittelee hevosurheilua (Bird & McRae, 1987). Suomen vedonlyöntimarkkinat elävät mielenkiintoista aikaa yksittäisen urheiluvedonlyöjän kannalta. Muutaman Euroopan Unionin jäsenmaan vedonlyöntimonopoli on jo murtunut, lähinnä Euroopan Unionin sekä ulkomaisten vedonlyöntitoimistojen painostuksen takia. Näin kävi esimerkiksi Italian valtiolliselle vedonlyöntimonopolille. (Yhteisöjen tuomioistuimen tuomio, lehdistötiedote < Kotimaisen Veikkauksen monopoliasema saattaa muuttua tulevaisuudessa ainakin vedonlyönnissä. 5
6 Suomalaisten vedonlyöjien on mahdollista lyödä vetoa kahdella eri tavalla: kotimaisissa, Veikkaus Oy:n asiamiespisteissä tai Internetin välityksellä. Internetin kautta on mahdollista pelata satojen eri ulkomaisten vedonlyöntitoimistojen tarjoamia kohteita. Ulkomaisten vedonlyöntitoimistojen houkuttelevuutta lisäsi ennakkotapaus, kun Ahvenanmaalainen, Elisabeth Lindman voitti ruotsalaisen Svenska Spelin rahaarvasta miljoona kruunua, Suomen valtio tulkitsi Lindmanin voiton verotettavaksi tuloksi. EY-tuomioistuin päätti, ettei pelaajan tarvitse maksaa kyseen omaisesta voitosta kotimaahan veroa, ettei vero kaksinkertaistu EU sisällä. Edellä mainittu tapaus toimii Suomen kohdalla myös ennakkotapauksena EU:n sisällä tapahtuvasta vedonlyönnin verotuksesta. (EU:n tiedote, verotus Diana Lindman < 1.2 Tutkimuksen tarkoitus ja tavoitteet Tutkimuksen tarkoituksena on tutkia suomalaisten Internet-vedonlyöjien käyttäytymistä. Tutkimuksen tavoitteena on tutkia suomalaisten Internet-vedonlyöjien käytössä olevia keinoja ja resursseja ja selvittää, riittävätkö ne kannattavaan vedonlyöntiin. Lisäksi tutkimuksessa tehdään vedonlyöntimarkkinoita käsittelevä kirjallisuuskatsaus. 1.3 Rajaukset Kaikista mahdollisista pelimuodoista rajaus tehdään urheiluvedonlyöntiin. Tarkastelun ulkopuolelle on rajattu puhtaat onnenpelit kuten esimerkiksi kasinopelit sekä lotto. Onnenpelien todennäköisyydet ovat objektiivisia, eli toisin sanoen eri tulosvaihtoehtojen tarkka ja oikea todennäköisyys on määritettävissä. Urheiluvedonlyönnissä on kyse subjektiivisen todennäköisyyden määrittämisestä, ja juuri tämä tekijä tekee sen tarkastelusta erityisen mielenkiintoisen. Subjektiivisella todennäköisyydellä tarkoitetaan markkinoiden tai yksittäisen vedonlyöjän näkemystä eri urheilutapahtumien tulosvaihtoehtojen todennäköisyyksistä (Ali, 1977). 6
7 1.4 Tutkimuksen rakenne Tämä tutkimus koostuu teoriaosuudesta sekä empiirisestä tutkimusosuudesta. Empiirinen tutkimus toteutettiin kyselytutkimuksena. Tutkimuksen empiiriseen osuuteen osallistuneet vastaajat saatiin vedonlyöntiaiheinen keskustelupalstan ylikerroin.comin rekisteröityneistä käyttäjistä. Johdannon jälkeen luvussa kaksi perehdytään vedonlyöntiteoriaan. Kolmannessa luvussa tehdään vedonlyöntimarkkinoiden tehokkuutta käsittelevä kirjallisuus katsaus ja verrataan eri vedonlyöntitoimistojen tarjoamia kiinteitä kertoimia sekä toimistojen kohdetarjonnan laajuutta. Neljännessä luvussa tehdään arvopaperimarkkinoiden ja vedonlyöntimarkkinoiden yhtäläisyyksiä ja vedonlyöntikäyttäytymistä käsittelevä kirjallisuuskatsaus. Tutkimuksen viidennessä luvussa esitellään empiirisessä osassa käytetty kyselytutkimusaineisto ja tutkimuksen toteutus. Kuudes luku koostuu empiirisen kyselytutkimuksen tuloksista. Seitsemännessä luvussa esitetään johtopäätökset. 1.5 Tutkimusote ja -menetelmä Tämän tutkimuksen tutkimusote on lähinnä nomoteettinen. Nomoteettinen tutkimusote perustuu pitkälti positivismiin. Positivismia voidaan pitää kattavana ylänimikkeenä sille tieteenfilosofiselle suuntaukselle, jonka peruskäsitteitä ovat mm. objektiivisuus, luonnontieteenomaisuus, kausaalisuus, selittäminen, analyyttisyys, empiriapohjaisuus sekä tutkijan neutraalisuus. Positivismiin perustuvaa lähestymistapaa, jonka kautta positivistiset tunnuspiirteet empiriaa korostavassa muodossa yrityksen taloustieteessä esiintyy, kutsutaan nomoteettiseksi tutkimusotteeksi. Nomoteettinen tutkimusote on varsin yleinen, ja sillä on erittäin merkittävä asema suomalaisessa liiketaloustieteessä. (Neilimo, Näsi, 1980, 61.) Positivismiin sekä nomoteettiseen tutkimusotteeseen liittyy vahvasti hypoteettisdeduktiivinen ajatusmalli. Hypoteettis-deduktiivisessa tutkimuksessa teoriasta pyritään 7
8 johtamaan uusia hypoteeseja, joiden tulee olla koeteltavassa muodossa. Koettelu tapahtuu empiriasta havaintojen tai mittausten avulla. (Kaikkonen, 1996, 78.) Perinteinen nomoteettinen tutkimus pyrkii etsimään lainalaisuuksia sekä syy- ja seuraussuhteita tilastollisen yleistyksen kautta. Nomoteettinen tutkimusote nojautuu kulloinkin yhteen teoriaan ja vähintään kohtuulliseen määrään tilastollisia havaintoja. Usein testataan havaintoja tilastollisesti havaintoaineiston avulla. Tutkimuksen testaaminen tilastollisin menetelmin onkin nomoteettisen tutkimusotteen eräs perusominaisuuksista. Nomoteettisen tutkimusotteen muita perusominaisuuksia ovat mm. tilastollisia havaintojoukkoja tarkasteleva havainnointiajattelu sekä deduktiivinen lähestymistapa, jossa teorioiden perusteella rakennetaan hypoteeseja ja malleja joiden validiteettia testataan empiirisen havaintoaineiston avulla. (Salmi, Järvenpää ) Tässä tutkimuksessa nomoteettinen tutkimusote ilmenee vahvimmin juuri havaintojen testaamisessa tilastollisten menetelmien avulla. Tutkimuksen nomoteettista tutkimusotetta kuvastaa myös tutkimuksen kausaalisuus sekä tutkimuksen selittävä luonne. Tutkimuksesta voidaan myös selkeästi havaita hypoteettis-deduktiivisia piirteitä. Hypoteettis-deduktiivinen tutkimusote kuvastuu tämän tutkimuksen deduktiivisena päättelynä ja tutkimuksen koettelevana luonteena. 8
9 2 VEDONLYÖNTITEORIA Luvussa kaksi on kuvattuna vedonlyöntiteoriaa sekä selitetty tässä tutkimuksessa käytettyjä vedonlyöntitermejä ja vedonlyöntimuotoja. Luvun lähteinä on käytetty ylikerroin.comin vedonlyönnin tietopakettia ( sekä Vuoksenmaan (1999) urheiluvedonlyöntiopasta. 2.1 Palautusprosentti Vedonlyöjän eli pelaajan palautusprosentti on hänen saamiensa bruttovoittojen prosentuaalinen osuus hänen käyttämistään panoksista. Pelin palautusprosentti ilmaisee kokonaisvaihdosta pelaajille voittoina palautettavan rahamäärän prosentteina. Vedonvälittäjän teoreettinen palautusprosentti pystytään selvittämään laskemalla kohteen eri lopputuloksille annettavien kertoimien käänteisluvut ja laskemalla ne yhteen. Vedonvälittäjän tarjoama palautusprosentti on saadun luvun käänteisluku. Oletetaan esimerkiksi, että tennisottelussa Jarkko Niemisen kerroin Andre Agassia vastaan on 2,8 ja Agassin kerroin 1,5. Käänteisluvuiksi saadaan 0,357 sekä 0,667. Tällöin käänteislukujen summaksi saadaan 0, ,667 = 1,024. Vedonvälittäjän palautusprosentti on tämän luvun käänteisluku 0,977 eli noin 98 %. Vedonlyöjälle palautusprosentti merkitsee hänen voittamiensa rahojen suhdetta sijoitettuun rahasummaan. Esimerkiksi kun pelaajan voittamien rahojen summa on euroa ja hänen sijoittamiensa rahojen summa euroa, hänen voidaan laskea saavuttaneen 111 % palautusprosentti ( / ) sijoittamalleen pääomalle. 9
10 2.2 Kertoimet ja niiden muodostuminen Kertoimella tarkoitetaan vedonvälittäjän tarjoamaa lukua, jonka perusteella vedonlyöjä tekee oman pelipäätöksensä (Vedonlyöntipörsseissä vedonlyöjä pelaa muiden vedonlyöjien tarjoamia kertoimia). Jos vedonlyöjä esimerkiksi saa kohteelle kertoimeksi 2,2, ja hän panostaa kohteeseen 10 euroa, hän saa kohteen mennessä oikein 22 euroa. Tällöin hänen voittonsa on 12 euroa (22-10). Mikäli vedonvälittäjä esimerkiksi tarjoaa HIFK - Tappara otteluun kertoimia 3,05 4,2 1,75 tarkoittaa tämä sitä, että vedonvälittäjä yrittää myydä omia todennäköisyysarvioitaan kohteista, joista on vähennetty vedonvälittäjän komissio. Seuraavassa on esitettynä edellä mainitun ottelun kertoimien käänteisluvut. kotivoitto (1 / 3,05) => 33 % tasapeli (1 / 4,20) => 24 % vierasvoitto (1 / 1,75) => 57 % Mikäli vedonlyöjän omat arviot ylittävät nämä arviot, voi hän tällöin panostaa ylikertoimeen. Huomioitavaa on, että vedonvälittäjän prosenttiarvioiden summa ylittää 100 %, koska välittäjä ottaa oman osansa pelivaihdosta (komissio). Vedonlyöntimarkkinoilla on tarjolla kahdenlaisia kertoimia: muuttuvia ja kiinteitä. Kiinteät kertoimet ovat vedonlyöntitoimistojen tarjoamia kertoimia. Muuttuvat eli totalisaattorikertoimet muuttuvat vedonlyöjien panostuksen kautta, eli ne toisin sanoen määräytyvät markkinoilla vapaasti. Seuraavassa esitellään, kuinka ne asetetaan tai kuinka ne määräytyvät Kiinteät kertoimet Kiinteät kertoimet ovat vedonvälittäjien, käytännössä vedonlyöntitoimistojen kertoimenlaskijoiden asettamia kertoimia heidän arvioimillaan (laskemillaan) todennäköisyyksillä. Kertoimenlaskijoiden tehtävänä on arvioida jonkin 10
11 urheilutapahtuman tulosvaihtoehtojen todennäköisyyksiä ja asettaa kertoimet niin, että vedonlyöntitoimiston voitto maksimoituisi. Kiinteiden kertoimien asetannan tulee tapahtua niin aikaisin, että vedonlyöjille jää tarpeeksi aikaa vedonlyöntiin. Kertoimen julkaisemisen jälkeen tapahtuvia, pelitapahtuman todennäköisyyksiin vaikuttavia tekijöitä ei tällöin voida ottaa huomioon kertoimen määrittämisessä. Kiinteitä kertoimia tarjoavien toimistojen voitto riippuu onnistuneen kertoimen asetannan lisäksi toimiston ottaman komission suuruudesta. Komission ja kiinteän kertoimen suuruus ovat riippuvaisia toisistaan. Mitä suurempi vedonlyöntitoimiston ottama komissio on, sitä pienemmät ovat toimiston tarjoamat kertoimet. Tämä johtaa vedonlyöjien kohdalla pienempään kiinnostukseen vedonlyöntiin, koska mahdolliset voitot pienenevät. Käytännössä mitkään kertoimet eivät ole täysin kiinteitä, koska vedonlyöntitoimistoilla on oikeus halutessaan muuttaa kertoimiaan Muuttuvat kertoimet (totalisaattoripeli) Muuttuvat kertoimet määräytyvät periaatteessa markkinoilla vapaasti. Vedonlyöntitoimisto tällöin vain muodostaa markkinapaikan eli tarjoaa pelialustan ja monitoroi muuttuvia kertoimia suhteessa kunkin tulosvaihtoehdon panostukseen. Muuttuvat kertoimet siis määräytyvät markkinoilla sen mukaan, kuinka paljon kyseenomaista tulosvaihtoehtoa pelataan. Vedonlyöntitoimistolle nämä totalisaattoripelit ovat riskitön vaihtoehto. Vedonlyöntitoimisto vain tarjoaa vedonlyöjille pelialustan ja ottaa tästä pelivaihtoon perustuvan kiinteän komission, eikä se näin ollen kanna riskiä pelin lopputuloksesta tai kertoimen asetannasta. Totalisaattorivedonlyöntimarkkinoilla kertoimen muodostuminen vastaa hyvin hinnan muodostumista pääomamarkkinoilla. Vedonlyöntimarkkinoilla on eri sijoituskohteita, joille määräytyy hinta sijoittajien tai sijoittajien tapaan toimivien vedonlyöjien näkemyksen mukaisesti. Oletetaan esimerkiksi, että jalkapallo-ottelussa Zyklon Jerkku, vedonlyönnin kohteena on ottelun lopputulos. Vedonlyöntitoimiston palautusprosentti on 80 %. Pelikohdetta 11
12 pelataan yhteensä eurolla, joten voittoina palautetaan yhteensä euroa. Tarkastelun kohteeksi otetaan tulos 1 1, jota on pelattu yhteensä eurolla. Tuloksen osuus kaikista veikatuista tuloksista on 10 %. Kun otetaan huomioon palautusprosentti 80 %, muodostuisi tuloksen 1 1 kertoimeksi 8. Tämä saadaan laskemalla euron osuus eurosta, joka on 10 %, jonka käänteisluvusta puolestaan saadaan tuloksen kertoimeksi 10, joka tulee vielä kertoa palautusprosentilla 0,8. Samalla tavalla määrittyvät myös kaikkien muiden lopputulosten kertoimet sitä mukaa ja sen verran, kuin niitä veikataan. 2.3 Todennäköisyyden määrittäminen Todennäköisyyttä voidaan tarkastella kahdesta eri näkökulmasta: subjektiivisesta ja objektiivisesta. Jako näiden todennäköisyyksien välillä riippuu siitä, millä aikavälillä todennäköisyyttä tarkastellaan Subjektiivinen todennäköisyys Alin (1977) mukaan, subjektiivisella todennäköisyydellä tarkoitetaan yleisesti markkinoiden näkemystä eri urheilutapahtumien tulosvaihtoehtojen todennäköisyyksistä. Omassa hevosurheiluvedonlyöntimarkkinoita käsittelevässä tutkimuksessaan Ali käyttää metodologiaa, joka perustuu subjektiivisiin ja objektiivisiin hevosten voittotodennäköisyyksiin. Subjektiivisella todennäköisyydellä tarkoitetaan markkinoiden näkemystä hevosen todennäköisyydestä voittaa lähtö. Subjektiivinen voittotodennäköisyys π hevoselle h voidaan määrittää hevoseen h panostettujen panosten X osuutena kokonaisvaihdosta W. (1) π = X / W h h 12
13 2.3.2 Objektiivinen todennäköisyys Objektiivisen voittotodennäköisyyden Ali (1977) määrittelee seuraavasti: Tietyn hevosen voittosuhde voidaan määritellä, kun lähtö toistetaan äärettömän monta kertaa, ja näin hevoselle saadaan objektiivinen voiton todennäköisyys. Toisin sanoen objektiivisella todennäköisyydellä tarkoitetaan minkä tahansa urheilutapahtuman tulosvaihtoehdon oikeaa todennäköisyyttä. Alin (1977) mukaan hevosurheiluvedonlyönnissä yksittäinen hevoskilpailu voidaan ajatella binomitoistokokeena, ja tällöin objektiivinen todennäköisyys määrittää hevosen todennäköisyyden voittaa kilpailu. Kaikkien hevoskilpailijoiden osallistujien objektiivisten todennäköisyyksien summa on yksi. Sekä subjektiiviset että objektiiviset todennäköisyydet vaihtelevat hevosten ja yksittäisten lähtöjen mukaan. Toisin sanoen samassa lähdössä on eri todennäköisyyden omaavia hevosia. Täysin samanlaisten lähtölistojen esiintyminen kahdessa eri lähdössä on myös hyvin harvinaista, eli samat hevoset osallistuisivat useampaan lähtöön. Näin ollen objektiivisten todennäköisyyksien arviointi on mahdotonta, koska sama lähtö käydään ainoastaan kerran. (Ali, 1977.) 2.4 Odotusarvo Odotusarvo on kertoimen ja todennäköisyysarvion tulo. Rationaalinen vedonlyöjä pelaa ainoastaan pelejä, joiden odotusarvo ylittää yhden. Todennäköisyysarvio voi olla joko vedonlyöjän itsensä määrittämä tai jostain muualta saatu arvio, esimerkiksi keskustelupalstalta tai vihjepalvelusta. Seuraava esimerkki havainnollistaa odotusarvon määrittämistä. Vedonlyöjä on esimerkiksi arvioinut suosikkijoukkueelleen HIFK:lle 40 prosentin todennäköisyyden ja panostaa tähän kertoimella 2,4. Tällöin hän on pelannut odotusarvoltaan (0,4 x 2,4) => 0,96 tulosta ja on täten panostanut alikertoimeen. Vastaavasti lyömällä vetoa kertoimella 2,7 on hän pelannut odotusarvoltaan (0,4 x 2,7) => 1,08 tulosta ja panostanut näin ollen ylikertoimeen. 13
14 2.5 Pelikassa ja kirjanpito Pelikassalla tarkoitetaan rahamäärää, jonka vedonlyöjä on omistanut ainoastaan vedonlyöntiä varten. Pelikassa ei missään tapauksessa ole esimerkiksi vedonlyöjän kuukausipalkka. Vedonlyöjän pelikassan tulisi olla hänen muista kuukausimenoistaan täysin erillinen summa, jonka voi hävitä sen vaikuttamatta vedonlyöjän omaan elintasoon. Muiden ansioiden sijoittaminen suoraan pelikassaan vaikuttaa alitajuisesti vedonlyöjän panostukseen sekä hänen kykyyn ajatella asioita puolueettomasti, eikä tämä voi olla vaikuttamatta pelaamiseen pitkällä aikavälillä. McCunen (1999) mukaan erillisen pelikassan (money management) pitäminen on ensiarvoisen tärkeätä. Vaikka vedonlyöjä olisi kuinka hyvä arvioimaan oikeat todennäköisyydet kohteilleen, tulee hänelle välillä tappioputkia. Yksinkertaisella kolikonheittoesimerkillä voi havainnollistaa tätä. Vaikka klaavalle saataisiin kertoimeksi 2,5, tulee vedonlyöjälle jossain vaiheessa tappioputki, tämä on matemaattinen fakta.. Jotta vedonlyöjä onnistuu pääsemään näiden tappioputkien yli, hänen tulee olla tietoinen omasta pelikassastaan ja siitä, kuinka suurella panoksella hänen tulee pelata. Vararikkoon joutumisen todennäköisyys on pienempi, kun valitaan enemmän kohteita pienemmillä panoksilla kuin vähän kohteita suurilla panoksilla. (McCune, 1999.) Vedonlyöjälle on paljon hyötyä, jos hän pitää kaikista omista vedoistaan erillistä tarkkaa vedonlyöntikirjanpitoa. Tuhansien vetojen sarjassa vedonlyöjä pystyy mittaamaan omaa osaamistaan juuri tarkan kirjanpidon avulla. Jos vedonlyöjällä on useammassa kuin yhdessä vedonlyöntitoimistossa tili, hänen on vaikea seurata kaikkia vanhoja vetoja ilman kirjanpitoa. Erityisesti kirjanpidosta on hyötyä panoksen koon määrityksessä; esimerkiksi Kellyn kaavaa käytettäessä on erillisen kirjanpidon pitäminen ehdotonta. 14
15 2.6 Hajonnan ja riskin merkitys vedonlyönnissä Tärkein erottava tekijä onnenpelien kuten esimerkiksi Loton ja urheiluvedonlyönnin välillä on se, että urheilutapahtumien tarkka arviointi on mahdotonta. Onnenpeleissä kuten kasinopeleissä tarkka todennäköisyyden laskeminen on mahdollista mutta urheiluvedonlyönnissä käytännössä mahdotonta. Vedonlyönnissä todennäköisyysarvioiden oikeellisuutta ei ratkaise yksittäisten vetojen oikein tai väärin meneminen vaan pitkänaikavälin menestys. Tätä voidaan havainnollistaa seuraavan esimerkin avulla. Heitetään noppaa sata kertaa. Silmälukujen jakautuminen sadan heiton sarjassa ei ole tasaista. Jos silmäluvulle kuusi olisi näiden sadan heiton ajan tarjottu kerrointa 6,5, olisi vedonlyöjä ollut paremmassa asemassa vedon vastaanottajaan nähden. Vedonlyöjä olisi täten saanut niin sanotun ylikertoimen, eli tarjottava kerroin olisi suurempi kuin vedon todennäköisyys. Nopan silmäluvun todennäköisyys on 1/6. Tässä tilanteessa ei ole takuita sille, ettei vedonlyöjä vielä olisi voitolla. Sadan heittokerran jälkeen todennäköisyys voitolla olemiselle on noin 61 %. Jos tapaus toistetaan 400 kertaa, on todennäköisyys voitolla olemiselle 75 %. 2.7 Vedonlyönnissä käytettäviä kaavoja Kellyn kaava Monet vedonlyöjät käyttävät panoksensa määrittämiseen niin sanottua Kellyn (1956) kaavaa, jonka kehitti John Kelly. Hänen alkuperäinen AT&T:n Bell-laboratoriossa vuonna 1956 suunnittelema kaavansa oli tarkoitettu käytettäväksi kaukopuheluiden äänisignaaleiden lähettämiseen ja niiden laskuttamiseen. Ei kulunut aikaakaan, kun vedonlyöntiyhteisö tajusi, että sama lähestymistapa voi auttaa heitä määrittämään optimaalisen summan sijoitettavaksi hevoseen ja parhaan edun saavuttamiseen yli- ja 15
16 alikertoimista. Kellyn kaavan avulla kassan kasvu pystytään maksimoimaan pitkällä aikavälillä. Kellyn kaava: (2) B = (π k-1) / (k-1) B = Sijoitettava panos (osuus pelikassasta) π = Merkin arvioitu todennäköisyys k = Välittäjän tarjoama kerroin Esimerkiksi tuhannen euron pelikassalla panostettaessa urheilijaan, jonka todennäköisyys on 40 % ja välittäjän tarjoama kerroin 2,7, saadaan Kellyn kaavalla => (0,4 x 2,7-1) / (2,7-1) => jolloin sijoitettava prosenttiosuus pelikassasta olisi 4,7 % eli 47 euroa. Kellyn jakajaa käytetään usein yhdessä Kellyn kaavan kanssa pienentämään panostukseen liittyvää riskiä. Kellyn kaava takaa optimaalisen panostuksen, mutta se vaatii samalla todennäköisyyksien äärimmäistä tarkkuutta, joka on urheiluvedonlyönnissä usein hankalaa. Vedonlyöjän kannattaa pienentää riskiään käyttämällä Kellyn jakajaa. Kellyn kaavaan sijoitettuna => B = (π k - 1) / (k - 1) / 5 on otettu käyttöön jakaja viisi. Jokainen määrittelee oman jakajansa koon itse. Mitä suurempi vedonlyöjän käyttämä jakaja on, sitä pienempi on vedonlyöjän riski Harvillen kaava Harville (1973) tutki 335 eri hevoskilpailua ja kehitti näistä matemaattisia kaavoja hevosurheiluvedonlyönnin pelimuotojen väliseen tehokkuustutkimukseen. Kaavojen avulla on mahdollista johtaa voittokertoimista laskettujen voittotodennäköisyyksien avulla muidenkin mahdollisten tapahtumien todennäköisyyksiä. Kaavojen avulla voittokertoimista voidaan laskea todennäköisyydet eri hevosten sijoittumiselle kahden (place) tai kolmen (show) parhaan joukkoon. 16
17 Harvillen (1973) kaavaa on myös mahdollista soveltaa laskiessa Kaksari- (quinella) ja Superkaksari- (exacta) kombinaatioiden todennäköisyyksiä. Seuraavassa esimerkissä on kuvattuna Harvillen kaavan soveltamisesta Superkaksarissa. Oletetaan, että lähdössä on kahdeksan hevosta ja jokaisella hevosella on yhtä suuri todennäköisyys voittaa lähtö. Tällöin lähdön Superkaksarissa on 8 x 7 mahdollista kombinaatiota. Tällöin jokaisen kombinaation kerroin on 56, jos vedonvälittäjän ottamaa komissiota ei oteta huomioon. Oletetaan hevosen numero 8 olevan lähdön voittaja. Tällöin hevosen numero 5 todennäköisyys tulla lähdössä sijalle kaksi on mahdollista selvittää käyttäen Harvillen kaavaa. Kaavan avulla pyritään selvittämään, mikä olisi hevosen numero 5 voiton todennäköisyys, jos hevonen numero 8 jätetään huomioimatta. Todennäköisyys hevoselle Y tulla lähdössä toiseksi, kun hevonen Z voittaa lähdön lasketaan seuraavasti: (3) π /(1 π ) Y Z π Y = Hevosen Y voiton todennäköisyys π Z = Hevosen Z voiton todennäköisyys Edellisessä esimerkissä selvitettiin lähdön voittajahevonen, kun jokaisella hevosella oli yhtä suuret todennäköisyydet lähdön voittoon. Seuraavaksi Harvillen kaavaa soveltaen selvitetään jonkun lähdön hevosen todennäköisyys tulla lähdössä toiseksi. = (1 / 8) / (1 - (1 / 8)) = (1 / 8) / (7 / 8) = 1 / 7 Jos hevonen numero 8 voittaa lähdön todennäköisyydellä 1/8 ja hevonen numero 5 tulee lähdössä toiseksi todennäköisyydellä 1/7, tällöin Superkaksarin todennäköisyys on (1 / 8) x (1 / 7) = 1 /
18 Harvillen kaava toimii myös silloin, kun lähdön hevosilla on eri todennäköisyydet voittaa lähtö. Oletetaan, että kertoimissa ei oteta lainkaan huomioon vedonvälittäjän ottamaa komissiota. Simo Sukkela 3,33 1/3 Viesker 5,00 1/5 Apassi 6,00 1/6 Seuraavassa esimerkissä oletetaan, että lähdön voittaja on Simo Sukkela ja toiseksi tulee Viesker. Tällöin Superkaksarin todennäköisyys saadaan seuraavasti: Simo Sukkelan voiton todennäköisyys on 1/3 Vieskerin sijoittumisen toiseksi todennäköisyys, Simo Sukkelan voitaessa lähdön (1 / 3) / (1 - (1 / 5)) = 0,4167 Todennäköisyys, että Simo Sukkela voittaa ja Viesker tulee toiseksi: (1 / 3) x 0,4167 = 0,1389 Näin ollen Superkaksarin kertoimen tulisi olla 1 / 0,1389 = 7,2 Seuraavassa oletetaan, että lähdön voittaja on Viesker ja toiseksi tulee Simo Sukkela. Tällöin Superkaksarin todennäköisyys saadaan edellisen esimerkin mukaisesti: (1 / 5) / (1 - (1 / 3)) = 0,3 => (1 / 5) x 0,3 = 0,06 => 1 / 0,06 = 16, Poisson-kaava Simeon-Denis Poisson kehitti kaavan, jonka avulla on mahdollista laskea säännöllisesti toistuvien tapahtumien todennäköisyyksiä. Poisson-kaava soveltuu myös eri palloilulajien otteluiden todennäköisyyksien laskemiseen. Lähinnä Poisson-kaavaa voidaan käyttää jalkapallo- ja jääkiekko-otteluiden maalimäärien todennäköisyyksien laskemiseen. Poisson kaava on seuraavanlainen. 18
19 µ x (4) P( x) = [ e * µ ] x! x = tapahtumien määrä x! = kertoma luvusta x On myös asetettu, että 0! = 1 µ = tapahtumien esiintymisen arvio e = Neperin luku Seuraavassa on esitettynä Poisson-kaava esimerkin avulla 2,70 3 P(3) = (2,7183 * 2,70 ) / 3!~ 0,220 = 22% x = tapahtumien määrä, maalimäärä 3 x! = kertoma luvusta x, 3! = 1 * 2 * 3 = 6 µ = tapahtumien esiintymisen arvio, maaliodotusarvo 2,70 e = Neperin luku, joka on vakio (~2,7183) Tämä yllä oleva esimerkki antaa vastaukseksi 22 %. Poisson kaavan mukaan joukkue tekee ottelussa kolme maalia 22 %:n todennäköisyydellä, jos maaliodotusarvoksi on arvioitu 2,7 maalia. Näin voidaan laskea todennäköisyydet molempien joukkueiden jokaiselle eri maalimäärälle erikseen. Tämän jälkeen kerrotaan saatuja todennäköisyyksiä keskenään, jolloin saadaan laskettua eri tuloskombinaatioiden todennäköisyydet. Kotijoukkueen tehdessä esimerkiksi kolme maalia 22 %:n todennäköisyydellä ja vieras joukkueen tehdessä kaksi maalia 26 %:n todennäköisyydellä, niin lopputuloksen 3 2 todennäköisyys on 0,22 x 0,26 = 0,0572 eli 5,7 %. Kun lasketaan yhteen kaikki kotivoittotulokset, niin saadaan todennäköisyys kotivoitolle määritetyillä maaliodotusarvoilla. Vierasvoiton ja tasapelin todennäköisyydet on mahdollista laskea vastaavalla tavalla. 19
20 2.8 Arbitraasit Arbitraasilla tarkoitetaan kertoimien muodostumista markkinoilla siten, että ne eroavat riittävästi vastaavista tulosskenaarioiden todennäköisyyksistä. Tällöin vedonvälittäjän komissiosta huolimatta voidaan saavuttaa positiivinen tuoton odotusarvo. (Hausch & Ziemba, 1990.) Hausch & Ziemba (1990) tutkivat eri hevoskilparatojen välisen vedonlyönnin tehokkuutta. Tämä kilparatojen välinen vedonlyönti (cross-track betting) mahdollistaa vedonlyönnin paikallisella raviradalla jonkun muun raviradan lähdön osalta. Koska jokaisella radalla on oma vedonlyöntipoolinsa, kertoimet voivat vaihdella ratojen kesken. Tämä pelitapa vaatii kahden tai useamman poolin syntymistä samaa lähtöä varten. Tutkimuksessaan Hausch & Ziemba (1990) havaitsivat, että kertoimet vaihtelevat saman lähdön hevosten osalta ja usein vielä niin dramaattisesti, että se mahdollistaa arbitraasimahdollisuuden. Tällöin markkinoiden välillä voidaan sanoa olevan eroja eri raviratojen ja eri poolien kesken. Tutkielmassaan Hausch & Ziemba (1990) esittävät arbitraasin hyödyntämiseen perustuvaa riskitöntä vedonlyöntistrategiaa ja pyrkivät demonstroimaan kilparatojen välisen vedonlyönnin tehottomuutta. Tässä arbitraasin hyväksikäyttöön perustuvassa strategiassa käytettiin hyväksi pelikassan kasvua optimoivaa pääoman kasvumallia. Tämä kasvumalli vaatii arviot lähdön jokaisen hevosen voittotodennäköisyydestä. Hausch & Ziemba toteavatkin, että hevosten todellisista voittotodennäköisyyksistä saadaan hyvät arviot, kun voittokertoimista korjataan suosikki altavastaaja-harha pois. Hausch & Ziemba (1990) käyttävät yhtenä esimerkkinä kilparatojen välisestä tehottomuudesta kahden dollarin pelitositetta hevosesta nimeltä Ferdinand, joka voitti vuonna 1986 legendaarisen Kentucky Derbyn Yhdysvalloissa. Tämän kyseisen pelitositteen voittosumma Pomodan Fairplexissa, Californiassa oli 13,20 dollaria, kun taas Lafayetten Evangeline Downissa, Louisianassa voittosumma oli 90,00 dollaria. Luonnollisesti vedonlyöjät olisivat lyöneet Ferdinand vetonsa Evangeline Downissa. Totalisaattoripelien luonteen vuoksi tällainen tilanne johtaa tehottomuuteen lähdön kaikkien hevosten kohdalla. Näin ollen, jos pelaaja kykenee sekä lukemaan kertoimia 20
Vedonlyöntistrategioiden simulointi ja evaluointi
 Vedonlyöntistrategioiden simulointi ja evaluointi Aleksi Avela 15.10.2018 Ohjaaja: Juho Roponen Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin
Vedonlyöntistrategioiden simulointi ja evaluointi Aleksi Avela 15.10.2018 Ohjaaja: Juho Roponen Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta osin
Ylikerroinstrategiat ja Poissonmallit vedonlyönnissä (aihe-esittely) Jussi Kolehmainen
 Ylikerroinstrategiat ja Poissonmallit vedonlyönnissä (aihe-esittely) Jussi Kolehmainen 23.01.2012 Ohjaaja: Jussi Kangaspunta Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla
Ylikerroinstrategiat ja Poissonmallit vedonlyönnissä (aihe-esittely) Jussi Kolehmainen 23.01.2012 Ohjaaja: Jussi Kangaspunta Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla
VEDONLYÖNTI PELIOPAS
 VEDONLYÖNTI PELIOPAS PITKÄVETO Tiedätkö kumpi voittaa vai päättyykö peli tasan? NÄIN SE SUJUU Pitkävedossa lyöt vetoa yhdestä tai useammasta pelikohteesta. Pitkävedon kohteet ja kertoimet saat pelimyyjältä,
VEDONLYÖNTI PELIOPAS PITKÄVETO Tiedätkö kumpi voittaa vai päättyykö peli tasan? NÄIN SE SUJUU Pitkävedossa lyöt vetoa yhdestä tai useammasta pelikohteesta. Pitkävedon kohteet ja kertoimet saat pelimyyjältä,
Jalkapallovedonlyöntistrategioiden. evaluointi. Aleksi Avela Ohjaaja: Juho Roponen Valvoja: Ahti Salo
 Jalkapallovedonlyöntistrategioiden simulointi ja evaluointi Aleksi Avela 26.2.2019 Ohjaaja: Juho Roponen Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta
Jalkapallovedonlyöntistrategioiden simulointi ja evaluointi Aleksi Avela 26.2.2019 Ohjaaja: Juho Roponen Valvoja: Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta
Betradar-virtuaaliurheilu
 Betradar-virtuaaliurheilu Säännöt Versio 6.0 kesäkuu 2018 Sivu 1 Sisällys 1. Virtuaalijalkapallo... 3 1.1 Pelilogiikka... 4 1.2 Ottelupäivän / Cup-kierroksen aikataulu... 5 1.3 Turnauksen aikataulu...
Betradar-virtuaaliurheilu Säännöt Versio 6.0 kesäkuu 2018 Sivu 1 Sisällys 1. Virtuaalijalkapallo... 3 1.1 Pelilogiikka... 4 1.2 Ottelupäivän / Cup-kierroksen aikataulu... 5 1.3 Turnauksen aikataulu...
2. Toto-pelien kohteena voi olla yhden tai useamman kohdekilpailun voittajat tai oikeaksi määritellyt tulosyhdistelmät.
 Liite sisäasiainministeriön asetukseen SMDno/2013/1125 TOTO-PELIEN SÄÄNNÖT I YLEISTÄ 1. Toto-pelikohteista käytetään nimitystä kohde. Kohde sisältää yhden tai useampia kohdekilpailuja. Kohde voi olla ravikilpailu,
Liite sisäasiainministeriön asetukseen SMDno/2013/1125 TOTO-PELIEN SÄÄNNÖT I YLEISTÄ 1. Toto-pelikohteista käytetään nimitystä kohde. Kohde sisältää yhden tai useampia kohdekilpailuja. Kohde voi olla ravikilpailu,
Patrik Saarelainen TIEDONLOUHINTATEKNOLOGIAN HYÖDYNTÄMINEN URHEILUVEDONLYÖNNISSÄ
 Patrik Saarelainen TIEDONLOUHINTATEKNOLOGIAN HYÖDYNTÄMINEN URHEILUVEDONLYÖNNISSÄ JYVÄSKYLÄN YLIOPISTO INFORMAATIOTEKNOLOGIAN TIEDEKUNTA 2017 TIIVISTELMÄ Saarelainen, Patrik Tiedonlouhintateknologian hyödyntäminen
Patrik Saarelainen TIEDONLOUHINTATEKNOLOGIAN HYÖDYNTÄMINEN URHEILUVEDONLYÖNNISSÄ JYVÄSKYLÄN YLIOPISTO INFORMAATIOTEKNOLOGIAN TIEDEKUNTA 2017 TIIVISTELMÄ Saarelainen, Patrik Tiedonlouhintateknologian hyödyntäminen
Jalkapallovedonlyöntistrategioiden simulointi ja evaluointi
 Aalto-yliopisto Perustieteiden korkeakoulu Teknillisen fysiikan ja matematiikan tutkinto-ohjelma Jalkapallovedonlyöntistrategioiden simulointi ja evaluointi Kandidaatintyö 19. maaliskuuta 2019 Aleksi Avela
Aalto-yliopisto Perustieteiden korkeakoulu Teknillisen fysiikan ja matematiikan tutkinto-ohjelma Jalkapallovedonlyöntistrategioiden simulointi ja evaluointi Kandidaatintyö 19. maaliskuuta 2019 Aleksi Avela
Nollasummapelit ja bayesilaiset pelit
 Nollasummapelit ja bayesilaiset pelit Kristian Ovaska HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Seminaari: Peliteoria Helsinki 18. syyskuuta 2006 Sisältö 1 Johdanto 1 2 Nollasummapelit 1 2.1
Nollasummapelit ja bayesilaiset pelit Kristian Ovaska HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Seminaari: Peliteoria Helsinki 18. syyskuuta 2006 Sisältö 1 Johdanto 1 2 Nollasummapelit 1 2.1
Liite sisäasiainministeriön asetukseen SMDno/2012/2144 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT
 Liite sisäasiainministeriön asetukseen SMDno/2012/2144 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT 2 Sisältö LOTON SÄÄNNÖT... 3 LOTON LISÄARVONNAN SÄÄNNÖT... 7 KESTOLOTON JA KESTOLAUANTAI-JOKERIN LISÄARVONNAN SÄÄNNÖT...
Liite sisäasiainministeriön asetukseen SMDno/2012/2144 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT 2 Sisältö LOTON SÄÄNNÖT... 3 LOTON LISÄARVONNAN SÄÄNNÖT... 7 KESTOLOTON JA KESTOLAUANTAI-JOKERIN LISÄARVONNAN SÄÄNNÖT...
OPISKELIJOIDEN VEDONLYÖNTI- JA SIJOITUSKÄYTTÄYTYMINEN
 Esko Peltonen OPISKELIJOIDEN VEDONLYÖNTI- JA SIJOITUSKÄYTTÄYTYMINEN Case: Centria-ammattikorkeakoulun opiskelijat Opinnäytetyö CENTRIA-AMMATTIKORKEAKOULU Liiketalouden koulutusohjelma Kesäkuu 2016 TIIVISTELMÄ
Esko Peltonen OPISKELIJOIDEN VEDONLYÖNTI- JA SIJOITUSKÄYTTÄYTYMINEN Case: Centria-ammattikorkeakoulun opiskelijat Opinnäytetyö CENTRIA-AMMATTIKORKEAKOULU Liiketalouden koulutusohjelma Kesäkuu 2016 TIIVISTELMÄ
Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
 Heli Vaara ja Tiina Komulainen OuLUMA, sivu 1 MERIROSVOJEN AARTEENJAKOPELI Avainsanat: matematiikka, pelit, todennäköisyys Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
Heli Vaara ja Tiina Komulainen OuLUMA, sivu 1 MERIROSVOJEN AARTEENJAKOPELI Avainsanat: matematiikka, pelit, todennäköisyys Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
MS-C2105 Optimoinnin perusteet Malliratkaisut 5
 MS-C2105 Optimoinnin perusteet Malliratkaisut 5 Ehtamo Demo 1: Arvaa lähimmäksi Jokainen opiskelija arvaa reaaliluvun välillä [0, 100]. Opiskelijat, joka arvaa lähimmäksi yhtä kolmasosaa (1/3) kaikkien
MS-C2105 Optimoinnin perusteet Malliratkaisut 5 Ehtamo Demo 1: Arvaa lähimmäksi Jokainen opiskelija arvaa reaaliluvun välillä [0, 100]. Opiskelijat, joka arvaa lähimmäksi yhtä kolmasosaa (1/3) kaikkien
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Hallituksen esitys liittokokoukselle sääntömuutoksiksi Käsitelty hallituksen kokouksessa 13.4.2005
 Hallituksen esitys liittokokoukselle sääntömuutoksiksi Käsitelty hallituksen kokouksessa 13.4.2005 3.3.3.7 Kilpailujen arvontaa vastaan tehtävä vastalause voidaan esittää suullisesti ylituomarille, jonka
Hallituksen esitys liittokokoukselle sääntömuutoksiksi Käsitelty hallituksen kokouksessa 13.4.2005 3.3.3.7 Kilpailujen arvontaa vastaan tehtävä vastalause voidaan esittää suullisesti ylituomarille, jonka
Tenniksen pistelaskusäännöt, lukio/ammatilliset oppilaitokset
 Tenniksen pistelasku Useimmat meistä ovat joskus katsoneet TV:stä tennisottelua. Katsoja kokee jännitystä voidessaan seurata kuinka pisteden kertyminen johtaa ottelun päättymisen toisen pelaajan voittoon
Tenniksen pistelasku Useimmat meistä ovat joskus katsoneet TV:stä tennisottelua. Katsoja kokee jännitystä voidessaan seurata kuinka pisteden kertyminen johtaa ottelun päättymisen toisen pelaajan voittoon
KOTITALOUKSIEN SÄÄSTÄMISTUTKIMUS 2006. Kotitalouksien säästämistutkimus 2006 1
 KOTITALOUKSIEN SÄÄSTÄMISTUTKIMUS 2006 Kotitalouksien säästämistutkimus 2006 1 Arvopaperien omistaminen 2006 ( suomalaisista talouksista) (kohderyhmä 18-69 vuotiaat yks.hlöt) (n=1002) Omistaa arvopapereita
KOTITALOUKSIEN SÄÄSTÄMISTUTKIMUS 2006 Kotitalouksien säästämistutkimus 2006 1 Arvopaperien omistaminen 2006 ( suomalaisista talouksista) (kohderyhmä 18-69 vuotiaat yks.hlöt) (n=1002) Omistaa arvopapereita
Miten hyvin mallit kuvaavat todellisuutta? Tarvitaan havaintoja.
 Luku 1 Johdanto 1.1 Todennäköisyys ja tilastotiede Kurssi käsittelee todennäköisyyslaskentaa ja tilastotiedettä. Laaditaan satunnaisilmiöille todennäköisyysmalleja. Miten hyvin mallit kuvaavat todellisuutta?
Luku 1 Johdanto 1.1 Todennäköisyys ja tilastotiede Kurssi käsittelee todennäköisyyslaskentaa ja tilastotiedettä. Laaditaan satunnaisilmiöille todennäköisyysmalleja. Miten hyvin mallit kuvaavat todellisuutta?
Tilastollisten algoritmien soveltuvuus jääkiekkovedonlyöntiin
 Tilastollisten algoritmien soveltuvuus jääkiekkovedonlyöntiin Oulun yliopisto Tietojenkäsittelytieteen laitos Pro gradu -tutkielma Juha-Matti Tapani Hurnasti 7.5.2013 2 Sisällysluettelo Sisällysluettelo...
Tilastollisten algoritmien soveltuvuus jääkiekkovedonlyöntiin Oulun yliopisto Tietojenkäsittelytieteen laitos Pro gradu -tutkielma Juha-Matti Tapani Hurnasti 7.5.2013 2 Sisällysluettelo Sisällysluettelo...
Liite sisäasiainministeriön asetukseen SMDno/2014/1711 TOTO-PELIEN SÄÄNNÖT
 Liite sisäasiainministeriön asetukseen SMDno/2014/1711 TOTO-PELIEN SÄÄNNÖT 2 Sisällys I Yleiset säännökset... 3 II Minimipanokset... 6 III Porukkapelit... 6 IV Voittaja-peli... 6 V Sija-peli... 6 VI Kaksari...
Liite sisäasiainministeriön asetukseen SMDno/2014/1711 TOTO-PELIEN SÄÄNNÖT 2 Sisällys I Yleiset säännökset... 3 II Minimipanokset... 6 III Porukkapelit... 6 IV Voittaja-peli... 6 V Sija-peli... 6 VI Kaksari...
Rahapelaamisen riskirajoilla. Mirka Smolej, Salla Karjalainen, Tapio Jaakkola 5.11.2015
 Rahapelaamisen riskirajoilla Mirka Smolej, Salla Karjalainen, Tapio Jaakkola 5.11.2015 Rahapelaamisen riskirajoilla Arpa-projekti Arpa-projekti tukee aikuisten rahapelaamisen hallintaa Tietoa ja välineitä
Rahapelaamisen riskirajoilla Mirka Smolej, Salla Karjalainen, Tapio Jaakkola 5.11.2015 Rahapelaamisen riskirajoilla Arpa-projekti Arpa-projekti tukee aikuisten rahapelaamisen hallintaa Tietoa ja välineitä
Oletetaan, että virhetermit eivät korreloi toistensa eikä faktorin f kanssa. Toisin sanoen
 Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
b) Arvonnan, jossa 50 % mahdollisuus saada 15 euroa ja 50 % mahdollisuus saada 5 euroa.
 2.9. Epävarmuus ja odotetun hyödyn teoria Testi. Kumman valitset a) 10 euroa varmasti. b) Arvonnan, jossa 50 % mahdollisuus saada 15 euroa ja 50 % mahdollisuus saada 5 euroa. Odotettu arvo 0,5* 15 + 0,5*5
2.9. Epävarmuus ja odotetun hyödyn teoria Testi. Kumman valitset a) 10 euroa varmasti. b) Arvonnan, jossa 50 % mahdollisuus saada 15 euroa ja 50 % mahdollisuus saada 5 euroa. Odotettu arvo 0,5* 15 + 0,5*5
Luento 5: Peliteoriaa
 Luento 5: Peliteoriaa Tässä kappaleessa tutustutaan hieman peliteoriaan. Keskeisiä asioita ovat Nash-tasapaino ja sekastrategia. Cournot n duopolimalli vuodelta 1838 toimii oivallisena havainnollistuksena
Luento 5: Peliteoriaa Tässä kappaleessa tutustutaan hieman peliteoriaan. Keskeisiä asioita ovat Nash-tasapaino ja sekastrategia. Cournot n duopolimalli vuodelta 1838 toimii oivallisena havainnollistuksena
Liite sisäasiainministeriön asetukseen SMDno/2011/2027 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT
 Liite sisäasiainministeriön asetukseen SMDno/2011/2027 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT 2 Sisältö LOTON SÄÄNNÖT... 3 LOTON LISÄARVONNAN SÄÄNNÖT... 8 KESTOLOTON JA KESTOLAUANTAI-JOKERIN LISÄARVONNAN SÄÄNNÖT...10
Liite sisäasiainministeriön asetukseen SMDno/2011/2027 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT 2 Sisältö LOTON SÄÄNNÖT... 3 LOTON LISÄARVONNAN SÄÄNNÖT... 8 KESTOLOTON JA KESTOLAUANTAI-JOKERIN LISÄARVONNAN SÄÄNNÖT...10
Aloitamme yksinkertaisella leluesimerkillä. Tarkastelemme yhtä osaketta S. Oletamme että tänään, hetkellä t = 0, osakkeen hinta on S 0 = 100=C.
 Luku 1 Johdatteleva esimerkki Herra K. tarjoaa osto-option Aloitamme yksinkertaisella leluesimerkillä. Tarkastelemme yhtä osaketta S. Oletamme että tänään, hetkellä t = 0, osakkeen hinta on S 0 = 100=C.
Luku 1 Johdatteleva esimerkki Herra K. tarjoaa osto-option Aloitamme yksinkertaisella leluesimerkillä. Tarkastelemme yhtä osaketta S. Oletamme että tänään, hetkellä t = 0, osakkeen hinta on S 0 = 100=C.
Veikkauksen pelaajien pelaaminen suhteessa ulkomaisten vedonlyöntiyhtiöiden todennäköisyysarvioihin
 Veikkauksen pelaajien pelaaminen suhteessa ulkomaisten vedonlyöntiyhtiöiden todennäköisyysarvioihin Jussi Vesanen Tilastotieteen pro gradu -tutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen
Veikkauksen pelaajien pelaaminen suhteessa ulkomaisten vedonlyöntiyhtiöiden todennäköisyysarvioihin Jussi Vesanen Tilastotieteen pro gradu -tutkielma Jyväskylän yliopisto Matematiikan ja tilastotieteen
Veikkauksen tulosvetopelien pelikäyttäytymisestä
 Veikkaus Oy Veikkauksen tulosvetopelien pelikäyttäytymisestä TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio Ville Venojärvi, 54284B 4.8.2009 Sisällysluettelo 1 JOHDANTO... 1 2 VEIKKAUKSEN TULOSVETOPELIN
Veikkaus Oy Veikkauksen tulosvetopelien pelikäyttäytymisestä TEKNILLINEN KORKEAKOULU Systeemianalyysin laboratorio Ville Venojärvi, 54284B 4.8.2009 Sisällysluettelo 1 JOHDANTO... 1 2 VEIKKAUKSEN TULOSVETOPELIN
Pelaajaluettelot nähtävissä osoitteessa http://www.finhockey.fi/alueet/kymi-saimaa/tulospalvelu_2011-2012/tilastoitavat_sarjat/
 Kuntokiekon lisäohjeet: Pelaajaluettelot Joukkueet toimittavat aluepäällikölle joukkueensa pelaajaluettelot ennen sarjan alkua. Yhteyshenkilö ilmoittaa pelaajamuutokset välittömästi aluepäällikölle. Vain
Kuntokiekon lisäohjeet: Pelaajaluettelot Joukkueet toimittavat aluepäällikölle joukkueensa pelaajaluettelot ennen sarjan alkua. Yhteyshenkilö ilmoittaa pelaajamuutokset välittömästi aluepäällikölle. Vain
Markku Annala VEDONLYÖNNIN OPTIMOINTITYÖKALUN KEHITTÄMINEN
 Markku Annala VEDONLYÖNNIN OPTIMOINTITYÖKALUN KEHITTÄMINEN VEDONLYÖNNIN OPTIMOINTITYÖKALUN KEHITTÄMINEN Markku Annala Opinnäytetyö Syksy 2014 Tietotekniikan koulutusohjelma Oulun ammattikorkeakoulu TIIVISTELMÄ
Markku Annala VEDONLYÖNNIN OPTIMOINTITYÖKALUN KEHITTÄMINEN VEDONLYÖNNIN OPTIMOINTITYÖKALUN KEHITTÄMINEN Markku Annala Opinnäytetyö Syksy 2014 Tietotekniikan koulutusohjelma Oulun ammattikorkeakoulu TIIVISTELMÄ
VAASAN YLIOPISTO TALOUSMATEMATIIKKA Päätöksenteko epävarmuuden vallitessa Prof. Ilkka Virtanen TENTTI 5.3.1999
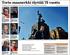 1(5) VAASAN YLIOPISTO TALOUSMATEMATIIKKA Päätöksenteko epävarmuuden vallitessa Prof. Ilkka Virtanen TENTTI 5.3.1999 Tehtävä 1. Liitteessä on kuvattu yksi luentojen perusesimerkeistä, Raiffan pallouurnia
1(5) VAASAN YLIOPISTO TALOUSMATEMATIIKKA Päätöksenteko epävarmuuden vallitessa Prof. Ilkka Virtanen TENTTI 5.3.1999 Tehtävä 1. Liitteessä on kuvattu yksi luentojen perusesimerkeistä, Raiffan pallouurnia
SEKASTRATEGIAT PELITEORIASSA
 SEKASTRATEGIAT PELITEORIASSA Matti Estola 8. joulukuuta 2013 Sisältö 1 Johdanto 2 2 Ratkaistaan sukupuolten välinen taistelu sekastrategioiden avulla 5 Teksti on suomennettu kirjasta: Gibbons: A Primer
SEKASTRATEGIAT PELITEORIASSA Matti Estola 8. joulukuuta 2013 Sisältö 1 Johdanto 2 2 Ratkaistaan sukupuolten välinen taistelu sekastrategioiden avulla 5 Teksti on suomennettu kirjasta: Gibbons: A Primer
Espoo Squash Rackets Club Hartwall Jaffa Cup Sivu 1 / 5 Kausi 2014-2015 Eero Salkala 30.11.2014
 Espoo Squash Rackets Club Hartwall Jaffa Cup Sivu 1 / 5 SÄÄNNÖT Kaudella pelataan kuusi osakilpailua Esport Centerissä klo 10-15: 13.09.2014, 04.10.2014, 29.11.2014, 31.01.2015, 14.03.2015 ja 25.04.2015.
Espoo Squash Rackets Club Hartwall Jaffa Cup Sivu 1 / 5 SÄÄNNÖT Kaudella pelataan kuusi osakilpailua Esport Centerissä klo 10-15: 13.09.2014, 04.10.2014, 29.11.2014, 31.01.2015, 14.03.2015 ja 25.04.2015.
Arvonlaskennan toiminta sijoitusten osalta
 Sivu 1/5 HEDGEHOG OY Arvonlaskennan toiminta sijoitusten osalta 6.10.2014 Tässä on kuvailtu Hedgehog Oy:n käyttämän arvonlaskentajärjestelmän toimintaa sijoitusten merkinnän, tuottosidonnaisten palkkioiden,
Sivu 1/5 HEDGEHOG OY Arvonlaskennan toiminta sijoitusten osalta 6.10.2014 Tässä on kuvailtu Hedgehog Oy:n käyttämän arvonlaskentajärjestelmän toimintaa sijoitusten merkinnän, tuottosidonnaisten palkkioiden,
Seuratiedote 2/09 LIITE 4
 CSA-järjestelmä Johdantoa USGAn Course Rating -järjestelmässä todetaan: USGAn Course Ratingin ja Slope Ratingin määritysten tulee vastata olosuhteita kauden aikana, jolloin suurin osa kierroksista pelataan.
CSA-järjestelmä Johdantoa USGAn Course Rating -järjestelmässä todetaan: USGAn Course Ratingin ja Slope Ratingin määritysten tulee vastata olosuhteita kauden aikana, jolloin suurin osa kierroksista pelataan.
1. Tässä tehtävässä päätellään kaksilapsisen perheen lapsiin liittyviä todennäköisyyksiä.
 TODENNÄKÖISYYS Aihepiirejä: Yhden ja kahden tapahtuman tuloksien käsittely ja taulukointi, ovikoodit, joukkueen valinta, bussin odotus, pelejä, urheilijoiden testaus kielletyn piristeen käytöstä, linnun
TODENNÄKÖISYYS Aihepiirejä: Yhden ja kahden tapahtuman tuloksien käsittely ja taulukointi, ovikoodit, joukkueen valinta, bussin odotus, pelejä, urheilijoiden testaus kielletyn piristeen käytöstä, linnun
Liite sisäasiainministeriön asetukseen SMDno/2015/635 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT
 Liite sisäasiainministeriön asetukseen SMDno/2015/635 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT 2 Sisältö LOTON SÄÄNNÖT... 3 LOTON LISÄARVONNAN SÄÄNNÖT... 7 KESTOLOTON JA KESTOLAUANTAI-JOKERIN LISÄARVONNAN SÄÄNNÖT...
Liite sisäasiainministeriön asetukseen SMDno/2015/635 VEIKKAUS OY:N RAHAPELIEN SÄÄNNÖT 2 Sisältö LOTON SÄÄNNÖT... 3 LOTON LISÄARVONNAN SÄÄNNÖT... 7 KESTOLOTON JA KESTOLAUANTAI-JOKERIN LISÄARVONNAN SÄÄNNÖT...
Työssä käytettyjä symboleita, merkintöjä ja lyhenteitä
 iii Työssä käytettyjä symboleita, merkintöjä ja lyhenteitä YD A T diag( 1, 2,..., p ) (.) satunnaismuuttuja Y noudattaa todennäköisyysjakaumaa D matriisin tai vektorin A transpoosi diagonaalimatriisi,
iii Työssä käytettyjä symboleita, merkintöjä ja lyhenteitä YD A T diag( 1, 2,..., p ) (.) satunnaismuuttuja Y noudattaa todennäköisyysjakaumaa D matriisin tai vektorin A transpoosi diagonaalimatriisi,
Tutkimustiedonhallinnan peruskurssi
 Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
Ratkaisut Summa on nolla, sillä luvut muodostavat vastalukuparit: ( 10) + 10 = 0, ( 9) + 9 = 0,...
 Ratkaisut 1 1. Summa on nolla, sillä luvut muodostavat vastalukuparit: ( 10) + 10 = 0, ( 9) + 9 = 0,.... Nolla, koska kerrotaan nollalla. 3. 16 15 50 = ( 8) 15 50 = (8 15) ( 50) = 1000 500 = 500 000. 4.
Ratkaisut 1 1. Summa on nolla, sillä luvut muodostavat vastalukuparit: ( 10) + 10 = 0, ( 9) + 9 = 0,.... Nolla, koska kerrotaan nollalla. 3. 16 15 50 = ( 8) 15 50 = (8 15) ( 50) = 1000 500 = 500 000. 4.
SUBSTANTIIVIT 1/6. juttu. joukkue. vaali. kaupunki. syy. alku. kokous. asukas. tapaus. kysymys. lapsi. kauppa. pankki. miljoona. keskiviikko.
 SUBSTANTIIVIT 1/6 juttu joukkue vaali kaupunki syy alku kokous asukas tapaus kysymys lapsi kauppa pankki miljoona keskiviikko käsi loppu pelaaja voitto pääministeri päivä tutkimus äiti kirja SUBSTANTIIVIT
SUBSTANTIIVIT 1/6 juttu joukkue vaali kaupunki syy alku kokous asukas tapaus kysymys lapsi kauppa pankki miljoona keskiviikko käsi loppu pelaaja voitto pääministeri päivä tutkimus äiti kirja SUBSTANTIIVIT
MONIVETOWEB MONI - JA TULOSVETO OHJELMISTO
 MONIVETOWEB MONI - JA TULOSVETO OHJELMISTO Sisällysluettelo INFO...2 KÄYTTÖOIKEUDET...2 Rekisteröimätön versio...2 Rekisteröity versio...2 OMINAISUUKSIA...2 YLIKERTOIMET...3 TERMEJÄ...3 Ylikerroin...3
MONIVETOWEB MONI - JA TULOSVETO OHJELMISTO Sisällysluettelo INFO...2 KÄYTTÖOIKEUDET...2 Rekisteröimätön versio...2 Rekisteröity versio...2 OMINAISUUKSIA...2 YLIKERTOIMET...3 TERMEJÄ...3 Ylikerroin...3
Turun seitsemäsluokkalaisten matematiikkakilpailu 18.1.2012 Tehtävät ja ratkaisut
 (1) Laske 20 12 11 21. Turun seitsemäsluokkalaisten matematiikkakilpailu 18.1.2012 Tehtävät ja ratkaisut a) 31 b) 0 c) 9 d) 31 Ratkaisu. Suoralla laskulla 20 12 11 21 = 240 231 = 9. (2) Kahden peräkkäisen
(1) Laske 20 12 11 21. Turun seitsemäsluokkalaisten matematiikkakilpailu 18.1.2012 Tehtävät ja ratkaisut a) 31 b) 0 c) 9 d) 31 Ratkaisu. Suoralla laskulla 20 12 11 21 = 240 231 = 9. (2) Kahden peräkkäisen
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Peliteoria Strategiapelit ja Nashin tasapaino. Sebastian Siikavirta sebastian.siikavirta@helsinki.fi
 Peliteoria Strategiapelit ja Nashin tasapaino Sebastian Siikavirta sebastian.siikavirta@helsinki.fi Helsinki 11.09.2006 Peliteoria Tomi Pasanen HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Sisältö
Peliteoria Strategiapelit ja Nashin tasapaino Sebastian Siikavirta sebastian.siikavirta@helsinki.fi Helsinki 11.09.2006 Peliteoria Tomi Pasanen HELSINGIN YLIOPISTO Tietojenkäsittelytieteen laitos Sisältö
ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2010 Harjoitus 3
 ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2010 Harjoitus 3 Ratkaisuehdotuksia 1. (a) Päätöspuu on matala, jos mitään sattumasolmua ei välittömästi seuraa sattumasolmu eikä mitään päätössolmua
ORMS2020 Päätöksenteko epävarmuuden vallitessa Syksy 2010 Harjoitus 3 Ratkaisuehdotuksia 1. (a) Päätöspuu on matala, jos mitään sattumasolmua ei välittömästi seuraa sattumasolmu eikä mitään päätössolmua
Todennäköisyyslaskenta I, kesä 2017 Helsingin yliopisto/avoin Yliopisto Harjoitus 1, ratkaisuehdotukset
 Todennäköisyyslaskenta I, kesä 207 Helsingin yliopisto/avoin Yliopisto Harjoitus, ratkaisuehdotukset. Kokeet ja Ω:n hahmottaminen. Mitä tarkoittaa todennäköisyys on? Olkoon satunnaiskokeena yhden nopan
Todennäköisyyslaskenta I, kesä 207 Helsingin yliopisto/avoin Yliopisto Harjoitus, ratkaisuehdotukset. Kokeet ja Ω:n hahmottaminen. Mitä tarkoittaa todennäköisyys on? Olkoon satunnaiskokeena yhden nopan
TEAMGOLF-KUTSU. Kilpailu järjestetään Veritas-Stadionin sisähallissa (Hippoksentie 6, Kupittaa, Turku) sunnuntaina 22.1.2006.
 TEAMGOLF-KUTSU Ajankohta Kilpailu järjestetään Veritas-Stadionin sisähallissa (Hippoksentie 6, Kupittaa, Turku) sunnuntaina 22.1.2006. Lähtöaika Ensimmäinen lähtö klo 10.00. Pelitapa Kierrokset Parikilpailu
TEAMGOLF-KUTSU Ajankohta Kilpailu järjestetään Veritas-Stadionin sisähallissa (Hippoksentie 6, Kupittaa, Turku) sunnuntaina 22.1.2006. Lähtöaika Ensimmäinen lähtö klo 10.00. Pelitapa Kierrokset Parikilpailu
TURNAUSSÄÄNNÖT 2014. Ottelut pelataan kahden minuutin vaihdoilla. Vaihdot kuulutetaan.
 OTTELUIDEN PELAAMINEN Ottelut pelataan 4 vs 4 peleinä. Ottelut pelataan puolikkaassa kaukalossa kaukalon suuntaisesti. Maalien koko on 122 cm x 183 cm. Ottelut pelataan mustilla kiekoilla. Ottelut pelataan
OTTELUIDEN PELAAMINEN Ottelut pelataan 4 vs 4 peleinä. Ottelut pelataan puolikkaassa kaukalossa kaukalon suuntaisesti. Maalien koko on 122 cm x 183 cm. Ottelut pelataan mustilla kiekoilla. Ottelut pelataan
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
Matematiikan tukikurssi Kurssikerta 6 Sarjojen suppeneminen Kiinnostuksen kohteena on edelleen sarja a k = a + a 2 + a 3 + a 4 +... k= Tämä summa on mahdollisesti äärellisenä olemassa, jolloin sanotaan
1.3 Prosenttilaskuja. pa b = 100
 1.3 Prosenttilaskuja Yksi prosentti jostakin luvusta tai suureesta on tämän sadasosa ja saadaan siis jakamalla ao. luku tai suure luvulla. Jos luku b on p % luvusta a, toisin sanoen jos luku b on p kpl
1.3 Prosenttilaskuja Yksi prosentti jostakin luvusta tai suureesta on tämän sadasosa ja saadaan siis jakamalla ao. luku tai suure luvulla. Jos luku b on p % luvusta a, toisin sanoen jos luku b on p kpl
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä
 Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
Fysiikan laboratoriotyöt 1, työ nro: 2, Harmoninen värähtelijä Tekijä: Mikko Laine Tekijän sähköpostiosoite: miklaine@student.oulu.fi Koulutusohjelma: Fysiikka Mittausten suorituspäivä: 04.02.2013 Työn
2.2 Neliöjuuri ja sitä koskevat laskusäännöt
 . Neliöjuuri ja sitä koskevat laskusäännöt MÄÄRITELMÄ 3: Lukua b sanotaan luvun a neliöjuureksi, merkitään a b, jos b täyttää kaksi ehtoa: 1o b > 0 o b a Esim.1 Määritä a) 64 b) 0 c) 36 a) Luvun 64 neliöjuuri
. Neliöjuuri ja sitä koskevat laskusäännöt MÄÄRITELMÄ 3: Lukua b sanotaan luvun a neliöjuureksi, merkitään a b, jos b täyttää kaksi ehtoa: 1o b > 0 o b a Esim.1 Määritä a) 64 b) 0 c) 36 a) Luvun 64 neliöjuuri
Rahoitusriskit ja johdannaiset Matti Estola. luento 7 Swap sopimuksista lisää
 Rahoitusriskit ja johdannaiset Matti Estola luento 7 Swap sopimuksista lisää 1. Pankki swapin välittäjänä Yleensä 2 eri-rahoitusalan yritystä eivät tee swap sopimusta keskenään vaan pankin tai yleensäkin
Rahoitusriskit ja johdannaiset Matti Estola luento 7 Swap sopimuksista lisää 1. Pankki swapin välittäjänä Yleensä 2 eri-rahoitusalan yritystä eivät tee swap sopimusta keskenään vaan pankin tai yleensäkin
Suomen Curlingliiton alaisten curlingin SMkilpailuiden säännöt kaudella 2010-2011
 Suomen Curlingliiton alaisten curlingin SMkilpailuiden säännöt kaudella 2010-2011 Näitä sääntöjä sovelletaan kaikissa Suomen Curlingliiton järjestämissä kilpailuissa, joilla on SM-status. Tällaisia kilpailuja
Suomen Curlingliiton alaisten curlingin SMkilpailuiden säännöt kaudella 2010-2011 Näitä sääntöjä sovelletaan kaikissa Suomen Curlingliiton järjestämissä kilpailuissa, joilla on SM-status. Tällaisia kilpailuja
KANSANTALOUSTIETEEN PÄÄSYKOE 4.6.2015 MALLIVASTAUKSET
 KANSANTALOUSTIETEEN ÄÄSYKOE 4.6.05 MALLIVASTAUKSET Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti ohjola, Taloustieteen oppikirja,. painos, 04] sivuihin. () (a) Bretton Woods -järjestelmä:
KANSANTALOUSTIETEEN ÄÄSYKOE 4.6.05 MALLIVASTAUKSET Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti ohjola, Taloustieteen oppikirja,. painos, 04] sivuihin. () (a) Bretton Woods -järjestelmä:
Suur Hollola Ajo. säännöt. Kilpailun järjestää Lahden Hevosystäväinseura ry Lahden raviradalla vuosittain kesä heinäkuun aikana.
 Suur Hollola Ajo säännöt Kilpailun järjestää Lahden Hevosystäväinseura ry Lahden raviradalla vuosittain kesä heinäkuun aikana. Kilpailu ajetaan 2140 metrin ryhmäajona autolähetyksellä. Loppukilpailuun
Suur Hollola Ajo säännöt Kilpailun järjestää Lahden Hevosystäväinseura ry Lahden raviradalla vuosittain kesä heinäkuun aikana. Kilpailu ajetaan 2140 metrin ryhmäajona autolähetyksellä. Loppukilpailuun
Todennäköisyyslaskenta - tehtävät
 Todennäköisyyslaskenta - tehtävät Todennäköisyyslaskentaa käsitellään Pitkän matematiikan kertauskirjan sivuilla 253 276. Klassinen todennäköisyys Kombinatoriikka Binomitodennäköisyys Satunnaismuuttuja,
Todennäköisyyslaskenta - tehtävät Todennäköisyyslaskentaa käsitellään Pitkän matematiikan kertauskirjan sivuilla 253 276. Klassinen todennäköisyys Kombinatoriikka Binomitodennäköisyys Satunnaismuuttuja,
III- Divisioona playoff- ottelut Etelän loppusarjan ylempi jatkosarja ja Kymi-Saimaan loppusarja
 6.3.2014 III- Divisioona playoff- ottelut Etelän loppusarjan ylempi jatkosarja ja Kymi-Saimaan loppusarja Huom. Välierät ja finaalit pelataan paras kahdesta järjestelmällä (ja 2 pisteen systeemillä) peliajan
6.3.2014 III- Divisioona playoff- ottelut Etelän loppusarjan ylempi jatkosarja ja Kymi-Saimaan loppusarja Huom. Välierät ja finaalit pelataan paras kahdesta järjestelmällä (ja 2 pisteen systeemillä) peliajan
VERKKOKUMPPANUUS PÄHKINÄNKUORESSA VEIKKAUS
 VERKKOKUMPPANUUS PÄHKINÄNKUORESSA VEIKKAUS sivu MIKÄ VERKKOKUMPPANUUS? Seuranne nettisivuille asennetaan nettibanneri, josta on linkkaus Veikkauksen sivuille Aktivoimalla seuran jäsenet, kannattajat ja
VERKKOKUMPPANUUS PÄHKINÄNKUORESSA VEIKKAUS sivu MIKÄ VERKKOKUMPPANUUS? Seuranne nettisivuille asennetaan nettibanneri, josta on linkkaus Veikkauksen sivuille Aktivoimalla seuran jäsenet, kannattajat ja
KANSANTALOUSTIETEEN PÄÄSYKOE : Mallivastaukset
 KANSANTALOUSTIETEEN PÄÄSYKOE.6.016: Mallivastaukset Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti Pohjola, Taloustieteen oppikirja, 014] sivuihin. (1) (a) Julkisten menojen kerroin (suljetun
KANSANTALOUSTIETEEN PÄÄSYKOE.6.016: Mallivastaukset Sivunumerot mallivastauksissa viittaavat pääsykoekirjan [Matti Pohjola, Taloustieteen oppikirja, 014] sivuihin. (1) (a) Julkisten menojen kerroin (suljetun
4. laskuharjoituskierros, vko 7, ratkaisut
 4. laskuharjoituskierros, vko 7, ratkaisut D1. Kone valmistaa kuulalaakerin kuulia, joiden halkaisija vaihtelee satunnaisesti. Halkaisijan on oltava tiettyjen rajojen sisällä, jotta kuula olisi käyttökelpoinen.
4. laskuharjoituskierros, vko 7, ratkaisut D1. Kone valmistaa kuulalaakerin kuulia, joiden halkaisija vaihtelee satunnaisesti. Halkaisijan on oltava tiettyjen rajojen sisällä, jotta kuula olisi käyttökelpoinen.
Tilinpäätöksen rakenne ja tulkinta Erkki Laitila. E Laitila 1
 Tilinpäätöksen rakenne ja tulkinta Erkki Laitila E Laitila 1 YRITYSTOIMINNAN TAVOITTEENA ON TAVALLISESTI VOITON MAKSIMOINTI TULOT MENOT = MAHDOLLISIMMAN SUURI LUKU VOITTOA VOIDAAN MAKSIMOIDA JOKO LYHYELLÄ
Tilinpäätöksen rakenne ja tulkinta Erkki Laitila E Laitila 1 YRITYSTOIMINNAN TAVOITTEENA ON TAVALLISESTI VOITON MAKSIMOINTI TULOT MENOT = MAHDOLLISIMMAN SUURI LUKU VOITTOA VOIDAAN MAKSIMOIDA JOKO LYHYELLÄ
PELISIJOITTAMINEN OSANA SIJOITUSTOIMINTAA
 Opinnäytetyö (AMK) Liiketalous BisnesAkatemia 2017 Teemu Kesänen ja Daniel Rantanen PELISIJOITTAMINEN OSANA SIJOITUSTOIMINTAA OPINNÄYTETYÖ (AMK ) TIIVISTELMÄ TURUN AMMATTIKORKEAKOULU Liiketalouden koulutusohjelma
Opinnäytetyö (AMK) Liiketalous BisnesAkatemia 2017 Teemu Kesänen ja Daniel Rantanen PELISIJOITTAMINEN OSANA SIJOITUSTOIMINTAA OPINNÄYTETYÖ (AMK ) TIIVISTELMÄ TURUN AMMATTIKORKEAKOULU Liiketalouden koulutusohjelma
A. Huutokaupat ovat tärkeitä ainakin kolmesta syystä. 1. Valtava määrä taloudellisia transaktioita tapahtuu huutokauppojen välityksellä.
 HUUTOKAUPOISTA A. Huutokaupat ovat tärkeitä ainakin kolmesta syystä 1. Valtava määrä taloudellisia transaktioita tapahtuu huutokauppojen välityksellä. 2. Huutokauppapelejä voidaan käyttää taloustieteen
HUUTOKAUPOISTA A. Huutokaupat ovat tärkeitä ainakin kolmesta syystä 1. Valtava määrä taloudellisia transaktioita tapahtuu huutokauppojen välityksellä. 2. Huutokauppapelejä voidaan käyttää taloustieteen
Sisällysluettelo ESIPUHE KIRJAN 1. PAINOKSEEN...3 ESIPUHE KIRJAN 2. PAINOKSEEN...3 SISÄLLYSLUETTELO...4
 Sisällysluettelo ESIPUHE KIRJAN 1. PAINOKSEEN...3 ESIPUHE KIRJAN 2. PAINOKSEEN...3 SISÄLLYSLUETTELO...4 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN...6 1.1 INDUKTIO JA DEDUKTIO...7 1.2 SYYT JA VAIKUTUKSET...9
Sisällysluettelo ESIPUHE KIRJAN 1. PAINOKSEEN...3 ESIPUHE KIRJAN 2. PAINOKSEEN...3 SISÄLLYSLUETTELO...4 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN...6 1.1 INDUKTIO JA DEDUKTIO...7 1.2 SYYT JA VAIKUTUKSET...9
5/11 6/11 Vaihe 1. 6/10 4/10 6/10 4/10 Vaihe 2. 5/11 6/11 4/11 7/11 6/11 5/11 5/11 6/11 Vaihe 3
 Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Verkot todennäköisyyslaskennassa Satunnaismuuttujat ja todennäköisyysjakaumat Jakaumien tunnusluvut Kertymäfunktio, Momentit, Odotusarvo,
Mat-.9 Sovellettu todennäköisyyslasku A / Ratkaisut Aiheet: Avainsanat: Verkot todennäköisyyslaskennassa Satunnaismuuttujat ja todennäköisyysjakaumat Jakaumien tunnusluvut Kertymäfunktio, Momentit, Odotusarvo,
INNOVAATIOIDEN SUOJAAMINEN LIIKESALAISUUKSIEN JA PATENTTIEN AVULLA: YRITYKSIIN VAIKUTTAVIA TEKIJÖITÄ EU:SSA TIIVISTELMÄ
 INNOVAATIOIDEN SUOJAAMINEN LIIKESALAISUUKSIEN JA PATENTTIEN AVULLA: YRITYKSIIN VAIKUTTAVIA TEKIJÖITÄ EU:SSA TIIVISTELMÄ Heinäkuu 2017 INNOVAATIOIDEN SUOJAAMINEN LIIKESALAISUUKSIEN JA PATENTTIEN AVULLA:
INNOVAATIOIDEN SUOJAAMINEN LIIKESALAISUUKSIEN JA PATENTTIEN AVULLA: YRITYKSIIN VAIKUTTAVIA TEKIJÖITÄ EU:SSA TIIVISTELMÄ Heinäkuu 2017 INNOVAATIOIDEN SUOJAAMINEN LIIKESALAISUUKSIEN JA PATENTTIEN AVULLA:
Blackjack on korttipeli, jossa pelaajan tavoitteena on voittaa pelinhoitaja.
 POHDIN projekti Blackjack Blackjack on pelinhoitajaa vastaan pelattava korttipeli mutta myös ns. uhkapeli 1. Kun kyseessä on ns. rahapeli, niin ikäraja Suomessa on tällaiselle pelille K-18. Blackjackissä
POHDIN projekti Blackjack Blackjack on pelinhoitajaa vastaan pelattava korttipeli mutta myös ns. uhkapeli 1. Kun kyseessä on ns. rahapeli, niin ikäraja Suomessa on tällaiselle pelille K-18. Blackjackissä
Järvitesti Ympäristöteknologia T571SA 7.5.2013
 Hans Laihia Mika Tuukkanen 1 LASKENNALLISET JA TILASTOLLISET MENETELMÄT Järvitesti Ympäristöteknologia T571SA 7.5.2013 Sarkola Eino JÄRVITESTI Johdanto Järvien kuntoa tutkitaan monenlaisilla eri menetelmillä.
Hans Laihia Mika Tuukkanen 1 LASKENNALLISET JA TILASTOLLISET MENETELMÄT Järvitesti Ympäristöteknologia T571SA 7.5.2013 Sarkola Eino JÄRVITESTI Johdanto Järvien kuntoa tutkitaan monenlaisilla eri menetelmillä.
Luentokalvoja tilastollisesta päättelystä. Kalvot laatinut Aki Taanila Päivitetty 30.11.2012
 Luentokalvoja tilastollisesta päättelystä Kalvot laatinut Aki Taanila Päivitetty 30.11.2012 Otanta Otantamenetelmiä Näyte Tilastollinen päättely Otantavirhe Otanta Tavoitteena edustava otos = perusjoukko
Luentokalvoja tilastollisesta päättelystä Kalvot laatinut Aki Taanila Päivitetty 30.11.2012 Otanta Otantamenetelmiä Näyte Tilastollinen päättely Otantavirhe Otanta Tavoitteena edustava otos = perusjoukko
ohjekortti #1 Tämä on ehto. Kun se täyttyy pelissä, seuraa tämän siirron sääntöjä.
 ohjekortti #1 tämä on siirron nimi Tämä on ehto. Kun se täyttyy pelissä, seuraa tämän siirron sääntöjä. Tässä on säännöt, joita siirto noudattaa. Säännöt käydään läpi ylhäältä alaspäin Noppien kohdalla
ohjekortti #1 tämä on siirron nimi Tämä on ehto. Kun se täyttyy pelissä, seuraa tämän siirron sääntöjä. Tässä on säännöt, joita siirto noudattaa. Säännöt käydään läpi ylhäältä alaspäin Noppien kohdalla
Kansainvälinen rahatalous Matti Estola. Termiinikurssit ja swapit valuuttariskien hallinnassa
 Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Kansainvälinen rahatalous Matti Estola ermiinikurssit ja swapit valuuttariskien hallinnassa 1. Valuuttariskien suojauskeinot Rahoitusalan yritykset tekevät asiakkailleen valuuttojen välisiä termiinisopimuksia
Pohjoismaiden osakkeet ulottuvillasi Taurus tekee sijoittamisesta helpon. Taurus Capital Ltd 24.04. 2010
 Pohjoismaiden osakkeet ulottuvillasi Taurus tekee sijoittamisesta helpon Taurus Capital Ltd 24.04. 2010 The Little Book that Beats the Market 2006 ilmestyi kirja, jonka tekijä väitti kehittäneensä osakevalintamenetelmän
Pohjoismaiden osakkeet ulottuvillasi Taurus tekee sijoittamisesta helpon Taurus Capital Ltd 24.04. 2010 The Little Book that Beats the Market 2006 ilmestyi kirja, jonka tekijä väitti kehittäneensä osakevalintamenetelmän
Oletko Bull, Bear vai Chicken?
 www.handelsbanken.fi/bullbear Handelsbankenin bull & Bear -sertifikaatit Oletko Bull, Bear vai Chicken? Bull Valmiina hyökkäykseen sarvet ojossa uskoen markkinan nousuun. Mikäli olet oikeassa, saat nousun
www.handelsbanken.fi/bullbear Handelsbankenin bull & Bear -sertifikaatit Oletko Bull, Bear vai Chicken? Bull Valmiina hyökkäykseen sarvet ojossa uskoen markkinan nousuun. Mikäli olet oikeassa, saat nousun
LIITE 1 VIRHEEN ARVIOINNISTA
 Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
Oulun yliopisto Fysiikan opetuslaboratorio Fysiikan laboratoriotyöt 1 1 LIITE 1 VIRHEEN RVIOINNIST Mihin tarvitset virheen arviointia? Mittaustuloksiin sisältyy aina virhettä, vaikka mittauslaite olisi
INTERVALLIPÄÄTÖSPUUT JANNE GUSTAFSSON 45433E. Mat Optimointiopin seminaari Referaatti
 12.11.1999 INTERVALLIPÄÄTÖSPUUT JANNE GUSTAFSSON 45433E Mat-2.142 Optimointiopin seminaari Referaatti Syksy 1999 1. JOHDANTO Thomas M. Stratin artikkeli Decision Analysis Using Belief Functions käsittelee
12.11.1999 INTERVALLIPÄÄTÖSPUUT JANNE GUSTAFSSON 45433E Mat-2.142 Optimointiopin seminaari Referaatti Syksy 1999 1. JOHDANTO Thomas M. Stratin artikkeli Decision Analysis Using Belief Functions käsittelee
Prof. Marko Terviö Assist. Jan Jääskeläinen
 Harjoitukset 3. 1. (a) Dismalandissa eri puolueiden arvostukset katusiivoukselle ovat Q A (P ) = 60 6P P A (Q) = 10 Q/6 Q B (P ) = 80 5P P B (Q) = 16 Q/5 Q C (P ) = 50 2P P C (Q) = 25 Q/2 Katusiivous on
Harjoitukset 3. 1. (a) Dismalandissa eri puolueiden arvostukset katusiivoukselle ovat Q A (P ) = 60 6P P A (Q) = 10 Q/6 Q B (P ) = 80 5P P B (Q) = 16 Q/5 Q C (P ) = 50 2P P C (Q) = 25 Q/2 Katusiivous on
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO
 Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
Kirjoita ohjelma jossa luetaan kokonaislukuja taulukkoon (saat itse päättää taulun koon, kunhan koko on vähintään 10)
 Tehtävä 40. Kirjoita ohjelma, jossa luetaan 20 lukua, joiden arvot ovat välillä 10 100. Kun taulukko on täytetty, ohjelma tulostaa vain ne taulukon arvot, jotka esiintyvät taulukossa vain kerran. Tehtävä
Tehtävä 40. Kirjoita ohjelma, jossa luetaan 20 lukua, joiden arvot ovat välillä 10 100. Kun taulukko on täytetty, ohjelma tulostaa vain ne taulukon arvot, jotka esiintyvät taulukossa vain kerran. Tehtävä
Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... 5 SISÄLLYSLUETTELO... 6 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN... 8 2. TODENNÄKÖISYYS...
 Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... 5 SISÄLLYSLUETTELO... 6 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN... 8 1.1 INDUKTIO JA DEDUKTIO... 9 1.2 SYYT JA VAIKUTUKSET... 11 TEHTÄVIÄ... 13
Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... 5 SISÄLLYSLUETTELO... 6 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN... 8 1.1 INDUKTIO JA DEDUKTIO... 9 1.2 SYYT JA VAIKUTUKSET... 11 TEHTÄVIÄ... 13
TOTO-PELIT PÄHKINÄNKUORESSA
 Peliopas TOTO-PELIT TOTO-PELIT PÄHKINÄNKUORESSA Toto-pelit tarjoavat sinulle monia erilaisia mahdollisuuksia pelata ja jännittää. Totoa voit pelata raveihin joka päivä Suomeen ja ulkomaille. Totossa pelataan
Peliopas TOTO-PELIT TOTO-PELIT PÄHKINÄNKUORESSA Toto-pelit tarjoavat sinulle monia erilaisia mahdollisuuksia pelata ja jännittää. Totoa voit pelata raveihin joka päivä Suomeen ja ulkomaille. Totossa pelataan
Markkinariskipreemio Suomen osakemarkkinoilla
 Markkinariskipreemio Suomen osakemarkkinoilla Tutkimus Marraskuu 2005 *connectedthinking Sisällysluettelo Yhteenveto... 3 Yleistä... 3 Kyselytutkimuksen tulokset... 3 Markkinariskipreemio Suomen osakemarkkinoilla...
Markkinariskipreemio Suomen osakemarkkinoilla Tutkimus Marraskuu 2005 *connectedthinking Sisällysluettelo Yhteenveto... 3 Yleistä... 3 Kyselytutkimuksen tulokset... 3 Markkinariskipreemio Suomen osakemarkkinoilla...
11 Oligopoli ja monopolistinen kilpailu (Mankiw & Taylor, Ch 17)
 11 Oligopoli ja monopolistinen kilpailu (Mankiw & Taylor, Ch 17) Oligopoli on markkinamuoto, jossa markkinoilla on muutamia yrityksiä, jotka uskovat tekemiensä valintojen seurauksien eli voittojen riippuvan
11 Oligopoli ja monopolistinen kilpailu (Mankiw & Taylor, Ch 17) Oligopoli on markkinamuoto, jossa markkinoilla on muutamia yrityksiä, jotka uskovat tekemiensä valintojen seurauksien eli voittojen riippuvan
1. laskuharjoituskierros, vko 4, ratkaisut
 1. laskuharjoituskierros, vko 4, ratkaisut D1. Heitetään kahta virheetöntä noppaa, joiden kuudella tahkolla on silmäluvut 1, 2, 3, 4, 5 ja 6. Tällöin heittotuloksiin liittyvä otosavaruus on S = {(x, y)
1. laskuharjoituskierros, vko 4, ratkaisut D1. Heitetään kahta virheetöntä noppaa, joiden kuudella tahkolla on silmäluvut 1, 2, 3, 4, 5 ja 6. Tällöin heittotuloksiin liittyvä otosavaruus on S = {(x, y)
BtoB-markkinoinnin tutkimus
 BtoB-markkinoinnin tutkimus Tiivistelmä tutkimustuloksista Anna-Mari West 19.6.2008 Tutkimuksen tavoitteet ja toteutus Tutkimuksen tavoitteet Tutkimuksen tavoitteena oli selvittää markkinointipäättäjien
BtoB-markkinoinnin tutkimus Tiivistelmä tutkimustuloksista Anna-Mari West 19.6.2008 Tutkimuksen tavoitteet ja toteutus Tutkimuksen tavoitteet Tutkimuksen tavoitteena oli selvittää markkinointipäättäjien
Bayesin pelit. Kalle Siukola. MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly
 Bayesin pelit Kalle Siukola MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Toistetun pelin esittäminen automaatin avulla Ekstensiivisen muodon puu on tehoton esitystapa, jos peliä
Bayesin pelit Kalle Siukola MS-E2142 Optimointiopin seminaari: Peliteoria ja tekoäly 12.10.2016 Toistetun pelin esittäminen automaatin avulla Ekstensiivisen muodon puu on tehoton esitystapa, jos peliä
(b) Tarkista integroimalla, että kyseessä on todella tiheysfunktio.
 Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
Todennäköisyyslaskenta I, kesä 7 Harjoitus 4 Ratkaisuehdotuksia. Satunnaismuuttujalla X on ns. kaksipuolinen eksponenttijakauma eli Laplacen jakauma: sen tiheysfunktio on fx = e x. a Piirrä tiheysfunktio.
PALLOVERKKO SÄHKÖINEN OTTELUPÖYTÄKIRJA
 PALLOVERKKO SÄHKÖINEN OTTELUPÖYTÄKIRJA 30.6.2011 KÄYTTÄJÄTUNNUKSEN TILAAMINEN LÖYTYY SIVUN ALAREUNASTA TUNNUSTEN TILAAMINEN: JOTTA PÄÄSEE KIRJAUTUMAAN JÄRJESTELMÄÄN TULOSPALVELUVASTAAVANA, PITÄÄ OLLA TUNNUKSET
PALLOVERKKO SÄHKÖINEN OTTELUPÖYTÄKIRJA 30.6.2011 KÄYTTÄJÄTUNNUKSEN TILAAMINEN LÖYTYY SIVUN ALAREUNASTA TUNNUSTEN TILAAMINEN: JOTTA PÄÄSEE KIRJAUTUMAAN JÄRJESTELMÄÄN TULOSPALVELUVASTAAVANA, PITÄÄ OLLA TUNNUKSET
SUOMEN SALIBANDYLIITTO JOUKKUESIVUSTON OHJE VERSIO 2.4. PÄIVITETTY joukkuesivusto KOKOONPANOT
 sivu 1 joukkuesivusto KOKOONPANOT KOKOONPANON LUOMINEN JA YLLÄPITO PALVELUSIVUSTOLLA Molemmat joukkueet (koti/vieras) ilmoittavat omalla joukkuetunnuksellaan päivän ottelukokoonpanon. Kokoonpano voidaan
sivu 1 joukkuesivusto KOKOONPANOT KOKOONPANON LUOMINEN JA YLLÄPITO PALVELUSIVUSTOLLA Molemmat joukkueet (koti/vieras) ilmoittavat omalla joukkuetunnuksellaan päivän ottelukokoonpanon. Kokoonpano voidaan
4. www-harjoitusten mallivastaukset 2016
 TU-91.1001 Kansantaloustieteen perusteet 4. www-harjoitusten mallivastaukset 2016 Tehtävä 1. Oikea vastaus: C Voitto maksimoidaan, kun MR=MC. Kyseisellä myyntimäärällä Q(m) voittomarginaali yhden tuotteen
TU-91.1001 Kansantaloustieteen perusteet 4. www-harjoitusten mallivastaukset 2016 Tehtävä 1. Oikea vastaus: C Voitto maksimoidaan, kun MR=MC. Kyseisellä myyntimäärällä Q(m) voittomarginaali yhden tuotteen
Tilastollisia peruskäsitteitä ja Monte Carlo
 Tilastollisia peruskäsitteitä ja Monte Carlo Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo Tutkimustiedonhallinnan peruskurssi Tilastollisia peruskäsitteitä ja Monte Carlo 1/13 Kevät 2003 Tilastollisia
Tilastollisia peruskäsitteitä ja Monte Carlo Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo Tutkimustiedonhallinnan peruskurssi Tilastollisia peruskäsitteitä ja Monte Carlo 1/13 Kevät 2003 Tilastollisia
SUOMEN PÖYTÄTENNISLIITTO MIESTEN RANKINGJÄRJESTELMÄN PERUSTEET
 SUOMEN PÖYTÄTENNISLIITTO MIESTEN RANKINGJÄRJESTELMÄN PERUSTEET VERSIO 1.6 Sisällysluettelo 1 Dokumentin tiedot...2 1.1 Dokumentin historia...2 2 Yleistä...3 3 Pelaajan pistearvo...3 4 Kilpailuista saatavat
SUOMEN PÖYTÄTENNISLIITTO MIESTEN RANKINGJÄRJESTELMÄN PERUSTEET VERSIO 1.6 Sisällysluettelo 1 Dokumentin tiedot...2 1.1 Dokumentin historia...2 2 Yleistä...3 3 Pelaajan pistearvo...3 4 Kilpailuista saatavat
PELIOHJEET (suomeksi) Koira. Peli on kaksivaiheinen: Vaihe 1:
 PELIOHJEET (suomeksi) Koira Peli on kaksivaiheinen: Vaihe 1: Jokaiselle osanottajalle/pelaajalle jaetaan kolme (3) korttia. Loput kortit asetetaan pelipöydälle pinoon, pakaksi. Huomattavaa on, että pakan
PELIOHJEET (suomeksi) Koira Peli on kaksivaiheinen: Vaihe 1: Jokaiselle osanottajalle/pelaajalle jaetaan kolme (3) korttia. Loput kortit asetetaan pelipöydälle pinoon, pakaksi. Huomattavaa on, että pakan
TOTO-PELIT PÄHKINÄNKUORESSA
 Peliopas TOTO-PELIT TOTO-PELIT PÄHKINÄNKUORESSA Toto-pelit tarjoavat sinulle monia erilaisia mahdollisuuksia pelata ja jännittää. Totoa voit pelata raveihin joka päivä Suomeen ja ulkomaille. Totossa pelataan
Peliopas TOTO-PELIT TOTO-PELIT PÄHKINÄNKUORESSA Toto-pelit tarjoavat sinulle monia erilaisia mahdollisuuksia pelata ja jännittää. Totoa voit pelata raveihin joka päivä Suomeen ja ulkomaille. Totossa pelataan
Toiminta ennen ensimmäistä ottelua (1/2)
 Toiminta ennen ensimmäistä ottelua (1/2) Kotijoukkue kirjautuu järjestelmään omalla joukkuekoodillaan Joukkue- /seuratunnus -kohdasta. Kirjoita joukkueesi tunnus siihen ja paina Kirjaudu -kohdasta. Tunnukset
Toiminta ennen ensimmäistä ottelua (1/2) Kotijoukkue kirjautuu järjestelmään omalla joukkuekoodillaan Joukkue- /seuratunnus -kohdasta. Kirjoita joukkueesi tunnus siihen ja paina Kirjaudu -kohdasta. Tunnukset
Salasuhteita. esimerkiksi espanjaksi nimi tarkoittaa pientä pusua.
 Salasuhteita Avioliittopeleistä kehiteltiin edelleen uusia pelejä, joissa varsinaisten avioliittojen lisäksi kohdataan sopimattomia suhteita kuningatarten ja sotilaiden välillä vieläpä maiden rajat ylittäen!
Salasuhteita Avioliittopeleistä kehiteltiin edelleen uusia pelejä, joissa varsinaisten avioliittojen lisäksi kohdataan sopimattomia suhteita kuningatarten ja sotilaiden välillä vieläpä maiden rajat ylittäen!
Palvelusetelihanke Hinnoitteluprojekti / hinnoittelupolitiikan vaihtoehtoja ja malleja 16.4.2010
 Palvelusetelihanke Hinnoitteluprojekti / hinnoittelupolitiikan vaihtoehtoja ja malleja 16.4.2010 Sisältö Sivu Johdanto 3 Palvelusetelin hinnoittelun elementit 5 Palvelun hinta: hintakatto tai markkinahinta
Palvelusetelihanke Hinnoitteluprojekti / hinnoittelupolitiikan vaihtoehtoja ja malleja 16.4.2010 Sisältö Sivu Johdanto 3 Palvelusetelin hinnoittelun elementit 5 Palvelun hinta: hintakatto tai markkinahinta
LIITE 1 VIRHEEN ARVIOINNISTA
 1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
1 LIITE 1 VIRHEEN ARVIOINNISTA Mihin tarvitset virheen arviointia? Mittaustulokset ovat aina todellisten luonnonvakioiden ja tutkimuskohdetta kuvaavien suureiden likiarvoja, vaikka mittauslaite olisi miten
MAT Todennäköisyyslaskenta Tentti / Kimmo Vattulainen
 MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
MAT-25 Todennäköisyyslaskenta Tentti 12.4.216 / Kimmo Vattulainen Funktiolaskin sallittu. Palauta kaavakokoelma 1. a) Pelaajat A ja B heittävät noppaa vuorotellen ja pelin voittaa se, joka saa ensimmäiseksi
