Aikasarjamallit. Pekka Hjelt
|
|
|
- Markku Hänninen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Pekka Hjelt Aikasarjamallit Aikasarja koostuu järjestyksessä olevista havainnoista, ja yleensä se on tasavälinen ja diskreetti eli havaintopisteet ovat erillisiä. Lisäksi aikasarjassa on yleensä autokorrelaatiota eli havaintojen keskinäistä riippuvuutta, minkä vuoksi otoksiin tarkoitetut tilastolliset menetelmät eivät sovellu aikasarjojen käsittelyyn. G.E.P. Box ja G.M. Jenkins julkaisivat 1970 kirjan ARIMA-malleista, ja se aloitti uuden aikakauden aikasarja-analyysissa. Heidän esittämänsä mallit oli tunnettu jo vuosikymmeniä, mutta vasta nyt saatiin systemaattinen kokonaisesitys siitä, miten nämä mallit tunnistetaan, estimoidaan niitten tuntemattomat parametrit, testataan mallin kelvollisuus ja laaditaan ennusteita. Tietokoneiden tuo yleiseen käyttöön mahdollisti menetelmien soveltamisen käytäntöön. ARIMA-malleissa lähdetään siitä, että havaitun aikasarjan on synnyttänyt jokin stokastinen eli satunnaisprosessi. Näitä prosesseja on kolmea tyyppiä: autoregressiiviset (AR), liukuvakeskiarvo- (MA) ja yhdistetyt autoregressiiviset liukuvakeskiarvoprosessit (ARMA). Ennalta ei tiedetä, mistä prosessista on kyse, mutta kun jokaisella tyypillä on oma autokorrelaatiorakenteensa, aikasarjan havaitut autokorrelaatiot antavat lähtökohdan mallin tunnistamiseen. Kun malliin sisältyvät parametrit on estimoitu, pystytään tilastotieteen teorian keinon päättelemään, kelpaako valittu malli. Jos se ei kelpaa, kokeillaan uutta mallia niiden tietojen pohjalta, jotka saadaan ensimmäisen mallin tuloksista. Näin jatketaan, kunnes löydetään sopiva malli. Mahdollisia malleja ei käytännössä ole kovin runsaasti, koska ehdottomana periaatteena on, että valitaan niukkaparametrinen, riittävä malli. Ei siis tavoitella kuten eräillä aloilla täydellistä mallia. Tähän on ainakin kolme pääsyytä: 1) tieteessä yleisen taloudellisuuden ja varovaisuuden periaatetta noudattaen tyydytään mieluummin yksinkertaiseen kuin monimutkaiseen selitykseen; 2) koska parametrien estimointi on varsin vaativa matemaattinen tehtävä, se onnistuu parhaiten, kun estimoitavia parametreja ei ole kovin monta; 3) tulevaisuuden ennustaminen tapahtuu parhaiten yksinkertaisella mallilla.
2 ARIMA-malleja voi käyttää vain stationaarisiin aikasarjoihin. Stationaarisuutta voidaan kuvata siten, että aikasarjan keskiarvo ja varianssi ovat likimain samat aikavälin jokaisessa kohdassa. Koska etenkin taloudelliset aikasarjat ovat yleensä epästationaarisia trendin vuoksi, ne on ennen mallin sovittamista stationarisoitava. Keskiarvon osalta se tapahtuu käyttämällä havaintojen differenssejä eli erotuksia ja varianssin stationarisointi tapahtuu yleensä logaritmimuunnoksen avulla. ARIMA(p,d,q) tarkoittaa mallia, jossa on p kappaletta autoregressiiviparametreja, q liukuvakeskiarvoparametria ja d ilmoittaa differenssiasteen. Yleensä nämä luvut ovat pieniä, 0 ja 1 ovat tavallisia, d=2 harvinainen ja 3:ea suurempi p:n tai q:n arvo ei esiinny kovinkaan usein. Lisäksi mukana voi olla ns. vakiotermi, jonka olemassaolo liittyy trendiin. Monia ilmiöitä havainnoidaan useammin kuin kerran vuodessa, jolloin aikasarjassa ilmenee kausivaihtelua. Se voidaan mallintaa samalla tavalla kuin ns. perusvaihtelukin, ja ne yhdistetään yleiseksi kerrannaiseksi kausivaihtelumalliksi ARIMA(p,d,q) (P,D,Q) s. s tarkoittaa kausivaihtelujakson pituutta (kuukausisarjassa 12, neljännesvuosisarjassa 4). Täydellinen malli voidaan kirjoittaa: (1-B) d (1-B s ) D Y t = C+[(1-θ1B- -θqb q )(1-Θ1B- -ΘQ Qs )] / [(1-1B- - p B p )(1-Φ1B- -ΦP Ps )]at. Siinä (1-B) d tarkoittaa d:ttä differenssiä, (1-B s ) D D:ttä kausidifferenssiä; d ja D ovat yleensä 0 tai 1. Vastaavasti B:t ovat viiveoperaattoreja eli BY t = Y t-1, B p Y t = Y t-p. Olennaisia päättelyn kannalta ovat ns. vakio C, liukuvakeskiarvoparametrit θ 1,,θ q, Θ 1,,Θ Q, autoregressiiviset parametrit 1,, p, ϕ1,,ϕp sekä jäännöshajonta σ a. Versaalit tarkoittavat aina kausivaihteluosaa, gemenat ns. perusosaa. Kun ARIMA-malli esitetään edelliseen tapaan osamäärämuotoisena eli molemmat puolet jaetaan autoregressiiviset termit sisältävällä hakasulkulausekkeella, C ilmoittaa suoraan aikasarjan trendin. Ellei sen estimaatti ole tilastollisesti merkitsevä ja d = 0 ja D = 0, C:n arvo on likimain sama luin sarjan keskiarvo, jonka ympärillä heilahtelu tapahtuu. Jos d =1 ja D = 0, C antaa keskimääräisen muutoksen kuukaudesta tai vuosineljänneksestä toiseen, ja jos d = 0 ja D = 1, C ilmoittaa keskimääräisen vuosimuutoksen. Muut tapaukset ovatkin harvinaisempia. Ilmastoaikasarjat ovat joko jo alun alkaen stationaarisia eli differenssit nollia tai tarvitaan kausidifferenssiä ( D = 1), ja jos siinä tilanteessa C poikkeaa merkitsevästi nollasta, sarjalla on jokin suunta.
3 Mallin valinta on iteratiivinen prosessi. Ensimmäisessä vaiheessa tutkitaan aikasarjan autokorrelaatiorakennetta, sillä jokaisella kyseeseen tulevalla stokastisella prosessilla on tyypillinen autokorrelaatiorakenteensa. Koska kyse on empiirisistä havainnoista, sen havaitseminen ei ole aina helppoa, mutta jokin alustava malli voidaan aina löytää. Vanhemmista menetelmistä poiketen valinta ei ole siis mielivaltainen, vaan sarjan oma historia on aina lähtökohtana. Parametrien estimoinnin jälkeen nähdään, täyttääkö malli vaaditut ehdot, ja ellei täytä, muutetaan mallia ensimmäisten tulosten viitoittamaan suuntaan. Monissa nykyisissä tietokoneohjelmissa mallin tunnistaminen ja alustava estimointi on pitkälle automatisoitu, mutta tulos ei ole välttämättä hyväksyttävä. Valinnassa käytetään useita tilastotieteen teoriaan pohjautuvia kriteerejä: AR-kerrointen on täytettävä stationaarisuusehdot, MA-kerrointen käännettävyysehdot; kerrointen väliset korrelaatiot eivät saa olla liian suuria; usein käytetään vaatimusta, että niiden itseisarvo on alle puolen; kerrointen on oltava tilastollisesti merkitseviä; todennäköisyystasona käytetään 0,95:tä tai tätä korkeampaa arvoa, jos aikasarja on pitkä; jäännössarjan on oltava riittävästi satunnainen eli siinä ei saa esiintyä merkitseviä autokorrelaatioita ainakaan tärkeillä viiveillä (1 ja 2; s ja 2s), mutta muuten huomiota ei kiinnitetä niinkään yksittäisiin kertoimiin, vaan koko rakenteeseen; jäännössarjan keskiarvo ei saa poikkea merkitsevästi nollasta: näiden lisäksi voidaan kiinnittää huomiota myös jäännössarjan normaalisuuteen ja sen etumerkkien satunnaisuuteen ym., mutta usein tällaiset tarkastelut sivuutetaan. Parametrien estimointi on vaativa matemaattinen minimointitehtävä, joka edellyttää tietokoneen käyttöä. Käytössä on jossain määrin toisistaan poikkeavia menetelmiä, jotka voivat johtaa hiukan erilaisiin tuloksiin. Sen lisäksi kerrointen etumerkit voivat olla vastakkaiset menetelmästä riippuen, mutta analyysin tärkeimmässä tehtävässä eli ennustamisessa ne tietenkin toimivat oikein.
4 SUOMEN KESKILÄMPÖ Vuosisarja Riittävä malli on yksinkertainen ARIMA(0,1,1) eli IMA(1,1). Stationarisointi edellyttää siis ensimmäistä differenssiä. Estimaatit ovat: θ 1 = 0,91, jonka keskivirhe on 0,33 eli se on sekä tilastollisesti merkitsevä että täyttää käännettävyysehdon (estimaatti + 2 kertaa keskivirhe on pienempi kuin 1). Jäännössarjan keskiarvo ei poikkea merkitsevästi nollasta (t = 1,44), jäännöshajonta σ a = 1,10 eikä malliin sisälly vakiotermiä C. Tämä tarkoittaa, ettei sarjalla ole trendiä, vaan kaikki ennusteet vuodesta 2011 alkaen ovat 2,49 astetta. Kun jäännössarjassa ei ole myöskään merkitsevää autokorrelaatiota, tämä malli osoittautuu riittäväksi. Vuosisarja Malliksi saadaan ARIMA(1,0,0) eli AR(1). Differenssiä ei ole. Estimointitulokset: 1 = 0,29, keskivirhe 0,095 eli estimaatti on merkitsevä ja täyttää stationaarisuusehdon, joka on ihan samanlainen kuin MA-kertoimen kohdalla edellä. C = 1,84, jonka ympärillä sarja siis vaihtelee ja joka on myös ennuste tulevaisuuteen. Jäännöshajonta σ a = 1,03 astetta, jäännöskeskiarvo ei merkitsevä (t = 0,51). Kaikki jäännösautokorrelaatiokertoimet ovat pieniä. Siis: Suomen keskilämpö ei osoita viimeisen sadan vuoden ajalta kehitystä mihinkään suuntaan. Tulos on oleellisesti sama, vaikka jätän pois kylmät vuodet 2009 ja Vuodenaikasarja Tämän 656 havainnon aikasarjan malliksi tulee ARIMA(1,0,0) (0,1,1) 4, siis kausidifferenssi mukana ja kaksi kerrointa. 1 = 0,22, Θ 1 = 0,95. Molemmat ovat tilastollisesti merkitseviä ja täyttävät stationaarisuus- ja käännettävyysehdon. Tähänkään malliin ei tule vakiotermiä, mutta jäännöskeskiarvo on aika lähellä merkitsevyysrajaa (t = 1,91). Jäännöshajonta σ a = 1,82 on tietenkin suurempi kuin vuosisarjojen kohdalla, koska lämpötilan vaihtelu vuodenaikojen kesken on paljon laajempaa. Autokorrelaatiokertoimet täyttävät satunnaisuusvaatimuksen, joskin viiveen 3 kerroin ylittää merkitsevyysrajan, vaikka sen arvo onkin vain 0,085. Pitkissä aikasarjoissa ilmenee helposti merkitsevyyksiä, vaikka absoluuttiset luvut ovatkin pieniä.
5 Vuodenaikaennusteet tulevaisuudessa ovat talvi -8,5 kevät 1,0 kesä 14,0 syksy 2,6 astetta. Talvi sisältää edellisen vuoden joulukuun ja tilastovuoden tammi- ja helmikuun, kevät maalis-, huhti- ja toukokuun, kesä kesä-, heinä- ja elokuun sekä syksy syys-, loka- ja marraskuun. Jos malliin pakotetaan vakio C, sen arvoksi tulee 0,012 eli hiukan enemmän kuin asteen sadasosa, ja se on tilastollisesti merkitsevä. Kertoimet pysyvät liki samoina, mutta kausivaihtelun MA-kerroin kohoaa hyvin lähelle käännettävyysehdon rajaa. Jäännöshajonta on 1,81 ja jäännössarja liki samanlainen kuin edellä, ja ennusteet osoittavat hidasta suuntaa lämpimämpään. Vuodet Malli ARIMA(1,0,0) (1,1,1) 4, kertoimet 1 = 0,18, ϕ1 = 0,14, Θ 1 = 0,98, jotka täyttävät muut ehdot, mutta kausivaihtelun MA-kerroin ylittää käännettävyysrajan. Vakiokerroin ei ole merkitsevä eikä jäännöskeskiarvo (t = 1,52) myöskään, ja autokorrelaatiokertoimet riittävän pienet. Jäännöshajonta on 1,77. Tämä on paras vähäparametrinen, jonka vikana on tuo MAkerroin. Sen korkea arvo kaikissa Suomen ilmastomalleissa johtuu sään voimakkaasta kausiriippuvuudesta. Vuodenaikaennusteet ovat kauttaaltaan 2-4 kymmenesosa-astetta alemmat kuin koko jakson mallissa. RUOTSIN KESKILÄMPÖ ARIMA(0,1,1); θ 1 = 0,94, täyttää ehdot. Vakio C = 0,011 ja juuri ja juuri merkitsevä (t = 2.08). Jäännöshajonta 0,93 astetta, jäännöskeskiarvo ei ole merkitsevä (t = -0,87), jäännösautokorrelaatiot riittävän pienet. Ennuste vuodeksi 2011 on 3,82 astetta ja se kasvaa jokseenkin yhden sadasosa-asteen vuodessa, joten mitään äkillistä ja valtavaa ilmastonmuutosta ei ole näkyvissä.
6 Vuodet ARIMA(1,0,0), 1 = 0,32, täyttää ehdot. C = 3,2, ja koska ei ole differenssejä, se ilmoittaa keskiarvotason ja samalla vakioennusteen. Jäännöshajonta on 0,93 astetta, jäännössarjan keskiarvo ei poikkea nollasta (t = 1,03), jäännösautokorrelaatiokertoimet ovat pieniä. NORJAN KESKILÄMPÖ ARIMA(0,1,1), θ 1 = 0,87, täyttää ehdot. Vakio ei ole merkitsevä (t = 1,17), jäännöskeskiarvo ei myöskään (t = 0,88). Jäännöshajonta on 0,77 astetta ja jäännösautokorrelaatiot matalia. Ennuste on koko ajan 4,8 astetta. Vuodet ARIMA(1,0,0), 1 = 0,36, täyttää ehdot. C = 4,1, ja koska ei ole differenssejä, se ilmoittaa keskiarvotason ja samalla vakioennusteen. Jäännöshajonta on 0,77 astetta, jäännössarjan keskiarvo ei poikkea nollasta (t = 1,40), jäännösautokorrelaatiokertoimet ovat riittävän matalia. TANSKAN KESKILÄMPÖ ARIMA(0,1,1), θ 1 = 0,82, täyttää ehdot. Vakio ei ole merkitsevä (t = 1,05), jäännöskeskiarvo ei myöskään (t = 0,74). Jäännöshajonta on 0,72 astetta ja jäännösautokorrelaatiot matalia. Ennuste on koko ajan 8,6 astetta.
7 Vuodet ARIMA(1,0,0), 1 = 0,36, täyttää ehdot. C = 7,9, ja koska ei ole differenssejä, se ilmoittaa keskiarvotason ja samalla vakioennusteen. Jäännöshajonta on 0,77 astetta, jäännössarjan keskiarvo ei poikkea nollasta (t = 1,48), jäännösautokorrelaatiokertoimet ovat riittävän matalia. Tulokset Missään pohjoismaassa ei keskilämpö ole muuttunut tilastollisesti merkitsevästi ainakaan viimeisen sadan vuoden aikana, vaan vaihdellut keskiarvonsa ympärillä, ja siksi myöskään ennusteet tulevaisuuteen eivät sisällä Ilmatieteen laitoksen uhkailemaa monen asteen nousua vuoteen 2100 mennessä. Kaikkien maiden sarjojen kuvaajissa näkyy sama muoto ja selvää noin 65 vuoden sykli luvun alkukymmenen lämpimät vuodet eivät olleet mitään poikkeuksia, vaan vastaavaa on koettu jo 1930-luvulla (kuvassa numeroiden 58 ja 67 välillä suunnilleen) Suomi Ruotsi Norja Tanska Lähteenä olevat aikasarjat ovat kyseisten maiden ilmatieteen laitosten julkaisemia. Analyysiohjelmana on ollut Espanjan keskuspankin tekemä Tramo/Seats, jota Eurostat suosittelee EU:n jäsenvaltioille ja joka onkin käytössä keskuspankeissa, valtiovarain- ja muissa ministeriöissä, tilastovirastoissa, tutkimuslaitoksissa ym. kautta maailman.
8
Dynaamiset regressiomallit
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Tilastolliset aikasarjat voidaan jakaa kahteen
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Tilastolliset aikasarjat voidaan jakaa kahteen
Harjoitukset 4 : Paneelidata (Palautus )
 31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitukset 4 : Paneelidata (Palautus 7.3.2017) Tämän harjoituskerran tarkoitus on perehtyä
31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitukset 4 : Paneelidata (Palautus 7.3.2017) Tämän harjoituskerran tarkoitus on perehtyä
4. Tietokoneharjoitukset
 4. Tietokoneharjoitukset Demotehtävät 4.1 Tarkastellaan seuraavia aikasarjoja. Tiedosto (.txt) Muuttuja Kuvaus Havaintoväli Aikasarjan pituus INTEL Intel_Close Intelin osakekurssi Pörssipäivä n = 20 Intel_Volume
4. Tietokoneharjoitukset Demotehtävät 4.1 Tarkastellaan seuraavia aikasarjoja. Tiedosto (.txt) Muuttuja Kuvaus Havaintoväli Aikasarjan pituus INTEL Intel_Close Intelin osakekurssi Pörssipäivä n = 20 Intel_Volume
4. Tietokoneharjoitukset
 4. Tietokoneharjoitukset Demotehtävät 4.1 Tarkastellaan seuraavia aikasarjoja. Tiedosto (.txt) Muuttuja Kuvaus Havaintoväli Aikasarjan pituus INTEL Intel_Close Intelin osakekurssi Pörssipäivä n = 20 Intel_Volume
4. Tietokoneharjoitukset Demotehtävät 4.1 Tarkastellaan seuraavia aikasarjoja. Tiedosto (.txt) Muuttuja Kuvaus Havaintoväli Aikasarjan pituus INTEL Intel_Close Intelin osakekurssi Pörssipäivä n = 20 Intel_Volume
Viikon 5 harjoituksissa käytämme samoja aikasarjoja kuin viikolla 4. Tiedosto Muuttuja Kuvaus Havaintoväli Aikasarjan pituus
 MS-C2128 Ennustaminen ja aikasarja-analyysi 5. harjoitukset / Tehtävät Kotitehtävät: 2 Aihe: ARMA-mallit Viikon 5 harjoituksissa käytämme samoja aikasarjoja kuin viikolla 4. Tehtävä 5.1. Tarkastellaan
MS-C2128 Ennustaminen ja aikasarja-analyysi 5. harjoitukset / Tehtävät Kotitehtävät: 2 Aihe: ARMA-mallit Viikon 5 harjoituksissa käytämme samoja aikasarjoja kuin viikolla 4. Tehtävä 5.1. Tarkastellaan
Harjoitus 7 : Aikasarja-analyysi (Palautus )
 31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitus 7 : Aikasarja-analyysi (Palautus 28.3.2017) Tämän harjoituskerran tarkoitus on perehtyä
31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitus 7 : Aikasarja-analyysi (Palautus 28.3.2017) Tämän harjoituskerran tarkoitus on perehtyä
STOKASTISET PROSESSIT
 TEORIA STOKASTISET PROSESSIT Satunnaisuutta sisältävän tapahtumasarjan kulkua koskevaa havaintosarjaa sanotaan aikasarjaksi. Sana korostaa empiirisen, kokeellisesti havaitun tiedon luonnetta. Aikasarjan
TEORIA STOKASTISET PROSESSIT Satunnaisuutta sisältävän tapahtumasarjan kulkua koskevaa havaintosarjaa sanotaan aikasarjaksi. Sana korostaa empiirisen, kokeellisesti havaitun tiedon luonnetta. Aikasarjan
Tiedosto Muuttuja Kuvaus Havaintoväli Aikasarjan pituus. Intelin osakekurssi. (Pörssi-) päivä n = 20 Intel_Volume. Auringonpilkkujen määrä
 MS-C2128 Ennustaminen ja aikasarja-analyysi 4. harjoitukset / Tehtävät Kotitehtävät: 3, 5 Aihe: ARMA-mallit Tehtävä 4.1. Tutustu seuraaviin aikasarjoihin: Tiedosto Muuttuja Kuvaus Havaintoväli Aikasarjan
MS-C2128 Ennustaminen ja aikasarja-analyysi 4. harjoitukset / Tehtävät Kotitehtävät: 3, 5 Aihe: ARMA-mallit Tehtävä 4.1. Tutustu seuraaviin aikasarjoihin: Tiedosto Muuttuja Kuvaus Havaintoväli Aikasarjan
Johtuuko tämä ilmastonmuutoksesta? - kasvihuoneilmiön voimistuminen vaikutus sääolojen vaihteluun
 Johtuuko tämä ilmastonmuutoksesta? - kasvihuoneilmiön voimistuminen vaikutus sääolojen vaihteluun Jouni Räisänen Helsingin yliopiston fysiikan laitos 15.1.2010 Vuorokauden keskilämpötila Talvi 2007-2008
Johtuuko tämä ilmastonmuutoksesta? - kasvihuoneilmiön voimistuminen vaikutus sääolojen vaihteluun Jouni Räisänen Helsingin yliopiston fysiikan laitos 15.1.2010 Vuorokauden keskilämpötila Talvi 2007-2008
Regressioanalyysi. Vilkkumaa / Kuusinen 1
 Regressioanalyysi Vilkkumaa / Kuusinen 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Halutaan selittää selitettävän muuttujan havaittujen arvojen vaihtelua selittävien muuttujien havaittujen
Regressioanalyysi Vilkkumaa / Kuusinen 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Halutaan selittää selitettävän muuttujan havaittujen arvojen vaihtelua selittävien muuttujien havaittujen
MTTTP5, luento Otossuureita ja niiden jakaumia (jatkuu)
 21.11.2017/1 MTTTP5, luento 21.11.2017 Otossuureita ja niiden jakaumia (jatkuu) 4) Olkoot X 1, X 2,..., X n satunnaisotos (, ):sta ja Y 1, Y 2,..., Y m satunnaisotos (, ):sta sekä otokset riippumattomia.
21.11.2017/1 MTTTP5, luento 21.11.2017 Otossuureita ja niiden jakaumia (jatkuu) 4) Olkoot X 1, X 2,..., X n satunnaisotos (, ):sta ja Y 1, Y 2,..., Y m satunnaisotos (, ):sta sekä otokset riippumattomia.
Työ 2: 1) Sähkönkulutuksen ennustaminen SARIMAX-mallin avulla 2) Sähkön hankinnan optimointi
 Ma-2.3132 Syseemianalyysilaboraorio I Työ 2: 1) Sähkönkuluuksen ennusaminen SARIMAX-mallin avulla 2) Sähkön hankinnan opimoini 1 yö 2 Aikasarjamalli erään yriyksen sähkönkuluukselle SARIMAX-malli: kausivaihelu,
Ma-2.3132 Syseemianalyysilaboraorio I Työ 2: 1) Sähkönkuluuksen ennusaminen SARIMAX-mallin avulla 2) Sähkön hankinnan opimoini 1 yö 2 Aikasarjamalli erään yriyksen sähkönkuluukselle SARIMAX-malli: kausivaihelu,
Estimointi. Estimointi. Estimointi: Mitä opimme? 2/4. Estimointi: Mitä opimme? 1/4. Estimointi: Mitä opimme? 3/4. Estimointi: Mitä opimme?
 TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
Regressioanalyysi. Kuusinen/Heliövaara 1
 Regressioanalyysi Kuusinen/Heliövaara 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun joidenkin
Regressioanalyysi Kuusinen/Heliövaara 1 Regressioanalyysin idea ja tavoitteet Regressioanalyysin idea: Oletetaan, että haluamme selittää jonkin selitettävän muuttujan havaittujen arvojen vaihtelun joidenkin
MS-C2128 Ennustaminen ja aikasarja-analyysi ARMA esimerkkejä
 MS-C2128 Ennustaminen ja aikasarja-analyysi ARMA esimerkkejä Tehtävä 4.1. Ncss-ohjelmiston avulla on generoitu AR(1)-, AR(2)-, MA(1)- ja MA(2)-malleja vastaavia aikasarjoja erilaisilla parametrien arvoilla.
MS-C2128 Ennustaminen ja aikasarja-analyysi ARMA esimerkkejä Tehtävä 4.1. Ncss-ohjelmiston avulla on generoitu AR(1)-, AR(2)-, MA(1)- ja MA(2)-malleja vastaavia aikasarjoja erilaisilla parametrien arvoilla.
805324A (805679S) Aikasarja-analyysi Harjoitus 4 (2016)
 805324A (805679S) Aikasarja-analyysi Harjoitus 4 (2016) Tavoitteet (teoria): Hallita autokovarianssifunktion ominaisuuksien tarkastelu. Osata laskea autokovarianssifunktion spektriiheysfunktio. Tavoitteet
805324A (805679S) Aikasarja-analyysi Harjoitus 4 (2016) Tavoitteet (teoria): Hallita autokovarianssifunktion ominaisuuksien tarkastelu. Osata laskea autokovarianssifunktion spektriiheysfunktio. Tavoitteet
Johdatus tilastotieteeseen Estimointi. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
8. Muita stokastisia malleja 8.1 Epölineaariset mallit ARCH ja GARCH
 8. Muita stokastisia malleja 8.1 Epölineaariset mallit ARCH ja GARCH Osa aikasarjoista kehittyy hyvin erityyppisesti erilaisissa tilanteissa. Esimerkiksi pörssikurssien epävakaus keskittyy usein lyhyisiin
8. Muita stokastisia malleja 8.1 Epölineaariset mallit ARCH ja GARCH Osa aikasarjoista kehittyy hyvin erityyppisesti erilaisissa tilanteissa. Esimerkiksi pörssikurssien epävakaus keskittyy usein lyhyisiin
Otoskeskiarvo on otossuure, jonka todennäköisyysjakauma tiedetään. Se on normaalijakauma, havainnollistaminen simuloiden
 1 KERTAUSTA JA TÄYDENNYSTÄ Luento 30.9.2014 Olkoon satunnaisotos X 1, X 2,, X n normaalijakaumasta N(µ, σ 2 ), tällöin ~ N(µ, σ 2 /n), kaava (6). Otoskeskiarvo on otossuure, jonka todennäköisyysjakauma
1 KERTAUSTA JA TÄYDENNYSTÄ Luento 30.9.2014 Olkoon satunnaisotos X 1, X 2,, X n normaalijakaumasta N(µ, σ 2 ), tällöin ~ N(µ, σ 2 /n), kaava (6). Otoskeskiarvo on otossuure, jonka todennäköisyysjakauma
1. Tilastollinen malli??
 1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
Pakkaset ja helteet muuttuvassa ilmastossa lämpötilan muutokset ja vaihtelu eri aikaskaaloissa
 Pakkaset ja helteet muuttuvassa ilmastossa lämpötilan muutokset ja vaihtelu eri aikaskaaloissa Jouni Räisänen Helsingin yliopiston fysiikan laitos Kimmo Ruosteenoja Ilmatieteen laitos Sisältöä ACCLIM-skenaariot
Pakkaset ja helteet muuttuvassa ilmastossa lämpötilan muutokset ja vaihtelu eri aikaskaaloissa Jouni Räisänen Helsingin yliopiston fysiikan laitos Kimmo Ruosteenoja Ilmatieteen laitos Sisältöä ACCLIM-skenaariot
3. Tietokoneharjoitukset
 3. Tietokoneharjoitukset Aikasarjan logaritmointi Aikasarjoja analysoidaan usein logaritmisessa muodossa. Asialooginen perustelu logaritmoinnille: Muuttujan arvojen suhteelliset muutokset ovat usein tärkeämpiä
3. Tietokoneharjoitukset Aikasarjan logaritmointi Aikasarjoja analysoidaan usein logaritmisessa muodossa. Asialooginen perustelu logaritmoinnille: Muuttujan arvojen suhteelliset muutokset ovat usein tärkeämpiä
805324A (805679S) Aikasarja-analyysi Harjoitus 6 (2016)
 805324A (805679S) Aikasarja-analyysi Harjoitus 6 (2016) Tavoitteet (teoria): Hahmottaa aikasarjan klassiset komponentit ideaalisessa tilanteessa. Ymmärtää viivekuvauksen vaikutus trendiin. ARCH-prosessin
805324A (805679S) Aikasarja-analyysi Harjoitus 6 (2016) Tavoitteet (teoria): Hahmottaa aikasarjan klassiset komponentit ideaalisessa tilanteessa. Ymmärtää viivekuvauksen vaikutus trendiin. ARCH-prosessin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 16. marraskuuta 2007 Antti Rasila () TodB 16. marraskuuta 2007 1 / 15 1 Epäparametrisia testejä χ 2 -yhteensopivuustesti Homogeenisuuden testaaminen Antti
Sovellettu todennäköisyyslaskenta B Antti Rasila 16. marraskuuta 2007 Antti Rasila () TodB 16. marraskuuta 2007 1 / 15 1 Epäparametrisia testejä χ 2 -yhteensopivuustesti Homogeenisuuden testaaminen Antti
7.4 Normaalijakauma (kertausta ja täydennystä) Taulukosta P(Z 1,6449) = 0,05, P(Z -1,6449) = 0,05 P(Z 1,96) = 0,025, P(Z -1,96) = 0,025
 26.3.2019/1 MTTTP1, luento 26.3.2019 7.4 Normaalijakauma (kertausta ja täydennystä) Z ~ N(0, 1), tiheysfunktion kuvaaja 0,5 0,4 0,3 0,2 0,1 Taulukosta P(Z 1,6449) = 0,05, P(Z -1,6449) = 0,05 P(Z 1,96)
26.3.2019/1 MTTTP1, luento 26.3.2019 7.4 Normaalijakauma (kertausta ja täydennystä) Z ~ N(0, 1), tiheysfunktion kuvaaja 0,5 0,4 0,3 0,2 0,1 Taulukosta P(Z 1,6449) = 0,05, P(Z -1,6449) = 0,05 P(Z 1,96)
1 Aritmeettiset ja geometriset jonot
 1 Aritmeettiset ja geometriset jonot Johdatus Johdatteleva esimerkki 1 Kasvutulille talletetaan vuoden jokaisen kuukauden alussa tammikuusta alkaen 100 euroa. Tilin nettokorkokanta on 6%. Korko lisätään
1 Aritmeettiset ja geometriset jonot Johdatus Johdatteleva esimerkki 1 Kasvutulille talletetaan vuoden jokaisen kuukauden alussa tammikuusta alkaen 100 euroa. Tilin nettokorkokanta on 6%. Korko lisätään
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
Ilkka Mellin Aikasarja-analyysi Aikasarjat
 Ilkka Mellin Aikasarja-analyysi Aikasarjat TKK (c) Ilkka Mellin (2007) 1 Aikasarjat >> Aikasarjat: Johdanto Aikasarjojen esikäsittely Aikasarjojen dekomponointi TKK (c) Ilkka Mellin (2007) 2 Aikasarjat:
Ilkka Mellin Aikasarja-analyysi Aikasarjat TKK (c) Ilkka Mellin (2007) 1 Aikasarjat >> Aikasarjat: Johdanto Aikasarjojen esikäsittely Aikasarjojen dekomponointi TKK (c) Ilkka Mellin (2007) 2 Aikasarjat:
Identifiointiprosessi
 Alustavia kokeita Identifiointiprosessi Koesuunnittelu, identifiointikoe Mittaustulosten / datan esikäsittely Ei-parametriset menetelmät: - Transientti-, korrelaatio-, taajuus-, Fourier- ja spektraalianalyysi
Alustavia kokeita Identifiointiprosessi Koesuunnittelu, identifiointikoe Mittaustulosten / datan esikäsittely Ei-parametriset menetelmät: - Transientti-, korrelaatio-, taajuus-, Fourier- ja spektraalianalyysi
Testejä suhdeasteikollisille muuttujille
 Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testejä suhdeasteikollisille muuttujille TKK (c) Ilkka Mellin (007) 1 Testejä suhdeasteikollisille muuttujille >> Testit normaalijakauman
Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testejä suhdeasteikollisille muuttujille TKK (c) Ilkka Mellin (007) 1 Testejä suhdeasteikollisille muuttujille >> Testit normaalijakauman
Monitasomallit koulututkimuksessa
 Metodifestivaali 9.5.009 Monitasomallit koulututkimuksessa Mitä ihmettä? Antero Malin Koulutuksen tutkimuslaitos Jyväskylän yliopisto 009 1 Tilastollisten analyysien lähtökohta: Perusjoukolla on luonnollinen
Metodifestivaali 9.5.009 Monitasomallit koulututkimuksessa Mitä ihmettä? Antero Malin Koulutuksen tutkimuslaitos Jyväskylän yliopisto 009 1 Tilastollisten analyysien lähtökohta: Perusjoukolla on luonnollinen
ARMA mallien ominaisuudet ja rakentaminen
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Viikko 4: 1 ARMA-mallien ominaisuudet 1 Stationaaristen
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Viikko 4: 1 ARMA-mallien ominaisuudet 1 Stationaaristen
Ilkka Mellin Aikasarja-analyysi ARMA-mallit
 Ilkka Mellin Aikasarja-analyysi ARMA-mallit TKK (c) Ilkka Mellin (007) 1 ARMA-mallit >> ARMA-mallit ja niiden ominaisuudet ARMA-mallien auto- ja osittaisautokorrelaatiofunktiot ARMA-mallien spektri ARMA-mallien
Ilkka Mellin Aikasarja-analyysi ARMA-mallit TKK (c) Ilkka Mellin (007) 1 ARMA-mallit >> ARMA-mallit ja niiden ominaisuudet ARMA-mallien auto- ja osittaisautokorrelaatiofunktiot ARMA-mallien spektri ARMA-mallien
/1. MTTTP1, luento Normaalijakauma (jatkoa) Olkoon Z ~ N(0, 1). Määritellään z siten, että P(Z > z ) =, graafisesti:
 4.10.2016/1 MTTTP1, luento 4.10.2016 7.4 Normaalijakauma (jatkoa) Olkoon Z ~ N(0, 1). Määritellään z siten, että P(Z > z ) =, graafisesti: Samoin z /2 siten, että P(Z > z /2 ) = /2, graafisesti: 4.10.2016/2
4.10.2016/1 MTTTP1, luento 4.10.2016 7.4 Normaalijakauma (jatkoa) Olkoon Z ~ N(0, 1). Määritellään z siten, että P(Z > z ) =, graafisesti: Samoin z /2 siten, että P(Z > z /2 ) = /2, graafisesti: 4.10.2016/2
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
Tilastollisen analyysin perusteet Luento 9: Moniulotteinen lineaarinen. regressio
 Tilastollisen analyysin perusteet Luento 9: lineaarinen lineaarinen Sisältö lineaarinen lineaarinen lineaarinen Lineaarinen Oletetaan, että meillä on n kappaletta (x 1, y 1 ), (x 2, y 2 )..., (x n, y n
Tilastollisen analyysin perusteet Luento 9: lineaarinen lineaarinen Sisältö lineaarinen lineaarinen lineaarinen Lineaarinen Oletetaan, että meillä on n kappaletta (x 1, y 1 ), (x 2, y 2 )..., (x n, y n
Estimointi populaation tuntemattoman parametrin arviointia otossuureen avulla Otossuure satunnaisotoksen avulla määritelty funktio
 17.11.2015/1 MTTTP5, luento 17.11.2015 Luku 5 Parametrien estimointi 5.1 Piste-estimointi Estimointi populaation tuntemattoman parametrin arviointia otossuureen avulla Otossuure satunnaisotoksen avulla
17.11.2015/1 MTTTP5, luento 17.11.2015 Luku 5 Parametrien estimointi 5.1 Piste-estimointi Estimointi populaation tuntemattoman parametrin arviointia otossuureen avulla Otossuure satunnaisotoksen avulla
Osa 2: Otokset, otosjakaumat ja estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
ARIMA- ja GARCH-mallit sekä mallin sovittaminen osakeaineistoon
 TAMPEREEN YLIOPISTO Pro gradu -tutkielma Laura Lizana Bister ARIMA- ja GARCH-mallit sekä mallin sovittaminen osakeaineistoon Informaatiotieteiden laitos Matematiikka Syyskuu 2011 Tampereen yliopisto Informaatiotieteiden
TAMPEREEN YLIOPISTO Pro gradu -tutkielma Laura Lizana Bister ARIMA- ja GARCH-mallit sekä mallin sovittaminen osakeaineistoon Informaatiotieteiden laitos Matematiikka Syyskuu 2011 Tampereen yliopisto Informaatiotieteiden
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 15 1 Tilastollisia testejä Z-testi Normaalijakauman odotusarvon testaus, keskihajonta tunnetaan
Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 15 1 Tilastollisia testejä Z-testi Normaalijakauman odotusarvon testaus, keskihajonta tunnetaan
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2015 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
MS-C2128 Ennustaminen ja Aikasarja-analyysi, 5 op Esittely Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2015 Aikataulu ja suoritustapa (Katso MyCourses) Luennot
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 30. lokakuuta 2007 Antti Rasila () TodB 30. lokakuuta 2007 1 / 23 1 Otos ja otosjakaumat (jatkoa) Frekvenssi ja suhteellinen frekvenssi Frekvenssien odotusarvo
Sovellettu todennäköisyyslaskenta B Antti Rasila 30. lokakuuta 2007 Antti Rasila () TodB 30. lokakuuta 2007 1 / 23 1 Otos ja otosjakaumat (jatkoa) Frekvenssi ja suhteellinen frekvenssi Frekvenssien odotusarvo
Kertaus. MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017 Viikko 1: Yleinen lineaarinen malli 1 Määritelmä
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017 Viikko 1: Yleinen lineaarinen malli 1 Määritelmä
Tilastotieteen kertaus. Kuusinen/Heliövaara 1
 Tilastotieteen kertaus Kuusinen/Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla reaalimaailman ilmiöistä voidaan tehdä johtopäätöksiä tilanteissa, joissa
Tilastotieteen kertaus Kuusinen/Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla reaalimaailman ilmiöistä voidaan tehdä johtopäätöksiä tilanteissa, joissa
Ennustaminen ARMA malleilla ja Kalmanin suodin
 Ennustaminen ARMA malleilla ja Kalmanin suodin MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017
Ennustaminen ARMA malleilla ja Kalmanin suodin MS-C2128 Ennustaminen ja Aikasarja-analyysi, Lauri Viitasaari Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2017
9. Tila-avaruusmallit
 9. Tila-avaruusmallit Aikasarjan stokastinen malli ja aikasarjasta tehdyt havainnot voidaan esittää joustavassa ja monipuolisessa muodossa ns. tila-avaruusmallina. Useat aikasarjat edustavat dynaamisia
9. Tila-avaruusmallit Aikasarjan stokastinen malli ja aikasarjasta tehdyt havainnot voidaan esittää joustavassa ja monipuolisessa muodossa ns. tila-avaruusmallina. Useat aikasarjat edustavat dynaamisia
tilastotieteen kertaus
 tilastotieteen kertaus Keskiviikon 24.1. harjoitukset pidetään poikkeuksellisesti klo 14-16 luokassa Y228. Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla
tilastotieteen kertaus Keskiviikon 24.1. harjoitukset pidetään poikkeuksellisesti klo 14-16 luokassa Y228. Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla
r = 0.221 n = 121 Tilastollista testausta varten määritetään aluksi hypoteesit.
 A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
Kertaus. MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä
 MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2015 Viikko 1: Yleinen lineaarinen malli 1 Määritelmä
MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2015 Viikko 1: Yleinen lineaarinen malli 1 Määritelmä
Aki Taanila AIKASARJAENNUSTAMINEN
 Aki Taanila AIKASARJAENNUSTAMINEN 26.4.2011 SISÄLLYS JOHDANTO... 1 1 AIKASARJA ILMAN SYSTEMAATTISTA VAIHTELUA... 2 1.1 Liukuvan keskiarvon menetelmä... 2 1.2 Eksponentiaalinen tasoitus... 3 2 AIKASARJASSA
Aki Taanila AIKASARJAENNUSTAMINEN 26.4.2011 SISÄLLYS JOHDANTO... 1 1 AIKASARJA ILMAN SYSTEMAATTISTA VAIHTELUA... 2 1.1 Liukuvan keskiarvon menetelmä... 2 1.2 Eksponentiaalinen tasoitus... 3 2 AIKASARJASSA
Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio
 Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio Sisältö Regressioanalyysissä tavoitteena on tutkia yhden tai useamman selittävän muuttujan vaikutusta selitettävään muuttujaan. Sen avulla
Tilastollisen analyysin perusteet Luento 7: Lineaarinen regressio Sisältö Regressioanalyysissä tavoitteena on tutkia yhden tai useamman selittävän muuttujan vaikutusta selitettävään muuttujaan. Sen avulla
Matematiikan tukikurssi
 Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Matematiikan tukikurssi Kurssikerta 4 Jatkuvuus Jatkuvan funktion määritelmä Tarkastellaan funktiota f x) jossakin tietyssä pisteessä x 0. Tämä funktio on tässä pisteessä joko jatkuva tai epäjatkuva. Jatkuvuuden
Tilastotieteessä aikasarja tarkoittaa yleensä sarjaa, jossa peräkkäisten havaintojen aikaväli on aina sama.
 Aikasarjat Tilastotieteessä aikasarja tarkoittaa yleensä sarjaa, jossa peräkkäisten havaintojen aikaväli on aina sama. Aikasarja on laajassa mielessä stationäärinen (wide sense stationary, WSS), jos odotusarvo
Aikasarjat Tilastotieteessä aikasarja tarkoittaa yleensä sarjaa, jossa peräkkäisten havaintojen aikaväli on aina sama. Aikasarja on laajassa mielessä stationäärinen (wide sense stationary, WSS), jos odotusarvo
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
ACCLIM II Ilmastonmuutosarviot ja asiantuntijapalvelu sopeutumistutkimuksia varten Kirsti Jylhä, Ilmatieteen laitos ISTO-loppuseminaari 26.1.
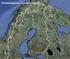 http://www.fmi.fi/acclim II Ilmastonmuutosarviot ja asiantuntijapalvelu sopeutumistutkimuksia varten Kirsti Jylhä, Ilmatieteen laitos ISTO-loppuseminaari 26.1.211 TEHTÄVÄ: tuottaa ilmaston vaihteluihin
http://www.fmi.fi/acclim II Ilmastonmuutosarviot ja asiantuntijapalvelu sopeutumistutkimuksia varten Kirsti Jylhä, Ilmatieteen laitos ISTO-loppuseminaari 26.1.211 TEHTÄVÄ: tuottaa ilmaston vaihteluihin
Tilastotieteen kertaus. Vilkkumaa / Kuusinen 1
 Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Tarkastusmuistio Poliisin toimintojen yhdistäminen ja liikennevalvonnan määrä
 Tarkastusmuistio Poliisin toimintojen yhdistäminen ja liikennevalvonnan määrä Liittyy tarkastukseen: 5/2019 Poliisin liikennevalvonta Tekijä: Ville Vehkasalo Päivämäärä: 24.9.2018 Diaarinumero: 248/54/2017
Tarkastusmuistio Poliisin toimintojen yhdistäminen ja liikennevalvonnan määrä Liittyy tarkastukseen: 5/2019 Poliisin liikennevalvonta Tekijä: Ville Vehkasalo Päivämäärä: 24.9.2018 Diaarinumero: 248/54/2017
5.3 Ensimmäisen asteen polynomifunktio
 Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
Yllä olevat polynomit P ( x) = 2 x + 1 ja Q ( x) = 2x 1 ovat esimerkkejä 1. asteen polynomifunktioista: muuttujan korkein potenssi on yksi. Yleisessä 1. asteen polynomifunktioissa on lisäksi vakiotermi;
Työvoiman tarpeen ennustaminen SARIMA-aikasarjamallilla
 Aalto-yliopisto Perustieteiden korkeakoulu Teknillisen fysiikan ja matematiikan tutkinto-ohjelma Työvoiman tarpeen ennustaminen SARIMA-aikasarjamallilla Kandidaatintyö 27.5.2015 Touko Väänänen Työn saa
Aalto-yliopisto Perustieteiden korkeakoulu Teknillisen fysiikan ja matematiikan tutkinto-ohjelma Työvoiman tarpeen ennustaminen SARIMA-aikasarjamallilla Kandidaatintyö 27.5.2015 Touko Väänänen Työn saa
Kysynnän ennustaminen muuttuvassa maailmassa
 make connections share ideas be inspired Kysynnän ennustaminen muuttuvassa maailmassa Nina Survo ja Antti Leskinen SAS Institute Mitä on kysynnän ennustaminen? Ennakoiva lähestymistapa, jolla pyritään
make connections share ideas be inspired Kysynnän ennustaminen muuttuvassa maailmassa Nina Survo ja Antti Leskinen SAS Institute Mitä on kysynnän ennustaminen? Ennakoiva lähestymistapa, jolla pyritään
Oletetaan, että virhetermit eivät korreloi toistensa eikä faktorin f kanssa. Toisin sanoen
 Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
Yhden faktorin malli: n kpl sijoituskohteita, joiden tuotot ovat r i, i =, 2,..., n. Olkoon f satunnaismuuttuja ja oletetaan, että tuotot voidaan selittää yhtälön r i = a i + b i f + e i avulla, missä
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
1. Tutkitaan tavallista kahden selittäjän regressiomallia
 TA7, Ekonometrian johdantokurssi HARJOITUS 5 RATKAISUEHDOTUKSET 232215 1 Tutkitaan tavallista kahden selittäjän regressiomallia Y i = β + β 1 X 1,i + β 2 X 2,i + u i (a) Kirjoita regressiomalli muodossa
TA7, Ekonometrian johdantokurssi HARJOITUS 5 RATKAISUEHDOTUKSET 232215 1 Tutkitaan tavallista kahden selittäjän regressiomallia Y i = β + β 1 X 1,i + β 2 X 2,i + u i (a) Kirjoita regressiomalli muodossa
pitkittäisaineistoissa
 Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi [email protected] Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Puuttuvan tiedon käsittelystä p. 1/18 Puuttuvan tiedon käsittelystä pitkittäisaineistoissa Tapio Nummi [email protected] Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto Puuttuvan tiedon
Ilkka Keskiväli Kiinan energiankäytön aikasarja-analysointi
 PRO GRADU -TUTKIELMA Ilkka Keskiväli Kiinan energiankäytön aikasarja-analysointi TAMPEREEN YLIOPISTO Informaatiotieteiden yksikkö Tilastotiede Joulukuu 2012 2 Tampereen yliopisto Informaatiotieteiden yksikkö
PRO GRADU -TUTKIELMA Ilkka Keskiväli Kiinan energiankäytön aikasarja-analysointi TAMPEREEN YLIOPISTO Informaatiotieteiden yksikkö Tilastotiede Joulukuu 2012 2 Tampereen yliopisto Informaatiotieteiden yksikkö
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 3B Tilastolliset datajoukot Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi 2016
Stationaariset stokastiset prosessit ja ARMA-mallit
 Stationaariset stokastiset prosessit ja ARMA-mallit MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy
Stationaariset stokastiset prosessit ja ARMA-mallit MS-C2128 Ennustaminen ja Aikasarja-analyysi, Heikki Seppälä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy
1. Tutkitaan regressiomallia Y i = β 0 + β 1 X i + u i ja oletetaan, että tavanomaiset
 TA7, Ekonometrian johdantokurssi HARJOITUS 7 RATKAISUEHDOTUKSET 16.3.2015 1. Tutkitaan regressiomallia Y i = β 0 + X i + u i ja oletetaan, että tavanomaiset regressiomallin oletukset pätevät (Key Concept
TA7, Ekonometrian johdantokurssi HARJOITUS 7 RATKAISUEHDOTUKSET 16.3.2015 1. Tutkitaan regressiomallia Y i = β 0 + X i + u i ja oletetaan, että tavanomaiset regressiomallin oletukset pätevät (Key Concept
Auringonpilkkujen jaksollisuus
 Mat-2.108 Sovelletun matematiikan erikoistyöt 16.1.2004 Auringonpilkkujen jaksollisuus Teknillinen korkeakoulu Systeemianalyysin laboratorio Keijo Jaakola 51624B 1 1. Johdanto...3 2. Aikasarjamalleja...3
Mat-2.108 Sovelletun matematiikan erikoistyöt 16.1.2004 Auringonpilkkujen jaksollisuus Teknillinen korkeakoulu Systeemianalyysin laboratorio Keijo Jaakola 51624B 1 1. Johdanto...3 2. Aikasarjamalleja...3
Mikä muuttuu, kun kasvihuoneilmiö voimistuu? Jouni Räisänen Helsingin yliopiston fysiikan laitos
 Mikä muuttuu, kun kasvihuoneilmiö voimistuu? Jouni Räisänen Helsingin yliopiston fysiikan laitos 15.4.2010 Sisältöä Kasvihuoneilmiö Kasvihuoneilmiön voimistuminen Näkyykö kasvihuoneilmiön voimistumisen
Mikä muuttuu, kun kasvihuoneilmiö voimistuu? Jouni Räisänen Helsingin yliopiston fysiikan laitos 15.4.2010 Sisältöä Kasvihuoneilmiö Kasvihuoneilmiön voimistuminen Näkyykö kasvihuoneilmiön voimistumisen
Odotusarvoparien vertailu. Vilkkumaa / Kuusinen 1
 Odotusarvoparien vertailu Vilkkumaa / Kuusinen 1 Motivointi Viime luennolta: yksisuuntaisella varianssianalyysilla testataan nollahypoteesia H 0 : μ 1 = μ 2 = = μ k = μ Jos H 0 hylätään, tiedetään, että
Odotusarvoparien vertailu Vilkkumaa / Kuusinen 1 Motivointi Viime luennolta: yksisuuntaisella varianssianalyysilla testataan nollahypoteesia H 0 : μ 1 = μ 2 = = μ k = μ Jos H 0 hylätään, tiedetään, että
Teollisuuden ja metalliteollisuuden uusien tilausten trendisarjat Indeksi (2010=100), viimeinen havainto 12/2013
 Teollisuuden ja metalliteollisuuden uusien tilausten trendisarjat Indeksi (21=1), viimeinen havainto 12/213 16 14 12 1 8 C Tehdasteollisuus 24-3 Metalliteollisuus 6 4 2 25 26 27 28 29 21 211 212 213 Suhdannetilanne:
Teollisuuden ja metalliteollisuuden uusien tilausten trendisarjat Indeksi (21=1), viimeinen havainto 12/213 16 14 12 1 8 C Tehdasteollisuus 24-3 Metalliteollisuus 6 4 2 25 26 27 28 29 21 211 212 213 Suhdannetilanne:
Männyn laaturajojen integrointi runkokäyrän ennustamisessa. Laura Koskela Tampereen yliopisto 9.6.2003
 Männyn laaturajojen integrointi runkokäyrän ennustamisessa Laura Koskela Tampereen yliopisto 9.6.2003 Johdantoa Pohjoismaisen käytännön mukaan rungot katkaistaan tukeiksi jo metsässä. Katkonnan ohjauksessa
Männyn laaturajojen integrointi runkokäyrän ennustamisessa Laura Koskela Tampereen yliopisto 9.6.2003 Johdantoa Pohjoismaisen käytännön mukaan rungot katkaistaan tukeiksi jo metsässä. Katkonnan ohjauksessa
pitkittäisaineistoissa
 Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi [email protected] Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi [email protected] Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Matemaatikot ja tilastotieteilijät
 Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Harjoitukset 2 : Monimuuttujaregressio (Palautus )
 31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitukset 2 : Monimuuttujaregressio (Palautus 24.1.2017) Tämän harjoituskerran tarkoitus
31C99904, Capstone: Ekonometria ja data-analyysi TA : markku.siikanen(a)aalto.fi & tuuli.vanhapelto(a)aalto.fi Harjoitukset 2 : Monimuuttujaregressio (Palautus 24.1.2017) Tämän harjoituskerran tarkoitus
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Kojemeteorologia. Sami Haapanala syksy 2013. Fysiikan laitos, Ilmakehätieteiden osasto
 Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Mittalaitteiden staattiset ominaisuudet Mittalaitteita kuvaavat tunnusluvut voidaan jakaa kahteen luokkaan Staattisiin
Kojemeteorologia Sami Haapanala syksy 2013 Fysiikan laitos, Ilmakehätieteiden osasto Mittalaitteiden staattiset ominaisuudet Mittalaitteita kuvaavat tunnusluvut voidaan jakaa kahteen luokkaan Staattisiin
Signaalien tilastollinen mallinnus T-61.3040 (5 op) Syksy 2006 Harjoitustyö
 Signaalien tilastollinen mallinnus T-61.3040 (5 op) Syksy 2006 Harjoitustyö Harjoitustyön sekä kurssin suorittaminen Kurssin suorittaminen edellyttää sekä tentin että harjoitustyön hyväksyttyä suoritusta.
Signaalien tilastollinen mallinnus T-61.3040 (5 op) Syksy 2006 Harjoitustyö Harjoitustyön sekä kurssin suorittaminen Kurssin suorittaminen edellyttää sekä tentin että harjoitustyön hyväksyttyä suoritusta.
Ei välttämättä, se voi olla esimerkiksi Reuleaux n kolmio:
 Inversio-ongelmista Craig, Brown: Inverse problems in astronomy, Adam Hilger 1986. Havaitaan oppositiossa olevaa asteroidia. Pyörimisestä huolimatta sen kirkkaus ei muutu. Projisoitu pinta-ala pysyy ilmeisesti
Inversio-ongelmista Craig, Brown: Inverse problems in astronomy, Adam Hilger 1986. Havaitaan oppositiossa olevaa asteroidia. Pyörimisestä huolimatta sen kirkkaus ei muutu. Projisoitu pinta-ala pysyy ilmeisesti
Identifiointiprosessi
 Alustavia kokeita Identifiointiprosessi Koesuunnittelu, identifiointikoe Mittaustulosten / datan esikäsittely Ei-parametriset menetelmät: - Transientti-, korrelaatio-, taajuus-, Fourier- ja spektraalianalyysi
Alustavia kokeita Identifiointiprosessi Koesuunnittelu, identifiointikoe Mittaustulosten / datan esikäsittely Ei-parametriset menetelmät: - Transientti-, korrelaatio-, taajuus-, Fourier- ja spektraalianalyysi
4.0.2 Kuinka hyvä ennuste on?
 Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Luonteva ennuste on käyttää yhtälöä (4.0.1), jolloin estimaattori on muotoa X t = c + φ 1 X t 1 + + φ p X t p ja estimointivirheen varianssi on σ 2. X t }{{} todellinen arvo Xt }{{} esimaattori = ε t Esimerkki
Estimointi. Vilkkumaa / Kuusinen 1
 Estimointi Vilkkumaa / Kuusinen 1 Motivointi Tilastollisessa tutkimuksessa oletetaan jonkin jakauman generoineen tutkimuksen kohteena olevaa ilmiötä koskevat havainnot Tämän mallina käytettävän todennäköisyysjakauman
Estimointi Vilkkumaa / Kuusinen 1 Motivointi Tilastollisessa tutkimuksessa oletetaan jonkin jakauman generoineen tutkimuksen kohteena olevaa ilmiötä koskevat havainnot Tämän mallina käytettävän todennäköisyysjakauman
Työvoima Palvelussuhdelajeittain %-jakautumat
 Hallinto 2510 Hyvinvointitoimiala tammikuu 134,9 121,3-13,6 82,8 84,4 3,2 5,4 11,8 7,3 2,3 2,9 3,9 5,8 55,6 38,6 123,1 107,6 91,3 % 88,7 % helmikuu 133,9 118,8-15,1 82,3 83,4 3,9 5,5 11,1 7,6 2,6 3,6 8,1
Hallinto 2510 Hyvinvointitoimiala tammikuu 134,9 121,3-13,6 82,8 84,4 3,2 5,4 11,8 7,3 2,3 2,9 3,9 5,8 55,6 38,6 123,1 107,6 91,3 % 88,7 % helmikuu 133,9 118,8-15,1 82,3 83,4 3,9 5,5 11,1 7,6 2,6 3,6 8,1
Otannasta ja mittaamisesta
 Otannasta ja mittaamisesta Tilastotiede käytännön tutkimuksessa - kurssi, kesä 2001 Reijo Sund Aineistot Kvantitatiivisen tutkimuksen aineistoksi kelpaa periaatteessa kaikki havaintoihin perustuva informaatio,
Otannasta ja mittaamisesta Tilastotiede käytännön tutkimuksessa - kurssi, kesä 2001 Reijo Sund Aineistot Kvantitatiivisen tutkimuksen aineistoksi kelpaa periaatteessa kaikki havaintoihin perustuva informaatio,
Väkiluku ja sen muutokset 31.12.2013
 KUUKAUSIRAPORTOINTI Väkiluku ja sen muutokset 31.12. Väkiluvun kehitys 54800 Mikkelin kaupungin väkilukuennakko kuukausittain 1.1. lukien (joulukuun 2012 luvussa on myös Ristiina ja Suomenniemi vertailun
KUUKAUSIRAPORTOINTI Väkiluku ja sen muutokset 31.12. Väkiluvun kehitys 54800 Mikkelin kaupungin väkilukuennakko kuukausittain 1.1. lukien (joulukuun 2012 luvussa on myös Ristiina ja Suomenniemi vertailun
Teema 8: Parametrien estimointi ja luottamusvälit
 Teema 8: Parametrien estimointi ja luottamusvälit Todennäköisyyslaskennan perusteet (Teemat 6 ja 7) antavat hyvän pohjan siirtyä kurssin viimeiseen laajempaan kokonaisuuteen, nimittäin tilastolliseen päättelyyn.
Teema 8: Parametrien estimointi ja luottamusvälit Todennäköisyyslaskennan perusteet (Teemat 6 ja 7) antavat hyvän pohjan siirtyä kurssin viimeiseen laajempaan kokonaisuuteen, nimittäin tilastolliseen päättelyyn.
Menetelmä Markowitzin mallin parametrien estimointiin (valmiin työn esittely)
 Menetelmä Markowitzin mallin parametrien estimointiin (valmiin työn esittely) Lauri Nyman 17.9.2015 Ohjaaja: Eeva Vilkkumaa Valvoja: Harri Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla
Menetelmä Markowitzin mallin parametrien estimointiin (valmiin työn esittely) Lauri Nyman 17.9.2015 Ohjaaja: Eeva Vilkkumaa Valvoja: Harri Ehtamo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla
