PLANKTON RECOGNITION FROM IMAGING FLOW CYTOMETER DATA USING CONVOLUTIONAL NEURAL NETWORKS
|
|
|
- Ilona Kivelä
- 5 vuotta sitten
- Katselukertoja:
Transkriptio
1 Lappeenranta-Lahti University of Technology School of Engineering Science Computational Engineering Intelligent Computing Osku Grönberg PLANKTON RECOGNITION FROM IMAGING FLOW CYTOMETER DATA USING CONVOLUTIONAL NEURAL NETWORKS Master s Thesis Examiners: Supervisors: Prof. Heikki Kälviäinen Prof. Lasse Lensu D.Sc. Tuomas Eerola Prof. Lasse Lensu Prof. Heikki Kälviäinen Prof. Heikki Haario M.Sc. Kaisa Kraft
2 ABSTRACT Lappeenranta-Lahti University of Technology School of Engineering Science Computational Engineering Intelligent Computing Osku Grönberg PLANKTON RECOGNITION FROM IMAGING FLOW CYTOMETER DATA US- ING CONVOLUTIONAL NEURAL NETWORKS Master s Thesis pages, 21 figures, 9 tables, 4 appendices. Examiners: Prof. Heikki Kälviäinen Prof. Lasse Lensu Keywords: convolutional neural networks, imaging flow cytometer, image processing, phytoplankton, classification Research on plankton populations is bottlenecked by the ability to obtain species-level information within a required time frame. Recent technological advances in imaging hardware have made it possible to obtain large amounts of image data from plankton populations. Because of the large number of images, there is a need for an automated solution to classify plankton. This thesis focuses on plankton recognition from images captured with an imaging flow cytometer using convolutional neural networks (CNN). A CNN to classify plankton images is trained and compared to a random forest solution that utilizes handcrafted features. The plankton images are resized for the CNN because there are large disparities in the image sizes. There is also a large class imbalance in the number of samples per class. The trained CNN has an accuracy of and the random forest implementation has an accuracy of on the same dataset. By using data augmentation methods and larger input images, the CNN reaches a accuracy.
3 TIIVISTELMÄ Lappeenrannan-Lahden teknillinen yliopisto School of Engineering Science Laskennallinen tekniikka Älykäs laskenta Osku Grönberg PLANKTONLAJIEN TUNNISTAMINEN KUVANTAVASTA VIRTAUSSYTOMET- RIADATASTA KONVOLUTIIVISILLA NEUROVERKOILLA Diplomityö sivua, 21 kuvaa, 9 taulukkoa, 4 liitettä. Tarkastajat: Prof. Heikki Kälviäinen Prof. Lasse Lensu Hakusanat: konvolutiivinen neuroverkko, kuvantava virtaussytometri, kuvankäsittely, kasviplankton, luokittelu Keywords: convolutional neural networks, imaging flow cytometer, image processing, phytoplankton, classification Planktonpopulaatioiden tutkimisen pullonkaula on kyky saada lajitason tietoa planktonpopulaatioista riittävän lyhyessä ajanjaksossa. Viimeaikaiset teknologiset edistysaskeleet kuvauslaitteissa ovat mahdollistaneet suuren kuvamäärän tuottamisen planktonpopulaatioista. Koska kuvia on paljon, on tarvetta automatisoidulle ratkaisulle planktonlajien luokitteluun. Tämä opinnäytetyö keskittyy planktonlajien tunnistamiseen kuvantavasta virtaussytometriadatasta konvolutiivisilla neuroverkoilla (CNN). Planktoneita luokitteleva CNN opetetaan ja sen toimintakykyä verrataan Random Forest-menetelmään (RF), joka käyttää käsin valittuja kuvapiirteitä. Planktonkuvien kokoa muutetaan CNN:ää varten, koska kuvien ko oissa on suuria eroja. Näytteiden luokkakohtaisessa määrässä on myös suuria luokkien välisiä eroja. Opetetulla CNN:llä on luokittelutarkkuus ja RF:llä on tarkkuus samalla datasetillä. Käyttämällä datan augumentointimenetelmiä ja suurempia syötekuvia, CNN saavuttaa tarkkuuden.
4 4 CONTENTS 1 INTRODUCTION Background Objectives and delimitations Structure of the thesis CONVOLUTIONAL NEURAL NETWORKS Machine learning Neural network layers and structure Convolutional layers Pooling layers Fully-connected layers Spatial pyramid pooling Universal approximation theorem and activation functions A typical network structure Neural network training Loss functions Gradient descent and backpropagation Vanishing and exploding gradients Deep residual networks Preventing overfitting and optimizing neural networks Dropout Data augmentation Few-shot learning Transfer learning PLANKTON RECOGNITION Plankton imaging Phytoplankton classes Existing methods for automated plankton recognition utilizing hand crafted features Support vector machine Random decision forest based plankton recognition Existing deep learning methods for automated plankton recognition Summary of plankton recognition studies EXPERIMENTS AND RESULTS Data
5 5 4.2 Data preprocessing Proposed network structures Description of experiments Evaluation criteria Results DISCUSSION Current study Future work CONCLUSION 64 REFERENCES 65 APPENDICES Appendix 1: The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 100 samples (Subset100). Appendix 2: The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 50 samples (Subset50). Appendix 3: The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 20 samples (Subset20). Appendix 4: The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 10 samples (Subset10).
6 6 LIST OF ABBREVIATIONS CNN IFCB NDSB RF ReLU sp. SPP SVM Convolutional neural network Imaging FlowCytobot National Data Science Bowl Random Forest Rectified linear unit Species Spatial pyramid pooling Support vector machine
7 7 1 INTRODUCTION 1.1 Background Plankton [1] are a diverse collection of aquatic micro-organisms defined mainly by their size and inability to resist a water current. The organisms include mainly bacteria, archaea, algae, protozoa and microscopic animals. Plankton can be roughly divided into three trophic groups: producers, consumers and decomposers. Phytoplankton consists of producers that perform photosynthesis, zooplankton consists of consumers that feed on other plankton and bacterioplankton and mycoplankton consist of decomposers that break down nutrients. There are many plankton species that are able to act on multiple different trophic levels. This is known as mixotrophy [2] [3] and it is part of the reason why dividing plankton into well defined groups is hard. As a primary producer phytoplankton is an important part of the food-chain, supplying food for larger aquatic organisms like fish and whales. Phytoplankton populations are proven to be good indicators of environmental conditions, like the quality of water. Additionally, changes in phytoplankton populations can indicate changes in these conditions. Phytoplankton is also a major contributor of oxygen in the Earth s atmosphere. [4] [5] Research on plankton populations is bottlenecked by the ability to classify plankton into species within a required time frame. This bottleneck is caused by the fast turnover rates of plankton, meaning that the species distribution of plankton populations can change very rapidly [4]. Recent technological advances have made it possible to make automated plankton imaging instruments capturing tens of thousands of images per hour. By such means, it is possible to capture enough images of a plankton population withing a small enough time frame to study the dynamics and structure of the plankton population. However, it is very infeasible for humans to screen through all the collected images in order to classify the plankton into species. Example phytoplankton images can be seen in Figure 1. The images have been assigned to classes by human experts. Computer vision is a field that deals with the automation of tasks that the human vision system can do [6]. A computer vision application seems well suited to automate the process of classifying images of plankton species. Classification is a machine learning problem of teaching a classifier to assign input samples into correct output classes. A computer vision system usually works in four steps: acquire images, preprocess images, extract features and make decisions.
8 8 Centrales Chroococcales Dinophysis Dolichospermum Oocystis acuminata Anabaenopsis Figure 1. Example phytoplankton images of different classes with different aspect ratios. There are many different methods for classification in the make decisions step. For instance, the classification can be done using a random forest or a neural network [7]. A classifier outputs either the class of the input or a distribution of the posterior probabilities of the different classes. A decision tree is an example of a classifier where the classifier directly outputs the class of the input. A neural network is an example of a classifier where the output is the distribution of the posterior probabilities. If the output of a classifier is the distribution of the posterior probabilities of the different classes, the input is usually classified to the class with the largest posterior probability. The traditional classification methods for image data use handcrafted features. In the feature extraction step of a computer vision system, predefined image features are extracted from the input images and the classification of the input images are done based on these features in the make decisions step. Feature extraction is a dimensionality reduction process where ideally the more informative characteristics of the data are preserved in terms of the classification problem [8]. Feature extraction is beneficial because it can help to reduce the computational overhead associated with a classification task. Additionally, feature extraction can allow humans to gain insight of the underlying structures of the data and to find outliers. For example, it may be possible to find correlations between different classes and features.
9 9 Convolutional neural networks (CNN) are a state-of-the-art method for image classification. CNNs utilize deep learning which is a machine learning method for learning data representations. Contrary to more traditional machine learning methods that utilize handcrafted features, deep learning methods attempt to also learn the features to be extracted. Deep learning automates the process of determining what features are good for a specific classification task. [9] The overall process of a CNN based plankton recognition system is depicted in Figure 2. First large amounts of images are captured with an automated in-situ imaging equipment, then the images are preprocessed for a classifier and finally the preprocessed images are classified using a CNN. In-situ refers to the case of imaging plankton in an environment where the plankton naturally exist. 1.2 Objectives and delimitations The main objectives of this thesis are the following: 1. Design a CNN for plankton classification and explore methods to improve the classification accuracy. 2. Compare the CNN with an existing random forest classifier. 3. Solve problems related to the large class imbalance in the number of available sample images per class. 4. Solve problems related to the large variations in the image sizes and aspect ratios. 5. Find a way to take into account the errors in the ground truth of the expert labeled classes. This thesis deals mainly with phytoplankton, but the employed machine learning approaches are also applicable for other trophic groups of plankton. The classification task is limited to micro- and nanophytoplankton images collected from the Baltic Sea. The image data consists of species in the size range of µm.
10 Figure 2. The process of acquiring, preprocessing and classifying a plankton image with convolutional neural networks. 10
11 Structure of the thesis Chapter 2 contains an introduction to supervised learning and contains an in-depth description of CNN components and how the networks can be trained and used. Chapter 3 introduces the overall aspects of plankton recognition, existing solutions and the random decision forest method. Chapter 4 contains a description of the implemented methods for plankton recognition and describes the experiments with these methods and the results of these experiments. In Chapter 5, the results are discussed and possible future works are described. Finally, Chapter 6 contains the conclusions of this thesis.
12 12 2 CONVOLUTIONAL NEURAL NETWORKS 2.1 Machine learning Machine learning is a science of making computer systems perform tasks without being explicitly programmed. Rather than explicitly programming an algorithm to perform a specific task, the training data is used to teach an algorithm how to perform the task. Machine learning methods can roughly be divided into two categories: supervised learning methods and unsupervised learning methods. Unsupervised learning methods learn to perform a task from data that has not been labeled. Unsupervised learning methods are usually used to solve the clustering task, where the objective is to group samples into clusters based on a some type of similarity measure. [7] Supervised learning methods use labeled training data. The labeled training data consists of pairs of input samples and desired output labels. Supervised learning methods are used to solve classification and regression problems. In regression the objective is to train a model to estimate a quantity. A regression problem can be thought of as a problem of fitting a function to a set of data points. In classification the objective is to teach a classifier to correctly classify input data into predefined discrete classes. The classes are predefined, meaning they have been defined by a human and the classes are discrete, meaning a sample has to either belongs to a particular class or not belong to the particular class. Supervised learning models for classification are typically fed training data and the model parameters are then adjusted so that the model outputs would match the desired model input labels. Neural networks are one example of supervised learning methods. [10] [7] 2.2 Neural network layers and structure CNNs are a supervised learning method for deep feature extraction and classification [11] [12]. A typical CNN consists of sequential layers of varying types. Common layers in CNNs are convolutional layers, pooling layers and fully-connected layers. A CNN usually begins with convolutional layers with a mix of pooling layers, then followed by a few fully connected layers. CNNs are a type of black box classification as it is difficult to fully understand what is represented in the extracted deep features. CNNs were inspired by the human vision system and the different types of layers can be seen analogous to various cells found in a visual cortex [13]. An example CNN can be seen in Figure 3. The network is split depth-wise to achieve a higher level of parallelism and to avoid the
13 13 problem of limited hardware memory and computing power [14]. Figure 3. The illustration of AlexNet [14] Convolutional layers A convolutional layer performs discrete convolution [15] on a input matrix, typically an image or a feature map, with different filters and outputs a stack of convoluted matrices. The filters in convolutional layers are two-dimensional or three-dimensional matrices. Multidimensional matrices are typically referred to as tensors. Different parameters involved in discrete convolution are the size of the filters, stride, and the zero-padding. The mapping of discrete convolution between two three-dimensional tensors in a convolutional layer can be defined as g(x, y) = A B(ax, by) = w h d A(i, j, k)b(ax + i, by + j, k) (1) i=0 j=0 k=0 where g(x, y) is the convoluted tensor, A is the convolutional filter, B is the tensor to be convoluted, w, h and d are the width, height and depth of A respectively and a and b are the horizontal and vertical convolutional strides respectively. Note that in this thesis the point of reference, also know and origin of the tensors, is always located at the first element of the tensors and the coordinate references for the cells in a tensor are always combinations of natural numbers. Natural numbers refer to all non-negative integers in this thesis. In convolutional layers the depths of the filters are equal to the depth of the input tensor [16]. Zero-padding is the number of zero valued rows and columns that are padded to the input tensor in horizontal and vertical directions prior to convolution. The depth of the output of a convolutional layer corresponds to the number of filters in the layer. The
14 14 height of the output can be calculated from the height of the input tensor, the stride and the zero-padding with the formula H o = H i F h + 2P S v + 1 (2) where H o is the output height, H i is the height of the input tensor, F h is the height of the filter, P is the zero-padding and S v is the vertical convolutional stride. The width of the output can be calculated from the width of the input tensor, the stride and the zero-padding with the formula W o = W i F w + 2P S h + 1 (3) where W o is the output width, W i is the width of the input tensor, F w is the width of the filter, P is the zero-padding and S h is the horizontal convolutional stride. An example of three-dimensional convolution of the parrots image can be seen in Figure 4. The original (a) (b) Figure 4. Example of three-dimensional convolution: (a) Original image; (b) Convoluted image. The white pixels correspond to positive values and the black pixels correspond to negative values. image is convoluted with the 3x3x3 tensor A(:, :, 0) = , A(:, :, 1) = , A(:, :, 2) = (4) The idea behind convolutional layers is that they perform the feature extraction part of the classification. The output of a convolutional layer can be seen as a feature map of the input. [11] [12]
15 Pooling layers In the CNN architecture, it is common to use a pooling layer to downsample the feature maps from a convolutional layer [11] [12]. The common pooling methods are averagepooling and max-pooling, max-pooling being the most common. Parameters involved in the pooling layers are the pooling window size and the stride. Pooling operations downsample the input tensor independently in each depth slice of the tensor. The mapping of the max-pooling operation can be defined as g(x, y, z) = max(b([ax, ax + w], [by, by + h], z)) (5) where g is the pooled tensor, B is the input tensor, a and b are the respective vertical and horizontal strides and w and h are the respective width and height of the pooling window. A pooling window, in this context a rectangle, is a shape that defines the specific regions in the input tensor that are used to calculate the different output elements of the output tensor. The notation [a, b] is used for discrete intervals in this thesis. The mapping of the average pooling operation can be defined as g(x, y, z) = 1 wh w i=0 h B(ax + i, by + j, z). (6) j=0 The purpose of the pooling layer is to reduce the network size in a fashion where the most useful information is kept [17]. The max-pooling layers should outperform the average pooling layers because the largest local activations from the convolutional layers can be considered locally the most important features. Another purpose of the pooling layers is to make the network more shift invariant. Shift invariance refers to the networks ability to correctly classify images that have had changes in the positions of the regions of interest Fully-connected layers Fully-connected layers are what traditional neural networks consist of [12]. All neurons in a fully-connected layer take input from all the activations in the previous layer. Convolutional layers can be seen as a way to extract features from the input image, whereas the fully-connected layers perform the classification task based on the features. That is why the last layers of a CNN are fully connected. An illustration of the connections in a fully-connected layer can be seen in Figure 5. The connections in a fully connected layer
16 16 contain trainable weights and the output nodes contain trainable biases. The output value of an output node in a fully connected layer is the weighted sum of its inputs and the bias. Figure 5. An illustration of the connections in a fully connected layer with four input nodes and six output nodes Spatial pyramid pooling A typical CNN takes in only images of fixed sizes because the fully-connected layers need to have a constant input size. Spatial pyramid pooling (SPP) [18] is a pooling method that allows the CNN to use input images of unfixed sizes and aspect ratios. The convolutional layers do not necessarily need to have a fixed input, but the input size does affect the size of the layer output. The only real restriction for a convolutional layer is that the input should not be too small because very small input images can collapse to single pixel feature maps. The SPP layer is typically implemented between the last convolutional layer and the first fully-connected layer. The SPP layer intakes a feature map and creates pooled feature-bins of various regions
17 17 in the feature map using the Bag-of-Words approach [19]. The input feature map is divided into subregions of varying scales and features are pooled in each subregion. The subregions of different scales may overlap with each other. The pooled outputs of the subregions are basically feature histograms [20] that have a fixed number of bins. A histogram is a representation of numerical data where the distribution of the data is represented by the number of samples included in fixed sized intervals such that each sample is included in exactly one interval. The intervals are called bins and the number of samples in a bin is called the bin height. The features in the SPP input subregions can also be pooled with other methods like max-pooling or average-pooling. The output of the SPP layer is a feature vector consisting of all pooled feature-bins. The addition of a SPP-layer has been shown to improve classification accuracies in different network architectures. An illustration of a SPP layer can be seen in Figure 6. Figure 6. The illustration of a spatial pyramid pooling layer [18] Universal approximation theorem and activation functions The universal approximation theorem states that a neural network with a single hidden layer can approximate continuous functions on compact subsets in n dimensions. This means that in theory, a network with a single hidden layer with appropriate parameters can perform as well as any network. However, the theorem does not cover any methods
18 18 to solve the parameters of such a network. [21] [22] A linear combination of linear functions is yet a linear function. To make sure that a network is not redundant to a single hidden layer network, the outputs of fully-connected layers and convolutional layers are passed through a non-linear activation function. It is shown that it is the feedforward architecture of neural networks that allows them to work as universal approximators and the choice of a particular activation function is of secondary importance [23]. Common non-linear activation functions in CNNs are the rectified linear unit (ReLU) and the sigmoid function. The ReLU function is defined as [24] and the sigmoid function is defined as [25] f(x) = max(x, 0) (7) f(x) = The activation functions have been plotted in Figure 7. ex e x + 1. (8) Figure 7. The plot of the rectified linear unit and the sigmoid function from -4 to 4. There exists a large number of other usable activation functions, and ReLU is one of the computationally cheapest options [14]. A parametric ReLU is an activation function that contains a trainable parameter. The parametric ReLU can be defined as [26] x if x > 0 f(x) = (9) ax if x 0 where a is a trainable parameter for the network. The choice of using parametric ReLUs
19 19 contrary to using standard ReLUs has been shown to increase classification accuracies in CNNs A typical network structure A typical CNN structure begins with convolutional layers with a mix of pooling layers, then followed by a few fully connected layers. Usually a larger stride and filter size is used in the first few convolutional layers to help to reduce the size of the network. The network becomes more shift invariant as the spatial size of the feature maps are progressively reduced with the convolutional layers and the pooling layers. Consequently, the total number of features represented in the feature maps also decreases. However, this can be compensated by having more convolutional filters in the convolutional layers that are located deeper in the network. [12] The number of different features the network could be looking for also increases in the convolutional layers that are located deeper in the network. As an example, the first convolutional layer of the network could be looking for edges in different orientations, the second convolutional layer could be looking for corners made from the edges in specific orientations and the third convolutional layer could be looking for different shapes defined by the edges and the corners in specific orientations. It is easy to see that there exist significantly more different kinds of shapes than different kinds of lines that the network could be looking for. Zeiler and Fergus [27] study and visualize the activations in different convolutional layers when a CNN is given different input images. They also studied how covering portions of an input image affects the classification result of a CNN. Example visualizations from their publication can be seen in Figure 8. For instance, it can be seen in the first row of Figure 8 that covering the dog s face has the largest negative impact on the classification accuracy. 2.3 Neural network training The process and different concepts related to training a CNN are outlined in this section. A CNN can be trained by iteratively minimizing a loss function. A loss function is used to determine the difference between the network output and the desired network output. After this difference is known, the network parameters are adjusted to minimize the difference. This can be achieved via gradient descent. However, simply calculating the gradient by applying the difference quotient can be computationally expensive. Backpropagation
20 20 Figure 8. The illustration of how covering a portion of an input image affects the classification result of a convolutional neural network [27]: (a) The input image; (b) The sum of the activations in the feature map with the strongest activation with the unoccluded image as a function of the position of the gray square; (c) Visualization of the feature map with the strongest activation with the unoccluded image projected back to the input of the network; (d) The probability of a correct classification as a function of the position of the gray square; (e) The most probable label of the classification as a function of the position of the gray square. is a method for efficiently calculating the partial derivatives of the gradient for the network weights and biases with regards to a loss function. Vanishing and exploding gradients are a problem related to using gradient descent in neural networks. [12] Loss functions A CNN is trained by minimizing a loss function. A training sample is first passed through the network and the network output is compared with the desired output. A loss function is used to define the difference between the network output and desired output. There exists a wide variety of different loss functions. When dealing with classification, we ideally want to minimize the Kullback Leibler divergence that measures how one probability distribution differs from another reference probability distribution. The Kullback Leibler divergence in a discrete domain can be defined as [28]
21 21 H(p, q) = x X p(x) log q(x) p(x) (10) = x X(p(x) log(q(x)) p(x) log(p(x))) (11) where p(x) is the probability of event x, q(x) is the predicted probability of event x and X is the support of p and q. Seemingly the most common loss function utilized in CNNs is the categorical cross entropy and in discrete domain it can be defined as [29] H(p, q) = x X p(x) log(q(x)). (12) Assuming p(x) is the true probability, then minimizing the categorical cross entropy becomes equivalent to minimizing the Kullback-Leibler divergence. It is easy to see that the term p(x) log(p(x)) in Equation 11 has no bearing on the partial derivatives of the weights and biases in q(x) when p(x) is fixed by the assumption that it is the true probability. This means that minimizing the categorical cross entropy is simply the computationally cheaper option Gradient descent and backpropagation Gradient descent is an iterative numerical method for estimating a local minimum of a function. This can be applied to estimate a local minimum of a loss function. Backpropagation [30] is a method for efficiently calculating the partial derivatives of the gradient for all the weights and biases in a network. The outputs of the neurons in convolutional and fully-connected layers can be formulated to be sums of linear functions as Out = i w i x i + b (13) where x i is the ith input component, w i is the respective weight for x i and b is the bias. The gradient of a loss function can be numerically estimated by calculating the difference quotient with regards to each variable. as [31] f (x) = The difference quotient is usually formulated f(x + h) f(x) h where f (x) is the difference quotient of f(x) and h is an arbitrarily small number. The gradient points in the direction of the largest growth in the loss function, the negation of (14)
22 22 the gradient represents the desired change in the weights of the layer. Based on the network output and the desired output, the gradient of the loss function can be calculated with regards to the weights in the last layer. Calculating the partial derivatives for the weights in the preceding layer can be achieved by applying the chain rule and this allows for the propagation of the error backwards in the network, hence the name backpropagation. The chain rule can be formulated as [30] dz dx = dz dy dy dx. (15) After the partial derivatives have been calculated for all the weights in all the layers, the weights can be updated by subtracting the gradient components of their respective weights [30]. The pooling layers and the activation functions do not usually have trainable weights and the error can be propagated backwards through them. For example, in the case of max-pooling, the error is propagated only to the nodes that had the largest forwardpasses in the pooling windows. A learning rate constant is usually defined for a network training and it is used as a multiplier for the gradient when calculating new weights. Because there are usually multiple input samples for gradient descend, it is possible to create a batch of samples [32]. A batch of samples is a collection of samples that are used during an iteration of gradient descent. During the iteration the samples in a batch are passed through the network, the respective costs for each sample are calculated in the last layer, the errors are propagated backwards in the network, the gradients are calculated and then the average of the gradients is used to update the weights of the network. It is usually not feasible to use all the training samples for every gradient update due to memory and computational limitations. Stochastic gradient descend is a popular method where the training data is split randomly into many smaller batches and the network weights are updated one batch at a time. Stochastic gradient descend usually results in a faster network convergence contrary to using every training sample for every gradient update. Convergence refers to the progress of gradient descent numerically stabilizing to a local minimum of a function. In many machine learning solutions, the gradient descend algorithm can be described as the backbone for minimizing a loss function. However, the learning process can usually be further improved. Gradient descent methods utilizing momentum use global update vectors that the gradients adjust. Instead of using gradients, the update vectors are used to update the weights in each layer of the network. The update vector can be updated with the formula [33] v i+1 = αv i lg (16)
23 23 where v is the update vector, α is the momentum, l is the learning rate and g is the gradient. Nesterov s accelerated gradient descent also utilizes momentum. The update rule for Nesterov s method is [33] v i+1 = α(αv i lg) lg. (17) The benefit of utilizing momentum in gradient descent is that the methods utilizing momentum are more likely to find smaller local minima. Nesterov s method can be seen as a more optimistic algorithm for gradient descent and it converges faster for convex functions. A real-valued function on an n-dimensional interval is a convex function if the second derivative of the function is always greater than or equal to zero in the defined interval. [33] Vanishing and exploding gradients The vanishing gradient problem is a problem related to the network training where the network weight update becomes increasingly small and the network becomes unable to learn [34]. The vanishing gradient problem can have many causes. The use of ReLUs is less likely to cause a vanishing gradient compared some of the more traditional activation functions [35]. The exploding gradient problem refers to the case where the network weights become increasingly large and consequently make the gradient also very large [36]. The exploding gradient problem can be solved for instance by employing a regularization function that penalizes the network training for assigning large weights. Problems related to exploding and vanishing gradients are typically encountered when dealing with recurrent or very deep network architectures [37]. Recurrent neural networks are neural networks that do not follow the traditional feed-forward architecture of neural networks. Deep network architectures refer to network architectures with a large number of layers Deep residual networks It has been shown in different visual recognition tasks that the neural network depth is an important parameter and increasing the number of layers in a network can increase the network s classification accuracy [38]. Vanishing and exploding gradients are not the only training problems related to deep neural networks. One would expect the accuracy
24 24 of a neural network to get saturated at some point when progressively increasing the number of layers in a network. However, it has been shown that the network accuracy saturates and then starts to decrease rapidly. This decrease is not due to overfitting. This network accuracy degradation can be prevented by using a residual network architecture and this has enabled the training of very deep networks with hundreds of layers. A residual network architecture contains shortcuts. A residual network consists of building blocks, which are just stacks of layers. The shortcuts make it so that some building blocks take input from the two preceding building blocks in the network architecture. If a stack of layers is thought of as a function Out = F (In) (18) where Out is the output and In is the input, then in residual networks the output of a building block with a shortcut becomes Out = F (In) + In. (19) The inspiration of the residual networks comes from the fact that when adding more layers to a network, at some point the network accuracy surely saturates and when even more layers are added, in the extreme case some layers in the network may be required to perform an identity mapping. An identity mapping is a mapping whose output is equal to its input. It may be that this identity mapping is not easy to optimize for a stack of nonlinear layers, but in case of residual networks, the term F (In) in Equation 19 can be easily made equal to a zero matrix by gradient descent. A zero matrix is a matrix containing only zeros. If the term F (In) becomes equal to a zero matrix in a block that has a shortcut, then the output of the block becomes equal to the input of the block. [38] 2.4 Preventing overfitting and optimizing neural networks When a small amount of training data is available, a classifier is more prone to overfitting. Overfitting is a problem where a function fits the data too well. It is very rare that a complete representation of data is available and hence, functions usually have to be fit with partial data. When dealing with partial data, overfitting can have negative effects on the reliability of interpolation and extrapolation of the fitted function. Classifiers are also functions and overfitting classifiers usually emerges as a classifiers inability to generalize. [39]
25 25 There are multiple ways to avoid overfitting to a degree and ultimately improve a classifier s accuracy. Methods to prevent overfitting in neural networks are surveyed in this section. Dropout is a method to prevent overfitting in neural networks [40]. Another way to avoid overfitting is to simply use more data. Data augmentation describes methods for generating seemingly new data from existing data [41]. Data augmentation can help in creating a more complete representation of the data from partial data. Few-shot learning is the machine learning problem where a classifier is required to learn from a very small amount of training data [42]. Transfer learning is a machine learning problem of using knowledge from solving one problem to solve another different problem and it can be applied to few-shot learning problems [43] Dropout Dropout is a method to avoid overfitting in neural networks [40]. Dropout is typically implemented in the fully-connected layers. The method involves randomly switching off nodes in the network layers. Depending on the implementation, each node has a probability of not contributing to the network for a given training sample or a training batch. The dropped-out nodes are also ignored in the network backpropagation. A common probability used for dropout in the fully connected layers is 0.5. Smaller probabilities are advised to be used for the input layer as data is directly lost if input nodes are ignored. Dropout slows the network convergence significantly, but also prevents overfitting very effectively.
26 Data augmentation Data augmentation can be used to reduce overfitting. In the context of machine learning, data augmentation consists of methods to derive seemingly new data from the existing data [41]. It is important that the derived data keeps key characteristics of the original data while appearing as completely new data to a machine learning method. Simplest methods include extrapolation and interpolation of data. When dealing with image data, there are multiple image transformations that work very well as data augmentation methods. It is important to note that different classification methods can be invariant to different image transformations. Common image transformations used for data augmentation include the following [44]: Affine transformations: Reflection: The image is flipped along an axis. Scale: The image is scaled along the image main axes. Rotate: The image is rotated along its center. Shear: The image is sheared along an axis. Image filtering methods: Methods for blurring and sharpening an image. Methods for adding and removing noise. Cropping: Output image is a subregion of the input image. Both rotating an image by 90-degrees and reflecting an image can be particularly good data augmentation methods because they do not cause any loss in the image quality. Resizing images can also be used for data augmentation. There are many ways to resize images. The most common methods include nearest-neighbor interpolation and bicubic interpolation. The mapping of the nearest-neighbor interpolation can be defined as Out(x, y) = In( ax, by ) (20) where Out is the output image, In is the input image, a is the inverse of the horizontal scaling factor and b is the inverse of the vertical scaling factor. is the notation for
27 27 rounding to nearest integer. The nearest-neighbor interpolation assigns to the output image pixels the values of the input image pixels with the closes relative positions in the input image. [45] The bicubic interpolation uses the weighted average of the closest relative 4-by-4 neighborhood in the input image to calculate the pixel values of the output image. The nearest neighbor interpolation can be thought of as fitting a static function to a point and then extrapolating that function. The bicubic interpolation can be thought of as fitting a second degree polynomial to a 4-by-4 region and then interpolating the 4-by-4 region with that polynomial. [45] Few-shot learning Few-shot learning refers to a case where a classifier is required to learn from a small number of samples, usually between one and a few dozen. This is often due to a lack of annotated data. In general, few-shot machine learning problems are solved by two ways. The first solution is simply to acquire more training data, either through data augmentation or external data sources. The second solution is to take the lack of samples into account in the model. This can be achieved for instance by different regularization techniques or other methods that compel the model to generalize more when the data at hand contains fewer samples. For example, in case of prototypical networks [46], a variable space with class prototypes is learned and the classification can be performed by a distance measure to the nearest class prototype. The class prototypes can be seen as generalizations of the classes. Matching networks [47] can also be used to solve a few-shot learning problem. Matching networks use a small support set of training samples to define classes in a variable space. The classification can be performed using the k-nearest neighbors method in the variable space. In the k-nearest neighbors method, an input is classified to the class with the largest amount of samples in the k-nearest neighbors of the input sample. The main difference between prototypical networks and matching networks is that the prototypical networks create one class prototype which is used for classifications, whereas the matching networks use a small support set of samples and the k-nearest neighbors method for classification. Both the prototypical networks and the matching networks can be used to detect classes that do not fit into any class, this is based on the distance of the input sample to the closes class prototype or k-nearest neighbors. Additionally, both of these classification methods make it easy to introduce new classes to an already trained model.
28 28 This can be achieved by adding a new class prototype or a support set to the model. Another way to account for the lack of samples involves meta-learning [48]. In metalearning, the aim is to learn the learning algorithm itself in the scope of the available data. Unfortunately, meta-learning can be computationally very expensive Transfer learning Transfer learning is a machine learning research problem of taking knowledge gained from solving one problem and applying it to another problem. The general idea of the transfer of knowledge is closely related to multi-task learning [49]. In multi-task learning, multiple tasks are solved jointly. The aim of multi-task learning is to transfer knowledge of commonalities and differences between tasks. In terms of classification tasks, multi-task learning can result in more accurate classifiers than solving the tasks separately. An example of multi-task learning is the task of training spam filters for different users [50]. There is clearly room for spam filters to learn from one another, but different users may also have different views of what is and is not spam. The main difference between transfer learning and multi-task learning is that in transfer learning, only one task is solved and the current task at hand is unable to transfer knowledge to the already solved reference tasks. As an example of transfer learning, a good CNN model to recognize hawks could have a similar structure to a good CNN model trained to recognize birds. As another example, the convolutional layers of a trained CNN can be used to perform feature extraction from image data for other classification methods [43]. Transfer learning can be used to reduce the required training time for CNN models [51]. Training a CNN model with pre-trained convolutional filters can speed up the network convergence significantly as the network does not need to learn the convolutional filters. The process of training a network with pre-trained convolutional filters is called fine-tuning a network. Fine-tuning a network is how transfer learning is applied to CNNs in practice. Fine-tuning a network can also be used to compensate the lack of samples in a few-shot learning problem.
29 29 3 PLANKTON RECOGNITION The outline of this chapter is the following. Different methods for plankton imaging are described. The taxonomy of phytoplankton is outlined. The random decision forest method is described. Existing handcrafted feature based and deep learning methods for plankton classification are surveyed. 3.1 Plankton imaging Plankton imaging solutions can be divided into in-situ and ex-situ systems [52]. Ex-situ refers to the case of imaging plankton in an environment where the plankton does not naturally exist, for instance the plankton are moved to a laboratory for imaging. Ex-situ imaging of a plankter can for instance be done by using a microscope. In-situ imaging solutions typically consist of a way to detect a plankter and a way to image the plankter. There are different techniques for imaging plankton of different sizes. Flow cytometers are devices designed to capture images and other characteristics of particles suspended in fluid that is injected into the device [52]. Imaging flow cytometers usually use light scatter and fluorescence from particles to detect them. The light scatter or fluorescence is usually caused by a laser beam. Plankton on average give a different kind of light florescence and scatter when compared to other particles in the sea. Phytoplankton can for instance be detected by chlorophyll-a fluorescence. Consequently, it is possible for the device to semi-reliably distinguish between plankton and other particles. The detection of a plankter then triggers the device camera to take an image of the plankter. Imaging flow cytometry is a highly applicable technique for capturing images and other data from plankton. There are many different commercially available hardware implementations of flow cytometry designed for plankton imaging including the Imaging FlowCytobot (IFCB), FlowCAM and CytoSense [53]. Digital holography [54] can be used to efficiently image plankton in a volume. In digital holography, a multidimensional image is created. The imaging is done with a camera and it is based on imaged interferograms. An interferogram is a pattern formed by the wave interference of light. The captured interferograms are used with numerical methods to construct a multidimensional image. The main benefit of digital holography is the ability to image particles in a volume simultaneously at different focuses.
30 30 The video plankton recorder [55] is a towed microscope device for in-situ plankton imaging. The video plankton recorder can be used to capture images of plankton that are larger than 50 µm. 3.2 Phytoplankton classes Taxonomy is the science of defining groups of biological organisms based on shared characteristics [56]. A created group is called a taxon, it is assigned a taxonomic rank and it can be further split into smaller taxonomic groups forming a tree like structure. The major taxonomic ranks for grouping animals and plants include domain, kingdom, division, class, order, family, genus and species. Species are at the lowest hierarchic level and these groups are not split any further. In case of phytoplankton, it is unclear if well defined species even exist and sometimes phytoplankton is divided into groups at higher taxonomic levels [57]. Phytoplankton can be divided into taxa based on the phylogeny of organisms or based on their functional roles in the ecosystem. In the future, plankton will likely be split into different taxa based on genetic information, but at this moment, mostly external characteristics are used. Typical features used to classify plankton into taxa include shape, texture, size and other characteristics like whether they live in colonies or have flagella. Sournia et al. [58] estimated that towards the end of 1980s, the living flora of the world oceans amounted to species. 3.3 Existing methods for automated plankton recognition utilizing hand crafted features The top-k accuracy is a common way to measure the performance of a classifier. The top-k accuracy is defined as A k = T k T k + F k (21) where A k is the top-k accuracy, T k is the number of samples whose classes were in the best k model predictions, F k is the number of samples whose classes were not in the best k model predictions and k is a natural number. Bueno et al. [59] studied handcrafted features to classify diatoms they acquired from rivers. Their dataset consisted of 80 classes with roughly 100 samples per class. They achieved a top-1 accuracy with a support vector machine (SVM) and a top-1 accuracy with a random forest implementation. They also showed how data aug-
31 31 mentation can improve the results. Their feature vector consisted of seven morphological features, 32 statistical features, 241 texture features, seven Hu moment features and 964 frequency features. They also studied the usefulness of the features for diatom classification Support vector machine The SVM is a supervised learning method for binary linear classification that utilizes handcrafted features [60]. Binary classifiers classify input into two discrete classes. In the SVM, a liner decision boundary is defined that separates the two classes. The decision boundary is defined based on the training data. The SVM method has multiple extensions. For instance, a non-linear classifier can be trained by performing a non-linear mapping on the extracted features. The SVM can also be extended to classify input into multiple classes. This can be achieved by formulating the classification problem into multiple binary classification problems Random decision forest based plankton recognition A decision tree is a supervised learning method for classification that utilizes handcrafted features [7]. Decision trees can also be used for regression. A decision tree is a treelike graph consisting of an input node, interior nodes, output nodes and connections. In a binary tree structure, every interior node is connected to a parent node and two child nodes. The input data enters the graph at the input node and is then sequentially evaluated at the node and passed forward to an appropriate child node until the data exits the graph. The rule deciding how to pass an input sample to an appropriate child node is called an attribute test. An attribute test compares the value of an attribute of the input to a threshold value. The attributes correspond to the features. The main benefits of decision trees compared to other classifiers are that decision trees are generally computationally very fast to use, and the classification process is completely transparent [7]. Transparency of the decision tree refers to the ability of a human to easily see and understand why a decision tree made a particular choice. Like many other classification methods, a decision tree usually requires feature extraction to be performed. A binary decision tree can be created from training data in a recursive fashion [7]. Two child nodes are recursively added to an impure output node in the decision tree based on
32 32 how they split the training data subset that corresponds to this particular impure node. This would make the output node into an interior node and the child nodes would be considered new additional output nodes. The training data subset that corresponds to a node is the set of samples that would arrive at the particular node if classified. An impure node refers to a node where the corresponding training data subset contains samples from more than a single class. The recursion is completed when all output nodes of the decision tree are pure nodes. Pure nodes are nodes where the corresponding training data subset contains samples from a single class. A typical way to decide how samples are split in an impure node into two child nodes is to minimize the sum of Gini impurities of the two child nodes. The Gini impurity of a node is defined as G = i P (i)(1 P (i)) (22) where G is the Gini impurity and P (i) is the fraction of samples of class i in the training data subset corresponding to this particular node. A simple decision tree can be seen in Figure 9. Figure 9. A simple decision tree. Random decision forest is a widely used supervised learning method for classification and regression [7]. The basic idea is to have many smaller decision trees rather than having one larger decision tree. A collection of multiple weaker classifiers is referred to as an ensemble. The classification task can be performed by having the ensemble of trees majority vote for the appropriate class of an input sample. The decision trees for the ensemble can be created from random sample subsets of the training data [61]. Having many weaker classifiers is an effective way to avoid overfitting and hence the random classification forest tends to yield better results than a single large decision tree [7]. Additionally, a random decision forest provides a confidence measure for its classification results in the form of the vote distribution. A confidence measure measures the credibility of the re-
33 33 sults. For instance, if the class with the most votes has a large majority of all the votes, then the classifier could be said to be confident of the result. However, if the class with the most votes did not collect a large majority of the votes or if there are multiple other classes with roughly equal amounts of votes, then the classification result does not look very credible. A random forest is also robust to features that do not consistently represent any changes between classes. The random forest can even be used to determine which of the used features are the most useful ones for the classification task. This is simply done by observing how often a particular feature is used in the nodes of the decision trees relative to the position of the respective nodes. A random forest requires feature extraction to be performed when dealing with image data. When dealing with plankton data, example extracted features could include the sum of the filled area, sum of the estimated biovolume, convex area, convex perimeter, major and minor axis lengths, eccentricity, extent, orientation, bounding box dimensions, perimeter, Feret diameter, solidity, number of blobs, texture entropy, texture uniformity, texture smoothness, texture entropy, different moment invariants, different shape histograms, different wedges and rings and histograms of gradients [62]. The idea is to extract all kinds of features and then let the decision forest calculate which features minimize the Gini impurities the best [7]. The spectral properties of plankton are also applicable features for classifiers. [63]. 3.4 Existing deep learning methods for automated plankton recognition There have been multiple works for classifying different plankton groups with different deep learning methods. Some of these methods are surveyed in this section. Correa at al. [64] proposed a CNN for microalgae classification. The study showed the ability of CNNs to classify FlowCAM particle analyzer data from the South Atlantic Ocean and also showed how data augmentation methods could improve the results. The dataset was composed of 19 classes with a total of 29,449 samples and a top-1 classification accuracy of was reported. Dai et al. [65] proposed ZooplanktoNet, a CNN architecture for zooplankton classification and reported a top-1 classification accuracy of The dataset consisted of microscopic grayscale zooplankton images captured by the ZooScan system. The data included 13 classes with a total of 9,460 samples. Different CNN architectures were surveyed,
34 34 like AlexNet, CaffeNet, VGGNet and GoogLeNet. The results showed that when data augmentation is used, the ZooplanktoNet architecture with appropriate parameters had a larger top-1 accuracy than the other surveyed architectures. In addition to comparing the classification accuracies, the training times of the networks were also compared. AlexNet and CaffeNet could be trained roughly in half an hour, VGGNet and GoogLeNet could be trained in roughly 55 minutes and the best performing ZooplanktoNet architecture could be trained roughly in 40 minutes. AlexNet, CaffeNet, VGGNet and GoogLeNet were also compared to each other when data augmentation was not used. Additionally, it was shown that parametric ReLU activations outperform standard ReLU activations by a small margin in the ZooplanktoNet architecture. Dai et al. [66] proposed a hybrid CNN architecture to improve plankton classification accuracies. The study used the WHOI-Plankton dataset as a base to create a data subset consisting of 30 classes with more than 1000 samples each. They used preprocessing methods to create local and global feature maps from their images and showed that a hybrid CNN architecture consisting of 3 separate inputs and convolutional channels could outperform a network with a single input and a convolutional channel. They applied this three-channel approach to the AlexNet and GoogLeNet architectures and reported a roughly percentage point increase in the classification accuracy. They reached a top-1 accuracy with the GoogLeNet hybrid architecture. The illustration of the hybrid architecture from their publication can be seen in Figure 10. The original input image, a locally preprocessed version of the input image and a globally preprocessed version of the input image are passed to three separate inputs leading to three separate convolutional channels. The three convolutional channels are combined in the fully connected layers to a single output layer. Li and Cui [67] proposed a deep residual network for plankton classification. The network architecture was based on VGGNet. Their dataset consisted of 30,336 grayscale images with 121 classes and they reported a top-5 accuracy of and a top-1 accuracy of This dataset was used for the National Data Science Bowl (NDSB), a data science competition hosted on the Kaggle platform. This dataset is referred to as the NDSB dataset. The winner of this competition was Deep Sea and they reached the top-1 accuracy of and the top-5 accuracy of Orenstein and Beijbom [43] studied transfer learning and deep feature extraction for plankton images. Their datasets included a recategorization of the NDSB data containing 37 classes and 30,336 samples captured using an In Situ Ichthyoplankton Imaging System near the straits of Florida, a recategorization of IFCB data captured at Martha s Vineyard
35 35 Figure 10. The illustration of a Hybrid CNN. FC refers to fully-connected layers and the numbers under FC refer to the number of neurons in the particular fully-connected layer. Conv11 and Conv3 refer to convolutional layers with filter sizes of 11x11 and 3x3 respectively and the numbers directly under them refer to the number of filters in the particular convolutional layers. [66] Coastal Observatory containing 53,239 samples separated into 95 classes and the Scripps Plankton Camera System data captured at Scripps Pier containing 3,200 samples separated into 4 classes. Their goal was to study the utility of using out-of-domain data to improve classification accuracies. They reached an 0.86 top-1 accuracy on the IFCB data using a CNN architecture based on AlexNet that was fine-tuned for the IFCB data. They reached a 0.83 top-1 accuracy on the NDSB dataset using a CNN architecture based on
36 36 AlexNet fine-tuned for the NDSB data. They reached a 0.77 top-1 accuracy on the Scripps Plankton Camera System data using a random forest utilizing hand crafted features and deep features extracted using a CNN. They showed a roughly 0.10 unit increase in accuracy when fine-tuning AlexNet weights compared to training the CNN from scratch. They also showed that the random forest utilizing only handcrafted features could reach a top-1 accuracy of 0.56 on the IFCB data, top-1 accuracy of 0.62 on the NDSB data and a top-1 accuracy of 0.69 on the Scripps Plankton Camera System data. Pedraza et al. [68] proposed a fine-tuned AlexNet for automatic diatom classification. The dataset consisted of 80 classes with 69,350 samples and the impacts of segmenting and normalizing the image data were studied. Three datasets were defined, the original dataset, a normalized version of the original dataset and a heterogeneous dataset containing both the normalized and original datasets. They reached a accuracy using the heterogeneous dataset. 3.5 Summary of plankton recognition studies Seemingly most common methods for automated plankton classification have been CNNs and random decision forests. CNN solutions for plankton classification tend to perform better than the random forest approaches. This is mainly because the deep feature extraction method of CNNs is superior to traditional feature extraction methods in terms of plankton classification [43] [68] [59]. The most relevant studies are shown in Table 1 to enable some degree of comparison and to illustrate how the average number of samples per class and the total number of classes impacts the classification accuracies. It is worth noting that some plankton taxa may be significantly easier to differentiate than others. Also based on taxonomic relations, some misclassifications of plankton may be more understandable than others. There are certainly more characteristics to consider in plankton recognition than just classification accuracy. A trend can be observed between the studies that used taxonomically similar data. Comparing [68] and [59], [65] and [43], and [43] and [67], it can be observed that having more classes in the data results in a decrease in the classification accuracy of the classifier and having less average samples per class in the data results in a decrease in the classification accuracy of the classifier.
37 37 Table 1. Comparison of solutions for plankton classification. Publication Data Classes Average Top-1 number of accuracy of samples per class Pedraza et al. [68] Diatoms Bueno et al. [59] Diatioms Dai et al. [66] The WHOI-Plankton dataset Dai et al. [65] Zooplankton Correa et al. [64] Microalgae Orenstein and Beijbom [43] Zooplankton Orenstein and Beijbom [43] Recategorization of the NDSB dataset Li and Cui [67] The NDSB dataset
38 38 4 EXPERIMENTS AND RESULTS The outline of this chapter is the following. The data is described. The data preprocessing methods are defined. The classification methods are described. The experiments are outlined. The evaluation criteria for the classifiers are defined. The results of the experiments are given. 4.1 Data The plankton data related to this thesis has been captured with an IFCB [69]. The IFCB is an in-situ automated submersible imaging flow cytometer. The IFCB captures roughly 3.4 pixels per µm resolution images of suspended particles in the size range of 10 to 150 µm. The device samples seawater at a rate of 15 ml per hour and can produce tens of thousands of images per hour. IFCB also gives analog-to-digital converted data from the photomultiplier tubes of the device. The photomultiplier tubes are used to detect light scatter and fluorescence from particles hit by the device laser and the analog-to-digital converted values of the photomultiplier tubes are used to determine whether a particle should be imaged or not. Example images can be seen in Figure 11. The dataset used to train and to test CNNs is the annotated and labeled portion of the image set collected by Kraft et al. from the Marine Research Centre of the Finnish Environment Institute during autumn 2016 and during spring 2017 to summer The 2017 data has been collected from the Utö Atmospheric and Marine Research Station [70] and the 2016 data from the Algaline ferrybox system of M/S Finnmaid and Silja Serenade. The event and analog-to-digital converted data is referred to as ADC-data and it is a portion of the dataset. The even data contains information about the performed imaging events like for instance the time of the imaging event. The dataset contains grayscale images and ADC-data of phytoplankton divided into 82 different classes. There is a large difference in the sizes of the images. The vertical axes of the images can range from 21 pixels to 770 pixels and the horizontal axes of the images can range from 52 pixels to 1,359 pixels. The pixel values of the images are scaled to values between zero and one. There is also a very large imbalance in the number of samples per class. Some classes have thousands of samples whereas some other classes have a single sample. The names of all the classes in the dataset and the corresponding number of samples in the classes can be seen in Table 2. The sp. is an abbreviation of species and it is used when the
39 39 Figure 11. Example phytoplankton images in the data. species name is unknown or can not be named. The taxonomic relations of the different classes are depicted in Figure 12. The taxonomic relations in the figure are based on [71]. In this thesis, only in the Figure 12 does the term class refer to the taxonomic rank and everywhere else it is used to describe the group a sample is labeled into. Three particular classes are removed from the dataset: Unclassified, Nanoplankton and Flagellates. Unclassified contains samples that could not be visually classified into any other class with reasonable certainty by a human expert. This makes up for roughly 50% of all screened samples. Nanoplankton and Flagellates are removed because they are classes that do not adhere to a real taxonomic rank and are similar to Unclassified. Nanoplankton and Flagellates both contain samples that could not be classified into any other class with a reasonable certainty by a human expert. The used features from the ADC-data include the original image dimensions and analogto-digital converted data of the average and peak values of the photomultiplier tubes during a laser pulse. The ADC-data is pseudo normalized to have values between 1 and 1. This is done by dividing the values of the features with the largest absolute value of each respective feature.
40 40 Table 2. Classes and the number of samples per class in the dataset. Class Samples Class Samples Unclassified Dinophysis acuminata 73 Nanoplankton 3200 Cluster A 72 Snowella Woronichinia sp. dense 2385 Uroglenopsis sp. 69 Dino small funny shaped 2070 Licmophora sp. 62 Chroococcus small 1446 Cyclotella choctawhatcheeana 55 Heterocapsa triquetra 1433 Euglenophyceae 42 Snowella Woronichinia sp. loose 1325 Cryptophyceae small 39 Dolichospermum Anabaenopsis 1223 Ceratoneis closterium 33 Chaetoceros sp. 916 Gymnodiniales 31 Peridiniella catenata single 871 Aphanothece paralleliformis 29 Pseudopedinella sp. 829 Pennales sp. curvy 28 Aphanizomenon flosaquae 821 Pennales sp. basic 25 Skeletonema marinoi 756 Chaetoceros similis 24 Thalassiosira levanderi 650 Melosira arctica 24 Pyramimonas sp. 623 Akinete 23 Heterocapsa rotundata 569 Amylax triacantha 21 Oocystis sp. 458 Monoraphidium contortum 19 Teleaulax sp. 413 Oscillatoriales 15 Mesodinium rubrum shrunken 346 Binuclearia lauterbornii 13 Mesodinium rubrum 287 Pauliella taeniata 13 Centrales sp. 249 Scenedesmus sp. 13 Prorocentrum cordatum 230 Chaetoceros throndsenii 12 Heterocyte 225 Apedinella radians 10 Dinophyceae under Chaetoceros resting stage 8 Eutreptiella sp. 190 Cryptophyceae Euglenophyceae 8 Flagellates 189 Chaetoceros subtilis 5 Cymbomonas tetramitiformis 150 Pauliella taeniata resting stage 5 Cyst like 150 Aphanizomenon sp. 4 Pennales sp. boxy 145 Dinobryon balticum 4 Peridiniella catenata chain 140 Nitzschia paleacea 4 Cryptomonadales 138 Chaetoceros danicus 3 Merismopedia sp. 138 Dinophysis norvegica 3 Cryptophyceae drop 136 Melosira arctica resting stage 3 Gymnodinium like 133 Nostocales 3 Ciliata strawberry 126 Coscinodiscus granii 2 Chroococcales 107 Dinophysis sp. 2 Beads 100 Gymnodinium sp. 2 Chlorococcales 88 Nodularia spumigena heterocyte 2 Katablepharis remigera 85 Rotifera 2 Nodularia sp.umigena 80 Amoeba 1 Ciliata 75 Dinophyceae over 20 1
41 Figure 12. Taxonomy of the classes in the dataset. The classes in the dataset are written in italics. 41
42 Figure 12. (continued). 42
43 43 The classes in the dataset are divided into four new data subsets called Subset100, Subset50, Subset20 and Subset10. The numbers in the subset names describe the threshold value that was used when the data subsets were created. For instance, Subset100 contains all the classes in the data with at least one hundred samples per class. Details of these data subsets can be seen in Table 3. The data subsets are randomly split into training sets and testing sets. A number of samples in a data subset are assigned to the testing set equal to 25% of the threshold value of the subset. The remaining samples are then assigned to the training set, up to one thousand. Table 3. Data subsets for the experiments. Name Thresholding Number Minimum number Test of of training samples samples classes per class per class Subset100 Classes with 100 samples Subset50 Classes with 50 samples Subset20 Classes with 20 samples Subset10 Classes with 10 samples Data preprocessing A traditional CNN requires the input images to have a predefined size. Resizing plankton images to a uniform size is done by reducing the size of the large images so that the larger axis of the image matches the target frame. The image aspect ratio is kept as constant as possible. Then the image is padded to match the target frame dimensions. The target frame refers to the desired size of the resized images. Images that are smaller than the target frame are enlarged to have their larger axis match the target frame and then the images are padded to fit the target frame. The images are resized with bicubic interpolation. Also, the effects of using the nearest-neighbor interpolation are tested. As there is a lot of background in the images, the mode of the image is used as the padding color for the image. The mode of an image is the most common pixel value in the image. The effects of using both black and white as padding colors are also tested. The implemented data augmentation methods include reflecting, 90-degree rotations and cropping 10 percent off the both ends of the larger image axis. The cropping is performed before the images are resized to a uniform size. Adding the reflected versions of the train-
44 44 ing samples to the training data doubles the amount of training data. Adding the cropped versions of the training samples to the training data doubles the amount of training data. Adding the rotated versions of the training samples to the training data quadruples the amount of training data. These augmentation methods allow for the generation of 16 times more training data for classes with few training samples. Because of the small number of samples in number of classes, data augmentation is performed on the training sets until each class contains one thousand samples. Duplicates of the samples are added if there are less than one thousand samples in a class after the data augmentation methods are used. 4.3 Proposed network structures The proposed network structures are based on AlexNet [14]. Validating any results related to class specific classification accuracies becomes computationally expensive because there are few samples in a moderate number of classes. As a result, smaller network architectures are more ideal for studying the impact of different methods related to increasing the classification accuracies of the CNNs in the scope of phytoplankton classification. The sequential network structures of the proposed networks can be seen in Tables 4 and 5, where n is the number of classes in data, p is the probability to dropout an activation and ADC_data is the number of features passed to the network form a secondary input. The feature vector passed from the secondary input is concatenated with the flattened feature map of the last convolutional layer. CNN256 takes in 256x256 sized images and CNN128 takes in 128x128 sized images. CNN256 consists of roughly four million trainable parameters and CNN128 consists of roughly three million trainable parameters. As a comparison, the AlexNet architecture consists of roughly 60 million trainable parameters [14]. It has been very clear that larger input images yield better classification accuracies, but also require increasingly more training time. CNN256 is merely the scaled up version of CNN128 for larger input images. The samples in the data subsets are resized to uniform 256x256 pixels for CNN256 and 128x128 pixels for CNN128. Examples of the resized 256x256 images can be seen in Figure 13.
45 45 Table 4. The sequential structure of CNN256. The network consists of roughly four million trainable parameters. The number of parameters depends on the number of classes. Layer Layer dimensions Parameters Output dimensions input 256x x256 convolutional 96x10x10 stride = 2x2 96x124x124 convolutional 96x6x6 stride = 2x2 96x60x60 maxpooling 2x2 stride = 2x2 96x30x30 convolutional 128x4x4 stride = 1x1 128x27x27 convolutional 160x4x4 stride = 1x1 160x24x24 maxpooling 2x2 stride = 2x2 160x12x12 convolutional 192x3x3 stride = 1x1 192x10x10 maxpooling 2x2 stride = 2x2 192x5x5 flatten 4800x1 fully-connected 512x x1 dropout 512x1 p = x1 fully-connected 512x x1 dropout 512x1 p = x1 fully-connected nx512 nx1 Table 5. The sequential structure of CNN128. The network consists of roughly three million trainable parameters. The number of parameters depends on the number of classes and the number of features given form the secondary input. Layer Layer dimensions Parameters Output dimensions input 128x x128 convolutional 96x10x10 stride = 2x2 96x60x60 convolutional 96x6x6 stride = 2x2 96x28x28 maxpooling 2x2 stride = 2x2 96x14x14 convolutional 128x3x3 stride = 1x1 128x12x12 convolutional 160x3x3 stride = 1x1 160x10x10 convolutional 192x3x3 stride = 1x1 192x8x8 maxpooling 2x2 stride = 2x2 192x4x4 flatten (3072+ADC_data)x1 fully-connected 512x x1 dropout 512x1 p = x1 fully-connected 512x x1 dropout 512x1 p = x1 fully-connected nx512 nx1
46 46 Centrales Chroococcales Dinophysis Dolichospermum Oocystis acuminata Anabaenopsis Figure 13. Examples of the resized plankton images. 4.4 Description of experiments CNN256 was trained for 70 epochs on the Subset100, Subset50, Subset20 and Subset10 training data with Nesterov s method [33] using learning rate of 0.01, momentum of 0.9 and batch size of 256. The parameters are based on small scale empiric tests and it was observed that the CNN can be trained successfully with these parameters. The network accuracy was tested every 5 epochs with the appropriate testing set. Additionally, CNN256 was trained on a variation of Subset50 where the images that were too small for the network input were only padded, instead of having them enlarged first and then having them padded. CNN128 was trained for 70 epochs on the Subset50 training data with Nesterov s method using learning rate of 0.01, momentum of 0.9 and batch size of 256. The network accuracy was tested every 5 epochs with the appropriate testing set. CNN128 was not given any ADC-data from the secondary input. Different variations of this experiment were
47 47 performed as follows: The height and width of the original images were given to the network from the secondary input, instead of giving nothing from the secondary input. The height and width of the original images and the average and the peak analogto-digital converted photomultiplier tube values were given to the network from the secondary input, instead of giving nothing from the secondary input. The network was trained using samples that were padded with white, instead of using samples padded with the mode of the images. The network was trained using samples that were padded with black, instead of using samples padded with the mode of the images. The network was trained using samples resized with the nearest-neighbor interpolation, instead of using samples resized with the bicubic interpolation. The network was trained using the parametric ReLU activation function in all the fully-connected and convolutional layers of the network, instead of using the ReLU activation function. The network was trained using only 90-degree rotations and reflections of the images as data augmentation methods, instead of also using cropping as a data augmentation method. The network was trained using no data augmentation methods, instead of using data augmentation methods. The network was trained using no dropout layers, instead of using the two dropout layers in the network. The network was trained using 1024 nodes in the fully connected layers, instead of 512 nodes. The network was trained without a pooling layer after the last convolutional layer, instead of having a pooling layer after the last convolutional layer. Random decision forests were created from the Subset100, Subset50, Subset20 and Subset10 training data consisting of a thousand decision trees that were created from subsets of 31 samples of the training data. The MATLAB toolboxes ifcb-analysis [72] and
48 48 DIPUM [62] were used for the feature extraction. DIPUM is a MATLAB toolbox containing implementations of digital image processing methods. The feature vector consisted of 237 features. The names of the features are listed in Table 6. The features included seven different moment invariants, 48 different wedges, 50 different rings and 81 different histograms of gradients. The feature extraction was performed on the original images in the data subsets, not on the resized versions. Table 6. Names of the extracted features. roi number Biovolume BoundingBox ywidth ConvexPerimeter EquivDiameter FeretDiameter H90 MajorAxisLength Orientation RWcenter2total powerratio Solidity shapehist kurtosis normeqd shapehist median normeqd shapehist skewness normeqd summedbiovolume summedconvexperimeter summedmajoraxislength summedperimeter texture average gray level texture smoothness texture uniformity RotatedBoundingBox xwidth Area over PerimeterSquared H90 over Hflip Hflip over H180 rotated BoundingBox solidity Rings Moment invariants Area BoundingBox xwidth ConvexArea Eccentricity Extent H180 Hflip MinorAxisLengt Perimeter RWhalfpowerintegral numblobs shapehist mean normeqd shapehist mode normeqd summedarea summedconvexarea summedferetdiameter summedminoraxislength texture average contrast texture entropy texture third moment RotatedArea RotatedBoundingBox ywidth Area over Perimeter H90 over H180 summedconvexperimeter over Perimeter Wedges Histograms of gradients Three class distributions were also created and studied. The first was the distribution of all the samples in Subset10, referred as the labeled distribution. The second one was the distribution of the class Unclassified that was classified using CNN256 trained on the Subset10, referred as the unclassified distribution. The idea was to see how similar these two distributions were and perhaps the similarity would allow for the identification of
49 49 some of the more problematic classes. The last distribution was the sum of the labeled and CNN classified distributions, referred as the estimated distribution. 4.5 Evaluation criteria To evaluate performance and to compare different methods, the classification performances were measured using top-k accuracies as defined in Section 3.3 Equation 21 and confusion matrices. A confusion matrix consists of correct class labels on one axis and class predictions on the other axis. The confusion matrix cells contain the number of samples that had the respective correct class and classification results. The diagonal of the confusion matrix corresponds to the number of correctly classified samples in each class. The confusion matrix can be normalized so that the sums along the axis representing the correct class labels is equal to one. This can be done by dividing the value of each cell by the number of test samples in each corresponding class. The class specific accuracies of the classifiers correspond to the values from the diagonals of the normalized confusion matrices. Cross validation was used to validate the results. The top-k accuracies in Section 4.6 and the confusion matrices in the Appendices are the average top-k accuracies and the average confusion matrices of the cross validations. The standard deviations were also calculated for the top-1 accuracies of the cross validations. The standard deviation can be defined as s = N i=1 (x i x) 2 N 1 (23) where N is the number of cross validations, x i is the top-1 accuracy of the ith cross validation and x is the average top-1 accuracy of the cross validations. The top-1 accuracies are given with the notation of top-1 accuracy±standard deviation. 4.6 Results The number of cross validations depend on the number of testing samples in the different data subsets. Classifiers trained with the data subsets containing less testing samples per class are cross validated more in order to have a reasonable certainty of the result. The training of CNN256 on the data subsets Subset100, Subset50, Subset20 and Subset10 and the respective top-1, top-2, top-3 and top-5 accuracies on the testing set can be seen in
50 50 Figures The confusion matrices can be found from the Appendices 1-4. The results for CNN256 for the data subsets Subset100, Subset50, Subset20 and Subset10 have been cross validated 30, 30, 30 and 60 times respectively. Based on the confusion matrices and the Figure 12, the largest confusions in the confusion matrices tend to be between taxonomically more closely related classes Accuracy Epoch Top-1 accuracy Top-2 accuracy Top-3 accuracy Top-5 accuracy Figure 14. Accuracies of CNN256 with Subset100. The classification accuracies of different classes with CNN256 on Subset10 and the total number of samples in the classes in the whole dataset can be seen in Table 7. A comparison of the top-1 accuracies between CNN256 and the random forest implementation can be seen in Table 8. The results of the random forest implementation for the data subsets Subset100, Subset50, Subset20 and Subset10 were cross validated 10, 10, 30 and 60 times respectively. The results from the random forest classifier have not been cross validated as much as the results from CNN256, because a lesser number of cross validations was enough to show the significant gap between the classification accuracies of the two classification methods. CNN256 performs significantly better than the random forest implementation with the same data. This is likely due to the deep feature extraction being superior to traditional feature extraction methods and this result agrees with other studies surveyed in Section 3.4. Also, the lack of data augmentation for the random forest
51 51 Accuracy Epoch Figure 15. Accuracies of CNN256 with Subset50. Top-1 accuracy Top-2 accuracy Top-3 accuracy Top-5 accuracy Accuracy Epoch Figure 16. Accuracies of CNN256 with Subset20. Top-1 accuracy Top-2 accuracy Top-3 accuracy Top-5 accuracy
52 Accuracy Epoch Figure 17. Accuracies of CNN256 with Subset10. Top-1 accuracy Top-2 accuracy Top-3 accuracy Top-5 accuracy implementation explains the lower classification accuracy of the forest to some degree. Training CNN256 on the variation of Subset50, where the images that were too small for the network input were only padded, instead of enlarging them first and then padding them resulted in a top-1 classification accuracy of 0.800± It was thought that the network might benefit from information about the original sizes of the images, but this resulted in a decrease in the top-1 classification accuracy when compared to training CNN256 on Subset50. It seems to be beneficial in this particular case to enlarge images that would otherwise be too small for the CNN. The results with the different variations of CNN128 can be seen in Table 9. These results have been cross validated 30 times. From Table 9, it can be seen that giving CNN128 ADC-data does not increase the top-1 classification accuracy of the network. It can be seen that using the mode of the images as a padding color results in an increased top- 1 classification accuracy, contrary to using white or black as a padding color. Resizing images with the bicubic interpolation also results in a better top-1 accuracy than using the nearest-neighbor interpolation. A small increase in the top-1 accuracy of CNN128 is observed when using the parametric ReLU activation function instead of the ReLU activation function.
53 53 Table 7. A table of the classes in Subset10, the total number of samples in the classes and the classification accuracies of the classes with CNN256 on Subset10. Class Samples Accuracy Snowella Woronichinia sp. dense Dino small funny shaped Chroococcus small Heterocapsa triquetra Snowella Woronichinia sp. loose Dolichospermum Anabaenopsis Chaetoceros sp Peridiniella catenata single Pseudopedinella sp Aphanizomenon flosaquae Skeletonema marinoi Thalassiosira levanderi Pyramimonas sp Heterocapsa rotundata Oocystis sp Teleaulax sp Mesodinium rubrum shrunken Mesodinium rubrum Centrales sp Prorocentrum cordatum Heterocyte Dinophyceae under Eutreptiella sp Cymbomonas tetramitiformis Cyst like Pennales sp. boxy Peridiniella catenata chain Cryptomonadales Merismopedia sp Cryptophyceae drop Gymnodinium like A small decrease in the top-1 accuracy of the network is observed when opting to no use cropping as a data augmentation method. A signification decrease in the network top-1 accuracy can be seen when no data augmentation methods are used. This accuracy is higher than the top-1 accuracy of the random forest trained on Subset50 and further goes to show the superior performance of the deep feature extraction compared to hand crafted feature approaches. The importance of using dropout can also be seen. The top-1 accuracy of the network drops drastically when opting to use not dropout.
54 54 Table 7. (continues). Class Samples Accuracy Ciliata strawberry Chroococcales Beads Chlorococcales Katablepharis remigera Nodularia sp.umigena Ciliata Dinophysis acuminata Cluster A Uroglenopsis sp Licmophora sp Cyclotella choctawhatcheeana Euglenophyceae Cryptophyceae small Ceratoneis closterium Gymnodiniales Aphanothece paralleliformis Pennales sp. curvy Pennales sp. basic Chaetoceros similis Melosira arctica Akinete Amylax triacantha Monoraphidium contortum Oscillatoriales Binuclearia lauterbornii Pauliella taeniata Scenedesmus sp Chaetoceros throndsenii Apedinella radians Table 8. The top-1 classification accuracies of CNN256 and the random forest, with the different data subsets. Data subset CNN256 The random forest subset ± ± subset ± ± subset ± ± subset ± ± 0.031
55 55 Having 1024 nodes in the fully-connected layers resulted in a 0.804± top-1 accuracy at 70 epochs, the network was then trained to 100 epochs and the top-1 accuracy increased to 0.813± Increasing the number of nodes at the fully-connected layers has clear potential to increase the top-1 accuracies. The increase from 512 nodes to 1028 nodes roughly doubled the number of parameters in the network and resulted in a need to train the network longer. Consequently, increasing the network size rapidly increases the amount of time it takes to train the network. Removing the last pooling layer of the network clearly reduced the network top-1 accuracy. Removing the last pooling layer from the network roughly quadruples the number of parameters in the network. It can be hypothesized that continuing the training for dozens of epochs may result in an increased top-1 accuracy. It can be seen that the CNN256 performs better on Subset50 than CNN128, clearly the size of the input images impacts the performance of the networks. Table 9. The top-1 classification accuracies with the variations of CNN128. Variation The top-1 accuracy No variation 0.809± Original image dimensions as features 0.807± Original image dimensions, average and peak 0.809± photomultiplier tube values as features White as a padding color 0.801± Black as a padding color 0.793± Resize images with the nearest-neighbor interpolation 0.804± Parametric ReLU 0.812± No cropping as an augmentation method 0.800± No data augmentation 0.713± No dropout layers 0.727± nodes in fully-connected layers 0.804± Last pooling layer removed 0.793± The normalized plankton distributions as introduced in Section 4.4 can be seen in Figure18. The CNN classified distribution has been cross validated 60 times. Examples of samples from Subset10 that were misclassified with CNN256 with some of the highest and lowest classification confidences can be seen in Figures 19 and 20. The classification confidence of a sample corresponds to the posterior probability of the class with the largest posterior probability given by the network.
56 Figure 18. Bar diagram of the normalized plankton distributions. Estimate is the estimated distribution, Labeled is the labeled distribution and Unclassified is the unclassified distribution. 56
57 Figure 19. Misclassified images with some of the highest classification confidences. Misclassified images on the left and example images from the corresponding correct class on the right. The number before the name of the misclassified sample is the classification confidence of the CNN. 57
58 Figure 19. (continued). 58
59 Figure 20. Misclassified images with some of the lowest classification confidences. Misclassified images on the left and example images from the corresponding correct class on the right. The number before the name of the misclassified sample is the classification confidence of the CNN. 59
60 60 5 DISCUSSION 5.1 Current study CNN256 was trained on Subset100, Subset50, Subset20 and Subset 10 and the results were compared to a random forest implementation trained on the same data subsets. CNN256 was also trained on a variation of Subset50. CNN128 was trained on Subset50 and multiple variations of this experiment were done. Three distributions were created based on the results with training CNN256 on Subset10. For the CNN implementation, problems related to the class imbalance in the number of samples per class were avoided to a large degree by augmenting the data. Using 90-degree rotations and reflections, the top-1 classification accuracy of cnn128 was significantly improved and using cropping as an additional data augmentation method further improved the results by a small margin. The effectiveness of data augmentation for plankton images agrees with other studies surveyed in Section 3.4. Problems related to the variations in the image sizes were solved to a degree by resizing and padding the images. The bicubic interpolation works better in this case than the nearest-neighbor interpolation. Additionally, it was shown that it is beneficial to enlarge images rather than only add padding to them. It can clearly be beneficial to have enlarged regions of interest. The smallest images in the dataset have dimensions equaling 21x52 pixels and the convolutional filters in the first convolutional layer of the CNN256 have dimensions of 10x10. It may also be that the size of the convolutional filters in the first convolutional layer are simply too large to efficiently extract good consistent features from the regions of interest in the smallest images in the dataset. Problems related to the errors in the ground truth were solved to an unknown degree by implementing dropout that forces the CNN to generalize. By forcing the network to generalize, the impact of outliers and erroneously labeled samples diminishes. This is likely to works well because of the relatively small number of expected actual errors in the ground truth. There are a few additional things worth noting about the results. Dropout proved to be very effective for preventing overfitting. Overfitting was not observed in any CNN that had incorporated dropout. This result agrees with [40]. The variations in the image sizes do not cause problems for the random forest implementation. The random forest is an ensemble of classifiers; hence, it inherently forces generalization, and thus dilutes the effects of erroneously labeled training samples.
61 61 The few-shot learning problem is real. Table 8 shows that the classification accuracy of the CNN and the random forest decreases as more classes with less samples are introduced. Also, the classification accuracies of the classes in Table 7 are on average seemingly smaller for the classes with fewer samples. However, many of the classes with less than 100 samples are classified with high accuracies. For instance, Pauliella taeniata has only 13 samples and the samples are classified with a 0.94 accuracy. The top-1 accuracy of the CNNs could be compared to the top-1 accuracies of the classifiers listed in Section 3.5 Table 1. From the table, the microalgae data in Correa et al. [64] is taxonomically the most similar data to the phytoplankton data used in this thesis. However, due to the diversity of phytoplankton species, the results are not directly comparable. Studies on the same data are required to compare the accuracies of different classification methods. Nevertheless, the classification accuracies of the CNNs in this thesis seem to fit the trend that more classes in the data results in a decrease in the classification accuracy and less samples per class in the data results in a decrease in the classification accuracy. It is possible to identify a few problematic classes from the confusion matrix found in Appendix 2. Two problematic classes can be identified, which are Chlorococcales and Ciliata with classification accuracies of 0.48 and 0.47 respectively. The confusion matrices are important knowledge for biologists as the classification accuracies of the classes should correlate to a degree with the errors in the ground truth. Some of the confusions are significantly more reasonable than others. For instance, from the confusion matrix in Appendix 3, misclassifications between Pennales sp. curvy and Pennales sp. boxy can be seen. These classes are taxonomically more closely related than classes like Chlorococcales and Snowella Woronichinia sp. loose and hence the misclassifications can be better understood. The distributions of the labeled training samples and the CNN classified samples clearly correlate despite the large fluctuations as shown in Figure 18. There are several ways how the differences in the distributions can be explained and one probably should not expect the distributions to match too well. For instance, important features may be hard for humans to detect for some plankton species, resulting in most of these samples being left in Unclassified. The reverse case is also true where plankton species with easily visible clear features are likely to have most of their samples labeled. Nevertheless, the relative differences between the labeled distribution and the unclassified distribution are indicators of possible problems. For instance, Chaetoceros throndsenii has roughly 14 times more CNN classified samples than labeled samples, Cluster A has roughly 9 times more CNN classified samples than labeled samples and Centrales sp. has roughly 7 times
62 62 more labeled samples than CNN classified samples. The large relative difference in the number of Chaetoceros throndsenii samples in the distributions can be explained by the few-shot learning problem as there are only 12 samples in this particular class. However, this is not the case for Cluster A and Centrales sp., both of these classes have a reasonable number of labeled samples and both of these classes exhibit good top-1 classification accuracies of over 0.80, as seen in Table 7. There are also other classes with similar cases. Logically the samples in Unclassified are more likely to belong to and to be classified into classes of higher taxonomic rank. This is because the samples do not have clear features by definition to match the characteristics of classes with lower taxonomic ranks, otherwise they probably could have been labeled by human experts. Nevertheless, it is unclear to what extent does this explain the fluctuations between the labeled and CNN classified distributions. The real distribution of the plankton species in the original dataset was estimated by summing the labeled and CNN classified distributions. The estimated distribution can give us an estimate of how important it is to correctly classify samples in a particular class. Practically all of the classes that make up an above average portion of the estimated distribution are classified with an above 0.80 accuracy or have very reasonable confusions. This is obviously caused partially by the above average amount of available labeled samples in these classes. However, there is one class that has a high number of labeled samples yet boasts a 0.63 accuracy: Dino small funny shaped. This class has the second largest number of labeled samples and it is the second largest class in the estimation of the real distribution. Dino small funny shaped is mainly confused with Heterocapsa triquetra and these two classes are taxonomically under the same class. 5.2 Future work Due to the CNN platform and the time limitations, the spatial pyramid pooling was not implemented in this thesis work. It would be interesting to see how much the classification result could be improved. The unlabeled portion of the data contains images of scraps, trash, bubbles, other inanimate particles, unknown plankton and images with multiple plankton in them. To have a CNN work in practice for automated plankton classification, a way to appropriately classify the unlabeled portion of the data, is required. Other studies in Section 3.4 have shown success for CNNs when dealing with zooplank-
63 63 ton. There are clear grounds to believe in the applicability of the proposed CNN architectures when dealing with plankton not limited to phytoplankton nor to the Baltic Sea. Training a significantly larger network is likely to increase the top-1 classification accuracy, it would be interesting to see to what extent can the top-1 accuracy be increased. Employing transfer learning can be beneficial and it would be interesting to see the results of fine-tuning networks that have been trained on different plankton data sets.
64 64 6 CONCLUSION The objectives of this thesis were to train a CNN classifier for automated phytoplankton classification, to explore methods to increase the classification accuracy and to compare the CNN to an existing random forest classifier. The task was limited to micro- and nanophytoplankton collected from the Baltic Sea. Additionally, there were three data related challenges: the large disparity in the image sizes, the large disparity in the number of samples per class, and erroneously labeled samples were expected in the data. A CNN based on AlexNet was trained on phytoplankton data which clearly outperformed the random forest solution in the experiments. Class imbalance was solved by data augmentation methods. Augmenting the data with 90-degree rotations and reflections of the samples improved the CNN s top-1 accuracy and augmenting the data with a cropping based method further increased the top-1 accuracy. With the subset of data containing all the classes with at least 50 samples, the best achieved top-1 accuracy was The large disparity in the image sizes were solved by resizing and padding the images to uniform size. The bicubic interpolation provided a better classification accuracy than the nearest neighbor interpolation. The impact of the errors in the ground truth were alleviated by forcing the CNN to generalize, which was achieved by employing dropout which also prevented the networks from overfitting. The real distribution of the data was estimated as the sum of the labeled distribution of samples and the CNN classified distribution of samples. Potentially problematic classes were identified from the dataset based on the confusion matrices and the different distributions. Potential future work was also outlined, including studying the applicability of CNNs for plankton classification not limited to the Baltic Sea nor to phytoplankton and studying the benefits of a spatial pooling pyramid, larger network architectures and transfer learning.
65 65 REFERENCES [1] Carol Lalli and Timothy R Parsons. Biological Oceanography: an Introduction. Elsevier, [2] Diane K Stoecker. Conceptual models of mixotrophy in planktonic protists and some ecological and evolutionary implications. European Journal of Protistology, 34(3): , [3] Ben A Ward and Michael J Follows. Marine mixotrophy increases trophic transfer efficiency, mean organism size, and vertical carbon flux. In Proceedings of the National Academy of Sciences, volume 113, pages , [4] Iain M Suthers and David Rissik. Plankton: a Guide to Their Ecology and Monitoring for Water Quality. Commonwealth Scientific and Industrial Research Organisation, [5] Paul G Falkowski. The role of phytoplankton photosynthesis in global biogeochemical cycles. Photosynthesis Research, 39(3): , [6] Milan Sonka, Vaclav Hlavac, and Roger Boyle. Image Processing, Analysis, and Machine Vision. Cengage Learning, [7] Jerome Friedman, Trevor Hastie, and Robert Tibshirani. The Elements of Statistical Learning, volume 1. Springer, [8] Ethem Alpaydin. Introduction to Machine Learning. MIT Press, [9] Yoshua Bengio, Aaron Courville, and Pascal Vincent. Representation learning: a review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, 35(8): , [10] Stuart J Russell and Peter Norvig. Artificial Intelligence: a Modern Approach. Prentice-Hall, Inc., 3rd edition, [11] Kunihiko Fukushima. Neocognitron: a self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position. Biological Cybernetics, 36(4): , [12] Yann LeCun, Patrick Haffner, Léon Bottou, and Yoshua Bengio. Object recognition with gradient-based learning. In Lecture Notes in Computer Science: Shape, Contour and Grouping in Computer Vision, pages Springer, 1999.
66 66 [13] David H Hubel and Torsten N Wiesel. Receptive fields and functional architecture of monkey striate cortex. The Journal of Physiology, 195(1): , [14] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. Imagenet classification with deep convolutional neural networks. In Proceedings of Advances in Neural Information Processing Systems, pages , [15] Steven B Damelin and Willard Miller Jr. The Mathematics of Signal Processing. Cambridge University Press, [16] Cs231n convolutional neural networks for visual recognition. Online; accessed: March, 30, [17] Dominik Scherer, Andreas Müller, and Sven Behnke. Evaluation of pooling operations in convolutional architectures for object recognition. In Proceedings of International Conference on Artificial Neural Networks, pages [18] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Spatial pyramid pooling in deep convolutional networks for visual recognition. In Proceedings of European Conference on Computer Vision, pages , [19] Josef Sivic and Andrew Zisserman. Video Google: a text retrieval approach to object matching in videos. In Proceedings of Ninth IEEE International Conference on Computer Vision, page 1470, [20] Karl Pearson. Contributions to the mathematical theory of evolution. II. skew variation in homogeneous material. Philosophical Transactions of the Royal Society of London.(A.), (186): , [21] Balázs Csanád Csáji. Approximation with artificial neural networks. Master s thesis, Faculty of Sciences, Etvs Lornd University, Hungary, [22] George Cybenko. Approximations by superpositions of a sigmoidal function. Mathematics of Control, Signals and Systems, 2: , [23] Kurt Hornik. Approximation capabilities of multilayer feedforward networks. Neural Networks, 4(2): , [24] Richard HR Hahnloser, Rahul Sarpeshkar, Misha A Mahowald, Rodney J Douglas, and H Sebastian Seung. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature, 405(6789):947, 2000.
67 67 [25] Jun Han and Claudio Moraga. The influence of the sigmoid function parameters on the speed of backpropagation learning. In Proceedings of International Workshop on Artificial Neural Networks, pages Springer, [26] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving deep into rectifiers: surpassing human-level performance on imagenet classification. In Proceedings on the IEEE International Conference on Computer Vision, pages , [27] Matthew D Zeiler and Rob Fergus. Visualizing and understanding convolutional networks. In Proceedings of European Conference on Computer Vision, pages Springer, [28] Solomon Kullback and Richard A Leibler. On information and sufficiency. The Annals of Mathematical Statistics, 22(1):79 86, [29] Kevin P Murphy. Machine Learning: a Probabilistic Perspective. MIT Press, [30] David E Rumelhart, Geoffrey E Hinton, and Ronald J Williams. Learning representations by back-propagating errors. Nature, 323(6088):533, [31] Peter D Lax and Maria Shea Terrell. Calculus with Applications. Springer, [32] Herbert Robbins and Sutton Monro. A stochastic approximation method. The Annals of Mathematical Statistics, pages , [33] Yurii Nesterov. Introductory Lectures on Convex Optimization: a Basic Course. Springer Science & Business Media, [34] Sepp Hochreiter, Yoshua Bengio, Paolo Frasconi, and Jürgen Schmidhuber. Gradient flow in recurrent nets: the difficulty of learning long-term dependencies. In A Field Guide to Dynamical Recurrent Neural Networks. Wiley-IEEE Press, [35] Xavier Glorot, Antoine Bordes, and Yoshua Bengio. Deep sparse rectifier neural networks. In Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, pages , [36] Yoshua Bengio, Patrice Simard, and Paolo Frasconi. Learning long-term dependencies with gradient descent is difficult. IEEE Transactions on Neural Networks, 5(2): , [37] Razvan Pascanu, Tomas Mikolov, and Yoshua Bengio. On the difficulty of training recurrent neural networks. In Proceeding of International Conference on Machine Learning, pages , 2013.
68 68 [38] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings on the IEEE Conference on Computer Vision and Pattern Recognition, pages , [39] Douglas M Hawkins. The problem of overfitting. Journal of Chemical Information and Modeling, 44(1):1 12, [40] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: a simple way to prevent neural networks from overfitting. The Journal of Machine Learning Research, 15(1): , [41] Olaf Ronneberger, Philipp Fischer, and Thomas Brox. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, pages , [42] Li Fei-Fei. Knowledge transfer in learning to recognize visual objects classes. In Proceedings on International Conference on Development and Learning, pages 1 8, [43] Eric C Orenstein and Oscar Beijbom. Transfer learning and deep feature extraction for planktonic image data sets. In Proceedings of 2017 IEEE Winter Conference on Applications of Computer Vision, pages , [44] Rafael C Gonzalez and Richard E Woods. Digital Image Processing. Prentice-Hall, Inc., 3rd edition, [45] Robert Keys. Cubic convolution interpolation for digital image processing. IEEE Transactions on Acoustics, Speech, and Signal Processing, 29(6): , [46] Jake Snell, Kevin Swersky, and Richard Zemel. Prototypical networks for few-shot learning. In Proceedings of Advances in Neural Information Processing Systems, pages , [47] Oriol Vinyals, Charles Blundell, Timothy Lillicrap, Daan Wierstra, et al. Matching networks for one shot learning. In Proceedins on Advances in Neural Information Processing Systems, pages , [48] Christiane Lemke, Marcin Budka, and Bogdan Gabrys. Metalearning: a survey of trends and technologies. Artificial Intelligence Review, 44(1): , [49] Rich Caruana. Multitask learning. Machine Learning, 28(1):41 75, 1997.
69 69 [50] Josh Attenberg, Kilian Weinberger, Anirban Dasgupta, Alex Smola, and Martin Zinkevich. Collaborative -spam filtering with the hashing trick. In Proceedings on the Sixth Conference on and Anti-Spam, [51] Francisco Caio Maia Rodrigues, Nina ST Hirata, Antonio A Abello, T Leandro, De La Cruz, Rubens M Lopes, and Roberto Hirata Jr. Evaluation of transfer learning scenarios in plankton image classification. In Proceedings of International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (5: International Conference on Computer Vision Theory and Applications), pages , [52] Howard M Shapiro. Practical Flow Cytometry. John Wiley & Sons, [53] Bengt Karlson, Felipe Artigas, Veronique Créach, Arnaud Louchart, Guilliaume Wacquet, and Jukka Seppälä. Novel methods for automated in situ observations of phytoplankton diversity. WP 3, D3.1, Version 9. IFREMER for JERICO-NEXT, [54] Joseph W Goodman and RW Lawrence. Digital image formation from electronically detected holograms. Applied physics letters, 11(3):77 79, [55] Video plankton recorder. Online; accessed: May, 5, [56] Walter S Judd, Christopher S Campbell, Elizabeth A Kellogg, Peter F Stevens, and Michael J Donoghue. Plant Systematics. Sinauer Sunderland, [57] Colin S Reynolds. The Ecology of Phytoplankton. Cambridge University Press, [58] Alain Sournia, M-J Chrdtiennot-Dinet, and Michel Ricard. Marine phytoplankton: How many species in the world ocean? Journal of Plankton Research, 13(5): , [59] Gloria Bueno, Oscar Deniz, Anibal Pedraza, Jesús Ruiz-Santaquiteria, Jesús Salido, Gabriel Cristóbal, María Borrego-Ramos, and Saúl Blanco. Automated diatom classification (Part A): Handcrafted feature approaches. Applied Sciences, 7(8):753, [60] Kai-Bo Duan and S Sathiya Keerthi. Which is the best multiclass SVM method? An empirical study. In International Workshop on Multiple Classifier Systems, pages Springer, 2005.
70 70 [61] Iñigo Barandiaran. The random subspace method for constructing decision forests. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(8), [62] Rafael C Gonzalez, Richard E Woods, and Steven L Eddins. Digital Image Processing Using MATLAB. Gatesmark Publishing, 2nd edition, [63] Lynne Boddy, CW Morris, MF Wilkins, GA Tarran, and PH Burkill. Neural network analysis of flow cytometric data for 40 marine phytoplankton species. Cytometry: The Journal of the International Society for Analytical Cytology, 15(4): , [64] Iago Correa, Paulo Drews, Silvia Botelho, Marcio Silva de Souza, et al. Deep learning for microalgae classification. In Proceedings of 16th IEEE International Conference on Machine Learning and Applications, pages 20 25, [65] Jialun Dai, Ruchen Wang, Haiyong Zheng, Guangrong Ji, and Xiaoyan Qiao. Zooplanktonet: Deep convolutional network for zooplankton classification. In Proceedings of OCEANS 2016-Shanghai, pages 1 6, [66] Jialun Dai, Zhibin Yu, Haiyong Zheng, Bing Zheng, and Nan Wang. A hybrid convolutional neural network for plankton classification. In Proceedings of Asian Conference on Computer Vision, pages , [67] Xiu Li and Zuoying Cui. Deep residual networks for plankton classification. In Proceedings of OCEANS 2016 MTS/IEEE Monterey, pages 1 4, [68] Anibal Pedraza, Gloria Bueno, Oscar Deniz, Gabriel Cristóbal, Saúl Blanco, and María Borrego-Ramos. Automated diatom classification (Part B): A deep learning approach. Applied Sciences, 7(5):460, [69] Robert J Olson and Heidi M Sosik. A submersible imaging-in-flow instrument to analyze nano-and microplankton: Imaging FlowCytobot. Limnology and Oceanography: Methods, 5(6): , [70] Kaisa Kraft, Jukka Seppälä, Heidi Hällfors, Sanna Suikkanen, Sílvia Anglès, Sami Kielosto, Harri Kuosa, Lauri Laakso, Sirpa Lehtinen, Johanna Oja, and Timo Tamminen. Unpublished data. [71] Guy Hällfors. Checklist of Baltic Sea Phytoplankton Species (including some heterotrophic protistan groups). Helsinki Commission, Baltic Marine Environment Protection Commission, [72] ifcb-analysis. Online; accessed: April, 11, 2019.
71 Appendix 1. The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 100 samples (Subset100). The confusions are shown as percentages (%).
72 Appendix 2. The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 50 samples (Subset50). The confusions are shown as percentages (%).
73 Appendix 3. The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 20 samples (Subset20). The confusions are shown as percentages (%).
74 Appendix 4. The confusion matrix of convolutional neural network (CNN256) classification of classes with at least 10 samples (Subset10). The confusions are shown as percentages (%).
Capacity Utilization
 Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Capacity Utilization Tim Schöneberg 28th November Agenda Introduction Fixed and variable input ressources Technical capacity utilization Price based capacity utilization measure Long run and short run
Efficiency change over time
 Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
Efficiency change over time Heikki Tikanmäki Optimointiopin seminaari 14.11.2007 Contents Introduction (11.1) Window analysis (11.2) Example, application, analysis Malmquist index (11.3) Dealing with panel
The CCR Model and Production Correspondence
 The CCR Model and Production Correspondence Tim Schöneberg The 19th of September Agenda Introduction Definitions Production Possiblity Set CCR Model and the Dual Problem Input excesses and output shortfalls
The CCR Model and Production Correspondence Tim Schöneberg The 19th of September Agenda Introduction Definitions Production Possiblity Set CCR Model and the Dual Problem Input excesses and output shortfalls
Other approaches to restrict multipliers
 Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Other approaches to restrict multipliers Heikki Tikanmäki Optimointiopin seminaari 10.10.2007 Contents Short revision (6.2) Another Assurance Region Model (6.3) Cone-Ratio Method (6.4) An Application of
Gap-filling methods for CH 4 data
 Gap-filling methods for CH 4 data Sigrid Dengel University of Helsinki Outline - Ecosystems known for CH 4 emissions; - Why is gap-filling of CH 4 data not as easy and straight forward as CO 2 ; - Gap-filling
Gap-filling methods for CH 4 data Sigrid Dengel University of Helsinki Outline - Ecosystems known for CH 4 emissions; - Why is gap-filling of CH 4 data not as easy and straight forward as CO 2 ; - Gap-filling
Returns to Scale II. S ysteemianalyysin. Laboratorio. Esitelmä 8 Timo Salminen. Teknillinen korkeakoulu
 Returns to Scale II Contents Most Productive Scale Size Further Considerations Relaxation of the Convexity Condition Useful Reminder Theorem 5.5 A DMU found to be efficient with a CCR model will also be
Returns to Scale II Contents Most Productive Scale Size Further Considerations Relaxation of the Convexity Condition Useful Reminder Theorem 5.5 A DMU found to be efficient with a CCR model will also be
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward.
 START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
START START SIT 1. SIT. The handler and dog stop with the dog sitting at heel. When the dog is sitting, the handler cues the dog to heel forward. This is a static exercise. SIT STAND 2. SIT STAND. The
16. Allocation Models
 16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
16. Allocation Models Juha Saloheimo 17.1.27 S steemianalsin Optimointiopin seminaari - Sks 27 Content Introduction Overall Efficienc with common prices and costs Cost Efficienc S steemianalsin Revenue
National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007
 National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007 Chapter 2.4 Jukka Räisä 1 WATER PIPES PLACEMENT 2.4.1 Regulation Water pipe and its
National Building Code of Finland, Part D1, Building Water Supply and Sewerage Systems, Regulations and guidelines 2007 Chapter 2.4 Jukka Räisä 1 WATER PIPES PLACEMENT 2.4.1 Regulation Water pipe and its
Alternative DEA Models
 Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
Mat-2.4142 Alternative DEA Models 19.9.2007 Table of Contents Banker-Charnes-Cooper Model Additive Model Example Data Home assignment BCC Model (Banker-Charnes-Cooper) production frontiers spanned by convex
Bounds on non-surjective cellular automata
 Bounds on non-surjective cellular automata Jarkko Kari Pascal Vanier Thomas Zeume University of Turku LIF Marseille Universität Hannover 27 august 2009 J. Kari, P. Vanier, T. Zeume (UTU) Bounds on non-surjective
Bounds on non-surjective cellular automata Jarkko Kari Pascal Vanier Thomas Zeume University of Turku LIF Marseille Universität Hannover 27 august 2009 J. Kari, P. Vanier, T. Zeume (UTU) Bounds on non-surjective
Information on preparing Presentation
 Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
Information on preparing Presentation Seminar on big data management Lecturer: Spring 2017 20.1.2017 1 Agenda Hints and tips on giving a good presentation Watch two videos and discussion 22.1.2017 2 Goals
Results on the new polydrug use questions in the Finnish TDI data
 Results on the new polydrug use questions in the Finnish TDI data Multi-drug use, polydrug use and problematic polydrug use Martta Forsell, Finnish Focal Point 28/09/2015 Martta Forsell 1 28/09/2015 Esityksen
Results on the new polydrug use questions in the Finnish TDI data Multi-drug use, polydrug use and problematic polydrug use Martta Forsell, Finnish Focal Point 28/09/2015 Martta Forsell 1 28/09/2015 Esityksen
The Viking Battle - Part Version: Finnish
 The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
The Viking Battle - Part 1 015 Version: Finnish Tehtävä 1 Olkoon kokonaisluku, ja olkoon A n joukko A n = { n k k Z, 0 k < n}. Selvitä suurin kokonaisluku M n, jota ei voi kirjoittaa yhden tai useamman
Characterization of clay using x-ray and neutron scattering at the University of Helsinki and ILL
 Characterization of clay using x-ray and neutron scattering at the University of Helsinki and ILL Ville Liljeström, Micha Matusewicz, Kari Pirkkalainen, Jussi-Petteri Suuronen and Ritva Serimaa 13.3.2012
Characterization of clay using x-ray and neutron scattering at the University of Helsinki and ILL Ville Liljeström, Micha Matusewicz, Kari Pirkkalainen, Jussi-Petteri Suuronen and Ritva Serimaa 13.3.2012
T Statistical Natural Language Processing Answers 6 Collocations Version 1.0
 T-61.5020 Statistical Natural Language Processing Answers 6 Collocations Version 1.0 1. Let s start by calculating the results for pair valkoinen, talo manually: Frequency: Bigrams valkoinen, talo occurred
T-61.5020 Statistical Natural Language Processing Answers 6 Collocations Version 1.0 1. Let s start by calculating the results for pair valkoinen, talo manually: Frequency: Bigrams valkoinen, talo occurred
Valuation of Asian Quanto- Basket Options
 Valuation of Asian Quanto- Basket Options (Final Presentation) 21.11.2011 Thesis Instructor and Supervisor: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta
Valuation of Asian Quanto- Basket Options (Final Presentation) 21.11.2011 Thesis Instructor and Supervisor: Prof. Ahti Salo Työn saa tallentaa ja julkistaa Aalto-yliopiston avoimilla verkkosivuilla. Muilta
Network to Get Work. Tehtäviä opiskelijoille Assignments for students. www.laurea.fi
 Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
Network to Get Work Tehtäviä opiskelijoille Assignments for students www.laurea.fi Ohje henkilöstölle Instructions for Staff Seuraavassa on esitetty joukko tehtäviä, joista voit valita opiskelijaryhmällesi
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31)
 On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
On instrument costs in decentralized macroeconomic decision making (Helsingin Kauppakorkeakoulun julkaisuja ; D-31) Juha Kahkonen Click here if your download doesn"t start automatically On instrument costs
Statistical design. Tuomas Selander
 Statistical design Tuomas Selander 28.8.2014 Introduction Biostatistician Work area KYS-erva KYS, Jyväskylä, Joensuu, Mikkeli, Savonlinna Work tasks Statistical methods, selection and quiding Data analysis
Statistical design Tuomas Selander 28.8.2014 Introduction Biostatistician Work area KYS-erva KYS, Jyväskylä, Joensuu, Mikkeli, Savonlinna Work tasks Statistical methods, selection and quiding Data analysis
7.4 Variability management
 7.4 Variability management time... space software product-line should support variability in space (different products) support variability in time (maintenance, evolution) 1 Product variation Product
7.4 Variability management time... space software product-line should support variability in space (different products) support variability in time (maintenance, evolution) 1 Product variation Product
Toppila/Kivistö 10.01.2013 Vastaa kaikkin neljään tehtävään, jotka kukin arvostellaan asteikolla 0-6 pistettä.
 ..23 Vastaa kaikkin neljään tehtävään, jotka kukin arvostellaan asteikolla -6 pistettä. Tehtävä Ovatko seuraavat väittämät oikein vai väärin? Perustele vastauksesi. (a) Lineaarisen kokonaislukutehtävän
..23 Vastaa kaikkin neljään tehtävään, jotka kukin arvostellaan asteikolla -6 pistettä. Tehtävä Ovatko seuraavat väittämät oikein vai väärin? Perustele vastauksesi. (a) Lineaarisen kokonaislukutehtävän
Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition)
 Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen Click here if your download doesn"t start automatically Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen
Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen Click here if your download doesn"t start automatically Uusi Ajatus Löytyy Luonnosta 4 (käsikirja) (Finnish Edition) Esko Jalkanen
Metsälamminkankaan tuulivoimapuiston osayleiskaava
 VAALAN KUNTA TUULISAIMAA OY Metsälamminkankaan tuulivoimapuiston osayleiskaava Liite 3. Varjostusmallinnus FCG SUUNNITTELU JA TEKNIIKKA OY 12.5.2015 P25370 SHADOW - Main Result Assumptions for shadow calculations
VAALAN KUNTA TUULISAIMAA OY Metsälamminkankaan tuulivoimapuiston osayleiskaava Liite 3. Varjostusmallinnus FCG SUUNNITTELU JA TEKNIIKKA OY 12.5.2015 P25370 SHADOW - Main Result Assumptions for shadow calculations
LYTH-CONS CONSISTENCY TRANSMITTER
 LYTH-CONS CONSISTENCY TRANSMITTER LYTH-INSTRUMENT OY has generate new consistency transmitter with blade-system to meet high technical requirements in Pulp&Paper industries. Insurmountable advantages are
LYTH-CONS CONSISTENCY TRANSMITTER LYTH-INSTRUMENT OY has generate new consistency transmitter with blade-system to meet high technical requirements in Pulp&Paper industries. Insurmountable advantages are
BLOCKCHAINS AND ODR: SMART CONTRACTS AS AN ALTERNATIVE TO ENFORCEMENT
 UNCITRAL EMERGENCE CONFERENCE 13.12.2016 Session I: Emerging Legal Issues in the Commercial Exploitation of Deep Seabed, Space and AI BLOCKCHAINS AND ODR: SMART CONTRACTS AS AN ALTERNATIVE TO ENFORCEMENT
UNCITRAL EMERGENCE CONFERENCE 13.12.2016 Session I: Emerging Legal Issues in the Commercial Exploitation of Deep Seabed, Space and AI BLOCKCHAINS AND ODR: SMART CONTRACTS AS AN ALTERNATIVE TO ENFORCEMENT
C++11 seminaari, kevät Johannes Koskinen
 C++11 seminaari, kevät 2012 Johannes Koskinen Sisältö Mikä onkaan ongelma? Standardidraftin luku 29: Atomiset tyypit Muistimalli Rinnakkaisuus On multicore systems, when a thread writes a value to memory,
C++11 seminaari, kevät 2012 Johannes Koskinen Sisältö Mikä onkaan ongelma? Standardidraftin luku 29: Atomiset tyypit Muistimalli Rinnakkaisuus On multicore systems, when a thread writes a value to memory,
7. Product-line architectures
 7. Product-line architectures 7.1 Introduction 7.2 Product-line basics 7.3 Layered style for product-lines 7.4 Variability management 7.5 Benefits and problems with product-lines 1 Short history of software
7. Product-line architectures 7.1 Introduction 7.2 Product-line basics 7.3 Layered style for product-lines 7.4 Variability management 7.5 Benefits and problems with product-lines 1 Short history of software
AYYE 9/ HOUSING POLICY
 AYYE 9/12 2.10.2012 HOUSING POLICY Mission for AYY Housing? What do we want to achieve by renting apartments? 1) How many apartments do we need? 2) What kind of apartments do we need? 3) To whom do we
AYYE 9/12 2.10.2012 HOUSING POLICY Mission for AYY Housing? What do we want to achieve by renting apartments? 1) How many apartments do we need? 2) What kind of apartments do we need? 3) To whom do we
Capacity utilization
 Mat-2.4142 Seminar on optimization Capacity utilization 12.12.2007 Contents Summary of chapter 14 Related DEA-solver models Illustrative examples Measure of technical capacity utilization Price-based measure
Mat-2.4142 Seminar on optimization Capacity utilization 12.12.2007 Contents Summary of chapter 14 Related DEA-solver models Illustrative examples Measure of technical capacity utilization Price-based measure
( ( OX2 Perkkiö. Rakennuskanta. Varjostus. 9 x N131 x HH145
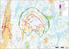 OX2 9 x N131 x HH145 Rakennuskanta Asuinrakennus Lomarakennus Liike- tai julkinen rakennus Teollinen rakennus Kirkko tai kirkollinen rak. Muu rakennus Allas Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 2 km
OX2 9 x N131 x HH145 Rakennuskanta Asuinrakennus Lomarakennus Liike- tai julkinen rakennus Teollinen rakennus Kirkko tai kirkollinen rak. Muu rakennus Allas Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 2 km
Land-Use Model for the Helsinki Metropolitan Area
 Land-Use Model for the Helsinki Metropolitan Area Paavo Moilanen Introduction & Background Metropolitan Area Council asked 2005: What is good land use for the transport systems plan? At first a literature
Land-Use Model for the Helsinki Metropolitan Area Paavo Moilanen Introduction & Background Metropolitan Area Council asked 2005: What is good land use for the transport systems plan? At first a literature
Kvanttilaskenta - 1. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 9, 0 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem False, sillä 0 0. Problem False, sillä 0 0 0 0. Problem A quantum state
Tynnyrivaara, OX2 Tuulivoimahanke. ( Layout 9 x N131 x HH145. Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a
 , Tuulivoimahanke Layout 9 x N131 x HH145 Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 km 2 SHADOW - Main Result Assumptions for shadow calculations
, Tuulivoimahanke Layout 9 x N131 x HH145 Rakennukset Asuinrakennus Lomarakennus 9 x N131 x HH145 Varjostus 1 h/a 8 h/a 20 h/a 0 0,5 1 1,5 km 2 SHADOW - Main Result Assumptions for shadow calculations
WindPRO version joulu 2012 Printed/Page :47 / 1. SHADOW - Main Result
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Calculation: N117 x 9 x HH141 Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG
SHADOW - Main Result Calculation: N117 x 9 x HH141 Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Constructive Alignment in Specialisation Studies in Industrial Pharmacy in Finland
 Constructive Alignment in Specialisation Studies in Industrial Pharmacy in Finland Anne Mari Juppo, Nina Katajavuori University of Helsinki Faculty of Pharmacy 23.7.2012 1 Background Pedagogic research
Constructive Alignment in Specialisation Studies in Industrial Pharmacy in Finland Anne Mari Juppo, Nina Katajavuori University of Helsinki Faculty of Pharmacy 23.7.2012 1 Background Pedagogic research
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.9.269
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.9.269
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Alternatives to the DFT
 Alternatives to the DFT Doru Balcan Carnegie Mellon University joint work with Aliaksei Sandryhaila, Jonathan Gross, and Markus Püschel - appeared in IEEE ICASSP 08 - Introduction Discrete time signal
Alternatives to the DFT Doru Balcan Carnegie Mellon University joint work with Aliaksei Sandryhaila, Jonathan Gross, and Markus Püschel - appeared in IEEE ICASSP 08 - Introduction Discrete time signal
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
WindPRO version joulu 2012 Printed/Page :42 / 1. SHADOW - Main Result
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 13.6.2013 19:42 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 13.6.2013 19:42 / 1 Minimum
SIMULINK S-funktiot. SIMULINK S-funktiot
 S-funktio on ohjelmointikielellä (Matlab, C, Fortran) laadittu oma algoritmi tai dynaamisen järjestelmän kuvaus, jota voidaan käyttää Simulink-malleissa kuin mitä tahansa valmista lohkoa. S-funktion rakenne
S-funktio on ohjelmointikielellä (Matlab, C, Fortran) laadittu oma algoritmi tai dynaamisen järjestelmän kuvaus, jota voidaan käyttää Simulink-malleissa kuin mitä tahansa valmista lohkoa. S-funktion rakenne
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 5.11.2013 16:44 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 5.11.2013 16:44 / 1 Minimum
Use of spatial data in the new production environment and in a data warehouse
 Use of spatial data in the new production environment and in a data warehouse Nordic Forum for Geostatistics 2007 Session 3, GI infrastructure and use of spatial database Statistics Finland, Population
Use of spatial data in the new production environment and in a data warehouse Nordic Forum for Geostatistics 2007 Session 3, GI infrastructure and use of spatial database Statistics Finland, Population
MUSEOT KULTTUURIPALVELUINA
 Elina Arola MUSEOT KULTTUURIPALVELUINA Tutkimuskohteena Mikkelin museot Opinnäytetyö Kulttuuripalvelujen koulutusohjelma Marraskuu 2005 KUVAILULEHTI Opinnäytetyön päivämäärä 25.11.2005 Tekijä(t) Elina
Elina Arola MUSEOT KULTTUURIPALVELUINA Tutkimuskohteena Mikkelin museot Opinnäytetyö Kulttuuripalvelujen koulutusohjelma Marraskuu 2005 KUVAILULEHTI Opinnäytetyön päivämäärä 25.11.2005 Tekijä(t) Elina
Master's Programme in Life Science Technologies (LifeTech) Prof. Juho Rousu Director of the Life Science Technologies programme 3.1.
 Master's Programme in Life Science Technologies (LifeTech) Prof. Juho Rousu Director of the Life Science Technologies programme 3.1.2017 Life Science Technologies Where Life Sciences meet with Technology
Master's Programme in Life Science Technologies (LifeTech) Prof. Juho Rousu Director of the Life Science Technologies programme 3.1.2017 Life Science Technologies Where Life Sciences meet with Technology
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Taulukon edut Taulukon haitat Taulukon haittojen välttäminen Dynaamisesti linkattu lista Linkatun listan solmun määrittelytavat Lineaarisen listan toteutus dynaamisesti linkattuna
Tietorakenteet ja algoritmit Taulukon edut Taulukon haitat Taulukon haittojen välttäminen Dynaamisesti linkattu lista Linkatun listan solmun määrittelytavat Lineaarisen listan toteutus dynaamisesti linkattuna
( ,5 1 1,5 2 km
 Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 4 5 3 1 2 6 7 8 9 10 0 0,5 1 1,5 2 km
Tuulivoimala Rakennukset Asuinrakennus Liikerak. tai Julkinen rak. Lomarakennus Teollinen rakennus Kirkollinen rakennus Varjostus "real case" h/a 1 h/a 8 h/a 20 h/a 4 5 3 1 2 6 7 8 9 10 0 0,5 1 1,5 2 km
S Sähkön jakelu ja markkinat S Electricity Distribution and Markets
 S-18.3153 Sähkön jakelu ja markkinat S-18.3154 Electricity Distribution and Markets Voltage Sag 1) Kolmivaiheinen vastukseton oikosulku tapahtuu 20 kv lähdöllä etäisyydellä 1 km, 3 km, 5 km, 8 km, 10 km
S-18.3153 Sähkön jakelu ja markkinat S-18.3154 Electricity Distribution and Markets Voltage Sag 1) Kolmivaiheinen vastukseton oikosulku tapahtuu 20 kv lähdöllä etäisyydellä 1 km, 3 km, 5 km, 8 km, 10 km
Huom. tämä kulma on yhtä suuri kuin ohjauskulman muutos. lasketaan ajoneuvon keskipisteen ympyräkaaren jänteen pituus
 AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
AS-84.327 Paikannus- ja navigointimenetelmät Ratkaisut 2.. a) Kun kuvan ajoneuvon kumpaakin pyörää pyöritetään tasaisella nopeudella, ajoneuvon rata on ympyränkaaren segmentin muotoinen. Hitaammin kulkeva
ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin. Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana
 ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana Taustaa KAO mukana FINECVET-hankeessa, jossa pilotoimme ECVETiä
ECVETin soveltuvuus suomalaisiin tutkinnon perusteisiin Case:Yrittäjyyskurssi matkailualan opiskelijoille englantilaisen opettajan toteuttamana Taustaa KAO mukana FINECVET-hankeessa, jossa pilotoimme ECVETiä
TM ETRS-TM35FIN-ETRS89 WTG
 VE1 SHADOW - Main Result Calculation: 8 x Nordex N131 x HH145m Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please
VE1 SHADOW - Main Result Calculation: 8 x Nordex N131 x HH145m Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please
Paikkatiedon semanttinen mallinnus, integrointi ja julkaiseminen Case Suomalainen ajallinen paikkaontologia SAPO
 Paikkatiedon semanttinen mallinnus, integrointi ja julkaiseminen Case Suomalainen ajallinen paikkaontologia SAPO Tomi Kauppinen, Eero Hyvönen, Jari Väätäinen Semantic Computing Research Group (SeCo) http://www.seco.tkk.fi/
Paikkatiedon semanttinen mallinnus, integrointi ja julkaiseminen Case Suomalainen ajallinen paikkaontologia SAPO Tomi Kauppinen, Eero Hyvönen, Jari Väätäinen Semantic Computing Research Group (SeCo) http://www.seco.tkk.fi/
Returns to Scale Chapters
 Return to Scale Chapter 5.1-5.4 Saara Tuurala 26.9.2007 Index Introduction Baic Formulation of Retur to Scale Geometric Portrayal in DEA BCC Return to Scale CCR Return to Scale Summary Home Aignment Introduction
Return to Scale Chapter 5.1-5.4 Saara Tuurala 26.9.2007 Index Introduction Baic Formulation of Retur to Scale Geometric Portrayal in DEA BCC Return to Scale CCR Return to Scale Summary Home Aignment Introduction
I. Principles of Pointer Year Analysis
 I. Principles of Pointer Year Analysis Fig 1. Maximum (red) and minimum (blue) pointer years. 1 Fig 2. Principle of pointer year calculation. Fig 3. Skeleton plot graph created by Kinsys/Kigraph programme.
I. Principles of Pointer Year Analysis Fig 1. Maximum (red) and minimum (blue) pointer years. 1 Fig 2. Principle of pointer year calculation. Fig 3. Skeleton plot graph created by Kinsys/Kigraph programme.
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 22.12.2014 11:33 / 1 Minimum
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table 22.12.2014 11:33 / 1 Minimum
EUROOPAN PARLAMENTTI
 EUROOPAN PARLAMENTTI 2004 2009 Kansalaisvapauksien sekä oikeus- ja sisäasioiden valiokunta 2008/0101(CNS) 2.9.2008 TARKISTUKSET 9-12 Mietintöluonnos Luca Romagnoli (PE409.790v01-00) ehdotuksesta neuvoston
EUROOPAN PARLAMENTTI 2004 2009 Kansalaisvapauksien sekä oikeus- ja sisäasioiden valiokunta 2008/0101(CNS) 2.9.2008 TARKISTUKSET 9-12 Mietintöluonnos Luca Romagnoli (PE409.790v01-00) ehdotuksesta neuvoston
Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat
 Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat Esityksen sisältö: 1. EU:n energiapolitiikka on se, joka ei toimi 2. Mihin perustuu väite, etteivät
Tarua vai totta: sähkön vähittäismarkkina ei toimi? 11.2.2015 Satu Viljainen Professori, sähkömarkkinat Esityksen sisältö: 1. EU:n energiapolitiikka on se, joka ei toimi 2. Mihin perustuu väite, etteivät
3 9-VUOTIAIDEN LASTEN SUORIUTUMINEN BOSTONIN NIMENTÄTESTISTÄ
 Puhe ja kieli, 27:4, 141 147 (2007) 3 9-VUOTIAIDEN LASTEN SUORIUTUMINEN BOSTONIN NIMENTÄTESTISTÄ Soile Loukusa, Oulun yliopisto, suomen kielen, informaatiotutkimuksen ja logopedian laitos & University
Puhe ja kieli, 27:4, 141 147 (2007) 3 9-VUOTIAIDEN LASTEN SUORIUTUMINEN BOSTONIN NIMENTÄTESTISTÄ Soile Loukusa, Oulun yliopisto, suomen kielen, informaatiotutkimuksen ja logopedian laitos & University
Exercise 1. (session: )
 EEN-E3001, FUNDAMENTALS IN INDUSTRIAL ENERGY ENGINEERING Exercise 1 (session: 24.1.2017) Problem 3 will be graded. The deadline for the return is on 31.1. at 12:00 am (before the exercise session). You
EEN-E3001, FUNDAMENTALS IN INDUSTRIAL ENERGY ENGINEERING Exercise 1 (session: 24.1.2017) Problem 3 will be graded. The deadline for the return is on 31.1. at 12:00 am (before the exercise session). You
1.3Lohkorakenne muodostetaan käyttämällä a) puolipistettä b) aaltosulkeita c) BEGIN ja END lausekkeita d) sisennystä
 OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
OULUN YLIOPISTO Tietojenkäsittelytieteiden laitos Johdatus ohjelmointiin 81122P (4 ov.) 30.5.2005 Ohjelmointikieli on Java. Tentissä saa olla materiaali mukana. Tenttitulokset julkaistaan aikaisintaan
toukokuu 2011: Lukion kokeiden kehittämistyöryhmien suunnittelukokous
 Tuula Sutela toukokuu 2011: Lukion kokeiden kehittämistyöryhmien suunnittelukokous äidinkieli ja kirjallisuus, modersmål och litteratur, kemia, maantiede, matematiikka, englanti käsikirjoitukset vuoden
Tuula Sutela toukokuu 2011: Lukion kokeiden kehittämistyöryhmien suunnittelukokous äidinkieli ja kirjallisuus, modersmål och litteratur, kemia, maantiede, matematiikka, englanti käsikirjoitukset vuoden
TM ETRS-TM35FIN-ETRS89 WTG
 SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
SHADOW - Main Result Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered by the blade Please look in WTG table WindPRO version 2.8.579
Genome 373: Genomic Informatics. Professors Elhanan Borenstein and Jay Shendure
 Genome 373: Genomic Informatics Professors Elhanan Borenstein and Jay Shendure Genome 373 This course is intended to introduce students to the breadth of problems and methods in computational analysis
Genome 373: Genomic Informatics Professors Elhanan Borenstein and Jay Shendure Genome 373 This course is intended to introduce students to the breadth of problems and methods in computational analysis
KONEISTUSKOKOONPANON TEKEMINEN NX10-YMPÄRISTÖSSÄ
 KONEISTUSKOKOONPANON TEKEMINEN NX10-YMPÄRISTÖSSÄ https://community.plm.automation.siemens.com/t5/tech-tips- Knowledge-Base-NX/How-to-simulate-any-G-code-file-in-NX- CAM/ta-p/3340 Koneistusympäristön määrittely
KONEISTUSKOKOONPANON TEKEMINEN NX10-YMPÄRISTÖSSÄ https://community.plm.automation.siemens.com/t5/tech-tips- Knowledge-Base-NX/How-to-simulate-any-G-code-file-in-NX- CAM/ta-p/3340 Koneistusympäristön määrittely
anna minun kertoa let me tell you
 anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
anna minun kertoa let me tell you anna minun kertoa I OSA 1. Anna minun kertoa sinulle mitä oli. Tiedän että osaan. Kykenen siihen. Teen nyt niin. Minulla on oikeus. Sanani voivat olla puutteellisia mutta
,0 Yes ,0 120, ,8
 SHADOW - Main Result Calculation: Alue 2 ( x 9 x HH120) TuuliSaimaa kaavaluonnos Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered
SHADOW - Main Result Calculation: Alue 2 ( x 9 x HH120) TuuliSaimaa kaavaluonnos Assumptions for shadow calculations Maximum distance for influence Calculate only when more than 20 % of sun is covered
Fighting diffuse nutrient load: Multifunctional water management concept in natural reed beds
 PhD Anne Hemmi 14.2.2013 RRR 2013 Conference in Greifswald, Germany Fighting diffuse nutrient load: Multifunctional water management concept in natural reed beds Eutrophication in surface waters High nutrient
PhD Anne Hemmi 14.2.2013 RRR 2013 Conference in Greifswald, Germany Fighting diffuse nutrient load: Multifunctional water management concept in natural reed beds Eutrophication in surface waters High nutrient
MRI-sovellukset. Ryhmän 6 LH:t (8.22 & 9.25)
 MRI-sovellukset Ryhmän 6 LH:t (8.22 & 9.25) Ex. 8.22 Ex. 8.22 a) What kind of image artifact is present in image (b) Answer: The artifact in the image is aliasing artifact (phase aliasing) b) How did Joe
MRI-sovellukset Ryhmän 6 LH:t (8.22 & 9.25) Ex. 8.22 Ex. 8.22 a) What kind of image artifact is present in image (b) Answer: The artifact in the image is aliasing artifact (phase aliasing) b) How did Joe
Kvanttilaskenta - 2. tehtävät
 Kvanttilaskenta -. tehtävät Johannes Verwijnen January 8, 05 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem The inner product of + and is. Edelleen false, kts. viikon tehtävä 6..
Kvanttilaskenta -. tehtävät Johannes Verwijnen January 8, 05 edx-tehtävät Vastauksissa on käytetty edx-kurssin materiaalia.. Problem The inner product of + and is. Edelleen false, kts. viikon tehtävä 6..
Operatioanalyysi 2011, Harjoitus 4, viikko 40
 Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
Operatioanalyysi 2011, Harjoitus 4, viikko 40 H4t1, Exercise 4.2. H4t2, Exercise 4.3. H4t3, Exercise 4.4. H4t4, Exercise 4.5. H4t5, Exercise 4.6. (Exercise 4.2.) 1 4.2. Solve the LP max z = x 1 + 2x 2
FinFamily PostgreSQL installation ( ) FinFamily PostgreSQL
 FinFamily PostgreSQL 1 Sisällys / Contents FinFamily PostgreSQL... 1 1. Asenna PostgreSQL tietokanta / Install PostgreSQL database... 3 1.1. PostgreSQL tietokannasta / About the PostgreSQL database...
FinFamily PostgreSQL 1 Sisällys / Contents FinFamily PostgreSQL... 1 1. Asenna PostgreSQL tietokanta / Install PostgreSQL database... 3 1.1. PostgreSQL tietokannasta / About the PostgreSQL database...
Mat Seminar on Optimization. Data Envelopment Analysis. Economies of Scope S ysteemianalyysin. Laboratorio. Teknillinen korkeakoulu
 Mat-2.4142 Seminar on Optimization Data Envelopment Analysis Economies of Scope 21.11.2007 Economies of Scope Introduced 1982 by Panzar and Willing Support decisions like: Should a firm... Produce a variety
Mat-2.4142 Seminar on Optimization Data Envelopment Analysis Economies of Scope 21.11.2007 Economies of Scope Introduced 1982 by Panzar and Willing Support decisions like: Should a firm... Produce a variety
Categorical Decision Making Units and Comparison of Efficiency between Different Systems
 Categorical Decision Making Units and Comparison of Efficiency between Different Systems Mat-2.4142 Optimointiopin Seminaari Source William W. Cooper, Lawrence M. Seiford, Kaoru Tone: Data Envelopment
Categorical Decision Making Units and Comparison of Efficiency between Different Systems Mat-2.4142 Optimointiopin Seminaari Source William W. Cooper, Lawrence M. Seiford, Kaoru Tone: Data Envelopment
Use of Stochastic Compromise Programming to develop forest management alternatives for ecosystem services
 Use of Stochastic Compromise Programming to develop forest management alternatives for ecosystem services Kyle Eyvindson 24.3.2014 Forest Science Department / Kyle Eyvindson 3/26/2014 1 Overview Introduction
Use of Stochastic Compromise Programming to develop forest management alternatives for ecosystem services Kyle Eyvindson 24.3.2014 Forest Science Department / Kyle Eyvindson 3/26/2014 1 Overview Introduction
Oma sininen meresi (Finnish Edition)
 Oma sininen meresi (Finnish Edition) Hannu Pirilä Click here if your download doesn"t start automatically Oma sininen meresi (Finnish Edition) Hannu Pirilä Oma sininen meresi (Finnish Edition) Hannu Pirilä
Oma sininen meresi (Finnish Edition) Hannu Pirilä Click here if your download doesn"t start automatically Oma sininen meresi (Finnish Edition) Hannu Pirilä Oma sininen meresi (Finnish Edition) Hannu Pirilä
GOOD WORK LONGER CAREER:
 Juhani Ilmarinen, Ville Ilmarinen, Pekka Huuhtanen, Veikko Louhevaara, Ove Näsman GOOD WORK LONGER CAREER: WORK WELL-BEING IN FINNISH TECHNOLOGY INDUSTRIES 2010-2015 Background Collective agreement between
Juhani Ilmarinen, Ville Ilmarinen, Pekka Huuhtanen, Veikko Louhevaara, Ove Näsman GOOD WORK LONGER CAREER: WORK WELL-BEING IN FINNISH TECHNOLOGY INDUSTRIES 2010-2015 Background Collective agreement between
Collaborative & Co-Creative Design in the Semogen -projects
 1 Collaborative & Co-Creative Design in the Semogen -projects Pekka Ranta Project Manager -research group, Intelligent Information Systems Laboratory 2 Semogen -project Supporting design of a machine system
1 Collaborative & Co-Creative Design in the Semogen -projects Pekka Ranta Project Manager -research group, Intelligent Information Systems Laboratory 2 Semogen -project Supporting design of a machine system
Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine Centre for Language and Communication Studies
 Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine 4.1.2018 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve
Information on Finnish Language Courses Spring Semester 2018 Päivi Paukku & Jenni Laine 4.1.2018 Centre for Language and Communication Studies Puhutko suomea? -Hei! -Hei hei! -Moi! -Moi moi! -Terve! -Terve
E80. Data Uncertainty, Data Fitting, Error Propagation. Jan. 23, 2014 Jon Roberts. Experimental Engineering
 Lecture 2 Data Uncertainty, Data Fitting, Error Propagation Jan. 23, 2014 Jon Roberts Purpose & Outline Data Uncertainty & Confidence in Measurements Data Fitting - Linear Regression Error Propagation
Lecture 2 Data Uncertainty, Data Fitting, Error Propagation Jan. 23, 2014 Jon Roberts Purpose & Outline Data Uncertainty & Confidence in Measurements Data Fitting - Linear Regression Error Propagation
RANTALA SARI: Sairaanhoitajan eettisten ohjeiden tunnettavuus ja niiden käyttö hoitotyön tukena sisätautien vuodeosastolla
 TURUN YLIOPISTO Hoitotieteen laitos RANTALA SARI: Sairaanhoitajan eettisten ohjeiden tunnettavuus ja niiden käyttö hoitotyön tukena sisätautien vuodeosastolla Pro gradu -tutkielma, 34 sivua, 10 liitesivua
TURUN YLIOPISTO Hoitotieteen laitos RANTALA SARI: Sairaanhoitajan eettisten ohjeiden tunnettavuus ja niiden käyttö hoitotyön tukena sisätautien vuodeosastolla Pro gradu -tutkielma, 34 sivua, 10 liitesivua
RINNAKKAINEN OHJELMOINTI A,
 RINNAKKAINEN OHJELMOINTI 815301A, 18.6.2005 1. Vastaa lyhyesti (2p kustakin): a) Mitkä ovat rinnakkaisen ohjelman oikeellisuuskriteerit? b) Mitä tarkoittaa laiska säikeen luominen? c) Mitä ovat kohtaaminen
RINNAKKAINEN OHJELMOINTI 815301A, 18.6.2005 1. Vastaa lyhyesti (2p kustakin): a) Mitkä ovat rinnakkaisen ohjelman oikeellisuuskriteerit? b) Mitä tarkoittaa laiska säikeen luominen? c) Mitä ovat kohtaaminen
OP1. PreDP StudyPlan
 OP1 PreDP StudyPlan PreDP The preparatory year classes are in accordance with the Finnish national curriculum, with the distinction that most of the compulsory courses are taught in English to familiarize
OP1 PreDP StudyPlan PreDP The preparatory year classes are in accordance with the Finnish national curriculum, with the distinction that most of the compulsory courses are taught in English to familiarize
Windows Phone. Module Descriptions. Opiframe Oy puh. +358 44 7220800 eero.huusko@opiframe.com. 02600 Espoo
 Windows Phone Module Descriptions Mikä on RekryKoulutus? Harvassa ovat ne työnantajat, jotka löytävät juuri heidän alansa hallitsevat ammatti-ihmiset valmiina. Fiksuinta on tunnustaa tosiasiat ja hankkia
Windows Phone Module Descriptions Mikä on RekryKoulutus? Harvassa ovat ne työnantajat, jotka löytävät juuri heidän alansa hallitsevat ammatti-ihmiset valmiina. Fiksuinta on tunnustaa tosiasiat ja hankkia
Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi
 Ideasta projektiksi - kumppanuushankkeen suunnittelun lähtökohdat Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi Erasmus+ -ohjelman hakuneuvonta ammatillisen koulutuksen kumppanuushanketta
Ideasta projektiksi - kumppanuushankkeen suunnittelun lähtökohdat Hankkeiden vaikuttavuus: Työkaluja hankesuunnittelun tueksi Erasmus+ -ohjelman hakuneuvonta ammatillisen koulutuksen kumppanuushanketta
The role of 3dr sector in rural -community based- tourism - potentials, challenges
 The role of 3dr sector in rural -community based- tourism - potentials, challenges Lappeenranta, 5th September 2014 Contents of the presentation 1. SEPRA what is it and why does it exist? 2. Experiences
The role of 3dr sector in rural -community based- tourism - potentials, challenges Lappeenranta, 5th September 2014 Contents of the presentation 1. SEPRA what is it and why does it exist? 2. Experiences
LX 70. Ominaisuuksien mittaustulokset 1-kerroksinen 2-kerroksinen. Fyysiset ominaisuudet, nimellisarvot. Kalvon ominaisuudet
 LX 70 % Läpäisy 36 32 % Absorptio 30 40 % Heijastus 34 28 % Läpäisy 72 65 % Heijastus ulkopuoli 9 16 % Heijastus sisäpuoli 9 13 Emissiivisyys.77.77 Auringonsuojakerroin.54.58 Auringonsäteilyn lämmönsiirtokerroin.47.50
LX 70 % Läpäisy 36 32 % Absorptio 30 40 % Heijastus 34 28 % Läpäisy 72 65 % Heijastus ulkopuoli 9 16 % Heijastus sisäpuoli 9 13 Emissiivisyys.77.77 Auringonsuojakerroin.54.58 Auringonsäteilyn lämmönsiirtokerroin.47.50
Skene. Games Refueled. Muokkaa perustyyl. napsautt. @Games for Health, Kuopio. 2013 kari.korhonen@tekes.fi. www.tekes.fi/skene
 Skene Muokkaa perustyyl. Games Refueled napsautt. @Games for Health, Kuopio Muokkaa alaotsikon perustyyliä napsautt. 2013 kari.korhonen@tekes.fi www.tekes.fi/skene 10.9.201 3 Muokkaa Skene boosts perustyyl.
Skene Muokkaa perustyyl. Games Refueled napsautt. @Games for Health, Kuopio Muokkaa alaotsikon perustyyliä napsautt. 2013 kari.korhonen@tekes.fi www.tekes.fi/skene 10.9.201 3 Muokkaa Skene boosts perustyyl.
Kysymys 5 Compared to the workload, the number of credits awarded was (1 credits equals 27 working hours): (4)
 Tilasto T1106120-s2012palaute Kyselyn T1106120+T1106120-s2012palaute yhteenveto: vastauksia (4) Kysymys 1 Degree programme: (4) TIK: TIK 1 25% ************** INF: INF 0 0% EST: EST 0 0% TLT: TLT 0 0% BIO:
Tilasto T1106120-s2012palaute Kyselyn T1106120+T1106120-s2012palaute yhteenveto: vastauksia (4) Kysymys 1 Degree programme: (4) TIK: TIK 1 25% ************** INF: INF 0 0% EST: EST 0 0% TLT: TLT 0 0% BIO:
Information on Finnish Language Courses Spring Semester 2017 Jenni Laine
 Information on Finnish Language Courses Spring Semester 2017 Jenni Laine 4.1.2017 KIELIKESKUS LANGUAGE CENTRE Puhutko suomea? Do you speak Finnish? -Hei! -Moi! -Mitä kuuluu? -Kiitos, hyvää. -Entä sinulle?
Information on Finnish Language Courses Spring Semester 2017 Jenni Laine 4.1.2017 KIELIKESKUS LANGUAGE CENTRE Puhutko suomea? Do you speak Finnish? -Hei! -Moi! -Mitä kuuluu? -Kiitos, hyvää. -Entä sinulle?
Siirtymä maisteriohjelmiin tekniikan korkeakoulujen välillä Transfer to MSc programmes between engineering schools
 Siirtymä maisteriohjelmiin tekniikan korkeakoulujen välillä Transfer to MSc programmes between engineering schools Akateemisten asioiden komitea Academic Affairs Committee 11 October 2016 Eija Zitting
Siirtymä maisteriohjelmiin tekniikan korkeakoulujen välillä Transfer to MSc programmes between engineering schools Akateemisten asioiden komitea Academic Affairs Committee 11 October 2016 Eija Zitting
Infrastruktuurin asemoituminen kansalliseen ja kansainväliseen kenttään Outi Ala-Honkola Tiedeasiantuntija
 Infrastruktuurin asemoituminen kansalliseen ja kansainväliseen kenttään Outi Ala-Honkola Tiedeasiantuntija 1 Asemoitumisen kuvaus Hakemukset parantuneet viime vuodesta, mutta paneeli toivoi edelleen asemoitumisen
Infrastruktuurin asemoituminen kansalliseen ja kansainväliseen kenttään Outi Ala-Honkola Tiedeasiantuntija 1 Asemoitumisen kuvaus Hakemukset parantuneet viime vuodesta, mutta paneeli toivoi edelleen asemoitumisen
HITSAUKSEN TUOTTAVUUSRATKAISUT
 Kemppi ARC YOU GET WHAT YOU MEASURE OR BE CAREFUL WHAT YOU WISH FOR HITSAUKSEN TUOTTAVUUSRATKAISUT Puolitetaan hitsauskustannukset seminaari 9.4.2008 Mikko Veikkolainen, Ratkaisuliiketoimintapäällikkö
Kemppi ARC YOU GET WHAT YOU MEASURE OR BE CAREFUL WHAT YOU WISH FOR HITSAUKSEN TUOTTAVUUSRATKAISUT Puolitetaan hitsauskustannukset seminaari 9.4.2008 Mikko Veikkolainen, Ratkaisuliiketoimintapäällikkö
Research plan for masters thesis in forest sciences. The PELLETime 2009 Symposium Mervi Juntunen
 Modelling tree and stand characteristics and estimating biomass removals and harvesting costs of lodgepole pine (Pinus contorta) plantations in Iceland Research plan for masters thesis in forest sciences
Modelling tree and stand characteristics and estimating biomass removals and harvesting costs of lodgepole pine (Pinus contorta) plantations in Iceland Research plan for masters thesis in forest sciences
4x4cup Rastikuvien tulkinta
 4x4cup Rastikuvien tulkinta 4x4cup Control point picture guidelines Päivitetty kauden 2010 sääntöihin Updated for 2010 rules Säännöt rastikuvista Kilpailijoiden tulee kiinnittää erityistä huomiota siihen,
4x4cup Rastikuvien tulkinta 4x4cup Control point picture guidelines Päivitetty kauden 2010 sääntöihin Updated for 2010 rules Säännöt rastikuvista Kilpailijoiden tulee kiinnittää erityistä huomiota siihen,
Supply Chain Management and Material Handling in Paper Industry Case Tervakoski Oy
 Tampere University of Applied Sciences Paper technology International Pulp and Paper Technology Supply Chain Management and Material Handling in Paper Industry Case Tervakoski Oy Supervisor Commissioned
Tampere University of Applied Sciences Paper technology International Pulp and Paper Technology Supply Chain Management and Material Handling in Paper Industry Case Tervakoski Oy Supervisor Commissioned
