Matematiikkaa tiedekerhoihin II Kiehtovaa geometriaa
|
|
|
- Hannu-Pekka Manninen
- 10 vuotta sitten
- Katselukertoja:
Transkriptio
1 Matematiikkaa tiedekerhoihin II Kiehtovaa geometriaa Vesa-Matti Sarenius Versio 1.0
2 Sisältö 1 Kochin lumihiutale (1h) Välipala-1, helppo ja vaikea vaakatehtävä Laatoituksia (1 2h) Välipala-2: yksipuolinen paperi Paradokseja Tetrominot (1h) 10 4 Puolisäännöllisiä monitahokkaita (1 2h) Välipala-3: Noppaventti Rakennelmia kuutioista (2h) 15 6 Kaaria viivoittimella (1h) 16 7 Kirjallisuutta 18 A Monistepohjia 19 B Rakennelmia-kappaleen tehtävät 35 1
3 Johdatus matematiikan maailmaan Kädessäsi on toinen Matematiikkaa tiedekerhoihin -opas. Tällä kertaa teemaksi on valittu geometria, jota käsitellään monelta eri kantilta. Mukana on tasogeometriaa, fraktaaleja ja kolmiulotteista geometriaa. Geometria valittiin teemaksi siksi, että sitä on koulumatematiikassa varsin vähän ja oppaassa esiteltäviä erikoisempia aiheita koulutunneilla tehdään harvoin. Ohjelmat ovat sellaisia, että ne painottavat kerholaisen omaa tekemistä ja havaitsemista. Ohjelmat sopivat hyvin myös oppitunneille. Kaikki oppaan ohjelmat ovat kirjoittajan ja monen muun kerhonohjaajan todellisessa kerho- tai luokkatilanteessa testaamia ja toimiviksi havaitsemia. Ohjelmiin on kerätty ideoita eri lähteistä, joita on lueteltu oppaan lopusta löytyvässä lähdeluettelossa. Oppaassa oleva materiaali on kirjottajan toteuttamaa ja siihen on vapaat kopiointioikeudet. Ohjelmiin tarvittavat materiaalit on ilmoitettu yhtä oppilasta kohden. Lisäksi yleensä tarvitaan saksia, kyniä, liimapuikkoja ja viivainta. Monet oppaan ohjelmista on laadittu niin, että jos ne käy kokonaisuudessaan läpi, aikaa saattaa hyvinkin mennä tunti tai kaksikin. Ajateltu toteutusaika on merkattu otsikkoon sulkuihin ja se on ajateltu nelosluokkalaisen tietotaidoille sopivaksi. Mikäli aikaa tuntuu olevan liikaa, opas sisältää kolme välipalatehtävää, jotka eivät tarvitse juurikaan materiaalia. Välipalatehtävät löytyvät sivuilta 4, 8 ja 14. Jälleen kerran haluan kiittää Mariaa, Allia, Eveliinaa, Kanervaa, Ansaa, Riikkaa, Emiliaa, Hannaa, Meeriä, Tiinaa, Anna-Maijaa, Jarnaa, Virpiä, Saria, Benjamia ja Tarjaa. Ilman teitä tätä opasta ei olisi koskaan kirjoitettu. Teidän ja monien muidenkin henkilöiden kanssa minulla on ollut onni pitää kerhoja ja leirejä ja suunnitella ohjelmia, joista osan esittelen oppaassani tai sitten muuten vain keskustella aiheesta. Erityiskiitos Hintan koululle, jossa olen monet oppaan ohjelmista saanut testata. Matematiikka odottaa seuraavalla sivulla. Käännä sivua ja hämmästy, mitä kaikkea mielenkiintoista ja kaunista matematiikka onkaan. Oulussa 11. syyskuuta 2005, Vesa-Matti Sarenius
4 1 Kochin lumihiutale (1h) Fraktaalit ovat äärettömän paljon yksityiskohtia sisältäviä geometrisia objekteja. Se tarkoittaa sitä, että mentiinpä kuinka lähelle tahansa, aina löytyy uusia yksityiskohtia. Fraktaalia ei pystytä kokonaan koskaan piirtämään, mutta fraktaalin idea voidaan tuoda esille tekemällä esimerkiksi osa niin sanotusta Kochin lumihiutaleesta. Materiaali A4-kokoinen kartonki, jolle lumihiutale kasataan. Sivu 20 kopioituna jokaiselle oppilaalle. Kopiot voi tehdä myös värillisille papereille. Toteutus Kaikki sivulla olevat kolmiot leikataan irti, jonka jälkeen ne liimataan isoimmista alkaen kartongille alla olevan kuvan tavalla. Kuvassa 1.1 on toteutettu vain ylin kolmio loppuun saakka, sama tehdään kaikille kulmille. 2 Kuva 1.1: Kochin lumihiutaleen kasaaminen kolmioista
5 Kuvion kasaamisen jälkeen kerholaiset vahvistavat esimerkiksi värikynällä kuvan reunaviivan. Reunaviivaa vahvistaessa huomataan, miten pitkäksi se on muodostunut. Kochin lumihiutale on juuri tämä reunaviiva. Kuvassa 1.2 on piirrettynä Kochin lumihiutaletta hieman kolmiomallia pidemmälle. Pohdiskeltavaa 1. Miksi kuvion nimi on Kochin lumihiutale? 2. Jos menetelmää jatkettaisiin vielä pienemmillä ja pienemmillä kolmioilla loputtomiin, minkälainen kuviosta tulisi? 3. Kuinka pitkä kuvion reunaviiva olisi, jos menetelmää jatkettaisiin loputtomiin? Vastauksia pohdiskelukysymyksiin 1. Koska mitä pidemmälle kuviota tehdään, sitä enemmän se näyttää lumihiutaleelta. 2. Todella rypyläreunainen. 3. Äärettömän pitkä. Kuva 1.2: Kochin lumihiutale 3
6 1.1 Välipala-1, helppo ja vaikea vaakatehtävä Vaakatehtäviä on olemassa kymmeniä, ellei satoja. Vaakatehtävissä pyritään aina etsimään eripainoista kappaletta käyttämällä kuvan 1.3 kaltaista kuppivaakaa. Kuva 1.3: Kuppivaaka Helppo vaakatehtävä Pinossa on yhdeksän yhden euron kolikkoa. Niistä yksi on väärennetty ja siksi kevyempi kuin muut kolikot. Käytössäsi on kuppivaaka. Kuinka monta punnitusta tarvitset, että voit paljastaa väärennetyn kolikon. Vastaus: Kolme punnitusta Vaikea vaakatehtävä Sinulle annetaan kaksitoista kuulaa, joista yksi on eripainoinen kuin muut, siis kevyempi tai painavampi. Tehtäväsi on kolmella punnituksella selvittää mikä kuulista on eripainoinen, kuin muut ja lisäksi, onko kuula kevyempi vai painavampi. Kuinka teet tämän? Vinkkejä: Tässä tehtävässä oleellista on, että punnitut kuulat pystytään merkitsemään punnituksen jälkeen. Myöskään jo punnittuja kuulia ei kannata laittaa sivuun. Vastaus: Koska tehtävä on mielenkiintoinen opettajallekin, vastausta ei anneta tässä. 4
7 2 Laatoituksia (1 2h) Laatoitus tarkoittaa äärettömän tason täyttämistä aukottomasti samanlaisilla tai erilaisilla palasilla. Laatoitus voi olla säännöllinen tai epäsäännöllinen. Säännöllinen laatoitus on sellainen, että taso voidaan täyttää millä tahansa osalla, joka on otettu laatoituksesta. Materiaali sivujen monistepohja joka oppilaalle kartonkia Toteutus Tunnin aluksi oppilaiden kanssa voi keskustella ja etsiä laatoituksia koulurakennuksesta, pihalta, ja niin edelleen. Lisäksi jo ennakkoon voi miettiä, minkämuotoisia laattoja on olemassa ja minkämuotoisilla laatoilla laatoitus voisi onnistua. Kannattaa keskustella myös siitä, löytyykö laatoituksia luonnosta. Jokainen oppilas liimaa kopionsa kartongille ja leikkaa yhdenlaiset palaset kerrallaan irti. Tarkoituksena on tutustua millä palasilla tason voi täyttää. Tätä varten ovat sivujen 31 ja 32 laatat. Sivun 33 laatoilla voi kokeilla laatoittamista monenmuotoisilla laatoilla. Väritettyjä laatoituksia voi liimata kartongille kauniiksi taideteoksiksi. Penrose-laatoitus Penrose-laatoitus on saanut nimensä keksijänsä Roger Penrosen mukaan. Se on epäsäännöllinen laatoitus. Penrose laattojen kaaviot löytyvät sivulta 34. Kun laattoja yhdistellään kuvan 2.1 tavalla mustalla pikkuympyrällä merkityt kulmat vastakkain ja valkoisella ympyrällä merkityt kulmat vastakkain, saadaan aikaan kuvan 2.2 kaltaisia laatoituksia. 5
8 Kuva 2.1: Penrose-laatoituksen teko-ohje Pohdiskeltavaa Kuva 2.2: Eräs Penrose-laatoitus Tuliko luokassa Penrose-laatoista samanlaisia laatoituksia? Kopioi jokin Penrose-laatoitus kalvolle ja kokeile pyörittää kalvoa alkuperäisen laatoituksen päällä. Mitä huomaat? Seuraavan sivun kuvassa 2.3 on tehty tämä. Voiko Penrose-laatoilla täyttää tason säännöllisesti, jos unohtaa mustat ja valkoiset pikkuympyrät? 6
9 Kuva 2.3: Penrose-laatoituksen kääntäminen 7
10 2.1 Välipala-2: yksipuolinen paperi Paperiarkissa on aina kaksi puolta. Jotta paperin molemmille puolille voisi piirtää viivan, täytyy kynää nostaa välillä ja siirtää se paperin toiselle puolelle. Vuonna 1858 saksalaiset matemaatikot August Ferdinand Möbius ja Johann Benedict Listing kehittivät toisistaan riippumatta tavan taittaa paperisuikale niin, että saadulla paperikappaleella on vain yksi puoli ja yksi reuna. Tällaista kappaletta kutsutaa Möbiuksen nauhaksi ja se tehdään seuraavalla tavalla. Leikataan paperista sopivanlevyinen suikale. Liimataan suikaleen päät yhteen kääntäen toista päätä 180. Siis yhdistetään kuvassa 2.4 ykköset keskenään ja kakkoset keskenään. Näin saadaan kuvan 2.5 näköinen Möbiuksen nauha Kuva 2.4: Paperinauha Kuva 2.5: Möbiuksen nauha Möbiuksen nauhan yksipuolisuuden voi todeta esimerkiksi piirtämällä kynällä viiva nauhan keskiviivaa pitkin. Näin tullaan piirtäneeksi kynää nostamatta alkuperäisen suikaleen molemmille puolille. Möbiuksen nauha kannattaa myös kokeilla leikata halki keskiviivaa pitkin ja katsoa, mitä syntyy. Kannattaa kokeilla myös tehdä sellainen nauha, jossa toista 8
11 päätä käännetään 360 tekovaiheessa ja leikata näin syntynyt nauha keskeltä halki. Möbiuksen nauhalla on myös vain yksi reuna, jonka voi todeta kuljettamalla sormea reunaa pitkin. Möbiuksen nauhoja voidaan käyttää moottoreissa hihnoina, jolloin hihnat saadaan kestävämmiksi, kun kulutuspintaa on kaksinkertaisesti normaaliin hihnaan verrattuna. 2.2 Paradokseja Paradoksit ovat lausumia, jotka ovat yhtä aikaa sekä tosia että epätosia. Paradokseihin törmää usein ja monesti ne johtuvat kielestä. Alla muutamia paradokseja mielen virkistämiseksi. Jos sanon: Minä valehtelen!, puhunko silloin totta vai valehtelenko? Kerrostalossa asuu miesparturi, joka ajaa kaikkien niiden miesten parrat, jotka eivät aja partaansa itse. Ajaako parturi oman partansa? Kirjoita paperilapun toiselle puolelle lause: Paperin toisella puolella oleva lause on totta. ja toiselle puolelle: Paperin toisella puolella oleva lause ei ole totta. Kääntele paperia ja mieti tarkkaan, mitä tulit kirjoittaneeksi. Älä lue tätä lausetta! Seuraava ei varsinaisesti ole paradoksi, mutta mietityttää varmasti siltikin kummallisuudellaan. Jos koolla on 23 sattumanvaraisesti valittua ihmistä, on todennäköisempää, että kahdella on sama syntymäpäivä (päivä ja kuukausi), kuin että kaikilla on eri syntymäpäivä. 9
12 3 Tetrominot (1h) Tetrominot ovat neljästä samankokoisesta neliöstä muodostuvia monikulmioita. Neliöt asetellaan tetrominoon niin, että vähintään kaksi neliötä on aina sivuistaan kiinni toisissaan ja niin, että sivut ovat kokonaan kiinni toisiinsa. Mahdollisia tetrominoja ovat näin muodostaen siis kuvan 3.1 viisi monikulmiota. Kuva 3.1: Tetrominot Materiaali Jokaiselle oppilaalle kaksi sarjaa tetrominoja (kopio sivulla 21). Nuoremmille lapsille mallia kannattaa suurentaa, mutta peliä pelatessa täytyy muistaa suurentaan myös sivun 22 pelilautaa samassa suhteessa. Kartonkia. 10
13 Toteutus Ensimmäisenä kannattaa selittää oppilaille tetrominojen periaate ja pyytää oppilaita piirtämään kaikki mahdolliset tetrominot ruutupaperille. Kun oppilaat ovat tehneet itselleen kaksi settiä tetrominoja, pelataan pareittain tetromino-peliä. Pelilauta löytyy sivulta 22. Pelin säännöt ovat seuraavat. Kumpikin pelaaja laittaa vuorotellen pelilaudalle tetrominopalan. Pelin voittaa se, joka saa laitettua pelilaudalle viimeisen palan. Tetrominoilla voi myöskin testata laatoituksia (katso kappale 2). Kuva 3.2: Esimerkkipeli, jonka sininen voittaa 11
14 4 Puolisäännöllisiä monitahokkaita (1 2h) HUOM! Tämä ohjelma soveltuu huonosti alle 3-luokkalaisille, koska taittelu vaatii sorminäppäryyttä. Oppaan ykkösosassa käsiteltiin Platonin kappaleita. Tässä kappaleessa taitellaan pahvista niinsanottuja Arkhimedeen kappaleita. Arkhimedeen kappaleita on 13 kappaletta. Ne ovat sellaisia puolisäännöllisiä kappaleita, jotka koostuvat kahden- tai useammanlaisesta säännöllisestä monikulmiosta. Arkhimedeen kappaleiden kärjet ovat aina keskenään samanlaisia ja särmät yhtä pitkiä. Arkhimedeen kappaleet ominaisuuksineet on lueteltu allaolevassa taulukossa. Kirjoittaja on suomentanut nimet parhaaksi katsomallaan tavalla. Kappale tahkoja särmiä kärkiä kuboktaedri (kaava sivulla 23) ikosidodekaedri (kaava sivulla 24) rombikuboktaedri (kaava sivulla 25) rombi-ikosidodekaedri rombitypistetty kuboktaedri rombitypistetty ikosidodekaedri pullistettu kuutio pullistettu dodekaedri typistetty kuutio typistetty dodekaedri typistetty ikosaedri typistetty oktaerdi typistetty tetraedri Taulukko 4.1: Arkhimedeen kappaleet 12
15 Eräitä Arkhimedeen kappaleita kartongista taiteltuna Materiaali Kopioita sivujen kaavakuvista suurennettuna mahdollisimman isoksi (suositeltavinta on suurentaa ne A3-paperille), kartonkia nappi tai helmi ja naru ripustamista varten. Toteutus Valmiita kappaleita voi tutkia aivan kuten Platonin kappaleitakin. Kappaleita voi luokitella tahkojen muodon mukaan ja oppilaat voivat kustakin kappaleesta kertoa, mitkä monikulmiot muodostavat aina kärjen. Kuvassa 4.1 on vasemmalta lukien typistetty tetraedri, ikosidodekaedri, kuboktaedri, rombikuboktaedri ja typistetty oktaedri. Kuva 4.1: Arkhimedeen kappaleita 13
16 4.1 Välipala-3: Noppaventti Noppaventti on erinomainen tapa kehittää yhteen- ja vähennyslaskutaitoa. Peli soveltuu myös ekaluokkalaisille, jos käytetään normaaleja noppia. Noppaventillä voi opettaa myöskin todennäköisyyskäsitettä. Materiaali Jokaiselle oppilaalle kuusi tavallista noppaa tai multinoppasetti (4-, 6-, 8-, 10-, 12- ja 20-tahkoiset nopat). Toteutus Tavoitteena pelissä on päästä mahdollisimman lähelle 21:tä. Pelaajat heittävät vuorotellen noppaa ja laskevat tulokset yhteen. Se, joka pääsee lähimmäs 21:tä on voittaja. Kaikkia noppia ei tarvitse käyttää. Jos käytössä on multinopat, pelaaja saa valita käyttämänsä nopan aina ennen heittoa. Toinen tapa pelata on heittää edelleenkin vuorotellen, mutta nyt kaikki heittävät kaikki nopat ja päättävät aina ennen heittoa vähennetäänkö vai lisätäänkö nopan tulos edellisiin. Multinoppia käytettäessä voi oppilaiden kanssa pohtia myös sitä, millä nopalla kannattaisi aloittaa ja miksi. 14
17 5 Rakennelmia kuutioista (2h) Rakennelmien kokoaminen perspektiivikuvista ja kaavioista kehittää spatiaalista hahmotuskykyä. Spatiaalisilla kyvyillä on suuri merkitys erityisesti modernissa, teknologisesti suuntautuneessa yhteiskunnassa. Aiemmin spatiaalisten kykyjen hyöty nähtiin lähinnä sellaisille ammateille, joissa tarvitaan suoraan varsinaista avaruudellista hahmottamista, esimerkiksi lentäjille, insinööreille ja teknisille piirtäjille. Myöhemmin useissa tutkimuksissa on havaittu hyvien spatiaalisten kykyjen auttavan ongelmanratkaisussa, matematiikassa, fysiikassa, kemiassa, maantiedossa, biologiassa, tähtitieteessä ja jopa lukutaidon kehittymisessä. Tämä ohjelma on muita vaativampi, koska se tarvitsee enemmän esitöitä. Esityöt voi hyvin tehdä lasten kanssa vaikka edellisellä kerralla. Jokainen kolmen neljän hengen ryhmä tarvitsee kpl samanlaisia kartonkikuutioita, joten jokaisen oppilaan pitää tehdä ryhmälleen 5 kpl kuutioita. Myös valmiita, esimerkiksi puukuutioita voi käyttää. Sivulla 28 on sopivan kokoisen kuution kaavio, josta kartongille liimaamalla ja taittelemalla saa käyttöön sopivia kuutioita. Koska kuutioita käytetään yhdessä sivun 29 kuvan kanssa, niitä ei kannata pienentää tai suurentaa kopioidessa. Tehtävät soveltuvat mainiosti ykkösluokalta eteenpäin. Materiaali Sivun 28 kaavakuvien kokoisia kuutioita noin kpl ryhmää kohti. Liiteen B (alkaa sivulta 35) tehtävät kopioituna jokaiselle ryhmälle. Lisäksi sivulla 29 oleva rakentelualusta kopioituna jokaiselle ryhmälle. Toteutus Ohjelma kannattaa toteuttaa niin, että ohjaaja kertoo ensin esimerkiksi piirtoheitintä käyttäen mitä perspektiivi-, etu-, sivu- ja yläkuva tarkoittavat. Tämän jälkeen voidaan alkaa tehdä tehtäviä yksi kerrallaan. Tehtävät kannattaa myös jakaa ryhmille yksi kerrallaan ja tarkastaa edellisen tehtävän lopputulos ennen uuden antamista. Monet tehtävät vaativat myös luokan töiden vertailua, joten kaikkien ryhmien pitää pysyä suunnilleen samassa tahdissa. Vaikka rakentelu ja kaavioiden luku saattaa vaikuttaa vaikealta, niin ykkösluokkalaiset pystyvät hyvin tekemään annetut tehtävät. 15
18 6 Kaaria viivoittimella (1h) Ylläolevassa kuvassa näkyvät kaksi kaarta on tehty käyttäen pelkästään janoja. Materiaali Paperia, kynä, viivain Toteutus 1) Piirrä kaksi yhtä pitkää (esim. 16 cm) janaa niin, että ne leikkaavat keskeltä. 16
19 2) Merkkaa janoille pisteet 1 cm:n välein. 3) Kirjoita jokaisen pisteen kohdalle luku alla kuvatulla tavalla ) Yhdistä luvut janalla niin, että saat aina saman summan. Tässä tapauksessa yhdistetään siis 1 ja 8, 2 ja 7 ja niin edelleen Vastaavalla tavalla voi toteuttaa muitakin taideteoksia. Kannattaa kokeilla esimerkiksi, minkälainen kuvio syntyy, kun sivun 30 kuvan pisteet yhdistää ohjeen mukaan. Yhdistelemisen jälkeen kuvat voi leikata paperista, värittää ja liimata kartongille, näin saadaan aikaan hienoja taideteoksia. Vastaavia teoksia voi tehdä myös piirtämällä edelläkuvatun kuvion laudanpätkälle ja käyttämällä pisteiden kohdilla pieniä nauloja ja yhdistämiseen lankaa. 17
20 7 Kirjallisuutta Björklund, Jenni, Lehto, Saara, Pasanen, Sampo ja Viljanen, Meeri Sukkia ja muuta matematiikkaa. MFKA-Kustannus. Vantaa Boyer, Carl Tieteiden kuningatar, matematiikan historia, osat I ja II. Bookwell. Juva Kelly, Gwen; Ewers, Tim ja Proctor, Lanna Developing Spatial Sense: Comparing Appearance with Reality. Mathematics Teacher, 95, Pappas, Theoni Matematiikan ilot. Terra Cognita. Helsinki Pappas, Theoni Lisää matematiikan iloja. Terra Cognita. Helsinki Monitahokkaista. 18
21 Liite A Monistepohjia 19
22 20
23 21
24 22
25 kuboktaedri 23
26 24 ikosidodekaedri
27 rombikuboktaedri 25
28 26 typistetty oktaedri
29 typistetty tetraedri 27
30 28
31 Sivu Etupuoli 29
32 Yhdistä kirjain lähimpiin samanlaisiin kirjaimiin. e a b c d d c e b a a b e c d d c e b a a e d c b 30
33 31
34 32
35 33
36 34
37 Liite B Rakennelmia-kappaleen tehtävät Huomaa kopioidessa, että tehtävät 1. ja 2. ovat kaksipuoleisia. 35
38 Tehtävä 1. Sivu Etupuoli Tehtävänänne on rakentaa kuvan mukainen rakennelma käyttämällä samankokoisia kuutioita. Toimintaohje 1) Rakentakaa kuvan rakennelma ruudukon päälle kuutioista. 2) Verratkaa tekemäänne rakennelmaa tehtäväpaperin toisella puolella oleviin kaaviokuviin. Muuttakaa rakennelmaa tarvittaessa. Pohdittavaa 1) Oliko tekemänne rakennelma samanlainen, kuin viereisissä pöydissä? 2) Muutitteko rakennelmaa sen jälkeen, kun olitte katsoneet kuvan kaavioita? 3) Oliko kaavioissa tai perspektiivikuvassa liikaa tietoa? Olisiko vähempi tieto riittänyt rakennelman tekemiseen? 36
39 37 Etupuoli Sivu Päältä
40 Tehtävä 2. Tehtässä rakennetaan kaaviokuvien mukainen rakennelma. Toimintaohje 1) Rakentakaa kuvan kaaviokuvien mukainen rakennelma. 2) Verratkaa rakennelmaa kääntöpuolen perspektiivikuvaan. Etupuoli Sivu Päältä Pohdittavaa 1) Oliko kaavioissa tai perspektiivikuvassa liikaa tietoa? Olisiko vähempi tieto riittänyt rakennelman tekemiseen? 2) Miksi kaaviokuvassa eri neliöt on piirretty eri harmaan sävyillä? Olisiko kaavion tai perspektiivikuvan voinut piirtää käyttäen pelkästään valkoista? 38
41 Sivu Etupuoli 39
42 Tehtävä 3. Tomintaohje Piirtäkää allaolevat perspektiivikuvat ruudukoihin. Rakentakaa rakennelmat ensin ja käyttäkää valmista rakennelmaa apuna piirtämisessä. Sivu Etupuoli Sivu Etupuoli Etupuoli Sivu Päältä Etupuoli Sivu Päältä 40
43 Tehtävä 4. Tässä tehtävässä päätellään päältäpäin katsottava kuva sivukuvien perusteella. Toimintaohje 1) Rakentakaa sivu- ja etukuvan mukainen rakennelma. Verratkaa muiden ryhmien rakennelmiin. Ovatko kaikki samanlaisia? 2) Piirtäkää jokin mahdollinen yläkuva allaolevaan ruudukkoon. Merkatkaa eri korkeuksilla olevia palikoita eri numeroilla. 3) Kuinka monta erilaista yläkuvaa luokassa syntyi? Etupuoli Sivu Päältä 41
44 Tehtävä 5. Tässä tehtävässä suunnitellaan oma rakennelma. Toimintaohje 1) Suunnitelkaa ryhmänä oma rakennelma ryhmän kaikista kuutioista. 2) Verratkaa rakennelmaa muiden rakennelmiin, tuliko millään muulla ryhmällä samanlaista? 3) Piirtäkää rakennelmasta yläkuva allaolevaan ruudukkoon. Merkatkaa eri korkeuksilla olevia palikoita eri numeroilla. Päältä 42
Platonin kappaleet. Avainsanat: geometria, matematiikan historia. Luokkataso: 6-9, lukio. Välineet: Polydron-rakennussarja, kynä, paperia.
 Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
Tero Suokas OuLUMA, sivu 1 Platonin kappaleet Avainsanat: geometria, matematiikan historia Luokkataso: 6-9, lukio Välineet: Polydron-rakennussarja, kynä, paperia Tavoitteet: Tehtävässä tutustutaan matematiikan
MATEMATIIKKA JA TAIDE I
 1 MATEMATIIKKA JA TAIDE I Tehtävät sopivat peruskoulun alaluokille. Ne on koostettu Matematiikkalehti Solmun Matematiikkadiplomeista I VI. Sivunumerot viittaavat näiden diplomitehtävien sivuihin. Aihepiirejä:
1 MATEMATIIKKA JA TAIDE I Tehtävät sopivat peruskoulun alaluokille. Ne on koostettu Matematiikkalehti Solmun Matematiikkadiplomeista I VI. Sivunumerot viittaavat näiden diplomitehtävien sivuihin. Aihepiirejä:
Kenguru 2010 Cadet (8. ja 9. luokka) sivu 1 / 5
 Kenguru 2010 Cadet (8. ja 9. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru 2010 Cadet (8. ja 9. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
MATEMATIIKKA JA TAIDE II
 1 MATEMATIIKKA JA TAIDE II Aihepiirejä: Hienomotoriikkaa harjoittavia kaksi- ja kolmiulotteisia väritys-, piirtämis- ja askartelutehtäviä, myös sellaisia, joissa kuvio jatkuu loputtomasti, ja sellaisia,
1 MATEMATIIKKA JA TAIDE II Aihepiirejä: Hienomotoriikkaa harjoittavia kaksi- ja kolmiulotteisia väritys-, piirtämis- ja askartelutehtäviä, myös sellaisia, joissa kuvio jatkuu loputtomasti, ja sellaisia,
Möbiuksen nauha. Välineet: paperisuikaleita, paperiristejä (liitteenä) lyijykynä, teippiä, sakset, värikyniä, liimaa ja värillistä paperia
 Möbiuksen nauha Avainsanat: yksipuolinen paperi, kaksiulotteinen pinta, topologia Luokkataso: 1.-2. luokka, 3.-5. luokka, 6.-9. luokka, lukio Välineet: paperisuikaleita, paperiristejä (liitteenä) lyijykynä,
Möbiuksen nauha Avainsanat: yksipuolinen paperi, kaksiulotteinen pinta, topologia Luokkataso: 1.-2. luokka, 3.-5. luokka, 6.-9. luokka, lukio Välineet: paperisuikaleita, paperiristejä (liitteenä) lyijykynä,
Kenguru 2013 Student sivu 1 / 7 (lukion 2. ja 3. vuosi)
 Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Student sivu 1 / 7 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2015 Student (lukiosarja)
 sivu 1 / 9 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 9 NIMI RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
4. Varastossa on 24, 23, 17 ja 16 kg:n säkkejä. Miten voidaan toimittaa täsmälleen 100 kg:n tilaus avaamatta yhtään säkkiä?
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 3.2.2012 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 3.2.2012 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja, kuvia tai muita perusteluja näkyviin.
Pienoismallien rakentaminen Linnanmäen laitteista
 Pienoismallien rakentaminen Linnanmäen laitteista Suunnittelu ja ohjeet: Hannele Ikäheimo ja Leena Kokko Valokuvat: Leena Kokko Pienoismallien rakentaminen Linnanmäen laitteista Suunnittelu ja ohjeet:
Pienoismallien rakentaminen Linnanmäen laitteista Suunnittelu ja ohjeet: Hannele Ikäheimo ja Leena Kokko Valokuvat: Leena Kokko Pienoismallien rakentaminen Linnanmäen laitteista Suunnittelu ja ohjeet:
Kenguru 2012 Cadet (8. ja 9. luokka)
 sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Kenguru 2011 Cadet (8. ja 9. luokka)
 sivu 1 / 7 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
sivu 1 / 7 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
Tässä osassa ei käytetä laskinta. Selitä päätelmäsi lyhyesti tai perustele ratkaisusi laskulausekkeella, kuviolla tms.
 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Selitä päätelmäsi lyhyesti tai perustele ratkaisusi laskulausekkeella, kuviolla tms. 1. Mikä on suurin kokonaisluku, joka toteuttaa
OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Selitä päätelmäsi lyhyesti tai perustele ratkaisusi laskulausekkeella, kuviolla tms. 1. Mikä on suurin kokonaisluku, joka toteuttaa
Kenguru 2013 Cadet (8. ja 9. luokka)
 sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6
 Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru Student (lukion 2. ja 3. vuosi) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Monikulmiot 1/5 Sisältö ESITIEDOT: kolmio
 Monikulmiot 1/5 Sisältö Monikulmio Monikulmioksi kutsutaan tasokuviota, jota rajaa perättäisten janojen muodostama monikulmion piiri. Janat ovat monikulmion sivuja, niiden päätepisteet monikulmion kärkipisteitä.
Monikulmiot 1/5 Sisältö Monikulmio Monikulmioksi kutsutaan tasokuviota, jota rajaa perättäisten janojen muodostama monikulmion piiri. Janat ovat monikulmion sivuja, niiden päätepisteet monikulmion kärkipisteitä.
Kenguru 2019 Student lukio
 sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta
Kenguru 2019 Benjamin 6. ja 7. luokka
 sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai
sivu 0 / 7 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Koodi: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai
Kenguru 2017 Student lukio
 sivu 1 / 9 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai 5 pistettä.
sivu 1 / 9 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Oikeasta vastauksesta saa 3, 4 tai 5 pistettä.
Peruskoulun matematiikkakilpailu Loppukilpailu 2010 Ratkaisuja OSA 1
 Peruskoulun matematiikkakilpailu Loppukilpailu 010 Ratkaisuja OSA 1 1. Mikä on suurin kokonaisluku, joka toteuttaa seuraavat ehdot? Se on suurempi kuin 100. Se on pienempi kuin 00. Kun se pyöristetään
Peruskoulun matematiikkakilpailu Loppukilpailu 010 Ratkaisuja OSA 1 1. Mikä on suurin kokonaisluku, joka toteuttaa seuraavat ehdot? Se on suurempi kuin 100. Se on pienempi kuin 00. Kun se pyöristetään
LUMATE-tiedekerhokerta, suunnitelma AIHE: PELIT JA TAKTIIKAT
 LUMATE-tiedekerhokerta, suunnitelma AIHE: PELIT JA TAKTIIKAT 1. Alkupohdintaa Mitä lempipelejä oppilailla on? Ovatko ne pohjimmiltaan matemaattisia? (laskeminen, todennäköisyys ) Mitä taktiikoita esimerkiksi
LUMATE-tiedekerhokerta, suunnitelma AIHE: PELIT JA TAKTIIKAT 1. Alkupohdintaa Mitä lempipelejä oppilailla on? Ovatko ne pohjimmiltaan matemaattisia? (laskeminen, todennäköisyys ) Mitä taktiikoita esimerkiksi
LUKUJONOT. 1) Jatka lukujonoja. 0, 1, 2,,,, 6, 8, 10,,,, 8, 12, 16,,,, 18, 15, 12,,,, 30, 25, 20,,,, 2) Täydennä lukujonoihin puuttuvat luvut.
 LUKUJONOT 2 1) Jatka lukujonoja. 0, 1, 2,,,, 6, 8, 10,,,, 8, 12, 16,,,, 18, 15, 12,,,, 30, 25, 20,,,, 2) Täydennä lukujonoihin puuttuvat luvut. 2, 4,, 8,, 12,,, 7,, 3, 1 3) Keksi oma lukujono ja kerro
LUKUJONOT 2 1) Jatka lukujonoja. 0, 1, 2,,,, 6, 8, 10,,,, 8, 12, 16,,,, 18, 15, 12,,,, 30, 25, 20,,,, 2) Täydennä lukujonoihin puuttuvat luvut. 2, 4,, 8,, 12,,, 7,, 3, 1 3) Keksi oma lukujono ja kerro
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ a) jana, jonka pituus on 3 b) kulma, jonka suuruus on 45 astetta c)
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ a) jana, jonka pituus on 3 b) kulma, jonka suuruus on 45 astetta c)
Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja tai perusteluja näkyviin, ellei muuta ole mainittu.
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 6..009 OSA Ratkaisuaika 30 min Pistemäärä 0 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja tai perusteluja näkyviin, ellei muuta
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 6..009 OSA Ratkaisuaika 30 min Pistemäärä 0 Tässä osassa ei käytetä laskinta. Kaikkiin tehtäviin laskuja tai perusteluja näkyviin, ellei muuta
Kenguru Cadet, ratkaisut (1 / 6) luokka
 Kenguru Cadet, ratkaisut (1 / 6) 3 pisteen tehtävät 1. Mikä luvuista on parillinen? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 Ainoa parillinen on 200 9 = 1800. 2. Kuvan tähti koostuu 12
Kenguru Cadet, ratkaisut (1 / 6) 3 pisteen tehtävät 1. Mikä luvuista on parillinen? (A) 2009 (B) 2 + 0 + 0 + 9 (C) 200 9 (D) 200 9 (E) 200 + 9 Ainoa parillinen on 200 9 = 1800. 2. Kuvan tähti koostuu 12
Kenguru 2014 Cadet (8. ja 9. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Kenguru 2016 Cadet (8. ja 9. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Koostaneet Juulia Lahdenperä ja Rami Luisto. Kochin lumihiutale
 Kochin lumihiutale Avainsanat: fraktaalit Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio Välineet: kynä, viivoitin, (sakset), (teippiä) Kuvaus: Tehdään oma fraktaali! Kochin lumihiutaleen voi toteuttaa
Kochin lumihiutale Avainsanat: fraktaalit Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio Välineet: kynä, viivoitin, (sakset), (teippiä) Kuvaus: Tehdään oma fraktaali! Kochin lumihiutaleen voi toteuttaa
Kenguru 2012 Student sivu 1 / 8 (lukion 2. ja 3. vuosi)
 Kenguru 2012 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2012 Student sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Matematiikkaa tiedekerhoihin
 Matematiikkaa tiedekerhoihin Vesa-Matti Sarenius Versio. Sisältö Caesarin salakirjoitus ( h). Salauskiekon valmistaminen.................... Materiaali............................... Toteutus.................................
Matematiikkaa tiedekerhoihin Vesa-Matti Sarenius Versio. Sisältö Caesarin salakirjoitus ( h). Salauskiekon valmistaminen.................... Materiaali............................... Toteutus.................................
Matematiikkaa tiedekerhoihin
 Matematiikkaa tiedekerhoihin Vesa-Matti Sarenius Versio. Sisältö Caesarin salakirjoitus ( h). Salauskiekon valmistaminen.................... Materiaali............................... Toteutus.................................
Matematiikkaa tiedekerhoihin Vesa-Matti Sarenius Versio. Sisältö Caesarin salakirjoitus ( h). Salauskiekon valmistaminen.................... Materiaali............................... Toteutus.................................
Kenguru 2016 Benjamin (6. ja 7. luokka)
 sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ (ja MITTAA) a) jana toinen jana, jonka pituus on 3 b) kulma toinen kulma, jonka
Tasogeometriaa GeoGebran piirtoalue ja työvälineet Näissä harjoituksissa työskennellään näkymässä Näkymät->Geometria PIIRRÄ (ja MITTAA) a) jana toinen jana, jonka pituus on 3 b) kulma toinen kulma, jonka
PERUSKOULUN MATEMATIIKKAKILPAILU LOPPUKILPAILU PERJANTAINA
 PERUSKOULUN MATEMATIIKKAKILPAILU LOPPUKILPAILU PERJANTAINA 4..005 OSA 1 Laskuaika 30 min Pistemäärä 0 pistettä 1. Mikä on lukujonon seuraava jäsen? Minkä säännön mukaan lukujono muodostuu? 1 4 5 1 1 1
PERUSKOULUN MATEMATIIKKAKILPAILU LOPPUKILPAILU PERJANTAINA 4..005 OSA 1 Laskuaika 30 min Pistemäärä 0 pistettä 1. Mikä on lukujonon seuraava jäsen? Minkä säännön mukaan lukujono muodostuu? 1 4 5 1 1 1
Kenguru 2011 Benjamin (6. ja 7. luokka)
 sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa
 Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
Lieriö ja särmiö Tarkastellaan pintaa, joka syntyy, kun tasoa T leikkaava suora s liikkuu suuntansa säilyttäen pitkin tason T suljettua käyrää (käyrä ei leikkaa itseään). Tällöin suora s piirtää avaruuteen
10. Kerto- ja jakolaskuja
 10. Kerto- ja jakolaskuja * Kerto- ja jakolaskun käsitteistä * Multiplikare * Kertolaatikot * Lyhyet kertotaulut * Laskujärjestys Aiheesta muualla: Luku 14: Algoritmien konkretisointia s. 87 Luku 15: Ajan
10. Kerto- ja jakolaskuja * Kerto- ja jakolaskun käsitteistä * Multiplikare * Kertolaatikot * Lyhyet kertotaulut * Laskujärjestys Aiheesta muualla: Luku 14: Algoritmien konkretisointia s. 87 Luku 15: Ajan
I Geometrian rakentaminen pisteestä lähtien
 I Geometrian rakentaminen pisteestä lähtien Koko geometrian voidaan ajatella koostuvan pisteistä. a) Matemaattinen piste on sellainen, millä EI OLE LAINKAAN ULOTTUVUUKSIA. Oppilaita voi johdatella pisteen
I Geometrian rakentaminen pisteestä lähtien Koko geometrian voidaan ajatella koostuvan pisteistä. a) Matemaattinen piste on sellainen, millä EI OLE LAINKAAN ULOTTUVUUKSIA. Oppilaita voi johdatella pisteen
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet
 TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Valitse Näkymät->Geometria PIIRRETÄÄN KOLMIOITA: suorakulmainen kolmio keksitkö, miten korostat suoraa kulmaa? tasakylkinen kolmio keksitkö,
TYÖPAJA 1: Tasogeometriaa GeoGebran piirtoalue ja työvälineet Valitse Näkymät->Geometria PIIRRETÄÄN KOLMIOITA: suorakulmainen kolmio keksitkö, miten korostat suoraa kulmaa? tasakylkinen kolmio keksitkö,
Kenguru 2011 Cadet RATKAISUT (8. ja 9. luokka)
 sivu / 2 IKET VSTUSVIHTEHDT N LLEVIIVTTU. 3 pistettä. Minkä laskun tulos on suurin? () 20 (B) 20 (C) 20 (D) + 20 (E) : 20 20 20, 20, 20 20 20 202 ( suurin ) ja : 20 0,0005 2. Hamsteri Fridolin suuntaa
sivu / 2 IKET VSTUSVIHTEHDT N LLEVIIVTTU. 3 pistettä. Minkä laskun tulos on suurin? () 20 (B) 20 (C) 20 (D) + 20 (E) : 20 20 20, 20, 20 20 20 202 ( suurin ) ja : 20 0,0005 2. Hamsteri Fridolin suuntaa
Kuva Suomen päätieverkko 1 Moottoritiet on merkitty karttaan vihreällä, muut valtatiet punaisella ja kantatiet keltaisella värillä.
 POHDIN projekti TIEVERKKO Tieverkon etäisyyksien minimointi ja esimerkiksi maakaapeleiden kokonaismäärän minimointi sekä ylipäätään äärellisen pistejoukon yhdistäminen reitityksillä toisiinsa niin, että
POHDIN projekti TIEVERKKO Tieverkon etäisyyksien minimointi ja esimerkiksi maakaapeleiden kokonaismäärän minimointi sekä ylipäätään äärellisen pistejoukon yhdistäminen reitityksillä toisiinsa niin, että
Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5
 Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru 2010 Benjamin (6. ja 7. luokka) sivu 1 / 5 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
 Heli Vaara ja Tiina Komulainen OuLUMA, sivu 1 MERIROSVOJEN AARTEENJAKOPELI Avainsanat: matematiikka, pelit, todennäköisyys Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
Heli Vaara ja Tiina Komulainen OuLUMA, sivu 1 MERIROSVOJEN AARTEENJAKOPELI Avainsanat: matematiikka, pelit, todennäköisyys Pelaajien lukumäärä: suositus 3 4 pelaajaa; peliä voi soveltaa myös muille pelaajamäärille
Kenguru 2013 Cadet (8. ja 9. luokka)
 sivu 1 / 12 3 pistettä 1. Annalla on neliöistä koostuva ruutupaperiarkki. Hän leikkaa paperista ruutujen viivoja pitkin mahdollisimman monta oikeanpuoleisessa kuvassa näkyvää kuviota. Kuinka monta ruutua
sivu 1 / 12 3 pistettä 1. Annalla on neliöistä koostuva ruutupaperiarkki. Hän leikkaa paperista ruutujen viivoja pitkin mahdollisimman monta oikeanpuoleisessa kuvassa näkyvää kuviota. Kuinka monta ruutua
Kolmion kulmien summa. Maria Sukura
 Kolmion kulmien summa Maria Sukura Oppituntien johdanto Oppilaat kuulevat triangelin äänen. He voivat katsoa sitä ja yrittää nimetä tämän soittimen. Tutkimme, miksi triangelia kutsutaan tällä nimellä,
Kolmion kulmien summa Maria Sukura Oppituntien johdanto Oppilaat kuulevat triangelin äänen. He voivat katsoa sitä ja yrittää nimetä tämän soittimen. Tutkimme, miksi triangelia kutsutaan tällä nimellä,
 Osoite: https://ggbm.at/tewz3jsv Tehtävä 1. Tutkitaan appletin kuutioita. a) Kuinka monta eripituista janaa voidaan piirtää yhdistämällä kaksi kuution kärkeä? b) Mikä a-kohdan janoista on pisin? Perustelkaa.
Osoite: https://ggbm.at/tewz3jsv Tehtävä 1. Tutkitaan appletin kuutioita. a) Kuinka monta eripituista janaa voidaan piirtää yhdistämällä kaksi kuution kärkeä? b) Mikä a-kohdan janoista on pisin? Perustelkaa.
Avaruuslävistäjää etsimässä
 Avaruuslävistäjää etsimässä Avainsanat: avaruusgeometria, mittaaminen Luokkataso: 6.-9. lk, lukio Välineet: lankaa, särmiön muotoisia kartonkisia pakkauksia(esim. maitotölkki tms.), sakset, piirtokolmio,
Avaruuslävistäjää etsimässä Avainsanat: avaruusgeometria, mittaaminen Luokkataso: 6.-9. lk, lukio Välineet: lankaa, särmiön muotoisia kartonkisia pakkauksia(esim. maitotölkki tms.), sakset, piirtokolmio,
Avaruuden muoto. Kuvaus: Tehtävässä pohditaan avaruuden muotoa ja pelataan ristinollaa erilaisilla pinnoilla.
 Avaruuden muoto Avainsanat: torus, Kleinin pullo, topologia Luokkataso: 6.-9. luokka, lukio Välineet: kyniä, pelilaudat (liitteenä) Kuvaus: Tehtävässä pohditaan avaruuden muotoa ja pelataan ristinollaa
Avaruuden muoto Avainsanat: torus, Kleinin pullo, topologia Luokkataso: 6.-9. luokka, lukio Välineet: kyniä, pelilaudat (liitteenä) Kuvaus: Tehtävässä pohditaan avaruuden muotoa ja pelataan ristinollaa
Kenguru 2012 Junior sivu 1 / 8 (lukion 1. vuosi)
 Kenguru 2012 Junior sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2012 Junior sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
LUKUKORTIT Lukukorteista on moneksi Toiminnallista matematiikkaa 1.-6. luokille. Riikka Lyytikäinen Liikkuva koulu Helsinki 2016
 LUKUKORTIT Lukukorteista on moneksi Toiminnallista matematiikkaa 1.-6. luokille Riikka Lyytikäinen Liikkuva koulu Helsinki 2016 Lukujonot Tarvikkeet: siniset ja vihreät lukukortit Toteutus: yksin, pareittain,
LUKUKORTIT Lukukorteista on moneksi Toiminnallista matematiikkaa 1.-6. luokille Riikka Lyytikäinen Liikkuva koulu Helsinki 2016 Lukujonot Tarvikkeet: siniset ja vihreät lukukortit Toteutus: yksin, pareittain,
Tehtävä 1 2 3 4 5 6 7 Vastaus
 Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Kenguru Ecolier, vastauslomake Nimi Luokka/Ryhmä Pisteet Kenguruloikka Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos
Kenguru 2011 Ecolier (4. ja 5. luokka)
 sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
Lataa Geometristen kuvien värittäminen - Sympsionics Design. Lataa
 Lataa Geometristen kuvien värittäminen - Sympsionics Design Lataa Kirjailija: Sympsionics Design ISBN: 9789526787824 Sivumäärä: 59 Formaatti: PDF Tiedoston koko: 29.30 Mb Kirja sisältää runsaasti ohjeita
Lataa Geometristen kuvien värittäminen - Sympsionics Design Lataa Kirjailija: Sympsionics Design ISBN: 9789526787824 Sivumäärä: 59 Formaatti: PDF Tiedoston koko: 29.30 Mb Kirja sisältää runsaasti ohjeita
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla
 Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
Peilaus pisteen ja suoran suhteen Pythonin Turtle moduulilla ALKUHARJOITUS Kynän ja paperin avulla peilaaminen koordinaatistossa a) Peilaa pisteen (0,0) suhteen koordinaatistossa sijaitseva - neliö, jonka
Kenguru 2014 Junior sivu 1 / 8 (lukion 1. vuosikurssi)
 Kenguru 2014 Junior sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2014 Junior sivu 1 / 8 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Laatoitukset. Tessellations. Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto
 Laatoitukset Tessellations Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.-7.10.2012 1 / 9 R. Kangaslampi Laatoitukset Laatoitukset Matematiikassa laatoitus tarkoittaa äärettömän
Laatoitukset Tessellations Riikka Kangaslampi Matematiikan ja systeemianalyysin laitos Aalto-yliopisto 5.-7.10.2012 1 / 9 R. Kangaslampi Laatoitukset Laatoitukset Matematiikassa laatoitus tarkoittaa äärettömän
Tasogeometria. Tasogeometrian käsitteitä ja osia. olevia pisteitä. Piste P on suoran ulkopuolella.
 Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
Tasogeometria Tasogeometrian käsitteitä ja osia Suora on äärettömän pitkä. A ja B ovat suoralla olevia pisteitä. Piste P on suoran ulkopuolella. Jana on geometriassa kahden pisteen välinen suoran osuus.
Kenguru 2013 Ecolier sivu 1 / 8 (4. ja 5. luokka)
 Kenguru 2013 Ecolier sivu 1 / 8 3 pistettä 1. Missä kuviossa mustia kenguruita on enemmän kuin valkoisia kenguruita? Kuvassa D on 5 mustaa kengurua ja 4 valkoista. 2. Nelli haluaa rakentaa samanlaisen
Kenguru 2013 Ecolier sivu 1 / 8 3 pistettä 1. Missä kuviossa mustia kenguruita on enemmän kuin valkoisia kenguruita? Kuvassa D on 5 mustaa kengurua ja 4 valkoista. 2. Nelli haluaa rakentaa samanlaisen
Kenguru 2011 Ecolier RATKAISUT (4. ja 5. luokka)
 sivu 1 / 7 OIKEAT VASTAUSVAIHTOEHDOT ON ALLEVIIVATTU. JOISSAKIN TEHTÄVISSÄ ON MYÖS RATKAISUN SELITYS TAI PERUSTELU. 3 pistettä 1. Pasi haluaa maalata sanan KENGURU. Hän maalaa yhden kirjaimen joka päivä
sivu 1 / 7 OIKEAT VASTAUSVAIHTOEHDOT ON ALLEVIIVATTU. JOISSAKIN TEHTÄVISSÄ ON MYÖS RATKAISUN SELITYS TAI PERUSTELU. 3 pistettä 1. Pasi haluaa maalata sanan KENGURU. Hän maalaa yhden kirjaimen joka päivä
Avaruusgeometrian perusteita
 Avaruusgeometrian perusteita Määritelmä: Kolmiulotteisen avaruuden taso on sellainen pinta, joka sisältää kokonaan jokaisen sellaisen suoran, jonka kanssa sillä on kaksi yhteistä pistettä. Ts. taso on
Avaruusgeometrian perusteita Määritelmä: Kolmiulotteisen avaruuden taso on sellainen pinta, joka sisältää kokonaan jokaisen sellaisen suoran, jonka kanssa sillä on kaksi yhteistä pistettä. Ts. taso on
Kenguru 2012 Cadet (8. ja 9. luokka) Ratkaisut.
 sivu 1 / 16 3 pistettä 1. Kello laitetaan pöydälle viisaripuoli ylöspäin juuri silloin, kun minuuttiviisari osoittaa etelään. Kuinka monen minuutin kuluttua minuuttiviisari seuraavan kerran osoittaa itään?
sivu 1 / 16 3 pistettä 1. Kello laitetaan pöydälle viisaripuoli ylöspäin juuri silloin, kun minuuttiviisari osoittaa etelään. Kuinka monen minuutin kuluttua minuuttiviisari seuraavan kerran osoittaa itään?
Kenguru 2013 Junior sivu 1 / 9 (lukion 1. vuosikurssi)
 Kenguru 2013 Junior sivu 1 / 9 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Junior sivu 1 / 9 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
3. Harjoitusjakso I. Vinkkejä ja ohjeita
 3. Harjoitusjakso I Tämä ensimmäinen harjoitusjakso sisältää kaksi perustason (a ja b) ja kaksi edistyneen tason (c ja d) harjoitusta. Kaikki neljä harjoitusta liittyvät geometrisiin konstruktioihin. Perustason
3. Harjoitusjakso I Tämä ensimmäinen harjoitusjakso sisältää kaksi perustason (a ja b) ja kaksi edistyneen tason (c ja d) harjoitusta. Kaikki neljä harjoitusta liittyvät geometrisiin konstruktioihin. Perustason
Kenguru 2011 Junior (lukion 1. vuosi)
 sivu 1 / 8 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
sivu 1 / 8 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Jätä ruutu tyhjäksi, jos et halua
Kenguru Ecolier, ratkaisut (1 / 5) 4. - 5. luokka
 3 pisteen tehtävät Kenguru Ecolier, ratkaisut (1 / 5) 1. Missä kenguru on? (A) Ympyrässä ja kolmiossa, mutta ei neliössä. (B) Ympyrässä ja neliössä, mutta ei kolmiossa. (C) Kolmiossa ja neliössä, mutta
3 pisteen tehtävät Kenguru Ecolier, ratkaisut (1 / 5) 1. Missä kenguru on? (A) Ympyrässä ja kolmiossa, mutta ei neliössä. (B) Ympyrässä ja neliössä, mutta ei kolmiossa. (C) Kolmiossa ja neliössä, mutta
LASKUTOIMITUKSET. Montako ötökkää on kussakin ruudussa? Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos:
 LASKUTOIMITUKSET Montako ötökkää on kussakin ruudussa? Nimi: 1 Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Jos laskit ötökät yksitellen, harjoittele ja mieti, miten voit tehdä laskun
LASKUTOIMITUKSET Montako ötökkää on kussakin ruudussa? Nimi: 1 Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Tulos: Jos laskit ötökät yksitellen, harjoittele ja mieti, miten voit tehdä laskun
Kenguru 2019 Cadet (8. ja 9. luokka)
 Sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse vastaus tehtävän numeron alle. Oikeasta vastauksesta saa 3, 4 tai
Sivu 0 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Tunnistekoodi (ope täyttää): Irrota tämä vastauslomake tehtävämonisteesta. Merkitse vastaus tehtävän numeron alle. Oikeasta vastauksesta saa 3, 4 tai
Valmistelut: Aseta kartiot numerojärjestykseen pienimmästä suurimpaan (alkeisopiskelu) tai sekalaiseen järjestykseen (pidemmälle edenneet oppilaat).
 Laske kymmeneen Tavoite: Oppilaat osaavat laskea yhdestä kymmeneen ja kymmenestä yhteen. Osallistujamäärä: Vähintään 10 oppilasta kartioita, joissa on numerot yhdestä kymmeneen. (Käytä 0-numeroidun kartion
Laske kymmeneen Tavoite: Oppilaat osaavat laskea yhdestä kymmeneen ja kymmenestä yhteen. Osallistujamäärä: Vähintään 10 oppilasta kartioita, joissa on numerot yhdestä kymmeneen. (Käytä 0-numeroidun kartion
Kenguru 2010 Ecolier (4. ja 5. luokka) sivu 1 / 6
 Kenguru 2010 Ecolier (4. ja 5. luokka) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
Kenguru 2010 Ecolier (4. ja 5. luokka) sivu 1 / 6 NIMI LUOKKA/RYHMÄ Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto.
lehtipajaan! Opettajan aineisto
 Tervetuloa lehtipajaan! Opettajan aineisto Opettajalle Ennen kuin ryhdyt lehtipajaan lue myös oppilaan aineisto Lehtipaja on tarkoitettu tt 3.-6.-luokkalaisille l ill Voit käyttää aineistoa myös 1.-2.-luokkalaisille,
Tervetuloa lehtipajaan! Opettajan aineisto Opettajalle Ennen kuin ryhdyt lehtipajaan lue myös oppilaan aineisto Lehtipaja on tarkoitettu tt 3.-6.-luokkalaisille l ill Voit käyttää aineistoa myös 1.-2.-luokkalaisille,
Hannele Ikäheimo www.opperi.fi 1(3)
 Hannele Ikäheimo www.opperi.fi 1(3) Junnauskoe 0 20 A ja B Opettajan ohje Tarkoitus: Tavoite: Testaus: Junnauskokeen 0-20 avulla saadaan selville oppilaiden käyttämät käyttämät laskustrategiat sekä yhteen-
Hannele Ikäheimo www.opperi.fi 1(3) Junnauskoe 0 20 A ja B Opettajan ohje Tarkoitus: Tavoite: Testaus: Junnauskokeen 0-20 avulla saadaan selville oppilaiden käyttämät käyttämät laskustrategiat sekä yhteen-
OMINAISUUS- JA SUHDETEHTÄVIEN KERTAUS. Tavoiteltava toiminta: Kognitiivinen taso: Ominaisuudet ja suhteet -kertaus
 Harjoite 12: Tavoiteltava toiminta: Materiaalit: OMINAISUUS- JA SUHDETEHTÄVIEN KERTAUS Kognitiivinen taso: Ominaisuudet ja suhteet -kertaus Toiminnan tavoite ja kuvaus: Oppilaat ratkaisevat paperi- ja
Harjoite 12: Tavoiteltava toiminta: Materiaalit: OMINAISUUS- JA SUHDETEHTÄVIEN KERTAUS Kognitiivinen taso: Ominaisuudet ja suhteet -kertaus Toiminnan tavoite ja kuvaus: Oppilaat ratkaisevat paperi- ja
Siltaaminen: Piaget Matematiikka Inductive Reasoning OPS Liikennemerkit, Eläinten luokittelu
 Harjoite 2 Tavoiteltava toiminta: Materiaalit: Eteneminen: TUTUSTUTAAN OMINAISUUS- JA Toiminnan tavoite ja kuvaus: SUHDETEHTÄVIEN TUNNISTAMISEEN Kognitiivinen taso: IR: Toiminnallinen taso: Sosiaalinen
Harjoite 2 Tavoiteltava toiminta: Materiaalit: Eteneminen: TUTUSTUTAAN OMINAISUUS- JA Toiminnan tavoite ja kuvaus: SUHDETEHTÄVIEN TUNNISTAMISEEN Kognitiivinen taso: IR: Toiminnallinen taso: Sosiaalinen
Kenguru 2016 Student lukiosarja
 sivu 1 / 9 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 9 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6
 Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö
Kenguru Benjamin (6. ja 7. luokka) ratkaisut sivu 1 / 6 3 pisteen tehtävät 1) Mikä on pienin? A) 2 + 0 + 0 + 8 B) 200 : 8 C) 2 0 0 8 D) 200 8 E) 8 + 0 + 0 2 2) Millä voidaan korvata, jotta seuraava yhtälö
Fiskars Boordilävistäjä
 Fiskars Boordilävistäjä Paperi on helppo kohdistaa oikeaan kohtaan boordilävistäjän apuviivojen avulla. Suuri painike, jota on helppo käyttää. Useita eri kuviovaihtoehtoja Maksimipaperinpaksuus 180 g,
Fiskars Boordilävistäjä Paperi on helppo kohdistaa oikeaan kohtaan boordilävistäjän apuviivojen avulla. Suuri painike, jota on helppo käyttää. Useita eri kuviovaihtoehtoja Maksimipaperinpaksuus 180 g,
Kirjoita ohjelma jossa luetaan kokonaislukuja taulukkoon (saat itse päättää taulun koon, kunhan koko on vähintään 10)
 Tehtävä 40. Kirjoita ohjelma, jossa luetaan 20 lukua, joiden arvot ovat välillä 10 100. Kun taulukko on täytetty, ohjelma tulostaa vain ne taulukon arvot, jotka esiintyvät taulukossa vain kerran. Tehtävä
Tehtävä 40. Kirjoita ohjelma, jossa luetaan 20 lukua, joiden arvot ovat välillä 10 100. Kun taulukko on täytetty, ohjelma tulostaa vain ne taulukon arvot, jotka esiintyvät taulukossa vain kerran. Tehtävä
Kenguru 2012 Benjamin sivu 1 / 8 (6. ja 7. luokka) yhteistyössä Pakilan ala-asteen kanssa
 Kenguru 2012 Benjamin sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2012 Benjamin sivu 1 / 8 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2015 Ecolier (4. ja 5. luokka)
 sivu 1 / 13 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
sivu 1 / 13 NIMI LUOKKA Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta saat miinuspisteitä
Kenguru 2010, Benjamin, ratkaisut sivu 1 / 9
 Kenguru 2010, Benjamin, ratkaisut sivu 1 / 9 3 pistettä 1. Kun tiedetään, että + + 6 = + + +, mikä luku voidaan sijoittaa kolmion paikalle? A) 2 B) 3 C) 4 D) 5 E) 6 Ratkaisu: Kun poistetaan kummaltakin
Kenguru 2010, Benjamin, ratkaisut sivu 1 / 9 3 pistettä 1. Kun tiedetään, että + + 6 = + + +, mikä luku voidaan sijoittaa kolmion paikalle? A) 2 B) 3 C) 4 D) 5 E) 6 Ratkaisu: Kun poistetaan kummaltakin
Oppimateriaali oppilaalle ja opettajalle : GeoGebra oppilaan työkaluna ylioppilaskirjoituksissa 2016 versio 0.8
 Oppimateriaali oppilaalle ja opettajalle : GeoGebra oppilaan työkaluna ylioppilaskirjoituksissa 2016 versio 0.8 Piirtoalue ja algebraikkuna Piirtoalueelle piirretään työvälinepalkista löytyvillä työvälineillä
Oppimateriaali oppilaalle ja opettajalle : GeoGebra oppilaan työkaluna ylioppilaskirjoituksissa 2016 versio 0.8 Piirtoalue ja algebraikkuna Piirtoalueelle piirretään työvälinepalkista löytyvillä työvälineillä
Fibonaccin luvut ja kultainen leikkaus
 Fibonaccin luvut ja kultainen leikkaus Avainsanat: Fibonacci, lukujono, kultainen leikkaus, suhde, yhtälö Luokkataso: 6.-9.-luokka, lukio, yliopisto Välineet: Kynä, paperi (kulmaviivain, sakset) Kuvaus:
Fibonaccin luvut ja kultainen leikkaus Avainsanat: Fibonacci, lukujono, kultainen leikkaus, suhde, yhtälö Luokkataso: 6.-9.-luokka, lukio, yliopisto Välineet: Kynä, paperi (kulmaviivain, sakset) Kuvaus:
Avainsanat: peli, matematiikka, polynomi, yhteen- ja vähennyslasku, kertolasku
 Pasi Leppäniemi OuLUMA, sivu 1 POLYNOMIPELI Avainsanat: peli, matematiikka, polynomi, yhteen- ja vähennyslasku, kertolasku Luokkataso: 8-9 lk Välineet: pelilauta, polynomikortit, monomikortit, tuloskortit,
Pasi Leppäniemi OuLUMA, sivu 1 POLYNOMIPELI Avainsanat: peli, matematiikka, polynomi, yhteen- ja vähennyslasku, kertolasku Luokkataso: 8-9 lk Välineet: pelilauta, polynomikortit, monomikortit, tuloskortit,
1. Jaa blini kolmella suoralla a) neljään, b) viiteen, c) kuuteen ja d) seitsemään osaan. Osien ei tarvitse olla samanlaisia. Piirrä suorat kuviin.
 Peruskoulun matematiikkakilpailu 2015 2016 alkukilpailu 29.10.2015. Ratkaisut 1. Jaa blini kolmella suoralla a) neljään, b) viiteen, c) kuuteen ja d) seitsemään osaan. Osien ei tarvitse olla samanlaisia.
Peruskoulun matematiikkakilpailu 2015 2016 alkukilpailu 29.10.2015. Ratkaisut 1. Jaa blini kolmella suoralla a) neljään, b) viiteen, c) kuuteen ja d) seitsemään osaan. Osien ei tarvitse olla samanlaisia.
Pelin tavoitteena on kerätä eniten eläin-pelimerkkejä ennen takaisin leiriin palaamista.
 OHJE / PELIOHJE 1 (5) Eläinsafari yli 5-vuotiaille pelilauta 4 värikästä jeeppi-pelikorttia 4 värikästä kortinpidikettä 2 noppaa 40 eläinkorttia, joissa 1-3 eläintä laskutaitoa taktikointia Kasatkaa pelilauta.
OHJE / PELIOHJE 1 (5) Eläinsafari yli 5-vuotiaille pelilauta 4 värikästä jeeppi-pelikorttia 4 värikästä kortinpidikettä 2 noppaa 40 eläinkorttia, joissa 1-3 eläintä laskutaitoa taktikointia Kasatkaa pelilauta.
Kenguru 2015 Mini-Ecolier (2. ja 3. luokka) RATKAISUT
 sivu 1 / 10 3 pistettä 1. Kuinka monta pilkkua kuvan leppäkertuilla on yhteensä? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21 Ratkaisu: Pilkkuja on 1 + 1 + 1 + 2 + 2 + 1 + 3 + 2 + 3 + 3 = 19. 2. Miltä kuvan pyöreä
sivu 1 / 10 3 pistettä 1. Kuinka monta pilkkua kuvan leppäkertuilla on yhteensä? (A) 17 (B) 18 (C) 19 (D) 20 (E) 21 Ratkaisu: Pilkkuja on 1 + 1 + 1 + 2 + 2 + 1 + 3 + 2 + 3 + 3 = 19. 2. Miltä kuvan pyöreä
Impedanssitomografia-peli
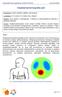 Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
Impedanssitomografia-peli Avainsanat: inversio-ongelmat, päättely, satunnaisuus Luokkataso: 3.-5. luokka, 6.-9. luokka, lukio, yliopisto Välineet: kynä, paperia, 2 pelinappulaa, 4 kolikkoa tai kolikonheittokortit
2.1 Yhtenevyyden ja yhdenmuotoisuuden käsite
 2.1 Yhtenevyyden ja yhdenmuotoisuuden käsite Tämän päivän lukiogeometrian sisältöjä on melkoisesti supistettu siitä, mitä ne olivat joku vuosikymmen sitten. Sisällöistä ei enää kasata sellaista rakennelmaa,
2.1 Yhtenevyyden ja yhdenmuotoisuuden käsite Tämän päivän lukiogeometrian sisältöjä on melkoisesti supistettu siitä, mitä ne olivat joku vuosikymmen sitten. Sisällöistä ei enää kasata sellaista rakennelmaa,
Kenguru 2013 Benjamin sivu 1 / 7 (6. ja 7. luokka) yhteistyössä Pakilan ala-asteen kanssa
 Kenguru 2013 Benjamin sivu 1 / 7 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
Kenguru 2013 Benjamin sivu 1 / 7 Nimi Ryhmä Pisteet: Kenguruloikan pituus: Irrota tämä vastauslomake tehtävämonisteesta. Merkitse tehtävän numeron alle valitsemasi vastausvaihtoehto. Väärästä vastauksesta
3. Kuvio taitetaan kuutioksi. Mikä on suurin samaa kärkeä ympäröivillä kolmella sivutahkolla olevien lukujen tulo?
 Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 4.2.2011 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Esitä myös lasku, kuvio, päätelmä tai muu lyhyt perustelu.
Peruskoulun matematiikkakilpailu Loppukilpailu perjantaina 4.2.2011 OSA 1 Ratkaisuaika 30 min Pistemäärä 20 Tässä osassa ei käytetä laskinta. Esitä myös lasku, kuvio, päätelmä tai muu lyhyt perustelu.
Sisällysluettelo. 1. Johdanto
 Säännöt Sisällysluettelo 1. Johdanto 3 2. Sisältö 4 3. Alkuvalmistelut 5 4. Pelin aloitus ja kulku 6 5. Pelin lopetus 9 6. Vaikea peli ja muut pelimuunnelmat 10 1. Johdanto Pelilauta on 25 ruudusta muodostuva
Säännöt Sisällysluettelo 1. Johdanto 3 2. Sisältö 4 3. Alkuvalmistelut 5 4. Pelin aloitus ja kulku 6 5. Pelin lopetus 9 6. Vaikea peli ja muut pelimuunnelmat 10 1. Johdanto Pelilauta on 25 ruudusta muodostuva
Monitahokkaat. MHK-SciFest 2011: työpajan Koe Matematiikka! osaraportti. Mitro Makkonen, Alpo Voutilainen ja Kaisa Ronkanen Joensuussa 8.5.
 Monitahokkaat MHK-SciFest 2011: työpajan Koe Matematiikka! osaraportti Mitro Makkonen, Alpo Voutilainen ja Kaisa Ronkanen Joensuussa 8.5.2011 Fysiikan ja matematiikan laitos Itä-Suomen yliopisto Joensuun
Monitahokkaat MHK-SciFest 2011: työpajan Koe Matematiikka! osaraportti Mitro Makkonen, Alpo Voutilainen ja Kaisa Ronkanen Joensuussa 8.5.2011 Fysiikan ja matematiikan laitos Itä-Suomen yliopisto Joensuun
2 + = 10 0 + = 10 10 3 = 10 5 = + 4 = 10 + 9 = 10 10 8 = 10 1 = 7 + = 10 5 + = 10 10 6 = 10 10 =
 Traggelprov 0 20 A Namn: 2 + = 10 0 + = 10 10 3 = 10 5 = + 4 = 10 + 9 = 10 10 8 = 10 1 = 7 + = 10 5 + = 10 10 6 = 10 10 = Dubbelt + Dubbelt 4 + 4 = 6 + 6 = 8 4 = 14 7 = 9 + 9 = 3 + 3 = 18 9 = 20 10 = 7
Traggelprov 0 20 A Namn: 2 + = 10 0 + = 10 10 3 = 10 5 = + 4 = 10 + 9 = 10 10 8 = 10 1 = 7 + = 10 5 + = 10 10 6 = 10 10 = Dubbelt + Dubbelt 4 + 4 = 6 + 6 = 8 4 = 14 7 = 9 + 9 = 3 + 3 = 18 9 = 20 10 = 7
Pinta-ala- ja tilavuuskäsitteiden oppimispeli
 Pinta-ala- ja tilavuuskäsitteiden oppimispeli Kari Mikkola, FM, OSAO, Kaukovainion yksikkö, tekniikka Geometriaa on perinteisesti osattu heikoiten matematiikan osa-alueista peruskoulun päättyessä [1],
Pinta-ala- ja tilavuuskäsitteiden oppimispeli Kari Mikkola, FM, OSAO, Kaukovainion yksikkö, tekniikka Geometriaa on perinteisesti osattu heikoiten matematiikan osa-alueista peruskoulun päättyessä [1],
Kenguru 2019 Student Ratkaisut
 sivu 0 / 22 3 pistettä TEHTÄVÄ 1 2 3 4 5 6 7 8 VASTAUS C B D C B E C A 4 pistettä TEHTÄVÄ 9 10 11 12 13 14 15 16 VASTAUS B B E D A E A A 5 pistettä TEHTÄVÄ 17 18 19 20 21 22 23 24 VASTAUS E E D D C C B
sivu 0 / 22 3 pistettä TEHTÄVÄ 1 2 3 4 5 6 7 8 VASTAUS C B D C B E C A 4 pistettä TEHTÄVÄ 9 10 11 12 13 14 15 16 VASTAUS B B E D A E A A 5 pistettä TEHTÄVÄ 17 18 19 20 21 22 23 24 VASTAUS E E D D C C B
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon
 Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Matikkaa KA1-kurssilaisille, osa 3: suoran piirtäminen koordinaatistoon KA1-kurssi on ehkä mahdollista läpäistä, vaikkei osaisikaan piirtää suoraa yhtälön perusteella. Mutta muut kansiksen kurssit, no
Lataa Geometristen kappaleiden piirtäminen - Sympsionics Design. Lataa
 Lataa Geometristen kappaleiden piirtäminen - Sympsionics Design Lataa Kirjailija: Sympsionics Design ISBN: 9789526787817 Sivumäärä: 64 Formaatti: PDF Tiedoston koko: 36.69 Mb Kirjasta löytyvät täsmälliset,
Lataa Geometristen kappaleiden piirtäminen - Sympsionics Design Lataa Kirjailija: Sympsionics Design ISBN: 9789526787817 Sivumäärä: 64 Formaatti: PDF Tiedoston koko: 36.69 Mb Kirjasta löytyvät täsmälliset,
4.3 Kehäkulma. Keskuskulma
 4.3 Kehäkulma. Keskuskulma Sellaista kulmaa, jonka kärki on ympyrän kehällä ja kumpikin kylki leikkaa (rajatapauksessa sivuaa) ympyrän kehää, sanotaan kehäkulmaksi, ja sitä vastaavan keskuskulman kyljet
4.3 Kehäkulma. Keskuskulma Sellaista kulmaa, jonka kärki on ympyrän kehällä ja kumpikin kylki leikkaa (rajatapauksessa sivuaa) ympyrän kehää, sanotaan kehäkulmaksi, ja sitä vastaavan keskuskulman kyljet
Matemaattisten Aineiden Opettajien Liitto MAOL ry Valtakunnallinen yhdeksännen luokan matematiikan koe 2012
 Matemaattisten Aineiden Opettajien Liitto MAOL ry Valtakunnallinen yhdeksännen luokan matematiikan koe 2012 MFKA-Kustannus Oy Rautatieläisenkatu 6, 00520 HELSINKI, puh. (09) 1502 378 http://www.mfka.fi
Matemaattisten Aineiden Opettajien Liitto MAOL ry Valtakunnallinen yhdeksännen luokan matematiikan koe 2012 MFKA-Kustannus Oy Rautatieläisenkatu 6, 00520 HELSINKI, puh. (09) 1502 378 http://www.mfka.fi
