3. Pinot, jonot ja linkitetyt listat
|
|
|
- Tapani Nieminen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 3. Pinot, jonot ja linkitetyt listat Pinot ja jonot ovat yksinkertaisimpia tietorakenteita, mutta myös tärkeimpiä. Niitä käytetään lukuisissa sovelluksissa ja monimutkaisten tietorakenteiden osina. Yksinkertaisuutensa vuoksi ne ovat niitä harvoja, joita on toteutettu myös laitteistotason mikrokäskyissä keskusyksikkötasolla Pinot Pino (stack) sisältää alkioita, joita lisätään ja poistetaan pinon huipulta viimeksi-pinoon-ensiksi-pinosta -periaatteen mukaan (LIFO last-in-first-out). Alkioita voidaan lisätä koska tahansa, mutta poistaa voidaan kulloinkin ainoastaan viimeksi pinoon lisätty. Tietorakenteen pino perusoperaatiot ovat pinoa ja pura lisäämistä ja poistamista varten (push ja pop). 3. luku 63 Esim Verkkoselain tallettaa käydyt osoitteet pinoon. Käyttäjän tullessa uuteen verkko-osoitteeseen kyseinen osoite työnnetään osoitepinoon. Selain sallii käyttäjän purkaa pinoa takaisin viittaavalla painikkeella. Esim Monipuoliset tekstinkäsittelyjärjestelmät käsittävät nykyään aina käskyn peruutuksen (undo), joka toteutetaan pinon avulla, kun pinoon talletaan tehdyt muutokset. Pino abstraktina tietotyyppinä Pino S on abstrakti tietotyyppi, joka käsittää seuraavat perusmetodit: push(o): Lisää alkion o pinon huipulle. Syöte: alkio 3. luku 64 pop(): Antaa päällimmäisen alkion poistaen sen samalla pinosta; virhe seuraa, mikäli pino oli tyhjä. Tulos: alkio Lisäksi voidaan käyttää pino-operaatioita: Esim Oheinen taulukko esittää sarjan pino-operaatioita ja näiden vaikutuksen alunperin tyhjään pinoon S, johon talletetaan yksinkertaisuuden vuoksi kokonaislukuja. size(): Palauttaa pinon alkioiden määrän. Tulos: kokonaisluku isempty(): Palauttaa totuusarvon sen mukaan, onko pino tyhjä vai ei. Tulos: totuusarvo Top(): Palauttaa pinon huippualkion poistamatta sitä pinosta; virhe seuraa pinon ollessa tyhjä. Tulos: alkio 3. luku 65 operaatio tulos S push(5) - (5) push(3) - (5,3) pop() 3 (5) push(7) - (5,7) pop() 7 (5) top() 5 (5) 3. luku 66
2 pop() 5 () pop() virhe () isempty() tosi () push(9) - (9) push(7) - (9,7) push(3) - (9,7,3) push(5) - (9,7,3,5) size() 4 (9,7,3,5) pop() 5 (9,7,3) 3. luku 67 Pino on sisäänrakennettuna luokkana Javassa. Tärkeimmät metodit ovat push, pop, peek (vastaa top-operaatiota), size ja empty. Seuraavana (koodi 3.1.) esitetään yleisellä tasolla (mielivaltaisesti valittuja olioita) rajapintaluokka vastaamaan pinon abstraktia tietotyyppiä. Mukana on lisäksi virheenkäsittelymetodeita pop ja top varten pinon ollessa tyhjä (koodi 3.2.). public interface Stack { // accessor methods public int size(); // return the number of elements stored in the stack public boolean isempty(); // test whether the stack is empty public Object top() // return the top element throws StackEmptyException; // thrown if called on an empty stack // update methods public void push (Object element); // insert an element onto the stack public Object pop() // return and remove the top element of the stack throws StackEmptyException; // thrown if called on an empty stack Koodi 3.1. Pinon rajapintaluokka. 3. luku 68 public class StackEmptyException extends RuntimeException { public StackEmptyException(String err) { super(err); S t N-1 Koodi 3.2. Pinon metodien pop ja top poikkeusten käsittely. Yksinkertainen taulukkoon perustuva toteutus Kuvataan pinon toteutus, jossa alkiot talletetaan taulukkoon. Kun taulukon koko on määrättävä se luotaessa, annetaan sille jokin maksimikoko N. Niinpä pino S sisältää N-alkioisen taulukon ja kokonaislukumuuttujan t, joka osoittaa pinon huippualkion paikan taulukossa (kuva 3.1.). Kuva 3.1. Pinon toteutus taulukkona S, jossa huippualkio on paikassa S[t]. Pinon indeksimuuttuja alustetaan arvoksi -1, koska Javassa taulukot alkavat indeksin arvosta 0. Lisäksi annetaan uusi poikkeus pinon ylitäytön estämiseksi. Nyt voidaan esittää abstrakti tietotyyppi pseudokoodina. 3. luku luku 70
3 Algorithm size(): return t + 1 Algorithm isempty(): return (t < 0) Algorithm top(): if isempty() then throw StackEmptyException return S[t] Koodi 3.3. Pinon abstraktia tietotyyppiä. Algorithm push(o): if size()=n then throw StackFullException t t + 1 S[t] o Algorithm pop(): if isempty() then throw StackEmptyException e S[t] S[t] null t t - 1 return e Koodi 3.3. (jatkoa) Pinon abstraktia tietotyyppiä. 3. luku luku 72 Kielestä riippuen automaattista roskienkeräystä voisi käyttää sen sijaan, että tässä asetettiin poistetun alkion paikalle null-arvo, mutta tehtävä on kuitenkin hoidettava tavalla tai toisella. Esitetyt pinometodit toimivat kaikki kompleksisuudeltaan ajassa O(1), ts. ovat riippumattomia alkioiden määrästä pinossa n tai taulukon koosta N. Tilavaatimus on luonnollisesti O(N). Tietorakenne pino on käytössä lukuisissa sovelluksissa. Sen taulukkototeutus on erittäin yksinkertainen ja tehokas. Täysin ideaalinen se ei kuitenkaan ole, kun taulukon koko on rajoitettu. Myöhemmin tässä luvussa tarkastellaan taulukon dynaamisempaa toteutustapaa. Seuraavana on pinon Javatoteutus. public class ArrayStack implements Stack { // Implementation of the Stack interface using an array. public static final int CAPACITY = 1000; // default capacity of the stack private int capacity; // maximum capacity of the stack. private Object S[]; // S holds the elements of the stack private int top = -1; // the top element of the stack. public ArrayStack() { // Initialize the stack with default capacity this(capacity); public ArrayStack(int cap) { // Initialize the stack with given capacity capacity = cap; S = new Object[capacity]; Koodi 3.4. Pinon taulukkototeutusta Javalla. 3. luku luku 74
4 public int size() { // Return the current stack size return (top + 1); public boolean isempty() { // Return true iff the stack is empty return (top < 0); public void push(object obj) throws StackFullException{ // Push a new object on the stack if (size() == capacity) throw new StackFullException("Stack overflow."); S[++top] = obj; Koodi 3.4. (jatkoa) Pinon taulukkototeutusta Javalla. public Object top() // Return the top stack element throws StackEmptyException { if (isempty()) throw new StackEmptyException("Stack is empty."); return S[top]; public Object pop() // Pop off the stack element throws StackEmptyException { Object elem; if (isempty()) throw new StackEmptyException("Stack is Empty."); elem = S[top]; S[top--] = null; // Dereference S[top] and decrement top return elem; 3. luku 75 Koodi 3.4. (jatkoa) Pinon taulukkototeutusta Javalla. 3. luku 76 Javan käyttö abstraktin tietotyypin toteutuksessa mahdollistaa geneeristen olioiden tallettamisen pinoon niiden kuuluessa mielivaltaisesti valittuihin luokkiin, kuten luokkiin kokonaisluvut tai opiskelijat. Jotta saadaan alkio määrätyn luokan ilmentymänä, on suoritettava tyypinmuunnos (cast), jonka avulla olio nähdään määrättyyn luokkaan kuuluvana eikä yleisempänä, yliluokkaan kuuluvana (Object tässä). Tämä esitetään eräälle tapaukselle seuraavassa. public static Integer[ ] reverse(integer[ ] a) { ArrayStack S = new ArrayStack(a.length); Integer[ ] b = new Integer[a.length]; for (int i=0; i<a.length; i++) S.push(a[i]); for (int i=0; i<a.length; i++) b[i] = (Integer) (S.pop()); return b; Koodi 3.5. Tämä metodi kääntää alkioiden järjestyksen taulukossa aputaulukkoa käyttäen. Tyypinmuunnos suoritetaan pakottamalla pop-metodin palauttama olio kokonaislukutyyppiseksi. Java antaa muuttujan eli kentän length (taulukon koko) käyttöön. 3. luku luku 78
5 Pinoja Javan virtuaalikoneessa Java-ohjelma käännetään välikieleen, jota ajetaan Javan virtuaalikoneessa - näin saavutetaan laiteriippumattomuus. Pinot ovat tärkeä osa Java-ohjelman suoritusaikaista ympäristöä. Javan metodipinossa pidetään kirjaa lokaaleista muuttujista ja muusta tärkeästä metodien tiedosta näitä kutsuttaessa (kuva 3.3.). Virtuaalikone ylläpitää ohjelmalaskuria, rekisteriä, jossa on kulloinkin suoritettavana olevan metodin osoite. Virtuaalikone ylläpitää pinoa, jonka alkiot ovat sillä hetkellä aktiivisten metodikutsujen tiedot. Päällimmäisenä pinossa on suorittevana oleva metodi ja sen alapuolella tilapäisesti keskeytetyt. Nämä muodostavat kutsujen ketjun, jossa järjestyksen määrää se, miten ne on pinoon asetettu eli metodeja kutsuttu. 3. luku 79 Java käyttää arvoparametreja, mikä merkitsee, että muuttujan tai lausekkeen nykyinen arvo välitetään kutsutulle metodille. Jos kutsuttu metodi muuttaa lokaalin muuttujan arvoa, se ei muuta kutsuneen vastaavan muuttujan arvoa. Kuvassa 3.3. Metodi cool on juuri kutsunut metodia fool ja edellistä sitä ennen metodi main. Ohjelmalaskurin (PC) arvo, parametrit ja lokaalit muuttujat on talletettu pinon alkioihin. Metodipinoa käytetään tässä metodikutsujen toteutukseen ja parametrinvälitykseen. Tämä ei ole toki vain Javan erityispiirre, vaan vastaavia on ollut jo kauan käytössä ohjelmointikielten ajoaikaisissa ympäristöissä. 3. luku 80 fool: PC = 320 m = 7 cool: PC = 216 j = 5 k = 7 main: PC = 14 i = 5 Javan pino Kuva 3.3. Esimerkki Javan pinosta. main() { int i=5;.. 14 cool(i);.. cool(int j) { int k=7; fool(k); fool(int m) {.. Java-ohjelma 3. luku 81 Yhtenä pinon käytön etuna on rekursion ohjelmoinnin tekeminen helpoksi. Tällöin metodi voi kutsua itseään ikään kuin aliohjelmana. Rekursio on varsin hyödyllinen, koska se sallii yksinkertaisten ja tehokkaiden ohjelmien suunnittelun melko vaikeille ongelmille. Eräs tyypillinen (hyvin yksinkertainen) esimerkki on kertomafunktion n! =n(n-1)(n-2) 1 laskeminen seuraavasti. public static long factorial(long n){ if (n<=1) return 1; else return n*factorial(n-1); Koodi 3.6. Rekursiivisesti kertomaa laskeva ohjelma. 3. luku 82
6 Ohjelma kutsuu itseään rekursiivisesti, kunnes parametrin arvoksi tulee 1, jolloin tämä palautetaan ja kerrotaan 2:n kanssa jne. Tässä nähdään myös se tärkeä yksityiskohta, että rekursiivisen metodin pitää aina käsittää metodin lopetus, sillä muuten aiheutuisi äärettömästi rekursiivinen metodi, joka päätyisi lopulta suoritusaikaiseen virheeseen pinolle varatun tilan loppuessa. kutsu factorial(3) kutsu factorial(2) palautus 3 2=6 palautus 2 1=2 Tällaista lineaarista rekursiota voidaan hyvin havainnollistaa kuvan 3.4. tapaan. Siinä lasketaan kertoma 3! kutsu palautus 1 factorial(1) Kuva 3.4. Kertoman 3!=1 3=6 laskenta rekursiivisesti. 3. luku luku Jonot Javan virtuaalikone soveltaa myös operandipinoa, jota käytetään aritmeettisten lausekkeiden, kuten ((a+b)*(c+d))/e, laskennassa. Yksinkertainen binäärioperaatio, esim. a+b, suoritetaan pinoamalla symboli a operandipinoon, samoin symboli b ja sitten kutsumalla käskyä, joka purkaa nämä kaksi pinon päällimmäistä alkiota laskien kyseisen binäärioperaation niille ja pinoaa tuloksen takaisin operandipinon huippualkioksi. Jono (queue) on pinoa muistuttava tärkeä tietorakenne. Jonossa alkioita lisätään ja poistetaan ensiksi-sisään-ensiksi-ulos - periaatteen (FIFO first-in first-out) mukaisesti. Alkioita voidaan lisätä milloin vain, mutta poistaa voidaan ainoastaan se, joka on ollut kauimmiten jonossa. Tämä esitetään niin, että alkiot lisätään jonon loppuun ja niitä poistetaan sen alusta. Jonon abstrakti tietotyyppi Jonon abstrakti tietotyyppi määritellään sellaisena, jossa alkion saanti ja poistaminen on rajoitettu jonon ensimmäiseen alkioon ja lisäys loppuun. Se käsittää kaksi perusmetodia: 3. luku luku 86
7 enqueue(o): Lisää olion o jonon loppuun. Syöte: olio dequeue(): Poistaa ja palauttaa alkion jonon alusta. Tulos: olio Yleensä sisällytetään jonon abstraktiin tietotyyppiin vielä: size(): Palauttaa jonon alkioiden määrän. Tulos: kokonaisluku isempty(): Palauttaa totuusarvon siitä, onko jono tyhjä. Tulos: totuusarvo front(): Palauttaa, mutta ei poista, jonon ensimmäisen alkion; virhe tapahtuu jonon ollessa tyhjä. Tulos: alkio 3. luku 87 Tietorakenteella jono on lukuisia sovellusmahdollisuuksia. Esimerkkinä voisi olla erilaiset varausjärjestelmät, joissa asiakkaita palvellaan tulojärjestyksessä. Kysymyksessä on tapahtumien (transaktio) käsittely. Esim Seuraava taulukko kuvaa sarjan jono-operaatioita ja näiden vaikutuksen aluksi tyhjään kokonaislukujen jonoon Q. operaatio tulos Q enqueue(5) - (5) enqueue(3) - (5,3) dequeue() 5 (3) enqueue(7) - (3,7) 3. luku 88 dequeue() 3 (7) front() 7 (7) dequeue() 7 () dequeue() virhe () isempty() tosi () enqueue(9) - (9) enqueue(7) - (9,7) size() 2 (9,7) enqueue(3) - (9,7,3) enqueue(5) - (9,7,3,5) dequeue() 9 (7,3,5) Jonon abstraktin tietotyypin Java-kielinen rajapinta on esitetty oheisena, joka sallii mielivaltaisesti valittujen luokkien olioita lisättävän jonoon. public interface Queue { // accessor methods public int size(); // return the number of elements stored in the queue public boolean isempty(); // test whether the queue is empty public Object front() // return the front element of the queue throws QueueEmptyException; // thrown if called on an empty queue // update methods public void enqueue (Object element); // insert an element at the rear public Object dequeue() // return and remove the front element throws QueueEmptyException; // thrown if called on an empty queue Koodi 3.7. Jonon rajapinta. 3. luku luku 90
8 Jonon yksinkertainen taulukkopohjainen toteutus Kiinnitetään jälleen aluksi taulukon koko arvoksi N. Kun jono noudattaa FIFO-periaatetta, huomiota pitää kiinnittää, miten hallitaan jonon alkua ja loppua. Yksi mahdollisuus olisi muuntaa pinoa niin, että jonon alku olisi paikassa Q[0], josta lukien jono kasvaisi taulukon loppua kohti. Tämä olisi kuitenkin huono ratkaisu, koska se vaatisi melkein kaikkien (n-1) alkioiden siirtämistä poistettaessa (dequeue) jonon alusta, joka on (n) n:lle alkiolle jonossa. Poisto voidaan tehdä vakioajassa määriteltäessä kaksi muuttujaa, f ja r, seuraavasti: Jonon Q ensimmäinen alkio osoitetaan indeksillä f. Se on seuraava poistettava, ellei jono ole tyhjä, jolloin f=r. Jonon Q seuraavan vapaan paikan osoittaa indeksi r. 3. luku 91 Aluksi määritellään f = r = 0 eli jono tyhjäksi. Poistettaessa alkio yksinkertaisesti lisätään muuttujan f arvoa ykkösellä, ja lisättäessä alkio lisätään muuttujan r arvoa ykkösellä eli seuraavaan vapaseen paikkaan. Näin operaatiot sekä dequeue että enqueue ovat O(1) aikakompleksisuudeltaan. Erikoistapauksina jää käsiteltäviksi tilanteet, joissa tullaan taulukon alkuun ja loppuun ja pitää kuitenkin tehdä vielä lisäyksiä tai poistoja. Tämä hallitaan helposti määriteltäessä taulukko rengasrankenteena, jossa jono jatkuu alkiosta Q[N-1] alkioon Q[0] ja päinvastoin (kuva 3.5.). Toteutus on helppo käytettäessä modulo-laskentaa, (f+1) mod N tai(r+1) mod N, operaatiosta riippuen. Modulo-operaattori mod (Javassa %) tuottaa kokonaislukujaon jakojäännöksen eli (y 0) x mod y = x- x/y y. 3. luku 92 Q Q f r N-1 (a) r f N-1 (b) Kuva 3.5. Taulukon Q käyttö rengasrakenteena: (a) normaali tilanne, kun f r, ja (b) kierretty tilanne, kun r f. Käytössä olevat paikat on väritetty (powerpoint-esityksessä). Ongelmana on hallita tilanne, kun taulukko on täyttymässä eli N alkiota haluttaisiin tallettaa ja tällöin f=r. Tämä on hankalasti samankaltainen kuin jonon ollessa tyhjä. Yksinkertaisin tapa väistää ongelma on rajoittaa talletettavien alkioiden määräksi N- 1. Tämä voidaan testata ehdolla (N-f+r) mod N sekä normaalissa että kierretyssä tapauksessa (kuva 3.5.). 3. luku 93 Seuraavaksi esitetään pseudokoodinen kuvaus jono-operaatioille. Kunkin niistä aikavaatimus on vakio, O(1). Muistitilavaatimus on pinon tapaan (riippumaton arvosta n N) O(N). Algorithm size(): return (N-f+r) mod N Algorithm isempty(): return (f=r) Algorithm front(): if isempty() then throw QueueEmptyException return Q[f] Koodi 3.8. Jonon taulukkototeutus pseudokoodisena. 3. luku 94
9 Algorithm dequeue(): if isempty() then throw QueueEmptyException temp Q[f] Q[f] null f (f+1) mod N return temp Algorithm enqueue(o): if size()=n-1 then throw QueueFullException Q[r] o r (r+1) mod N Koodi 3.8. (jatkoa) Jonon taulukkototeutus pseudokoodisena. Jonon heikkous on sama kuin pinon. Alkioiden määrä on rajoitettu. Jos alkioiden maksimimäärästä on hyvä arvio, ei rajoituksella ole kuitenkaan suurta merkitystä. Muistin hallinta Javassa Javassa oliolle voidaan varata muistia dynaamisesti metodin suoritusaikana, kun metodi hyödyntää Javan käskyä new. Esim. voidaan luoda 12-alkioinen olio Vector käskyllä: Vector items = new Vector(12) Tätä oliota voidaan käyttää taulukon tapaan paitsi, että sen koko kasvaa ja kutistuu tarpeen mukaan. Lisäksi se ei häviä, vaikka sen luonut metodi päätetään. 3. luku luku 96 Pinon sijasta Javassa sovelletaan jonoa olioiden muistinhallinnassa. Muistia (kuva 3.6.) varataan muistikasasta tai -keosta (heap), jota ei pidä sekoittaa myöhemmin esiteltävään kasa tai keko nimiseen tietorakenteeseen. Tämä muisti jaetaan lohkoihin (block), jotka ovat peräkkäisiä muistialueita. Java soveltaa jono-operaatioita näille lohkoille (koko esim tavua). Muitakin jonosovelluksia Javassa on olemassa. Säikeiden (thread) käyttö rajoitetun moniohjelmoinnin mahdollistamiseksi hyödyntää jonoa, missä säie sijoitetaan jonon alkioon ja sille annetaan aikaviipaleita vuorotellen muiden jonossa olevien säikeiden kanssa Linkitetyt listat ohjelman koodi Javan pino vapaa muisti muistikasa Kuva 3.6. Javan virtuaalikoneen muistin käyttöä. Edellä tarkasteltiin pinojen ja jonojen abstrakteja tietotyyppejä taulukkototeutuksin. Vaikka toteutukset olivat sangen yksinkertaisia, ne eivät olleet joustavia ratkaisuja, koska taulukon koko on kiinnitettävä etukäteen. Linkitetty lista tarjoaa tälle joustavan vaihtoehdon. 3. luku luku 98
10 Yhteen suuntaan linkitetty lista Linkitetty tai ketjutettu lista on yksinkertaisimmillaan lineaarisesti järjestettyjen solmujen kokoelma. Kukin solmu käsittää varsinaisen tiedon lisäksi viittauksen tai osoittimen seuraavaan (next) solmuun (kuva 3.7.). pää seuraaja seuraaja seuraaja seuraaja alkio alkio alkio alkio Baltimore Rooma Seattle Toronto Kuva 3.7. Yhteen suuntaan linkitetty lista. Viittaukset varsinaisiin alkioihin on esitetty alas suunnatuin (sinisin) nuolin ja viittaukset seuraaviin oikealle suunnatuin nuolin. Tyhjä olio null on kuvattu symbolilla. 3. luku 99 Listan alkua ja loppua voidaan kutsua myös pääksi (head) ja hännäksi (tail). Jälkimmäisestä on viittaus tyhjä-arvoon (null). Tässä listassa on linkitys yksinkertaisimmillaan, so. yhteen suuntaan. Taulukon tapaan alkiot ovat listassa lineaarisessa järjestyksessä, joka sallii ketjutuksen alkioiden eli solmujen välillä. Lista ei kuitenkaan edellytä kiinteää kokoa. Alkio vaatii tilaa O(1) tietoa ja viittausta seuraavaan varten. Kaikkiaan tilaa tarvitaan O(n), kun solmuja on n. Määritellään luokka Node oheisena, joka esittelee listan solmujen oliot. Lisäksi pitäisi antaa luokka viittauksen ylläpitämiseksi listan alkuun. 3. luku 100 public class Node { private Object element ; // element stored in this node private Node next; // reference to the next node in the list // constructors public Node() { // create a node with a null element and next reference this(null, null); public Node(Object e, Node n) { // create a node given element // and next element = e; next = n; Koodi 3.9. Yhteen suuntaan linkitetyn listan solmun toteutus. // update methods public void setelement(object newelem) { element = newelem; public void setnext(node newnext) { next = newnext; // accessor methods public Object getelement() { return element; public Node getnext() {return next; Koodi 3.9. (jatkoa) Yhteen suuntaan linkitetyn listan solmun toteutus. Lisäys tai poisto on helposti tehtävissä listan alkuun eli päähän ajassa O(1), kuten kuvassa luku luku 102
11 pää pää seuraaja seuraaja seuraaja alkio alkio alkio pää Rooma (a) Seattle Toronto Baltimore Rooma Seattle (c) Toronto Baltimore Rooma Seattle (b) Toronto Kuva 3.8. Alkion lisäys listaan: (a) ennen lisäystä, (b) uuden solmun luominen. 3. luku 103 Kuva 3.8. (jatkoa) (c) Lisäyksen jälkeen. Alkion poistaminen listasta on lisäykselle symmetrinen toiminta, jota voidaan kuvata käänteisessä järjestyksessä: (c), (b) ja (a). Lisäys voidaan suorittaa myös listan loppuun eli häntään niin ikään ajassa O(1), kuten kuvassa luku 104 pää häntä pää häntä pää Rooma (a) Seattle häntä Toronto Rooma Seattle Toronto Zürich (c) Kuva 3.9. (jatkoa) (c) Lisäyksen jälkeen. Rooma Seattle Toronto Zürich (b) Kuva 3.9. Alkion lisäys listan loppuun: (a) ennen lisäystä, (b) uuden solmun luonti. 3. luku 105 Poistoa ei voida tehdä listan loppuun vakioajassa. Vaikka on olemassa viittaus listan viimeiseen solmuun, on päästävä myös sitä edeltävään solmuun käsiksi viimeisen poistamiseksi, so. ketjutuksen katkaisemiseksi viimeisen ja toiseksi viimeisen väliltä. 3. luku 106
12 Viimeisen solmun poistamista varten on käytävä lista alusta loppuun, jotta päästään viimeistä edelliseen solmuun käsiksi. Tämä vaatii ajan (n). Pinon toteutus yhteen suuntaan linkitetyn listan avulla Koska poiston suorittaminen listan lopusta ei ole vakioajassa mahdollista, on järkevää sijoittaa pinon huippu listan alkuun, jossa sekä lisäys että poisto ovat tehtävissä ajassa O(1), kuten kaikki muutkin operaatiot, myös size, kun talletettujen alkioiden määrästä ylläpidetään tietoa. Tilaa tietorakenne vaatii O(n). Pinottaessa uusi alkio e luodaan sille uusi solmu n ja lisätään tämä listan alkuun. Java-toteutus on oheisena (koodi 3.10.). public class LinkedStack implements Stack { private Node top; // reference to the top node private int size; // number of elements in the stack public LinkedStack() { // Initialize the stack top = null; size = 0; public int size() { // Returns the current stack size return size; public boolean isempty() { // Returns true iff the stack is empty if (top == null) return true; return false; Koodi Pinon toteuttaminen listan avulla. 3. luku luku 108 public void push(object obj) { // Push a new object on the stack Node n = new Node(); n.setelement(obj); n.setnext(top); top = n; size++; public Object top() // Return the top stack element throws StackEmptyException { if (isempty()) throw new StackEmptyException("Stack is empty."); return top.getelement(); Koodi (jatkoa) Pinon toteuttaminen listan avulla. public Object pop() // Pop off the top stack element throws StackEmptyException { Object temp; if (isempty()) throw new StackEmptyException("Stack is empty."); temp = top.getelement(); top = top.getnext(); // link-out the top node size--; return temp; Koodi (jatkoa) Pinon toteuttaminen listan avulla. 3. luku luku 110
13 Jonon toteutus käyttäen yhteen suuntaan linkitettyä listaa Jono voidaan toteuttaa tehokkaasti listana, kun alkioiden poisto jonon alusta suoritetaan nimenomaan listan alusta eli päästä ja lisäys jonon loppuun tehdään nimenomaan listan loppuun eli häntään. Tilanteen ollessa päinvastainen toteutus olisi tehoton. Mieti, miksi on näin! Kaikki jonon listatoteutuksen metodit toimivat ajassa O(1). Metodit ovat hieman pinon tapausta mutkikkaampia, koska erikoistapauksina ovat tilanteet, joissa jono on tyhjä ennen lisäystä ja jono tyhjenee poiston jälkeen. Abstrakti tietotyyppi on esitetty oheisena, koodi public void enqueue(object obj) { // Place a new object at the rear of the queue Node node = new Node(); node.setelement(obj); node.setnext(null); // node will be new tail node if (size == 0) head = node; // special case of a previously empty queue else tail.setnext(node); // add node at the tail of the list tail = node; // update the reference to the tail node size++; Koodi Metodi enqueue lisäystä varten yhteen suuntaan linkitetyssä listassa jonon abstraktina tietotyyppinä. 3. luku luku 112 public Object dequeue() throws QueueEmptyException { // Remove the first object from the queue Object obj; if (size == 0) throw new QueueEmptyException("Queue is empty."); obj = head.getelement(); head = head.getnext(); size--; if (size == 0) tail = null; // the queue is now empty return obj; Koodi (jatkoa) Metodi dequeue poistoa varten yhteen suuntaan linkitetyssä listassa jonon abstraktina tietotyyppinä Kaksiloppuiset jonot Käsitellään jonomaista tietorakennetta, jossa lisäys ja poisto voidaan tehdä sekä alkuun että loppuun. Tällaista jonon laajennusta kutsutaan kaksiloppuiseksi jonoksi (doubleended queue tai deque (ei siis dequeue)). Kaksiloppuisen jonon abstrakti tietotyyppi Tämä on monipuolisempi kuin pinon tai jonon vastaavat. Seuraavissa perusmetodeissa D viittaa kaksiloppuiseen jonoon. 3. luku luku 114
14 insertfirst(e): Lisää uuden alkion e jonon D alkuun. Syöte: olio insertlast(e): Lisää uuden alkion e jonon D loppuun. Syöte: olio removefirst(): Poistaa ja palauttaa jonon D ensimmäisen alkion. Tulos: olio removelast(): Poistaa ja palauttaa jonon D viimeisen alkion. Tulos: olio Myös muita metodeita on käytettävissä. first(): last(): size(): isempty(): Palauttaa jonon D ensimmäisen alkion. Tulos: olio Palauttaa jonon D viimeisen alkion. Tulos: olio Palauttaa jonon D alkioiden määrän. Tulos: kokonaisluku Tutkii, onko D tyhjä. Tulos: totuusarvo 3. luku luku 116 Esim Sarja operaatioita ja niiden vaikutus alunperin tyhjään kaksiloppuiseen kokonaislukujonoon D. operaatio tulos D insertfirst(3) - (3) insertfirst(5) - (5,3) removefirst() 5 (3) insertlast(7) - (3,7) removefirst() 3 (7) removelast() 7 () removefirst() virhe () isempty() tosi () insertfirst(9) - (9) insertlast(7) - (9,7) size() 2 (9,7) insetfirst(3) - (3,9,7) insertlast(5) - (3,9,7,5) removelast() 5 (3,9,7) Pinojen ja jonojen toteutus kaksiloppuisilla jonoilla Seuraavat yksinkertaiset vastaavuudet ovat voimassa pinon ja kaksiloppuisen jonon välillä. 3. luku luku 118
15 pinon metodi kaksiloppuisen jonon toteutus jonon metodi kaksiloppuisen jonon toteutus size() isempty() top() push(e) pop() size() isempty() last() insertlast(e) removelast() size() isempty() front() enqueue(e) dequeue() size() isempty() first() insertlast(e) removefirst() Vastaavasti jonon ja kaksiloppuisen jonon välillä ovat seuraavat vastaavuudet. Kaksiloppuista jonoa käyttäen esitetään pinon rajapinta. Tämän luokan metodit käsittävät kaksiloppuisen jonon metodien suoraviivaisia kutsuja (koodi 3.12.). Mukana on virheidentarkastelu yritettäessä saada tai poistaa tyhjästä jonosta. 3. luku luku 120 public class DequeStack implements Stack { private Deque D; // holds the elements of the stack public DequeStack() { // Initialize the stack D = new MyDeque(); public int size() { // Return the number of elements of the stack return D.size(); public boolean isempty() { // Return true iff the stack has no elements return D.isEmpty(); public void push(object obj) { // Insert an element into the stack D.insertLast(obj); Koodi Pinon rajapinnan toteutus kaksiloppuisen jonon avulla. public Object top() // Access the top element of the stack throws StackEmptyException { // thrown if the stack is empty try { return D.last(); // since the deque throws its own exception, we catch it // and throw the StackEmptyException catch (DequeEmptyException ece) { throw new StackEmptyException("Stack is empty!"); Koodi (jatkoa) Pinon rajapinnan toteutus kaksiloppuisen jonon avulla. 3. luku luku 122
16 Kaksiloppuisten jonojen toteutus kaksoislinkitetyillä listoilla public Object pop() // Remove and return the top element of the stack throws StackEmptyException { // thrown if the stack is empty try { return D.removeLast(); catch (DequeEmptyException ece) { throw new StackEmptyException("Stack is empty!"); Koodi (jatkoa) Pinon rajapinnan toteutus kaksiloppuisen jonon avulla. Käytettäessä yhteen suuntaan linkitettyä listaa eo. tapaan ei voitu listan lopusta poistaa alkiota ajassa O(1). Listarakennetta voidaan kuitenkin tehostaa lisäämällä siihen toinen linkitys, jolloin myös kyseinen poisto toimii vakioajassa. Kaksoislinkitetyssä listassa on seuraava-linkin (next) lisäksi linkki edeltävään (prev) solmuun. Toteutuksen yksinkertaistamiseksi on kätevää asettaa listan alkuun erillinen alkusolmu (header) ja loppuun loppusolmu (trailer). Nämä vale- tai vartijasolmut eivät sisällä listan alkioita, vaan ovat ainoastaan listan alun ja lopun merkkeinä. Alkusolmun viittaus edeltävään ja vastaavasti loppusolmun viittaus seuraajaan ovat luonnollisesti tyhjiä (null) (kuva 3.10.). 3. luku luku 124 alku loppu alku loppu Baltimore New York Providence Philadelphia alku New York Providence Philadelphia (a) loppu alku Baltimore (c) loppu New York Providence Philadelphia (d) New York Providence Philadelphia alku loppu Baltimore (b) Kuva Kaksoislinkitetyn listan päivitys käytettäessä erillisiä alku- ja loppusolmuja: (a) ennen lisäystä ja (b) uuden solmun luonti. 3. luku 125 Baltimore New York Providence (e) Kuva (jatkoa) Kaksoislinkitetyn listan päivitys käytettäessä erillisiä alku- ja loppusolmuja: (c) lisäyksen jälkeen ja ennen viimeisen alkion poistoa, (d) viimeisen alkion poisto sekä (e) poiston jälkeen. 3. luku 126
17 Kaksoislinkitetyn listan sekä alkuun että loppuun on lisäys tehtävissä ajassa O(1). Täten kaikki kaksiloppuisen listan metodit voidaan toteuttaa kaksoislinkitetyn listan avulla ajassa O(1). Tilavaatimus on luonnollisesti O(n). Hieman enemmän tietorakenne vaatii tilaa täsmällisesti laskien kuin edelliset listat, koska käytettiin kahta linkitystä yhden sijasta ja lisänä vielä alkuja loppusolmua. 3. luku Yleisesti linkitetyistä listoista eli sekvensseistä Edellä käytettiin listoja vain siten, että pinon tai jonon periaatteen mukaan käsiteltiin listan toista tai molempia päitä. Yleisemmin listaa ajatellen on monipuolisempi käyttö toki mahdollista. Voidaan puhua yleisestä listasta tai sekvenssistä. Tämä on toteutettavissa sekä taulukon avulla että linkitetyn, kätevimmin kaksoislinkitetyn listan avulla. Kuvassa päästään taulukkototeutuksena tehdyssä listassa keskelle lisäämään tai poistamaan alkio. Vaikka itse lisäys tai poisto tapahtuu ajassa O(1), pahimmassa tapauksessa muiden alkioiden siirto vaatii ajan O(n). Keskimäärin tämä on (n), koska keskimäärin on siirrettävä n/2 alkiota. Koodi kuvaa lisäyksen ja poiston indeksin arvolla r. 3. luku 128 S S r n-1 N-1 (a) r n-1 N-1 (b) Kuva Taulukkoon perustuva sekvenssin toteutus: (a) siirto eteenpäin taulukossa lisäystä varten indeksin arvolla r ja (b) siirto takaisinpäin poistoa indeksillä r varten. Algorithm insertelem(r,e): if r n-1 for i = n-1, n-2,.., r do S[i+1] S[i] S[r] e n n+1 Algorithm removeelem(r): e S[r] for i = r, r+1,, n-2 do S[i] S[i+1] n n-1 return e Koodi Taulukkoon perustuvat sekvenssin lisäys- ja poistometodit. 3. luku luku 130
18 alku loppu Toteutus käyttäen kaksoislinkitettyä listaa Sekvenssi voidaan toteuttaa myös kaksoislinkitetyllä listalla. Alkion löytämiseksi pitää lähteä listan jommastakummasta päästä ja kulkea haluttuun alkioon. Tehokkainta on valita näistä lyhyempi reitti, jolloin saanti tapahtuu ajassa O(min(r+1, n-r)), joka on O(n). Pahin tapaus sattuu, kun r = n/2. alku Baltimore Pariisi Providence (a) loppu Baltimore Pariisi Providence Operaatiot insertelem(r,e) ja removeelem(r) lisäystä ja poistoa varten vaativat myös kulkemisen päästä kyseiseen alkioon asti, jonka indeksiarvo on r. Niiden suoritusaika on vastaavasti O(min(r+1, n-r+1)), joka on O(n). Nämä on esitetty kuvassa luku 131 New York (b) Kuva Kaksoislinkitetyn listan (mukana alku- ja loppusolmu vartijoina) päivitysoperaatiot: (a) ennen solmun lisäystä ja (b) uuden solmun luonti. 3. luku 132 alku loppu alku alku Baltimore New York Pariisi Providence (c) loppu Baltimore New York Pariisi Providence (d) loppu Kaksoislinkitetty lista vaatii tilaa vain O(n), kun taas taulukkototeutus ei ollut tässä niin taloudellinen. Huonona puolena on, että alkion haku vaatii ajan O(n) pahimmassa tapauksessa, kun taulukkototeutuksessa se oli O(1). Muuten suoritusajat olivat samat molemmissa toteutuksissa. Toisaalta muunlaisia lisäyksiä ja poistoja voidaan tehdä nopeasti kaksoislinkitetyssä listassa. Baltimore New York Providence (e) Kuva Kaksoislinkitetyn listan (mukana alku- ja loppusolmu vartijoina)päivitysoperaatiot (jatkoa): (c) solmun lisäyksen jälkeen ja ennen solmunpoistoa, (d) solmun poisto sekä (e) poiston jälkeen. 3. luku luku 134
19 3.6. Yleisen listan käyttö alkioiden lajittelussa Kuvataan sekvenssiä soveltava toteutus kuplalajittelua (bubble sort) varten. Lajittelussa (sorting) on tehtävänä järjestää syötealkiot niin, että ne tulevat joko kasvavaan tai vähenevään järjestykseen. Tässä yhteydessä käsitellään ei-vähenevää eli tarkemmin ilmaisten kasvavaa tai osin samansuuruisten perättäisten alkioparien sekvenssiä. Alkiot voivat olla toki muitakin kuin lukuja, esim. leksikograafisesti järjestettäviä (tekstiä), mutta niiden välillä pitää olla jokin järjestysrelaatio voimassa, kuten tässä pienempi tai yhtä suuri. Kuplalajittelualgoritmi Tarkastellaan listaa, jossa mitä tahansa kahta perättäistä alkiota voidaan verrata keskenään ja asettaa suuruusjärjestykseen. Tämä algoritmi on ensimmäinen yksinkertainen menetelmä, jota käsitellään tärkeän lajitteluongelman yhteydessä. 3. luku 135 Kuplalajittelualgoritmi ratkaisee lajitteluongelman yksinkertaisella, mutta samalla asymptoottisesti melko tehottomalla tavalla. Siinä suoritetaan sarja vaiheita (pass) listassa (kuva 3.13.). Kussakin vaiheessa alkiot selataan indeksiä kasvattaen arvosta 0 vielä lajittelemattomien alkioiden loppuun. Vaiheen jokaisessa paikassa alkiota verrataan naapuriinsa ja nämä kaksi perättäistä alkiota vaihdetaan keskenään, mikäli suhteellinen järjestys on väärä, so. edeltävä alkio on seuraavaa suurempi. Lajittelu käsittää kaikkiaan n tällaista vaihetta. 3. luku 136 Olkoon n alkioiden lukumäärä. Kuplalajittelualgoritmilla on seuraavat ominaisuudet: vaihe vaihdot lista eli sekvenssi (5, 7, 2, 6, 9, 3) , 7 6, 9 3 (5, 2, 6, 7, 3, 9) , 7 3 (2, 5, 6, 3, 7, 9) (2, 5, 3, 6, 7, 9) (2, 3, 5, 6, 7, 9) Ensimmäisessä vaiheessa sen jälkeen, kun suurin alkio on saavutettu, jatketaan vaihtamista, kunnes päästään sekvenssin viimeiseen paikkaan. Toisessa vaiheessa, kun toiseksi suurin alkio on saavutettu, jatketaan vaihtamista, kunnes päästään toiseksi viimeiseen paikkaan. Eo. menettelyä toistetaan niin kauan, kunnes kaikki alkiot on käyty läpi. Kuva Kuplalajittelu kokonaislukujen sekvenssille, jossa kunkin vaiheen vaihdot on esitetty ja sekvenssi vaihtojen jälkeen. Itse asiassa vaiheita on näiden jälkeen vielä kaksi, mutta niitä ei ole esitetty, koska niissä ei tapahdu vaihtoja. 3. luku 137 Täten i:nnen vaiheen lopussa i oikeanpuolimmaista alkiota (indeksin arvosta n-1 alas arvoon n-i) ovat lopullisissa paikoissaan. Tämä osoittaa, että n vaihetta riittää alkioiden lajittelemiseksi ja kussakin vaiheessa i riittää lajitella ensimmäiset n-i+1 alkiota. 3. luku 138
20 Kuplalajittelun analyysi Oletetaan sekvenssin toteutuksen sallivan yksittäisten alkioiden saannin ja vaihdon ajassa O(1). Tällöin i:nnen vaiheen suoritusaika on O(n-i+1). Kokonaissuoritusajaksi tulee siten Edellisestä saadaan summan perusteella tulos O(n 2 ) suoritusajaksi edellyttäen, että vaihdot ja saanti olivat vakioaikaisia. Tämä voidaan kirjoittaa muotoon Koodi käsittää kaksi kuplalajittelun toteutusta lajiteltaessa kokonaislukuja. Ne eroavat alkion saannissa ja listan muuttamisessa käytettävien metodien suhteen. 3. luku luku 140 Metodi bubblesort1 hakee alkiot rajapintametodin atrank kautta. Se on sovelias ainoastaan sekvenssin taulukkototeutuksessa, jossa atrank tarvitsee ajan O(1). Tällöin metodin kokonaissuoritusaika on O(n 2 ). Jos algoritmi toteutettaisiin kaksoislinkitetyn listan avulla, silloin jokainen metodin atrank kutsu vaatisi ajan O(n) pahimmassa tapauksessa ja kokonaissuoritusaika olisi O(n 3 ). Metodi bubblesort2 saa alkiot sekvenssistä metodien first ja after avulla. Se on sopiva sekä taulukkoa että kaksoislinkitettyä listaa hyödynnettäessä. Näin on, koska molemmat tavat tuottavat vakiollisen suoritusajan metodeille first ja after. Koko suoritusaika on (n 2 ) sekvenssin toteutustavasta riippumatta. public void static bubblesort1(integersequence s) { int n = s.size(); for (int i=0; i<n; i++) // i:s vaihe for (int j=1; j<n-i; j++) if (s.atrank(j-1).element().intvalue() > s.atrank(j).element().intvalue()) swap(s.atrank(j-1), s.atrank(j)); Koodi Kuplalajittelun ensimmäinen toteutusversio. Metodi swap vaihtaa alkioita keskenään. 3. luku luku 142
21 public void static bubblesort2(integersequence s) { int n = s.size(); IntegerSequencePosition prec, succ; for (int i=0; i<n; i++) { // i:s vaihe prec = s.first(); for (int j=0; j<n-i; j++) { succ = s.after(prec); if (prec.element().intvalue() > succ.element().intvalue()) swap(prec,succ); prec = succ; Kuplalajittelu on hyvin yksinkertainen, mutta se on myös varsin tehoton lajiteltavien määrän n kasvaessa aikakompleksisuuden ollessa neliöllinen. Myöhemmin palataan lajitteluun, jolle on olemassa tehokkaampia algoritmeja, aikakompleksisuudeltaan O(n log n). Koodi (jatkoa) Kuplalajittelun toinen toteutusversio. Tässä first antaa listan ensimmäisen alkion ja after nykyistä seuraavan. 3. luku luku Rekursio Edellä pinojen yhteydessä käsiteltiin suppeasti lineaarista rekursiota. Tarkastellaan tässä vähän monimutkaisempaa rekursiota ikään kuin siirtymänä seuraavaan, puita käsittelevään lukuun. Lasketaan Fibonaccin lukuja rekursiivisesti oheisella kaavalla: F 0 =0 F 1 =1 F i = F i-1 + F i-2, kun i>1. Voidaan laskea suoraan määritelmän mukaan binäärisellä rekursiolla seuraavasti. Algorithm BinaryFib(k) Input: ei-negatiivinen luku k Output: k:s Fibonaccin luku F k if k 1 then return k else return BinaryFib(k-1)+BinaryFib(k-2) Koodi Fibonacci binäärisellä rekursiolla. 3. luku luku 146
22 Vaikka Koodin ratkaisu on suoraviivainen, se on hyvin tehoton. Silmäillään seuraavaa laskentaa, jossa n k tarkoittaa kutsujen määrää suoritettaessa BinaryFib(k): BinaryFib(4) BinaryFib(5) BinaryFib(3) n 0 =1 n 1 =1 n 2 =n 1 +n 0 +1=1+1+1=3 n 3 =n 2 +n 1 +1=3+1+1=5 n 4 =n 3 +n 2 +1=5+3+1=9 n 5 =n 4 +n 3 +1=9+5+1=15 n 6 =n 5 +n 4 +1=15+9+1=25 BinaryFib(3) BinaryFib(2) BinaryFib(1) BinaryFib(1) BinaryFib(0) BinaryFib(2) BinaryFib(2) BinaryFib(1) BinaryFib(1) BinaryFib(0) BinaryFib(1) BinaryFib(0) Seurattaessa laskentaa eteenpäin nähdään kutsujen lukumäärän enemmän kuin kaksinkertaistuvan kullekin kahdelle peräkkäiselle indeksin arvolle. Täten n 4 on enemmän kuin n 2 kahdesti, n 5 on enemmän kuin n 3 kahdesti (Kuva 3.14.) jne. Yleisesti saadaan, että n k >2 k/2, joka on eksponentiaalinen. 3. luku 147 Kuva Fibonacci binäärisen rekursion avulla laskettaessa lähtien arvosta k=5. Lehdet (kutsut arvolla 0 tai 1) ovat alkuarvotilanteita. Näiden lukumäärä on eksponentiaalinen suhteessa arvoon k. 3. luku 148 Fibonaccin laskenta on kuitenkin luonteeltaan lineaarinen, joten se on tällaiseksi muunnettavissa laskemalla kussakin vaiheessa lukupari (Koodi 3.16.). Käytetään lisäksi uutta alkuarvoa F -1 =0. Algorithm LinearFib(k) Input: ei-negatiivinen luku k Output: pari Fibonaccin lukuja (F k, F k-1 ) if k 1 then return (k,0) else (i,j LinearFib(k-1) return (i+j,i) Koodi Fibonacci lineaarisella rekursiolla. Lineaarinen rekursio pudottaa tarvittavien kutsujen määrän k:hon, sillä jokaisella kutsulla argumenttia vähennetään 1:llä. Tämä on merkittävä ero verrattuna binääriseen rekursioon. Tätä voitaisiin edelleen tehostaa käytännön suoritusajan mielessä - mutta ei kompleksisuuden - muuttamalla rekursiivinen ratkaisu iteratiiviseksi. Algoritmi on tällaisen muunnoksen jälkeen pidempi, mutta ajankäytön kannalta tehokkaampi, koska ei ole kutsuja eli datan välittämistä. Se olisi kuitenkin eri asia, koska tässä tarkasteltiin rekursiota, joka on kätevä tapa toteuttaa monia algoritmeja, kuten jatkossa käsiteltäessä puita. Rekursiota voidaan tarvittaessa laajentaa binäärisestä yleisemmin nk. k-ariseksi, esim. tilanteissa, joissa puun solmulla olisi enemmän kuin kaksi jälkeläistä. Ei tarkastella kuitenkaan näitä tilanteita. 3. luku luku 150
3. Pinot, jonot ja linkitetyt listat
 3 Pinot, jonot ja linkitetyt listat Pinot ja jonot ovat yksinkertaisimpia tietorakenteita, mutta myös tärkeimpiä Niitä käytetään lukuisissa sovelluksissa ja monimutkaisten tietorakenteiden osina Yksinkertaisuutensa
3 Pinot, jonot ja linkitetyt listat Pinot ja jonot ovat yksinkertaisimpia tietorakenteita, mutta myös tärkeimpiä Niitä käytetään lukuisissa sovelluksissa ja monimutkaisten tietorakenteiden osina Yksinkertaisuutensa
3. Pinot, jonot ja linkitetyt listat
 3. Pinot, jonot ja linkitetyt listat Pinot ja jonot ovat yksinkertaisimpia tietorakenteita, mutta myös tärkeimpiä. Niitä käytetään lukuisissa sovelluksissa ja monimutkaisten tietorakenteiden osina. Yksinkertaisuutensa
3. Pinot, jonot ja linkitetyt listat Pinot ja jonot ovat yksinkertaisimpia tietorakenteita, mutta myös tärkeimpiä. Niitä käytetään lukuisissa sovelluksissa ja monimutkaisten tietorakenteiden osina. Yksinkertaisuutensa
Pino S on abstrakti tietotyyppi, jolla on ainakin perusmetodit:
 Pino (stack) Pino: viimeisenä sisään, ensimmäisenä ulos (LIFO, Last In, First Out) -tietorakenne kaksi perusoperaatiota: alkion lisäys pinon päälle (push), ja päällimmäisen alkion poisto (pop) Push(alkio)
Pino (stack) Pino: viimeisenä sisään, ensimmäisenä ulos (LIFO, Last In, First Out) -tietorakenne kaksi perusoperaatiota: alkion lisäys pinon päälle (push), ja päällimmäisen alkion poisto (pop) Push(alkio)
4. Sekvenssit Astetta soveltavat sekvenssit
 4. Sekvenssit Sekvenssit edustavat lineaarisesti järjestettyä alkioiden kokoelmaa, jolle on määritelty metodit alkion saantia, lisäystä ja poistoa varten. Täten sen jokaisella alkiolla on edeltäjä, paitsi
4. Sekvenssit Sekvenssit edustavat lineaarisesti järjestettyä alkioiden kokoelmaa, jolle on määritelty metodit alkion saantia, lisäystä ja poistoa varten. Täten sen jokaisella alkiolla on edeltäjä, paitsi
Kaksiloppuinen jono D on abstrakti tietotyyppi, jolla on ainakin seuraavat 4 perusmetodia... PushFront(x): lisää tietoalkion x jonon eteen
 Viimeksi käsiteltiin pino: lisäys ja poisto lopusta jono: lisäys loppuun, poisto alusta Pinon ja jonon yleistävä tietorakenne: kaksiloppuinen jono alkion lisäys/poisto voidaan kohdistaa jonon alkuun tai
Viimeksi käsiteltiin pino: lisäys ja poisto lopusta jono: lisäys loppuun, poisto alusta Pinon ja jonon yleistävä tietorakenne: kaksiloppuinen jono alkion lisäys/poisto voidaan kohdistaa jonon alkuun tai
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT PERUSTIETORAKENTEET LISTA, PINO, JONO, PAKKA ABSTRAKTI TIETOTYYPPI Tietotyyppi on abstrakti, kun se on määritelty (esim. matemaattisesti) ottamatta kantaa varsinaiseen
A274101 TIETORAKENTEET JA ALGORITMIT PERUSTIETORAKENTEET LISTA, PINO, JONO, PAKKA ABSTRAKTI TIETOTYYPPI Tietotyyppi on abstrakti, kun se on määritelty (esim. matemaattisesti) ottamatta kantaa varsinaiseen
Algoritmit 1. Luento 4 Ke Timo Männikkö
 Algoritmit 1 Luento 4 Ke 18.1.2017 Timo Männikkö Luento 4 Tietorakenteet Pino Pinon toteutus Jono Jonon toteutus Lista Listaoperaatiot Algoritmit 1 Kevät 2017 Luento 4 Ke 18.1.2017 2/29 Pino Pino, stack,
Algoritmit 1 Luento 4 Ke 18.1.2017 Timo Männikkö Luento 4 Tietorakenteet Pino Pinon toteutus Jono Jonon toteutus Lista Listaoperaatiot Algoritmit 1 Kevät 2017 Luento 4 Ke 18.1.2017 2/29 Pino Pino, stack,
Sisällys. 18. Abstraktit tietotyypit. Johdanto. Johdanto
 Sisällys 18. bstraktit tietotyypit Johdanto abstrakteihin tietotyyppeihin. Pino ja jono. Linkitetty lista. Pino linkitetyllä listalla toteutettuna. 18.1 18.2 Johdanto Javan omat tietotyypit ovat jo tuttuja:
Sisällys 18. bstraktit tietotyypit Johdanto abstrakteihin tietotyyppeihin. Pino ja jono. Linkitetty lista. Pino linkitetyllä listalla toteutettuna. 18.1 18.2 Johdanto Javan omat tietotyypit ovat jo tuttuja:
18. Abstraktit tietotyypit 18.1
 18. Abstraktit tietotyypit 18.1 Sisällys Johdanto abstrakteihin tietotyyppeihin. Pino ja jono. Linkitetty lista. Pino linkitetyllä listalla toteutettuna. 18.2 Johdanto Javan omat tietotyypit ovat jo tuttuja:
18. Abstraktit tietotyypit 18.1 Sisällys Johdanto abstrakteihin tietotyyppeihin. Pino ja jono. Linkitetty lista. Pino linkitetyllä listalla toteutettuna. 18.2 Johdanto Javan omat tietotyypit ovat jo tuttuja:
Algoritmit 1. Luento 3 Ti Timo Männikkö
 Algoritmit 1 Luento 3 Ti 17.1.2017 Timo Männikkö Luento 3 Algoritmin analysointi Rekursio Lomituslajittelu Aikavaativuus Tietorakenteet Pino Algoritmit 1 Kevät 2017 Luento 3 Ti 17.1.2017 2/27 Algoritmien
Algoritmit 1 Luento 3 Ti 17.1.2017 Timo Männikkö Luento 3 Algoritmin analysointi Rekursio Lomituslajittelu Aikavaativuus Tietorakenteet Pino Algoritmit 1 Kevät 2017 Luento 3 Ti 17.1.2017 2/27 Algoritmien
811312A Tietorakenteet ja algoritmit II Perustietorakenteet
 811312A Tietorakenteet ja algoritmit 2017-2018 II Perustietorakenteet Sisältö 1. Johdanto 2. Pino 3. Jono 4. Lista 811312A TRA, Perustietorakenteet 2 II.1. Johdanto Tietorakenne on tapa, jolla algoritmi
811312A Tietorakenteet ja algoritmit 2017-2018 II Perustietorakenteet Sisältö 1. Johdanto 2. Pino 3. Jono 4. Lista 811312A TRA, Perustietorakenteet 2 II.1. Johdanto Tietorakenne on tapa, jolla algoritmi
TIETORAKENTEET JA ALGORITMIT
 TIETORAKENTEET JA ALGORITMIT Timo Harju 1999-2004 1 typedef link List; /* Vaihtoehtoisia nimiä */ typedef link Stack; /* nodepointterille */ typedef link Queue typedef struct node Node; /* itse nodelle
TIETORAKENTEET JA ALGORITMIT Timo Harju 1999-2004 1 typedef link List; /* Vaihtoehtoisia nimiä */ typedef link Stack; /* nodepointterille */ typedef link Queue typedef struct node Node; /* itse nodelle
Sekvenssi: kokoelma peräkkäisiä alkioita (lineaarinen
 Sekvenssi Sekvenssi: kokoelma peräkkäisiä alkioita (lineaarinen järjestys) Timo Esim. pino, jono ja kaksiloppuinen jono ovat sekvenssin erikoistapauksia sekvenssejä, jotka kohdistavat operaationsa ensimmäiseen/viimeiseen
Sekvenssi Sekvenssi: kokoelma peräkkäisiä alkioita (lineaarinen järjestys) Timo Esim. pino, jono ja kaksiloppuinen jono ovat sekvenssin erikoistapauksia sekvenssejä, jotka kohdistavat operaationsa ensimmäiseen/viimeiseen
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Rekursio Rekursion käyttötapauksia Rekursio määritelmissä Rekursio ongelmanratkaisussa ja ohjelmointitekniikkana Esimerkkejä taulukolla Esimerkkejä linkatulla listalla Hanoin
Tietorakenteet ja algoritmit Rekursio Rekursion käyttötapauksia Rekursio määritelmissä Rekursio ongelmanratkaisussa ja ohjelmointitekniikkana Esimerkkejä taulukolla Esimerkkejä linkatulla listalla Hanoin
Tietorakenteet, laskuharjoitus 3, ratkaisuja
 Tietorakenteet, laskuharjoitus 3, ratkaisuja 1. (a) Toistolauseen runko-osassa tehdään yksi laskuoperaatio, runko on siis vakioaikainen. Jos syöte on n, suoritetaan runko n kertaa, eli aikavaativuus kokonaisuudessaan
Tietorakenteet, laskuharjoitus 3, ratkaisuja 1. (a) Toistolauseen runko-osassa tehdään yksi laskuoperaatio, runko on siis vakioaikainen. Jos syöte on n, suoritetaan runko n kertaa, eli aikavaativuus kokonaisuudessaan
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Merkintöjen tulkintoja *++Pstack->top = item *Pstack->top++ = item (*Pstack->top)++ *(Pstack++)->top = item *(++Pstack)->top = item Lisää pinon toteutuksia Dynaaminen taulukko
Tietorakenteet ja algoritmit Merkintöjen tulkintoja *++Pstack->top = item *Pstack->top++ = item (*Pstack->top)++ *(Pstack++)->top = item *(++Pstack)->top = item Lisää pinon toteutuksia Dynaaminen taulukko
Tietorakenteet ja algoritmit Johdanto Lauri Malmi / Ari Korhonen
 Tietorakenteet ja algoritmit Johdanto Lauri Malmi / Ari 1 1. JOHDANTO 1.1 Määritelmiä 1.2 Tietorakenteen ja algoritmin valinta 1.3 Algoritmit ja tiedon määrä 1.4 Tietorakenteet ja toiminnot 1.5 Esimerkki:
Tietorakenteet ja algoritmit Johdanto Lauri Malmi / Ari 1 1. JOHDANTO 1.1 Määritelmiä 1.2 Tietorakenteen ja algoritmin valinta 1.3 Algoritmit ja tiedon määrä 1.4 Tietorakenteet ja toiminnot 1.5 Esimerkki:
useampi ns. avain (tai vertailuavain) esim. opiskelijaa kuvaavassa alkiossa vaikkapa opintopistemäärä tai opiskelijanumero
 Alkioiden avaimet Usein tietoalkioille on mielekästä määrittää yksi tai useampi ns. avain (tai vertailuavain) esim. opiskelijaa kuvaavassa alkiossa vaikkapa opintopistemäärä tai opiskelijanumero 80 op
Alkioiden avaimet Usein tietoalkioille on mielekästä määrittää yksi tai useampi ns. avain (tai vertailuavain) esim. opiskelijaa kuvaavassa alkiossa vaikkapa opintopistemäärä tai opiskelijanumero 80 op
Algoritmit 2. Luento 2 To Timo Männikkö
 Algoritmit 2 Luento 2 To 14.3.2019 Timo Männikkö Luento 2 Tietorakenteet Lineaarinen lista, binääripuu Prioriteettijono Kekorakenne Keko-operaatiot Keon toteutus taulukolla Algoritmit 2 Kevät 2019 Luento
Algoritmit 2 Luento 2 To 14.3.2019 Timo Männikkö Luento 2 Tietorakenteet Lineaarinen lista, binääripuu Prioriteettijono Kekorakenne Keko-operaatiot Keon toteutus taulukolla Algoritmit 2 Kevät 2019 Luento
Tietorakenteet ja algoritmit - syksy 2015 1
 Tietorakenteet ja algoritmit - syksy 2015 1 Tietorakenteet ja algoritmit - syksy 2015 2 Tietorakenteet ja algoritmit Johdanto Ari Korhonen Tietorakenteet ja algoritmit - syksy 2015 1. JOHDANTO 1.1 Määritelmiä
Tietorakenteet ja algoritmit - syksy 2015 1 Tietorakenteet ja algoritmit - syksy 2015 2 Tietorakenteet ja algoritmit Johdanto Ari Korhonen Tietorakenteet ja algoritmit - syksy 2015 1. JOHDANTO 1.1 Määritelmiä
1.1 Pino (stack) Koodiluonnos. Graafinen esitys ...
 1. Tietorakenteet Tietorakenteet organisoivat samankaltaisten olioiden muodostaman tietojoukon. Tämä järjestys voidaan saada aikaan monin tavoin, esim. Keräämällä oliot taulukkoon. Liittämällä olioihin
1. Tietorakenteet Tietorakenteet organisoivat samankaltaisten olioiden muodostaman tietojoukon. Tämä järjestys voidaan saada aikaan monin tavoin, esim. Keräämällä oliot taulukkoon. Liittämällä olioihin
Algoritmit 1. Luento 6 Ke Timo Männikkö
 Algoritmit 1 Luento 6 Ke 25.1.2017 Timo Männikkö Luento 6 Järjestetty lista Listan toteutus dynaamisesti Linkitetyn listan operaatiot Vaihtoehtoisia listarakenteita Puurakenteet Binääripuu Järjestetty
Algoritmit 1 Luento 6 Ke 25.1.2017 Timo Männikkö Luento 6 Järjestetty lista Listan toteutus dynaamisesti Linkitetyn listan operaatiot Vaihtoehtoisia listarakenteita Puurakenteet Binääripuu Järjestetty
Kääreluokat (oppikirjan luku 9.4) (Wrapper-classes)
 Kääreluokat (oppikirjan luku 9.4) (Wrapper-classes) Kääreluokista Javan alkeistietotyypit ja vastaavat kääreluokat Autoboxing Integer-luokka Double-luokka Kääreluokista Alkeistietotyyppiset muuttujat (esimerkiksi
Kääreluokat (oppikirjan luku 9.4) (Wrapper-classes) Kääreluokista Javan alkeistietotyypit ja vastaavat kääreluokat Autoboxing Integer-luokka Double-luokka Kääreluokista Alkeistietotyyppiset muuttujat (esimerkiksi
Algoritmit 2. Luento 2 Ke Timo Männikkö
 Algoritmit 2 Luento 2 Ke 15.3.2017 Timo Männikkö Luento 2 Tietorakenteet Lineaarinen lista, binääripuu Prioriteettijono Kekorakenne Keko-operaatiot Keon toteutus taulukolla Algoritmit 2 Kevät 2017 Luento
Algoritmit 2 Luento 2 Ke 15.3.2017 Timo Männikkö Luento 2 Tietorakenteet Lineaarinen lista, binääripuu Prioriteettijono Kekorakenne Keko-operaatiot Keon toteutus taulukolla Algoritmit 2 Kevät 2017 Luento
2. Perustietorakenteet
 2. Perustietorakenteet Tässä osassa käsitellään erilaisia perustietorakenteita, joita algoritmit käyttävät toimintansa perustana. Aluksi käydään läpi tietorakenteen abstrakti määritelmä. Tämän jälkeen
2. Perustietorakenteet Tässä osassa käsitellään erilaisia perustietorakenteita, joita algoritmit käyttävät toimintansa perustana. Aluksi käydään läpi tietorakenteen abstrakti määritelmä. Tämän jälkeen
Abstraktit tietotyypit. TIEA341 Funktio ohjelmointi 1 Syksy 2005
 Abstraktit tietotyypit TIEA341 Funktio ohjelmointi 1 Syksy 2005 Data abstraktio Abstraktio on ohjelmoinnin tärkein väline Data abstraktio abstrahoi dataa Abstrakti tietotyyppi Koostuu kolmesta asiasta:
Abstraktit tietotyypit TIEA341 Funktio ohjelmointi 1 Syksy 2005 Data abstraktio Abstraktio on ohjelmoinnin tärkein väline Data abstraktio abstrahoi dataa Abstrakti tietotyyppi Koostuu kolmesta asiasta:
Algoritmit 1. Luento 10 Ke Timo Männikkö
 Algoritmit 1 Luento 10 Ke 14.2.2018 Timo Männikkö Luento 10 Algoritminen ongelmanratkaisu Suunnittelumenetelmät Raaka voima Järjestäminen eli lajittelu Kuplalajittelu Lisäyslajittelu Valintalajittelu Permutaatiot
Algoritmit 1 Luento 10 Ke 14.2.2018 Timo Männikkö Luento 10 Algoritminen ongelmanratkaisu Suunnittelumenetelmät Raaka voima Järjestäminen eli lajittelu Kuplalajittelu Lisäyslajittelu Valintalajittelu Permutaatiot
Algoritmit 1. Demot Timo Männikkö
 Algoritmit 1 Demot 2 1.-2.2.2017 Timo Männikkö Tehtävä 1 (a) Ei-rekursiivinen algoritmi: laskesumma(t, n) sum = t[0]; for (i = 1; i < n; i++) sum = sum + t[i]; return sum; Silmukka suoritetaan n 1 kertaa
Algoritmit 1 Demot 2 1.-2.2.2017 Timo Männikkö Tehtävä 1 (a) Ei-rekursiivinen algoritmi: laskesumma(t, n) sum = t[0]; for (i = 1; i < n; i++) sum = sum + t[i]; return sum; Silmukka suoritetaan n 1 kertaa
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 5 Vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 5 Vastaukset Harjoituksen aiheena ovat aliohjelmat ja abstraktit tietotyypit sekä olio-ohjelmointi. Tehtävät tehdään C-, C++- ja Java-kielillä.
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 5 Vastaukset Harjoituksen aiheena ovat aliohjelmat ja abstraktit tietotyypit sekä olio-ohjelmointi. Tehtävät tehdään C-, C++- ja Java-kielillä.
Tehtävän V.1 ratkaisuehdotus Tietorakenteet, syksy 2003
 Tehtävän V.1 ratkaisuehdotus Tietorakenteet, syksy 2003 Matti Nykänen 5. joulukuuta 2003 1 Satelliitit Muunnetaan luennoilla luonnosteltua toteutusta seuraavaksi: Korvataan puusolmun p kentät p. key ja
Tehtävän V.1 ratkaisuehdotus Tietorakenteet, syksy 2003 Matti Nykänen 5. joulukuuta 2003 1 Satelliitit Muunnetaan luennoilla luonnosteltua toteutusta seuraavaksi: Korvataan puusolmun p kentät p. key ja
811312A Tietorakenteet ja algoritmit Kertausta kurssin alkuosasta
 811312A Tietorakenteet ja algoritmit 2017-2018 Kertausta kurssin alkuosasta II Perustietorakenteet Pino, jono ja listat tunnettava Osattava soveltaa rakenteita algoritmeissa Osattava päätellä operaatioiden
811312A Tietorakenteet ja algoritmit 2017-2018 Kertausta kurssin alkuosasta II Perustietorakenteet Pino, jono ja listat tunnettava Osattava soveltaa rakenteita algoritmeissa Osattava päätellä operaatioiden
Tieto- ja tallennusrakenteet
 Tieto- ja tallennusrakenteet Sisältö Tyyppi, abstrakti tietotyyppi, abstraktin tietotyypin toteutus Tallennusrakenteet Taulukko Linkitetty rakenne Abstraktit tietotyypit Lista (Puu) (Viimeisellä viikolla)
Tieto- ja tallennusrakenteet Sisältö Tyyppi, abstrakti tietotyyppi, abstraktin tietotyypin toteutus Tallennusrakenteet Taulukko Linkitetty rakenne Abstraktit tietotyypit Lista (Puu) (Viimeisellä viikolla)
(p j b (i, j) + p i b (j, i)) (p j b (i, j) + p i (1 b (i, j)) p i. tähän. Palaamme sanakirjaongelmaan vielä tasoitetun analyysin yhteydessä.
 Loppu seuraa suoralla laskulla: n n Tave TR = p j (1 + b (i, j)) j=1 = 1 + 1 i
Loppu seuraa suoralla laskulla: n n Tave TR = p j (1 + b (i, j)) j=1 = 1 + 1 i
Ohjelmointi 2 / 2010 Välikoe / 26.3
 Ohjelmointi 2 / 2010 Välikoe / 26.3 Välikoe / 26.3 Vastaa neljään (4) tehtävään ja halutessa bonustehtäviin B1 ja/tai B2, (tuovat lisäpisteitä). Bonustehtävät saa tehdä vaikkei olisi tehnyt siihen tehtävään
Ohjelmointi 2 / 2010 Välikoe / 26.3 Välikoe / 26.3 Vastaa neljään (4) tehtävään ja halutessa bonustehtäviin B1 ja/tai B2, (tuovat lisäpisteitä). Bonustehtävät saa tehdä vaikkei olisi tehnyt siihen tehtävään
8. Lajittelu, joukot ja valinta
 8. Lajittelu, joukot ja valinta Yksi tietojenkäsittelyn klassisista tehtävistä on lajittelu (järjestäminen) (sorting) jo mekaanisten tietojenkäsittelylaitteiden ajalta. Lajiteltua tietoa tarvitaan lukemattomissa
8. Lajittelu, joukot ja valinta Yksi tietojenkäsittelyn klassisista tehtävistä on lajittelu (järjestäminen) (sorting) jo mekaanisten tietojenkäsittelylaitteiden ajalta. Lajiteltua tietoa tarvitaan lukemattomissa
815338A Ohjelmointikielten periaatteet Harjoitus 6 Vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 6 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet Harjoitus 3 vastaukset
 815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 3 vastaukset Harjoituksen aiheena ovat imperatiivisten kielten muuttujiin liittyvät kysymykset. Tehtävä 1. Määritä muuttujien max_num, lista,
815338A Ohjelmointikielten periaatteet 2015-2016. Harjoitus 3 vastaukset Harjoituksen aiheena ovat imperatiivisten kielten muuttujiin liittyvät kysymykset. Tehtävä 1. Määritä muuttujien max_num, lista,
private TreeMap<String, Opiskelija> nimella; private TreeMap<String, Opiskelija> numerolla;
 Tietorakenteet, laskuharjoitus 7, ratkaisuja 1. Opiskelijarekisteri-luokka saadaan toteutetuksi käyttämällä kahta tasapainotettua binäärihakupuuta. Toisen binäärihakupuun avaimina pidetään opiskelijoiden
Tietorakenteet, laskuharjoitus 7, ratkaisuja 1. Opiskelijarekisteri-luokka saadaan toteutetuksi käyttämällä kahta tasapainotettua binäärihakupuuta. Toisen binäärihakupuun avaimina pidetään opiskelijoiden
Listarakenne (ArrayList-luokka)
 Listarakenne (ArrayList-luokka) Mikä on lista? Listan määrittely ArrayList-luokan metodeita Listan läpikäynti Listan läpikäynti indeksin avulla Listan läpikäynti iteraattorin avulla Listaan lisääminen
Listarakenne (ArrayList-luokka) Mikä on lista? Listan määrittely ArrayList-luokan metodeita Listan läpikäynti Listan läpikäynti indeksin avulla Listan läpikäynti iteraattorin avulla Listaan lisääminen
Algoritmit 2. Luento 7 Ti Timo Männikkö
 Algoritmit 2 Luento 7 Ti 4.4.2017 Timo Männikkö Luento 7 Joukot Joukko-operaatioita Joukkojen esitystapoja Alkiovieraat osajoukot Toteutus puurakenteena Algoritmit 2 Kevät 2017 Luento 7 Ti 4.4.2017 2/26
Algoritmit 2 Luento 7 Ti 4.4.2017 Timo Männikkö Luento 7 Joukot Joukko-operaatioita Joukkojen esitystapoja Alkiovieraat osajoukot Toteutus puurakenteena Algoritmit 2 Kevät 2017 Luento 7 Ti 4.4.2017 2/26
Ohjelmoinnin peruskurssien laaja oppimäärä
 Ohjelmoinnin peruskurssien laaja oppimäärä Luento 5: Sijoituslause, SICP-oliot, tietorakenteen muuttaminen (mm. SICP 33.1.3, 3.33.3.2) Riku Saikkonen 6. 11. 2012 Sisältö 1 Muuttujan arvon muuttaminen:
Ohjelmoinnin peruskurssien laaja oppimäärä Luento 5: Sijoituslause, SICP-oliot, tietorakenteen muuttaminen (mm. SICP 33.1.3, 3.33.3.2) Riku Saikkonen 6. 11. 2012 Sisältö 1 Muuttujan arvon muuttaminen:
811312A Tietorakenteet ja algoritmit, 2014-2015, Harjoitus 7, ratkaisu
 832A Tietorakenteet ja algoritmit, 204-205, Harjoitus 7, ratkaisu Hajota ja hallitse-menetelmä: Tehtävä 7.. Muodosta hajota ja hallitse-menetelmää käyttäen algoritmi TULOSTA_PUU_LASKEVA, joka tulostaa
832A Tietorakenteet ja algoritmit, 204-205, Harjoitus 7, ratkaisu Hajota ja hallitse-menetelmä: Tehtävä 7.. Muodosta hajota ja hallitse-menetelmää käyttäen algoritmi TULOSTA_PUU_LASKEVA, joka tulostaa
Sisältö. 22. Taulukot. Yleistä. Yleistä
 Sisältö 22. Taulukot Yleistä. Esittely ja luominen. Alkioiden käsittely. Kaksiulotteinen taulukko. Taulukko metodin parametrina. Taulukko ja HelloWorld-ohjelma. Taulukko paluuarvona. 22.1 22.2 Yleistä
Sisältö 22. Taulukot Yleistä. Esittely ja luominen. Alkioiden käsittely. Kaksiulotteinen taulukko. Taulukko metodin parametrina. Taulukko ja HelloWorld-ohjelma. Taulukko paluuarvona. 22.1 22.2 Yleistä
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
A274101 TIETORAKENTEET JA ALGORITMIT PUURAKENTEET, BINÄÄRIPUU, TASAPAINOTETUT PUUT MIKÄ ON PUUTIETORAKENNE? Esim. Viereinen kuva esittää erästä puuta. Tietojenkäsittelytieteessä puut kasvavat alaspäin.
Sisältö. 2. Taulukot. Yleistä. Yleistä
 Sisältö 2. Taulukot Yleistä. Esittely ja luominen. Alkioiden käsittely. Kaksiulotteinen taulukko. Taulukko operaation parametrina. Taulukko ja HelloWorld-ohjelma. Taulukko paluuarvona. 2.1 2.2 Yleistä
Sisältö 2. Taulukot Yleistä. Esittely ja luominen. Alkioiden käsittely. Kaksiulotteinen taulukko. Taulukko operaation parametrina. Taulukko ja HelloWorld-ohjelma. Taulukko paluuarvona. 2.1 2.2 Yleistä
Yleistä. Nyt käsitellään vain taulukko (array), joka on saman tyyppisten muuttujien eli alkioiden (element) kokoelma.
 2. Taulukot 2.1 Sisältö Yleistä. Esittely ja luominen. Alkioiden käsittely. Kaksiulotteinen taulukko. Taulukko operaation parametrina. Taulukko ja HelloWorld-ohjelma. Taulukko paluuarvona. 2.2 Yleistä
2. Taulukot 2.1 Sisältö Yleistä. Esittely ja luominen. Alkioiden käsittely. Kaksiulotteinen taulukko. Taulukko operaation parametrina. Taulukko ja HelloWorld-ohjelma. Taulukko paluuarvona. 2.2 Yleistä
Olion elinikä. Olion luominen. Olion tuhoutuminen. Olion tuhoutuminen. Kissa rontti = null; rontti = new Kissa();
 Sisällys 7. Oliot ja viitteet Olio Java-kielessä. Olion luominen, elinikä ja tuhoutuminen. Viitteiden käsittelyä: sijoitus, vertailu ja varautuminen null-arvoon. Viite metodin paluuarvona.. 7.1 7.2 Olio
Sisällys 7. Oliot ja viitteet Olio Java-kielessä. Olion luominen, elinikä ja tuhoutuminen. Viitteiden käsittelyä: sijoitus, vertailu ja varautuminen null-arvoon. Viite metodin paluuarvona.. 7.1 7.2 Olio
14. Poikkeukset 14.1
 14. Poikkeukset 14.1 Sisällys Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla poikkeuksella? Poikkeusten heittäminen.
14. Poikkeukset 14.1 Sisällys Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla poikkeuksella? Poikkeusten heittäminen.
Algoritmit 1. Luento 9 Ti Timo Männikkö
 Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
Algoritmit 1 Luento 9 Ti 7.2.2017 Timo Männikkö Luento 9 Graafit ja verkot Kaaritaulukko, bittimatriisi, pituusmatriisi Verkon lyhimmät polut Floydin menetelmä Lähtevien ja tulevien kaarien listat Forward
3. Binääripuu, Java-toteutus
 3. Binääripuu, Java-toteutus /*-------------------------------------------------------------/ / Rajapinta SearchTree: binäärisen hakupuun käsittelyrajapinta / / Metodit: / / void insert( Comparable x );
3. Binääripuu, Java-toteutus /*-------------------------------------------------------------/ / Rajapinta SearchTree: binäärisen hakupuun käsittelyrajapinta / / Metodit: / / void insert( Comparable x );
Java kahdessa tunnissa. Jyry Suvilehto
 Java kahdessa tunnissa Jyry Suvilehto Ohjelma Ohjelmointiasioita alkeista nippelitietoon n. 45 min Tauko 10 min Oliot, luokat ja muut kummajaiset n. 45 min Kysykää Sisältöä ei oikeasti ole 2x45 min täytteeksi,
Java kahdessa tunnissa Jyry Suvilehto Ohjelma Ohjelmointiasioita alkeista nippelitietoon n. 45 min Tauko 10 min Oliot, luokat ja muut kummajaiset n. 45 min Kysykää Sisältöä ei oikeasti ole 2x45 min täytteeksi,
Algoritmit 2. Luento 14 Ke Timo Männikkö
 Algoritmit 2 Luento 14 Ke 3.5.2017 Timo Männikkö Luento 14 Ositus ja rekursio Rekursion toteutus Kertaus ja tenttivinkit Algoritmit 2 Kevät 2017 Luento 14 Ke 3.5.2017 2/30 Ositus Tehtävän esiintymä ositetaan
Algoritmit 2 Luento 14 Ke 3.5.2017 Timo Männikkö Luento 14 Ositus ja rekursio Rekursion toteutus Kertaus ja tenttivinkit Algoritmit 2 Kevät 2017 Luento 14 Ke 3.5.2017 2/30 Ositus Tehtävän esiintymä ositetaan
58131 Tietorakenteet ja algoritmit (syksy 2015)
 58131 Tietorakenteet ja algoritmit (syksy 2015) Harjoitus 2 (14. 18.9.2015) Huom. Sinun on tehtävä vähintään kaksi tehtävää, jotta voit jatkaa kurssilla. 1. Erään algoritmin suoritus vie 1 ms, kun syötteen
58131 Tietorakenteet ja algoritmit (syksy 2015) Harjoitus 2 (14. 18.9.2015) Huom. Sinun on tehtävä vähintään kaksi tehtävää, jotta voit jatkaa kurssilla. 1. Erään algoritmin suoritus vie 1 ms, kun syötteen
2. Seuraavassa kuvassa on verkon solmujen topologinen järjestys: x t v q z u s y w r. Kuva 1: Tehtävän 2 solmut järjestettynä topologisesti.
 Tietorakenteet, laskuharjoitus 11, ratkaisuja 1. Leveyssuuntaisen läpikäynnin voi toteuttaa rekursiivisesti käsittelemällä jokaisella rekursiivisella kutsulla kaikki tietyllä tasolla olevat solmut. Rekursiivinen
Tietorakenteet, laskuharjoitus 11, ratkaisuja 1. Leveyssuuntaisen läpikäynnin voi toteuttaa rekursiivisesti käsittelemällä jokaisella rekursiivisella kutsulla kaikki tietyllä tasolla olevat solmut. Rekursiivinen
58131 Tietorakenteet ja algoritmit (kevät 2016) Ensimmäinen välikoe, malliratkaisut
 58131 Tietorakenteet ja algoritmit (kevät 2016) Ensimmäinen välikoe, malliratkaisut 1. Palautetaan vielä mieleen O-notaation määritelmä. Olkoon f ja g funktioita luonnollisilta luvuilta positiivisille
58131 Tietorakenteet ja algoritmit (kevät 2016) Ensimmäinen välikoe, malliratkaisut 1. Palautetaan vielä mieleen O-notaation määritelmä. Olkoon f ja g funktioita luonnollisilta luvuilta positiivisille
Algoritmit 1. Luento 5 Ti Timo Männikkö
 Algoritmit 1 Luento 5 Ti 24.1.2017 Timo Männikkö Luento 5 Järjestetty lista Järjestetyn listan operaatiot Listan toteutus taulukolla Binäärihaku Binäärihaun vaativuus Algoritmit 1 Kevät 2017 Luento 5 Ti
Algoritmit 1 Luento 5 Ti 24.1.2017 Timo Männikkö Luento 5 Järjestetty lista Järjestetyn listan operaatiot Listan toteutus taulukolla Binäärihaku Binäärihaun vaativuus Algoritmit 1 Kevät 2017 Luento 5 Ti
Ohjelmoinnin peruskurssien laaja oppimäärä
 Ohjelmoinnin peruskurssien laaja oppimäärä Luento 4: Symbolit, derivojaesimerkki, kierroksen 1 ratkaisut (mm. SICP 2.32.3.2) Riku Saikkonen 1. 11. 2011 Sisältö 1 Symbolit ja sulkulausekkeet 2 Lisää Schemestä:
Ohjelmoinnin peruskurssien laaja oppimäärä Luento 4: Symbolit, derivojaesimerkki, kierroksen 1 ratkaisut (mm. SICP 2.32.3.2) Riku Saikkonen 1. 11. 2011 Sisältö 1 Symbolit ja sulkulausekkeet 2 Lisää Schemestä:
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset
 815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
815338A Ohjelmointikielten periaatteet 2014-2015. Harjoitus 7 Vastaukset Harjoituksen aiheena on funktionaalinen ohjelmointi Scheme- ja Haskell-kielillä. Voit suorittaa ohjelmat osoitteessa https://ideone.com/
Rajapinta (interface)
 1 Rajapinta (interface) Mikä rajapinta on? Rajapinta ja siitä toteutettu luokka Monimuotoisuus ja dynaaminen sidonta Rajapinta vs periytyminen 1 Mikä rajapinta on? Rajapintoja käytetään, kun halutaan määritellä
1 Rajapinta (interface) Mikä rajapinta on? Rajapinta ja siitä toteutettu luokka Monimuotoisuus ja dynaaminen sidonta Rajapinta vs periytyminen 1 Mikä rajapinta on? Rajapintoja käytetään, kun halutaan määritellä
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 11.2.2009 T-106.1208 Ohjelmoinnin perusteet Y 11.2.2009 1 / 33 Kertausta: listat Tyhjä uusi lista luodaan kirjoittamalla esimerkiksi lampotilat = [] (jolloin
Ohjelmoinnin perusteet Y Python T-106.1208 11.2.2009 T-106.1208 Ohjelmoinnin perusteet Y 11.2.2009 1 / 33 Kertausta: listat Tyhjä uusi lista luodaan kirjoittamalla esimerkiksi lampotilat = [] (jolloin
Algoritmit 1. Luento 14 Ke 25.2.2015. Timo Männikkö
 Algoritmit 1 Luento 14 Ke 25.2.2015 Timo Männikkö Luento 14 Heuristiset menetelmät Heuristiikkoja kapsäkkiongelmalle Kauppamatkustajan ongelma Lähimmän naapurin menetelmä Kertaus ja tenttivinkit Algoritmit
Algoritmit 1 Luento 14 Ke 25.2.2015 Timo Männikkö Luento 14 Heuristiset menetelmät Heuristiikkoja kapsäkkiongelmalle Kauppamatkustajan ongelma Lähimmän naapurin menetelmä Kertaus ja tenttivinkit Algoritmit
A215 Tietorakenteet. Tietojenkäsittelytieteiden laitos Tampereen yliopisto. Periodit I-II, syksy 2007
 Kurssiesittely Tietojenkäsittelytieteiden laitos Tampereen yliopisto 25 Tietorakenteet Periodit I-II, syksy 2007 Luennot/vastuuhenkilö: Heikki Hyyrö Sähköposti: heikki.hyyro@cs.uta.fi Kurssin kotisivu:
Kurssiesittely Tietojenkäsittelytieteiden laitos Tampereen yliopisto 25 Tietorakenteet Periodit I-II, syksy 2007 Luennot/vastuuhenkilö: Heikki Hyyrö Sähköposti: heikki.hyyro@cs.uta.fi Kurssin kotisivu:
Algoritmit 2. Luento 3 Ti Timo Männikkö
 Algoritmit 2 Luento 3 Ti 20.3.2018 Timo Männikkö Luento 3 Järjestäminen eli lajittelu Kekorakenne Kekolajittelu Hajautus Yhteentörmäysten käsittely Ketjutus Algoritmit 2 Kevät 2018 Luento 3 Ti 20.3.2018
Algoritmit 2 Luento 3 Ti 20.3.2018 Timo Männikkö Luento 3 Järjestäminen eli lajittelu Kekorakenne Kekolajittelu Hajautus Yhteentörmäysten käsittely Ketjutus Algoritmit 2 Kevät 2018 Luento 3 Ti 20.3.2018
Informaatioteknologian laitos Olio-ohjelmoinnin perusteet / Salo 15.2.2006
 TURUN YLIOPISTO DEMO III Informaatioteknologian laitos tehtävät Olio-ohjelmoinnin perusteet / Salo 15.2.2006 1. Tässä tehtävässä tarkastellaan erääntyviä laskuja. Lasku muodostaa oman luokkansa. Laskussa
TURUN YLIOPISTO DEMO III Informaatioteknologian laitos tehtävät Olio-ohjelmoinnin perusteet / Salo 15.2.2006 1. Tässä tehtävässä tarkastellaan erääntyviä laskuja. Lasku muodostaa oman luokkansa. Laskussa
A274101 TIETORAKENTEET JA ALGORITMIT
 A274101 TIETORAKENTEET JA ALGORITMIT ALGORITMIEN ANALYYSISTÄ 1.ratkaisu Laskentaaika hakkeri - optimoitu ALGORITMIANALYYSIÄ hyvä algoritmi hakkeri -optimoitu hyvä algoritmi Tehtävän koko Kuva mukailtu
A274101 TIETORAKENTEET JA ALGORITMIT ALGORITMIEN ANALYYSISTÄ 1.ratkaisu Laskentaaika hakkeri - optimoitu ALGORITMIANALYYSIÄ hyvä algoritmi hakkeri -optimoitu hyvä algoritmi Tehtävän koko Kuva mukailtu
Jakso 4 Aliohjelmien toteutus
 Jakso 4 Aliohjelmien toteutus Tyypit Parametrit Aktivointitietue (AT) AT-pino Rekursio 1 Aliohjelmatyypit (2) Korkean tason ohjelmointikielen käsitteet: aliohjelma, proseduuri parametrit funktio parametrit,
Jakso 4 Aliohjelmien toteutus Tyypit Parametrit Aktivointitietue (AT) AT-pino Rekursio 1 Aliohjelmatyypit (2) Korkean tason ohjelmointikielen käsitteet: aliohjelma, proseduuri parametrit funktio parametrit,
Ohjelmointitaito (ict1td002, 12 op) Kevät 2008. 1. Java-ohjelmoinnin alkeita. Tietokoneohjelma. Raine Kauppinen raine.kauppinen@haaga-helia.
 Ohjelmointitaito (ict1td002, 12 op) Kevät 2008 Raine Kauppinen raine.kauppinen@haaga-helia.fi 1. Java-ohjelmoinnin alkeita Tietokoneohjelma Java-kieli ja Eclipse-ympäristö Java-ohjelma ja ohjelmaluokka
Ohjelmointitaito (ict1td002, 12 op) Kevät 2008 Raine Kauppinen raine.kauppinen@haaga-helia.fi 1. Java-ohjelmoinnin alkeita Tietokoneohjelma Java-kieli ja Eclipse-ympäristö Java-ohjelma ja ohjelmaluokka
Rinnakkaisohjelmointi kurssi. Opintopiiri työskentelyn raportti
 Rinnakkaisohjelmointi kurssi Opintopiiri työskentelyn raportti Opintopiiri: Heikki Karimo, Jesse Paakkari ja Keijo Karhu Päiväys: 15.12.2006 Ohjelmointitehtävä C i C i : Säikeet ja kriittisen vaiheen kontrollointi
Rinnakkaisohjelmointi kurssi Opintopiiri työskentelyn raportti Opintopiiri: Heikki Karimo, Jesse Paakkari ja Keijo Karhu Päiväys: 15.12.2006 Ohjelmointitehtävä C i C i : Säikeet ja kriittisen vaiheen kontrollointi
Tietorakenteet ja algoritmit
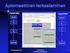 Tietorakenteet ja algoritmit Elegantti toteutus funktiolle insert_to_list_end Alkion lisäys sisällön mukaan järjestettyyn listaan (insert_to_list) Linkatun listan yleisyys alkiotyypin suhteen source-tasolla
Tietorakenteet ja algoritmit Elegantti toteutus funktiolle insert_to_list_end Alkion lisäys sisällön mukaan järjestettyyn listaan (insert_to_list) Linkatun listan yleisyys alkiotyypin suhteen source-tasolla
Sisällys. 14. Poikkeukset. Johdanto. Johdanto
 Sisällys 14. Poikkeukset Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla poikkeuksella? Poikkeusten heittäminen.
Sisällys 14. Poikkeukset Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla poikkeuksella? Poikkeusten heittäminen.
Olio-ohjelmointi Syntaksikokoelma
 C++-kielen uusia ominaisuuksia Olio-ohjelmointi Syntaksikokoelma 31.10.2008 Bool-tietotyyppi: Totuusarvo true (1), jos ehto on tosi ja false (0) jos ehto epätosi. Dynaaminen muistinvaraus: Yhden muuttuja
C++-kielen uusia ominaisuuksia Olio-ohjelmointi Syntaksikokoelma 31.10.2008 Bool-tietotyyppi: Totuusarvo true (1), jos ehto on tosi ja false (0) jos ehto epätosi. Dynaaminen muistinvaraus: Yhden muuttuja
Algoritmit 1. Luento 12 Ti Timo Männikkö
 Algoritmit 1 Luento 12 Ti 19.2.2019 Timo Männikkö Luento 12 Osittamisen tasapainoisuus Pikalajittelun vaativuus Lajittelumenetelmien vaativuus Laskentalajittelu Lokerolajittelu Kantalukulajittelu Algoritmit
Algoritmit 1 Luento 12 Ti 19.2.2019 Timo Männikkö Luento 12 Osittamisen tasapainoisuus Pikalajittelun vaativuus Lajittelumenetelmien vaativuus Laskentalajittelu Lokerolajittelu Kantalukulajittelu Algoritmit
A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä.
 Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Esimerkki otteluvoiton todennäköisyys A ja B pelaavat sarjan pelejä. Sarjan voittaja on se, joka ensin voittaa n peliä. Yksittäisessä pelissä A voittaa todennäköisyydellä p ja B todennäköisyydellä q =
Opintojakso TT00AA11 Ohjelmoinnin jatko (Java): 3 op Taulukot & Periytyminen
 Opintojakso TT00AA11 Ohjelmoinnin jatko (Java): 3 op Taulukot & Periytyminen Taulukot: Array Taulukko Javassa pitää aina perustaa (new) Yksinkertaisessa tilanteessa taulukon koko tiedetään etukäteen ja
Opintojakso TT00AA11 Ohjelmoinnin jatko (Java): 3 op Taulukot & Periytyminen Taulukot: Array Taulukko Javassa pitää aina perustaa (new) Yksinkertaisessa tilanteessa taulukon koko tiedetään etukäteen ja
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 15.3.2010 T-106.1208 Ohjelmoinnin perusteet Y 15.3.2010 1 / 56 Tiedostoista: tietojen tallentaminen ohjelman suorituskertojen välillä Monissa sovelluksissa ohjelman
Ohjelmoinnin perusteet Y Python T-106.1208 15.3.2010 T-106.1208 Ohjelmoinnin perusteet Y 15.3.2010 1 / 56 Tiedostoista: tietojen tallentaminen ohjelman suorituskertojen välillä Monissa sovelluksissa ohjelman
14. Poikkeukset 14.1
 14. Poikkeukset 14.1 Sisällys Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Miten varautua poikkeukseen metodissa? Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla
14. Poikkeukset 14.1 Sisällys Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Miten varautua poikkeukseen metodissa? Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla
Algoritmit 2. Luento 3 Ti Timo Männikkö
 Algoritmit 2 Luento 3 Ti 21.3.2017 Timo Männikkö Luento 3 Järjestäminen eli lajittelu Kekorakenne Kekolajittelu Hajautus Yhteentörmäysten käsittely Ketjutus Algoritmit 2 Kevät 2017 Luento 3 Ti 21.3.2017
Algoritmit 2 Luento 3 Ti 21.3.2017 Timo Männikkö Luento 3 Järjestäminen eli lajittelu Kekorakenne Kekolajittelu Hajautus Yhteentörmäysten käsittely Ketjutus Algoritmit 2 Kevät 2017 Luento 3 Ti 21.3.2017
Algoritmit 1. Demot Timo Männikkö
 Algoritmit 1 Demot 2 7.-8.2.2018 Timo Männikkö Tehtävä 1 (a) Ei-rekursiivinen algoritmi: etsipienin(t, n) { pnn = t[0]; for (i = 1; i < n; i++) { pnn = min(pnn, t[i]); return pnn; Silmukka suoritetaan
Algoritmit 1 Demot 2 7.-8.2.2018 Timo Männikkö Tehtävä 1 (a) Ei-rekursiivinen algoritmi: etsipienin(t, n) { pnn = t[0]; for (i = 1; i < n; i++) { pnn = min(pnn, t[i]); return pnn; Silmukka suoritetaan
Ohjelmoinnin perusteet Y Python
 Ohjelmoinnin perusteet Y Python T-106.1208 1.4.2009 T-106.1208 Ohjelmoinnin perusteet Y 1.4.2009 1 / 56 Tentti Ensimmäinen tenttimahdollisuus on pe 8.5. klo 13:00 17:00 päärakennuksessa. Tämän jälkeen
Ohjelmoinnin perusteet Y Python T-106.1208 1.4.2009 T-106.1208 Ohjelmoinnin perusteet Y 1.4.2009 1 / 56 Tentti Ensimmäinen tenttimahdollisuus on pe 8.5. klo 13:00 17:00 päärakennuksessa. Tämän jälkeen
Sisällys. 14. Poikkeukset. Johdanto. Johdanto
 Sisällys 14. Poikkeukset Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Miten varautua poikkeukseen metodissa? Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla
Sisällys 14. Poikkeukset Johdanto. Tarkistettavat ja tarkistamattomat poikkeukset. Miten varautua poikkeukseen metodissa? Poikkeusten tunnistaminen ja sieppaaminen try-catchlauseella. Mitä tehdä siepatulla
JAVA-PERUSTEET. JAVA-OHJELMOINTI 3op A274615 JAVAN PERUSTEET LYHYT KERTAUS JAVAN OMINAISUUKSISTA JAVAN OMINAISUUKSIA. Java vs. C++?
 JAVA-OHJELMOINTI 3op A274615 JAVAN PERUSTEET LYHYT KERTAUS Teemu Saarelainen teemu.saarelainen@kyamk.fi Lähteet: http://java.sun.com/docs/books/tutorial/index.html Vesterholm, Kyppö: Java-ohjelmointi,
JAVA-OHJELMOINTI 3op A274615 JAVAN PERUSTEET LYHYT KERTAUS Teemu Saarelainen teemu.saarelainen@kyamk.fi Lähteet: http://java.sun.com/docs/books/tutorial/index.html Vesterholm, Kyppö: Java-ohjelmointi,
lähtokohta: kahden O(h) korkuisen keon yhdistäminen uudella juurella vie O(h) operaatiota vrt. RemoveMinElem() keossa
 Kekolajittelu Prioriteettijonolla toteutettu keko InsertItem ja RemoveMinElem: O(log(n)) Lajittelu prioriteettijonolla: PriorityQueueSort(lajiteltava sekvenssi S) alusta prioriteettijono P while S.IsEmpty()
Kekolajittelu Prioriteettijonolla toteutettu keko InsertItem ja RemoveMinElem: O(log(n)) Lajittelu prioriteettijonolla: PriorityQueueSort(lajiteltava sekvenssi S) alusta prioriteettijono P while S.IsEmpty()
Hakupuut. tässä luvussa tarkastelemme puita tiedon tallennusrakenteina
 Hakupuut tässä luvussa tarkastelemme puita tiedon tallennusrakenteina hakupuun avulla voidaan toteuttaa kaikki joukko-tietotyypin operaatiot (myös succ ja pred) pahimman tapauksen aikavaativuus on tavallisella
Hakupuut tässä luvussa tarkastelemme puita tiedon tallennusrakenteina hakupuun avulla voidaan toteuttaa kaikki joukko-tietotyypin operaatiot (myös succ ja pred) pahimman tapauksen aikavaativuus on tavallisella
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Pino Pinon määritelmä Pinon sovelluksia Järjestyksen kääntäminen Palindromiprobleema Postfix-lausekkeen laskenta Infix-lausekkeen muunto postfix-lausekkeeksi Sisäkkäiset funktiokutsut
Tietorakenteet ja algoritmit Pino Pinon määritelmä Pinon sovelluksia Järjestyksen kääntäminen Palindromiprobleema Postfix-lausekkeen laskenta Infix-lausekkeen muunto postfix-lausekkeeksi Sisäkkäiset funktiokutsut
Algoritmit 1. Luento 10 Ke 11.2.2015. Timo Männikkö
 Algoritmit 1 Luento 10 Ke 11.2.2015 Timo Männikkö Luento 10 Algoritminen ongelman ratkaisu Suunnittelumenetelmät Raaka voima Järjestäminen eli lajittelu Kuplalajittelu Väliinsijoituslajittelu Valintalajittelu
Algoritmit 1 Luento 10 Ke 11.2.2015 Timo Männikkö Luento 10 Algoritminen ongelman ratkaisu Suunnittelumenetelmät Raaka voima Järjestäminen eli lajittelu Kuplalajittelu Väliinsijoituslajittelu Valintalajittelu
puuta tree hierarkkinen hierarchical
 4. Puut Seuraavaksi käsitellään yhtä tärkeimmistä tietojenkäsittelytieteen ei-lineaarisista käsitteistä, puuta (tree). Puut ovat olleet keksintönä todellinen läpimurto, koska niissä luotiin tehokas eilineaari
4. Puut Seuraavaksi käsitellään yhtä tärkeimmistä tietojenkäsittelytieteen ei-lineaarisista käsitteistä, puuta (tree). Puut ovat olleet keksintönä todellinen läpimurto, koska niissä luotiin tehokas eilineaari
Imperatiivisen ohjelmoinnin peruskäsitteet. Meidän käyttämän pseudokielen lauseiden syntaksi
 Imperatiivisen ohjelmoinnin peruskäsitteet muuttuja muuttujissa oleva data voi olla yksinkertaista eli primitiivistä (esim. luvut ja merkit) tai rakenteista jolloin puhutaan tietorakenteista. puhuttaessa
Imperatiivisen ohjelmoinnin peruskäsitteet muuttuja muuttujissa oleva data voi olla yksinkertaista eli primitiivistä (esim. luvut ja merkit) tai rakenteista jolloin puhutaan tietorakenteista. puhuttaessa
Luku 8. Aluekyselyt. 8.1 Summataulukko
 Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
Luku 8 Aluekyselyt Aluekysely on tiettyä taulukon väliä koskeva kysely. Tyypillisiä aluekyselyitä ovat, mikä on taulukon välin lukujen summa tai pienin luku välillä. Esimerkiksi seuraavassa taulukossa
ITKP102 Ohjelmointi 1 (6 op)
 ITKP102 Ohjelmointi 1 (6 op) Tentaattori: Antti-Jussi Lakanen 7. huhtikuuta 2017 Vastaa kaikkiin tehtäviin. Tee jokainen tehtävä erilliselle konseptiarkille. Kirjoittamasi luokat, funktiot ja aliohjelmat
ITKP102 Ohjelmointi 1 (6 op) Tentaattori: Antti-Jussi Lakanen 7. huhtikuuta 2017 Vastaa kaikkiin tehtäviin. Tee jokainen tehtävä erilliselle konseptiarkille. Kirjoittamasi luokat, funktiot ja aliohjelmat
Se mistä tilasta aloitetaan, merkitään tyhjästä tulevalla nuolella. Yllä olevassa esimerkissä aloitustila on A.
 Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
Tehtävä. Tämä tehtävä on aineistotehtävä, jossa esitetään ensin tehtävän teoria. Sen jälkeen esitetään neljä kysymystä, joissa tätä teoriaa pitää soveltaa. Mitään aikaisempaa tehtävän aihepiirin tuntemusta
ITKP102 Ohjelmointi 1 (6 op)
 ITKP102 Ohjelmointi 1 (6 op) Tentaattori: Antti-Jussi Lakanen 20. huhtikuuta 2018 Vastaa kaikkiin tehtäviin. Tee kukin tehtävä omalle konseptiarkille. Noudata ohjelmointitehtävissä kurssin koodauskäytänteitä.
ITKP102 Ohjelmointi 1 (6 op) Tentaattori: Antti-Jussi Lakanen 20. huhtikuuta 2018 Vastaa kaikkiin tehtäviin. Tee kukin tehtävä omalle konseptiarkille. Noudata ohjelmointitehtävissä kurssin koodauskäytänteitä.
Tietorakenteet, laskuharjoitus 6,
 Tietorakenteet, laskuharjoitus, 23.-2.1 1. (a) Kuvassa 1 on esitetty eräät pienimmistä AVL-puista, joiden korkeus on 3 ja 4. Pienin h:n korkuinen AVL-puu ei ole yksikäsitteinen juuren alipuiden keskinäisen
Tietorakenteet, laskuharjoitus, 23.-2.1 1. (a) Kuvassa 1 on esitetty eräät pienimmistä AVL-puista, joiden korkeus on 3 ja 4. Pienin h:n korkuinen AVL-puu ei ole yksikäsitteinen juuren alipuiden keskinäisen
Rakenteiset tietotyypit Moniulotteiset taulukot
 C! Rakenteiset tietotyypit Moniulotteiset taulukot 22.2.2018 Agenda Rakenteiset tietotyypit Vilkaisu 6. kierroksen tehtäviin Moniulotteiset taulukot Esimerkki Seuraava luento to 8.3. Ilmoittautuminen ohjelmointikokeeseen
C! Rakenteiset tietotyypit Moniulotteiset taulukot 22.2.2018 Agenda Rakenteiset tietotyypit Vilkaisu 6. kierroksen tehtäviin Moniulotteiset taulukot Esimerkki Seuraava luento to 8.3. Ilmoittautuminen ohjelmointikokeeseen
Algoritmit 1. Luento 12 Ke Timo Männikkö
 Algoritmit 1 Luento 12 Ke 15.2.2017 Timo Männikkö Luento 12 Pikalajittelu Pikalajittelun vaativuus Osittamisen tasapainoisuus Lajittelumenetelmien vaativuus Laskentalajittelu Lokerolajittelu Kantalukulajittelu
Algoritmit 1 Luento 12 Ke 15.2.2017 Timo Männikkö Luento 12 Pikalajittelu Pikalajittelun vaativuus Osittamisen tasapainoisuus Lajittelumenetelmien vaativuus Laskentalajittelu Lokerolajittelu Kantalukulajittelu
Luento 4 Aliohjelmien toteutus
 Luento 4 Aliohjelmien toteutus Tyypit Parametrit Aktivointitietue (AT) AT-pino Rekursio 1 Aliohjelmatyypit (2) Korkean tason ohjelmointikielen käsitteet: aliohjelma, proseduuri parametrit funktio parametrit,
Luento 4 Aliohjelmien toteutus Tyypit Parametrit Aktivointitietue (AT) AT-pino Rekursio 1 Aliohjelmatyypit (2) Korkean tason ohjelmointikielen käsitteet: aliohjelma, proseduuri parametrit funktio parametrit,
Algoritmit 2. Luento 4 To Timo Männikkö
 Algoritmit 2 Luento 4 To 21.3.2019 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2019 Luento 4
Algoritmit 2 Luento 4 To 21.3.2019 Timo Männikkö Luento 4 Hajautus Yhteentörmäysten käsittely Avoin osoitteenmuodostus Hajautusfunktiot Puurakenteet Solmujen läpikäynti Algoritmit 2 Kevät 2019 Luento 4
Luku 6. Dynaaminen ohjelmointi. 6.1 Funktion muisti
 Luku 6 Dynaaminen ohjelmointi Dynaamisessa ohjelmoinnissa on ideana jakaa ongelman ratkaisu pienempiin osaongelmiin, jotka voidaan ratkaista toisistaan riippumattomasti. Jokaisen osaongelman ratkaisu tallennetaan
Luku 6 Dynaaminen ohjelmointi Dynaamisessa ohjelmoinnissa on ideana jakaa ongelman ratkaisu pienempiin osaongelmiin, jotka voidaan ratkaista toisistaan riippumattomasti. Jokaisen osaongelman ratkaisu tallennetaan
15. Ohjelmoinnin tekniikkaa 15.1
 15. Ohjelmoinnin tekniikkaa 15.1 Sisällys For-each-rakenne. Geneerinen ohjelmointi. Lueteltu tyyppi enum. 15.2 For-each-rakenne For-rakenteen variaatio taulukoiden ja muiden kokoelmien silmukoimiseen:
15. Ohjelmoinnin tekniikkaa 15.1 Sisällys For-each-rakenne. Geneerinen ohjelmointi. Lueteltu tyyppi enum. 15.2 For-each-rakenne For-rakenteen variaatio taulukoiden ja muiden kokoelmien silmukoimiseen:
Tietorakenteet ja algoritmit
 Tietorakenteet ja algoritmit Taulukon edut Taulukon haitat Taulukon haittojen välttäminen Dynaamisesti linkattu lista Linkatun listan solmun määrittelytavat Lineaarisen listan toteutus dynaamisesti linkattuna
Tietorakenteet ja algoritmit Taulukon edut Taulukon haitat Taulukon haittojen välttäminen Dynaamisesti linkattu lista Linkatun listan solmun määrittelytavat Lineaarisen listan toteutus dynaamisesti linkattuna
Alkuarvot ja tyyppimuunnokset (1/5) Alkuarvot ja tyyppimuunnokset (2/5) Alkuarvot ja tyyppimuunnokset (3/5)
 Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
Alkuarvot ja tyyppimuunnokset (1/5) Aiemmin olemme jo antaneet muuttujille alkuarvoja, esimerkiksi: int luku = 123; Alkuarvon on oltava muuttujan tietotyypin mukainen, esimerkiksi int-muuttujilla kokonaisluku,
