Yhtälöryhmän iteratiivinen ratkaiseminen

Transkriptio

1 Yhtälöryhmän iteratiivinen ratkaiseminen V V I Berg Matematiikan pro gradu Jyväskylän yliopisto Matematiikan ja tilastotieteen laitos Kesä 2015

2

3 Tiivistelmä: V V I Berg, Yhtälöryhmän iteratiivinen ratkaiseminen (engl Iterative solving of linear system), matematiikan pro gradu -tutkielma, 35 s, Jyväskylän yliopisto, Matematiikan ja tilastotieteen laitos, kesä 2015 Tämän kirjoitelman tarkoituksena on näyttää eri ratkaisumenetelmiä lineaarisen yhtälöryhmän a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a n1 x 1 + a n2 x n2 + + a nn x n = b n ratkaisemiseksi iteratiivisesti ja osoittaa miksi kyseiset menetelmät toimivat ja millä ehdoilla Kirjoitelmassa käydään läpi Jacobin menetelmä, Gaussin ja Seidelin menetelmä ja konjugaattigradienttimenetelmä Edellä mainittua yhtälöryhmää vastaa matriisiyhtälö Ax = b, missä A = A n n on kompleksikertoiminen neliömatriisi Jacobin menetelmällä hajotetaan matriisi A osiin diagonaalimatriisiksi D ja matriisiksi E F, jonka diagonaalialkiot ovat nollia, ja A = D E F Tällöin saadaan matriisiyhtälö sellaiseen muotoon, että voidaan iteroida vektorille x m ratkaisuja alkioittain käyttämällä laskuissa pelkästään edellistä ratkaisua x m 1 Gaussin ja Seidelin menetelmässä lähtökohta on sama kuin Jacobin menetelmässä Ero Jacobin menetelmään on siinä, että vektorin alkion x m j ratkaisua iteroitaessa käytetään kyseisen iteraatiokierroksen saatujen arvojen x m 1,, x m j 1 lisäksi edelliseltä kierrokselta arvoja x m 1 j,, x m 1 n Tällöin Gaussin ja Seidelin menetelmä näyttäisi olevan laskennallisesti tehokkaampi kuin Jacobin menetelmä Konjugaattigradienttimenetelmässä etsitään neliömuodon f(x) = 1 2 x Ax b x gradientin f(x) = Ax b nollakohtaa kun A on itseadjungoitu ja positiivisesti definiitti Kirjoitelmassa lähdetään liikkeelle jyrkimmän laskun menetelmästä, jossa käytetään tietoa siitä, että gradientti vähenee voimakkaimmin negatiivisen gradientin suuntaan, jolloin kyseisen suuntavektorin ja neliömuodon leikkauspiste on jokaisen iteraatiokierroksen ratkaisu vektoriksi x m Tämän jälkeen parannetaan jyrkimmän laskun menetelmää etsimällä yleisiä keskenään ortogonaalisia A-konjugaatteja suuntavektoreita p k Lopuksi määritellään tapa määrittää eksaktisti etsintäsuuntavektorit käyttämällä Krylovin aliavaruuksia, jolloin päädytään konjugaattigradienttimenetelmään Kirjoitelman lopussa arvioidaan empiirisesti kahden esimerkin avulla menetelmien laskennallista tehokkuutta Pienten matriisien tapauksissa näyttäisi konjugaattigradienttimenetelmä olevan tehokkaampi kuin Jacobin menetelmä ja Gaussin ja Seidelin menetelmä i

4

5 Sisältö Johdanto 1 Luku 1 Lineaarialgebrasta ja matriisiteoriasta 3 11 Matriisin ominaisarvo 3 12 Matriisijono 4 13 Ortogonaalisuudesta ja aliavaruuksista 4 14 Matriisin eräitä ominaisuuksia 5 15 Normi 6 Luku 2 Jacobin ja Gaussin ja Seidelin iteratiiviset menetelmät Jacobin iterointimenetelmä Gaussin ja Seidelin iterointimenetelmä 18 Luku 3 Konjugaattigradienttimenetelmä Matriisin neliömuoto Jyrkimmän laskun menetelmä A-konjugaatit etsintäsuunnat Konjugaattigradienttimenetelmä 27 Kirjallisuutta 35 iii

6

7 Johdanto Tämän kirjoitelman tarkoituksena on näyttää eri ratkaisumenetelmiä lineaarisen yhtälöryhmän a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 a n1 x 1 + a n2 x n2 + + a nn x n = b n ratkaisemiseksi tai approksimoimiseksi iteratiivisesti ja osoittaa miksi kyseiset menetelmät toimivat ja millä ehdoilla Kirjoitelmassa käydään läpi Jacobin menetelmä, Gaussin ja Seidelin menetelmä ja konjugaattigradienttimenetelmä Esitietoina oletetaan tunnetuiksi peruslineaarialgebran kurssit Lähdeluettelossakin mainituilta matriisiteorian [3] ja matriisiseminaarin [4] kurssien käsitellyistä asioista esitellään ensimmäisessä kappaleessa tarpeellinen esitieto Kirjoitelmassa käsiteltävät matriisit ovat kompleksikertoimisia neliömatriiseja M C(n, n) Myöhemmin kirjoitelmassa käytetään kompleksikertoimisten neliömatriisien joukolle merkintää M n (C) Kirjoitelmassa mainitaan erikseen mikäli matriisit ovat jotain muuta Lisäksi mikäli matriisia kerrotaan vektorilla, matriisia matriisilla tai vektoria vektorilla, niin oletuksena on laskutoimitusten yhteensopivuus dimensioiden suhteen Ensimmäisessä kappaleessa esitellään jo peruslineaarialgebran kursseilla käydyistä asioista ominaisarvoteoriaa Tämän jälkeen esitellään matriisiteoria ja -seminaarikursseilla esitelty määritelmä matriisijonolle ja esitellään matriisin ominaisuuksista itseadjungoituvuus, pseudoinverttisyys, similaarisuus ja matriisinormi, joka johdetaan kompleksisen vektoriavaruuden normista matriisille sopivan ehdon avulla Lisäksi kappaleessa käsitellään vektorijoukon ortogonaalisuus, ortogonaaliprojektio ja matriisin normaalius Toisessa kappaleessa käsitellään Jacobin menetelmä ja Gaussin ja Seidelin menetelmä Jacobin menetelmällä hajotetaan matriisi summamatriisiksi, jonka toinen osa on diagonaalimatriisi ja toinen osa matriisiksi, jonka diagonaalialkiot ovat nollia Tällöin saadaan matriisiyhtälö sellaiseen muotoon, että voidaan iteroida ratkaisuvektorin arvoja alkioittain käyttämällä laskuissa pelkästään edellistä ratkaisua Gaussin ja Seidelin menetelmässä lähtökohta on sama kuin Jacobin menetelmässä Ero Jacobin menetelmään on kuitenkin siinä, että ratkaisuvektorin arvoja iteroitaessa käytetään aina tuoreimpia arvoja eli kyseisen iteraatiokierroksen saatujen arvojen lisäksi tarvittaessa edelliseltä kierrokselta saatuja arvoja Toinen kappale pohjautuu vahvasti Denis Serren Matrices: Theory and Applications [2] teokseen ja osittain myös Gene H Golubin ja Charles F Van Loanin Matrix computations [1] teokseen 1

8 2 JOHDANTO Konjugaattigradienttimenetelmässä etsitään neliömuodon f(x) = 1 2 x Ax b x gradientin f(x) = Ax b nollakohtaa kun A on itseadjungoitu ja positiivisesti definiitti Kirjoitelmassa lähdetään liikkeelle jyrkimmän laskun menetelmästä, jossa käytetään tietoa siitä, että gradientti vähenee voimakkaimmin negatiivisen gradientin suuntaan, jolloin kyseisen suuntavektorin ja neliömuodon leikkauspiste on jokaisen iteraatiokierroksen ratkaisu vektoriksi x m Tämän jälkeen parannetaan jyrkimmän laskun menetelmää etsimällä yleisiä keskenään ortogonaalisia A-konjugaatteja suuntavektoreita p k Lopuksi määritellään tapa määrittää eksaktisti etsintäsuuntavektorit käyttämällä Krylovin aliavaruuksia, jolloin päädytään konjugaattigradienttimenetelmään Kolmas kappale pohjautuu suurimmilta osin Gene H Golubin ja Charles F Van Loanin Matrix computations [1] teokseen Normien osalta painotus on kuitenkin Denis Serren Matrices: Theory and Applications [2] teoksessa Kuvaajien osalta lähteenä on käytetty Jonathan R Shewchukin An Introduction to the Conjugate Gradient Method Without the Agonizing Pain [5] teosta ja jyrkimmän laskun menetelmän yhteydessä gradientin voimakkaimman vähenemisen osalta on viitattu Robert A Adamsin Calculus: A Complete Course [6] teokseen

9 LUKU 1 Lineaarialgebrasta ja matriisiteoriasta Tässä kappaleessa esitetään iteraatiomenetelmissä käytävien asioiden kannalta oleellisimpia esitietoja todistuksineen tai viittauksineen todistuksiin 11 Matriisin ominaisarvo Lineaarikuvaukselle L : V V, missä V on sisätuloavaruus, jollekin luvulle λ ja vektorilla v V, v 0, on voimassa ominaisarvoyhtälö L(v) = λv, missä λ on kuvauksen L ominaisarvo ja v siihen liittyvä ominaisvektori Äärellisulotteista lineaarikuvausta L vastaa yksikäsitteisesti neliömatriisi A = A n n, jolloin määritellään ominaisarvo λ ja ominaisvektori v vastaavalla matriisiyhtälöllä Tämä saadaan muodostettua lauseeksi: Av = λv (11) Lause 11 Luku λ on matriisin A = A n n ominaisarvo täsmälleen silloin, kun se toteuttaa matriisin A karakteristisen yhtälön det(a λi) = 0 Todistus Yhtälö (11) toteutuu, kun (A λi)v = 0 Sellainen ratkaisu, missä v 0 löytyy vain, jos kuvaus A λi ei ole injektio Tämä on yhtäpitävää sen kanssa, että A λi ei ole kääntyvä, eli det(a λi) = 0 Matriisin A ominaisarvojen joukkoa sanotaan sen spektriksi ja käytetään sille merkintää σ(a) Matriisin A = A n n spektraalisäde on luku ρ(a) = max{ λ, λ σ(a)} Otettaessa huomioon myös mahdolliset kompleksiset ominaisarvot spektri sisältyy sen spektraalisäteiseen suljettuun kiekkoon eli σ(a) B(0, ρ(a)) Matriisin ominaisarvojen määrittämistä tarvitaan erityisesti matriisin normin määrityksessä 3

10 4 1 LINEAARIALGEBRASTA JA MATRIISITEORIASTA 12 Matriisijono Olkoon (A k ) k=0, missä A k = [a k i,j] on äärellisulotteinen matriisi, jono matriiseja Matriisijono (A k ) suppenee kohti matriisia A = [a i,j ], jos suppeneminen tapahtuu alkioittain eli jos a k i,j a i,j Tällöin voidaan käyttää merkintää lim A k = A, tai k A k A, kun k Lause 12 Suppeneville matriisijonoille A k A ja B k B, suppenevalle lukujonolle λ k λ ja kääntyvälle matriisille C pätevät seuraavat ominaisuudet: A k + B k A + B (1) A k B k AB (2) λ k A k λa (3) C 1 A k C C 1 AC (4) Todistus Olkoot matriisijonot A k = [a k i,j] ja B k = [b k i,j], sekä kääntyvä matriisi C = [c i,j ] ja matriisien A ja B alkiot a k i,j a i,j ja b k i,j b i,j Kohta (1): Koska matriisien A k ja B k yhteenlasku on alkioittain yhteenlaskua, niin ne suppenevat alkioittain, eli (A k + B k ) i,j = a k i,j + b k i,j a i,j + b i,j = (A + B) i,j Kohta (2): Matriisitulon A k B k alkiolle paikassa (i, j) on a k i,lb k l,j a i,l b l,j, l=1 sillä matriisijonojen A k ja B k alkioittaisen suppenevuuden perusteella a k i,l a i,l ja b k l,j b l,j eli myös matriisien tulo suppenee alkioittain Kohta (3): Koska matriisin A k ja skalaarin λ kertolaskussa kerrotaan matriisin A k alkioita skalaarilla λ, niin l=1 (λa k ) i,j = λa k i,j λa i,j = (λa) i,j, eli matriisin ja skalaarin tulossa alkioittainen suppeneminen säilyy Kohta(4) Seuraa suoraan kohdasta (2) Matriisijonon suppeneminen on erittäin olennaista iteratiivisen ratkaisun löytämiseksi 13 Ortogonaalisuudesta ja aliavaruuksista Äärellinen vektorijoukko V on ortogonaalinen, jos sen vektorit ovat pareittain kohtisuorassa toisiaan vastaan Olkoon vektorit s V ja v V ortogonaalisen vektorijoukon jäseniä Tällöin niiden sisätulo antaa nollan eli (s v) = s v = 0 Jos ortogonaalisen vektorijoukon V vektorit ovat yksikkövektoreita eli v = 1 kaikilla v V, niin vektorijoukko V on ortonormaali Jos vektorijoukko V muodostaa sisätuloavaruuden, niin sillä on ortonormaali kanta [3, s 31]

11 14 MATRIISIN ERÄITÄ OMINAISUUKSIA 5 Osajoukot S ja T ovat ortogonaaliset, jos (s t) = 0 kaikilla s S ja t T Osajoukon S V ortogonaalikomplementti on aliavaruus S = {s V (x s) = 0 kaikilla s S} Olkoon vektorijoukko {v 1,, v n } R m Joukkoa kaikista vektorijoukon lineaarikombinaatioista merkitään span {v 1,, v n } = { β j v i : β j R} j=1 Jos V on avaruuden R m aliavaruus eli V R m, niin on olemassa lineaarisesti riippumattomat kantavektorit {v 1,, v n } V siten, että V = span {v 1,, v n } Aliavaruuden V kantavektoreiden lukumäärälle eli dimensiolle käytetään merkintää dim(v ) Olkoon v = λ 1 v λ n v n, λ j R Samaistamalla tämä vektori sarakevektorin kanssa, saadaan [v 1, v 2,, v n ] T (v 1, v 2,, v n ) R n Tällöin matriisin A yhteys lineaarikuvaukseen L : V V saadaan samaistetun sarakevektorin v avulla Lv = Av Käyttämällä samaistettuja sarakevektoreita matriisi saadaan sarakehajotelmamuotoon A = [a 1,, a n ], jolloin sen sarakeavaruus ran(a) = span {a 1,, a n } ja sen ranki rank(a) = dim(ran(a)) Määritellään vielä ortogonaaliprojektio, joka on lineaarikuvaus P : V V, jolle P 2 = P on projektio kuvauksen P kuvajoukolta Im(P ) kuvauksen P ytimen eli aliavaruuden Ker(P ) suuntaan, jos Ker(P ) Im(P ) Ortogonaaliprojektiolle P pätee Im(P ) = U Ker(P ) = U, missä U on avaruuden V aliavaruus 14 Matriisin eräitä ominaisuuksia Käsitellään tutkielmassa käytettyjä matriisin ominaisuuksia, joita ei ole käsitelty johdannon alussa mainituilla kursseilla tai ovat muuten oleellisia tutkielman kannalta Määritelmä 13 Olkoon kompleksikertoiminen n n neliömatriisi A M n (C) Matriisi A on itseadjungoitu, jos se on itsensä konjugaattitranspoosi eli A = A T ja sen alkioille a i,j = a ji Käytetään tälle merkintää A Määritelmä 14 Olkoon kompleksikertoiminen n n neliömatriisi A M n (C) Matriisi X on matriisin A pseudoinverssi, jos pätee seuraavat ehdot: AXA = A XAX = X (AX) = AX (XA) = XA Tällöin sekä AX, että XA ovat itseadjungoituja Käytetään matriisin A pseudoinverssille merkintää A + (ks [1, s ])

12 6 1 LINEAARIALGEBRASTA JA MATRIISITEORIASTA Jos rank(a) = n, niin n m matriiseille A + = (A A) 1 A ja n n neliömatriiseille on A + = A 1 Lisäksi AA + ja A + A ovat ortogonaaliprojektioita sarakeavaruuksiin ran(a) ja ran(a ) Määritelmä 15 Neliömatriisit A ja B ovat similaareja toistensa suhteen, jos on olemassa kääntyvä matriisi P, jolle pätee A = P BP 1 (ks [2, s 9] ja [1, s 311]) Tutkitaan seuraavaksi similaarien matriisien ominaisarvoja Lause 16 Jos neliömatriisit A ja B ovat similaarit, niin niillä on sama karakteristinen polynomi ja samat ominaisarvot monikertoineen Todistus Jos A = P BP 1, niin det(a λi) = det(p BP 1 λp P 1 ) = det(p (B λ)p 1 ) = det(p ) det(b λ) det(p 1 ) = det(b λi) Määritelmä 17 Olkoon kompleksikertoiminen n n neliömatriisi A M(n, n, C) Matriisi A on unitaarinen, jos A 1 = A Neliömatriisi on unitaarinen täsmälleen silloin, kun sen rivivektorit ovat ortonormaalit ja kun sen sarakevektorit ovat ortonormaalit Määritelmä 18 Matriisi A on normaali, jos sillä on normaali ominaiskanta avaruudessa C n, eli jos matriisin ominaisvektorit muodostavat avaruuden C n kannan ja kantavektoreiden pituudet ovat ykkösiä Matriisi A on normaali silloin, kun A A = AA (ks [2, s 313] Mikäli matriisi A on normaali, niin on olemassa unitaarinen matriisi U niin, että A = UDU, missä D on diagonaalimatriisi (ks [3, s 36] ja [2, s 28 29]) Tällöin matriisit A ja D ovat similaarit ja siten niiden ominaisarvot ovat samat 15 Normi Määritelmä 19 Kuvaus : V R on normi kompleksisessa vektoriavaruudessa V, jos kaikilla x, y V ja w C pätee (1) x 0 ja x = 0 jos ja vain jos x = 0 (2) wx = w x (3) x + y x + y Kompleksisen vektoriavaruuden C n normeja ovat mm x 1 = x x n = x i x p = ( x p ) 1 p, kun p > 1 x = max{ x 1,, x n }

13 15 NORMI 7 Todistus Siihen, että edellä mainitut normit toteuttavat normin ehdot, tarvitaan Minkowskin epäyhtälöä ja Hölderin epäyhtälöä Minkowskin epäyhtälö on kaikilla x, y C n Hölderin epäyhtälö on missä yhtälön x + y p x p + y p (x, y) x p y p, 1 p + 1 p = 1 lukuja p ja p sanotaan konjugaattieksponenteiksi Näiden todistukset löytyvät Serren kirjasta [2, s 61 63] Olkoon vektorit x ja y C n ja w C Tarkastellaan aluksi normia 1 Selvästi jos x = 0, niin x 1 = 0 Edelleen jos jokin vektorin x komponentti x i 0, niin x 1 > 0 Lisäksi wx 1 = wx i = w x i = w x 1 Lopuksi x + y 1 = x i + y i x i + y i = x 1 + y 1 Seuraavaksi tarkastellaan normia p Selvästi jos x = 0, niin x p = 0 Edelleen jos jokin vektorin x alkio x i 0, niin x p > 0 Lisäksi Koska p > 1, niin Jos q = saadaan wx p = ( wx i p ) 1 p = ( w p x i p ) 1 p = ( w p ) 1 p ( x i p ) 1 p = w x p x i + y i p = x i + y i x i + y i p 1 ( x i + y i ) x i + y i p 1 = x i x i + y i p 1 + y i x i + y i p 1 p p 1, niin 1 p + 1 q = 1, 1 p = 1 1 q ja (p 1)q = p Tällöin Hölderin epäyhtälöllä x i x i + y i p 1 ( x i p ) 1 p ( x i + y i (p 1)q ) 1 q

14 8 1 LINEAARIALGEBRASTA JA MATRIISITEORIASTA ja Nyt ( y i x i + y i p 1 ( y i p ) 1 p ( x i + y i (p 1)q ) 1 q n x i + y i p ) 1 p = ( x i + y i p ) 1 1 q = x i + y i p ( n x i + y i p ) 1 q ( n x i p ) 1 p ( n x i + y i (p 1)q ) 1 q + ( n y i p ) 1 p ( n x i + y i (p 1)q ) 1 q ( n x i + y i (p 1)q ) 1 q = ( x i p ) 1 p + ( y i p ) 1 p Tarkastellaan vielä normia Selvästi jos x = 0, niin x = 0 Edelleen jos jokin vektorin x alkio on nollasta poikkeava eli x i 0, niin x > 0 Lisäksi ja lopulta wx = max { wx 1,, wx n } = w max { x 1,, x n } = w x x + y = max { x 1 + y 1,, x n + y n } max { x 1 + y 1,, x n + y n } max { x 1,, x n } + max { y 1,, y n } = x + y Siispä annetut normit toteuttavat normin ehdot Vektoriavaruuden normien ehdot eivät kuitenkaan riitä matriiseille Määritellään siis erikseen ehto matriisinormille Määritelmä 110 Kuvausta : M n (C) R kutsutaan matriisinormiksi, jos matriiseille A, B M n (C) pätee AB A B (12) Kirjoitelmassa oleellisin matriisinormi on operaattorinormi tai indusoitu matriisinormi Olkoon nyt vektoriavaruus C n varustettu normilla v Tämän normin indusoima matriisinormi määritellään asettamalla A = sup x 0 Ax v x v = max x v Ax v (13) kaikille A M n (C) Tarkistetaan, että indusoidulle matriisinormille pätee määritelmän 19 ehdot normille ja matriisinormin ehto (1) Olkoon vektori z C n, jolle z v = 1 ja A = Az v Tällöin kaikille vektoreille x C n, joille x v = 1, on Ax v Az v Jos A = 0, niin 0 = Ax v Az v kaikille x C n, jolloin A = 0 Jos A = Az v = 0, niin A = 0 (2) Olkoon c C n cax ca = sup v x 0 x v c Ax = sup v x 0 x v Ax = c sup v = c A x 0 x v

15 15 NORMI 9 (3) Olkoon x 0 Nyt (A + B)x v x v Tällöin = Ax + Bx v x v (4) Olkoon Bx = y 0 Tällöin Ax v + Bx v x v A + B A + B A + B ABx AB = sup v x 0 x v ABx = sup v Bx v x 0,Bx 0 Bx v x v Ay sup v Bx sup v y 0 y v x 0 x v = A B Toisaalta jokaiselle x, jolle Bx = 0 on ABx v ABx = 0 sup v, x v x 0,Bx 0 x v jolloin epäyhtälö pätee myös toiseen suuntaan Lause 111 Aikaisemmin annettujen normien indusoimat matriisinormit ovat: A 1 = a i,j (14) A p = ( i,j=1 a i,j p ) 1 p, kun p > 1 (15) i,j=1 A = max 1 i n a i,j (16) j=1 Todistus Tarkistetaan, että edellä mainitut matriisinormit täyttävät matriisinormin ehdon (110) Olkoon A, B M n (C) siten, että A = [a i,j ] ja B = [b i,j ] Nyt saadaan normille (14) AB 1 = (AB) i,j = a i,k b k,j = j=1 j=1 k=1 a i,k b k,j j=1 k=1 m=1 = A 1 B 1 j=1 k=1 j=1 k=1 m=1 a i,k b m,j = ( k=1 a i,k b m,j a i,k )( j=1 m=1 b m,j )

16 10 1 LINEAARIALGEBRASTA JA MATRIISITEORIASTA Normia (15) eli p-normia varten todistetaan aluksi, että p-normifunktio p on vähenevä muuttujan p R n suhteen Olkoon p ja q R n siten, että 0 < p < q ja vektori x C n Jos x = 0, niin x p = x q ja väite pätee Jos x 0, niin olkoon komponentti y k = x k Tällöin y x k 1 jokaiselle k = 1,, n ja y p q k yq k Siis y p 1, jolloin x p x q ja p-normifunktio on vähenevä Nyt saadaan Hölderin epäyhtälöstä p a i,k b k,j ( a i,k b k,j ) p (( a i,k p ) 1 p ( b k,j q ) 1 q ) p k=1 k=1 k=1 k=1 = (( a i,k p ) 1 p ( a i,k q p 1 ) p ) p = ( a i,k p )( b k,j q ) p 1, k=1 missä q = p, niin = 1, 1 = 1 1 ja (p 1)q = p p 1 p q p q Saadaan AB p = ( (AB) i,j p ) 1 p = ( a i,k b k,j p) 1 p (( (( = ( Normille (16) on taas j=1 k=1 k=1 a i,k p ) k=1 j=1 a i,k p )( k=1 j=1 k=1 k=1 ( b k,j q ) p 1 ) 1 p k=1 k=1 j=1 a i,k p ) 1 p ( k=1 j=1 = A p B q A p B p b k,j q ) p 1 ) 1 p b k,j q ) 1 q k=1 AB = max 1 i n max 1 i n j=1 j=1 k=1 max ( a i,j 1 i n j=1 = A B a k,j b i,k max 1 i n a i,j b i,j = max 1 i n k=1 j=1 k=1 a i,j b i,j j=1 b i,k ) ( max 1 i n a k,j b i,k j=1 Tällöin jokainen normi täyttää matriisinormin ehdon a i,j )( max 1 i n b i,k ) k=1 Eräs käyttökelpoinen matriisinormin (15) erikoistapaus on euklidisen normin 2 indusoima spektraalinormi (ks [2, s 65] ja [1, s 57]) A 2 = ρ(a A)

17 15 NORMI 11 Lause 112 Olkoon avaruuden C n normi ja kääntyvä neliömatriisi P M n (C) Siten N(x) := P x on normi avaruudessa C n Tällöin N(A) = P AP 1 Todistus Olkoon y = P x Nyt P Ax N(A) = sup x 0 P x = sup P AP 1 y y 0 y = P AP 1 Lause 113 (Householderin lause) Jokaiselle matriisille B M n (C) ja jokaiselle ɛ > 0 on olemassa avaruuden C n normi siten, että indusoitu normi B ρ(b) + ɛ (17) Todistus Oletetaan tunnetuksi (ks [2, s 29 30]), että jokaiselle B M n (C) on olemassa kääntyvä neliömatriisi P siten, että T = P BP 1 on yläkolmiomatriisi Indusoiduille normeille pätee ρ(a) A (ks [2, s 66]), sillä on olemassa ominaisvektori x, joka vastaa itseisarvoltaan suurinta ominaisarvoa eli matriisin A spektraalisädettä ρ(a) ja jolloin ρ(a) x = λx = Ax A x Nyt matriisit B ja T ovat similaarit ja lauseesta 16 johtuen matriiseilla B ja T on sama spektraalisäde, jolloin B 2 = T 2 Edelleen löydetään matriisin T similaari diagonaalimatriisi D = diag(t 1,, t n ) (ks [2, s 48]) Olkoon kääntyvä neliömatriisi Q M n (C) siten, että Q(y) = diag(1, y, y 2,, y n 1 ) Tällöin lim y Q(y)T Q(y) 1 = D Käyttämällä euklidisen normin 2 indusoimaa matriisinormia saadaan inf T = lim Q(y)T Q(y) 1 = D 2 = ρ(d D) = max t i = ρ(t ) 2 y Householderin lauseella on seuraava seuraus potenssijonojen suppenevuuteen Seuraus 114 Olkoon matriisi B M n (C) Matriisijono B k 0, kun k, jos ja vain jos ρ(b) < 1 Todistus Todistetaan aluksi, että matriisijonon B k suppenevuudesta seuraa se, että myös matriisijono B k v 0, kun k, kaikilla vektoreilla v C n Tämä seuraa suoraan epäyhtälöstä B k v B k v Jos nyt ρ(b) 1, niin on olemassa vektori u ja luku λ siten, että Tällöin myös B k u = λ k u ja Bu = λu B k u = λ k u λ k u = B k u,

18 12 1 LINEAARIALGEBRASTA JA MATRIISITEORIASTA eli kun matriisijono B k 0, kun k, pitäisi myös λ k 0, kun k, mutta se on oletuksen vastaista Siis ρ(b) < 1 Jos taas ρ(b) < 1, niin Householderin lauseen nojalla jokaisella ɛ > 0 on Tällöin matriisijono B k 0, kun k B k B k ρ(b) + ɛ

19 LUKU 2 Jacobin ja Gaussin ja Seidelin iteratiiviset menetelmät Lineaarinen systeemi on muotoa Ax = b Yleisesti hajottamalla matriisi A muotoon M N ja sillä oletuksella, että M on kääntyvä, saadaan vektoriksi x = M 1 (Nx + b) Nyt jono (x m ) m N saadaan induktiivisesti kun x m+1 = M 1 (Nx m + b) (21) Määritelmä 21 Matriisin suppenemisehto: Olettaen, että matriisit A ja M ovat kääntyviä, A = M N, sanotaan että iteratiivinen metodi (21) on suppeneva mikäli jokaiselle parille (x 0, b) C n C n on lim m xm = A 1 b Tästä päästään ehtoon iteratiivisen metodin suppenevuudelle: Lause 22 Iteratiivinen metodi (21) on suppeneva jos ja vain jos spektraalisäde ρ(m 1 N) < 1 Todistus Olkoon x 0 alkuvektori Nyt x 1 = M 1 (Nx 0 + b) = M 1 Nx 0 + M 1 b x 2 = M 1 (Nx 1 + b) = M 1 Nx 1 + M 1 b = M 1 N(M 1 Nx 0 + M 1 b) + M 1 b = (M 1 N) 2 x 0 + M 1 NM 1 b + M 1 b x 3 = M 1 (Nx 2 + b) = M 1 Nx 2 + M 1 b = M 1 N((M 1 N) 2 x 0 + M 1 NM 1 b + M 1 b) + M 1 b = (M 1 N) 3 x 0 + (M 1 N) 2 M 1 b + M 1 NM 1 b + M 1 b Näin ollen voidaan päätellä, että vektori m 1 x m+1 = (M 1 N) m x 0 + (M 1 N) k M 1 b k=0 Todistetaan tämä induktiolla Induktio-oletus on k 2 x k = (M 1 N) k 1 x 0 + (M 1 N) i M 1 b i=0 13

20 14 2 JACOBIN JA GAUSSIN JA SEIDELIN ITERATIIVISET MENETELMÄT ja induktioväite on k 1 x k+1 = (M 1 N) k x 0 + (M 1 N) i M 1 b i=0 Todistetaan induktioväite sijoittamalla yhtälöön (21) induktio-oletuksen vektori x k, niin saadaan x k+1 = M 1 (Nx k + b) k 2 = M 1 (N((M 1 N) k 1 x 0 + (M 1 N) i M 1 b) + b) i=0 k 2 = (M 1 N) k x 0 + M 1 (N (M 1 N) i M 1 b) + M 1 b i=0 k 1 = (M 1 N) k x 0 + (M 1 N) i M 1 b, i=0 eli induktioväite on tosi Jos ρ(m 1 N) < 1, on olemassa matriisinormi siten, että M 1 N < 1, jolloin potenssijono (M 1 N) m suppenee kohti nollamatriisia ja sarja k 1 i=0 (M 1 N) i suppenee geometrisenä sarjana kohti (I M 1 N) 1, jolloin k 1 (M 1 N) i M 1 b i=0 (M 1 N) k M 1 b = (I M 1 N) 1 M 1 b k=0 Merkitään y = (I M 1 N) 1 M 1 b, jolloin M 1 b = (I M 1 N)y = y M 1 Ny, b = My Ny = Ay ja y = A 1 b Tällöin x m 0 + A 1 b Jos taas ρ(m 1 N) < 1, niin seurauksen (114) nojalla lim m M 1 N = 0 Tällöin x m A 1 b = (M 1 N) m (x 0 A 1 b) 0 ja iteratiivinen metodi on suppeneva Jos metodi on suppeneva ja b = 0, niin lim m (M 1 N) m x 0 = 0 jokaiselle x 0 C n, jolloin myös lim m (M 1 N) m = 0 Seurauksen (114) nojalla ρ(m 1 N) < 1 Määritetään raja-arvo lim m x m iteroimalla Jacobin menetelmällä ja Gaussin ja Seidelin menetelmällä 21 Jacobin iterointimenetelmä Olkoon n n matriisi A jaettu sen diagonaaliosaan D, jonka alkiot ovat nollasta poikkeavia, yläkolmiomatriisiksi F ja alakolmiomatriisiksi E Valitaan nyt M = D ja N = E +F ja saadaan iteraatiomatriisiksi J := D 1 (E +F ) Tarkastellaan yhtälöä Ax = b, missä A = A n n yleisessä tapauksessa:

21 21 JACOBIN ITEROINTIMENETELMÄ 15 Jaetaan matriisi A diagonaaliosaan a 1,1 a 1,n a n,1 a n,n Ax = b x 1 x n = a 1,1 0 0 D = a n,n b 1 b n ja matriisiksi 0 a 1,2 a 1,3 a E F = 2,1 a n 1,n a n,1 a n,n 1 0 Nyt A = D E F ja yhtälö Ax = b saadaan muotoon x = D 1 (b + (E + F )x) Koska yhtälöiden vasemmalla ja oikealla puolella olevat termit ovat samat, niin huomataan, että x = D 1 (b + (E + F )x) jolloin yhtälö on induktiivisessa muodossa (x m ) m=1 = (D 1 (b + (E + F )x m )) m=1, x m+1 = D 1 (b + (E + F )x m ) Voidaan approksimoida vektorijonoa aina vektorijonon edellisen jäsenen avulla Jacobin menetelmä toimii siten, että kun tunnetaan vektori x m, niin saadaan ratkaistua vektorin x m+1 alkio x m+1 i ( ) x m+1 i = 1 i 1 b i a i,j x m j a i,j x m j (22) a i,i j=1 j=i+1 Tutkitaan Jacobin iterointimenetelmää suppenemisehdon avulla, kun b = 0 Nyt siis matriisi A on muotoa A = M N = D E F, missä matriisi D on matriisin A diagonaali ja matriisit E ja F ovat sen ylä- ja alakolmiomatriisit ja riittää tutkia matriisin D 1 (E +F ) spektraalisädettä Käyttämällä normin indusoimaa matriisinormia saadaan

22 16 2 JACOBIN JA GAUSSIN JA SEIDELIN ITERATIIVISET MENETELMÄT ρ(d 1 (E + F )) D 1 (E + F ) 1 0 a 12 a 1,n a 11 0 = a an 1,n a nn a n,1 a n,n 1 0 = max a i,j a i,i 1 i j j=1,j i Matriisi A on diagonaalisesti dominoiva kun sen alkioille pätee a i,i a i,j (23) j=1,j i kaikille i Vastaavasti on kyse aidosta dominoituvuudesta, kun epäyhtälö on aito Nyt siis aidosti diagonaalisesti dominoivalle matriisille max a i,j < 1 (24) 1 i j a i,i j=1,j i Esimerkiksi tapauksessa (24) jokaisen matriisin A rivin i diagonaalialkion a i,i itseisarvon täytyy olla suurempi kuin muiden sen rivin alkioiden itseisarvojen summa Ehto (23) takaa sen, milloin vähintään Jacobin menetelmä toimii Neliömatriisin A = A 3 3 tapauksessa matriisiyhtälö on muotoa Ax = b a 11 a 12 a 13 a 21 a 22 a 23 x 1 x 2 = b 1 b 2 a 31 a 32 a 33 x 3 b 3 ja vektorin x m+1 alkioista saadaan muodostettua yhtälöryhmä x m+1 1 = 1 a 11 (b 1 a 12 x m 2 a 13 x m 3 ) x m+1 2 = 1 a 22 (b 2 a 21 x m 1 a 13 x m 3 ) x m+1 3 = 1 a 33 (b 3 a 31 x m 1 a 32 x m 2 ) Esimerkki 23 Olkoon yhtälöryhmä 5x 1 2x 2 + 3x 3 = 1 3x 1 + 9x 2 + x 3 = 2 2x 1 x 2 7x 3 = 3 Tätä vastaa matriisiyhtälö x 1 x 2 = x 3

23 21 JACOBIN ITEROINTIMENETELMÄ 17 Jacobin menetelmällä saadaan iteraatiokierroksen m + 1 vektoriksi 1 ( xm 2 3x m 3 ) x m+1 1 = ( xm 1 x m 3 ) 1 (3 7 2xm 1 + x m 2 ) Alkuarvauksella x 0 = = 0 0 saadaan ensimmäisen iteraatiokierroksen jäl- 0 keen vektoriksi x 1 = x0 1 x 0 2 x 0 3 ( 1 + 2(0) 3(0)) (2 + 3(0) (0)) (3 2(0) + (0)) = Toisella iteraatiokierroksella saadaan 1 ( x1 2 3x 1 3) x 2 1 = ( x1 1 x 1 3) 1 (3 7 2x1 1 + x 1 2) = 1 ( 1 + 2( 2) 3( 3)) (2 + 3( 1) ( 3)) (3 2( 1) + ( 2)) = Taulukoimalla iteraatiokierroksia saadaan taulukko n x n 1 x n 2 x n Yhdeksännen kierroksen jälkeen x 9 x 8 < 0001 ja saadaan ratkaisun approksimaatioksi x =

24 18 2 JACOBIN JA GAUSSIN JA SEIDELIN ITERATIIVISET MENETELMÄT Esimerkki 24 Olkoon yhtälöryhmää 1 x x 2 + 3x 3 = 1 3x 1 + 9x 2 + x 3 = 2 2x 1 x 2 7x 3 = 3 vastaava matriisiyhtälö x 1 x 2 = Ehdon (24) perusteella huomataan, että matriisi ei ole diagonaalisesti dominoiva, koska 1 < = 5 Ehto ei kuitenkaan poissulje sitä mahdollisuutta, että 10 matriisi silti suppenisi, joten tutkitaan matriisiyhtälöä Jacobin menetelmällä alkuarvauksella x 0 = x0 1 x 0 2 x 0 3 x 3 = Jacobin menetelmällä iteroimalla saadaan taulukko n x n 1 x n 2 x n Huomataan, että iteraatiokierrosten määrän kasvaessa vektorijonon (x m ) arvot alkavat oskilloimaan voimakkaasti hajaantuen jolloin jono ei suppene 22 Gaussin ja Seidelin iterointimenetelmä Olkoon n n matriisi A jaettu sen diagonaaliosaan D, jonka alkiot ovat erisuuria kuin nolla, yläkolmiomatriisiksi F ja alakolmiomatriisiksi E Nyt yhtälö Ax = b saadaan samaan muotoon kuin Jacobin iteraatiomenetelmässä, eli Ax = (D E F )x = b Gaussin ja Seidelin iterointimenetelmällä käytetään aina tuoreinta laskettua arvoa kunkin vektorin laskemiseksi Kun tunnetaan vektori x m, niin saadaan laskettua vektori ( x m+1 i = 1 i 1 b i a i,i j=1 a i,j x m+1 j j=n j=i+1 a i,j x m j ) (25)

25 22 GAUSSIN JA SEIDELIN ITEROINTIMENETELMÄ 19 Esimerkki 25 Olkoon yhtälöryhmä 5x 1 2x 2 + 3x 3 = 1 3x 1 + 9x 2 + x 3 = 2 2x 1 x 2 7x 3 = 3 Tätä vastaa matriisiyhtälö Olkoon alkuarvaus x 0 = x 1 x 2 = x 3 3 x0 1 x 0 2 x 0 3 = 0 0 Gaussin ja Seidelin menetelmällä 0 x 1 1 = 1 5 ( 1 + 2x0 2 3x 0 3) = 0, 2 x 1 2 = 1 9 (2 + 3x1 1 x 0 3) 0, 1556 x 1 3 = 1 7 (3 2x1 1 + x 1 2) 0, 5079 Taulukoimalla iteraatiokierroksia saadaan taulukko n x n 1 x n 2 x n Kuuden iteraation jälkeen x m+1 x m < 0001, jolloin saadaan ratkaisuksi 0, 1861 x = 0, , 4226 Esimerkki 26 Olkoon yhtälöryhmää { 3x 1 + x 3 + ix 3 = i x 1 + ix 1 + x 3 = 3 vastaava matriisiyhtälö Alkuarvauksella [ ] [ ] i x1 = 1 i 1 x 2 x 0 = [ [ ] 0 x 0 1 = 0 ] [ ] 1 10

26 20 2 JACOBIN JA GAUSSIN JA SEIDELIN ITERATIIVISET MENETELMÄT saadaan Jacobin menetelmällä iteroimalla taulukko n x n 1 x n i i i i i i i i i i i i Ehdolla x 15 x 16 < 0001 saadaan ratkaisun approksimaatioksi x = [ i, i] Vastaava taulukko Gaussin ja Seidelin menetelmällä n x n 1 x n i i i i i i i i i i i i Ehdolla x 10 x 9 < 0001 saadaan ratkaisun approksimaatioksi x = [ i, i] Huomataan ensinnäkin, että jopa yksinkertaiset kompleksikertoimiset matriisit vaativat reaalikertoimisia enemmän iteraatioita ja että Jacobin menetelmä vaatii noin kaksinkertaisen määrän iteraatioita Gaussin ja Seidelin menetelmään nähden

27 LUKU 3 Konjugaattigradienttimenetelmä Konjugaattigradienttimenetelmä on eräs menetelmä, jolla voidaan ratkaista lineaarisia yhtälöryhmiä Tässä kappaleessa esitellään aluksi matriisin neliömuoto ja jyrkimmän laskun menetelmä, jolla approksimoidaan neliömuodon minimiä gradientin avulla lineaarisen yhtälön ratkaisemiseksi Sen jälkeen parannetaan menetelmää A- konjugaattien etsintäsuuntien avulla ja kehitetään sitä käyttökelpoiseksi konjugaattigradienttimenetelmäksi Matriisin A neliömuoto on 31 Matriisin neliömuoto f(x) = x Ax = a i,j x i x j (31) Mikäli matriisi A on itseadjungoitu, niin matriisi A ja sen kompleksikonjugaatin transpoosi A ovat samat, eli A = A Määritelmä 31 Olkoon matriisi A itseadjungoitu neliömatriisi Jos kaikille x C n, x 0 on (1) x Ax > 0, on matriisi A positiivisesti definiitti ja käytetään tälle merkintää A > 0 (2) x Ax 0, on matriisi A positiivisesti semidefiniitti ja käytetään tälle merkintää A 0 (3) x Ax < 0, on matriisi A negatiivisesti definiitti ja käytetään tälle merkintää A < 0 (4) x Ax 0, on matriisi A negatiivisesti semidefiniitti ja käytetään tälle merkintää A 0 Jos matriisi ei ole mikään edellisistä, niin se on indefiniitti matriisi Tutkitaan seuraavaksi itseadjungoidun matriisin A spektriä eli sen ominaisarvojen joukkoa Matriisin neliömuodosta (31) ja yhtälöstä (11) saadaan Nyt saadaan ominaisarvoille lauseke i,j x Ax = x λ i x = λ i x x λ i = x Ax x x (32) Huomataan, että jokaiselle λ i σ(a) pätee (1) λ i > 0 jokaiselle i jos ja vain jos A > 0 (2) λ i 0 jokaiselle i jos ja vain jos A 0 (3) λ i < 0 jokaiselle i jos ja vain jos A < 0 21

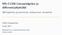
28 22 3 KONJUGAATTIGRADIENTTIMENETELMÄ (4) λ i 0 jokaiselle i jos ja vain jos A 0 (5) λ i on reaalinen [ ] 5 2 Esimerkki 32 Olkoon matriisi A =, Tämä on positiivisesti definiittinen, 2 3 sillä sen karakteristinen polynomi on det(a λi) = 5 λ λ = (5 λ)(3 λ) 4 = λ 2 8λ + 11 ja sen juuret eli matriisin A ominaisarvot ovat λ = 4 ± 5 > 0 Matriisin A neliömuodon f(x) = x Ax kuvaaja on kuvassa 31 Kuva 31 Positiivisesti definiitin matriisin A = A 2 2 neliömuoto Matriisiyhtälölle Ax = b sopiva neliömuoto on f(x) = 1 2 x Ax b x, (33) missä x C n, x 0 ja b ovat vektoreita Tutkitaan milloin neliömuoto f on pienimmillään käyttämällä siihen neliömuodon gradienttia

29 32 JYRKIMMÄN LASKUN MENETELMÄ 23 Määritelmä 33 Olkoon f matriisin neliömuoto Neliömuodon f gradientti on x 1 f(x) f(x) = (34) x n f(x) Olkoot vektorit x = [x 1,, x n ] ja b = [b 1,, b n ] ja matriisi A M(n, n, C) Nyt saadaan neliömuodosta f(x) = 1 2 x Ax b x = 1 x i (x j a i,j ) 2 j=1 b l x l l=1 gradientti 2x 1 a 11 + n i=2 x ia i1 + n j=2 x ja 1j b 1 2x 2 a 22 + n,i 2 f(x) = 1 x ia i2 + n j=1,j 2 x ja 2j b 2 2 2x k a kk + n,i k x ia ik + n j=1,j k x ja kj b k 2x n a nn + n 1 x ia in + n 1 j=1 x ja nj b n n x n n ia i1 = 1 x x n ia 1i b 1 ia i x ia 2i 2 b 2 n x n ia in x ia ni b n = 1 2 Ax A x b Huomataan, että jos matriisi A on itseadjungoitu niin gradientti tulee muotoon f(x) = Ax b ja jos A on positiivisesti definiittinen, niin neliömuoton (33) globaali minimi saadaan, kun f(x) = Ax b = 0 32 Jyrkimmän laskun menetelmä Jyrkimmän laskun menetelmässä minimoidaan neliömuodon gradienttia Oletetaan tunnetuksi (ks [6, s 714]), että gradientti vähenee voimakkaimmin negatiivisen gradientin suuntaan Tällöin pisteen x c ympäristössä neliömuodon gradientin väheneminen voimakkaimmin on negatiivisen gradientin f(x c ) = b Ax c suuntaan Käytetään erotukselle r c = b Ax c

30 24 3 KONJUGAATTIGRADIENTTIMENETELMÄ nimitystä pisteen x c residuaali Jyrkimmän laskun menetelmässä seuraava iteraatiopiste löytyy negatiivisen gradientin suuntaisen janan ja neliömuotoisen matriisin kuvaajan leikkauspisteestä x c+1 Selkeyden vuoksi merkitään iteraatiokierroksen lähtöpistettä indeksillä 0 ja loppupistettä indeksillä 1 Nyt siis loppupiste x 1 = x 0 + αx 0 jollekin α Tiedetään, että pistessä x 1 residuaali r 1 antaa seuraavan vähenemispisteen suunnan Pisteen x 1 selvittämistä varten tarvitsee vielä selvittää kerroin α Valitaan α siten, että residuaalien r 0 ja r 1 pistetulo on 0, jolloin 0 = r 1r 0 0 = (b Ax 1 ) r 0 0 = (b A(x 0 + αx 1 )) r 0 0 = (b Ax 0 ) r 0 α(ar 0 ) r 0 r 0r 0 = αr 0Ar 0 α = r 0r 0 r 0Ar 0, jos r 0 0 Tällöin on olemassa α R siten, että f(x c + αr c ) < f(x c ) Yleisesti asettamalla arvoksi α = rcr c /rcar c saadaan f(x c + αr c ) = 1(x 2 c + αr c ) A(x c + αr c ) (x c + αr c ) b = 1 2 (x cax c + αrcax c + α 2 rcar c + αx car c ) x cb αrcb = f(x c ) α2 rcar c αrcr c = f(x c ) 1 2 αr cr c f(x c + αr c ) = f(x c ) 1 (rcr c ) 2 2 rcar c Pitää vielä osoittaa, että jono f(x c ) suppenee eli f(x c + αr c ) f(x c ) Matriisi A on itseadjungoituna myös normaali, sillä se täyttää normaalin matriisin ehdon A A = AA Tällöin on olemassa unitaarinen matriisi U siten, että A = U DU, missä D on diagonaalimatriisi, joka on similaari matriisin A kanssa Merkitään vektoria z = Ur c Nyt jolloin sen jokaiselle komponentille on r car c = r cu DUr c = z c Dz, z i d i z i = z i z i d i = z i 2 d i Matriisin D diagonaalin alkiot koostuvat sen ominaisarvoista λ i, jotka ovat similaarisuuden perusteella samat kuin matriisin A ominaisarvot ja siten myös λ i > 0 Siis 1 (rcr c ) 2 > 0 2 rcar c

31 ja 33 A-KONJUGAATIT ETSINTÄSUUNNAT 25 f(x c ) 1 (rcr c ) 2 < f(x 2 rcar c ) c Tällöin jono f(x c ) on suppeneva ja kun residuaali r k on tarpeeksi lähellä nollaa niin saadaan ratkaisuksi x k Nyt saadaan algoritmiksi: Algoritmi 34 (Konjugaattigradienttimenetelmän esiversio) Olkoon x 0 alkuvektori, k iteraatioindeksi ja r residuaali Konjugaattimenetelmän esiversio yhtälön Ax = b ratkaisemiseksi on nyt k = 0 r = b Ax 0 ρ 0 = r 2 2 toista, kunnes r = 0 : k = k + 1 α k = rk 1 r k 1/rk 1 Ar k 1 x k = x k 1 + α k r k 1 r k = b Ax x = x k Menetelmänä tämä on heikohko, sillä kyseistä menetelmää käyttäen oskilloidaan ratkaisun ympärillä puolelta toiselle sen sijaan että lähestytään ratkaisua sulavasti 33 A-konjugaatit etsintäsuunnat Konjugaattigradienttimenetelmää varten täytyy parantaa jyrkimmän laskun menetelmää tutkimalla yleistä suuntavektoria p k Kuten aikaisemmin, osoitetaan, että yleisen suuntavektorin p k avulla päästään lähemmäksi ratkaisua, eli asettamalla α = α k = p k r k 1/p k Ap k: f(x k 1 + αp k ) < f(x k 1 ) f(x k 1 + αp k ) = 1 2 (x k 1 + αp k ) A(x k 1 + αp k ) (x k 1 + αp k ) b f(x k 1 + αp k ) = f(x k 1 ) 1 2 (p k r k 1) 2 p k Ap, k kun p k r k 1 0 eli kun p k ja r k 1 eivät ole keskenään ortogonaaliset Näin on siis millä tahansa edellä mainitun ehdon täyttävällä suuntavektorilla eli etsintäsuunnalla p k Jos etsintäsuunnat span{p 1, p 2,, p k } ovat lineaarisesti riippumattomia ja x k antaa minimin min f(x), (35) x x 0 +span {p 1,p 2,,p k } missä k = 1, 2,, niin iteraatiolla n saadaan ratkaisu x n yhtälölle Ax n = b Määritelmä 35 Olkoot vektorit {p 1, p 2,, p k } lineaarisesti riippumattomia Niitä sanotaan A-konjugaateiksi, jos pätee p i Ap j = 0 kaikille i j

32 26 3 KONJUGAATTIGRADIENTTIMENETELMÄ Seuraavaksi määritetään etsintäsuunta p n Olkoot P k 1 = [p 1,, p k 1 ], y R k 1 ja α R siten, että x k = x 0 + P k 1 y + αp k, jolloin f(x k ) = f(x 0 + P k 1 y + αp k ) = f(x 0 + P k 1 y) + αy P k 1Ap k + α2 2 p kap k αp kr 0 Jos p k kuuluu vektoreiden {Ap 1, Ap 2,, Ap k 1 } virittämään aliavaruuden ortogonaalikomplementtiin eli p k (span {Ap 1, Ap 2,, Ap k 1 }), niin αy P k 1 Ap k = 0 Tällöin päästään tilanteeseen, jossa minimoidaan lauseketta (35) vektorin y ja skalaarin α yli Tällöin (35) tulee muotoon min f(x) = min f(x 0 + P k 1 y + αp k ) x x 0 +span{p 1,p 2,,p k } y,α = min y,α (f(x 0 + P k 1 y) + αy P k 1Ap k + α2 2 p kap k αp kr 0 ) = min y f(x 0 + P k 1 y) + min( α2 α 2 p kap k αp kr 0 ) Jos y k 1 = min y f(x 0 + P k 1 y), niin min α ( α2 2 p k Ap k αp k r 0) = α k = p k r 0 p k Ap k antaa ratkaisun yhtälölle α 2 2 p kap k αp kr 0 = (p k r 0) 2 2p k Ap k (p k r 0) 2 p k Ap k sillä se A-konjugaattisuuden nojalla p kr k 1 = p k(b Ax k 1 ) = p k(b A(x 0 + P k 1 y k 1 )) = p kr 0 Tästä seuraa x k = x k 1 + α k p k Tämä ei kuitenkaan anna kovinkaan tarkkaa määrittelyä sille, miten vektori p k saadaan määritettyä tai edes sitä onko se olemassa Lemma 36 Jos on olemassa residuaali r k 1 0, niin on olemassa jokin etsintäsuunta p k span {Ap 1, Ap 2,, Ap k 1 } siten, että p k r k 1 = 0 Todistus Jos k = 1, niin asetetaan p 1 = r 0 Olkoon r k 1 0 Jos k > 1, niin A 1 b / x 0 + span {p 1,, p k 1 } b / Ax 0 + span {Ap 1,, Ap k 1 } r 0 / span {Ap 1,, Ap k 1 }

33 34 KONJUGAATTIGRADIENTTIMENETELMÄ 27 Nyt on siis olemassa p span {Ap 1,, Ap k 1 } siten, että p r 0 0 Koska x k1 x 0 + span {p 1,, p k 1 }, niin r k 1 r 0 + span {Ap 1,, Ap k 1 } Tällöin p r k 1 = p r 0 0 On siis todistettu, että vektorisuunta p k todellakin on olemassa Valitaan vektori p k siten, että se on mahdollisimman lähellä residuaalia r k 1, jolloin p k = min( p r k 1 2 ) kaikille vektoreille p span{ap 1,, Ap k 1 } Lemma 37 Jos k 2, niin vektorille p k on p k = r k 1 AP k 1 z k 1, missä P k 1 = [p 1,, p k ] ja z k 1 antavat ratkaisun pienimmän neliösumman ongelmalle min z R k 1 r k 1 AP k 1 z 2 Todistus Olkoon p oletuksissa mainitun pienimmän neliösumman ongelman ratkaisu, jolloin p = r k 1 AP k 1 z k 1 Tästä ja siitä tiedosta, että p kuuluu vektorijoukon {Ap 1,, Ap k } lineaarikombinaatioiden ortogonaalikomplementtiin seuraa se, että vektorin p ja vektorin AP k 1 sisätulo on nolla eli p AP k 1 = 0 Lisäksi pseudoinverssin ominaisuuksien perusteella p = [I (AP k 1 )(AP k 1 ) + ]r k 1 antaa vektorin r k 1 ortogonaaliprojektion sarakeavaruuteen ran(apk 1 ), jolloin se on lähin sarakeavaruuden ran(ap k 1 ) vektori vektorille r k 1 Siis p = p k 34 Konjugaattigradienttimenetelmä Määritelmä 38 Olkoot vektori v C n ja matriisi A M n (C) Muotoa κ k (v, A) = span{v, Av, A 2 v,, A k 1 v} olevia aliavaruuksia sanotaan Krylovin aliavaruuksiksi Lause 39 Konjugaattigradienttimenetelmälle on k 2 iteraation jälkeen r k = r k 1 α k Ap k (36) P k r k = 0, (37) span {p 1,, p k } = span {r 0,, r k 1 } = κ k (v, A), (38) p k span {p k 1, r k 1 }, (39) joissa residuaalit r 0,, r k 1 ovat keskenään ortogonaalisia Todistus (36): Algoritmista 34 saadaan vektori x k = x k 1 + α k r k 1 Ax k = Ax k 1 + Aα k r k 1

34 28 3 KONJUGAATTIGRADIENTTIMENETELMÄ Sovelletaan tähän residuaalin määritelmää r k = b Ax k Ax k = b r k, niin saadaan b r k = b r k 1 + Aα k r k 1 r k = r k 1 α k Ar k 1 (37): Koska x k = x 0 + P k y k missä y k antaa minimin lausekkeelle f(x 0 + P k y) Koska f(x 0 + P k y) = f(x 0 ) (P k AP k )y y P k (b Ax 0 ), niin y k on ratkaisu lineaariselle yhtälölle (P k AP k)y = P k (b Ax 0), jolloin 0 = P k (b Ax 0 ) (P k AP k )y = P k (b A(x 0 + P k y k )) = P k r k (38): Kohdasta (36) huomataan, että jokainen vektori r k on lineaarikombinaatio vektoreista r k 1 ja Ap k, jolloin vektorijoukko {Ap 1,, Ap k 1 } on aliavaruuden span {r 0,, r k 1 } aliavaruus eli Lemmasta 37 saadaan jolloin {Ap 1,, Ap k 1 } span {r 0,, r k 1 } p k = r k 1 [Ap 1,, Ap k 1 ]z k 1 span {r 0,, r k 1 }, [p 1,, p k ] = [r 0,, r k 1 ]T, missä T on yläkolmiomatriisi ja epäsingulaarinen, sillä etsintäsuunnat ovat lineaarisesti riippumattomia Tällöin etsintäsuuntien ja residuaalien lineaarikombinaatiot ovat samat eli span {p 1,, p k } = span {r 0,, r k 1 } Yhteys Krylovin aliavaruuksiin on nähtävissä siitä, että kohdan (36) mukaan residuaalit koostuvat aina edellisistä residuaaleista ja koska uusin residuaali on aina ortogonaalinen edellisiin nähden, sillä se kuuluu aliavaruuteen, jonka jäseninä on edellinen residuaali r k 1 ja Ap k Tällöin se kuuluu myös aliavaruuteen, jonka virittäviä vektoreita ovat {r 0,, r k 1 } Siis r k span {r k 1, Ap k } span {r k 1, Ar 0,, Ar k 1 } = span {r 0, Ar 0, A 2 r 0,, A k 1 r 0 } = κ k (v, A) (39): Jos k = 2, niin etsintäsuunta p 2 span {r 0, r 1 } = span {p 1, r 1 } koska p 1 = r 0, jolloin p 2 on lineaarikombinaatio etsintäsuunnasta p 1 ja residuaalista r 1

35 34 KONJUGAATTIGRADIENTTIMENETELMÄ 29 Jos k > 2, niin tutkitaan lemman 37 vektoria z k 1 lohkoina siten, että [ w z k 1 =, µ] missä w koostuu vektorin z k 1 k 2 ensimmäisestä komponentista ja µ on vektorin z k 1 viimeinen alkio Koska missä vektori r k 1 = r k 2 α k 1 Ap k 1, niin p k = r k 1 Ap k 1 z k 1 = r k 1 Ap k 2 w µap k 1 = (1 + µ α k 1 )r k 1 + s k 1, s k 1 = µ α k 1 r k 2 AP k 2 w ja vektori s k 1 kuuluu vektoreiden r k 2 ja AP k 2 w virittämään aliavaruuteen, joka taas on vektoreiden r k 2, Ap 1,, Ap k 2 virittämän aliavaruuden aliavaruus, joka taas vastaavasti on residuaalien r 0,, r k 2 virittämän aliavaruuden aliavaruus Edellä mainittujen residuaalien keskenäisen ortogonaalisuuden nojalla vektori s k 1 on ortogonaalinen vektoriin r k 1 nähden, jolloin minimoitavaksi tulee vektorin p k normin neliö, joka on lemman 37 nojalla p k 2 2 = (1 + µ α k 1 ) 2 r k s k Koska vektori z k 2 on lausekkeen r k 2 AP k 2 z 2 minimi ja p k 1 on riippuvainen vektorista z k 2, niin vektori s k 1 on vektorin p k 1 monikerta ja sen seurauksena p k on residuaalin r k 1 ja vektorin p k 1 lineaarikombinaatio, jolloin p k span {r k 1, p k 1 } Nyt siis p k = r k 1 + β k p k 1 jollekin skalaarille β k, joten p k = r k 1 + β k p k 1 p k 1Ap k = p k 1Ar k 1 + p k 1Aβ k p k 1 Koska p k 1 Ap k = 0, niin saadaan β = p k 1 Ar k 1 p k 1 Ap k 1 Nyt konjugaattigradienttimenetelmä saadaan seuraavaan muotoon Algoritmi 310 (Konjugaattigradienttimenetelmä) Olkoon matriisi A R n n itseadjungoitu ja positiivisesti definiittinen, vektori b R ja x 0 alkuvektori Tällöin seuraava algoritmi antaa ratkaisun x R yhtälölle Ax = b

36 30 3 KONJUGAATTIGRADIENTTIMENETELMÄ k = 0 r = b Ax 0 toista, kunnes r k = 0 : k = k + 1 jos k = 1, niin p = r muuten β k = p k 1 Ar k 1/p k 1 Ap k 1 p k = r k 1 + β k p k 1 α k = p k r k 1/p k Ap k x k = x k 1 + α k p k r k = b Ax k x = x k on ratkaisu Säädetään vielä algoritmia laskennallisesti kevyemmäksi käyttämällä edellisen todistuksen tietoa residuaalin rekursiivisuudesta, eli r k = r k 1 αap k ja otetaan huomioon se, että iteratiivinen menetelmä ei kuitenkaan aina päädy eksaktiin ratkaisuun vaan se saattaa lähestyä ratkaisua äärettömästi, jolloin ratkaisua voidaan approksimoida residuaalin euklidisen normin r avulla asettamalla ρ = r r = r 2 2 ja ottamalla ehdoksi ρ < ɛ b 2 Toisaalta laskennallisesti ajateltuna voidaan rajoittaa iteraatioiden määrää jollain vakiolla k max, jolloin toiseksi ehdoksi tulee k < k max Nyt konjugaattigradienttimenetelmä saadaan muotoon: Algoritmi 311 (Konjugaattigradienttimenetelmä) Olkoon matriisi A R n n itseadjungoitu ja positiivisesti definiittinen, vektori b R ja x 0 alkuvektori Tällöin seuraava algoritmi antaa ratkaisun approksimaation x R yhtälölle Ax = b k = 0 r = b Ax 0 ρ 0 = r 2 2 toista, kunnes ρ < ɛ b 2 tai k k max : k = k + 1 jos k = 1, niin p = r muuten β k = ρ k 1 /ρ k 2 p = r + β k p α k = ρ k 1 /p Ap x k = x k 1 + α k p r k = r k 1 α k Ap ρ k = r 2 2 x = x k Esimerkki 312 Tutkitaan esimerkin 13 matriisyhtälöryhmää 5x 1 2x 2 + 3x 3 = 1 3x 1 + 9x 2 + x 3 = 2 2x 1 x 2 7x 3 = 3

37 vastaavaa matriisiyhtälöä 34 KONJUGAATTIGRADIENTTIMENETELMÄ 31 Ax = b x 1 x 2 = x 3 Koska matriisin A likiarvoiset ominaisarvot ovat , ja 26503, niin A on positiivisesti definiitti Lisäksi matriisi A on itseadjungoitu, joten voidaan käyttää konjugaattigradienttimenetelmää yhtälön ratkaisemiseksi Ratkaistaan yhtälö käyttämällä alkuarvausta x 0 = = 0 0 ja asettamalla 0 ɛ b 2 = 0001 Ensimmäisellä iteraatiokierroksella menetelmää käyttämällä saadaan x0 1 x 0 2 x 0 3 r = b Ax 0 = ρ 0 = r 2 2 = = 14 k = 1 p = r = α 1 = ρ 0 /p Ap = 14/ [ ] = 14/ x 1 = x 0 + α 1 p = r 1 = r 0 α 1 Ap = ρ 1 = r Koska > 0001, niin menetelmässä siirrytään toiseen iteraatioon

38 32 3 KONJUGAATTIGRADIENTTIMENETELMÄ k = k + 1 = 2 β 2 = ρ 1 /ρ / p = r + β 2 p = α 2 = ρ 1 /p Ap = 18864/ [ ] x 2 = x 1 + α 2 p = r 2 = r 1 α 2 Ap = ρ 2 = r Koska > 0001, niin menetelmässä siirrytään kolmanteen iteraatioon Kolmannen iteraation jälkeen ρ < ja ratkaisuapproksimaatioksi saadaan x 3 = Esimerkki 313 Tarkastellaan esimerkin 26 tapausta eli kompleksikertoimista matriisiyhtälöä [ ] [ ] [ ] i x1 1 = 1 i 1 x 2 10 Alkuarvauksella [ 0 x 0 = 0] saadaan konjugaattigradienttimenetelmällä kahden iteraation jälkeen ratkaisuksi x = [ i, i] Koska 2 2 neliömatriiseja pystyy kuvaamaan matriisin neliömuodon kuvaajalla, niin vertaillaan Jacobin menetelmää, Gaussin ja Seidelin menetelmää ja konjugaattigradienttimenetelmää myös graafisesti Esimerkki 314 Olkoon yhtälöryhmää vastaava matriisiyhtälö [ ] [ ] [ 5 2 x1 0 = 2 3 x 2 0]

39 34 KONJUGAATTIGRADIENTTIMENETELMÄ 33 [ ] 5 2 Koska matriisi on positiivisesti definiitti ominaisarvoilla 4 ± 5, niin voidaan 2 3 käyttää konjugaattigradienttimenetelmää Alkuarvauksella [ 2 x 0 = 2] saadaan Jacobin iterointimenetelmällä yhdeksän iteraation jälkeen ehdolla x j x j 1 < 001 approksimaatioksi x = [ 00040, 00067], Gaussin ja Seidelin menetelmällä kuuden iteraation jälkeen ehdolla x j x j 1 < 001 approksimaatioksi x = [ 00011, 00007] ja konjugaattigradienttimenetelmällä kahden iteraation jälkeen ehdolla ɛ b 2 < 001 approksimaatioksi x = [ 00000, 00000] Graafinen vertailu matriisin neliömuodon kuvaajalla eri menetelmien lähestymisestä yhtälön ratkaisua kohden matriisin neliömuodon yhtälöä käyttäen on kuvassa 32 Esimerkkejä 26, 34 ja 314 vertailemalla näyttäisi olevan niin, että pienten matriisien tapauksessa konjugaattigradienttimenetelmä on laskennallisesti huomattavasti tehokkaampi kuin Jacobin iteraatiomenetelmä ja Gaussin ja Seidelin iterointimenetelmä

40 34 3 KONJUGAATTIGRADIENTTIMENETELMÄ Kuva 32 Eri iteraatiomenetelmien graafinen vertailu

41 Kirjallisuutta [1] Gene H Golub ja Charles F Van Loan: Matrix computations third edition, The John Hopkins University Press, 1996 [2] Denis Serre: Matrices: Theory and Applications Springer-Verlag New York, Inc,2002 [3] Mikko Saarimäki: Matriisiteoria kurssimoniste, kevät 2013 [4] Mikko Saarimäki: Matriisiseminaari kurssimuistiinpanot, kevät 2013 [5] Jonathan R Shewchuk: An Introduction to the Conjugate Gradient Method Without the Agonizing Pain School of Computer Science Carnegie Mellon University Pittsburgh, 1994 [6] Robert A Adams: Calculus: A Complete Course seventh edition, Pearson: Adisson Wesley,