Taloudelliset vahingot rakennuspaloissa. Kati Tillander, Towe Lindblom & Olavi Keski-Rahkonen ESPOO 2002 VTT TIEDOTTEITA Rakennuksen vahinko 1,0
|
|
|
- Eeva Rantanen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 ESPOO 2002 VTT TIEDOTTEITA ,0 Rakennuksen vahinko 1,0 Irtaimistovahinko 0,8 0,8 Kertymä 0,6 0,4 Kertymä 0,6 0,4 0,2 0,2 0,0 0,0 1E+0 1E+2 1E+4 1E+6 1E+0 1E+2 1E+4 1E+6 Vahinko [mk] Vahinko [mk] 1,0 Keskeytysvahinko 0,8 Kertymä 0,6 0,4 0,2 0,0 1E+0 1E+2 1E+4 1E+6 1E+8 Vahinko [mk] Kati Tillander, Towe Lindblom & Olavi Keski-Rahkonen Taloudelliset vahingot rakennuspaloissa
2 VTT TIEDOTTEITA RESEARCH NOTES 2159 Taloudelliset vahingot rakennuspaloissa Kati Tillander, Towe Lindblom & Olavi Keski-Rahkonen VTT Rakennus- ja yhdyskuntatekniikka
3 ISBN (nid.) ISSN (nid.) ISBN (URL: ISSN (URL: Copyright VTT 2002 JULKAISIJA UTGIVARE PUBLISHER VTT, Vuorimiehentie 5, PL 2000, VTT puh. vaihde (09) 4561, faksi (09) VTT, Bergsmansvägen 5, PB 2000, VTT tel. växel (09) 4561, fax (09) VTT Technical Research Centre of Finland, Vuorimiehentie 5, P.O.Box 2000, FIN VTT, Finland phone internat , fax VTT Rakennus- ja yhdyskuntatekniikka, Kivimiehentie 4, PL 1803, VTT puh. vaihde (09) 4561, faksi (09) VTT Bygg och transport, Stenkarlsvägen 4, PB 1803, VTT tel. växel (09) 4561, fax (09) VTT Building and Transport, Kivimiehentie 4, P.O.Box 1803, FIN VTT, Finland phone internat , fax Otamedia Oy, Espoo 2002
4 Tillander, Kati, Lindblom, Towe & Keski-Rahkonen, Olavi. Taloudelliset vahingot rakennuspaloissa [Economical losses in structural fires]. Espoo Valtion teknillinen tutkimuskeskus, VTT Tiedotteita Research Notes s. + liitt. 5 s. Avainsanat fire safety, residential buildings, statistics, economic evaluation, economic analysis, losses, damage, distribution, fire risk, value Tiivistelmä Matemaattisessa analyysissä tulipalon riskin ajatellaan muodostuvan kahdesta pääkomponentista, joista ensimmäinen on tulipalon syttymän todennäköisyys ja toinen sen aiheuttamien vahinkojen todennäköinen laajuus. Tässä tutkimuksessa on paneuduttu riskin jälkimmäiseen komponenttiin, joka tähän mennessä on ollut yleisesti melko tuntematon. Seurausten laajuuden mittana käytettiin palon aiheuttamia taloudellisia vahinkoja, ja käytettävissä olevaa aineistoa tutkittiin ensin koko joukkona ja edelleen jaotellen pienempiin joukkoihin niin pitkälle kuin tilastollisen tarkkuuden puitteissa oli käytännöllistä etsien selviä lainalaisuuksia. Jo alkuvaiheessa tehty tärkeä havainto oli, että jakaumien ääripäät poikkeavat merkittävästi perusjoukon massasta, mutta tämän tutkimuksen painopiste oli vahinkojakauman keskivaiheen ominaisuuksien ja erityispiirteiden määritys. Tilastoaineisto osoitti, että ääripäitä lukuun ottamatta, taloudellisen vahingon jakauma on likimain logaritmisesti normaali. Kun oletetaan palovahingon noudattavan logaritmista normaalijakaumaa, voidaan Ramachandranin aiemmin esittämän mallin avulla määrittää vahingon odotusarvo yksittäiselle rakennukselle, jonka uhatun omaisuuden arvo on tunnettu. Suomen tilastoaineiston ja teoreettisen mallin yhteensopivuus oli heikko, johon osaltaan vaikuttivat mallin oletukset ja rajoitukset. Siten mallin antamat numeroarvoiset tulokset ovat vain suuntaa antavia. Kahden logaritmisen normaalijakauman summan soveltaminen teoriaan ei parantanut sen toimivuutta. Parempaan sovitteeseen päästiin vapauttamalla jakauman parametrit. Tämä on luultavasti toimivampi tapa määrittää parametrien arvot, sillä koko rakennuskannan todellisen uhatun omaisuuden jakauma ei ole tunnettu. Toiminnallisessa suunnittelussa kerrosala on uhatun omaisuuden arvoa käytännöllisempi mitta. Havaintoaineiston pikainen tarkastelu osoitti rakennuksen uhatun omaisuuden ja kerrosalan välisen yhteyden. Siten rakennuksessa oleva uhattu omaisuus voidaan lausua joko rahana tai kerrosneliöinä. Jaettaessa havainnot käyttötapaluokkaryhmiin: asuinrakennukset, teollisuus- ja varastorakennukset sekä kaikki muut rakennukset edellä mainittuja lukuun ottamatta nousi esiin selvä nyppylä keskimääräisessä vahingossa, jonka huippu asettui asuinrakennuksissa n. 600 m 2 :n kohdalle. Nyppylä selittyi lähemmällä tarkastelulla, joka osoitti että 3
5 kerrosalajakauman alkupäähän sijoittuvat erilliset pientalot käsittävät yleisesti ottaen vain yhden palo-osaston ja niissä vahinko kasvaa kerrosalan funktiona selvästi. Kerrostalot puolestaan sijoittuvat kerrosalajakauman loppupäähän ja niissä vahinko usein rajoittuu vain yhteen asuntoon ja siten koko rakennuksen kerrosalan ja vahingon välillä ei ole samankaltaista riippuvuutta. Nyppylä sijoittuu kohtaan, jossa rakennuskannassa vallitsevat rakennukset vaihtuvat pienistä erillisistä pientaloista kerrostaloiksi, jolloin koko rakennuksen kerrosalan funktiona määritetty vahinko vakiintuu hieman huippuarvoa alemmalle tasolle. Tämä osoittaa, että koko rakennuksen kerrosala ei ole oleellinen mitta suurten kerrostalojen riskin määrittelyssä. Parempi suure olisi syttymisosaston koko, jonka vuoksi se tulisi kirjata palotilastoihin nykyistä tarkemmin. Vahinkojen aikajakaumissa ei ollut kuukausittaista vaihtelua. Erityisesti asuinrakennuksissa sekä ryhmässä kaikki muut rakennukset, joka kattoi kaikki käyttötapaluokat asuin-, teollisuus- ja varastorakennuksia lukuun ottamatta, vahingot olivat keskimääräistä suuremmat öiseen aikaan. Palokuolemien osalta päivitettiin aiempia tutkimustuloksia uudella tilastoaineistolla. Aiemmasta poiketen käytettävissä oli myös tieto taloudellisesta vahingosta, jotka osoittautuivat olevan yleensä ottaen suuremmat kuolemaan johtaneissa tulipaloissa kaikkiin rakennuspaloihin verrattuna. Uhatun omaisuuden jakaumassa ei kuitenkaan ollut vastaavaa eroa, vaan tulokset osoittivat, että usein tulipalo on ollut jo hyvin pitkälle kehittynyt palokunnan saapuessa sekä vahingot ovat päässeet leviämään laajemmalle verrattuna keskimääräiseen rakennuspaloon. Tämän tutkimuksen aineiston perusteella palokunnan toimintavalmiusajalla tai asuinrakennustyypillä ei havaittu olevan vaikutusta palokuolemien syntyyn. 4
6 Tillander, Kati, Lindblom, Towe & Keski-Rahkonen, Olavi. Taloudelliset vahingot rakennuspaloissa [Economical losses in structural fires]. Espoo Valtion teknillinen tutkimuskeskus, VTT Tiedotteita Research Notes p. + app. 5 p. Keywords fire safety, residential buildings, statistics, economic evaluation, economic analysis, losses, damage, distribution, fire risk, value Abstract Generally the risk can be expressed as a product of two components: ignition frequency and probable consequences. Until now detailed information on the latter component, economical losses, has not been publicly available. Top down analysis method was adopted and the data was at first analyzed as one group. Then it was divided into smaller groups as far as the statistical accuracy allowed. It is known for long that the distributions of the fire loss are skewed. Here it is shown that it can be described fairly well by lognormal distribution. It turned out that at tails of the distributions differed considerably from lognormal but here the focus was the characteristic features of the fire loss in the middle part of the distribution. The behavior and dependencies of the fire loss were examined as well as different statistical methods were applied to the data. When the assumption of the lognormality is considered correct, the expected value of individual building can be determined using a theory presented by Ramachandran. When the parameters for the model were determined from the data set, the compatibility of the theoretical curve and the observations was fair but still weak for quantitative work. The sum of two lognormal distributions added to the theory did not improve the agreement. By releasing the connection of the parameters to the data set a good fit was obtained. This is presumably a better way to determine the parameters because the actual distribution of the value at risk in the total building stock is not known. The data revealed the dependency between the value at risk and the floor area. Thus the value at risk can be expressed as monetary value or floor area. The further analysis brought out the peculiar behavior of the loss as a function of the floor area. A peak of loss appeared especially in residential buildings around 600 m 2. As the residential buildings were divided into apartment, row and detached houses it turned out that the loss grows rapidly as function of the floor area in detached houses while in row and apartment houses the growth is much slower. Examination of the building stock revealed that the peak appears when the majority in the building stock changes at 600 m 2 from detached houses to apartment houses and the loss drops little lower from the peak value of detached houses to the constant level of the apartment houses. It indicates that a total floor area of the building is not a proper descriptor of the value at risk in large 5
7 apartment houses. As a suggestion for improvement of fire statistics data on fire compartment floor area should be recorded carefully. Monthly variation was not observed in the time distributions of the fire loss. Especially in residential buildings and in group of all other buildings except residential, industrial and warehouses the loss was above average during the night-time. The comparison of all building fires and fires where at least one person has died showed that the economical losses are in general larger in fatal fires. No differences were found in values at risk or the fire department response times. However it became apparent that the fatal fires have usually spread wider before the fire department reached the scene than an average building fire. 6
8 Alkusanat Kiitokset Teknilliselle korkeakoululle tutkijankoulutusstipendin myöntämisestä Kati Tillanderille. Stipendi on mahdollistanut hänen osuutensa tässä tutkimuksessa. Lisäksi kiitokset Suomen Paloinsinööriyhdistykselle sekä Suomen Riskienhallintayhdistykselle, jotka ovat rahoittaneet Towe Lindblomin työn osuuden. Kiitokset myös sisäasiainministeriön pelastusosastolle PRONTO-tietokannan sekä Suomen Vakuutusyhtiöiden keskusliitolle suurvahinkotietojen luovuttamisesta käyttöömme. 7
9 Sisällysluettelo Tiivistelmä...3 Abstract...5 Alkusanat...7 Symboliluettelo Johdanto Taloudellinen vahinko rakennuspaloissa Matemaattinen jakauma Vahingon odotusarvo Omavastuinen vakuutus Riippuvuus kerrosalasta Rakennuspalot PRONTO-tietokannasta ja rakennuskanta Tilastokeskuksesta Rakennuspalot PRONTOsta Tilastokeskuksen rakennuskanta Lukumäärän tiheysjakauma Teoreettinen sovite Taloudellinen vahinko Helsingin ja koko maan rakennuspaloissa Vahinkojen kertymäfunktiot Vahinkojen tiheysfunktiot Koko maan havaintojen jako luokkiin uhatun omaisuuden perusteella Sovitteiden hyvyys Yleistä Kaikki rakennuspalot Luokkajako uhatun omaisuuden perusteella Yhteenveto Kokonaisvahingon odotusarvo uhatun omaisuuden funktiona Helsinki Koko maa Yhteenveto Vahingon suuruuden todennäköisyys Helsinki Koko maa Yhteenveto Uhatun omaisuuden riippuvuus kerrosalasta
10 4.7.1 Helsinki ja koko maa Kokonaisvahingon odotusarvon riippuvuus kerrosalasta Helsinki Koko maa Rakennus- ja irtaimistovahingot Keskeytysvahingon poisto Pienten vahinkojen poisto havaintojoukosta Rakennuspalojen taloudellinen vahinko eri lääneissä Kokonaisvahingon matemaattinen jakauma Taloudellisen vahingon riippuvuus kerrosalasta Käyttötapaluokkaryhmät Yleistä Logaritminen normaalijakauma Asuinrakennusten jako luokkiin uhatun omaisuuden perusteella Kahden logaritmisen normaalijakauman summa Kahden logaritmisen normaalijakauman summa kaikissa käyttötapaluokkaryhmissä Rakennuksen ja irtaimiston vahingon odotusarvo uhatun omaisuuden funktiona Rakennuksen ja irtaimiston vahingon odotusarvo kerrosalan funktiona Käyttötapaluokkaryhmät Asuinrakennukset Asuinkerrostalot, rivi- ja ketjutalot sekä erilliset pientalot Uhatun omaisuuden ja kerrosalan riippuvuus Taloudellinen vahinko käyttötapaluokassa muut rakennukset Taloudellisen vahingon erikoiskysymyksiä Keskeytysvahinko Yleistä Matemaattinen jakauma Riippuvuus rakennuksen ja irtaimiston vahingosta Tuhoutumisaste Kaikki rakennukset koko maassa Käyttötapaluokkaryhmät Syttymisosaston koon vaikutus taloudelliseen vahinkoon Kaikki rakennukset Asuinrakennukset Vahinkojen aikajakaumat Vuosittainen jakauma
11 8.2 Kuukausittainen jakauma Vuorokaudenaikajakaumat Palokuolemat Taustaa Taloudellinen vahinko Palokunnan toimintavalmiusaika Kuolemaan johtaneiden tulipalojen vertailu kaikkiin rakennuspaloihin Palokuoleman taajuustiheys eri asuinrakennustyypeissä Aikajakaumat Yhteenveto Lähdeluettelo Liitteet Liite A: Vahingon tiheysfunktiot uhatun omaisuuden eri luokissa Liite B: Vahingon tiheysfunktiot lääneittäin Liite C: Keskeytysvahingon jakaumia 10
12 Symboliluettelo µ Keskiarvo σ Keskihajonta A Kerrosala (m 2 ) D F(z) f(z) G(t) g(t) h(z) N V Omavastuu (mk) Muuttujan z kertymäfunktio Muuttujan z tiheysfunktio Normaalijakauman kertymäfunktio Normaalijakauman tiheysfunktio Vioittuvuusfunktio (hasardifunktio) Rakennusten lukumäärä Uhatun omaisuuden arvo (mk) v N (A) Rakennusten lukumäärän tiheysjakauma [1/m 2 ] x z Vahingon suuruus (mk) ln(x), vahingon logaritmi 11
13
14 1. Johdanto Matemaattisessa analyysissä tulipalon riskin ajatellaan muodostuvan kahdesta pääkomponentista, joista ensimmäinen on tulipalon syttymän todennäköisyys ja toinen sen aiheuttamien vahinkojen todennäköinen laajuus. Molemmat ovat luonteeltaan stokastisia, vaikka jälkimmäiseen sisältyykin jonkin verran myös deterministisiä piirteitä. Suuria rakennusmääriä käsiteltäessä otaksutaan ennakkoon, että tilastollinen lähestymistapa on oikeutettua. Syttymän todennäköisyydestä käyttötavaltaan erilaisissa rakennuksissa on tutkimustietoa (Rahikainen 1998a, Rahikainen & Keski-Rahkonen 1998a, b, 2002, Tillander & Keski-Rahkonen 2001), mutta riskin toista komponenttia, tulipalon seurauksia koskeva tieto on tahän asti ollut hyvin vaikeasti saatavilla. SM:n PRONTO-tietokantaan on kerätty arvioita palovahingon suuruudesta vuodesta Alkuvuosien haparoinnin jälkeen tämä tieto on muuttunut käyttökelpoiseksi. Tampereelta ja hiukan myöhemmin Helsingistä saatiin pari vuotta sitten rakennuspalojen vahinkojen tarkistetut arviot, joiden nopea analyysi paljasti niiden periaatteessa monipuolisen tietosisällön. Lindblom sai tehtäväksi diplomityössään (2001) vertailla eri lähteistä saatuja tietoja keskenään. Hänen tuloksensa vahvistavat edellä arvellun: PRONTOn vahinkotiedot ovat puutteistaan huolimatta kelvollinen taloudellisen vahingon mittari.tässä työssä käsitellään PRONTOn taloudellisen vahingon aineistoa ensimmäistä kertaa laajana kokonaisuutena tavoitteena määrittää sen tyypillisimpiä ominaispiirteitä. Varsinkin toiminnallisessa suunnittelussa tieto palon määräisistä vaikutuksista on hyvin olennainen. Kun vahingon matemaattinen käyttäytyminen on tunnettu, odotetusta vahingon laajuudesta sekä sen todennäköisyydestä saadaan arvokasta tietoa. Tässä työssä vahingon mittana on käytetty palon taloudellisia seurauksia, esitetty muutamia perusjakaumia ja verrattu niitä Ramachandranin (1979/80, 1982, 1998) esittämän teorian ennustamiin malleihin. Lisäksi lyhyesti on analysoitu tulipaloissa aiheutuneita henkilövahinkoja ja verrattu eri muuttujien käyttäytymistä aiempiin tuloksiin (Rahikainen 1998a, Rahikainen & Keski-Rahkonen 1999a, b). Palon seurausten laajuus riippuu useiden tekijöiden yhteisvaikutuksesta ja siihen voidaan vaikuttaa useilla suojaustoimenpiteillä. Kun ominaisuuksiltaan samanlaisessa, riittävän suuressa ryhmässä tapahtuneita palovahinkoja sekä syttymistodennäköisyyttä analysoidaan ja molempien matemaattinen käyttäytyminen tunnetaan, voidaan yksinkertaisesti arvioida ryhmän yhden rakennuksen tulipalon riski. Lisäksi riski voidaan lausua kvantitatiivisella tasolla rahana, jolloin eri suunnitteluratkaisujen vertailu on helppoa. 13
15 Todellisuudessa tulipalon aiheuttamaa riskiä yksittäiselle rakennukselle tai pienelle rakennusluokalle ei ole helppoa kuvata, koska ihmisen toiminta vaikuttaa merkittävästi sen palovaaraan. Lisäksi kohteiden kirjo on suuri ja monet huomattavat käytännössä esiin tulevat kohteet ovat joko ainutlaatuisia yksilöitä tai pieniä erikoisryhmiä. Nämä yksilölliset piirteet saattavat vaikuttaa ratkaisevasti palovahingon suuruuteen. Silloin mikään tilastomenetelmä ei periaatteessa ole kovin käyttökelpoinen. Esimerkin tällaisesta vaikeasta yksilöjoukosta tarjoavat yleensä historialliset rakennukset, meillä erityisesti puukirkkomme, tärkein historiallinen muistomerkkijoukkomme. Vanhoissa rakennuksissa on ominaisuuksia, jotka edistävät syttymän leviämistä nopeasti suurvahingoksi jo palon kokona mitattuna muista korvaamattomista arvoista puhumattakaan. Tässä esitetty tilastollinen analyysi osoittaa, että vahinkojen hajonta on suurta kaikissa ryhmissä eikä mikään yllä esitetyn kaltainen ryhmä erotu siitä selvästi. Tässä raportissa etenemisjärjestys onkin päinvastainen. Perusoletuksen mukaisesti koko käytettävissä olevaa aineistoa käsitellään ylhäältä alaspäin ja etsitään selviä lainalaisuuksia. Kaikki havainnot yhtenä ryhmänä noudattavatkin ihmeteltävän hyvin melko yksinkertaisia jakaumia, jolloin on epäiltävissä, että niiden takana piileekin jokin yleisempi lainalaisuus. Kun havaintomassa jaetaan kokeillen erilaisiin pienempiin ryhmiin, jakaumiin ilmaantuu lisää hienorakennetta. Rakennuspaloista havaintoja on kuitenkin niin vähän, että kovin yksityiskohtaiseen jaotteluun ei voida mennä ennenkuin todelliset ilmiöt peittyvät tilastokohinaan. Tässä on kokeillen jaottelu viety aina niin lähelle kohinarajaa kuin käytännöllistä. Koska rakennusten tulipalot ovat onneksi melko harvinaisia, yleisenä tuloksena oli, että vasta huomattavan kokoinen osa rakennuskannasta saadaan periaatteessa erottumaan joukosta. Toinen käytännössä tärkeä havainto oli, että jakaumien ääripäät poikkeavat merkittävästi perusjoukon massasta. Epäsäännöllisyydet asteikon alapäässä voidaan merkitä tilastointivirheiksi; katsomalla vasta tietyn kynnysarvon ylittäviä tapahtumia ongelmasta päästään eroon. Asteikon yläpäässä havaitaan taasen poikkeavuutta, mitä vakuutusyhtiöt ovat kautta aikain kutsuneet suurvahingoiksi. Aineiston yllä kuvatut erikoisryhmät saattavat kuulua tähän joukkoon. Pienuudestaan huolimatta joukko on merkittävä, koska näihin tapahtumiin kuluu merkittävä osa koko palovahinkojen summasta. Suurvahinkojen tilastollinen tarkastelu rajattiin erillisen tutkimuksen aiheeksi. Tämän tutkimuksen painopiste on vahinkojakauman keskipaikkeilla: mitkä ovat taloudellisen vahingon ominaispiirteet sen laajassa ympäristössä? Teoreettisten mallien ja tilastolähteiden esittelyn jälkeen tarkastellaan erilaisia vahingon ja uhatun omaisuuden jakaumia koko maassa ja erikseen Helsingissä sekä myöhemmin vielä lääneittäin. Seuraavaksi tarkastellaan sekä rakennuskantaa että palovahinkoja käyttötapaluokittain. Erikseen otetaan esille vahingot tilastoinniltaan ongelmallisessa käyttötapaluokassa 'muut rakennukset'. Uhatun omaisuuden ja vahingon riippuvuutta 14
16 kerrosalasta, vahingon riippuvuutta uhatusta omaisuudesta sekä palo-osaston koon vaikutusta vahinkoon on selvitetty yksityiskohtaisemmin. Vahinkojen aikajakaumat on piirretty virherajoineen. Lopuksi on verrattu kuolemaan johtaneiden palojen vahinkojakaumia koko havaintojoukon jakaumiin ja tarkasteltu tuloksia aiempien havaintojen perusteella. 15
17 2. Taloudellinen vahinko rakennuspaloissa 2.1 Matemaattinen jakauma Todennäköisten palovahinkojen suuruus kasvaa rakennuksen kerrosalan kasvaessa. Tuhojen suuruus riippuu luonnollisesti myös palon laajuudesta, johon vaikuttaa palon syttymispaikka sekä mahdollisten sammutuslaitteistojen toiminta. Tässä käytetyn Ramachandranin (1979/80, 1982, 1998) teorian mukaisesti tulipalon aiheuttamia taloudellisia vahinkoja voidaan käsitellä stokastisina muuttujina, joilla on määrätty todennäköisyys. Palovahinkoja kuvaava matemaattinen jakauma on tunnetusti vino. Merkitään tulipalossa aiheutunutta vahinkoa x:llä. Muuntamalla vahinkoasteikko logaritmiseksi, z = ln(x) saadaan jakauma, joka on z-asteikolla likimain symmetrinen keskiarvon suhteen. Symmetristen jakaumien käsittelyssä voimme käyttää laajempaa joukkoa yleisiä tilastollisia työkaluja kuin epäsymmetristen. Fysikaalisiin lähtökohtiin nojautuen voidaan olettaa, että palokestoajan todennäköisyysjakauma on eksponentiaalista tyyppiä. Lisäksi voidaan olettaa, että vahingon logaritmi z on likimain verrannollinen palonkestoaikaan ja siten z = ln(x):n todennäköisyysjakauma on myös eksponentiaalista tyyppiä (Ramachandran 1979/80). Vioittuvuus- eli hasardifunktio määritellään seuraavasti f ( z) h( z) = 1 F( z) (1) missä F(z) on muuttujan z kertymäfunktio ja f(z) tiheysfunktio. d f ( z) = F( z) dz (2) Hasardifunktio kuvaa ehdollista todennäköisyyttä, että tulipalo sammuu aikavälillä (z, z+dz), kun se on palanut vähintään ajan z. Välittömästi syttymishetken jälkeen (z on pieni) hasardifunktion arvo on oletettavasti korkea, koska jostain syystä palo sammuu ja leviäminen pysähtyy. Tätä vaihetta kutsutaan niin sanotuksi lastentautijaksoksi. Jos palo jatkuu tämän jakson ajan, sillä on mahdollisuus levitä, jolloin myös hasardifunktion arvo pienenee. Tällöin sen arvo pysyy vakiona jonkun aikaa, kunnes suurilla z:n arvoilla se alkaa jälleen kasvaa. Muuttujan z hasardifunktio on siis ns. kylpyammekäyrän muotoinen. Näistä syistä palovahinkoja voidaan kuvata funktiolla, jonka hasardifunktio on kasvava suurilla z:n arvoilla. Tällainen jakauma on esimerkiksi normaalijakauma, ja koska z = ln(x) tulipaloissa sattuvia rahallisia vahinkoja voidaan kuvata logaritmisella normaalijakaumalla, jonka tiheysfunktio on (McCormick 1981) 16
18 f ( x) = 1 1 exp 2πσ x 1 ( 2 ln( x) µ ) σ 2 (3) missä x on vahingon suuruus (mk), µ ln(x):n keskiarvo ja σ ln(x):n keskihajonta. Tällöin vahingon logaritmin z = ln(x) jakauma on f ( z) = 1 exp 2πσ 1 ( 2 z µ ) σ 2 (4) missä µ on z:n keskiarvo ja σ z:n keskihajonta. Tilastohavainnoista kaavan (1) avulla määritetty kokonaisvahingon hasardifunktio on esitetty kuvassa 1. Kuva 1 osoittaa, että hasardifunktio h(z) kasvaa koko tilastoista näkyvän z:n vaihtelualueella. Tämä näyttäisi olevan ristiriidassa Ramachandranin kylpyammekäyräoletuksen kanssa. Lähempi tarkastelu osoittaa, että näin ei tarvitse välttämättä silti olla. Lastentautijakso vain on ajallisesti niin lyhyt ja rahallisesti niin pieni, että se on leikkautunut tilastoista pois 1. 1 Asian mahdollista tilaa voidaan valottaa karkeasti liioitellun esimerkin avulla. Mikä on tulipalo? Tässä työssä se on rakennuspalo, johon palokunta hälytetään. Periaatteessa paljon pienempikin tapahtuma on syttymä. Käryävä sähkölaite, joka irrotetaan verkosta tai jopa jokainen raapaistu tulitikku huolimattomasti käsiteltynä on mahdollinen palon aiheuttaja. Lisäksi osa pienemmistä syttymistä sammutetaan omatoimisesti eikä niistä tule tietoa palokuntaan. Kun tutkimme varsinaisia tulipalojen alkusyitä, valtaosa niistä on aiheutunut edellä mainittujen kaltaisista hallituista tulen käsittelyistä, joista pieni murto-osa riistäytyy hallitsemattomiksi. Jos haluamme saada tietoa tästä lastentautijaksosta, tässä käyttämämme tilastomenetelmä ei ole siihen tarkoitukseen tehokas. Läheltä piti tapausten tarkastelu tai simulointimalleista saatavat tulokset lienevät tapoja lähestyä tätä ongelmaa. 17
19 h(z) z = ln(x) Kuva 1. Tilastohavainnoista määritetty kokonaisvahingon hasardifunktio. 2.2 Vahingon odotusarvo Kun vahingon jakaumaa merkitään f(x):llä, saadaan sen odotusarvo kaavasta [ X ] E = xf ( x) dx (5) Kun tunnetaan palovahingon jakauma rakennuksessa, jonka uhatun omaisuuden arvo on V (mk), voidaan määrittää vahingon odotusarvo kyseisessä rakennuksessa. Vahingon jakauma voidaan likimääräisesti määrittää pääjakauman avulla ns. katkaistuna jakaumana (Ramachandran 1982). Jos oletetaan, että vahinko on logaritmisesti normaalijakautunut, katkaistu jakauma on muotoa f V ( x) = V 1 exp( 2πσx 1 exp( 2πσx 1 ln( ( 2 1 ln( ( 2 x) µ ) σ x) µ ) σ 2 2 ) ) dx (6) missä µ ja σ ovat ln(x):n keskiarvo ja keskihajonta. Kun z = ln(x) (7) Jolloin 18
20 x = exp(z) (8) ja dx = exp( z) dz (9) Lisäksi normitettu muuttuja µ t = z σ (10) Jolloin z = µ + σt (11) ja dz = σdt (12) Saadaan kaavasta (6) f V ( z) = 1 1 z µ exp( ( ) 2πσ 2 σ G( k) 2 ) (13) Missä normitustekijä 2 1 t G( k) = exp( ) dt 2π 2 k (14) G(t) on normaalijakauman kertymäfunktio, jonka keskiarvo on nolla ja keskihajonta 1. Lisäksi ln V µ (15) k = σ Katkaistu vahingon jakauma (kaava (13)) olettaa, ettei vahinko voi ylittää uhatun omaisuuden arvoa V. Eli 19
21 z ln(v ) (16) Kaavasta (6) tai (13) saadaan vahingon odotusarvo rakennuksessa, jonka uhatun omaisuuden arvo on V x V = V 0 1 = G( k) xf ( x) dx 1 = G( k) G( k) k 0 G( k σ ) σ = exp( µ + G( k) ) 1 exp( 2πσx 2 1 t 2 exp( + σt + µ ) dt 2π 2 V 1 ln( x) µ ( ) 2 σ 2 ) dx (17) Missä k σ 2 1 t (18) G ( k σ ) = exp( ) dt 2π 2 Todennäköisyydeksi F v (z), että vahingon arvo on pienempi kuin x saadaan (Ramachandran 1979/80) Fv ( z) = fv ( z) = z G( u) G( k) (19) missä ln x µ (20) u = σ 2.3 Omavastuinen vakuutus Jos kiinteistö on vakuutettu, omavastuuosuutta merkitään D:llä (mk). Tapahtunut palovahinko x v (mk) saadaan kaavasta (17), josta kiinteistön omistaja on velvollinen korvaamaan korkeintaan summan D. Omistajan osuus vahingosta saadaan kaavasta (Ramachandran 1998) 20
22 x D 2 G( w σ ) σ G( w) (21) = exp( µ + ) + D(1 ) G( k) 2 G( k) missä ln D µ (22) w = σ Vakuutusyhtiö korvaa summan, joka ylittää omavastuun D. Summa saadaan kaavasta R D 2 G( k σ ) G( w σ ) σ G( w) (23) = exp( µ + ) D(1 ) G( k) 2 G( k) Kokonaisvahinko on siten x + v = x D R D (24) Esimerkkinä lasketaan vahingon suuruus ja jakautuminen esimerkkirakennukselle. Oletetaan koko kiinteistön arvoksi V = 1 mmk ja palovahingon omavastuuosuudeksi mk. Oletetaan palovahingot logaritmisesti normaalijakautuneiksi keskiarvolla µ = 9,8 ja keskihajonnalla σ = 2,2. Odotetuksi kokonaisvahingoksi saadaan kaavasta (17) mk, josta vakuutusyhtiön korvaama osuus mk saadaan kaavasta (23) ja omavastuuosuus mk kaavasta (21). 2.4 Riippuvuus kerrosalasta Helsingin aineiston pikainen tarkastelu (vrt. kuva 18) osoitti uhatun omaisuuden ja rakennuksen kerrosalan riippuvan toisistaan seuraavasti V q = V 0 A (25) missä A on rakennuksen kerrosala (m 2 ) ja V 0 sekä q sovitettavia parametreja. Lindblom (2001) laajensi tarkastelua muihin ryhmiin, ja havaitsi sen pitävän likimain paikkansa. Tässä kirjataan tulokset koko käytettävissä olevasta aineistosta. Kun potenssifunktiosta otetaan logaritmi molemmin puolin saadaan suora ln( V ) = b + a ln( A) (26) missä 21
23 a = q (27) ja b = ln( V 0 ) (28) Regressioyhtälön kertoimien luottamusvälit voidaan muodostaa t-jakauman avulla ja niiden hypoteesit voidaan testata t-testillä. Kertoimen β i (1-α) %:n luottamusväli saadaan kaavasta (Laininen 1998) β = b ± t se( b ), df = n 2 (29) i i α / 2 i missä b i on regressiokerroin, se(b i ) kertoimen keskivirhe ja n havaintojen lukumäärä. 22
24 3. Rakennuspalot PRONTO-tietokannasta ja rakennuskanta Tilastokeskuksesta 3.1 Rakennuspalot PRONTOsta Tilastoaineisto kattoi PRONTOsta poimitut koko maan rakennuspalohavainnot vuosina (Lindblom 2001). Lisäksi tarkasteltiin tapahtuneita palovahinkoja Helsingissä vuosina Kelvollisiksi havainnoiksi luettiin ensimmäisessä vaiheessa ne, joissa sekä kokonaisvahingon että uhatun omaisuuden arvot olivat nollaa suurempia. Kelvollisen havaintojoukon koko Helsingissä oli siten ja koko maassa kpl. Taulukossa 1 on esitetty Helsingin ja koko maan havainnoista laskettuja tilastosuureita. Taulukko 1. Tilastoiduissa rakennuspaloissa syntyneiden kokonaisvahinkojen vertailu Helsingissä ja koko maassa. Helsinki Koko maa Lukumäärä Minimi (mk) 10 1 Maksimi (mk) Keskiarvo (mk) ± ± Keskihajonta (mk) Mediaani (mk) % fraktiili (mk) % fraktiili (mk) % fraktiili (mk) Helsingissä tilastoitujen palovahinkojen keskiarvo oli mk ja mediaani mk. Koko maassa samat arvot olivat likimain yhtä suuria, keskiarvon ollessa mk ja mediaanin mk. Myös eri fraktiilit olivat hyvin lähellä toisiaan. 3.2 Tilastokeskuksen rakennuskanta Lukumäärän tiheysjakauma Rakennuskantatiedot pohjautuivat Tilastokeskuksen sähköiseen aineistoon rakennuskannasta Suomessa Tilastokeskuksen rakennuskantaan ei lueta maatalous- 23
25 rakennuksia, vapaa-ajan rakennuksia eikä muita rakennuksia paitsi silloin, kun ko. rakennuksissa on asuttuja asuntoja tai toimitiloja. Siihen ei ole laskettu mukaan esimerkiksi kesämökkejä, joissa ei ole ympärivuotista asutusta, eläinsuojia, turkistarhoja, ym. Kun rakennuskannan rakennukset jaettiin kerrosalan mukaisesti luokkiin, lukumäärän tiheysjakauma saatiin kaavasta f Ni ni ( A) =, N A (30) missä n i on kerrosalaluokkaan kuuluvien rakennusten lukumäärä, N kaikkien rakennusten lukumäärä yhteensä ja A kerrosalaluokan koko. Näin saatu rakennusten lukumäärän tiheysjakauma on esitetty kuvassa 2. f N (A) (1/m 2 ) 1E-2 1E-3 1E-4 1E-5 1E-6 1E-7 1E-8 1E-9 1E-10 1E-11 1E+0 1E+2 1E+4 1E+6 Kerrosala (m 2 ) Kuva 2. Rakennuskantaan kuuluvien rakennusten lukumäärän tiheysjakauma kerrosalan funktiona. Olettaen, että uhatun omaisuuden ja kerrosalan välillä on potenssimuotoinen riippuvuus (25), saadaan lukumäärän tiheysjakauma myös uhatun omaisuuden funktiona muuntamalla kerrosala kaavassa (30) uhatuksi omaisuudeksi. Tiheysjakauma on tällöin muotoa f V ) n 1 i Ni ( = q 1 N V0qA 1, A (31) joka on esitetty kuvassa 3. 24
26 1E-5 1E-6 f N (V) (1/mk) 1E-7 1E-8 1E-9 1E-10 1E-11 1E+4 1E+5 1E+6 1E+7 1E+8 Uhattu omaisuus (mk) Kuva 3. Rakennuskantaan kuuluvien rakennusten lukumäärän tiheysjakauma uhatun omaisuuden funktiona Teoreettinen sovite Tiheysjakaumaan sovitettiin Pareton ja kahden logaritmisen normaalijakauman summa, johon päädyttiin aiemmin rakennusten lukumäärän tiheysjakaumaa määritettäessä (Tillander & Keski-Rahkonen 2001). v N ( 1N 1N 2N 2N + 3N 3N A A) = c v ( A) + c v ( A) c v ( ), (32) missä v 1 ( A N ) S λn A λ 1 λ N N (33) = N ja v in 1 1 ln A µ in 2 ( A) = exp ( ), i = 2,3. 2πσ A 2 σ in in (34) Summafunktio (32) on sovitettu kuvassa 4 kaikkien sekä kuvassa 5 asuinrakennusten tilastohavaintoihin. Soviteparametrien arvot on esitetty taulukossa 2. 25
27 f N (V) (1/mk) 2,5E-6 Kaikki, Rakennuskanta 2,0E-6 1,5E-6 1,0E-6 5,0E-7 0,0E+0 1E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus (mk) f N (V) (1/mk) 1E-5 Kaikki, Rakennuskanta 1E-6 1E-7 1E-8 1E-9 1E-10 1E-11 1E-12 1E-13 1E-14 1E-15 1E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus (mk) Kuva 4. Kaikkien rakennusten lukumäärän kerrosalajakauma. Tilastohavainnot pisteinä ja teoreettinen sovite (viiva). f N (V) (1/mk) 2,0E-6 Asuin, Rakennuskanta 1,5E-6 1,0E-6 5,0E-7 0,0E+0 1E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus (mk) f N (V) (1/mk) 1E-5 Asuin, Rakennuskanta 1E-6 1E-7 1E-8 1E-9 1E-10 1E-11 1E-12 1E-13 1E-14 1E-15 1E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus (mk) Kuva 5. Asuinrakennusten lukumäärän kerrosalajakauma. Tilastohavainnot pisteinä ja teoreettinen sovite (viiva). Taulukko 2. Rakennusten lukumäärän tiheysjakaumasovitteen (32) parametrien arvot. Rakennukset c 1N λ N S N c 2N µ 2N σ 2N c 3N µ 3N σ 3N Kaikki 0,05 0, ,85 12,6 0,7 0,10 14,8 1,3 Asuin 0,13 0, ,8 12,7 0,6 0,04 15,4 0,7 26
28 4. Taloudellinen vahinko Helsingin ja koko maan rakennuspaloissa 4.1 Vahinkojen kertymäfunktiot Tilastoidut palovahingot voidaan jakaa neljään ryhmään (Lindblom 2001), kokonaisvahingot, kiinteistölle aiheutuneet vahingot, irtaimistovahingot sekä keskeytysvahingot. Tässä kappaleessa on keskitytty kolmeen ensimmäiseen ryhmään. PRONTOsta poimittujen tilastohavaintojen (Lindblom 2001) kertymäfunktioihin sovitettiin logaritminen normaalijakauma käyttäen apuna tilasto-ohjelma STATISTICAa. Sovitteet Helsingin ja koko maan havaintojoukkoihin on esitetty kuvassa 6 ja 7. Logaritmisen normaalijakauman soviteparametrit, keskiarvo ja keskihajonta on esitetty taulukossa 3. 1,0 Kokonaisvahingot Helsinki 1,0 Rakennuksen vahingot Helsinki 0,8 0,8 Ke rtym ä 0,6 0,4 Ke rtym ä 0,6 0,4 0,2 0,2 0, , Vahingon suuruus (m k) Vahingon suuruus (m k) 1,0 Irtaimistovahingot Helsinki 0,8 Ke r tym ä 0,6 0,4 0,2 0, Vahingon suuruus (m k) Kuva 6. Kokonais-, rakennus- ja irtaimistovahinkojen kertymäfunktiot Helsingissä sekä havaintoihin sovitettu logaritminen normaalijakauma. 27
29 1,0 0,8 Kokonaisvahingot Koko maa 1,0 0,8 Rakennuksen vahingot Koko maa Kertymä 0,6 0,4 Kertymä 0,6 0,4 0,2 0,2 0,0 0,0 1E+0 1E+2 1E+4 1E+6 1E+0 1E+2 1E+4 1E+6 Vahinko (mk) Vahinko (mk) 1,0 0,8 Irtaimistovahingot Koko maa Kertymä 0,6 0,4 0,2 0,0 1E+0 1E+2 1E+4 1E+6 Vahinko (mk) Kuva 7. Kokonais-, rakennus- ja irtaimistovahinkojen kertymäfunktiot koko maassa sekä havaintoihin sovitettu logaritminen normaalijakauma. Taulukko 3. Helsingin ja koko maan omaisuusvahinkohavaintoihin sovitettujen logaritmisten normaalijakaumien keskiarvot ja -hajonnat. Helsinki Keskiarvo Keskihajonta Kokonaisvahingot 9,67 2,18 Kiinteistön vahingot 9,58 1,95 Irtaimistovahingot 8,87 2,07 Koko maa Kokonaisvahingot 9,80 2,21 Kiinteistön vahingot 9,63 2,09 Irtaimistovahingot 8,77 2, Vahinkojen tiheysfunktiot Edellä esitetyt sovitteet tehtiin tilastohavaintojen kertymäfunktioihin. Kertymä integraalifunktiona ei kuitenkaan tuo esille pieniä muutoksia havaintojoukossa, jotka puolestaan tiheysfunktiossa tulevat esiin paremmin. Voidaan todeta, että jos vahinko x on 28
30 logaritmisesti normaalijakautunut, sen logaritmin ln(x) tulee noudattaa normaalijakaumaa. Kuvassa 8 on piirretty vahinkojen logaritmin tiheysfunktio koko maassa samaan kuvaan normaalijakauman kanssa. Normaalijakauman parametrit saatiin taulukosta 3. 0,20 0,15 Kokonaisvahingot Koko maa 0,25 0,20 Rakennuksen vahingot Koko maa f(z) 0,10 f(z) 0,15 0,10 0,05 0,05 0, z = ln(x) 0, z = ln(x) 0,25 0,20 Irtaimistovahingot Koko maa f(z) 0,15 0,10 0,05 0, z = ln(x) Kuva 8. Koko maassa tulipaloissa syntyneiden vahinkojen logaritmin tiheysfunktio (kolmiot) piirrettynä samaan kuvaan normaalijakauman kanssa. Kuvasta 8 nähdään, ettei vahinko ole niin tarkasti logaritmisesti normaalijakautunut kuin kuvaa 7 tarkastelemalla vaikuttaa, vaan pieniä poikkeamia teoreettisesta käyrästä on havaittavissa. Kuvassa 9 koko maan ja kuvassa 10 Helsingin aineistosta määritetyt tiheysfunktiot on esitetty markkoina. Vasemmalla molemmat koordinaattiakselit ovat logaritmisia, oikealla y-akseli on lineaarinen. Samaan kuvaan on piirretty myös logaritminen normaalijakauma, jonka parametrit on esitetty taulukossa 3. Kuvat 8 10 osoittavat vanhastaan tunnetun tosiasian, että tiheysfunktio kuvaa jakaumaa kertymäfunktiota huomattavasti tarkemmin. Vaikka kertymäfunktioiden sovitteita voidaan pitää erittäin hyvinä, tiheysfunktioissa on merkittäviä eroja. Kuvista 9 ja 10 huomataan yleiskuvan ja yksityiskohtien erojen merkitys. Vasemmalla logaritmisella pystyasteikolla sovitteen havaitaan kuvaavan ilmiötä likimääräisellä tavalla koko alueella. Oikealla lineaarista pystyakselia käytettäessä pienten arvojen havaitaan poikkeavan sovitteesta jopa tekijällä 3, mitä perinteisesti ei ole totuttu pitämään kovin hyvänä sovitteena! Nämä esimerkit osoittavat, että vahingon kuvaaminen yksityiskohdittain tarkasti vaatisi huomattavasti monimutkaisempia funktioita, kuin kaavat (32) (34) esittävät; sama havainto tehtiin myös syttymistaajuuksia mallitettaessa (Tillander & Keski-Rahkonen 2001). Tässäkään 29
31 kohdassa emme pyri suurimpaan mahdolliseen tarkkuuteen, vaan tyydymme nyt ilmiöiden yleiskuvaukseen jakaumien keskivaiheilla. Jos haluamme suurta tarkkuutta, jakaumien rakennetta on lisättävä ja ehkä yleistettävä jatkuvista epäjatkuviin. Niistä on laskettava myös eri suureet numeerisesti. Tällaisen menettelyn haittana on epähavainnollisuus. Siksi tässä yritetään viedä analyysi läpi analyyttisenä ja vasta lopussa arvioidaan menettelytavan hyvyys sekä mahdolliset vaadittavat lisätoimet. 1E-4 Kokonaisvahingot Koko maa 1,2E-4 1,0E-4 Kokonaisvahingot Koko maa f(x) (1/mk) 1E-6 1E-8 1E-10 f(x) (1/mk) 8,0E-5 6,0E-5 4,0E-5 2,0E-5 1E-12 0,0E+0 1E+1 1E+2 1E+3 1E+4 1E+5 1E+6 1E+7 1E+8 1E+1 1E+2 1E+3 1E+4 1E+5 1E+6 1E+7 1E+8 Vahinko, x (mk) Vahinko, x (mk) 1E-4 Irtaimistovahingot Koko maa 3E-4 Irtaimistovahingot Koko maa f(x) (1/mk) 1E-6 1E-8 1E-10 f(x) (1/mk) 2E-4 1E-4 1E-12 1E+1 1E+3 1E+5 1E+7 1E+9 Vahinko, x (mk) 0E+0 1E+1 1E+3 1E+5 1E+7 1E+9 Vahinko, x (mk) f(x) (1/mk) 1E-3 1E-4 1E-5 1E-6 1E-7 1E-8 1E-9 1E-10 1E-11 1E+1 1E+3 1E+5 1E+7 1E+9 Vahinko, x (mk) Rakennuksen vahingot Koko maa f(x) (1/mk) 1,2E-4 1,0E-4 Rakennuksen vahingot Koko maa 8,0E-5 6,0E-5 4,0E-5 2,0E-5 0,0E+0 1E+1 1E+3 1E+5 1E+7 1E+9 Vahinko, x (mk) Kuva 9. Koko maassa tulipaloissa syntyneiden vahinkojen tiheysfunktiot piirrettynä samaan kuvaan logaritmisen normaalijakauman kanssa. Vasemmalla logaritmiset x- ja y-akselit, oikealla logaritminen x- ja lineaarinen y-akseli. 30
32 1E-3 1E-4 Kokonaisvahingot Helsinki 1,4E-4 1,2E-4 Kokonaisvahingot Helsinki f(x) (1/mk) 1E-5 1E-6 1E-7 1E-8 f(x) (1/mk) 1,0E-4 8,0E-5 6,0E-5 4,0E-5 1E-9 2,0E-5 1E-10 0,0E+0 1E+1 1E+2 1E+3 1E+4 1E+5 1E+6 1E+7 1E+8 1E+1 1E+2 1E+3 1E+4 1E+5 1E+6 1E+7 1E+8 Kokonaisvahinko, x (mk) Kokonaisvahinko, x (mk) Kuva 10. Kokonaisvahingon tiheysfunktio ja logaritminen normaalijakauma Helsingissä. Vasemmalla logaritmiset x- ja y-akselit, oikealla logaritminen x- ja lineaarinen y-akseli. 4.3 Koko maan havaintojen jako luokkiin uhatun omaisuuden perusteella Koko maan kokonaisvahinkohavainnot jaettiin uhatun omaisuuden perusteella seitsemään luokkaan, koska haluttiin selvittää onko vahinkojen jakauman matemaattinen muoto sama myös luokkien sisällä. Käytettyjen luokkien rajat on esitetty taulukossa 4. Kokonaisvahingon kertymäfunktiot eri luokissa on esitetty kuvassa 11. Taulukko 4. Uhatun omaisuuden perusteella tehdyn luokkajaon rajat ja eri luokkien havaintoihin sovitetun logaritmisen normaalijakauman parametrit. Luokka Rajat (mk) Keskiarvo Keskihajonta ,20 1, ,31 2, ,30 2, ,66 2, ,57 2, ,59 2, ,56 2,53 31
33 1,0 Kertymä 0,8 0,6 0,4 0,2 Luokka 1 Luokka 2 Luokka 3 Luokka 4 Luokka 5 Luokka 6 Luokka 7 0,0 1E+0 1E+2 1E+4 1E+6 1E+8 Vahingon suuruus (mk) Kuva 11. Kokonaisvahingon kertymä eri uhatun omaisuuden luokissa. Luokkajako on esitetty taulukossa 4. Kuvasta 11 nähdään eri luokkien kertymäjakaumien poikkeavan toisistaan jonkin verran. Näihin kertymäfunktioihin sovitettiin logaritminen normaalijakauma, jotta nähtäisiin ovatko myös uhatun omaisuuden perusteella luokkiin jaotellut palovahingot logaritmisesti normaalijakautuneita. Määritetyt keskiarvot ja keskihajonnat on esitetty taulukossa 4. 32
34 1,0 Luokka 1 1,0 Luokka 2 0,8 0,8 Kertymä 0,6 0,4 Kertymä 0,6 0,4 0,2 0,2 0,0 0,0 1E+0 1E+2 1E+4 1E+6 1E+8 1E+0 1E+2 1E+4 1E+6 1E+8 Vahingon suuruus (mk) Vahingon suuruus (mk) 1,0 Luokka 3 1,0 Luokka 4 0,8 0,8 Kertymä 0,6 0,4 Kertymä 0,6 0,4 0,2 0,2 0,0 0,0 1E+0 1E+2 1E+4 1E+6 1E+8 1E+0 1E+2 1E+4 1E+6 1E+8 Vahingon suuruus (mk) Vahingon suuruus (mk) 1,0 Luokka 5 1,0 Luokka 6 0,8 0,8 Kertymä 0,6 0,4 Kertymä 0,6 0,4 0,2 0,2 0,0 0,0 1E+0 1E+2 1E+4 1E+6 1E+8 1E+0 1E+2 1E+4 1E+6 1E+8 Vahingon suuruus (mk) Vahingon suuruus (mk) 1,0 Luokka 7 0,8 Kertymä 0,6 0,4 0,2 0,0 1E+0 1E+2 1E+4 1E+6 1E+8 Vahingon suuruus (mk) Kuva 12. Kokonaisvahinkojen kertymäfunktioiden logaritmisen normaalijakauman sovitteet eri luokissa. Kuvasta 12 nähdään, että jo kertymäfunktiossa näkyy poikkeamia oletetusta teoreettisesta jakaumasta erityisesti luokissa 1, 2 ja 7. Tiheysfunktiot, jotka on esitetty liitteessä A osoittivat, että vain luokka 4 näyttäisi silmävaraisesti olevan logaritmisesti normaali- 33
35 jakautunut. Ennen sovitteiden numeerista vertailua katsotaan kuvan 12 tuloksia silmävaraisesti. Niistä on nähtävissä, että luokissa 1, 2 ja 7 kertymät koostuvat selvästi erillisistä ryhmistä. Kertymäfunktio olisikin muodostettava näiden yhdelmänä. 4.4 Sovitteiden hyvyys Yleistä Kun otetaan tarkasteluun n toisistaan riippumatonta N(0,1)-jakautunutta satunnaismuuttujaa X 1, X 2,, X n ja merkitään niiden neliöiden summaa χ n = X 1 + X X n (35) saadaan satunnaismuuttuja, jota kutsutaan χ 2 -jakautuneeksi vapausasteilla n (Lokki 1980, Laininen 1998). Vapausaste n ilmoittaa kuinka monta toisistaan riippumatonta satunnaismuuttujaa on käytetty neliösummaa muodostettaessa. χ 2 -jakauman tiheysfunktio on f χ 2 ( x) = Γ 1 n 2 n ( ) 2 2 x n 1 2 x exp( ) 2 (36) Tiheysfunktion kulku eri vapausasteiden arvoilla on esitetty kuvassa 13. 0,2 0,15 n = 4 f x 2 (x) 0,1 n = 10 0,05 n = 30 p x χ 2 n (p) Kuva 13. χ 2 -jakauman tiheysfunktio eri vapausasteiden n arvoilla. 34
36 Kuvaan 13 piirretty viivoitettu alue kuvaa yhteensopivuustestissä käytettyä todennäköisyyttä p, joka ilmoittaa, kun x = χ 2 n ( p) kuinka monta prosenttia tiheysfunktion ja x- 2 akselin väliin jäävästä pinta-alasta on välillä ( χ ( p), ). χ 2 -yhteensopivuustestin avulla voidaan tarkastella esimerkiksi sovitteiden hyvyyttä. Yhteensopivuustestissä tarkastellaan, onko satunnaismuuttujasta X poimittu satunnaisotos sopusoinnussa X:n jakaumasta tehdyn ennakkohypoteesin kanssa. (Laininen 1998). Edellä satunnaismuuttuja X on vahingon suuruus, jonka kertymäfunktio on F(x). G(x) on nyt logaritmisen normaalijakauman kertymäfunktio. Testattavat hypoteesit ovat H H 0 1 : F( x) G( x) valitulla riskitasolla α n : F( x) = G( x) kaikilla x (37) joillakin x Sovitteen hyvyyttä kuvaa edellä mainittu todennäköisyys p, joka ilmoittaa kuinka suuret mahdollisuudet sattumalla on enintään aiheuttaa vähintään havaitun suuruinen poikkeama. Tavallisesti poikkeama tulkitaan merkitseväksi eli pääasiassa muusta kuin sattumasta johtuvaksi, jos p on pienempi tai yhtä suuri kuin 0,05 (Laininen 1998). Yhteensopivuustestissä 2 2 = P( χ χ ( p)) α H hylätään (38) p n Kaikki rakennuspalot Arvioitaessa tehtyjen sovitteiden hyvyyttä käytettiin STATISTICA-ohjelman tekemää yhteensopivuustestiä. Logaritmisen normaalijakauman sovitteeseen liittyvä yhteensopivuustesti on likimääräinen, joka perustuu uskottavuusfunktion maksimiarvoon ja on melko tehoton. Tämän vuoksi sovitteen hyvyyttä testattiin vertaamalla havainnoista otettuja logaritmeja normaalijakaumaan sillä perusteella, että jos logaritmia ei voida hyväksyä normaalijakautuneeksi ei myöskään alkuperäistä muuttujaa voida hyväksyä logaritmisesti normaalijakautuneeksi. Taulukossa 5 on esitetty kappaleessa 4.1 tehtyjen logaritmisesti normaalien sovitteiden yhteensopivuustestillä saadut χ n 2(p)-arvot sekä vapausasteiden n arvot sekä niiden perusteella määritetyt todennäköisyydet p. 35
37 Taulukko 5. Helsingin vuosien ja koko maan vuosien logaritmisiin havaintoihin sovitetun normaalijakauman sovitteen hyvyyttä mittaavien parametrien arvot. Helsinki χ 2 n (p) n p Kokonaisvahingot 60,1 10 3E-09 Rakennusvahingot 118,0 8 9E-22 Irtaimistovahingot 122,8 9 4E-22 Koko maa Kokonaisvahingot 482,8 13 6E-95 Rakennusvahingot E-251 Irtaimistovahingot E-250 Koska todennäköisyys p on kaikissa tapauksissa pienempi kuin 0,05, yhteensopivuustestin perusteella logaritminen normaalijakauma ei sovellu kuvaamaan havaintoja missään yllä olevista tapauksista. Silmävaraisesti kertymäfunktiot vaikuttivat noudattavan logaritmista normaalijakaumaa melko hyvin. Kuitenkin kappaleen 4.2 tiheysfunktiot osoittivat, että poikkeamia teoreettisesta käyrästä oli selvästi havaittavissa Luokkajako uhatun omaisuuden perusteella Taulukossa 6 on esitetty yhteensopivuustestin avulla saatu todennäköisyys p, jonka arvon alittaessa 0,05 voidaan olettaa oletushypoteesin (havainnot noudattavat logaritmista normaalijakaumaa) pitävän paikkansa. Taulukosta 6 nähdään, että p ei ylitä arvoa 0,05 missään luokassa. Tämän perusteella voidaan päätellä, että logaritminen normaalijakauma soveltuu kuvaamaan havaintoja kaikissa luokissa melko huonosti. Parhaiten jakauma soveltui havaintoihin luokissa 4 ja 6. 36
38 Taulukko 6. Eri luokkiin sovitetun logaritmisen normaalijakauman yhteensopivuustestin perusteella määritetty sovitteen hyvyys p. Luokka p 1 2E E E ,04 5 1E ,03 7 8E Yhteenveto Tulipaloissa syntyneet taloudelliset vahingot näyttivät kertymäfunktioon tehtyjen sovitteiden perusteella noudattavan logaritmista normaalijakaumaa hyvin. Tiheysfunktiot kuitenkin paljastivat, että pieniä eroja havaintojen ja teoreettisen jakauman välillä oli havaittavissa. On kuitenkin epätodennäköistä, että mikään yksinkertainen matemaattinen jakauma pystyisi kuvaamaan havaintoja täydellisesti ja siten logaritminen normaalijakauma on melko hyvä sovite poikkeamista huolimatta. 4.5 Kokonaisvahingon odotusarvo uhatun omaisuuden funktiona Helsinki Tietyssä rakennuksessa syttyvässä tulipalossa syntyvän vahingon odotusarvo voidaan määrittää Ramachandranin teorian mukaisesti kaavasta (17), kun tunnetaan rakennuksen uhatun omaisuuden arvo. Lisäksi teoria olettaa, että tarkasteltavan ryhmän palovahingot ovat logaritmisesti normaalijakautuneet tunnetuin parametrein. Analyysia varten tilastohavainnot jaettiin uhatun omaisuuden mukaisesti kuuteen luokkaan. Luokkien rajat sekä havaintojen lukumäärä kussakin luokassa on esitetty taulukossa 7. 37
39 Taulukko 7. Uhatun omaisuuden luokkajaon rajat. Luokka Uhattu omaisuus (mk) Lkm Yhteensä Kuvassa 14 on pisteillä piirretty kunkin luokan tilastohavainnoista määritetty kokonaisvahingon keskiarvo. Virhejana kuvaa keskiarvon keskivirhettä, joka saadaan kaavasta σ = x σ n (39) missä σ on keskihajonta ja n havaintojen lukumäärä. Samaan kuvaan 14 on tilastohavaintojen kanssa piirretty kaavasta (17) määritetty teoreettinen vahingon odotusarvo. Logaritmisen normaalijakauman parametrien arvot on saatiin taulukosta Vahingon odotusarvo, x v (mk) E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus, V (mk) Kuva 14. Vahingon odotusarvo uhatun omaisuuden funktiona Helsingissä. Pisteillä on piirretty todellisten vahinkojen luokkakohtaiset keskiarvot. Virhejana kuvaa keskiarvon keskivirhettä. 38
40 Silmävaraisen tarkastelun perusteella teoreettinen käyrä näyttää sopivan tilastohavaintoihin kohtalaisesti Koko maa Koko maan havainnot muodostivat huomattavasti suuremman joukon, kpl, jolloin ne voitiin jakaa 24 luokkaan uhatun omaisuuden perusteella. Käytetyn luokkajaon rajat on esitetty taulukossa 8. Taulukko 8. Uhatun omaisuuden luokkajaon rajat. Luokka Uhattu omaisuus (mk) Luokka Uhattu omaisuus (mk) Kuvaan 15 on piirretty tilastohavainnoista määritetty vahingon keskiarvo keskivirheineen (pisteet) samaan kuvaan teoreettisen vahingon odotusarvon kanssa (kaava (17)). 39
41 Vahingon odotusarvo, x v (mk) 1E+7 1E+6 1E+5 1E+4 µ = 9,80 σ = 2,21 1E+3 1E+3 1E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus, V (mk) Kuva 15. Vahingon odotusarvo uhatun omaisuuden funktiona koko maassa. Pisteillä on piirretty todellisten vahinkojen luokkakohtaiset keskiarvot. Virhejanat kuvaavat keskiarvon keskivirhettä. Kuten kuvasta 15 nähdään, teoreettinen käyrä jää selvästi alemmaksi kuin tilastohavaintopisteet. Kun logaritmisen normaalijakauman parametreja muutettiin, käyrä saatiin kulkemaan tilastohavaintopisteiden kautta. Silmävaraisen sovituksen tuloksena parametrien arvoiksi saatiin µ = 11,5 ja σ = 1,5. Sovituksen tulos on esitetty kuvassa 16. Vahingon odotusarvo, x v (mk) 1E+7 1E+6 1E+5 1E+4 µ = 11,5 σ = 1,5 1E+3 1E+3 1E+4 1E+5 1E+6 1E+7 1E+8 1E+9 1E+10 Uhattu omaisuus, V (mk) Kuva 16. Vahingon odotusarvo uhatun omaisuuden funktiona. Koko maan vahinkojen luokkakohtaiset keskiarvot on piirretty kuvaan pisteinä Yhteenveto Kuvien teoreettisten käyrien perusteella näyttäisi, että uhatun omaisuuden ylittäessä 1 10 mmk, odotettu vahinko ei enää kasva. Käyrä vastasi melko hyvin Helsingin tilastohavaintoja, mutta havaintojoukon pienuuden takia tulos on vain suuntaa antava. Koko maalle piirretty teoreettinen käyrä jäi selvästi todellisia havaintoja alemmaksi, sen 40
42 muodon ollessa kuitenkin samankaltainen. Muuttamalla logaritmisen normaalijakauman parametreja käyrä saatiin sopimaan havaintoihin. Kuvien 15 ja 16 tilastohavaintopisteiden perusteella näyttäisi myöskin, että vahingon keskiarvo vakiintuu tietylle tasolle 100 mmk omaisuuden arvoon saakka. Sitä suuremmilla uhatun omaisuuden arvoilla oli kuitenkin niin vähän havaintoja, ettei johtopäätöksiä asiasta voida enää tehdä. Tämä asia on vakuutusmaailmassa hyvin tunnettu jälleenvakuutusten arvioinnin probleema. Teoreettisen käyrän ja tilastohavaintojen heikkoon yhteensopivuuteen vaikuttivat osaltaan sovelletun mallin rajoitukset. Periaatteessa tarvitsisimme vahingon todennäköisyysjakauman kullekin rakennukselle, jossa uhatun omaisuuden arvo on V (mk). Näiden jakaumien muodostaminen olisi kuitenkin vaivalloista ja aikaa vievää, jonka vuoksi jakaumat approksimoidaan kokonaisjakaumasta. Jos kokonaisjakauma on logaritmisesti normaali keskiarvolla µ ja keskihajonnalla σ, tiheysfunktio on kokonaisjakauman katkaistu versio. Siten vahingon tiheysfunktio rakennuksessa, jossa uhatun omaisuuden arvo on V (mk) on 1 1 z µ 2 (40) f V ( z) = exp ( ) G( k) 2πσ 2 σ missä G(k) saadaan kaavasta (14). Tiheysfunktiosta (40) saadaan integroimalla kaavassa (19) esitetty kertymäfunktio. Lisäksi teoria olettaa, että syntynyt vahinko voi olla korkeintaan uhatun omaisuuden suuruinen. Suomen tilastohavainnoissa kokonaisvahinkoon on kuitenkin laskettu myös keskeytysvahingot, jolloin vahinko voi kasvaa suuremmaksi kuin uhattu omaisuus. Uhattuun omaisuuteen keskeytysvahinkoja ei ole laskettu mukaan lainkaan. Myös nämä seikat voivat vaikuttaa mallin sovellettavuuteen kyseiseen aineistoon, jonka vuoksi mallista saadut tulokset ovat tässä vaiheessa vain suuntaa antavia. Yhteenvetona voidaan todeta, että Ramachandranin teorian suoraviivainen soveltaminen poikkeaa havaituista arvoista niin selvästi, ettei teoria sellaisenaan sovellu ennustetyökaluksi. 4.6 Vahingon suuruuden todennäköisyys Helsinki Kun uhatun omaisuuden arvo on tunnettu, voidaan kaavan (19) avulla määrittää myös vahingon suuruuden todennäköisyys. Kuvassa 17 on esitetty todennäköisyyskäyriä eri uhatun omaisuuden V arvoilla. x-akselilla on vahingon suuruus ja seuraamalla valittua uhatun omaisuuden käyrää, y-akselilta voidaan lukea todennäköisyys, jolla vahingon suuruus on korkeintaan x mk. Teorian perusoletuksena on, että vahinko on logaritmi- 41
Kuvista B1 ja B2 nähdään, että syttymistaajuus asuntoa kohden on korkein erillisissä pientaloissa.
 Ignition frequency [1/a*flat] Ignition frequency [1/m 2 a] Ignition frequency [1/a*inhabitant] Liite 9. Tausta-aineistoa liittyen asuinrakennusten riskeihin Viimeaikaiset tutkimukset ovat osoittaneet,
Ignition frequency [1/a*flat] Ignition frequency [1/m 2 a] Ignition frequency [1/a*inhabitant] Liite 9. Tausta-aineistoa liittyen asuinrakennusten riskeihin Viimeaikaiset tutkimukset ovat osoittaneet,
PELASTUSTOIMEN MÄÄRÄISET MITTARIT
 PELASTUSTOIMEN MÄÄRÄISET MITTARIT TIIVISTELMÄ Kati Tillander, Timo Korhonen & Olavi Keski-Rahkonen VTT Rakennus- ja yhdyskuntatekniikka PL 83, 244 VTT Tutkimuksessa on kerätty pelastustoimen mittareiksi
PELASTUSTOIMEN MÄÄRÄISET MITTARIT TIIVISTELMÄ Kati Tillander, Timo Korhonen & Olavi Keski-Rahkonen VTT Rakennus- ja yhdyskuntatekniikka PL 83, 244 VTT Tutkimuksessa on kerätty pelastustoimen mittareiksi
r = 0.221 n = 121 Tilastollista testausta varten määritetään aluksi hypoteesit.
 A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
A. r = 0. n = Tilastollista testausta varten määritetään aluksi hypoteesit. H 0 : Korrelaatiokerroin on nolla. H : Korrelaatiokerroin on nollasta poikkeava. Tarkastetaan oletukset: - Kirjoittavat väittävät
Harjoitus 7: NCSS - Tilastollinen analyysi
 Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Harjoitus 7: NCSS - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tilastollinen testaus Testaukseen
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 18. lokakuuta 2007 Antti Rasila () TodB 18. lokakuuta 2007 1 / 19 1 Tilastollinen aineisto 2 Tilastollinen malli Yksinkertainen satunnaisotos 3 Otostunnusluvut
Sovellettu todennäköisyyslaskenta B Antti Rasila 18. lokakuuta 2007 Antti Rasila () TodB 18. lokakuuta 2007 1 / 19 1 Tilastollinen aineisto 2 Tilastollinen malli Yksinkertainen satunnaisotos 3 Otostunnusluvut
Jatkuvat satunnaismuuttujat
 Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Jatkuvat satunnaismuuttujat Satunnaismuuttuja on jatkuva jos se voi ainakin periaatteessa saada kaikkia mahdollisia reaalilukuarvoja ainakin tietyltä väliltä. Täytyy ymmärtää, että tällä ei ole mitään
Tilastollinen testaus. Vilkkumaa / Kuusinen 1
 Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
Tilastollinen testaus Vilkkumaa / Kuusinen 1 Motivointi Viime luennolla: havainnot generoineen jakauman muoto on usein tunnettu, mutta parametrit tulee estimoida Joskus parametreista on perusteltua esittää
Paloriskin arvioinnin tilastopohjaiset tiedot Kati Tillander, VTT Esa Kokki, Pelastusopisto Tuuli Oksanen, VTT
 Paloriskin arvioinnin tilastopohjaiset tiedot Kati Tillander, VTT Esa Kokki, Pelastusopisto Tuuli Oksanen, VTT Palotutkimuksen päivät 25-26.8.2009 Tausta Liittyy hankkeeseen Paloriskin arvioinnin tilastopohjaiset
Paloriskin arvioinnin tilastopohjaiset tiedot Kati Tillander, VTT Esa Kokki, Pelastusopisto Tuuli Oksanen, VTT Palotutkimuksen päivät 25-26.8.2009 Tausta Liittyy hankkeeseen Paloriskin arvioinnin tilastopohjaiset
Rakennuspalojen omaisuusvahinkoriskin ennakointi
 TEKNOLOGIAN TUTKIMUSKESKUS VTT OY Rakennuspalojen omaisuusvahinkoriskin ennakointi Palotutkimuksen päivät 2015 Antti Paajanen, Tuula Hakkarainen ja Kati Tillander Johdanto Onnettomuusvahingot pelastustoimen
TEKNOLOGIAN TUTKIMUSKESKUS VTT OY Rakennuspalojen omaisuusvahinkoriskin ennakointi Palotutkimuksen päivät 2015 Antti Paajanen, Tuula Hakkarainen ja Kati Tillander Johdanto Onnettomuusvahingot pelastustoimen
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 16. marraskuuta 2007 Antti Rasila () TodB 16. marraskuuta 2007 1 / 15 1 Epäparametrisia testejä χ 2 -yhteensopivuustesti Homogeenisuuden testaaminen Antti
Sovellettu todennäköisyyslaskenta B Antti Rasila 16. marraskuuta 2007 Antti Rasila () TodB 16. marraskuuta 2007 1 / 15 1 Epäparametrisia testejä χ 2 -yhteensopivuustesti Homogeenisuuden testaaminen Antti
Harjoitus 2: Matlab - Statistical Toolbox
 Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
Harjoitus 2: Matlab - Statistical Toolbox Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen tavoitteet Satunnaismuuttujat ja todennäköisyysjakaumat
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
MS-A0502 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 4A Parametrien estimointi Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016, periodi
Tilastollisen analyysin perusteet Luento 11: Epäparametrinen vastine ANOVAlle
 Tilastollisen analyysin perusteet Luento 11: Epäparametrinen vastine ANOVAlle - Sisältö - - - Varianssianalyysi Varianssianalyysissä (ANOVA) testataan oletusta normaalijakautuneiden otosten odotusarvojen
Tilastollisen analyysin perusteet Luento 11: Epäparametrinen vastine ANOVAlle - Sisältö - - - Varianssianalyysi Varianssianalyysissä (ANOVA) testataan oletusta normaalijakautuneiden otosten odotusarvojen
Estimointi. Vilkkumaa / Kuusinen 1
 Estimointi Vilkkumaa / Kuusinen 1 Motivointi Tilastollisessa tutkimuksessa oletetaan jonkin jakauman generoineen tutkimuksen kohteena olevaa ilmiötä koskevat havainnot Tämän mallina käytettävän todennäköisyysjakauman
Estimointi Vilkkumaa / Kuusinen 1 Motivointi Tilastollisessa tutkimuksessa oletetaan jonkin jakauman generoineen tutkimuksen kohteena olevaa ilmiötä koskevat havainnot Tämän mallina käytettävän todennäköisyysjakauman
Johdatus tilastotieteeseen Estimointi. TKK (c) Ilkka Mellin (2005) 1
 Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
Johdatus tilastotieteeseen Estimointi TKK (c) Ilkka Mellin (2005) 1 Estimointi Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin ominaisuudet TKK (c) Ilkka Mellin (2005) 2 Estimointi:
MTTTA1 Tilastomenetelmien perusteet 5 op Luento Kokonaisuudet johon opintojakso kuuluu
 10.1.2019/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 10.1.2019 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2018 10.1.2019/2
10.1.2019/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 10.1.2019 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2018 10.1.2019/2
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 18 1 Kertausta: momenttimenetelmä ja suurimman uskottavuuden menetelmä 2 Tilastollinen
Testit järjestysasteikollisille muuttujille
 Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testit järjestysasteikollisille muuttujille TKK (c) Ilkka Mellin (2007) 1 Testit järjestysasteikollisille muuttujille >> Järjestysasteikollisten
Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testit järjestysasteikollisille muuttujille TKK (c) Ilkka Mellin (2007) 1 Testit järjestysasteikollisille muuttujille >> Järjestysasteikollisten
Väliestimointi (jatkoa) Heliövaara 1
 Väliestimointi (jatkoa) Heliövaara 1 Bernoulli-jakauman odotusarvon luottamusväli 1/2 Olkoon havainnot X 1,..., X n yksinkertainen satunnaisotos Bernoulli-jakaumasta parametrilla p. Eli X Bernoulli(p).
Väliestimointi (jatkoa) Heliövaara 1 Bernoulli-jakauman odotusarvon luottamusväli 1/2 Olkoon havainnot X 1,..., X n yksinkertainen satunnaisotos Bernoulli-jakaumasta parametrilla p. Eli X Bernoulli(p).
2. TILASTOLLINEN TESTAAMINEN...
 !" # 1. 1. JOHDANTO... 3 2. 2. TILASTOLLINEN TESTAAMINEN... 4 2.1. T-TESTI... 4 2.2. RANDOMISAATIOTESTI... 5 3. SIMULOINTI... 6 3.1. OTOSTEN POIMINTA... 6 3.2. TESTAUS... 7 3.3. TESTIEN TULOSTEN VERTAILU...
!" # 1. 1. JOHDANTO... 3 2. 2. TILASTOLLINEN TESTAAMINEN... 4 2.1. T-TESTI... 4 2.2. RANDOMISAATIOTESTI... 5 3. SIMULOINTI... 6 3.1. OTOSTEN POIMINTA... 6 3.2. TESTAUS... 7 3.3. TESTIEN TULOSTEN VERTAILU...
Osa 2: Otokset, otosjakaumat ja estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2007) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Estimointi. Estimointi. Estimointi: Mitä opimme? 2/4. Estimointi: Mitä opimme? 1/4. Estimointi: Mitä opimme? 3/4. Estimointi: Mitä opimme?
 TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
TKK (c) Ilkka Mellin (2004) 1 Johdatus tilastotieteeseen TKK (c) Ilkka Mellin (2004) 2 Mitä opimme? 1/4 Tilastollisen tutkimuksen tavoitteena on tehdä johtopäätöksiä prosesseista, jotka generoivat reaalimaailman
Tilastollisen analyysin perusteet Luento 1: Lokaatio ja hajonta
 Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Testejä suhdeasteikollisille muuttujille
 Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testejä suhdeasteikollisille muuttujille TKK (c) Ilkka Mellin (007) 1 Testejä suhdeasteikollisille muuttujille >> Testit normaalijakauman
Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Testejä suhdeasteikollisille muuttujille TKK (c) Ilkka Mellin (007) 1 Testejä suhdeasteikollisille muuttujille >> Testit normaalijakauman
Tilastotieteen kertaus. Vilkkumaa / Kuusinen 1
 Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Tilastotieteen kertaus Vilkkumaa / Kuusinen 1 Motivointi Reaalimaailman ilmiöihin liittyy tyypillisesti satunnaisuutta ja epävarmuutta Ilmiöihin liittyvien havaintojen ajatellaan usein olevan peräisin
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 2. luento: Tilastolliset testit Kai Virtanen 1 Tilastollinen testaus Tutkimuksen kohteena olevasta perusjoukosta esitetään väitteitä oletuksia joita
Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 2. luento: Tilastolliset testit Kai Virtanen 1 Tilastollinen testaus Tutkimuksen kohteena olevasta perusjoukosta esitetään väitteitä oletuksia joita
Tilastollinen aineisto Luottamusväli
 Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
Tilastollinen aineisto Luottamusväli Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Tilastollinen aineisto p.1/20 Johdanto Kokeellisessa tutkimuksessa tutkittavien suureiden
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 15 1 Tilastollisia testejä Z-testi Normaalijakauman odotusarvon testaus, keskihajonta tunnetaan
Sovellettu todennäköisyyslaskenta B Antti Rasila 8. marraskuuta 2007 Antti Rasila () TodB 8. marraskuuta 2007 1 / 15 1 Tilastollisia testejä Z-testi Normaalijakauman odotusarvon testaus, keskihajonta tunnetaan
FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa. 6. luento. Pertti Palo
 FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa 6. luento Pertti Palo 1.11.2012 Käytännön asioita Harjoitustöiden palautus sittenkin sähköpostilla. PalautusDL:n jälkeen tiistaina netistä löytyy
FoA5 Tilastollisen analyysin perusteet puheentutkimuksessa 6. luento Pertti Palo 1.11.2012 Käytännön asioita Harjoitustöiden palautus sittenkin sähköpostilla. PalautusDL:n jälkeen tiistaina netistä löytyy
pisteet Frekvenssi frekvenssi Yhteensä
 806118P JOHDATUS TILASTOTIETEESEEN Loppukoe 15.3.2018 (Jari Päkkilä) 1. Kevään -17 Johdaus tilastotieteeseen -kurssin opiskelijoiden harjoitusaktiivisuudesta saatujen pisteiden frekvenssijakauma: Harjoitus-
806118P JOHDATUS TILASTOTIETEESEEN Loppukoe 15.3.2018 (Jari Päkkilä) 1. Kevään -17 Johdaus tilastotieteeseen -kurssin opiskelijoiden harjoitusaktiivisuudesta saatujen pisteiden frekvenssijakauma: Harjoitus-
MTTTA1 Tilastomenetelmien perusteet 5 op Luento , osa 1. 1 Kokonaisuudet johon opintojakso kuuluu
 5.3.2018/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 5.3.2018, osa 1 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2017
5.3.2018/1 MTTTA1 Tilastomenetelmien perusteet 5 op Luento 5.3.2018, osa 1 1 Kokonaisuudet johon opintojakso kuuluu https://www10.uta.fi/opas/opintojakso.htm?rid=14600 &idx=1&uilang=fi&lang=fi&lvv=2017
Johdatus todennäköisyyslaskentaan Normaalijakaumasta johdettuja jakaumia. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2005) 1 Normaalijakaumasta johdettuja jakaumia Johdanto χ 2 -jakauma F-jakauma t-jakauma TKK (c) Ilkka Mellin
Johdatus todennäköisyyslaskentaan Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2005) 1 Normaalijakaumasta johdettuja jakaumia Johdanto χ 2 -jakauma F-jakauma t-jakauma TKK (c) Ilkka Mellin
Tilastotieteen kertaus. Kuusinen/Heliövaara 1
 Tilastotieteen kertaus Kuusinen/Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla reaalimaailman ilmiöistä voidaan tehdä johtopäätöksiä tilanteissa, joissa
Tilastotieteen kertaus Kuusinen/Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla reaalimaailman ilmiöistä voidaan tehdä johtopäätöksiä tilanteissa, joissa
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Lineaarinen erotteluanalyysi (LDA, Linear discriminant analysis) Erotteluanalyysin avulla pyritään muodostamaan selittävistä muuttujista
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE Ratkaisut ja arvostelu < X 170
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 4.6.2013 Ratkaisut ja arvostelu 1.1 Satunnaismuuttuja X noudattaa normaalijakaumaa a) b) c) d) N(170, 10 2 ). Tällöin P (165 < X < 175) on likimain
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 4.6.2013 Ratkaisut ja arvostelu 1.1 Satunnaismuuttuja X noudattaa normaalijakaumaa a) b) c) d) N(170, 10 2 ). Tällöin P (165 < X < 175) on likimain
Otoskoko 107 kpl. a) 27 b) 2654
 1. Tietyllä koneella valmistettavien tiivisterenkaiden halkaisijan keskihajonnan tiedetään olevan 0.04 tuumaa. Kyseisellä koneella valmistettujen 100 renkaan halkaisijoiden keskiarvo oli 0.60 tuumaa. Määrää
1. Tietyllä koneella valmistettavien tiivisterenkaiden halkaisijan keskihajonnan tiedetään olevan 0.04 tuumaa. Kyseisellä koneella valmistettujen 100 renkaan halkaisijoiden keskiarvo oli 0.60 tuumaa. Määrää
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 3. marraskuuta 2007 Antti Rasila () TodB 3. marraskuuta 2007 1 / 18 1 Varianssin luottamusväli, jatkoa 2 Bernoulli-jakauman odotusarvon luottamusväli 3
Sovellettu todennäköisyyslaskenta B Antti Rasila 3. marraskuuta 2007 Antti Rasila () TodB 3. marraskuuta 2007 1 / 18 1 Varianssin luottamusväli, jatkoa 2 Bernoulli-jakauman odotusarvon luottamusväli 3
Jos nyt on saatu havaintoarvot Ü ½ Ü Ò niin suurimman uskottavuuden
 1.12.2006 1. Satunnaisjakauman tiheysfunktio on Ü µ Üe Ü, kun Ü ja kun Ü. Määritä parametrin estimaattori momenttimenetelmällä ja suurimman uskottavuuden menetelmällä. Ratkaisu: Jotta kyseessä todella
1.12.2006 1. Satunnaisjakauman tiheysfunktio on Ü µ Üe Ü, kun Ü ja kun Ü. Määritä parametrin estimaattori momenttimenetelmällä ja suurimman uskottavuuden menetelmällä. Ratkaisu: Jotta kyseessä todella
tilastotieteen kertaus
 tilastotieteen kertaus Keskiviikon 24.1. harjoitukset pidetään poikkeuksellisesti klo 14-16 luokassa Y228. Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla
tilastotieteen kertaus Keskiviikon 24.1. harjoitukset pidetään poikkeuksellisesti klo 14-16 luokassa Y228. Heliövaara 1 Mitä tilastotiede on? Tilastotiede kehittää ja soveltaa menetelmiä, joiden avulla
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Sovellettu todennäköisyyslaskenta B Antti Rasila 22. marraskuuta 2007 Antti Rasila () TodB 22. marraskuuta 2007 1 / 17 1 Epäparametrisia testejä (jatkoa) χ 2 -riippumattomuustesti 2 Johdatus regressioanalyysiin
Normaalijakaumasta johdettuja jakaumia
 Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2007) 1 Normaalijakaumasta johdettuja jakaumia >> Johdanto χ 2 -jakauma F-jakauma
Ilkka Mellin Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Normaalijakaumasta johdettuja jakaumia TKK (c) Ilkka Mellin (2007) 1 Normaalijakaumasta johdettuja jakaumia >> Johdanto χ 2 -jakauma F-jakauma
Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä
 Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä arvon Sisältö arvon Bootstrap-luottamusvälit arvon arvon Oletetaan, että meillä on n kappaletta (x 1, y 1 ),
Tilastollisen analyysin perusteet Luento 8: Lineaarinen regressio, testejä ja luottamusvälejä arvon Sisältö arvon Bootstrap-luottamusvälit arvon arvon Oletetaan, että meillä on n kappaletta (x 1, y 1 ),
Todennäköisyyden ominaisuuksia
 Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
Todennäköisyyden ominaisuuksia 0 P(A) 1 (1) P(S) = 1 (2) A B = P(A B) = P(A) + P(B) (3) P(A) = 1 P(A) (4) P(A B) = P(A) + P(B) P(A B) (5) Tapahtuman todennäköisyys S = {e 1,..., e N }. N A = A. Kun alkeistapaukset
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A050 Todennäköisyyslaskennan ja tilastotieteen peruskurssi B Satunnaismuuttujat ja todennäköisyysjakaumat Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
GeoGebra tutkivan oppimisen välineenä: havainto-hypoteesi-testaus
 GeoGebra tutkivan oppimisen välineenä: havainto-hypoteesi-testaus Mitä jäi mieleen viime viikosta? Mitä mieltä olet tehtävistä, joissa GeoGebralla työskentely yhdistetään paperilla jaettaviin ohjeisiin
GeoGebra tutkivan oppimisen välineenä: havainto-hypoteesi-testaus Mitä jäi mieleen viime viikosta? Mitä mieltä olet tehtävistä, joissa GeoGebralla työskentely yhdistetään paperilla jaettaviin ohjeisiin
1. Tilastollinen malli??
 1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
1. Tilastollinen malli?? https://fi.wikipedia.org/wiki/tilastollinen_malli https://en.wikipedia.org/wiki/statistical_model http://projecteuclid.org/euclid.aos/1035844977 Tilastollinen malli?? Numeerinen
Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia
 Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Todennäköisyyslaskenta Osa 3: Todennäköisyysjakaumia Lisää Diskreettejä jakaumia Lisää Jatkuvia jakaumia Normaalijakaumasta johdettuja jakaumia KE (2014) 1 Hypergeometrinen jakauma Hypergeometrinen jakauma
Ilkka Mellin Tilastolliset menetelmät. Osa 3: Tilastolliset testit. Tilastollinen testaus. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Tilastollinen testaus TKK (c) Ilkka Mellin (2007) 1 Tilastolliset testit >> Tilastollinen testaus Tilastolliset hypoteesit Tilastolliset
Ilkka Mellin Tilastolliset menetelmät Osa 3: Tilastolliset testit Tilastollinen testaus TKK (c) Ilkka Mellin (2007) 1 Tilastolliset testit >> Tilastollinen testaus Tilastolliset hypoteesit Tilastolliset
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 30. lokakuuta 2007 Antti Rasila () TodB 30. lokakuuta 2007 1 / 23 1 Otos ja otosjakaumat (jatkoa) Frekvenssi ja suhteellinen frekvenssi Frekvenssien odotusarvo
Sovellettu todennäköisyyslaskenta B Antti Rasila 30. lokakuuta 2007 Antti Rasila () TodB 30. lokakuuta 2007 1 / 23 1 Otos ja otosjakaumat (jatkoa) Frekvenssi ja suhteellinen frekvenssi Frekvenssien odotusarvo
Matematiikan kotitehtävä 2, MAA 10 Todennäköisyys ja tilastot
 Matematiikan kotitehtävä 2, MAA 10 Todennäköisyys ja tilastot Sievin lukio Tehtävien ratkaisut tulee olla esim. Libre officen -writer ohjelmalla tehtyjä. Liitä vastauksiisi kuvia GeoGebrasta ja esim. TI-nSpire
Matematiikan kotitehtävä 2, MAA 10 Todennäköisyys ja tilastot Sievin lukio Tehtävien ratkaisut tulee olla esim. Libre officen -writer ohjelmalla tehtyjä. Liitä vastauksiisi kuvia GeoGebrasta ja esim. TI-nSpire
H0: otos peräisin normaalijakaumasta H0: otos peräisin tasajakaumasta
 22.1.2019/1 MTTTA1 Tilastomenetelmien perusteet Luento 22.1.2019 Luku 3 2 -yhteensopivuus- ja riippumattomuustestit 3.1 2 -yhteensopivuustesti H0: otos peräisin tietystä jakaumasta H1: otos ei peräisin
22.1.2019/1 MTTTA1 Tilastomenetelmien perusteet Luento 22.1.2019 Luku 3 2 -yhteensopivuus- ja riippumattomuustestit 3.1 2 -yhteensopivuustesti H0: otos peräisin tietystä jakaumasta H1: otos ei peräisin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi
 Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Ilkka Mellin Tilastolliset menetelmät Osa 2: Otokset, otosjakaumat ja estimointi Estimointi TKK (c) Ilkka Mellin (2006) 1 Estimointi >> Todennäköisyysjakaumien parametrit ja niiden estimointi Hyvän estimaattorin
Tilastollisen analyysin perusteet Luento 2: Tilastolliset testit
 Tilastollisen analyysin perusteet Luento 2: Tilastolliset testit Sisältö Tilastollisia testejä tehdään jatkuvasti lukemattomilla aloilla. Meitä saattaa kiinnostaa esimerkiksi se, että onko miesten ja
Tilastollisen analyysin perusteet Luento 2: Tilastolliset testit Sisältö Tilastollisia testejä tehdään jatkuvasti lukemattomilla aloilla. Meitä saattaa kiinnostaa esimerkiksi se, että onko miesten ja
Todennäköisyyslaskun kertaus. Vilkkumaa / Kuusinen 1
 Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Todennäköisyyslaskun kertaus Vilkkumaa / Kuusinen 1 Satunnaismuuttujat ja todennäköisyysjakaumat Vilkkumaa / Kuusinen 2 Motivointi Kokeellisessa tutkimuksessa tutkittaviin ilmiöihin liittyvien havaintojen
Tilastollisen analyysin perusteet Luento 3: Epäparametriset tilastolliset testit
 Tilastollisen analyysin perusteet Luento 3: Epäparametriset tilastolliset testit s t ja t kahden Sisältö t ja t t ja t kahden kahden t ja t kahden t ja t Tällä luennolla käsitellään epäparametrisia eli
Tilastollisen analyysin perusteet Luento 3: Epäparametriset tilastolliset testit s t ja t kahden Sisältö t ja t t ja t kahden kahden t ja t kahden t ja t Tällä luennolla käsitellään epäparametrisia eli
V T T T I E D O T T E I T A
 2 1 1 9 V T T T I E D O T T E I T A V T T T I E D O T T E I T A Kati Tillander & Olavi Keski-Rahkonen Rakennusten syttymistaajuudet PRONTO-tietokannasta 1996 1999 Syttymistaajuustiheys (1/m 2 a) Asuinrakennukset
2 1 1 9 V T T T I E D O T T E I T A V T T T I E D O T T E I T A Kati Tillander & Olavi Keski-Rahkonen Rakennusten syttymistaajuudet PRONTO-tietokannasta 1996 1999 Syttymistaajuustiheys (1/m 2 a) Asuinrakennukset
MTTTP5, luento Otossuureita ja niiden jakaumia (jatkuu)
 21.11.2017/1 MTTTP5, luento 21.11.2017 Otossuureita ja niiden jakaumia (jatkuu) 4) Olkoot X 1, X 2,..., X n satunnaisotos (, ):sta ja Y 1, Y 2,..., Y m satunnaisotos (, ):sta sekä otokset riippumattomia.
21.11.2017/1 MTTTP5, luento 21.11.2017 Otossuureita ja niiden jakaumia (jatkuu) 4) Olkoot X 1, X 2,..., X n satunnaisotos (, ):sta ja Y 1, Y 2,..., Y m satunnaisotos (, ):sta sekä otokset riippumattomia.
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Satunnaismuuttujat ja todennäköisyysjakaumat Mitä tänään? Jos satunnaisilmiötä halutaan mallintaa matemaattisesti, on ilmiön tulosvaihtoehdot kuvattava numeerisessa muodossa. Tämä tapahtuu liittämällä
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO
 Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
Aki Taanila YHDEN SELITTÄJÄN REGRESSIO 26.4.2011 SISÄLLYS JOHDANTO... 1 LINEAARINEN MALLI... 1 Selityskerroin... 3 Excelin funktioita... 4 EKSPONENTIAALINEN MALLI... 4 MALLIN KÄYTTÄMINEN ENNUSTAMISEEN...
edellyttää valintaa takaisinpanolla Aritmeettinen keskiarvo Jos, ½ Ò muodostavat satunnaisotoksen :n jakaumasta niin Otosvarianssi Ë ¾
 ËØÙ ÓØÓ Ø Mitta-asteikot Nominaali- eli laatueroasteikko Ordinaali- eli järjestysasteikko Intervalli- eli välimatka-asteikko ( nolla mielivaltainen ) Suhdeasteikko ( nolla ei ole mielivaltainen ) Otos
ËØÙ ÓØÓ Ø Mitta-asteikot Nominaali- eli laatueroasteikko Ordinaali- eli järjestysasteikko Intervalli- eli välimatka-asteikko ( nolla mielivaltainen ) Suhdeasteikko ( nolla ei ole mielivaltainen ) Otos
Tutkimustiedonhallinnan peruskurssi
 Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
Tutkimustiedonhallinnan peruskurssi Hannu Toivonen, Marko Salmenkivi, Inkeri Verkamo hannu.toivonen, marko.salmenkivi, inkeri.verkamo@cs.helsinki.fi Helsingin yliopisto Hannu Toivonen, Marko Salmenkivi,
Tilastollisen analyysin perusteet Luento 6: Korrelaatio ja riippuvuus tilastotieteessä
 Tilastollisen analyysin perusteet Luento 6: Korrelaatio ja riippuvuus tilastotieteessä Sisältö Riippumattomuus Jos P(A B) = P(A)P(B), niin tapahtumat A ja B ovat toisistaan riippumattomia. (Keskustelimme
Tilastollisen analyysin perusteet Luento 6: Korrelaatio ja riippuvuus tilastotieteessä Sisältö Riippumattomuus Jos P(A B) = P(A)P(B), niin tapahtumat A ja B ovat toisistaan riippumattomia. (Keskustelimme
Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... 5 SISÄLLYSLUETTELO... 6 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN... 8 2. TODENNÄKÖISYYS...
 Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... 5 SISÄLLYSLUETTELO... 6 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN... 8 1.1 INDUKTIO JA DEDUKTIO... 9 1.2 SYYT JA VAIKUTUKSET... 11 TEHTÄVIÄ... 13
Sisällysluettelo ESIPUHE... 4 ALKUSANAT E-KIRJA VERSIOON... 5 SISÄLLYSLUETTELO... 6 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN... 8 1.1 INDUKTIO JA DEDUKTIO... 9 1.2 SYYT JA VAIKUTUKSET... 11 TEHTÄVIÄ... 13
χ = Mat Sovellettu todennäköisyyslasku 11. harjoitukset/ratkaisut
 Mat-2.091 Sovellettu todennäköisyyslasku /Ratkaisut Aiheet: Yhteensopivuuden testaaminen Homogeenisuuden testaaminen Riippumattomuuden testaaminen Avainsanat: Estimointi, Havaittu frekvenssi, Homogeenisuus,
Mat-2.091 Sovellettu todennäköisyyslasku /Ratkaisut Aiheet: Yhteensopivuuden testaaminen Homogeenisuuden testaaminen Riippumattomuuden testaaminen Avainsanat: Estimointi, Havaittu frekvenssi, Homogeenisuus,
Sisällysluettelo ESIPUHE KIRJAN 1. PAINOKSEEN...3 ESIPUHE KIRJAN 2. PAINOKSEEN...3 SISÄLLYSLUETTELO...4
 Sisällysluettelo ESIPUHE KIRJAN 1. PAINOKSEEN...3 ESIPUHE KIRJAN 2. PAINOKSEEN...3 SISÄLLYSLUETTELO...4 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN...6 1.1 INDUKTIO JA DEDUKTIO...7 1.2 SYYT JA VAIKUTUKSET...9
Sisällysluettelo ESIPUHE KIRJAN 1. PAINOKSEEN...3 ESIPUHE KIRJAN 2. PAINOKSEEN...3 SISÄLLYSLUETTELO...4 1. JOHDANTO TILASTOLLISEEN PÄÄTTELYYN...6 1.1 INDUKTIO JA DEDUKTIO...7 1.2 SYYT JA VAIKUTUKSET...9
2 exp( 2u), kun u > 0 f U (u) = v = 3 + u 3v + uv = u. f V (v) dv = f U (u) du du f V (v) = f U (u) dv = f U (h(v)) h (v) = f U 1 v (1 v) 2
 HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
HY, MTO / Matemaattisten tieteiden kandiohjelma Todennäköisyyslaskenta IIa, syksy 208 Harjoitus 4 Ratkaisuehdotuksia Tehtäväsarja I. Satunnaismuuttuja U Exp(2) ja V = U/(3 + U). Laske f V käyttämällä muuttujanvaihtotekniikkaa.
Sovellettu todennäköisyyslaskenta B
 Sovellettu todennäköisyyslaskenta B Antti Rasila 30. marraskuuta 2007 Antti Rasila () TodB 30. marraskuuta 2007 1 / 19 1 Lineaarinen regressiomalli ja suurimman uskottavuuden menetelmä Minimin löytäminen
Sovellettu todennäköisyyslaskenta B Antti Rasila 30. marraskuuta 2007 Antti Rasila () TodB 30. marraskuuta 2007 1 / 19 1 Lineaarinen regressiomalli ja suurimman uskottavuuden menetelmä Minimin löytäminen
Luento KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja
 1 Luento 23.9.2014 KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja 2 Ristiintaulukko Esim. Toyota Avensis farmariautoja, nelikenttä (2x2-taulukko) 3 Esim. 5.2.6. Markkinointisuunnitelma
1 Luento 23.9.2014 KERTAUSTA Kaksiulotteinen jakauma Pisteparvi, Toyota Avensis -farmariautoja 2 Ristiintaulukko Esim. Toyota Avensis farmariautoja, nelikenttä (2x2-taulukko) 3 Esim. 5.2.6. Markkinointisuunnitelma
Yhteenveto kynttilöiden sytyttämistä tulipaloista vuosina 2000-2002
 1 (12) Yhteenveto kynttilöiden sytyttämistä tulipaloista vuosina 2000-2002 Sisältö Sisältö... 1 1 Johdanto... 2 1.1 Tausta... 2 1.2 Tilastoaineisto... 2 2 Kynttilästä syttyneiden tulipalojen lukumäärä...
1 (12) Yhteenveto kynttilöiden sytyttämistä tulipaloista vuosina 2000-2002 Sisältö Sisältö... 1 1 Johdanto... 2 1.1 Tausta... 2 1.2 Tilastoaineisto... 2 2 Kynttilästä syttyneiden tulipalojen lukumäärä...
Johdatus todennäköisyyslaskentaan Kertymäfunktio. TKK (c) Ilkka Mellin (2005) 1
 Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
Johdatus todennäköisyyslaskentaan Kertymäfunktio TKK (c) Ilkka Mellin (2005) 1 Kertymäfunktio Kertymäfunktio: Määritelmä Diskreettien jakaumien kertymäfunktiot Jatkuvien jakaumien kertymäfunktiot TKK (c)
(b) Onko hyvä idea laske pinta-alan odotusarvo lähetmällä oletuksesta, että keppi katkeaa katkaisukohdan odotusarvon kohdalla?
 6.10.2006 1. Keppi, jonka pituus on m, taitetaan kahtia täysin satunnaisesti valitusta kohdasta ja muodostetaan kolmio, jonka kateetteina ovat syntyneet palaset. Kolmion pinta-ala on satunnaismuuttuja.
6.10.2006 1. Keppi, jonka pituus on m, taitetaan kahtia täysin satunnaisesti valitusta kohdasta ja muodostetaan kolmio, jonka kateetteina ovat syntyneet palaset. Kolmion pinta-ala on satunnaismuuttuja.
Harjoitus 9: Excel - Tilastollinen analyysi
 Harjoitus 9: Excel - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen regressioanalyysiin
Harjoitus 9: Excel - Tilastollinen analyysi Mat-2.2107 Sovelletun matematiikan tietokonetyöt Syksy 2006 Mat-2.2107 Sovelletun matematiikan tietokonetyöt 1 Harjoituksen aiheita Tutustuminen regressioanalyysiin
805306A Johdatus monimuuttujamenetelmiin, 5 op
 monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Logistinen regressioanalyysi Vastemuuttuja Y on luokiteltu muuttuja Pyritään mallittamaan havaintoyksikön todennäköisyyttä kuulua
monimuuttujamenetelmiin, 5 op syksy 2018 Matemaattisten tieteiden laitos Logistinen regressioanalyysi Vastemuuttuja Y on luokiteltu muuttuja Pyritään mallittamaan havaintoyksikön todennäköisyyttä kuulua
Tilastollisen analyysin perusteet Luento 1: Lokaatio ja hajonta
 Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Tilastollisen analyysin perusteet Luento 1: ja hajonta Sisältö Havaittujen arvojen jakauma Havaittujen arvojen jakaumaa voidaan kuvailla ja esitellä tiivistämällä havaintoarvot sopivaan muotoon. Jakauman
Matemaatikot ja tilastotieteilijät
 Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
Matemaatikot ja tilastotieteilijät Matematiikka/tilastotiede ammattina Tilastotiede on matematiikan osa-alue, lähinnä todennäköisyyslaskentaa, mutta se on myös itsenäinen tieteenala. Tilastotieteen tutkijat
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Jos nollahypoteesi pitää paikkansa on F-testisuuren jakautunut Fisherin F-jakauman mukaan
 17.11.2006 1. Kahdesta kohteesta (A ja K) kerättiin maanäytteitä ja näistä mitattiin SiO -pitoisuus. Tulokset (otoskoot ja otosten tunnusluvut): A K 10 16 Ü 64.94 57.06 9.0 7.29 Oletetaan mittaustulosten
17.11.2006 1. Kahdesta kohteesta (A ja K) kerättiin maanäytteitä ja näistä mitattiin SiO -pitoisuus. Tulokset (otoskoot ja otosten tunnusluvut): A K 10 16 Ü 64.94 57.06 9.0 7.29 Oletetaan mittaustulosten
Mat Sovellettu todennäköisyyslasku A
 TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 5 (vko 4/003) (Aihe: jatkuvia satunnaismuuttujia ja jakaumia, sekamalli, Laininen luvut 5.1 5.7, 6.1 6.3)
TKK / Systeemianalyysin laboratorio Nordlund Mat-.090 Sovellettu todennäköisyyslasku A Harjoitus 5 (vko 4/003) (Aihe: jatkuvia satunnaismuuttujia ja jakaumia, sekamalli, Laininen luvut 5.1 5.7, 6.1 6.3)
Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä palamisaikaa?
 21.3.2019/1 MTTTP1, luento 21.3.2019 7 TILASTOLLISEN PÄÄTTELYN PERUSTEITA Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä
21.3.2019/1 MTTTP1, luento 21.3.2019 7 TILASTOLLISEN PÄÄTTELYN PERUSTEITA Miten voidaan arvioida virheellisten komponenttien osuutta tuotannossa? Miten voidaan arvioida valmistajan kynttilöiden keskimääräistä
Lisätehtäviä ratkaisuineen luentomonisteen lukuun 6 liittyen., jos otoskeskiarvo on suurempi kuin 13,96. Mikä on testissä käytetty α:n arvo?
 MTTTP5, kevät 2016 15.2.2016/RL Lisätehtäviä ratkaisuineen luentomonisteen lukuun 6 liittyen 1. Valitaan 25 alkion satunnaisotos jakaumasta N(µ, 25). Olkoon H 0 : µ = 12. Hylätään H 0, jos otoskeskiarvo
MTTTP5, kevät 2016 15.2.2016/RL Lisätehtäviä ratkaisuineen luentomonisteen lukuun 6 liittyen 1. Valitaan 25 alkion satunnaisotos jakaumasta N(µ, 25). Olkoon H 0 : µ = 12. Hylätään H 0, jos otoskeskiarvo
Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria.
 5.10.2017/1 MTTTP1, luento 5.10.2017 KERTAUSTA Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria. Muodostetaan väli, joka peittää parametrin etukäteen valitulla todennäköisyydellä,
5.10.2017/1 MTTTP1, luento 5.10.2017 KERTAUSTA Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria. Muodostetaan väli, joka peittää parametrin etukäteen valitulla todennäköisyydellä,
ABHELSINKI UNIVERSITY OF TECHNOLOGY
 Tilastollinen testaus Tilastollinen testaus Tilastollisessa testauksessa tutkitaan tutkimuskohteita koskevien oletusten tai väitteiden paikkansapitävyyttä havaintojen avulla. Testattavat oletukset tai
Tilastollinen testaus Tilastollinen testaus Tilastollisessa testauksessa tutkitaan tutkimuskohteita koskevien oletusten tai väitteiden paikkansapitävyyttä havaintojen avulla. Testattavat oletukset tai
Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria.
 6.10.2016/1 MTTTP1, luento 6.10.2016 KERTAUSTA JA TÄYDENNYSTÄ Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria. Muodostetaan väli, joka peittää parametrin etukäteen valitulla
6.10.2016/1 MTTTP1, luento 6.10.2016 KERTAUSTA JA TÄYDENNYSTÄ Luottamisvälin avulla voidaan arvioida populaation tuntematonta parametria. Muodostetaan väli, joka peittää parametrin etukäteen valitulla
Mat Tilastollisen analyysin perusteet, kevät 2007
 Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen 1 Jakaumaoletuksien testaamiseen soveltuvat testit χ 2 -yhteensopivuustesti yksi otos otoksen
Mat-2.2104 Tilastollisen analyysin perusteet, kevät 2007 4. luento: Jakaumaoletuksien testaaminen Kai Virtanen 1 Jakaumaoletuksien testaamiseen soveltuvat testit χ 2 -yhteensopivuustesti yksi otos otoksen
6. laskuharjoitusten vastaukset (viikot 10 11)
 6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
6. laskuharjoitusten vastaukset (viikot 10 11) 1. a) Sivun 102 hypergeometrisen jakauman määritelmästä saadaan µ µ 13 39 13! 13 12 11 10 9 µ 0! 8! 1! 2 2! 2 1 0 49 48! 47!! 14440 120 31187200 120 1287
Tutkimusongelmia ja tilastollisia hypoteeseja: Perunalastupussien keskimääräinen paino? Nollahypoteesi Vaihtoehtoinen hypoteesi (yksisuuntainen)
 1 MTTTP3 Luento 29.1.2015 Luku 6 Hypoteesien testaus Tutkimusongelmia ja tilastollisia hypoteeseja: Perunalastupussien keskimääräinen paino? H 0 : µ = µ 0 H 1 : µ < µ 0 Nollahypoteesi Vaihtoehtoinen hypoteesi
1 MTTTP3 Luento 29.1.2015 Luku 6 Hypoteesien testaus Tutkimusongelmia ja tilastollisia hypoteeseja: Perunalastupussien keskimääräinen paino? H 0 : µ = µ 0 H 1 : µ < µ 0 Nollahypoteesi Vaihtoehtoinen hypoteesi
Ongelma: Poikkeaako perusjoukon suhteellinen osuus vertailuarvosta?
 Yhden otoksen suhteellisen osuuden testaus Ongelma: Poikkeaako perusjoukon suhteellinen osuus vertailuarvosta? Hypoteesit H 0 : p = p 0 H 1 : p p 0 tai H 1 : p > p 0 tai H 1 : p < p 0 Suhteellinen osuus
Yhden otoksen suhteellisen osuuden testaus Ongelma: Poikkeaako perusjoukon suhteellinen osuus vertailuarvosta? Hypoteesit H 0 : p = p 0 H 1 : p p 0 tai H 1 : p > p 0 tai H 1 : p < p 0 Suhteellinen osuus
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 6A Tilastolliset luottamusvälit Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 6A Tilastolliset luottamusvälit Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Syksy 2016,
Maximum likelihood-estimointi Alkeet
 Maximum likelihood-estimointi Alkeet Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Maximum likelihood-estimointi p.1/20 Maximum Likelihood-estimointi satunnaismuuttujan X
Maximum likelihood-estimointi Alkeet Keijo Ruotsalainen Oulun yliopisto, Teknillinen tiedekunta Matematiikan jaos Maximum likelihood-estimointi p.1/20 Maximum Likelihood-estimointi satunnaismuuttujan X
Matematiikan kotitehtävä 2, MAA 10 Todennäköisyys ja tilastot
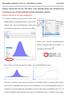 Matematiikan kotitehtävä 2, MAA 10 Todennäköisyys ja tilastot Sievin lukio Tehtävien ratkaisut tulee olla esim. Libre officen -writer ohjelmalla tehtyjä. Liitä vastauksiisi kuvia GeoGebrasta ja esim. TI-nSpire
Matematiikan kotitehtävä 2, MAA 10 Todennäköisyys ja tilastot Sievin lukio Tehtävien ratkaisut tulee olla esim. Libre officen -writer ohjelmalla tehtyjä. Liitä vastauksiisi kuvia GeoGebrasta ja esim. TI-nSpire
Tilastollisen analyysin perusteet Luento 10: Johdatus varianssianalyysiin
 Tilastollisen analyysin perusteet Luento 10: Sisältö Varianssianalyysi Varianssianalyysi on kahden riippumattoman otoksen t testin yleistys. Varianssianalyysissä perusjoukko koostuu kahdesta tai useammasta
Tilastollisen analyysin perusteet Luento 10: Sisältö Varianssianalyysi Varianssianalyysi on kahden riippumattoman otoksen t testin yleistys. Varianssianalyysissä perusjoukko koostuu kahdesta tai useammasta
HAVAITUT JA ODOTETUT FREKVENSSIT
 HAVAITUT JA ODOTETUT FREKVENSSIT F: E: Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies (1) 59 28 4 91 Nainen (2) 5 14 174 193 Yhteensä 64 42 178 284 Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies
HAVAITUT JA ODOTETUT FREKVENSSIT F: E: Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies (1) 59 28 4 91 Nainen (2) 5 14 174 193 Yhteensä 64 42 178 284 Usein Harvoin Ei tupakoi Yhteensä (1) (2) (3) Mies
Estimointi populaation tuntemattoman parametrin arviointia otossuureen avulla Otossuure satunnaisotoksen avulla määritelty funktio
 17.11.2015/1 MTTTP5, luento 17.11.2015 Luku 5 Parametrien estimointi 5.1 Piste-estimointi Estimointi populaation tuntemattoman parametrin arviointia otossuureen avulla Otossuure satunnaisotoksen avulla
17.11.2015/1 MTTTP5, luento 17.11.2015 Luku 5 Parametrien estimointi 5.1 Piste-estimointi Estimointi populaation tuntemattoman parametrin arviointia otossuureen avulla Otossuure satunnaisotoksen avulla
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 5B Bayesläiset piste- ja väliestimaatit Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
MS-A0501 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 5B Bayesläiset piste- ja väliestimaatit Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto
Johdatus tn-laskentaan torstai 16.2.2012
 Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
Johdatus tn-laskentaan torstai 16.2.2012 Muunnoksen jakauma (ei pelkkä odotusarvo ja hajonta) Satunnaismuuttujien summa; Tas ja N Vakiokerroin (ax) ja vakiolisäys (X+b) Yleinen muunnos: neulanheittoesimerkki
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi
 MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
MS-A0503 Todennäköisyyslaskennan ja tilastotieteen peruskurssi 2A Satunnaismuuttujan odotusarvo Lasse Leskelä Matematiikan ja systeemianalyysin laitos Perustieteiden korkeakoulu Aalto-yliopisto Lukuvuosi
Kaavakokoelma, testikaaviot ja jakaumataulukot liitteinä. Ei omia taulukoita! Laskin sallittu.
 Ka6710000 TILASTOLLISEN ANALYYSIN PERUSTEET 2. VÄLIKOE 9.5.2007 / Anssi Tarkiainen Kaavakokoelma, testikaaviot ja jakaumataulukot liitteinä. Ei omia taulukoita! Laskin sallittu. Tehtävä 1. a) Gallupissa
Ka6710000 TILASTOLLISEN ANALYYSIN PERUSTEET 2. VÄLIKOE 9.5.2007 / Anssi Tarkiainen Kaavakokoelma, testikaaviot ja jakaumataulukot liitteinä. Ei omia taulukoita! Laskin sallittu. Tehtävä 1. a) Gallupissa
pitkittäisaineistoissa
 Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Puuttuvan tiedon ongelma p. 1/18 Puuttuvan tiedon ongelma pitkittäisaineistoissa Tapio Nummi tan@uta.fi Matematiikan, tilastotieteen ja filosofian laitos Tampereen yliopisto mtl.uta.fi/tilasto/sekamallit/puupitkit.pdf
Ilkka Mellin Todennäköisyyslaskenta. Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat. Kertymäfunktio. TKK (c) Ilkka Mellin (2007) 1
 Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
Ilkka Mellin Todennäköisyyslaskenta Osa 2: Satunnaismuuttujat ja todennäköisyysjakaumat Kertymäfunktio TKK (c) Ilkka Mellin (2007) 1 Kertymäfunktio >> Kertymäfunktio: Määritelmä Diskreettien jakaumien
3. laskuharjoituskierros, vko 6, ratkaisut
 Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
Mat-.9 Sovellettu todennäköisyyslasku, kevät - eliövaara, Palo, Mellin. laskuharjoituskierros, vko 6, ratkaisut D. Uurnassa A on 4 valkoista ja 6 mustaa kuulaa ja uurnassa B on 6 valkoista ja 4 mustaa
