LAPPEENRANNAN TEKNILLINEN KORKEAKOULU Kemiantekniikan osasto Prosessitekniikan laboratorio
|
|
|
- Timo Laaksonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 LAPPEENRANNAN TEKNILLINEN KORKEAKOULU Kemiantekniikan osasto Prosessitekniikan laboratorio DIPLOMITYÖ: PYRIITTIPASUTTEEN SULAKALVOSULFATOINTIPROSESSI Työn tarkastaja Työn ohjaaja v.s. prof. Marja Oja tekn. lis. Matti Hiltunen Karhulassa Pasi Makkonen Mällinkatu 14 A KARHULA
2 TIIVISTELMÄ Pasi Makkonen Pyriittipasutteen sulakalvosulfatointiprosessi Diplomityö, Lappeenrannan teknillinen korkeakoulu Kemiantekniikan osasto, Lappeenranta lehteä, 64 kuvaa, 24 taulukkoa, 10 liitettä Tarkastaja Hakusanat: Keywords: vs. professori Marja Oja pasute, hematiitti, sinkkisulfaatti, sulfatointi, sulakalvosulfatointi, diffuusio, cinder, hematite, zinc sulphate, sulphation, melt film sulphation, diffusion Tässä työssä tutkittiin Kemira Oy:n Siilinjärven tehtaiden pasutteen sisältämän sinkin sulfatointia vesiliukoiseen muotoon sulakalvosulfatoinnilla. Kirjallisuusosassa perehdyttiin sulkalvosulfatoinnin teoriaan ja esiteltiin mittauksissa käytetyn pilot-laitteiston toiminnan kannalta oleellisia teorioita. Kokeellisessa osassa tehtiin sulakalvosulfatointi-pilot-laitteistolla 29 koeajon sarja ja mitattiin tulosten käsittelyn kannalta tärkeitä pasutteen ominaisuuksia laboratorio-olosuhteissa. Mittaustuloksista laskettiin ferrisulfaatin konversiot CFB-reaktorissa sekä sinkkisulfaatin konversiot CFB-reaktorissa ja kuilu-uunissa, sekä laadittiin mallit hematiitin ja sinkin sulfatoitumiselle pilot-laitteistossa. Pasutteen sisältämän, veteen liukenemattoman sinkin pitoisuus saatiin parhaassa koeajossa arvoon 200 ppm. Rautaruukin vaatimus teräksen raaka-aineeksi käytettävälle rautaoksidille on enintään 150 ppm sinkkiä. Koeajoissa ei kuitenkaan päästy sinkin sulfatoitumisen kannalta optimaalisiin olosuhteisiin. Koeajoja vaikeutti holvaantuminen ja pasutteen massavirran pysähtyminen kuilu-uunissa. Lisäksi lämmönsiirto kuilu-uunissa oli oletettua hitaampaa. CFB-reaktori toimi moitteettomasti pasutteen kaliumsulfaattipitoisuuteen 5 p-% saakka, tätä suuremmilla pasutteen kaliumsulfaattipitoisuuksilla CFB-reaktorin sekundäärikierto tukkeutui nopeasti.
3 ABSTRACT Pasi Makkonen Melt Film Sulphation Process for Pyrite Cinder Master's thesis, Lappeenranta University of Technology Department of Chemical Engineering, Lappeenranta pages, 64 pictures, 24 tables, 10 appendixes Supervisor Keywords: acting professor Marja Oja cinder, hematite, zinc sulphate, sulphation, melt film sulphation, diffusion The purpose of this study was to research sulphation of zinc in cinder into water soluble form by melt film sulphation. Cinder used in experiments was produced as side product of sulphur acid at Kemira Oy in Siilinjärvi. At the literature study the purpose was to get acquainted with the existing theory of melt film sulphation and also to get familiar with theories about the pilot-plant equipment and rate processes occurring in it. At the experimental part 29 test runs with the pilot-plant were performed. The experimental part also included laboratory measurements of cinder properties. From the results ferric sulphate conversion in CFB-reactor and zinc sulphate conversions in CFB-reactor and in vertical kiln were calculated. From calculated results models for sulphation of hematite and zinc in the pilotplant were formed. At the best test run the amount of not-water-soluble zinc in cinder was 200 ppm. Rautaruukki demands that the amount of zinc in cinder to be used for steel making must not be over 150 ppm. However, the optimum conditions for the sulphation of zinc in the pilot-plant were not reached. Problems which took place during test runs were bridging over of cinder and stopping of mass flow of cinder in vertical kiln. The actual heat transfer rate inside the vertical kiln was slower than the expected rate. The CFB-reactor performed without faults up to 5 w-% of potassium sulphate in cinder. With larger potassium sulphate concentrations in the feed stream the secondary return of CFB-reactor clogged up.
4 SISÄLLYSLUETTELO TIIVISTELMÄ ABSTRACT SISÄLLYSLUETTELO SYMBOLIT JA LYHENTEET 1 JOHDANTO 2 SULAKALVOSULFATOINTI 2.1 Sulakalvosulfatoinnin teoria 2.2 Sulakalvosulfatoinnin termodynaamiikka 2.3 Sulakalvosulfatoinnin reaktiokinetiikasta 2.4 Aineensiirto sulakalvosulfatoinnissa Aineensiirto kaasusta partikkeliin Aineensiirto jauhepatjassa 2.5 Rikkitrioksidin muodostuminen 2.6 Rautaoksidin sulfatoituminen 2.7 Sinkkioksidin ja sinkkiferriitin sulfatoituminen 2.8 Muut reaktiot 3 SULAKALVOSULFATOINTIPROSESSI 3.1 Yleistä sulakalvosulfatointiprosessista 3.2 Prosessin kuvaus 3.3 Prosessilaitteet CFB-reaktori Kaasusyklonit Kuilu-uuni Muut prosessilaitteet ja instrumentointi 3.4 Prosessin ainetaseet 3.5 Prosessin energiataseet 3.6 Lämmönsiirto Lämmönsiirto johtumalla Lämmönsiirto CFB-reaktorissa Lämmönsiirto kuilu-uunissa 4 LEIJUKERROSPROSESSIN UUDET METALLURGISET SOVELLUS- MAHDOLLISUUDET 5 TALOUDELLINEN TARKASTELU 5.1 Kustannuslaskennan perusteet 5.2 Sulakalvosulfatointiprosessin laitekustannukset 5.3 Liuotusprosessin laitekustannukset 5.4 Muut kustannukset 5.5 Kannattavuus
5 6 KOEAJOT 6.1 Laitteiston kuvaus CFB-reaktori Kuilu-uuni 6.2 Koeajojen toteutus Laitteiston kalibrointi Koeajot Koeajoja edeltäneet toimenpiteet Prosessiarvojen säätäminen Näytteenotto ja analysointi 6.3 Mittaukset Paineen mittaus Lämpötilan mittaus Happimittaus Pölymittaus Partikkelikokokanalyysit Ominaispinta-alan mittaus Huokoisuuden mittaus Elektronimikroskopia Kuva-analyysi 7 KOEAJOJEN TULOKSET 7.1 Syötteen ominaisuudet 7.2 Ferrisulfaatin muodostus Ferrisulfaatin muodostuminen CFB-reaktorissa Malli ferrisulfaatin muodos-tumiselle CFB-reaktorissa 7.3 Sinkin sulfatoituminen Sinkin sulfatoituminen CFB-reaktorissa Malli sinkin sulfatoitumiselle CFB-reaktorissa Sinkin sulfatoituminen kuilu-uunissa Malli sinkin sulfatoitumiselle kuilu-uunissa 7.4 Kuparin sulfatoituminen 7.5 Muut koeajot Panosajot CFB-reaktorilla Sulakalvosulfatoidun tuotteen valmistus liuotuskokeita varten 8 AINEENSIIRTO REAKTIONOPEUTTA KONTROLLOIVANA TEKIJÄNÄ 9 TULOSTEN TARKASTELU 9.1 CFB-reaktori 9.2 Kuilu-uuni 9.3 Kaasusyklonit 9.4 Muita huomioita 10 YHTEENVETO 11 JATKOTOIMENPITEET 12 KIRJALLISUUS
6 TYÖSSÄ KÄYTETYT SYMBOLIT JA LYHENTEET Symbolit A lähtöaine, - Ac syklonin palautusputken poikkileikkauspinta-ala, m 2 Ah,conv lämpöhäviöpinta-ala, m 2 Ap partikkelin kaasua vastaan kohtisuorassa oleva pinta-ala, m 2 As leijureaktorin poikkileikkauspinta-ala, m 2 a stökiometrinen kerroin, - a reaktion kertaluku, yhtälö (16), - ah kerroin, - atd terminen diffusiviteetti, W/m 2 K B lähtöaine, - Bc syklonin tuloputken halkaisija, m b stökiometrinen kerroin, - b reaktion kertaluku, yhtälö (16), - C tuote, - C absorptioenergiavakio, yhtälö (104), - CA,c komponentin A konsentraatio ytimen pinnalla, mol/dm 3 CA,g komponentin A konsentraatio kaasussa, mol/dm 3 CA,s komponentin A konsentraatio kiintoaineessa, mol/dm 3 Cd hiukkasen muotokerroin, - Cx aineen x konsentraatio, mol/dm 3 c stökiometrinen kerroin, - c reaktion kertaluku, yhtälö (16), - cp,g kaasun ominaislämpökapasiteetti, J/mol K D tuote, - DAB diffuusiokerroin A:n ja B:n välillä, m/s D e AB kokonaisdiffuusiokerroin A:n ja B:n välillä, m/s Dc syklonin halkaisija, m De kaasun diffuusiokerroin tuotekerroksen ja kaasun välillä, m/s Dg,p diffuusiokerroin kaasusta partikkeliin, m/s Dk Knudsenin diffuusiokerroin, m/s Dk,A diffuusiokerroin kaasusta partikkeliin, m/s Dp putken halkaisija, m Du yhdistetty diffuusiokerroin, m/s d stökiometrinen kerroin, - d reaktion kertaluku, yhtälö (16), - dp partikkelin halkaisija, m huokosen halkaisija, m dpore
7 dp,min pienin syklonilla erotettavissa oleva partikkelikoko, m ds,50 partikkelikoko, josta erottuu 50 %, m dt leijukerroksen halkaisija, m dv redusoitu halkaisija, m dv tilavuuden muutos, m 3 /s d partikkelissa olevien huokosten halkaisija, m Ea aktivoitumisenergia, J/mol ET,c syklonin erotustehokkuus, - Fp virtauksen partikkeliin aiheuttama voima, N Gc(x) syklonin erotustehokkuus, - Glähtöaineet lähtöaineiden Gibbsin vapaa energia, J/mol Gs kiintoaineen massavirran tiheys, kg/m 2 s Gtuotteet reaktiotuotteiden Gibbsin vapaa energia, J/mol g putoamiskiihtyvyys, m/s 2 Hc syklonin tuloputken korkeus, m ir sisäinen korko, - Kc kokeellisesti määritetty kerroin,- Kconv johtumisen kokonaislämmösiirtymiskerroin, W/m 2 K KFe2(SO4)3 ferrisulfaatin tasapainovakio, - KZnSO4 sinkkisulfaatin tasapainovakio, - Kp termodynaaminen tasapainovakio, - kg aineensiirtokerroin kaasufilmin läpi, m/s ks aineensiirtokerroin tuotekerroksesta ytimeen, m/s kv venturin korjauskerroin, - k0 frekvenssitekijä, - k1 reaktion nopeusvakio, m 3 /mol s k1' SO3:n muodostumisen nopeusvakio, m 3 /mol s k2 käänteisreaktion nopeusvakio, m 3 /mol s k2' SO3:n hajoamisen nopeusvakio, m 3 /mol s k3' SO3:n muodostumisen nopeusvakio katalyytin läsnäollessa, m 3 /mol s k4' SO3:n hajoamisen nopeusvakio katalyytin läsnäollessa, m 3 /mol s Lh lämmönsiirtoelementin pituus, m Lmf leijukerroksen korkeus minimileijutusnopeudella, m M suoran kulmakerroin, - MA A:n moolimassa, - m kokonaismassa, kg ms leijukerroksen massa, kg macc CFB-reaktoriin kertyvä massavirta, kg/s mi,g CFB-reaktoriin tulevan prosessikaasun massavirta, kg/s mi,s CFB-reaktoriin syötettävän pasutteen massavirta, kg/s mi,sk nestekaasun palamisesta syntyvän savukaasun massavirta, kg/s CFB-reaktorista poistuvan kaasun massavirta, kg/s mo,g
8 kuilu-uunista poistuvan kiintoaineen massavirta, kg/s CFB-reaktorista poistuvan pasutteen massavirta, kg/s kuilu-uuniin kertyvä massavirta, kg/s kiintoaineen massavirta sykloniin, kg/s syklonin alitteen massavirta, kg/s N vakio, - Np partikkeliin aiheutuva noste, N n eksponentti, - n reaktion kokonaiskertaluku, yhtälö (16), - ni investoinnin pitoaika, a na aineen A ainemäärä, mol na A:n ainevirta, mol/s nb B:n ainevirta, mol/s nmax maksimiainemäärä, mol Pi investointimeno, mk p paine, Pa ps saturaatiopaine, Pa p0 referenssipaine, Pa Qh,conv lämpöhäviö johtumalla, J/s Qi,g kaasun mukana tuleva lämpömäärä, J/s Qi,s pasutteen mukana tuleva lämpömäärä, J/s R moolinen kaasuvakio, J/mol K Ri vuosituotto, mk Rp partikkelin säde, m r sylinterikoordinaatiston r-koordinaatti, - ra syklonin poistoputken säde, m ra reaktionopeus, mol/s ra1 reaktion nopeus, mol/s ra2 käänteisreaktion nopeus, mol/s ri syklonin sisäsäde, m rm syklonin keskimääräinen säde, m Sc ytimen pinta-ala, m 2 mor,s mo,s mr,acc ms,in ms,r Sex partikkelin ulkokuoren pinta-ala, m 2 Sr reaktiotuotteen pinta-ala, m 2 si T Tg Ti To Tr Tref T0 materiaalin paksuus, m lämpötila, K kaasun lämpötila, K lämpötila sisällä, K lämpötila ulkona, K pasutteen lämpötila kuilu-uunissa, K referenssilämpötila, K referenssilämpötila, K
9 t aika, s tf ulkopinnan lämpötila, K V tilavuus, m 3 Vm monomolekulaarisen kerroksen tilavuus, m 3 Vr kuilu-uunin tilavuus, m 3 Vin tilavuusvirta reaktoriin, m 3 /s Vout tilavuusvirta reaktorista, m 3 /s Vs,in kiintoaineen tilavuusvirta kuilu-uuniin, m 3 /s WZn,f sinkin massaosuus syötteessä, kg/kg WZnFe2O4 sinkkiferriitin massaosuus, kg/kg wa kaasun nopeus syklonin poistoputkessa, m/s wc kaasun tulonopeus sykloniin, m/s wg kaasun virtausnopeus partikkelin ohi, m/s wi kaasun nopeus syklonin sisällä, m/s wm kaasun keskimääräinen nopeus syklonissa, m/s wmf minimileijutusnopeus, m/s wsr leijukerroksen nousunopeus, m/s wt maksimileijutusnopeus, m/s XB konversio B:n suhteen, - XFe2(SO4)3 ferrisulfaatin konversio, - XZnSO4 sinkkisulfaatin konversio, - X1 parametri, - X2 parametri, - X3 parametri, - X4 parametri, - xa A:n mooliosuus, mol/mol xb B:n mooliosuus, mol/mol xfe2(so4)3 ferrisulfaatin mooliosuus, mol/mol xk2so4 kaliumsulfaatin mooliosuus, mol/mol xso3 rikkitrioksidin mooliosuus, mol/mol xznso4 sinkkisulfaatin mooliosuus, mol/mol YZnSO4 sinkin sulfatoitumisaste, - [O2] hapen pitoisuus, mol/mol [SO2] rikkidioksidin pitoisuus, mol/mol [SO3] rikkitrioksidin pitoisuus, mol/mol
10 Kreikkalaiset aakkoset αh lämmönsiirtymiskerroin, W/m 2 K αh,cfb kokonaislämmönsiirtymiskerroin CFB-reaktorissa, W/m 2 K αi sisäpuolinen lämmönsiirtymiskerroin, W/m 2 K βo ulkopuolinen lämmönsiirtymiskerroin, W/m 2 K βg kaasun lämpölaajenemiskerroin, 1/K β1 regressioparametri, - β2 regressioparametri, - β3 regressioparametri, - β4 regressioparametri, - γ elohopean pintajännitys, G reaktion Gibbsin vapaa energia, J/mol G 0 Gibbsin vapaa energia, J/mol H 0 entalpian muutos, J/mol H 0 T entalpian muutos lämpötilassa T, J/mol p paine-ero leijukerroksen yli, Pa ph,c painehäviö kaasusyklonissa, Pa pmf painehäviö leijukerroksessa minimileijutusnopeudella, Pa pv venturin aiheuttama paine-ero, Pa S 0 entropian muutos, J/mol K S 0 T entropian muutos lämpötilassa T, J/mol K Ts,o lämpötilaero pinnan ja ilman välillä., K εmf leijukerroksen huokoisuus minimileijutusnopeudella, - εp partikkelin huokoisuus, - ξd virtausvastuskerroin, - ηc syklonin erotustehokkuus, - λc syklonin seinämäkitka, - λg kaasun lämmönjohtavuus, W/m K λi materiaalin lämmönjohtavuus, W/m K λs pasutteen lämmönjohtavuus, W/m K µg kaasun dynaaminen viskositeetti, Pa s ρb komponentin B moolitiheys, mol/m 3 ρg kaasun tiheys, kg/m 3 ρm keskimääräinen tiheys, kg/m 3 ρs partikkelin tiheys, kg/m 3 Σmi,i Σni ΣQi ΣQo CFB-reaktoriin tulevien polvi- purso- ja laimennusilmojen yhteenlaskettu massavirta, kg/s kokonaisainemäärä, mol prosessiin tuleva lämpömäärä, J/s prosessista poistuva lämpömäärä, J/s
11 τc aika, joka kuluu 100 % konversioon, s τg,c kaasun viipymäaika syklonissa, s τp huokosten kiemurtelavuus, - τr pasutteen viipymäaika kuilu-uunissa, s τs materiaalin viipymäaika kuilu-uunissa, s Φs hiukkasen muotokerroin, - φ' lämpötila, K Dimensiottomat luvut Bi Fo Frmf Gr Nu Pr Re Rec Rep,mf Rx Sc Vi θ θm θr θ0 Biotin luku dimensioton aika Frouden luku minimileijutusnopeudella Grashofin luku Nusseltin luku Prandtlin luku Reynolds-luku Syklonin Reynolds-luku Reynolds-luku partikkelin ohi minimileijutusnopeudella dimensioton etäisyys pinnasta Schmidtin luku viskositeettisuhde dimensioton lämpötila dimensioton keskilämpötila kuilu-uunissa dimensioton lämpötila etäisyydellä r dimensioton lämpötila pinnalla Lyhenteet: CFB Me p-% mol-% Circulating Fluidized Bed, kiertoleijukerros metalli painoprosentti mooliprosentti Muut merkinnät: p xa F(r) f(r) fin(x) fr(x) paineen muutosgradientti A:n mooliosuuden muutosgradientti integraalifunktio funktio syötteen tiheysfunktio alitteen tiheysfunktio
12 1 1 JOHDANTO Tutkimuksen tarkoituksena oli selvittää mahdollisuus sulfatoida pyriitin poltossa syntyvän pasutuskuonan sisältämät ei-rautametallit vesiliukoiseen muotoon sulakalvosulfatoinnilla. Sulakalvosulfatoinnissa metallioksidit ja metalliferriitit sulfatoidaan noin 1000 K lämpötilassa lisäaineiden läsnäollessa. Lisäaineina käytetään matalissa lämpötiloissa sulavia alkalimetallisuoloja ja ferrisulfaattia. Alkalimetallisuolat ja ferrisulfaatti muodostavat metallin pinnalle sulan kerroksen, joka nopeuttaa diffuusiota. Rastas ja Saikkonen /1/ ovat tutkineet pasutteen sulfatointia sulakalvomenetelmällä. Kemira Oy:n Siilinjärven tehtailla rikkihapon valmistuksessa tarvittava rikkidioksidi valmistetaan polttamalla pyriittiä. Pyriitti ja markasiitti, joiden kemiallinen koostumus on FeS2, ovat Sanderin et al. /2/ mukaan tärkeimmät rautasulfidimineraalit. Pyriitti on harmaa tai vihertävä mineraali, joka sisältää usein myös pyrrotiittiä tai magnetopyriittiä, Fe7S8. Lisäksi pyriittimalmissa on usein jonkin verran ei-rautametalleja, muun muassa sinkkiä, kuparia ja lyijyä, sekä pienissä pitoisuuksissa kobolttia, nikkeliä, mangaania ja arseenia. Pyriitin polttaminen tapahtuu Kemira Oy:n Siilinjärven tehtailla Lurgin leijukerrosprosessilla, kuva 1. Pyriittirikaste, joka sisältää pölyämisen estämiseksi 7 p-% vettä, syötetään leijukerrosuuniin, jossa rikaste poltetaan ilmakertoimen ollessa 1,05...1,1. Saatu tuotekaasu sisältää 14 mol-% rikkidioksidia, 1,5 mol-% happea, 6 mol-% vettä ja 78,5 mol-% typpeä. Prosessissa syntyy lisäksi pasutuskuonaa. 1 Kuva 1. Lurgin prosessin mukaisen leijukerrospasutuksen periaatekaavio, Sander et.al. /2, s. 181/. Pasutuskuona, josta käytetään myös nimitystä pasute, sisältää enimmäkseen ferrioksidia, Fe2O3. Ferrioksidi eli hematiitti esiintyy kahtena faasina: - ja -hematiittina, joilla on toisistaan poikkeava kiderakenne. Hematiitti on alle 200 C lämpötilassa väriltään punaista tai mustaa, väri muuttuu transitiolämpötilan jälkeen mustaksi. Pasute sisältää lisäksi jonkin verran muiden metallien oksideja ja metalliferriittejä. Tärkeimmät pasutteen sisältämät alkuaineet ja yhdisteet on esitetty taulukossa I.
13 2 TAULUKKO I Pasutteen alkuainekoostumus ja tärkeimmät yhdisteet Vuotoveden /3/ mukaan. Alkuaine/ yhdiste p-% Fe2O3 95,94 SiO2 1,86 S 0,64 Al2O3 0,39 CaO 0,30 BaO 0,27 MgO 0,26 Zn 0,19 Na2O 0,14 Cu 0,07 K2O 0,04 Co 0,01 Kemira Oy:n Siilinjärven tehtailla syntyvä pasute ei sellaisenaan kelpaa terästeollisuuden raakaaineeksi, koska pasutteen sisältämä sinkki rikastuu masuunikiertoon. Tästä syystä terästeollisuuden raaka-aineena käytettävän rautarikasteen sinkkipitoisuus ei Särkän et al. /4/ mukaan saa olla suurempi kuin 150 ppm. Sinkin erottaminen pasutteesta on mahdollista saattamalla sinkki vesiliukoiseen muotoon, esimerkiksi sulfaatiksi. Kirjallisuusosassa esitetään sulakalvosulfatoinnin teoria ja kokeellisessa osassa tutkitaan mahdollisuutta sulakalvosulfatoida pasutteen sisältämä sinkki käyttäen jatkuvatoimista pilotmittakaavaista prosessilaitteistoa.
14 3 2 SULAKALVOSULFATOINTI 2.1 Sulakalvosulfatoinnin teoria Sulakalvosulfatoinnilla tarkoitetaan metalliferriitin sulfatointia metallisulfaatiksi käyttäen aineensiirtoa nopeuttavaa sulakalvoa metallipartikkelin pinnalla. Rastaan ja Saikkosen /1/ mukaan sulakalvosulfatointi perustuu metalliferriitin ja ferrisulfaatin väliseen reaktioon 3 MeFe2O4(s)+ Fe2( SO4 ) (sula) _ 3 3 MeSO4(sula)+ 4 Fe2 O3(s) (1) jossa Me Zn, Cu, Co. Pasutteessa olevien ferriittien joutuessa K-Fe-sulfaattisulaan tapahtuu vastakkaisdiffuusio, jossa ferriitissä oleva Me 2+ -ioni diffuntoituu metalliferriitin hilasta sulaan faasiin ja ekvivalentti määrä Fe 3+ -ioneja diffuntoituu sulasta faasista metalliferriitin hilaan, jolloin metalliferriitin hila muuttuu Fe2O3-faasiksi. Kaaviollinen esitys sulfatoitumismekanismista sulakalvosulfatoitumisessa on esitetty kuvassa 2. Pasutteen sulakalvosulfatoinnissa sulan kalvon muodostavat ferrisulfaatti, Fe2(SO4)3, yhdessä kaliumsulfaatin, K2SO4, kanssa. Ferriittien lisäksi pasutteessa on myös metallien oksideja. Yhtälössä (2) on esitetty metallioksidin sulfatoitumisen yleinen reaktioyhtälö. MeO+ SO3 _ MeSO4 (2) Kuva 2. Kaaviollinen esitys sulfatoitumismekanismista sulakalvosulfatoitumisessa, Rastas ja Saikkonen /1, s. 1/.
15 4 Sulakalvosulfatoinnin etuina verrattuna sulfatointiin ilman aineensiirtoa nopeuttavaa sulakalvoa ovat nopeampi aineensiirto ja tätä kautta nopeampi kinetiikka sekä mahdollisuus vaikuttaa reaktion kinetiikkaan alkalisuolakonsentraatioita muuttamalla. Rastaan ja Saikkosen /1/ mukaan sulakalvosulfatoitumisen kannalta on välttämätöntä, että sulakalvosulfatoitavassa pasutteessa on reaktioon (1) riittävä määrä ferrisulfaattia ja sulan aikaansaamiseksi myös sopivasti kaliumsulfaattia. Reaktiovaiheessa on huolehdittava siitä, että metalliferriitti ja seokseen muodostuva K-Fe-sulfaattisula joutuvat keskenään kontaktiin ja ovat tässä kontaktissa riittävän kauan. Sopiva reaktiolämpötila on välillä C ja riittävä reaktioaika 0,5-1 tuntia. 2.2 Sulakalvosulfatoinnin termodynamiikka Sulakalvosulfatoinnissa tapahtuvien reaktioiden termodynaaminen tasapaino määrää sopivan sulfatointilämpötilan. Sulakalvosulfatoinnin kokonaisreaktio koostuu useista osa- ja sivureaktioista, joten termodynaaminen tarkastelu kannattaa tehdä kullekin osareaktiolle erikseen. Sulakalvosulfatointiprosessissa voidaan erottaa kaksi päävaihetta: ferrisulfaatin muodostuminen ja metalliferriittien sulakalvosulfatoituminen. Mittauksissa käytettävässä laitteistossa ferrisulfaatin muodostuminen tapahtuu leijukerroksessa, jossa partikkelit ovat suurimman osan ajasta kosketuksessa kaasun kanssa. Metalliferriittien sulakalvosulfatoituminen tapahtuu putkireaktorissa. Reaktioon osallistuvat metalliferriittien lisäksi ferrioksidi ja kaliumsulfaatti. Sulakalvosulfatoinnissa tapahtuvat reaktiot ovat tyyppiä a A+b B _ c C + d D (3) jossa A, B lähtöaineet C, D tuotteet a, b lähtöaineiden stökiometriset kertoimet c, d tuotteiden stökiometriset kertoimet.
16 5 Yhtälön (3) tyyppisen reaktion termodynaamiselle tasapainovakiolle on voimassa yhtälö K p c d [C ] [D ] = a b [A ] [B ] (4) jossa Kp termodynaaminen tasapainovakio. Termodynaamisen tasapainovakion avulla on mahdollista laskea Gibbsin vapaa energia, yhtälö G = - R T ln K p (5) jossa G Gibbsin vapaa energia R moolinen kaasuvakio T lämpötila. Gibbsin vapaa energia on mahdollista esittää muodossa G = H - T S (6) jossa H entalpian muutos S entropian muutos. Entalpian muutos voidaan laskea esimerkiksi Van't Hoffin isobaarista H T = R T d ln K dt p (7) jossa H T entalpian muutos lämpötilassa T.
17 6 Entropian muutos voidaan laskea yhtälöstä S T = R (T d ln K dt p - ln K P ) (8) jossa S T entropian muutos lämpötilassa T. Reaktion Gibbsin vapaa energia määritellään G = G tuotteet - G lähtöaineet (9) jossa G reaktion Gibbsin vapaa energia Gtuotteet Glähtöaineet reaktiotuotteiden Gibbsin vapaa energia lähtöaineiden Gibbsin vapaa energia. Reaktion termodynaaminen tasapaino määritellään reaktion Gibbsin vapaan energian minimikohtana. Reaktion Gibbsin vapaata energiaa kutsutaan myös potentiaaliksi. Reaktion termodynaaminen tasapaino voidaan Levenspielin /5/ mukaan määritellä seuraavasti: - Systeemi on termodynaamisesti tasapainossa, kun mikä tahansa muutos saa aikaan systeemin vapaan energian kasvun. Kätevin tapa laskea reaktion entalpia, entropia ja Gibbsin vapaa energia on käyttää tarkoitukseen suunniteltuja ohjelmistoja, joista Roineen et al. /6/ HSC-ohjelmisto on erittäin käyttökelpoinen. Ohjelmisto soveltuu yksittäisen reaktion termodynaamisten suureiden määrittämiseen. HSCohjelmistoa voidaan käyttää myös reaktioiden termodynaamisen tasapainon laskemiseen monikomponentti-monifaasi-systeemeissä.
18 7 2.3 Sulakalvosulfatoinnin reaktiokinetiikasta Reaktion etenemiseen vaikuttaa termodynamiikan lisäksi reaktiokinetiikka. Reaktiokinetiikalla tarkoitetaan reaktion dynamiikkaa, eli reaktioon osallistuvien komponenttien konsentraatioiden tai osapaineiden muutosnopeutta. Tutkitaan eräitä perusreaktiotyyppejä. Jos kyseessä on reversiibeli alkeisreaktio, reaktioyhtälö on muotoa k1 A+ B _ C + D k 2 (10) jossa k1 reaktion nopeusvakio käänteisreaktion nopeusvakio. k2 Yhtälön (10) mukaisen reaktion reaktionopeus voidaan esittää yhtälöllä r A = 1 V dn dt A (11) jossa ra reaktionopeus V reaktioseoksen tilavuus na t aineen A ainemäärä aika. Aineen A ainemäärän muutosnopeudelle voidaan kirjoittaa yhtälö dn dt A = k 1 C A C B - k 2 C C C D (12) jossa CX aineen X konsentraatio.
19 8 Reaktio on kineettisesti tasapainossa, kun r A = r A1 + r A2 = 0 (13) jossa ra1 reaktion nopeus käänteisreaktion nopeus ra2 Tällöin yhtälöistä (12) ja (13) saadaan reaktion nopeusvakioiden suhteelle yhtälö (14). k k 1 2 = C C C A C C D B (14) Lisäksi tiedetään, että alkeisreaktiolle tasapainotilanteessa on voimassa yhtälö (15). K p = k k 1 2 (15) Reaktion kineettinen tasapaino voidaan Levenspielin /5/ mukaan määritellä seuraavasti: - Systeemi on kineettisesti tasapainossa, kun eteenpäin tapahtuvien reaktioiden ja käänteisreaktioiden reaktionopeudet ovat yhtä suuria. Reaktion kinetiikkaan vaikuttaa myös reaktion kertaluku. Reaktion kertaluku kuvaa reaktionopeuden riippuvuutta reaktioon osallistuvien aineiden konsentraatioista. Reaktion kokonaiskertaluku määritellään alkeisreaktioiden kertalukujen summana, yhtälö n= a + b + c + d +... (16) jossa n reaktion kokonaiskertaluku a,b... alkeisreaktioiden kertaluvut.
20 9 Reaktionopeudelle voidaan kirjoittaa yhtälö (17). r A = k C a A C b B C c C C d D... (17) Reaktiomekanismi pyrkii selittämään reaktion todellisen kulun. Esimerkiksi jos reaktion A + B2 2 2 A B (18) kinetiikka osoittaa, että kyseessä ei ole alkeisreaktio, on mahdollista, että todellinen reaktiomekanismi sisältää seuraavat reaktiot, yhtälö (19). A2 _ 2 A A* + B2 _ A B + B A* + B* _ A B (19) Sulakalvosulfatoinnissa tapahtuvien reaktioiden reaktiomekanismeja ja kinetiikkaa on tutkittu varsin vähän. Rastas ja Saikkonen /1/ ovat tutkineet pasutteen sulakalvosulfatoinnin kinetiikkaa. He ovat esittäneet, että pasutteen sulakalvosulfatoinnissa tarvittava reaktioaika on noin 0,5...1 tuntia, jos halutaan päästä yli 90 % konversioon.
21 Aineensiirto sulakalvosulfatoinnissa Reaktioiden kinetiikkaan keskeisesti vaikuttava tekijä on aineensiirto. Aineensiirto sulakalvosulfatointi-prosessissa voidaan jakaa kolmeen päätyyppiin: aineensiirto CFBreaktorissa kaasun ja kiintoaineen välillä, aineensiirto kuilu-uunissa kiintoainepartikkeleiden välillä sekä aineensiirto kiintoainepartikkeleiden sisällä Aineensiirto kaasusta partikkeliin Reaktion nopeutta eniten rajoittava tekijä on yleensä aineensiirto eri faasien välillä. Jos tutkittava reaktio on tyyppiä A(g)+ bb(s) _ cc(g)+ dd(s) (20) voidaan Sohn ja Wadsworthin /7/ mukaan kokonaisreaktiossa erottaa kolme tapahtumaa: -aineensiirto kaasun ja kiintoaineen pinnan välillä -aineensiirto kiintoaineen huokosissa -lämmönsiirto kaasun ja kiintoaineen välillä. Levenspiel /5/ on esittänyt useita mahdollisia malleja aineensiirrolle ja kinetiikalle kaasu/kiintoaine-reaktioissa. Yksinkertaisin malli olettaa, että partikkelin koko pysyy vakiona, ja reaktio tapahtuu pinnalta partikkelin ydintä kohti. Tämän mallin, jota kutsutaan nimellä kutistuvan ytimen malli, ovat ensimmäisinä esittäneet Yagi ja Kunii /8/. Kuvassa 3 on esitetty kutistuvan ytimen malli. Kuva 3. Kutistuvan ytimen malli, Levenspiel /5, s. 362/. Ensin kaasu diffuntoituu partikkelin pinnalla olevan kaasufilmin läpi. Tämän jälkeen kaasu diffuntoituu partikkelin pinnalla olevan reaktiotuotekerroksen läpi. Näiden vaiheiden jälkeen tapahtuu reaktio kaasun ja reagoimattoman kiintoaineen välillä. Kutistuvan ytimen malli voidaan esittää vaiheittain yhtälöillä (21), (22) ja (23).
22 11 Kaasun sisältämän komponentin A diffuusio partikkelin pinnalla olevan kaasufilmin läpi voidaan esittää yhtälöllä (21). S 1 dn dt A - = k g ( C A,g C A, s ex ) (21) jossa Sex partikkelin ulkokuoren pinta-ala kg CA,g CA,s aineensiirtokerroin kaasufilmin läpi komponentin A konsentraatio kaasussa komponentin A konsentraatio kiinto-aineessa. Komponentin A diffuusio tuotekerroksen läpi voidaan esittää yhtälöllä 1 - S r d n dt A = D e d C dr A (22) jossa Sr reaktiotuotteen pinta-ala kaasun diffuusiokerroin tuotekerroksen läpi. De Reaktio komponentin A ja kiintoaineen komponentin B välillä voidaan esittää yhtälöllä 1 S dn dt A - = k s C A, c c (23) jossa Sc ytimen pinta-ala ks CA,c aineensiirtokerroin tuotekerroksesta ytimeen komponentin A konsentraatio ytimen pinnalla. Levenspielin /9/ mukaan kutistuvan ytimen mallia voidaan yksinkertaistaa, koska aineensiirtovastus reagoineen kerroksen läpi on huomattavasti suurempi kuin aineensiirtovastus partikkelin pinnalla olevan kaasufilmin läpi. Aineensiirtovastuksella partikkelin pinnalla olevan kaasufilmin läpi on yleensä merkitystä vain reaktion alkuvaiheessa.
23 12 Jos reaktionopeutta rajoittaa kaasun diffuusio partikkelin pinnalla olevan kaasufilmin läpi, voidaan reaktion konversio lähtöaineen B suhteen esittää yhtälöllä X B = t τ c (24) jossa XB konversio B:n suhteen aika, joka kuluu 100 % konversioon. τc Reaktion alussa τc määritellään yhtälöllä ρ B R p τ c = 3 b k g C A,g (25) jossa ρb komponentin B moolitiheys partikkelin säde. Rp Aineensiirtokerroin kaasufilmin läpi voidaan yksittäiselle partikkelille laskea yhtälöstä (26). k g D d g,p p = 2 +0,6 Re 1 2 Sc 1 3 (26) jossa dp partikkelin halkaisija Dg,p Re Sc diffuusiokerroin kaasusta partikkeliin kaasufilmin läpi Reynolds-luku kaasun virtaukselle partikkelin ohi Schmidtin luku.
24 13 Reynolds-luku kaasun virtaukselle partikkelin ohi määritellään yhtälöllä d Re= p w µ g g ρ g (27) jossa ρg kaasun tiheys wg kaasun virtausnopeus partikkelin ohi µg kaasun dynaaminen viskositeetti. Schmidtin luku määritellään yhtälöllä (28). Sc= ρ µ g g D (28) Kun partikkelin pinnalle on muodostunut tuotekerros, joka rajoittaa reaktion etenemistä, voidaan konversio B:n suhteen kirjoittaa seuraavaan muotoon, yhtälö (29). t τ c = 1-3(1 - X B 2 3 ) + 2(1 - X B ) (29) Tällöin τc voidaan esittää yhtälöllä (30). 2 ρ B R τ c = 6 b De C A,g (30) Jos reaktiota rajoittaa kiinteän ytimen ja kaasun välinen reaktio, voidaan konversio B:n suhteen esittää yhtälöllä (31). t τ c = 1 ( 1 X ) 3 1 b (31)
25 14 Tällöin voidaan τc esittää yhtälöllä (32). ρ R B τ c = b k s C A,g (32) Kutistuvan ytimen malli on yksinkertainen, mutta malli ei ota huomioon partikkelin huokoisuutta. Lisäksi malli olettaa, että partikkelia ympäröivän kaasun koostumus ei muutu. CFB-reaktorissa partikkelia ympäröivän kaasun keskimääräiselle koostumukselle voidaan käyttää reaktorista poistuvan kaasun arvoja. Eräs monipuolisimmista aineensiirtoa kaasusta partikkeliin käsittelevistä malleista on Basun ja Largen /10/ esittämä Masonin ja Malinauskasin malli, joka ottaa huomioon partikkelikoon muuttumisen ja reaktiot sekä kaasufaasissa että kiintoaineessa, - m n A xb n A - x A n B + = e Dg,A A B D AB 2 p x A d ε p x A - (1+ ) R T R T 8 µ Dg,A p (33) jossa na A:n ainevirta Dk,A m xa nb xb D e AB p xa d p diffuusiokerroin kaasusta partikkeliin kokonaismassa A:n mooliosuus B:n ainevirta B:n mooliosuus kokonaisdiffuusiokerroin A:n ja B:n välillä paine A:n mooliosuuden muutosgradientti partikkelissa olevien huokosten halkaisija paineen muutosgradientti.
26 15 Diffuusiokerroin kaasusta partikkeliin voidaan laskea yhtälöstä D k,a 2 ε = p 2 (4 r0 -π r 3τ p 2 g ) 0,5 8 R T ( π M A ) 0,5 (34) jossa MA A:n moolimassa p p partikkelin huokoisuus huokosten kiemurtelevuus. Kokonaisdiffuusiokerroin A:n ja B:n välillä määritellään yhtälöllä D e AB ε = τ p p D AB (35) jossa DAB diffuusiokerroin A:n ja B:n välillä. Masonin ja Malinauskasin malli on kuitenkin matemaattisesti monimutkainen ja malli vaatii tarkkoja tietoja kiintoainepartikkeleiden ominaisuuksista Aineensiirto jauhepatjassa Sulakalvosulfatoinnissa reaktiot tapahtuvat jauhepatjassa. Reaktionopeutta kontrolloivaksi tekijäksi muodostuu tässäkin tapauksessa aineensiirtonopeus. Sulakalvosulfatoinnissa aineensiirto tapahtuu partikkelista partikkeleiden välissä olevan sulakalvon kautta toiseen partikkeliin. Reaktiot tapahtuvat yhtälöiden (1) ja (2) mukaisesti. Levenspielin /5/ mukaan aineensiirto kiintoainekerroksessa noudattaa kutistuvan ytimen mallia, jolloin aineensiirron laskennassa voidaan käyttää hyväksi yhtälöitä (24)...(32).
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Luento 9 Kemiallinen tasapaino CHEM-A1250
 Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luento 9 Kemiallinen tasapaino CHEM-A1250 Kemiallinen tasapaino Kaksisuuntainen reaktio Eteenpäin menevän reaktion reaktionopeus = käänteisen reaktion reaktionopeus Näennäisesti muuttumaton lopputilanne=>
Luku 8. Reaktiokinetiikka
 Luku 8 Reaktiokinetiikka 234 8.1 Reaktion nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista
Luku 8 Reaktiokinetiikka 234 8.1 Reaktion nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista
Sähkökemian perusteita, osa 1
 Sähkökemian perusteita, osa 1 Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 4 - Luento 1 Teema 4: Suoritustapana oppimispäiväkirja Tehdään yksin tai pareittain Tehtävät/ohjeet löytyvät kurssin
Sähkökemian perusteita, osa 1 Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 4 - Luento 1 Teema 4: Suoritustapana oppimispäiväkirja Tehdään yksin tai pareittain Tehtävät/ohjeet löytyvät kurssin
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Termodynaamisten tasapainotarkastelujen tulokset esitetään usein kuvaajina, joissa:
 Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
Lämpötila (Celsius) Luento 9: Termodynaamisten tasapainojen graafinen esittäminen, osa 1 Tiistai 17.10. klo 8-10 Termodynaamiset tasapainopiirrokset Termodynaamisten tasapainotarkastelujen tulokset esitetään
- Termodynaamiset edellytykset - On olemassa ajava voima prosessin tapahtumiselle - Perusta - Kemiallinen potentiaali
 Luento 1: Yleistä kurssista ja sen suorituksesta Tiistai 9.10. klo 10-12 Kemiallisten prosessien edellytykset - Termodynaamiset edellytykset - On olemassa ajava voima prosessin tapahtumiselle - Perusta
Luento 1: Yleistä kurssista ja sen suorituksesta Tiistai 9.10. klo 10-12 Kemiallisten prosessien edellytykset - Termodynaamiset edellytykset - On olemassa ajava voima prosessin tapahtumiselle - Perusta
Luku 21. Kemiallisten reaktioiden nopeus
 Luku 21. Kemiallisten reaktioiden nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista tasapainoreaktiota:
Luku 21. Kemiallisten reaktioiden nopeus Reaktiokinetiikka tarkastelee reaktioiden nopeuksia (vrt. termodynamiikka) reaktionopeus = konsentraation muutos aikayksikössä Tarkastellaan yksinkertaista tasapainoreaktiota:
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
FLUPA I, syksy 2009 RIKASTUS. Tehtävä 1.
 FLUP I, syksy 29 RIKSTUS Tehtävä 1. Lyijymalmia rikastetaan 1 t/h vaahdottamalla käyttäen 43 g reagenssia (ksantaattia) malmitonnia kohti. Syötteen, jätteen ja rikasteen kiintoaineiden mineraalikoostumukset
FLUP I, syksy 29 RIKSTUS Tehtävä 1. Lyijymalmia rikastetaan 1 t/h vaahdottamalla käyttäen 43 g reagenssia (ksantaattia) malmitonnia kohti. Syötteen, jätteen ja rikasteen kiintoaineiden mineraalikoostumukset
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka. Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU
 MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
MIKKELIN AMMATTIKORKEAKOULU Tekniikka ja liikenne / Sähkövoimatekniikka T8415SJ Energiatekniikka Hannu Sarvelainen HÖYRYKATTILAN SUUNNITTELU HARJOITUSTYÖOHJE SISÄLLYS SYMBOLILUETTELO 3 1 JOHDANTO 4 2 TYÖOHJE
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
TKK, TTY, LTY, OY, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 31.5.2006
 TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
TKK, TTY, LTY, Y, TY, VY, ÅA / Insinööriosastot Valintakuulustelujen kemian koe 1.5.006 1. Uraanimetallin valmistus puhdistetusta uraanidioksidimalmista koostuu seuraavista reaktiovaiheista: (1) U (s)
 KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KULJETUSSUUREET Kuljetussuureilla tai -ominaisuuksilla tarkoitetaan kaasumaisen, nestemäisen tai kiinteän väliaineen kykyä siirtää ainetta, energiaa, tai jotain muuta fysikaalista ominaisuutta paikasta
KANDIDAATIN TYÖ: LÄMMÖN- JA AINEENSIIRTO HIILIPARTIKKELIN PALAMISESSA
 LAPPEENRANNA TEKNILLINEN YLIOPISTO Teknillinen tiedekunta Energiatekniikan koulutusohjelma KANDIDAATIN TYÖ: LÄMMÖN- JA AINEENSIIRTO HIILIPARTIKKELIN PALAMISESSA Lappeenrannassa 1.3.01 Elina Luttunen 0340015
LAPPEENRANNA TEKNILLINEN YLIOPISTO Teknillinen tiedekunta Energiatekniikan koulutusohjelma KANDIDAATIN TYÖ: LÄMMÖN- JA AINEENSIIRTO HIILIPARTIKKELIN PALAMISESSA Lappeenrannassa 1.3.01 Elina Luttunen 0340015
Lukion kemia 3, Reaktiot ja energia. Leena Piiroinen Luento 2 2015
 Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Lukion kemia 3, Reaktiot ja energia Leena Piiroinen Luento 2 2015 Reaktioyhtälöön liittyviä laskuja 1. Reaktioyhtälön kertoimet ja tuotteiden määrä 2. Lähtöaineiden riittävyys 3. Reaktiosarjat 4. Seoslaskut
Kuva 1. Virtauksen nopeus muuttuu poikkileikkauksen muuttuessa
 8. NESTEEN VIRTAUS 8.1 Bernoullin laki Tässä laboratoriotyössä tutkitaan nesteen virtausta ja virtauksiin liittyviä energiahäviöitä. Yleisessä tapauksessa nesteiden virtauksen käsittely on matemaattisesti
8. NESTEEN VIRTAUS 8.1 Bernoullin laki Tässä laboratoriotyössä tutkitaan nesteen virtausta ja virtauksiin liittyviä energiahäviöitä. Yleisessä tapauksessa nesteiden virtauksen käsittely on matemaattisesti
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
- Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka: kappaleiden liike)
 KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
KEMA221 2009 TERMODYNAMIIKAN 1. PÄÄSÄÄNTÖ ATKINS LUKU 2 1 1. PERUSKÄSITTEITÄ - Termodynamiikka kuvaa energian siirtoa ( dynamiikkaa ) systeemin sisällä tai systeemien kesken (vrt. klassinen dynamiikka:
4) Törmäysten lisäksi rakenneosasilla ei ole mitään muuta keskinäistä tai ympäristöön suuntautuvaa vuorovoikutusta.
 K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
K i n e e t t i s t ä k a a s u t e o r i a a Kineettisen kaasuteorian perusta on mekaaninen ideaalikaasu, joka on matemaattinen malli kaasulle. Reaalikaasu on todellinen kaasu. Reaalikaasu käyttäytyy
Demo 5, maanantaina 5.10.2009 RATKAISUT
 Demo 5, maanantaina 5.0.2009 RATKAISUT. Lääketieteellisen tiedekunnan pääsykokeissa on usein kaikenlaisia laitteita. Seuraavassa yksi hyvä kandidaatti eli Venturi-mittari, jolla voi määrittää virtauksen
Demo 5, maanantaina 5.0.2009 RATKAISUT. Lääketieteellisen tiedekunnan pääsykokeissa on usein kaikenlaisia laitteita. Seuraavassa yksi hyvä kandidaatti eli Venturi-mittari, jolla voi määrittää virtauksen
(b) Tunnista a-kohdassa saadusta riippuvuudesta virtausmekaniikassa yleisesti käytössä olevat dimensiottomat parametrit.
 Tehtävä 1 Oletetaan, että ruiskutussuuttimen nestepisaroiden halkaisija d riippuu suuttimen halkaisijasta D, suihkun nopeudesta V sekä nesteen tiheydestä ρ, viskositeetista µ ja pintajännityksestä σ. (a)
Tehtävä 1 Oletetaan, että ruiskutussuuttimen nestepisaroiden halkaisija d riippuu suuttimen halkaisijasta D, suihkun nopeudesta V sekä nesteen tiheydestä ρ, viskositeetista µ ja pintajännityksestä σ. (a)
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
Puhtaan kaasun fysikaalista tilaa määrittävät seuraavat 4 ominaisuutta, jotka tilanyhtälö sitoo toisiinsa: Paine p
 KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KEMA221 2009 KERTAUSTA IDEAALIKAASU JA REAALIKAASU ATKINS LUKU 1 1 IDEAALIKAASU Ideaalikaasu Koostuu pistemäisistä hiukkasista Ei vuorovaikutuksia hiukkasten välillä Hiukkasten liike satunnaista Hiukkasten
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma
 KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
PROSESSISUUNNITTELUN SEMINAARI. Luento 5.3.2012 3. vaihe
 PROSESSISUUNNITTELUN SEMINAARI Luento 5.3.2012 3. vaihe 1 3. Vaihe Sanallinen prosessikuvaus Taselaskenta Lopullinen virtauskaavio 2 Sanallinen prosessikuvaus Prosessikuvaus on kirjallinen kuvaus prosessin
PROSESSISUUNNITTELUN SEMINAARI Luento 5.3.2012 3. vaihe 1 3. Vaihe Sanallinen prosessikuvaus Taselaskenta Lopullinen virtauskaavio 2 Sanallinen prosessikuvaus Prosessikuvaus on kirjallinen kuvaus prosessin
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
CHEM-A1110 Virtaukset ja reaktorit. Laskuharjoitus 9/2016. Energiataseet
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
Luento 2: Lämpökemiaa, osa 1 Keskiviikko klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Luento 2: Lämpökemiaa, osa 1 Keskiviikko 12.9. klo 8-10 477401A - ermodynaamiset tasapainot (Syksy 2018) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen
Liite F: laskuesimerkkejä
 Liite F: laskuesimerkkejä 1 Lämpövirta astiasta Astiasta ympäristöön siirtyvää lämpövirtaa ei voida arvioida vain astian seinämien lämmönjohtavuuksilla sillä ilma seinämä ja maali seinämä -rajapinnoilla
Liite F: laskuesimerkkejä 1 Lämpövirta astiasta Astiasta ympäristöön siirtyvää lämpövirtaa ei voida arvioida vain astian seinämien lämmönjohtavuuksilla sillä ilma seinämä ja maali seinämä -rajapinnoilla
Teddy 2. välikoe kevät 2008
 Teddy 2. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Teddy 2. välikoe kevät 2008 Vastausaikaa on 2 tuntia. Kokeessa saa käyttää laskinta ja MAOL-taulukoita. Jokaiseen vastauspaperiin nimi ja opiskelijanumero! 1. Ovatko seuraavat väitteet oikein vai väärin?
Luvun 12 laskuesimerkit
 Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Luvun 12 laskuesimerkit Esimerkki 12.1 Mikä on huoneen sisältämän ilman paino, kun sen lattian mitat ovat 4.0m 5.0 m ja korkeus 3.0 m? Minkälaisen voiman ilma kohdistaa lattiaan? Oletetaan, että ilmanpaine
Chem-C2400 Luento 3: Faasidiagrammit Ville Jokinen
 Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
Chem-C2400 Luento 3: Faasidiagrammit 16.1.2019 Ville Jokinen Oppimistavoitteet Faasidiagrammit ja mikrorakenteen muodostuminen Kahden komponentin faasidiagrammit Sidelinja ja vipusääntö Kolmen faasin reaktiot
energiatehottomista komponenteista tai turhasta käyntiajasta
 LUT laboratorio- ato o ja mittauspalvelut ut Esimerkkinä energiatehokkuus -> keskeinen keino ilmastomuutoksen hallinnassa Euroopan sähkönkulutuksesta n. 15 % kuluu pumppusovelluksissa On arvioitu, että
LUT laboratorio- ato o ja mittauspalvelut ut Esimerkkinä energiatehokkuus -> keskeinen keino ilmastomuutoksen hallinnassa Euroopan sähkönkulutuksesta n. 15 % kuluu pumppusovelluksissa On arvioitu, että
:TEKES-hanke. 40121/04 Leijukerroksen kuplien ilmiöiden ja olosuhteiden kokeellinen ja laskennallinen tutkiminen
 FB-kupla :TEKES-hanke 40121/04 Leijukerroksen kuplien ilmiöiden ja olosuhteiden kokeellinen ja laskennallinen tutkiminen Ryhmähankkeen osapuolet: Tampereen teknillinen yliopisto Osahanke: Biopolttoaineiden
FB-kupla :TEKES-hanke 40121/04 Leijukerroksen kuplien ilmiöiden ja olosuhteiden kokeellinen ja laskennallinen tutkiminen Ryhmähankkeen osapuolet: Tampereen teknillinen yliopisto Osahanke: Biopolttoaineiden
Prosessi- ja ympäristötekniikan perusta
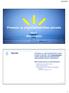 Prosessi- ja ympäristötekniikan perusta Aihe 2: Materiaalitaseet Tavoite Tavoitteena on oppia tasetarkastelun käsite ja oppia tuntemaan, miten materiaalitaseita voidaan hyödyntää kokonaisprosessien sekä
Prosessi- ja ympäristötekniikan perusta Aihe 2: Materiaalitaseet Tavoite Tavoitteena on oppia tasetarkastelun käsite ja oppia tuntemaan, miten materiaalitaseita voidaan hyödyntää kokonaisprosessien sekä
L7 Kaasun adsorptio kiinteän aineen pinnalle
 CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle 1
CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle 1
Kellogg-diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2012 Teema 1 - Luento 1
 Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy Teema - Luento Eetu-Pekka Heikkinen, Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Eetu-Pekka
Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy Teema - Luento Eetu-Pekka Heikkinen, Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Eetu-Pekka
Mitä on huomioitava kaasupäästöjen virtausmittauksissa
 Mitä on huomioitava kaasupäästöjen virtausmittauksissa Luotettavuutta päästökauppaan liittyviin mittauksiin 21.8.2006 Paula Juuti 2 Kaupattavien päästöjen määrittäminen Toistaiseksi CO2-päästömäärät perustuvat
Mitä on huomioitava kaasupäästöjen virtausmittauksissa Luotettavuutta päästökauppaan liittyviin mittauksiin 21.8.2006 Paula Juuti 2 Kaupattavien päästöjen määrittäminen Toistaiseksi CO2-päästömäärät perustuvat
1. Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta
 766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
766328A Termofysiikka Harjoitus no. 5, ratkaisut syyslukukausi 204). Yksiulotteisen harmonisen oskillaattorin energiatilat saadaan lausekkeesta E n n + ) ω, n 0,, 2,... 2 a) Oskillaattorin partitiofunktio
Entalpia - kuvaa aineen lämpösisältöä - tarvitaan lämpötasetarkasteluissa (usein tärkeämpi kuin sisäenergia)
 Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
Luento 4: Entroia orstai 12.11. klo 14-16 47741A - ermodynaamiset tasaainot (Syksy 215) htt://www.oulu.fi/yomet/47741a/ ermodynaamisten tilansuureiden käytöstä Lämökaasiteetti/ominaislämö - kuvaa aineiden
L7 Kaasun adsorptio kiinteän aineen pinnalle
 CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle Oppimistavoitteet
CHEM-C2230 Pintakemia L7 Kaasun adsorptio kiinteän aineen pinnalle Monika Österberg Barnes&Gentle, 2005, luku 8 Aikaisemmin käsitellyt Adsorptio kiinteälle pinnalle nesteessä Adsorptio nestepinnalle Oppimistavoitteet
y 2 h 2), (a) Näytä, että virtauksessa olevan fluidialkion tilavuus ei muutu.
 Tehtävä 1 Tarkastellaan paineen ajamaa Poisseuille-virtausta kahden yhdensuuntaisen levyn välissä Levyjen välinen etäisyys on 2h Nopeusjakauma raossa on tällöin u(y) = 1 dp ( y 2 h 2), missä y = 0 on raon
Tehtävä 1 Tarkastellaan paineen ajamaa Poisseuille-virtausta kahden yhdensuuntaisen levyn välissä Levyjen välinen etäisyys on 2h Nopeusjakauma raossa on tällöin u(y) = 1 dp ( y 2 h 2), missä y = 0 on raon
Luku 5: Diffuusio kiinteissä aineissa
 Luku 5: Diffuusio kiinteissä aineissa Käsiteltävät aiheet... Mitä on diffuusio? Miksi sillä on tärkeä merkitys erilaisissa käsittelyissä? Miten diffuusionopeutta voidaan ennustaa? Miten diffuusio riippuu
Luku 5: Diffuusio kiinteissä aineissa Käsiteltävät aiheet... Mitä on diffuusio? Miksi sillä on tärkeä merkitys erilaisissa käsittelyissä? Miten diffuusionopeutta voidaan ennustaa? Miten diffuusio riippuu
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
Esimerkiksi ammoniakin valmistus typestä ja vedystä on tyypillinen teollinen tasapainoreaktio.
 REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
REAKTIOT JA TASAPAINO, KE5 REAKTIOTASAPAINO Johdantoa: Usein kemialliset reaktiot tapahtuvat vain yhteen suuntaan eli lähtöaineet reagoivat keskenään täydellisesti reaktiotuotteiksi, esimerkiksi palaminen
Lämmityksen lämpökerroin: Jäähdytin ja lämmitin ovat itse asiassa sama laite, mutta niiden hyötytuote on eri, jäähdytyksessä QL ja lämmityksessä QH
 Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
Muita lämpökoneita Nämäkin vaativat työtä toimiakseen sillä termodynamiikan toinen pääsääntö Lämpökoneita ovat lämpövoimakoneiden lisäksi laitteet, jotka tekevät on Clausiuksen mukaan: Mikään laite ei
HSC-ohje laskuharjoituksen 1 tehtävälle 2
 HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
1 Eksergia ja termodynaamiset potentiaalit
 1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
1 PHYS-C0220 Termodynamiikka ja statistinen fysiikka, kevät 2017 Emppu Salonen 1 Eksergia ja termodynaamiset potentiaalit 1.1 Suurin mahdollinen hyödyllinen työ Tähän mennessä olemme tarkastelleet sisäenergian
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut
 Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Astrokemia Kevät 2011 Harjoitus 1, Massavaikutuksen laki, Ratkaisut 1 a Kaasuseoksen komponentin i vapaa energia voidaan kirjoittaa F i (N,T,V = ln Z i (T,V missä on ko hiukkasten lukumäärä tilavuudessa
Kellogg-diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 1 - Luento 1
 Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy 6 Teema - Luento Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
Kellogg-diagrammit Ilmiömallinnus rosessimetallurgiassa Syksy 6 Teema - Luento Tavoite Oia tulkitsemaan ja laatimaan ns. Kellogg-diagrammeja eli vallitsevuusaluekaavioita Aluksi tutustutaan yleisesti tasaainoiirroksiin
Ainemäärien suhteista laskujen kautta aineiden määriin
 REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
REAKTIOT JA ENERGIA, KE3 Ainemäärien suhteista laskujen kautta aineiden määriin Mitä on kemia? Kemia on reaktioyhtälöitä, ja niiden tulkitsemista. Ollaan havaittu, että reaktioyhtälöt kertovat kemiallisen
2. Prosessikaavioiden yksityiskohtainen tarkastelu
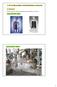 2. Prosessikaavioiden yksityiskohtainen tarkastelu 2.1 Reaktorit Teolliset reaktorit voidaan toimintansa perusteella jakaa seuraavasti: panosreaktorit (batch) panosreaktorit (batch) 1 virtausreaktorit
2. Prosessikaavioiden yksityiskohtainen tarkastelu 2.1 Reaktorit Teolliset reaktorit voidaan toimintansa perusteella jakaa seuraavasti: panosreaktorit (batch) panosreaktorit (batch) 1 virtausreaktorit
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
Luku 2. Kemiallisen reaktion tasapaino
 Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Luku 2 Kemiallisen reaktion tasapaino 1 2 Keskeisiä käsitteitä 3 Tasapainotilan syntyminen, etenevä reaktio 4 Tasapainotilan syntyminen 5 Tasapainotilan syntyminen, palautuva reaktio 6 Kemiallisen tasapainotilan
Muita lämpökoneita. matalammasta lämpötilasta korkeampaan. Jäähdytyksen tehokerroin: Lämmityksen lämpökerroin:
 Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Muita lämpökoneita Nämäkin vaativat ovat työtälämpövoimakoneiden toimiakseen sillä termodynamiikan pääsääntö Lämpökoneita lisäksi laitteet,toinen jotka tekevät on Clausiuksen mukaan: laiteilmalämpöpumppu
Luku 13 KAASUSEOKSET
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2010 Luku 13 KAASUSEOKSET Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction
TKK, TTY, LTY, OY, ÅA, TY ja VY insinööriosastojen valintakuulustelujen fysiikan koe 31.5.2006, malliratkaisut ja arvostelu.
 1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
1 Linja-autoon on suunniteltu vauhtipyörä, johon osa linja-auton liike-energiasta siirtyy jarrutuksen aikana Tätä energiaa käytetään hyväksi kun linja-autoa taas kiihdytetään Linja-auto, jonka nopeus on
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
KJR-C1001 Statiikka ja dynamiikka Luento 16.3.2016 Susanna Hurme Päivän aihe: Translaatioliikkeen kinetiikka (Kirjan luvut 12.6, 13.1-13.3 ja 17.3) Oppimistavoitteet Ymmärtää, miten Newtonin toisen lain
Diplomi-insinöörien ja arkkitehtien yhteisvalinta - dia-valinta 2013 Insinöörivalinnan fysiikan koe 29.5.2013, malliratkaisut
 A1 Ampumahiihtäjä ampuu luodin vaakasuoraan kohti maalitaulun keskipistettä. Luodin lähtönopeus on v 0 = 445 m/s ja etäisyys maalitauluun s = 50,0 m. a) Kuinka pitkä on luodin lentoaika? b) Kuinka kauaksi
A1 Ampumahiihtäjä ampuu luodin vaakasuoraan kohti maalitaulun keskipistettä. Luodin lähtönopeus on v 0 = 445 m/s ja etäisyys maalitauluun s = 50,0 m. a) Kuinka pitkä on luodin lentoaika? b) Kuinka kauaksi
Tärkeitä tasapainopisteitä
 Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
Tietoa tehtävistä Tasapainopiirrokseen liittyviä käsitteitä Tehtävä 1 rajojen piirtäminen Tehtävä 2 muunnos atomi- ja painoprosenttien välillä Tehtävä 3 faasien koostumus ja määrät Tehtävä 4 eutektinen
KJR-C2003 Virtausmekaniikan perusteet, K2017 Tentti, perjantai klo 12:00-16:00 Lue tehtävät huolellisesti. Selitä tehtävissä eri vaiheet.
 KJR-C2003 Virtausmekaniikan perusteet, K2017 Tentti, perjantai 1.9.2017 klo 12:00-16:00 Lue tehtävät huolellisesti. Selitä tehtävissä eri vaiheet. Pelkät kaavat ja ratkaisu eivät riitä täysiin pisteisiin.
KJR-C2003 Virtausmekaniikan perusteet, K2017 Tentti, perjantai 1.9.2017 klo 12:00-16:00 Lue tehtävät huolellisesti. Selitä tehtävissä eri vaiheet. Pelkät kaavat ja ratkaisu eivät riitä täysiin pisteisiin.
Ellinghamin diagrammit
 Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
Ellinghamin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 1 - Luento 2 Tavoite Oppia tulkitsemaan (ja laatimaan) vapaaenergiapiirroksia eli Ellinghamdiagrammeja 1 Tasapainopiirrokset
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Käyttämällä annettua kokoonpuristuvuuden määritelmää V V. = κv P P = P 0 = P. (b) Lämpölaajenemisesta johtuva säiliön tilavuuden muutos on
 766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
766328A ermofysiikka Harjoitus no. 3, ratkaisut (syyslukukausi 201) 1. (a) ilavuus V (, P ) riippuu lämpötilasta ja paineesta P. Sen differentiaali on ( ) ( ) V V dv (, P ) dp + d. P Käyttämällä annettua
Reaktiotekniikka. Prosessi- ja ympäristötekniikan perusta Teema 4 Kaisa Lamminpää
 Reaktiotekniikka Prosessi- ja ympäristötekniikan perusta Teema 4 Kaisa Lamminpää Luennon sisältö Johdanto ja termejä Reaktiotekniikka Kemiallinen prosessitekniikka Kemialliset reaktiot Reaktioiden jaottelu
Reaktiotekniikka Prosessi- ja ympäristötekniikan perusta Teema 4 Kaisa Lamminpää Luennon sisältö Johdanto ja termejä Reaktiotekniikka Kemiallinen prosessitekniikka Kemialliset reaktiot Reaktioiden jaottelu
LAPPEENRANNAN TEKNILLINEN YLIOPISTO KEMIANTEKNIIKAN OSASTO PERMUURAHAISHAPON VALMISTAMINEN PUTKIREAKTORISSA
 LAPPEENRANNAN TEKNILLINEN YLIOPISTO KEMIANTEKNIIKAN OSASTO PERMUURAHAISHAPON VALMISTAMINEN PUTKIREAKTORISSA Työn tarkastajana ja ohjaajana toimi DI Eero Kolehmainen Lappeenrannassa 26.3.2008 Jukka Räsänen
LAPPEENRANNAN TEKNILLINEN YLIOPISTO KEMIANTEKNIIKAN OSASTO PERMUURAHAISHAPON VALMISTAMINEN PUTKIREAKTORISSA Työn tarkastajana ja ohjaajana toimi DI Eero Kolehmainen Lappeenrannassa 26.3.2008 Jukka Räsänen
Termodynamiikan suureita ja vähän muutakin mikko rahikka
 Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Termodynamiikan suureita ja vähän muutakin mikko rahikka 2006 m@hyl.fi 1 Lämpötila Suure lämpötila kuvaa kappaleen/systeemin lämpimyyttä (huono ilmaisu). Ihmisen aisteilla on hankala tuntea lämpötilaa,
Mekaniikan jatkokurssi Fys102
 Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 10 Noste Nesteeseen upotettuun kappaleeseen vaikuttaa nesteen pintaa kohti suuntautuva nettovoima, noste F B Kappaleen alapinnan kohdalla nestemolekyylien
Mekaniikan jatkokurssi Fys10 Kevät 010 Jukka Maalampi LUENTO 10 Noste Nesteeseen upotettuun kappaleeseen vaikuttaa nesteen pintaa kohti suuntautuva nettovoima, noste F B Kappaleen alapinnan kohdalla nestemolekyylien
Luento 16: Fluidien mekaniikka
 Luento 16: Fluidien mekaniikka Johdanto ja käsitteet Sovelluksia Bernoullin laki Luennon sisältö Johdanto ja käsitteet Sovelluksia Bernoullin laki Jatkuvan aineen mekaniikka Väliaine yhteisnimitys kaasuilla
Luento 16: Fluidien mekaniikka Johdanto ja käsitteet Sovelluksia Bernoullin laki Luennon sisältö Johdanto ja käsitteet Sovelluksia Bernoullin laki Jatkuvan aineen mekaniikka Väliaine yhteisnimitys kaasuilla
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Korkealämpötilakemia
 Korkealämpötilakemia Metallurgiset liuosmallit Yleistä To 15.11.218 klo 8-1 PR126A Tavoite Tutustua ideaali- ja reaaliliuosten käsitteisiin Tutustua liuosmalleihin yleisesti - Jaottelu - Hyvän liuosmallin
Korkealämpötilakemia Metallurgiset liuosmallit Yleistä To 15.11.218 klo 8-1 PR126A Tavoite Tutustua ideaali- ja reaaliliuosten käsitteisiin Tutustua liuosmalleihin yleisesti - Jaottelu - Hyvän liuosmallin
MOOLIMASSA. Vedyllä on yksi atomi, joten Vedyn moolimassa M(H) = 1* g/mol = g/mol. ATOMIMASSAT TAULUKKO
 MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
MOOLIMASSA Moolimassan symboli on M ja yksikkö g/mol. Yksikkö ilmoittaa kuinka monta grammaa on yksi mooli. Moolimassa on yhden moolin massa, joka lasketaan suhteellisten atomimassojen avulla (ATOMIMASSAT
kuonasula metallisula Avoin Suljettu Eristetty S / Korkealämpötilakemia Termodynamiikan peruskäsitteitä
 Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
Termodynamiikan peruskäsitteitä The Laws of thermodynamics: (1) You can t win (2) You can t break even (3) You can t get out of the game. - Ginsberg s theorem - Masamune Shirow: Ghost in the shell Systeemillä
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]
![KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille]](/thumbs/24/3803781.jpg) KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
KAASUJEN YLEISET TILANYHTÄLÖT ELI IDEAALIKAASUJEN TILANYHTÄLÖT (Kaasulait) [pätevät ns. ideaalikaasuille] A) p 1, V 1, T 1 ovat paine tilavuus ja lämpötila tilassa 1 p 2, V 2, T 2 ovat paine tilavuus ja
Top Analytica Oy Ab. XRF Laite, menetelmät ja mahdollisuudet Teemu Paunikallio
 XRF Laite, menetelmät ja mahdollisuudet Teemu Paunikallio Röntgenfluoresenssi Röntgensäteilyllä irroitetaan näytteen atomien sisäkuorilta (yleensä K ja L kuorilta) elektroneja. Syntyneen vakanssin paikkaa
XRF Laite, menetelmät ja mahdollisuudet Teemu Paunikallio Röntgenfluoresenssi Röntgensäteilyllä irroitetaan näytteen atomien sisäkuorilta (yleensä K ja L kuorilta) elektroneja. Syntyneen vakanssin paikkaa
PHYS-A0120 Termodynamiikka syksy 2016
 PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
PHYS-A0120 Termodynamiikka syksy 2016 Emppu Salonen Prof. Peter Liljeroth Viikko 6: Faasimuutokset Maanantai 5.12. Kurssin aiheet 1. Lämpötila ja lämpö 2. Työ ja termodynamiikan 1. pääsääntö 3. Lämpövoimakoneet
Luento 2: Lämpökemiaa, osa 1 Torstai klo Termodynamiikan käsitteitä
 Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Luento 2: Lämpökemiaa, osa 1 orstai 11.10. klo 14-16 477401A - ermodynaamiset tasapainot (Syksy 2012) ermodynamiikan käsitteitä - Systeemi Eristetty - suljettu - avoin Homogeeninen - heterogeeninen Faasi
Kurssin toteutus ja ryhmiinjako Ma 2.9. klo 13-15 PR104 Aki Sorsa (SÄÄ) Pe 13.9. klo 8-10 (oma huone) Ke 18.9. Tehtävien palautus
 PROSESSI- JA YMPÄRISTÖTEKNIIKAN PERUSTA I Aikataulu, syksy 2013 TEEMA AIKATAULU VASTUU Kurssin toteutus ja ryhmiinjako Ma 2.9. klo 13-15 PR104 Aki Sorsa (SÄÄ) Yksikköprosessit ja taseajattelu Ympäristövaikutukset
PROSESSI- JA YMPÄRISTÖTEKNIIKAN PERUSTA I Aikataulu, syksy 2013 TEEMA AIKATAULU VASTUU Kurssin toteutus ja ryhmiinjako Ma 2.9. klo 13-15 PR104 Aki Sorsa (SÄÄ) Yksikköprosessit ja taseajattelu Ympäristövaikutukset
KJR-C2003 Virtausmekaniikan perusteet, K2017 Tentti, pe :00-17:00 Lue tehtävät huolellisesti. Selitä tehtävissä eri vaiheet.
 KJR-C2003 Virtausmekaniikan perusteet, K2017 Tentti, pe 16.2.2018 13:00-17:00 Lue tehtävät huolellisesti. Selitä tehtävissä eri vaiheet. Pelkät kaavat ja ratkaisu eivät riitä täysiin pisteisiin. Arvioinnin
KJR-C2003 Virtausmekaniikan perusteet, K2017 Tentti, pe 16.2.2018 13:00-17:00 Lue tehtävät huolellisesti. Selitä tehtävissä eri vaiheet. Pelkät kaavat ja ratkaisu eivät riitä täysiin pisteisiin. Arvioinnin
PYP I / TEEMA 8 MITTAUKSET JA MITATTAVUUS
 1 PYP I / TEEMA 8 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittausprojekti Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen
1 PYP I / TEEMA 8 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittausprojekti Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen
CHEM-A1410 Materiaalitieteen perusteet
 CHEM-A1410 Materiaalitieteen perusteet Laskuharjoitus 18.9.2017, Materiaalien ominaisuudet Tämä harjoitus ei ole arvioitava, mutta tämän tyyppisiä tehtäviä saattaa olla tentissä. Tehtävät perustuvat kurssikirjaan.
CHEM-A1410 Materiaalitieteen perusteet Laskuharjoitus 18.9.2017, Materiaalien ominaisuudet Tämä harjoitus ei ole arvioitava, mutta tämän tyyppisiä tehtäviä saattaa olla tentissä. Tehtävät perustuvat kurssikirjaan.
www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet
 www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet Masuunihiekka stabiloinnit (sideaineena) pehmeikkörakenteet sidekivien alusrakenteet putkijohtokaivannot salaojan ympärystäytöt alapohjan
www.ruukki.com MINERAALI- TUOTTEET Kierrätys ja Mineraalituotteet Masuunihiekka stabiloinnit (sideaineena) pehmeikkörakenteet sidekivien alusrakenteet putkijohtokaivannot salaojan ympärystäytöt alapohjan
(c) Kuinka suuri suhteellinen virhe painehäviön laskennassa tehdään, jos virtaus oletetaan laminaariksi?
 Tehtävä 1 Vettä (10 astetta) virtaa suorassa valurautaisessa (cast iron) putkessa, jonka sisähalkaisija on 100 mm ja pituus 70 m. Tilavuusvirta on 15 litraa minuutissa. (a) Osoita, että virtaus on turbulenttia.
Tehtävä 1 Vettä (10 astetta) virtaa suorassa valurautaisessa (cast iron) putkessa, jonka sisähalkaisija on 100 mm ja pituus 70 m. Tilavuusvirta on 15 litraa minuutissa. (a) Osoita, että virtaus on turbulenttia.
Käytännön esimerkkejä on lukuisia.
 PROSESSI- JA Y MPÄRISTÖTEKNIIK KA Ilmiömallinnus prosessimet allurgiassa, 01 6 Teema 4 Tehtävien ratkaisut 15.9.016 SÄHKÖKEMIALLISTEN REAKTIOIDEN TERMODYNAMIIKKA JA KINETIIKKA Yleistä Tämä dokumentti sisältää
PROSESSI- JA Y MPÄRISTÖTEKNIIK KA Ilmiömallinnus prosessimet allurgiassa, 01 6 Teema 4 Tehtävien ratkaisut 15.9.016 SÄHKÖKEMIALLISTEN REAKTIOIDEN TERMODYNAMIIKKA JA KINETIIKKA Yleistä Tämä dokumentti sisältää
KJR-C1001 Statiikka ja dynamiikka. Luento Susanna Hurme
 KJR-C1001 Statiikka ja dynamiikka Luento 23.3.2016 Susanna Hurme Rotaatioliikkeen kinetiikka: hitausmomentti ja liikeyhtälöt (Kirjan luvut 17.1, 17.2 ja 17.4) Osaamistavoitteet Ymmärtää hitausmomentin
KJR-C1001 Statiikka ja dynamiikka Luento 23.3.2016 Susanna Hurme Rotaatioliikkeen kinetiikka: hitausmomentti ja liikeyhtälöt (Kirjan luvut 17.1, 17.2 ja 17.4) Osaamistavoitteet Ymmärtää hitausmomentin
MUISTIO No CFD/MECHA pvm 22. kesäkuuta 2011
 Aalto yliopisto Insinööritieteiden korkeakoulu Virtausmekaniikka / Sovelletun mekaniikan laitos MUISTIO No CFD/MECHA-17-2012 pvm 22. kesäkuuta 2011 OTSIKKO Hilatiheyden määrittäminen ennen simulointia
Aalto yliopisto Insinööritieteiden korkeakoulu Virtausmekaniikka / Sovelletun mekaniikan laitos MUISTIO No CFD/MECHA-17-2012 pvm 22. kesäkuuta 2011 OTSIKKO Hilatiheyden määrittäminen ennen simulointia
Teddy 10. harjoituksen malliratkaisu syksy 2011
 Teddy. harjoituksen malliratkaisu syksy 2. Tarkastellaan reaktioketjua k O 3 O2 +O () O 2 +O k O 3 (2) O 3 +O k 2 O 2 +O 2 (3) Vakiotilaolettamuksen mukaan välituotteen konsentraatio pysyy vakiona lyhyen
Teddy. harjoituksen malliratkaisu syksy 2. Tarkastellaan reaktioketjua k O 3 O2 +O () O 2 +O k O 3 (2) O 3 +O k 2 O 2 +O 2 (3) Vakiotilaolettamuksen mukaan välituotteen konsentraatio pysyy vakiona lyhyen
Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen
 KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
KEMA221 2009 YKSINKERTAISET SEOKSET ATKINS LUKU 5 1 YKSINKERTAISET SEOKSET Gibbsin energia ja kemiallinen potentiaali määräävät seosten käyttäytymisen Seoksia voidaan tarkastella osittaisten moolisuureitten
KOTITEKOINEN PALOSAMMUTIN (OSA II)
 Johdanto KOTITEKOINEN PALOSAMMUTIN (OSA II) Monet palosammuttimet, kuten kuvassa esitetty käsisammutin, käyttävät hiilidioksidia. Jotta hiilidioksidisammutin olisi tehokas, sen täytyy vapauttaa hiilidioksidia
Johdanto KOTITEKOINEN PALOSAMMUTIN (OSA II) Monet palosammuttimet, kuten kuvassa esitetty käsisammutin, käyttävät hiilidioksidia. Jotta hiilidioksidisammutin olisi tehokas, sen täytyy vapauttaa hiilidioksidia
PHYS-A3121 Termodynamiikka (ENG1) (5 op)
 PHYS-A3121 Termodynamiikka (ENG1) (5 op) Sisältö: Nestevirtaukset Elastiset muodonmuutokset Kineettinen kaasuteoria Termodynamiikan käsitteet Termodynamiikan pääsäännöt Termodynaamiset prosessit Termodynaamiset
PHYS-A3121 Termodynamiikka (ENG1) (5 op) Sisältö: Nestevirtaukset Elastiset muodonmuutokset Kineettinen kaasuteoria Termodynamiikan käsitteet Termodynamiikan pääsäännöt Termodynaamiset prosessit Termodynaamiset
