Menetelmä soveltuu WQ-palkin alalaipassa käytettävän palosuojamaalauksen lämmönjohtavuusarvojen
|
|
|
- Mari Myllymäki
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 TRY TERÄSNORMIKORTTI N:o 16/2004 [KORVAA NORMIKORTIN N:o14/2001] Plosuojmlien lämmönjohvuusrvojen määriäminen, kun suojv eräsos on WQ-lkin lli Yheyshenkilö: Jyri Ouinen Teräsrkenneyhdisys ry Unioninku 14, HELSINKI uh , fx e-mil: Meneelmän kuvus: Meneelmän rjoiukse: Teräsnormikoriss esieään meneelmä losuojmlien lämmönjohvuusrvojen määriykseen, kun suojv rkenne on hisun WQ-lkin lli. Teräsnormikorin eruseell lskeu lämmönjohvuuden ominisrvo on rkoieu ohjeiden B7 mukisen mioiusrvojen lskemiseen WQ-lkin llin losuojukselle. Meneelmä soveluu WQ-lkin lliss käyeävän losuojmluksen lämmönjohvuusrvojen määriykseen, kun lkin loluokk on R15-R120 lorsius on ISO 834-sndrdin mukinen koejärjesely ov eräsnormikorin mukise. Tämän eräsnormikorin eruseell määriey losuojmlin lämmönjohvuusrvo erusuv yksinkeriseuihin yhälöihin j mlin kuivklvonksuueen, joen niiä ei s ole losuojmlin odellisiksi ineominisuuksiksi eikä käyää elemenimeneelmään erusuvss lskennss. Teräsrkenneyhdisyksen Normioimikun on käsielly j hyväksyny Teräsnormikorin. Teräsnormikorin käyäjällä on vsuu korin ohjeiden käyösä. Tämä Teräsnormikori on voimss oisiseksi. Helsingissä huhikuun 20. äivänä 2004 TERÄSRAKENNEYHDISTYS RY TRY Teräsrkenneyhdisys ry Unioninku 14, 4.krs. Puh.: (09) HELSINKI Fx: (09)
2 1. JOHDANTO Tus Hisujen WQ-lkkien käyö P1 j P2 luokn rkennuksiss edellyää vllisesi lkin llin losuojus. Plosuojmlus soveluu WQ-lkin llin losuojukseen j losuojmlu in ei erou vnomisill mleill mlus inns. Knvien WQ-lkkien loluokkvimus on usein R60-R120, jok soveluu losuojmlille. WQ-lkkien llin losuojmlien klvoksuuden määriämisessä on ikisemmin käyey voimille i suljeuille eräsrofiileille määrieyjä mioiuskäyriä i yksiäisiä olokoeuloksi. Plosuojmlin isumisrekio on erilinen uki-, I- j levymäisen (esim. WQ-lkin lli) eräsosien innll. Plosuojmlin suojusvikuus on remi WQ-lkin lliss kuin suljeujen j yleensä myös voimien rofiilien innll. Suljeujen rofiilien mioiuskäyriä voidn sien sovel suorn myös WQ-lkeille. Avoimille j suljeuille rofiileille määriey mioiuskäyrä lkv kuienkin yleensä vs oikkileikkusekijän A /V rvos / m j jkuv oikkileikkusekijän rvoon / m. WQlkkien llin ksuude vihelev vllisesi 10 j 30 mm välillä j näiden oikkileikkusekijän rvo ov , kun llin leveys on 450 mm. Avoimien j suljeujen rofiilien mioiuskäyrä eivä siis yleensä k koko WQ-lkkien käyölue. Yheismillisen mioiuskäyräsöjen määriämiseksi Teräsrkenneyhdisys ry:n losuojmliyöryhmä on kehiäny WQ-lkin llin losuojmlukselle soveluvn olokoe- j lskenmeneelmän. Normikoriss esiey koe- j lskenmeneelmä erusuu Nordes NT FIRE 021 /1/ meneelmään j losuojmlej vren ehyyn lisäohjeeseen Nordes echnicl reor 122 /2/. Koemeneelmän mukn lskeujen lämmönjohvuuden ominisrvojen vull on mhdollis määriää Suomen rkenmismääräyskokoelmn ohjeiden B7 /3/ mukise yleisesi hyväksyy mioiuskäyräsö i - uluko WQ-lkin llin losuojuksen eriseksuuden määriämisä vren. Polokoemeneelmän vull määrieään losuojmlin suojuskyky WQ-lkin lliss sndrdin ISO 834 /4/ mukisess loss. Tämän ohjeen eruseell määriey losuojmlin lämmönjohvuusrvo erusuv yksinkeriseuihin yhälöihin j mlin kuivklvoksuueen, joen niiä ei s ole losuojmlin odellisiksi ineominisuuksiksi eikä käyää elemenimeneelmään erusuvss lskennss. 1.2 Normikorin mukisess lskennss käyeävä WQ-lkin llin oikkileikkusekijä Poikkileikkusekijällä A /V rkoien lolle liin olevn eräsosn in-ln j ilvuuden suhde [1/m]. WQ-lkin lli on mioiln yleensä smnlinen koko lkiss. Kuvss 1.1 esieään WQlkin llin oikkileikkusekijän A /V määriämiseen rviv mi kun llin oikkileikkus ysyy lkin iuussuunnss muuumomn.
3 3 b Kuv 1.1 WQ-lkin llin oikkileikkusekijä A /V määrieään kvs (1), kun llin oikkileikkus lkin iuussuunnss ysyy muuumomn. A b + 2 = (1) V b missä b on llin leveys [m] on llin ksuus [m] 2. LÄMMMÖNJOHTAVUUSARVOJEN JA TERÄSLÄMPÖTILOJEN LASKENNAN PERUSTEET Lskenmeneelmä erusuu WQ-lkeill ehäviin olokokeisiin, jok ehdään ISO 834 /4/ mukise vimukse äyävässä olouuniss. Polokokees miujen eräs- j loiln lämöilojen vull määrieään losuojmlin lämmönjohvuus memisen mllin vull. Lskennss määrieään kunkin yksiäisen koekleen losuojmlin lämmönjohvuusrvo o C lämöiloiss 25 o C:n välein. Koesrjn ulosen vull lsken lämmönjohvuuksien keskirvo lämöilvälille o C. Peruskoesrjn koekleill määrieyihin lämmönjohvuuden keskirvouloksiin lisäään koesrjn keskihjon kerroun vkiorvoll k = 1,0. Mikäli käyeään kohdn 3.4 mukis muunneun lämmönjohvuuden koe- j lskenmeneelmää, käyeään keskihjonkeroimelle vkiorvo k = 0. Plosuojmlin lämmönjohvuuden ominisrvojen vull voidn määriää eräsosn lämöil eri lonkesojoille kisinlskennn vull. Memisen mllin käyö mhdollis eräsosn lämöilojen lskennss ineroloinnin koeulosen rjoimss lueess j ässä ohjeess esieyissä rjoiss huvn eksroloinnin suojvn eräsosn oikkileikkusekijän j losuojmlin kuivklvoksuuden suheen.
4 4 3. KOEKAPPALEET 3.1 Yleisä Polokoesrjn koeklee vlin sien, eä niiden oikkileikkusekijä j losuojmlin kuivklvoksuude kv käyännössä esiinyvän lueen. WQ-lkkien lliojen A /V - suhde vlin vllisesi 35 j / m sekä losuojmlin kuivklvoksuus d 200 j 1500 µm välilä. Koeklee vlmisen S235, S275, S355, S420, S460 i muus vsvs rkenneeräsljis. Polokokeiss käyeävien koekleiden oikkileikkusmi rkisen. Poikkileikkusekijän lskennss käyeään nimellisiä oikkileikkusmioj mikäli miu oikkileikkusmi ov Rkenmismääräyskokoelmn osn B7 /3/ olernssien mukise. 3.2 Peruskoesrj Peruskoesrjn koekleiden lukumäärä on vähinään kuusi. Koeklee vlin sien, eä ne kv käyännössä esiinyvän lueen klvoksuuden j oikkileikkusekijän osl. Plkkien vähimmäisiuudeksi suosielln 1250 mm j ne voidn es kuormimomin. Koekleiden oikkileikkusekijä vlin oleeujen käyökoheiden mukn sien, eä kuskin rofiiliryhmäsä esn inkin ienin j suurin A /V-suhde käyäen vähinään kolme eri mliklvoksuu (ieni, suuri j keskimääräinen käyölueen klvoksuus). Tulukoss 3.1 j kuvss 3.1 esieään esimerkkikoesrj eruskoesrjn koekleis. Mikäli mioiuskäyräsö on rkoieu ääsiss loluokkn R60, ulukon 3.1 mukisess koesrjss on rkoiuksenmukis ksv koekleen 1 klvoksuu j mhdollisesi ienenää koekleen 6 klvoksuu jonkin verrn. Kuivklvoksuude ulee in vli uskohisesi. Tulukko 3.1 Esimerkki eruskoesrjn koekleis. Nro Allin leveys [mm] Allin ksuus [mm] Poikkileikkusekijä A /V [ 1 / m ] Kuivklvoksuus d [µm]
5 Mlin kuivklvon ksuus [µm] Kuv 3.1 Esimerkki eruskoesrjn koekleis. 3.3 Koekleiden sennus uuniin Poikkileikkusekijä A /V [ 1 / m ] Koeklee sennen uuniin sien, eä niiden llin lin j sivu ov kokonisuudessn lolle liin. Alliojen äälle sennen höyrykrkisus kevybeonis vlmiseu elemeni, kuvn 3.2 mukisesi. Elemenien ulee oll senneess kuivi. Elemenien j WQlkin välinen sum iiviseään kuivll hiekll. WQ-lkin ylälin äälle sennen vähinään 50 mm kuiv hiekk j 50 mm luokn A2-s1,d0 vimukse äyävää minerlivill lämöhäviöiden minimoimiseksi. Mikäli koelki knnen uunin seinärkeneis ulee lämmön johuminen esää lkeis uunin ulkouolelle. Koeklee suosielln riusevksi uunin korkeneis Kuv 3.2 Esimerkki WQ-lkkien sijoimises olouuniin. Väli- j yläohjiss WQ-lkin llin ukeuuu vllisesi sumvleu onelolso. Käyämällä olokokeiss väliohjss beonirkeneiden sijs kuivi höyrykrkisus kevybeonis vlmiseuj elemenejä j kuiv sumhiekk sdn vrmll uolell olevi eräsosn lämöiloj. Lämö ei johdu niin helosi höyrykrkisuun kevybeoniin kuin vlliseen beoniin j beonin sisälämä koseus hids odellisiss rkeneiss llin lämöiln nousu.
6 6 3.4 Muunneun lämmönjohvuuden määriysmeneelmä Plosuojmlin lämmönjohvuuden rvojen on hviu olevn lhisemi ohuill klvoksuuksill j hoikkien eräsosien innoill kuin ksuill klvoksuuksill j ksumien eräsosien innoill. Plosuojmlien lämmönjohvuueen viku sien lämöiln lisäksi myös mlin kuivklvon ksuus d j llin oikkileikkusekijä A /V. Kohdss 6.2 esieään meneelmä muunneun lämmönjohvuuden määriämiseksi. Jos losuojmlin klvoksuuden j eräsosn oikkileikkusekijän vikuus lämmönjohvuuden ominisrvoihin ei oe huomioon eräsosn lämöil määrieäessä, s seuruksen oll ohuill klvoill j suurill oikkileikkusekijän rvoill losuojmlin selvä ylimioiminen j ksuill klvoill j ienillä oikkileikkusekijän rvoill mliklvon limioiminen. Teräsrkeneen lämöil sndrdiloss sdn rkemmin lskeuksi eri mliklvon ksuuksill käyämällä lämmönjohvuuksien määriämisessä NT echnicl reor 122:ss esieyä mliklvon ksuuden j oikkileikkusekijän muunnosmeneelyä. Plosuojmlin muunneun kuivklvoksuuden j oikkileikkusekijän käyäminen edellyää eruskoesrj suurem koeklemäärää. Meneelmää vren rvin vähinään yhdeksän koekle eruskoesrjn kuuden sijs. Koekleiden oikkileikkusekijä j mliklvo vlin oleeujen käyökoheiden mukn sien, eä kuskin rofiiliryhmäsä esn inkin ienin, keskimmäinen j suurin A /V-suhde käyäen vähinään kolme eri kuivklvoksuu (ieni, suuri j keskimääräinen käyölueen klvoksuus). Koesrj koskev muu vimukse ov sm kuin eruskoesrjll. Tulukoss 3.2 j kuvss 3.3 esieään esimerkkikoesrj muunneun lämmönjohvuuden määriysmeneelmän koekleis. Tulukko 3.2 Esimerkki muunneun lämmönjohvuuden määriysmeneelmän koekleis. Nro Allin leveys [mm] Allin ksuus [mm] Poikkileikkusekijä A /V [ 1 / m ] Kuivklvoksuus d [µm]
7 Mlin kuivklvon ksuus [µm] Poikkileikkusekijä A /V [ 1 / m ] Kuv 3.3 Esimerkki muunneun lämmönjohvuuden meneelmän koesrjs. 4. KOEKAPPALEIDEN MAALAUS JA MAALIKALVON PAKSUUDEN MÄÄRITTÄ- MINEN Koekleiden losuojvn innn mlus suorien mlin vlmisjn ohjeen mukisesi ruiskull elll i sivelimellä sisesi leviäen koko lolle liin olevlle innlle. Plosuojmli ei s keskiää lämöilmiiseiden ymärille. Ruiskumll mlujen koekleiden losuojmlin klvoksuuksin käyeään klvonksuusmirill miujen yksiäisen ulosen keskirvo jos vähenneään ohj- j inmlin osuude. Mlikerrosen ksuuden mimiseen käyeään klibroiu sähkömgneeis kuivklvomiri. Mliklvon ksuuden määriämiseksi miuksi suorien vähinään 30 llin yhä lolle lis lkv neliömeriä kohden. Miukse suorien ohj-, losuoj- j inmlin leviämisen jälkeen. Yksi miusulos rkoi n. 1 cm 2 lueel suorieun kolmen miuksen (koskeuksen) keskirvo. Tel i sivellinä käyeäessä mlin määrä voidn määriää klvoksuusmirill edellä esieyllä vll i unnisemll mlisi mleineen j leviysvälineineen ennen j jälkeen mluksen. Punnisemll määrieyn mliklvon ksuus sdn kyseiselle mlille ominisen märkäklvo [g/m 2 ] vsvn kuivklvoksuuden eruseell. Plosuojmlin ulee oll äysin kuivunu ennen olokokeiden suorimis. Koekleiden mlus ulee suori vähinään kksi viikko ennen olokoe. Mlin vähimmäiskuivumisik ulee vrmis losuojmlin vlmisjl ennen olokokeen suorimis.
8 8 Plosuojmlille määrieyjä lämmönjohvuuden ominisrvoj voidn käyää eräslämöilojen lskennss vin olokokeiss esuille mliyhdiselmille (ohjmli, losuojmli j inmli). Koesrjs oikkevn inmli- j/i ohjmliyhdiselmän käyö losuojmlin knss vii vrmenvn olokokeen suorimisen mliyhdiselmän soveluvuuden vrmismiseksi. Vrmenv olokoe losuojmlin knss käyeäville eri in- j ohjmliyhdiselmille voidn ehdä esimerkiksi käyäen yhdelä uolel lolle liin olevi mm eräslevyjä i eruskoesrj vsvi koeklei. Kokeess olen sekä lämmönjohvuuden ominisrvojen määriyksessä käyey hyväksyy eä uusi mliyhdiselmä. Plosuojmlin klvoksuuksien j eräsosien (muoo j oikkileikkusekijä) ulee oll verilviss koekleiss smnlise. Tähän kokeeseen käyeävä losuojmlin klvoksuus vlin käyöksuuden ylärjoil. Mikäli esvn losuojmluksen eräsinnn lämöiln nousu on yhä noe i him kuin verilumlun eräsosn voidn uu mliyhdiselmää käyää vnhn rinnll smoin mioiuserusein. Vrmenviss olokokeiss ulee noud sndrdin ISO 834 /4/ mukis lämöilnousu j olokoe voidn ehdä myös kuuiouuniss. 5. POLTTOKOKEET JA LÄMPÖTILOJEN MITTAUS 5.1 Polokokeiden suoriminen Polokokee suorien olouuniss jok äyää ISO 834 /4/ mukise vimukse. Polokokeiss uunin lämöil nosen ISO 834 -sndrdilokäyrän mukisesi. Uunin miu keskimääräinen lämöil s oike sndrdilokäyräsä eninään sndrdiss ISO 834 esieyjen olernssien verrn. Polokokei jken, kunnes WQ-lkkien lliojen keskilämöil on vähinään C i voieen ollu lonkesoik on yliyny. Kokeen ikn seurn isumisrekio sekä losuojmlin kiinniysyvyyä. Tehdy hvinno kirjn ukimusselosukseen. 5.2 Uunin j eräslämöilojen mius Lämmönjohvuuden ominisrvojen lsken vren kunkin koekleen lämöiln nousu j uunin lämöil min j llennen ieokoneelle. Miusieojen llennusväliksi suosielln eninään 30 sekuni. Lämöil vihelee uunin eri osiss jonkin verrn, joen uunin lämöiloj ulee mi uses kohds koekleiden ymärilä. Miisee ulee sijoi sien, eä niiden vull voidn määriää uunin lämöil vähinään khden miiseen keskirvon kunkin koekleen ymärilä. Uunin lämöil min 3 mm ksuill visuojuill ermoelemeneillä. WQ-lkin lämöilmiisee ulee sijoi llin sien, eä miusieojen erusell voidn määriää llin keskimääräinen lämöil. Allin lämöil ulee mi yheensä vähinään seisemäsä eri miiseesä khdes eri leikkuksess kuvn 5.1 mukisesi. Teräslämöilojen miusrkkuuden ulee oll vähinään ± 5 o C j uunin lämöiln ± 15 o C. Termoelemenien kiinniysv esieään sndrdiss NT FIRE 021. Teräslämöilojen miuksess käyeään ermolnk jonk mellilngn ksuus on noin 1,5 mm.
9 Kuv 5.1 Esimerkki ermoelemenien sijinnis WQ-lkin lliss. Termoelemenien sijini j osien mi riiuv koesevs koeklees. 6. LASKENTAMENETELMÄ 6.1 Peruskoesrjn mukinen lskenmeneelmä Plosuojmlin lämmönjohvuuden lskennss käyeään NT FIRE 021 -sndrdiss esieyä lskenmeneelyä j sndrdiin losuojmlej vren ehyä lisäohje Nordes echnicl reor 122. Lskennss käyeään ominislämmölle NT FIRE 021 -sndrdis oikeen vkiorvo 600 J/kg o C. Lämmönjohvuuden lskennss käyeävä yleinen kv losuoj-ineille on muoo λ θ θ φ /10 g, V φ [ + ( e 1) ] d ρ c (1 + ) A 3 = (2) θ θ g, missä λ on losuojmlin lämmönjohvuus [W/m o C] d on losuojmlin kuivklvoksuus [m] ρ α on eräksen iheys, 7850 kg/m 3 c on eräksen ominislämö, vkiorvo 600 J/kg o C A /V on WQ-lkin llin oikkileikkusekijä [m -1 ] θ g, on loiln lämöil [ o C] θ on eräsosn lämöil [ o C] θ on eräsosn lämöiln muuos [ o C] θ g, on loiln lämöiln muuos [ o C] on lsken-ikväli [s] c ρ φ = d A /V on losuoj-ineen j suojvn eräsosn lämöksieeien välinen suhde, erise-syseemin c ρ suheellinen erminen mssiivisuus.
10 10 Käyeäessä losuojmli kv (2) yksinkerisuu kvksi (3), kun losuojuksen j eräsosn lämöksieeien välinen suhde θ seen nollksi. λ θ V d ρ c A = (3) θ θ g, Koekleiden jokisen miusiseen uloksis lsken kv (3) käyäen losuojmlin lämmönjohvuusrvo o C lämöiloiss 25 o C:n välein. Kun kunkin koekleen lämmönjohvuude on su, lsken koko koesrjn lämmönjohvuuksien rimeeinen keskirvo j keskihjon. Plosuojmlin lämmönjohvuuden ominisrvo λ d lsken koesrjn keskirvon j keskihjonnn eruseell edellä miniuiss lämöiloiss kvs (4). λ = λ + k s (4) d k λ missä λ d on lämmönjohvuuden ominisrvo [W/m 2o C] λ k on koesrjn lämmönjohvuusrvojen keskirvo [W/m 2o C] s λ on koesrjn lämmönjohvuusrvojen keskihjon [W/m 2o C] k on koesrjn vrmuu kuvv vkiokerroin (1,0) Ploiln lämöiln käyeään lämmönjohvuusrvojen lskennss miusuloksiin ienimmän neliösummn eruseell sovieu sndrdilokäyrän muoois logrimifunkio θ g, = b + log(8 +1). Logrimifunkion määriäminen suorien erikseen koekleiden ymärilä miujen uunin lämöilmiusiseiden vull. WQ-lkin llin keskimääräisen eräslämöiln lskennss käyeään kv (5), joss losuojmlin lämmönjohvuuen käyeään kvn (4) vull suj lämmönjohvuuden ominisrvoj λ d. θ = λ d d 1 A ( θ g, θ ) ρ c V (5) 6.2 Muunneun lämmönjohvuuden meneelmän mukinen lskenmeneelmä Plosuojmlien lämmönjohvuusrvoihin on odeu vikuvn lämöiln lisäksi myös eräsosn oikkileikkusekijä j losuojmlin kuivklvoksuus. Lsken suorien käyäen NT echnicl reor 122 esieyä muunneun lämmönjohvuuden ominisrvojen lskenmeneelmää, kun koekleiden lukumäärä j vlin on suorieu kohdn 3.4 mukisesi. Muunneuihin lämmönjohvuuden ominisrvoihin ei viku eriseksuus eikä eräsrkeneen oikkileikkusekijä. Muunneujen lämmönjohvuuksien ominisrvo määrieään kvs (4) käyäen keskihjonkerroin k = 0. WQ-lkin llin lämöiln nousun lskennss ulee käyää kv (6), joss losuojmlin lämmönjohvuuden rvoin käyeään muunneuj ominisrvoj.
11 11 θ λd ' = d ρ 1 c A V ( θ g, θ ) (6) Käyeäessä muunneuj lämmönjohvuuksien ominisrvoj eräslämöilojen lskennss korvn kvn (5) klvoksuus d j oikkileikkusekijä A /V muunneull klvoksuudell d j oikkileikkusekijällä [A /V], kv (7) j (8). d ' d c 1 1 = (7) b1 + 1 d 2 missä d' on muunneu losuojmlin klvoksuus [m] d 1 on lkueräinen losuojmlin klvoksuus [m] d 2 = d [m] 1, b 1 j c 1 ov klvoksuuden suheen suorieun muunnoksen ikn määrieyjä vkiorvoj A V A ' ( b ) = V c 2 A V (8) missä [A /V] on muunneu WQ-lkin llin oikkileikkusekijä [1/m] A /V on WQ-lkin llin oikkileikkusekijä [1/m] 2, b 2 j c 2 ov oikkileikkusekijän suheen suorieun muunnoksen ikn määrieyjä vkiorvoj Kvojen (7) j (8) vkiokeroime i, b i j c i (i=1 i 2) määrieään NT echnicl reor 122 ohjeen mukn. Keroime 2, b 2 j c 2 ulee määriää sien, eä kikill slliuill oikkileikkusekijän rvoill llin lämöil nousee oikkileikkusekijän suurenuess. 7. LASKENTAMENETELMÄN EKSTRAPOLOINTISÄÄNNÖT Plosuojmlien suojusksuuden lskennllinen mioius mhdollis eksroloinnin klvoksuuden j oikkileikkusekijän suheen. Eksroloini s suori vin ulukon 7.1 osoimill slliuill lueill kosk eksroloini s n näiden lueiden ulkouolell eävrmll uolell olevi eräslämöiloj. Pisunu mlikerros voi kuoriuu i vlu loss jos sen run- i leikkuskesävyys ei ole riiävä. Toisl isumisrekio voi jäädä uueelliseksi, kun eräsrkeneen oikkileikkusekijä on ieni.
12 12 Kokeiden eruseell eksroloinnin on hviu olevn urvllisem oikkileikkusekijän suheen ylösäin j klvoksuuden suheen lsäin. Tulukoss 7.1 esieään suurimm slliu eksroloiniluee eräsrofiilin oikkileikkusekijän j losuojmlin kuivklvoksuuden suheen. Tulukko 7.1 Teräslämöilojen lskennss käyeävä suurimm slliu eksroloiniluee eräsrofiilin oikkileikkusekijän j mlin klvoksuuden suheen. Eksroloiv ekijä Slliu eksroloiniluee Teräsrofiilin oikkileikkusekijä A /V [1/m] - 10 % % Plosuojmlin kuivklvoksuus d [m] - 25 % % 8. LÄHTEET 1. NT FIRE 021, Insulion of seel srucures: Fire roecion. Finlnd 1985, Nordes. 14 s. 2. Niels E. Andersen, Guidelines o use of NT FIRE 021. NT echn reor 122, Finlnd 1989, Nordes rojec no s. 3. Suomen rkenmismääräyskokoelm os B7, Teräsrkenee, Ohjee Helsinki 1996, Ymärisöminiseriö. 4. ISO 834-1:1999, Fire resisnce ess - Elemens of building consrucion Pr 1:generl Requiremens. Swizerlnd 1999, Inernionl orgnision for sndrdision. 25 s.
5 Jatkuvan funktion integraali
 5 Jkuvn funkion inegrli Derivlle kääneisä käsieä kusun inegrliksi. Aloien inegrliin uusuminen esimerkillä. Esimerkki 5.. Tuonolioksess on phunu kemiklivuoo. Määriellään funkio V sien, eä V () on vuoneen
5 Jkuvn funkion inegrli Derivlle kääneisä käsieä kusun inegrliksi. Aloien inegrliin uusuminen esimerkillä. Esimerkki 5.. Tuonolioksess on phunu kemiklivuoo. Määriellään funkio V sien, eä V () on vuoneen
Tehtävän 1 moottorin kuormana an työkone, jonka momentti on vakio T=30 Nm. Laske
 SÄHKÖENERGAEKNKKA Hrjoius - lueno 9 ehävä 1 Oheisess kuvss on ssähkökoneen sijiskykenämlli. Joh pyörimisnopeuden kv momenin funkion, kun mgneoinivuo φ j nkkurijännie V ov vkioin. Piirrä johmsi kv -ω soss,
SÄHKÖENERGAEKNKKA Hrjoius - lueno 9 ehävä 1 Oheisess kuvss on ssähkökoneen sijiskykenämlli. Joh pyörimisnopeuden kv momenin funkion, kun mgneoinivuo φ j nkkurijännie V ov vkioin. Piirrä johmsi kv -ω soss,
ILVESVUORI POHJOINEN
 NURMIJÄRVEN KUNTA ILVESVUORI POHJOINEN ILVESVUORI POHJOINEN, KUUSIMÄEN TYÖPAIKKA-ALUEEN LAAJENNUKSEN ASEMAKAAVA JA ASEMAKAAVANMUUTOS, KAAVATUNNUS -19 Asinro 8/10.0.0/01 Asemkvn j -muuoksen selosus Asemkv
NURMIJÄRVEN KUNTA ILVESVUORI POHJOINEN ILVESVUORI POHJOINEN, KUUSIMÄEN TYÖPAIKKA-ALUEEN LAAJENNUKSEN ASEMAKAAVA JA ASEMAKAAVANMUUTOS, KAAVATUNNUS -19 Asinro 8/10.0.0/01 Asemkvn j -muuoksen selosus Asemkv
2. Taloudessa käytettyjä yksinkertaisia ennustemalleja. ja tarkasteltavaa muuttujan arvoa hetkellä t kirjaimella y t
 Tilasollinen ennusaminen Seppo Pynnönen Tilasoieeen professori, Meneelmäieeiden laios, Vaasan yliopiso. Tausaa Tulevaisuuden ennusaminen on ehkä yksi luoneenomaisimpia piireiä ihmiselle. On ilmeisesi aina
Tilasollinen ennusaminen Seppo Pynnönen Tilasoieeen professori, Meneelmäieeiden laios, Vaasan yliopiso. Tausaa Tulevaisuuden ennusaminen on ehkä yksi luoneenomaisimpia piireiä ihmiselle. On ilmeisesi aina
Voutila ASEMAKAAVAN SELOSTUS. 2519 Dnro 788/2015. Hongistonkuja Asemakaavan muutos 25. kaup. osa, Kortteli 74, tontti 3 ja katualue
 SEMV SESS 59 Dnro 788/5 Vouil Hongisonuj semvn muuos 5 up os, oreli 74, oni 3 j ulue iljjohj äivi Slorn Vireille ulo 35 Yhdysunluun 5 Yhdysunluun 75 invoiminen SSYSEE ERS- J SEED 3 v-lueen sijini 3 vn
SEMV SESS 59 Dnro 788/5 Vouil Hongisonuj semvn muuos 5 up os, oreli 74, oni 3 j ulue iljjohj äivi Slorn Vireille ulo 35 Yhdysunluun 5 Yhdysunluun 75 invoiminen SSYSEE ERS- J SEED 3 v-lueen sijini 3 vn
4. Integraalilaskenta
 4. Inegrlilsken Joh8elev esimerkki: kun hiukksen pikk s( erivoin jn suheen, sn hiukksen nopeus: v( = s'( Kun nopeus erivoin jn suheen sn kiihyvyys ( = v'( Kääneinen ongelm: hiukksen kiihyvyys on (. Mikä
4. Inegrlilsken Joh8elev esimerkki: kun hiukksen pikk s( erivoin jn suheen, sn hiukksen nopeus: v( = s'( Kun nopeus erivoin jn suheen sn kiihyvyys ( = v'( Kääneinen ongelm: hiukksen kiihyvyys on (. Mikä
SELOSTUS Halolanpolun_muutos 1 LIETO KIRKONSEUTU HALOLANPOLUN ASEMAKAAVAN MUUTOS
 SELOSTUS Hlolnpolun_muuos L:\KAAA\TEXT\KAAASEL\0\ Hlolnpolun_m.docx\PS KAAAN LAATJA: HOLANPOLUN ASEMAKAAAN MUUTOS LEDON KUNTA / KAAOTUS JATEKNSET PELUT: Kvoiusinsinööri Juh Mäki p. 00 0 Kvoiusriehi Pe
SELOSTUS Hlolnpolun_muuos L:\KAAA\TEXT\KAAASEL\0\ Hlolnpolun_m.docx\PS KAAAN LAATJA: HOLANPOLUN ASEMAKAAAN MUUTOS LEDON KUNTA / KAAOTUS JATEKNSET PELUT: Kvoiusinsinööri Juh Mäki p. 00 0 Kvoiusriehi Pe
VUOLTEENPELLON ASEMAKAAVA MELUSELVITYS
 Vsnoj Mänsälän kun Asikirjyyppi Meluselviys Päivämäärä 8..09 VUOLTEENPELLON ASEMAAAVA MELUSELVTYS VUOLTEENPELLON ASEMAAAVA, MÄNTSÄLÄ Päivämäärä 8..09 Lij Trksj Ville Virnen Timo orkee Viie 007 Rpori sisälää
Vsnoj Mänsälän kun Asikirjyyppi Meluselviys Päivämäärä 8..09 VUOLTEENPELLON ASEMAAAVA MELUSELVTYS VUOLTEENPELLON ASEMAAAVA, MÄNTSÄLÄ Päivämäärä 8..09 Lij Trksj Ville Virnen Timo orkee Viie 007 Rpori sisälää
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.2014 Ratkaisut ja arvostelu
 VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
VALTIOTIETEELLINEN TIEDEKUNTA TILASTOTIETEEN VALINTAKOE 3.6.4 Rtkisut j rvostelu. Koululisen todistuksen keskirvo x on lskettu ) b) c) d) kymmenen ineen perusteell. Jos koululinen nostisi neljän ineen
Kuvausta f sanotaan tällöin isomorfismiksi.
 Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Määritelmä..12. Oletetn, että 1 =(V 1,E 1 ) j 2 =(V 2,E 2 ) ovt yksinkertisi verkkoj. Verkot 1 j 2 ovt isomorfiset, jos seurvt ehdot toteutuvt: (1) on olemss bijektio f : V 1 V 2 (2) kikill, b V 1 pätee,
Painopiste. josta edelleen. x i m i. (1) m L A TEX 1 ( ) x 1... x k µ x k+1... x n. m 1 g... m n g. Kuva 1. i=1. i=k+1. i=1
 Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
Pinopiste Snomme ts-ineiseksi kpplett, jonk mteriliss ei ole sisäisiä tiheyden vihteluj. Tällisen kppleen pinopisteen sijinti voidn joskus päätellä kppleen muodon perusteell. Esimerkiksi ts-ineisen pllon
Kaupunkikehityspalvelut. Kaupunkisuunnittelu KAAVA-ALUE 457:6:87 457:6:88 457:6:95 457:6:82 418:1: :1: :11:0 457:6:21 457:6:83 457:6:89
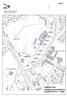 Kupunkisuunnielu Kupunkikehiysplvelu KAAVA-ALUE 8::8 8:: 8::9 8:: 8::8 8::9 8::9 8:: 8:: 8:: 8:: 8:: 8:: 8::8 8::9 8::80 8: 8::8 8::89 8::90 8::9 8:: 8::9 8: 8::0 8::0 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8::8
Kupunkisuunnielu Kupunkikehiysplvelu KAAVA-ALUE 8::8 8:: 8::9 8:: 8::8 8::9 8::9 8:: 8:: 8:: 8:: 8:: 8:: 8::8 8::9 8::80 8: 8::8 8::89 8::90 8::9 8:: 8::9 8: 8::0 8::0 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8:: 8::8
4 Pinta-alasovelluksia
 Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Pint-lsovelluksi. Kuvjn lle jäävä pint-l voidn määrittää, jos kuvj on -kselin yläpuolell. Välillä [, 5] funktion f kuvj on -kselin lpuolell. Peiltn funktion f kuvj -kselin suhteen, jolloin sdn funktion
Lähiympäristö- ja rakentamistapaohje 10.12.2014 33109 KIRKKONUMMEN KUNTA / 540 ARKKITEHTITOIMISTO PETRI ROUHIAINEN OY
 T I N A N P U I S T O Lähiympärisö- j rkenmispohje 10.12.2014 33109 KIRKKONUMMEN KUNTA / 540 Sisällyslueelo: 1 Alkusn s.3 Rkenne j rkoius Tekijä 2 Yleisä s.4 Kvhnke Sijini 3 Lähiympärisöohje s.5 3.1 Tori,
T I N A N P U I S T O Lähiympärisö- j rkenmispohje 10.12.2014 33109 KIRKKONUMMEN KUNTA / 540 Sisällyslueelo: 1 Alkusn s.3 Rkenne j rkoius Tekijä 2 Yleisä s.4 Kvhnke Sijini 3 Lähiympärisöohje s.5 3.1 Tori,
2.4 Pienimmän neliösumman menetelmä
 2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
2.4 Pienimmän neliösummn menetelmä Optimointimenetelmiä trvitn usein kokeellisen dtn nlysoinniss. Mittuksiin liittyy virhettä, joten mittus on toistettv useit kertoj. Oletetn, että mittn suurett c j toistetn
DVC. VARIZON Piennopeuslaite säädettävällä hajotuskuviolla. Pikavalintataulukko
 VARIZON Piennoeuslaie säädeävällä hajouskuviolla Lyhyesi Säädeävä hajouskuvio ja lähivyöhyke Soii kaikenyyisiin iloihin Miausyhde Helosi uhdiseava Peiey ruuviliiännä Eri värivaihoehoja Pikavalinaaulukko
VARIZON Piennoeuslaie säädeävällä hajouskuviolla Lyhyesi Säädeävä hajouskuvio ja lähivyöhyke Soii kaikenyyisiin iloihin Miausyhde Helosi uhdiseava Peiey ruuviliiännä Eri värivaihoehoja Pikavalinaaulukko
Korkotuettuja osaomistusasuntoja
 Korkotuettuj osomistussuntoj Hvinnekuv suunnitelmst. Titeilijn näkemys Asunto Oy Espoon Stulmkri Stulmkrintie 1, 02780 ESOO Asunto Oy Espoon Stulmkri Kerv Kuklhti Iso Mntie 2 Espoo Vihdintie Keh III Hämeenlinnnväylä
Korkotuettuj osomistussuntoj Hvinnekuv suunnitelmst. Titeilijn näkemys Asunto Oy Espoon Stulmkri Stulmkrintie 1, 02780 ESOO Asunto Oy Espoon Stulmkri Kerv Kuklhti Iso Mntie 2 Espoo Vihdintie Keh III Hämeenlinnnväylä
Dynaaminen optimointi ja ehdollisten vaateiden menetelmä
 Dynaaminen opimoini ja ehdollisen vaaeiden meneelmä Meneelmien keskinäinen yheys S yseemianalyysin Laboraorio Esielmä 10 - Peni Säynäjoki Opimoiniopin seminaari - Syksy 2000 / 1 Meneelmien yhäläisyyksiä
Dynaaminen opimoini ja ehdollisen vaaeiden meneelmä Meneelmien keskinäinen yheys S yseemianalyysin Laboraorio Esielmä 10 - Peni Säynäjoki Opimoiniopin seminaari - Syksy 2000 / 1 Meneelmien yhäläisyyksiä
Finavian ympäristötyö 2006: Vesipäästöjen hallintaa ja tehokkaita prosesseja
 9 Y M P Ä R I S T Ö K A T S A U S 2006 2 Finavian ympärisöyö 2006: Vesipääsöjen hallinaa ja ehokkaia prosesseja Jääneson aiheuama kuormius aseiain hallinaan Finavia vasaa maahuolinayriysen jäänesoon käyämän
9 Y M P Ä R I S T Ö K A T S A U S 2006 2 Finavian ympärisöyö 2006: Vesipääsöjen hallinaa ja ehokkaia prosesseja Jääneson aiheuama kuormius aseiain hallinaan Finavia vasaa maahuolinayriysen jäänesoon käyämän
Syksyn 2015 Pitkän matematiikan YO-kokeen TI-Nspire CAS -ratkaisut
 Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
Sksn 0 Pitkän mtemtiikn YO-kokeen TI-Nspire CAS -rtkisut Tekijät: Olli Krkkulinen Rtkisut on ldittu TI-Nspire CAS -tietokoneohjelmll kättäen Muistiinpnot -sovellust. Kvt j lskut on kirjoitettu Mth -ruutuihin.
Kertymäfunktio. Kertymäfunktio. Kertymäfunktio: Mitä opimme? 2/2. Kertymäfunktio: Mitä opimme? 1/2. Kertymäfunktio: Esitiedot
 TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
TKK (c) Ilkk Mellin (24) 1 Johdtus todennäköisyyslskentn TKK (c) Ilkk Mellin (24) 2 : Mitä opimme? 1/2 Jos stunnisilmiötä hlutn mllint mtemttisesti, on ilmiön tulosvihtoehdot kuvttv numeerisess muodoss.
(x) (tasaisesti suppeneva sarja)
 6.3 MATEMAATTISET OPERAATIOT SARJOIE Jos srjss o äärellie äärä erejä, void derivoii i iegroii suori huole ereiäi. Ääreöä srj puksess ereiäi operoii o slliu, jos srj suppeee sisesi. Esi. Trksell ääreöä
6.3 MATEMAATTISET OPERAATIOT SARJOIE Jos srjss o äärellie äärä erejä, void derivoii i iegroii suori huole ereiäi. Ääreöä srj puksess ereiäi operoii o slliu, jos srj suppeee sisesi. Esi. Trksell ääreöä
Kontulan vauvaperhehanke
 Helsingin kupungin sosilivirso. Selviyksiä 2008:5 Konuln vuvperhehnke Vrhisen uen hnke 2005-2007 Kri Lninen j Kirsi Lukk HELSINGIN KAUPUNKI SOSIAALIVIRASTO HELSINGFORS STAD SOCIALVERKET Tekijä() - Förfre
Helsingin kupungin sosilivirso. Selviyksiä 2008:5 Konuln vuvperhehnke Vrhisen uen hnke 2005-2007 Kri Lninen j Kirsi Lukk HELSINGIN KAUPUNKI SOSIAALIVIRASTO HELSINGFORS STAD SOCIALVERKET Tekijä() - Förfre
1.3 Toispuoleiset ja epäoleelliset raja-arvot
 . Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
. Toisuoleiset j eäoleelliset rj-rvot Rj-rvo lim f () A olemssolo edellyttää että muuttuj täytyy void lähestyä rvo kummst suust hyväsä. Jos > ii sot että lähestyy rvo oikelt ositiivisest suust. Jos ts
II.1. Suppeneminen., kun x > 0. Tavallinen lasku
 II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
II. EPÄOLEELLISET INTEGRAALIT nt II.. Suppeneminen Esim. Olkoon f() =, kun >. Tvllinen lsku = / =. Kuitenkn tätä integrli ei ole ikisemmss mielessä määritelty, kosk f ei ole rjoitettu välillä [, ] (eikä
KOMISSION VALMISTELUASIAKIRJA
 EUROOPAN UNIONIN NEUVOSTO Bryssel, 23. oukokuua 2007 (24.05) (OR. en) Toimielinen välinen asia: 2006/0039 (CNS) 9851/07 ADD 2 N 239 RESPR 5 CADREN 32 LISÄYS 2 I/A KOHTAA KOSKEVAAN ILMOITUKSEEN Läheäjä:
EUROOPAN UNIONIN NEUVOSTO Bryssel, 23. oukokuua 2007 (24.05) (OR. en) Toimielinen välinen asia: 2006/0039 (CNS) 9851/07 ADD 2 N 239 RESPR 5 CADREN 32 LISÄYS 2 I/A KOHTAA KOSKEVAAN ILMOITUKSEEN Läheäjä:
θ 1 θ 2 γ γ = β ( n 2 α + n 2 β = l R α l s γ l s 22 LINSSIT JA LINSSIJÄRJESTELMÄT 22.1 Linssien kuvausyhtälö
 22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
22 LINSSIT JA LINSSIJÄRJSTLMÄT 22. Linssien kuvusyhtälö Trkstelln luksi vlon tittumist pllopinnll (krevuussäde R j krevuuskeskipiste C) kuvn mukisess geometriss. Tässä vlo siis tulee ineest ineeseen 2
missä t on matkaan raosta varjostimelle kuluva aika. Jos suihkun elektronien liikemäärä x- sunnassa on p x,on min y0min 0min
 S-11446 Fysiikk IV (Sf), I Välikoe 154 1 Elektronisuihku, joss elektronien noeus on v, suu kohtisuorsti rkoon, jonk leveys on d Ron läi kuljettun elektronit osuvt etäisyydellä D olevn vrjostimeen Mikä
S-11446 Fysiikk IV (Sf), I Välikoe 154 1 Elektronisuihku, joss elektronien noeus on v, suu kohtisuorsti rkoon, jonk leveys on d Ron läi kuljettun elektronit osuvt etäisyydellä D olevn vrjostimeen Mikä
Lähiympäristö- ja rakentamistapaohje 21.12.2015 33109 KIRKKONUMMEN KUNTA / 540 ARKKITEHTITOIMISTO PETRI ROUHIAINEN OY
 T I N A N P U I S T O Lähiympärisö- j rkenmispohje 33109 KIRKKONUMMEN KUNTA / 540 Sisällyslueelo: 1 Alkusn s.3 Rkenne j rkoius Tekijä 2 Yisä s.4 Kvhnke Sijini 3 Lähiympärisöohje s.5 3.1 Tori, puiso j lähivirkisysluee
T I N A N P U I S T O Lähiympärisö- j rkenmispohje 33109 KIRKKONUMMEN KUNTA / 540 Sisällyslueelo: 1 Alkusn s.3 Rkenne j rkoius Tekijä 2 Yisä s.4 Kvhnke Sijini 3 Lähiympärisöohje s.5 3.1 Tori, puiso j lähivirkisysluee
6 Integraali ja derivaatta
 ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 9 6 Inegrli j deriv 6. Inegrli ylärjns funkion. Olkoon Määriä kun () [, ], (b) ], 3]., kun [, ],, kun ], 3]. f() d, [, 3],. Osoi, eä jos funkio f on Riemnn-inegroiuv
ANALYYSI B, HARJOITUSTEHTÄVIÄ, KEVÄT 9 6 Inegrli j deriv 6. Inegrli ylärjns funkion. Olkoon Määriä kun () [, ], (b) ], 3]., kun [, ],, kun ], 3]. f() d, [, 3],. Osoi, eä jos funkio f on Riemnn-inegroiuv
( ) ( ) x t. 2. Esitä kuvassa annetun signaalin x(t) yhtälö aikaalueessa. Laske signaalin Fourier-muunnos ja hahmottele amplitudispektri.
 ELEC-A7 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS Sivu 1/11 1. Johda anneun pulssin Fourier-muunnos ja hahmoele ampliudispekri. Käyä esim. derivoinieoreemaa, ja älä unohda 1. derivaaan epäjakuvuuskohia!
ELEC-A7 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS Sivu 1/11 1. Johda anneun pulssin Fourier-muunnos ja hahmoele ampliudispekri. Käyä esim. derivoinieoreemaa, ja älä unohda 1. derivaaan epäjakuvuuskohia!
AOR II e=0.3 AOR III. II e=0.3. e=0.65 AO-37 36: K2/ K14/ K11/1. 1/3 I e=0, :0 KL-4. sv-1 23:71. s 1. e=0.8. e=0.
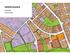 -K/ 0-K/ 0-K/ -K/ -K/ -K/ 0-K/ -K/ 000-K/ 000-K0/ -K/ 0-K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ 00-K/ -K/ -K/ 0-0- -0- : 0-0- -0- -0-0 : : :0 : :0-0- : :0 : : : : : : 0 0 0 0 0-0- -0- -0- Suvikuj
-K/ 0-K/ 0-K/ -K/ -K/ -K/ 0-K/ -K/ 000-K/ 000-K0/ -K/ 0-K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ -K/ 00-K/ -K/ -K/ 0-0- -0- : 0-0- -0- -0-0 : : :0 : :0-0- : :0 : : : : : : 0 0 0 0 0-0- -0- -0- Suvikuj
Mittaus- ja säätölaitteet IRIS, IRIS-S ja IRIS-M
 Miaus- ja sääölaiee IRIS, IRIS-S ja IRIS-M KANSIO 4 VÄLI ESITE Lapinleimu Miaus- ja sääölaiee IRIS, IRIS-S ja IRIS-M IRIS, IRIS-S Rakenne IRIS muodosuu runko-osasa, sääösäleisä, sääömuerisa ai sääökahvasa
Miaus- ja sääölaiee IRIS, IRIS-S ja IRIS-M KANSIO 4 VÄLI ESITE Lapinleimu Miaus- ja sääölaiee IRIS, IRIS-S ja IRIS-M IRIS, IRIS-S Rakenne IRIS muodosuu runko-osasa, sääösäleisä, sääömuerisa ai sääökahvasa
LINSSI- JA PEILITYÖ TEORIAA. I Geometrisen optiikan perusaksioomat
 (0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
(0) LINSSI- JA PEILITYÖ MOTIVOINTI Tutustutn linsseihin j peileihin geometrisen optiikn mittuksiss Tutkitn vlon käyttäytymistä linsseissä j peileissä Määritetään linssien j peilien polttopisteet Optiset
SATE2180 Kenttäteorian perusteet syksy / 6 Laskuharjoitus 7 / Siirrosvirta ja indusoitunut sähkömotorinen voima
 ATE18 Kenäeorin perusee syksy 18 1 / 6 Lskuhrjoius 7 / iirrosvir j inusoiunu sähkömoorinen voim Tehävä 1. All olevn kuvn mukinen piiri on sinimuooisesi värähelevässä j epähomogeenisess mgneeikenässä sin
ATE18 Kenäeorin perusee syksy 18 1 / 6 Lskuhrjoius 7 / iirrosvir j inusoiunu sähkömoorinen voim Tehävä 1. All olevn kuvn mukinen piiri on sinimuooisesi värähelevässä j epähomogeenisess mgneeikenässä sin
Integraalilaskentaa. 1. Mihin integraalilaskentaa tarvitaan? MÄNTÄN LUKIO
 Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
Integrlilskent Tämä on lukion oppimterileist hiemn poikkev yksinkertistettu selvitys määrätyn integrlin lskemisest. Kerromme miksi integroidn, mitä integroiminen trkoitt, miten integrli lsketn j miten
OUML6421B3004. 3-tilaohjattu venttiilimoottori KÄYTTÖKOHTEET TEKNISET TIEDOT OMINAISUUDET SOPIVAT VENTTIILIT TUOTETIEDOT
 OUML6421B3004 3-tilohjttu venttiilimoottori KÄYTTÖKOHTEET i Lämmityksen säätö i Ilmnvihtojärjestelmät TUOTETIEDOT OMINAISUUDET Helppo j nope sent Ei trvitse erillistä sennustelinettä Ei trvitse liikepituuden
OUML6421B3004 3-tilohjttu venttiilimoottori KÄYTTÖKOHTEET i Lämmityksen säätö i Ilmnvihtojärjestelmät TUOTETIEDOT OMINAISUUDET Helppo j nope sent Ei trvitse erillistä sennustelinettä Ei trvitse liikepituuden
OUML7421B3003. Jänniteohjattu venttiilimoottori KÄYTTÖKOHTEET TEKNISET TIEDOT OMINAISUUDET SOPIVAT VENTTIILIT TUOTETIEDOT. i OUV5049 i OUV5050
 OUML7421B3003 Jänniteohjttu venttiilimoottori TUOTETIEDOT OMINAISUUDET Helppo j nope sent Ei trvitse erillistä sennustelinettä Ei trvitse liikepituuden säätöä Momenttirjkytkimet Käsikäyttömhdollisuus Mikroprosessorin
OUML7421B3003 Jänniteohjttu venttiilimoottori TUOTETIEDOT OMINAISUUDET Helppo j nope sent Ei trvitse erillistä sennustelinettä Ei trvitse liikepituuden säätöä Momenttirjkytkimet Käsikäyttömhdollisuus Mikroprosessorin
XII RADIOAKTIIVISUUSMITTAUSTEN TILASTOMATEMATIIKKAA
 II ADIOAKTIIVISUUSMITTAUSTEN TILASTOMATEMATIIKKAA Laskenaaajuus akiivisuus Määrieäessä radioakiivisen näyeen akiivisuua (A) uloksena saadaan käyeyn miausyseemin anama laskenaaajuus (). = [II.I] jossa =
II ADIOAKTIIVISUUSMITTAUSTEN TILASTOMATEMATIIKKAA Laskenaaajuus akiivisuus Määrieäessä radioakiivisen näyeen akiivisuua (A) uloksena saadaan käyeyn miausyseemin anama laskenaaajuus (). = [II.I] jossa =
Vastaa tehtäviin 1-4 ja valitse toinen tehtävistä 5 ja 6. Vastaat siis enintään viiteen tehtävään.
 S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
S-8. Sähkönsiirtoärstlmät Tntti 8..7 Vst thtäviin -4 vlits toinn thtävistä 5 6. Vstt siis nintään viitn thtävään.. Tutkitn ll piirrttyä PV-käyrää, ok kuv sllist vrkko, oss on tuotntolu kuormituslu niidn
VÄRÄHTELYMEKANIIKKA SESSIO 14: Yhden vapausasteen vaimeneva pakkovärähtely, harmoninen kuormitusheräte
 4/ VÄRÄHTELYMEKANIIKKA SESSIO 4: Yhden vaausaseen vaieneva akkvärähely, harninen kuriusheräe LIIKEYHTÄLÖN JOHTO JA RATKAISU Kuvassa n esiey visksisi vaienneun yhden vaausaseen harnisen akkvärähelijän erusalli.
4/ VÄRÄHTELYMEKANIIKKA SESSIO 4: Yhden vaausaseen vaieneva akkvärähely, harninen kuriusheräe LIIKEYHTÄLÖN JOHTO JA RATKAISU Kuvassa n esiey visksisi vaienneun yhden vaausaseen harnisen akkvärähelijän erusalli.
Riemannin integraalista
 Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
Lebesguen integrliin sl. 2007 Ari Lehtonen Riemnnin integrlist Johdnto Tämän luentomonisteen trkoituksen on tutustutt lukij Lebesgue n integrliin j sen perusominisuuksiin mhdollisimmn yksinkertisess tpuksess:
Näytä tai jätä tarkistettavaksi tämän jakson tehtävät viimeistään tiistaina 18.6. ylimääräisessä tapaamisessa.
 Jkso 12. Sähkömgneettinen induktio Tässä jksoss käsitellään sähkömgneettist induktiot, jok on tärkeimpiä sioit sähkömgnetismiss. Tätä tphtuu koko jn rkisess ympäristössämme, vikk emme sitä välttämättä
Jkso 12. Sähkömgneettinen induktio Tässä jksoss käsitellään sähkömgneettist induktiot, jok on tärkeimpiä sioit sähkömgnetismiss. Tätä tphtuu koko jn rkisess ympäristössämme, vikk emme sitä välttämättä
Preliminäärikoe Pitkä Matematiikka 5.2.2013
 Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
Preliminäärikoe Pitkä Mtemtiikk 5..0 Kokeess s vstt enintään kymmeneen tehtävään. Tähdellä ( * ) merkittyjen tehtävien mksimipistemäärä on 9, muiden tehtävien mksimipistemäärä on 6.. ) Rtkise yhtälö b)
Tehtävä 1. Jatka loogisesti oheisia jonoja kahdella seuraavaksi tulevalla termillä. Perustele vastauksesi
 Tehtävä. Jtk loogisesti oheisi jonoj khdell seurvksi tulevll termillä. Perustele vstuksesi lyhyesti. ), c, e, g, b),,, 7,, Rtkisut: ) i j k - oike perustelu j oiket kirjimet, nnetn p - oike perustelu,
Tehtävä. Jtk loogisesti oheisi jonoj khdell seurvksi tulevll termillä. Perustele vstuksesi lyhyesti. ), c, e, g, b),,, 7,, Rtkisut: ) i j k - oike perustelu j oiket kirjimet, nnetn p - oike perustelu,
VÄRÄHTELYMEKANIIKKA SESSIO 16: Yhden vapausasteen vaimeneva pakkovärähtely, yleinen jaksollinen kuormitus
 6/ VÄRÄHTELYMEKANIIKKA SESSIO 6: Yhde vpussee vimeev poväähely, yleie jsollie uomius YLEINEN JAKSOLLINEN KUORMITUS Hmois heäeä vsv pysyvä poväähely lusee löyyy helposi oeilemll. Hmoise heäee eoi void hyödyää
6/ VÄRÄHTELYMEKANIIKKA SESSIO 6: Yhde vpussee vimeev poväähely, yleie jsollie uomius YLEINEN JAKSOLLINEN KUORMITUS Hmois heäeä vsv pysyvä poväähely lusee löyyy helposi oeilemll. Hmoise heäee eoi void hyödyää
( ) ( ) 2. Esitä oheisen RC-ylipäästösuotimesta, RC-alipäästösuotimesta ja erotuspiiristä koostuvan lineaarisen järjestelmän:
 ELEC-A700 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS 3 Sivu /8. arkasellaan oheisa järjeselmää bg x Yksikköviive + zbg z bg z d a) Määriä järjeselmän siirofunkio H Y = X b) Määriä järjeselmän
ELEC-A700 Signaali ja järjeselmä Laskuharjoiukse LASKUHARJOIUS 3 Sivu /8. arkasellaan oheisa järjeselmää bg x Yksikköviive + zbg z bg z d a) Määriä järjeselmän siirofunkio H Y = X b) Määriä järjeselmän
12. ARKISIA SOVELLUKSIA
 MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
MAA. Arkiia ovellukia. ARKISIA SOVELLUKSIA Oleeaan, eä kappale liikkuu ykiuloeia raaa, eimerkiki -akelia pikin. Kappaleen nopeuden vekoriluonne riiää oaa vauhdin eumerkin avulla huomioon, ja on ehkä arkoiukenmukaiina
FDPa. Rei itetty seinään asennettava poistoilmalaite
 Rei iey seinään asenneava poisoilmalaie Lyhyesi Säädeävä Kiineä miausyhde Suuri poisoehokkuus Helposi puhdiseava Eri värivaihoehoja Pikavalinaaulukko I L M A V I R T A Ä Ä N I T A S O l/s Koko db(a) db(a)
Rei iey seinään asenneava poisoilmalaie Lyhyesi Säädeävä Kiineä miausyhde Suuri poisoehokkuus Helposi puhdiseava Eri värivaihoehoja Pikavalinaaulukko I L M A V I R T A Ä Ä N I T A S O l/s Koko db(a) db(a)
LAUSUNTO FIRETEX FX2000 JA FIRETEX FX1000 PALOSUOJAMAALIEN SAMANKALTAISUUDESTA
 LAUSUNTO LAUSUNTO FIRETEX FX2000 JA FIRETEX FX1000 PALOSUOJAMAALIEN SAMANKALTAISUUDESTA Aika teräslämpötilan 550 C saavuttamiseen [min] 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 Varmennettu
LAUSUNTO LAUSUNTO FIRETEX FX2000 JA FIRETEX FX1000 PALOSUOJAMAALIEN SAMANKALTAISUUDESTA Aika teräslämpötilan 550 C saavuttamiseen [min] 90 85 80 75 70 65 60 55 50 45 40 35 30 25 20 15 10 5 Varmennettu
DVC. VARIZON Piennopeuslaite säädettävällä hajotuskuviolla LYHYESTI
 VARIZON Piennoeuslaie säädeävällä hajouskuviolla LYHYESTI Säädeävä hajouskuvio ja lähivyöhyke Soii kaikenyyisiin iloihin Miausyhde Helosi uhdiseava Peiey ruuviliiännä Vakioväri Valkoinen RAL 9003 -- 5
VARIZON Piennoeuslaie säädeävällä hajouskuviolla LYHYESTI Säädeävä hajouskuvio ja lähivyöhyke Soii kaikenyyisiin iloihin Miausyhde Helosi uhdiseava Peiey ruuviliiännä Vakioväri Valkoinen RAL 9003 -- 5
Laskennan mallit (syksy 2010) 1. kurssikoe, ratkaisuja
 582206 Lskennn mllit (syksy 2010) 1. kurssikoe, rtkisuj 1. [2+2+2 pistettä] Säännöllisissä lusekkeiss on käytetty tuttu lyhennysmerkintää Σ = ( ). () merkkijonot, joiden kksi ensimmäistä merkkiä ovt joko
582206 Lskennn mllit (syksy 2010) 1. kurssikoe, rtkisuj 1. [2+2+2 pistettä] Säännöllisissä lusekkeiss on käytetty tuttu lyhennysmerkintää Σ = ( ). () merkkijonot, joiden kksi ensimmäistä merkkiä ovt joko
SARJAT JA DIFFERENTIAALIYHTÄLÖT Funktiojonot 1
 SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 JOUNI PARKKONEN Sisältö 0. Tästä tekstistä. Funktiojonot 0. Tästä tekstistä Tämä moniste on trkoitettu käytettäväksi kurssin Srjt j differentiliyhtälöt luentomterilin.
SARJAT JA DIFFERENTIAALIYHTÄLÖT 2003 JOUNI PARKKONEN Sisältö 0. Tästä tekstistä. Funktiojonot 0. Tästä tekstistä Tämä moniste on trkoitettu käytettäväksi kurssin Srjt j differentiliyhtälöt luentomterilin.
KÄYTTÖOPAS. -järjestelmän sisäyksikkö HXHD125A8V1B
 KÄYÖOPAS -järjeselmän sisäyksikkö SISÄLÖ 1. Määrielmä... 1 1.1. Merkkien ja varoiusen arkoiukse... 1 1.2. Käyeyjen ermien merkiys... 1 2. Yleise varooime... 2 3. Johdano... 2 3.1. Yleisä... 2 3.2. ämän
KÄYÖOPAS -järjeselmän sisäyksikkö SISÄLÖ 1. Määrielmä... 1 1.1. Merkkien ja varoiusen arkoiukse... 1 1.2. Käyeyjen ermien merkiys... 1 2. Yleise varooime... 2 3. Johdano... 2 3.1. Yleisä... 2 3.2. ämän
SELOSTUS. Dnro KAUS/463/2014 VP 12/6.4.2004 11.3.2014 ASEMAKAAVAN MUUTOS (KÄPPÄRÄ 22. JA MUSA 23.) VALTATIE 2 JA 8 UUSI LIITTYMÄ JA RINNAKKAISTIE
 Dnro KUS//0 VP /..00..0 0 SELOSTUS SEMKVN MUUTOS (KÄPPÄRÄ. J MUS.) VLTTE J UUS LTTYMÄ J RNNKKSTE Vireille:..00 KH hyväsyny: KV hyväsyny: SEMKVN MUUTOS (KÄPPÄRÄ. J MUS.) VLTTE J UUS LTTYMÄ J RNNKKSTE PERUS-
Dnro KUS//0 VP /..00..0 0 SELOSTUS SEMKVN MUUTOS (KÄPPÄRÄ. J MUS.) VLTTE J UUS LTTYMÄ J RNNKKSTE Vireille:..00 KH hyväsyny: KV hyväsyny: SEMKVN MUUTOS (KÄPPÄRÄ. J MUS.) VLTTE J UUS LTTYMÄ J RNNKKSTE PERUS-
Esimerkki 8.1 Määritellään operaattori A = x + d/dx. Laske Af, kun f = asin(bx). Tässä a ja b ovat vakioita.
 8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
8. Operttorit, mtriisit j ryhmäteori Mtemttinen operttori määrittelee opertion, jonk mukn sille nnettu funktiot muoktn. Operttorit ovt erityisen tärkeitä kvnttimekniikss, kosk siinä jokist suurett vst
Elintarvikealan pk yritysten markkinointiosaamisen kasvattaminen: kohti tutkijoiden, kehittäjien ja pk yrittäjien yhteistyömallia
 Tukimusprofessori Hrri Luoml Elinrvikeln pk yriysen mrkkinoiniosmisen ksvminen: kohi ukijoiden, kehiäjien j pk yriäjien yheisyömlli Esiys Ruok Suomi seminriss 20.11.2008, Arkikum, Rovniemi Hnkkeen lähökohd
Tukimusprofessori Hrri Luoml Elinrvikeln pk yriysen mrkkinoiniosmisen ksvminen: kohi ukijoiden, kehiäjien j pk yriäjien yheisyömlli Esiys Ruok Suomi seminriss 20.11.2008, Arkikum, Rovniemi Hnkkeen lähökohd
KÄYTTÖOPAS. Ilma vesilämpöpumppujärjestelmän sisäyksikkö ja lisävarusteet RECAIR OY EKHBRD011ADV1 EKHBRD014ADV1 EKHBRD016ADV1
 EKHBRD011ADV1 EKHBRD014ADV1 EKHBRD016ADV1 EKHBRD011ADY1 EKHBRD014ADY1 EKHBRD016ADY1 KÄYÖOPAS Ilma vesilämpöpumppujärjeselmän sisäyksikkö ja lisävarusee EKHBRD011ADV1+Y1 EKHBRD014ADV1+Y1 EKHBRD016ADV1+Y1
EKHBRD011ADV1 EKHBRD014ADV1 EKHBRD016ADV1 EKHBRD011ADY1 EKHBRD014ADY1 EKHBRD016ADY1 KÄYÖOPAS Ilma vesilämpöpumppujärjeselmän sisäyksikkö ja lisävarusee EKHBRD011ADV1+Y1 EKHBRD014ADV1+Y1 EKHBRD016ADV1+Y1
Tehokasta talvipitoa MICHELIN-renkailla
 Tehokasa alvipioa MICHELIN-renkailla y y 2014 www.michelinranspor.com 1 Lainsäädänö koskien kuorma- ja linja-auonrenkaiden käyöä alvella Lainsäädänö koskien kuormaja linja-auonrenkaiden käyöä alvella Seuraavassa
Tehokasa alvipioa MICHELIN-renkailla y y 2014 www.michelinranspor.com 1 Lainsäädänö koskien kuorma- ja linja-auonrenkaiden käyöä alvella Lainsäädänö koskien kuormaja linja-auonrenkaiden käyöä alvella Seuraavassa
Asennusohje EPP-0790-FI-4/02. Kutistemuovijatkos Yksivaiheiset muovieristeiset. Cu-lanka kosketussuojalla 12 kv & 24 kv.
 Asennusohje EPP-0790-FI-4/02 Kutistemuovijtkos Yksiviheiset muovieristeiset kpelit Cu-lnk kosketussuojll 12 kv & 24 kv Tyyppi: MXSU Tyco Electronics Finlnd Oy Energy Division Konlntie 47 F 00390 Helsinki
Asennusohje EPP-0790-FI-4/02 Kutistemuovijtkos Yksiviheiset muovieristeiset kpelit Cu-lnk kosketussuojll 12 kv & 24 kv Tyyppi: MXSU Tyco Electronics Finlnd Oy Energy Division Konlntie 47 F 00390 Helsinki
SUOMEN PANKIN KANSANTALOUSOSASTON TYÖPAPEREITA
 SUOMEN PANKIN KANSANTALOUSOSASTON TYÖPAPEREITA 10.10.2004 1/2004 Hannes Kaadu Kuluajahinainflaaion miaaminen Yhdysvalloissa 2 Kuluajahinainflaaion miaaminen Yhdysvalloissa Kansanalousosason yöpapereia
SUOMEN PANKIN KANSANTALOUSOSASTON TYÖPAPEREITA 10.10.2004 1/2004 Hannes Kaadu Kuluajahinainflaaion miaaminen Yhdysvalloissa 2 Kuluajahinainflaaion miaaminen Yhdysvalloissa Kansanalousosason yöpapereia
Valmennuksen ja arvioinnin tukijärjestemä (VAT)
 Vlmennuksen j rvioinnin tukijärjestemä (VAT) Työhön kuntoutuksen trkoitus on utt sikst kuntoutumn siten, että siirtyminen koulutukseen ti työelämään on mhdollist. VAT -järjestelmä on kehitetty kuntoutumisen
Vlmennuksen j rvioinnin tukijärjestemä (VAT) Työhön kuntoutuksen trkoitus on utt sikst kuntoutumn siten, että siirtyminen koulutukseen ti työelämään on mhdollist. VAT -järjestelmä on kehitetty kuntoutumisen
Matematiikan tukikurssi
 Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Mtemtiikn tukikurssi Kurssikert 4 Tilvuuden j vipn ln lskeminen Kuten iemmin käsittelimme, määrätyn integrlin vull voi lske pintloj j tilvuuksi. Tyypillisenä sovelluksen tilvuuden lskemisest on tpus, joss
Asennusopas. Daikin Altherma - Matalan lämpötilan Monoblocin varalämmitin EKMBUHCA3V3 EKMBUHCA9W1. Asennusopas. Suomi
 Dikin Altherm - Mtln lämpötiln Monolocin vrlämmitin EKMBUHCAV EKMBUHCA9W Suomi Sisällysluettelo Sisällysluettelo Tietoj sikirjst. Tieto tästä sikirjst... Tietoj pkkuksest. Vrlämmitin..... Vrusteiden poistminen
Dikin Altherm - Mtln lämpötiln Monolocin vrlämmitin EKMBUHCAV EKMBUHCA9W Suomi Sisällysluettelo Sisällysluettelo Tietoj sikirjst. Tieto tästä sikirjst... Tietoj pkkuksest. Vrlämmitin..... Vrusteiden poistminen
2:154. lak.yht. lak.yht. lak.yht. 2:156 2:156 6-9901-0 2:156. lak.yht. 2:155. 35 dba. sr-1. No330. YY/s-1. Työväentalo 8-9903-0. No30. sr-2.
 00 lak.yh. lak.yh. lak.yh. lak.yh. lak.yh. ras.m ras.m lak.yh. lak.yh. lak.yh. lak.yh. lak.yh. 0 0 No No No0 No0 0:::M0 0:::M0 0:::M0 0:::M0 0:::M0 0::0:M0 0:::M0 0:::M0 0:::M 0 0 0 0 0 0 0 0 0 0 0 0 0
00 lak.yh. lak.yh. lak.yh. lak.yh. lak.yh. ras.m ras.m lak.yh. lak.yh. lak.yh. lak.yh. lak.yh. 0 0 No No No0 No0 0:::M0 0:::M0 0:::M0 0:::M0 0:::M0 0::0:M0 0:::M0 0:::M0 0:::M 0 0 0 0 0 0 0 0 0 0 0 0 0
5 VALON ETENEMINEN. Säteille voidaan antaa tarvittaessa myös polarisaatio-ominaisuuksia.
 113 5 VAON ETENEMINEN Opsell lueell (nfrpun, näkyvä, ulrvole) sähkömgneenen kenä värähelee hyvn suurell juudell (luokk 1 15 Hz). Vsvs llonpuus on hyvn lyhy (luokk 1-5 m). On ss odoevss, eä hyvä pproksmo
113 5 VAON ETENEMINEN Opsell lueell (nfrpun, näkyvä, ulrvole) sähkömgneenen kenä värähelee hyvn suurell juudell (luokk 1 15 Hz). Vsvs llonpuus on hyvn lyhy (luokk 1-5 m). On ss odoevss, eä hyvä pproksmo
VESIPATTERIN ASENNUS TBLA Thermo Guard-jäätymissuojalla GOLD koko 11-32, versio B
 VESIPATTERIN ASENNUS TBLA -jäätymissuojll GOLD koko 11-32, versio B ASENNUS 1. Knvliitäntä on tehtävä seurvsti: ) TBLA 000-031 j 000-040 Vesiptteri voidn sent suorn kierresumttuun knvn. Ptteri on vrustettu
VESIPATTERIN ASENNUS TBLA -jäätymissuojll GOLD koko 11-32, versio B ASENNUS 1. Knvliitäntä on tehtävä seurvsti: ) TBLA 000-031 j 000-040 Vesiptteri voidn sent suorn kierresumttuun knvn. Ptteri on vrustettu
BETONI-TERÄS LIITTORAKENTEIDEN SUUNNITTELU EUROKOODIEN MUKAAN (TTY 2009) Betonipäivät 2010
 DIPLOMITYÖ: BETONI-TERÄS LIITTORAKENTEIDEN SUUNNITTELU EUROKOODIEN MUKAAN (TTY 29) Beonipäivä 21 DIPLOMITYÖ prosessina Aie: yön eeäjän aloieesa Selviykse beonin, eräksen ja puun osala oli jo ey/käynnissä
DIPLOMITYÖ: BETONI-TERÄS LIITTORAKENTEIDEN SUUNNITTELU EUROKOODIEN MUKAAN (TTY 29) Beonipäivä 21 DIPLOMITYÖ prosessina Aie: yön eeäjän aloieesa Selviykse beonin, eräksen ja puun osala oli jo ey/käynnissä
ELEC- E8419 välikoe b) Yhtiö A ilmoittaa että sillä on liian korkea jännite solmussa 1.
 ELE- E89 väliko 8..5 rkiu. ll olvn kuvn muki vrko on onglmi. Tiln ov kuvillii ikä kiki vihohdoi ol kyä mnlinn vrkko. Vli opivi oimnpiiä, oill onglm dn poiu miä hdään minn nn rkiulli prulu. Vikk ohonkin
ELE- E89 väliko 8..5 rkiu. ll olvn kuvn muki vrko on onglmi. Tiln ov kuvillii ikä kiki vihohdoi ol kyä mnlinn vrkko. Vli opivi oimnpiiä, oill onglm dn poiu miä hdään minn nn rkiulli prulu. Vikk ohonkin
SATE1050 Piirianalyysi II syksy / 8 Laskuharjoitus 2 / Transientti-ilmiö (ratkaisut muodostaen diff. yhtälöt, EI saa käyttä Laplace-muunnosta!
 SAT5 Piirinlyysi II syksy 6 / 8 skuhrjoius / Trnsini-ilmiö (rkisu muodosn diff. yhälö, I s käyä plc-muunnos!) Thävä. All olvss kuvss siyssä piirissä kykin siiryy hkllä = snnos snoon viivä (= induknssin
SAT5 Piirinlyysi II syksy 6 / 8 skuhrjoius / Trnsini-ilmiö (rkisu muodosn diff. yhälö, I s käyä plc-muunnos!) Thävä. All olvss kuvss siyssä piirissä kykin siiryy hkllä = snnos snoon viivä (= induknssin
Teoriaa tähän jaksoon on talvikurssin luentomonisteessa luvussa 10. Siihen on linkki sivulta
 Jkso 10. Sähkömgneettinen induktio Näytä ti plut tämän jkson tehtävät viimeistään tiistin 13.6.2017. Ekstr-tehtävät vstvt kolme tvllist tehtävää, kun lsketn lskuhrjoituspisteitä. Teori tähän jksoon on
Jkso 10. Sähkömgneettinen induktio Näytä ti plut tämän jkson tehtävät viimeistään tiistin 13.6.2017. Ekstr-tehtävät vstvt kolme tvllist tehtävää, kun lsketn lskuhrjoituspisteitä. Teori tähän jksoon on
Kuukausi- ja kuunvaihdeanomalia Suomen osakemarkkinoilla vuosina 2005-2013
 Kauppaieeellinen iedekuna Talousjohaminen Kandidaainukielma Kuukausi- ja kuunvaihdeanomalia Suomen osakemarkkinoilla vuosina 2005-2013 Monhly and Turn-of-he-Monh anomaly in he Finnish sock marke during
Kauppaieeellinen iedekuna Talousjohaminen Kandidaainukielma Kuukausi- ja kuunvaihdeanomalia Suomen osakemarkkinoilla vuosina 2005-2013 Monhly and Turn-of-he-Monh anomaly in he Finnish sock marke during
b) (max 3p) Värähtelijän jaksonajan ja taajuuden välinen yhteys on T = 1/ f, eli missä k on jousen jousivakio. Neliöimällä yllä oleva yhtälö saadaan
 A1 Lbortoriokokeess keveen kierrejouseen ripustettiin eri mssisi punnuksi. Punnust vedettiin lspäin j sntneen hrmonisen värähteln jksonik mitttiin. Värähtelijän tjus f = 2π 1 k mp. Oheisess tulukoss on
A1 Lbortoriokokeess keveen kierrejouseen ripustettiin eri mssisi punnuksi. Punnust vedettiin lspäin j sntneen hrmonisen värähteln jksonik mitttiin. Värähtelijän tjus f = 2π 1 k mp. Oheisess tulukoss on
Y m p ä r i s t ö k a t s a u s
 Y m p ä r i s ö k a s a u s 2007 Finavia ja ympärisö vuonna 2007 Ympärisölupia vireillä ympäri maaa Vuonna 2007 Länsi-Suomen ympärisölupaviraso anoi pääöksen ympärisönsuojelulain mukaisesa luvasa Tampere-
Y m p ä r i s ö k a s a u s 2007 Finavia ja ympärisö vuonna 2007 Ympärisölupia vireillä ympäri maaa Vuonna 2007 Länsi-Suomen ympärisölupaviraso anoi pääöksen ympärisönsuojelulain mukaisesa luvasa Tampere-
Differentiaali- ja integraalilaskenta 1 (CHEM) Laskuharjoitus 4 / vko 47, mallivastaukset
 Differentili- j integrlilskent (CHEM) Lskuhrjoitus / vko 7, mllivstukset Johdntotehtävä x dx = ln.693, joten rvo ln voidn pproksimoid integroimll numeerisesti funktiot x välillä [,]. Jetn väli [,] khteen
Differentili- j integrlilskent (CHEM) Lskuhrjoitus / vko 7, mllivstukset Johdntotehtävä x dx = ln.693, joten rvo ln voidn pproksimoid integroimll numeerisesti funktiot x välillä [,]. Jetn väli [,] khteen
Suorakaidekanavat. lindab suorakaidekanavat
 Suorkideknvt lind suorkideknvt lind suorkideknvt Sisällysluettelo Suorkideknvt Knv LKR... Liitosost Liitoslist LS... Liitoslist LS-... Kulmyhde LBR... Liitoslist LS... S-mutk LBXR... LBSR... Liitoslist
Suorkideknvt lind suorkideknvt lind suorkideknvt Sisällysluettelo Suorkideknvt Knv LKR... Liitosost Liitoslist LS... Liitoslist LS-... Kulmyhde LBR... Liitoslist LS... S-mutk LBXR... LBSR... Liitoslist
2. Suoraviivainen liike
 . Suoraviivainen liike . Siirymä, keskinopeus ja keskivauhi Aika: unnus, yksikkö: sekuni s Suoraviivaisessa liikkeessä kappaleen asema (paikka) ilmoieaan suoralla olevan piseen paikkakoordinaain (unnus
. Suoraviivainen liike . Siirymä, keskinopeus ja keskivauhi Aika: unnus, yksikkö: sekuni s Suoraviivaisessa liikkeessä kappaleen asema (paikka) ilmoieaan suoralla olevan piseen paikkakoordinaain (unnus
Geometrinen lukujono. Ratkaisu. a2 = 50 4 = 200 a3 = = 800 a4 = = 3 200
 Geometrie lukujoo 7. Geometrise lukujoo esimmäie jäse o = 0 j peräkkäiste jäsete suhde =. Määritä lukujoo kolme seurv jäsetä. = 0 = 00 = 0 = 800 = 0 = 00 8. Geometrie lukujoo lk seurvsti: ), 0, 0, b) 000,
Geometrie lukujoo 7. Geometrise lukujoo esimmäie jäse o = 0 j peräkkäiste jäsete suhde =. Määritä lukujoo kolme seurv jäsetä. = 0 = 00 = 0 = 800 = 0 = 00 8. Geometrie lukujoo lk seurvsti: ), 0, 0, b) 000,
ETERAN TyEL:n MUKAISEN VAKUUTUKSEN ERITYISPERUSTEET
 TRAN TyL:n MUKASN AKUUTUKSN RTYSPRUSTT Tässä peruseessa kaikki suuree koskea eraa, ellei oisin ole määriely. Tässä peruseessa käyey lyhenee: LL Lyhyaikaisissa yösuheissa oleien yönekijäin eläkelaki TaL
TRAN TyL:n MUKASN AKUUTUKSN RTYSPRUSTT Tässä peruseessa kaikki suuree koskea eraa, ellei oisin ole määriely. Tässä peruseessa käyey lyhenee: LL Lyhyaikaisissa yösuheissa oleien yönekijäin eläkelaki TaL
Puolijohdekomponenttien perusteet A Ratkaisut 6, Kevät 2017
 OY/PJKOMP R6 017 Puolijohdoponnin pru 571A Riu 6, Kvä 017 1. MOSondnori (MlOxidSiconducor) oouu ninä uii lli hil, oidiriä j doupu puolijoh (Kuv 1). Idlii hilll u jänni G ippuu oidirro jännin vrrn j puolijohn
OY/PJKOMP R6 017 Puolijohdoponnin pru 571A Riu 6, Kvä 017 1. MOSondnori (MlOxidSiconducor) oouu ninä uii lli hil, oidiriä j doupu puolijoh (Kuv 1). Idlii hilll u jänni G ippuu oidirro jännin vrrn j puolijohn
Asennusopas. Daikin Altherma Matalan lämpötilan Monoblocin varalämmitin EKMBUHCA3V3 EKMBUHCA9W1. Asennusopas. Suomi
 Dikin Altherm Mtln lämpötiln Monolocin vrlämmitin EKMBUHCAV EKMBUHCA9W Dikin Altherm Mtln lämpötiln Monolocin vrlämmitin Suomi Sisällysluettelo Sisällysluettelo Tietoj sikirjst. Tieto tästä sikirjst...
Dikin Altherm Mtln lämpötiln Monolocin vrlämmitin EKMBUHCAV EKMBUHCA9W Dikin Altherm Mtln lämpötiln Monolocin vrlämmitin Suomi Sisällysluettelo Sisällysluettelo Tietoj sikirjst. Tieto tästä sikirjst...
Polynomien laskutoimitukset
 Polyomie lskutoimitukset Polyomi o summluseke, joss jokie yhteelskettv (termi) sisältää vi vkio j muuttuj välisiä kertolskuj. Esimerkki 0. Mm., 6 j ovt polyomej. Polyomist, joss o vi yksi termi, käytetää
Polyomie lskutoimitukset Polyomi o summluseke, joss jokie yhteelskettv (termi) sisältää vi vkio j muuttuj välisiä kertolskuj. Esimerkki 0. Mm., 6 j ovt polyomej. Polyomist, joss o vi yksi termi, käytetää
OSINKOJEN JA PÄÄOMAVOITTOJEN VEROTUKSEN VAIKUTUKSET OSAKKEEN ARVOON
 AMPN YLIOPISO Kauppaieeien laios OSINKOJN JA PÄÄOMAVOIOJN VOUKSN VAIKUUKS OSAKKN AVOON Laskenaoimi Seminaariukielma Helmikuu 2004 Ohjaaja: Ismo Vuorinen apani Höök 3 SISÄLLYS JOHDANO... 4. ukielman ausaa...4.2
AMPN YLIOPISO Kauppaieeien laios OSINKOJN JA PÄÄOMAVOIOJN VOUKSN VAIKUUKS OSAKKN AVOON Laskenaoimi Seminaariukielma Helmikuu 2004 Ohjaaja: Ismo Vuorinen apani Höök 3 SISÄLLYS JOHDANO... 4. ukielman ausaa...4.2
RIIPUKSENKADUN ASEMAKAAVAMUUTOKSEN NRO 8471 HULEVESISELVITYS
 S U U N N T T EL U JA T E N A TAMPEREEN AUPUN RPUSENADUN ASEMAAAVAMUUTOSEN NRO HULEVESSELVTYS LOPPURAPORTT D FCG SUUNNTTELU JA TENA OY.. P Loppurpori ().. Sisällyslueelo JOHDANTO.... Työn lähökohd j voiee....
S U U N N T T EL U JA T E N A TAMPEREEN AUPUN RPUSENADUN ASEMAAAVAMUUTOSEN NRO HULEVESSELVTYS LOPPURAPORTT D FCG SUUNNTTELU JA TENA OY.. P Loppurpori ().. Sisällyslueelo JOHDANTO.... Työn lähökohd j voiee....
6 Integraalilaskentaa
 6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
6 Integrlilskent 6. Integrlifunktio Funktion f integrlifunktioksi snotn funktiot F, jonk derivtt on f. Siis F (x) = f (x) määrittelyjoukon jokisell muuttujn rvoll x. Merkitään F(x) = f (x) dx. Integrlifunktion
Matematiikan perusteet taloustieteilijöille 2 800118P
 Mtemtiikn perusteet tloustieteilijöille 2 800118P Luentomoniste Kri Myllylä Niin Korteslhti Oulun yliopisto Mtemttisten tieteiden litos Kevät 2014 Sisältö 1 Mtriisilgebr j optimointi 4 11 Määritelmä 4
Mtemtiikn perusteet tloustieteilijöille 2 800118P Luentomoniste Kri Myllylä Niin Korteslhti Oulun yliopisto Mtemttisten tieteiden litos Kevät 2014 Sisältö 1 Mtriisilgebr j optimointi 4 11 Määritelmä 4
Öljyn hinnan ja Yhdysvaltojen dollarin riippuvuussuhde
 Öljyn hinnan ja Yhdysvalojen dollarin riippuvuussuhde Kansanalousiede Pro gradu -ukielma Talousieeiden laios Tampereen yliopiso Toukokuu 2010 Jari Hännikäinen TIIVISTLMÄ Tampereen yliopiso Talousieeiden
Öljyn hinnan ja Yhdysvalojen dollarin riippuvuussuhde Kansanalousiede Pro gradu -ukielma Talousieeiden laios Tampereen yliopiso Toukokuu 2010 Jari Hännikäinen TIIVISTLMÄ Tampereen yliopiso Talousieeiden
TIELIIKENNEMELUSELVITYS
 PR44-Y01 28.5.2018 Harela Eelä-Suomi Oy TIELIIKENNEMELUSELTYS Asemakaavan muuos A-2701, Hirsimesänie 5 ja 7, Lahi HELSINKI iikinpori 4 B 18 00790 Helsinki puh. 050 377 6565 TURKU Rauakau 5 A 200 Turku
PR44-Y01 28.5.2018 Harela Eelä-Suomi Oy TIELIIKENNEMELUSELTYS Asemakaavan muuos A-2701, Hirsimesänie 5 ja 7, Lahi HELSINKI iikinpori 4 B 18 00790 Helsinki puh. 050 377 6565 TURKU Rauakau 5 A 200 Turku
Ilmavirransäädin. Mitat
 Ilmairransäädin Mia (MF, MP, ON, MOD, KNX) Ød nom (MF-D, MP-D, ON-D, MOD-D, KNX-D) Tuoekuaus on ilmairasäädin pyöreälle kanaalle. Se koosuu sääöpellisä ja miaaasa oimilaieesa ja siä oidaan ohjaa huonesääimen
Ilmairransäädin Mia (MF, MP, ON, MOD, KNX) Ød nom (MF-D, MP-D, ON-D, MOD-D, KNX-D) Tuoekuaus on ilmairasäädin pyöreälle kanaalle. Se koosuu sääöpellisä ja miaaasa oimilaieesa ja siä oidaan ohjaa huonesääimen
MS-A010{3,4} (ELEC*) Differentiaali- ja integraalilaskenta 1 Luento 8: Integraalifunktio ja epäoleellinen integraali
 MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
MS-A1{3,4} (ELEC*) Differentili- j integrlilskent 1 Luento 8: Integrlifunktio j epäoleellinen integrli Pekk Alestlo, Jrmo Mlinen Alto-yliopisto, Mtemtiikn j systeeminlyysin litos 5.1.216 Pekk Alestlo,
Fireflex -palosuojamaali
 Käyttöseloste uusittu 13.11.2007 VARMENNETTU KÄYTTÖSELOSTE Liitteet uusittu 14.2.2008 TRY-69-2007 Fireflex -palosuojamaali Valmistaja Tikkurila Coatings Oy Kuninkaalantie 1 01300 VANTAA Varmennetun käyttöselosteen
Käyttöseloste uusittu 13.11.2007 VARMENNETTU KÄYTTÖSELOSTE Liitteet uusittu 14.2.2008 TRY-69-2007 Fireflex -palosuojamaali Valmistaja Tikkurila Coatings Oy Kuninkaalantie 1 01300 VANTAA Varmennetun käyttöselosteen
Magneettisessa profiilitulkinnassa saaduista suskeptibiliteettiarvoista. käytettäessä kaksidimensionaalista levymallia.
 Ou kumpu O} vlalminesinä ARKSTO ' ple. '-1 Magneeisessa priiliulkinnassa saaduisa suskepibilieeiarvisa ja keskimääräisen suskepibilieein laskemisesa käyeäessä kaksidimensinaalisa levymallia. Yheenvedssa
Ou kumpu O} vlalminesinä ARKSTO ' ple. '-1 Magneeisessa priiliulkinnassa saaduisa suskepibilieeiarvisa ja keskimääräisen suskepibilieein laskemisesa käyeäessä kaksidimensinaalisa levymallia. Yheenvedssa
766328A Termofysiikka Harjoitus no. 12, ratkaisut (syyslukukausi 2014)
 7668A Termofysiikk Hrjoitus no 1, rtkisut (syyslukukusi 14) 1 Lämpötilss T K elektronien energit eivät ylitä Fermin energi (ɛ i ɛ F ), lämpötilprmetri β j kemillinen potentili vst Fermin energi (µ() ɛ
7668A Termofysiikk Hrjoitus no 1, rtkisut (syyslukukusi 14) 1 Lämpötilss T K elektronien energit eivät ylitä Fermin energi (ɛ i ɛ F ), lämpötilprmetri β j kemillinen potentili vst Fermin energi (µ() ɛ
Sanomalehtien kysyntä Suomessa Sanomalehtien kysynnän kehittymistä selittävä ekonometrinen malli
 Sanomalehien kysynä Suomessa Sanomalehien kysynnän kehiymisä seliävä ekonomerinen malli Heikki Nikali, Iella BI Research series - Tukimussarja 7/2014 12.3.2014 FOR INTERNAL USE ONLY VAIN SISÄISEEN KÄYTTÖÖN
Sanomalehien kysynä Suomessa Sanomalehien kysynnän kehiymisä seliävä ekonomerinen malli Heikki Nikali, Iella BI Research series - Tukimussarja 7/2014 12.3.2014 FOR INTERNAL USE ONLY VAIN SISÄISEEN KÄYTTÖÖN
Digitaalinen videonkäsittely Harjoitus 5, vastaukset tehtäviin 25-30
 Digitlinen videonkäsittely Hrjoitus 5, vstukset tehtäviin 5-30 Tehtävä 5. ) D DCT sdn tekemällä ensin D DCT kullekin riville, j toistmll D DCT tuloksen sdun kuvn srkkeill. -D N-pisteen DCT:, k 0 N ( k),
Digitlinen videonkäsittely Hrjoitus 5, vstukset tehtäviin 5-30 Tehtävä 5. ) D DCT sdn tekemällä ensin D DCT kullekin riville, j toistmll D DCT tuloksen sdun kuvn srkkeill. -D N-pisteen DCT:, k 0 N ( k),
EFG 213-320. Käyttöohjeet 09.09 - 03.13. EFG 213 EFG 215 EFG 216k EFG 216 EFG 218k EFG 218 EFG 220 EFG 316k EFG 316 EFG 318k EFG 318 EFG 320
 EFG 213-320 09.09 - Käyöohjee 51151911 03.13 s EFG 213 EFG 215 EFG 216k EFG 216 EFG 218k EFG 218 EFG 220 EFG 316k EFG 316 EFG 318k EFG 318 EFG 320 Vaaimusenmukaisuusvakuuus Jungheinrich AG, Am Sadrand
EFG 213-320 09.09 - Käyöohjee 51151911 03.13 s EFG 213 EFG 215 EFG 216k EFG 216 EFG 218k EFG 218 EFG 220 EFG 316k EFG 316 EFG 318k EFG 318 EFG 320 Vaaimusenmukaisuusvakuuus Jungheinrich AG, Am Sadrand
Reaalinen lukualue. Millainen on luku, jossa on päättymätön ja jaksoton desimaalikehitelmä?
 Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Relinen lukulue POLYNOMIFUNKTIOT JA -YHTÄLÖT, MAA Millinen on luku, joss on päättymätön j jksoton desimlikehitelmä? Onko sellisi? Trkstelln Pythgorn luseest stv yksikköneliön lävistäjää, luku + = x x =.
Signaalit aika- ja taajuustasossa
 Sili lomuoo Sili ik- uussoss Alomuoo kuv sili käyäyymisä fukio li iksoss. Ylsä lomuoo rksll simrkiksi oskilloskoopi äyöllä. Siimuooi sili Asiφ Asiπf φ i Acosφ Acosπf φ muodos prus kikki sili uussisällö
Sili lomuoo Sili ik- uussoss Alomuoo kuv sili käyäyymisä fukio li iksoss. Ylsä lomuoo rksll simrkiksi oskilloskoopi äyöllä. Siimuooi sili Asiφ Asiπf φ i Acosφ Acosπf φ muodos prus kikki sili uussisällö
4. Määritä oheisen kehän plastinen rajakuorma. Tarkista, ettei myötöehtoa rikota missään. Piirrä tasapainoehdot toteuttava taivutusmomenttijakauma.
 Rk-4.00 Rkenteiden mekniikk I tentti/exm,..0 Kirjoit jokiseen koeeriin selvästi - ointojkson nimi, koodi j tentin äivämäärä - kikki nimesi uhuttelunimi lleviivttun - koulutusohjelm, oiskelijnumero, myös
Rk-4.00 Rkenteiden mekniikk I tentti/exm,..0 Kirjoit jokiseen koeeriin selvästi - ointojkson nimi, koodi j tentin äivämäärä - kikki nimesi uhuttelunimi lleviivttun - koulutusohjelm, oiskelijnumero, myös
Integraalilaskenta. Määrätty integraali
 9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
9..08 Integrlilskent Määräämätön Etsitään funktiot Derivoinnille käänteistoimenpide integroiminen Integrlifunktio F(x), jolle F x = f x, lisäksi integrlifunktioille G x = F x + C. Vkion C lisäys (merkitys),
