Vetypolttokennojen dynaamiset mallit
|
|
|
- Teuvo Lehtonen
- 8 vuotta sitten
- Katselukertoja:
Transkriptio
1 SÄÄTÖTEKNIIKAN LABORATORIO Vetypolttokennojen dynaamiset mallit Janne Aarnio ja Kauko Leiviskä Raportti B No 67, Kesäkuu 008
2 Oulun yliopisto Säätötekniikan laboratorio Raportti B No 6, Kesäkuu 008 Vetypolttokennojen dynaamiset mallit Janne Aarnio ja Kauko Leiviskä Oulun yliopisto, Säätötekniikan laboratorio Lyhennelmä: Tässä kirjallisuustyössä tutustutaan vedyllä toimivien polttokennojen mallinnuksiin. Kirjallisuustyössä kuvataan ensin polttokennon toimintaa. Lisäksi esitellään lyhyesti bioetanolin reformointia, josta saadaan tuotteena vetyä. Tutkimuksessa keskitytään matalalämpötilassa toimivien polymeeripolttokennojen dynaamisiin malleihin, joista esitellään kaksi mallia, joiden Matlab/Simulink-mallit on helposti saatavissa. Alkalipolttokennoista suoraetanoli-polttokennoille, joissa etanolin reformointi tapahtuu itse polttokennossa, esitetään vain joitakin kirjallisuusviitteitä. Tämä kirjallisuusselvitys liittyy projektiin Polttokennoon soveltuvan vedyn tuottaminen bioetanolia reformoimalla (REFORMH). Hakusanat: Polttokenno, PEM, etanolin reformointi, dynamiset prosessimallit ISBN ISSN Oulun yliopisto Säätötekniikan laboratorio PL 4300 FIN OULUN YLIOPISTO ii
3 Sisällysluettelo 1 Johdanto...1 Polttokennot....1 Yleistä polttokennoista.... Polttokennon termodynamiikkaa Polymeeripolttokenno Alkalipolttokenno Reformoinnin perusteita PEM-polttokennojen dynaamiset mallit Kirjallisuuskatsaus dynaamisista malleista Mallien rakenteesta Sähkökemiallinen malli Ainetasemalli Lämpötasemalli Alkalipolttokennon dynaamiset mallit Malleja yhdistetylle reformoinnille ja polttokennolle Suoraetanoli-alkalipolttokenno Suoraetanoli-polymeeripolttokenno... 6 Yhteenveto... 3 LÄHDELUETTELO... 4 iii
4 1 JOHDANTO Polttokennot ovat suhteellisen vanha keksintö. Ensimmäiset maininnat polttokennoista ovat jo 1840-luvulta, mutta vasta viimeisen parin vuosikymmenen aikana niiden tutkimus on kasvanut voimakkaasti. Osaltaan tähän on vaikuttanut ihmisten kiinnostus puhtaampaan energian tuotantoon. Vetypolttokennot tarjoavat mahdollisuuden tuottaa sähköä vedystä, niin että tuotteena syntyy sähkön lisäksi vain lämpöä ja vettä. Polttokennon hyötysuhde on myös korkeampi kuin perinteisillä lämpövoimakoneilla, joten autoteollisuuskin on osoittanut mielenkiintoa polttokennotekniikkaan. Polttokennot voidaan tehdä kooltaan ja tehoiltaan erikokoisiksi. Niillä on siten lukuisia mahdollisuuksia erilaisiin käyttökohteisiin. Kannettavaan elektroniikkaan niitä on ajateltu energialähteeksi akun korvikkeina. Korkeammissa lämpötiloissa toimivia polttokennoja voidaan hyödyntää rakennuksissa sähkön ja lämmön tuottamiseen. Polttokennon suosiota lisää myös mahdollisuus käyttää uusiutuvaa vetyä polttoaineena. Vetyä on mahdollista tehdä fossiilisten polttoaineiden lisäksi biologisista vaihtoehdoista. Bioetanolia voidaan hyödyntää matalalämpötilassa toimivissa polttokennoissa ja biokaasu soveltuu hyvin korkealämpötila-polttokennoihin. Vedyn lähteiksi on kaavailtu myös kaatopaikoilla syntyvää metaania. Maatalousjätteistä taas voidaan kaasuttaa bioetaania tai valmistaa käymisprosessilla bioetanolia. Biopolttoaineen valmistamiseen tarvittavaa biomassaa voi valmistaa myös viljelemällä sopivia kasveja, mutta eettisistä syistä se ei vielä ole saanut suuren yleisön hyväksyntää. Polttokennot ovat vielä esikaupallisessa vaiheessa ja ne yleistyvät hiljalleen. Teknologia ei ole vielä aivan valmis edullisiin polttokennosovelluksiin. Myös polttoaineen varastointi ja jakelu kaipaisivat yhdenmukaistamista. Tämä kirjallisuuskatsaus antaa tietoa polttokennojen toiminnasta, biopolttoaineen käsittelystä vedyksi ja kahden polttokennotyypin mallintamisesta.
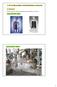
5 POLTTOKENNOT.1 Yleistä polttokennoista Polttokenno on sähkökemiallinen laite, joka muuttaa polttoaineen hapettimen avulla sähköksi ja lämmöksi jatkuvatoimisesti (Ramakumar 001). Polttokenno koostuu positiivisesti varautuneesta elektrodista (katodista), negatiivisesti varautuneesta elektrodista (anodista) ja ne toisistaan erottavasta elektrolyytistä. Elektrolyytti estää polttoaineen ja hapettimen suoran kosketuksen, joten varsinaista palamisreaktiota polttokennossa ei tapahdu. Polttokennot luokitellaan yleensä käytetyn elektrolyytin mukaan ja niitä on käytössä erilaisia: kiinteitä, nestemäisiä ja kalvomaisia. Polttokennon rakenne ja reaktiot riippuvat polttokennotyypistä. Polttokennossa polttoaine hajoaa ja ionisoituu anodilla. Elektronit siirtyvät elektrodia pitkin ulkoiselle kuormitukselle, jossa niiden virtaus hyödynnetään sähköenergiana. Positiivinen ioni siirtyy elektrolyytin läpi katodille, missä ilman happi hapettimena pelkistyy. Joissakin polttokennotyypeissä taas negatiivinen ioni liikkuu anodille. Polttokennoissa käytetään yleensä polttoaineena vetyä, joko puhtaana tai sitoutuneena eri yhdisteisiin. Hapettimena käytetään ilmaa tai puhdasta happea. Teoriassa polttoaineena ja hapettimena voitaisiin käyttää lähes mitä tahansa hapettuvaa ja pelkistyvää ainetta. Puhdasta vetyä ja puhdasta happea käytettäessä tuotteena syntyy sähkön lisäksi vain lämpöä ja vettä. Polttokennon toiminnan yleinen periaate on esitetty kuvassa 1. Kuva 1. Polttokennon toimintaperiaate (Fuel cell handbook 004, 1).
6 . Polttokennon termodynamiikkaa Polttokennon tuottama sähköenergia saadaan reagoivien aineiden kemiallisesta energiasta. Energia vapautuu hapetus-pelkistys reaktioiden avulla. Sähkökemiallisen reaktion avulla saadaan energia lämpönä ja sähkönä. Energia, joka saadaan talteen tietyssä lämpötilassa, voidaan ilmaista Gibbsin vapaan energian avulla. Muutos Gibbsin vapaassa energiassa ( G) saadaan, kun entalpian muutoksesta ( H) vähennetään entropian muutos ( S) tietyssä lämpötilassa (T) (Ramakumar 001). G = H T S (1) Kokonaisentalpianmuutos saadaan, kun tuotteiden (p) entalpioiden muutoksesta vähennetään lähtöaineiden (r) entalpioiden muutos. H = Σ H p Σ H r () Hapetus-pelkistysreaktioiden tyyppi vaikuttaa kennon tuottamaan sähkötehoon. Reaktiossa moolia kohden vapautuvien elektronien lukumäärän (n), Faradayn vakion (F) ja Gibbsin energian muutoksen avulla saadaan lasketuksi maksimaalinen jännite (V). Paine ja lämpötila vaikuttavat Gibbsin energian kautta yhtälöön 3, joten maksimaalinen ulostulojännite riippuu toimintapisteestä. V G = volttia (3) nf.3 Polymeeripolttokenno PEM (polymeeri-elektrolyytti-membraani) polttokennoissa puhdas vetykaasu johdetaan platinalla pinnoitetun hiilielektrodin läheisyyteen (anodille). Siellä vetyatomi ionisoituu ja hajoaa protoniksi luovuttaen elektronin. Platinalla katalysoidussa katodireaktiossa ilman happi yhtyy membraanin läpi tulleeseen vetyprotoniin. Reaktiossa syntyy vettä ja lämpöä. Sähkö muodostuu hapetus- ja pelkistysreaktioista elektrodeilla. Polttokenno toimii C lämpötilassa, joten se on nopea käynnistymään. Kennosta saatava maksimaalinen jännite on E o = 1.16 V (Farrauto 005). Elektrodeilla tapahtuvat reaktiot ovat esitetty seuraavissa yhtälöissä : anodireaktio: H H + + e - (4) katodireaktio: ½ O + H + + e - H O (5) kennoreaktio: H + ½ O H O (6) 3
7 Edellä esitetyn yksikkökennon tuottama jännite on suhteellisen pieni, joten suurempaa jännitettä tarvittaessa polttokennossa kytketään sarjaan useita yksikkökennoja. Yksikkökennojen välissä on bipolaarilevy, jossa virtaavat molemmat reagenssit. Levyt toimivat myös virranjohtimina. Kennoston päädyissä on yksipuolinen virtauskanavalevy. Polttokennon rakenne ja eo. yhtälöt ovat nähtävissä kuvasta (Haddad et al. 006). Kuva. Polymeeripolttokenno yhtälöineen (Haddad et al. 006)..4 Alkalipolttokenno Alkalipolttokennojen (Alkaline Fuel Cell, AFC) historia ulottuu yli sadan vuoden taakse: vuonna 190 Reid ja 1904 Noel esittelivät polttokennon, joka käytti nestemäistä kaliumhydroksidia elektrolyyttinä. Sadan vuoden aikana alkalipolttokennojen kehityksessä on kohdattu monia ongelmia ja osa niistä on saatu myös ratkaistuksi. (Gülzow 1996) Alkalipolttokennossa käytetään elektrolyyttinä kaliumhydroksidin vesiliuosta. Näitä polttokennoja käytetään esim. avaruussukkuloissa, koska reaktiot ovat tehokkaita ja tuotteena saadaan sähkön lisäksi juomakelpoista vettä. Alkalipolttokennot vaativat toimiakseen puhdasta vetyä ja puhdasta happea, sillä elektrolyytin teho heikkenee ilman hiilidioksidin vaikutuksesta. (Romm 004, s 3) Alkalipolttokennojen hyödyntämisen mahdollisuudet erilaisissa kohteissa ovat hyvät. Polttokennoja voidaan rakentaa kooltaan pieniksi ja liikuteltaviksi, esim pienten 4
8 sähkölaitteiden energialähteiksi tai paikallisesti asennettaviksi suurempaa tehoa vaativien laitteiden energialähteeksi. (Gülzow 1996) Alkalipolttokennolla on muutamia etuja polymeeripolttokennoon verrattuna. Platinakatalyytit voidaan korvata nikkelillä anodilla ja hopealla katodilla. Alkalipolttokennossa elektrolyyttinä käytetään kaliumhydroksidia kalliin membraanikalvon sijaan. Huonona puolena alkalipolttokennossa on sen sieto hiilidioksidia vastaan, kun hapettimena käytetään ilman happea (Gülzow et al. 006). Tällöin kaliumhydroksidi reagoi hiilidioksidin läsnäollessa kaliumkarbonaatiksi (Laramie and Dicks 003, s 16): KOH + CO K CO3 + H O (7) Alkalipolttokennon kennoreaktiot poikkeavat hieman polymeeripolttokennoista. Merkittävin ero on siinä, että elektrolyytin läpi liikkuvat hydroksyyli-ionit protonien sijaan. Seuraavissa yhtälöissä on esitetty elektrodireaktiot ja kokonaisreaktio: H + ( OH ) H O + e (8) H O +.5O + e ( OH ) (9) 0 H O H O (10).5 Reformoinnin perusteita Bioetanolia reformoimalla voidaan tuottaa vetyä. Yleisesti reformointi voidaan jakaa kahteen menetelmään: höyryreformointiin ja autotermiseen reformointiin. Näiden lisäksi polttokennoihin liittyen voidaan puhua sisäisestä reformoinnista (internal reforming), jolloin reformointi tapahtuu suoraan polttokennossa. Höyryreformointia voidaan kuvata useilla erilaisilla reaktioyhtälöillä, riippuen siitä, minkälaisia osareaktioita haluaa käyttää kuvaamaan kokonaisreaktiota. Reaktio-olosuhteet ja mooliosuudet syötteissä ja käytetyt katalyytit vaikuttavat osareaktioiden todennäköisyyksiin. Seuraavassa on esitetty yksi tapa höyryreformoinnin kuvaamiseen reaktioyhtälöillä (Francesconi et al. 007): C + (11) H 5OH CH 3CHO H CH 3 COH CH 4 + CO (1) CH + + (13) 4 H O CO 3H CO + H + (14) O CO H 5
9 Autoterminen reformointi on toinen tapa valmistaa bioetanolista vetyä. Siinä vetyä muodostetaan osittaishapetuksella (Ni et al. 007). Tällä tavoin vedyn selektiivisyys jää kuitenkin pieneksi. Osittaishapetus on esitetty seuraavalla reaktioyhtälöllä: 1 CHOH 5 + O CO+ 3H (15) Parempaan lopputulokseen päästään autotermisessä reformoinnissa, kun yhdistetään osittaishapetus ja höyryreformointi. Seuraavassa reaktioyhtälössä nähdään, miten vedyn tuotanto paranee yhtä moolia etanolia kohden: 1 CHOH 5 + HO + O CO + 5H (16) Etanolia voidaan valmistaa fermentoimalla biomassaa (Ni et al. 007). Biomassaa saadaan esimerkiksi maatalousjätteistä. Biomassaa voidaan tuottaa myös viljelemällä sopivia kasveja. Fermentaatiota (käymistä) on helppo hallita ja siinä orgaaninen aines pilkkoutuu yleensä hapettomassa ympäristössä. Glukoosin fermentaatiossa muodostuu etanolia ja hiilidioksidia C + CO (17) 6H1O6 CH 3CH OH Yhteenveto reformointiprosessin malleista löytyy viitteestä (Ohenoja 008). 6
10 3 PEM-POLTTOKENNOJEN DYNAAMISET MALLIT 3.1 Kirjallisuuskatsaus dynaamisista malleista Kirjallisuudessa on referoitu useita perusilmiöihin pohjautuvia PEM-polttokennojen malleja. Del Real et al. (007) ovat esittäneet mallin, joka on parametroitu vastaamaan Ballardin 1. kw PEM polttokennoa, mitä monet tutkimusryhmät ovat käyttäneet myös omissa tutkimuksissaan. Lisäksi mallin toimintaa on verrattu todellisesta polttokennosta mitattuihin arvoihin. Malli koostuu pääpiirteissään kolmesta kokonaisuudesta: sähkökemiallisesta staattisesta osasta, aineensiirron dynamiikasta ja termodynamiikasta. Mallin tuloja ovat (kuva 3): ilmapumpun jännite, jolla ohjataan hapettimen kulkua kennolle, jäähdytystuulettimen jännite, jolla vaikutetaan kennon lämpötilaan, ja vetyventtiiliin asento, jolla säädetään reagoivan polttoaineen määrää. Muita tuloja ovat ympäristön lämpötila ja kennon virta. Näihin muuttujiin voidaan yhdistää suoraan mitattua aineistoa ja mallintaa näin kennon toimintaa. Mallin lähtösuureina ovat kennon lämpötila ja jännite. Kuva 3. Mallin tulo- ja lähtösuureet (del Real et al. 007). Haddad et al. (006) ovat esittäneet 17 tilayhtälöstä koostuvan mallin, jonka dynamiikassa on otettu huomioon sekä aineensiirtoon perustuvat diffuusioyhtälöt että sähkökemiaan liittyvät yhtälöt. Mallissa on kuusi tuloa ja viisi lähtöä ja kaavio sen Simulink-toteutuksesta on esitetty kuvassa 4. Tärkeimmät kennon dynamiikkaa kuvaavat lähdöt ovat kennon jännite ja virta, sillä kaikki tulot vaikuttavat niihin. Wang et al. (005) ovat esittäneet vastaavanlaisen mallin, joka on toteutettu Matlab /Simulink - ympäristössä. Artikkelissa on myös verrattu Simulink -toteutusta vastaavaan sähköiseen analogiaan, joka on toteutettu PSPICE työkalulla. Tuloksia on myös vertailtu kokeellisiin mittaustuloksiin. Kuvassa 5 on esitetty mallin peruskaavio. 7
11 Toinen Ballardin PEM polttokennolle tehty dynaaminen malli simuloi 5 kw:n tehoista Ballardin MK-5 E polttokennoa (Khan and Iqbal 004). Malli on myös tehty Matlabilla ja sillä on mahdollista simuloida dynaamisesti sähkövirran vaihtelua ja syötekaasujen paineita. Polttokennon ulkoisen kuormituksen resistanssin kasvattaminen havaitaan mallissa virran arvon laskemisena ja jännitteen kasvamisena. Tämä malli on myös modulaarinen ja se sisältää sähkökemiallisen, termodynaamisen ja reaktanttien virtausta kuvaavan osion. Sähkökemiallinen malli käsittää yhtälöt kennon jännitteelle, termodynaamiselle potentiaalille, aktivaatioylipotentiaalille (activation overvoltage) ja ohmiselle ylipotentiaalille (ohmic overvoltage). Termodynaaminen malli sisältää energiatasapainoyhtälön, missä terminen kapasitanssi tietyllä ajanhetkellä saadaan, kun kokonaistehosta vähennetään lämpöhukka kennon pinnalta, jäähdytyksen aiheuttama häviö ja ulosottoteho. Reaktanttien virtausmalli koostuu vedyn ja hapen ainetaseyhtälöistä. Kuvaa 5 vastaava Simulink -kaavio on kuvassa 6. Kuva 4. Simulink -mallin peruskaavio (Haddad et al. 006). Merkintöjen selitykset löytyvät alkuperäisestä viitteestä. Kuva 5. Simulink -mallin peruskaavio (Wang et al. 005). 8
12 Kuva 6. Simulink-mallin peruskaavio (Khan and Iqbal. 004). Kirjallisuudessa on raportoitu myös hybridimalleista. Bucholz ja Krebs (007) ovat esittäneet mallin, jossa epälineaarinen staattinen osa on toteutettu neuroverkolla ja dynaaminen osa on lineaarinen tilamalli. Malli sisältää viisi tuloa ja yhden lähdön. Dynaamisessa osassa on kaksi tuloa ja yksi lähtö. Muuttujat on esitetty kuvassa 7. (Buchholz ja Krebs 007) Kuva 7. Hybridimalli polttokennolle (Buchholz ja Krebs 007). Li et al. (007) ovat esittäneet polttokennolle Hammersteinin mallin, jota on identifioitu tukivektorimenetelmällä (SVM) Malli on toteutettu kolmella tulolla ja kahdella lähdöllä. Hapen stökiometria, sähkövirran tiheyden arvo ja jäähdytysveden virtausmäärä ovat 9
13 tulosuureita. Lähdöt on hapen osapaine ja kennon lämpötila, joilla ohjataan kennon jännitettä. Malli on rakennettu Matlabilla ja perustuu 3kW polymeeripolttokennoon. 3. Mallien rakenteesta Polttokennomallit ovat usein modulaarisia, kuten edellisessä kappaleessa mainittiin. Ne sisältävät erikseen mallit sähkökemiaan, termodynaamiikkaan ja reagoivien aineiden taseisiin. Seuraavassa on verratu lähinnä Khanin ja Iqbalin (004) ja Wang et al. (005) malleja. Molemmista on olemassa Simulink -versio. Wangin mallin yksinkertaistamiseen on käytetty oletuksia, joita on käytetty myös muissa tutkimuksissa: Malli on yksiulotteinen. Kaasut ovat ideaalisia ja tasaisesti levinneitä. Paineet kaasujen virtauskanavissa ovat vakioita. Hapetin ja oksidantti ovat kostutettuja. Lämpötila alle 100 C, joten tuotteen faasi on nestemäinen. Lämpötila on yhtenevä kennossa ja samoin lämpökapasiteetti. Yksikkökennojen parametrit ovat voimassa sarjaan kytkettynä koko kennostolle. Sähkökemiallinen malli Sähkökemiallinen malli kuvaa jännitteen käyttäytymistä virrantiheyden funktiona (polaarisaatiokäyrä) (kuva 8). Polttokennosta ei saada ulos teoreettista maksimijännitettä, vaan erilaiset vastukset aiheuttavat jännitehäviötä. Malleissa on usein otettu huomioon kolme häviöitä aiheuttavaa termiä: aktivaatioylijännite (activation overvoltage), V act, ohminen häviö, V ohmic ja konsentraatioylijännite (consentration overvoltage), V con. Jännitettä voidaan kuvata seuraavasti (Wang et al. 005) Vcell = Ecell Vact Vohmic Vcon (18) Sisäinen jännite, E cell, lasketaan molemmissa malleissa Nernstin yhtälön avulla 0.5 [ p ( p ] RT E (19) cell = E0, cell + ln H ) O F * * Yhtälön ratkaisemiseen tarvitaan hapen ja vedyn osapaineet( p, p ). Lisäksi H O kemiallisen reaktion olosuhteet vaikuttavat jännitteen arvoon. E 0,cell kuvaa maksimaalista jännitettä standardiolosuhteissa (1.9 V, T=98.15 K, p= 1 atm). T on kennon lämpötila (K), R on yleinen kaasuvakio (8.314 J/molK) ja F on Faradayn vakio (96485). E 0,cell :n lämpötilariippuvuus on sisällytetty Khanin ja Iqbalin (004) malliin muodossa 10
14 E 3 0, cell ( T 98.15) = (0) Wang et al. (005) antavat riippuvuuden E0, cell = E0, cell ke ( T 98), (1) joka tietyin oletuksin vastaa yhtälöä (0). Vakioille on annettu arvot K E = V/K. Li et al. (007) antavat erilaisen riippuvuuden E 0,cell =58.9 V ja E = 1, *10 ( T 98.15) *10 Tln( p ) + 0.5ln( p ) () 3 5 * * cell H O Sama yhtälö on myös viitteessä Mann et al. (000). Haddad et al. (006) ovat antaneet Nernstin yhtälön muodossa E E cell 0, cell RT p = E + F p * * H O 0, cell * HO = p 4 T (3) Nernstin yhtälöä käytetään malleissa kuvaamaan termodynaamista jännitettä. Yhtälön avulla saadaan lasketuksi ideaalijännite (Kuva 8). Aktivaatioylijännite laskee nopeimmin jännitettä pienillä virrantiheyden arvoilla ja se korostuu erityisesti matalassa lämpötilassa toimivissa polttokennoissa kuten PEM-polttokennoissa. Aktivaatioylijännite koostuu elektronien liikkeen hitauksista elektrodeilla. Elektrodireaktioiden aktivaatioenergiat vaikuttavat jännitehäviön suuruuteen, joten sitä voidaan vähentää reaktionopeutta kasvattamalla, esimerkiksi lämpötilaa tai painetta lisäämällä. Kuva 8. Polarisaatiokuvaaja (Fuel cell handbook 004, 64). 11
15 Aktivaatioylijännitteen laskenta poikkeaa tarkastelluissa malleissa. Khan ja Iqbal (004) lähtevät alunperin Amphlett et alin (1995) esittämästä staattisesta mallista, jossa polttokennon aktiivinen ala (A, cm ), virran arvo (i, A), lämpötila (T, K) ja syötekaasujen * * konsentraatiot ( c, c, mol/cm 3 ) otetaan huomioon H O * ( O ) η = ξ + ξ T + ξ ln( c ) + ξ Tln( i) (4) act Sijoittamalla tähän viitteessä Mann et al. (000) kokeellisesti määritetyt kertoimet saadaan η act = ( ln( A) + [ ] ln( ch )) + ( T ln c ) ( ln( ) ) O + T i (5) Vedyn ja hapen konsentraatiot lasketaan osapaineista Henryn lain avulla c c 77 = p exp T 498 = p exp T * 7 * H H * 7 * O O (6) Dynamiikka on otettu huomioon seuraavilla yhtälöillä (Khan ja Iqbal 004) V V R i dvact i Vact = dt C R C act act = ηact; act = dl act dl (7) Edellä C dl on double-layer kapasitanssi (0.035 Fcm - ). Kuvan 9 Simulink -malli selventänee yhtälöitä. Kuva 9. Yhtälön 7 Simulink -toteutus (Khan ja Iqbal 004). 1
16 Wang et al. (005) ovat laajentaneet Tafelin yhtälöä vakiotermillä η 0 (0.145 V) Amphlett et alin (1995) mukaisesti ja laskevat aktivaatioylijannitteen kahdessa osassa, joissa V act1 sisältää vain vakiotermin ja lämpötilariippuvuuden ja V act sekä lämpötilaettä virtariipuvuuden V = V + V V act act1 act act1 0 act = η + a( T 98) V = btln( i) (8) Vakiolle a on annettu arvo V/K. Ohmiset häviöt ovat vallitsevia virrantiheyden keskivaiheilla, joten Ohmin lakia noudattaen kyseinen alue on hyvin lineaarinen. Näihin jännitehäviöihin sisältyy polttokennon osien sisäisiä vastuksia, kuten elektrodien resistanssit, membraanin resistanssi ja kontaktiresistanssit (Khan ja Iqbal 004). Membraanin resistanssi riippuu membraanin paksuudesta, alasta ja resistiivisyydestä. Resistiivisyys saa taas eri arvoja riippuen membraanin kosteudesta, lämpötilasta ja anodikaasun stökiömetriasta. V ohmic = ir (9) ohm Sisäinen vastus (R ohm, Ω) saadaan seuraavasta yhtälöstä R r l A M M ohm =, (30) missä r M on membraanin resistiivisyys (Ω), l M membraanin paksuus (cm) ja A kennon tehollinen pinta-ala (cm ). Membraanin resistiivisyydelle Khan ja Iqbal (004) antavat yhtälön r M i T i A 303 A = 3i T 303 λ exp 4.18 A T (31) Yhtälö pätee Dow membraaneille ja parametrille λ on annettu arvo 1.5. Wang et al (005) ovat kirjoittaneet sisäisen vastuksen virta- ja lämpötilariippuvuuden muotoon R = R + k i k T, (3) ohm ohm0 RI RT jossa R ohm0 (.793 Ω) on sisäisen vastuksen perusarvo ja k RI ja k RT ovat kokeellisia parametreja. 13
17 Konsentraatioylipotentiaali rajoittaa maksimitehoa suurilla virrantiheyden arvoilla. Tällöin reaktanttien kulutus elektrodeilla on suurempi kuin niiden diffuusio kyseiselle alueelle. Tämä termi ei sisälly Khanin ja Iqbalin (004) malliin, mutta Wang et al (005) ovat kirjoittaneet sen muotoon V R con con RT i = ln 1 zf i limit Vcon RT i = = ln 1 i zfi i limit (33) Wang et al (005) käsittelevät myös katodin ja membraanin välisen sähkökemiallisen kaksoiskerroksen (double layer) kapasitiivista vaikutusta hieman eri tavalla yhtälöön 7 verrattuna. He yhdistävät yhtälön 33 mukaisen vastuksen ja yhtälön 7 vastuksen ja kirjoittavat dynaamisen yhtälön muotoon dv V = i C R + R dt ( ) C C dl act con (34) Tällöin yhtälön 18 asemasta voidaan käyttää yhtälöä Vcell = Ecell VC Vohmic Vact1 (35) Ainetasemalli Ainetasemalliin lasketaan komponenttien taseet kullekin tasealueelle. Komponentteina ovat aina vety ja happi. Ilmaa hapettimena käytettäessa typpi otetaan usein tarkasteluun ja tuotteena syntyvä vesi otetaan myös joissain malleissa huomioon. Tasealueitten määrät vaihtelevat faasien ja kennoston kuvaustarkkuuden mukaan. Ainetasemallit perustuvat ideaalikaasulakiin. Vedyn ja hapen osapaineille anodilla ja katodilla voidaan kirjoittaa seuraavat yhtälöt (Wang et al. 005) * V dp a H i = mh, in mh, out RT dt F i = mh, net F * V dp c O i = mo, in mo, out RT dt 4F i = mo, net 4F (36) 14
18 Edellä virtausnopeudet ovat yksikössä mol/s. V a ja V c ovat anodin ja katodin tilavuudet. Tasapainotilassa dp m dp = = 0 dt i = m = F * * H O dt H, net O, net (37) Wang et al. (005) antavat myös seuraavan yhtälön mukaisen dynaamisen mallin moolivirtauksille dm τ dt dm τ dt i F i 4F H, net a = mh, net O, net C = mo, net (38) Khan ja Iqbal (004) ovat ratkaisseet yo. ainetaseyhtälöt hieman eri tavalla (kuvat 10 ja 11). Moolinen lähtövirtaus anodilta lasketaan yhtälöstä * ( ) m = k p p, (39) H, out a H tank missä k a on anodin virtauskerroin (0.065 mol/(s atm)) ja p tank on vedyn paine tulovirtauksessa (3 atm). Vedyn tulovirtaus lasketaan kuvan 10 mukaisella PIDsäätimellä. Kuva 10. Anodin massataseen Simulink -kaavio (Khan ja Iqbal 004). Vastaavasti katodin massataseessa poistuva happivirtaus lasketaan yhtälöstä * ( ) m = k p p, (40) O, out c O BPR 15
19 missä k c on katodin virtauskerroin (0.065 mol/(s atm)) ja p BPR on hapen paine ulostulossa (3 atm). Hapen tulovirtaus lasketaan kertomalla ilman tulovirtausta hapen mooliosuudella (1%). Kuva 11. Katodin massataseen Simulink -kaavio (Khan ja Iqbal 004). Hieman yksityiskohtaisemmin esitettynä tasealueet voidaan jakaa viiteen osaan polttokennon rakenteen mukaan (kuva 1, del Real 007). Silloin membraanin lisäksi tasealueiksi on määritelty anodin ja katodin virtauskanavat ja kaasudiffuusiokerros. Mallissa on lisäksi otettu huomioon kaasun kosteus, typpi ja vesi kaasu- ja nestefaasissa. Kuva 1. Vaihtoehtoinen ainetaseen määrittely (del Real 007). Lämpötasemalli Polttokennolle tehty lämpötasemalli kuvaa energiatasetta. Se voidaan ilmaista yksinkertaisesti; systeemin sisältämä energia on yhtäsuuri kuin siihen tuotu energia vähennettynä siitä lähtevä energia. Polttokennoon tuodaan energiaa reagenssien mukana. Niihin on sitoutunut lämpöenergia ja kennossa tapahtuvan reaktion avulla vapautuva energia. Systeemissä oleva energia (lämpömäärä) tietyllä ajanhetkellä voidaan esittää seuraavasti (Khan ja Iqbal 004). 16
20 C t dt dt ' = P tot P elec Q cool Q loss (41) C t on lämpökapasiteetti (J/ C) ja T on lämpötila (huom. C ). Kokonaisenergia P tot (W) on vedyn palamisentalpia, reaktiossa kuluneesta vedystä laskettuna. Kuorman sähkön kulutus P elec (W) kuvaa kennosta otettua tehoa. Q-termit (J/s) kuvaavat lämpönä poistuvaa energiaa. Se voi tapahtua sisäisellä jäähdytyksellä, ulkoisella vapaalla konvektiolla tai pakotettuna esim. puhaltimen avulla (kuva 13). Kuva 13. Lämpötasemallin termit (Khan ja Iqbal 004). Kokonaisenergia saadaan yhtälöstä Ni Ptot = mh, used H = H (4) F jossa N on polttokennojen määrä ja H on vedyn palamislämpö (85.5 kj/mol). Kuormituksen ottama teho saadaan yhtälöstä P = V i V elec stack stack = NV cell (43) Jäähdytysveden mukana poistuva lämpömäärä taas saadaan yhtälöistä Q = UA LMDT = UA cool HX HX UA = h h i HX cond conv ( T' Tcw, in ) ( T' Tcw, out ) ( T Tcw, in ) ( T Tcw, out ) ln ' ' (44) jossa UA on lämmönsiirtokerroin (W/ C), ja T cw,in ja T cw,out ovat jäähdytysnesteen tulo- ja lähtölämpötilat ( C). Kennoston pinnalta tapahtuva lämpöhäviö saadaan yhtälöstä 17
21 T' Tamb Q loss (45) R t Edellä T amb on ulkoilman lämpötila ja R t lämmönsiirtovastus. Lämmönsiirtovastuksen ja lämpökapasiteetin tulo määrittelee systeemin aikavakion, τ τ = R C (46) t t Mallissa käytettyjen vakioiden arvot on esitetty Taulukossa 1 (Khan ja Iqbal 004). Taulukko 1. Lämpötasessa käytettyjen vakioiden arvoja (Khan ja Iqbal 004). Wang et al. (005) ovat esittäneet periaatteessa samanlaisen energiataseen. Dynaaminen yhtälö on annettu muodossa dt M FCCFC Qnet dt =, (47) missä M FC on kennon massa (kg), C FC on ominaislämpökapasiteetti (J/kgK) ja T on lämpötila (K). Kokonaisenergiamäärä on Q = Q Q Q Q (48) net tot elec sens+ latent loss Eri termeille on annettu seuraavat yhtälöt * * ( ) 0.5 Q tot = mh, used Go RTln ph ( p O (49) 18
22 missa G o on Gibbsin vapaa energia normaalitilassa. Kuormituksen ottama teho saadaan yhtälöstä 43. Tuntuvalle ja latentille lämmölle on annettu yhtälö (,, ) (,, ) Q + = m T m T C sens latent H out H in amb H + m T m T C O out O in amb O ( ) + m T T C + m H HOgen, amb HOl, HOgen, V (50) Yhtälössä 50 C i on kyseisen aineen ominaislämpökapasiteetti (J/molK), alaindeksi H O,gen viittaa syntyneseen veteen ja H O,l nestemäiseen veteen. Parametri H V on veden höyrystymislämpö (J/mol). Lämpöhäviöiden on ajateltu syntyvän pääasiassa konvektiosta ilmaan ( ) Q = h T T NA, (51) loss cell amb cell missä lämmönsiirtokerroin h cell (W/m K) on ajateltu määritettävän kokeellisesti. 19
23 4 ALKALIPOLTTOKENNON DYNAAMISET MALLIT Alkalipolttokennojen dynaamisen toiminnan mallintaminen ei ole niin massiivista kuin polymeeripolttokennolla. Ensimmäinen julkaistu dynaaminen malli esiteltiin vasta vuonna 007 (Duerr et al. 007). Kyseinen malli perustuu staattiseen matemaattiseen malliin, joka on esitetty jo vuonna 1999 (Jang-Ho ja Shung-Chul 1999). Alkalipolttokennon toiminta on monimutkainen ja siihen vaikuttaa lukuisia parametreja. Malliin valitut parametrit voidaan luokitella neljään ryhmään: Olosuhdeparametrit, kuten syötekaasujen paineet ja lämpötilat ja elektrolyytin konsentraatio. Sähkökemialliset parametrit, kuten virrantiheydet elektrodeilla, sekä hapetuksen ja pelkistyksen siirtoilmiöiden vakiot. Materiaaliparametrit, kuten elektrodien koostumus, kollektorin koostumus, materiaalin huokoisuus ja elektrodien johtavuus. Rakenteelliset parametrit, kuten diffuusio ja muiden kerrosten paksuudet, yksikkökennojen lukumäärä ja aktivaatio-alojen koot. Huolimatta lukuisista parametreista varsinaiseen dynaamisen malliin on valittu tuloksi virran arvo ja lähdöksi kennon jännite. Tällä dynaamisella mallilla on siis mahdollista tutkia erisuuruisten ulkoisten kuormituksien vaikutusta polttokennon jännitteeseen. Lisäksi mallin avulla voi tarkkailla tasapainoilmiöitä kennon sisällä, kuten hapen ja vedyn konsentraatioita eri virran arvoilla. Alkalipolttokennon rakenne ja toiminta nähdään kuvasta 14. Kuva 14. Alkalipolttokennon rakenne mallinnettaessa sen toimintaa (Duerr et al. 007). 0
24 5 MALLEJA YHDISTETYLLE REFORMOINNILLE JA POLTTOKENNOLLE Reformoinnin ja polttokennoprosessin yhdistämisellä saavutetaan joitakin etuja. Prosessiketjun yksikköprosessien toiminnan voi tuolloin optimoida toimimaan yhdessä tehokkaammin. Lisäksi se mahdollistaa energiaintegroinnin, jolloin hyötysuhde saadaan nostetuksi. Osa polttoaineista on myös logistiikan kannalta helpommassa muodossa ennen reformointia. Kaupallisella HYSYS simulointiohjelmistolla on simuloitu reformoinnin ja PEMpolttokennon systeemiä (Francesconi et al. 007). Reformointi on siinä suoritettu höyryreformoinnilla ja sen lisänä on käytetty vesikaasu-reaktiota hiilimonoksidin minimoimiseen. Simuloinnin päämääränä oli luoda oikeanlainen reformointipolttokennosysteemi, hyödyntäen energia-integrointia. Reformoinnin voi myös jättää kokonaan pois, jolloin etanolia käytetään suoraan polttoaineena. Dynaamista mallia suoraetanoli-polttokennolle ei löytynyt, mutta staattisia matemaattisia malleja on kehitetty. 5.1 Suoraetanoli-alkalipolttokenno Alkalipolttokennosta on tehty myös staattinen malli suoraan etanolia hyödyntämällä. Kehitettyä mallia voidaan etanolin lisäksi testata metanolilla ja natriumboorihydridillä (NaBH 4 ) (Verma ja Basu 007). Malli perustuu reaktiomekanismeihin ja siinä tarkastellaan virran ja jännitteen riippuvuuksia. Mallissa otetaan huomioon myös muissa malleissa tutuiksi tulleet häviöt kuten, aktivaatio-, ohmiseen- ja konsentraatiopolarisaatioon perustuvat jännitehäviöt. Hapetus-pelkistysreaktiot suoraetanolipolttokennossa ovat seuraavanlaisia: C ad 3 + H 5OH CH 3CO + 3H + e (5) OH OH ad + e (53) CH 3COad + OH ad CH 3COOH (54) Artikkelissa testattiin mallin toimintaa eri toimintapisteissä: elektrolyytin konsentraatiolle, polttoaineen konsentraatiolle ja lämpötilalle annettiin erisuuruisia arvoja. Katalyytteinä käytettiin platinaa ja mangnesiumdioksidia. 1
25 5. Suoraetanoli-polymeeripolttokenno Matemaattisia malleja on kehitetty myös suoraetanoli-polymeeripolttokenoille. Mallit eivät ole dynaamisia, mutta niillä on silti hyvä analysoida polttokennon toimintaa. Etanolin reaktiot ovat seuravanlaisia polymeeripolttokennolle (Andreadis ja Panagiotis 006): CH CH OH + 3H O CO + 1H + e (55) + 3O + 1H + 1e 6H O (56) CH 3CH OH + 3 O CO + 3H O (57) Jännitemallissa on otettu huomioon samat häviölähteet kuin kaasumaista polttoainetta hyödyntävissä polttokennomalleissa. Veden ja etanolin diffuusiomalliin membraanin läpi huomioidaan elektro-osmoosi ja konsentraatiodiffuusio. Pakotettu diffuusio jätetään huomioon ottamatta olettamalla paine yhtäsuureksi molemmilla elektrodeilla. Elektroosmoottinen kulkeutuminen (electro-osmotic drag) kuvaa tapahtumaa, jossa vesi- ja etanoli-molekyylejä kulkeutuu liikkuvien protonien mukana kalvon läpi. Virrantiheys vaikuttaa sen suuruuteen. Anodin ja katodin välinen konsentraatioero vaikuttaa puolestaan konsentraatiodiffuusion suuruuteen.
26 6 YHTEENVETO Kirjallisuuskatsaus alkaa polttokennojen esittelyllä. Työssä käydään lyhyesti läpi erityyppiset polttokennot ja polttokennon toiminta. Polttokennot jaoteltiin niissä käytetyn elektrolyytin ja polttoaineen perusteella. Kirjallisuuskatsauksessa esiteltiin polymeeri- ja alkalipolttokennot, niiden toiminta ja niissä tapahtuvat reaktiot. Polttokennojen esittelyn jälkeen käytiin läpi sitä edeltävää vedyn valmistamista bioetanolia reformoimalla. Reformoinnista kuvattiin höyryreformointi ja autoterminen reformointi ja niiden reaktioyhtälöt. Reformoinnin malleista löytyy yhteenveto vasta valmistuneesta diplomityöstä (Ohenoja 008). Mallinnusselvityksessä keskityttiin PEM-polttokennon dynaamiseen toimintaan liittyviin artikkeleihin eikä tarkasteltu niinkään polttokennon rakenteen vaikutuksia, ts. kehitetyt virtausmallit jäivät tarkastelun ulkopuolelle. Tarkempaan käsittelyyn otettiin kaksi suhteellisen uutta dynaamista mallia, joista löytyi myös Matlab/Simulink-mallit. Yleisesti polttokennojen sähkökemiallisen toiminnan kuvaamiseen käytettiin kirjallisuuslähteissä sähkö-, lämpö- ja ainetaseita. Raportin lopussa esiteltiin joitakin kirjallisuusviitteita matemaattisista malleista, joita on tehty yhdistetyille polttokennoille ja reformoinnille. Näiden osalta tutkimusta voitaisiin täydentää. Dynaamisia malleja voitaisiin käyttää säätötarkastelujen lisäksi etsittäessä optimaaliset toimintaolosuhteet erilaisille reformoinnin ja polttokennojen yhdistelmille. Samoin voitaisiin menetellä myös suoraan etanolia hyödyntävien polttokennojen suhteen. 3
27 LÄHDELUETTELO Amphlett J, Baumert R, Mann R, Peppley B, Roberge P. Performance modeling of the Ballard Mark IV solid polymer electrolyte fuel cell, I. Mechanistic model development. Journal of the Electrochemical Society 14(1995)1. Andreadis G, Panagiotis T. Ethanol crossover and direct ethanol PEM fuel cell performance modeling and experimental validation. Chemical Engineering Science 61 (006) Buchholz M, Krebs V. Dynamic modelling of a polymer electrolyte membrane fuel cell stack by nonlinear system identifigation. Fuel Cells 07(007) Duerr M, Gair S, Cruden A, McDonald J. Dynamic elevtrochemical model of an alkaline fuel cell stack. Journal of Power Sources 171 (007) Farrauto, R J. Introduction to solid polymer membrane fuel cells and reforming natural gas for production of hydrogen. Applied Catalysis B: Environmental, 56(005)3-7. Francesconi J A, Mussati M C, Mato R O, Aguirre PA. Analysis of the energy efficiency of an integrated ethanol processor for PEM fuel cell systems. Journal of Power Sources 167(007) Fuel Cell Handbook, 7 th (004). edition, National Energy Technology Laboratory (NETL), Haddad A, Bouyekhf R, Moudni A, Wack M. Non-linear dynamic modeling of proton exhange membrane fuel cell. Journal of Power Sources 163(006) Giilzow E. Alkaline fuel cells: a critical view. Journal of Power Sources 61 ( 1996) Gülzow E, Schulze M, Gerke U. Bipolar concept for alkaline fuel cells. Journal of Power Sources 156(006) 1 7. Jang-Ho J, Shung-Chul Y. A computational simulation of an alkaline fuel cell. Journal of Power Sources 84(1999) Khan M, Iqbal M. Modelling and Analysis of Electrochemical, Thermal, and Reactant Flow Dynamics for a PEM Fuel Cell System. Fuel cells 05(005) Larminie J, Dicks A. Fuel Cell Systems Explained, John Wiley & Sons Ltd, England, 003, 433 p, ISBN X. 4
28 Li C-H, Zhu X-J, Cao G-Y, Sui S, Hu M-R. Identification of the Hammerstein model of a PEMFC stack based on least squares support vector machines. Journal of Power Sources 175(008) Mann R F, Amphlett J C, Hooper M A I, Jensen H M, Peppley BA, Roberge P R. Development and application of a generalised steady-state electrochemical model for a PEM fuel cell. Journal of Power Sources 86(000) Ni M, Leung D, Leung M. A review on reforming bio-ethanol for hydrogen production. International Journal of Hydrogen Energy 3(007) Ohenoja M. Diplomityö. Oulun yliopisto, prosessi- ja ympäristötekniikan osasto Ramakumar R. Fuel Cells An Introduction, Proceedings of IEEE-PES Summer Meeting, Vancouver, B. C., Canada July 15-19,001, p Romm J. The Hype About Hydrogen, Island Press, Washington, DC, 004, 5 p, ISBN X. Verma A, Basu S. Experimental evaluation and mathematical modelling of a direct alkaline fuel cell. Journal of Power Sources 168(007) Wang C, Nehir M H, Shaw S R. Dynamic models and model validation for PEM fuel cells using electrical circuits. Electrical and Computer Engineering Department, Montana State University. IEEE Transactions on Energy Conversion 0(005)
vetyteknologia Polttokennon tyhjäkäyntijännite 1 DEE-54020 Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
DEE-5400 olttokennot ja vetyteknologia olttokennon tyhjäkäyntijännite 1 DEE-5400 Risto Mikkonen 1.1.014 g:n määrittäminen olttokennon toiminta perustuu Gibbsin vapaan energian muutokseen. ( G = TS) Ideaalitapauksessa
Polymeerielektrolyyttimembraanipolttokennojen
 SÄÄTÖTEKNIIKAN LABORATORIO Polymeerielektrolyyttimembraanipolttokennojen dynaaminen malli Markku Ohenoja ja Kauko Leiviskä Raportti B No 68, Elokuu 2008 Oulun yliopisto Säätötekniikan laboratorio Raportti
SÄÄTÖTEKNIIKAN LABORATORIO Polymeerielektrolyyttimembraanipolttokennojen dynaaminen malli Markku Ohenoja ja Kauko Leiviskä Raportti B No 68, Elokuu 2008 Oulun yliopisto Säätötekniikan laboratorio Raportti
Polttokennolaboratoriotyö
 Polttokennolaboratoriotyö Polttokennot ovat sähkökemiallisia laitteita, jotka muuntavat polttoaineen kemiallisen energian suoraan sähköksi ja lämmöksi [1]. Ne eivät nimensä mukaisesti kuitenkaan polta
Polttokennolaboratoriotyö Polttokennot ovat sähkökemiallisia laitteita, jotka muuntavat polttoaineen kemiallisen energian suoraan sähköksi ja lämmöksi [1]. Ne eivät nimensä mukaisesti kuitenkaan polta
vetyteknologia Muut kennotyypit 1 Polttokennot ja vetyteknologia Risto Mikkonen
 DEE-5400 Polttokennot ja vetyteknologia Muut kennotyypit 1 Polttokennot ja vetyteknologia Risto Mikkonen Alkaalipolttokennot Anodi: Katodi: H 4OH 4 H O 4e O e H O 4OH 4 Avaruussovellutukset, ajoneuvokäytöt
DEE-5400 Polttokennot ja vetyteknologia Muut kennotyypit 1 Polttokennot ja vetyteknologia Risto Mikkonen Alkaalipolttokennot Anodi: Katodi: H 4OH 4 H O 4e O e H O 4OH 4 Avaruussovellutukset, ajoneuvokäytöt
Sähkökemian perusteita, osa 1
 Sähkökemian perusteita, osa 1 Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 4 - Luento 1 Teema 4: Suoritustapana oppimispäiväkirja Tehdään yksin tai pareittain Tehtävät/ohjeet löytyvät kurssin
Sähkökemian perusteita, osa 1 Ilmiömallinnus prosessimetallurgiassa Syksy 2015 Teema 4 - Luento 1 Teema 4: Suoritustapana oppimispäiväkirja Tehdään yksin tai pareittain Tehtävät/ohjeet löytyvät kurssin
HANNA NURMILO VETYPOLTTOKENNON HYÖDYNTÄMINEN LINJA-AUTOSSA
 HANNA NURMILO VETYPOLTTOKENNON HYÖDYNTÄMINEN LINJA-AUTOSSA Diplomityö Tarkastaja: Lehtori Risto Mikkonen Tarkastaja ja aihe hyväksytty Tieto- ja sähkötekniikan tiedekuntaneuvoston kokouksessa 6. huhtikuuta
HANNA NURMILO VETYPOLTTOKENNON HYÖDYNTÄMINEN LINJA-AUTOSSA Diplomityö Tarkastaja: Lehtori Risto Mikkonen Tarkastaja ja aihe hyväksytty Tieto- ja sähkötekniikan tiedekuntaneuvoston kokouksessa 6. huhtikuuta
Tutkimuksellinen lähestymistapa polttokennojen kemian opetukseen
 Tutkimuksellinen lähestymistapa polttokennojen kemian opetukseen Matleena Ojapalo Pro gradu -tutkielma Ohjaaja: Maija Aksela Kemian opettajankoulutusyksikkö Kemian laitos Helsingin yliopisto 29.10.2010
Tutkimuksellinen lähestymistapa polttokennojen kemian opetukseen Matleena Ojapalo Pro gradu -tutkielma Ohjaaja: Maija Aksela Kemian opettajankoulutusyksikkö Kemian laitos Helsingin yliopisto 29.10.2010
= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]
![= P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ] = P 0 (V 2 V 1 ) + nrt 0. nrt 0 ln V ]](/thumbs/62/46694692.jpg) 766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
766328A Termofysiikka Harjoitus no. 7, ratkaisut (syyslukukausi 2014) 1. Sylinteri on ympäristössä, jonka paine on P 0 ja lämpötila T 0. Sylinterin sisällä on n moolia ideaalikaasua ja sen tilavuutta kasvatetaan
vetyteknologia Polttokennon termodynamiikkaa 1 DEE Risto Mikkonen
 DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
DEE-5400 olttokennot ja vetyteknologia olttokennon termodynamiikkaa 1 DEE-5400 Risto Mikkonen ermodynamiikan ensimmäinen pääsääntö aseraja Ympäristö asetila Q W Suljettuun systeemiin tuotu lämpö + systeemiin
Käsitteitä. Hapetusluku = kuvitteellinen varaus, jonka atomi saa elektronin siirtyessä
 Sähkökemia Nopea kertaus! Mitä seuraavat käsitteet tarkoittivatkaan? a) Hapettuminen b) Pelkistyminen c) Hapetusluku d) Elektrolyytti e) Epäjalometalli f) Jalometalli Käsitteitä Hapettuminen = elektronin
Sähkökemia Nopea kertaus! Mitä seuraavat käsitteet tarkoittivatkaan? a) Hapettuminen b) Pelkistyminen c) Hapetusluku d) Elektrolyytti e) Epäjalometalli f) Jalometalli Käsitteitä Hapettuminen = elektronin
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I
 Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
Kemialliset reaktiot ja reaktorit Prosessi- ja ympäristötekniikan perusta I Juha Ahola juha.ahola@oulu.fi Kemiallinen prosessitekniikka Sellaisten kokonaisprosessien suunnittelu, joissa kemiallinen reaktio
CHEM-A1110 Virtaukset ja reaktorit. Laskuharjoitus 9/2016. Energiataseet
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 9/2016 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa D406 Energiataseet Tehtävä 1. Adiabaattisen virtausreaktorin
Polttokennoteknologian tarjoamat mahdollisuudet suomalaiselle kulkuneuvo-, kone- ja elektroniikkateollisuudelle 02-11/2001
 Polttokennoteknologian tarjoamat mahdollisuudet suomalaiselle kulkuneuvo-, kone- ja elektroniikkateollisuudelle 02-11/2001 Hankkeen pääsisältö Teknologian kehitystilannekartoitus Yrityskysely kotimaisesta
Polttokennoteknologian tarjoamat mahdollisuudet suomalaiselle kulkuneuvo-, kone- ja elektroniikkateollisuudelle 02-11/2001 Hankkeen pääsisältö Teknologian kehitystilannekartoitus Yrityskysely kotimaisesta
KYMENLAAKSON AMMATTIKORKEAKOULU Merenkulun ko / Merenkulkualan insinöörin sv
 KYMENLAAKSON AMMATTIKORKEAKOULU Merenkulun ko / Merenkulkualan insinöörin sv Mikko Oksanen MAAKAASUA JA METANOLIA KÄYTTÄVIEN KIINTEÄOKSIDIPOLTTO- KENNOJEN (SOFC) KÄYTTÖ LAIVOISSA Opinnäytetyö 2011 TIIVISTELMÄ
KYMENLAAKSON AMMATTIKORKEAKOULU Merenkulun ko / Merenkulkualan insinöörin sv Mikko Oksanen MAAKAASUA JA METANOLIA KÄYTTÄVIEN KIINTEÄOKSIDIPOLTTO- KENNOJEN (SOFC) KÄYTTÖ LAIVOISSA Opinnäytetyö 2011 TIIVISTELMÄ
AS.84-3134 Energiatekniikan automaatio. Polttokennot. Matias Halinen. DI, Tutkija VTT, Polttokennot
 AS.84-3134 Energiatekniikan automaatio Polttokennot Matias Halinen DI, Tutkija VTT, Polttokennot AS-84.3134 Energiatekniikan automaatio, Syksy 2007 Sisältö Luento 1 Polttokennot yleisesti Polttokennojen
AS.84-3134 Energiatekniikan automaatio Polttokennot Matias Halinen DI, Tutkija VTT, Polttokennot AS-84.3134 Energiatekniikan automaatio, Syksy 2007 Sisältö Luento 1 Polttokennot yleisesti Polttokennojen
DEE Polttokennot ja vetyteknologia
 DEE-54020 Polttokennot ja vetyteknologa Polttokennon hävöt 1 Polttokennot ja vetyteknologa Rsto Mkkonen Polttokennon tyhjäkäyntjännte Teoreettnen tyhjäkäyntjännte E z g F Todellnen kennojännte rppuu er
DEE-54020 Polttokennot ja vetyteknologa Polttokennon hävöt 1 Polttokennot ja vetyteknologa Rsto Mkkonen Polttokennon tyhjäkäyntjännte Teoreettnen tyhjäkäyntjännte E z g F Todellnen kennojännte rppuu er
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA!
 ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
ENY-C2001 Termodynamiikka ja lämmönsiirto TERVETULOA! Luento 14.9.2015 / T. Paloposki / v. 03 Tämän päivän ohjelma: Aineen tilan kuvaaminen pt-piirroksella ja muilla piirroksilla, faasimuutokset Käsitteitä
Teddy 7. harjoituksen malliratkaisu syksy 2011
 Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Teddy 7. harjoituksen malliratkaisu syksy 2011 1. Systeemin käyttäytymistä faasirajalla kuvaa Clapeyronin yhtälönä tunnettu keskeinen relaatio dt = S m. (1 V m Koska faasitasapainossa reaktion Gibbsin
Matemaattisesta mallintamisesta
 Matemaattisesta mallintamisesta (Fysikaalinen mallintaminen) 1. Matemaattisen mallin konstruointi dynaamiselle reaalimaailman järjestelmälle pääpaino fysikaalisella mallintamisella samat periaatteet pätevät
Matemaattisesta mallintamisesta (Fysikaalinen mallintaminen) 1. Matemaattisen mallin konstruointi dynaamiselle reaalimaailman järjestelmälle pääpaino fysikaalisella mallintamisella samat periaatteet pätevät
Käytännön esimerkkejä on lukuisia.
 PROSESSI- JA Y MPÄRISTÖTEKNIIK KA Ilmiömallinnus prosessimet allurgiassa, 01 6 Teema 4 Tehtävien ratkaisut 15.9.016 SÄHKÖKEMIALLISTEN REAKTIOIDEN TERMODYNAMIIKKA JA KINETIIKKA Yleistä Tämä dokumentti sisältää
PROSESSI- JA Y MPÄRISTÖTEKNIIK KA Ilmiömallinnus prosessimet allurgiassa, 01 6 Teema 4 Tehtävien ratkaisut 15.9.016 SÄHKÖKEMIALLISTEN REAKTIOIDEN TERMODYNAMIIKKA JA KINETIIKKA Yleistä Tämä dokumentti sisältää
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus
 Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
Mamk / Tekniikka ja liikenne / Sähkövoimatekniikka / Sarvelainen 2015 T8415SJ ENERGIATEKNIIKKA Laskuharjoitus KEMIALLISIIN REAKTIOIHIN PERUSTUVA POLTTOAINEEN PALAMINEN Voimalaitoksessa käytetään polttoaineena
FYSA220/K2 (FYS222/K2) Vaimeneva värähtely
 FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
FYSA/K (FYS/K) Vaimeneva värähtely Työssä tutkitaan vaimenevaa sähköistä värähysliikettä. Erityisesti pyritään havainnollistamaan kelan inuktanssin, konensaattorin kapasitanssin ja ohmisen vastuksen suuruuksien
HENRI KARIMÄKI AJONEUVOKÄYTÖN POLTTOKENNOTEHOLÄHTEEN HYBRIDISOINTI TEOREETTINEN JA KOKEELLINEN TARKASTELU. Diplomityö
 HENRI KARIMÄKI AJONEUVOKÄYTÖN POLTTOKENNOTEHOLÄHTEEN HYBRIDISOINTI TEOREETTINEN JA KOKEELLINEN TARKASTELU Diplomityö Tarkastaja: lehtori Risto Mikkonen Tarkastaja ja aihe hyväksytty Tieto- ja sähkötekniikan
HENRI KARIMÄKI AJONEUVOKÄYTÖN POLTTOKENNOTEHOLÄHTEEN HYBRIDISOINTI TEOREETTINEN JA KOKEELLINEN TARKASTELU Diplomityö Tarkastaja: lehtori Risto Mikkonen Tarkastaja ja aihe hyväksytty Tieto- ja sähkötekniikan
SISÄLLYSLUETTELO SYMBOLILUETTELO 4
 1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
1 SISÄLLYSLUETTELO SYMBOLILUETTELO 4 1 KEMIALLISESTI REAGOIVA TERMODYNAAMINEN SYSTEEMI 6 11 Yleistä 6 12 Standarditila ja referenssitila 7 13 Entalpia- ja entropia-asteikko 11 2 ENTALPIA JA OMINAISLÄMPÖ
Normaalipotentiaalit
 Normaalipotentiaalit MATERIAALIT JA TEKNOLOGIA, KE4 Yksittäisen elektrodin aiheuttaman jännitteen mittaaminen ei onnistu. Jännitemittareilla voidaan havaita ja mitata vain kahden elektrodin välinen potentiaaliero
Normaalipotentiaalit MATERIAALIT JA TEKNOLOGIA, KE4 Yksittäisen elektrodin aiheuttaman jännitteen mittaaminen ei onnistu. Jännitemittareilla voidaan havaita ja mitata vain kahden elektrodin välinen potentiaaliero
Sähkökemia. Sähkökemiallinen jännitesarja, galvaaninen kenno, normaalipotentiaali
 Sähkökemia Sähkökemiallinen jännitesarja, galvaaninen kenno, normaalipotentiaali Esimerkki 1 Pohdi kertauksen vuoksi seuraavia käsitteitä a) Hapettuminen b) Pelkistin c) Hapetusluku d) Elektrolyytti e)
Sähkökemia Sähkökemiallinen jännitesarja, galvaaninen kenno, normaalipotentiaali Esimerkki 1 Pohdi kertauksen vuoksi seuraavia käsitteitä a) Hapettuminen b) Pelkistin c) Hapetusluku d) Elektrolyytti e)
Elektrolyysi Anodilla tapahtuu aina hapettuminen ja katodilla pelkistyminen!
 Elektrolyysi MATERIAALIT JA TEKNOLOGIA, KE4 Monet kemialliset reaktiot ovat palautuvia eli reversiibeleitä. Jo sähkökemian syntyvaiheessa oivallettiin, että on mahdollista rakentaa kahdenlaisia sähkökemiallisia
Elektrolyysi MATERIAALIT JA TEKNOLOGIA, KE4 Monet kemialliset reaktiot ovat palautuvia eli reversiibeleitä. Jo sähkökemian syntyvaiheessa oivallettiin, että on mahdollista rakentaa kahdenlaisia sähkökemiallisia
Diplomityö, joka on jätetty tarkastettavaksi diplomi-insinöörin tutkintoa varten
 VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Jussi Sievänen KYTKENTÄSUOJAPIIRIEN VERTAILU ERÄÄN POLTTOKENNOJÄRJESTELMÄN KOKOAALTOSILTAMUUNTIMEN TASASUUNTAAJASSA Diplomityö, joka on jätetty tarkastettavaksi
VAASAN YLIOPISTO TEKNILLINEN TIEDEKUNTA SÄHKÖTEKNIIKKA Jussi Sievänen KYTKENTÄSUOJAPIIRIEN VERTAILU ERÄÄN POLTTOKENNOJÄRJESTELMÄN KOKOAALTOSILTAMUUNTIMEN TASASUUNTAAJASSA Diplomityö, joka on jätetty tarkastettavaksi
Tehtävä 1. Tasapainokonversion laskenta Χ r G-arvojen avulla Alkyloitaessa bentseeniä propeenilla syntyy kumeenia (isopropyylibentseeniä):
 CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
CHEM-A1110 Virtaukset ja reaktorit Laskuharjoitus 10/017 Lisätietoja s-postilla reetta.karinen@aalto.fi tai tiia.viinikainen@aalto.fi vastaanotto huoneessa E409 Kemiallinen tasapaino Tehtävä 1. Tasapainokonversion
Reaktiosarjat
 Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Reaktiosarjat Usein haluttua tuotetta ei saada syntymään yhden kemiallisen reaktion lopputuotteena, vaan monen peräkkäisten reaktioiden kautta Tällöin edellisen reaktion lopputuote on seuraavan lähtöaine
Energian talteenotto liikkuvassa raskaassa työkoneessa. 20.01.2010 Heinikainen Olli
 Energian talteenotto liikkuvassa raskaassa työkoneessa 20.01.2010 Heinikainen Olli Esityksen sisältö Yleistä Olemassa olevat sovellukset Kineettisen energian palauttaminen Potentiaalienergian palauttaminen
Energian talteenotto liikkuvassa raskaassa työkoneessa 20.01.2010 Heinikainen Olli Esityksen sisältö Yleistä Olemassa olevat sovellukset Kineettisen energian palauttaminen Potentiaalienergian palauttaminen
Termodynamiikka. Fysiikka III 2007. Ilkka Tittonen & Jukka Tulkki
 Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
Termodynamiikka Fysiikka III 2007 Ilkka Tittonen & Jukka Tulkki Tilanyhtälö paine vakio tilavuus vakio Ideaalikaasun N p= kt pinta V Yleinen aineen p= f V T pinta (, ) Isotermit ja isobaarit Vakiolämpötilakäyrät
2. Prosessikaavioiden yksityiskohtainen tarkastelu
 2. Prosessikaavioiden yksityiskohtainen tarkastelu 2.1 Reaktorit Teolliset reaktorit voidaan toimintansa perusteella jakaa seuraavasti: panosreaktorit (batch) panosreaktorit (batch) 1 virtausreaktorit
2. Prosessikaavioiden yksityiskohtainen tarkastelu 2.1 Reaktorit Teolliset reaktorit voidaan toimintansa perusteella jakaa seuraavasti: panosreaktorit (batch) panosreaktorit (batch) 1 virtausreaktorit
Bensiiniä voidaan pitää hiilivetynä C8H18, jonka tiheys (NTP) on 0,703 g/ml ja palamislämpö H = kj/mol
 Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
Kertaustehtäviä KE3-kurssista Tehtävä 1 Maakaasu on melkein puhdasta metaania. Kuinka suuri tilavuus metaania paloi, kun täydelliseen palamiseen kuluu 3 m 3 ilmaa, jonka lämpötila on 50 C ja paine on 11kPa?
BIOMETANOLIN TUOTANTO
 LAPPEENRANNAN TEKNILLINEN YLIOPISTO Kemiantekniikan osasto Teknillisen kemian laboratorio Ke3330000 Kemianteollisuuden prosessit BIOMETANOLIN TUOTANTO Tekijä: Hiltunen Salla 0279885, Ke2 20.2.2006 SISÄLLYS
LAPPEENRANNAN TEKNILLINEN YLIOPISTO Kemiantekniikan osasto Teknillisen kemian laboratorio Ke3330000 Kemianteollisuuden prosessit BIOMETANOLIN TUOTANTO Tekijä: Hiltunen Salla 0279885, Ke2 20.2.2006 SISÄLLYS
Puun termiset aineominaisuudet pyrolyysissa
 1 Puun termiset aineominaisuudet pyrolyysissa V Liekkipäivä Otaniemi, Espoo 14.1.2010 Ville Hankalin TTY / EPR 14.1.2010 2 Esityksen sisältö TTY:n projekti Biomassan pyrolyysin reaktiokinetiikan tutkimus
1 Puun termiset aineominaisuudet pyrolyysissa V Liekkipäivä Otaniemi, Espoo 14.1.2010 Ville Hankalin TTY / EPR 14.1.2010 2 Esityksen sisältö TTY:n projekti Biomassan pyrolyysin reaktiokinetiikan tutkimus
Hapetus-pelkistymisreaktioiden tasapainottaminen
 Hapetus-pelkistymisreaktioiden tasapainottaminen hapetuslukumenetelmällä MATERIAALIT JA TEKNO- LOGIA, KE4 Palataan hetkeksi 2.- ja 3.-kurssin asioihin ja tarkastellaan hapetus-pelkistymisreaktioiden tasapainottamista.
Hapetus-pelkistymisreaktioiden tasapainottaminen hapetuslukumenetelmällä MATERIAALIT JA TEKNO- LOGIA, KE4 Palataan hetkeksi 2.- ja 3.-kurssin asioihin ja tarkastellaan hapetus-pelkistymisreaktioiden tasapainottamista.
4. Kontrollitilavuusajattelu ja massan säilyminen. KJR-C2003 Virtausmekaniikan perusteet
 4. Kontrollitilavuusajattelu ja massan säilyminen KJR-C2003 Virtausmekaniikan perusteet Päivän anti Miten partikkelisysteemiin liittyvän suuren säilyminen esitetään tarkastelualueen taseena ja miten massan
4. Kontrollitilavuusajattelu ja massan säilyminen KJR-C2003 Virtausmekaniikan perusteet Päivän anti Miten partikkelisysteemiin liittyvän suuren säilyminen esitetään tarkastelualueen taseena ja miten massan
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe
 Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
Kemian koe kurssi KE5 Reaktiot ja tasapaino koe 1.4.017 Tee kuusi tehtävää. 1. Tämä tehtävä koostuu kuudesta monivalintaosiosta, joista jokaiseen on yksi oikea vastausvaihtoehto. Kirjaa vastaukseksi numero-kirjainyhdistelmä
= 1 kg J kg 1 1 kg 8, J mol 1 K 1 373,15 K kg mol 1 1 kg Pa
 766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
766328A Termofysiikka Harjoitus no. 8, ratkaisut syyslukukausi 2014 1. 1 kg nestemäistä vettä muuttuu höyryksi lämpötilassa T 100 373,15 K ja paineessa P 1 atm 101325 Pa. Veden tiheys ρ 958 kg/m 3 ja moolimassa
HALLIN ILMIÖ 1. TUTKITTAVAN ILMIÖN TEORIAA
 1 ALLIN ILMIÖ MOTIVOINTI allin ilmiötyössä tarkastellaan johteen varauksenkuljettajiin liittyviä suureita Työssä nähdään kuinka all-kiteeseen generoituu all-jännite allin ilmiön tutkimiseen soveltuvalla
1 ALLIN ILMIÖ MOTIVOINTI allin ilmiötyössä tarkastellaan johteen varauksenkuljettajiin liittyviä suureita Työssä nähdään kuinka all-kiteeseen generoituu all-jännite allin ilmiön tutkimiseen soveltuvalla
Lääketiede Valintakoeanalyysi 2015 Fysiikka. FM Pirjo Haikonen
 Lääketiede Valintakoeanalyysi 5 Fysiikka FM Pirjo Haikonen Fysiikan tehtävät Väittämä osa C (p) 6 kpl monivalintoja, joissa yksi (tai useampi oikea kohta.) Täysin oikein vastattu p, yksikin virhe/tyhjä
Lääketiede Valintakoeanalyysi 5 Fysiikka FM Pirjo Haikonen Fysiikan tehtävät Väittämä osa C (p) 6 kpl monivalintoja, joissa yksi (tai useampi oikea kohta.) Täysin oikein vastattu p, yksikin virhe/tyhjä
Puupohjainen Bio-SNG kaasutusteknologian kehitysnäkymiä. Gasumin kaasurahaston seminaari / Bankin auditorio / ti 10.12.2013 tutkija Ilkka Hannula VTT
 Puupohjainen Bio-SNG kaasutusteknologian kehitysnäkymiä Gasumin kaasurahaston seminaari / Bankin auditorio / ti 10.12.2013 tutkija Ilkka Hannula VTT 2 Lämpötila 700-900 C Paine 1-20 bar CO, H 2, CH 4,
Puupohjainen Bio-SNG kaasutusteknologian kehitysnäkymiä Gasumin kaasurahaston seminaari / Bankin auditorio / ti 10.12.2013 tutkija Ilkka Hannula VTT 2 Lämpötila 700-900 C Paine 1-20 bar CO, H 2, CH 4,
Vesi. Pintajännityksen Veden suuremman tiheyden nesteenä kuin kiinteänä aineena Korkean kiehumispisteen
 Vesi Hyvin poolisten vesimolekyylien välille muodostuu vetysidoksia, jotka ovat vahvimpia molekyylien välille syntyviä sidoksia. Vetysidos on sähköistä vetovoimaa, ei kovalenttinen sidos. Vesi Vetysidos
Vesi Hyvin poolisten vesimolekyylien välille muodostuu vetysidoksia, jotka ovat vahvimpia molekyylien välille syntyviä sidoksia. Vetysidos on sähköistä vetovoimaa, ei kovalenttinen sidos. Vesi Vetysidos
Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen
 KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
KEMA221 2009 PUHTAAN AINEEN FAASIMUUTOKSET ATKINS LUKU 4 1 PUHTAAN AINEEN FAASIMUUTOKSET Esimerkkejä faasimuutoksista? Tässä luvussa keskitytään faasimuutosten termodynaamiseen kuvaukseen Faasi = aineen
Polttokennojärjestelmät
 AS.84-3134 Energiatekniikan automaatio Polttokennojärjestelmät Matias Halinen DI, Tutkija VTT, Polttokennot Sisältö SOFC -järjestelmät Rakenne Vaatimuksia automaatiojärjestelmälle Kiinteäoksidipolttokenno,
AS.84-3134 Energiatekniikan automaatio Polttokennojärjestelmät Matias Halinen DI, Tutkija VTT, Polttokennot Sisältö SOFC -järjestelmät Rakenne Vaatimuksia automaatiojärjestelmälle Kiinteäoksidipolttokenno,
Johdantoa. Kemia on elektronien liikkumista/siirtymistä. Miksi?
 Mitä on kemia? Johdantoa REAKTIOT JA ENERGIA, KE3 Kemia on elektronien liikkumista/siirtymistä. Miksi? Kaikissa kemiallisissa reaktioissa tapahtuu energian muutoksia, jotka liittyvät vanhojen sidosten
Mitä on kemia? Johdantoa REAKTIOT JA ENERGIA, KE3 Kemia on elektronien liikkumista/siirtymistä. Miksi? Kaikissa kemiallisissa reaktioissa tapahtuu energian muutoksia, jotka liittyvät vanhojen sidosten
REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos
 ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
ympäristö ympäristö 15.12.2016 REAKTIOT JA ENERGIA, KE3 Ekso- ja endotermiset reaktiot sekä entalpian muutos Kaikilla aineilla (atomeilla, molekyyleillä) on asema- eli potentiaalienergiaa ja liike- eli
Konventionaalisessa lämpövoimaprosessissa muunnetaan polttoaineeseen sitoutunut kemiallinen energia lämpö/sähköenergiaksi höyryprosessin avulla
 Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Termodynamiikkaa Energiatekniikan automaatio TKK 2007 Yrjö Majanne, TTY/ACI Martti Välisuo, Fortum Nuclear Services Automaatio- ja säätötekniikan laitos Termodynamiikan perusteita Konventionaalisessa lämpövoimaprosessissa
Pellettien ja puunkuivauksessa syntyneiden kondenssivesien biohajoavuustutkimus
 Pellettien ja puunkuivauksessa syntyneiden kondenssivesien biohajoavuustutkimus FM Hanna Prokkola Oulun yliopisto, Kemian laitos EkoPelletti-seminaari 11.4 2013 Biohajoavuus Biohajoavuudella yleensä tarkoitetaan
Pellettien ja puunkuivauksessa syntyneiden kondenssivesien biohajoavuustutkimus FM Hanna Prokkola Oulun yliopisto, Kemian laitos EkoPelletti-seminaari 11.4 2013 Biohajoavuus Biohajoavuudella yleensä tarkoitetaan
Aktiiviset piirikomponentit. DEE Piirianalyysi Risto Mikkonen
 DEE-11000 Piirianalyysi Aktiiviset piirikomponentit 1 Aktiiviset piirikomponentit Sähköenergian lähteitä Jännitelähteet; jännite ei merkittävästi riipu lähteen antamasta virrasta (akut, paristot, valokennot)
DEE-11000 Piirianalyysi Aktiiviset piirikomponentit 1 Aktiiviset piirikomponentit Sähköenergian lähteitä Jännitelähteet; jännite ei merkittävästi riipu lähteen antamasta virrasta (akut, paristot, valokennot)
Kondensaattorin läpi kulkeva virta saadaan derivoimalla yhtälöä (2), jolloin saadaan
 VAIHTOVIRTAPIIRI 1 Johdanto Vaihtovirtapiirien käsittely perustuu kolmen peruskomponentin, vastuksen (resistanssi R), kelan (induktanssi L) ja kondensaattorin (kapasitanssi C) toimintaan. Tarkastellaan
VAIHTOVIRTAPIIRI 1 Johdanto Vaihtovirtapiirien käsittely perustuu kolmen peruskomponentin, vastuksen (resistanssi R), kelan (induktanssi L) ja kondensaattorin (kapasitanssi C) toimintaan. Tarkastellaan
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Kuparin korroosio hapettomissa olosuhteissa
 Kuparin korroosio hapettomissa olosuhteissa Olof Forsén, Antero Pehkonen, Jari Aromaa Aalto-yliopisto Timo Saario VTT 1 Kuparin korroosio hapettomissa olosuhteissa Taustaa Aikaisemmat tutkimukset Tutkimuksen
Kuparin korroosio hapettomissa olosuhteissa Olof Forsén, Antero Pehkonen, Jari Aromaa Aalto-yliopisto Timo Saario VTT 1 Kuparin korroosio hapettomissa olosuhteissa Taustaa Aikaisemmat tutkimukset Tutkimuksen
Elektroniikan perusteet, Radioamatööritutkintokoulutus
 Elektroniikan perusteet, Radioamatööritutkintokoulutus Antti Karjalainen, PRK 30.10.2014 Komponenttien esittelytaktiikka Toiminta, (Teoria), Käyttö jännite, virta, teho, taajuus, impedanssi ja näiden yksiköt:
Elektroniikan perusteet, Radioamatööritutkintokoulutus Antti Karjalainen, PRK 30.10.2014 Komponenttien esittelytaktiikka Toiminta, (Teoria), Käyttö jännite, virta, teho, taajuus, impedanssi ja näiden yksiköt:
MT Sähkökemialliset tutkimusmenetelmät
 .9. MT-. Sähkökemialliset tutkimusmenetelmät POTENTIO- JA GALVANOSTAATTISET MITTAUKSET Potentiostaattisissa menetelmissä näytettä pidetään vakiopotentiaalissa ja samalla mitataan kennosysteemin läpi kulkevaa
.9. MT-. Sähkökemialliset tutkimusmenetelmät POTENTIO- JA GALVANOSTAATTISET MITTAUKSET Potentiostaattisissa menetelmissä näytettä pidetään vakiopotentiaalissa ja samalla mitataan kennosysteemin läpi kulkevaa
Alkuaineita luokitellaan atomimassojen perusteella
 IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
IHMISEN JA ELINYMPÄRISTÖN KEMIAA, KE2 Alkuaineen suhteellinen atomimassa Kertausta: Isotoopin määritelmä: Saman alkuaineen eri atomien ytimissä on sama määrä protoneja (eli sama alkuaine), mutta neutronien
Tehtävä 1. Valitse seuraavista vaihtoehdoista oikea ja merkitse kirjain alla olevaan taulukkoon
 Tehtävä 1. Valitse seuraavista vaihtoehdoista oikea ja merkitse kirjain alla olevaan taulukkoon A. Mikä seuraavista hapoista on heikko happo? a) etikkahappo b) typpihappo c) vetykloridihappo d) rikkihappo
Tehtävä 1. Valitse seuraavista vaihtoehdoista oikea ja merkitse kirjain alla olevaan taulukkoon A. Mikä seuraavista hapoista on heikko happo? a) etikkahappo b) typpihappo c) vetykloridihappo d) rikkihappo
Energian tuotanto haasteita ja mahdollisuuksia Pohjois- Suomessa. Pekka Tynjälä Ulla Lassi
 Energian tuotanto haasteita ja mahdollisuuksia Pohjois- Suomessa Pekka Tynjälä Ulla Lassi Pohjois-Suomen suuralueseminaari 9.6.2009 Johdanto Mahdollisuuksia *Uusiutuvan energian tuotanto (erityisesti metsäbiomassan
Energian tuotanto haasteita ja mahdollisuuksia Pohjois- Suomessa Pekka Tynjälä Ulla Lassi Pohjois-Suomen suuralueseminaari 9.6.2009 Johdanto Mahdollisuuksia *Uusiutuvan energian tuotanto (erityisesti metsäbiomassan
T F = T C ( 24,6) F = 12,28 F 12,3 F T K = (273,15 24,6) K = 248,55 K T F = 87,8 F T K = 4,15 K T F = 452,2 F. P = α T α = P T = P 3 T 3
 76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
76628A Termofysiikka Harjoitus no. 1, ratkaisut (syyslukukausi 2014) 1. Muunnokset Fahrenheit- (T F ), Celsius- (T C ) ja Kelvin-asteikkojen (T K ) välillä: T F = 2 + 9 5 T C T C = 5 9 (T F 2) T K = 27,15
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016
 PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
PHYS-C0220 Termodynamiikka ja statistinen fysiikka Kevät 2016 Emppu Salonen Lasse Laurson Toni Mäkelä Arttu Lehtinen Luento 6: Vapaaenergia Pe 11.3.2016 1 AIHEET 1. Kemiallinen potentiaali 2. Maxwellin
Evansin diagrammit. Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 4
 Evansin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 4 Tavoite Oppia hyödyntämään Evansin diagrammeja esimerkiksi hydrometallurgisissa tai korroosiotarkasteluissa 1 Termodynamiikka
Evansin diagrammit Ilmiömallinnus prosessimetallurgiassa Syksy 2016 Teema 4 - Luento 4 Tavoite Oppia hyödyntämään Evansin diagrammeja esimerkiksi hydrometallurgisissa tai korroosiotarkasteluissa 1 Termodynamiikka
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko klo 8-10
 Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Kertausluennot: Mahdollisuus pisteiden korotukseen ja rästisuorituksiin Keskiviikko 25.10 klo 8-10 Jokaisesta oikein ratkaistusta tehtävästä voi saada yhden lisäpisteen. Tehtävä, joilla voi korottaa kotitehtävän
Oikeat vastaukset: Tehtävän tarkkuus on kolme numeroa. Sulamiseen tarvittavat lämmöt sekä teräksen suurin mahdollinen luovutettu lämpö:
 A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
A1 Seppä karkaisee teräsesineen upottamalla sen lämpöeristettyyn astiaan, jossa on 118 g jäätä ja 352 g vettä termisessä tasapainossa Teräsesineen massa on 312 g ja sen lämpötila ennen upotusta on 808
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA
 PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-C0220 TERMODYNAMIIKKA JA STATISTINEN FYSIIKKA Kevät 2016 Emppu Salonen Lasse Laurson Arttu Lehtinen Toni Mäkelä Luento 8: Kemiallinen potentiaali, suurkanoninen ensemble Pe 18.3.2016 1 AIHEET 1. Kanoninen
PHYS-A0120 Termodynamiikka syksy 2017
 PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
PHYS-A0120 Termodynamiikka syksy 2017 Emppu Salonen Prof. Peter Liljeroth Viikko 5: Termodynaamiset potentiaalit Maanantai 27.11. ja tiistai 28.11. Kotitentti Julkaistaan ti 5.12., palautus viim. ke 20.12.
KEMA221 2009 KEMIALLINEN TASAPAINO ATKINS LUKU 7
 KEMIALLINEN TASAPAINO Määritelmiä Kemiallinen reaktio A B pyrkii kohti tasapainoa. Yleisessä tapauksessa saavutetaan tasapainoa vastaava reaktioseos, jossa on läsnä sekä lähtöaineita että tuotteita: A
KEMIALLINEN TASAPAINO Määritelmiä Kemiallinen reaktio A B pyrkii kohti tasapainoa. Yleisessä tapauksessa saavutetaan tasapainoa vastaava reaktioseos, jossa on läsnä sekä lähtöaineita että tuotteita: A
Jännite, virran voimakkuus ja teho
 Jukka Kinkamo, OH2JIN oh2jin@oh3ac.fi +358 44 965 2689 Jännite, virran voimakkuus ja teho Jännite eli potentiaaliero mitataan impedanssin yli esiintyvän jännitehäviön avulla. Koska käytännön radioamatöörin
Jukka Kinkamo, OH2JIN oh2jin@oh3ac.fi +358 44 965 2689 Jännite, virran voimakkuus ja teho Jännite eli potentiaaliero mitataan impedanssin yli esiintyvän jännitehäviön avulla. Koska käytännön radioamatöörin
Luento 2. DEE Piirianalyysi Risto Mikkonen
 DEE-11000 Piirianalyysi Luento 2 1 Luento 1 - Recap Opintojakson rakenne ja tavoitteet Sähkötekniikan historiaa Sähköiset perussuureet Passiiviset piirikomponentit 2 Luento 2 - sisältö Passiiviset piirikomponentit
DEE-11000 Piirianalyysi Luento 2 1 Luento 1 - Recap Opintojakson rakenne ja tavoitteet Sähkötekniikan historiaa Sähköiset perussuureet Passiiviset piirikomponentit 2 Luento 2 - sisältö Passiiviset piirikomponentit
Osio 1. Laskutehtävät
 Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
Osio 1. Laskutehtävät Nämä palautetaan osion1 palautuslaatikkoon. Aihe 1 Alkuaineiden suhteelliset osuudet yhdisteessä Tehtävä 1 (Alkuaineiden suhteelliset osuudet yhdisteessä) Tarvitset tehtävään atomipainotaulukkoa,
P = kv. (a) Kaasun lämpötila saadaan ideaalikaasun tilanyhtälön avulla, PV = nrt
 766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
766328A Termofysiikka Harjoitus no. 2, ratkaisut (syyslukukausi 204). Kun sylinterissä oleva n moolia ideaalikaasua laajenee reversiibelissä prosessissa kolminkertaiseen tilavuuteen 3,lämpötilamuuttuuprosessinaikanasiten,ettäyhtälö
Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA
 Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
Thermodynamics: An Engineering Approach, 7 th Edition Yunus A. Cengel, Michael A. Boles McGraw-Hill, 2011 Luku 8 EXERGIA: TYÖPOTENTIAALIN MITTA Copyright The McGraw-Hill Companies, Inc. Permission required
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma
 KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
KOE 3, A-OSIO Agroteknologia Agroteknologian pääsykokeessa saa olla mukana kaavakokoelma Sekä A- että B-osiosta tulee saada vähintään 10 pistettä. Mikäli A-osion pistemäärä on vähemmän kuin 10 pistettä,
YLEINEN KEMIA. Alkuaineiden esiintyminen maailmassa. Alkuaineet. Alkuaineet koostuvat atomeista. Atomin rakenne. Copyright Isto Jokinen
 YLEINEN KEMIA Yleinen kemia käsittelee kemian perusasioita kuten aineen rakennetta, alkuaineiden jaksollista järjestelmää, kemian peruskäsitteitä ja kemiallisia reaktioita. Alkuaineet Kaikki ympärillämme
YLEINEN KEMIA Yleinen kemia käsittelee kemian perusasioita kuten aineen rakennetta, alkuaineiden jaksollista järjestelmää, kemian peruskäsitteitä ja kemiallisia reaktioita. Alkuaineet Kaikki ympärillämme
PYP I / TEEMA 8 MITTAUKSET JA MITATTAVUUS
 1 PYP I / TEEMA 8 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittausprojekti Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen
1 PYP I / TEEMA 8 MITTAUKSET JA MITATTAVUUS Aki Sorsa 2 SISÄLTÖ YLEISTÄ Mitattavuus ja mittaus käsitteinä Mittauksen vaiheet Mittausprojekti Mittaustarkkuudesta SUUREIDEN MITTAUSMENETELMIÄ Mittalaitteen
kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin?
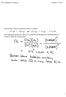 Esimerkki: Mihin suuntaan etenee reaktio CO (g) + H 2 O (g) CO 2 (g) + H 2 (g), K = 0,64, kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin? 1 Le Châtelier'n
Esimerkki: Mihin suuntaan etenee reaktio CO (g) + H 2 O (g) CO 2 (g) + H 2 (g), K = 0,64, kun hiilimonoksidia ja vettä oli 0,0200 M kumpaakin ja hiilidioksidia ja vetyä 0,0040 M kumpaakin? 1 Le Châtelier'n
Molaariset ominaislämpökapasiteetit
 Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Molaariset ominaislämpökapasiteetit Yleensä, kun systeemiin tuodaan lämpöä, sen lämpötila nousee. (Ei kuitenkaan aina, kannattaa muistaa, että työllä voi olla osuutta asiaan.) Lämmön ja lämpötilan muutoksen
Kaikki ympärillämme oleva aine koostuu alkuaineista.
 YLEINEN KEMIA Yleinen kemia käsittelee kemian perusasioita kuten aineen rakennetta, alkuaineiden jaksollista järjestelmää, kemian peruskäsitteitä ja kemiallisia reaktioita. Alkuaineet Kaikki ympärillämme
YLEINEN KEMIA Yleinen kemia käsittelee kemian perusasioita kuten aineen rakennetta, alkuaineiden jaksollista järjestelmää, kemian peruskäsitteitä ja kemiallisia reaktioita. Alkuaineet Kaikki ympärillämme
Tasapainotilaan vaikuttavia tekijöitä
 REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA TASAPAINO, KE5 Tasapainotilaan vaikuttavia tekijöitä Fritz Haber huomasi ammoniakkisynteesiä kehitellessään, että olosuhteet vaikuttavat ammoniakin määrään tasapainoseoksessa. Hän huomasi,
REAKTIOT JA ENERGIA, KE3. Kaasut
 Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
Kaasut REAKTIOT JA ENERGIA, KE3 Kaasu on yksi aineen olomuodosta. Kaasujen käyttäytymistä kokeellisesti tutkimalla on päädytty yksinkertaiseen malliin, ns. ideaalikaasuun. Määritelmä: Ideaalikaasu on yksinkertainen
2.1 Sähköä kemiallisesta energiasta
 2.1 Sähköä kemiallisesta energiasta Monet hapettumis ja pelkistymisreaktioista on spontaaneja, jolloin elektronien siirtyminen tapahtuu itsestään. Koska reaktio on spontaani, vapautuu siinä energiaa, yleensä
2.1 Sähköä kemiallisesta energiasta Monet hapettumis ja pelkistymisreaktioista on spontaaneja, jolloin elektronien siirtyminen tapahtuu itsestään. Koska reaktio on spontaani, vapautuu siinä energiaa, yleensä
Reformointi- ja pelkistysprosessien kaasuvirtausten simulointi ReGenGasprojektissa
 SÄÄTÖTEKNIIKAN LABORATORIO Reformointi- ja pelkistysprosessien kaasuvirtausten simulointi ReGenGasprojektissa Timo Mäki Outi Mäyrä Raportti B No 63, Tammikuu 6 Oulun yliopisto Säätötekniikan laboratorio
SÄÄTÖTEKNIIKAN LABORATORIO Reformointi- ja pelkistysprosessien kaasuvirtausten simulointi ReGenGasprojektissa Timo Mäki Outi Mäyrä Raportti B No 63, Tammikuu 6 Oulun yliopisto Säätötekniikan laboratorio
SÄHKÖSTATIIKKA JA MAGNETISMI. NTIETS12 Tasasähköpiirit Jussi Hurri syksy 2013
 SÄHKÖSTATIIKKA JA MAGNETISMI NTIETS12 Tasasähköpiirit Jussi Hurri syksy 2013 1. RESISTANSSI Resistanssi kuvaa komponentin tms. kykyä vastustaa sähkövirran kulkua Johtimen tai komponentin jännite on verrannollinen
SÄHKÖSTATIIKKA JA MAGNETISMI NTIETS12 Tasasähköpiirit Jussi Hurri syksy 2013 1. RESISTANSSI Resistanssi kuvaa komponentin tms. kykyä vastustaa sähkövirran kulkua Johtimen tai komponentin jännite on verrannollinen
Magneettinen energia
 Luku 11 Magneettinen energia 11.1 Kelojen varastoima energia Sähköstatiikan yhteydessä havaittiin, että kondensaattori kykenee varastoimaan sähköstaattista energiaa. astaavalla tavalla kela, jossa kulkee
Luku 11 Magneettinen energia 11.1 Kelojen varastoima energia Sähköstatiikan yhteydessä havaittiin, että kondensaattori kykenee varastoimaan sähköstaattista energiaa. astaavalla tavalla kela, jossa kulkee
VOIMALAITOSMITTAKAAVAN POLTTOKENNOJÄRJESTELMIEN TEKNIS-TALOUDELLINEN VERTAILU. Antti Teräsvirta Prizztech Oy
 VOIMALAITOSMITTAKAAVAN POLTTOKENNOJÄRJESTELMIEN TEKNIS-TALOUDELLINEN VERTAILU Antti Teräsvirta Prizztech Oy II ESIPUHE Vetyä pidetään sen korkean energiatiheyden, vähäisten päästöjen ja säilöttävyyden
VOIMALAITOSMITTAKAAVAN POLTTOKENNOJÄRJESTELMIEN TEKNIS-TALOUDELLINEN VERTAILU Antti Teräsvirta Prizztech Oy II ESIPUHE Vetyä pidetään sen korkean energiatiheyden, vähäisten päästöjen ja säilöttävyyden
Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste.
 TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
TYÖ 36b. ILMANKOSTEUS Tehtävä Työssä määritetään luokkahuoneen huoneilman vesihöyryn osapaine, osatiheys, huoneessa olevan vesihöyryn massa, absoluuttinen kosteus ja kastepiste. Välineet Taustatietoja
DEE-53010 Aurinkosähkön perusteet
 DEE-53010 Aurinkosähkön perusteet Toisen luennon aihepiirit Lyhyt katsaus aurinkosähkön historiaan Valosähköinen ilmiö: Mistä tässä luonnonilmiössä on kyse? Pinnallinen tapa aurinkokennon virta-jännite-käyrän
DEE-53010 Aurinkosähkön perusteet Toisen luennon aihepiirit Lyhyt katsaus aurinkosähkön historiaan Valosähköinen ilmiö: Mistä tässä luonnonilmiössä on kyse? Pinnallinen tapa aurinkokennon virta-jännite-käyrän
HSC-ohje laskuharjoituksen 1 tehtävälle 2
 HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
HSC-ohje laskuharjoituksen 1 tehtävälle 2 Metanolisynteesin bruttoreaktio on CO 2H CH OH (3) 2 3 Laske metanolin tasapainopitoisuus mooliprosentteina 350 C:ssa ja 350 barin paineessa, kun lähtöaineena
AKKU- JA PARISTOTEKNIIKAT
 AKKU- JA PARISTOTEKNIIKAT H.Honkanen Kemiallisessa sähköparissa ( = paristossa ) ylempänä oleva, eli negatiivisempi, metalli syöpyy liuokseen. Akussa ei elektrodi syövy pois, vaan esimerkiksi lyijyakkua
AKKU- JA PARISTOTEKNIIKAT H.Honkanen Kemiallisessa sähköparissa ( = paristossa ) ylempänä oleva, eli negatiivisempi, metalli syöpyy liuokseen. Akussa ei elektrodi syövy pois, vaan esimerkiksi lyijyakkua
Erään piirikomponentin napajännite on nolla, eikä sen läpi kulje virtaa ajanhetkellä 0 jännitteen ja virran arvot ovat. 500t.
 DEE- Piirianalyysi Harjoitus / viikko 4 Erään piirikomponentin napajännite on nolla, eikä sen läpi kulje virtaa ajanhetkellä jännitteen ja virran arvot ovat t Kun t, v te t 5t 8 V, i te t 5t 5 A, a) Määritä
DEE- Piirianalyysi Harjoitus / viikko 4 Erään piirikomponentin napajännite on nolla, eikä sen läpi kulje virtaa ajanhetkellä jännitteen ja virran arvot ovat t Kun t, v te t 5t 8 V, i te t 5t 5 A, a) Määritä
Kemiallinen reaktio
 Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Kemiallinen reaktio REAKTIOT JA ENERGIA, KE3 Johdantoa: Syömme elääksemme, emme elä syödäksemme! sanonta on totta. Kun elimistömme hyödyntää ravintoaineita metaboliassa eli aineenvaihduntareaktioissa,
Rak Tulipalon dynamiikka
 Rak-43.3510 Tulipalon dynamiikka 7. luento 14.10.2014 Simo Hostikka Palopatsaat 1 Luonnollisten palojen liekki 2 Palopatsas 3 Liekin korkeus 4 Palopatsaan lämpötila ja virtausnopeus 5 Ideaalisen palopatsaan
Rak-43.3510 Tulipalon dynamiikka 7. luento 14.10.2014 Simo Hostikka Palopatsaat 1 Luonnollisten palojen liekki 2 Palopatsas 3 Liekin korkeus 4 Palopatsaan lämpötila ja virtausnopeus 5 Ideaalisen palopatsaan
PERMITTIIVISYYS. 1 Johdanto. 1.1 Tyhjiön permittiivisyyden mittaaminen tasokondensaattorilla . (1) , (2) (3) . (4) Permittiivisyys
 PERMITTIIVISYYS 1 Johdanto Tarkastellaan tasokondensaattoria, joka koostuu kahdesta yhdensuuntaisesta metallilevystä Siirretään varausta levystä toiseen, jolloin levyissä on varaukset ja ja levyjen välillä
PERMITTIIVISYYS 1 Johdanto Tarkastellaan tasokondensaattoria, joka koostuu kahdesta yhdensuuntaisesta metallilevystä Siirretään varausta levystä toiseen, jolloin levyissä on varaukset ja ja levyjen välillä
m h = Q l h 8380 J = J kg 1 0, kg Muodostuneen höyryn osuus alkuperäisestä vesimäärästä on m h m 0,200 kg = 0,
 76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
76638A Termofysiikka Harjoitus no. 9, ratkaisut syyslukukausi 014) 1. Vesimäärä, jonka massa m 00 g on ylikuumentunut mikroaaltouunissa lämpötilaan T 1 110 383,15 K paineessa P 1 atm 10135 Pa. Veden ominaislämpökapasiteetti
Sähköstatiikan laskuissa useat kaavat yksinkertaistuvat hieman, jos vakio C kirjoitetaan muotoon
 30 SÄHKÖVAKIO 30 Sähkövakio ja Coulombin laki Coulombin lain mukaan kahden tyhjiössä olevan pistevarauksen q ja q 2 välinen voima F on suoraan verrannollinen varauksiin ja kääntäen verrannollinen varausten
30 SÄHKÖVAKIO 30 Sähkövakio ja Coulombin laki Coulombin lain mukaan kahden tyhjiössä olevan pistevarauksen q ja q 2 välinen voima F on suoraan verrannollinen varauksiin ja kääntäen verrannollinen varausten
782630S Pintakemia I, 3 op
 782630S Pintakemia I, 3 op Ulla Lassi Puh. 0400-294090 Sposti: ulla.lassi@oulu.fi Tavattavissa: KE335 (ma ja ke ennen luentoja; Kokkolassa huone 444 ti, to ja pe) Prof. Ulla Lassi Opintojakson toteutus
782630S Pintakemia I, 3 op Ulla Lassi Puh. 0400-294090 Sposti: ulla.lassi@oulu.fi Tavattavissa: KE335 (ma ja ke ennen luentoja; Kokkolassa huone 444 ti, to ja pe) Prof. Ulla Lassi Opintojakson toteutus
SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas Tampereen teknillinen yliopisto Elektroniikan laitos
 SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas jari.kangas@tut.fi Tampereen teknillinen yliopisto Elektroniikan laitos Sähkömagnetiikka 2009 1 1 Maxwellin & Kirchhoffin laeista Piirimallin
SMG-5250 Sähkömagneettinen yhteensopivuus (EMC) Jari Kangas jari.kangas@tut.fi Tampereen teknillinen yliopisto Elektroniikan laitos Sähkömagnetiikka 2009 1 1 Maxwellin & Kirchhoffin laeista Piirimallin
ELEC-C6001 Sähköenergiatekniikka, laskuharjoitukset oppikirjan lukuun 10 liittyen.
 ELEC-C6001 Sähköenergiatekniikka, laskuharjoitukset oppikirjan lukuun 10 liittyen. X.X.2015 Tehtävä 1 Bipolaaritransistoria käytetään alla olevan kuvan mukaisessa kytkennässä, jossa V CC = 40 V ja kuormavastus
ELEC-C6001 Sähköenergiatekniikka, laskuharjoitukset oppikirjan lukuun 10 liittyen. X.X.2015 Tehtävä 1 Bipolaaritransistoria käytetään alla olevan kuvan mukaisessa kytkennässä, jossa V CC = 40 V ja kuormavastus
Erilaisia entalpian muutoksia
 Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Erilaisia entalpian muutoksia REAKTIOT JA ENERGIA, KE3 Erilaisille kemiallisten reaktioiden entalpiamuutoksille on omat terminsä. Monesti entalpia-sanalle käytetään synonyymiä lämpö. Reaktiolämmöllä eli
Vastksen ja diodin virta-jännite-ominaiskäyrät sekä valodiodi
 Sivu 1/10 Fysiikan laboratoriotyöt 1 Työ numero 3 Vastksen ja diodin virta-jännite-ominaiskäyrät sekä valodiodi Työn suorittaja: Antero Lehto 1724356 Työ tehty: 24.2.2005 Uudet mittaus tulokset: 11.4.2011
Sivu 1/10 Fysiikan laboratoriotyöt 1 Työ numero 3 Vastksen ja diodin virta-jännite-ominaiskäyrät sekä valodiodi Työn suorittaja: Antero Lehto 1724356 Työ tehty: 24.2.2005 Uudet mittaus tulokset: 11.4.2011
